Методика устного быстрого счета: A potentially dangerous Request.Path value was detected from the client (?).

Способы быстрого устного счета – презентация онлайн

Невозможно отобразить презентацию

Похожие презентации:

Приемы быстрого счета

«Устный счет – гимнастика для ума»

Приемы устных вычислений. Формирование навыков устных вычислений на уроках математики

«Устный счет – гимнастика для ума». Способы быстрого счёта

Вычислительные навыки на уроках математики

Приёмы быстрого счёта без калькулятора

Интересные и быстрые способы и приемы вычислений

Делители и кратные. 6 класс

Приёмы быстрого счёта. 5 класс

Методика изучения арифметических действий

Немногие умеют считать быстро и правильно.

Я покажу несколько быстрых и удобных способов которые пригодятся в математике.

Способы быстрого устного счёта Можно очень просто умножать такие числа.

К одному из чисел надо прибавить количество единиц другого, умножить на 10 и прибавить произведение единиц чисел.

Например: 16*18=(16+8)10+6*8=288, или 17*17=(17+7)10+7*7=289.

Умножение чисел от 10-ти до 20-ти Умножение на 25 Чтобы умножить какое-нибудь число, нужно данное число разделить 4.

Ответ – полные сотни, остаток – неполные (1, 2, 3 или 25, 50, 75).

Например 135*25=(135:4=100:4+35:4)=33 сотни, остаток 3 (или неполная сотня – 75)=3375.

Возведение в квадрат чисел , оканчивающихся цифрой 5 Для того чтобы возвести в квадрат число оканчивающееся на 5, надо найти значение выражения 100*количество десятков числа*(количество десятков+1)+25.Например 185 в квадрате=100*18*(18+1)+25=34 225.

Увеличение и уменьшение суммы в выражении Если от суммы двух чисел отнять разность тех же чисел, то в результате получится удвоенное меньшее число, то есть (a+b)-(a-b)=2b (3+2)-(3-2)=2*2=4 Если к сумме двух чисел прибавить их разность, то получится удвоенное большее число, то есть (a+b)+(a-b)=2a(3+2)+(3-2)=3*2=6 Умножение на 5, на 50, на 25, на 125 При умножении на эти числа можно воспользоваться следующими выражениями: a*5=a*10:2 a*50=a*100:2 a*25=a*100:4 а*125=а*1000:8 Например: 17*5=17*10:2=170:2=85 43*50=43*100:2=4300:2=2150 27*25=27*100:4=2700:4=675 96*125=96*1000:8=96000:8=12000 Деление на 5, на 50, на 25 При делении на эти числа можно воспользоваться следующими выражениями: a:5=a*2:10 a:50=a*2:100 a:25=a*4:100 Например: 35:5=35*2:10=70:10=7 3750:50=3750*2:100=7500:100=75 6400:25=6400*4:100=25600:100=256 Способы быстрого сложения и вычитания натуральных чисел 1.

Если одно из слагаемых увеличить на несколько единиц, то из полученной суммы надо вычесть столько же единиц.

Например: 785+963=785+(963+7)-7= 785+970-7= 1748 Способы быстрого сложения и вычитания натуральных чисел 2.Если одно из слагаемых увеличить на несколько единиц, а второе уменьшить на столько же единиц, то сумма не измениться.

Например: 762+639=(762+8)+(639-8)=770+ 631=1401 Способы быстрого сложения и вычитания натуральных чисел 3.Если вычитаемое уменьшить на несколько единиц и уменьшаемое увеличить на столько же единиц, то разность не измениться.

Например: 529-435=(529-5)-(435+5)=524- 440=84 Способы быстрого умножения и деления натуральных чисел Для получения единиц произведения перемножают единицы множителей, для получения десятков умножают десятки одного на единицы другого множителя и наоборот и результаты складывают, для получения сотен перемножают десятки.

Например: 62*58=3596 а)8*2=16, пишем 6 помним 1.

б)8*6+5*2+1=59, пишем 9, помним 5.

в)5*6+5=35.

Умножение чисел, у которых число десятков одинаково, а сумма равна10 Число десятков любого множителя умножить на число, которое больше на 1, затем перемножить отдельно единицы этих чисел и, наконец, к первому результату справа приписать второй.

Например: 204*206=42024 а)20*(20+1)=420, пишем 420 б)6*4=24, пишем 24 Умножение числа вида cc Нужно умножить данное число сначала на c , потом на 11.

Например: 12*66=(12*6)*11=72*11=792 Приёмы быстрого устного счёта известны давно.

Великолепные способности к устному счёту таких блестящих математиков, как Гаусс, фон Нейман, Эйлер или Валлис, вызывают настоящий восторг.

Об этом тоже много написано.

Учителю иногда полезно рассказывать и показывать известные вычислительные секреты.

Тогда перед учениками откроется

English     Русский Правила

Приемы и методы устного счета на уроках математики. | Методическая разработка по алгебре (5, 6 класс):

Методы и приемы устного счета на уроках математики.

Назаревская С.Д. – преподаватель математики ГБПОУ Педагогического колледжа № 4.

«Старайся дать уму как можно больше пищи» Л.Н. Толстой.

Одним из важных этапов организации урока математики в начальной школе и в 5-6 классах является устный счет.

Данный этап способствует развитию мыслительной деятельности учащихся. Выполнение устных упражнений развивает память, воображение, внимание, наблюдательность,  умение сосредоточиться, способность воспринимать сказанное на слух, речь, точность, быстроту реакции учащихся.

Многие психологи отмечают, что устный счет способствует гармоничному развитию двух полушарий человека.

Использование устных упражнений на уроках математики преследует следующие цели, стоящие перед учителем при подготовке к уроку:

1. Повторение изученного материала;  отработка умений и навыков применения знаний по определенной теме на практике.
2. Пропедевтика нового материала (т.е. система заданий и упражнений для подготовки к изучению нового материала).
3. Развитие вычислительных умений и навыков.

Понимая важность использования устных упражнений, учитель должен не только грамотно спланировать содержание устной работы, но и форму ее проведения. Устная работа должна быть разнообразной, т.к. она направлена не только на активизацию мыслительной деятельности  учащихся, на развитие интеллектуальных способностей учащихся,  но и на развитие интереса к математике.

Существуют различные формы организации устной работы на уроках математики:

1. Математический диктант.

Например:

1. I слагаемое 28, II слагаемое 57. Найдите сумму этих чисел.
2. Уменьшаемое 64, вычитаемое 46. Найдите разность этих чисел.
3. Число 75 увеличьте на 17.
4. Найдите разность 51 и 38.
5. Найдите сумму 43 и 49.
6. Число 81 уменьшите на 24.
7. I слагаемое 25, а второе на 14 больше. Найдите сумму этих чисел.

2. Цепочка.

Учитель просит учащихся записать число. Учитель просит изменить данное число при помощи определенного математического действия, запомнить промежуточный результат и выполнить следующее действие, предлагаемое учителем, снова запомнить результат и т.д.

На первых уроках можно разрешать учащимся писать промежуточные результаты, а в дальнейшем попробовать производить операции с промежуточными числами в уме и записать только конечный результат.

3. Круглые примеры.

Предлагается найти последний пример среди определенного числа примеров, записанных в разнобой. Учащиеся находят результат первого примера, далее им надо найти тот, который начинается с цифры, которая является результатом предыдущего примера и т.д. до тех пор, пока результат последнего примера не совпадет с начальной цифрой первого.

Данную работу можно организовать фронтально и индивидуально.

4. Ручеек.

На листочке даны примеры по количеству учащихся, сидящих на одном ряду. Решив первый пример, учащийся передает листочек сидящему за ним однокласснику. Тот должен найти ответ следующего по порядку примеру и передать листочек сидящему за ним однокласснику.

5. Лесенка.

На доске изображена лесенка примеров. Дается определенное время, за которое необходимо подняться на верхнюю ступеньку этой лесенки.

6. Расшифруй слово или фразу.

Таких заданий очень много в учебниках  Л.Г. Петерсон и Г.В. Дорофеева.

Можно придумать и зашифровать тему урока или фамилию того или иного математика, ученого, которые внесли большой вклад в развитие математики.

7. Ромашка.

На доске изображены по кругу числа, а в середине или какое-то действие, или круг, разделенный на четыре или две части. В данных частях круга арифметические действия. Это задание направлено не только на отработку вычислительных навыков, но и на развитие внимания учащихся. Учитель поочередно связывает числа, расположенные по кругу, показывая на них указкой, определенными действиями из маленького круга.

8. Математический марафон.

На доске изображены примеры. Необходимо в уме быстро и правильно найти их результат и записать ответы в тетради.

Через определенное время проверить с классом данное задание и разобрать те задания, которые вызвали трудность.

9. Восстанови пример.

Учитель предлагает ученикам примеры, в которых пропущены или действия, или один из компонентов. Надо восстановить пропущенную запись.

10. Математическое лото.

Учащимся выдаются конверты с карточкой, на которой записаны примеры, расположенные в таблице, как в лото.

Данные карточки можно предлагать или каждому ученику, или двум, сидящим на одной парте.

Учащиеся решают примеры и закрывают ответы маленькими карточками, на которых изображены цифры, являющиеся ответами к примерам на карточке.

По команде учителя ученики прекращают работу и переворачивают маленькие карточки. На большой карточке должен получиться рисунок, или какая-нибудь геометрическая фигура.

11. Найди ошибку.

Эту форму устной работы чаще всего использую при работе над единицами измерения.

Предлагаю ученикам столбик равенств  с метрическими величинами. Ученикам необходимо проверить правильно ли поставлены знаки равно и у себя в тетради отметить это в виде графической записи.

Если ученик согласен с поставленным знаком равно, то он в тетради изображает дугу, размером в две клеточки, если же не согласен, то отрезек, длиной две клеточки.

Например:

Верно ли, что:

5 дм = 50 см                                                   9 км 27 м = 927 м

6 мм = 60 см                                                   65 см = 6 дм 5 см

8 км 78 м = 8780 м                                        369 мм = 3 см 69 мм

3 м 2 см = 302 см                                           973 см = 9 м 73 см

7 см 9 мм = 79 мм                                         5643 м = 5 км 643 м

1 дм 5 мм = 105 мм                                      730 дм = 73 м?

12. Оглянись назад.

 Учитель предлагает ученикам определенное число и записывает его на доске, например 10,5.

Далее учитель называет какое-то число меньшее или большее, чем данное. Учащиеся устно должны назвать число, которое поможет вернуться к данному числу.

13. Качели.

Это задание способствует развитию памяти учащихся.

Учитель называет числа, например трехзначные. Учащиеся записывают данные числа наоборот, в обратном порядке, сначала пользуясь записями в тетради, а потом только по памяти.

14. «Числовые фокусы». 5 – 6 класс.

Можно в устные упражнения включать всевозможные числовые фокусы. Данные задания разнообразят урок и привнесут в него новизну.

Например:

«Проблема Гольдбаха».

Живший в 18 веке в России математик Гольдбах открыл удивительную вещь:

каждое четное число ему удавалось представить в виде суммы двух простых чисел

 (включая число «1»).

Задание: можно предложить 6-тиклассникам при изучении темы «Простые и составные числа» на одном уроке представить в виде суммы простых чисел первые 20 четных чисел; на втором уроке представить в виде суммы простых чисел  числа от 20 до 50.

15. «Любопытные свойства натуральных чисел».

Возьмем любое число из 4-х цифр (например, 2365) и расставим их сначала в порядке возрастания (2356), затем убывания (6532). Из большего числа вычтем меньшее: 6532 – 2356 = 4176. С полученным числом проделаем то же самое: 7641 – 1467 = 6174. Интересно то, что к этому числу не более чем за 7 шагов мы приходим вышеуказанным способом от любого, взятого наугад четырехзначного числа.

3) 7641 – 1467 = 6174

Пример: 6598.                                                                 Пример: 3582.

1. 9865 – 5689 = 4176                                                  1) 8532 – 2358 = 6174
2. 7641 – 1467 = 6174.

                Пример: 3198.

1. 9831 – 1389 =8442
2. 8442 – 2448 = 5994
3. 9954 – 4599 = 5355
4. 5553 – 3555 = 1998
5. 9981 – 1899 = 8082
6. 8820 – 288 = 8532
7. 8532 – 2358 = 6174

Применение различных видов устной работы в основном зависит от творчества учителя.

Какой бы вид работы не выбрал учитель на уроке надо понимать, что устные упражнения способствуют не только развитию математических способностей учащихся, но и развитию вычислительных навыков. Как не странно, учащиеся, которые хорошо считают,  порой лучше и быстрее справляются с заданиями по математике, чем даже те ученики, которые по природе своей имеют лучшие математические способности.

Применяя в организации устной работы задания вычислительного характера, учитель тем самым экономит время на вычисления при решении задач, уравнений, неравенств.

Существует ряд приемов устного счета, которые полезно показать учащимся, и использовать их при решении заданий, требующих всевозможных арифметических вычислений.

1.  «Промежуточное» приведение к «круглым» числам.

Пример: 187 + 198.

1. одно из слагаемых необходимо привести к «круглому» числу десятков, сотен, тысяч и т.д.;
2. выполнить действие сложения;
3. учесть поправку.

187 + 198 = 200 + 187 -2 = 387 – 2=385.

2. Способ «корневых» чисел.

34 + 37 + 36 + 34 + 38 + 39 = 30*6 + (4 + 7 +6 +8 +9) = 180 + 34 = 214

37.  34 + 33 + 35 +3 4 + 33 + 34 = 34*7 + (3 + 0 -1 + 1 – 1 +0 ) = 238 + 2 = 240

3. Использование изменения порядка счета.

При сложении чисел нередко бывает полезно складывать их, начиная со старшего разряда.

5879. 654 = 9533

4. Использование дополнения числа для упрощения вычитания из числа.

700. – 238 = 700 – (300 – 2) = 400 + 2 = 402

5. Переход от вычитания к сложению.

3000 – 1264 = (3000 + 736) – 2000 = 1736

6. Приемы умножения чисел на 9, 99, 999.

А) 56 * 9 = 56 * 10 – 56 = 560 – 56 = 504

Б) 68 * 99 = 68 * 100 – 68 = 6800 – 68 = 6732

В) 73 * 999 = 73 * 1000 – 73 = 73000 – 73 = 72927

7. Приемы умножения чисел на 11.

26 * 11 = 2 * 6 , вместо * пишем число, которое является суммой 2 и 6.

67 * 11 = 6 * 7, вместо * надо записать результат суммы чисел 6 и 7, но это двузначное число, а на месте разряда десятков можно записать только одну цифру, поэтому на месте десятков мы пишем 3, а к 6 единицам, которые должны стоять на месте сотен прибавляем 1 и получаем 7.

Итак, 67 * 11 = 737

8. Приемы умножения на 111.

Пример:  359 * 111=…9 

На последнем месте в результате пишем 9, т.к. 9 * 1 = 9.

Слева от 9 записываем цифру, которая получилась в результате сложения двух последних цифр в числе 359. Это 5 + 9 = 14, т.е. пишем цифру 4.

Затем находят суммы цифр, взятых по три и прибавляют 1 (если есть переход через разряд).

(3 + 5 + 9) + 1 = 18

Перед цифрой 4 пишем цифру 8.

Затем находим сумму двух последних цифр: (3 + 5) + 1 = 9.

Перед цифрой 8 пишем 9.

На первом месте запишем цифру 3, т.к. она первая цифра в данном множителе.

Итак, 359 * 11 = 39849.

Пример: 2356 * 111 = …6

5 + 6 = 11, тогда записываем …16

(3 + 5 + 6) + 1 = 15, тогда записываем …516

(2 + 3 + 5) + 1 = 11, тогда записываем …1516

(2 + 3) + 1 = 6, тогда записываем …61516

Итак, 2356 * 111 = 261516.

Пример: 895123 * 111 = …3

2 + 3 = 5             …53

1 + 2 + 3 = 6       …653

5 + 1 + 2 = 8       …8553

9 + 5 + 1 = 15     …58553

(8 + 9 + 5) + 1 = 23    ….358553

(8 + 9) + 2 = 19         …9358553

8 + 1 = 9

Итак, 895123 * 111 = 99358653

9. Умножение крестиком.

Данный прием применялся еще в древней Индии и назывался «молниеносным».

Пример: 54 * 26.

1. Умножаем 4 на 6, получаем 24, пишем на месте единиц 4, а 2 запоминаем.
2. 5 умножаем на 6, получаем 30 и прибавляем цифру, которую запомнили, т.е. 2. Получаем 32. Запомним цифру 32.
3. 2 умножаем на 4, получаем 8 и прибавляем 32,получаем 40. Цифру 0 пишем перед 4.
4. 2 умножаем на 5 и прибавляем 4, получаем 14.
5. Пишем 14 перед всеми записанными цифрами.
6. Получили число 1404.

  Пример: 67 * 39 .

1. 7 * 9 = 63     …3
2. 6 * 9 + 6 = 60
3. 3 * 7 + 60 = 81  …1
4. 3 * 6 + 8 = 26

Итак, 67 * 39 = 2613

Пример: 48 * 67.

1. 8 * 7 = 56   …6
2. 7 * 4 + 5 = 33
3. 6 * 8 + 33 = 81 …16
4. 6 * 4 + 8 = 32

Итак, 48 * 67 = 3216

10. Способ умножения путем изменения сомножителей.

Если один из сомножителей уменьшить в несколько раз, а другой увеличить во столько же раз, итог произведения не изменится, однако умножение может стать проще и быстрее.

Примеры: 24 * 25 = (24:4) * (25 * 4) = 6 * 100 = 600

                    17 * 12 = (17 * 4) * (12 : 4) = 68 * 3 = 204

                    28 * 55 = (28 : 2) * ( 55 * 2) = 14 * 110 = 1540

                    256 *5 = (256 : 2) * ( 5 * 2) = 128 * 10 = 1280

           48 * 25 = (48 : 4) * (25 * 4) = 12 * 100 = 1200

           64 * 125 = (64 : 8) * (125 * 8) = 8 * 1000 = 8000

11.  Способ дополнения для умножения чисел, близких к .

94 * 97 = (100 – 6 – 3) * 100 + 6 *3 = 91 * 100 + 18 = 9118

98 * 96 = (100 – 2 – 4) * 100 + 2 * 4 = 94 * 100 + 8 = 9408

89 * 78 = (100 – 11 – 22) * 100 + 11 * 22 = 67 * 100 + 242 = 6942

113 * 108 = ( 100 + 13 + 8) * 100 + 13 * 8 = 121 * 100 + 104 = 12100 + 104 = 12204

106 * 98 = (100 + 6 -2) * 100 – 6 * 2 = 10400 – 12 = 10388

115 * 91 = (100 +15 – 9) * 100 – 15 * 9 = 10600 – 135 = 10465

108 * 112 = (100 + 8 + 12) * 100 + 8 * 12 = 12000 + 96 = 12096

1002 * 993 = (1000 + 2 – 7) * 1000 -2 * 7 = 995000 – 14 = 99 4986

1012 * 1005 = ( 1000 + 12 + 5) * 1000 + 12 * 5 = 1017000 + 60 = 107060

12. Способ вычитания дополнения при умножении чисел.

Пример: 196 * 198

1. Из какого-нибудь сомножителя вычитаем дополнение второго сомножителя.  

198 – 4 = 194 или 196 – 2 = 194

2. Полученный результат умножаем на 2, т.к. оба числа дополняли до 200.  

194 * 2 = 388  

3. К полученному результату алгебраически (с учетом знака) и разрядности прибавляем произведение дополнений.

198 * 196 = 388 * 100 + 2 * 4 = 38800 + 8 = 38808  

                     Пример: 65 * 78.

Округляем до 80.

1. 78 – 15 = 63
2. 63 * 8 = 504
3. 65 * 78 = 504 * 10 + 15 * 2 = 5040 + 30 = 5070

Пример: 87 * 73.

Округляем до 80.

1. 87 – 7 = 80
2. 80 * 8 = 640
3. 87 * 73 = 640 * 10 – 7 * 7 = 6400 – 49 = 6351

13. Признак делимости на 11.

Если сумма данного многозначного числа через одну равна сумме остальных цифр через одну или разность этих сумм делится на 11, то и данное число делится на 11.

Если суммы цифр через одну данного числа или их разность не делится на 11, то данное число не делится на 11.

Пример: Делится ли 390137 на 11?

Решение: 1) 3 + 0 + 3 = 6

            2)9 + 1 + 7 = 17

            3) 17 – 6 = 11

            4) 11 : 11, значит и число 390137 делится на 11.

 Пример: Делится ли 6880357 на 11?

 Решение: 1) 6 + 8 + 3 + 7 = 24

             2)8 + 0 + 5 = 13

             3) 24 – 13 = 11

             4) 11 : 11, значит данное число делится на 11.

Пример: Делится ли 985621 на 11?

 Решение: 1) 9 + 5 + 2 = 16

                    2)8 + 6 + 1 = 15

             3) 16 – 15 = 1

              4) 1 не делится на 11, значит и число 985621 не делится на 11.    

                 

14. Возведение в квадрат чисел, оканчивающихся на 5.

Пример: 65 * 65 = 4225

6 дес. * 7 дес. = 42 с.

5 * 5 = 25

42 с. + 25 = 4225

Пример: 95 * 95 =

9 дес. * 10 дес. = 90 с.

5 * 5 = 25

90 с. + 25 = 9025

Пример: 385 * 385 = 148225

38 дес. * 39 дес. = 1482 с.

5 * 5  = 25

1482 с. + 25 = 148225

Пример: 685 * 685 =469225

68 дес. * 69 дес. = 4692 с.

4692** + 25 = 469225

Пример: 7435 * 7435

743 дес. * 744 дес. = 552792 с.

552792 с. + 25 = 55279225

15. Умножение трехзначных чисел, оканчивающихся на 25.

Пример: 425 * 425.

1. В конце числа пишем 625.
2. Число сотен в числе (4) умножаем на 5. Получаем 20. Перед числом 625 пишем последнюю цифру числа 20, а цифру 2 запоминаем. (0625)
3. Число сотен данного числа возводим в квадрат, т.е. . Получаем 16. К 16 прибавляем ту цифру, которую мы запомнили, т.е. 2. Получаем 18.
4. Полученную цифру 18 припишем перед 0625.
5. Получили 180625.

Пример: 725 * 725.

1. В конце числа пишем 625.
2. 7 * 5 = 35.

5625

3. .

49 + 3 = 52

4. Получили 525625

Учащиеся  любят использовать данные приемы, которые отличаются от традиционных решений в столбик. Важно только, показав на каком-нибудь уроке один из приемов устного счета, стараться применять его на практике, не забывая о нем.

Литература:

1. Гончар Д.Р. Устный счет и память: загадки, приемы развития, игры;

Лурия А. Р. Маленькая книжка о большой памяти;

Вильям В. Аткинсон. Память и забота о ней. – Д.: Сталкер, 1998.

2. Шейнина О. С., Соловьева Г. М. Математика. Занятия школьного кружка. 5 – 6 кл. – М.: Изд-во НЦ ЭНАС, 2005.

                       

Принципы счета – счет и количество элементов

Развитие счета и количества

Успех в математике начинается с развития чувства числа посредством счета и количества. Может показаться, что дети учатся считать почти так же, как учатся алфавиту — просто повторяя числа наизусть. Хотя обучение наших детей счету от 1 до 10, 20 или даже 100 полезно, сам по себе этот навык не то же самое, что научиться считать. Чтобы у детей в начальных и средних классах сформировалась гибкость с числами, очень важно выработать прочную основу для счета и количества. Когда учащийся начинает испытывать трудности в изучении математики, виновником часто могут быть пробелы в знаниях из предыдущих классов. Работая со многими учениками в коррекционных математических классах, я часто обнаруживал, что трудности могут быть связаны с отсутствием концептуального понимания счета и количества. Эта памятка по принципам счета и количества предназначена для того, чтобы помочь родителям и учителям лучше понять, как помочь своим детям в счете и количестве в раннем возрасте.

Посвятив большую часть своей профессиональной жизни преподаванию математики в средней школе и наставничеству учителей математики среднего (с 7 по 10 классы), моя новая роль консультанта по математике K-12 привела меня на путь к новым знаниям, которые я хотел бы иметь во время учебы. лет, проведенных в классе. В прошлом мои беседы с учителями средних и старших классов о потребностях учащихся в обучении всегда, казалось, наталкивались на пробелы в понимании учащихся, однако редко нам удавалось копнуть достаточно далеко в математическом континууме обучения, чтобы точно определить, где именно начинались эти пробелы. Несмотря на то, что Рошель Гельман и Рэнди Галлистел ввели пять принципов счета в 1978, этот ресурс познакомит вас с этими пятью и дополнительными пятью, которые очень полезны, чтобы помочь учащимся глубже понять счет и количество числа .

1. Стабильный порядок

Первый принцип счета заключается в том, что учащийся использует список слов для счета в повторяемом порядке. Этот упорядоченный или «стабильный» список счетных слов должен быть не меньше количества подсчитываемых элементов.

Например, если учащийся хочет сосчитать 20 элементов, его стабильный список чисел должен быть не менее 20. Размышляя о стабильном порядке глубже, мы могли бы рассмотреть механический счет с 0, считая с числа (т. е.: «начать на 6 и считать до 18″) и считать в обратном порядке (т. е. “считать в обратном порядке от 15”), которые связаны со стабильным порядком.

Tweet This

Помощь учащимся в приобретении этих навыков и гибкости, чтобы считать и считать в обратном порядке, потребует времени, но поможет сформировать глубокое понимание счета и количества.

Посмотреть эту анимацию в видеоформате можно здесь.

Стратегии, способствующие обучению учащихся

• Расстановка изображений предметов по порядку от меньшего к большему в зависимости от количества и их подсчет в прямом и обратном порядке.
• Упорядочивание объектов по порядку, сначала без номеров, а затем с добавлением символов.

Если вы заметили:

• Ребенок неправильно считает наизусть или с помощью предметов…

Подумайте:

• Намеренно ошиблись в счете и попросите ребенка сказать вам, какое число вы пропустили.

2. Соответствие один к одному

Понимание того, что каждый объект в группе можно пересчитать один и только один раз. На ранних этапах полезно, чтобы дети помечали или касались каждого подсчитываемого предмета и убирали его в сторону по мере подсчета.

Посмотреть эту анимацию в видеоформате можно здесь.

Чтобы учащиеся поняли и применяли принцип счета один к одному, они должны уметь считать наизусть устно. Мы можем способствовать развитию этого навыка, регулярно считая предметы во время игры и повседневной жизни. Также полезно поощрять учащихся показывать количество на пальцах.

Твитнуть это

Стратегии, поддерживающие обучение учащихся

• Поощрение учащихся «отмечать» или убирать предметы во время счета.
• Сопоставление предметов с картинками. Например, с помощью поиска и поиска книг.
• Предложите учащимся составить таблицу для подсчета и отслеживания количества еды, игрушек, звуков (например, ударов по барабану), букв в слове или слов в предложении.

Если вы заметили:

• Ребенок, играющий на кухне и готовящий еду для мягких игрушек…

Подумайте:

• Спросите, сколько блюд они готовят или для скольких людей они готовят.

3. Количество элементов

Понимание того, что последнее число, используемое для подсчета группы объектов, показывает, сколько объектов в группе. Ребенок, который пересчитывает, когда его спрашивают, сколько конфет в наборе, который он только что посчитал, может не понимать принципа кардинальности.

Посмотреть эту анимацию в видеоформате можно здесь.

Если вам трудно определить, твердо ли учащийся усвоил основной принцип, попросите его сосчитать группу предметов, а затем попросите их положить такое же количество в мешок. Если они должны пересчитывать, у них может не быть твердого понимания кардинальности.

Стратегии, поддерживающие обучение учащихся

• Побуждение учащихся показать вам группу элементов, соответствующих определенному числу.
• Попросите учащихся сосчитать группу предметов в наборе. Затем явно попросите их показать вам, сколько объектов в этой группе представляет эту сумму.

Tweet This

Если вы заметите:

• Ребенок строит башню из лего…

Подумайте:

• Спросите, могут ли они использовать такое же количество лего для создания пути.

4. Сохранение

Понимание того, что счет для заданной группы объектов остается неизменным независимо от того, разбросаны они или близко друг к другу. Если учащийся считает группу предметов, стоящих близко друг к другу, а затем ему нужно пересчитать после того, как вы их разложили, возможно, он не развил понимание принципа сохранения.

Посмотреть эту анимацию в видеоформате можно здесь.

Tweet This

Совет по подсчету и количеству: не торопитесь с символами

Слишком часто мы спешим к символам в математике, и счет ничем не отличается. Помогите детям развить твердое представление о количестве, связанном с каждым конкретным числом, прежде чем мы формально введем символическую форму числа.

УЗНАТЬ БОЛЬШЕ

Переход от конкретного к визуальному к абстрактному в математике часто называют моделью затухания конкретности.

Загрузите 15-страничную памятку по подсчету и количеству и завершите обучение с доступом в Интернет или без него с вашего любимого устройства!

СКАЧАТЬ РУКОВОДСТВО

5. Порядок не имеет значения

Порядок подсчета предметов не имеет значения. Учащиеся понимают, что порядок не имеет значения, когда они могут сосчитать группу предметов, начиная с разных мест. Например, считая от крайнего левого элемента к крайнему правому и наоборот.

Посмотреть эту анимацию в видеоформате можно здесь.

В то время как принцип неуместности порядка может показаться взрослым очевидным, многие ученики до 4 класса придерживаются ошибочного представления о том, что порядок, в котором вы считаете предметы, имеет значение. Четкое преподавание этого принципа важно. Следует также отметить, что только потому, что ребенок силен в этом принципе, он все еще может быть слаб в других принципах счета. 9.

Счетные наборы уникальных предметов (разного цвета, формы и т.д.) в различных порядках.

Твитнуть это

Если вы заметили:

• Ребенок считает набор машинок…

Подумайте:

• Спросите, могут ли они предсказать, сколько машин было бы, если бы они начали считать с другого места.

6. Абстракция

Абстракция требует понимания того, что мы можем сосчитать любой набор объектов, материальных или нет. Например, количество пяти больших предметов равно количеству пяти маленьких предметов или смешанной группе из пяти маленьких и больших предметов. Другой пример может заключаться в том, что учащийся может считать связанные кубики, представляющие какой-либо другой набор объектов, таких как автомобили, собаки или велосипеды.

Посмотреть эту анимацию в видеоформате можно здесь.

Дети часто считают, что группы более крупных предметов имеют большую ценность, чем группы более мелких предметов. Например, ребенок может полагать, что количество 3-х машин на парковке больше, чем 3-х игрушечных машинок, размещенных на игровом коврике

Стратегии, поддерживающие обучение учащихся

• Подсчет неосязаемых величин, таких как звуки, действия , слова, вопросы или шаги.
• Сопоставление групп разных предметов с одинаковым количеством.

Твитнуть это

Если вы заметите:

• Ребенок, играющий с игрушками разного размера…

Рассмотрим:

• Берем группу из 2 больших предметов и группу из 3 меньших предметов и спрашиваем, у кого больше.

7.

Субитирование

В общем, субитирование — это способность «видеть» или визуализировать небольшое количество объектов и знать, сколько их, не считая. Хотя эта идея может показаться простой на первый взгляд, субитизация на самом деле довольно сложна. Если мы копнем глубже, мы увидим, что есть два типа субитизации, которые могут происходить в нашем уме, когда мы учимся считать, называемые 9.0007 перцептивное субитизирование  и  концептуальное субитизирование .

Перцептивная субитизация

Перцептивная субитизация имеет место, когда вы можете смотреть на группу объектов и знать, сколько существует объектов, не задумываясь. Часто, когда мы смотрим на группы из 5 или менее объектов, мы субитизируем восприятие.

Примеры

перцептивного субитизации могут включать:

• Знание того, что на столе 3 конфеты, не считая конфет.
• Зная, что вы выбросили 5 одним кубиком, не считая точек.
• Зная, что на подъездной дорожке стоят 2 машины, не считая машин.

Концептуальная субитизация

Концептуальная субитизация имеет место, когда вы все еще можете «видеть», сколько объектов находится в группе, но количество объектов слишком велико, чтобы субитизировать без разбиения на две или более меньшие группы. Мы часто переходим от субитизации восприятия к субитизации концептуальной, когда количество объектов в группе превышает 5.

Вы можете обнаружить, что способны перцептивно субитизировать групп из более чем 5 элементов, когда элементы организованы знакомым образом. Например, большинство «знают», что они выбросили 6 на одном кубике из-за знакомого расположения точек. Тем не менее, вам может быть трудно воспринимать эти 6 точек, если они расположены незнакомым образом, и прибегать к концептуальной субитизации, разбивая 6 точек на две группы по 3 в уме, даже не осознавая этого!

В то время как многие могут полагать, что использование 5- и 10-фреймов в ранней математике просто потому, что 5 и 10 являются очень удобными числами в нашей системе счисления с основанием 10, мы можем видеть, что организация элементов в 5-фрейме может быть важным инструментом. помочь учащимся перейти от перцептивного субитизации к концептуальному субитизации.

Стратегии, поддерживающие обучение учащихся

• Попросите детей подсчитать, сколько предметов находится в наборе, который находится вне досягаемости или трудно физически пометить с помощью однозначного соответствия (например, автомобили на подъездной дорожке, стулья за столом). , и т. д.).
• Создавайте карты с точками, используя листы бумаги с небольшим количеством точек на каждой, расположенные в различных конфигурациях, и играйте с ними в игры на совпадение, войну и другие забавные карточные игры.

Tweet This

Если вы заметили:

• Ребенок играет с небольшим количеством предметов…

Подумайте:

• Спросите их, со сколькими предметами они играют.

Хотите больше действий по субитализации?

Вы можете узнать больше о перцептивной и концептуальной субитизации и получить доступ к полезным действиям, загрузив руководство по субитизации.

СКАЧАТЬ РУКОВОДСТВО

8. Иерархическое включение

Понимание того, что все числа, предшествующие числу, могут быть или систематически включены в значение другого выбранного числа. Например, зная, что в группе из 5 элементов есть также группа из 4 элементов в этой группе; 3 элемента в этой группе; 2 предмета… и так далее.

Посмотреть эту анимацию в видеоформате можно здесь.

Tweet Это

Иерархическое включение является важной вехой, которую учащиеся должны достичь, чтобы полностью понять кардинальность и начать составлять числа (т. е. составлять набор из 5 элементов путем объединения набора из 2 элементов с набором из 3 элементы) и разложение чисел (т. е. разложение набора из 6 элементов путем разделения на набор из 4 элементов и набор из 2 элементов).

Стратегии, поддерживающие обучение учащихся

• Попросите детей назвать число, которое «на единицу больше» или «на единицу меньше» числа.
• Запрос числа, которое находится «внутри» числа 7.

9. Движение – это Величина

Понимание того, что при движении вверх по счетной последовательности (или вперед) количество увеличивается на единицу, а при движении вниз (или назад) количество уменьшается на единицу или на любую другую величину, которую вы поднимаете /вниз мимо.

Несмотря на то, что многие считают, что выучить алфавит — это то же самое, что научиться считать, наша система счисления намного сложнее алфавита. Буквы в алфавите расположены в порядке без какой-либо особой причины, тогда как стабильный список чисел, который мы используем для измерения количества посредством счета, упорядочен по величине.

Tweet This

Посмотреть эту анимацию в видеоформате можно здесь.

10. Объединение

Объединение относится к пониманию того, что вы можете подсчитать большую группу предметов, разбив группу на более мелкие, равные группы элементов, а затем подсчитать их. Например, если на столе есть большая группа конфет, можно создать группы (или «единицы») по 2 штуки (часто делая это путем перцептивного субитизации этих групп) и пропустить подсчет до 2-х.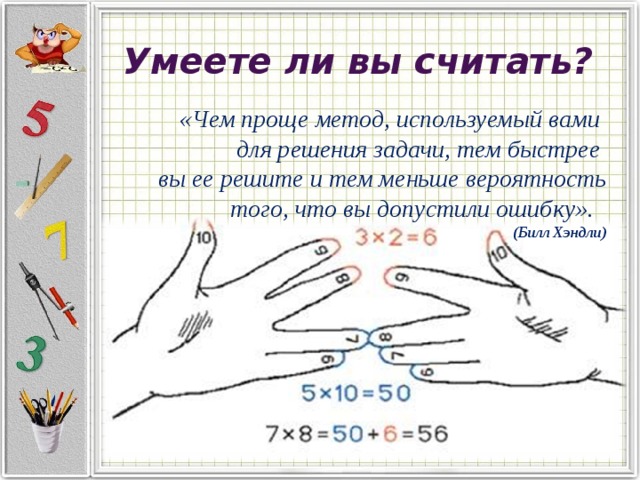 Некоторые могут решить создать «единицы» из 3 и пропустить счет на 3.

Мы могли бы подумать о соединении объединения обратно с соответствием 1-к-1 , думая об объединении групп из 2 как « соответствие 2-к-1 » в ситуации, когда мы подсчитываем 2 конфеты на каждую 1 группу или объединяем группы по 3 как « соответствие 3-к-1 » в ситуации, когда мы считаем 3 конфеты на каждую 1 группу. Я обнаружил, что, думая об объединении таким образом, он может начать обнаруживать связи с умножением и лежащими в его основе соотношениями, которые существуют всякий раз, когда мы считаем какое-либо количество.

Tweet This

Понимание разрядного значения посредством объединения

Единение также важно для учащихся, чтобы понять, что объекты сгруппированы в десятки в нашей системе счисления с основанием десять. Например, когда количество превышает 9, это обозначается 1 в разряде десятков числа.

Посмотреть эту анимацию в видеоформате можно здесь.

Ссылки и ресурсы

Интернет-ресурс

• Наглядные материалы для подсчета и количества
• Считай глазами: руководство по субитизации
• Как 5 принципов счета закладывают основу для гибкого мышления в старших классах
• Математика в младших классах: счет и мощность
• Основные принципы подсчета

Книги, чтобы узнать больше о счете, количестве и ранней математике

ПРОЧИТАТЬ КНИГУ

ПРОЧИТАТЬ КНИГУ

ПРОЧИТАТЬ КНИГУ

Исследования

• Bermejo, V., Osuna, Garcia, S. Поддержка развития понимания кардинальности у детей, Learning and Instruction, 14: 381–9.8. [PDF]
• DCSF (Департамент по делам детей, школ и семей) (2009 г.), Дети, мыслящие математически: PSRN, необходимые знания для специалистов по раннему развитию. Ноттингем: DCSF. [PDF]
• Гельман, Р. и Галлистел, К. (1978) Понимание числа ребенком. Кембридж, Массачусетс. Издательство Гарвардского университета. [PDF]
• Клементс, Д. и Сарама, Дж. (2010) Траектории обучения в ранней математике – последовательности приобретения и обучения. Баффало, Нью-Йорк. [PDF]

По мере того, как мы изучаем принципы счета и переходим к объединению, я быстро понимаю, насколько важно это понимание для учащихся, когда мы изучаем разрядное значение, дроби, умножение/деление (т. связаны с чувством числа, измерением и пропорциональным мышлением. Я что-то пропустил? У вас есть отличные идеи, которые можно добавить к этим описаниям? Другие вещи, которые мы должны учитывать, сосредотачиваясь на подсчете и количестве? Пожалуйста, поделитесь в комментариях!

СКАЧАТЬ БЕСПЛАТНУЮ Шпаргалку!

Вам предстоит многое узнать о счете и количестве! Загрузите 15-страничную печатную памятку по подсчету и количеству, чтобы поделиться ею с коллегами, родителями или просто для своей личной стопки материалов для изучения математики!

СКАЧАТЬ РУКОВОДСТВО

Что должен знать каждый учитель

Математические советы и стратегии развития чувства числа до 20 в детском саду и первом классе: Включен обширный список заданий и ресурсов для развития чувства числа: книги, материалы, математические манипуляции , и БЕСПЛАТНЫЕ мероприятия!

Математические советы и стратегии, необходимые для развития чувства числа до 20, находятся прямо здесь. У вас будет все, что вам нужно, чтобы быстро внедрить множество заданий, игр и центров, связанных с числами, в свой класс или домой.

Building Number Sense to 20

Занятия, книги, предложения ресурсов (включая БЕСПЛАТНУЮ) охватывают множество концепций числового смысла и идеально подходят для детского сада и первого класса. Кроме того, вы найдете ценные материалы по численному смыслу и манипулятивные предложения, а также бесплатные подарки, которые вы можете получить уже сегодня! Предупреждение: он ДЛИННЫЙ, но в нем так много всего, что вы не захотите ничего пропустить!

Почему важен смысл номера здания?

Детям нужны возможности изучать числа и знакомиться с ними. Научиться считать, определять числа и понимать количество — это лишь некоторые из основных понятий. Повторяющийся опыт способствует пониманию и свободному обращению с числами. Этот опыт помогает расширить знания и узнать новые идеи. Сильное чувство числа жизненно важно для будущего понимания более сложных математических тем.

Приведенные ниже действия успешно использовались. Используйте их так, как они описаны, или адаптируйте их к своим потребностям. Быть гибким. Обсуждайте числа и поощряйте вопросы. Когда есть возможность заказать, посчитать, сопоставить или описать вместе с ребенком, дерзайте! Им выгодно видеть числа естественным и плавным образом.

Каждый день уделяйте время веселым и увлекательным занятиям с числами и наблюдайте за развитием беглости речи.

Чувство числа. Концепции и упражнения

Развивайте чувство числа посредством счета

Очень важно считать с детьми каждый день. Повторяющийся устный счет помогает им услышать, как звучат числа, и запомнить их порядок. Использование математических манипуляций, таких как подсчет фишек, может помочь установить связь с вербальным счетом и счетом объектов. Этот счет один к одному является важным навыком, который необходимо часто практиковать.

Занятия

• Считайте вслух всем классом, начиная с единицы и постепенно увеличивая число.
• Сядьте с партнером или в круг и по очереди считайте по 1.
• По мере того, как счет будет развиваться, учите модели чисел и счет 2, 5 и 10.
• Используйте числовую диаграмму, чтобы посмотреть, как числа выглядят визуально. Укажите на каждое число, как оно сказано.
• Поощряйте детей практиковать прямой счет с маленькими предметами. Поставьте небольшие группы предметов в центре, чтобы их можно было сосчитать.
• Раздайте детям карточки с цифрами (подобные показанным ниже), чтобы они могли изображать их с помощью счетных фишек.

Развивайте чувство числа, сопоставляя числа с количествами

Предоставьте детям материалы для счета и связи с предметами и числами. Это побуждает детей видеть, что цифры — это больше, чем слова. Объясните детям, что числа имеют множество представлений, таких как точки, пальцы, счетчики, цифры, объекты, десять рамок и т. д.

Занятия

• Сопоставьте вместе объекты двух разных типов, например пять счетных медведей и домино с пятью точками.
• Используйте ссылки, чтобы создать числовую цепочку для номера.
• Работайте до показа количества с более чем двумя типами объектов (как видно на фото).
• Имейте множество различных предметов для занятий, таких как игральные кости, домино, магниты с числами, медведи, счетные фишки, кубики и числовые карты.

• Сопоставьте числовые карты из карточной колоды или игры Уно с точками на домино. Найдите все комбинации чисел на костяшках домино.

• Соберите головоломки с числами, каждая из которых имеет свое числовое представление. Они помогают детям увидеть, что числа можно моделировать разными способами. Эти числовые головоломки до 20 доступны для БЕСПЛАТНОЙ загрузки далее.

• Поощряйте индивидуальный счет с карточками с вырезками. Дети считают группы предметов и вырезают цифру, которая соответствует нужному количеству.

• Десять рамок отлично подходят для систематизации чисел, чтобы их можно было легко сосчитать. Сопоставление числовых карточек с десятью изображениями рамок является простым, но эффективным способом связи количества с числами.

Развивайте чувство числа с числом дня

Когда дети видят числа разными способами одновременно и многократно, их чувство числа развивается. Выберите число дня, начинающееся с единицы, и проанализируйте его во время математического блока.

Занятия

• Узнайте о конкретном номере за каждый день вашего пребывания в школе. Научите и проанализируйте это число в течение календарного времени. Представьте это число на числовой прямой, сосчитайте до этого числа, покажите это число с помощью соломинок или кубиков и т. д.
•  Используйте номер постера дня или якорную диаграмму, чтобы разбить числа. Создайте свой плакат с номером дня с помощью БЕСПЛАТНЫХ шаблонов плакатов.
• Поощряйте детей к участию и демонстрируйте свое понимание на бумаге или мини-досках. Задайте вопрос, например: «Как мы покажем 5 с подсчетом баллов?» и дайте им время попробовать самостоятельно. Это отличная разминка для развития беглости перед уроками математики.
• Прочтите дополнительные советы о том, как начать распорядок дня в классе.

Распознавание чисел путем заказа номеров

Предоставьте детям возможность упорядочивать числа. Располагая числа или объекты с числами в правильном порядке, они считают и развивают чувство числа.

Занятия

• Предоставьте возможности с помощью числовой линии и числовой диаграммы, которые упорядочивают числа для нас.
• Расставьте наборы чисел в правильном порядке, найдя их на числовой прямой.
• Заклейте разные числа на таблице с числами стикерами и попросите детей назвать недостающие числа.
• Собирайте наборы Lego, собирая детали в порядке, указанном на блоках.

• Вместе с партнером закажите карточки с числами от 0 до 20. Создайте гусеницу с числами, как показано ниже.

• Головоломки с числами — это интересный способ упорядочить числа. Поместите полоски в правильном порядке, чтобы открыть изображение.

• Пазлы просты и легки в создании. Возьмите старую головоломку и напишите числа на обратной стороне каждой части.
• Возьмите лист бумаги и напишите числа в ряд. Вырежьте произвольно кусочки и торгуйте с партнером. Снова соберите пазл для практики.

• Пройдите лабиринт с порядковым номером, начиная с 0. Это упражнение можно использовать повторно, если положить его в карманный протектор.

Смысл номера сборки с позиционным значением Действия

Обучение детей порядковому значению должно начинаться с обучения их видеть десять разными способами. Перейдите к иллюстрированию чисел с помощью десятичных блоков.

Занятия

• Потренируйтесь составлять группы из десяти предметов. Сгруппируйте соломинки, бобы, прилавки или любые мелкие предметы.
• Обучайте счет десятками для групп. Сначала перейдите к обучению групп, а затем одиночных занятий.
• Объединитесь в группы по десять человек, чтобы добраться до 100-го дня.
• Показать и изучить блок десятков и блок единиц. Обсудите, что в блоке десятков сложено десять единиц.
• Используйте блоки десятичной системы счисления для представления чисел. Сделайте много примеров, где дети должны использовать и считать кубики. Используйте диаграмму, чтобы помочь сосчитать блоки.
• Скажите: «Покажи (или нарисуй) мне 14 кубиков разряда!»
• Представляет количество десятков и единиц на матах разряда (см. ниже). Задавайте вопросы типа «Сколько их?» или «Сколько групп по десять человек?». Убедитесь, что они понимают, что означает каждое число в числе (например, 1 из 18 — это десятка, а не единица).

• Представление числа различными способами: расширенная форма, стандартная форма, словоформа, цифра и т. д. Рабочие листы, подобные приведенному ниже, могут помочь установить эту связь.

Чтение и запись цифр

Дети постоянно окружены числами в своем окружении. Они быстро учатся распознавать отдельные цифры от 0 до 9 с помощью различного опыта. Продолжайте поощрять это знакомство, размещая цифры на стене. Плакаты, числовые строки и календари являются полезными инструментами.

Занятия

• Собери числа из пластилина в математическом центре. Даже такая простая вещь, как это пластилин, показывает активность.
• Ежедневно печатайте числа от 0 до 9 разными способами – в буклетах, на досках во время уроков математики и т. д.
• Нарисуйте числа на бумаге и дайте учащимся расставить точки маркерами или бинго-дабберами, чтобы расставить точки.

• Используйте доску Boogie Board (см. ниже) или белую доску, чтобы быстро практиковать числа снова и снова.

• Часто повторяйте числа, чтобы построить координацию и правильную форму. Мини-книга ниже поощряет это, а также номера местонахождения.

• Поощряйте правильное формирование чисел, обучая этому явным образом. Плакаты (см. ниже) являются полезными инструментами для использования и размещения на стене.
• Запоминающиеся стихотворения о числах помогают учащимся визуализировать и запомнить формирование чисел. Используйте все свое тело, чтобы совершать действия или рисовать в воздухе.

Чтение и запись числовых слов

Научите детей читать числовые слова, пока они учатся читать. Учите каждое числовое слово по одному и произносите их фонетически (если применимо).

Мероприятия

• Имейте плакаты с цифрами и числовым словом.
• Включите числовые слова в списки правописания, чтобы дети научились читать и писать числовые слова.
• Используйте номер распорядка дня, чтобы учить и сосредотачиваться на одном слове каждый день.
• Сопоставьте карточки со словами с числами и карточками с числами (см. ниже).
• Играйте в память с партнером со словами-цифрами и карточками с числами. Ищите пары (двенадцать и 12).

• Развивайте распознавание и скорость с помощью флеш-карточек для ментальной арифметики. Карточки для детей, и они соревнуются, чтобы назвать то, что они видят (счет, цифры, числовые слова и т. д.).

Развивайте чувство числа, считая вперед и назад

Обучайте детей стратегии счета вперед и назад, чтобы подготовить детей к сложению и вычитанию.

Упражнения

• Дайте учащимся число и группу мелких предметов, которые они будут считать. Спросите: «Сколько у меня еще есть?» дается 7 для начала и группа из 9 жетонов, на которые можно рассчитывать.
• Играйте в игры с мелкими предметами и колодами карт, где необходим расчет.
• Сыграйте в групповую счетную игру под названием «Вокруг света». Произнесите число, и каждый человек будет считать и называть следующее число, пока вы идете по кругу.
• Используйте маленькие предметы, чтобы считать в прямом или обратном направлении от заданного числа (кубики, жетоны, игральные кости и т. д.).
• Расположите числа в обратном порядке. Возьмите описанные выше действия по упорядочиванию и измените их.

Build Number Sense by Estimating

Предоставьте детям множество возможностей угадать, сколько вещей они видят в своей повседневной жизни. Задавайте наводящие вопросы, чтобы стимулировать это мышление. Убедитесь, что дети знают, что они оценивают и что это всего лишь догадки. Подчеркните, что оценки не обязательно должны быть точными, но они должны быть продуманными. С большей практикой оценки должны стать ближе к фактическому количеству объектов.

Занятия

• Наполните прозрачные или открытые контейнеры предметами разного размера, чтобы дети могли угадать. Держите их простыми и работайте над сложностью и размером объектов. Меньшие объекты и большие контейнеры обычно сложнее.
• Создайте оценочную станцию», где устанавливаются контейнеры с объектами внутри. Дети могут внимательно посмотреть и сделать оценки.

• В качестве общего группового задания возьмите кучу предметов, чтобы быстро их показать. Накройте их и пусть дети делают предположения.
• Играйте в «Покажи и спрячь» с партнером. Используйте чашку и поместите внутрь несколько маленьких счетных мишек. Быстро покажите партнера, а затем спрячьте его. Они делают оценку, а затем вы вместе считаете, чтобы проверить.

Развивайте чувство числа путем сравнения чисел

По мере того, как растет знакомство с числами, растет и способность сравнивать числа друг с другом. Обеспечьте возможность сравнивать числа ежедневно. Задавайте вопросы о том, какое число больше, меньше или одинаково.

Действия

• Используйте диаграмму или числовую линейку для сравнения чисел.
• Используйте маленькие предметы, чтобы упростить сравнение. Скажите «Покажи 11 и 15 кубиками». Спросите: «Какое число меньше?».
• Научите символы < > и = и их значение. Используйте стратегию аллигатора (Аллигатор любит есть побольше), чтобы запомнить знаки и их значение.
• Создание числовых башен. Дети используют кубики для формирования башен для представления чисел. Сравните две башни, чтобы увидеть, какая из них самая высокая и, следовательно, большее число. Аллигатор съедает большую башню.
• Сравните числа с помощью математических инструментов и укажите правильный символ на карточках с картинками (см. ниже). Когда дети станут свободно говорить, они должны распознавать правильный символ без посторонней помощи.

Действия, показанные в этом посте, можно найти в следующих ресурсах, которые можно найти на сайте «Учителя платят учителям».

Числа до 5 для детского сада

Числа до 10 для детского сада

Числа от 11 до 20 для детского сада

Учебная программа Mindful Math для детского сада

Числа до 10 для первоклассников

Числа до 20 для первоклассников

Учебная программа Mindful Math для первоклассников

Бесплатные головоломки со смыслом до 20

Подготовьте этот забавный набор числовых головоломок для своих учебных центров и помогите детям построить свое число смысл!

Возьмите 20 БЕСПЛАТНЫХ числовых головоломок с разными изображениями на каждой части, щелкнув изображение ниже .

Книги Number Sense

I Spy Numbers Jean Marzollo
1,2,3 Peas от Кита Бейкера
Chicka Chicka 1,2,3 от Bill Martin Jr.
Splash! Энн Джонас (счет)
Очень голодная гусеница Эрик Карл (счет)
Как динозавры считают до 10? Джейн Йолен
Число везде Эллиот Кауфман
10 черных точек Дональд Крюс
Сколько жуков в коробке? Дэвид Картер
Сколько улиток? Пол Гиганти-младший.
Десять хитрых пираний, Уильям Уайз.
Нет числа, Оливер Джефферс.0703 «Больше или меньше», Стюарт Мерфи
Tally O’Mally, Стюарт Мерфи
Place Value, Дэвид Адлер
What’s Place Value, Ширли Дьюк
Quack and Count, Кит Бейкер
Держу пари! Стюарт Дж. Мерфи

Материалы для определения числа

Попробуйте комплексную программу Mindful Math

Прочитайте о программе Mindful Math и о том, как она может изменить ваш математический блок в лучшую сторону! Эта всеобъемлющая учебная программа по математике доступна для детского сада, первого и второго класса.