ПРИЕМЫ БЫСТРОГО СЧЕТА НА УРОКАХ МАТЕМАТИКИ В НАЧАЛЬНОЙ ШКОЛЕ
Автор: Мозжегорова Алиса Олеговна
1024×768
Normal
0
false
false
false
RU
X-NONE
X-NONE
/* Style Definitions */
table.MsoNormalTable
{mso-style-name:”Обычная таблица”;
mso-tstyle-rowband-size:0;
mso-tstyle-colband-size:0;
mso-style-noshow:yes;
mso-style-priority:99;
mso-style-qformat:yes;
mso-style-parent:””;
mso-padding-alt:0cm 5.4pt 0cm 5.4pt;
mso-para-margin:0cm;
mso-para-margin-bottom:.0001pt;
mso-pagination:widow-orphan;
font-size:10.0pt;
font-family:”Calibri”,”sans-serif”;
mso-bidi-font-family:”Times New Roman”;}
ПРИЕМЫ БЫСТРОГО СЧЕТА НА УРОКАХ МАТЕМАТИКИ В НАЧАЛЬНОЙ ШКОЛЕ
А.О. Мозжегорова
Государственное бюджетное профессиональное образовательное учреждение Ямало-Ненецкого автономного округа «Новоуренгойский многопрофильный колледж»
Научный руководитель Н.
В. Смирнова, преподаватель дисциплин общеобразовательного и профессионального цикла
Немецкого ученого Карла Гаусса называли королем математиков. Его математическое дарование проявилось уже в детстве. Однажды в школе (Гауссу было 10 лет) учитель предложил классу сложить все числа от 1 до 100. Пока он диктовал задание, у Гаусса уже был готов ответ. На его грифельной доске было написано: 101·50=5050. Как он вычислил? Очень просто – он применил прием быстрого счета, он складывал первое число с последним, второе с предпоследним и т.д. таких сумм всего 50 и каждая равна 101, поэтому он смог почти мгновенно дать правильный ответ.
1+2+…+50+51+…+99+100=(1+100)+(2+99)+…+(50+51)=101·50=5050.
Этот пример, лучше всего показывает, что можно считать практически устно всем школьникам, для этого всего лишь нужно знать приемы быстрого счета.
В настоящее время практически у каждого ученика начальной школы есть телефон, а значит и калькулятор, что никак не способствует повышению вычислительной культуры.
Вместе с тем, главная задача учителя начальных классов – научить всех своих обучающихся вычислительным навыкам, в том числе, навыкам устного счета.
Устный счет как обязательный этап урока должен проводиться на уроках математики во всех классах, он может быть представлен разнообразными формами работы: математический, арифметический или графический диктанты, вычисление по цепочке, математическое лото, ребусы, кроссворды, тесты, беседы, опрос и многое другое. В комплекс упражнений устного счета может входить алгебраический и геометрический материал, решение простых задач и задач на смекалку, свойства действий над числами и величинами и т.д.
Предлагаю некоторые приемы быстрого счета, которые просты в понимании и могут с легкостью применяться обучающимися начальной школы на уроках математики и в повседневной жизни.
Прием 1. Умножение и деление числа на 4. Чтобы умножить число на 4, нужно его дважды умножить на 2. Например: 28·4=(28·2)·2=56·2=112; 526·4=(526·2)·2=1052·2=2104.
Чтобы разделить число на 4, нужно его дважды разделить на 2. Например: 324:4=(324:2):2=162:2=81.
Прием 2. Умножение числа на 5. Чтобы умножить число на 5, нужно его умножить на 10 и разделить на 2. Например: 236·5=(236·10):2=2360:2=1180.
Прием 3. Умножение числа на 9. Чтобы умножить число на 9, нужно к нему приписать 0 и отнять исходное число. Например: 72·9=720-72=648.
Прием 4. Умножение на 25 числа, делящегося на 4. Чтобы умножить на 25 число, делящееся на 4, нужно его разделить на 4 и получившееся число умножить на 100. Например: 124·25=(124:4)·100=31·100=3100.
Прием 5. Умножение двузначного числа на 11. При умножении двузначного числа на 11, нужно между цифрой единиц и цифрой десятков вписать сумму этих цифр, причем, если сумма цифр больше 10, то единицу нужно прибавить к старшему разряду (первой цифре). Например: 23·11=253, т.к. 2+3=5, поэтому между 2 и 3 ставим цифру 5; 57·11=627, т.к. 5+7=12, цифру 2 ставим между 5 и 7, а к 5 прибавляем 1, вместо 5 пишем 6.
Прием 7. Умножение двузначного числа на 101. Для того, чтобы число умножить на 101, нужно приписать данное число к самому себе. Например: 34·101 = 3434. Поясним, 34·101 = 34·100+34·1=3400+34=3434.
Прием 8. Умножение на 22, 33, …, 99. Чтобы двузначное число умножить на 22, 33, …, 99, надо этот множитель представить в виде произведения однозначного числа (от 2 до 9) на 11 и умножить сначала на однозначное число, а потом на 11 или наоборот. Например, 33=3·11, значит, 21·33=(21·3)·11=63·11=693.
Прием 9. Возведение в квадрат двузначного числа, оканчивающегося на 5. Чтобы возвести в квадрат двузначное число, оканчивающееся на 5, нужно цифру десятков умножить на цифру, большую на единицу, и к полученному произведению приписать справа число 25. Например: 352=1225, т.е. 3·4=12 и к 12 приписываем 25, получаем 1225.
Прием 10. Возведение в квадрат двузначного числа, начинающегося на 5. Для возведения в квадрат двузначного числа, начинающегося на пять, нужно прибавить к 25 вторую цифру числа и приписать справа квадрат второй цифры, причем если квадрат второй цифры – однозначное число, то перед ним надо приписать цифру 0.
Например: 522= 2704, т.к. 25+2=27 и 22=04; 582= 3364, т.к. 25+8=33 и 82=64.
Особенность применения устных упражнений и приемов быстрого счета на уроках математики заключается в следующем:
– активизируется мыслительную деятельность ;
– повышается общий уровень математического образования и сознательное усвоение школьного курса математики;
– развиваются навыки быстро выделять из известных им фактов те, которые следует применить для решения предложенных или возникших в практике задач, расчетов и вычислений;
– развивается память, речь, способность зрительного восприятия математических фактов, совершенствуется пространственное воображение.
Знание приемов быстрого счета позволяет упрощать вычисления, экономит время, развивает логическое мышление и гибкость ума.
Проект “Приемы устного счета и их применение”
Автор работы:
Супрун Никита Сергеевич
Руководитель проекта:
Дутова Людмила Павловна
Учреждение:
МБОУ «СОШ №2 » пгт.
Кировский
В процессе исследовательской работы по математике “Приемы устного счета и их применение” учеником 8 класса была поставлена цель изучить методы и приёмы быстрого счёта и доказать необходимость умения быстрого счёта и эффективного использования этих приёмов. В проекте рассматривается первые книги о способах счета и приемы приобретения навыков умножения “на пальцах”.
В исследовательской работе по математике “Приемы устного счета и их применение” автор описывает упрощённые, нестандартные способы устных вычислений при умножении натуральных чисел, рассматривает и показывает на примерах применение нестандартных способов при умножении и делении чисел.
В предложенном проекте по математике “Приемы устного счета и их применение” автором была представлена практическая часть, в которой он демонстрирует приемы устного счета для разных категорий цифр на практике, примеры и эксперименты умножения различных чисел.
Рассматриваются интересные алгоритмы умножения чиселю
Оглавление
Введение
1. Исследование теории.
1.1. Возникновение счета у первобытных людей.
1.2. Изменение счета при появлении цивилизации.
1.3. Первая литература по способам счёта.
1.4. Таблица умножения на пальцах.
1.5. Люди – феномены быстрого счёта.
2. Эксперименты и анализ решения.
2.1. Умножение на 11 числа, сумма цифр которого меньше.
2.2. Умножение на 11 числа, сумма цифр которого больше.
2.3 Умножение на одиннадцать (по Трахтенбергу).
2.4 Умножение на 22,33,…,99.
2.5 Умножение на число 111, 1111 и т. д., зная правила
умножения двузначного числа на число 11.
2.6. Умножение двузначного числа на 101, 1001 и т.д.
2.7. Умножение на 37.
2.8. Алгоритм перемножения двузначных чисел, близких к 100.
2.9. Умножение трёхзначного числа на 999.
2.10. Умножение на шесть ( по Трахтенбергу).
Выводы
Список использованной литературы
Приложение
Введение
В наш век высоких технологий и повсеместного использования компьютера умение быстро и правильно производить в уме достаточно сложные вычисления ни в коем случае не утратило своей актуальности.
Кроме того, быстрый счёт – настоящая гимнастика для ума, приучающая в самых сложных жизненных ситуациях находить в кратчайшее время хорошие и нестандартные решения. Производя математические вычисления в уме, человек пользуется, по сути, теми же правилами, что и при письменных вычислениях.
И оказалось, что большие познания можно получить, обратившись к литературе. Проанализировав очень многие статьи, я открыл для себя очень интересные исторические данные о необычных способах быстрого счёта, а также много закономерностей и неожиданных результатов.
И, казалось бы, «сухие» цифры всего лишь примеры, но сколько полезного и красивого в этих преобразованиях. Для меня было необычно, что приложив немного усилий, я теперь смогу и сам вести быстрый счёт и поделиться этими познаниями с одноклассниками, со взрослыми и со знакомыми.
И, как правило, они, заинтересованные этим, начинают использовать такие приёмы и способы.
А ведь большинство моих сверстников считают плохо. То ли думать им лень (зачем загружать себя лишней работой, если есть калькуляторы), то ли в своё время этому никто не научил. Приёмов рациональных вычислений в учебниках практически нет. Сложные формулы и алгоритмы школьной программы всё дальше и дальше уводят учеников от простых, понятных навыков устного счёта.
Я выбрал тему «Нестандартные приемы устного счета»потому, что я люблю математику и хотел бы научиться считать быстро и правильно, не прибегая к использованию калькулятора.
Актуальность выбранной темы заключается в том, что нижеперечисленные способы быстрого счёта рассчитаны на ум «
Цель исследовательской работы: изучить методы и приёмы быстрого счёта и доказать необходимость умения быстрого счёта и эффективного использования этих приёмов.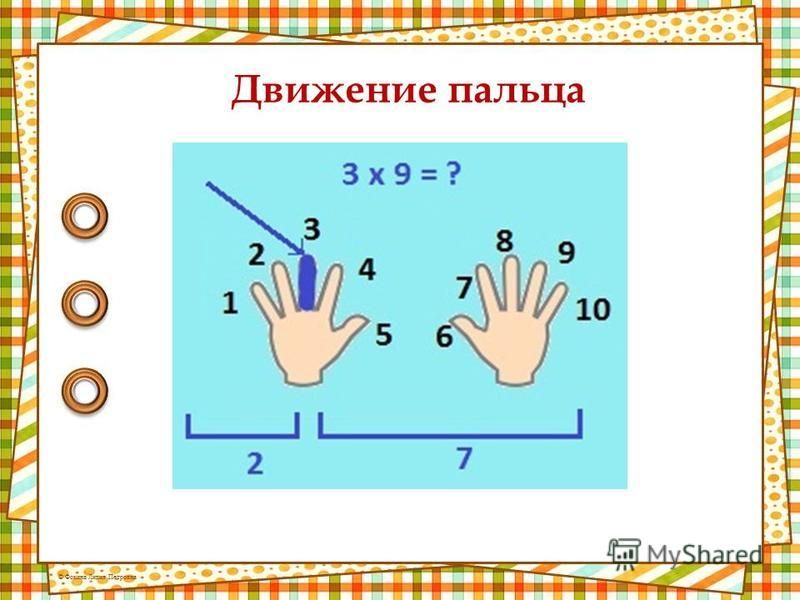
Задачи – 1)узнать об упрощённых, нестандартных способах устных вычислений при умножении натуральных чисел.
2)рассмотреть и показать на примерах применение нестандартных способов при умножении и делении чисел.
Я поставил перед собой проблему: найти и рассмотреть нестандартные приёмы устного быстрого счёта, не рассматриваемые непосредственно в школьном курсе математики.
Объект исследования – вычислительные навыки и быстрый счёт на уроках предметов естественно – математического цикла.
Гипотеза исследования – если показать, что применение приемов быстрого счета, облегчает вычисления, то можно добиться того, что повысится вычислительная культура учащихся, и им будет легче решать практические задачи.
Методы исследования:
1) сбор информации;
2) систематизация и обобщение.
Для того чтобы выяснить, знают ли современные школьники другие способы выполнения арифметических действий, кроме умножения, сложения, вычитания столбиком и деления «уголком» и хотели бы узнать новые способы, был проведен тестовый опрос.
Я провел анкетирование среди учащихся 5, 8 и 10 классов. Задавал учащимся простые вопросы:
1. Умеешь ли ты быстро и правильно считать?
2. Как часто ты пользуешься калькулятором?
3. Знаешь ли ты какие-либо приемы быстрого счета?
Результаты опроса:
1. Умею 11; считаю медленно 38; не умею 10.
2. Часто 3; иногда 42; не пользуюсь 14.
3. Да 17; нет 42.
4. Да 49; нет 10.
Проведя статистическую обработку данных, я сделал вывод, что далеко не все учащиеся знают приемы быстрого счета, поэтому необходимо сделать для учеников 5-6-х классов памятки с приемами быстрого счета, чтобы использовать их при выполнении вычислений.
(Приложение 1
Перейти к разделу: 1. Исследование теории
Как считать быстрее, чем калькулятор « Математика :: WonderHowTo
- По Бобински
Когда вам нужно быстро обработать цифры — я имею в виду действительно быстро — есть классный метод, который вы можете использовать, чтобы перемножить два числа вместе всего за несколько секунд.
Это удобно, когда вам нужно ускорить домашнее задание по умножению, а также для того, чтобы произвести впечатление на учителя математики или сверстников, или просто в качестве классного трюка на вечеринке (в зависимости от вашей толпы). Ментальная математика для победы! Теперь этот трюк будет применяться только в нескольких настройках умножения, но об этом позже.
Для первого примера рассчитаем следующее:
24 x 26 =
Начните с первой цифры первого числа (2 вместо 24) и умножьте ее на число, непосредственно превышающее ее, что даст вам первые цифры ответа. Таким образом, для 24, умноженного на 26, будет 2 (первая цифра в первом числе), умноженная на 3 (на одну цифру выше) = 6.
Это означает, что 6 — наша первая цифра в ответе.
Теперь возьмите вторую цифру первого числа (4 для 24) и умножьте ее на вторую цифру второго числа (6 для 26), что даст вам оставшиеся цифры ответа. Таким образом, если 24 умножить на 26, получится 4 (вторая цифра в первом числе) x 6 (вторая цифра во втором числе) = 24,9.
0021
2 и 4 — последние цифры ответа.
Итак, 24 х 26 = 624 .
Вуаля! Готово. Это магия следующего уровня в стиле Гарри Поттера, верно?
Несколько ограничений
Не пропустите:
Ненавидите математику? Эти умственные трюки заставят вас умножать быстрее, чем когда-либо мог Эйнштейн!
Если вы думали, что этот метод слишком хорош, чтобы быть правдой, вы правы. Есть несколько ограничений или предостережений, которых необходимо придерживаться:
- первые цифры обоих чисел должны быть одинаковыми
- последняя цифра обоих чисел должна быть равна 10
, а последние цифры в каждом (4, 6) равны 10 . Давайте сделаем еще несколько примеров, чтобы понять этот момент.
37 x 33 =
Для 37, умноженного на 33, будет 3 (первая цифра в первом числе), умноженная на 4 (на одну цифру больше) = 12,
Значит, 1 и 2 — наши первые цифры в ответе.
Для второй части фокуса это будет 7 (вторая цифра в первом числе), умноженное на 3 (вторая цифра во втором числе) = 21.
Это означает, что 2 и 1 являются последними цифры ответа.
Итак, 37 х 33 = 1,221 .
122 x 128 =
Если 122 умножить на 128, то получится 12 (первые цифры в первом числе) умножить на 13 (на одну цифру больше) = 156,
Итак, 1 , 5 и 6 — наши первые цифры в ответе.
Для второй части фокуса это будет 2 (вторая цифра в первом числе), умноженное на 8 (вторая цифра во втором числе) = 16. отвечать.
Итак, 122 х 128 = 15 616 .
Не пропустите: как найти процент от данных двух чисел
59 x 51 =
Итак, приведенные выше примеры были довольно простыми. Теперь давайте попробуем вариант, в котором цифры единиц (вторые цифры, те, которые должны равняться 10) умножаются вместе, но не превышают 10.
В этом случае вы должны добавить ноль перед ответом.
Если 59 умножить на 51, получится 5 (первые цифры в первом числе), умноженные на 6 (на одну цифру больше) = 30.
Для второй части трюка это будет 9(вторая цифра в первом числе) умножается на 1 (вторая цифра во втором числе) = 9. Поскольку это меньше 10, мы должны заранее добавить ноль.
Это означает, что 0 и 9 являются последними цифрами ответа.
Итак, 59 х 51 = 3,009 .
Чтобы получить более наглядное руководство, посмотрите приведенное ниже видео от Roger73026 на YouTube, в котором есть больше примеров этого математического трюка в действии:
Не пропустите: Math Craft: Mathmatically Inspired Art Projects
Хотите освоить Microsoft Excel и поднять перспективы работы на дому на новый уровень? Начните свою карьеру с нашего учебного комплекта Microsoft Excel Premium от А до Я в новом магазине Gadget Hacks Shop и получите пожизненный доступ к более чем 40 часам базовых и продвинутых инструкций по функциям, формулам, инструментам и многому другому.
Купить сейчас (скидка 97 %) >
Другие выгодные предложения:
- Скидка 97 % The Ultimate 2021 White Hat Hacker Certification Bundle
- Скидка 98 % на комплект Accounting Mastery Bootcamp 2021
- Скидка 99 % на универсальный набор Data Scientist Mega Bundle 2021
- Скидка 59 % на XSplit VCam: пожизненная подписка (Windows)
- Скидка 98 % на Premium to Learn 2021 Code Certification Bundle
- Скидка 62 % Программное обеспечение MindMaster Mind Mapping: бессрочная лицензия
- Скидка 41 % NetSpot Home Wi-Fi Analyzer: пожизненные обновления
33 комментария
- Горячий
- Последние
Основной принцип счета (Правило счета умножения)
Вероятность и статистика > Вероятность > Основной принцип счета
Определение основного принципа счета.
Фундаментальный принцип подсчета (также называемый правилом подсчета) — это способ подсчитать количество результатов в вероятностной задаче. По сути, вы перемножаете события вместе, чтобы получить общее количество результатов. Формула:
Если у вас есть событие «а» и другое событие «b», то все различные исходы событий равны a * b.
Если вы смотрели игру Squid Game на Netflix, вы узнаете правило счета в сцене со стеклянными ступеньками. Посмотрите это видео, чтобы увидеть, как они использовали это правило (и как математик в сериале ошибся!):
Кальмар игра Блупер: они ошиблись в вероятности
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Примеры основных принципов счета
Посмотрите видео с пятью рабочими примерами использования формулы правила счета:
Примеры основных принципов счета
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Основной принцип счета: Пример задачи №1
В ресторане быстрого питания есть специальное меню: 5 долларов за напиток, бутерброд, гарнир и десерт. Возможные варианты:
- Сэндвич: жареная курица, говяжья котлета, вегебургер и рыбное филе.
- Гарнир: Обычный картофель фри, Картофель фри, Картофельные дольки.
- Десерт: печенье с шоколадной крошкой или яблочный пирог.
- Напиток: Fanta, Dr. Pepper, Coke, Diet Coke и Sprite.
В. Сколько комбо блюд возможно?
А. Всего 4 ступени:
- Выбери бутерброд.
- Выберите сторону.
- Выбери десерт.
- Выбери напиток.
Есть 4 вида сэндвичей, 3 вида гарниров, 2 вида десертов и пять видов напитков.
Количество возможных комбинаций еды равно 4 * 3 * 2 * 5 = 120.
Основной принцип подсчета: Пример задачи №2.
В. Вы проходите опрос с пятью ответами «да» или «нет».
Сколькими способами вы могли бы заполнить анкету?
A. Есть 5 этапов: вопрос 1, вопрос 2, вопрос 3, вопрос 4 и вопрос 5.
На каждый вопрос есть 2 варианта ответа (Да или Нет).
Таким образом, общее количество возможных ответов равно:
2 * 2 * 2 * 2 * 2 = 32.
Пример задачи №3.
В: Компания наносит код на каждый продаваемый продукт. Код состоит из 3 цифр и 2 букв. Сколько различных кодов возможно?
A. Всего 5 ступеней (цифра 1, цифра 2, цифра 3, буква 1 и буква 2).
Возможны 10 чисел: 0 – 9.
Возможны 26 букв: A – Z.
Итак, имеем:
10 * 10 * 10 * 26 * 26 = 676000 возможных кодов.
Проблемы с фундаментальным принципом счета: Ваша очередь!
Нажмите на вопрос, чтобы открыть ответ.
Вопрос 1: Вы подбрасываете три десятицентовика. Сколько возможных исходов?
Вопрос 2: В вашей школе есть два урока английского языка, три урока математики и три урока истории. Вы хотите взять по одному из каждого класса.
Сколько существует различных способов организовать свое расписание?
Вопрос 3: Кейтеринг на свадьбу предлагает вам три варианта основного блюда, шесть вариантов закуски и пять вариантов десерта. Сколько существует различных блюд (состоящих из закуски, ужина и десерта)?
Вопрос 4: Вы проходите тест с несколькими вариантами ответов, состоящий из 10 вопросов. Каждый вопрос имеет 4 варианта ответа. Сколько различных способов ответить на тест (при условии, что вы не оставили вопрос пустым)?
Вопрос 5: Интернет-компания предлагает специальное предложение для свиданий: выберите один фильм из четырех вариантов, один ресторан из шести вариантов и цветы, шоколад или вино. Сколько возможных вариантов свидания существует?
Посетите наш канал на YouTube, чтобы получить дополнительную статистику, справку и советы!
Ссылки
Dodge, Y. (2008). Краткая энциклопедия статистики. Спрингер.
Уилан, К. (2014). Голая статистика.