Метод Жордана-Гаусса для решения СЛАУ: основные понятия, примеры, определения
В данной статье мы рассмотрим метод Жордана-Гаусса для решения систем линейных уравнений, отличие метода Гаусса от метода Жордана-Гаусса, алгоритм действий, а также приведем примеры решений СЛАУ.
Основные понятия
Определение 1Метод Жордана-Гаусса — один из методов, предназначенный для решения систем линейных алгебраических уравнений.
Этот метод является модификацией метода Гаусса — в отличие от исходного (метода Гаусса) метод Жордана-Гаусса позволяет решить СЛАУ в один этап (без использования прямого и обратного ходов).
ПримечаниеМатричная запись СЛАУ: вместо обозначения А в методе Жордана-Гаусса для записи используют обозначение Ã — обозначение расширенной матрицы системы.
Пример 1Решить СЛАУ методом Жордана-Гаусса:
4×1-7×2+8×3=-232×1-4×2+5×3=-13-3×1+11×2+x3=16
Как решить?
Записываем расширенную матрицу системы:
Ã=4-78|-232-45|-13-3111|16
Напоминаем, что слева от черты записывается матрица системы А:
A=4-782-45-3111
Замечание 1На каждом шаге решения необходимо выбирать разрешающие элементы матрицы.
В этой статье мы покажем оба способа решения.
Произвольный способ выбора разрешающих элементов
- Первый этап:
Следует обратиться к 1-му столбцу матрицы Ã — необходимо выбрать ненулевой (разрешающий) элемент.
В 1-ом столбце есть 3 ненулевых элемента: 4, 2, -3. Можно выбрать любой, но, по правилам, выбирается тот, чей модуль ближе всего к единице. В нашем примере таким числом является 2.
Цель: обнулить все элементы, кроме разрешающего, т.е. необходимо обнулить 4 и -3:
4-782-45-3111
Произведем преобразование: необходимо сделать разрешающий элемент равным единице. Для этого делим все элементы 2-ой строки на 2. Такое преобразование имеет обозначение: II:2:
4-78|-232-45|-13-3111|16II÷2→4-78|-232-45/2|-13/2-3111|16
Теперь обнуляем остальные элементы: 4 и -3:
4-78|-232-45/2|-13/2-3111|16 I-4×IIIII-(-3)×II
Необходимо выполнить преобразования:
I-4×II и III-(-3)×II=III+3×II
Запись I-4×II означает, что от элементов 1-ой строки вычитаются соответствующие элементы 2-ой строки, умноженные на 4.
Запись III+3×II означает, что к элементам 3-ей строки прибавляются соответствующие элементы 2-ой строки, умноженные на 3.
I-4×II=4 -78 -23-41 -25/2 -13/2==4 -78 -23-4 -810 -26=0 1-2 3
Записываются такие изменения следующим образом:
4-78|-232-45/2|-13/2-3111|16I-4×IIIII-(-3)×II→01-2|31-25/2|-13/20517/2|-7/2
- Второй этап
Необходимо обнулить 2-ой столбец, следовательно, нужно выбрать разрешающий элемент: 1, -2, 5. Однако 2-ую строку матрицы мы использовали в первом этапе, так что элемент -2 не может быть использован.
Поскольку необходимо выбирать число, чей модуль ближе всего к единице, то выбор очевиден — это 1. Обнуляем остальные элементы 2-го столбца:
01-2|31-25/2|-13/20517/2|-7/2II-(-2)×IIII-5×I
Итог:
01-2|31-25/2|-13/20517/2|-7/2II+2×IIII-5×I→01-2|310-3/2|-1/20037/2|-37/2
- Третий этап
Теперь требуется обнулить элементы 3-го столбца. Поскольку первая и вторая строки уже использованы, поэтому остается только один вариант: 37/2. Обнуляем с его помощью элементы третьего столбца:
Обнуляем с его помощью элементы третьего столбца:
01-2|310-3/2|-1/20037/2|-37/2
Выполнив преобразования
I-(-2)×III=I+2×III и II-(-32)×III=II+32×II
получим следующий результат:
01-2|310-3/2|-1/2001|-1I+2×IIIII+3/2×III→010|1100|-2001|-1
Полное решение:
4-78|-232-45|-13-3111|16II÷2→4-78|-232-45/2|-13/2-3111|16I-4×IIIII-(-3)×II→
→01-2|31-25/2|-13/20517/2|-7/2II-(-2)×IIII-5×I→01-2|310-3/2|-1/20037/2|-37/2III÷372→
→01-2|310-3/2|-1/2001|-1I+2×IIIII+3/2×III→010|1100|-2001|-1.
Выбор разрешающих элементов на главной диагонали матрицы системы
Определение 2Принцип выбора разрешающих элементов строится на простом отборе соответствующих элементов: в 1-ом столбце выбирается элемент 1-го столбца, во 2-ом — второй, в 3-ем — третий и т.д.
- Первый этап
В первом столбце необходимо выбрать элемент первой строки, т.е. 4. Но поскольку в первом столбце есть число 2, чей модуль ближе к единице, чем 4, то можно поменять местами первую и вторую строку:
4-78|-232-45|-13-3111|16→2-45|-134-78|-23-3111|16
Теперь разрешающий элемент — 2. Как показано в первом способе, делим первую строку на 2, а затем обнуляем все элементы:
Как показано в первом способе, делим первую строку на 2, а затем обнуляем все элементы:
4-78|-232-45|-13-3111|16I÷2→2-45/2|-13/24-78|-23-3111|16II-4×IIII+3×I→1-25/2|-13/201-2|30517/2|-7/2
- Второй этап
На втором этапе требуется обнулить элементы второго столбца. Разрешающий элемент — 1, поэтому никаких изменений производить не требуется:
01-2|31-25/2|-13/20517/2|-7/2I+2×IIIII-5×II→01-2|310-3/2|-1/20037/2|-37/2
- Третий этап
На третьем этапе необходимо обнулить элементы третьего столбца. Разрешающий элемент — 37/2. Делим все элементы на 37/2 (чтобы сделать равными 1), а затем обнуляем:
01-2|310-3/2|-1/20037/2|-37/2III÷372→10-3/2|-1/201-2|3001|-1I+2×IIIII+3/2×III→100|-2010|1001|-1
Ответ: x1=-2; x2=1; x3=-1.
4-78|-232-45|-13-3111|16I÷2→2-45/2|-13/24-78|-23-3111|16II-4×IIII+3×I→01-2|31-25/2|-13/20517/2|-7/2I+2×IIIII-5×II→
→01-2|310-3/2|-1/20037/2|-37/2III÷372→10-3/2|-1/201-2|3001|-1I+2×IIIII+3/2×III→100|-2010|1001|-1
Пример 2Решить СЛАУ методом Жордана-Гаусса:
3×1+x2+2×3+5×4=-63×1+x2+2×4=-106×1+4×2+11×3+11×4=-27-3×1-2×2-2×3-10×4=1
Как решить?
Записать расширенную матрицу данной системы Ã:
3125|-63102|10641111|-27-3-2-2-10|1
Для решения используем второй способ: выбор разрешающих элементов на главной диагонали системы. На первом этапе выбираем элемент первой строки, на втором — второй строки, на третьем — третьей и т.д.
На первом этапе выбираем элемент первой строки, на втором — второй строки, на третьем — третьей и т.д.
- Первый этап
Необходимо выбрать разрешающий элемент первой строки, т.е. 3. Затем обнуляем все элементы столбца, разделяя на 3 все элементы:
3125|-63102|-10641111|-27-3-2-2-10|1I÷3→11/32/35/3|-23102|-10641111|-27-3-2-2-10|1II-3×IIII-6×IIV+3×I→
→11/32/35/3|-200-2-3|-40271|-150-10-5|-5
- Второй этап
Необходимо обнулить элементы второго столбца. Для этого выделяем разрешающий элемент, но элемент первой строки второго столбца равен нулю, поэтому необходимо менять строки местами.
Поскольку в четвертой строке есть число -1, то меняем местами вторую и четвертую строки:
11/32/35/3|-200-2-3|-40271|-150-10-5|-5→11/32/35/3|-20-10-5|-50271|-1500-2-3|-4
Теперь разрешающий элемент равен -1. Делим элементы второго столбца на -1, а затем обнуляем:
11/32/35/3|-20-10-5|-50271|-1500-2-3|-4II÷(-1)→11/32/35/3|-20105|50271|-1500-2-3|-4I-1/3×IIIII-2×I→
→102/30|-11/30105|5007-9|-2500-2-3|-4
- Третий этап
На третьем этапе необходимо также обнулить элементы третьего столбца. Для этого находим разрешающий элемент в третьей строке — это 7. Но на 7 делить неудобно, поэтому необходимо менять строки местами, чтобы разрешающий элемент стал -2:
Для этого находим разрешающий элемент в третьей строке — это 7. Но на 7 делить неудобно, поэтому необходимо менять строки местами, чтобы разрешающий элемент стал -2:
102/30|-11/30105|5007-9|-2500-2-3|-4→102/30|-11/30105|500-2-3|-4007-9|-25
Теперь делим все элементы третьего столбца на -2 и обнуляем все элементы:
102/30|-11/30105|500-2-3|-4007-9|-25III÷(-2)→102/30|-11/30105|50013/2|2000-9|-25I-2/3×IIIIV-7×III→
100-1|-50105|50013/2|2000-39/2|-39
- Четвертый этап
Обнуляем четвертый столбец. Разрешающий элемент — -392:
100-1|-50105|50013/2|2000-39/2|-39IV÷(-392)→100-1|-50105|50013/2|20001|2I+IVII-5×IVIII-3/2×IV→
→1000|-30100|-50010|-10001|2.
Ответ: x1=-3; x2=-5; x3=-1; x4=2
Решение задач
от 1 дня / от 150 р. Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Тема 3. Решение систем линейных уравнений методом Жордана – Гаусса.
Общим решением системы m линейных уравнений с n неизвестными называется
решение, в котором свободные неизвестные произвольны
!решение, в котором базисные неизвестные линейно выражаются через свободные неизвестные
сумма частных решений этой системы
сумма частных и базисных решений этой системы
Частным решением системы m линейных уравнений с n неизвестными называется
!решение, полученное из общего решения, если свободным неизвестным придать произвольные значения
решение, состоящее только из свободных неизвестных
решение, в котором все компоненты – дробные
частное от деления общего решения на базисное
При отыскании общего решения системы m линейных уравнений с n неизвестными методом Жордана – Гаусса в качестве разрешающего элемента выбирается
элемент таблицы, удовлетворяющий условию
элемент таблицы, удовлетворяющий условию
!любой отличный от нуля элемент таблицы, кроме элементов столбца свободных членов и контрольного столбца
любой элемент таблицы
Система m линейных уравнений с n неизвестными не имеет решений, если на некоторой итерации
все элементы какой либо строки таблицы Жордана – Гаусса равны нулю
две какие – либо строки таблицы Жордана – Гаусса одинаковы
какой – либо из свободных членов
!все элементы какой – либо строки таблицы Жордана – Гаусса, кроме свободного члена, равны нулю
Базисным решением системы m линейных уравнений с n неизвестными называется
!решение, полученное из общего решения системы, в котором свободные неизвестные равны 0
решение, в котором базисные неизвестные произвольны
решение, в котором свободные неизвестные произвольны
система, приведенная к единичному базису
Если r – число базисных неизвестных, а n – общее число неизвестных в произвольной системе m линейных уравнений, то система имеет бесконечное множество решений при
!
Если дано матричное уравнение , то его решение определяется по формуле
!
Если в таблице Жордана – Гаусса – разрешающий элемент, то элемент находится по формуле (правило прямоугольника)
!
Итерацией в методе Жордана – Гаусса называется
расчет одной строки в таблице Жордана – Гаусса
!расчет элементов одной таблицы Жордана – Гаусса
вычисление элементов одного столбца в таблице Жордана – Гаусса
вычисление элементов вводимой строки
Метод Жордана – Гаусса это
нахождение производной
нахождение разрешающего уравнения
!последовательное исключение неизвестных
нахождение разрешающего элемента
Если в таблице Жордана – Гаусса имеются две одинаковые строки, то
их нужно сложить
их нужно перемножить
одну из них сложить со строкой, элементы которой отличаются
!одну из них можно вычеркнуть
Единичным называется столбец таблицы Жордана – Гаусса, который состоит из
единиц
!одной единицы и остальных 0
двух единиц и нулей
нулей
Переменная называется базисной, если в таблице Жордана – Гаусса столбец коэффициентов перед ней является
нулевым
отрицательным
!единичным
положительным
Если в таблице Жордана – Гаусса имеются две пропорциональные строки, то
одну можно вычесть из другой
их нужно сложить
их нужно перемножить
!одну из них нужно вычеркнуть
Переменная называется свободной, если в таблице Жордана – Гаусса
столбец коэффициентов при ней нулевой
!она не входит в столбец – базис
столбец коэффициентов при ней состоит из единиц
она входит в столбец – базис
Система m линейных уравнений с n неизвестными называется однородной, если свободные члены
!равны 0
положительны
отрицательны
принимают любые значения
Матрица коэффициентов при неизвестных системы m линейных уравнений с n неизвестными является
квадратной
диагональной
!прямоугольной
матрицей столбцом
Число частных решений равно
числу базисных решений
числу опорных решений
числу допустимых решений
!бесчисленному множеству решений
Переход от одного базисного решения к другому осуществляется путем
!проведения еще одной итерации метода Жордана – Гаусса
выбора разрешающей строки
выбора разрешающего столбца
проведения симплексных преобразований
Элементы вводимой строки в таблице Жордана – Гаусса находятся
умножением элементов разрешающей строки предыдущей таблицы на (-1)
делением элементов разрешающей строки предыдущей таблицы на (-1)
!делением элементов разрешающей строки предыдущей таблицы на разрешающей элемент
умножением элементов разрешающей строки предыдущей таблицы на разрешающий элемент
Число базисных решений произвольной системы m линейных уравнений с n неизвестными определяется
!формулой
числом уравнений
числом неизвестных
размерностью матрицы системы
Решение системы m линейных уравнений с n неизвестными, в котором базисные неизвестные линейно выражаются через свободные, называется
частным
допустимым
!общим
единственным
Систему можно решить матричным способом, если
число уравнений не равно числу неизвестных
!число уравнений равно числу неизвестных
число уравнений меньше числа неизвестных
число уравнений больше числа неизвестных
Решение, полученное из общего решения, если свободным неизвестным придать произвольные значения, называется
допустимым
опорным
!частным
единственным
Значение базисных переменных в таблице Жордана – Гаусса находится в
вводимой строке
!столбце
контрольном столбце
в разрешающей строке
В контрольный столбец 1-й таблицы Жордана – Гаусса записывается
сумма элементов по каждой строке, включая свободные члены
!сумма коэффициентов при неизвестных по каждой строке
разность коэффициентов при неизвестных и
произведение коэффициентов при неизвестных по каждой строке
Матрица коэффициентов при неизвестных при решении системы n линейных уравнений с n неизвестными матричным способом является
прямоугольной
!невырожденной
диагональной
вырожденной
При решении системы m линейных уравнений с n неизвестными методом Жордана – Гаусса контроль вычислений в таблицах Гаусса, начиная со 2 –ой, проводится путем
сравнения элементов столбца с элементами контрольного столбца
сравнения сумм коэффициентов при неизвестных с элементами контрольного столбца
нахождение разности элементов столбца и контрольного столбца
!сравнения суммы элементов по каждой строке, включая свободные члены, с элементами контрольного столбца
В столбце таблицы Жордана – Гаусса находятся значения неизвестных
свободных
искусственных
!базисных
отрицательных
Решение системы линейных уравнений с n неизвестными находится с применением обратной матрицы, если число уравнений равно
!n
m
n+m
n-m
Решение, матричного уравнения находится по формуле , если оно имеет вид
!
Решение, полученное из общего решения, если свободным неизвестным придать нулевые значения называется
частным
единственным
опорным
!базисным
Если в таблице Жордана – Гаусса все элементы какой – либо строки, кроме свободного члена, равны нулю, то система m линейных уравнений с n неизвестными
имеет единственное решение
!не имеет решений
имеет бесчисленное множество решений
имеет m решений
Если в системе m линейных уравнений с n неизвестными r – число базисных неизвестных и при этом , то система имеет
единственное решение
r решений
m решений
!бесчисленное множество решений
Если при решении системы m линейных уравнений c n неизвестными в разрешающей строке таблицы Жордана – Гаусса находится нуль, то столбец, содержащий этот нуль
!переносится в следующую таблицу без изменения
рассчитывается по правилу прямоугольника
становится единичным
становится нулевым
Если при решении системы m линейных уравнений c n неизвестными в разрешающем столбце таблицы Жордана – Гаусса имеется нуль, то строка, содержащая этот нуль
в следующей таблице состоит из нулей
!переносится в следующую таблицу без изменения
рассчитывается по правилу прямоугольника
в следующую таблицу переносится с обратными знаками
Если в базисном решении системы линейных уравнений , − базисные переменные, то равно
35
3
!30
20
Если в базисном решении системы линейных уравнений , − базисные переменные, то равно
!16
20
2
4
Если в системе m линейных уравнений с n неизвестными , то система называется
переопределенной
однородной
несовместной
!неопределенной
Если в системе m линейных уравнений с n неизвестными , то система называется
!переопределенной
несовместной
однородной
неопределенной
В системе m линейных уравнений с n неизвестными число базисных решений равно
только m
только n
n–m
!
Если в базисном решении системы линейных уравнений , − базисные переменные, то равно
8
1
!6
0
Если в базисном решении системы линейных уравнений , − базисные переменные, то равно
!6
8
0
2
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 2 из 7Следующая ⇒ Общим решением системы m линейных уравнений с n неизвестными называется +—решение, в котором базисные неизвестные линейно выражаются через свободные неизвестные
Частным решением системы m линейных уравнений с n неизвестными называется +—решение, полученное из общего решения, если свободным неизвестным придать произвольные значения
При отыскании общего решения системы m линейных уравнений с n неизвестными методом Жордана – Гаусса в качестве разрешающего элемента выбирается +—любой отличный от нуля элемент таблицы, кроме элементов столбца свободных членов и контрольного столбца
Система m линейных уравнений с n неизвестными не имеет решений, если на некоторой итерации +—все элементы какой – либо строки таблицы Жордана – Гаусса, кроме свободного члена, равны нулю
Базисным решением системы m линейных уравнений с n неизвестными называется +—решение, полученное из общего решения системы, в котором свободные неизвестные равны 0
Если r – число базисных неизвестных, а n – общее число неизвестных в произвольной системе m линейных уравнений, то система имеет бесконечное множество решений при +—
Если дано матричное уравнение , то его решение определяется по формуле +— Если в таблице Жордана – Гаусса – разрешающий элемент, то элемент находится по формуле (правило прямоугольника) +— Итерацией в методе Жордана – Гаусса называется +—расчет элементов одной таблицы Жордана – Гаусса
Метод Жордана – Гаусса это +—последовательное исключение неизвестных
Если в таблице Жордана – Гаусса имеются две одинаковые строки, то +—одну из них можно вычеркнуть
Единичным называется столбец таблицы Жордана – Гаусса, который состоит из +—одной единицы и остальных 0
Переменная называется базисной, если в таблице Жордана – Гаусса столбец коэффициентов перед ней является +—единичным
Если в таблице Жордана – Гаусса имеются две пропорциональные строки, то +—одну из них нужно вычеркнуть
Переменная называется свободной, если в таблице Жордана – Гаусса +—она не входит в столбец в базис
Система m линейных уравнений с n неизвестными называется однородной, если свободные члены +—равны 0
Матрица коэффициентов при неизвестных системы m линейных уравнений с n неизвестными является +—прямоугольной
Число частных решений равно +—бесчисленному множеству решений
Переход от одного базисного решения к другому осуществляется путем +—проведения еще одной итерации метода Жордана – Гаусса
Элементы вводимой строки в таблице Жордана – Гаусса находятся +—делением элементов разрешающей строки предыдущей таблицы на разрешающей элемент
Число базисных решений произвольной системы m линейных уравнений с n неизвестными определяется +—формулой
Решение системы m линейных уравнений с n неизвестными, в котором базисные неизвестные линейно выражаются через свободные, называется +—общим
Систему можно решить матричным способом, если +—число уравнений равно числу неизвестных
Решение, полученное из общего решения, если свободным неизвестным придать произвольные значения, называется +—частным
Значение базисных переменных в таблице Жордана – Гаусса находится в +—столбце
В контрольный столбец 1-й таблицы Жордана – Гаусса записывается +—сумма элементов по каждой строке, включая свободные члены
Матрица коэффициентов при неизвестных при решении системы n линейных уравнений с n неизвестными матричным способом является +—невырожденной
При решении системы m линейных уравнений с n неизвестными методом Жордана – Гаусса контроль вычислений в таблицах Гаусса, начиная со 2 –ой, проводится путем +—сравнения суммы элементов по каждой строке, включая свободные члены, с элементами контрольного столбца
В столбце таблицы Жордана – Гаусса находятся значения неизвестных +—базисных
Решение системы линейных уравнений с n неизвестными находится с применением обратной матрицы, если число уравнений равно +—n
Решение, матричного уравнения находится по формуле , если оно имеет вид +— Решение, полученное из общего решения, если свободным неизвестным придать нулевые значения называется +—базисным
Если в таблице Жордана – Гаусса все элементы какой – либо строки, кроме свободного члена, равны нулю, то система m линейных уравнений с n неизвестными +—не имеет решений
Если в системе m линейных уравнений с n неизвестными – число базисных неизвестных и при этом , то система имеет +—бесчисленное множество решений
Если при решении системы m линейных уравнений c n неизвестными в разрешающей строке таблицы Жордана – Гаусса находится нуль, то столбец, содержащий этот нуль +—переносится в следующую таблицу без изменения
Если в базисном решении системы линейных уравнений , − базисные переменные, то равно +—30 Если в базисном решении системы линейных уравнений , − базисные переменные, то равно +—16
Если в системе m линейных уравнений с n неизвестными , то система называется +—неопределенной
Если в системе m линейных уравнений с n неизвестными , то система называется +—переопределенной
В системе m линейных уравнений с n неизвестными число базисных решений равно +— Если в базисном решении системы линейных уравнений , − базисные переменные, то равно +—6 Если в базисном решении системы линейных уравнений , − базисные переменные, то равно +—6 Если в базисном решении системы линейных уравнений , − базисные переменные, то равно +—0 Если в базисном решении системы линейных уравнений , − базисные переменные, то равно +—12 Если в базисном решении системы линейных уравнений , − базисные переменные, то равно +—12 Если в базисном решении системы линейных уравнений , − базисные переменные, то равно +—-4 Если в базисном решении системы линейных уравнений , − базисные переменные, то равно +—2
Если разрешающим элементом в преобразованиях однократного замещения является , то новые элементы в таблице Гаусса определяются по формуле +— В системе линейных уравнений базисное решение имеет вид +—(0,5,0,3)
⇐ Предыдущая1234567Следующая ⇒ Читайте также: Психологические особенности спортивного соревнования Приготовление дезинфицирующих растворов различной концентрации Занятость населения и рынок труда Социальный статус семьи и её типология |
|
Последнее изменение этой страницы: 2016-08-25; просмотров: 1216; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
линейных уравнений — ГАУСС ДЖОРДАН. Как использовать Python для решения линейных… | от J3 | Jungletronics
Как использовать Python для решения линейной системы #PySeries#Episode 32
!
Числовая линейная алгебра , иногда называемая прикладной линейной алгеброй , представляет собой исследование того, как матричные операции могут использоваться для создания компьютерных алгоритмов, которые эффективно и точно дают приблизительные ответы на вопросы непрерывной математики.
Вот задача для решения:
Инженер-технолог электронной промышленности анализирует производственный процесс, в котором он учитывает время сборки (t), количество сотрудников (x) и количество компонентов (n), используемых в конечный продукт, и пришли к этой системе уравнений.Системное уравнение для решения этим методом: GAUSS JORDAN
Инженер хочет достичь идеальных условий для достижения всех целей с оценочной точностью 0,01 (одна сотая каждой переменной).
КАК РЕШИТЬ ЭТУ ПРОБЛЕМУ С ИСПОЛЬЗОВАНИЕМ GAUSS JORDAN (настройка разрешения матрицы)?
Первая задача состоит в том, чтобы преобразовать систему в матрицы:
(уравнение_0) КОЭФФИЦИЕНТЫ] * [ПЕРЕМНАЯ] = [ЗАДАЧА] [A] * [X] = [B]
Решение может быть получено с помощью матрицы ИДЕНТИЧНОСТИ используя это уравнение:
(equation_1) (IDENTITY) * (VAR) = (SOLVE) [I] * [X] = [S]
Как мы можем работать с матрицей IDENTITY?
Мы знаем, что:
Сама матрица, умноженная на обратную, дает МАТРИЦУ ИДЕНТИЧНОСТИ, верно?
(уравнение_2) [A] * inv[A] = [I]
Итак, В НАШЕЙ ЗАДАЧЕ (уравнение_0):
[A] * [X] = [B]
РЕШЕНИЕ БУДЕТ (уравнение_1 ):
[I] * [X] = [S]
Подставляя I в уравнение (1 и 2):
([A] * inv[A]) * [X] = [S]
Перестановка:
inv[A] * ([A] * [X]) = [S]
Но из уравнения (1) имеем [A] * [X] = [B] :
Отсюда следует:
(s_equation) inv[A] * [B] = [S]
Итак, решение будет дано:
умножение обратная матрица [A] с матрицей [B] \o/
или:
[S] = inv[A] * [B]
ЭТО ОБОСНОВАНИЕ ДОЛЖНО ПРИМЕНЯТЬСЯ ЗДЕСЬ!
ДАВАЙТЕ ПРИГОТОВИМСЯ С ПИТОНОМ!!!
Нажмите, чтобы перейти к решению для ноутбука colab ниже 🙂
01#Step — инициализация метода Gauss-jordan (импорт библиотек)
из матрицы импорта numpy, linalg
import numpy as np
02#Step — создание матриц с Массивы Numpy (и печать используемой логики:)
print("Для 'A * X = B' нам нужно написать как 'I * X = S'") Для 'A * X = B' нам нужно записать как «I * X = S»
matrix_A
matrix_A = np.array([[2.0, 1.0, 1.0],[0.30, 2.0, 0.25],[1.0, 1.0, 2.0]])
Печать matrix_A
print('matrix_A')
print(matrix_A) matrix_A [[2. 1. 1. ]
[0,3 2. 0,25]
[1. 1. 2. ]] matrix_B
matrix_B = np.array([[39.0],[13.0],[45.0]])
Печать matrix_B
print('matrix_B')
print(matrix_07)
print(matrix_07) matrix_B
[[39.]
[13.]
[45.]] 03#Шаг — Создание обратной матрицы A:
print("Зная, что 'A * A_inv = I', решение сводится к 'S = A_inv * B'") # создание обратной матрицы matrix_A
matrix_A_inv = linalg.inv(matrix_A)
print(matrix_A_inv) [[ 0.68807339 -0.18348624 -0.32110092]
[-0.06422018 0.55045872 -0.03669725]
[-0.31192661 -0.18348624 0.67889908]]
04#Step — РЕШЕНИЕ ( s_equation ):
matrix_S = np.matmul(matrix_A_inv, matrix_B)900:590 Вот и все
print('matrix_S')
print(matrix_S) matrix_S
[[10.]
[ 3.]
[16.]]
print("Все! Спасибо за прочтение!") Готово! Спасибо за прочтение поста! 👉 Блокнот Colab : ссылка
Основано на: Uninter Course Computer Engineer Graduation — Date Aug/2021
Благодарность:
Fernanda Fonseca Degree — докторант в области образования, магистр физики и математики и философия — UNINTER — Бразилия — PR
32#PySeries#Episode — Линейные уравнения — GAUSS JORDAN — Как использовать Python для решения линейной системы (этот)
33#PySeries#Episode — Линейные уравнения — ПРАВИЛО КРЕМЕРА — Как использовать Python для решения линейной системы
34#PySeries#Episode — Линейные уравнения — Линейные уравнения — ГАУСС ЗАЙДЕЛЬ — Как использовать Python для решения линейной системы
Рис. 1. Секрет метода Гаусса-Джордана: обратная матрица! (изображение отсюда)🧮 Метод Гаусса-Джордана для решения систем линейных уравнений — документация
Карл Фридрих Гаусс был математиком и физиком, родившимся в Германии в 1777 году. и разработал такое огромное количество работ в стольких различных областях, что любой
студент, изучающий естественные науки, найдет его имя много раз в разных предметах, вплоть до
точка веры в то, что Гаусс повсюду.
и разработал такое огромное количество работ в стольких различных областях, что любой
студент, изучающий естественные науки, найдет его имя много раз в разных предметах, вплоть до
точка веры в то, что Гаусс повсюду.
Среди всех вкладов Гаусса в математику мы находим метод решения систем линейных уравнений, которые широко используются сейчас, когда компьютеры могут быть запрограммированным на выполнение всей тяжелой работы. Этот метод имеет то преимущество, что легко программируется, поскольку использует последовательность повторяющихся операций после уравнения сохраняются в памяти компьютера в виде массива термов, подобного матрица, содержащая коэффициенты каждого уравнения в одной строке.
Гаусс решил эту проблему, используя некоторые свойства систем Линейные уравнения, чтобы внести изменения в матрицу, изменив коэффициенты на получение эквивалентных уравнений, которые не изменят Систему. Эти изменения могут быть:
A) Поменяйте местами два ряда, поместив каждый ряд на место другого
B) Умножить каждое слагаемое в одной из строк (уравнений) на одно и то же число отличное от нуля.

C) Добавьте или вычтите каждое слагаемое в одной из строк (уравнений) из соответствующий термин из другой строки, в результате чего получается новая строка, которая также принадлежит к той же системе уравнений.
Вы можете выполнить любую из этих операций, и система уравнений останется прежней. решения будут одинаковыми. Гаусс придумал способ использовать это для преобразования исходную группу уравнений в одну, которую будет легче решить.
Метод Гаусса
Метод очень оригинальный и очень простой. Давайте покажем, как он это сделал это с одним примером; система из 4 уравнений с 4 неизвестными (w, x, y, z):
В матрице столько столбцов, сколько уравнений (и неизвестных), сколько в системе, плюс один столбец из-за постоянных членов, поэтому в этом случае матрица имеет 5 столбцы х 4 ряда.
Гаусс считал, что хорошим способом решения этих систем является «избавление» от некоторых
члены, сделав их равными нулю, пока он не смог получить уравнение только с нулями
за исключением одного неизвестного и постоянного члена, что позволяет очень легко найти тогда
неизвестный. Как это сделать?
Как это сделать?
Мы должны помнить операции (A, B, C), которые мы можем выполнять, не меняя система. Теперь давайте сосредоточимся на втором уравнении:
ш-4х-2у+2г=-5
Первая неизвестная (w) умножается на коэффициент 1, не пишется. Это почему первый член во второй строке матрицы равен 1,
Как я могу избавиться от этого неизвестного, внеся изменения во второе уравнение? Как могу ли я превратить эту 1 в ноль, чтобы w просто исчезла из уравнения?
Не самая очевидная идея – умножать все уравнение на ноль. Если мы снова прочитаем
операцию B, как объяснялось ранее, мы находим там очень ясно сказано, что
мы не можем умножать на ноль. Другой способ – добавить -1 к первому члену.
Третья операция, о которой мы говорили ранее, C, утверждает, что мы можем сложить два
уравнения, принадлежащие системе, почленно, и полученное уравнение
тоже принадлежит системе. Итак, если бы в системе было еще одно уравнение
системы с -1 в качестве первого коэффициента, мы бы только добавили это уравнение, член на
срок, ко второму и первый член стал бы просто нулем, он пошел бы
прочь. Но, конечно, нет этого желаемого уравнения с -1, умножающим w.
Жизнь никогда не бывает такой легкой.
Но, конечно, нет этого желаемого уравнения с -1, умножающим w.
Жизнь никогда не бывает такой легкой.
Какое решение нашел Гаусс? Ну, он думал умножить любой другой уравнение на число, которое превратит его первый коэффициент в -1. Если мы умножьте каждый член линейного уравнения на одно и то же число, в результате уравнение эквивалентно исходному, как указано на Б.
Если мы сделаем это с первым уравнением (3w – 2x + 3y + z = 12), коэффициент умножая неизвестное w, первое, равно 3, поэтому в этом случае нам понадобится умножить все первое уравнение член за членом на число, которое 3 в -1. Это число будет равно -1/3, так что операция будет выглядеть как это:
Где искомый -1 является первым коэффициентом. Теперь мы можем добавить это уравнение к второе уравнение системы, чтобы превратить его первый коэффициент в нуль.
Мы видим, что первый коэффициент во втором уравнении теперь равен нулю, поэтому теперь на один срок меньше.
Система уравнений и матрица коэффициентов теперь будут выглядеть так:
Теперь мы на шаг ближе к решению системы, так как оно у нас есть
уравнение с тремя неизвестными вместо четырех. Можем ли мы продолжать делать то же самое
с большим количеством уравнений? Конечно можем, и Гаусс сделал именно это для третьего
и четвертое уравнения. Его метод избавляется от всех первых членов, кроме
случай первого уравнения; вам всегда понадобится хотя бы одно уравнение с
первый член, чтобы можно было вычислить значение w.
Можем ли мы продолжать делать то же самое
с большим количеством уравнений? Конечно можем, и Гаусс сделал именно это для третьего
и четвертое уравнения. Его метод избавляется от всех первых членов, кроме
случай первого уравнения; вам всегда понадобится хотя бы одно уравнение с
первый член, чтобы можно было вычислить значение w.
Повторение шагов вниз
Итак, проделав аналогичные операции над третьим и четвертым уравнениями, получим:
Теперь система, если игнорировать первое уравнение, имеет только три неизвестных (x, y, z) и три уравнения (второе, третье и четвертое уравнения).
Как только мы поймем, что мы здесь сделали, мы сможем понять весь метод Гаусса.
придумано так умно, потому что если мы забудем о первом уравнении и повторим
предыдущий процесс, оставив теперь второе уравнение нетронутым, и мы модифицируем
третье и четвертое уравнения так, что их первый член (коэффициент при
x) равно нулю, мы получим меньшую систему уравнений только с двумя неизвестными и
два уравнения.
Метод Гаусса продолжает уменьшать размер системы уравнений до меньших системы, которые легче решить. Вот так выглядит система уравнений как только это сводится всего к двум уравнениям:
Таким образом, мы можем продолжать уменьшать размер системы, пока не получим только один уравнение и одно неизвестное, которое решается напрямую:
Добиться результатов и переломить ситуацию, чтобы двигаться вверх
Таким образом, из четвертого уравнения мы можем получить непосредственно значение z, наше первое результат:
До этого момента метод работает сверху вниз, получая наш первый результат из последнего уравнения, но теперь поток меняется на противоположный, и мы начинаем двигаться вверх. Имея значение z, мы можем использовать его в третьем уравнении (z=4, тогда 3z=12) получение:
-10 лет + 12 = -18
Откуда мы можем получить непосредственно следующий результат, значение для y:
г = (-18-12) / (-10) = 3
Затем, имея z=4 и y=3, мы можем продолжить движение вверх и использовать эти значения в
второе уравнение, чтобы получить следующее неизвестное, x, и, наконец, мы используем эти
три результата (x, y, z) в первом уравнении, чтобы получить последний результат,
неизвестный ж.
Следуя этой процедуре, мы подсчитали все результаты:
ш=1 х=2 у=3 з=4
И этот метод можно использовать для любой системы линейных уравнений, независимо от ее размера. сколько же у него уравнений, спасибо Карлу Фридриху Гауссу.
Некоторые детали, которые следует учитывать при программировании этого метода
Когда мы работали над преобразованием первого столбца в нули, мы оставили первый
уравнение нетронуто, оно было использовано для изменения других уравнений, сосредоточив внимание на
первый член первого уравнения; этот термин, который мы используем, известен как «стержень». Один раз
мы изменили все коэффициенты ниже этого первого члена на нули, мы переместились вниз
и использовал второе уравнение, оставив его нетронутым, чтобы изменить третье и четвертое
уравнение. Мы использовали первый ненулевой член, чтобы превратить в нули все
коэффициенты ниже (второй столбец), так что в этом случае этот второй член является
вращаться. Когда мы повторяем процедуру, используя третье уравнение, третий член равен
стержень и так далее.
Матрица, которую мы показывали в правой части системы, представляет собой представление о том, как коэффициенты могут быть сохранены на компьютере, чтобы сделать все эти операции в цифровом виде, используя программируемую версию этого метода, алгоритм. Есть некоторые детали, которые следует учитывать при разработке этого алгоритма.
Элемент, который мы используем в качестве точки опоры, не может быть нулем. Чтобы этого не произошло,
обычная процедура использует уравнение, которое имеет большее число, поскольку оно
первый коэффициент как основное уравнение. Мы должны помнить, что мы можем поменять местами два
уравнения из системы без изменения системы, поэтому перед использованием первого
уравнение, чтобы изменить другие, мы ищем уравнение с большей первой
коэффициент и поменять местами его на первую строку, далее продолжаем. То же самое происходит, когда
мы будем использовать второе уравнение, мы сравниваем его второй коэффициент (поскольку
первая единица была заменена нулем) с соответствующими коэффициентами на
третье и четвертое уравнения, а затем поменять местами то с наибольшим
коэффициент во вторую строку.
Такую же замену следует выполнять до тех пор, пока весь нижний левый треугольник не будет заполнен нулями, так что последнее уравнение готово к прямому решению. Это способ гарантировать, что каждый стержень не будет нулем.
Улучшение Джордана
Вильгельм Йордан был немецким геодезистом, родившимся в 1842 году, а также писателем. с интересом к математике и геометрии. Работал по методу, разработанному Гауссом и улучшил его, пока пытался применить к некоторым геодезическим данным. Позже он опубликовал свою методику в своей книге «Учебник геодезии».
Чтобы понять работу Джордана, мы должны помнить, что метод Гаусса превращает
в нули весь нижний левый треугольник матрицы. У Джордана была идея сохранить
используя ту же процедуру для верхнего правого треугольника, повернув все эти
коэффициенты тоже в нули, оставив только члены по диагонали, т.е.
повороты, так что каждое уравнение будет иметь только одно неизвестное, а затем оперируя
эти члены, чтобы они были заменены единицами (1) и каждое уравнение
приносят сразу один результат. Мы можем лучше понять все это, взглянув на
системы после того, как верхний правый треугольник был заменен нулями, а
шарниры по диагонали превратились в единицы.
Мы можем лучше понять все это, взглянув на
системы после того, как верхний правый треугольник был заменен нулями, а
шарниры по диагонали превратились в единицы.
В системе уравнения мы оставили обнуленные члены, чтобы сделать очевидным соответствие уравнений матрице, а обычный способ записи эти уравнения были бы проще, не записывая нулевые члены и не записывая число 1 при умножении неизвестных, например:
Глядя на упрощенные уравнения, становится ясно, почему Джордан хотел добавить эти шаги к методу Гаусса. Каждое уравнение является просто результатом для каждый неизвестный. Очень элегантный.
Хотя эти методы были разработаны задолго до компьютеров, очевидно,
авторы хотели разработать алгоритм с простыми и повторяющимися шагами, который
будет работать даже для больших систем уравнений; идеально подходит для компьютеров,
итеративный процесс может быть запрограммирован и выполнен в цифровом виде очень точным образом
просто вводя матрицу коэффициентов. Собственно говоря, вот как
компьютеры решают системы линейных уравнений в настоящее время, иногда запуская
Метод Гаусса, а иногда и вариация Гаусса-Жордана.
Собственно говоря, вот как
компьютеры решают системы линейных уравнений в настоящее время, иногда запуская
Метод Гаусса, а иногда и вариация Гаусса-Жордана.
Мы можем только восхищаться такими умами, которые, посылая свои интеллект и мудрость сквозь века могут помочь нам решить наши проблемы Cегодня.
Об авторе
Хорхе Араика Графический дизайнер с техническим образованием, профессионал старой школы с некоторыми знаниями в области инженерии и программирования, а также сторонник критических и рациональных мышление как способ распространения научного отношения к знаниям. Свобода это его другая страсть, и он будет отстаивать ее при каждом удобном случае.
Решите систему линейных уравнений, используя метод исключения Гаусса-Жордана
Решите систему линейных уравнений, используя метод исключения Гаусса-Жордана. (Если решения нет, введите NO SOLUTION. Если решений бесконечно много, выразите ответ через параметры t и/или s.)
х+2у+г=-4
−2x−3y−z=2
4x+8y+4z=−16
Спросить эксперта 1 Посмотри ответы
Вы все еще можете обратиться за помощью к специалисту
youtube.com/embed/4PCktDZJH8E” title=”YouTube video player” allow=”accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture” allowfullscreen=””>Ответ эксперта
Мы получили систему уравнений
x + 2y + z = −4
−2x − 3y − z = 24
x + 8y + 4z = −16
Расширенная матрица данной системы равна
[121|−4− 2−3−1|2484|−16]
Опорный элемент в первой строке и первом столбце равен 1.
Теперь применяем следующие преобразования строк к расширенной матрице.
R2→R2+2R1
R3→R3−4R1
[121|−4011|−6000|0]
Поворотный элемент во второй строке и втором столбце равен 1.
Применить следующее преобразование к предыдущей матрице.
R1→R1−2R2
[10−1|8011|−6000|0] Переписав систему уравнений из приведенной строки матрицы,
x − z=8y + z = −6 Количество уравнений = 2
Количество уравнений переменных = 3
Количество переменных больше, чем количество уравнений, поэтому данная система имеет бесконечно много решений.
Количество свободных переменных = Количество переменных – Количество уравнений = 3 – 2 = 1
Подставьте t вместо z.
⇒x − t=8 и y + t = −6
⇒x = t + 8 и y = −t −6
Следовательно, x = t + 8, y = −t − 6 и z = t.
Ответ: Данная система имеет бесконечно много решений, множество решений x = t + 8, y = −t − 6, z = t.
Вам может быть интересно
Предположим, что строка A эквивалентна строке B. Найдите основания для Nul A и Col A.
Для приведенной ниже матрицы A найдите ненулевой вектор в Nul A и ненулевой вектор в Col A.
A=[235−9−8−9−11214−3−1727]
Найти ненулевой вектор в Nul A.
А=[−3201]
Найдите явное описание Nul A, перечислив векторы, охватывающие нулевое пространство.
А=[15−4−3101−21000000]
Две трехмерные точки. A[x1,y1,z1] и B[x2,y2,z2]. Нужно найти матрицу преобразования, которая при умножении на A даст мне B, а при умножении на B даст мне A. Преобразование должно быть отражением от плоскости, перпендикулярной середине сегмента AB и проходящей через середину сегмента. АБ.
АБ.
Решите следующую систему уравнений, используя обратную матрицу коэффициентов A.
(AX=B), х+5у=-10, -2х+7у=-31
Пусть T:R3→R3 — линейное преобразование такое, что
T[111]=[−25−2],T[110]=[414],T[100]=[1−11]
а) Найдите такую матрицу A, что T(x)=Ax для каждого x ∈R3
b) Найдите линейно независимый набор векторов в R3, который охватывает диапазон T
Найти матрицу линейного преобразования по базе собственных векторов
Преобразование R2->R2 представлено матрицей (1210).
Новые вопросы
Предположим, V — n-мерное линейное векторное пространство. {s1,s2,…,sn} и {e1,e2,…,en} — два набора ортонормированных базисов с матрицей преобразования базиса U, для которых ei=∑jUijsj.
Теперь рассмотрим n2 размерное векторное пространство V⨂V (произведение Кронекера) с эквивалентными базисными наборами {s1s1,s1s2,…,snsn} и {e1e1,e1e2,…,enen}. Теперь можем ли мы найти матрицу преобразования базиса для этого в терминах U?
Если матрица линейного преобразования :RN→RN относительно некоторого базиса симметрична, что она говорит о преобразовании? Есть ли способ геометрически интерпретировать преобразование красивым/простым способом?
Преобразование 10 метров в футы. Округлите ответ до десятых
Округлите ответ до десятых
Приведите стандартную матрицу линейного преобразования, которое сначала переводит (x, y, z) в (y, y, z) и поворачивает этот вектор на 90 градусов против часовой стрелки вокруг начала координат в плоскости x = y. Найдите стандартную матрицу линейного преобразования.
Дана матрица Y∈Rm×n. Найдите матрицу преобразования Θ∈Rn×p такую, что
1mΘTYTYΘ=Ip×p,
, где 𝐼𝑝×𝑝 — единичная матрица.
Моя попытка: 1mYΘ является ортогональной матрицей, и я попытался найти Θ, удовлетворяющую ей, но это не работает.
Вектор, u:=[u1,…,un]T. Я пытаюсь найти невырожденную матрицу преобразования координат Q∈Rn×n, удовлетворяющую:
[0⋮0||u||]=Qu.
Каждая матрица представляет собой линейное преобразование, но в зависимости от характеристик матрицы линейное преобразование, которое она представляет, может быть ограничено определенным типом. Например, ортогональная матрица представляет поворот (и, возможно, отражение). Есть ли что-то подобное в треугольных матрицах? Представляют ли они какой-либо конкретный тип преобразования?
Найдите матрицу T следующего линейного преобразования
T:R2(x)−>R2(x), определяемого формулой T(ax2+bx+c)=2ax+b
Без построения найти координаты точек пересечения графика функции y = -0,6x + 3 с осями координат.

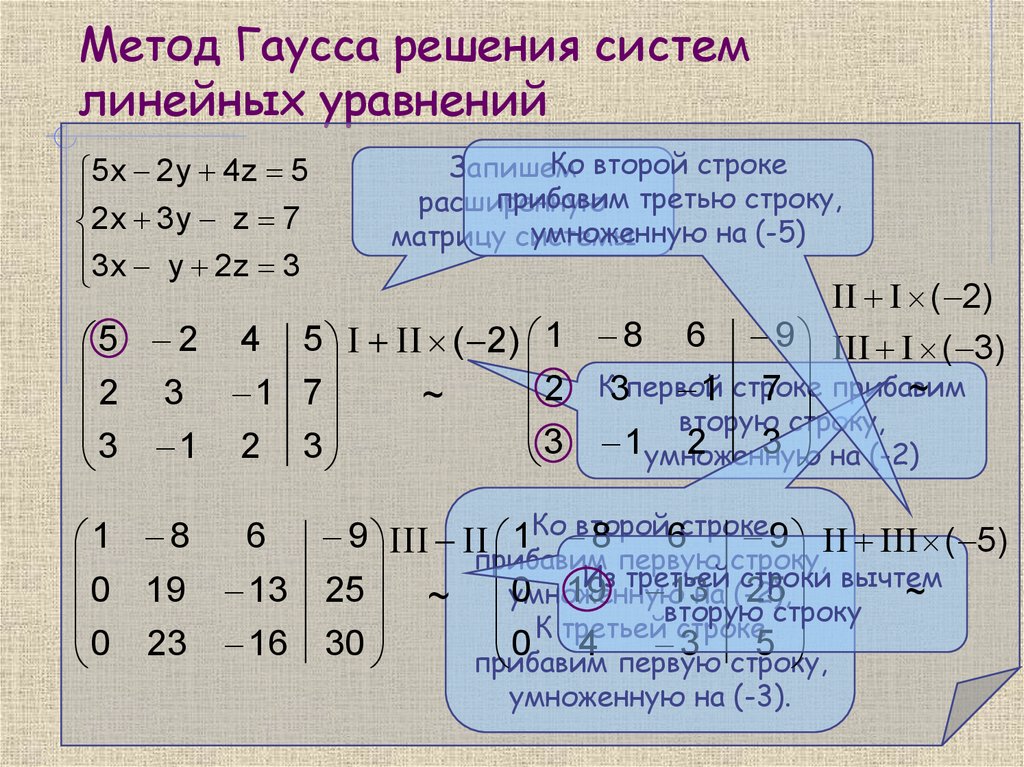
 Решение систем линейных уравнений методом Жордана – Гаусса
Решение систем линейных уравнений методом Жордана – Гаусса Все правила по сольфеджио
Все правила по сольфеджио
 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь – 161.97.168.212 (0.013 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь – 161.97.168.212 (0.013 с.)
 array([[2.0, 1.0, 1.0],[0.30, 2.0, 0.25],[1.0, 1.0, 2.0]])
array([[2.0, 1.0, 1.0],[0.30, 2.0, 0.25],[1.0, 1.0, 2.0]])  ]
] 