Научная работа по математике на тему “Приёмы быстрого счёта”
Содержание
Введение………………………………………………………………………………………………………..4
Глава 1. Использование устного счёта……………………………………………………………6
1.1 «Устный счет» на картине Н. П. Богданова-Бельского ………………………..6
1.2 Приёмы быстрых устных вычислений в 5,6 классах…………………………………..9
1.3 Приёмы быстрых устных вычислений в 7 классе……………………………………..12
1.4 Приёмы быстрых устных вычислений в 8 классе……………………………13
Глава 2. Исследовательская часть………………………………….……….……15
2.1 Выработка умений решать примеры, используя упрощенные способы вычислений…………………………………………………………………………15
Выводы………………………………………………………………………………19
Заключение………… ………………………………………………………………………………………..20
………………………………………………………………………………………..20
Список литературы……………………………………………………………………………………….21
Приложение
« Сборник упражнений по устному счёту»
Пифагор Самосский
Введение
Вычислять
быстро, подчас на ходу – это требование времени. Числа окружают нас повсюду, а
выполнение арифметических действий над ними приводит к результату, на основании
которого мы принимаем то или иное решение. Понятно, что без вычислений не
обойтись, как в повседневной жизни, так и во время учёбы в школе.
Числа окружают нас повсюду, а
выполнение арифметических действий над ними приводит к результату, на основании
которого мы принимаем то или иное решение. Понятно, что без вычислений не
обойтись, как в повседневной жизни, так и во время учёбы в школе.
А какую огромную роль в школьном курсе обучения имеют вычислительные навыки. Ни один пример, ни одну задачу по математике, физике, химии, черчению и так далее нельзя решить, не обладая навыками элементарных способов вычисления. Не секрет, что у учащихся с прочными вычислительными навыками гораздо меньше проблем с математикой.
Повышение вычислительной культуры способствует полноценно усваивать предметы физико-математического цикла. Вычислительные навыки по-прежнему остаются актуальными, в особенности, когда под рукой нет калькулятора, так как приходится очень много времени тратить на вычисления в «столбик».
Цель работы – повысить вычислительную
культуру учащихся, научить использовать приемы быстрого счета при выполнении различных
математических тестов, при подготовке итоговых аттестаций в 9 и 11 классах.
Задачи работы:
1. Рассмотреть приемы быстрого счета подобранных соответственно для 6, 7, 8 классов;
2. Изучить предложенные способы быстрого счёта и применить их при решении различных видов вычислительных примеров;
3. Провести анкетирование в 6,7,8 классов на применение навыков устного счета;
4. Выявить основные ошибки, возникающие при вычислениях
Методы исследования: Изучение литературы, анкетирование среди учащихся, синтез и анализ данных полученных в ходе работы.
Предмет исследования – различные способы устного счета на уроках математики соответствующие каждому классу относительно школьной программы.
Объект исследования – учащиеся 6-8 классов КГУ «Гимназия № 93»
Гипотеза: использование на уроках
математики знаний и умений быстрых способов вычисления способствует повышению
вычислительной культуры учащихся 6-8 классов: умножения двузначного на
двузначное, умножение на 11, применение формул сокращенного умножения,
возведения в квадрат и т. д.
д.
Глава 1. Использование устного счёта
1.1 «Устный счёт» на картине Н.П. Богданова – Бельского.
Вычислительная
культура формируется у учащихся на всех этапах изучения курса математики, но
основа ее закладывается в первые 5-6 лет обучения. В этот период школьники
обучаются именно умению осознанно использовать законы математических действий
(сложение, вычитание, умножение, деление, возведение в степень). В последующие
годы, полученные умения и навыки совершенствуются и закрепляются в процессе
изучения математики, физики, химии и других предметов.
Счёт в уме (устные вычисления) является самым древним и простым способом вычислений. Устному счёту уделял большое внимание известный русский деятель в области просвещения доктор естественных наук, профессор ботаники Московского университета Сергей Александрович Рачинский (1832-1902). В 1872 г. он переехал из Москвы в своё имение, село Татево Смоленской губернии. Там организовал начальную школу и сам преподавал в ней, стремясь развить у крестьянских детей математические способности и привить им интерес к математике. Всем известна картина Н. П. Богданова-Бельского “Устный счёт”. На ней изображён С. А. Рачинский со своими учениками. Обратимся к картине. На доске записан пример для устного счёта:
Мальчик, конечно
же, догадался, что сумма квадратов первых трёх натуральных чисел равна сумме
квадратов следующих чисел, т.е. . Таким
образом, данное на картине числовое выражение равно 2. Под силу ли эта задача
нашим нынешним ученикам начальных классов? Скажем сразу: нет! Не под силу эта
задача и среднему звену современных учащихся.
В настоящее время среди учащихся бытует мнение, что вычислительная работа должна стать уделом компьютеров, а человек может отойти от этого рутинного занятия. При этом мы не замечаем, что всё более и более освобождая себя от вычислений, фактически освобождаем свой разум от умственного развития.
“Развитие навыков должно предшествовать развитию ума”. Это сказал Аристотель 25 веков назад. На мой взгляд, в этой цитате навыки рассматриваются как необходимое условие развитие ума, а их совершенствование как важная составляющая развития каждого из нас.
В школе
Рачинского, умели возводить в квадрат числа до 100 в уме. Не столбиком, а
именно в уме. Как они это делали? Казалось бы, процесс достаточно трудоемкий,
однако при ближайшем рассмотрении выясняется, что освоить возведение в квадрат
может любой, даже не слишком продвинутый в математике ученик. Ну, например,
сколько будет 96 в квадрате? Конечно, можно взять калькулятор, набрать нужные
кнопки и получить ответ. Можно взять листок бумаги и подсчитать это столбиком. А можно и в уме.
А можно и в уме.
Нужна технология, способная за короткое время дать правильный ответ, тем самым ускорить процесс формирования у учащихся вычислительных навыков.
Качество вычислительных умений определяется знанием правил и алгоритмов вычислений. Поэтому степень овладения вычислительными умениями зависит от четкости сформулированного правила и от понимания принципа его использования.
Как в письменных, так и в устных вычислениях используются разнообразные правила и приемы. Уровень овладения вычислительными навыками определяется систематичностью закрепления ранее усвоенных приемов вычислений и приобретением новых в связи с изучаемым материалом.
Вычисления активизируют память учащихся, внимание, стремление к рациональной организации деятельности, которые оказывают существенное влияние на развитие личности.
Вычислительные
умения и навыки можно считать сформированными только в том случае, если
учащиеся умеют с достаточной беглостью выполнять математические действия с
натуральными числами, десятичными и обыкновенными дробями, рациональными
числами, а также производить тождественные преобразования различных числовых
выражений и приближенные вычисления.
Хорошо развитые у учащихся навыки устного счёта – одно из условий их успешного обучения в старших классах.
1. 2
Приёмы быстрых устных вычислений в 5, 6 классах
2
Приёмы быстрых устных вычислений в 5, 6 классах
Для формирования у школьников сознательных прочных вычислительных навыков, используются различные приемы устного счёта.
В 5 и 6 – ом классах ученики должны уметь выполнять все арифметические действия с натуральными (многозначными) числами. Согласно школьной программе учащиеся могут выполнять основные действия с десятичными дробями, применять законы умножения к вычислению примеров, использовать основные признаки делимости, определять порядок действий при вычислении значения выражения, выполнять действия с положительными и отрицательными числами. Рассмотрим некоторые приёмы устного счёта в данный промежуток обучения учащихся.
1. Признаки деления. Признаки делимости — алгоритмы, позволяющие сравнительно быстро определить, является ли число кратным заранее заданному.
Признак делимости на 2
Число делится на 2 тогда и только тогда, когда его
последняя цифра делится на 2, то есть является чётной.
Признак делимости на 3
Число делится на 3 тогда и только тогда, когда
сумма его цифр делится на 3.
Признак делимости на 4
Число делится на 4 тогда и только тогда,
когда число из двух последних его цифр нули или делится на 4.
Признак делимости на 5
Число делится на 5 тогда и только тогда,
когда последняя цифра делится на 5 (то есть равна 0 или 5).
Признак делимости на 6
Число делится на 6 тогда и только тогда,
когда оно делится на 2 и на 3.
Признак делимости на 7
Число делится на 7 тогда и только тогда,
когда результат вычитания удвоенной последней цифры из этого числа без
последней цифры делится на 7.
Признак делимости на 8
Число делится на 8 тогда и только тогда, когда три его
последние цифры – нули или образуют число, которое делится на 8.
Признак делимости на 9
Число делится на 9 тогда и только тогда,
когда сумма его цифр делится на 9.
Признак делимости на 10
Число делится на 10 тогда и только тогда,
когда оно оканчивается на ноль.
Признак делимости на 11
Число делится на 11 тогда и только тогда,
когда сумма цифр с чередующимися знаками делится на 11
Признак делимости на 25
Число делится на 25 тогда и только тогда,
когда две его последние цифры делятся на 25 или число кратно 5.
2. Умножение чисел на 11. Данный способ устного счёта используется очень часто в 5 классе при решении больших примеров и математических «цепочек».
А) Сумма десятков и единиц умножаемого числа меньше 10:
1) Слева ставим число десятков, а справа единиц, оставляя место между ними
2) Между записанными числами записываем сумму данных чисел
3) Переписать данные числа, которые и будут ответом.
Пример:
Б) Сумма десятков и единиц умножаемого числа больше 10:
1) Так же как и верхнем способе слева пишем число десятков, а справа единиц.
2) Между ними записать их сумму
3) К числу единиц исходного числа прибавить 1
Пример:
3. Умножение
двухзначного числа на двухзначное.
Умножение
двухзначного числа на двухзначное.
Данный алгоритм используется при решении многих примеров в 5,6 и последующих классах.
1) цифры десяток перемножить между собой, умножив на 100,
2) перемножить “крайние” цифры чисел между собой попарно (справа и слева), и перемножить внутренние цифры между собой при записи в строчку. Результат сложить и умножить на 10.
3) перемножить цифры единиц.
4) Сложить все числа, полученные в ходе предыдущих вычислений
Пример:
4. Умножение натуральных чисел, используя законы умножения. Отталкиваясь от общего представления об умножении натуральных чисел, можно отметить ряд результатов, характерных для этого действия. Эти результаты называются свойствами умножения натуральных чисел.
Сочетательный закон
Чтобы произведение двух множителей умножить на третий множитель, можно первый множитель умножить на произведение второго и третьего множителей:
Переместительный закон
От перестановки множителей произведение не изменяется:
Распределительный закон
Чтобы умножить число на сумму, можно умножить это число на каждое из слагаемых и полученные произведения сложить:
1. 3
Приёмы быстрых устных вычислений в 7 классе
3
Приёмы быстрых устных вычислений в 7 классе
В 7-ом классе вычислительные соображения школьников закрепляются при выполнении тождественных преобразований над степенями с натуральным и целым показателями, с различными действиями над одночленами и многочленами, при решении примеров с помощью сокращенного умножения, а также при нахождении значения рациональных выражений. Но в основном у школьников вызывает большой интерес возведение чисел в квадрат с помощью формул сокращенного умножения:
1. Возведение чисел в квадрат, используя формулы квадрата суммы и разности .
1) Вначале, мы должны «разбить» данное число на сумму десятков и единиц, входящих в это число и возвести в квадрат
2) По формулам : , где а – число десятков, в – число единиц, посчитать результат.
Пример:
2. Вычисления с применением формулы разности квадратов :
1) Перемножаемые числа должны соответствовать формуле
2) Числа нужно разбить на одинаковое число десятков и единиц, отличающихся друг от друга только знаком
Пример:
1. 4
Приёмы быстрых устных вычислений в 8 классах
4
Приёмы быстрых устных вычислений в 8 классах
В 8-ом классе мы сталкиваемся с изучением таких тем как: «Квадратные корни и их свойства», «квадратные неравенства и уравнения», а точнее в ходе нахождения корней квадратного уравнения, его дискриминанта, вычислений, связанных в возведением чисел в квадрат и их умножением.
1. Возведение в квадрат чисел, оканчивающихся на 5 :
Способ 1: 1) Возведём в квадрат число десятков.
2) К полученному произведению прибавим число десятков, которое возводили в квадрат. Число, полученное в результате действий 1 и 2 будет являться числом сотен.
3) Справа от результата допишем квадрат числа единиц.
Пример:
Способ 2: 1) К числу десятков допишем следующее по счёту число и перемножим их.
2) К результату справа, как и в предыдущем случае, допишем квадрат числа единиц, т.е. числа 5.
Пример:
Способ 3: 1) Число десятков, так же как в прошлый
раз, умножим на следующее число по счёту и объединим цифры, связанные между
собой знаком умножения в скобки.
2) Данное произведение умножим на 100. Т.е. к полученному результату добавим 2 нуля.
3) К полученному результату прибавляем квадрат числа 5.
Пример:
2. Возведение в квадрат двухзначного числа:
1) К числу, которое нужно возвести в квадрат нужно прибавить его единицы
2) Сумму следует умножить на десятки данного числа
3) В окончании, надо к полученному результату прибавить квадрат единиц данного числа, что очень похоже на предыдущие способы.
3. Квадраты близких чисел:
1) Вначале, нужно разобраться, к какому числу данное число расположено ближе: к 5 или к 10. Числа от 0 до 3 следует округлять до целого ( 10,20…), а от 4 и более до числа, десяток которого на 10 единиц больше.
2) К округленному числу прибавим единицы, которые следует умножить на сумму числа, которое нужно возвести в квадрат.
4. Умножение чисел, у которых цифры десятков одинаковые:
1) Для этого нужно к числу десятков приписать следующую по счёту цифры и записать данное произведение
2) Перемножить числа единиц и дописать их справа
Пример:
Глава 2. Исследовательская часть.
Исследовательская часть.
2.1 Выработка умений решать примеры, используя упрощенные способы вычислений
Для того, чтобы определить как учащиеся владеют быстрыми устными способами вычислений было проведено анкетирование среди учащихся 6 «Г», 7 «Б», 8 «В» классов КГУ «Гимназия № 93» по следующим вопросам:
1. Часто ли Вы используете при вычислениях приёмы устного счёта:
2. Как вы думаете, знание данных приемов устного счёта будут ли использованы Вами в дальнейшем?
Данные об анкетировании можно представить в виде таблицы:
Класс | Всего опрошено | 1 вопрос | 2 вопрос | ||
«Да» | «Нет» | «Да» | «Нет» | ||
6 «Г» | 27 | 24 | 3 | 27 | 0 |
7 «Б» | 12 | 8 | 4 | 8 | 4 |
8 «В» | 23 | 11 | 12 | 21 | 2 |
Судя по таблице
можно сказать, что многие учащиеся используют при вычислениях приёмы устного
счёта (см. 1 вопрос). По результатам второго вопроса видно, что 56 из 62
опрошенных будут использовать показанные приёмы устных вычислений.
Количественное соотношение можно увидеть на следующих диаграммах:
1 вопрос). По результатам второго вопроса видно, что 56 из 62
опрошенных будут использовать показанные приёмы устных вычислений.
Количественное соотношение можно увидеть на следующих диаграммах:
Также учащимся было предложено выполнить задания по примерам, соответствующим их учебной программе. Для каждого класса составлено по 3 задания:
Задание для 6 класса 1.Перемножьте числа 27 и 93 2.Умножьте 25 на 11 3.Выполните умножение, используя нужный закон умножения: 1) ; 2) ; 3) | Задание для 7 класса 1.Возведите число 59 в квадрат, используя формулу квадрата суммы 2.Возведите число 38 используя формулу квадрата разности 3.Перемножьте числа 56 и 44, используя формулу разности квадратов | Задание для 8 класса 1. 2.Возведите число 45 в квадрат 3.Извлеките из – под знака корня |
Данные по результатам внесены в следующую таблицу:
Класс | Выполняли | 1 задание | 2 задание | 3 задание | ||||
Справ. | Н/с | Справ. | Н/с | Справ. | Н/с | Справились частично | ||
6 «Г» | 27 | 2 | 25 | 25 | 18 | 18 | 3 | 6 |
7 «Б» | 12 | 9 | 3 | 8 | 8 | 8 | 4 | – |
8 «В» | 23 | 19 | 4 | 22 | 20 | 20 | 3 | – |
Анализируя
результаты ответов ребят, я пришёл к выводу, что способы устного быстрого счёта
поняты учениками. В основном учащиеся справились с предложенными им заданиями.
У них появился интерес и потребность к расширениям их знаний. Они с
удовольствием участвовали в приёмах устного счёта. Но, не смотря на это, в
вычислениях были допущены и ошибки. Рассмотрим эти ошибки относительно каждого
класса:
В основном учащиеся справились с предложенными им заданиями.
У них появился интерес и потребность к расширениям их знаний. Они с
удовольствием участвовали в приёмах устного счёта. Но, не смотря на это, в
вычислениях были допущены и ошибки. Рассмотрим эти ошибки относительно каждого
класса:
У учеников 6 «Г» класса:
1. Возникли трудности в выполнении умножения двухзначного на двухзначное число;
2. Неверное применение сочетательного закона умножения;
3. Неверная постановка знаков между произведением чисел в третьем примере, третьего задания;
4. Неправильное сложение двухзначных и трехзначных чисел.
У учеников 7 «Б» класса:
1. Неверное применение формул сокращенного умножения;
2. Неправильное сложение чисел.
У учеников 8 «В» класса:
1. Путаница в применении таблицы умножения;
2.
Ошибочное
восприятие информации об извлечении чисел, оканчивающихся на 25 из под знака
арифметического квадратного корня.
Количественное соотношение можно увидеть на следующих диаграммах:
На основании полученных данных мы можем утверждать, что данная работа востребована и будет иметь практическое значение и применение в ходе учебной деятельности учащихся.
Выводы
В ходе данной работы я пришёл к следующим выводам:
1) Рассмотренные приёмы быстрого счёта подобранны соответственно для 6,7,8 классов из разных источников литературы
2) Проводя анкетирование в 6,7,8 классах на применение навыков устного счёта, в ходе которого некоторые учащиеся данных классов открыли для себя новые приёмы
3) Я думаю, что вычислительная культура учащихся данных классов повысилась, так как некоторые из них впервые слышали о данных способах приемов устного счета
4) Мной были Выявлены основные ошибки, возникающие при вычислениях, при проведении исследования
5) Моя гипотеза о том, что
использование на уроках математики знаний и умений быстрых способов вычисления
способствуют повышению культуры учащихся 6-8 классов подтвердилась, т. к. при
вычислениях обычным способом (умножение «столбиком», деление «уголком»)
потребовало затратить больше времени, чем практическое применение данных
приёмов устного счёта.
к. при
вычислениях обычным способом (умножение «столбиком», деление «уголком»)
потребовало затратить больше времени, чем практическое применение данных
приёмов устного счёта.
Заключение
Устный счёт имеет
широкое применение в повседневной жизни: он развивает сообразительность
учащихся, находчивость, сообразительность, память, гибкость мышления, ставя нас
перед необходимостью подбирать приёмы вычислений, удобные для конкретного
случая. Устные вычисления дают возможность не только быстро производить расчёты
в уме, но и контролировать, оценивать, находить и исправлять свои ошибки в результатах
вычислений, выполненных без помощи калькулятора и соответствующих таблиц. На
данный момент, изучив методы решения быстрого счёта, я могу помогать своим
друзьям, одноклассникам и сверстникам. Поэтому, думаю, что полезно знать приёмы
устного счёта, связанные с вычислениями, которые в дальнейшем будут
использованы нами при написании итоговых экзаменов в 9 классе и итоговых
аттестаций в 11 классе.
Поэтому, думаю, что полезно знать приёмы
устного счёта, связанные с вычислениями, которые в дальнейшем будут
использованы нами при написании итоговых экзаменов в 9 классе и итоговых
аттестаций в 11 классе.
Список литературы
1. Т.А. Алдамуратова, Т.С. Байшоланов // Математика. Учебник для 6 класса общеобразовательной школы, Алматы – 2006 год
2. А.Н. Шыныбеков // Алгебра. Учебник для 7 класса общеобразовательной школы, Алматы – 2011 год
3. А.Е. Абылкасымова, А.Абдиев, З.А. Жумагулова // Алгебра. Учебник для 8 класса общеобразовательной школы, Алматы – 2012 год
4. Л. Федотова // Повышение
вычислительной культуры учащихся 5-9 классов, журнал « Математика в школе»,
Москва – 2004 год. – № 35. – с. 3
– № 35. – с. 3
5. Э.П. Струнникова, Н.И. Мельникова // Устный счёт, Москва – 2007 год
6. Ф.Ф. Нагибин, Е.С. Канин // Математическая шкатулка, Москва – 1988 год
Как научить ребенка быстро считать в уме
01.12.2020
Чтобы ребенок успешно учился и развивался в целом, он должен быстро считать в уме. Начинать прививать это умение нужно в 3-5 лет. Считается, что такой возраст наиболее благоприятен для обучения: дети уже с легкостью осваивают сложение и вычитание.
Содержание:
- В чем польза устного счета
- Подготовка к обучению
- Методики обучения
- Игры для тренировки счета в уме
- Чего не нужно делать
- Несколько советов
В чем польза устного счета
Быстрый устный счет полезен каждому человеку. И это умение пригодится не только при посещении магазина, планировании семейного бюджета и в других жизненных ситуациях. Постоянные арифметические вычисления в уме способствуют развитию мышления, воображения и интеллектуальных способностей, они улучшают память, формируют аналитический склад ума, а еще придают уверенность в себе. Любой счет, даже если это элементарные примеры, делает наш мозг активным – он будет «подвижным», готовым воспринимать большое количество информации.
Постоянные арифметические вычисления в уме способствуют развитию мышления, воображения и интеллектуальных способностей, они улучшают память, формируют аналитический склад ума, а еще придают уверенность в себе. Любой счет, даже если это элементарные примеры, делает наш мозг активным – он будет «подвижным», готовым воспринимать большое количество информации.
Устные вычисления заставляют оба полушария мозга функционировать слажено и продуктивно, на полную мощность своих возможностей. Ученики, практикующие счет в уме, быстрее других усваивают информацию, легче воспринимая ее на слух и зрительно. Они без проблем переключаются с одного предмета на другой, и им легко дается не только математика, но также иностранные языки и другие дисциплины.
Подготовка к обучению
Перед началом обучения устному счету ребенок должен понимать, что такое число, а также ориентироваться в понятии «меньше-больше», сравнивать размеры предметов, различать круг, квадрат, треугольник, линию.
Начните обучение с того, что дайте понять ребенку: каждое число может обозначать группу определенного количества предметов. То есть недостаточно посчитать до четырех и показать написание цифры 4. Покажите ученику 4 пальца, 4 конфеты, нарисуйте 4 кружочка. Свяжите все простые числа со знаменитыми сказочными героями: три поросенка, четыре черепашки-ниндзя, семь гномиков.
То есть недостаточно посчитать до четырех и показать написание цифры 4. Покажите ученику 4 пальца, 4 конфеты, нарисуйте 4 кружочка. Свяжите все простые числа со знаменитыми сказочными героями: три поросенка, четыре черепашки-ниндзя, семь гномиков.
Методики обучения
Обучать счету можно несколькими методиками. Например, способ Глена Домана заключается в обучении по специальным карточкам с изображенными на них красными точками. Можно выбрать устный счет на основе знания состава чисел. К примеру, нужно сложить 7 и 5. Первое число дополняем с помощью тройки до 10. А зная, что 5 можно представить как 2+3, «забираем» из пятерки эту тройку, получая 2. Прибавляем его к полученной ранее 10. Общий итог – 12.
Заучивание таблиц – еще один метод. В таблицах содержатся примеры на сложение и вычитание простых, а затем и более сложных чисел, и заучить их нужно до автоматизма. Распространена и методика Полякова. Она основана на игре с кубиками или карточками, в которых имеются гнезда для вставки пронумерованных фишек. Этот способ также основан на знании состава числа. Каждое число ребенок запоминает как комбинацию (сумму) фишек с простыми числами. А ментальная арифметика использует в обучении специальный счетный инструмент – соробан, аналог древневосточных счетов абакуса.
Этот способ также основан на знании состава числа. Каждое число ребенок запоминает как комбинацию (сумму) фишек с простыми числами. А ментальная арифметика использует в обучении специальный счетный инструмент – соробан, аналог древневосточных счетов абакуса.
Для облегчения устного счета используются разнообразный лайфхаки и хитрости. Один из самых известных приемов – перестановка слагаемых: например, 8+7+2 удобнее считать в виде 8 + 2 + 7 = 10 + 7 = 17. Еще один вариант – так называемое «присчитывание». Например, 36+38 можно посчитать как 36+40-2.
Игры для тренировки счета в уме
Навыки устного счета будут развиваться при регулярных тренировках, и их можно проводить в игровом формате. Подойдет сюжетная игра «Магазин», арифметическое лото, настольные игры на основе арифметики. Есть немало приложений для телефонов и онлайн-игр на эту тему.
Можно соединить занятия математикой с физической нагрузкой и организовать игру «Веселый счет». Ведущий в ней кидает мяч игроку и называет простой пример, который последнему нужно решить, тот считает в уме и сообщает результат.
Чего не нужно делать
Устный счет – потому и устный, раз происходит исключительно в уме. Не нужно начинать учить ребенка считать на палочках, ракушках или с помощью пальцев: так научить счету легко, а отучить будет весьма сложно. При счете на пальцах или при помощи каких-то предметов у ученика не задействован механизм памяти, результаты действий и математические закономерности в мозгу не откладываются.
Столь же вреден модный в последнее время метод счета по линейке, когда от искомого числа на линейке отсчитывают вправо (при сложении) или влево (при вычитании) второе число. Эта методика также не приучает ребенка думать и запоминать, не тренирует память и тормозит умственное развитие.
Несколько советов
На первом этапе обучения лучше оперировать не цифрами, а любыми предметами, так как у детей такого возраста преобладает пока образное мышление. Уроки должны проходить с регулярностью, но обязательно в ненавязчивой форме. Важно не только решать абстрактные примеры, но использовать примеры из жизни. Обязательно хвалите ребенка за достигнутые успехи, а за неудачи – ни в коем случае не ругайте.
Обязательно хвалите ребенка за достигнутые успехи, а за неудачи – ни в коем случае не ругайте.
Методику нужно выбирать по возможностям и способностям ребенка, причем можно использовать не один метод, а комбинировать два или даже три.
Что такое устная арифметика и как улучшить свои математические навыки
Наша повседневная деятельность зависит от математики. Мы используем математические идеи и принципы в нашей повседневной жизни, осознаем мы это или нет. Счет в уме — одна из самых важных математических способностей, которыми вы можете овладеть. Способность производить математические расчеты в уме без помощи калькулятора или любого другого внешнего устройства называется ментальной арифметикой. В этой части будет обсуждаться определение ментальной арифметики, а также ее преимущества, методы и инструменты для развития ваших способностей.
Что такое ментальная арифметика?
Без помощи калькулятора, ручки или листа бумаги ментальная арифметика представляет собой процесс проведения математических вычислений в вашей голове. Это влечет за собой использование умственных методов, таких как визуализация, запоминание и распознавание образов, для решения математических задач.
Преимущества ментальной арифметики
Умение считать в уме имеет много преимуществ. Это может помочь в развитии ваших арифметических способностей, что является одним из самых важных преимуществ. Ваша память, внимание и навыки решения проблем могут быть улучшены с помощью ментальной арифметики. Кроме того, когда вам нужно произвести быстрые вычисления — например, во время тестов, конкурсов или в повседневной жизни — ментальная арифметика может помочь вам сэкономить время.
Методы ментальной арифметики
Вы можете использовать различные методы, чтобы отточить свои способности к ментальной арифметике. Самый удачный метод — воображение. Визуализация влечет за собой воображение цифр и выполнение вычислений в уме. Запоминание — это другая стратегия, которая предполагает заучивание наизусть арифметических таблиц, обычных математических формул и других математических идей. Другим эффективным методом решения математических задач является идентификация образов, включающая выявление закономерностей и связей между числами.
Самый удачный метод — воображение. Визуализация влечет за собой воображение цифр и выполнение вычислений в уме. Запоминание — это другая стратегия, которая предполагает заучивание наизусть арифметических таблиц, обычных математических формул и других математических идей. Другим эффективным методом решения математических задач является идентификация образов, включающая выявление закономерностей и связей между числами.
Ресурсы для изучения устной арифметики
Вы можете изучать и практиковать устную арифметику с помощью ряда инструментов. Счеты, также известные как соробан, являются распространенным инструментом для выполнения вычислений в уме. Это древнее счетное устройство, используемое в Японии. Вы также можете заниматься ментальной арифметикой, используя различные приложения и веб-инструменты, включая рабочие листы, практические задачи и загадки. Вы также можете принять участие в ряде соревнований и курсов, чтобы развить свои способности.
- olymp.
 abakus-center.eu
abakus-center.eu - abakus-center.eu/онлайн
- https://x.abakus-center.eu/
- Приведены некоторые китайские цифры и примеры. Попробуйте понять, что означает каждый иероглиф
- Заполните пропуски в этом магическом квадрате, зная, что сумма каждой строки должна быть равна 111
Подробнее «Думай быстро и считай быстрее: лайфхаки для развития навыков счета в уме»
Развитие навыков счета в уме
Есть несколько способов улучшить вычислительные способности мозга. Первоначально начните с регулярного выполнения ментальной арифметики. Простые вычисления — хорошее место для начала, и со временем вы сможете перейти к более сложным задачам. Во-вторых, используйте стратегии решения проблем, такие как образы, память и распознавание образов. Наконец, используйте такие инструменты, как курсы, приложения и интернет-ресурсы, которые помогут вам тренировать и развивать свои способности.
youtube.com/embed/wuZ6GGjb1LA” frameborder=”0″ allowfullscreen=”allowfullscreen”>Часто задаваемые вопросы
Как лучше всего практиковать ментальную арифметику?
Лучший способ попрактиковаться в ментальной арифметике — начать с простых сумм и постепенно переходить к более сложным задачам. Другие методы решения проблем включают выявление закономерностей, запоминание и визуализацию.
Существуют ли какие-либо приложения или онлайн-инструменты, которые я могу использовать для оттачивания своих математических способностей в уме?
Да, существует множество приложений и интернет-инструментов, таких как математические рабочие листы, практические вопросы и головоломки, которые могут помочь вам отточить и развить свои способности к устному счету.
Что такое счеты и соробаны?
Счеты, также известные как соробан, представляют собой древнее счетное устройство, используемое в Японии и позволяющее производить вычисления в уме.
Могут ли занятия в уме помочь мне улучшить память и сосредоточиться?
Ответ: Вы можете укрепить свою память, внимание и навыки решения задач, изучая и применяя ментальную арифметику.
Существуют ли какие-либо программы или мероприятия, в которых я могу принять участие, чтобы отточить свои математические способности?
Ряд онлайн-курсов и конкурсов, а также соревнований по устной арифметике помогут вам отточить свои способности к умственным вычислениям.
Стратегии и советы по ментальной арифметике, которые должен знать каждый ребенок
Когда мы думаем о стратегиях ментальной арифметики, мы в основном думаем о тех математических навыках, которые мы можем выполнять в уме, без использования формальных письменных методов, которые мы использовали бы дольше вопросы и стандартные методы алгоритма.
В этой статье мы познакомим вас с некоторыми стратегиями ментальной арифметики, которым вы можете научить своих учеников, чтобы развить их навыки ментальной арифметики в начальной школе.
Что такое математические стратегии в уме?
Стратегии ментальной арифметики — это общепринятые способы решения математических задач в уме, которые помогают нам срезать путь и эффективно находить правильный ответ.
Почему важны математические стратегии в уме?
Стратегии ментальной математики лежат в основе большинства областей математики, в которых используются числа. Без эффективных умственных стратегий дети часто не могут быстро и бегло считать.
Умственные стратегии также являются основой любого письменного или формального метода в математике. Ссылаясь на это как на умственную математику, это не означает, что вы вообще ничего не можете записать, но любая письменная работа будет представлять собой быстрые наброски, помогающие запомнить через многошаговые задачи.
По мере того, как дети начинают использовать более формальные методы, начиная примерно с 3-го класса, и по мере того, как числа, с которыми они работают, становятся все более ценными, навыки счета в уме жизненно важны для обеспечения беглости и точности в математике.
Развитие истинной беглости в математике
Эффективные мыслительные стратегии важны, если дети хотят развить «истинную» беглость
Истинную беглость лучше всего можно определить как способность детей уверенно использовать и применять свои знания о числовых отношениях, числовых фактах и нашу систему счисления для расчета и решения задач.
Стоит помнить, что свободное владение математикой не ограничивается способностью вспоминать известные факты. Точнее, важно то, как дети могут использовать и применять эти факты, в том числе с помощью ряда умственных математических стратегий.
«Отстающие часто являются отстающими не потому, что знают меньше, а потому, что не умеют гибко использовать числа». – Джо Боалер
Индивидуальное онлайн-обучение Third Space Learning уделяет большое внимание формированию у учащихся уверенности и беглости в математике. Наши еженедельные уроки с репетиторством, разработанные с учетом индивидуальных потребностей каждого ребенка, направлены на то, чтобы укрепить понимание учениками числовых фактов и способов их применения в широком круге вопросов.
Будьте осторожны, чтобы не ошибиться в обозначениях математических навыков в уме.
При работе над развитием «истинной» беглости речи важно помнить, что точность — это не то же самое, что беглость речи.
Например, рассмотрим следующие сценарии, которые, хотя и являются точными, не обязательно могут быть классифицированы как беглые:
- Первоклассник вычисляет 40 + 8, считая единицами;
- Третьеклассник, вычисляющий 1003 – 998 формальным письменным методом;
- Пятиклассник вычисляет 41,79 + 25,3 + 25,7 – 41,79сложив первые три числа, а затем вычтя четвертое.
Этот отрывок из исследовательской работы «Развитие вычислительной беглости с целыми числами», опубликованной в 2000 году С. Дж. Расселом, остается одним из лучших объяснений беглости:
«Беглость опирается на хорошо построенную математическую основу, состоящую из трех частей:
- понимание смысла операций и их отношений друг к другу — например, обратное отношение между умножением и делением;
- знание большого набора числовых отношений, включая «факты» сложения и умножения, а также другие отношения, например, как 4 × 5 связано с 4 × 50;
- и глубокое понимание системы счисления с основанием 10, того, как числа устроены в этой системе и как система разрядов ведет себя в различных операциях — например, что 24 + 10 = 34 или 24 × 10 = 240′ .

Быстрое вспоминание и вычисления в уме с заметками
Когда мы обсуждаем вычисления в уме по математике в старших классах начальной школы, нам нужно четко понимать различие между фактами, которые дети должны уметь быстро вспоминать, и типами вычислений, которые дети должны уметь производить в уме, иногда с помощью заметок.
Практика припоминания и быстрого припоминания числовых фактов важна, потому что, если дети способны автоматически вспоминать числовые факты, это позволяет им высвободить свою рабочую память при столкновении с более сложными вопросами.
Они также способны более эффективно и точно решать проблемы, рассуждать и устанавливать связи, если им не приходится постоянно вычислять одни и те же «базовые» факты.
«Обучая процедурным и фактическим знаниям, убедитесь, что учащиеся доходят до автоматизма. Объясните учащимся, что автоматизм [с ключевыми фактами] важен, потому что он освобождает их разум для размышлений о концепциях». – Дэниел Уиллингем – когнитивист, в теме «Правда ли, что некоторые люди просто не умеют считать?»
– Дэниел Уиллингем – когнитивист, в теме «Правда ли, что некоторые люди просто не умеют считать?»
Концепция должна быть понята, прежде чем вводить стратегию
Прежде чем мы сможем ожидать быстрого припоминания и автоматизма числовых фактов с нашими стратегиями ментальной математики, нам необходимо научить основным математическим концепциям. Например, только когда у детей есть надежное концептуальное понимание числовых связей до 10, следует пытаться быстро вспоминать.
Исходя из этого понимания числовых связей до 10, можно использовать стратегию разделения. Например, к 5-му классу большинство детей должны уметь вычислять в уме 34 х 5 (30 х 5 + 4 х 5), используя разбиение и свои знания закона распределения, подкрепленные базовыми вычислениями.
Хотя учащиеся будут узнавать все больше и больше математических фактов, которые они могут запомнить «наизусть», жизненно важно, чтобы они понимали концепции. Работа с манипуляторами может помочь в этом, переходя к виртуальным манипуляторам на интерактивной доске, когда числа становятся слишком большими, чтобы удерживать их физически.
Оценка математических стратегий в уме, которые использует ваш класс
Один из действительно интересных способов проверить стратегии в устной арифметике – представить группам разные письменные версии одних и тех же математических задач.
- Представьте одну задачу
Если вы представите задачу, например 64 + 17, в предложении, подобном этому, те дети, которые уверены в своих математических стратегиях в уме, решат ее в уме.
Обычно они, даже подсознательно, если владеют беглым языком, разбивают числа и вычисляют 60 + 10, а затем 4 + 7, или 60 + 17, затем прибавляют 4. Некоторые делают 64 + 10, а затем прибавляют 7.
Некоторые могут округлять числа, например, 64 + 20, используя числовые связи, до 20 знаний, а затем минус 3.
Некоторые могут снова использовать свои числовые связи, чтобы вычислить 64 + 17, добавив 63 + 17, чтобы получить 80, а затем добавить 1.
Вы ожидаете, что ваш класс даст ряд ответов относительно своего метода, но, надеюсь, все говорят бегло. и может найти правильный ответ, не более чем быстро записывая некоторые числа при добавлении нескольких шагов.
и может найти правильный ответ, не более чем быстро записывая некоторые числа при добавлении нескольких шагов.
- Создайте две версии одного и того же набора из 10 вопросов
Теперь составьте лист из 10 похожих вопросов с диапазоном сложения и вычитания, которые, как вы ожидаете, ваш класс сможет выполнить в уме. Создайте вторую версию этого, которая излагает те же вопросы, с теми же точными числами и тем же ожидаемым ответом, в стандартном формате метода алгоритма.
Раздайте половине класса первый лист в виде числового предложения, а другой половине — вторую версию, где вопросы представлены в формате стандартного метода алгоритма.
Не говорите группам, что у них разные листы, и раздавайте их за разные столы, чтобы они не видели другой формат тех же вопросов. Дайте им время, чтобы они индивидуально ответили на вопросы и записали свои ответы.
- Попросите детей поделиться своими методами
Ответьте на первый вопрос и попросите кого-нибудь добровольно поделиться своим методом. Затем попросите кого-нибудь поделиться, затем еще кого-нибудь и так далее. Убедитесь, что вы получили пару примеров из таблиц с горизонтальным расположением вопросов и пару примеров из таблиц с вертикальным расположением столбцов.
Затем попросите кого-нибудь поделиться, затем еще кого-нибудь и так далее. Убедитесь, что вы получили пару примеров из таблиц с горизонтальным расположением вопросов и пару примеров из таблиц с вертикальным расположением столбцов.
Вы, скорее всего, обнаружите, что группы, у которых была горизонтальная схема, с гораздо большей вероятностью просто обдумывали это в уме, в то время как группы, у которых была вертикальная схема, тратили время на выполнение стандартного алгоритмического метода, чтобы найти и записать свои ответы, включая каждый шаг, хотя они могли бы легко решить эти задачи в уме.
Это упражнение является отличным напоминанием о том, что даже когда мы видим формальные вычисления, мы должны использовать наши математические стратегии в уме, чтобы ускориться там, где мы можем.
Укрепление уверенности в умственных математических стратегиях
При введении любого нового математического понятия — от сложения до процентов и десятичных дробей — детям будет полезно показать физическое представление чисел (с использованием математических манипуляций) и операций перед использованием графических представлений (например, числовые линии или модели столбцов), а затем, наконец, написанные методы с использованием символов числа и операции.
Подробнее: Конкретно-иллюстрированный абстрактный метод
По пути вам придется много повторять и тренироваться мысленно вспоминать факты. Мы надеемся, что по мере того, как дети становятся старше и переходят в старшие классы начальной школы, переход от физического к письменному будет происходить быстрее для новых концепций, поскольку они строятся на прочном фундаменте.
Разные дети могут переходить к умственным стратегиям в разных точках каждого блока. Некоторые могут перейти от физического к ментальному, если они быстро схватывают концепцию и уже имеют четкое понимание.
Другие, возможно, не смогут достичь беглости запоминания и применения до тех пор, пока они не попрактикуются в написании своих ответов и не укрепят уверенность в этих новых числовых фактах и стратегиях.
Возможно, вам также придется распаковать любые неправильные представления на этих этапах, и это может включать возвращение «назад» к физическому. Хорошей практикой является всегда иметь под рукой манипуляторы во время выполнения самостоятельных заданий, даже в 5-м классе и для всех способностей. Иногда быстрое сравнение с использованием палочек с основанием 10 или палочек Кюизенера может помочь ребенку «закрепить» эту стратегию в голове.
Иногда быстрое сравнение с использованием палочек с основанием 10 или палочек Кюизенера может помочь ребенку «закрепить» эту стратегию в голове.
Также важно не учить детей выполнять математические трюки, например, «прибавлять ноль» при умножении на десять, так как это может вызвать проблемы в более позднем возрасте с пониманием разрядности. Однако можно надеяться, что дети заметят такие закономерности в своих ответах, и это должно привести к обсуждению и сравнению, а также предоставить детям возможность проверить свою теорию там, где они заметили возможную закономерность. Даже если вы знаете, что это неправильно/правильно, они выиграют от возможности проверить и применить это предположение.
Подробнее: Математические приемы, которых следует избегать и умственный труд, арифметика и рассуждение. Они фактически формируют прогрессию, начиная с 3-го класса, поэтому важно, чтобы в детском саду – 2-м классе уже была сделана основа, чтобы дети могли выполнять вычисления в уме.
Таким образом, эти навыки лучше всего рассматривать как прогресс, а не как набор ожиданий годовой группы.
Как улучшать математику в уме год за годом
Наряду с расширением диапазона детских вычислений в уме по мере прохождения ими элементарных предметов, убедитесь, что они также каждый год уверены в количестве фактов.
Как развить в уме математические стратегии, необходимые для сложения и вычитания
В младших классах дети узнают основные сведения о числах, включая сложение и вычитание. Это будет включать количество облигаций до 20 к тому времени, когда они закончат 1-й класс. Они будут много работать с физическими объектами и играть в ролевые игры, поэтому в эти годы хорошей практикой является не только практиковать математические навыки во время уроков математики, но и создавать возможности для вопросов вне этих уроков.
Попросите детей подсчитать, сколько учеников сегодня отсутствовало, посчитав карандаши на каждом столе, чтобы увидеть, достаточно ли у них (или слишком много, или слишком мало), и пополнить словарный запас на уроках математики.
Как только дети усвоят концепцию фактов сложения и фактов вычитания, а также то, что они являются обратными операциями (хотя они могут еще не знать этого конкретного слова), они начнут укреплять свое быстрое запоминание числовых связей и применять их в своей работе.
Никогда не рано вводить различные стратегии для отработки своих расчетов, если базовое понимание правильное. Спросить их, есть ли другой способ, которым они могли бы найти ответ, можно задать на официальных уроках, в ролевой игре или в спорте.
Основные факты сложения, которые дети должны знать ко 2-му классуСтратегии сложения и вычитания в уме в старших классах
Счет в прямом и обратном порядке
Счет в прямом и обратном порядке впервые встречается в младших классах, начиная с единицы и считая до единиц .
Чувство числа у учащихся расширяется за счет того, что они начинают с разных чисел и считают в прямом и обратном порядке не только единицы, но и двойки, пятерки, десятки, сотни, десятые и так далее.
Прогресс в счете в прямом и обратном порядке
Вот способы, которыми вы можете помочь своему классу прогрессировать в счете в прямом и обратном порядке:
- Счет в десятках или в обратном порядке от любого числа (например, работая над 27 + 60= ? путем подсчета десятками от 27)
- Счет до пятерок или обратно от любого числа, кратного 5 (например, 35+15=? путем счета с шагом 5 от 35.)
- Счет до сотен или обратно от любого числа (например, 570 + 300= ?, считая сотни от 570.)
- Счет вперед или назад в десятых и/или сотых долях (например, 3,2 + 0,6 = ? при счете в десятых долях. 1,7 + 0,55=? в счете в десятых и сотых долях.)
Разбиение для сложения и вычитания
Стратегии разбиения учат детей разбивать большие числа на меньшие.
Важно, чтобы дети знали, что числа могут быть разделены – как по границам разрядного значения (канонически), так и другими способами (неканонически).
Затем они могут использовать свое разбиение, чтобы помочь им в вычислениях сложения и вычитания.
 Это может быть расширено по мере того, как дети продвигаются по старшей начальной школе.
Это может быть расширено по мере того, как дети продвигаются по старшей начальной школе.Прогресс в делении на части
Вот способы, которыми вы можете помочь своему классу в делении на части:
- Вычисления с целыми числами, которые не требуют пересечения границ разрядных значений. Например. 23 + 45= ? на 40 + 5 +20 + 3 или 40 + 23 + 5
- Вычисления с целыми числами, которые включают пересечение границ разрядного значения. Например. 49– 32= ? на 49 – 9 – 23 или 57 + 34 = ? на 57 + 3 + 31
- Вычисления с десятичными числами, не связанные с пересечением границ разряда 5.6 + 3.7= ? на 5,6 + 3 +0,7 или 540 + 380= ? на 540 + 300 + 80 или 540 + 360 + 20
- Вычисления с десятичными числами, которые включают пересечение границ разрядного значения. Например. 1,4 + 1,7= ? на 1,4 + 0,6 + 1,1 и 0,8 + 0,35 = ? на 0,8 + 0,2 + 0,15
Компенсация и корректировка
Компенсация заключается в том, чтобы добавить больше, чем нужно, а затем вычесть лишнее.

Эта стратегия полезна для сложения чисел, близких к кратным 10, например чисел, оканчивающихся на 1 или 2, 8 или 9.
Добавляемое число округляется до кратного 10 плюс или минус небольшое число.
Например, добавление 9 выполняется путем прибавления 10, а затем вычитания 1. Аналогичная стратегия работает для добавления десятичных дробей, близких к целым числам.
Вот как вы можете помочь своему классу добиться прогресса в компенсации и корректировке:
- Компенсация и настройка на 10. (например, 34 + 9=? на 34 + 10 – 1 или 34 – 11= ? на 34 – 100 – 1 = ?)
- Компенсация и настройка, кратные 10. (например, 38 + 68 = ? на 38 + 70 – 2 или 45 – 29 = 45 – 30 + 1)
- Компенсация и корректировка, кратные 10 или 100. (например, 138 + 69= ? на 138 + 70 – 1 или 299 – 48 = 300 – 48 – 1)
- Компенсация и корректировка кратных с десятичными дробями. (например, 2 ½ + 1 ¾ на 2½ + 2 – ¼ или 5,7 + 3,9 на 5,7 + 4,0 – 0,1)
Расчет с использованием почти двойных чисел
Когда дети автоматически вспоминают основные двойные факты, они могут использовать эту информацию при сложении двух чисел, которые очень близки друг к другу.

Вот способы, которыми вы можете помочь своему классу прогрессировать в почти двойных числах:
- Почти двойных числах до 20. Например. 18 + 16 равно удвоению 18 и вычитанию 2 или удвоению 16 и прибавлению 2.
- Почти удвоение числа, кратного 10. 60 + 70 — это удвоить 60 и прибавить 10, или удвоить 70 и вычесть 10, или 75 + 76 — это удвоить 76 и вычесть 1, или удвоить 75 и прибавить 1.
- Десятичное число почти удваивается до целых чисел. Например. 2,5 + 2,6 — это удвоить 2,5, добавить 0,1 или удвоить 2,6, вычесть 0,1.
Как разработать математические стратегии в уме, необходимые для умножения и деленияПо мере прохождения начальной школы учащиеся узнают факты умножения. Им потребуется свободное владение фактами умножения, чтобы они могли вспомнить их достаточно быстро для тестирования сейчас и в высшем образовании. Опять же жизненно важно, чтобы они понимали концепцию умножения, а не просто повторяли факты наизусть.
Тем не менее, практика имеет решающее значение, так как ежедневное вспоминание известных фактов жизненно важно, чтобы новые факты не вытесняли старые там, где они не полностью укоренились.

Дети начинают понимать умножение с помощью удвоения и деления пополам в начальной школе. Это вводит понятия как умножения, так и деления, и они должны начать замечать их закономерности и применять это к математическим вопросам.
Они также узнают факты умножения для 5 и 10, и это начинается со счета вперед и назад в 5s и 10s, что они также должны делать с любого заданного числа, а не только с нуля.
Умственные математические факты, которые дети должны знать к концу 3-го классаК концу 3-го класса учащиеся должны уметь запоминать все произведения двух однозначных чисел. А потом в 4 классе факты умножения 11 и 12. Они также должны применять их к задачам со словами и многошаговым задачам по мере повышения уверенности, чтобы убедиться, что они могут применять числовые факты, а не просто повторять их.
Эти навыки счета в уме и их беглость будут иметь жизненно важное значение в тестовых ситуациях. К тому времени, когда они пойдут в старшую школу, они должны иметь очень твердое представление о системе счисления, а также о известных фактах и закономерностях.
38 новых фактов об умножении (и делении), которые дети должны знать к концу 4-го класса. и факты деления на числа, кратные 10 и 100, чтобы мысленно рассчитать увеличивающийся диапазон вопросов на умножение.
Вот способы, с помощью которых вы можете помочь своему классу повысить разрядность:
- Умножьте двузначное число на однозначное путем разбиения. Например. 26 х 3 = 20 х 3 + 6 х 3
- Умножение десятичного числа, содержащего до 2 знаков после запятой, на одну цифру путем разбиения. Например. 3,42 x 4 = 3 x 4 + 0,4 x 4 + 0,02 x 4
Стратегии удвоения и деления пополам
Дети должны уметь распознавать деление пополам как результат, обратный удвоению, и уметь быстро вычислять двойные и половинные числа.
Некоторые двойные и половинчатые факты быстро запоминаются, а не те, которые дети должны вычислять каждый раз, и они описаны в списках выше.
Вот способы, которыми вы можете помочь своему классу прогрессировать в удвоении и делении пополам:
- Найдите двойные и половинные числа любого двузначного числа и любого числа, кратного 10 или 100.
 (например, половина 680 или двойное 73)
(например, половина 680 или двойное 73) - Умножьте и разделите на 4, дважды удвоив/делив пополам, и на 8, снова удвоив/поделив пополам. (например, 34 x 4 = 34 x 2 x 2.)
- Найдите двойные числа и половинки любого числа до 10 000 путем разбиения. (например, половина от 32 202 за счет деления вдвое 3000, 2000, 200 и 2)
- Умножить на 50 путем умножения на 100 и деления пополам. (например, 8 x 50 = 8 x 100 разделить на 2)
- Разделить число, кратное 25, на 25, разделить на 100 и умножить на 4 (путем удвоения и повторного удвоения). (например, 350 ÷ 25 = 350 ÷ 100 x 2 x 2)
- Разделите число, кратное 50, на 50 путем деления на 100, а затем удвоения. (например, 450 ÷ 50= 450 ÷ 10 x 2)
- Двойное и половинное десятичное число с точностью до одного десятичного знака при порционировании. (например, половина 8,4 путем уменьшения вдвое 8 и уменьшения вдвое 0,4)
Стратегии вычисления в уме дробей, десятичных знаков и процентовПо мере прохождения начальной школы дети должны лучше понимать дроби, десятичные числа и проценты и то, как они связаны с делением.

Таким образом, к 5-му классу они должны уметь быстро вспоминать факты умножения и деления, чтобы вычислять в уме некоторые вопросы, связанные с дробями, десятичными знаками и процентами.
Вот как вы можете помочь своему классу освоить дроби, десятичные числа и проценты:
- Найдите в уме дроби чисел в таблице умножения на 2, 3, 4, 5 и 10, используя известные факты умножения и деления. (например, 3/5 от 45 на 45 ÷ 5 x 3.)
- Проценты отзыва эквивалентны ½, 1/3, ⅕, ⅙, 1/10 и 1/100. (например, ¼ = 25%)
- Найдите 10% или кратные 10% целых чисел и величин. (например, 30 % от 50 на 50 ÷ 10 x 3)
- Мысленно найдите 50 % путем деления пополам и 25 % путем деления чисел и величин на 4 или 2. (например, 25% от 150 на 150 ÷ 4)
Взлом математических вычислений в уме
Этот вирусный твит — очень хороший пример математического трюка в уме. Это также отличный способ использовать математические трюки в уме, чтобы произвести впечатление на своих друзей!
Лучшие советы по ментальной арифметике: как обучать стратегиям ментальной арифметикиМы достаточно подробно рассмотрели вопрос «что», но как мы на самом деле приступаем к обучению стратегиям ментальной арифметики? Вот краткое изложение наших лучших советов:
- Обучайте математическим приемам в уме и методам вычисления в уме, а не просто полагайтесь на то, что дети «соберут их».
 Важно, чтобы время урока было посвящено концептуальному обучению стратегиям и оказанию помощи детям в установлении связи между известными им фактами и расчетами в уме. Лучше всего это достигается с помощью моделирования и использования манипулятивных средств и т. д.
Важно, чтобы время урока было посвящено концептуальному обучению стратегиям и оказанию помощи детям в установлении связи между известными им фактами и расчетами в уме. Лучше всего это достигается с помощью моделирования и использования манипулятивных средств и т. д. - Вовлекайте детей в обсуждение. Детей следует поощрять к обсуждению своих умственных стратегий друг с другом и всем классом, а взрослые в классе должны присоединиться к этому обсуждению. Дети будут видеть и подходить к вычислениям в уме разными (и в равной степени обоснованными) способами, и, делясь ими, они знакомят друг друга с разными способами мышления и «видения» вычисления.
- Обеспечьте регулярную практику умственного счета. Дети должны иметь регулярную практику умственного счета, которая фокусируется на стратегиях умственного счета. Наряду с обучением стратегиям на основном уроке математики, школы, где дети имеют высокий уровень компетентности и беглости в умственных стратегиях, часто посвящают 15-20 минут в день практике и развитию умственных стратегий и быстрому воспроизведению вне основного урока математики.
 .
. - Не думайте, что тестирование по времени — единственный способ добиться быстрого отзыва. Многие исследования показали, что тестирование на время является одним из наименее эффективных способов развития быстрого припоминания. Вместо этого предоставьте детям множество возможностей использовать, применять и вспоминать факты, которые вы хотите, чтобы они могли быстро вспоминать.
- Играйте в игры и создавайте возможности для значимой деятельности. Если занятия будут веселыми и осмысленными, дети получат поддержку в развитии чувства числа и беглости в увеличивающемся диапазоне вычислений.
- Обеспечьте соблюдение «базовых» числовых фактов. Важно, чтобы вы не пренебрегали «базовыми» числовыми фактами, например, числовыми связями в пределах 10, 20 и 100 и таблицей умножения 1-12x. Часто такие факты, как числовые связи, практикуются только в начальных классах, но жизненно важно, чтобы они практиковались, и детей поощряют использовать эти факты в своих умственных вычислениях.
 Помните, если вы не предоставите им возможность ею воспользоваться, они ее потеряют!
Помните, если вы не предоставите им возможность ею воспользоваться, они ее потеряют!
Подробнее:
- Как учить факты умножения, чтобы ученики быстро запоминали
- Что такое свободное владение математикой?
Ссылки:
Рассел, Сьюзан Джо (2007). Развитие вычислительной беглости с целыми числами в начальных классах
Есть ли у вас учащиеся, которым нужна дополнительная помощь по математике?
Предоставьте своим учащимся четвертого и пятого классов больше возможностей для закрепления навыков обучения и практики с помощью персонализированного обучения элементарной математике с их собственным онлайн-репетитором по математике.Каждый учащийся получает дифференцированное обучение, предназначенное для устранения индивидуальных пробелов в обучении, а организованное обучение гарантирует, что каждый учащийся учится в нужном темпе. Уроки соответствуют стандартам и оценкам вашего штата, плюс вы будете получать регулярные отчеты о каждом шаге.


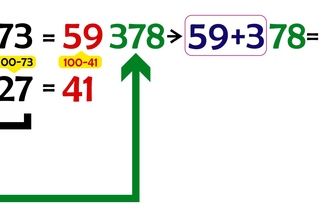 Выполните
умножение: 92∙98
Выполните
умножение: 92∙98 abakus-center.eu
abakus-center.eu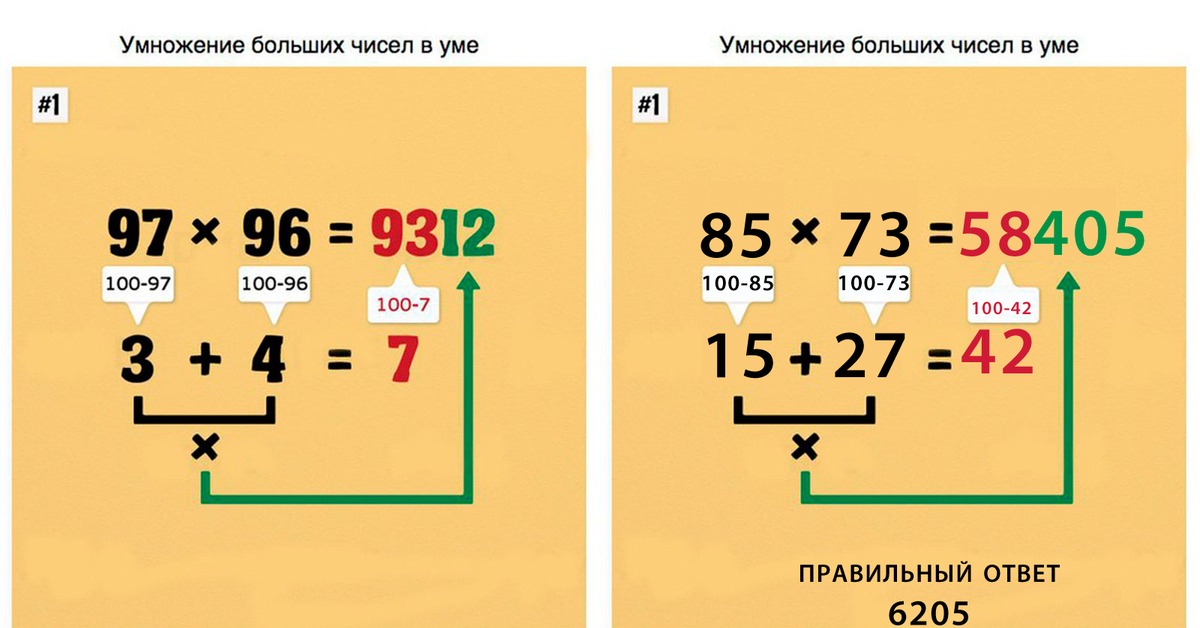
 Это может быть расширено по мере того, как дети продвигаются по старшей начальной школе.
Это может быть расширено по мере того, как дети продвигаются по старшей начальной школе.



 (например, половина 680 или двойное 73)
(например, половина 680 или двойное 73)
 Важно, чтобы время урока было посвящено концептуальному обучению стратегиям и оказанию помощи детям в установлении связи между известными им фактами и расчетами в уме. Лучше всего это достигается с помощью моделирования и использования манипулятивных средств и т. д.
Важно, чтобы время урока было посвящено концептуальному обучению стратегиям и оказанию помощи детям в установлении связи между известными им фактами и расчетами в уме. Лучше всего это достигается с помощью моделирования и использования манипулятивных средств и т. д. .
. Помните, если вы не предоставите им возможность ею воспользоваться, они ее потеряют!
Помните, если вы не предоставите им возможность ею воспользоваться, они ее потеряют!