| Менеджмент и маркетинг РАЙНЕР ФЁЛЬКЕР • С помощью теории игр предприятие получает возможность предусмотреть ходы своих партнеров и конкурентов • Сложный инструментарий следует использовать только при принятии принципиально важных стратегических решений В последние годы значение теории игр существенно возросло во многих областях экономических и социальных наук. В экономике она применима не только для решения общехозяйственных задач, но и для анализа стратегических проблем предприятий, разработок организационных структур и систем стимулирования. Уже в момент ее зарождения, которым считают публикацию в 1944 г. монографии Дж. Неймана и О. Моргенштерна “Теория игр и экономическое поведение”, многие предсказали революцию в экономических науках благодаря использованию нового подхода. Первые работы по теории игр отличались упрощенностью предположений и высокой степенью формальной абстракции, что делало их малопригодными для практического использования. За последние 10 – 15 лет положение резко изменилось. Бурный прогресс в промышленной экономике показал плодотворность методов игр в прикладной сфере. В последнее время эти методы проникли и в управленческую практику. Вполне вероятно, что теория игр наряду с теориями трансакционных издержек и “патрон – агент” будет восприниматься как наиболее экономически обоснованный элемент теории организации. Основные положения теории игрЧтобы описать игру, необходимо сначала выявить ее участников. Это условие легко выполнимо, когда речь идет об обычных играх типа шахмат, канасты и т.п. Иначе обстоит дело с “рыночными играми”. Здесь не всегда просто распознать всех игроков, т.е. действующих или потенциальных конкурентов. Практика показывает, что не обязательно идентифицировать всех игроков, надо обнаружить наиболее важных. Игры охватывают, как правило, несколько периодов, в течение которых игроки предпринимают последовательные или одновременные действия. Эти действия обозначаются термином “ход”. Действия могут быть связаны с ценами, объемами продаж, затратами на научные исследования и разработки и т. Еще одним основным понятием данной теории является стратегия игрока. Под ней понимаются возможные действия, позволяющие игроку на каждом этапе игры выбирать из определенного количества альтернативных вариантов такой ход, который представляется ему “лучшим ответом” на действия других игроков. Относительно концепции стратегии следует заметить, что игрок определяет свои действия не только для этапов, которых фактически достигла конкретная игра, но и для всех ситуаций, включая и те, которые могут и не возникнуть в ходе данной игры. Важна и форма предоставления игры. Обычно выделяют нормальную, или матричную, форму и развернутую, заданную в виде дерева. Эти формы для простой игры представлены на рис. Чтобы установить первую связь со сферой управления, игру можно описать следующим образом. Два предприятия, производящие однородную продукцию, стоят перед выбором. В одном случае они могут закрепиться на рынке благодаря установлению высокой цены, которая обеспечит им среднюю картельную прибыль П При отсутствии жестких условий обоим предприятиям выгодно назначить низкую цену. Стратегия “низкой цены” является доминирующей для любой фирмы: вне зависимости от того, какую цену выбирает конкурирующая фирма, самой всегда предпочтительней устанавливать низкую цену. Стратегическая комбинация “низкие цены/низкие цены” с соответствующими платежами представляет собой равновесие Нэша, при котором ни одному из игроков невыгодно сепаратно отходить от выбранной стратегии. Подобная концепция равновесия является принципиальной при разрешении стратегических ситуаций, но при определенных обстоятельствах она все же требует усовершенствования. Что касается указанной выше дилеммы, то ее разрешение зависит, в частности, от оригинальности ходов игроков. Если предприятие имеет возможность пересмотреть свои стратегические переменные (в данном случае цену), то может быть найдено кооперативное решение проблемы даже без жесткого договора между игроками. Интуиция подсказывает, что при многократных контактах игроков появляются возможности добиться приемлемой “компенсации”. Так, при известных обстоятельствах нецелесообразно стремиться к краткосрочным высоким прибылям путем ценового демпинга, если в дальнейшем может возникнуть “война цен”. Как отмечалось, оба рисунка характеризуют одну и ту же игру. Предоставление игры в нормальной форме в обычном случае отражает “синхронность”. Однако это не означает “одновременность” событий, а указывает на то, что выбор стратегии игроком осуществляется в условиях неведения о выборе стратегии соперником. При развернутой форме такая ситуация выражается через овальное пространство (информационное поле). При отсутствии этого пространства игровая ситуация приобретает иной характер: сначала решение должен бы принимать один игрок, а другой мог бы делать это вслед за ним. Применение теории игр для принятия стратегических управленческих решенийВ качестве примеров здесь можно назвать решения по поводу проведения принципиальной ценовой политики, вступления на новые рынки, кооперации и создания совместных предприятий, определения лидеров и исполнителей в области инноваций, вертикальной интеграции и т. n Инструментарий теории игр особенно целесообразно применять, когда между участниками процесса существуют важные зависимости в области платежей. Ситуация с возможными конкурентами приведена на рис. 2. |
Игра в развернутой форм – Энциклопедия по экономике
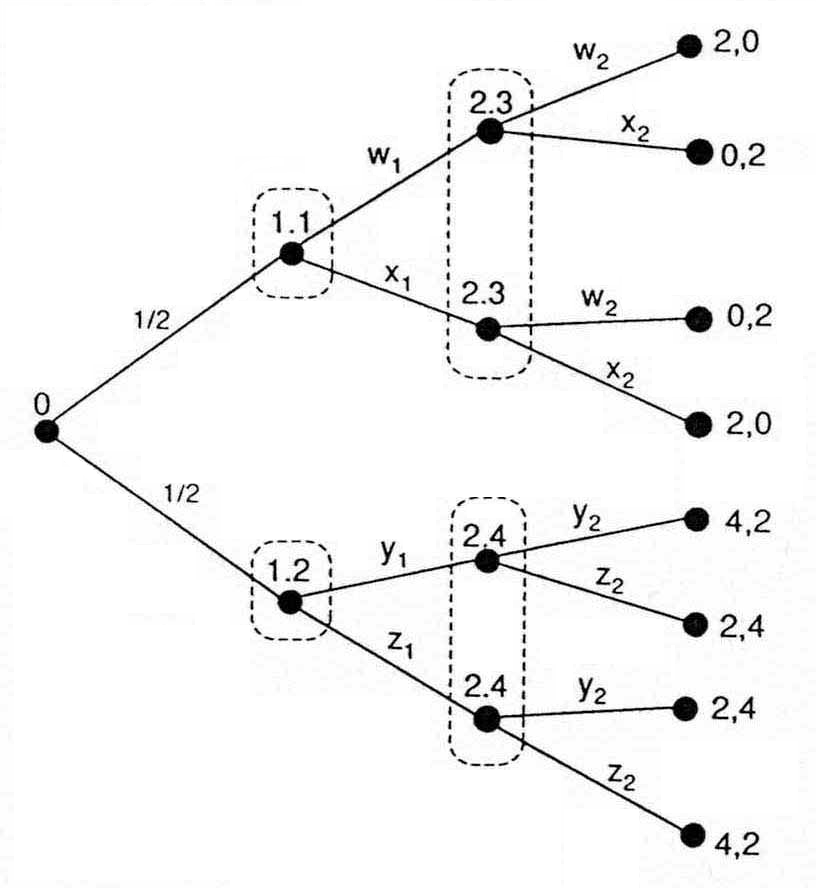
Лучший способ моделирования игры с последовательным выбором — использовать древо игры. Древо игры напоминает древо решений, за тем исключением, что в первом случае решение принимает не один, а большее число игроков. На рис. 4.6 приведен пример со стратегиями и результатами, иллюстрирующий описанный выше случай с новичком и старожилом.
| Рис. 4.6. Игра в развернутой форме с последовательным выбором |
 Если между состоянием равновесия и реальными событиями обнаруживается разница, как, по-вашему, это можно объяснить
[c.73]
Если между состоянием равновесия и реальными событиями обнаруживается разница, как, по-вашему, это можно объяснить
[c.73]Кроме того, удобно представить ситуацию как игру в развернутой форме. Можно изобразить последовательность ходов и выигрыши игроков с помощью следующего дерева игры [c.47]
Игры в развернутой форме (динамические) с совершенной информацией о ходах [c.94]
В игре в развернутой форме (чистая) стратегия — это полный план действий игрока что он будет делать в каждой из вершин, в которой ход принадлежит ему. Это должен быть действительно полный план, то есть в нем должно быть определено, что игрок выберет в любой своей вершине, даже если из каких-либо соображений ясно, что процесс игры вряд ли может привести в эту вершину. То есть это должен быть настолько полный план, что доверенное лицо игрока может использовать его в качестве инструкции, будучи уверенным, что его поведение будет совпадать с поведением самого игрока. [c.657]
Таким образом, существуют два представления любой игры — представление в нормальной и развернутой форме. Выше мы показали, как динамическую игру с совершенной информацией представить в нормальной форме, а статическую игру — в развернутой форме. Таким образом, любую динамическую игру с совершенной информацией можно представить в нормальной форме, а затем, — на основе этой нормальной формы — построить развернутую форму соответствующей игры. Приведем пример такого построения.
[c.666]
Выше мы показали, как динамическую игру с совершенной информацией представить в нормальной форме, а статическую игру — в развернутой форме. Таким образом, любую динамическую игру с совершенной информацией можно представить в нормальной форме, а затем, — на основе этой нормальной формы — построить развернутую форму соответствующей игры. Приведем пример такого построения.
[c.666]
Этой нормальной форме соответствует дерево игры, представленное на Рис. 166. Как видим, при таком двойном переводе частично потеряна информация о структуре игры и мы получили другую игру в развернутой форме. Очевидно, что принципиально разным играм может соответствовать одна и та же нормальная форма. [c.666]
Игра в развернутой (экстенсивной) форме [c.466]
Равновесие Нэша (NE). NE при наблюдаемых ходах и близоруком поведении, или в популяции участников. NE в развернутой форме игры игра “перекресток” – борьба за лидерство. Соответствие между развернутой и нормальной формами игры. NE в примерах с непрерывной стратегией ценовое соревнование взаимозаменяемых товаров. Вложение DE в NE.
[c.93]
Вложение DE в NE.
[c.93]
Представление игры в виде дерева соответствует развернутой форме игры. В дальнейшем мы увидим, как можно представить динамическую игру в нормальной форме. А сейчас перечислим, что должно включать описание динамической игры (с совершенной информацией) в развернутой форме [c.654]
Множество игроков, конечно, должно быть одним и тем же в нормальной форме и в развернутой форме игры. Прежде всего уточним понятие стратегии для игр такого типа. [c.657]
В СССР система С. ф. складывалась постепенно. На различных этапах социалистич. строительства разные виды С. ф. играли ведущую роль. В период военного коммунизма преобладали государственные натуральные С. ф. Впоследствии (в 20-х гг.) главное значение приобрел фонд государственного страхования, к-рый обслуживал и государственный сектор произ-ва. В период коллективизации с. х-ва стали возникать колхозные С. ф. С переходом на централизованный метод создания С. ф. через государственный бюджет постепенно суживалась сфера применения фонда государственного страхования. Большое значение, особенно в послевоенные годы, получили общественные фонды потребления, имеющие в известной мере значение С. ф. (фонды социального страхования и социального обеспечения), возросло значение фонда государственного личного страхования. В период развернутого коммунистич. строительства роль С. ф. повышается. Они во все большей степени содействуют слаженности и бесперебойности производственного процесса, поддержанию определенного уровня жизни людей. С построением материально-технич. базы коммунизма и переходом к единой общенародной форме собственности отпадет необходимость в разнообразных формах С. ф. Коммунистич. об-во будет располагать мощным централизованным резервным фондом, полностью гарантирующим бесперебойность общественного вос-произ-ва и высокий уровень жизни трудящихся.
[c.396]
Большое значение, особенно в послевоенные годы, получили общественные фонды потребления, имеющие в известной мере значение С. ф. (фонды социального страхования и социального обеспечения), возросло значение фонда государственного личного страхования. В период развернутого коммунистич. строительства роль С. ф. повышается. Они во все большей степени содействуют слаженности и бесперебойности производственного процесса, поддержанию определенного уровня жизни людей. С построением материально-технич. базы коммунизма и переходом к единой общенародной форме собственности отпадет необходимость в разнообразных формах С. ф. Коммунистич. об-во будет располагать мощным централизованным резервным фондом, полностью гарантирующим бесперебойность общественного вос-произ-ва и высокий уровень жизни трудящихся.
[c.396]
Эта форма обмена, выражающая новую ступень его развития, носит название полной, или развернутой, формы стоимости. Она характеризует расширение и упрочение производственных связей. В этих условиях возрастает и значение точности количественных соотношений между товарами, поскольку обмен начинает играть все большую роль в возмещении затраченного на их производство труда.
[c.52]
В этих условиях возрастает и значение точности количественных соотношений между товарами, поскольку обмен начинает играть все большую роль в возмещении затраченного на их производство труда.
[c.52]
Противоречия развернутой формы стоимости преодолеваются в ходе развития товарного производства и обмена. По мере того как в результате разделения труда между земледелием, скотоводством и ремеслом увеличивалось производство товаров на рынок, среди них все более выделялись товары, пользующиеся всеобщим спросом. У скотоводческих племен таким товаром был скот, у земледельцев – зерно, кофе, у охотничьих племен – шкуры диких зверей и т.д. В этом случае возникающие противоречия развернутой формы стоимости начинают разрешаться через одну ступень товарного обмена все товары выражали свою относительную стоимость только в одном из них, но пользующимся всеобщим спросом. Получаются ряды товарного обмена, в которых разные товары в определенных пропорциях обмениваются на один и тот же товар. Например, 0,25 т пшеницы = 1 овце, 0,5 бочонка меда = 2 овцам, 7,5 м ткани = 1 овце и т. д. Овцы на таком рынке играют роль всеобщей формы стоимости всех остальных товаров, как это и было у скотоводческих народов.
[c.145]
д. Овцы на таком рынке играют роль всеобщей формы стоимости всех остальных товаров, как это и было у скотоводческих народов.
[c.145]
Как видим, развернутая форма игр с несовершенной информацией несколько более сложна, чем развернутая форма игр с совершенной информацией. Дополнительно к тем составляющим, которые были указаны в прежнем определении, требуется также перечислить информационные множества, которые задают разбиение множества вершин (кроме конечных). Информационные множества должны быть заданы так, чтобы каждая вершина, кроме конечных, принадлежала одному и только одному из них. Кроме того, по смыслу определения информационного множества, во всех его вершинах ход должен принадлежать одному и тому же игроку. [c.665]
Таким образом, нормальная форма игры не является в общем случае адекватной для описания динамических игр. С помощью нее можно представлять корректно только статические игры. Если операцию двойного перевода из развернутой формы в нормальную и обратно осуществить со статической игрой, представленной на Рис. 163, то дерево игры не поменяется (с точностью до выбора порядка ходов, что в данном случае несущественно).
[c.666]
163, то дерево игры не поменяется (с точностью до выбора порядка ходов, что в данном случае несущественно).
[c.666]
Игры могут быть представлены в нормальной (матричной) и развернутой (в виде древа игры) формах. Как правило, игры с одновременным выбором представлены нормальной формой, а игры с последовательным выбором — развернутой. [c.70]
ДЕНЬГИ И ДЕНЕЖНОЕ ОБРАЩЕНИЕ в СССР. Деньги являются особым товаром — всеобщим эквивалентом в нем выражается стоимость всех других товаров и при его посредстве непрерывно совершается обмен продуктами труда между товаропроизводителями. Деньги возникли несколько тысяч лет тому назад в связи с появлением и развитием товарного обмена. При социализме деньги как общий эквивалент всех товаров являются необходимой и всеобщей формой планомерного учета затрат общественного труда, хозрасчетной организации произ-ва и распределения общественного продукта, контроля над мерой труда и потребления. Деньги будут существовать и играть важную роль в течение всего периода развернутого строительства коммунизма В коммунистическом строительстве,— подчеркивается в Программе Коммунистической партии Сов. Союза,— необходимо полностью использовать товарно-денежные отношения в соответствии с новым содержанием, присущим им в период социализма (1961, с. 89). Деньги отомрут на высшей фазе коммунизма, когда произойдет переход к единой коммунистич. форме собственности и когда не будет необходимости в товарных отношениях, связанных с распределением общественного продукта среди трудящихся по количеству и качеству труда и в хозрасчетных товарных отношениях между социалистич. предприятиями.
[c.186]
Союза,— необходимо полностью использовать товарно-денежные отношения в соответствии с новым содержанием, присущим им в период социализма (1961, с. 89). Деньги отомрут на высшей фазе коммунизма, когда произойдет переход к единой коммунистич. форме собственности и когда не будет необходимости в товарных отношениях, связанных с распределением общественного продукта среди трудящихся по количеству и качеству труда и в хозрасчетных товарных отношениях между социалистич. предприятиями.
[c.186]
Для формального анализа игру обычно записывают в одной из форм развернутой (детальное описание возможных ходов), характеристической (описываются значения выигрышей каждой коалиции, для анализа кооперативных игр) или стратегической (нормальной). Последний вариант, изучаемый далее, означает, что игра есть [c.3]
Не изучаемое здесь, но популярное, понятие PNE (обычно называемое просто “Perfe t Equilibrium”) задается для игр в развернутой форме с деревом последовательности ходов. Это понятие означает, что исход х g PNE является Нэшевским равновесием не только во всей игре, но и во всех подыграх (ветвях дерева). [c.5]
[c.5]
Более важная теорема Куна на эту тему касается игр в развернутой форме из нее, в частности, следует, что в шахматах есть SE (оно пока неизвестно). [c.7]
ДЕРЕВО ИГРЫ [game tree] — способ описания игры с помощью графа “дерево”, последовательно по ходам фиксирующего, какой информацией располагают игроки перед каждым ходом, какие варианты они могут выбирать и какими могут быть предельные размеры платежей в конце игры. Игра, описываемая с помощью подобного “дерева”, называется игрой в развернутой (экстенсивной) форме, а иногда — позиционной игрой. [c.77]
Подыгра игры G, где G — игра с совершенной информацией в развернутой форме, — это игра, построенная на основе исходной игры. Начальной вершиной подыгры служит любая вершина исходной игры, кроме конечных. В подыгру входят все вершины, следующие за ее начальной вершиной. Выигрыши в подыгре совпадают с выигрышами в соответствующих конечных вершинах полной игры. [c.660]
ФОРМА СТОИМОСТИ – форма выражения стоимости товара на различных этапах развития товарного производства и обмена. Стоимость как общественное свойство товара может проявиться лишь при приравнивании одного товара к другому в процессе обмена. Обобщив огромный материал по истории обмена, К. Маркс впервые проанализировал процесс развития формы стоимости. Ступени этого процесса таковы I) простая, единичная, или случайная, форма стоимости, 2) полная, или развернутая, 3) всеобщая и 4) денежная форма стоимости. Простая, единичная, или случайная, форма стоимости свойственна начальному этапу развития товарного производства, когда продукты труда превращались в товары лишь посредством единичных и случайных актов обмена. При простой форме стоимость отдельного товара только случайно выражалась в каком-либо другом товаре. Она может быть представлена уравнением товар А = товару Б. В данном случае два разнородных товара — товар А и товар Б — играют две различные роли. Товар А выражает свою стоимость в товаре Б, поэтому он играет активную роль и находится в относительной форме стоимости. Товар Б служит материалом для выражения стоимости товара А, играет пассивную роль и находится в эквивалентной форме стоимости.
Стоимость как общественное свойство товара может проявиться лишь при приравнивании одного товара к другому в процессе обмена. Обобщив огромный материал по истории обмена, К. Маркс впервые проанализировал процесс развития формы стоимости. Ступени этого процесса таковы I) простая, единичная, или случайная, форма стоимости, 2) полная, или развернутая, 3) всеобщая и 4) денежная форма стоимости. Простая, единичная, или случайная, форма стоимости свойственна начальному этапу развития товарного производства, когда продукты труда превращались в товары лишь посредством единичных и случайных актов обмена. При простой форме стоимость отдельного товара только случайно выражалась в каком-либо другом товаре. Она может быть представлена уравнением товар А = товару Б. В данном случае два разнородных товара — товар А и товар Б — играют две различные роли. Товар А выражает свою стоимость в товаре Б, поэтому он играет активную роль и находится в относительной форме стоимости. Товар Б служит материалом для выражения стоимости товара А, играет пассивную роль и находится в эквивалентной форме стоимости. Превращение простой, единичной, или случайной, формы стоимости в полную, или развернутую, обуслов-
[c.444]
Превращение простой, единичной, или случайной, формы стоимости в полную, или развернутую, обуслов-
[c.444]
Совершенное в подыграх равновесие (SPE). Игра “Пилот и террорист”. Обратная индукция (алгоритм Куна) для нахождения SPE. Связь между развернутой и нормальной формами игры. Примеры повестки дня при голосовании, игра в спички, “пираты”, конечные и бесконечные процедуры торга по Нэшу в игре “дележ пирога с дисконтированием”. Отношение SPE к NE, к SE. Теоремы существования SPE, SE, и единственность при “неповторимости исходов”. [c.94]
Командный тренинг корпоративного управления фирмой осуществляется в форме участия обучающихся в комплексной компьютерной деловой игре, имитирующей деятельность производственной организации в реальном масштабе времени, в приближенных к реальным условиях конкуренции. Приводится развернутое описание компьютерной деловой игры СИПРОМЕК, рекомендуемой авторами для командного тренинга. [c.8]
(PDF) Teoriya igr v upravlenii organizatsionnymi sistemami (Game Theory for Mechanism Design in Organizations)
ВВЕДЕНИЕ
Данная книга посвящена описанию подходов и результатов
теории игр
к постановке и решению задач управления организа-
ционными системами. Теория игр – раздел прикладной матема-
Теория игр – раздел прикладной матема-
тики, исследующий модели принятия решений в условиях несов-
падения интересов сторон (игроков
), когда каждая сторона стре-
мится воздействовать на развитие ситуации в собственных инте-
ресах [19].
Среди литературы по теории игр можно выделить: моногра-
фии [1, 3, 5, 18, 19, 21, 20, 23, 26, 33, 35, 41, 42, 48, 62, 63, 74, 81,
82, 87 и др.], содержащие изложение фундаментальных результа-
тов; малочисленные, к сожалению, учебные пособия [20, 24, 35,
37, 47, 46, 62, 65, 74, 79, 82] и сборники задач и упражнений [30,
45]. Основной акцент при описании прикладных результатов
обычно делается на применении теоретико-игровых моделей в
социальных, экономических системах и в военном деле. Наряду с
этим, аппарат теории игр широко используют многочисленные
математические модели управления организационными система-
ми [9-14, 21, 29, 37, 49-58, 79, 80, 83, 85], многие из которых изу-
чаются в ВУЗах при подготовке специалистов по управлению.
Конечно, в рамках учебного пособия невозможно, да и нецелесо-
образно, привести детальную картину современного состояния
теория игр (так, ниже, например, практически не рассматривают-
ся дифференциальные [1, 28, 32, 33] и повторяющиеся [21, 33, 52,
58, 74, 82] игры). Такая задача и не ставится. Цель данной книги
– дать общее представление о подходах и результатах теории игр,
которые используются в моделях управления именно организа-
ционными системами. Многочисленные ссылки дают возмож-
Под игрой будем понимать взаимодействие сторон, интересы кото-
рых не совпадают. Возможны и другие определения игры – см. [5, 6,
19, 20, 21, 48, 62, 65]. В частности, в [67, C.475] приводится следую-
щее определение: «Игра – вид непродуктивной деятельности, мотив
которой заключается не в ее результатах, а в самом процессе».
Понятия, вводимые впервые, выделены курсивом. Основные определе-
ния выделены рубленым шрифтом.
Создание таблицы и добавление полей
В базе данных можно хранить данные в виде таблиц — тематических списков строк и столбцов. Например, вы можете создать таблицу “Контакты” для хранения имен, адресов и телефонных номеров или таблицу “Товары” для хранения сведений о товарах. В этой статье описано, как создать таблицу, добавить в нее поля, настроить первичный ключ и свойства таблицы и полей.
Перед созданием таблиц и добавлением полей изучите основные понятия. Дополнительные сведения см. в статье Общие сведения о таблицах.
В этой статье
Создание таблицы
В простой базе данных, такой как список контактов, может быть всего одна таблица. Однако во многих базах данных используется несколько таблиц. При создании базы данных на компьютере создается файл, который используется как контейнер для всех ее объектов, включая таблицы.
Есть несколько способов создать таблицу: вы можете создать новую базу данных, вставить таблицу в существующую базу данных или импортировать таблицу из другого источника данных, например книги Microsoft Office Excel, документа Microsoft Office Word, текстового файла или другой базы данных, либо связать таблицу с этим источником. Когда вы создаете новую базу данных, в нее автоматически вставляется новая пустая таблица. Затем вы можете ввести в нее данные, чтобы начать определение полей.
Когда вы создаете новую базу данных, в нее автоматически вставляется новая пустая таблица. Затем вы можете ввести в нее данные, чтобы начать определение полей.
К началу страницы
Создание таблицы в новой базе данных
-
Щелкните Файл > Создать и выберите пункт Пустая база данных рабочего стола.
-
В поле Файл введите имя файла новой базы данных.
-
Чтобы сохранить базу данных в другом месте, щелкните значок папки.
-
Нажмите кнопку Создать.
Откроется новая база данных, в которой будет создана и открыта в режиме таблицы новая таблица с именем “Таблица1”.
К началу страницы
Создание таблицы в существующей базе данных
-
Щелкните Файл > Открыть и выберите базу данных, если она указана в разделе Последние.
 В противном случае выберите один из вариантов поиска базы данных.
В противном случае выберите один из вариантов поиска базы данных. -
В диалоговом окне Открытие файла базы данных найдите базу данных, которую вы хотите открыть,и нажмите кнопку Открыть.
-
на вкладке Создание в группе Таблицы нажмите кнопку Таблица.
В базу данных будет вставлена новая таблица, которая откроется в режиме таблицы.
К началу страницы
Использование импорта или связывания для создания таблицы
Чтобы создать таблицу, вы можете импортировать данные из другого файла (например, из листа Excel, списка SharePoint, XML-файла, другой базы данных Access, папки Microsoft Outlook и т. д.) либо связать таблицу с ним.
При импорте данных создается их копия в новой таблице текущей базы данных. Последующие изменения, вносимые в исходные данные, не будут влиять на импортированные данные, и наоборот. После подключения к источнику и импорта данных можно использовать импортированные данные без подключения к источнику. В структуру импортированной таблицы можно вносить изменения.
Последующие изменения, вносимые в исходные данные, не будут влиять на импортированные данные, и наоборот. После подключения к источнику и импорта данных можно использовать импортированные данные без подключения к источнику. В структуру импортированной таблицы можно вносить изменения.
Когда осуществляется связывание с данными, в текущей базе данных создается связанная таблица, обеспечивающая динамическое подключение к данным, хранящимся в другом месте. Изменения данных в связанной таблице отражаются в источнике, а изменения в источнике — в связанной таблице. Для работы со связанной таблицей необходимо подключение к источнику данных. Изменить структуру связанной таблицы нельзя.
Примечание: Нельзя изменять данные на листе Excel с помощью связанной таблицы. В качестве обходного способа можно импортировать исходные данные в базу данных Access, а затем создать связь с базой данных из Excel.
К началу страницы
Создание таблицы с помощью импорта внешних данных или связи с ними
-
Откройте меню Файл и выберите команду Открыть.

-
В диалоговом окне Открытие файла базы данных выберите и откройте базу данных, в которой вы хотите создать таблицу.
-
На вкладке Внешние данные в группе Импорт и связи выберите один из доступных источников данных.
-
Следуйте инструкциям в появляющихся диалоговых окнах.
Будет создана таблица, имя которой появится в области навигации.
К началу страницы
Для создания таблицы базы данных можно использовать импортировать список SharePoint или создать связь с ним. Кроме того, вы можете создать новый список SharePoint на основе готового шаблона. В Access доступны такие шаблоны, как “Контакты”, “Задачи”, “Вопросы” и “События”.
Кроме того, вы можете создать новый список SharePoint на основе готового шаблона. В Access доступны такие шаблоны, как “Контакты”, “Задачи”, “Вопросы” и “События”.
-
Откройте меню Файл и выберите команду Открыть.
-
В диалоговом окне Открытие файла базы данных выберите базу данных, в которой вы хотите создать таблицу, и нажмите кнопку Открыть.
-
На вкладке Создание в группе Таблицы нажмите кнопку Списки SharePoint.
-
Выполните одно из указанных ниже действий.
Создание списка SharePoint на основе шаблона
-
Выберите пункт Контакты, Задачи, Вопросы или События.

-
В диалоговом окне Создание нового списка введите URL-адрес сайта SharePoint, на котором вы хотите создать список.
-
Введите имя и описание для нового списка в полях Укажите имя нового списка и Описание.
-
Чтобы открыть связанную таблицу после ее создания, установите флажок Открыть список по окончании экспорта (он установлен по умолчанию).
Создание настраиваемого списка
-
Выберите пункт Другой.
-
В диалоговом окне Создание нового списка введите URL-адрес сайта SharePoint, на котором вы хотите создать список.

-
Введите имя и описание для нового списка в полях Укажите имя нового списка и Описание.
-
Чтобы открыть связанную таблицу после ее создания, установите флажок Открыть список по окончании экспорта (он установлен по умолчанию).
Импорт данных из существующего списка
-
Выберите пункт Существующий список SharePoint.
-
В диалоговом окне Внешние данные введите URL-адрес сайта SharePoint, содержащего данные, которые нужно импортировать.
-
Выберите пункт Импортировать данные источника в новую таблицу в текущей базе данных и нажмите кнопку Далее.

-
Установите флажки всех списков SharePoint, которые нужно импортировать.
Связь со списком
-
Выберите пункт Существующий список SharePoint.
-
В диалоговом окне Внешние данные — сайт SharePoint введите URL-адрес сайта SharePoint, содержащего список, связь с которым нужно создать.
-
Выберите пункт Создать связанную таблицу для связи с источником данных и нажмите кнопку Далее.
-
Установите флажки всех списков SharePoint, связи с которыми нужно создать.
-
К началу страницы
Создание таблицы с использованием веб-службы
В базе данных можно создать таблицу, подключенную к данным на веб-сайте с интерфейсом веб-службы. Таблицы веб-служб доступны только для чтения.
Таблицы веб-служб доступны только для чтения.
-
На вкладке Внешние данные в группе Импорт и связи нажмите кнопку Дополнительно и выберите команду Службы данных.
-
Если нужное подключение уже установлено, перейдите к действию 5. В противном случае перейдите к следующему действию.
-
Нажмите кнопку Установить новое подключение.
-
Выберите нужный файл подключения и нажмите кнопку ОК.
-
В диалоговом окне Создание связи с данными веб-службы разверните нужное подключение.
-
Выберите таблицу, связь с которой требуется создать. Ее поля отобразятся в правой части диалогового окна.

-
Можно ввести имя связанной таблицы в поле Укажите имя ссылки. Access будет выводить это имя связанной таблицы в области навигации.
-
Нажмите кнопку ОК. Будет создана связанная таблица.
К началу страницы
Настройка свойств таблицы
Кроме настройки свойств полей, можно задать свойства, которые применяются ко всей таблице или ко всем записям.
-
Выберите таблицу, для которой требуется задать свойства.
-
На вкладке Главная в группе Представления нажмите кнопку Представление и выберите пункт Конструктор.
-
На вкладке Конструктор в группе Показать или скрыть выберите пункт Страница свойств.

Откроется страница свойств таблицы.
-
На странице свойств откройте вкладку Общие.
-
Щелкните поле слева от свойства, которое вы хотите задать, и введите значение.
Чтобы сохранить изменения, не забудьте нажать клавиши CTRL+S.
Свойство таблицы
Задача
Представления на веб-сайте SharePoint
Укажите, должны ли представления, основанные на таблице, отображаться на сайте SharePoint.

Примечание: Действие этого параметра зависит от значения свойства базы данных Отображать все представления на сайте SharePoint.
Развернутая подтаблица
Укажите, следует ли развертывать все подтаблицы при открытии таблицы.
Высота подтаблицы
Выполните одно из указанных ниже действий.
-
Чтобы в окне подтаблицы отображались все строки, оставьте значение 0.

-
Чтобы задать высоту подтаблицы, введите нужное значение.
Ориентация
Укажите направление отображения данных в соответствии с направлением письма (слева направо или справа налево).
Описание
Укажите описание таблицы, которое будет появляться в качестве всплывающей подсказки для этой таблицы.
Режим по умолчанию
Укажите режим открытия таблицы, используемый по умолчанию (Режим таблицы, Сводная таблица или Сводная диаграмма).
 Режимы сводной таблицы и сводной диаграммы в Access недоступны, начиная с Access 2013.
Режимы сводной таблицы и сводной диаграммы в Access недоступны, начиная с Access 2013.Условие на значение
Введите выражение, которое должно быть истинно при добавлении или изменении любой записи.
Сообщение об ошибке
Введите сообщение, отображаемое в том случае, если запись не соответствует выражению в свойстве Правило проверки.
Фильтр
Определите условия отображения строк в режиме таблицы.

Порядок сортировки
Выберите одно или несколько полей, чтобы задать порядок сортировки по умолчанию для строк в режиме таблицы.
Имя подтаблицы
Укажите, должна ли подтаблица отображаться в режиме таблицы. Если да, укажите таблицу или запрос, из которых подтаблица должна получать строки.
Подчиненные поля
Укажите поля в таблице или запросе, используемые в подтаблице и соответствующие свойству Основные поля, заданному для таблицы.

Основные поля
Укажите поля таблицы, соответствующие свойству Подчиненные поля, заданному для таблицы.
Фильтр при загрузке
Укажите, необходимо ли автоматически применять условия фильтра, заданные с помощью свойства Фильтр (если присвоено значение Да), при открытии таблицы в режиме таблицы.
Сортировка при загрузке
Укажите, необходимо ли автоматически применять условия сортировки, заданные с помощью свойства Порядок сортировки (если присвоено значение Да), при открытии таблицы в режиме таблицы.

Совет. Если в поле свойства недостаточно места для ввода или изменения значения, нажмите сочетание клавиш SHIFT+F2, чтобы открыть поле Область ввода. Если при назначении выражению свойства Правило проверки требуется помощь, нажмите кнопку рядом с полем свойства Правило проверки, чтобы открыть построитель выражений.
-
К началу страницы
Сохранение таблицы
После создания или изменения таблицы следует сохранить ее структуру. При первом сохранении таблице необходимо присвоить имя, описывающее содержащиеся в ней данные. Можно использовать до 64 знаков (букв или цифр), включая пробелы. Например, вы можете назвать таблицу “Клиенты”, “Перечень запасных частей” или “Товары”.
Access предоставляет вам гибкие возможности при именовании таблиц, однако есть и некоторые ограничения. Имя может сдержать до 64 знаков, включать любое сочетание букв, цифр, пробелов и специальных символов, за исключением точек (.), восклицательных знаков (!), квадратных скобок ([]), начального пробела, начального знака равенства (=) или непечатаемых символов, таких как возврат каретки. Кроме того, имя не должно содержать следующие символы: ` / \ : ; * ? ” ‘ < > | # <TAB> { } % ~ &.
Имя может сдержать до 64 знаков, включать любое сочетание букв, цифр, пробелов и специальных символов, за исключением точек (.), восклицательных знаков (!), квадратных скобок ([]), начального пробела, начального знака равенства (=) или непечатаемых символов, таких как возврат каретки. Кроме того, имя не должно содержать следующие символы: ` / \ : ; * ? ” ‘ < > | # <TAB> { } % ~ &.
Совет: Договоритесь о том, по какому принципу будете называть объекты в базе данных, и следуйте этим правилам.
-
Выберите Файл > Сохранить или нажмите клавиши CTRL+S.
-
Если вы сохраняете таблицу в первый раз, введите ее имя и нажмите кнопку ОК.
К началу страницы
Настройка первичного ключа
Для таблицы следует задать первичный ключ, если только у вас нет веских оснований не делать этого. Access автоматически создает индекс для первичного ключа, что повышает производительность базы данных. Кроме того, Access гарантирует, что каждая запись имеет значение в поле первичного ключа и это значение всегда уникально. Это крайне важно, поскольку в противном случае нельзя надежно отличить одну строку от другой.
Access автоматически создает индекс для первичного ключа, что повышает производительность базы данных. Кроме того, Access гарантирует, что каждая запись имеет значение в поле первичного ключа и это значение всегда уникально. Это крайне важно, поскольку в противном случае нельзя надежно отличить одну строку от другой.
При создании таблицы в режиме таблицы Access автоматически создает первичный ключ с именем “Код” и присваивает ему тип данных “Счетчик”.
Изменить или удалить первичный ключ, а также задать первичный ключ для таблицы, в которой его еще нет, можно в Конструкторе.
К началу страницы
Определение полей, используемых в качестве первичного ключа
Иногда данные, которые можно использовать в качестве первичного ключа, уже есть. Например, у сотрудников уже могут быть идентификационные номера. Если вы создаете таблицу для отслеживания данных о сотрудниках, в качестве первичного ключа можно использовать их идентификаторы. Иногда идентификаторы сотрудников уникальны только в сочетании с кодами отделов; в этом случае в качестве первичного ключа необходимо использовать сочетание этих полей. Первичный ключ должен обладать следующими характеристиками:
Иногда идентификаторы сотрудников уникальны только в сочетании с кодами отделов; в этом случае в качестве первичного ключа необходимо использовать сочетание этих полей. Первичный ключ должен обладать следующими характеристиками:
-
Значение данного поля или сочетания полей должно быть уникальным для каждой записи.
-
Поле или сочетание полей не должно быть пустым (у них всегда должно быть значение).
-
Значения не должны изменяться.
Если данных, подходящих на роль первичного ключа, нет, для этого можно создать новое поле. При создании поля для использования в качестве первичного ключа выберите для него тип “Счетчик” — это обеспечит соответствие трем характеристикам, указанным выше.
К началу страницы
Настройка или изменение первичного ключа
-
Выберите таблицу, для которой вы хотите задать или изменить первичный ключ.

-
На вкладке Главная в группе Представления нажмите кнопку Представление и выберите пункт Конструктор.
-
На бланке таблицы выберите поле или поля, которые вы хотите использовать в качестве первичного ключа.
Чтобы выделить одно поле, щелкните область выделения строки для него.
Чтобы выделить несколько полей, щелкните область выделения для каждого поля, удерживая нажатой клавишу CTRL.
-
На вкладке Конструктор в группе Элементы нажмите кнопку Ключевое поле.
Индикатор ключа будет добавлен слева от поля или полей, определенных как первичный ключ.
К началу страницы
Удаление первичного ключа
-
Выберите таблицу, первичный ключ которой вы хотите удалить.

-
На вкладке Главная в группе Представления нажмите кнопку Представление и выберите пункт Конструктор.
-
Щелкните область выделения строки для текущего первичного ключа. Если первичный ключ состоит из нескольких полей, щелкните область выделения строки для каждого из них, удерживая нажатой клавишу CTRL.
-
На вкладке Конструктор в группе Элементы нажмите кнопку Ключевое поле.
Индикатор ключа будет удален из поля или полей, ранее определенных в качестве первичного ключа.
Если попытаться сохранить новую таблицу без первичного ключа, Access предложит создать поле для него. Если нажать кнопку Да, Access создаст поле “Код” с типом данных “Счетчик”, в котором будет хранится уникальное значение для каждой записи. Если в таблице уже есть поле с типом “Счетчик”, оно будет использовано в качестве первичного ключа. Если нажать кнопку Нет, Access не добавит новое поле и не задаст первичный ключ.
Если в таблице уже есть поле с типом “Счетчик”, оно будет использовано в качестве первичного ключа. Если нажать кнопку Нет, Access не добавит новое поле и не задаст первичный ключ.
К началу страницы
Добавление полей
Чтобы сохранить новый фрагмент данных для уже имеющейся таблицы Access, рекомендуется добавить в нее поле. Например, предположим, что есть таблица с полями, в которых указаны фамилия, имя, адрес электронной почты, номер телефона и почтовый адрес каждого клиента. Если нужно начать отслеживать предпочтительный способ связи для каждого клиента, для хранения таких данных добавляется поле.
Все элементы данных, которые необходимо отслеживать, хранятся в отдельных полях. Например, в таблице контактов можно создать поля “Имя”, “Фамилия”, “Телефон” и “Адрес”, а в таблице товаров — поля “Название товара”, “Код товара” и “Цена”.
У каждого поля есть некоторые основные характеристики, например имя, которое уникальным образом определяет его в пределах таблицы, тип данных, указывающий на характер данных, операции, которые можно выполнять с данными, и объем места, выделяемого для каждого значения.
Прежде чем создавать поля, разделите данные на минимальные полезные элементы. Потом вам будет намного проще объединить данные, чем разделить их. Например, вместо поля “Полное имя” лучше создать отдельные поля “Имя” и “Фамилия”. Благодаря этому вам будет проще искать и сортировать данные по имени, фамилии или их сочетанию. Если вы собираетесь создавать отчет, выполнять сортировку, поиск или вычисления по элементу данных, выделите его в отдельное поле.
Для поля можно задать свойства, определяющие его вид и поведение. Например, свойство Формат задает отображение данных в таблице или форме, включающей поле.
К началу страницы
Добавление поля путем ввода данных
Чтобы при создании новой или открытии существующей таблицы в режиме таблицы добавить в нее поле, введите данные в столбец таблицы Добавить поле(1). В зависимости от того, какое значение введено, тип данных для поля назначается автоматически. Если введенное значение не имеет определенного типа данных, Access выбирает текстовый тип, но при необходимости его можно изменить.
В зависимости от того, какое значение введено, тип данных для поля назначается автоматически. Если введенное значение не имеет определенного типа данных, Access выбирает текстовый тип, но при необходимости его можно изменить.
Ввод данных в столбец Добавить поле:
-
Чтобы создать или открыть таблицу в режиме таблицы, в области навигации щелкните нужную таблицу правой кнопкой мыши и затем в контекстном меню выберите пункт Режим таблицы.
-
Введите имя создаваемого поля в столбец Добавить поле.
Используйте описательное имя, помогающее идентифицировать поле.
-
Введите данные в новое поле.
К началу страницы
Добавление поля с помощью шаблона
Иногда проще выбрать поле из готового списка, чем создавать его вручную. Для выбора поля из списка шаблонов используется список Другие поля. Шаблон поля – это заданный набор характеристик и свойств, описывающих его. Определение шаблона поля включает имя поля, тип данных, значение свойства Формат и ряд других свойств.
Для выбора поля из списка шаблонов используется список Другие поля. Шаблон поля – это заданный набор характеристик и свойств, описывающих его. Определение шаблона поля включает имя поля, тип данных, значение свойства Формат и ряд других свойств.
-
На вкладке Главная в группе Представления нажмите кнопку Представление и выберите пункт Режим таблицы.
-
На вкладке Поля в группе Добавление и удаление нажмите кнопку Другие поля.
-
Чтобы вставить новый столбец, выберите поле в списке Другие поля. Access помещает поле справа от столбца, в котором находится курсор. Если вы выберете один из заголовков Quick Start, например “Адрес”, Access воздаст множество полей в таблице для разных составляющих частей адреса.

К началу страницы
Задание свойств полей
Для поля можно задать свойства, определяющие его вид и поведение.
Например, с помощью свойств поля можно:
-
изменить вид данных в поле;
-
предотвратить ввод неправильных данных в поле;
-
задать для поля значение по умолчанию;
-
ускорить поиск и сортировку по полю.
Некоторые свойства поля можно настроить в режиме таблицы, однако для доступа ко всем свойствам и их настройки необходимо использовать конструктор.
Настраиваемые свойства зависят от типа данных поля.
К началу страницы
Задание свойств поля в режиме таблицы
В режиме таблицы можно переименовать поле, изменить его тип, свойство Формат и некоторые другие свойства.
-
В области навигации щелкните правой кнопкой мыши таблицу, которую вы хотите открыть.
-
В контекстном меню выберите пункт Режим таблицы.
К началу страницы
Переименование поля
Когда вы добавляете поле путем ввода данных в режиме таблицы, Access автоматически присваивает ему универсальное имя. Первому новому полю назначается имя “Поле1”, второму — “Поле2” и т. д. По умолчанию имя поля используется в качестве его метки везде, где поле отображается (например, в заголовке столбца таблицы). Если вы присвоите полям описательные имена, вам будет легче просматривать и изменять записи.
-
Щелкните правой кнопкой мыши заголовок поля, которое требуется переименовать (например, “Поле1”).

-
В контекстном меню выберите пункт Переименовать поле.
-
Введите новое имя в заголовок поля.
Имена полей могут содержать до 64 символов (цифр или букв), включая пробелы.
К началу страницы
Изменение типа данных поля
При создании поля путем ввода данных в режиме таблицы приложение Access анализирует данные, чтобы определить подходящий тип данных для поля. Например, если ввести значение 01.01.2017, Access распознает его как дату и назначит полю тип даты-времени. Если Access не может однозначно определить тип данных, по умолчанию полю назначается текстовый тип. (Короткий текст, если используется Access 2016).
Тип данных поля определяет, какие еще свойства вы можете для него задать. Например, свойство Только добавление можно задать только для поля с типом данных “Гиперссылка” или “Поле МЕМО” (или “Длинный текст” в Access 2016).
Например, свойство Только добавление можно задать только для поля с типом данных “Гиперссылка” или “Поле МЕМО” (или “Длинный текст” в Access 2016).
Бывают ситуации, когда нужно изменить тип данных поля вручную. Представьте, что вам нужно ввести номера комнат, напоминающие даты (например, 10.2017). Если ввести значение 10.2017 в новое поле в режиме таблицы, функция автоматического определения типа данных выберет для поля тип данных “Дата и время”. Поскольку номера комнат являются метками, а не датами, для них должен быть установлен тип данных “Текст”. Чтобы изменить тип данных поля, выполните указанные ниже действия.
-
На ленте откройте вкладку Поля.
-
В группе Форматирование в списке Тип данных выберите нужный тип данных.
Доступные типы данных
Полный список доступных типов данных для баз данных Access вы найдете в статье Типы данных для баз данных Access рабочего стола.

Советы по типам данных
-
Максимальный размер файла базы данных Access составляет 2 ГБ.
-
Чтобы оптимизировать производительность, при создании текстовых и числовых полей укажите оптимальный Размер поля. Например, если вы собираетесь хранить почтовые индексы известной длины, задайте соответствующие размеры поля. Для этого введите нужное значение в поле Размер поля. Дополнительные сведения см. в разделе Задание других свойств поля.
-
Для телефонных номеров, артикулов и других номеров, которые не предполагается использовать в математических вычислениях, вместо числового необходимо выбрать текстовый тип данных. Числовые значения, которые хранятся как текст, проще сортировать и фильтровать.

-
К началу страницы
Изменение формата поля
Кроме определения типа данных нового поля Access может задать для него значение свойства Формат, зависящее от введенных данных. Например, если ввести значение 10:50, Access выберет тип данных “Дата и время” и присвоит свойству Формат значение “Средний формат времени”. Чтобы вручную изменить значение свойства Формат, сделайте следующее.
-
На ленте откройте вкладку Поля.
-
В группе Форматирование в поле Формат введите нужный формат.
Примечание: Для полей некоторых типов (например, текстовых) список Формат может быть недоступен.

К началу страницы
Задание других свойств поля
-
В режиме таблицы щелкните поле, для которого нужно задать свойство.
-
На вкладке Поля в группах Свойства, Форматирование или Проверка поля выберите нужные свойства.
К началу страницы
Задание свойств поля в Конструкторе
При работе с таблицей в Конструкторе можно настраивать любые свойства полей. Тип данных поля задается на бланке таблицы, а другие свойства — в области Свойства поля.
-
В области навигации щелкните таблицу правой кнопкой мыши.

-
В контекстном меню выберите пункт Конструктор.
К началу страницы
Изменение типа данных поля
После создания поля можно изменить его различные параметры.
Предупреждение: Эти параметры можно изменять также у полей, которые были созданы ранее. Тем не менее если в поле уже есть данные, некоторые действия могут быть недоступны или привести к повреждению данных.
-
На бланке таблицы найдите поле, для которого вы хотите задать тип данных.
-
В столбце Тип данных выберите значение из списка.
Доступные типы данных
Полный список доступных типов данных для баз данных Access вы найдете в статье Типы данных для баз данных Access рабочего стола.

Советы по типам данных
-
Максимальный размер файла базы данных Access составляет 2 ГБ.
-
Для телефонных номеров, артикулов и других номеров, которые не предполагается использовать в математических вычислениях, вместо числового необходимо выбрать текстовый тип данных. Числовые значения, которые хранятся как текст, проще сортировать и фильтровать, но их сложно использовать в вычислениях.
-
Для текстового и числового типа данных вы можете более точно задать размер поля или тип данных с помощью свойства Размер поля.
-
К началу страницы
Задание других свойств поля
Примечание: Не все форматы доступны для всех типов данных. Сначала задайте тип данных, а затем при необходимости настройте формат.
Сначала задайте тип данных, а затем при необходимости настройте формат.
-
На бланке таблицы выберите поле, для которого вы хотите задать свойства. Свойства поля выводятся в области Свойства поля.
Свойства, которые можно задать, зависят от типа данных этого поля.
-
В области Свойства поля введите нужные параметры для каждого свойства или нажмите клавишу F6 и выберите свойство с помощью клавиш со стрелками.
Какие свойства полей доступны?
Полный список свойств полей, доступных для каждого типа данных в базах данных приложения Access см. в статье Введение в использование типов данных и свойств полей.
Примечание: Не все свойства доступны для каждого поля.
 Свойства поля определяются его типом данных.
Свойства поля определяются его типом данных. -
Если требуется больше места для ввода или изменения значений в поле свойства, нажмите клавиши SHIFT+F2 для отображения поля Область ввода.
Совет: Если вам требуется помощь в создании маски ввода или выражения условия на значение, нажмите кнопку рядом с полем свойства для отображения соответствующего построителя.
-
Чтобы сохранить изменения, нажмите клавиши CTRL+S.
К началу страницы
Перемещение поля
Чтобы переместить поле, перетащите его на нужное место. Чтобы выбрать несколько соседних полей для перемещения, щелкните первое поле, и, удерживая нажатой клавишу SHIFT, щелкните последнее поле. После этого можно перетащить выделенную группу полей на новое место.
После этого можно перетащить выделенную группу полей на новое место.
При перетаскивании поля меняется его положение в таблице, порядок полей в конструкторе при этом не изменяется. При программном доступе к полям используется исходный порядок. Например, если перетащить поле в новое положение в режиме таблицы, а затем с помощью кнопки “Форма” создать на основе этой таблицы форму, поле будет расположено в исходном положении.
К началу страницы
См. также
Добавление вычисляемого поля в таблицу
Добавление поля в форму или отчет
Инструкция начинающего разработчика игр / Хабр
В данной инструкции я попытался осветить основные моменты разработки игр. Инструкция будет полезна для людей, собирающихся заняться разработкой игр в роли лидера (главного разработчика и организатора).
Хочу отметить, что игры бывают разные – большие и маленькие, сложные и лёгкие, и поэтому для каждой игры эта инструкция верна в какой-то своей определённой степени. Охватить всё не удалось, но передать общие моменты, думаю, получилось.
И так Вы решили сделать свою игру, о чём Вам нужно подумать…
Думаем – нужно ли это тебе
Перед тем, как за что-то взяться, необходимо всё обдумать. А перед тем, как заняться разработкой игр, необходимо обдумать всё очень хорошо. Очень часто начинающие разработчики, достигнув определённых успехов в чём-то (сделал мод для игры, небольшой фан-сайт и пр.), начинают грезить созданием своей игры. Это происходит из-за того, что они имеют слабое представление о процессе разработки игр.
Я перечислю основные ошибки в их представлении:
- Нет романтики. Многие начинающие разработчики, наигравшись вдоволь в игры, приходят к мысли, что создавать игры также интересно, как и играть, только чуть-чуть сложнее. Это очень частая ошибка.
 Чем больше и сложнее игра тем, скучнее и безынтереснее процесс её разработки. Романтики совершенно нет.
Чем больше и сложнее игра тем, скучнее и безынтереснее процесс её разработки. Романтики совершенно нет. - Трудно и даже невозможно. Многие после нескольких (или даже одного) успешного проекта наполняются уверенностью, что написать игровой проект им по силам. На самом деле, игры – это одно из самых сложных направлений разработки. И чем «серьёзнее» игра, тем проект сложнее. В процессе создания игры разработчик может столкнуться с нерешаемыми проблемами, которые убивают на корню энтузиазм даже у самых упёртых.
- Отвращение к играм. Со временем у каждого матёрого разработчика игр развивается отвращение к играм. Сначала просто они становится менее интересными. Затем начинаешь замечать, что они вовсе не интересны, а интересно только, как они работают. Чем дальше, тем хуже.
- Конкуренция и качество продукта. Играми занимаются многие студии и независимые разработчики. Существует своеобразный «уровень вхождения» в этот бизнес. Сейчас нельзя сделать успешную игру, нарисованную акварелью (да, такие игры встречались в начале 2000-х).
 Она просто не выдержит конкуренции. Соответственно, абы что не сделаешь. Тут скрывается важный психологический момент – начинающий разработчик вынужден делать хороший продукт, иначе он будет испытывать постоянное чувство страха неуспешности своего продукта.
Она просто не выдержит конкуренции. Соответственно, абы что не сделаешь. Тут скрывается важный психологический момент – начинающий разработчик вынужден делать хороший продукт, иначе он будет испытывать постоянное чувство страха неуспешности своего продукта. - Время и ресурсы. И самая распространенная ошибка – это то, что ресурсов (время, деньги, знания) им хватит. Чтобы понять объём работ, читайте следующие пункты.
Концепция и ТЗ
Когда-то давно я написал довольно неплохую
статьюо концепции проекта. За последние пару лет мои взгляды слегка поменялись, но суть осталась та же.
- Что же такое концепция? Концепция игрового проекта — это документ, описывающий цели, задачи, основные особенности проекта, исследование рынка и целевой аудитории, условия его выполнения. Также, так как проект игровой, обязательно описание игровой механики, игровых понятий, примерный сценарий и концепт-арт. Если Вы ещё рассчитываете делать проект не в одиночку (что весьма вероятно), то понадобится ещё техническое задание (ТЗ) – документ, содержащий описание необходимых работ, сроки и условия.

- Зачем нужна концепция? Очень хороший вопрос. Зачем заниматься какой-то «писаниной», когда нужно собирать команду и писать код?
В первую очередь концепция нужна, чтобы самому получить полноценное представление о конечном результате и оценить объём работ. Без чёткой и продуманной концепции у Вас в итоге получится, соответственно, противоречивая и непродуманная игра. Без концепции существует большая вероятность возникновения ошибок организации игровой механики или ошибок реализации.
Во вторую очередь концепция нужна для того, что бы другие поняли то, что Вы хотите сделать. Все члены команды должны работать над одним общим проектом. Об этом общем проекте члены команды узнают из документа концепции проекта. Это нужно, чтобы не было расхождений в представлениях о конечном результате. Если Вы решили создать игру и для этого собираете команду, то первые вопросы от будущих членов команды будут: «А что предстоит мне сделать? Что в итоге мы должны получить?». Вы должны будете им предоставить концепцию проекта и ТЗ. Без концепции и ТЗ Вы не привлечёте ни одного нормального специалиста.
Вы должны будете им предоставить концепцию проекта и ТЗ. Без концепции и ТЗ Вы не привлечёте ни одного нормального специалиста. - Объёмы. Весьма интересен вопрос объёма концепции. Тут необходимо отталкиваться от сложности игры и её разработки. Если у Вас простая игра, Вы работаете один и Вы способны удержать идею игры в своей голове, то можно вообще не писать концепцию. Если удержать в памяти все моменты нельзя, то необходимо перенести их на бумагу (или другой носитель). Если Вы будете работать в команде или использовать помощь других людей (инвесторы, художники и прочие), то Вам просто необходима развёрнутая концепция и ТЗ для каждого человека. Критерий один – понятность. Нужно чтобы любой человек, ознакомившись с концепцией и ТЗ, представил конечный результат, так же как и Вы.
Обратите внимание на то, что, если Вы понимаете свою концепцию, то это не значит, что её поймут другие. Написание концепции выполняет роль «лакмусовой бумажки». Если Вы не можете написать понятную концепцию (примерно, 5 страниц для небольшой игры, несколько десятков страниц для большой), то вряд ли Вы закончите в итоге проект.
- Детальность. В концепции должны быть ответы на все вопросы. После прочтения концепции должно сформироваться полное представление о проекте. Специалисты первым делом смотрят на концепцию, если концепция окажется для них не полной и непонятной, то они не будут с Вами работать.
Отдельно стоит упомянуть концепт-арт. Он должен быть, хотя бы в простейшем виде. Он является доказательством решения проблемы с контентом, содержимым игры (смотрите следующий раздел). - Русский язык. Для многих это серьёзная проблема. Если документ концепции содержит множество грамматических, орфографических и синтаксических ошибок, то ни один специалист не воспримет его всерьёз. Помните: незнание русского языка очень вредит бизнесу.
- Время. Желательно в сразу в ТЗ указать сроки выполнения работ. Проблема в том, как оценить это время, если никогда подобным не занимался. Точно ответа на этот вопрос Вы никогда не получите, всё придёт с опытом. Я только дам один совет: учитывайте не только время разработки, но и время на исправление ошибок (примерно 50% от времени на разработку).

Контент
Я специально выделил этот раздел, так как он является решающим в процессе разработки игр. Под контентом понимается всё содержимое игры, с которым взаимодействует пользователь. Это графика (растровая, векторная, 3D), музыкальное и звуковое сопровождение, видеоряд, сценарий и текст. Также сюда следует добавить медиаматериалы, используемые для продвижения игры (реклама, банеры и прочие).
В английском языке есть такое понятие как «artist» обозначающие сразу художников, музыкантов, режиссёров, писателей и прочих творцов. К сожалению, в русском языке нет нормального аналога этого слова, поэтому я дальше буду использовать понятие «создатель контента».
Разберём основные моменты этого раздела.
- Сложность. Это самая главная проблема в вопросе контента. Оказывается, в большинстве случаев подготовка контента является самой сложной задачей, сложнее написания программного кода, сложнее тестирования и отладки, и сложнее реализации игры.
 Естественно, если игра маленькая, то это не так заметно, а если большая, то на долю создателя контента выпадает до 80% работы по проекту.
Естественно, если игра маленькая, то это не так заметно, а если большая, то на долю создателя контента выпадает до 80% работы по проекту. - Объёмы. Часто из-за того, что разработчики никогда не выполняли задачи создателей контента, им очень сложно оценить объёмы. Кажется, что там такого ¬– пара десятков картинок и 3-4 звука. Но если посчитать, то получается 40 крупноразмерных изображений, 400 мелких изображений, два десятка звуков (я привел пример среднестатистической BMMORPG). Хорошо, что это всё можно подсчитать при подготовке концепции.
- Качество. Во-первых, надо понимать, что игроки работают непосредственно с контентом. Во-вторых, надо помнить, что существует огромное количество игр-конкурентов с хорошим контентом. Можно сделать вывод: игра с плохим контентом будет не конкурентоспособна, т.е. контент в игре должен быть высокого качества.
- Время. Вполне логично, что на подготовку больших объёмов качественного контента уходит очень много времени.
 Времени уходит больше, чем на все остальные направления вместе взятые (маленькие игры не в счёт). Учитывайте это, когда будете планировать и рассчитывать сроки.
Времени уходит больше, чем на все остальные направления вместе взятые (маленькие игры не в счёт). Учитывайте это, когда будете планировать и рассчитывать сроки. - Стоимость контента. Хороший контент стоит «хороших» денег. Очень «хороших» денег, которых у начинающих разработчиков игр обычно нет. Многие разработчики питают иллюзорную надежду найти «бесплатного» создателя контента (или дешёвого). Найти можно, но он либо будет создавать низкопробный контент, либо создаст для Вас немного контента, а затем переметнётся к тем, кто будет ему платить. Короче говоря, «бесплатного» создателя хорошего контента Вы никогда не найдёте. Именно по этой причине нет хороших «OpenSource» игр.
- Воровство. Из-за существования проблемы дорогого контента, иногда появляются разработчики игр, которые его воруют. Мол, что такого?.. возьму-ка я из этой игры десяток картинок, а фоновые изображения найду на DA, а в качестве фоновой музыки поставлю пару любимых песенок Rammstein.
 Проблема в том, что авторское право контента достаточно легко подтвердить. У «жертвы» воровства есть либо исходные файлы контента, либо документ о передаче контента от его создателя. Для воров контента очень велик шанс нарваться на статью 146 УК РФ.
Проблема в том, что авторское право контента достаточно легко подтвердить. У «жертвы» воровства есть либо исходные файлы контента, либо документ о передаче контента от его создателя. Для воров контента очень велик шанс нарваться на статью 146 УК РФ. - Единый стиль. Ещё один важный момент, о котором часто забывают. Что бы игра смотрелась цельной и продуманной, ей нужно иметь единый стиль. Создатели контента не роботы, поэтому делают работы в своём индивидуальном стиле. Отсюда можно сделать вывод: желательно чтобы содержимое игры создавало как можно меньше человек.
- Дилемма. После прочтения описанных выше моментов можно построить следующую цепочку: Конкурентоспособная игра требует использование качественного контента. Качественный контент может сделать только профессиональный создатель контента. Профессиональный создатель контента стоит недёшево. Решений данной проблемы всего лишь три:
- Не делать игру, то есть отказаться от направления разработки игр.

- Найти инвестора. Но тут сразу нас поджидает проблема концепт-арта. Кто будет подготавливать концепт-арт, если нет денег на художника? А без концепт-арта никто не будет инвестировать в Вас.
- Решать проблему собственными силами. То есть кто-то из членов команды должен быть создателем контента и должен получать зарплату, даже если все остальные сосут палец.
- Не делать игру, то есть отказаться от направления разработки игр.
Программирование
Как ни странно, создание программного кода для игр не является самой сложной задачей, но в тоже время и не является простой.
- Команда. В отличие от создателей контента программистов для своей команды найти легко. Это объясняется тем, что при определённом уровне подготовки написание программного кода игры не такая уж сложная задача. Можно найти «бесплатных» программистов, готовых работать ради интереса. А за плату и «имя» (упоминание, как разработчика игры) можно найти программиста, который будет писать хороший годный код. Но… сейчас не начало 2000-х и программисты поумнели.
 Первым делом адекватный программист попросит разработчика продемонстрировать концепцию и ТЗ. Затем спросит про создание контента или финансирование, которое пойдёт на его создание. Специалисты прекрасно понимают, что незачем вкладывать силы в изначально провальный проект. Если у Вас нет концепции и не решен вопрос с контентом, то нормального программиста Вы не найдёте.
Первым делом адекватный программист попросит разработчика продемонстрировать концепцию и ТЗ. Затем спросит про создание контента или финансирование, которое пойдёт на его создание. Специалисты прекрасно понимают, что незачем вкладывать силы в изначально провальный проект. Если у Вас нет концепции и не решен вопрос с контентом, то нормального программиста Вы не найдёте. - Сначала делаем большое, потом маленькое. Достаточно простой совет, но ему чаще всего не следуют. Игровой проект в большинстве случаев сложен и имеет множество зависимостей. Все это сложно просчитать на уровне составления концепции, частенько приходиться что-то менять в планах. Поэтому, чтобы не выполнять двойную работу, сначала необходимо сделать общую работающую конструкцию (прототип), а затем углубляться в детали.
- Что сначала контент или код? Прочитав раздел про контент, Вы уже, наверное, поняли, что современные игры основаны на контенте, а не на программировании. Отсюда дилемма – код подгонять под контент или контент подгонять под код.
 Оба подхода имеют место в современном процессе разработки. Если подгонять код под контент, то нагрузка падает на программиста, время разработки увеличивается. Это дешёвый способ. Если контент подгонять под код, то нагрузка с программиста спадает, и при учёте, что контент подготавливают наёмные работники, время разработки сокращается. Это дорогой способ, так как нагрузка падает на наёмных создателей контента. Заранее оцените ситуацию и придерживайтесь одного из подходов.
Оба подхода имеют место в современном процессе разработки. Если подгонять код под контент, то нагрузка падает на программиста, время разработки увеличивается. Это дешёвый способ. Если контент подгонять под код, то нагрузка с программиста спадает, и при учёте, что контент подготавливают наёмные работники, время разработки сокращается. Это дорогой способ, так как нагрузка падает на наёмных создателей контента. Заранее оцените ситуацию и придерживайтесь одного из подходов. - Нерешаемые ошибки. Это даже не проблема, а предубеждение. Разработка игры весьма сложный процесс. Бывает, что разработчик сталкивается с нерешаемыми проблемами (либо решаемыми крайне тяжело) и ему приходиться пересматривать чуть ли не весь проект. Психологически это очень трудно. Многие, даже самые упёртые разработчики, попав в такой «тупик», теряют энтузиазм и закрывают проект. Предубеждение в том, что все считают, что с ними такого не случиться. Совет один: будьте психологически готовы пересмотреть весь проект и выполнить работу заново.

- Журналы. Совет лично от меня. Ведите три журнала:
- Журнал выполненной работы по проекту для отслеживания динамики разработки;
- Журнал идей по проекту, чтобы не забыть их и, если возможно, включить в концепцию;
- Журнал найденных багов и ошибок, которые необходимо исправить в будущем.
- Время. При определении времени, которое планируется на написание кода, часто делают одну ошибку – не учитывают затраты времени на исправление багов и отладку кода.
- Авторство программного кода. Определённый «маразм» наблюдается, у некоторых программистов. Они считают, что обладают абсолютными правами на код, который ими написан, что даже после релиза игры они могут предъявить права на «часть кода» игры. Что бы защитить это «священное» право они могут пойти на всякие низости (программные бомбы, бакдоры, отказ от передачи исходных кодов и прочие).
 Мой совет прост – остерегайтесь таких неадекватных программистов. Программный код не контент. Доказать его авторство очень сложно. Поэтому нормальный программист сначала договаривается, что он получит за код; затем его пишет; потом передаёт разработчику и получает вознаграждение; после чего уже ни на что не претендует. Также должно быть организовано и в команде.
Мой совет прост – остерегайтесь таких неадекватных программистов. Программный код не контент. Доказать его авторство очень сложно. Поэтому нормальный программист сначала договаривается, что он получит за код; затем его пишет; потом передаёт разработчику и получает вознаграждение; после чего уже ни на что не претендует. Также должно быть организовано и в команде.
Тестирование
О тестировании начинающие разработчики обычно не задумываются, а зря, так как на него тратиться немногим меньше времени, чем на написание программной части. В этом разделе есть два важных момента:
- Тестирование сторонними людьми. В процессе разработки тестирование проводиться в основном своими средствами. Со временем глаза привыкают к имеющимся игровым моментам, вырабатываются умение работать в данной системе, короче, ошибки становятся менее заметными. Поэтому устраивайте периодические тесты продукта сторонними людьми, которые никогда не видели ваш продукт. Следите за их реакцией на различные игровые моменты, как они воспринимают меню игры и, вообще, расспросите их общее впечатление.
 Поверьте мне, один такой тест даст Вам очень большой объём полезной информации. Проводите их чаще, прислушивайтесь к обратной связи, и Вы получите на выходе хорошую игру.
Поверьте мне, один такой тест даст Вам очень большой объём полезной информации. Проводите их чаще, прислушивайтесь к обратной связи, и Вы получите на выходе хорошую игру. - Женщины. Когда-то я написал неплохую статью про женщин и игры. Смысл в том, что женщины видят всё по другому. Поэтому, желательно, чтобы в тесте игры участвовала хотя бы одна женщина (девушка), даже если игра не рассчитана на женскую аудиторию. Их обратная связь будет невероятно полезна.
Организационные моменты
- Команда. Как Вы могли догадаться, созданием таких проектов, как игры, лучше заниматься командой. Это обосновано тем, что создание контента совершенно другой вид деятельности отличный от программирования и организации проекта и одному заниматься такими разными видами деятельности сложно. Минимальная команда – это два человека, создатель контента и разработчик. Чтобы не было непонимания, уточню – наёмный работник, по-моему, тоже в какой-то мере член команды.

Конечно, можно заниматься разработкой и в одиночку. Есть такие «сумасшедшие», которые и пишут код, и рисуют графику, и сочиняют музыку, но это их проблемы.
Собрать команду при наличии финансирования легко – форумы программистов и создателей контента, биржи фрилансеров Вам в помощь. При отсутствии финансирования можно найти только программиста, а вот нормального создателя контента не найдёте – здесь надо надеяться либо на себя, либо на удачу. - Юридическое оформление. Здесь всё просто. Хотите иметь с игры деньги и обезопасить себя от рейдерского захвата (когда кто-то внаглую ворует вашу игру), то вам нужно юридическое оформление на уровне индивидуального предпринимателя. Если Вы ещё собираетесь распределять проект по долям, то нужно оформление на уровне ООО. Поэтому если при поиске членов команды Вы обещаете долю в проекте, то не удивляйтесь, что Вас будут просить предъявить реквизиты вашей организации.
- Контакты. Никогда не пренебрегайте знакомствами.
 Знакомьтесь с другими разработчиками, общайтесь и обменивайтесь контактами. В будущем, возможно, знакомство с ними принесёт Вам пользу.
Знакомьтесь с другими разработчиками, общайтесь и обменивайтесь контактами. В будущем, возможно, знакомство с ними принесёт Вам пользу. - Реклама. Так как игр на рынке много, то чтобы пользователи выбрали именно вашу игру, нужно привлечь к себе внимание. Делается это при помощи рекламы на различных ресурсах. Логично, что реклама эта требует: во-первых денег, а во-вторых, рекламный контент (банеры, видеоролики, статьи). Возможны и другие способы ¬– связи, спам, рекламные акции и прочие, но они не всегда эффективны.
Без рекламы игра, точно также как и без контента, является провальным проектом. Обратите на это внимание. Но тут ситуация может достаточно легко исправлена инвестированием и сторонней помощью. - Инвестирование. Понятное дело, что с деньгами игру делать гораздо легче, но без развёрнутой концепции (с концепт-артом), команды и рабочего прототипа никто не будет финансировать ваш проект. То есть на начальных этапах на финансирование не надейтесь.
 А вот на последних этапах разработки ситуация может в корне поменяться – могут появиться инвесторы и Вам всё равно будут нужны деньги для организации рекламной компании.
А вот на последних этапах разработки ситуация может в корне поменяться – могут появиться инвесторы и Вам всё равно будут нужны деньги для организации рекламной компании.
Чтобы найти инвесторов, собирайте контакты. - Сторонняя помощь. Вместо инвесторов можно найти стороннюю помощь (реклама за рекламу, помощь в распространении за процент и прочие). Тут надо ориентироваться по ситуации. Чтобы найти стороннюю помощь, так же собирайте контакты.
Послесловие
Инструкция получилась большой, материала много. Крайне советую прочесть её начинающим разработчикам игр, так как, возможно, она поможет им избежать ошибок в будущем.
UPD: Статья получилась успешной, даже очень. Но в комментариях прослеживаются замечания по поводу отсуствия романтики и отвращения к играм. Поэтому я прокомментирую эти моменты.
Многие опускают тот факт, что статья для начинающих разработчиков игр, претендующих на роль лидера (первый абзац статьи). Не буду отрицать, что со временем, когда приобретаешь опыт разработки игр и жизнь складывается удачно, возвращается романтика и отвращение спадает. Но в самом начале, когда начинаешь с нуля, после того как столкнёшься с первыми серьёзными проблемами, эта романтика и любовь к играм исчезает ко всем чертям. Разработка игр — это не прогулка по ковровой дорожке в розывых очках, а блуждание в лабиринте Минотавра, где много тупиков.
Не буду отрицать, что со временем, когда приобретаешь опыт разработки игр и жизнь складывается удачно, возвращается романтика и отвращение спадает. Но в самом начале, когда начинаешь с нуля, после того как столкнёшься с первыми серьёзными проблемами, эта романтика и любовь к играм исчезает ко всем чертям. Разработка игр — это не прогулка по ковровой дорожке в розывых очках, а блуждание в лабиринте Минотавра, где много тупиков.
Я не собираюсь своей статьёй вселять в начинающих разработчиков уверенность. Они должны знать, что путь разработчика игр сложен, что они могут встретить нерешаемые проблемы, что их нерализованный проект будет для них символом поражения.
Теория игр 101 | Принятие решений с использованием игр в нормальной форме
Обзор
- Теория игр может быть невероятно полезна для принятия решений в соревновательных сценариях
- Понимать концепцию игр в нормальной форме в контексте теории игр
- Мы также рассмотрим применение теории игр на реальных примерах
Введение
Начнем эту статью по теории игр с примера игры (обожаю символику!). Футбол — самый популярный вид спорта в мире, поэтому мы рассмотрим сценарий оттуда.
Футбол — самый популярный вид спорта в мире, поэтому мы рассмотрим сценарий оттуда.
Предположим, что команде назначен пенальти. Эта ситуация ставит нападающего против вратаря в битве умов. Вратарь должен принять решение, прыгнуть ли ему влево или вправо (или стоять на своем). У нападающего аналогичная дилемма (какое направление выбрать).
А теперь вопрос к вам – что бы вы сделали? Если это упражнение с пенальти повторить 10 раз, какую сторону вы бы спасли как вратарь, чтобы свести к минимуму забитые голы? Или куда бы вы нанесли удар, чтобы максимизировать количество забитых голов? Какие действия вы предпримете, если у вас есть выводы из прошлого о действиях кикера и вратаря?
Это трудное решение.Здесь мы можем применить теорию игр и сделать логический вывод, соответствующий индивидуальным интересам:
.- Теория игр примет во внимание все большие данные при обработке решения
- Он поделится обоснованием предлагаемого решения, чтобы вы знали, как он пришел к этому решению
- Команды узнают, почему и как было принято это решение, используя теорию игр .
Принятие этого стратегического решения является разумным шагом с точки зрения бизнеса, учитывая тот факт, что наиболее вероятные результаты можно предсказать с помощью умозаключений и теории игр.
В этой статье мы в первую очередь рассмотрим игры в нормальной форме или одновременные игры и вычислим равновесие Нэша для соответствующих игр. Мы также научимся вычислять равновесие Нэша в играх с чистой стратегией и играх со смешанной стратегией. Наконец, мы найдем стратегию равновесия Нэша в приведенном выше примере с пенальти.
Прежде чем двигаться дальше, я бы посоветовал прочитать первую статью по теории игр. Это даст вам представление о теории игр с высоты птичьего полета и понимание того, как теория игр используется в области искусственного интеллекта.
Содержание
- Что такое теория игр?
- Теория игр – подготовка к играм в нормальной форме
- Чистая стратегия Эквилибриум Нэша
- Смешанная стратегия равновесия Нэша
- Получение решения с использованием теории игр
- Чем теория игр полезна для специалистов по науке о данных?
Что такое теория игр?
Проще говоря, теория игр является очень специализированным предметом для любого специалиста по данным.
Это позволяет принимать решения на основе выводов из данных наиболее оптимальным образом на основе выводов, сделанных после проведения анализа больших данных.
Принятие стратегических решений — разумный шаг с точки зрения бизнеса, учитывая тот факт, что наиболее вероятные результаты можно предсказать с помощью умозаключений и теории игр.
Теория игр помогает предсказать, как рациональные люди будут принимать решения, которые помогают специалистам по данным принимать эффективные решения, основанные на данных, в стратегических обстоятельствах.Вы можете ознакомиться с этим более подробно здесь.
Теория игр – подготовка к играм в нормальной форме
Прежде чем мы углубимся в концепцию игр в нормальной форме, повторите, пожалуйста, ключевые термины теории игр, которые мы рассмотрели во вводной статье.
Для справки я быстро изменю приведенные ниже термины:
- Игра : В общем смысле игра состоит из набора игроков, действий/стратегий и окончательного выигрыша.
 Пример: аукцион, шахматы, политика и т. д.
Пример: аукцион, шахматы, политика и т. д. - Игроки/Агенты : Игроки — разумные существа, участвующие в любой игре. Например:
- Участники аукциона
- Политики, участвующие в выборах и т. д.
- Действия: Это набор действий, которые каждый агент может выполнять в игре. Одно замечание — действия любого агента могут быть похожими или разными в зависимости от игры
- Матрица игры: Это систематическое представление всех возможных результатов и вознаграждений, основанное на том, какое действие выбрал каждый агент.Мы рассмотрим это в ближайшее время
- Вознаграждение/Выплата: Это просто вознаграждение, которое получает любой агент, когда достигается результат благодаря совместным действиям всех агентов
Теперь, когда у нас есть представление об основных терминах теории игр, давайте обсудим некоторые допущения, которым мы будем следовать в этой статье, чтобы понять игры в нормальной форме.
Предположение 1: Игры совершенной информации
В контексте теории игр мы должны обратить особое внимание на количество информации, которой владеет каждый агент.Бывают ситуации, когда агенты ничего не знают друг о друге. А с другой стороны, бывают сценарии, когда агенты знают друг о друге все.
Поскольку мы только начинаем изучение теории игр, мы будем иметь дело с играми совершенной информации (последний сценарий).
В идеальных информационных условиях каждый агент имеет информацию о следующем:
- Весь набор действий, которые могут выполнять другие агенты
- О мотивации другого агента
- Знание обо всех возможных исходах
- Вознаграждайте других агентов за каждый возможный результат
- Какие действия предпринимают другие агенты
- Все агенты рациональны
Или по существу:
Но бывают и игры с неполной и неполной информацией.Тем не менее, мы сосредоточимся на них в следующих статьях.
Допущение 2: одновременные действия
В играх нормальной формы мы предполагаем, что все агенты действуют одновременно и они не могут заранее знать, что собирается делать другой агент.
Однако существуют сценарии, в которых агенты играют в пошаговую игру — они известны как игры с расширенными формами . Мы будем исследовать эти формы игр в моей следующей статье.
Понимание игр в нормальной форме
Я предполагаю, что вы уже знакомы с Матрицей Игры, которую мы используем в Играх Нормальной Формы.В предыдущей статье мы подробно рассмотрели пример дилеммы заключенного. Выглядело это примерно так:
Теперь проще всего начать с использования этой игровой матрицы и узнать, как определяется эта игра. Помните: игра определяется как кортеж {Игроки, Действия, Полезность}.
Давайте посмотрим, что каждый из них представляет в соответствии с этой игровой матрицей выше.
игроков:
Количество игроков, участвующих в любой игре.В этой игре: игроков = {Алан, Бен} .
Действия:Действия представляют собой набор действий, которые может выполнять каждый агент. Мы должны иметь в виду, что не все игроки могут выполнять все действия. В этой игре:
- Действия Бена = {Признаться, Молчать}
- Действия Алана = {Признаться, Молчать}
Полезность или награда каждого игрока — это награда, которую получает каждый агент в соответствии с действиями, сыгранными ими обоими.Он определяется с помощью функции их действий.
Если мы представим действия Алана как {A исповедуемся , A молчишь }, а действия Бена как {B исповедуемся , B молчим } , то функция полезности может быть определена как:
- A признание , B признание = {-10,-10}
- A признаться , B молчать = {0,-15}
- А молчит , Б исповедь = {-15,0}
- A молча , B молча = {-1,-1}
Чтобы понять это обозначение, давайте разберем третью функцию полезности. В нем говорится, что , когда Алан молчит, а Бен признается, они получают полезность/награду -15 и 0 соответственно.
В нем говорится, что , когда Алан молчит, а Бен признается, они получают полезность/награду -15 и 0 соответственно.
И это нормальные игры!
Теперь, когда мы разобрались с игрой в нормальной форме, вот еще одна игровая матрица:
Прежде чем мы двинемся дальше, я хочу, чтобы вы кое-что сделали. Попробуйте определить Game{Players, Actions, Utility} для этой матрицы Game. Это действительно поможет вам усвоить концепции, которые мы рассмотрели в этом разделе.Опубликуйте свой ответ в разделе комментариев ниже!
Чистая стратегия Эквилибриум Нэша
Теперь, когда мы поняли нюансы игр в нормальной форме, давайте посмотрим, как найти равновесие Нэша для этих игр. Вы должны быть знакомы с тем, что означает равновесие Нэша, если вы прочитали предыдущую статью. Не волнуйтесь, если вы этого не сделали, я кратко расскажу об этом здесь.
Равновесие Нэша определяется как стратегия каждого агента, такая, что эта стратегия является наилучшей реакцией на все остальные агенты.

или
Равновесие по Нэшу — это набор стратегий, используемых каждым агентом таким образом, чтобы никто не захотел отклониться или изменить свою стратегию.
В Чистый Стратегия Равновесие Нэша, чистый означает одно действие, которое является лучшим ответом на все остальные агенты. Более того, это равновесие в чистой стратегии часто называют доминирующей стратегией .
Обратите особое внимание на два слова – доминирование и доминирование . Они звучат очень похоже и могут вызвать путаницу. Мы будем использовать оба этих слова в ближайшее время, так что просто имейте это в виду.
Повторное удаление доминируемой стратегии (IRDS)
Чтобы найти равновесие Нэша в чистой стратегии, мы следуем методу, известному как «Повторяющееся удаление доминируемой стратегии (IRDS)» . Это простой метод, который говорит, что мы можем удалить действие с доминированием из действий игрока, если над ним явно доминирует какое-то другое лучшее действие.
Это простой метод, который говорит, что мы можем удалить действие с доминированием из действий игрока, если над ним явно доминирует какое-то другое лучшее действие.
Давайте вернемся к примеру с дилеммой заключенного и отработаем эту стратегию:
Давайте сначала применим IRDS к действиям Алана:
Для Алана есть две возможности в зависимости от действий Бена:
- Если Бен решит признаться, для Алана разумно признаться, потому что 10 лет наказания лучше, чем 15 лет наказания
- Если Бен предпочитает хранить молчание, Алану разумно признаться, потому что нет лучшего наказания, чем 1 год наказания
В результате, что бы ни выбрал Бен, признание является доминирующей стратегией для Алана.Или отклонение от признания повлечет за собой большее наказание для Алана. Поэтому мы исключаем доминируемое действие (молчаливая строка для Алана выделена серым цветом) .
Теперь применим IRDS к действиям Бена. Есть две возможности в зависимости от того, что делает Алан:
- Если Алан решит признаться, для Бена разумно признаться, потому что 10 лет наказания лучше, чем 15 лет наказания
- Если Алан предпочитает хранить молчание, Бену разумно признаться, потому что нет лучшего наказания, чем 1 год наказания
И мы можем ясно заметить, что после удаления стратегии с чистым доминированием мы остаемся с равновесием Нэша {признаться, признаться} в дилемме заключенного, а результирующая полезность равна {-10, -10}.
Я бы хотел, чтобы вы опробовали метод IRDS на следующей игровой матрице, чтобы попрактиковаться:
Проблемы с чистой стратегией равновесия Нэша
Часто игры, с которыми мы сталкиваемся для принятия решений, не так просты и могут не иметь в них доминирующей стратегии. Популярным примером одной из таких игр является «Сопоставление пенни».
Это соревновательная игра, в которой у двух игроков противоречащие друг другу цели. Два игрока должны положить монету на стол и выбрать, какая сторона монеты должна быть обращена вверх.Цель игрока 1 состоит в том, чтобы сопоставить монету другого игрока, тогда как цель игрока 2 состоит в том, чтобы не соответствовать монете другого игрока. Результирующая игровая матрица выглядит так:
Игра «Собери монетки»
Теперь, если мы внимательно посмотрим на эту игру, применение IRDS невозможно. Для любых действий, заданных двумя игроками, у одного из них всегда будет стимул отклониться от текущего действия:
Мы ясно видим, что играть в чистую стратегию действий — плохая идея.В результате не существует равновесия Нэша в чистой стратегии. Так что же нам делать?
Смешанная стратегия равновесия Нэша
Мы собираемся все перепутать! Мы собираемся разыграть некоторую комбинацию доступных действий для любого агента. Теперь понятно, что мы не можем играть наполовину орлом или наполовину решкой в одной игре.
Поэтому мы воспользуемся помощью вероятности, чтобы смешать стратегии действий, когда игры повторяются.
Теперь, прежде чем мы перейдем к смешанной стратегии и вычислим равновесие Нэша для смешанной стратегии, давайте сначала проясним некоторые предположения о вероятности:
- Вероятность всех действий должна быть неотрицательной: Это означает, что любое действие, доступное любому данному игроку, должно быть числом от 0 до 1 (оно не может быть больше 1 или меньше 0)
- Общая вероятность = 1: Вероятности всех действий любого игрока должны суммироваться до значения 1
Итак, как работает смешанная стратегия?
Мы просто распределяем вероятность между действиями, доступными агентам.Рассмотрим приведенный выше пример совпадающих пенни. Игрок 1 играет «орлом» с вероятностью p и «решкой» с вероятностью «1-p». Точно так же Игрок 2 играет «орлом» и «решкой» с вероятностью q и 1-q.
Когда игроки используют эту смешанную стратегию, другие игроки просто не могут придерживаться простой или чистой стратегии действия. Следовательно, им также нужно будет играть аналогичным образом. Но остается вопрос — как найти равновесие Нэша?
Чтобы ответить на этот вопрос, нам нужно понять две вещи:
- Как рассчитать полезность/вознаграждение в стратегических играх
- Используйте определение равновесия Нэша
Давайте разберемся с каждым из них немного подробнее.
Как рассчитать полезность/вознаграждение в смешанных стратегических играх
Мы рассчитываем Ожидаемое вознаграждение/полезность, когда дело доходит до смешанных стратегических игр. Поскольку мы имеем дело с вероятностями, их необходимо учитывать для расчета ожидаемой полезности:
Ожидаемый выигрыш каждого игрока «i» в любой игре в нормальной форме задается как:
Сумма всех возможных исходов k (награда за получение исхода k * общая вероятность того, что этот исход k будет сыгран всеми игроками).
Давайте рассмотрим пример:
Для игрока 1:
- Ожидаемый выигрыш от первого исхода: (p)*(q)*(1)
- Ожидаемый выигрыш от второго исхода: (p)*(1 – q)*(-1)
- Ожидаемый выигрыш от третьего исхода: (1 – p)*(q)*(-1)
- Ожидаемый выигрыш от четвертого исхода: (1 – p)*(1 – q)*(1)
Общий ожидаемый выигрыш игрока 1 = сумма всех вышеуказанных исходов.
Аналогично для игрока 2:
- Ожидаемый выигрыш от первого исхода: (p)*(q)*(-1)
- Ожидаемый выигрыш от второго исхода: (p)*(1 – q)*(1)
- Ожидаемый выигрыш от третьего исхода: (1 – p)*(q)*(1)
- Ожидаемый выигрыш от четвертого исхода: (1 – p)*(1 – q)*(-1)
Общий ожидаемый выигрыш игрока 2 = сумма всех вышеуказанных исходов.
Использование определения равновесия Нэша для нахождения равновесия Нэша смешанной стратегии
Ранее мы обсуждали, что равновесие Нэша — это стратегия, от которой ни один игрок не захочет отклоняться. Но в игре с сопоставлением монет мы увидели, что какую бы чистую стратегию ни выбрали игроки, у каждого из них всегда был стимул отклониться от стратегии.
Но в игре с сопоставлением монет мы увидели, что какую бы чистую стратегию ни выбрали игроки, у каждого из них всегда был стимул отклониться от стратегии.
Итак, какой трюк мы можем использовать, чтобы установить равновесие Нэша?
Хитрость в поиске равновесия Нэша в разумной стратегии заключается в том, что игроки должны выбирать распределение вероятностей своих действий таким образом, чтобы другому игроку было безразлично, какие из его/ее доступных действий.Результатом этого является то, что у другого игрока не будет стимула отклоняться, если ему/ей безразличны его/ее действия.
Давайте снова посмотрим на игру с сопоставлением монет, чтобы найти равновесие Нэша.
Перспектива игрока 1:
Разделить вероятность между орлом (p) и решкой (1-p), чтобы Игрок 2 получил одинаковую награду независимо от того, что он/она выберет :
Награда Игрока 2, когда Игрок 2 выбирает «орел» = Награда Игрока 2, когда Игрок 2 выбирает «решку»
Награда игрока 2, когда игрок 2 выбирает решку = [(p)*(-1)] + [(1 – p)*(1)]
Награда Игрока 2, когда Игрок 2 выбирает решку = [(p)*(1)] + [(1 – p)*(-1)]
Используя вышеупомянутое отношение равенства:
[(p)*(-1)] + [(1 – p)*(1)] = [(p)*(1)] + [(1 – p)*(-1)]
При решении p: p = 0. 5 .
5 .
Следовательно, Игрок 1 должен с равной вероятностью выложить орла и решку, чтобы Игрок 2 не отклонился.
Перспектива Player2:
Разделить вероятность между орлом (q) и решкой (1-q) так, чтобы Игрок 1 получил одинаковую награду независимо от того, что он/она выберет :
Награда Игрока 1, когда Игрок 1 выбирает «орел» = Награда Игрока 1, когда Игрок 1 выбирает «решку»
Награда Игрока 1, когда Игрок r1 выбирает решку = [(q)*(1)] + [(1 – q)*(-1)]
Награда Игрока 1, когда Игрок 1 выбирает решку = [(q)*(-1)] + [(1 – q)*(1)]
Используя вышеупомянутое отношение равенства:
[(q)*(1)] + [(1 -q)*(-1)] = [(q)*(-1)] + [(1 – q)*(1)]
При решении q: q = 0.5 .
Следовательно, Игрок 1 должен с равной вероятностью выложить орла и решку, чтобы Игрок 2 не отклонился. В результате стратегия равновесия Нэша для игры «сопоставление монет» равна (0,5, 0,5) как для игрока 1, так и для игрока 2.
Краткое изложение смешанной стратегии (что именно означает играть смешанной стратегией):
- Это способ рандомизировать (расчетный) и запутать противников
- Рандомизация работает лучше, когда противник непредсказуем
- Смешанные стратегии — это краткое описание того, что на самом деле может произойти в реальном мире
Получение решения с использованием теории игр
До сих пор мы серьезно занимались проблемой модели, чтобы понять ключевые концепции теории игр.Пришло время вернуться к сценарию наказания, который мы видели во введении.
Рассмотрим следующую игровую матрицу для ситуации нападающий-вратарь:
Здесь нападающий представляет игрока ряда, а вратарь представляет игрока столбца. Выплаты/вознаграждения в этой матрице представляют собой вероятности успеха. Например, если и вратарь, и нападающий играют слева, то у последнего вероятность забить гол равна 0,58, а у вратаря вероятность спастись равна 0. 42. Обратите особое внимание на то, что сумма наград в каждой ячейке составляет 1.
42. Обратите особое внимание на то, что сумма наград в каждой ячейке составляет 1.
Благодаря тщательному исследованию, которое мы провели до сих пор, мы знаем, как рассчитать равновесие Нэша для этой игры, также известной как идеальная стратегия как для вратаря, так и для кикера:
Лучшая стратегия нападающего — сделать так, чтобы вратарю было безразлично, в какую сторону он прыгает. Поэтому:Награда за прыжок вратаря влево = Награда за прыжок вратаря вправо
[(0,42)*(р) + (0.07)*(1-п)] = [(0,05)*(п) + (0,30)*(1-п)]
При решении: p = 0,38
Это означает, что стратегия равновесия для нападающего такова: {слева (0,38), справа (0,62)}.
Точно так же лучшая стратегия вратаря — сделать нападающего безразличным, с какой стороны он бьет. Поэтому:Награда за удар кикером влево = Награда за удар кикером вправо
[(0,58)*(q) + (0,95)*(1-q)] = [(0,93)*(q) + (0,70)*(1-q)]
При решении: q = 0. 42
42
Это означает, что равновесная стратегия для вратаря — это {слева (0,42), справа (0,58)}.
Окончательная стратегия равновесия по Нэшу: кикер { левый (0,38), правый (0,62)} и вратарь { левый (0,42), правый (0,58)}.
Чем теория игр полезна для специалистов по науке о данных?
Сейчас мы решаем много разных игр, и я уверен, что большинство из вас должно быть уже задалось вопросом (возможно, кричало):
- Чем это полезно для специалистов по данным? Как мы узнаем значения выплат до решения игры?
- Обобщаются ли эти решения в реальном мире?
Награды в игре с пенальти, которую мы только что решили, на самом деле были основаны на данных, собранных в матчах чемпионата мира по футболу.Концепции теории игр, которые мы рассмотрели до сих пор, используются после того, как сделаны выводы из данных.
Выводы из нашего анализа данных затем можно использовать для моделирования игры в нормальной форме, которая позволяет нам найти наилучший возможный план действий в соответствии с игровой матрицей.
На самом деле теория игр тесно используется в сочетании с аналитикой больших данных для принятия оптимизированных и стратегических решений.
Равновесие Нэша очень хорошо моделирует динамику населения. Стратегии равновесия Нэша, как правило, точно следуют реальным сценариям .Например:
Пример пенальти, который мы только что обсуждали, является частью исследования, которое было опубликовано в 2003 году. Было обнаружено, что результаты равновесия Нэша поразительно близки к наблюдаемым стратегиям реального мира.
Конечные примечания
Чтобы узнать больше об этом исследовании, вы можете прочитать работу Игнасио Паласиоса Уэрты. Это исследование доказывает, как профессиональные футболисты играют стратегически, используя стратегию равновесия Нэша. Вы можете найти исследование здесь (см. стр. 399-402 для примера, который мы рассмотрели).
Я бы также посоветовал посмотреть выступление профессора Милинда Тамбе (директора отдела искусственного интеллекта для общественного блага) и узнать, как он использовал концепции теории игр и выводы из прошлых данных для общественного блага. Тем не менее, этот разговор будет иметь смысл только после того, как вы хорошо поймете эту статью:
Тем не менее, этот разговор будет иметь смысл только после того, как вы хорошо поймете эту статью:
Концепции теории игр используются в различных конкурентных областях, таких как экономика, политика, профессиональный спорт, бизнес и т. д. По мере роста доступности данных растут и перспективы применения теории игр.
Я с нетерпением жду вашего мнения в разделе комментариев ниже.
РодственныеИгра в развернутой форме — обзор
2 модели некооперативной игры
Простейший тип модели — это модель, в которой отсутствует динамика: каждый игрок должен принять только одно решение, и решения фактически принимаются одновременно, поскольку ни один игрок не знает о решение, принятое другим игроком. В качестве примера можно привести аукцион с закупкой запечатанных заявок: не зная ставок конкурентов, каждый игрок подает свою заявку в запечатанном конверте; игрок, делающий самую низкую ставку, получает контракт и, в свою очередь, получает платеж, равный, скажем, его ставке. Такая игра называется игрой в нормальной форме или также игрой в стратегической форме.
Такая игра называется игрой в нормальной форме или также игрой в стратегической форме.
Формальное математическое определение игры в нормальной форме с и игроками выглядит следующим образом. Пусть S i будет (конечным) набором возможных решений (также называемых действиями или стратегиями), которые может принять игрок i . Кроме того, пусть S=Xi−1nSi будет набором профилей стратегий, следовательно, s ∈ S определяет стратегию для каждого игрока в игре.Предположим, что предпочтения каждого игрока относительно набора результатов игры могут быть описаны функцией полезности (фон Нейман и Моргенштерн, 1944/1953), следовательно, каждый игрок хочет максимизировать свою полезность и заботится только об ожидаемой полезности. Фон Нейман и Моргенштерн (1944/1953) дают условия, при которых может быть найдена такая функция полезности; некоторые теории были разработаны и без этого предположения, но здесь удобно его сохранить. Каждый профиль стратегии s ∈ S дает определенный результат и право u i ( s ) для полезности игрока i , связанное с этим исходом.Тогда игра в нормальной форме полностью определяется наборами стратегий S i и функциями полезности u i с u i : S → ℓ S → S i ,…, S n, u i ,…, u n 〉.
Каждый профиль стратегии s ∈ S дает определенный результат и право u i ( s ) для полезности игрока i , связанное с этим исходом.Тогда игра в нормальной форме полностью определяется наборами стратегий S i и функциями полезности u i с u i : S → ℓ S → S i ,…, S n, u i ,…, u n 〉.
Игры, в которых игроки ходят более одного раза и/или в которых ходы разных игроков являются последовательными, могут быть представлены с помощью дерева. Формально такая игра называется экстенсивной.Узлы дерева соответствуют точкам принятия решений игроками, а дуги в узле представляют решения, которые возможны в этом узле. Каждая конечная точка дерева представляет собой результат игры и снова связана с полезностью для каждого из игроков. Особый тип игры с развернутой формой — это игра, в которой имеется полная информация: когда игрок должен сделать ход, у него есть полная информация о том, где он находится в игре и какие решения были приняты до этого. Шахматы можно рассматривать как игру в расширенной форме с совершенной информацией.Так называемые информационные наборы используются для представления ограниченной информации в дереве: когда игрок не может различить два узла в дереве, они находятся в одном и том же информационном наборе. Когда игрок должен двигаться, он может обусловить свое действие только набором информации, который ему открывается, а не фактическим узлом. Теория была разработана в основном для игр с совершенным воспоминанием, то есть предполагается, что каждый игрок полностью помнит свои предыдущие действия и информацию. Kuhn (1953) дает формальное развитие.О некоторых недавних работах, посвященных несовершенному воспоминанию, см. Rubinstein (1998).
Шахматы можно рассматривать как игру в расширенной форме с совершенной информацией.Так называемые информационные наборы используются для представления ограниченной информации в дереве: когда игрок не может различить два узла в дереве, они находятся в одном и том же информационном наборе. Когда игрок должен двигаться, он может обусловить свое действие только набором информации, который ему открывается, а не фактическим узлом. Теория была разработана в основном для игр с совершенным воспоминанием, то есть предполагается, что каждый игрок полностью помнит свои предыдущие действия и информацию. Kuhn (1953) дает формальное развитие.О некоторых недавних работах, посвященных несовершенному воспоминанию, см. Rubinstein (1998).
Фон Нейман (1928) ввел фундаментальное понятие стратегии, с помощью которого игра в экстенсивной форме может быть сведена к игре в нормальной форме. Формально стратегия игрока представляет собой полный план действий, определяющий для каждого набора информации этого игрока действие, которое этот игрок намеревается предпринять, если и когда этот набор информации будет достигнут. Ясно, что как только определена стратегия для каждого игрока, определяется и результат.Фон Нейман утверждал, что для рациональных игроков нет потери общности в том, чтобы заставить их продумать игру заранее, а значит, заставить их выбрать стратегию. Следовательно, экстенсивная форма может быть приведена к более простой нормальной форме.
Ясно, что как только определена стратегия для каждого игрока, определяется и результат.Фон Нейман утверждал, что для рациональных игроков нет потери общности в том, чтобы заставить их продумать игру заранее, а значит, заставить их выбрать стратегию. Следовательно, экстенсивная форма может быть приведена к более простой нормальной форме.
Приведенное выше описание основано на рандомизации. Однако перед началом игры игрок может случайным образом выбрать, какую (чистую) стратегию он может использовать во время игры. В качестве альтернативы они могут рандомизировать, чтобы определить, какое действие они выберут, когда будет достигнут определенный набор информации.Понятие смешанной стратегии используется для обозначения первого случая, понятие поведенческой стратегии относится ко второму случаю локальной рандомизации. Кун (1953) показал, что обе концепции эквивалентны для игр с совершенным припоминанием, то есть все, что игрок может делать со стратегией одного типа, он может делать и со стратегией другого типа, и наоборот. Заметим, что поскольку предполагается, что у игроков есть полезности фон Неймана–Моргенштерна, замена «выигрыша» (полезности) на «ожидаемый выигрыш» не создает особых трудностей.
Заметим, что поскольку предполагается, что у игроков есть полезности фон Неймана–Моргенштерна, замена «выигрыша» (полезности) на «ожидаемый выигрыш» не создает особых трудностей.
Традиционная теория была разработана для игр с полной информацией, то есть предполагается, что каждый игрок знает функции полезности всех игроков в игре. Часто у игрока не будет всей информации о своих конкурентах. Например, в упомянутом выше контексте закупок игрок может не знать, сколько заказов у конкурента есть на складе, следовательно, он может не знать, какую ценность противник придает выигрышу настоящего контракта. Harsanyi (1967–1968) показал, как включить в модель неполную информацию.Чтобы представить асимметричную информацию, Харсаньи вводит искусственный случайный ход в начале игры, который определяет, какая часть частной информации будет у каждого игрока. Эта часть личной информации также называется типом игрока. Предполагается, что набор возможных типов и распределение вероятностей по этому набору общеизвестны, однако результаты реализации типа для игрока и обычно известны только самому игроку и . Таким образом, игра в нормальной форме с неполной информацией определяет не только игроков и их функции полезности, но также их типы и совместное распределение вероятностей по типам игроков.Формально такая игра задается набором G=〈S 1 ,…, S n , T 1 ,…, T n , u 1 ,…, u 3 n p 〉 где s i – игрок i’ s набор стратегий, T i – множество возможных типов игроков, i → ❄ T2 is4, 9 u 90×202 i 90 функция выигрыша игрока i’ (где T=Xi−1nT), а p — распределение вероятностей на T .Ход игры протекает следующим образом: профиль типа t∈T определяется в соответствии с p , и игрок i информируется о своем типе t i . Основываясь на этой информации, игрок i обновляет информацию о типах остальных, вычисляя апостериорную вероятность p i ( t/t i ) и выбирает действие для максимизации ассоциированного ожидаемая отдача.
Таким образом, игра в нормальной форме с неполной информацией определяет не только игроков и их функции полезности, но также их типы и совместное распределение вероятностей по типам игроков.Формально такая игра задается набором G=〈S 1 ,…, S n , T 1 ,…, T n , u 1 ,…, u 3 n p 〉 где s i – игрок i’ s набор стратегий, T i – множество возможных типов игроков, i → ❄ T2 is4, 9 u 90×202 i 90 функция выигрыша игрока i’ (где T=Xi−1nT), а p — распределение вероятностей на T .Ход игры протекает следующим образом: профиль типа t∈T определяется в соответствии с p , и игрок i информируется о своем типе t i . Основываясь на этой информации, игрок i обновляет информацию о типах остальных, вычисляя апостериорную вероятность p i ( t/t i ) и выбирает действие для максимизации ассоциированного ожидаемая отдача. Техника моделирования Харшани оказалась очень мощной (см. Аукционы ; Информация, экономика ).
Техника моделирования Харшани оказалась очень мощной (см. Аукционы ; Информация, экономика ).
Что такое теория игр и каковы ее приложения?
Объясняет Сол И. Гасс, почетный профессор Школы бизнеса Роберта Х. Смита Университета Мэриленда.Игра: Соревновательная деятельность, требующая мастерства, случая или выносливости со стороны двух или более лиц, которые играют в соответствии с набором правил, обычно для собственного развлечения или для развлечения зрителей ( The Random House Dictionary of the English Language , 1967).
Рассмотрим следующие реальные конкурентные ситуации: противоракетная оборона, ценовые войны при продаже новых автомобилей, энергетическое регулирование, проверка налогоплательщиков, телешоу «Выживший», терроризм, гонки NASCAR, переговоры с руководством, военные конфликты, торги на аукцион, арбитраж, реклама, выборы и голосование, селекция сельскохозяйственных культур, разрешение конфликтов, фондовый рынок, страхование и телекоммуникации. Что у них общего?
Что у них общего?
Простой пример поможет проиллюстрировать это.Научившись играть в крестики-нолики, вы, вероятно, открыли для себя стратегию игры, позволяющую добиться как минимум ничьей и даже выиграть, если противник ошибется и вы это заметите. Придерживаясь этой стратегии, вы не проиграете.
Эта простая игра иллюстрирует основные аспекты того, что сейчас называется теорией игр. В нем игра — это набор правил, которые ее описывают. Экземпляр игры от начала до конца известен как игра в игру.И чистая стратегия — такая, как та, которую вы нашли для игры в крестики-нолики, — это общий план, определяющий ходы, которые следует предпринять во всех случаях, которые могут возникнуть в ходе игры. Говорят, что игра обладает полной информацией, если на протяжении всей игры все правила, возможные варианты выбора и предыдущая история игры любого игрока известны всем участникам. Такие игры, как крестики-нолики, нарды и шахматы, — это игры с полной информацией, и такие игры решаются с помощью чистых стратегий. Но в то время как вы можете описать все такие чистые стратегии для крестиков-ноликов, это невозможно сделать для шахмат, отсюда и вековая интрига последних.
Но в то время как вы можете описать все такие чистые стратегии для крестиков-ноликов, это невозможно сделать для шахмат, отсюда и вековая интрига последних.
Игры без полной информации, такие как сопоставление монет, камень-ножницы-бумага или покер, бросают вызов игрокам, потому что не существует чистой стратегии, гарантирующей выигрыш. Для сопоставления пенни у вас есть две чистые стратегии: играть орлом или решкой. Для «камень-ножницы-бумага» у вас есть три чистые стратегии: играть в камень, бумагу или ножницы. В обоих случаях вы не можете постоянно разыгрывать чистую стратегию, такую как орел или камень, потому что ваш противник скоро поймет и применит соответствующую выигрышную стратегию.Что делать? Вскоре мы научимся сбивать с толку нашего оппонента, случайным образом выбирая стратегию для каждого розыгрыша (для орла и решки просто подбросьте монету в воздух и посмотрите, что получится при разделении 50 на 50). Есть и другие способы контролировать то, как мы рандомизируем. Например, для «камень-ножницы-бумага» мы можем подбросить шестигранный кубик и решить выбрать камень в половине случаев (выпадают числа 1, 2 или 3), выбрать бумагу в трети случаев (числа 4 или 5). подбрасываются) или выберите ножницы в одной шестой части времени (выбрасывается число 6).Это может скрыть ваш выбор от оппонента. Но, смешивая стратегии таким образом, должны ли вы ожидать выигрыша или проигрыша в долгосрочной перспективе? Каково оптимальное сочетание стратегий, которые вы должны использовать? Сколько вы ожидаете выиграть? Здесь в игру вступает современная математическая теория игр.
Например, для «камень-ножницы-бумага» мы можем подбросить шестигранный кубик и решить выбрать камень в половине случаев (выпадают числа 1, 2 или 3), выбрать бумагу в трети случаев (числа 4 или 5). подбрасываются) или выберите ножницы в одной шестой части времени (выбрасывается число 6).Это может скрыть ваш выбор от оппонента. Но, смешивая стратегии таким образом, должны ли вы ожидать выигрыша или проигрыша в долгосрочной перспективе? Каково оптимальное сочетание стратегий, которые вы должны использовать? Сколько вы ожидаете выиграть? Здесь в игру вступает современная математическая теория игр.
Такие игры, как «орел-решка» и «камень-ножницы-бумага», называются играми с нулевой суммой для двух лиц. Нулевая сумма означает, что любая сумма денег, которую выигрывает (или проигрывает) Игрок 1, равна той же сумме денег, которую проигрывает (или выигрывает) Игрок 2.То есть, играя в игру, деньги не создаются и не теряются. Большинство салонных игр — это игры с нулевой суммой для многих игроков (но если вы играете в покер в игорном зале, где зал берет определенный процент банка для покрытия своих накладных расходов, игра не является игрой с нулевой суммой). Для игр с нулевой суммой двух лиц самый известный математик 20-го века Джон фон Нейман доказал, что все такие игры имеют оптимальные стратегии для обоих игроков с соответствующим ожидаемым значением игры. Здесь оптимальная стратегия, учитывая, что игра проводится много раз, представляет собой специализированную случайную смесь отдельных чистых стратегий.Ценность игры, обозначаемая как v, , — это ценность, при которой игрок, скажем, Игрок 1, гарантированно выиграет, если будет придерживаться обозначенного оптимального сочетания стратегий независимо от того, какое сочетание стратегий использует Игрок 2. Точно так же Игрок 2 гарантированно не проиграет больше, чем 90 342 против 90 343, если он будет придерживаться обозначенного оптимального набора стратегий независимо от того, какой набор стратегий использует Игрок 1. Если v — положительная сумма, то Игрок 1 может рассчитывать на выигрыш этой суммы, усредненной по многим розыгрышам, а Игрок 2 может рассчитывать на проигрыш этой суммы.
Для игр с нулевой суммой двух лиц самый известный математик 20-го века Джон фон Нейман доказал, что все такие игры имеют оптимальные стратегии для обоих игроков с соответствующим ожидаемым значением игры. Здесь оптимальная стратегия, учитывая, что игра проводится много раз, представляет собой специализированную случайную смесь отдельных чистых стратегий.Ценность игры, обозначаемая как v, , — это ценность, при которой игрок, скажем, Игрок 1, гарантированно выиграет, если будет придерживаться обозначенного оптимального сочетания стратегий независимо от того, какое сочетание стратегий использует Игрок 2. Точно так же Игрок 2 гарантированно не проиграет больше, чем 90 342 против 90 343, если он будет придерживаться обозначенного оптимального набора стратегий независимо от того, какой набор стратегий использует Игрок 1. Если v — положительная сумма, то Игрок 1 может рассчитывать на выигрыш этой суммы, усредненной по многим розыгрышам, а Игрок 2 может рассчитывать на проигрыш этой суммы. Противоположный случай, если v является отрицательной суммой. Такая игра называется честной, если v = 0. То есть оба игрока могут рассчитывать на выигрыш 0 в течение длительного периода игр. Математическое описание игры двух лиц с нулевой суммой построить нетрудно, а определение оптимальных стратегий и ценности игры не представляет сложности с вычислительной точки зрения. Мы можем показать, что игра «орел-решка» — это честная игра и что у обоих игроков одинаковое оптимальное сочетание стратегий, при котором случайным образом выпадает орел или решка в 50 % случаев для каждого.Камень-ножницы-бумага также является честной игрой, и у обоих игроков есть оптимальные стратегии, которые используют каждый выбор в одной трети случаев. Не все игры с нулевой суммой честны, хотя большинство салонных игр с нулевой суммой для двух человек являются честными играми. Так почему же мы тогда играем в них? Это весело, нам нравится конкуренция, и, поскольку мы обычно играем в течение короткого периода времени, средний выигрыш может отличаться от 0.
Противоположный случай, если v является отрицательной суммой. Такая игра называется честной, если v = 0. То есть оба игрока могут рассчитывать на выигрыш 0 в течение длительного периода игр. Математическое описание игры двух лиц с нулевой суммой построить нетрудно, а определение оптимальных стратегий и ценности игры не представляет сложности с вычислительной точки зрения. Мы можем показать, что игра «орел-решка» — это честная игра и что у обоих игроков одинаковое оптимальное сочетание стратегий, при котором случайным образом выпадает орел или решка в 50 % случаев для каждого.Камень-ножницы-бумага также является честной игрой, и у обоих игроков есть оптимальные стратегии, которые используют каждый выбор в одной трети случаев. Не все игры с нулевой суммой честны, хотя большинство салонных игр с нулевой суммой для двух человек являются честными играми. Так почему же мы тогда играем в них? Это весело, нам нравится конкуренция, и, поскольку мы обычно играем в течение короткого периода времени, средний выигрыш может отличаться от 0. Попробуйте свои силы в следующей игре, в которой против = 1/5.
Попробуйте свои силы в следующей игре, в которой против = 1/5.
The Skin Game: Два игрока получают по бубновому и трефовому тузам.Игроку 1 также дается двойка бубен, а игроку 2 — двойка треф. В ходе игры Игрок 1 показывает одну карту, а Игрок 2, не зная о выборе Игрока 1, показывает одну карту. Игрок 1 выигрывает, если масти совпадают, и Игрок 2 выигрывает, если они не совпадают. Выигранная сумма (выигрыш) является числовым значением карты победителя. Но, если показаны две двойки, выигрыш равен нулю. [Здесь, если выплаты выражены в долларах, Игрок 1 может рассчитывать на выигрыш 0,20 доллара. Эта игра является фаворитом карнавальных дельцов (Игрок 1); его оптимальная смешанная стратегия состоит в том, чтобы никогда не играть бубновым тузом, играть тузом треф в 60% случаев и бубновой двойкой в 40% случаев.]
Возможности теории игр далеко не ограничиваются анализом таких относительно простых игр, но при этом возникают сложности. У нас могут быть ситуации конкуренции между многими людьми, в которых игроки могут формировать коалиции и сотрудничать против других игроков; игры многих лиц с ненулевой суммой; игры с бесконечным количеством стратегий; и игры с ненулевой суммой для двух человек, и это лишь некоторые из них. Математический анализ таких игр привел к обобщению результата фон Неймана об оптимальном решении для игр с нулевой суммой двух лиц, называемого равновесным решением.Равновесное решение — это набор смешанных стратегий, по одной для каждого игрока, так что у каждого игрока нет причин отклоняться от этой стратегии, при условии, что все остальные игроки придерживаются своей равновесной стратегии. Затем мы получаем важное обобщение решения для теории игр: любая некооперативная игра с конечными стратегиями для многих лиц имеет по крайней мере одно равновесное решение. Этот результат был доказан Джоном Нэшем и показан в фильме «Игры разума ». Книга ( A Beautiful Mind, by Sylvia Nasar; Simon & Schuster, 1998) представляет собой более реалистичную и лучше рассказанную историю.
Математический анализ таких игр привел к обобщению результата фон Неймана об оптимальном решении для игр с нулевой суммой двух лиц, называемого равновесным решением.Равновесное решение — это набор смешанных стратегий, по одной для каждого игрока, так что у каждого игрока нет причин отклоняться от этой стратегии, при условии, что все остальные игроки придерживаются своей равновесной стратегии. Затем мы получаем важное обобщение решения для теории игр: любая некооперативная игра с конечными стратегиями для многих лиц имеет по крайней мере одно равновесное решение. Этот результат был доказан Джоном Нэшем и показан в фильме «Игры разума ». Книга ( A Beautiful Mind, by Sylvia Nasar; Simon & Schuster, 1998) представляет собой более реалистичную и лучше рассказанную историю.
К настоящему моменту вы пришли к выводу, что ответом на вступительный вопрос о конкурентных ситуациях является «теория игр». Аспекты всех названных направлений были подвергнуты анализу с использованием методов теории игр. Веб-сайт www.gametheory.net содержит около 200 сравнительно недавних упоминаний, сгруппированных в 20 категорий. Однако важно отметить, что во многих конкурентных ситуациях теория игр на самом деле не решает насущной проблемы. Наоборот, это помогает осветить проблему и предлагает нам другой способ интерпретации конкурентных взаимодействий и возможных результатов.Теория игр — это стандартный инструмент анализа для профессионалов, работающих в области исследования операций, экономики, финансов, регулирования, вооруженных сил, страхования, розничного маркетинга, политики, анализа конфликтов и энергетики. Для получения дополнительной информации о теории игр см. вышеупомянутый веб-сайт и
http://william-king.www.drexel.edu/top/eco/game/game.html.
Веб-сайт www.gametheory.net содержит около 200 сравнительно недавних упоминаний, сгруппированных в 20 категорий. Однако важно отметить, что во многих конкурентных ситуациях теория игр на самом деле не решает насущной проблемы. Наоборот, это помогает осветить проблему и предлагает нам другой способ интерпретации конкурентных взаимодействий и возможных результатов.Теория игр — это стандартный инструмент анализа для профессионалов, работающих в области исследования операций, экономики, финансов, регулирования, вооруженных сил, страхования, розничного маркетинга, политики, анализа конфликтов и энергетики. Для получения дополнительной информации о теории игр см. вышеупомянутый веб-сайт и
http://william-king.www.drexel.edu/top/eco/game/game.html.
Введение в разработку игр для Интернета – Разработка игр
Современный Интернет быстро стал жизнеспособной платформой не только для создания великолепных высококачественных игр, но и для их распространения.
Диапазон игр, которые можно создать, не уступает настольным и родным аналогам ОС. Благодаря современным веб-технологиям и последнему браузеру вполне возможно создавать потрясающие первоклассные игры для Интернета. И мы не говорим о простых карточных играх или многопользовательских социальных играх, которые в былые времена делались с использованием Flash®. Мы говорим об офигенных 3D-шутерах, ролевых играх и многом другом. Благодаря значительным улучшениям производительности в технологии JIT-компилятора JavaScript и новым API-интерфейсам вы можете создавать игры, которые запускаются в браузере (или на устройствах с поддержкой HTML5, например, на базе Firefox OS) без компромиссов.
Благодаря современным веб-технологиям и последнему браузеру вполне возможно создавать потрясающие первоклассные игры для Интернета. И мы не говорим о простых карточных играх или многопользовательских социальных играх, которые в былые времена делались с использованием Flash®. Мы говорим об офигенных 3D-шутерах, ролевых играх и многом другом. Благодаря значительным улучшениям производительности в технологии JIT-компилятора JavaScript и новым API-интерфейсам вы можете создавать игры, которые запускаются в браузере (или на устройствах с поддержкой HTML5, например, на базе Firefox OS) без компромиссов.
Вы действительно можете думать о Интернете как о лучшей целевой платформе для вашей игры. Как мы любим говорить, «Интернет — это платформа». Давайте взглянем на ядро веб-платформы:
. Как разработчик игр, независимо от того, являетесь ли вы отдельным лицом или крупной игровой студией, вы хотите знать, почему имеет смысл ориентировать свой следующий игровой проект на Интернет. Давайте посмотрим, как Интернет может вам помочь.
Давайте посмотрим, как Интернет может вам помочь.
- Возможности Интернета огромны; это везде. Игры, созданные с помощью HTML5, работают на смартфонах, планшетах, ПК и Smart TV.
- Маркетинг и возможность обнаружения улучшены. Вы не ограничены продвижением своего приложения в чужом магазине приложений. Вместо этого вы можете рекламировать и продвигать свою игру в Интернете, а также в других средствах массовой информации, используя присущую Интернету возможность связывания и обмена для привлечения новых клиентов.
- У вас есть контроль там, где это важно: Платежи. Вам не нужно передавать кому-то 30% своих доходов только потому, что ваша игра находится в их экосистеме. Вместо этого взимайте плату, которую хотите, и используйте любую услугу обработки платежей, которая вам нравится.
- Опять же, с большим контролем, вы можете обновить свою игру, когда захотите. Не нужно ждать, затаив дыхание, одобрения, пока кто-то из другой компании решает, будет ли выпущено ваше исправление критической ошибки сегодня или завтра.

- Контролируйте свою аналитику! Вместо того, чтобы полагаться на кого-то еще, чтобы принять все решения о том, какая аналитика вам нужна, вы можете собрать свою собственную — или выбрать третью сторону, которая вам больше нравится — для сбора информации о ваших продажах и охвате вашей игры.
- Вы сможете более тесно управлять отношениями с клиентами по-своему. Больше не нужно фильтровать отзывы клиентов через ограниченные механизмы магазина приложений. Взаимодействуйте со своими клиентами так, как вы хотите, без посредников.
- Ваши игроки могут играть в вашу игру где угодно и когда угодно. Поскольку Интернет вездесущ, ваши клиенты могут проверять статус своей игры на своих телефонах, планшетах, домашних ноутбуках, рабочих компьютерах и т. д.
Что касается технических специалистов, давайте углубимся в API, которые Интернет предлагает для разработчиков игр.Вот подробный список, чтобы дать вам представление о том, что Интернет может сделать для вас:
- Полноэкранный API
Этот простой API позволяет вашей игре занимать весь экран, тем самым погружая игрока в действие.

- API геймпада
Если вы хотите, чтобы ваши пользователи могли использовать геймпады или другие игровые контроллеры для работы с вашей игрой, вам понадобится этот API.
- HTML и CSS
Вместе эти две технологии позволяют создавать, стилизовать и компоновать пользовательский интерфейс вашей игры.Частью HTML является элемент
, который обеспечивает один из способов создания 2D-графики.- HTML аудио
Элемент
- ИндекседБД
Мощный API для хранения данных для хранения пользовательских данных на их собственном компьютере или устройстве.Отличный способ сохранить состояние игры и другую информацию локально, чтобы ее не приходилось загружать каждый раз, когда это необходимо.
 Также полезно, чтобы сделать вашу игру играбельной, даже если пользователь не подключен к Интернету (например, когда он часами застревает в самолете).
Также полезно, чтобы сделать вашу игру играбельной, даже если пользователь не подключен к Интернету (например, когда он часами застревает в самолете).- JavaScript
JavaScript, язык программирования, используемый в Интернете, стремительно развивается в современных браузерах и становится все быстрее. Используйте его возможности для написания кода для своей игры или попробуйте использовать такие технологии, как Emscripten или Asm.js, чтобы легко портировать существующие игры.
- API блокировки указателя
API блокировки указателя позволяет заблокировать мышь или другое указывающее устройство в интерфейсе вашей игры, чтобы вместо абсолютного позиционирования курсора вы получали дельты координат, которые дают вам более точные измерения того, что делает пользователь, и предотвращают случайную отправку пользователем своих данных. ввести где-то еще, тем самым пропустив важное действие.
- SVG (масштабируемая векторная графика)
Позволяет создавать векторную графику, которая плавно масштабируется независимо от размера или разрешения экрана пользователя.

- Типизированные массивы
Типизированные массивы JavaScript дают вам доступ к необработанным двоичным данным из JavaScript; это позволяет вам манипулировать текстурами GL, игровыми данными или чем-то еще, даже если это не в родном формате JavaScript.
- API веб-аудио
Этот API для управления воспроизведением, синтезом и манипулированием звуком из кода JavaScript позволяет создавать потрясающие звуковые эффекты, а также воспроизводить музыку и управлять ею в режиме реального времени.
- WebGL
Позволяет создавать высокопроизводительную трехмерную (и двухмерную) графику с аппаратным ускорением из веб-контента. Это поддерживаемая Интернетом реализация OpenGL ES 2.0.
- WebRTC
API WebRTC (коммуникации в реальном времени) дает вам возможность управлять аудио- и видеоданными, включая телеконференции и передачу данных других приложений туда и обратно между двумя пользователями.
 Хотите, чтобы ваши игроки могли разговаривать друг с другом во время взрыва монстров? Это API для вас.
Хотите, чтобы ваши игроки могли разговаривать друг с другом во время взрыва монстров? Это API для вас.- Веб-сокеты
API WebSocket позволяет подключить ваше приложение или сайт к серверу для передачи данных туда и обратно в режиме реального времени. Идеально подходит для многопользовательских игр, чатов и т. д.
- Веб-работники
Workers дают вам возможность создавать фоновые потоки, выполняющие собственный код JavaScript, чтобы использовать преимущества современных многоядерных процессоров.
- XMLHttpRequest и файловый API
Комбинация XMLHttpRequest и File API позволяет вам отправлять и получать любые данные, которые вы хотите (не позволяйте «XML» сбить вас с толку!) с веб-сервера.Это отличный способ делать что угодно: от загрузки новых игровых уровней и иллюстраций до передачи информации о состоянии игры не в режиме реального времени туда и обратно.
Обновление вашей игры: передовой опыт (документация Steamworks)
Основная функциональность Steam заключается в том, чтобы держать ваших игроков в курсе последних сборок вашей игры. Независимо от того, есть ли у вас небольшая ошибка, которую нужно исправить, или крупное добавление контента, в Steam есть надежный набор инструментов, чтобы объявить об обновлении и передать его в руки ваших игроков.
Независимо от того, есть ли у вас небольшая ошибка, которую нужно исправить, или крупное добавление контента, в Steam есть надежный набор инструментов, чтобы объявить об обновлении и передать его в руки ваших игроков.Далее следует общий набор рекомендаций, которые следует учитывать при обновлении, а также некоторые передовые практики, которые мы в Valve извлекли из основных обновлений, которые мы сделали для наших собственных продуктов, а также из многих других доступных продуктов. через Стим.
Независимо от того, является ли ваш продукт бесплатным игровым сервисом или однопользовательским повествованием, обновления могут расширить вашу пользовательскую базу и повысить вовлеченность. Чтобы получить общую информацию об общении с клиентами, ознакомьтесь с нашей документацией по лучшим практикам модерации и посмотрите полную презентацию Робина Уокера на Steam Dev Days.
Примечание . Клиенты ожидают, что смогут загружать вашу игру и будущие обновления в клиенте Steam. Важно, чтобы вы использовали Steam для обработки своих обновлений и не требовали от пользователей загрузки контента внутри вашей игры после ее запуска. Steam предоставляет унифицированный процесс загрузки и обновления для клиентов, который позволяет им легко управлять расписанием и расположением своих загрузок и может привести к значительному повышению производительности и экономии средств для разработчиков.
Важно, чтобы вы использовали Steam для обработки своих обновлений и не требовали от пользователей загрузки контента внутри вашей игры после ее запуска. Steam предоставляет унифицированный процесс загрузки и обновления для клиентов, который позволяет им легко управлять расписанием и расположением своих загрузок и может привести к значительному повышению производительности и экономии средств для разработчиков.
Обновление в любое время
Обновления являются важной частью жизненного цикла вашего продукта и важной формой связи с клиентами. Вам нужно будет делать обновления, чтобы исправлять ошибки и устранять проблемы, но крупные обновления также предоставляют огромные возможности для добавления нового контента, новых режимов игры или новых функций, которые помогут поддерживать интерес клиентов и привлекать новую аудиторию. Steam упрощает исправление вашей игры или добавление контента в любое время, когда вам нужно, чтобы наилучшим образом обслуживать вашу аудиторию в соответствии с вашим графиком. Не стесняйтесь обновлять так часто, как вам нужно, но помните, что игрокам, у которых установлена ваша игра, нужно будет загрузить каждое обновление, прежде чем они смогут снова запустить игру, поэтому будьте внимательны, если ваши обновления имеют большой размер.
Не стесняйтесь обновлять так часто, как вам нужно, но помните, что игрокам, у которых установлена ваша игра, нужно будет загрузить каждое обновление, прежде чем они смогут снова запустить игру, поэтому будьте внимательны, если ваши обновления имеют большой размер.
Планирование и цели
Чтобы получить максимальную отдачу от вашего обновления, вам нужно начать с размышлений о целях, которых вы хотите достичь. Вы, вероятно, захотите все время вносить исправления, чтобы исправлять проблемы, которые подняли игроки или которые вы обнаружили во время тестирования игры.Но вы также должны подумать о более долгосрочных обновлениях контента, которые заинтересуют ваших игроков и вернут их к игре.Независимо от того, большое у вас обновление или маленькое, каждое из них — это форма общения с игроками, демонстрирующая, что вы прислушиваетесь к отзывам игроков и заботитесь об улучшении игрового опыта.
Исправления ошибок и исправления
Обновление и исправление вашей игры — один из лучших способов общения с клиентами. Если вы слышите о клиентах, испытывающих проблемы с вашей игрой, нет лучшего ответа, чем устранить проблему как можно быстрее (если это разумно).Steam упрощает развертывание обновленных сборок в любое время, так что используйте его, чтобы дорабатывать свой продукт и помогать клиентам с проблемами.
Если вы слышите о клиентах, испытывающих проблемы с вашей игрой, нет лучшего ответа, чем устранить проблему как можно быстрее (если это разумно).Steam упрощает развертывание обновленных сборок в любое время, так что используйте его, чтобы дорабатывать свой продукт и помогать клиентам с проблемами.При развертывании обновления полезно опубликовать объявление в Центре сообщества Steam, чтобы клиенты могли сообщить, что изменилось. Это также демонстрирует клиентам, что вы слушаете их и работаете над решением выявленных проблем.
Значительные обновления содержимого
Переработка и обновление вашего продукта очень важны, но ваше сообщение об обновлении может иметь большое значение.Мы обнаружили, что для наших собственных игр лучше всего выпускать крупные обновления максимум каждые 1-2 месяца. Это позволило нам собрать достаточно большое обновление, чтобы оно было захватывающим и убедительным, а также дало время, чтобы дразнить или предварительно объявить об этих обновлениях до их выпуска, чтобы вызвать ожидание.
Ваш собственный подход может измениться, когда вы узнаете, на что положительно реагируют ваши игроки. Вот пример хорошо сработавшего для нас процесса, который мы отточили, пробуя различные подходы и прислушиваясь к отзывам игроков:
- Предложите обновление — Предложите обновление (возможно, в повествовательной форме) за 3-4 дня до его начала, давать намеки, разжигать спекуляции и возбуждать клиентов.Вы также предоставляете ресурсы для освещения вашего продукта в прессе.
- Мониторинг форумов и отзывов – Мониторинг форумов и отзывов до того, как обновление будет выпущено, и соответствующим образом улучшите или настройте свой контент или узнайте, какие элементы больше всего нравятся вашим клиентам, чтобы вы могли соответствующим образом выделить их.
- Выделите изменения в функциях и игровом процессе — Выделите изменения в функциях и игровом процессе в сообщениях перед обновлением, чтобы привлечь больше внимания, спекуляций и волнения.
 Показывая эти детали по частям, ваши игроки могут анализировать и переваривать контент до того, как он начнет его воспроизводить.
Показывая эти детали по частям, ваши игроки могут анализировать и переваривать контент до того, как он начнет его воспроизводить. - Создавайте метаигры или конкурсы – Создавайте метаигры или конкурсы, позволяя вашим клиентам эффективно продавать продукт своим друзьям или другим игрокам и предоставляя им возможность внести свой вклад в игровой мир.
Примеры В качестве примера страниц объявлений об обновлениях, которые мы в Valve создали для некоторых наших собственных игр, вы можете увидеть последние обновления для Counter-Strike: Global Offensive, перечисленные справа веб-сайт CS:GO или некоторые обновления для Dota 2 здесь и здесь.
Все эти элементы применимы к любому продукту, независимо от жанра или размера команды. Мы настоятельно рекомендуем, чтобы одна и та же команда, разрабатывающая и создающая контент, также напрямую общалась с клиентами и получала отзывы. Это НЕ означает, что ваш дизайнер уровней должен целый день отвечать на вопросы на форуме Steam. Однако это означает, что чтение отзывов и ответственность за сообщество должны быть частью роли команды разработчиков, а не делегироваться менеджерам сообщества или отдельной команде по связям с общественностью.Посмотрите полный доклад Dev Days, чтобы узнать о конкретных примерах и получить дополнительную информацию.
Однако это означает, что чтение отзывов и ответственность за сообщество должны быть частью роли команды разработчиков, а не делегироваться менеджерам сообщества или отдельной команде по связям с общественностью.Посмотрите полный доклад Dev Days, чтобы узнать о конкретных примерах и получить дополнительную информацию.
DLC или часть основной игры?
Когда вы выпускаете новый контент для своей игры, у вас есть несколько вариантов того, как вы можете предоставить этот контент игрокам. Вы можете продавать его как загружаемый контент (DLC) или внутриигровые покупки. Или вы можете просто включить его в базовую игру в качестве бесплатного обновления контента. Ниже приведены некоторые рекомендации, которые, как мы видели, хорошо работают в большинстве случаев:
- Бесплатный контент => часть игры — Если вы хотите, чтобы контент был бесплатным, мы обнаружили, что он работает. лучше всего просто включить этот новый контент как часть контента вашей основной игры.
 Таким образом, ваши игроки сразу же получат новейший контент без необходимости нажимать отдельную кнопку загрузки (как в случае, если вы выпустили свое обновление в виде бесплатного DLC).
Таким образом, ваши игроки сразу же получат новейший контент без необходимости нажимать отдельную кнопку загрузки (как в случае, если вы выпустили свое обновление в виде бесплатного DLC). - Небольшой платный контент => внутриигровые покупки — Если вы добавляете небольшие предметы платного контента, такие как головные уборы, индивидуальное оружие или расходные материалы, вы можете подумать о том, чтобы сделать их отдельными внутриигровыми покупками. Steamworks включает в себя простую в использовании службу инвентаря Steam, и, конечно же, вам нужно будет использовать микротранзакции Steam, которые обрабатывают всю обработку платежей и конвертацию валюты.
- Крупный платный контент => DLC — Если вы продаете значительное количество контента, такого как карты, новые игровые режимы или расширения, вам нужно использовать для этого DLC. Это позволяет устанавливать контент отдельно, чтобы уменьшить размер файла для игроков, которые не покупают дополнительный контент, и позволяет продавать значительный контент как часть страницы магазина вашей игры.

Тестирование
Перед развертыванием обновления вы, вероятно, захотите убедиться, что протестировали его самостоятельно из сборки Steam.Это можно сделать несколькими способами, поэтому обязательно ознакомьтесь с документацией по тестированию в Steam.Загрузка вашего обновления
Чтобы обновить игру или сборку программного обеспечения, просто следуйте тем же инструкциям, что и при создании исходных сборок в SteamPipe. Подробности смотрите в документации SteamPipe.Обратите внимание, что после того, как ваше приложение будет выпущено для клиентов, ваши клиенты получат сборку, помеченную как сборка по умолчанию. Чтобы протестировать свое обновление, вы должны загрузить новую сборку с помощью Steampipe, а затем установить эту сборку в тестовой ветке с паролем для тестирования, прежде чем перемещать ее в ветку по умолчанию.См. раздел «Управление загруженными сборками» выше, чтобы напомнить об управлении ветками сборки.
Оживите свою сборку
После того, как вы загрузили и протестировали свою сборку, вы готовы представить ее игрокам. Для этого вам нужно переключить желаемую сборку на новую сборку «по умолчанию». Если вы создали новые хранилища в процессе добавления этого нового контента, убедитесь, что вы добавили это новое хранилище во все хранилища и пакеты ключей. См. документацию по пакетам для получения более подробной информации.
Для этого вам нужно переключить желаемую сборку на новую сборку «по умолчанию». Если вы создали новые хранилища в процессе добавления этого нового контента, убедитесь, что вы добавили это новое хранилище во все хранилища и пакеты ключей. См. документацию по пакетам для получения более подробной информации.Анонс вашего обновления в Steam
Когда вы будете готовы выпустить свое обновление в Steam, вы захотите сообщить об этом клиентам и предоставить место для целенаправленной обратной связи.Steam предоставляет вам несколько способов объявить об обновлении и сообщить о нем:- Использовать переопределение обложки — вы можете использовать временный набор капсульных изображений, чтобы сообщить клиентам об обновлениях вашей игры. В разделе «Редактировать магазин» Steamworks на вкладке «Графические ресурсы» есть раздел для определения временной переопределения ресурсов. Подробнее о переопределениях иллюстраций
- Опубликовать объявление .
 Когда вы публикуете событие или объявление, оно будет отображаться для всех клиентов, которые следят за вашей игрой (что они могут сделать из вашего центра сообщества или страницы в магазине), на странице вашего магазина. , в библиотеке Steam и будет доступен из панели «загрузки» клиента Steam.Подробнее о событиях и объявлениях
Когда вы публикуете событие или объявление, оно будет отображаться для всех клиентов, которые следят за вашей игрой (что они могут сделать из вашего центра сообщества или страницы в магазине), на странице вашего магазина. , в библиотеке Steam и будет доступен из панели «загрузки» клиента Steam.Подробнее о событиях и объявлениях - Получите скидку . Чтобы получить максимальную отдачу от крупного обновления контента, вы можете подумать о том, чтобы приурочить его к скидке на вашу игру. Это может одновременно создать как можно больше шума и дать игрокам еще один повод приобрести вашу игру сейчас, когда вокруг игры накапливается куча волнений. Кроме того, игроки, у которых ваша игра есть в списке желаний, получат электронное письмо с уведомлением о том, что ваша игра продается со скидкой. Это работает очень хорошо в сочетании с переопределением временных иллюстраций, как описано выше.Подробнее о скидке
- Использование раунда видимости обновлений — Если это одно из ваших основных обновлений контента, вы можете использовать раунд показа обновлений Steam, чтобы ваше обновление появилось на главной странице магазина Steam.
 Это полезно для информирования новых и существующих клиентов о вашем обновлении. Это также перечисляет ваш заголовок на странице недавно обновленных продуктов.
Это полезно для информирования новых и существующих клиентов о вашем обновлении. Это также перечисляет ваш заголовок на странице недавно обновленных продуктов.
Чтобы использовать раунд видимости обновления, вам сначала нужно опубликовать объявление сообщества Steam с подробной информацией о вашем обновлении.Для получения более подробной информации ознакомьтесь с документацией раунда видимости обновлений Steam.
Руководство по разработке игр для Windows 10 — приложения UWP
- Статья
- 33 минуты на чтение
Пожалуйста, оцените свой опыт
да Нет
Любая дополнительная обратная связь?
Отзыв будет отправлен в Microsoft: при нажатии кнопки отправки ваш отзыв будет использован для улучшения продуктов и услуг Microsoft. Политика конфиденциальности.
Политика конфиденциальности.
Представлять на рассмотрение
Спасибо.
В этой статье
Добро пожаловать в руководство по разработке игр для Windows 10!
В этом руководстве содержится полный набор ресурсов и информации, которые вам понадобятся для разработки игры для универсальной платформы Windows (UWP). Английская (США) версия этого руководства доступна в формате PDF.
Введение в разработку игр для универсальной платформы Windows (UWP)
Когда вы создаете игру для Windows 10, у вас есть возможность обратиться к миллионам игроков по всему миру через телефон, ПК и Xbox One. Благодаря Xbox для Windows, Xbox Live, многопользовательской игре на нескольких устройствах, потрясающему игровому сообществу и новым мощным функциям, таким как универсальная платформа Windows (UWP) и DirectX 12, игры для Windows 10 захватывают игроков всех возрастов и жанров. Новая универсальная платформа Windows (UWP) обеспечивает совместимость вашей игры на устройствах с Windows 10 благодаря общему API для телефона, ПК и Xbox One, а также инструментам и параметрам, позволяющим адаптировать игру для каждого устройства.
Новая универсальная платформа Windows (UWP) обеспечивает совместимость вашей игры на устройствах с Windows 10 благодаря общему API для телефона, ПК и Xbox One, а также инструментам и параметрам, позволяющим адаптировать игру для каждого устройства.
В этом руководстве собрана исчерпывающая информация и ресурсы, которые помогут вам в разработке игры. Разделы организованы в соответствии с этапами разработки игры, поэтому вы будете знать, где искать информацию, когда она вам понадобится.
Если вы новичок в разработке игр для Windows или Xbox, вам может понадобиться руководство по началу работы. В разделе Ресурсы для разработки игр также представлен общий обзор документации, программ и других ресурсов, полезных при создании игры.Если вы хотите начать с просмотра некоторого кода UWP, см. раздел Образцы игр.
Это руководство будет обновляться по мере появления дополнительных ресурсов и материалов по разработке игр для Windows 10.
Ресурсы для разработки игр
От документации до программ для разработчиков, форумов, блогов и примеров — доступно множество ресурсов, которые помогут вам в разработке игр. Вот сводка ресурсов, о которых нужно знать, когда вы начинаете разработку игры для Windows 10.
Вот сводка ресурсов, о которых нужно знать, когда вы начинаете разработку игры для Windows 10.
Примечание
Некоторыми функциями можно управлять с помощью различных программ.Это руководство охватывает широкий спектр ресурсов, поэтому вы можете обнаружить, что некоторые ресурсы недоступны в зависимости от программы, в которой вы участвуете, или вашей конкретной роли в разработке. Примерами являются ссылки, которые разрешаются на developer.xboxlive.com, forums.xboxlive.com, xdi.xboxlive.com или в сети разработчиков игр (GDN). Сведения о партнерстве с корпорацией Майкрософт см. в разделе Программы для разработчиков.
Документация по разработке игр
В этом руководстве вы найдете глубокие ссылки на соответствующую документацию, упорядоченную по задачам, технологиям и этапам разработки игры.Чтобы дать вам общее представление о том, что доступно, вот основные порталы документации по разработке игр для Windows 10.
Партнерский центр
Регистрация учетной записи разработчика в Центре партнеров — это первый шаг к публикации вашей игры для Windows. Учетная запись разработчика позволяет зарезервировать название вашей игры и отправлять бесплатные или платные игры в Microsoft Store для всех устройств Windows. Используйте свою учетную запись разработчика для управления своей игрой и внутриигровыми продуктами, получения подробной аналитики и включения сервисов, которые создают отличные впечатления для ваших игроков по всему миру.
Учетная запись разработчика позволяет зарезервировать название вашей игры и отправлять бесплатные или платные игры в Microsoft Store для всех устройств Windows. Используйте свою учетную запись разработчика для управления своей игрой и внутриигровыми продуктами, получения подробной аналитики и включения сервисов, которые создают отличные впечатления для ваших игроков по всему миру.
Microsoft также предлагает несколько программ для разработчиков, которые помогут вам разрабатывать и публиковать игры для Windows. Мы рекомендуем посмотреть, подходят ли они вам, прежде чем регистрировать учетную запись Центра партнеров. Дополнительные сведения см. в разделе Программы для разработчиков
.Программы для разработчиков
Microsoft предлагает несколько программ для разработчиков, которые помогут вам разрабатывать и публиковать игры для Windows. Подумайте о том, чтобы присоединиться к программе для разработчиков, если вы хотите разрабатывать игры для Xbox One и интегрировать функции Xbox Live в свою игру. Чтобы опубликовать игру в Microsoft Store, вам также потребуется создать учетную запись разработчика в Центре партнеров.
Чтобы опубликовать игру в Microsoft Store, вам также потребуется создать учетную запись разработчика в Центре партнеров.
Программа для авторов Xbox Live
Программа Xbox Live Creators Program позволяет любому интегрировать Xbox Live в свою игру и публиковать ее на Xbox One и Windows 10. Существует упрощенный процесс сертификации, и утверждение концепции не требуется за пределами стандартных политик Microsoft Store.
Вы можете развернуть, спроектировать и опубликовать свою игру в программе Creators Program без специального комплекта для разработки, используя только розничное оборудование.Для начала загрузите приложение активации режима разработки на свой Xbox One.
Если вам нужен доступ к еще большему количеству возможностей Xbox Live, специализированная поддержка в области маркетинга и разработки, а также возможность быть представленным в основном магазине Xbox One, подайте заявку на участие в программе ID@Xbox.
ID@Xbox
Программа ID@Xbox помогает квалифицированным разработчикам игр самостоятельно публиковать игры для Windows и Xbox One. Если вы хотите разрабатывать для Xbox One или добавлять функции Xbox Live, такие как Gamerscore, достижения и списки лидеров, в свою игру для Windows 10, зарегистрируйтесь с помощью ID@Xbox.Станьте разработчиком ID@Xbox, чтобы получить инструменты и поддержку, необходимые для раскрытия вашего творчества и максимального успеха. Мы рекомендуем сначала подать заявку на ID@Xbox, прежде чем регистрировать учетную запись разработчика в Центре партнеров.
Если вы хотите разрабатывать для Xbox One или добавлять функции Xbox Live, такие как Gamerscore, достижения и списки лидеров, в свою игру для Windows 10, зарегистрируйтесь с помощью ID@Xbox.Станьте разработчиком ID@Xbox, чтобы получить инструменты и поддержку, необходимые для раскрытия вашего творчества и максимального успеха. Мы рекомендуем сначала подать заявку на ID@Xbox, прежде чем регистрировать учетную запись разработчика в Центре партнеров.
Инструменты Xbox и ПО промежуточного слоя
Программа инструментов и промежуточного программного обеспечения Xbox предоставляет лицензии на комплекты разработки Xbox профессиональным разработчикам игровых инструментов и промежуточного программного обеспечения. Разработчики, принятые в программу, могут делиться и распространять свои технологии Xbox XDK среди других лицензированных разработчиков Xbox.
Образцы игр
Существует множество примеров игр и приложений для Windows 10, которые помогут вам понять игровые функции Windows 10 и быстро приступить к разработке игр. Регулярно разрабатываются и публикуются дополнительные образцы, поэтому не забывайте время от времени заглядывать на порталы образцов, чтобы узнать, что нового. Вы также можете просматривать репозитории GitHub, чтобы получать уведомления об изменениях и дополнениях.
Регулярно разрабатываются и публикуются дополнительные образцы, поэтому не забывайте время от времени заглядывать на порталы образцов, чтобы узнать, что нового. Вы также можете просматривать репозитории GitHub, чтобы получать уведомления об изменениях и дополнениях.
Форумы разработчиков
Форумы разработчиков — отличное место, где можно задавать вопросы о разработке игр и отвечать на них, а также общаться с сообществом разработчиков игр.Форумы также могут быть прекрасным ресурсом для поиска существующих ответов на сложные вопросы, с которыми разработчики сталкивались и решали в прошлом.
Блоги разработчиков
Блоги разработчиков — еще один отличный источник последней информации о разработке игр. Вы найдете сообщения о новых функциях, деталях реализации, передовых практиках, истории архитектуры и многом другом.
Концепция и планирование
На этапе концепции и планирования вы решаете, какой будет ваша игра, а также какие технологии и инструменты вы будете использовать, чтобы воплотить ее в жизнь.
Обзор технологий разработки игр
Когда вы начинаете разработку игры для UWP, у вас есть несколько вариантов графики, ввода, звука, сети, утилит и библиотек.
Если вы уже определились со всеми технологиями, которые будете использовать в своей игре, отлично! Если нет, руководство по игровым технологиям для приложений UWP представляет собой отличный обзор многих доступных технологий, и его настоятельно рекомендуется прочитать, чтобы помочь вам понять варианты и то, как они сочетаются друг с другом.
Планирование игры
Вот некоторые общие концепции и темы планирования, которые следует учитывать при планировании игры.
Выбор графической технологии и языка программирования
Существует несколько языков программирования и графических технологий, доступных для использования в играх для Windows 10. Путь, который вы выберете, зависит от типа разрабатываемой вами игры, опыта и предпочтений вашей студии разработки, а также конкретных требований к функциям вашей игры. Будете ли вы использовать C#, C++ или JavaScript? DirectX, XAML или HTML5?
Будете ли вы использовать C#, C++ или JavaScript? DirectX, XAML или HTML5?
DirectX
Microsoft DirectX — это выбор для обеспечения высочайшей производительности 2D- и 3D-графики и мультимедиа.
DirectX 12 быстрее и эффективнее любой предыдущей версии. Direct3D 12 обеспечивает более насыщенные сцены, больше объектов, более сложные эффекты и полное использование современного оборудования графического процессора на ПК с Windows 10 и Xbox One.
Если вы хотите использовать знакомый графический конвейер Direct3D 11, вам по-прежнему будут полезны новые функции рендеринга и оптимизации, добавленные в Direct3D 11.3. И, если вы опытный разработчик Windows API для настольных ПК с корнями в Win32, у вас все еще будет эта возможность в Windows 10.
Широкие возможности и глубокая интеграция платформы DirectX обеспечивают мощность и производительность, необходимые для самых требовательных игр.
XAML
XAML — это простой в использовании декларативный язык пользовательского интерфейса с такими удобными функциями, как анимация, раскадровка, привязка данных, масштабируемая векторная графика, динамическое изменение размера и графы сцен. XAML отлично подходит для пользовательского интерфейса игр, меню, спрайтов и 2D-графики.Чтобы упростить макет пользовательского интерфейса, XAML совместим с инструментами проектирования и разработки, такими как Expression Blend и Microsoft Visual Studio. XAML обычно используется с C#, но C++ также является хорошим выбором, если вы предпочитаете этот язык или если ваша игра требует больших ресурсов ЦП.
XAML отлично подходит для пользовательского интерфейса игр, меню, спрайтов и 2D-графики.Чтобы упростить макет пользовательского интерфейса, XAML совместим с инструментами проектирования и разработки, такими как Expression Blend и Microsoft Visual Studio. XAML обычно используется с C#, но C++ также является хорошим выбором, если вы предпочитаете этот язык или если ваша игра требует больших ресурсов ЦП.
HTML 5
Язык гипертекстовой разметки (HTML) — это распространенный язык разметки пользовательского интерфейса, используемый для веб-страниц, приложений и многофункциональных клиентов. Игры для Windows могут использовать HTML5 в качестве полнофункционального уровня представления со знакомыми функциями HTML, доступом к универсальной платформе Windows и поддержкой современных веб-функций, таких как AppCache, Web Workers, холст, перетаскивание, асинхронное программирование и SVG.При рендеринге HTML за кулисами используется аппаратное ускорение DirectX, поэтому вы по-прежнему можете пользоваться преимуществами DirectX в производительности без написания дополнительного кода. HTML5 — хороший выбор, если вы разбираетесь в веб-разработке, портируете веб-игру или хотите использовать языковые и графические слои, которые проще использовать, чем другие варианты. HTML5 используется с JavaScript, но также может вызывать компоненты, созданные с помощью C# или C++/CX.
HTML5 — хороший выбор, если вы разбираетесь в веб-разработке, портируете веб-игру или хотите использовать языковые и графические слои, которые проще использовать, чем другие варианты. HTML5 используется с JavaScript, но также может вызывать компоненты, созданные с помощью C# или C++/CX.
Сочетание технологий презентации
Графическая инфраструктура Microsoft DirectX (DXGI) обеспечивает взаимодействие и совместимость нескольких графических технологий.Для высокопроизводительной графики можно комбинировать XAML и DirectX, используя XAML для меню и другого простого пользовательского интерфейса, а DirectX — для рендеринга сложных 2D- и 3D-сцен. DXGI также обеспечивает совместимость между Direct2D, Direct3D, DirectWrite, DirectCompute и Microsoft Media Foundation.
С++
C++/CX — это высокопроизводительный язык с низкими накладными расходами, который обеспечивает мощное сочетание скорости, совместимости и доступа к платформе. C++/CX упрощает использование всех замечательных игровых функций Windows 10, включая DirectX и Xbox Live. Вы также можете повторно использовать существующий код и библиотеки C++. C++/CX создает быстрый нативный код, который не требует дополнительных затрат на сборку мусора, поэтому ваша игра может иметь высокую производительность и низкое энергопотребление, что приводит к увеличению времени автономной работы. Используйте C++/CX с DirectX или XAML или создайте игру, в которой используется их комбинация.
Вы также можете повторно использовать существующий код и библиотеки C++. C++/CX создает быстрый нативный код, который не требует дополнительных затрат на сборку мусора, поэтому ваша игра может иметь высокую производительность и низкое энергопотребление, что приводит к увеличению времени автономной работы. Используйте C++/CX с DirectX или XAML или создайте игру, в которой используется их комбинация.
С#
C# (произносится как «си-шарп») — современный инновационный язык, простой, мощный, типобезопасный и объектно-ориентированный. C# обеспечивает быструю разработку, сохраняя привычность и выразительность языков C-стиля.Несмотря на простоту использования, C# имеет множество расширенных языковых функций, таких как полиморфизм, делегаты, лямбда-выражения, замыкания, методы итераторов, ковариантность и выражения LINQ. C# — отличный выбор, если вы ориентируетесь на XAML, хотите быстро приступить к разработке своей игры или уже имеете опыт работы с C#. C# в основном используется с XAML, поэтому, если вы хотите использовать DirectX, выберите вместо него C++ или напишите часть своей игры как компонент C++, взаимодействующий с DirectX. Или возьмем Win2D, графическую библиотеку прямого режима Direct2D для C# и C++.
Или возьмем Win2D, графическую библиотеку прямого режима Direct2D для C# и C++.
JavaScript
JavaScript — это динамический язык сценариев, широко используемый для современных веб-приложений и многофункциональных клиентских приложений.
Приложения JavaScript для Windows могут получить доступ к мощным функциям универсальной платформы Windows простым и интуитивно понятным способом — как методы и свойства объектно-ориентированных классов JavaScript. JavaScript — хороший выбор для вашей игры, если вы пришли из среды веб-разработки, уже знакомы с JavaScript или хотите использовать библиотеки HTML5, CSS, WinJS или JavaScript.Если вы ориентируетесь на DirectX или XAML, вместо этого выберите C# или C++/CX.
Используйте компоненты среды выполнения Windows для объединения языков
Универсальная платформа Windows позволяет легко комбинировать компоненты, написанные на разных языках. Создавайте компоненты среды выполнения Windows на C++, C# или Visual Basic, а затем вызывайте их из JavaScript, C#, C++ или Visual Basic. Это отличный способ запрограммировать части вашей игры на выбранном вами языке. Компоненты также позволяют вам использовать внешние библиотеки, которые доступны только на определенном языке, а также использовать устаревший код, который вы уже написали.
Это отличный способ запрограммировать части вашей игры на выбранном вами языке. Компоненты также позволяют вам использовать внешние библиотеки, которые доступны только на определенном языке, а также использовать устаревший код, который вы уже написали.
Какую версию DirectX следует использовать в вашей игре?
Если вы выбираете DirectX для своей игры, вам нужно решить, какую версию использовать: Microsoft Direct3D 12 или Microsoft Direct3D 11.
DirectX 12 быстрее и эффективнее любой предыдущей версии. Direct3D 12 обеспечивает более насыщенные сцены, больше объектов, более сложные эффекты и полное использование современного оборудования графического процессора на ПК с Windows 10 и Xbox One. Поскольку Direct3D 12 работает на очень низком уровне, он может предоставить опытной группе разработчиков графики или опытной команде разработчиков DirectX 11 все необходимые средства управления для максимальной оптимизации графики.
Direct3D 11.3 — это низкоуровневый графический API, который использует знакомую модель программирования Direct3D и решает для вас дополнительные сложности, связанные с рендерингом с помощью графического процессора. Он также поддерживается в Windows 10 и Xbox One. Если у вас есть существующий движок, написанный на Direct3D 11, и вы не совсем готовы перейти на Direct3D 12, вы можете использовать Direct3D 11 на 12 для достижения некоторых улучшений производительности. Версии 11.3+ содержат новые функции рендеринга и оптимизации, доступные также в Direct3D 12.
Он также поддерживается в Windows 10 и Xbox One. Если у вас есть существующий движок, написанный на Direct3D 11, и вы не совсем готовы перейти на Direct3D 12, вы можете использовать Direct3D 11 на 12 для достижения некоторых улучшений производительности. Версии 11.3+ содержат новые функции рендеринга и оптимизации, доступные также в Direct3D 12.
Мосты, игровые движки и промежуточное ПО
В зависимости от потребностей вашей игры использование мостов, игровых движков или промежуточного ПО может сэкономить время и ресурсы на разработку и тестирование. Вот некоторые обзоры и ресурсы для мостов, игровых движков и промежуточного программного обеспечения.
Мосты универсальной платформы Windows
Мосты универсальной платформы Windows — это технологии, которые переносят ваше существующее приложение или игру на UWP. Мосты — отличный способ быстро приступить к разработке игр для UWP.
PlayFab
Теперь часть семейства Microsoft, PlayFab представляет собой полную серверную платформу для живых игр и мощный способ начать работу для независимых студий. Повышайте доход, вовлеченность и удержание клиентов — при одновременном снижении затрат — с помощью игровых сервисов, аналитики в реальном времени и LiveOps.
Повышайте доход, вовлеченность и удержание клиентов — при одновременном снижении затрат — с помощью игровых сервисов, аналитики в реальном времени и LiveOps.
Единство
Unity предлагает платформу для создания красивых и увлекательных 2D-, 3D-, VR- и AR-игр и приложений. Это позволяет вам быстро реализовать свое творческое видение и доставляет ваш контент практически на любой носитель или устройство.
Начиная с Unity 5.4, Unity поддерживает разработку Direct3D 12.
Хавок
Модульный набор инструментов и технологийHavok помогает создателям игр выйти на новый уровень интерактивности и погружения. Havok обеспечивает очень реалистичную физику, интерактивные симуляции и потрясающую кинематографию. Версия 2015.1 и выше официально поддерживает UWP в Visual Studio 2015 на платформах x86, 64-разрядных версиях и ARM.
МоноИгра
MonoGame — это кроссплатформенная среда разработки игр с открытым исходным кодом, изначально основанная на Microsoft XNA Framework 4. 0. В настоящее время Monogame поддерживает Windows, Windows Phone и Xbox, а также Linux, macOS, iOS, Android и ряд других платформ.
0. В настоящее время Monogame поддерживает Windows, Windows Phone и Xbox, а также Linux, macOS, iOS, Android и ряд других платформ.
Cocos2d
Cocos2d-x — это кроссплатформенный механизм разработки игр с открытым исходным кодом и набор инструментов, который поддерживает создание игр UWP. Начиная с версии 3, также добавляются 3D-функции.
Нереальный движок
Unreal Engine 4 — это полный набор инструментов для разработки игр для всех типов игр и разработчиков. Разработчики игр по всему миру используют Unreal Engine для самых требовательных игр для консолей и ПК.
ВавилонJS
BabylonJS — это полная среда JavaScript для создания 3D-игр с использованием HTML5, WebGL, WebVR и веб-аудио.
Портирование вашей игры
Если у вас уже есть игра, существует множество ресурсов и руководств, которые помогут вам быстро перенести ее на UWP. Чтобы ускорить процесс переноса, вы также можете рассмотреть возможность использования моста универсальной платформы Windows.
Прототип и конструкция
Теперь, когда вы определились с типом игры, которую хотите создать, а также с инструментами и графическими технологиями, которые будете использовать для ее создания, вы готовы приступить к работе над дизайном и прототипом.По своей сути ваша игра представляет собой приложение для универсальной платформы Windows, и именно с этого вы и начнете.
Введение в универсальную платформу Windows (UWP)
В Windows 10 представлена универсальная платформа Windows (UWP), которая обеспечивает общую платформу API для устройств с Windows 10. UWP развивает и расширяет модель среды выполнения Windows и превращает ее в целостное унифицированное ядро. Игры, предназначенные для UWP, могут вызывать WinRT API, общие для всех устройств. Поскольку UWP предоставляет гарантированные уровни API, вы можете создать единый пакет приложения, который будет установлен на всех устройствах с Windows 10.И если вы хотите, ваша игра по-прежнему может вызывать API-интерфейсы (включая некоторые классические API-интерфейсы Windows из Win32 и . NET), специфичные для устройств, на которых работает ваша игра.
NET), специфичные для устройств, на которых работает ваша игра.
Ниже приведены отличные руководства, в которых подробно обсуждаются приложения универсальной платформы Windows. Их рекомендуется прочитать, чтобы лучше понять платформу.
Начало работы с разработкой UWP
Настройка и подготовка к разработке приложения для универсальной платформы Windows выполняется быстро и легко. Следующие руководства шаг за шагом проведут вас через этот процесс.
Если вы «абсолютный новичок» в программировании UWP и рассматриваете возможность использования XAML в своей игре (см. раздел Выбор графической технологии и языка программирования), серия видеороликов «Разработка Windows 10 для абсолютных новичков» — хорошее место для начала.
| Руководство для начинающих по разработке Windows 10 с помощью XAML (серия видеороликов) | Разработка Windows 10 для начинающих |
| Анонс серии Windows 10 для начинающих с использованием XAML (запись в блоге) | Разработка Windows 10 для начинающих |
Концепции разработки UWP
API Windows Desktop для UWP
Вот несколько ссылок, которые помогут вам перенести настольную игру Windows на UWP.
Управление временем жизни процесса
Управление жизненным циклом процесса или жизненным циклом приложения описывает различные состояния активации, через которые может проходить приложение универсальной платформы Windows. Ваша игра может быть активирована, приостановлена, возобновлена или прекращена, и может переходить через эти состояния различными способами.
Дизайн игры UX
Генезис великой игры — вдохновленный дизайн.
Игры имеют некоторые общие элементы пользовательского интерфейса и принципы дизайна с приложениями, но игры часто имеют уникальный внешний вид, ощущения и цель дизайна для их взаимодействия с пользователем.Игры успешны, когда продуманный дизайн применяется к обоим аспектам — когда в вашей игре должен использоваться проверенный UX, а когда она должна отличаться и вводить новшества? Технология представления, которую вы выберете для своей игры — DirectX, XAML, HTML5 или комбинация этих трех — повлияет на детали реализации, но применяемые вами принципы проектирования в значительной степени не зависят от этого выбора.
Помимо дизайна UX, дизайн геймплея, такой как дизайн уровней, темп, дизайн мира и другие аспекты, представляет собой самостоятельную форму искусства, которая зависит от вас и вашей команды и не рассматривается в этом руководстве по разработке.
Цветовая шкала и палитра
Следование единообразным цветовым рекомендациям в игре улучшает эстетику, облегчает навигацию и является мощным инструментом для информирования игрока о меню и функциях HUD. Последовательное окрашивание игровых элементов, таких как предупреждения, урон, опыт и достижения, может привести к более чистому пользовательскому интерфейсу и уменьшить потребность в явных метках.
Типография
Надлежащее использование типографики улучшает многие аспекты вашей игры, включая макет пользовательского интерфейса, навигацию, удобочитаемость, атмосферу, бренд и погружение игрока.
Карта пользовательского интерфейса
Карта пользовательского интерфейса — это макет игровой навигации и меню, представленный в виде блок-схемы. Карта пользовательского интерфейса помогает всем заинтересованным сторонам понять интерфейс игры и пути навигации, а также может выявить потенциальные препятствия и тупики на ранних этапах цикла разработки.
Карта пользовательского интерфейса помогает всем заинтересованным сторонам понять интерфейс игры и пути навигации, а также может выявить потенциальные препятствия и тупики на ранних этапах цикла разработки.
Звук игры
Руководства и справочники по реализации звука в играх с использованием XAudio2, XAPO и Windows Sonic. XAudio2 — это низкоуровневый аудио API, обеспечивающий основу для обработки и микширования сигналов для разработки высокопроизводительных аудиодвижков.XAPO API позволяет создавать кроссплатформенные объекты обработки звука (XAPO) для использования в XAudio2 как на Windows, так и на Xbox. Поддержка звука Windows Sonic позволяет добавить поддержку Dolby Atmos для домашнего кинотеатра, Dolby Atmos для наушников и поддержку Windows HRTF в вашу игру или приложение потокового мультимедиа.
Разработка DirectX
Руководства и справочники по разработке игр DirectX.
Обучение Direct3D 12
Узнайте, что изменилось в Direct3D 12 и как начать программировать с помощью Direct3D 12.
Набор инструментов и библиотеки DirectX
Набор инструментов DirectX, библиотека обработки текстур DirectX, библиотека обработки геометрии DirectXMesh, библиотека UVAtlas и библиотека DirectXMath предоставляют текстуры, сетки, спрайты и другие служебные функции, а также вспомогательные классы для разработки DirectX. Эти библиотеки могут помочь вам сэкономить время и усилия на разработку.
Ресурсы DirectX от партнеров
Это дополнительная документация по DirectX, созданная внешними партнерами.
Производство
Теперь ваша студия полностью занята и переходит к производственному циклу, а работа распределена по всей вашей команде. Вы полируете, реорганизуете и расширяете прототип, чтобы превратить его в полноценную игру.
Уведомления и живые плитки
Плитка — это представление вашей игры в меню «Пуск». Плитки и уведомления могут заинтересовать игроков, даже если они в данный момент не играют в вашу игру.
Включить покупку продуктов (надстроек) в приложении
Дополнение (внутриигровой продукт) — это дополнительный предмет, который игроки могут приобрести в игре. Дополнениями могут быть игровые уровни, предметы или что-то еще, что может понравиться вашим игрокам. При правильном использовании надстройки могут приносить доход, улучшая игровой процесс. Вы определяете и публикуете надстройки своей игры через Центр партнеров и включаете покупки в приложении в коде своей игры.
Дополнениями могут быть игровые уровни, предметы или что-то еще, что может понравиться вашим игрокам. При правильном использовании надстройки могут приносить доход, улучшая игровой процесс. Вы определяете и публикуете надстройки своей игры через Центр партнеров и включаете покупки в приложении в коде своей игры.
Отладка, оптимизация производительности и мониторинг
Чтобы оптимизировать производительность, воспользуйтесь игровым режимом в Windows 10, чтобы предоставить своим геймерам наилучшие игровые возможности, полностью используя возможности их текущего оборудования.
Windows Performance Toolkit (WPT) состоит из инструментов мониторинга производительности, которые создают подробные профили производительности операционных систем и приложений Windows. Это особенно полезно для мониторинга использования памяти и повышения производительности игры. Windows Performance Toolkit входит в состав Windows 10 SDK и Windows ADK. Этот набор инструментов состоит из двух независимых инструментов: средства записи производительности Windows (WPR) и анализатора производительности Windows (WPA). ProcDump, входящая в состав Windows Sysinternals, представляет собой утилиту командной строки, которая отслеживает всплески загрузки ЦП и создает файлы дампа во время сбоев игры.
ProcDump, входящая в состав Windows Sysinternals, представляет собой утилиту командной строки, которая отслеживает всплески загрузки ЦП и создает файлы дампа во время сбоев игры.
| Проверка производительности вашего кода | Нагрузочное тестирование в облаке |
| Получить тип консоли Xbox с помощью информации об игровом устройстве | Информация об игровом устройстве |
| Повышение производительности за счет получения эксклюзивного или приоритетного доступа к аппаратным ресурсам с помощью API игрового режима | Игровой режим |
| Получить Windows Performance Toolkit (WPT) из Windows 10 SDK | Windows 10 SDK |
| Получить Windows Performance Toolkit (WPT) из Windows ADK | Windows ADK |
| Устранение неполадок ненадлежащего пользовательского интерфейса с помощью анализатора производительности Windows (видео) | Анализ критического пути с помощью WPA |
| Диагностика использования памяти и утечек с помощью средства записи производительности Windows (видео) | Объем памяти и утечки |
| Получить ProcDump | Прокдамп |
| Обучение использованию ProcDump (видео) | Настройка ProcDump для создания файлов дампа |
Расширенные методы и концепции DirectX
Некоторые этапы разработки DirectX могут быть сложными и сложными. Когда вы дойдете до точки производства, когда вам нужно будет углубиться в детали вашего механизма DirectX или отладить сложные проблемы с производительностью, ресурсы и информация в этом разделе могут помочь.
Когда вы дойдете до точки производства, когда вам нужно будет углубиться в детали вашего механизма DirectX или отладить сложные проблемы с производительностью, ресурсы и информация в этом разделе могут помочь.
| PIX в Windows | Средство настройки производительности и отладки для DirectX 12 в Windows |
| Средства отладки и проверки для разработки D3D12 (видео) | Настройка производительности D3D12 и отладка с проверкой PIX и GPU |
| Оптимизация графики и производительности (видео) | Расширенная графика и производительность DirectX 12 |
| Отладка графики DirectX (видео) | Решите серьезные проблемы с графикой в игре с помощью инструментов DirectX |
| Инструменты Visual Studio 2015 для отладки DirectX 12 (видео) | Инструменты DirectX для Windows 10 в Visual Studio 2015 |
| Руководство по программированию Direct3D 12 | Руководство по программированию Direct3D 12 |
| Сочетание DirectX и XAML | Взаимодействие DirectX и XAML |
Разработка контента с расширенным динамическим диапазоном (HDR)
Создавайте игровой контент, в котором используются полноцветные возможности HDR.
| Введение в HDR и концепции цвета (видео) | Включение HDR и расширенных цветов в DirectX |
| Узнайте, как визуализировать HDR-контент и определить, поддерживает ли его текущий дисплей | HDR образец |
| Создание и настройка расширенного цвета с помощью DirectX | Образец рендеринга расширенных цветных изображений Direct2D |
Глобализация и локализация
Разрабатывайте игры для платформы Windows, готовые к использованию во всем мире, и узнайте о международных функциях, встроенных в лучшие продукты Microsoft.
Отправка и публикация игры
Следующие руководства и информация помогут максимально упростить процесс публикации и отправки.
Издательство
Вы будете использовать Центр партнеров для публикации пакетов игр и управления ими.
Упаковка и загрузка
Политика и сертификация
Не позволяйте проблемам с сертификацией задерживать выпуск вашей игры. Вот политики и распространенные проблемы сертификации, о которых следует знать.
Вот политики и распространенные проблемы сертификации, о которых следует знать.
Манифест магазина (StoreManifest.xml)
Манифест магазина (StoreManifest.xml) — это необязательный файл конфигурации, который можно включить в пакет приложения. Манифест магазина предоставляет дополнительные функции, которые не являются частью файла AppxManifest.xml. Например, вы можете использовать манифест магазина, чтобы заблокировать установку вашей игры, если целевое устройство не имеет указанного минимального уровня функций DirectX или указанного минимального объема системной памяти.
Управление жизненным циклом игры
После того, как вы закончили разработку и отправили свою игру, это не “игра окончена”.Возможно, вы закончили разработку первой версии, но продвижение вашей игры на рынке только началось. Вы захотите отслеживать использование и отчеты об ошибках, отвечать на отзывы пользователей и публиковать обновления для своей игры.
Партнерский центр аналитики и продвижения
Анализ приложений Visual Studio
Visual Studio Application Insights предоставляет аналитику производительности, телеметрии и использования для опубликованной игры. Application Insights помогает обнаруживать и решать проблемы после выпуска игры, постоянно отслеживать и улучшать использование, а также понимать, как игроки продолжают взаимодействовать с вашей игрой.Application Insights работает путем добавления SDK в ваше приложение, которое отправляет данные телеметрии на портал Azure.
Application Insights помогает обнаруживать и решать проблемы после выпуска игры, постоянно отслеживать и улучшать использование, а также понимать, как игроки продолжают взаимодействовать с вашей игрой.Application Insights работает путем добавления SDK в ваше приложение, которое отправляет данные телеметрии на портал Azure.
Сторонние решения для аналитики и продвижения
| Анализ поведения игроков с помощью GameAnalytics | Игровая аналитика |
| Подключите свою игру UWP к Google Analytics | Получить Windows SDK для Google Analytics |
| Узнайте, как использовать Windows SDK для Google Analytics (видео) | Начало работы с Windows SDK для Google Analytics |
| Используйте Facebook App Installs Ads для продвижения своей игры среди пользователей Facebook | Получить Windows SDK для Facebook |
| Узнайте, как использовать Facebook App Installs Ads (видео) | Начало работы с Windows SDK для Facebook |
| Используйте Vungle для добавления видеорекламы в свои игры | Получить Windows SDK для Vungle |
Создание обновлений содержимого и управление ими
Чтобы обновить опубликованную игру, отправьте новый пакет приложения с более высоким номером версии. После того, как пакет пройдет отправку и сертификацию, он будет автоматически доступен клиентам в качестве обновления.
После того, как пакет пройдет отправку и сертификацию, он будет автоматически доступен клиентам в качестве обновления.
Добавление Xbox Live в игру
Xbox Live — это первоклассная игровая сеть, объединяющая миллионы игроков по всему миру. Разработчики получают доступ к функциям Xbox Live, которые органично расширяют аудиторию их игр, включая присутствие в Xbox Live, списки лидеров, облачные сохранения, игровые центры, клубы, командный чат, игровой видеорегистратор и многое другое.
Примечание
Если вы хотите разрабатывать игры для Xbox Live, вам доступно несколько вариантов.Сведения о различных программах см. в разделе Обзор программы для разработчиков.
Для разработчиков, участвующих в программе Xbox Live Creators Program
Для управляемых партнеров и разработчиков в программе ID@Xbox
Дополнительные ресурсы
| Видео разработки игр | Видео с крупных конференций, таких как GDC и //сборка |
| Разработка инди-игр (видео) | Новые возможности для независимых разработчиков |
| Рекомендации для многоядерных мобильных устройств (видео) | Устойчивая игровая производительность на многоядерных мобильных устройствах |
| Разработка настольных игр для Windows 10 (видео) | Игры для ПК для Windows 10 |
Уравнение репликатора и другая игровая динамика
Игровая динамика моделирует, как люди или популяции меняют свою стратегию с течением времени, на основе сравнения выигрышей. Это контрастирует с классической некооперативной теорией игр, которая анализирует поведение рациональных игроков с помощью концепций статического решения, таких как равновесие Нэша (РН) (т. е. выбор стратегии для каждого игрока, при котором ни у одного человека нет одностороннего стимула изменить свое поведение). В общем, игровая динамика предполагает, что стратегии с более высоким выигрышем работают лучше. Как мы увидим, предельным поведением этой динамики (т. е. результатом эволюции) часто является НЭ с дополнительными свойствами стабильности.
Это контрастирует с классической некооперативной теорией игр, которая анализирует поведение рациональных игроков с помощью концепций статического решения, таких как равновесие Нэша (РН) (т. е. выбор стратегии для каждого игрока, при котором ни у одного человека нет одностороннего стимула изменить свое поведение). В общем, игровая динамика предполагает, что стратегии с более высоким выигрышем работают лучше. Как мы увидим, предельным поведением этой динамики (т. е. результатом эволюции) часто является НЭ с дополнительными свойствами стабильности.
Наиболее важной игровой динамикой является уравнение репликатора, определенное для одного вида Тейлором и Джонкером (1) и названное Шустером и Зигмундом (2). Уравнение репликатора — это первая динамика игры, изученная в связи с эволюционной теорией игр, которая была разработана Мейнардом Смитом и Прайсом (3) (см. также ссылку 4) с биологической точки зрения, чтобы предсказать эволюционный результат поведения популяции. без детального анализа таких биологических факторов, как влияние генетики или размера популяции. Если выигрыш интерпретируется как приспособленность (т. е. репродуктивный успех), частота стратегии у крупного, хорошо перемешанного одного вида изменяется в соответствии с уравнением репликатора (непрерывного времени) со скоростью на душу населения, равной разнице между его ожидаемым выигрышем и средний выигрыш населения (уравнение 1 ). Если выигрыш каждой стратегии постоянен (в частности, не зависит от частоты стратегий), конечным результатом эволюции будет то, что все будут использовать стратегию с наибольшим выигрышем, результат, который верен для любой игровой динамики, а не только для уравнения репликатора.С биологической точки зрения, у нас есть Дарвиновское выживание наиболее приспособленных посредством естественного отбора.
Если выигрыш интерпретируется как приспособленность (т. е. репродуктивный успех), частота стратегии у крупного, хорошо перемешанного одного вида изменяется в соответствии с уравнением репликатора (непрерывного времени) со скоростью на душу населения, равной разнице между его ожидаемым выигрышем и средний выигрыш населения (уравнение 1 ). Если выигрыш каждой стратегии постоянен (в частности, не зависит от частоты стратегий), конечным результатом эволюции будет то, что все будут использовать стратегию с наибольшим выигрышем, результат, который верен для любой игровой динамики, а не только для уравнения репликатора.С биологической точки зрения, у нас есть Дарвиновское выживание наиболее приспособленных посредством естественного отбора.
Более интересно то, что происходит, когда индивидуальный выигрыш зависит от действий других (т. е. когда речь идет о настоящей игре). Таким образом, ранний успех эволюционной теории игр является результатом того, что эволюционно стабильная стратегия (ЭСС) является динамически стабильной для уравнения репликатора одного вида, описанного выше (1, 5). ESS, интуитивная концепция неприкосновенности, первоначально обобщающая «непревзойденное» соотношение полов, проанализированное Гамильтоном (6), может быть определена исключительно в терминах сравнения выплат (4, 7).С тех пор стратегическое (т. е. теоретико-игровое) мышление стало играть все более заметную роль в прогнозировании поведения как индивидуума, так и популяции в биологических системах (8).
ESS, интуитивная концепция неприкосновенности, первоначально обобщающая «непревзойденное» соотношение полов, проанализированное Гамильтоном (6), может быть определена исключительно в терминах сравнения выплат (4, 7).С тех пор стратегическое (т. е. теоретико-игровое) мышление стало играть все более заметную роль в прогнозировании поведения как индивидуума, так и популяции в биологических системах (8).
Эволюционная теория игр уже давно вышла за пределы своих биологических корней и становится все более важной для анализа человеческого и/или социального поведения. Здесь изменения частоты стратегий не являются результатом естественного отбора; скорее, люди (или общества) меняют свое поведение в зависимости от последствий выигрыша.Уравнение репликатора затем возникает, например, когда люди принимают рациональные решения о том, как имитировать наблюдаемые стратегии, которые в настоящее время приносят более высокую отдачу. В зависимости от того, какой информацией обладают лица, принимающие решения (и как они используют эту информацию), возможен широкий спектр других игровых динамик (9⇓–11).
Эволюционная теория игр и соответствующая ей динамика игр также значительно расширились за пределы их первоначального акцента на одновидовые (т.е. симметричные) игры с конечным набором (чистых) стратегий, в которых выигрыши являются результатом случайных однократных взаимодействий между парами индивидуумов. (также называемые «симметричными играми в нормальной форме для двух игроков» или, проще говоря, «матричными играми»).В этой статье мы кратко выделяем некоторые особенности матричных игр в начале следующего раздела, прежде чем обобщить их на другие классы симметричных игр. Это популяционные игры, игры с континуумом чистых стратегий и многопользовательские игры. Затем мы рассматриваем асимметричные игры для двух игроков, в том числе игры с экстенсивной формой (где пары индивидуумов взаимодействуют друг с другом, и набор действий, доступных при более поздних взаимодействиях, может зависеть от того, какой выбор был сделан в предыдущих), а также асимметричные игры. популяционные игры и игры с непрерывными стратегическими пространствами.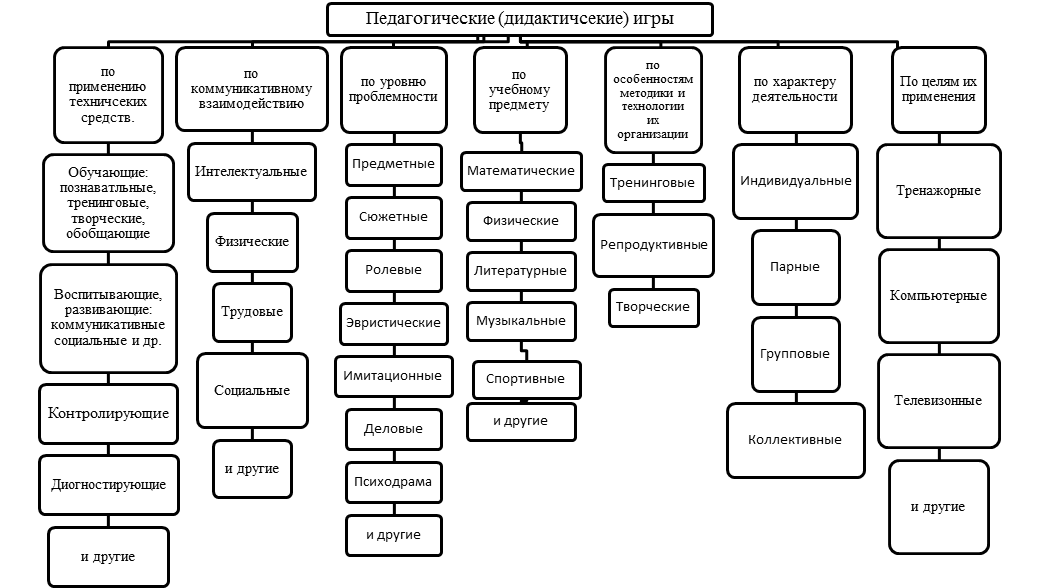
Симметричные игры
Матричные игры имеют конечный набор из m чистых стратегий {e1,e2,…,em}, доступных для индивидуальной игры. Матрица выигрышей m×m A имеет элементы aij=π(ei,ej) (выигрыш ei при игре против ej), для i,j=1,…,m. Чтобы получить уравнение репликатора с чистой стратегией непрерывного времени (уравнение 1 ) в соответствии с исходным подходом приспособленности (1), скорость роста числа ni индивидуумов на душу населения, использующих стратегию ei в момент времени t , принимается как ожидаемый выигрыш ei от одного взаимодействия со случайным индивидуумом в большой популяции.То есть n˙i=ni∑j=1mπ(ei,ej)pj≡niπ(ei,p), где p — состояние популяции в (смешанном) симплексе стратегий ∆m≡{(p1,p2,… ,pm}|∑j=1mpj=1,0≤pj≤1} с pi=ni/∑j=1mnj доля населения, использующего стратегию e i в момент времени t . Прямой расчет упражнение дает уравнение репликатора на Δm:p˙i=pi(π(ei,p)−π(p,p)) for i=1,…,m,[1], где π(p,p)=∑j =1mpiπ(ei,p) — средний выигрыш случайно выбранного индивидуума (т. е. средний выигрыш по популяции).Из теории динамических систем траектории [1] оставляют внутренность Δm инвариантной вперед, как и каждую из ее граней (12).
е. средний выигрыш по популяции).Из теории динамических систем траектории [1] оставляют внутренность Δm инвариантной вперед, как и каждую из ее граней (12).
Теорема 1. Уравнение репликатора для матричной игры удовлетворяет:
а) Точка устойчивого покоя является РН.
b) Сходящаяся траектория внутри пространства стратегии превращается в NE.
c) Строгий РН локально асимптотически устойчив.
Теорема 1 — Народная теорема эволюционной теории игр (9, 12, 13), примененная к уравнению репликатора [см. , раздел 1) и по всему тексту]. Эти три вывода верны для многих динамик матричных игр (как в дискретном, так и в непрерывном времени) и служат эталоном для проверки методов динамических систем, применяемых к общей динамике игр и к нематричным эволюционным играм, таким как рассмотренные в остальных разделах этой статьи.
Народная теорема означает, что биологи могут предсказывать эволюционный результат своих стабильных систем, исследуя поведение НЭ основной игры. Создается впечатление, что индивидуумы в этих системах являются рациональными лицами, принимающими решения, тогда как на самом деле именно естественный отбор посредством репродуктивной приспособленности приводит систему к стабильному результату. Это привело к сдвигу парадигмы в сторону стратегического мышления в популяционной биологии. Глубокое влияние, которое он оказал на анализ поведенческой экологии, больше, чем более ранние методы теории игр, примененные к биологии, такие как аргумент Фишера (14) [см. также Дарвина (15) и Гамильтона (6)] для распространенности 50: 50 соотношение полов у диплоидных видов и теория родственного отбора Гамильтона (16).
Важность стратегического мышления в популяционной биологии дополнительно усиливается Теоремой 2 , которая основана на интуитивной концепции ESS (3), определенной Мейнардом Смитом (ссылка 7, стр.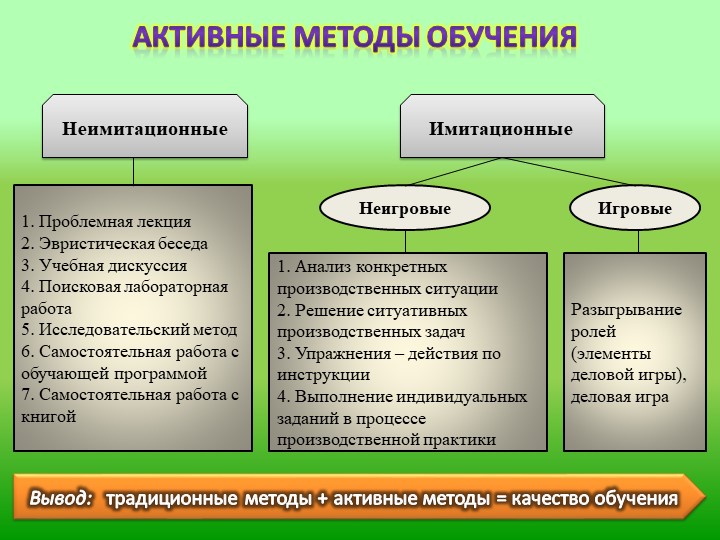 10) как «стратегия, такая, что , если все члены популяции примут ее, то никакая мутантная стратегия не сможет проникнуть в популяцию под влиянием естественного отбора». Мейнард Смит продолжает на той же странице, что «определение ESS как неприступной стратегии можно сделать более точным… если сделать точные предположения об эволюционирующей популяции.В матричной игре, если большинство особей в популяции используют p*∈Δm, а остальные используют мутантную стратегию p , то мутант вымрет в этой модели с двумя стратегиями ( SI Приложение , раздел 1), если и только если
10) как «стратегия, такая, что , если все члены популяции примут ее, то никакая мутантная стратегия не сможет проникнуть в популяцию под влиянием естественного отбора». Мейнард Смит продолжает на той же странице, что «определение ESS как неприступной стратегии можно сделать более точным… если сделать точные предположения об эволюционирующей популяции.В матричной игре, если большинство особей в популяции используют p*∈Δm, а остальные используют мутантную стратегию p , то мутант вымрет в этой модели с двумя стратегиями ( SI Приложение , раздел 1), если и только если
i ) π(p,p*)≤π(p*,p*) (условие NE) и
ii ) π(p*,p)>π( p,p), если π(p,p*)=π(p*,p*) (условие устойчивости).
p*∈Δm является ESS, если он удовлетворяет этим двум условиям для всех остальных p∈Δm.
Теорема 2.
а) p* является РСС матричной игры тогда и только тогда, когда π(p*,p)>π(p,p) для всех p∈ Δm достаточно близко (но не равно) к p*.

б) ESS p* является локально асимптотически устойчивой точкой покоя уравнения репликатора.
c) ESS p* внутри Δm является глобально асимптотически устойчивой точкой покоя уравнения репликатора.
Эквивалентное условие для ESS, содержащееся в Теорема 2a , является более полезной характеристикой при обобщении концепции ESS на другие эволюционные игры. Это называется «локальным превосходством» (17), «стратегией захватчиков по соседству» (NIS) (18) или «превосходством по соседству» (19). Одна из причин разных названий этой концепции заключается в том, что существует несколько способов обобщить локальное превосходство на другие эволюционные игры, и они имеют разные последствия для стабильности.
Наиболее элегантное доказательство (5) утверждений об устойчивости в теореме 2 b и c показывает, что V(p)≡∏pipi∗, где произведение взято по {i:pi∗>0}, является строгая локальная функция Ляпунова [т. е. V(p*)>V(p) и V˙(p)=V(p)(π(p*,p)−π(p,p))>0 для всех p∈ Δm достаточно близко, но не равно ESS p*]. Заманчиво добавить эти утверждения об устойчивости к Народной теореме, потому что они остаются в силе для многих динамик матричных игр благодаря использованию других функций Ляпунова.Есть несколько причин избегать этого искушения.
е. V(p*)>V(p) и V˙(p)=V(p)(π(p*,p)−π(p,p))>0 для всех p∈ Δm достаточно близко, но не равно ESS p*]. Заманчиво добавить эти утверждения об устойчивости к Народной теореме, потому что они остаются в силе для многих динамик матричных игр благодаря использованию других функций Ляпунова.Есть несколько причин избегать этого искушения.
Во-первых, эти утверждения неверны для динамики матричных игр с дискретным временем ( SI Приложение , раздел 1), как показано уже для игр с тремя стратегиями, которые демонстрируют циклическое доминирование. Во-вторых, глобальная устойчивость внутренней ЭСС в этих играх неверна для важных классов игровой динамики, таких как динамика монотонного выбора (17). Более того, игры с тремя стратегиями из примера 1 демонстрируют, что траектории для матричных игр могут сходиться к РН, не являющемуся РЭС, или приближаться к гетероклиническому циклу вокруг границы симплекса стратегий.Пример 1 (обобщенная игра «камень-ножницы-бумага») =RSP[06−4−4042−20].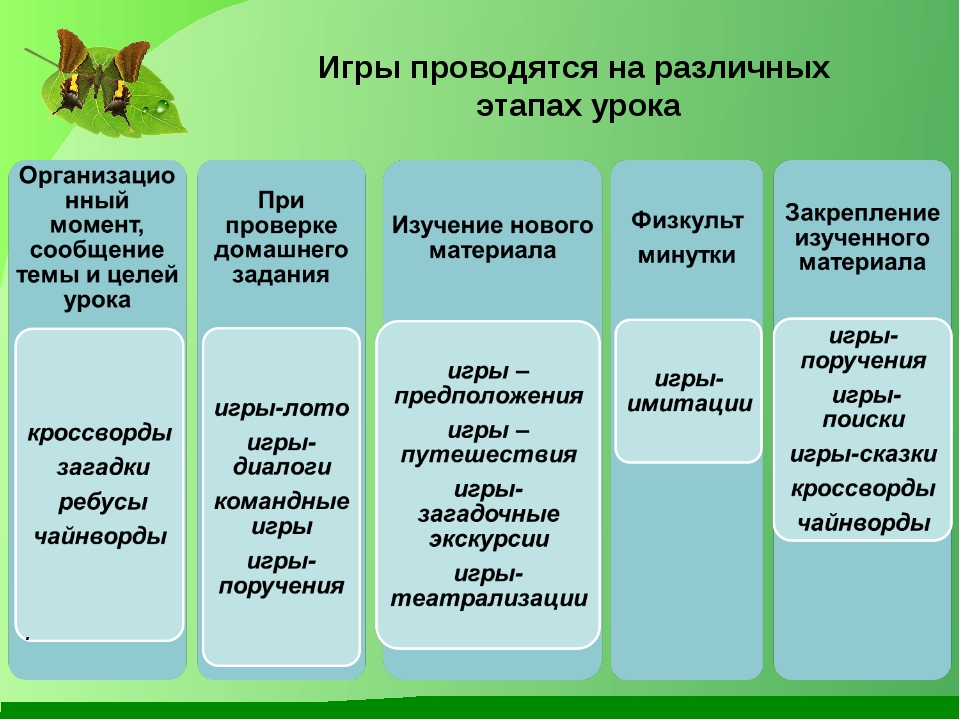 [2] Все такие игры с положительными параметрами ai и bi демонстрируют циклическое доминирование, в результате чего R побеждает S (т. е. R строго доминирует над S в двух -стратегическая игра, основанная на этих двух стратегиях), S превосходит P , а P превосходит R .Это доминирование означает отсутствие северо-восточного направления на границе ∆3. На самом деле единственным РН для [2] является полностью смешанная стратегия p*=(10/29,8/29,11/29) внутри. Он глобально асимптотически устойчив по уравнению репликатора (рис. 1), но p* не является ESS, поскольку π(e1,p*)=π(p*,p*)=4/29 и π(p*,e1) =-(10/29)<0=π(e1,e1).
[2] Все такие игры с положительными параметрами ai и bi демонстрируют циклическое доминирование, в результате чего R побеждает S (т. е. R строго доминирует над S в двух -стратегическая игра, основанная на этих двух стратегиях), S превосходит P , а P превосходит R .Это доминирование означает отсутствие северо-восточного направления на границе ∆3. На самом деле единственным РН для [2] является полностью смешанная стратегия p*=(10/29,8/29,11/29) внутри. Он глобально асимптотически устойчив по уравнению репликатора (рис. 1), но p* не является ESS, поскольку π(e1,p*)=π(p*,p*)=4/29 и π(p*,e1) =-(10/29)<0=π(e1,e1).
Траектории уравнения репликатора для игры RSP с матрицей выигрышей 2 .
Матричная игра с матрицей выигрышей -A также демонстрирует циклическое доминирование, и ее траектории в уравнении репликатора такие же, как на рис.1, за исключением того, что направление меняется на противоположное. То есть все внутренние траектории [1] (кроме той, которая изначально находилась в точке p*) приближаются к гетероклиническому циклу вокруг границы, соединяющей три чистые стратегии в порядке e3,e2,e1,e3. Также хорошо известно (12), что стандартная игра RSP (со всеми ai=bi=1 в [2] ) имеет периодические орбиты [1] вокруг уникального NE p*=(1/3,1 /3,1/3).
То есть все внутренние траектории [1] (кроме той, которая изначально находилась в точке p*) приближаются к гетероклиническому циклу вокруг границы, соединяющей три чистые стратегии в порядке e3,e2,e1,e3. Также хорошо известно (12), что стандартная игра RSP (со всеми ai=bi=1 в [2] ) имеет периодические орбиты [1] вокруг уникального NE p*=(1/3,1 /3,1/3).
Циклическое поведение распространено не только в биологии (например, системы хищник-жертва), но и в поведении человека (например,г., деловые циклы, появление и последующее исчезновение увлечений и т. д.). Таким образом, неудивительно, что эволюционная игровая динамика также включает в себя циклы. На самом деле, по мере увеличения количества стратегий может появиться еще более богатое динамическое поведение, такое как хаотические траектории (12).
Что может быть более удивительным, так это множество классов матричных игр (10), для которых эта сложная динамика не проявляется (например, потенциальные, устойчивые, супермодулярные, игры с нулевой суммой, дважды симметричные игры), и для них эволюционный результат часто предсказано с помощью аргументов рациональности, лежащих в основе теорем 1 и 2 . В оставшейся части статьи основное внимание уделяется таким ситуациям для нематричных игр.
В оставшейся части статьи основное внимание уделяется таким ситуациям для нематричных игр.
Прежде чем сделать это, важно отметить, что репликаторное уравнение для дважды симметричных матричных игр формально эквивалентно модели непрерывного времени естественного отбора в одиночном (диплоидном) локусе с m аллелями A1,…,Am ( 12, 20). В частности, если aij — приспособленность генотипа AiAj, а pi — частота аллеля Ai в популяции, то [1] — это уравнение отбора в непрерывном времени популяционной генетики (14).Затем можно показать, что средняя приспособленность популяции π(p,p) увеличивается (это одна из частей фундаментальной теоремы естественного отбора). Более того, локально асимптотически устойчивые точки покоя [1] точно соответствуют РЭС симметричной платежной матрицы A , и все траектории внутри ∆m сходятся к NE A (20). Аналогичные результаты справедливы для модели отбора непересекающихся поколений (жизнеспособности) (12).
Население Игры.
Симметричные популяционные игры являются наиболее простым обобщением матричных игр. В симметричной популяционной игре с фиксированным размером популяции и конечным числом чистых стратегий выигрыш π(ei,p) стратегии ei является произвольной непрерывной функцией состояния популяции p∈Δm. Тогда матричные игры соответствуют случаю, когда π(ei,p) линейно по компонентам p . Если выигрыш нелинейный, такие игры называются эволюционными играми «игрового поля» (7). В любом случае приравнивание приспособленности к репродуктивному успеху снова приводит к уравнению репликатора (уравнение 1 ) от Δm. Народная теорема верна для этих популяционных игр, как и теорема 2b , когда ESS определяется как локально превосходящая с использованием теоремы 2a . [Использование термина ESS становится проблематичным для нематричных игр, потому что он часто имеет несколько различных возможных значений. Например, ЭСС, как в Теорема 2b , Хофбауэр и Зигмунд (9) называют «локальной ЭСС», чтобы подчеркнуть, что условие π(p*,p)>π(p,p) выполняется только для p∈Δm которые достаточно близки (но не равны) к p*. Когда есть двусмысленность, мы вместо этого будем использовать фразу «локально выше» или «в окрестности выше», в зависимости от того, что подходит. быть более чем один такой ESS.
Когда есть двусмысленность, мы вместо этого будем использовать фразу «локально выше» или «в окрестности выше», в зависимости от того, что подходит. быть более чем один такой ESS.
Демографические игры имеют важные применения в биологии [например, игра с соотношением полов; Maynard Smith (7)], а также на человеческое поведение [например, игры с перегрузкой; Сандхольм (10)]. Следующий пример, взятый из поведенческой экологии, иллюстрирует, что важная игровая динамика, отличная от уравнения репликатора, возникает естественным образом.
Пример 2 (Игра по выбору среды обитания и идеальное бесплатное распространение): Основа игры по выбору среды обитания для одного вида была заложена Фретвеллом и Лукасом (21) до появления эволюционной теории игр. Их интересовало предсказание того, как вид (в частности, вид птиц) с фиксированным размером популяции должен распределяться между несколькими участками ресурсов, если особи будут перемещаться на участки с более высокой приспособленностью. Они утверждали, что результатом будет идеальное свободное распределение (IFD), определяемое как распределение участков, при котором приспособленность всех особей на любом занятом участке будет такой же и, по крайней мере, такой же высокой, как их приспособленность на любом незанятом участке (в противном случае некоторые люди перейдут на другой патч).Если существует H участков (или местообитаний) и чистая стратегия индивидуума ei соответствует нахождению на участке i (для i = 1,2,…,H), мы получаем популяционную игру, приравнивая выигрыш ei к фитнес в этом патче. Таким образом, словесное описание IFD в этой «игре выбора среды обитания» есть не что иное, как описание NE.
Они утверждали, что результатом будет идеальное свободное распределение (IFD), определяемое как распределение участков, при котором приспособленность всех особей на любом занятом участке будет такой же и, по крайней мере, такой же высокой, как их приспособленность на любом незанятом участке (в противном случае некоторые люди перейдут на другой патч).Если существует H участков (или местообитаний) и чистая стратегия индивидуума ei соответствует нахождению на участке i (для i = 1,2,…,H), мы получаем популяционную игру, приравнивая выигрыш ei к фитнес в этом патче. Таким образом, словесное описание IFD в этой «игре выбора среды обитания» есть не что иное, как описание NE.
Если приспособленность участка уменьшается по плотности участка (т. е. по размеру популяции на участке), Фретвелл и Лукас доказали, что существует уникальный IFD для каждого фиксированного общего размера популяции.Более того, IFD является ESS, глобально асимптотически устойчивой по уравнению репликатора (22). Чтобы увидеть это, пусть p∈ΔH будет распределением среди патчей, а π(ei,p) будет соответствием в патче i . Тогда π(ei,p) зависит только от доли pi в этом пятне (т. е. имеет вид π(ei,pi)]. Поскольку векторное поле (π(e1,p),…,π(eH,p)) является градиентом вещественнозначной функции F(p), определенной на ∆H, мы имеем потенциальную игру ( SI Приложение , раздел 1.1). Следуя Сэндхольму (10), это строго стабильная игра, и поэтому она имеет уникальную РЭС p*, которая глобально асимптотически устойчива согласно уравнению репликатора (а также во многих других игровых динамиках).
Чтобы увидеть это, пусть p∈ΔH будет распределением среди патчей, а π(ei,p) будет соответствием в патче i . Тогда π(ei,p) зависит только от доли pi в этом пятне (т. е. имеет вид π(ei,pi)]. Поскольку векторное поле (π(e1,p),…,π(eH,p)) является градиентом вещественнозначной функции F(p), определенной на ∆H, мы имеем потенциальную игру ( SI Приложение , раздел 1.1). Следуя Сэндхольму (10), это строго стабильная игра, и поэтому она имеет уникальную РЭС p*, которая глобально асимптотически устойчива согласно уравнению репликатора (а также во многих других игровых динамиках).
Хотя Фретвелл и Лукас (21) не добавили никакой динамики в свою модель, движение между участками обсуждается неявно. Вслед за Криваном и соавт. (22), пусть Iij(p) будет вероятностью того, что человек из участка j переместится на участок i в единицу времени, если текущее распределение участков равно p . Тогда соответствующая динамика миграции (или расселения) в непрерывном времени в векторной форме имеет вид p˙=I(p)p−p,[3], где I(p) — матрица миграции H×H с элементами Iij(p). Следующий результат (22) использует (убывающую) функцию Ляпунова W(p)≡max1≤i≤H π(ei,p).
Теорема 3 . Предположим, что приспособленность участков является убывающей функцией плотности участков в игре выбора среды обитания одного вида. Тогда любая миграционная динамика 3 , удовлетворяющая следующим двум условиям, эволюционирует в единственную IFD.
a) Люди никогда не переезжают на участок с более низкой физической подготовкой.
b) Если есть участок с более высокой приспособленностью, чем какой-либо занятый участок, некоторые особи переходят на участок с наивысшей приспособленностью.
Проиллюстрируем Теорему 3 при наличии трех заплат. Предположим, что при p пригодность патчей упорядочена π(e1,p)>π(e2,p)>π(e3,p), и рассмотрим две матрицы миграции I1(p)≡[111000000] I2(p)≡[ 11/31/302/31/3001/3].I1(p) соответствует ситуации, когда люди, которые перемещаются, переходят к патчу 1, потому что они знают, что он имеет наибольшую приспособленность. Соответствующая динамика игр p˙=BR(p)−p,[4], где BR(p) — стратегия наилучшего ответа, e1 to p называется динамикой наилучшего ответа ( СИ Приложение , раздел 1.1).
С другой стороны, I2(p) моделирует индивидуумов, которые получают информацию о приспособленности только путем случайной выборки одного участка, переходя к этому участку, если он имеет более высокую приспособленность, чем его текущий участок [например, индивидуум на участке 2 перемещается, если он производит выборку патч 1 и в противном случае остается в своем собственном патче (с вероятностью 1/3 и 2/3 соответственно)]. Несколько траекторий для каждой из этих двух миграционных динамик показаны на рис. 2 (см. также SI Приложение , рис. S1). Как видно, все они сходятся к IFD, как и должны согласно Теореме 3 , хотя их пути к этому рациональному исходу весьма различны.
Рис. 2.Траектории для игры выбора среды обитания с функциями приспособленности патчей π(e1,p)=1−p1,π(e2,p)=0,8[1−(10p2/9)] и π(e3,p) )=0,6[1−(10p3/8)]. ( A ) Динамика наилучшего ответа с матрицами миграции вида I1(p) и ( B ) динамика неидеальных животных с матрицами миграции вида I2(p).
Наконец, предположим, что информация получена путем выборки случайной особи, перемещающейся к ее участку с вероятностью, пропорциональной разнице приспособленности, только если отобранная особь имеет более высокую приспособленность.Хорошо известно (13), что это «правило пропорционального подражания» приводит к уравнению репликатора ( SI Приложение , раздел 1.1). Поскольку правило пропорционального подражания удовлетворяет двум условиям теоремы 3 , уникальная IFD глобально асимптотически устойчива при [1] .
Fretwell и Lucas (21) кратко рассматривают свою концепцию IFD, когда приспособленность участков увеличивается с плотностью участков, когда плотность низкая (так называемый эффект Allee). Хотя Теорема 3 больше не применяется, эти игры выбора среды обитания все еще являются потенциальными играми (но не строго стабильными).Таким образом, все внутренние траектории во многих игровых динамиках (включая уравнение репликатора и динамику наилучшего ответа) сходятся к РН (10). Несколько NE уже возможны для моделей с двумя патчами, некоторые из которых локально асимптотически устойчивы, а некоторые нет. Существуют разные мнения относительно того, следует ли определять IFD как любой из этих НЭ или ограничивать концепцию только теми, которые локально лучше и/или асимптотически стабильны (23).
Игры по выбору среды обитания также обеспечивают естественную среду для эффекта изменяющихся размеров популяции, темы очевидной важности в популяционной биологии, которой до сих пор уделялось мало внимания в моделях социального поведения.Динамика миграции популяции возникает, если размер популяции N развивается за счет приспособленности, воспринимаемой буквально как репродуктивный успех ( SI Приложение , раздел 1.1). Как обсуждалось в SI Приложение , раздел 1.1, если приспособленность участка положительна, когда он не занят, уменьшается с плотностью участка и в конечном итоге становится отрицательной, то система эволюционирует до пропускной способности всякий раз, когда матрица миграции I(p;N) удовлетворяет двум условиям в Теорема 3 для каждого N .В частности, эволюционный результат не зависит от временного масштаба миграции по сравнению с изменением размера популяции, что является примечательным результатом, поскольку это часто неверно, когда объединяются два динамических процесса.
Игры с непрерывными стратегическими пространствами.
Динамика игры, когда игроки могут выбирать из континуума чистых стратегий S , усложняется, особенно если индивидуальный выигрыш зависит от состояния популяции [которое теперь является распределением в наборе мер вероятности Δ(S) на S ] .Один из подходов, позволяющих избежать этих сложностей, состоит в том, чтобы предположить, что популяция всегда мономорфна в своем среднем значении x∈S. Когда S представляет собой выпуклое компактное подмножество R (т. е. замкнутый и ограниченный интервал), далее предполагается, что x эволюционирует посредством замещения признаков в направлении y ближайших мутантов, которые могут вторгаться из-за их более высокая отдача, чем x при игре против этого мономорфизма. Если π(y,x) является выигрышем мутанта, использующего стратегию y в мономорфной популяции x , то x увеличивается (убывает), если π(y,x) является возрастающей (убывающей) функцией y вместо y близко к x .
Наиболее элементарная динамика для моделирования этих предположений называется «каноническим уравнением адаптивной динамики», которое имеет вид (с точностью до изменения шкалы времени)x˙=∂π(y,x)∂y|y=x≡ π1(x,x).[5]Точка покоя x* [т.е. π1(x*,x*)=0] является устойчивой по сходимости (24), если она асимптотически устойчива относительно [5] . x* является устойчивой по сходимости тогда и только тогда, когда d/dx[∂π(y,x)/∂y|y=x]|x=x*=π11(x*,x*)+π12(x*,x* )<0. С другой стороны, x* является строгим по соседству NE тогда и только тогда, когда π11(x*,x*)<0 ( SI Приложение , раздел 1.2).
Таким образом, в адаптивной динамике строгий НЭ не обязательно достижим из близлежащих популяций (т. е. он не обязательно должен быть устойчив к конвергенции) и, наоборот, устойчивая к конвергенции точка покоя не обязательно должна быть РН. То есть части a и c Народной теоремы неверны. Стабильная конвергенция x*, которая не является строгой по соседству NE, называется «эволюционной точкой ветвления» (25), поскольку в диморфной популяции, где некоторые особи используют чистые стратегии по обе стороны от x*, эти близкие стратегии эволюционируют от x * [как может быть показано полиномиальным разложением Тейлора второго порядка π (y, x) относительно (x *, x *)].По этой причине только те x*, которые удовлетворяют обоим условиям i и ii , заданным как
i ) π11(x*,x*)<0 (условие строгого соседства NE) и
ii ) π11(x*,x*)+π12(x*,x*)<0 (условие устойчивости сходимости)
считаются устойчивыми для моделей, основанных на адаптивной динамике.
Условия i и ii соответственно эквивалентны тому, что π(x,x*)<π(x*,x*) и π(y,x)>π(x,x), если x близко до x* и y близко к x , но ближе к x*.Они определяют концепцию непрерывно стабильной стратегии (CSS) в терминах статических сравнений выигрышей, введенных ранее Эшелем (26) для обобщения ESS на одномерные (1D) пространства непрерывных стратегий. Тогда CSS стабилен для моделей, основанных на адаптивной динамике.
Однако CSS не является стабильным в соответствии с уравнением репликатора (уравнение 6 ) для непрерывных пространств стратегий. Когда выигрыши являются результатом парных взаимодействий между людьми, а π(x,y) интерпретируется как выигрыш до x против y , тогда ожидаемый выигрыш до x при случайном взаимодействии равен π(x,P)≡∫ Sπ(x,y)P(dy), где P — вероятностная мера на S , соответствующая текущему распределению стратегий населения.При π(P,P)≡∫Sπ(x,P)P(dx) среднем выигрыше населения и B борелевском подмножестве S уравнение репликатора (27)dPtdt(B)=∫B (π(x,Pt)−π(Pt,Pt))Pt(dx)[6] имеет единственное решение при любом начальном P0 в бесконечномерном пространстве ∆(S) борелевских вероятностных мер над пространством стратегий S (28) ( Приложение SI , раздел 1.2). Уравнение репликатора описывает эволюцию распределения стратегии популяции P∈Δ(S). С этой точки зрения каноническое уравнение становится эвристическим инструментом, который аппроксимирует эволюцию среднего значения популяции, игнорируя эффекты, связанные с разнообразием стратегий в популяции.
Из SI Приложение , раздел 1.2, чтобы гарантировать стабильность x* в соответствии с [6] , x* должен быть NE со строгим соседством, а также NIS, определяемым как π(x*,x)>π( x,x) для x около x* (29). Эти два условия эквивалентны тому, что x* превосходит соседство [т.е. π(x*,P)>π(P,P) для всех распределений P , поддержка которых достаточно близка, но не равна x*] (19).
Уравнение репликатора, а также концепции строгих по соседству NE, NIS и превосходства по соседству имеют прямые обобщения на многомерные непрерывные пространства стратегий, где результаты устойчивости остаются верными (19).CSS и каноническое уравнение адаптивной динамики также были обобщены (30, 31), но они зависят от направления (направлений), в котором более вероятно появление мутантов. Если x* стабилен для всех таких направлений (так называемая «сильная стабильность сходимости»), соответствующий CSS имеет такие же свойства сильной стабильности, как и ESS для матричных игр.
Многопользовательские игры.
Матричные игры — это особый тип популяционных игр, в которых люди участвуют в соревнованиях для двух игроков. В многопользовательских играх с конечным набором S чистых стратегий взаимодействия формируются между n игроками, где n>2 фиксировано.Например, при n=3 ожидаемый выигрыш ei при случайном взаимодействии, если популяция имеет состояние p∈Δ3, равен π(ei;p)=∑j,k=1mpjpkπ(ei;ej,ek), где выигрыш π Предполагается, что (ei;ej,ek) к ei в симметричной игре с тремя игроками зависит от двух других игроков, но не от их порядка [т. е. π(ei;ej,ek)=π(ei;ek,ej)] .
Многопользовательские игры являются классом популяционных игр, в которых выигрыши нелинейны в состоянии популяции. Таким образом, согласно разделу Игры населения Народная теорема и Теорема 2b верны для любой многопользовательской игры с конечным числом чистых стратегий в соответствии с уравнением репликатора (уравнение 1 ). Bukowski и Miekisz (32) (см. также ссылку 8) характеризуют ESS с точки зрения неприступности [т. е. локального превосходства, как в , теорема 2a ]. Тогда для игр с тремя игроками p* является РБС тогда и только тогда, когда для всех p≠p*
i ) π(p;p*,p*)≤π(p∗;p *,p*) (условие NE),
ii ) если π(p;p*,p*)=π(p*;p*,p*), то π(p;p*, p)≤π(p*;p*,p),
iii ), если π(p;p*,p*)=π(p*;p*,p*) и π(p; p*,p)=π(p*;p*,p), тогда π(p;p,p)<π(p*;p,p),
, где π(p;q,r) ≡∑j,k=1mpiqjrkπ(ei;ej,ek).То есть ESS удовлетворяет NE условию i , а также двум условиям устойчивости ii и iii .
Буковски и Микиш (32) продолжают классифицировать структуру РЭС всех игр с двумя стратегиями для трех игроков, показывая, в частности, что внутренняя РЭС не обязательно должна быть глобально асимптотически стабильной (сравните с Теорема 2c ). Фактически, они также дают пример суперсимметричной игры с двумя стратегиями для четырех игроков [т.е. π(ei;ej,ek,eℓ) одинаково для всех перестановок фиксированных индексов i,j,k,ℓ∈{ 1,2}], у которого есть два внутренних СЭС.Кроме того, для всех многопользовательских игр с двумя стратегиями p* локально асимптотически устойчиво тогда и только тогда, когда p* является ESS.
Приведенное выше обсуждение предполагает, что многопользовательская игра имеет конечное число чистых стратегий. В следующем примере это уже не так.
Пример 3 (Игра общественных благ): Игра общественных благ (PGG) — это многопользовательская игра, в которой каждому игроку дается начальный запас E>0, а затем он решает, сколько x этого вклада внести общий бассейн (т.е., 0≤x≤E). Все взносы в общий пул умножаются на коэффициент r>1 и затем равномерно распределяются между всеми n игроками. В этом случае выигрыш игрока равен остатку его вклада E-x плюс то, что он получает из общего фонда. Если он вносит x1, а другие n−1 игроков вносят x2,x3,…,xn соответственно, его выигрыш π(x1;x2,x3,…,xn) определяется какE−x1+rn∑i=1nxi=E+( rn−1)x1+rn∑i=2nxi.[7] Предполагается, что 1 Единственный РН для каждого игрока состоит в том, чтобы внести 0 (т. е. в безбилетный проезд), поскольку π(0;x2,x3,…,xn)>π(x1;x2,x3,…,xn) для всех x1> 0. С другой стороны, каждый игрок получает свой максимально возможный выигрыш rE, когда все игроки вносят E . PPG — это многопользовательская версия игры «Дилемма заключенного» (PD) (33) со свободной ездой (соответственно, вклад E ), соответствующей дефекту (соответственно, сотрудничеству). PGG и PD использовались в качестве стандартных примеров социальных дилемм для исследования эволюции сотрудничества в человеческом и других обществах (33, 34) как с теоретической, так и с эмпирической точек зрения. Поскольку PGG имеет непрерывное пространство стратегий, народная теорема может быть неприменима (как мы видели выше). Поэтому важно анализировать стабильность в игровой динамике, такой как уравнение репликатора и адаптивная динамика. Из [7] ожидаемый выигрыш π(y;P) индивидуума, играющего y в группе, остальные n−1 игроков которой выбираются случайным образом из популяции с состоянием P∈∆([0,E] ) равно E+[(r/n)−1]y+[r(n−1)/n]x¯, где x¯≡∫[0,E]xP(dx) – средний вклад особи в популяцию ( Приложение SI , раздел 1.3). Кроме того, средний выигрыш населения равен π(P;P)≡∫[0,E]π(y;P)P(dy)=E+[(r/n)−1]x¯+[r(n−1 )/n]x¯=E+(r−1)x¯. В соответствии с Cressman et al. (35), эволюция x¯ по уравнению репликатора (уравнение 6 ) есть dx¯/dt=[(r/n)−1]∫[0,E](x−x¯)2P(dx )≤0 с равенством тогда и только тогда, когда P является распределением δx, которое имеет весь свой вес на некотором x∈[0,E]. Поскольку Pt имеет тот же носитель, что и P0, для всех t≥0, x¯ эволюционирует до наименьшего элемента x* в носителе P0. В частности, если в исходном распределении населения есть несколько безбилетников, Pt эволюционирует до δ0 в слабой топологии.Этот результат также следует из того факта, что π(0;P)>π(P;P), если P ≠ δ0 [т. е. 0 (глобально) превосходит соседство в PGG]. Соответствующая адаптивная динамика dx/dt=[dπ(y;δx)/dy]|y=x=(r/n)−1<0 для x внутри [0,E] и, следовательно, x эволюционирует до 0 и для этой игровой динамики. То есть ни одна игровая динамика не предсказывает, что кооперативное поведение возникнет в социальной дилемме PGG. Асимметричная игра — это многопользовательская игра, в которой игрокам назначаются роли с определенной вероятностью, и для каждой роли существует набор стратегий.Если роль всего одна, то у нас симметричная игра. Здесь мы сосредоточимся на двухролевых асимметричных играх для двух игроков с конечными множествами чистых стратегий {e1,e2,…,em} и {f1,f2,…,fn} соответственно. Их еще называют «двухвидовыми играми» (роли соответствуют видам) с внутривидовыми (соответственно межвидовыми) взаимодействиями между игроками в одной роли (соответственно, разных ролях). Мы также предполагаем, что ожидаемые выигрыши π1(ei;p,q) и π2(fj;p,q) для ei у вида 1 и fj у вида 2 линейны по компонентам состояний популяции p∈Δm и q∈ Δн.Одна интерпретация линейности состоит в том, что каждый игрок участвует в одном внутривидовом и одном межвидовом случайном парном взаимодействии в единицу времени. Соответствующее уравнение репликатора на (m−1)+(n−1) мерном пространстве стратегий Δm×Δn тогда имеет вид p˙i=pi(π1(ei;p,q)−π1(p;p,q)) для i=1,…,mq˙j=qj(π2(fj;p,q)−π2(q;p,q)) для j=1,…,n,[8]где, например, π1( p;p,q)≡∑i=1mpiπ1(ei;p,q) — средний выигрыш вида 1. Народная теорема верна при [8] , где NE — пара стратегий (p*,q *) такое, что π1(p;p*,q*)≤π1(p*;p*,q*) для всех p≠p* и π2(q;p*,q*)≤π2(q*;p *,q*) для всех q≠q* (строгим, если оба неравенства строгие). Чтобы обобщить Теорему 2 , рассмотрим подход Мейнарда Смита и Прайса (3) к неуязвимости для системы резидент-мутант, где резиденты и мутанты используют пары стратегий (p*,q*) и (p0,q0) соответственно . (p*,q*) называется «двухвидовой ESS» (36), если она локально асимптотически устойчива при соответствующем двумерном (смешанном) уравнении репликатора для всех (p0,q0)≠(p*,q* ). Следующий результат (9, 12, 20) соответствует теореме 2 . Теорема 4. а) (p*,q*) является двухвидовой ЭСС тогда и только тогда, когда либо π1(p*;p,q)>π1(p;p,q), либо π2( q*;p,q)>π2(q;p,q)[9] для всех пар стратегий (p,q) , которые достаточно близки (но не равны) к (p*,q*) . b) Двухвидовая ESS (p*,q*) является локально асимптотически устойчивой точкой покоя уравнения репликатора ( Eq. 8 7 9). c) Двухвидовая ESS (p*,q*) внутри Δm×Δn является глобально асимптотически устойчивой точкой покоя уравнения репликатора. Таким образом, Условие 9 для (p*,q*) является логическим продолжением двухвидовых игр локального превосходства. В дальнейшем он был распространен на асимметричные игры, имеющие непрерывные пространства стратегий, где он называется «превосходным соседством» (19) применительно к парам чистых стратегий (x*, y*) и распределениям (P, Q) с близкой поддержкой.Высшая окрестность (x*,y*) тогда стабильна в соответствии с уравнением репликатора теории меры, которое расширяет [6] до двухвидовых систем. Родственное состояние (называемое «полупревосходное соседство») соответствует концепции CSS и стабильности при адаптивной динамике (19, 31). Теория с конечным числом чистых стратегий также была распространена на игры популяций двух видов с нелинейными выигрышами (10). В игре выбора среды обитания с двумя конкурирующими видами индивидуальная приспособленность снижается по мере увеличения плотности любого вида на его участке.Криван и др. (22) показывают, что IFD [определяемый как распределение, при котором приспособленность вида 1 на всех участках, занятых этим видом, одинакова и, по крайней мере, столь же высока, как на любом участке, не занятом этим видом (и то же самое для вида 2)] не всегда стабильна, если только она не является двухвидовой ESS. Этот результат ставит вопрос о том, как следует определять одновидовую IFD Фретвелла и Лукаса (21) для двух (или более) видов. Асимметричные игры без внутривидовых взаимодействий (т. е. вероятность взаимодействия индивидуумов в одной и той же роли равна 0) были рассмотрены Селтеном (37) на раннем этапе, который назвал их «истинно асимметричными играми».С двумя игроками, двумя ролями и нашим предположением о линейности ожидаемых выплат они становятся биматричными играми, поскольку π1(ei;p,q)=π1(ei,q)≡∑ℓ=1nAiℓqℓ и π2(fj;p,q)= π2(fj,p)≡∑k=1mBkjpk, где, например, A — матрица размера m×n с элементами Aij=π1(ei,fj). Хорошо известно (12), что (p*,q*) является локально асимптотически устойчивой точкой покоя биматричного уравнения репликатора (уравнение 8 ) тогда и только тогда, когда оно является строгим NE ( SI Приложение , раздел 2). При этом (38), (p*,q*) является строгим РН тогда и только тогда, когда он является двухвидовым РЭ [т.е.т. е., если (p,q)=(p,q*), то [9] влечет π1(p*,q*)>π1(p,q*) при p≠p*]. К сожалению, многие биматричные игры не имеют строгого РН, поэтому динамика игры не может предсказать для них результат РН. Однако можно сказать больше, когда эти биматричные игры в нормальной форме происходят из соответствующей расширенной формы (например, Теорема 5 в следующем разделе). Игры в расширенной форме, деревья решений которых описывают конечный ряд взаимодействий между одними и теми же двумя игроками (при этом набор действий, доступных при более поздних взаимодействиях, возможно, зависит от того, какой выбор был сделан ранее), были введены вместе с играми в нормальной форме фон Нейманом и Моргенштерном (39). ).С точки зрения эволюционной игры различия с интуицией в нормальной форме уже проявляются в играх с полной информацией ( SI, Приложение , раздел 2.1) с короткими деревьями решений, как показано в этом разделе (см. также ссылку 13). Рассмотрим элементарную игру с совершенной информацией на рис. 3 A , которая имеет несколько названий [например, «игра в сетевом магазине» (38), «игра с сдерживанием входа» (17)]. У игрока 1 есть один узел принятия решений u , в котором он выбирает между действиями L и R .Если он выполнит действие L , игрок 1 получит выигрыш 1, а игрок 2 получит 4. Если он выполнит действие R , то мы достигнем узла решения v игрока 2, который затем выбирает между ℓ и r , что приводит к оба игрока получают выигрыш 0 или оба выигрыша 2 соответственно. Экстенсивная форма ( A ) игры в сетевой магазин и траектории ( B ) уравнения репликатора (уравнение 8 ). Соответствующая биматричная нормальная форма [e.g., 1 и 4 — выигрыши игроков 1 и 2, соответственно, когда они играют (L,ℓ)]LR[1,41,40,02,2]ℓ с двумя NE-исходами. Одним из них является двухвидовая пара ESS и строгая NE (R, r). С другой стороны, если игрок 1 выбирает L , то игроку 2 безразлично, какую стратегию он использует, поскольку его выигрыш всегда равен 4. Кроме того, игрок 1 не выигрывает от того, что играет R с положительной вероятностью тогда и только тогда, когда игрок 2 играет ℓ как минимум в половине случаев. Таким образом, G≡{(L,q1ℓ+(1−q1)r)|12≤q1≤1} — это множество РН (называемое «компонентой НЭ», поскольку это связное множество РН, не содержащееся ни в большее связанное множество РН), все они соответствуют одному и тому же результату РН; а именно путь L , ведущий к выигрышам 1 и 4. Траектории уравнения репликатора (уравнение 8 ) показаны на рис. 3 B . Все точки на вертикальном ребре p1=1 (p1 — вероятность того, что игрок 1 сыграет L ) являются точками покоя, хотя только точки G являются предельными точками внутренних траекторий. Шесть приведенных ниже результатов для этого примера следуют из того, что q1 всегда строго убывает, а p1 строго возрастает (убывает) тогда и только тогда, когда q1>1/2 (q1<1/2) для любой внутренней траектории. Они выполняются, вообще говоря, по теореме 5 (13). 1) Каждый выход NE является единственным конечным узлом. 2) Каждый компонент сетевого элемента G включает пару чистых стратегий. 3) Исходы всех элементов G одинаковы. 4) Каждая внутренняя траектория сходится к СВ. 5) Если компонент РЭ является внутренним притягивающим, он включает совершенный РН подыгра (SPNE), определенный ниже. 6) НЭ локально асимптотически устойчиво тогда и только тогда, когда оно является строгим СФНЭ, тогда и только тогда, когда оно является всеобъемлющим (т.е., он достигает точки принятия решения каждым игроком). Теорема 5. Эти шесть результатов верны для всех общих игр с совершенной информацией без ходов по своей природе. Некоторые теоретики игр утверждают, что эти игры имеют только один рациональный NE-равновесный исход, который можно найти с помощью обратной индукции. Эта процедура начинается с конечного узла принятия решений игроком (т. е. с узла принятия решений игроком, за которым не следуют точки принятия решений игроком) и решает, какое уникальное действие этот игрок выберет, чтобы максимизировать свой выигрыш в подыгре с этим корнем.Затем исходное игровое дерево усекается в этом узле путем создания там конечного узла с выплатами двум игрокам, полученным в результате этого действия. Процесс дает SPNE, если он продолжается до тех пор, пока в игровом дереве не останется узлов решений игрока. То есть стратегия, построенная методом обратной индукции, порождает РН в каждой подыгре Γu, соответствующей поддереву с корнем в узле решения u . Это пара чистых стратегий, и она обозначена двойными линиями в дереве решений, как на рис.3 А . Если РН не является идеальной подыгрой, то эта точка зрения утверждает, что существует некоторый узел принятия решения игроком, в котором использовалась невероятная угроза, такая как игрок 2, форсирующий выплату 0, играя ℓ, если достигается узел против (38). Результаты 5 и 6 подтверждают этот аргумент, хотя, поскольку дерево решений становится более сложным, чем на рис. 3 A , SPNE (компонент) больше не должен быть стабильным (13). Нестабильность SPNE часто возникает, когда у игрока есть два (или более) узла принятия решений на пути в дереве или когда в игре нет полной информации, как в следующем примере. Пример 4 (Игра на распознавание добычи): Два типа добычи распределены по большому количеству участков (или микросред обитания) с не более чем одной добычей на каждом участке. Пусть pi — вероятность того, что участок, случайно выбранный одним хищником, содержит добычу типа i для i = 1,2, а p0 — вероятность того, что участок пуст (т. е. не содержит добычи) (рис. 4, уровень 1). Если хищник находит жертву за время поиска τs в выбранном пятачке, он сразу решает, атаковать ли его, перейти в другую микросреду обитания, чтобы начать новый поиск, или потратить время на распознавание, чтобы определить тип встречающейся жертвы с вероятностями qA,qM, qR соответственно [т.е.т. е., q≡(qA,qM,qR)∈∆3]. Горизонтальная пунктирная линия на рис. 4, соединяющая эти два события встречи (называемые «информационным набором»), указывает на то, что это решение должно быть принято без знания типа жертвы. Дерево решений для игры распознавания добычи. В редуцированном дереве удаляются пунктирные ребра. Если хищник решает потратить время распознавания τr, чтобы определить, что встречающаяся жертва относится к типу i , то он должен впоследствии решить, атаковать эту жертву или нет с вероятностями qAi и 1−qAi соответственно (рис.4, уровень 3). Если τih — время обращения с жертвами типа i , а πi — их питательная ценность, то суммарная пищевая ценность хищников в единицу времени f((qA,qR,qM),qA1,qA2) isp1π1(qA+qRqA1)+ p2π2(qA+qRqA2)τ,[10] , где τ=τs+p1qAτ1h+p1qR(qA1τ1h+τr)+p2qAτ2h+p2qR(qA2τ2h+τr) ( Приложение SI , раздел 2.2). Теория оптимального поиска пищи (40) постулирует, что хищник максимизирует f как функцию q, qA1, qA2. Теоретико-игровые методы могут быть использованы для поиска оптимального поведения при поиске пищи (41).В частности, нормальная форма агента на рис. 4 представляет собой игру-собирательство с тремя игроками, в которой игрок 1 выбирает q∈Δ3 в информационном наборе, игрок 2 выбирает qA2 в узле, помеченном как «распознанная добыча 2», а игрок 3 выбирает qA1 в «распознанной добыче». добыча 1». Оптимальное поведение при поиске пищи — НЭ этой игры. В СЗ хищник никогда не должен переходить на другой участок, когда он впервые находит добычу, поскольку, бросив эту добычу, хищник тратит впустую время, затраченное на ее поиск. Кроме того, если добыча типа 1 более прибыльна, чем тип 2 (т.т. е., π1/τ1h>π2/τ2h, как предполагалось в этом примере), то хищник должен атаковать любую добычу 1, которую он распознает ( SI Приложение , раздел 2.2). Таким образом, мы предполагаем, что qM=0 и qA1=1 в дереве решений на рис. 4, и анализируем усеченную игру-собирательство, которая устраняет три ребра, обозначенные там пунктирными линиями. В соответствии с Cressman et al. (41), если выгоды обоих типов жертв почти равны или время распознавания велико, единственное поведение НЭ игрока 1 состоит в том, чтобы немедленно атаковать любую встреченную добычу.Фактически тогда единственным компонентом NE является G≡{(q,qA2)|qA=1,0≤qA2≤1}. В противном случае подмножество G (см. сегмент красной линии в SI Приложение , рис. S2) является компонентом NE, и появляется другой результат NE, когда хищник тратит время на распознавание типа жертвы, с которой он столкнулся, и затем атакует только самый прибыльный тип (т.е. qA=0 и qA2=0 — это NE). Этот последний NE является строгим и единственным, который соответствует оптимальному поведению при поиске пищи. Кроме того, это единственный результат НЭ, локально асимптотически устойчивый при адаптивной динамике ( SI Приложение , раздел 2.2 и рис. S2)q˙A=qA(1−qA)∂∂qAf(qA,qA2)q˙B=qA2(1−qA2)∂∂qA2f(qA,qA2)[11], что сохраняет единичный квадрат инвариант. Хотя игра по распознаванию добычи не является обычной игрой в расширенной форме, поскольку выигрыши нелинейны в стратегии хищника (и игра имеет непрерывное пространство стратегий), динамика игры 11 удивительно похожа на динамику уравнения репликатора для сетевой магазин игры (рис. 3 B и SI Приложение , рис. S2). Асимметричные игры
Асимметричные игры в расширенной форме.

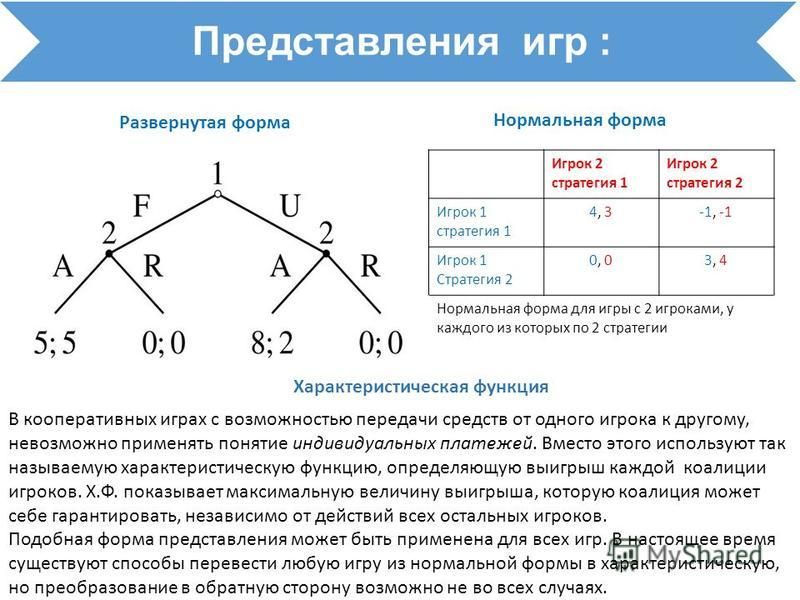
 Следует отметить, что уже в 80-х годах М. Портер ввел в обиход некоторые ключевые понятия теории, в частности такие, как “стратегический ход” и “игрок”. Правда, эксплицитный анализ, связанный с концепцией равновесия, в этом случае еще отсутствовал.
Следует отметить, что уже в 80-х годах М. Портер ввел в обиход некоторые ключевые понятия теории, в частности такие, как “стратегический ход” и “игрок”. Правда, эксплицитный анализ, связанный с концепцией равновесия, в этом случае еще отсутствовал.
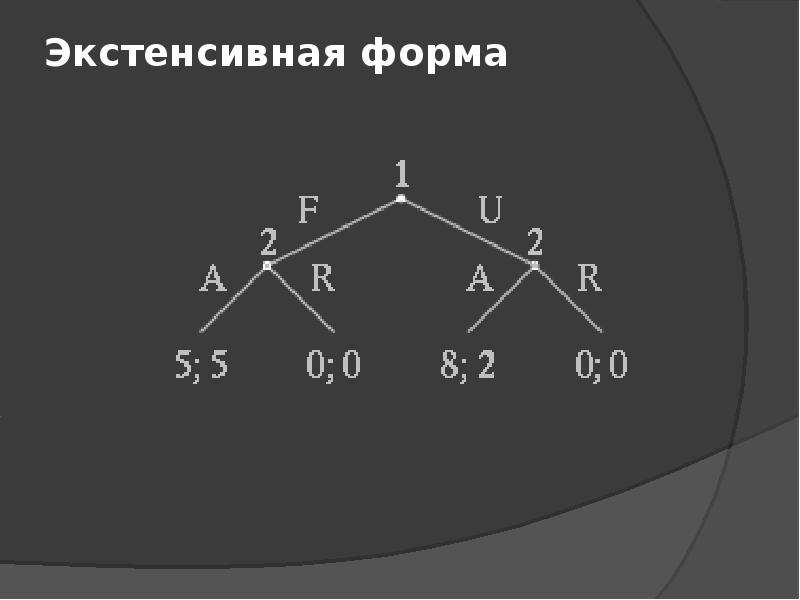 1а и 1б.
1а и 1б.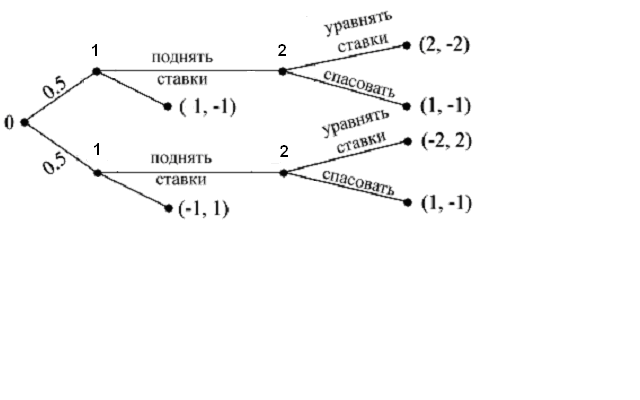

 д. Положения данной теории в принципе можно использовать для всех видов решений, если на их принятие влияют другие действующие лица. Этими лицами, или игроками, необязательно должны быть рыночные конкуренты; в их роли могут выступать субпоставщики, ведущие клиенты, сотрудники организаций, а также коллеги по работе.
д. Положения данной теории в принципе можно использовать для всех видов решений, если на их принятие влияют другие действующие лица. Этими лицами, или игроками, необязательно должны быть рыночные конкуренты; в их роли могут выступать субпоставщики, ведущие клиенты, сотрудники организаций, а также коллеги по работе. В противном случае выберите один из вариантов поиска базы данных.
В противном случае выберите один из вариантов поиска базы данных.
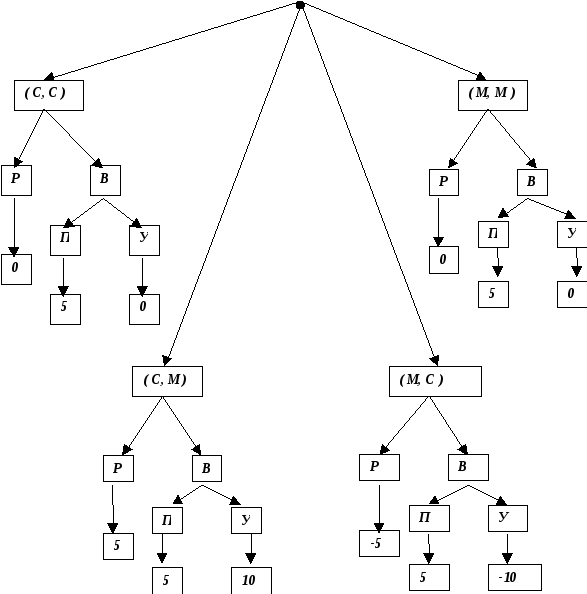






 Режимы сводной таблицы и сводной диаграммы в Access недоступны, начиная с Access 2013.
Режимы сводной таблицы и сводной диаграммы в Access недоступны, начиная с Access 2013.











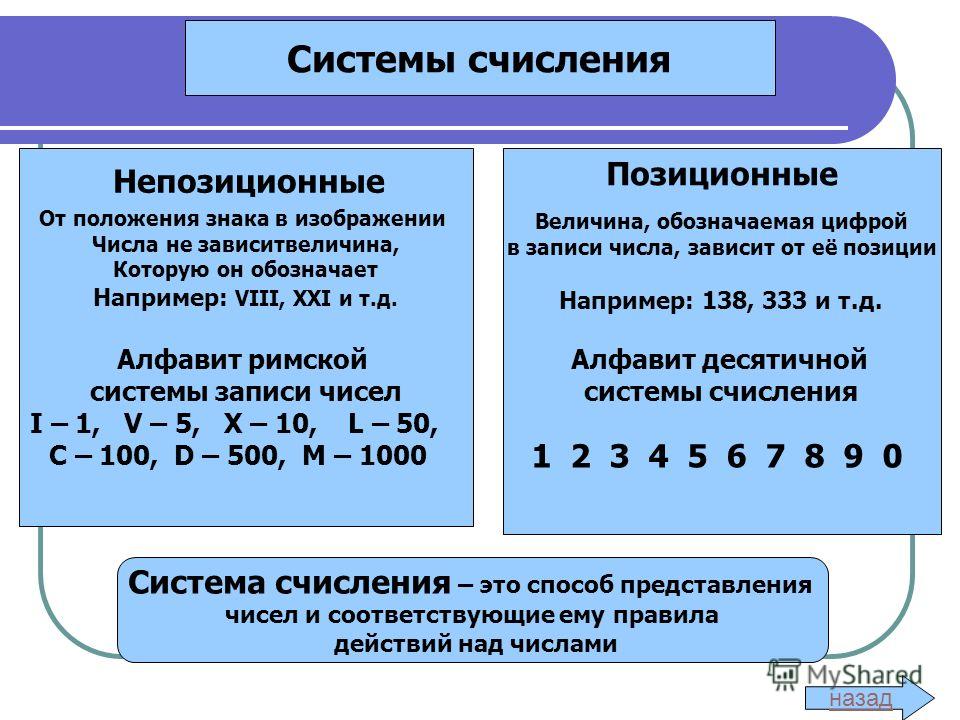 Свойства поля определяются его типом данных.
Свойства поля определяются его типом данных.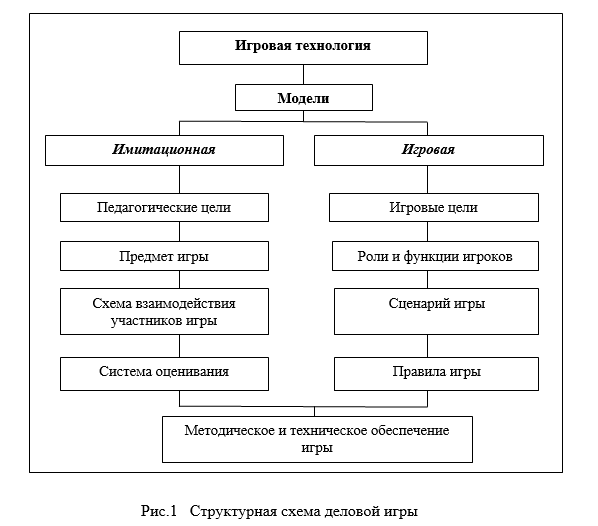 Чем больше и сложнее игра тем, скучнее и безынтереснее процесс её разработки. Романтики совершенно нет.
Чем больше и сложнее игра тем, скучнее и безынтереснее процесс её разработки. Романтики совершенно нет.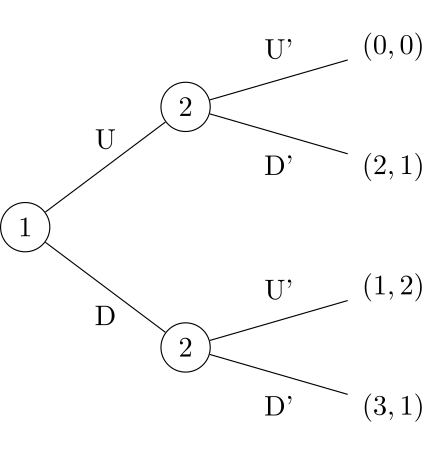 Она просто не выдержит конкуренции. Соответственно, абы что не сделаешь. Тут скрывается важный психологический момент – начинающий разработчик вынужден делать хороший продукт, иначе он будет испытывать постоянное чувство страха неуспешности своего продукта.
Она просто не выдержит конкуренции. Соответственно, абы что не сделаешь. Тут скрывается важный психологический момент – начинающий разработчик вынужден делать хороший продукт, иначе он будет испытывать постоянное чувство страха неуспешности своего продукта.
 Вы должны будете им предоставить концепцию проекта и ТЗ. Без концепции и ТЗ Вы не привлечёте ни одного нормального специалиста.
Вы должны будете им предоставить концепцию проекта и ТЗ. Без концепции и ТЗ Вы не привлечёте ни одного нормального специалиста.

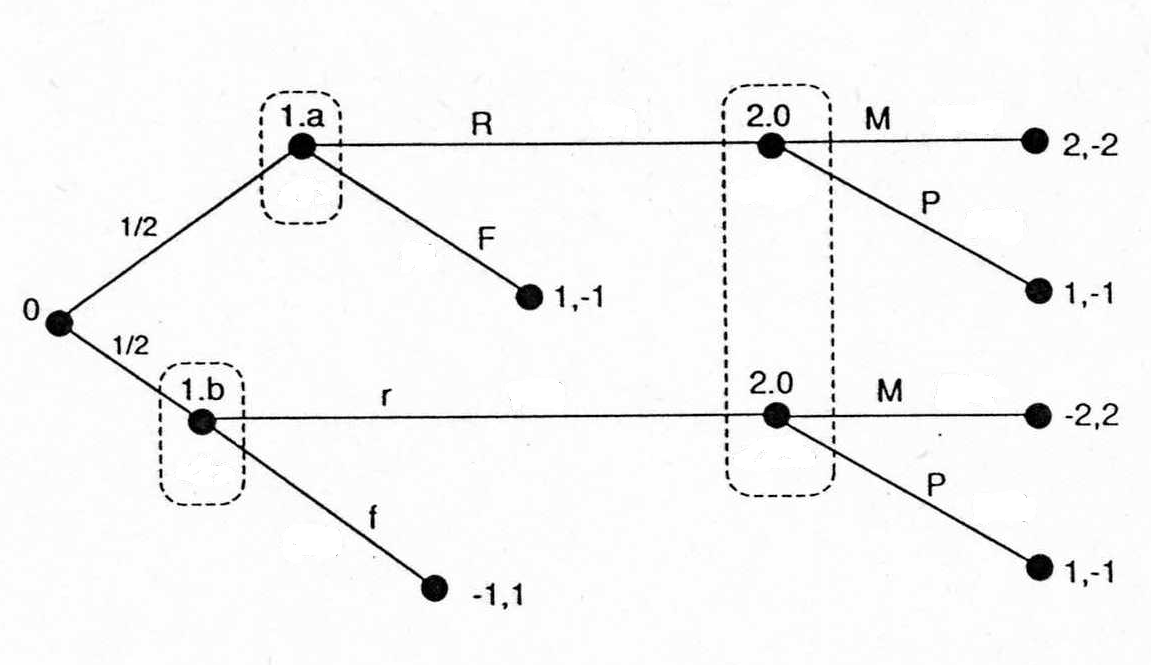 Естественно, если игра маленькая, то это не так заметно, а если большая, то на долю создателя контента выпадает до 80% работы по проекту.
Естественно, если игра маленькая, то это не так заметно, а если большая, то на долю создателя контента выпадает до 80% работы по проекту. Времени уходит больше, чем на все остальные направления вместе взятые (маленькие игры не в счёт). Учитывайте это, когда будете планировать и рассчитывать сроки.
Времени уходит больше, чем на все остальные направления вместе взятые (маленькие игры не в счёт). Учитывайте это, когда будете планировать и рассчитывать сроки. Проблема в том, что авторское право контента достаточно легко подтвердить. У «жертвы» воровства есть либо исходные файлы контента, либо документ о передаче контента от его создателя. Для воров контента очень велик шанс нарваться на статью 146 УК РФ.
Проблема в том, что авторское право контента достаточно легко подтвердить. У «жертвы» воровства есть либо исходные файлы контента, либо документ о передаче контента от его создателя. Для воров контента очень велик шанс нарваться на статью 146 УК РФ.
 Первым делом адекватный программист попросит разработчика продемонстрировать концепцию и ТЗ. Затем спросит про создание контента или финансирование, которое пойдёт на его создание. Специалисты прекрасно понимают, что незачем вкладывать силы в изначально провальный проект. Если у Вас нет концепции и не решен вопрос с контентом, то нормального программиста Вы не найдёте.
Первым делом адекватный программист попросит разработчика продемонстрировать концепцию и ТЗ. Затем спросит про создание контента или финансирование, которое пойдёт на его создание. Специалисты прекрасно понимают, что незачем вкладывать силы в изначально провальный проект. Если у Вас нет концепции и не решен вопрос с контентом, то нормального программиста Вы не найдёте. Оба подхода имеют место в современном процессе разработки. Если подгонять код под контент, то нагрузка падает на программиста, время разработки увеличивается. Это дешёвый способ. Если контент подгонять под код, то нагрузка с программиста спадает, и при учёте, что контент подготавливают наёмные работники, время разработки сокращается. Это дорогой способ, так как нагрузка падает на наёмных создателей контента. Заранее оцените ситуацию и придерживайтесь одного из подходов.
Оба подхода имеют место в современном процессе разработки. Если подгонять код под контент, то нагрузка падает на программиста, время разработки увеличивается. Это дешёвый способ. Если контент подгонять под код, то нагрузка с программиста спадает, и при учёте, что контент подготавливают наёмные работники, время разработки сокращается. Это дорогой способ, так как нагрузка падает на наёмных создателей контента. Заранее оцените ситуацию и придерживайтесь одного из подходов.
 Мой совет прост – остерегайтесь таких неадекватных программистов. Программный код не контент. Доказать его авторство очень сложно. Поэтому нормальный программист сначала договаривается, что он получит за код; затем его пишет; потом передаёт разработчику и получает вознаграждение; после чего уже ни на что не претендует. Также должно быть организовано и в команде.
Мой совет прост – остерегайтесь таких неадекватных программистов. Программный код не контент. Доказать его авторство очень сложно. Поэтому нормальный программист сначала договаривается, что он получит за код; затем его пишет; потом передаёт разработчику и получает вознаграждение; после чего уже ни на что не претендует. Также должно быть организовано и в команде. Поверьте мне, один такой тест даст Вам очень большой объём полезной информации. Проводите их чаще, прислушивайтесь к обратной связи, и Вы получите на выходе хорошую игру.
Поверьте мне, один такой тест даст Вам очень большой объём полезной информации. Проводите их чаще, прислушивайтесь к обратной связи, и Вы получите на выходе хорошую игру.
 Знакомьтесь с другими разработчиками, общайтесь и обменивайтесь контактами. В будущем, возможно, знакомство с ними принесёт Вам пользу.
Знакомьтесь с другими разработчиками, общайтесь и обменивайтесь контактами. В будущем, возможно, знакомство с ними принесёт Вам пользу. А вот на последних этапах разработки ситуация может в корне поменяться – могут появиться инвесторы и Вам всё равно будут нужны деньги для организации рекламной компании.
А вот на последних этапах разработки ситуация может в корне поменяться – могут появиться инвесторы и Вам всё равно будут нужны деньги для организации рекламной компании. Это позволяет принимать решения на основе выводов из данных наиболее оптимальным образом на основе выводов, сделанных после проведения анализа больших данных.
Это позволяет принимать решения на основе выводов из данных наиболее оптимальным образом на основе выводов, сделанных после проведения анализа больших данных. Пример: аукцион, шахматы, политика и т. д.
Пример: аукцион, шахматы, политика и т. д.

 На самом деле теория игр тесно используется в сочетании с аналитикой больших данных для принятия оптимизированных и стратегических решений.
На самом деле теория игр тесно используется в сочетании с аналитикой больших данных для принятия оптимизированных и стратегических решений.

 Также полезно, чтобы сделать вашу игру играбельной, даже если пользователь не подключен к Интернету (например, когда он часами застревает в самолете).
Также полезно, чтобы сделать вашу игру играбельной, даже если пользователь не подключен к Интернету (например, когда он часами застревает в самолете).
 Хотите, чтобы ваши игроки могли разговаривать друг с другом во время взрыва монстров? Это API для вас.
Хотите, чтобы ваши игроки могли разговаривать друг с другом во время взрыва монстров? Это API для вас. Показывая эти детали по частям, ваши игроки могут анализировать и переваривать контент до того, как он начнет его воспроизводить.
Показывая эти детали по частям, ваши игроки могут анализировать и переваривать контент до того, как он начнет его воспроизводить.  Таким образом, ваши игроки сразу же получат новейший контент без необходимости нажимать отдельную кнопку загрузки (как в случае, если вы выпустили свое обновление в виде бесплатного DLC).
Таким образом, ваши игроки сразу же получат новейший контент без необходимости нажимать отдельную кнопку загрузки (как в случае, если вы выпустили свое обновление в виде бесплатного DLC). 
 Когда вы публикуете событие или объявление, оно будет отображаться для всех клиентов, которые следят за вашей игрой (что они могут сделать из вашего центра сообщества или страницы в магазине), на странице вашего магазина. , в библиотеке Steam и будет доступен из панели «загрузки» клиента Steam.Подробнее о событиях и объявлениях
Когда вы публикуете событие или объявление, оно будет отображаться для всех клиентов, которые следят за вашей игрой (что они могут сделать из вашего центра сообщества или страницы в магазине), на странице вашего магазина. , в библиотеке Steam и будет доступен из панели «загрузки» клиента Steam.Подробнее о событиях и объявлениях  Это полезно для информирования новых и существующих клиентов о вашем обновлении. Это также перечисляет ваш заголовок на странице недавно обновленных продуктов.
Это полезно для информирования новых и существующих клиентов о вашем обновлении. Это также перечисляет ваш заголовок на странице недавно обновленных продуктов. 