Методы решения ду: Методы решения дифференциальных уравнений

Содержание

Численные методы решения дифференциальных уравнений третьего порядка. Численные методы решения дифференциальных уравнений

Введение

При решении научных и инженерно-технических задач часто бывает необходимо математически описать какую-либо динамическую систему. Лучше всего это делать в виде дифференциальных уравнений (ДУ ) или системы дифференциальных уравнений. Наиболее часто они такая задача возникает при решении проблем, связанных с моделированием кинетики химических реакций и различных явлений переноса (тепла, массы, импульса) – теплообмена, перемешивания, сушки, адсорбции, при описании движения макро- и микрочастиц.

В ряде случаев дифференциальное уравнение можно преобразовать к виду, в котором старшая производная выражена в явном виде. Такая форма записи называется уравнением, разрешенным относительно старшей производной (при этом в правой части уравнения старшая производная отсутствует):

Решением обыкновенного дифференциального уравнения называется такая функция y(x), которая при любых х удовлетворяет этому уравнению в определенном конечном или бесконечном интервале.

Процесс решения дифференциального уравнения называют интегрированием дифференциального уравнения.

Исторически первым и наиболее простым способом численного решения задачи Коши дляОДУ первого порядка является метод Эйлера. В его основе лежит аппроксимация производной отношением конечных приращений зависимой (y) и независимой (x) переменных между узлами равномерной сетки:

где y i+1 это искомое значение функции в точке x i+1 .

Точность метода Эйлера можно повысить, если воспользоваться для аппроксимации интеграла более точной формулой интегрирования –формулой трапеций .

Данная формула оказывается неявной относительно y i+1 (это значение есть и в левой и в правой части выражения), то есть является уравнением относительно y i+1 , решать которое можно, например, численно, применяя какой-либо итерационный метод (в таком виде его можно рассматривать как итерационную формула метода простой итерации).

Состав курсовой работы: Курсовая работа состоит из трех частей. В первой части краткое описание методов. Во второй части постановка и решение задачи. В третьей части – программная реализация на языке ЭВМ

Цель курсовой работы: изучить два метода решения дифференциальных уравнений-метод Эйлера-Коши и усовершенствованный методЭйлера.

1. Теоретическая часть

Численное дифференцирование

Дифференциальным называется уравнение, содержащее один или несколько производных. В зависимости от количества не зависимых переменных, дифференциальные уравнения делятся на две категории.

Обыкновенные дифференциальные уравнения (ОДУ)

Дифференциальные уравнения в частных производных.

Обыкновенными дифференциальными уравнениями называются такие уравнения, которые содержат одну или несколько производных от искомой функции . Их можно записать виде

независимая переменная

Наивысший порядок , входящий в уравнение (1) называется порядком дифференциального уравнения.

Простейшим (линейным) ОДУ является уравнение (1) порядка разрешенное относительно производной

Решением дифференциального уравнения (1) называется всякая функция,которая после ее подстановки в уравнение обращает его в тождество.

Основная задача, связанная с линейной ОДУ известно как задача Каши:

Найти решение уравнения (2) в виде функции удовлетворяющий начальному условию (3)

Геометрически это означает, что требуется найти интегральную кривую, проходящую через точку ) при выполнение равенства (2).

Численный с точки зрения задачи Каши означает: требуется построить таблицу значений функции удовлетворяющий уравнение (2) и начальное условие (3) на отрезке с некоторым шагом . Обычно считается, что то есть начальное условие задано в левом конце отрезка.

Простейшим из численных методов решения дифференциального уравнения является метод Эйлера. В его основе лежит идея графического построения решения дифференциального уравнения, однако этот метод дает одновременно и способ нахождения искомой функции в численной форме или таблицы.

Пусть дано уравнение (2) с начальным условием тоесть поставлена задача Каши. Решим вначале следующую задачу. Найти простейшим способом приближенное значение решения в некоторой точке где -достаточно малый шаг.

Уравнение (2) совместно с начальным условием (3) задают направление касательной искомой интегральной кривой в точке с координатами

Уравнение касательной имеет вид

Двигаясь вдоль этой касательной, получим приближенное значение решения в точке :

Располагая приближенным решением в точке можно повторить описанную ранее процедуру: построить прямую проходящую через эту точку с угловым коэффициентом , и по ней найти приближенное значение решения в точке

. Заметим, что эта прямая не является касательной к реальной интегральной кривой, поскольку точка нам не доступна, однако если достаточно мало то получаемые приближенные будут близки к точным значениям решения.

Продолжая эту идею, построим систему равно отстоящих точек

Получение таблицы значений искомой функции

по методу Эйлера заключается в циклическом применение формулы

Рисунок 1. Графическая интерпретация метода Эйлера

Методы численного интегрирования дифференциальных уравнений, в которых решения получаются от одного узла к другому, называются пошаговыми. Метод Эйлера самый простой представитель пошаговых методов. Особенностью любого пошагового метода является то, что начиная со второго шага исходное значение в формуле (5) само является приближенным, то есть погрешность на каждом следующем шаге систематически возрастает. Наиболее используемым методом оценки точности пошаговых методов приближенного численного решения ОДУ является способ двойного прохождения заданного отрезка с шагом и с шагом

1.1 Усовершенствованный метод Эйлера

Основная идея этого метода: вычисляемое по формуле (5) очередное значение будет точнее, если значение производной, то есть угловой коэффициент прямой замещающей интегральную кривую на отрезке будет вычисляться не по левому краю (то есть в точке ), а по центру отрезка . Но так как значение производной между точками не вычисляется, то перейдем к сдвоенным участкам центром, в которых является точка , при этом уравнение прямой получает вид:

А формула (5) получает вид

Формула (7) применена только для , следовательно, значения по ней получить нельзя, поэтому находят по методу Эйлера, при этом для получения более точного результата поступают так: с начало по формуле (5) находят значение

(8)

В точке а затем находится по формуле (7) с шагом

(9)

После того как найдено дальнейшие вычисления при производится по формуле (7)

Лабораторная работа 1

Численные методы решения

обыкновенных дифференциальных уравнений (4 часа)

При решении многих физических и геометрических задач приходится искать неизвестную функцию по данному соотношению между неизвестной функцией, ее производными и независимыми переменными.

Такое соотношение называется дифференциальным уравнением , а отыскание функции, удовлетворяющей дифференциальному уравнению, называется решением дифференциального уравнения.

Обыкновенным дифференциальным уравнением называется равенство

, (1)

в котором

– независимая переменная, изменяющаяся в некотором отрезке , а – неизвестная функция y (x ) и ее первые n

производные. называется порядком уравнения .

Задача заключается в нахождении функции y, удовлетворяющей равенству (1). Более того, не оговаривая это отдельно, будем предполагать, что искомое решение обладает той или иной степенью гладкости, необходимой для построения и «законного» применения того или иного метода.

Различают два типа обыкновенных дифференциальных уравнений

Уравнения без начальных условий

Уравнения с начальными условиями.

Уравнения без начальных условий – это уравнение вида (1).

Уравнение с начальными условиями – это уравнение вида (1), в котором требуется найти такую функцию

, которая при некотором удовлетворяет следующим условиям: ,

т.е. в точке

функция и ее первые производных принимают наперед заданные значения.

Задачи Коши

При изучении способов решения дифференциальных уравнений приближенными методами основной задачей считается задача Коши.

Рассмотрим наиболее популярный метод решения задачи Коши – метод Рунге-Кутта. Этот метод позволяет строить формулы расчета приближенного решения практически любого порядка точности.

Выведем формулы метода Рунге-Кутта второго порядка точности. Для этого решение представим куском ряда Тейлора, отбрасывая члены с порядком выше второго. Тогда приближенное значение искомой функции в точке

x 1 можно записать в виде:

(2)

Вторую производную y “( x 0 ) можно выразить через производную функции f ( x , y ) , однако в методе Рунге-Кутта вместо производной используют разность

соответственно подбирая значения параметров

Тогда (2) можно переписать в виде:

y 1 = y 0 + h [ β f ( x 0 , y 0 ) + α f ( x 0 + γh , y 0 + δh )], (3)

где α , β , γ и δ – некоторые параметры.

Рассматривая правую часть (3) как функцию аргумента h , разложим ее по степеням h :

y 1 = y 0 +( α + β ) h f ( x 0 , y 0 ) + αh 2 [ γ f x ( x 0 , y 0 ) + δ f y ( x 0 , y 0 )],

и выберем параметры α , β , γ и δ так, чтобы это разложение было близко к (2). Отсюда следует, что

α + β =1, αγ =0,5, α δ =0,5 f ( x 0 , y 0 ).

С помощью этих уравнений выразим β , γ и δ через параметры α , получим

y 1 = y 0 + h [(1 – α ) f ( x 0 , y 0 ) + α f ( x 0 +, y 0 + f ( x 0 , y 0 )], (4)

0 α ≤ 1.

Теперь, если вместо (x 0 , y 0 ) в (4) подставить (x 1 , y 1 ), получим формулу для вычисления y 2 – приближенного значения искомой функции в точке x 2 .

В общем случае метод Рунге-Кутта применяется на произвольном разбиении отрезка [ x 0 , X ] на n частей, т.е. с переменным шагом

x 0 , x 1 , …,x n ; h i = x i+1 – x i , x n = X. (5)

Параметры α выбирают равными 1 или 0,5. Запишем окончательно расчетные формулы метода Рунге-Кутта второго порядка с переменным шагом для α =1:

y i+1 =y i +h i f(x i + , y i + f(x i , y i)), (6.1)

i = 0, 1,…, n -1.

и α =0,5:

y i+1 =y i + , (6.2)

i = 0, 1,…, n -1.

Наиболее употребляемые формулы метода Рунге-Кутта – формулы четвертого порядка точности:

y i+1 =y i + (k 1 + 2k 2 + 2k 3 + k 4),

k 1 =f(x i , y i), k 2 = f(x i + , y i + k 1), (7)

k 3 = f(x i + , y i + k 2), k 4 = f(x i +h, y i +hk 3).

Для метода Рунге-Кутта применимо правило Рунге для оценки погрешности. Пусть y ( x ; h ) – приближенное значение решения в точке x , полученное по формулам (6.1), (6.2) или (7) с шагом h , а p – порядок точности соответствующей формулы. Тогда погрешность R ( h ) значения y ( x ; h ) можно оценить, используя приближенное значение y ( x ; 2 h ) решения в точке x , полученное с шагом 2 h :

(8)

где p =2 для формул (6. 1) и (6.2) и p =4 для (7).

Известно, что обыкновенное дифференциальное уравнение первого порядка имеет вид: .Решением этого уравнения является дифференцируемая функция, которая при подстановке в уравнение обращает его в тождество. График решения дифференциального уравнения (рис 1.) называетсяинтегральной кривой.

Производную в каждой точкеможно геометрически интерпретировать как тангенс угланаклона касательной к графику решения, проходящего через эту точку, т е.:.

Исходное уравнение определяет целое семейство решений. Чтобы выделить одно решение, задают начальное условие: , где – некоторое заданное значение аргумента, а–начальное значение функции.

Задача Коши заключается в отыскании функции , удовлетворяющей исходному уравнению и начальному условию. Обычно определяют решение задачи Коши на отрезке, расположенном справа от начального значения, т. е. для.

Даже для простых дифференциальных уравнений первого порядка не всегда удается получить аналитическое решение. Поэтому большое значение имеют численные методы решения. Численные методы позволяют определить приближенные значения искомого решения на некоторой выбранной сетке значений аргумента. Точкиназываютсяузлами сетки , а величина – шагом сетки. Часто рассматриваютравномерные сетки, для которых шаг постоянен,. При этом решение получается в виде таблицы, в которой каждому узлу сеткисоответствуют приближенные значения функциив узлах сетки.

Численные методы не позволяют найти решение в общем виде, зато они применимы к широкому классу дифференциальных уравнений.

Сходимость численных методов решения задачи Коши. Пусть – решение задачи Коши. Назовем погрешностью численного метода функцию , заданную в узлах сетки. В качестве абсолютной погрешности примем величину.

Численный метод решения задачи Коши называется сходящимся , если для него при. Говорят, что метод имеет-ый порядок точности, если для погрешности справедлива оценка, – константа, .

Метод Эйлера

Простейшим методом решения задачи Коши является метод Эйлера. Будем решать задачу Коши

на отрезке . Выберем шаги построим сетку с системой узлов. В методе Эйлера вычисляются приближенные значения функциив узлах сетки:. Заменив производнуюконечными разностями на отрезках,, получим приближенное равенство:,, которое можно переписать так:,.

Эти формулы и начальное условие являются расчетными формулами метода Эйлера.

Геометрическая интерпретация одного шага метода Эйлера заключается в том, что решение на отрезке заменяется касательной, проведенной в точкек интегральной кривой, проходящей через эту точку. После выполненияшагов неизвестная интегральная кривая заменяется ломаной линией(ломаной Эйлера).

Оценка погрешности. Для оценки погрешности метода Эйлера воспользуемся следующей теоремой.

Теорема. Пусть функция удовлетворяет условиям:

Тогда для метода Эйлера справедлива следующая оценка погрешности: , где– длина отрезка. Мы видим, что метод Эйлера имеет первый порядок точности.

Оценка погрешности метода Эйлера часто бывает затруднительна, так как требует вычисления производных функции . Грубую оценку погрешности даетправило Рунге (правило двойного пересчета), которое используется для различных одношаговых методов, имеющих -ый порядок точности. Правило Рунге заключается в следующем. Пусть– приближения, полученные с шагом, а– приближения, полученные с шагом. Тогда справедливо приближенное равенство:

Таким образом, чтобы оценить погрешность одношагового метода с шагом , нужно найти то же решение с шагоми вычислить величину, стоящую справа в последней формуле, т.е.. Так как метод Эйлера имеет первый порядок точности, т. е., то приближенное равенство имеет вид:.

Используя правило Рунге, можно построить процедуру приближенного вычисления решения задачи Коши с заданной точностью . Для этого нужно, начав вычисления с некоторого значения шага , последовательно уменьшать это значение в два раза, каждый раз вычисляя приближенное значение,. Вычисления прекращаются тогда, когда будет выполнено условие: . Для метода Эйлера это условие примет вид:. Приближенным решением будут значения,.

Пример 1. Найдем решение на отрезке следующей задачи Коши:,. Возьмем шаг. Тогда.

Расчетная формула метода Эйлера имеет вид:

, .

Решение представим в виде таблицы 1:

Таблица 1

Исходное уравнение есть уравнение Бернулли. Его решение можно найти в явном виде: .

Для сравнения точного и приближенного решений представим точное решение в виде таблицы 2:

Таблица 2

Из таблицы видно, что погрешность составляет

Для решения дифференциальных уравнений необходимо знать значение зависимой переменной и ее производных при некоторых значениях независимой переменной. Если дополнительные условия задаются при одном значении неизвестной, т.е. независимой переменной., то такая задача называется задачей Коши. Если начальные условия задаются при двух или более значениях независимой переменной, то задача называется краевой. При решении дифференциальных уравнений различных видов, функция, значения которой требуется определить вычисляется в виде таблицы.

Классификация численных методов для решения дифр. Ур. Типов.

Задача Коши – одношаговые: методы Эйлера, методы Рунге- Кутта; – многошаговые: метод Майна, Метод Адамса. Кроевая задача – метод сведения кроевой задачи к задаче Коши; –метод конечных разностей.

При решении задачи Коши должны быть заданы дифр. ур. порядка n или система дифр. ур. первого порядка из n уравнений и n дополнительных условий для ее решения. Дополнительные условия должны быть заданы при одном и том же значении независимой переменной. При решении кроевой задачи должны быть заданы ур. n-ого порядка или система из n уравнений и n дополнительных условий при двух или более значениях независимой переменной. При решении задачи Коши искомая функция определяется дискретно в виде таблицы с некоторым заданным шагом . При определении каждого очередного значения можно использовать информацию об одной предыдущей точке.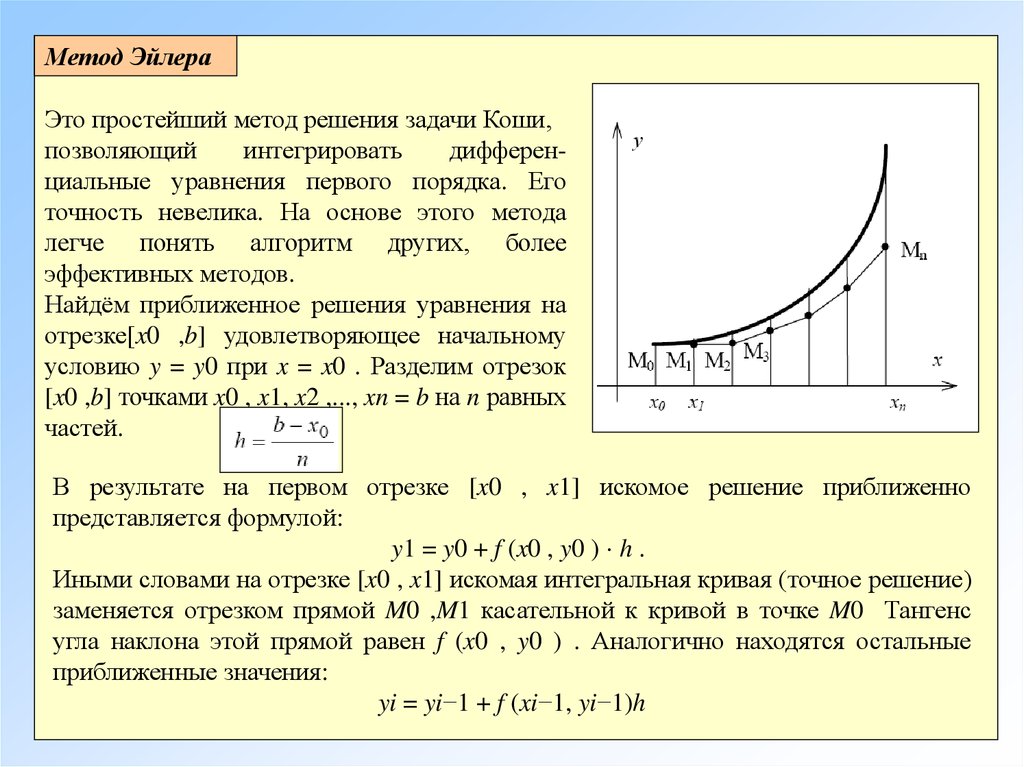 В этом случае методы называют одношаговым, либо можно использовать информацию о нескольких предыдущих точках – многошаговые методы.

Обыкновенные дифференциальные ур. Задача Коши. Одношаговые методы. Метод Эйлера.

Задано: g(x,y)y+h(x,y)=0, y=-h(x,y)/g(x,y)= f(x,y), x 0 , y(x 0)=y 0 . Известно: f(x,y), x 0 , y 0 . Определить дискретное решение: x i , y i , i=0,1,…,n. Метод Эйлера основан на разложении функции в ряд Тейлора окрестности точки x 0 . Окрестность описывается шагом h. y(x 0 +h)y(x 0)+hy(x 0)+…+ (1). В методе Эйлера учитываются только два слагаемых ряда Тейлора. Введем обозначения. Формула Эйлера примет вид: y i+1 =y i +y i , y i =hy(x i)=hf(x i ,y i), y i+1 =y i +hf(x i ,y i) (2), i=0,1,2…, x i+1 =x i +h

Формула (2) является формулой простого метода Эйлера.

Геометрическая интерпретация формулы Эйлера

Для получения численного решения используется ф-ла касательной, проходящей через урав. касательной: y=y(x 0)+y(x 0)(x-x 0), x=x 1 ,

y 1 =y(x 0)+f(x 0 ,y 0)  (x-x 0), т. к.

x-x 0 =h, то y 1 =y 0 +hf(x 0 ,y 0), f(x 0 ,y 0)=tg £.

Модифицированный метод Эйлера

Задано: y=f(x,y), y(x 0)=y 0 . Известно: f(x,y), x 0 , y 0 . Определить: зависимость y от x в виде табличной дискретной функции: x i , y i , i=0,1,…,n.

Геометрическая интерпертация

1) вычислим тангенс угла наклона в начальной точке

tg £=y(x n ,y n)=f(x n ,y n)

2) Вычислим значение  y n+1 на

конце шага по формуле Эйлера

 y n+1 =y n +f(x n ,y n) 3) Вычислим тангенс угла наклона

касательной в n+1 точке: tg £=y(x n+1 ,  y n+1)=f(x n+1 ,  y n+1) 4) Вычислим среднее арифметическое углов

наклона: tg £=½. 5) Используя тангенс угла наклона пересчитаем значение функции в n+1 точке: y n+1 =y n +htg £= y n +½h=y n +½h – формула модифицированного метода Эйлера. Можно показать, что полученная ф-ла соответствует разложению ф-ии в ряд Тейлора, включая слагаемы (до h 2). Модифицированный метод Эйлнра в отличии от простого является методом вторго порядка точности, т. к. погрешность пропорциональна h 2 .

Дифференциальные уравнения – это уравнения, в которые неизвестная функция входит под знаком производной. Основная задача теории дифференциальных уравнений — изучение функций, являющихся решениями таких уравнений.

Дифференциальные уравнения можно разделить на обыкновенные дифференциальные уравнения, в которых неизвестные функции являются функциями одной переменной, и на дифференциальные уравнения в частных производных, в которых неизвестные функции являются функциями двух и большего числа переменных.

Теория дифференциальных уравнений в частных производных более сложная и рассматривается в более полных или специальных курсах математики.

Изучение дифференциальных уравнений начнем с наиболее простого уравнения–уравнения первого порядка.

Уравнение вида

F(x,y,y”) = 0,(1)

где х — независимая переменная; у — искомая функция; у” — ее производная, называется дифференциальным уравнением первого порядка.

Если уравнение (1) можно разрешить относительно у”, то оно принимает вид

и называется уравнением первого порядка, разрешенным относительно производной.

В некоторых случаях уравнение (2) удобно записать в виде f (х, у) dх – dy = 0, являющемся частным случаем более общего уравнения

P(x,y)dx+Q(x,y)dy=O,(3)

где Р(х,у) и Q(х,у) — известные функции. Уравнение в симметричной форме (3) удобно тем, что переменные х и у в нем равноправны, т. е. каждую из них можно рассматривать как функцию другой.

Дадим два основных определения общего и частного решения уравнения.

Общим решением уравнения (2) в некоторой области G плоскости Оху называется функция у=ц(х,С), зависящая от х и произвольной постоянной С, если она является решением уравнения (2) при любом значении постоянной С, и если при любых начальных условиях y x=x0 =y 0 таких, что (x 0 ;y 0)=G, существует единственное значение постоянной С = С 0 такое, что функция у=ц(х,С 0) удовлетворяет данным начальным условиям у=ц(х 0 ,С).

Частным решением уравнения (2) в области G называется функция у=ц(х,С 0), которая получается из общего решения у=ц(х,С) при определенном значении постоянной С=С 0 .

Геометрически общее решение у=ц(х,С) представляет собой семейство интегральных кривых на плоскости Оху, зависящее от одной произвольной постоянной С, а частное решение у=ц(х,С 0) — одну интегральную кривую этого семейства, проходящую через заданную точку (х 0 ; у 0).

Приближенное решение дифференциальных уравнений первого порядка методом Эйлера. Суть этого метода состоит в том, что искомая интегральная кривая, являющаяся графиком частного решения, приближенно заменяется ломаной. Пусть даны дифференциальное уравнение

и начальные условия y |x=x0 =y 0 .

Найдем приближенно решение уравнения на отрезке [х 0 ,b], удовлетворяющее заданным начальным условиям.

Разобьем отрезок [х 0 ,b] точками х 0

Подставим значения х 0 и у 0 в правую часть уравнения y”=f(x,y) и вычислим угловой коэффициент y”=f(x 0 ,y 0) касательной к интегральной кривой в точке (х 0 ;у 0). Для нахождения приближенного значения у 1 искомого решения заменяем на отрезке [х 0 ,x 1 ,] интегральную кривую отрезком ее касательной в точке (х 0 ;у 0). При этом получаем

y 1 – y 0 =f(x 0 ;y 0)(x 1 – x 0),

откуда, так как х 0 , х 1 , у 0 известны, находим

y1 = y0+f(x0;y0)(x1 – x0).

Подставляя значения х 1 и y 1 , в правую часть уравнения y”=f(x,y), вычисляем угловой коэффициент y”=f(x 1 ,y 1) касательной к интегральной кривой в точке (х 1 ;y 1). Далее, заменяя на отрезке интегральную кривую отрезком касательной, находим приближенное значение решения у 2 в точке х 2:

y 2 = y 1 +f(x 1 ;y 1)(x 2 – x 1)

В этом равенстве известными являются х 1 , у 1 , х 2 , а у 2 выражается через них.

Аналогично находим

y 3 = y 2 +f(x 2 ;y 2) ?x, …, y n = y n-1 +f(x n-1 ;y n-1) ?x

Таким образом, приближенно построена искомая интегральная кривая в виде ломаной и получены приближенные значения y i искомого решения в точках х i . При этом значения у i вычисляются по формуле

y i = y i-1 +f(x i-1 ;y i-1) ?x (i=1,2, …, n).

Формула и является основной расчетной формулой метода Эйлера. Ее точность тем выше, чем меньше разность?x.

Метод Эйлера относиться к численным методам, дающим решение в виде таблицы приближенных значений искомой функции у(х). Он является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.

Степень точности метода Эйлера, вообще говоря, невелика. Существуют гораздо более точные методы приближенного решения дифференциальных уравнений.

Методы вычислений, Т.2

Березин И.С., Жидков Н.П. Методы вычислений, Т.2. М.: ГИФМЛ, 1959. – 620 с.

Во втором томе книги рассмотрены численные методы решения систем линейных алгебраических уравнений, уравнений высших степеней и трансцендентных уравнений, численные методы отыскания собственных значений, приближенные методы решения обыкновенных дифференциальных уравнений, уравнений в частных производных и интегральных уравнений.

Книга предназначена в качестве учебного пособия для студентов механико-математических и физико-математических факультетов, специализирующихся по вычислительной математике, и лиц, интересующихся теорией и практикой численных методов

ГЛАВА 6. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
§ 2. Метод исключения
1. Схема Гаусса с выбором главного элемента.
2. Компактная схема Гаусса.
3. Обращение матрицы.
4. Вычисление определителей.
5. Схема Жордана.
6. Схема без обратного хода.
§ 3. Метод квадратного корня
§ 4. Метод ортогонализации
§ 5. Метод сопряженных градиентов
§ 6. Метод разбиения на клетки
§ 7. Линейные операторы. Нормы операторов
1. Конечномерные линейные нормированные пространства.
2. Линейные операторы в конечномерном линейном нормированном пространстве и их связь с матрицами.
3. Сходимость последовательностей матриц и матричных рядов.

§ 8. Разновидности методов последовательных приближений
§ 9. Линейные полношаговые методы первого порядка
2. Метод Ричардсона.
3. Обращение матриц методом последовательных приближений.
§ 10. Линейные одношаговые методы первого порядка
2. Сходимость метода Зейделя.
3. Релаксационный метод.
§ 11. Метод скорейшего спуска
ГЛАВА 7. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ ВЫСШИХ СТЕПЕНЕЙ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ
§ 2. Отделение корней
2. Границы расположения корней алгебраического уравнения.
3. Число действительных корней алгебраического уравнения.
4. Отделение действительных корней алгебраического уравнения.
5. Отделение комплексных корней алгебраических уравнений.
§ 3. Метод Лобачевского решения алгебраических уравнений
2. Метод Лобачевского. Случай комплексных корней.
3. Метод Лобачевского. Случай близких или равных корней.
4. Погрешность метода Лобачевского.
5. Видоизменение Лемера метода Лобачевского.

§ 4. Итерационные методы решения алгебраических и трансцендентных уравнений
2. Простейшие итерационные методы: метод секущих и метод Ньютона.
3. Метод Чебышева построения итераций высших порядков.
4. Построение итераций высших порядков с помощью теоремы Кёнига.
5. Метод Эйткена построения итераций высших порядков.
6. Пример.
§ 5. Решение систем уравнений
2. Метод Ньютона.
3. Метод скорейшего спуска.
§ 6. Отыскание корней алгебраических уравнений методом выделения множителей
1. Метод Лина выделения множителей.
2. Метод Фридмана.
3. Метод Хичкока выделения квадратного множителя.
ГЛАВА 8. ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И СОБСТВЕННЫХ ВЕКТОРОВ МАТРИЦ
§ 2. Метод А. Н. Крылова
2. Отыскание собственных векторов матрицы.
§ 3. Метод Ланцоша
2. Отыскание собственных векторов.
§ 4. Метод Данилевского
1. Видоизменение метода Данилевского.
§ 5. Обзор других способов получения характеристического многочлена
§ 6. Определение границ собственных значений
§ 7.

Итерационные методы отыскания собственных значений и собственных векторов матриц
2. Отыскание других собственных значений и соответствующих им собственных векторов для симметрических матриц.
3. Отыскание собственных значений и собственных векторов несимметрических матриц, имеющих простую структуру.
4. Некоторые замечания об отыскании собственных значений и собственных векторов матриц общей структуры.
§ 8. Ускорение сходимости итерационных процессов при решении задач линейной алгебры
2. Метод М. К. Гавурина.
3. Метод Л. А. Люстерника.
4. «дельта квадрат»-процесс Эйткена.
5. Улучшение сходимости итерационных процессов для отыскания собственных значений матриц.
§ 9. Неустранимая погрешность при численном решении систем линейных алгебраических уравнений
ГЛАВА 9. ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
§ 2. Метод С. А. Чаплыгина
2. Способ Чаплыгина построения улучшенных приближений.
3. Второй способ построения улучшенных приближений.

4. Метод Чаплыгина приближенного решения линейных дифференциальных уравнений второго порядка.
§ 3. Метод малого параметра
§ 4. Метод Рунге — Кутта
2. Метод Рунге — Кутта решения систем дифференциальных уравнений первого порядка.
3. Метод Рунге-Кутта решения уравнений второго порядка.
§ 5. Разностные методы решения обыкновенных дифференциальных уравнений первого порядка
1. Некоторые экстраполяционные формулы для интегрирования дифференциальных уравнений первого порядка.
2. Примеры интерполяционных формул.
3. Метод неопределенных коэффициентов вывода разностных формул.
4. Метод Крылова отыскания начальных значений решения.
5. Примеры.
§ 6. Разностные методы решения обыкновенных дифференциальных уравнений высших порядков
§ 7. Оценка погрешности, сходимость и устойчивость разностных методов решения обыкновенных дифференциальных уравнений
2. Разностное уравнение для погрешности приближенного решения.
3. Оценки погрешности решений, получаемых по формулам Адамса.

4. Устойчивость разностных методов решения дифференциальных уравнений.
5. Оценка погрешности и сходимость устойчивых разностных методов решения дифференциальных уравнений.
§ 8. Решение краевых задач для обыкновенных дифференциальных уравнений методом конечных разностей
2. Метод конечных разностей решения краевых задач для нелинейных дифференциальных уравнений второго порядка.
§ 9. Метод прогонки
§ 10. Решение краевых задач для обыкновенных дифференциальных уравнений вариационными методами
1. Вариационные методы решения операторных уравнений в гильбертовом пространстве.
2. Метод Ритца решения вариационных задач.
3. Понятие о методе Галеркина.
ГЛАВА 10. ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ И ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ
§ 2. Метод сеток решения краевых задач для дифференциальных уравнений эллиптического типа
2. Аппроксимация дифференциальных уравнений разностными.
3. Аппроксимация граничных условий.
4.

Разрешимость разностных уравнений и способы их решения.
5. Оценка погрешности и сходимость метода сеток.
§ 3. Метод сеток решения линейных дифференциальных уравнений гиперболического типа
1. Метод сеток для решения задачи Коши.
2. Оценка погрешности и сходимость метода сеток для неоднородного волнового уравнения.
3. Метод сеток решения смешанной задачи.
4. Другие разностные схемы.
§ 4. Метод характеристик численного решения гиперболических систем квазилинейных дифференциальных уравнений в частных производных
2. Примеры.
3. Уравнения характеристик квазилинейного гиперболического дифференциального уравнения второго порядка.
4. Численное решение квазилинейной гиперболической системы двух дифференциальных уравнений первого порядка методом Массо.
5. Численное решение гиперболической системы трех квазилинейных дифференциальных уравнений первого порядка методом Массо.
6. Метод Массо численного решения квазилинейного гиперболического уравнения второго порядка.

7. Основные задачи, встречающиеся при исследовании плоского безвихревого сверхзвукового установившегося течения идеального газа.
§ 5. Метод сеток решения линейных дифференциальных уравнений параболического типа
2. Метод сеток для решения смешанных задач. Понятие устойчивости разностных схем.
§ 6. Метод прогонки решения краевых задач для уравнений в частных производных
2. Уравнение Пуассона.
§ 7. Сходимость и устойчивость разностных схем
2. Понятие корректности и устойчивости разностной схемы.
3. Связь сходимости с корректностью разностной схемы.
4. Некоторые приемы исследования устойчивости разностных схем.
5. Некоторые общие замечания.
§ 8. Метод прямых решения граничных задач для дифференциальных уравнений в частных производных
2. Метод прямых решения задачи Дирихле для уравнения Пуассона.
3. Метод прямых решения смешанной задачи для уравнения колебаний струны.
4. Метод прямых решения смешанной задачи для уравнения теплопроводности.

§ 9. Вариационные методы решения краевых задач для дифференциальных уравнений математической физики
2. Метод Ритца приближенного решения краевых задач для линейных дифференциальных уравнений в частных производных второго порядка эллиптического типа.
3. Некоторые другие вариационные методы.
4. Метод Ритца решения задачи о собственных значениях.
5. Метод Галеркина решения краевых задач.
§ 10. Приближенные методы решения интегральных уравнений
2. Решение интегральных уравнений Фредгольма второго рода методом замены ядра на вырожденное.
3. Метод моментов.
4. Метод наименьших квадратов.
5. Метод последовательных приближений.
6. Приближенное решение уравнений Вольтерра.

Алгебраические методы решения систем

Цели обучения

Использовать метод подстановки
- Решить систему уравнений методом подстановки.
- Распознавать системы уравнений, которые не имеют решений или имеют бесконечное число решений
Использовать метод исключения без умножения
- Решите систему уравнений, когда для исключения переменной не требуется умножения
Использовать метод исключения с умножением
- Использование умножения в сочетании с методом исключения для решения системы линейных уравнений
- Распознать, когда решение системы линейных уравнений подразумевает существование бесконечного числа решений

Решение системы уравнений методом подстановки

В последних парах разделов мы проверили, что упорядоченные пары являются решениями систем, и использовали графики для классификации количества решений системы двух линейных уравнений. Что, если нам не задана точка пересечения или она не очевидна из графика? Можем ли мы все же найти решение системы? Конечно можно, используя алгебру!

В этом разделе мы изучим метод подстановки для нахождения решения системы линейных уравнений с двумя переменными. В этом курсе мы использовали подстановку по-разному, например, когда использовали формулы площади треугольника и простых процентов. Мы подставили значения, которые мы знали, в формулу для решения на значения, которые мы не знали. Идея аналогична применительно к решению систем, в этом процессе всего несколько разных шагов. Вы сначала определите одну переменную, а затем подставите это выражение в другое уравнение. Давайте начнем с примера, чтобы понять, что это значит.

Вы можете заменить значение переменной, даже если это выражение. Вот пример.

Помните, что решение системы уравнений должно быть решением каждого уравнения в системе. Упорядоченная пара [латекс](4,−1)[/латекс] работает для обоих уравнений, поэтому вы знаете, что она также является решением системы.

Давайте рассмотрим еще один пример, замена которого связана с распределительным свойством.

В приведенных выше примерах одно из уравнений уже было дано нам в терминах переменной х или и . Это позволило нам быстро подставить это значение в другое уравнение и найти одно из неизвестных.

Иногда вам может потребоваться переписать одно из уравнений в терминах одной из переменных, прежде чем вы сможете произвести замену. В приведенном ниже примере вам сначала нужно изолировать одну из переменных, прежде чем вы сможете подставить ее в другое уравнение.

В следующем видео вам будет представлен пример решения системы двух уравнений методом подстановки.

Если бы вы выбрали другое уравнение для начала в предыдущем примере, вы все равно смогли бы найти такое же решение. На самом деле это вопрос предпочтений, потому что иногда нахождение переменной приводит к необходимости работать с дробями. Когда вы станете более опытными в алгебре, вы сможете предвидеть, какой выбор приведет к более желаемым результатам.

Распознавать системы уравнений, которые не имеют решений или имеют бесконечное число решений

Когда мы изучили методы решения линейных уравнений с одной переменной, то обнаружили, что одни уравнения не имеют решений, а другие имеют бесконечное число решений. Мы снова увидели это поведение, когда начали описывать решения систем уравнений с двумя переменными.

Вспомните этот пример из Модуля 1 для решения линейных уравнений с одной переменной:

Решите для x . [латекс]12+2x–8=7x+5–5x[/латекс]

[латекс] \displaystyle \begin{array}{l}12+2x-8=7x+5-5x\\\,\, \,\,\,\,\,\,\,\,\,\,\,\,2x+4=2x+5\end{массив}[/латекс]

[латекс]\begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,\,2x+4=2x+5\\\,\, \,\,\,\,\,\,\подчеркнуть{-2x\,\,\,\,\,\,\,\,\,\,-2x\,\,\,\,\,\ ,\,\,}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \,\,\,4= \,5\end{array}[/latex]

Это ложное утверждение означает, что нет решений этого уравнения. Точно так же вы можете увидеть подобный результат, когда используете метод подстановки для поиска решения системы линейных уравнений с двумя переменными. В следующем примере вы увидите пример системы двух уравнений, не имеющей решения.

Вы получаете ложное утверждение [латекс]−8=4[/латекс]. Что это значит? График этой системы проливает некоторый свет на происходящее.

Прямые параллельны, они никогда не пересекаются, и у этой системы линейных уравнений нет решения. Обратите внимание, что результат [латекс]−8=4[/латекс] — это , а не решение. Это просто ложное утверждение, и оно указывает на то, что нет решения .

Мы также видели линейные уравнения с одной переменной и системы уравнений с двумя переменными, которые имеют бесконечное число решений. В следующем примере вы увидите, что происходит, когда вы применяете метод подстановки к системе с бесконечным числом решений.

На этот раз вы получите верное утверждение: [латекс]−4,5x=−4,5x[/латекс]. Но что означает этот тип ответа? Опять же, графики могут помочь вам разобраться в этой системе.

Эта система состоит из двух уравнений, представляющих одну и ту же прямую; две линии коллинеарны. Каждая точка на линии будет решением системы, поэтому метод подстановки дает истинное утверждение. В этом случае существует бесконечное множество решений.

В следующем видео вы увидите пример решения системы, которая имеет бесконечное количество решений.

В следующем видео вы увидите пример решения системы уравнений, не имеющей решений.

Решение системы уравнений методом исключения

Метод исключения для решения систем линейных уравнений использует свойство сложения равенства. Вы можете добавить одно и то же значение к каждой стороне уравнения, чтобы исключить один из переменных членов. В этом методе вам может понадобиться или не понадобиться сначала умножать члены в одном уравнении на число. Сначала мы рассмотрим примеры, в которых умножение не требуется для использования метода исключения. В следующем разделе вы увидите примеры использования умножения после того, как познакомитесь с идеей метода исключения.

С помощью этого метода легче показать, чем рассказать, поэтому давайте сразу перейдем к некоторым примерам.

Если сложить вместе два уравнения,

[латекс]x–y=−6[/латекс] и [латекс]х+у=8[/латекс], посмотрите, что получится.

[латекс] \displaystyle \begin{array}{l}\,\,\,\,\,x-y=\,-6\\\underline{+\,x+y=\,\,\,8 }\\\,2x+0\,=\,\,\,\,2\end{array}[/latex]

Вы исключили член y , и это уравнение можно решить, используя методы для решение уравнений с одной переменной.

Давайте посмотрим, как решается эта система методом исключения.

К сожалению, не все системы работают так легко. Как насчет такой системы, как [латекс]2x+y=12[/латекс] и [латекс]−3x+y=2[/латекс]. Если вы сложите эти два уравнения вместе, никакие переменные не будут устранены.

[латекс] \displaystyle \begin{array}{l}\,\,\,\,2x+y=12\\\underline{-3x+y=\,\,\,2}\\-x +2y=14\end{array}[/latex]

Но вы хотите удалить переменную. Итак, давайте добавим противоположное одному из уравнений к другому уравнению. Это означает, что умножьте каждый член одного из уравнений на -1, чтобы знак каждого члена был противоположным.

[латекс]\begin{array}{l}\,\,\,\,2x+\,\,y\,=12\rightarrow2x+y=12\rightarrow2x+y=12\\−3x+\,\ ,y\,=2\rightarrow-\left(-3x+y\right)=-(2)\rightarrow3x-y=-2\\\,\,\,\,5x+0y=10\end{массив }[/latex]

Вы удалили переменную y , и теперь проблема может быть решена.

В следующем видео описывается аналогичная задача, в которой можно исключить одну переменную, сложив вместе два уравнения.

Внимание! Когда вы добавляете противоположность одного полного уравнения к другому, обязательно меняйте знак КАЖДОГО члена в обеих частях уравнения. Это очень распространенная ошибка.

Ниже приведены еще два примера, показывающие, как решать линейные системы уравнений с помощью исключения.

Проверьте этот последний пример — подставьте (2, 3) в оба уравнения. Вы получаете два верных утверждения: 14=14 и 16=16!

Обратите внимание, что вы могли бы использовать противоположное первому уравнению вместо второго уравнения и получить тот же результат.

Распознавание систем, не имеющих решений или имеющих бесконечное число решений

Как и в случае с методом подстановки, метод исключения иногда устраняет обе v переменных, и вы получите либо истинное утверждение, либо ложное утверждение. Напомним, что ложное утверждение означает отсутствие решения.

Давайте рассмотрим пример.

Графическое изображение этих линий показывает, что они являются параллельными линиями и поэтому не имеют общих точек, что подтверждает отсутствие решения.

Если обе переменные исключены, а у вас осталось истинное утверждение, это означает, что существует бесконечное число упорядоченных пар, удовлетворяющих обоим уравнениям. По сути, уравнения представляют собой одну и ту же строку.

Графики этих двух уравнений помогут проиллюстрировать происходящее.

В следующем видео методом исключения решается система уравнений, не имеющая решений.

Решите систему уравнений, когда умножение необходимо для исключения переменной

Много раз добавление уравнений или добавление противоположного одному из уравнений не приведет к исключению переменной. Посмотрите на систему ниже.

[латекс]\begin{array}{r}3x+4y=52\\5x+y=30\end{array}[/latex]

Если добавить приведенные выше уравнения или добавить противоположное одному из уравнения, вы получите уравнение, которое по-прежнему имеет две переменные. Итак, давайте теперь сначала воспользуемся свойством умножения равенства. Вы можете умножить обе части одного из уравнений на число, которое позволит исключить ту же переменную в другом уравнении.

Мы делаем это с помощью умножения. Обратите внимание, что первое уравнение содержит член 4 y , а второе уравнение содержит член y . Если вы умножите второе уравнение на -4, то при сложении обоих уравнений переменные y дадут в сумме 0.

Следующий пример проведет вас через все шаги, чтобы найти решение этой системы.

Внимание! Когда вы используете умножение для исключения переменной, вы должны умножать КАЖДЫЙ член в уравнении на выбранное вами число. Распространенной ошибкой является забывание умножить каждое слагаемое.

Есть и другие способы решения этой системы. Вместо того, чтобы умножать одно уравнение, чтобы исключить переменную при добавлении уравнений, вы могли бы умножить обоих уравнений на разные числа.

На этот раз удалим переменную x . Умножьте уравнение A на 5 и уравнение B на [латекс]-3[/латекс].

Эти уравнения были умножены на 5 и [латекс]-3[/латекс] соответственно, потому что это дало вам члены, которые в сумме давали бы 0. Обязательно умножьте все члены уравнения.

В следующем видео вы увидите пример использования метода исключения для решения системы уравнений.

Можно использовать метод исключения с умножением и получить результат, указывающий на отсутствие решений или бесконечное множество решений, как и в случае с другими изученными нами методами поиска решений систем. В следующем примере вы увидите систему, имеющую бесконечно много решений.

В следующем видео метод исключения используется для решения системы уравнений. Обратите внимание, что сначала нужно умножить одно из уравнений на отрицательное. Кроме того, эта система имеет бесконечное число решений.

Резюме

Метод подстановки является одним из способов решения систем уравнений. Чтобы использовать метод подстановки, используйте одно уравнение, чтобы найти выражение для одной из переменных через другую переменную. Затем подставьте это выражение вместо этой переменной во второе уравнение. Затем вы можете решить это уравнение, так как теперь оно будет иметь только одну переменную. Решение с использованием метода подстановки даст один из трех результатов: одно значение для каждой переменной в системе (указывающее одно решение), неверное утверждение (указывающее отсутствие решений) или истинное утверждение (указывающее бесконечное количество решений).

Объединение уравнений — мощный инструмент для решения системы уравнений. Сложение или вычитание двух уравнений для исключения общей переменной называется методом исключения (или добавления). Как только одна переменная исключена, становится намного проще найти другую.

Умножение можно использовать для сопоставления членов в уравнениях, прежде чем они будут объединены, чтобы помочь найти решение системы. При использовании метода умножения важно умножать все члены с обеих сторон уравнения, а не только один член, который вы пытаетесь исключить.

Решение линейных уравнений – 4 метода, пошаговые решения, примеры

Решение линейных уравнений означает нахождение значений переменных, заданных в линейных уравнениях. Линейное уравнение представляет собой комбинацию алгебраического выражения и символа равенства (=). Оно имеет степень 1 или его можно назвать уравнением первой степени. Например, x + y = 4 — это линейное уравнение. Иногда нам может понадобиться найти значения переменных, участвующих в линейном уравнении. Когда нам дано два или более таких линейных уравнения, мы можем найти значения каждой переменной, решая линейные уравнения. Существует несколько методов решения линейных уравнений. Остановимся подробно на каждом из этих методов.

1.	Решение линейных уравнений с одной переменной
2.	Решение линейных уравнений методом подстановки
3.	Решение линейных уравнений методом исключения
4.	Графический метод решения линейных уравнений
5.	Метод перекрестного умножения
6.	Часто задаваемые вопросы о решении линейных уравнений

Решение линейных уравнений с одной переменной

Линейное уравнение с одной переменной является уравнением первой степени и имеет только один переменный член. Он имеет вид «ax+b = 0», где «a» — ненулевое число, а «x» — переменная. Решая линейные уравнения с одной переменной, мы получаем только одно решение для данной переменной. Примером этого является 3x – 6 = 0. Переменная «x» имеет только одно решение, которое рассчитывается как 9.0262 3x – 6 = 0
3x = 6
х = 6/3
x = 2

Для решения линейных уравнений с одной переменной упростите уравнение так, чтобы все переменные члены переносились в одну сторону, а постоянное значение — в другую. Если есть какие-либо дробные члены, найдите LCM (наименьшее общее кратное) и упростите их так, чтобы переменные члены были с одной стороны, а постоянные члены — с другой. Давайте разработаем небольшой пример, чтобы понять это.

4x + 8 = 8x – 10. Чтобы найти значение «x», давайте упростим и перенесем члены «x» в одну сторону, а постоянные члены — в другую.

4x – 8x = -10 – 8
-4x = -18
4x = 18
х = 18/4
При упрощении получаем x = 9/2.

Решение линейных уравнений методом подстановки

Метод подстановки — один из методов решения линейных уравнений. В методе подстановки мы перестраиваем уравнение таким образом, что одно из значений подставляется во второе уравнение. Теперь, когда у нас осталось уравнение с одной переменной, мы можем решить его и найти значение этой переменной. В двух заданных уравнениях можно взять любое уравнение и найти значение переменной и подставить в другое уравнение. Для решения линейных уравнений методом подстановки выполните шаги, указанные ниже. Поясним это на примере решения следующей системы линейных уравнений.

х + у = 6 ————–(1)
2x + 4y = 20 ———–(2)

Шаг 1: Найдите значение одной из переменных с помощью любого из уравнений. В этом случае найдем значение «х» из уравнения (1).
х + у = 6 ———(1)
x = 6 – y

Шаг 2: Подставьте значение переменной, найденное на шаге 1, во второе линейное уравнение. Теперь давайте подставим значение «x» во второе уравнение 2x + 4y = 20,9.0031

х = 6 – у
Подставляя значение ‘x’ в 2x + 4y = 20, мы получаем

2(6 – y) + 4y = 20
12 – 2г + 4г = 20
12 + 2г = 20
2г = 20 – 12
2г = 8
у = 8/2
y = 4

Шаг 3: Теперь подставьте значение ‘y’ в уравнение (1) или (2). Подставим значение ‘y’ в уравнение (1).

х + у = 6
х + 4 = 6
х = 6 – 4
х = 2

Следовательно, методом подстановки решаются линейные уравнения, и значение x равно 2, а y равно 4.

Решение линейных уравнений методом исключения

Метод исключения — это еще один способ решения системы линейных уравнений. Здесь мы пытаемся умножить либо переменный термин «x», либо переменный термин «y» на постоянное значение, так что либо переменные члены «x», либо переменные члены «y» компенсируются и дают нам значение другая переменная. Давайте разберемся с этапами решения линейных уравнений методом исключения. Рассмотрим данные линейные уравнения:

2х + у = 11 ———– (1)
x + 3y = 18 ———- (2)

Шаг 1: Проверить, расположены ли термины таким образом, чтобы за термином «x» следовал термин «y» и знак равенства, а после знака равенства должен стоять постоянный член. Данный набор линейных уравнений уже устроен правильным образом: ax+by=c или ax+by-c=0.

Шаг 2: Следующим шагом является умножение одного или обоих уравнений на постоянное значение таким образом, чтобы сокращались либо члены «x», либо члены «y», что помогло бы нам найти значение другая переменная. Теперь в уравнении (2) давайте умножим каждый член на число 2, чтобы сделать коэффициенты x одинаковыми в обоих уравнениях.

x + 3y = 18 ———- (2)

Умножая все члены уравнения (2) на 2, получаем

2(x) + 2(3y) = 2 (18). Теперь уравнение (2) принимает вид

2x + 6y = 36 ———–(2)

Шаг 3: Следующим шагом является упрощение этих двух уравнений путем сложения или вычитания их ( в зависимости от того, какая операция требуется для отмены x терминов). Теперь, вычитая два уравнения, мы можем сократить члены «x» в обоих уравнениях.

Следовательно, у = 5,

Шаг 4: Используя значение, полученное на шаге 3, найдите значение другой переменной, подставив значение в любое из уравнений. Подставим значение ‘y’ в уравнение (1). Получаем,

2х+у=11
2х + 5 = 11
2х = 11 – 5
2х = 6
х = 6/2
x = 3

Следовательно, решая линейные уравнения, мы получаем значение x = 3 и y = 5.

Графический метод решения линейных уравнений

Другой метод решения линейных уравнений — использование графика. Когда нам дана система линейных уравнений, мы графически рисуем оба уравнения, находя значения «y» для разных значений «x» в системе координат. Как только это будет сделано, мы найдем точку пересечения этих двух линий. Значения (x, y) в точке пересечения дают решение этих линейных уравнений. Возьмем два линейных уравнения и решим их графическим методом.

х + у = 8 ——-(1)

y = x + 2 ——–(2)

Возьмем некоторые значения для ‘x’ и найдем значения ‘y’ для уравнения x + y = 8. Это также может быть переписывается как y = 8 – x.

х	0	1	2	3	4
у	8	7	6	5	4

Возьмем некоторые значения для «x» и найдем значения для «y» в уравнении y = x + 2.

x	0	1	2	3	4
у	2	3	4	5	6

Нанеся эти точки на координатную плоскость, получим вот такой график.

Теперь мы найдем точку пересечения этих линий, чтобы найти значения «x» и «y». Две прямые пересекаются в точке (3,5). Следовательно, x = 3 и y = 5 при использовании графического метода решения линейных уравнений.

Этот метод также используется для поиска оптимального решения задач линейного программирования. Рассмотрим еще один метод решения линейных уравнений — метод перекрестного умножения.

Метод перекрестного умножения для решения линейных уравнений

Метод перекрестного умножения позволяет нам решать линейные уравнения, выбирая коэффициенты всех членов («x», «y» и постоянных членов) в формате, показанном ниже, и применяя формулу для нахождения значений «x». и «у».

Темы, связанные с решением линейных уравнений

Просмотрите данные статьи, связанные с решением линейных уравнений.

Линейные уравнения
Применение линейных уравнений
Линейные уравнения с двумя переменными
Линейные уравнения и полуплоскости
Линейные уравнения и неравенства с одной переменной

Часто задаваемые вопросы о решении линейных уравнений

Что означает решение линейных уравнений?

Уравнение, имеющее степень 1, называется линейным уравнением. У нас могут быть линейные уравнения с одной переменной, линейные уравнения с двумя переменными, линейные уравнения с тремя переменными и многое другое в зависимости от количества переменных в нем. Решение линейных уравнений означает нахождение значений всех переменных, присутствующих в уравнении. Это можно сделать методом подстановки, методом исключения, графическим методом и методом перекрестного умножения. Все эти методы представляют собой разные способы нахождения значений переменных.

Как использовать метод подстановки для решения линейных уравнений?

Метод подстановки для решения уравнений гласит, что для данной системы линейных уравнений нужно найти значение «x» или «y» из любого из заданных уравнений, а затем подставить найденное значение «x» или «y» в другом уравнении, чтобы можно было найти другое неизвестное значение.

Как использовать метод исключения для решения линейных уравнений?

В методе исключения для решения линейных уравнений мы умножаем константу или число на одно уравнение или на оба уравнения так, чтобы члены «x» или члены «y» были одинаковыми. Затем мы сокращаем один и тот же член в обоих уравнениях, добавляя или вычитая их, и находим значение одной переменной (либо «x», либо «y»). Найдя одно из значений, подставляем значение в одно из уравнений и находим другое неизвестное значение.

Что такое графический метод решения линейных уравнений?

В графическом методе решения линейных уравнений мы находим значение ‘y’ из заданных уравнений, подставляя значения x как 0, 1, 2, 3 и т. д., и строим график в системе координат для линии для различных значений ‘x’ для обеих систем линейных уравнений. Мы увидим, что эти две прямые пересекаются в одной точке. Эта точка является решением данной системы линейных уравнений. Если между двумя прямыми нет точки пересечения, то мы рассматриваем их как параллельные прямые, а если мы обнаружили, что обе прямые лежат друг на друге, то они называются совпадающими прямыми и имеют бесконечно много решений.

Какие этапы решения линейных уравнений с одной переменной?

Линейное уравнение — это уравнение степени 1. Чтобы решить линейное уравнение с одной переменной, мы подносим переменную к одной стороне, а постоянное значение — к другой. Затем к обеим частям уравнения можно добавить, вычесть, умножить или разделить ненулевое число. Например, линейное уравнение с одной переменной будет иметь вид «х – 4 = 2». Чтобы найти значение «x», мы добавляем постоянное значение «4» к обеим частям уравнения. Следовательно, значение ‘x = 6’.