ГДЗ конспекты по физике 7 класс Задание: Сила явления тяготения Сила тяжести
Изображения обложек учебников приведены на страницах данного сайта исключительно в качестве иллюстративного материала (ст. 1274 п. 1 части четвертой Гражданского кодекса Российской Федерации)
Вид УМК: конспекты
Серия: Краткое содержание параграфов учебника для устного ответа
На данной странице представлено детальное решение задания Сила явления тяготения. Сила тяжести по физике для учеников 7 классa автор(ы)
Сила явления тяготения. Сила тяжести
Сила – мера взаимодействия тел.
При взаимодействии изменяются скорости тел.
Деформация – это любое изменение формы и размера тела.
F – сила
Результат действия силы зависит от числового значения, направления и точки приложения.
[F] – Н (ньютон)
1 кН = 1000 Н
1 МН = 1000000 Н
1 мН = 0,01 Н
1 мкН = 0,000001 Н
Сила тяжести – это сила, с которой Земля притягивает к себе другие тела.
Закон всемирного тяготения
Два тела притягиваются друг к другу с силой прямо пропорциональной массе каждого из них и обратно пропорциональной квадрату расстояния между ними.
Сила тяжести всегда направлена вертикально вниз из центра тяжести тела.
Свободное падение тела – движение тела без начальной скорости, только под действием силы тяжести.
Ускорение свободного падения показывает, как меняется скорость тела при свободном падении.
g – ускорение свободного падения
g = 9,8 \(\frac{Н}{кг}\) (= 10 \(\frac{Н}{кг}\))
Fт. = mg – сила тяжести
m – масса тела, кг
g – ускорение свободного падения, \(\frac{Н}{кг}\)
[Fт.] = Н
Вес тела – сила, с которой тело давит на опору или растягивает подвес.
Р – вес тела
Вес равен силе тяжести, если тело движется равномерно или покоится.
Р = Fт.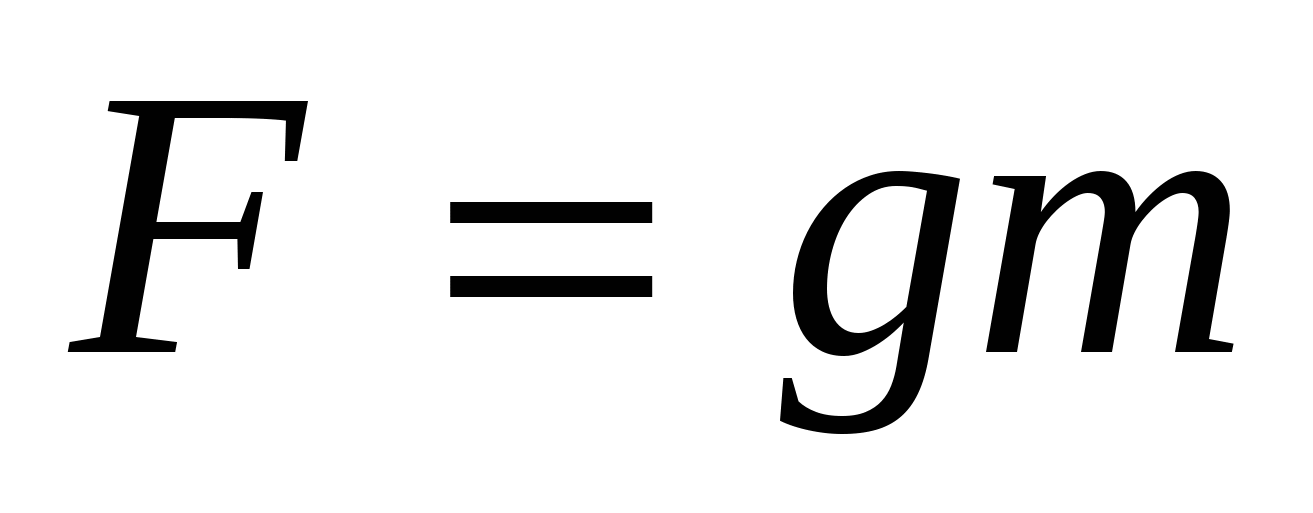
P = mg
Рис. 1. ГДЗ конспекты по физике 7 класс Задание: Сила явления тяготения Сила тяжести
Add
Новыe решебники
Презентация по физике по теме “Физика. Сила”
Презентация ВЕСЕЛОВОЙ ДАРЬИ ученицы 7д класса Учитель Веселова Эльмира Александровна
Силы, которые существуют в природе:
Сила тяжести
Сила упругости
Сила трения
Вес тела
Сила тяжести
Пусть тело падает с некоторой высоты
притягивает к себе тела .
Сила тяжести – сила с которой Земля
F m = mg
F m –
g – ускорение свободного падения
F тяж = 1Н(ньютон)
g = 9,8 м/с2
Сила тяжести всегда направлена к центру плане Земля .
Притягивает мальчика и мяч с силами, направленными вниз, то есть к центру планеты.
Сила упругости
Силой упругости называют силу, которая возникает в теле при изменении его формы или размеров. Это происходит, если тело сжимают, растягивают, изгибают или скручивают.
Сила упругости
Причины возникновения сил упругости – является взаимодействие молекул тела.
На малых расстояниях молекулы отталкиваются , а на больших – притягиваются .
В не деформированном теле молекулы находятся как раз на таком расстоянии, при котором силы притяжения , либо силы отталкивания уравновешиваются.
Когда мы растягиваем или сжимаем тело, расстояния между молекулами изменяются, поэтому начинают преобладать либо силы притяжения

В результате и возникает сила упругости , которая всегда направлена так, чтобы уменьшить величину деформации тела
Закон Гука
Сила упругости по модулю при упругой деформации прямо пропорциональна удлинению тела (пружины)
Закон Гука
- Для каждой ситуации В упругой деформации Все силы, как и водится, В пропорции находятся К увеличенью длин. А если при решении У длин есть уменьшение, Закон и тут закон:
- Пропорции упрямые –
Сила трения
Сила трения обозначается Fтр . Направлена сила трения всегда противоположно движению тела.
ВЕС ТЕЛА
Вес тела – это сила, с которой тело вследствие притяжения к Земле действует на опору или подвес.
Физика Подготовительные курсы
Тема 1. Механика (кинематика, динамика, статика, законы сохранения в механике, механические колебания и волны).1.1. Равномерное прямолинейное движение, равноускоренное прямолинейное движение, движение по окружности.
1.2. Законы Ньютона, закон всемирного тяготения, закон Гука, сила трения.
1.3. Закон сохранения импульса, кинетическая и потенциальные энергии, работа и мощность силы, закон сохранения механической энергии.
1.4. Условие равновесия твердого тела, закон Паскаля, сила Архимеда, математический и пружинный маятники, механические волны, звук.
1.5. Механика (объяснение явлений; интерпретация результатов, представленных в виде таблицы или графиков).
1.6. Механика (изменение величин в процессах).
1.7. Механика (установление соответствия между графиками и физическими величинами, между физическими величинами и формулами).
Тема 2. Молекулярная физика (молекулярно-кинетическая теория, термодинамика).
2.1. Связь между давлением и средней кинетической энергией, абсолютная температура, связь температуры со средней кинетической энергией, уравнение Менделеева – Клапейрона, изопроцессы.
2.2. Работа в термодинамике, первый закон термодинамики, КПД тепловой машины.
2.3. Относительная влажность, количество теплоты.
2.4. МКТ, термодинамика (объяснение явлений; интерпретация результатов опытов, представленных в виде таблицы или графиков).
2.5. МКТ, термодинамика (изменение физических величин в процессах, установление соответствия между графиками и физическими величинами и формулами).
Тема 3. Электродинамика и основы СТО (электрическое поле, постоянный ток, магнитное поле, электромагнитная индукция, электромагнитные колебания и волны , оптика, основы СТО).
3.1. Принцип супперпозиции электрических полей, магнитное поле проводника с током, сила Лоренца, правило Ленца (определение направления).
3.2. Закон сохранения электрического заряда, закон Кулона, конденсатор, сила тока, закон Ома для участка цепи, последовательное и параллельное соединение проводников, работа и мощность тока, Закон Джоуля-Ленца.
3.3. Поток вектора магнитной индукции, закон электромагнитной индукции Фарадея, индуктивность, энергия магнитного поля катушки с током, колебательный контур, законы отражения, преломления, ход лучей в линзе.
3.4. Электродинамика (объяснение явлений; интерпретация результатов опытов, представленных в виде таблицы или графиков).
3.5. Электродинамика (установление соответствия между графиками и физическими величинами, между физическими величинами и формулами).
Тема 4. Квантовая физика и элементы астрофизики (корпускулярно- волновой дуализм, физика атома, физика атомного ядра, элементы астрофизики).
4.1. Планетарная модель атома. Нуклонная модель ядра. Ядерные реакции.
4.2. Фотоны, линейчатые спектры, закон радиоактивного распада.
4.3. Квантовая физика (изменение физических величин в процессах; установление соответствия между графиками и физическими величинами, между физическими величинами и формулами).
Тема 5. Механика – квантовая физика (методы научного познания).
Решение задач по всем темам. Промежуточное и итоговое тестирование.
Урок физики по теме “Закон Гука – решение задач”
В 1635 году родился Роберт Гук, английский физик, член Лондонского королевского общества, его секретарь. В 1660 году открыл закон упругости для твердых тел (закон Гука).
В курсе 7 класса одной из сложных тем является условие равновесия груза на
пружине: kx=mg, но предварительно для более эффективного понимания этой темы
проводится эксперимент по закону Гука, а затем комментируются формулы: Fу=kx и
Fт=mg .
Задачи на данную тему
1) Какова жесткость пружины , если груз массой 10 кг растягивает пружину на 10 см.
: 1000Н/мОтвет
2) Используя полученный Ответет из предыдущей задачи определите какой груз нужно подвесить к пружине , чтобы растянуть ее на 20 см.
: 20 кг.Ответ
3) Груз массой 3 кг растягивает пружину на 5 см . Каким должен быть груз , который растянет пружину на 8см.
: 4,8 кг.Ответ
Фрагмент урока
Приложение 1
III. Изучение нового материала:
Вам уже известно, что на все тела, находящиеся на Земле, действует сила тяжести. В результате действия силы тяжести на Землю падает подброшенный камень, выпущенная из лука стрела, снежинки.
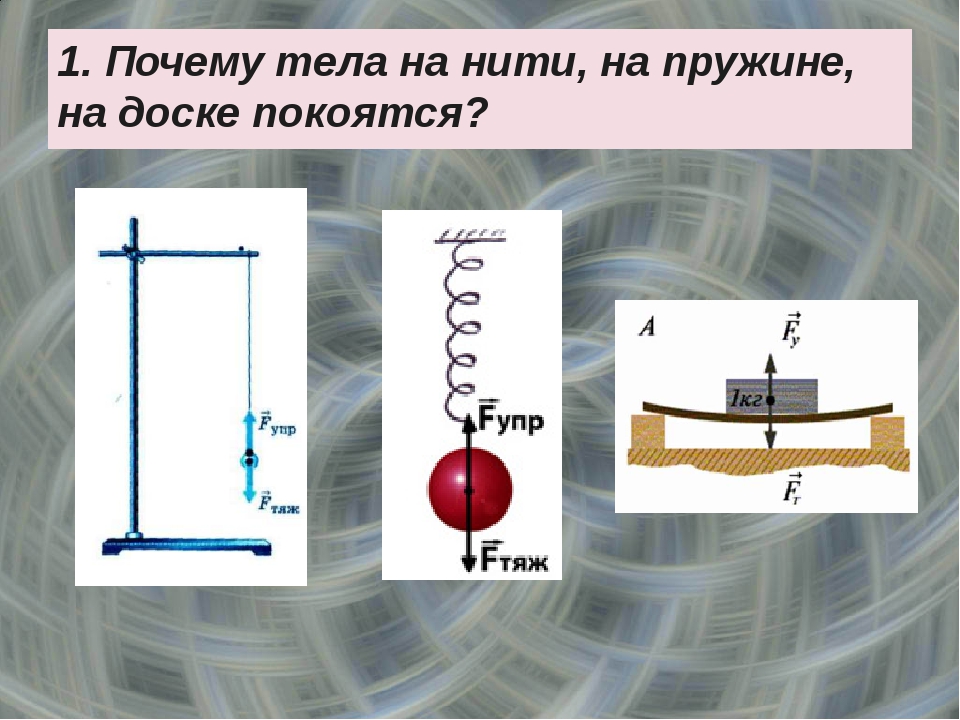
Почему же покоятся тела, подвешенные на нити или лежащие на опоре?
По-видимому, сила тяжести уравновешивается какой-то другой силой. Что это за
сила и как она возникает.
Что это за
сила и как она возникает.
Проведем опыт: на упругий подвес поместим гирю. Под действием силы тяжести гиря начнет двигаться вниз, и подвес деформируется – его длина увеличится. При этом возникнет сила, с которой подвес действует на тело. Когда эта сила уравновесит силу тяжести, тело остановится. Из этого опыта можно сделать вывод, что на гирю, кроме силы тяжести, направленной вертикально вниз, действует другая сила. Эта сила направлена вертикально вверх. Она и уравновешивает силу тяжести. Эту силу называют
Ребята, запишите, пожалуйста, в тетрадях определение силы упругости: Сила, возникающая в теле в результате его деформации, и стремящаяся вернуть тело в исходное положение называется силой упругости.
– Проведем эксперимент: линейка и пружина с указателем закреплены на
штативе.
Вопросы учащимся:
– Какую линию получили на графике?
– Как называется такая зависимость в математике?
– Что происходит с силой упругости, если длина пружины увеличивается? Уменьшается?
– Как изменится сила упругости, если длина пружины увеличится в 2 раза? Посмотрим на график.
– Найдем отношение силы упругости к удлинению пружины (первый результат считаю я, остальные вы – по вариантам):
∆F1/∆l1= ∆F2/∆l2=
∆F3/∆l3= ∆F4/∆l4=
– Какой вывод можно сделать об отношении силы упругости к удлинению пружины?
– Мы с вами получили закон, открытый английским физиком Робертом Гуком в
1660г.
– Закон Гука: Fупр = k∆l – сила упругости прямо пропорциональна величине деформации. Обсудим формулу закона и попытаемся определить, какие величины в нее входят (обсуждение формулы, записи величин и единиц их измерения).
Теперь мы можем написать условие равновесия груза на пружине : mg = k∆l , используем это условие при решении задачи №1:
1) Какова жесткость пружины , если груз массой 10 кг растягивает пружину на 0,1 м.
Дано: М=10кг
L=0,1м
k-?Решение: mg = k∆l
mg : ∆l = k
После подстановки получаем ответ: 1000Н/м
Теперь зная жесткость пружины, разберем ситуацию каким образом мы можем узнать массу тела, рассмотрим задачу №2:
2) Используя полученный ответ из предыдущей задачи определите какой груз
нужно подвесить к пружине, чтобы растянуть ее на 20 см.
Дано: k =1000Н/м
L=0,2м
М – ?Решение: mg = k ∆l
m = k ∆l:g
После подстановки получаем ответ: 20 кг
А теперь используем наши умения и навыки для решения более сложной задачи:
3) Груз массой 3 кг растягивает пружину на 5 см. Каким должен быть груз, который растянет пружину на 8см.
Дано: М1=3кг
L1=0,05м
L2=0,08м
М2=?Решение: М1 g = k L1
М1 g : L1 = k =600 Н/м
Нашли жесткость, теперь можем написать условие равновесия груза на пружине и найти массу груза:
М2 g = k∆l , М2=k L2: g=4,8 кг,
Ответ: 4,8 кг
|
Вес
ВесВсе физики согласны с тем, что:
Вес и масса , а не синоним.
Вес – это сила.
Вес предмета зависит от его местонахождения – вещи могут весить в разных местах по разному.
Вес НЕ является массой
Первое, что нужно понять о весе, это то, что вес не то же самое, что и масса, хотя термины используются как синонимы в повседневной жизни.Масса измеряет инерцию – это свойство объекта. Вес – это сила – что-то что происходит с объектом.
Вес – это сила, но КАКАЯ сила?
Все физики и инженеры согласны с тем, что вес является силой, но
существуют значительные разногласия и путаница в отношении того, какая сила
вес есть – в разных учебниках написано разное, а некоторые
учебники говорят разные вещи в разных местах.В основном мнение
делится на два лагеря. Для некоторых людей «вес — это сила
гравитация», а для других «вес — это то, что показывают весы».
думаю, что эти два утверждения эквивалентны, но это не так. Там
являются преимуществами и (к сожалению) недостатками с любой точки зрения
Посмотреть.
Для некоторых людей «вес — это сила
гравитация», а для других «вес — это то, что показывают весы».
думаю, что эти два утверждения эквивалентны, но это не так. Там
являются преимуществами и (к сожалению) недостатками с любой точки зрения
Посмотреть.
Вес как гравитационная сила
Наш текст, среди прочего, говорит:
Вес: сила тяжести на тело. 1
Преимущества:
- Вес всегда легко рассчитать. Вес предмета w = мг , где m — масса объекта, а g — ускорение свободного падения.
Недостатки:
Это не интуитивное определение веса для непрофессионалов. Ты не чувствует силы тяжести. Вы чувствуете, как пол подталкивает вы, а не нисходящее притяжение Земли.Вы не чувствуете тяги к Земля, даже когда вы прыгаете в воздух.
Вес соответствует показаниям весов:
Существует стандартное определение веса, данное Международная организация по стандартизации (ISO), которая говорит:
Вес тела в указанной ссылке система есть та сила, которая при приложении к телу давала бы это ускорение, равное местному ускорению свободного падения в эта система отсчета.– ISO 31-3 «Количества и единицы. Часть 3, Механика”, 1992 2
Можно ли это упростить без потери точности? Да! оказывается что это определение веса эквивалентно высказыванию:
Вес — это то, что показывают весы. 3
, что эквивалентно фразе:
Вес объекта равен силе, необходимой для поддержите это. 4
Преимущества:
Сначала кажется, что это гораздо более естественный, практичный и более удобный способ посмотреть на вес, чем напрямую связывать вес с сила тяжести.(«Что показывают весы» и «сила гравитация” не всегда эквивалентны – см. Проблема с лифтом подробнее…) Это определение – вес что показывают весы – также вполне естественно согласуется с идеей «невесомость».
Недостатки:
Чтобы эффективно использовать это определение в приложениях
требует довольно сложного понимания законов Ньютона –
в частности, третий закон Ньютона, который в большинстве начинающих физиков
студенты обычно не имеют. (Без обид…)
(Без обид…)
Что мы будем делать:
В этом курсе мы будем следовать указаниям текста и скажем, что вес объекта равен его массе, умноженной на g.
Каталожные номера:
1 Хьюитт, Концептуальная физика , стр. 32
2 Вес – официальное определение , Марио Иона, Учитель физики, Том 37, с.238 (апрель 1999 г.)
3 адаптировано из Вес – точный, актуальный, Определение непрофессионала , Рой Бишоп, Учитель физики, Vol. 37, с. 238-239 (апрель 1999 г.)
4 Там же.
Другие ссылки:
Вес и гравитация – необходимость согласованных определений , Ричард С. Моррисон, Учитель физики, том 37, с. 51-52 (январь 1999)
Вес – иллюстрированный вид , Анджей Соколовский, The Physics Учитель, Том 37, с.340 (апрель 1999 г.)
Вес – вообще не используйте слово , Рональд Браун, The
Учитель физики, Том. 37, с. 341 (апрель 1999 г.)
37, с. 341 (апрель 1999 г.)
последнее обновление 7 апреля 1999 г. по J L Стэнбро
«Расширить работу, чтобы заполнить время доступный на его доработку»
С.Норткот Паркинсон – Закон Паркинсона (1958)
- вес объекта есть сила с которой тело привлекает на землю.
- Вес = масса х ускорение свободного падения (w = мг)
- Так как “g” примерно одинаково везде на земной поверхности, вес часто указывается в единицах массы.
- Вес зависит от
местоположение, масса постоянна независимо от местоположения, например.
 ан
объект на
Луна весит около одной шестой своего веса на Земле, но
его масса
без изменений.
ан
объект на
Луна весит около одной шестой своего веса на Земле, но
его масса
без изменений. - Единицы: ньютоны (СИ), фунты (британские)
- Струны, веревки, провода, кабели и т. д. используются в качестве механизма для передачи сила.
- Напряжение в веревка равна передаваемой силе.
- Напряжение всегда а «тянущее» усилие. Веревка не может толкать предмет. Поэтому канат под натяжением «тянет» в обоих направлениях.
- Введение: Диаграмма свободного тела – это изображение сил, действующих на
объект
и это первый (и, возможно, самый важный) шаг
при решении силовых задач.

- Назначение: Назначение свободного тела диаграмма (FBD) должна помочь вам определять и анализировать силы, действующие на конкретный объект или тело.
о Типы Силы: Типы силы, обычно встречающиеся в классическом механика
а. ВЕС: Как мы видели, вес – это сила тяжести, действующая на объект со стороны Земля (или любой другое небесное тело). Если объект находится рядом с Землей поверхность и имеет масса, тогда объект имеет вес. Величина его веса w = мг и это направление – к центру Земли.
б. ПРИМЕНЯЕТСЯ СИЛА: Применено силы обычно возникают в результате физического соприкосновения вещей и действующий на тело.
От это определение, нормальные силы, силы натяжения и трения применяемый силы, но мы обычно выделяют их отдельно. В нашем случае применяется силы включать такие явления, такие как толкание объекта или сила, приложенная весна на объект.
в. НОРМАЛЬНЫЙ СИЛА: нормальный сила возникает из-за контакта внешней поверхности с объектом.То поверхность придает нормальную силу объекту из-за третьей силы Ньютона закон. Если два объекты находятся в контакте, существуют нормальные силы. Направление нормальная сила является перпендикулярно соприкасающимся поверхностям и направлено в тело под рассмотрение. Величина нормальной силы может быть только определенный от анализ всех сил, действующих на тело.
д. НАТЯЖЕНИЕ FORCE: (см. выше) Сила натяжения – это сила, приложенная к тело на веревке или строка. Веревки и струны не способны толкать тело; Oни всегда должен тянуть тело. Силы натяжения направлены от тела существование вытащил и вдоль направления веревки или струны.
эл. ФРИКЦИОННЫЙ СИЛ: Силы трения возникают из-за поверхностного сцепления между два объекта в контакт. Подробно рассмотрим силы трения. Поздняя дата.
о Чертеж ФБД . В резюме, шаги (более подробно обсуждается ниже) для рисования FBD:
а.
Изолировать в тело. Это шаг требует что вы отделяете тело (блок, колесо, тележка и т. д.), которые вы исследуете из все остальное и Нарисуй это.
б. Розыгрыш и обозначьте все силы, действующие на тело. Это самый сложный шаг. Здесь это предлагаемый метод использовать:
1) Список в возможные виды сил. Удобная мнемоника ХОЧУ СИЛ:
Вт Вт восемь
А А многослойный
Н Н обычный
Т Т номер
Силы Трение
2) Ответить в следующие вопросы о типах сил:
а) Делает тело есть масса? Если это так, вес должен быть включен.
б) Является там применяется сила, описанная в задаче?
в) Является там нормальный сила? Соприкасается ли тело с другой поверхностью? Если да, то там должен быть нормальный сила.
г) Является там веревка или веревка прикреплена к телу? Если да, то есть напряжение направленная сила в таком способ, как вытащить тело.
д) Является есть трение сила? Если поверхность без трения или гладкая, то нет сила трения является настоящее время.В противном случае сила трения присутствует и направленный параллельно к поверхность и противоположное движение или надвигающееся движение.
3) Определить где привлечь силы на FBD. Позиции векторы силы на диаграмме не будут повлиять на наш анализ.Однако если бы мы обсуждали вращательный движение, положение станет важным.
Используйте следующие правила:
а) Идентифицировать в точка приложения сила.
1) За однородная масса, вес действует в геометрической центр объект.
2) То точка приложения приложенных сил и сил растяжения обычно указано в постановка задачи.
3) Нормальная сила и сила трения связаны площади поверхностей на связи.По соглашению мы выберем центр поверхности в контакте как смысл приложения этих двух сил.
4) То нормальная сила направлена перпендикулярно поверхности связаться через в центр тела.
5) То сила трения направлена параллельно контакту поверхность.
б) линия действия силы определяется как прямой линии в направлении действия силы и проходя через точка применение.
в. Выбрать а систему координат (и направление положительный крутящий момент). Практически любой координатные оси могут использоваться в задаче; тем не менее, определенные выбор сделаю применение второго закона Ньютона намного проще математически. Немного правила найти хороший набор топоров:
1) Объект испытывает ускорение.
Выберите одну ось по направлению ускорения. Выберите другую ось перпендикулярно первый.
2) Объект движущийся постоянная скорость. Выберите одну ось по направлению движения. Выберите другую ось перпендикулярно в первый.
3) Объект в отдых. Выбрать одна ось параллельно поверхности, на которой объект отдыхает. Выберите другую ось, перпендикулярную первый.
направление из положительный крутящий момент будет обсуждаться позже в курсе, когда мы покрываем вращательный движение.
На данном этапе курса нам не нужно себя с крутящий момент.
д. Включая критический углы и размеры. Во многих случаях необходимо сломать сила векторов в их компоненты. Определение критических углов позволяет простой применение тригонометрических отношений.
Для всех проблем, связанных с применение 2-го закона Ньютона следуйте приведенному ниже рецепту:
Нарисуйте схему, описывающую ситуация, описанная в задаче.
Убедитесь, что вы знаете, какие объекты возможное движение относится к.
Рисование диаграмм свободного тела (FBD) для каждого рассматриваемого объекта, отдельно от вашего оригинальная схема.
Этот шаг является критическим. Разве что можно выявить и правильно сложить все силы воздействуя на каждый объект, вы не сможете решить проблема.
Выберите подходящую координату система для каждого объекта. В большинстве ситуаций для для каждого объекта вы выбираете оси так, чтобы любое движение происходит вдоль оси. Обратите внимание, что системы координат для каждого объекта не обязательно должны быть то же.
Наконец, примените метод Ньютона. 2
и закон для каждого объекта в каждом направлении (это будет включать разрешение сил вдоль выбранных координатных осей) и использовать некоторые общие смысл.Этот часто описывается как запись «уравнений движения».Один раз у вас есть уравнения движения, в принципе, вы можете решить их для желаемых неизвестных.
Пример Проблема
«Голосуй за человек, который обещает наименее; он будет меньше всего разочарование»
Бернард Барух
Др.C
7.3 Потенциальная гравитационная энергия – College Physics
Определение скорости американских горок по их высоте
(a) Какова конечная скорость американских горок, показанных на рисунке 7.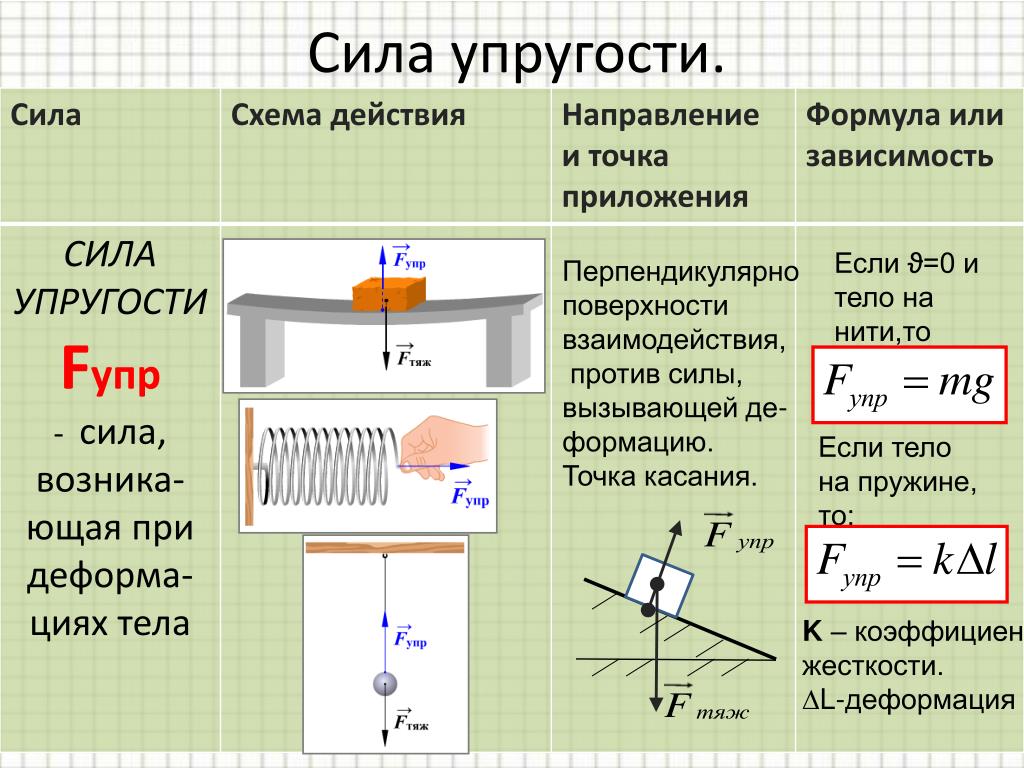 8, если он стартует из состояния покоя на вершине холма высотой 20 м и работа сил трения пренебрежимо мала? б) Какова его конечная скорость (опять же в предположении пренебрежимо малого трения), если его начальная скорость равна 5,00 м/с?
8, если он стартует из состояния покоя на вершине холма высотой 20 м и работа сил трения пренебрежимо мала? б) Какова его конечная скорость (опять же в предположении пренебрежимо малого трения), если его начальная скорость равна 5,00 м/с?
Стратегия
Американские горки теряют потенциальную энергию при спуске. Мы пренебрегаем трением, так что оставшаяся сила, действующая на гусеницу, является нормальной силой, которая перпендикулярна направлению движения и не совершает работы. В этом случае чистая работа на американских горках выполняется только за счет силы тяжести. Потеря гравитационной потенциальной энергии при движении вниз на расстояние hh размером 12{h} {} равна выигрышу в кинетической энергии. Это может быть записано в форме уравнения как -ΔPEg=ΔKE-ΔPEg=ΔKE размер 12{ – Δ”PE” rSub { размер 8{g} } =Δ”KE”} {}.Используя уравнения для PEgPEg размера 12{“PE” rSub {размер 8{g} } } {} и KEKE размера 12{“KE”} {}, мы можем решить для конечной скорости vv размера 12{v} {}, что является желаемым количеством.
Потеря гравитационной потенциальной энергии при движении вниз на расстояние hh размером 12{h} {} равна выигрышу в кинетической энергии. Это может быть записано в форме уравнения как -ΔPEg=ΔKE-ΔPEg=ΔKE размер 12{ – Δ”PE” rSub { размер 8{g} } =Δ”KE”} {}.Используя уравнения для PEgPEg размера 12{“PE” rSub {размер 8{g} } } {} и KEKE размера 12{“KE”} {}, мы можем решить для конечной скорости vv размера 12{v} {}, что является желаемым количеством.
Решение для (а)
Здесь начальная кинетическая энергия равна нулю, так что ∆KE=12mv2∆KE=12mv2. Уравнение изменения потенциальной энергии утверждает, что ∆PEg=mgh∆PEg=mgh. Поскольку в этом случае hh отрицательно, мы перепишем это как ΔPEg=−mg∣h∣ΔPEg=−mg∣h∣, чтобы ясно показать знак минус. Таким образом,
−ΔPEg=ΔKE−ΔPEg=ΔKE size 12{ – Δ”PE” rSub { size 8{g} } =Δ”KE”} {}7.34
становится
мг∣ч∣=12мв2.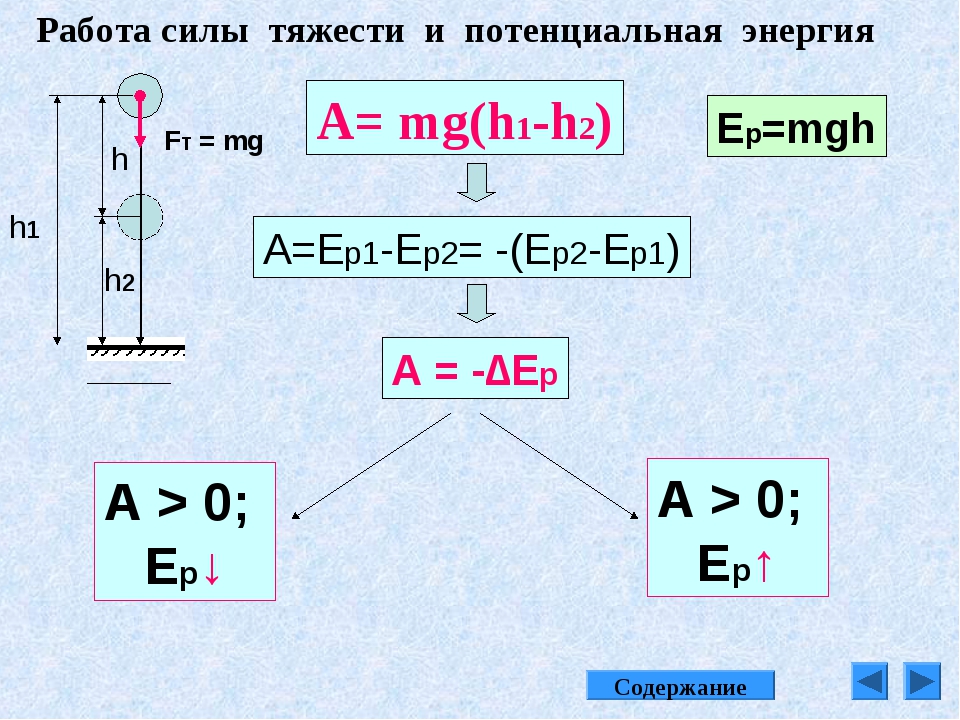 мг∣ч∣=12мв2. size 12{ ital “mg” llline h rline = { {1} over {2} } ital “mv” rSup { size 8{2} } “.” } {}
мг∣ч∣=12мв2. size 12{ ital “mg” llline h rline = { {1} over {2} } ital “mv” rSup { size 8{2} } “.” } {}7,35
Решая для размера vv 12{v} {}, мы находим, что масса сокращается и что
v=2g∣h∣.v=2g∣h∣. size 12{v= sqrt {2g lline h rline } } {}7,36
Подстановка известных значений,
v=29,80 м/с220,0 м= 19,8 м/с.v=29,80 м/с220,0 м= 19,8 м/с.alignl { stack { размер 12{v= sqrt {2 левый (9 “.” “80” “м/с” rSup { размер 8 {2} } правый) левый (“20” “.”0″ м” справа )} } {} # ” “=” 19″ “.” “8 м/с” “.” {} } } {}7.37
Решение для (b)
Снова −ΔPEg=ΔKE−ΔPEg=ΔKE размер 12{ – Δ”PE” rSub { размер 8{g} } =Δ”KE”} {}. В этом случае имеется начальная кинетическая энергия, поэтому ΔKE=12mv2−12mv02ΔKE=12mv2−12mv02 size 12{Δ”KE”= { {1} over {2} } ital “mv” rSup { size 8{2} } – { {1} более {2} } ital “mv” rSub { размер 8{0} rSup { размер 8{2} } } } {}. Таким образом,
мг∣ч∣=12мв2−12мв02.мг∣ч∣=12мв2−12мв02. size 12{ ital “mg” llline h rline = { {1} over {2} } ital “mv” rSup { size 8{2} } – { {1} over {2} } ital “mv” rSub { size 8 {0} rSup {размер 8{2} } } “.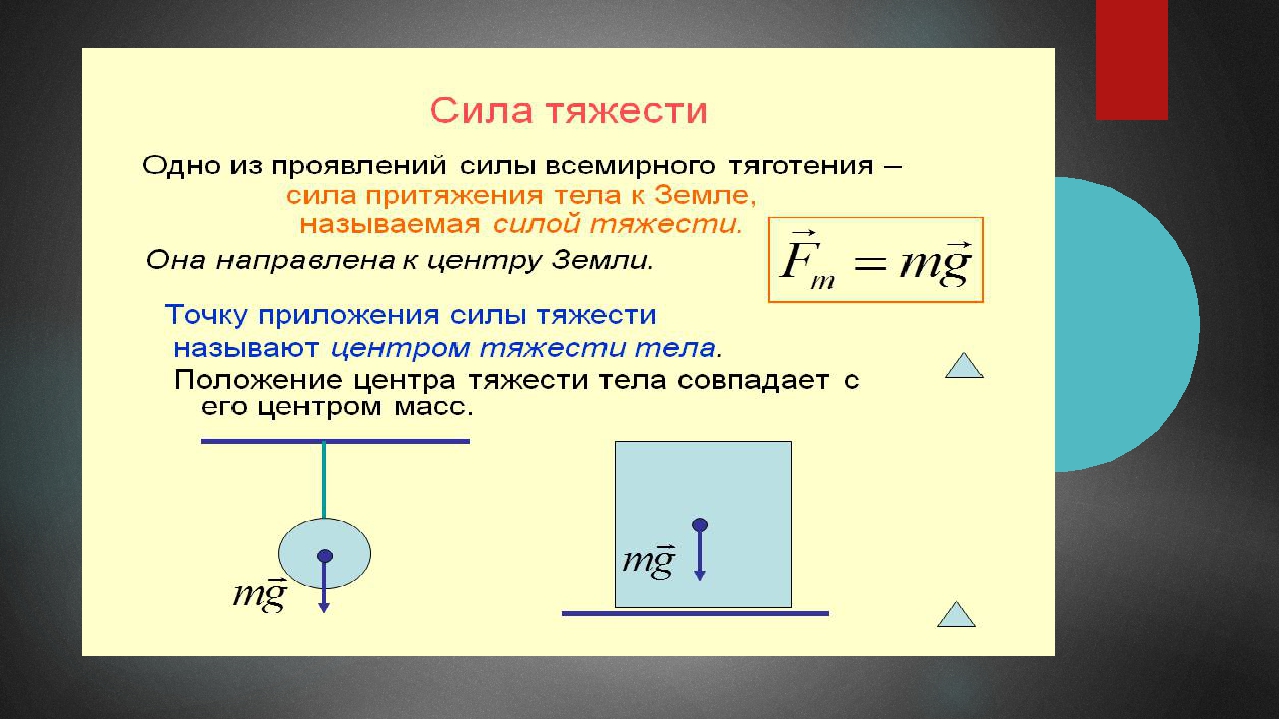 ” } {}
” } {}7.38
Перестановка дает
12mv2=мг∣ч∣+12мв02.12mv2=мг∣ч∣+12мв02. size 12{ { {1} over {2} } ital “mv” rSup { size 8{2} } = ital “mg” llline h rline + { {1} over {2} } ital “mv” rSub { size 8 {0} rSup { размер 8{2} } } “.” } {}7.39
Это означает, что конечная кинетическая энергия является суммой начальной кинетической энергии и гравитационной потенциальной энергии. Масса снова отменяется, и
v=2g∣h∣+v02.v=2g∣h∣+v02. size 12{v= sqrt {2g lline h rline +v rSub { size 8{0} rSup { size 8{2} } } } } {}7.40
Это уравнение очень похоже на уравнение кинематики v=v02+2adv=v02+2ad size 12{v= sqrt {v rSub { size 8{0} } rSup { size 8{2} } +2 ital “ad “} } {}, но оно является более общим — уравнение кинематики справедливо только для постоянного ускорения, тогда как наше вышеприведенное уравнение справедливо для любого пути независимо от того, движется ли объект с постоянным ускорением. Теперь подстановка известных значений дает
v=2(9,80 м/с2)(20,0 м)+(5,00 м/с)2= 20,4 м/сv=2(9,80 м/с2)(20,0 м)+(5,00 м/с). с)2= 20.4 м/с.alignl { стек {
size 12{v= sqrt {2 \( 9 “.” “80”” м/с” rSup { size 8{2} } \) \( “20” “.” 0″ m” \) + \( 5 “.” “00”” м/с” \) rSup { size 8{2} } } } {} #
” “=” 20″ “.” “4 м/с” “.” {}
} } {}
с)2= 20.4 м/с.alignl { стек {
size 12{v= sqrt {2 \( 9 “.” “80”” м/с” rSup { size 8{2} } \) \( “20” “.” 0″ m” \) + \( 5 “.” “00”” м/с” \) rSup { size 8{2} } } } {} #
” “=” 20″ “.” “4 м/с” “.” {}
} } {}7.41
Обсуждение и выводы
Во-первых, обратите внимание, что масса отменяется. Это вполне согласуется с наблюдениями, сделанными в Falling Objects, о том, что все объекты падают с одинаковой скоростью, если трением можно пренебречь. Во-вторых, учитывается только скорость американских горок; нет информации о его направлении ни в одной точке.Это раскрывает еще одну общую истину. Когда трением можно пренебречь, скорость падающего тела зависит только от его начальной скорости и высоты, а не от его массы или пройденного пути. Например, американские горки будут иметь одинаковую конечную скорость независимо от того, падают ли они с высоты 20,0 м прямо вниз или движутся по более сложной траектории, как показано на рисунке. В-третьих, и, возможно, неожиданно, конечная скорость в части (b) больше, чем в части (а), но намного меньше, чем 5,00 м/с. Наконец, обратите внимание, что скорость может быть найдена на любой высоте по пути, просто используя соответствующее значение размера hh 12{h} {} в интересующей точке.
Наконец, обратите внимание, что скорость может быть найдена на любой высоте по пути, просто используя соответствующее значение размера hh 12{h} {} в интересующей точке.
Единицы СИ – Масса | НИСТ
Килограмм (кг) определяется путем принятия фиксированного числового значения постоянной Планка h, равного 6,62607015 × 10 −34 при выражении в Дж с, что равно кг м 2 с −1 , где метр и секунда определяются через c и ∆ν Cs .
Основным эталоном массы для этой страны является американский прототип 20 килограммов, представляющий собой платино-иридиевый цилиндр, хранящийся в NIST.Килограмм, первоначально определяемый как масса одного кубического дециметра воды при температуре максимальной плотности, был известен как архивный килограмм. После Международной метрической конвенции в 1875 году он был заменен международным прототипом килограмма, который стал единицей массы без привязки к массе кубического дециметра воды или архивному килограмму. Каждой стране, подписавшейся на Международную метрическую конвенцию, была присвоена одна или несколько копий международных стандартов; они известны как национальные прототипы метров и килограммов.Узнайте больше об истории и текущем определении килограмма.
Каждой стране, подписавшейся на Международную метрическую конвенцию, была присвоена одна или несколько копий международных стандартов; они известны как национальные прототипы метров и килограммов.Узнайте больше об истории и текущем определении килограмма.
Среди основных единиц СИ килограмм (кг) является единственной единицей, название и символ которой по историческим причинам включают префикс. «Кило» префикс SI для 1000 или 10 3 . Названия и символы для десятичных кратных и дольных единиц массы образуются путем присоединения префиксных имен к названию единицы «грамм» и префиксных символов к символу единицы «г». Узнайте больше об этой исторической причуде.
| Единицы массы | ||
|---|---|---|
| 10 миллиграмм (мг) | = | 1 сантиграмм (г) |
| 10 сантиграмм | = | 1 дециграмм (дг) = 100 миллиграммов |
| 10 дециграмм | = | 1 грамм (г) |
| 10 дециграмм | = | 1000 миллиграммов |
| 10 грамм | = | 1 декаграмм (даг) |
| 10 декаграмм | = | 1 гектограмм (hg) |
| 10 декаграмм | = | 100 грамм |
| 10 гектограмм | = | 1 килограмм (кг) |
| 10 гектограмм | = | 1000 грамм |
| 1000 кг | = | 1 мегаграмм (Mg) или 1 метрическая тонна (т) |
Физик Ричард Штайнер настраивает электронный килограмм, экспериментальный прибор для определения массы с точки зрения основных свойств природы.
Кредит: © Роберт Рат
Ресурсы для студентов и преподавателей
Кредит: Дж. Ван и Б. Хейс/NIST
Лига супергероев SI – месье Килограмм
Этот анимационный видеосериал в стиле комиксов был разработан, чтобы помочь учащимся средних школ узнать о 7 основных единицах измерения SI.С его невероятно сильными руками месье Килограмм является мастером массы. Килограмм представляет собой цилиндр из специального металла шириной около 39 миллиметров и высотой 39 миллиметров, который служит мировым эталоном массы.
Часто задаваемые вопросы – В чем разница между терминами “масса” и “вес”?
Масса тела является мерой его инерционных свойств или количества вещества, которое оно содержит. Вес тела — это мера силы, действующей на него под действием силы тяжести, или силы, необходимой для его поддержания. Гравитация на Земле придает телу нисходящее ускорение около 9,8 м/с 2 . В просторечии вес часто используется как синоним массы в мерах и весах. Например, глагол «взвесить» означает «определить массу» или «иметь массу». Неправильное использование веса вместо массы должно быть постепенно прекращено, а термин «масса» должен использоваться, когда имеется в виду масса. Единицей массы в системе СИ является килограмм (кг). В науке и технике вес тела в конкретной системе отсчета определяется как сила, сообщающая телу ускорение, равное локальному ускорению свободного падения в этой системе отсчета.Таким образом, единицей СИ определяемой таким образом величины веса (силы) является ньютон (Н).
Гравитация на Земле придает телу нисходящее ускорение около 9,8 м/с 2 . В просторечии вес часто используется как синоним массы в мерах и весах. Например, глагол «взвесить» означает «определить массу» или «иметь массу». Неправильное использование веса вместо массы должно быть постепенно прекращено, а термин «масса» должен использоваться, когда имеется в виду масса. Единицей массы в системе СИ является килограмм (кг). В науке и технике вес тела в конкретной системе отсчета определяется как сила, сообщающая телу ускорение, равное локальному ускорению свободного падения в этой системе отсчета.Таким образом, единицей СИ определяемой таким образом величины веса (силы) является ньютон (Н).
Гравитационная потенциальная энергия – Гиперучебник по физике
Обсуждение
введение
Короткая часть исчисления.
| U г = – | ⌠ ⌡ | F · д с |
| р | ||||
| U г = – | ⌠ ⎮ ⌡ | − | Гм 1 м 2 | др |
| р 2 | ||||
| ∞ |
| U г = – | Гм 1 м 2 | ⎛ ⎜ ⎝ | 1 | − | 1 | ⎞ ⎟ ⎠ |
| р | ∞ |
и вот он…
где…
| У г = | гравитационная потенциальная энергия |
| м 1 м 2 = | массы любых двух объектов |
| r = | расстояние между их центрами |
| Г = | универсальная гравитационная постоянная (6. 67 × 10 −11 Н·м 2 /кг 2 ) 67 × 10 −11 Н·м 2 /кг 2 ) |
Обратите внимание, что в этом выражении нет ∆. Обсудить здесь.
Где-нибудь обсудите потенциал и потенциальную энергию.
А как насчет старого уравнения?
∆ U г = мг ∆ ч
Это скрыто в новом уравнении.
Позвольте мне показать вам.
| ∆ U г = | U f | − | У и | |
| ∆ U г = | U г ( r + ∆ ч ) | − | U г ( р ) | |
| ∆ U г = | − | Гм 1 м 2 | + | Гм 1 м 2 |
| р + ∆ ч | р |
Объединить члены под общим знаменателем.
| ∆ U г = |
| ||||
| ∆ U г = | |||||
Умножить на “один”.
| ∆ U г = | Гм 1 м 2 ∆ ч | р | |
| r ( r + ∆ ч ) | р |
Поменять местами члены в знаменателях.
| ∆ U г = | Гм 1 м 2 ∆ ч | р | |
| р 2 | р + ∆ ч |
Вынесите что-нибудь из числителя.
| ∆ U г = м 2 ч | Гм 1 | р | |
| р 2 | р + ∆ ч |
Видишь? Если r — радиус Земли, м 1 — масса Земли, а м 2 — масса поднимаемого предмета, то…
— это ускорение силы тяжести на поверхности Земли.Делая эту замену (и опуская индекс, так как у нас осталась только одна масса), мы получаем…
| ∆ U г = мг ∆ ч | р |
| р + ∆ ч |
Первая часть этого выражения — наш старый знакомый, исходное уравнение для гравитационной потенциальной энергии. Второй член является поправочным коэффициентом. Для обычных высот этот член по существу один.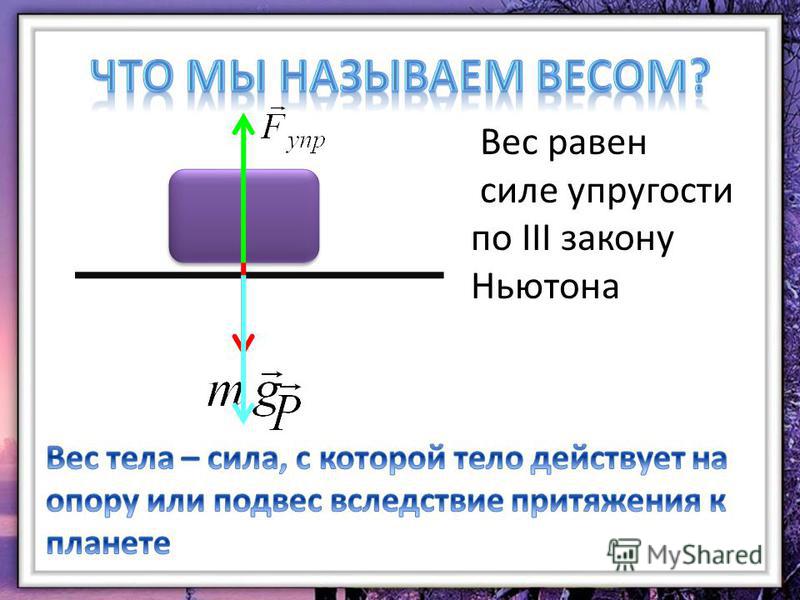 Подтвердим это, используя действительно большую высоту — вершину шпиля Бурдж-Халифа в Арабских Эмиратах (818 м).
Подтвердим это, используя действительно большую высоту — вершину шпиля Бурдж-Халифа в Арабских Эмиратах (818 м).
| р | = | 6 371 000 м |
| р + ∆ ч | 6 371 000 м + 818 м | |
| р | = | 0,999872 |
| р + ∆ ч |
Инженеры, спроектировавшие Бурдж, допустили ошибку в четвертом десятичном знаке в своих расчетах.Это отклонение, вероятно, меньше, чем неопределенность массы балок, используемых для строительства этого здания, поэтому ∆ U g = mg ∆ h вполне приемлемо для большинства практических приложений
Теперь давайте попробуем что-нибудь астрономическое. Можно ли использовать ∆ U g = мг ∆ h для измерения гравитационной потенциальной энергии Луны? Расстояние от Земли до Луны (384 400 000 м) измеряется от центра Земли, а не от ее поверхности. В этом случае r + ∆ h на самом деле будет разностью двух чисел.
В этом случае r + ∆ h на самом деле будет разностью двух чисел.
| р | = | 6,371000 м |
| р + ∆ ч | 384 400 000 м − 6 371 000 м | |
| р | = | 0,016853 |
| р + ∆ ч |
Это число явно ближе к нулю, чем к единице, поэтому…
используется для астрономических приложений.
Скорость убегания
Что поднимается, то должно опускаться. Правильно?
ммм. Нет. Не обязательно.
Если объект подбросить вверх достаточно быстро, он поднимется и никогда не упадет. Минимальная скорость, необходимая для этого, называется скоростью убегания .
Ни один человек никогда не путешествовал со скоростью, превышающей скорость убегания Земли. Астронавты Аполлона подошли очень близко, но они направлялись к Луне, которая под действием земного притяжения попала на замкнутую орбиту. В каком-то смысле они действительно не хотели бежать с Земли. Однако им удалось путешествовать быстрее, чем скорость убегания Луны, поэтому они смогли вернуться на Землю.
В каком-то смысле они действительно не хотели бежать с Земли. Однако им удалось путешествовать быстрее, чем скорость убегания Луны, поэтому они смогли вернуться на Землю.
Любому космическому кораблю, который когда-либо летал к другой планете или астероиду, удавалось превысить космическую скорость Земли. Считать их всех слишком трудоемко. Где-то в сотнях.
Пять космических зондов в настоящее время находятся на траекториях, которые выведут их за пределы Солнечной системы, что означает, что они превысили космическую скорость Солнца.Это миссии Pioneer 10 и 11 к Юпитеру и Сатурну, миссии Voyager 1 и 2 ко всем четырем планетам Юпитера (Юпитер, Сатурн, Уран, Нептун) и миссия New Horizons к Плутону. В 2012 году “Вояджер-1” стал первым созданным человеком объектом, который пересек межзвездное пространство на расстоянии от Солнца в 120 астрономических единиц (в 120 раз больше, чем расстояние от Земли до Солнца, или в 4 раза больше, чем расстояние от Нептуна до Солнца).
Рассмотрим факторы, влияющие на скорость убегания.
- У всех объектов с массой есть космическая скорость, но этот термин обычно используется только для астрономических объектов — объектов с большой массой.Скорость убегания Земли довольно высока (11 км/с), поэтому большинство людей никогда непосредственно не видели, как объект покидает Землю. Скорость убегания человека незаметно мала (0,3 мм/с), поэтому все, что человек когда-либо отпускал, так и не вернулось к нему из-за его гравитационного притяжения. Скорость убегания увеличивается с массой (но эти две величины не прямо пропорциональны).
- Спасательная скорость иногда описывается как скорость, необходимая для преодоления гравитации объекта, но это не совсем так.Вы никогда не сможете избежать гравитации. Никогда! Гравитация уменьшается с увеличением расстояния между объектами, но никогда не равна нулю. Гравитация бесконечна в своей досягаемости. Поскольку гравитация уменьшается с разделением , скорость убегания тоже уменьшается (но эти две величины не обратно пропорциональны).

Время заняться математикой. Начнем с закона сохранения энергии — полная энергия в начале равна полной энергии в конце.
E 0 = E
Для объекта, подброшенного вверх, соответствующими энергиями являются кинетический и гравитационный потенциал.
К 0 + У 0 = К + У
Замените символы энергии их уравнениями. (Помните, что кинетическая энергия всегда положительна, а гравитационная энергия всегда отрицательна.)
| ½ м 1 v 0 2 – | Гм 1 м 2 | = ½ м 1 v 2 − | Гм 1 м 2 |
| р 0 | р |
Пусть…
| м 1 = | масса объекта, который убегает (космический корабль, обломки взрыва, обломки падения метеорита и т. ) ) |
| м 2 = | масса астрономического объекта, от которого он улетает (Земля, Солнце, Млечный Путь и т. д.) |
| v 0 = | начальная скорость убегающего объекта |
| v = | скорость убегающего объекта в более позднее время |
| р 0 = | начальное разделение между двумя объектами |
| r = | расстояние между двумя объектами в более позднее время |
| Г = | универсальная гравитационная постоянная |
Подбросить предмет вверх и что произойдет? Гравитация притягивает его, замедляя по мере подъема.В конце концов объект остановится, развернется и упадет обратно на Землю. Бросьте его быстрее, и точка разворота будет выше. Бросьте его еще быстрее, и этот балл будет еще выше. Возьмите эту ситуацию и доведите ее до крайности.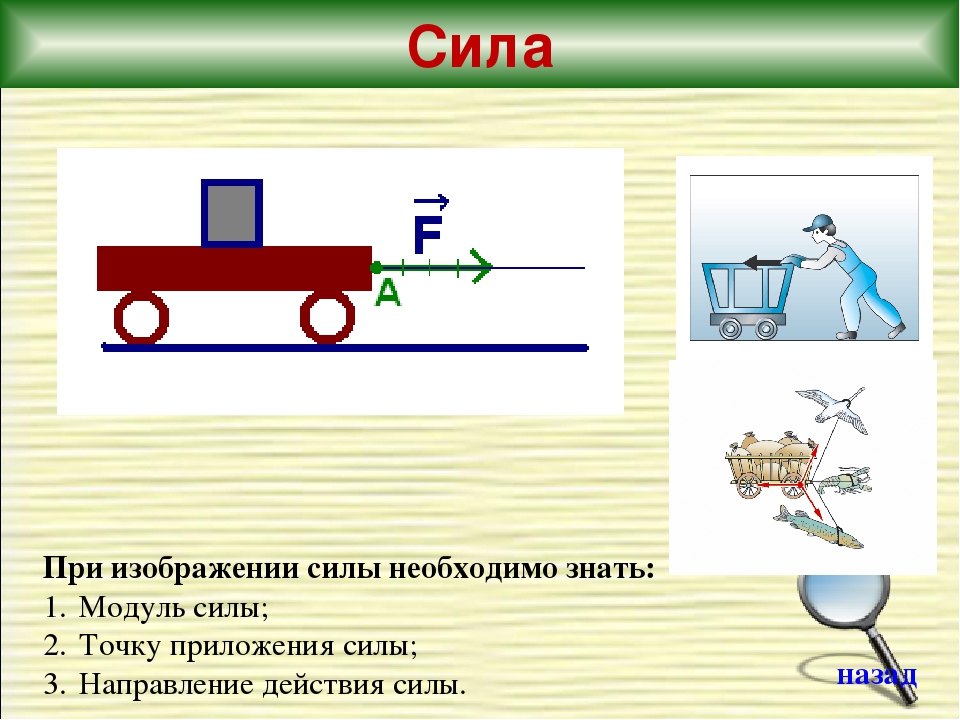 Сделайте эту точку поворота бесконечно далекой. На языке пределов пусть r → ∞ и v → 0. Когда мы это делаем, оба слагаемых справа от знака равенства исчезают. Если вы хотите убежать от Земли, Солнца или Млечного Пути, просто имейте нулевую общую энергию.
Сделайте эту точку поворота бесконечно далекой. На языке пределов пусть r → ∞ и v → 0. Когда мы это делаем, оба слагаемых справа от знака равенства исчезают. Если вы хотите убежать от Земли, Солнца или Млечного Пути, просто имейте нулевую общую энергию.
| ½ м 1 v 0 2 – | Гм 1 м 2 | + = 0 – 0 |
| р 0 |
Алгебра говорит, что мы можем исключить m 1 , поскольку оно встречается в каждом члене. Поскольку осталась только одна масса, я не вижу смысла больше писать индекс. Мы также можем сделать то же самое для индексов v 0 и r 0 .Если нет других значений скорости или разделения, о которых нужно беспокоиться, зачем беспокоиться об индексах? Давайте также сделаем небольшую перестановку, чтобы уменьшить количество терминов и убрать знак минус.
Решение для v дает нам следующее уравнение для скорости убегания…
где…
| v = | скорость убегания (минимальная скорость, необходимая объекту для перемещения на бесконечное расстояние от астрономического объекта в определенном месте) |
| Г = | универсальная гравитационная постоянная |
| м = | масса астрономического объекта |
| r = | начальное разделение между двумя объектами |
Обратите внимание, что хотя это называется побег скорость , на самом деле это побег скорость .Это не вектор, это скаляр. Пока направление, в котором вы движетесь, не находится в астрономическом объекте, убегающий объект ускользнет. Мы подошли к этому как к проблеме сохранения энергии, а энергия является скалярной величиной. Его не волнует направление. Вспомните также, что гравитация описывается как консервативная сила, что означает, что ей все равно, какой путь вы выберете.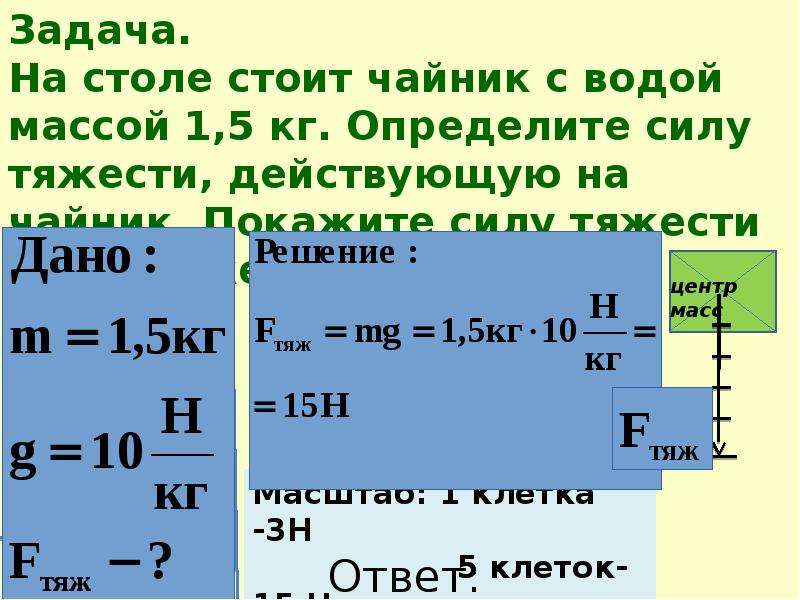
горизонт событий
Черная дыра — это звезда, которая схлопнулась в точку. В пределах определенного радиуса, известного как горизонт событий, скорость убегания больше скорости света.Поскольку ничто не может превысить скорость света, все, что пересекает горизонт событий, навсегда оказывается в ловушке внутри черной дыры.
Черные дыры разрушают объем, но не массу, энергию, угловой момент, заряд, энтропию и т. д.
Горизонт событий, также известный как радиус Шварцшильда. Точка невозврата.
Впервые теоретизировано Джоном Мишелем в 1784 году
Исходя из формулы скорости убегания, выведите уравнение для радиуса горизонта событий через м (масса черной дыры), G (гравитационная постоянная) и c (скорость светлый).
Перефразируя это, “может быть возможно создать черную дыру в лаборатории, ничто легче 10 мкг не может создать черную дыру, эта энергия все еще находится за пределами досягаемости современных коллайдеров частиц, но не очень энергичных космических лучей, поскольку Земля не была поглощена маленькими черными дырами, мы можем предположить, что они нестабильны».
космическое расширение
Закон Хаббла
Когда мы смотрим на галактики и другие объекты за пределами нашего Млечного Пути, мы видим, что они обычно удаляются от нас и что скорость их удаления почти прямо пропорциональна их расстоянию.То есть чем дальше от нас находится конкретная галактика, тем быстрее она от нас убегает. Если одна галактика находится в два раза дальше от Млечного Пути, чем другая, то и скорость ее будет в два раза больше. В три раза дальше путь означает в три раза быстрее и так далее. Это наблюдение было впервые сделано в 1929 году американским астрономом Эдвином Хабблом (1889–1953) и с тех пор стало известно как закон Хаббла . Математически закон Хаббла записывается как…
v = ч
где…
| v = | скорость удаления (составляющая скорости объекта вдали от Млечного Пути) |
| r = | расстояние от Млечного Пути |
| Н = | константа пропорциональности, известная как константа Хаббла . Предполагается, что эта постоянная изменяется со временем. Говоря о текущем значении, мы используем H 0 Предполагается, что эта постоянная изменяется со временем. Говоря о текущем значении, мы используем H 0 | .
Закон Хаббла важен, потому что он говорит нам, что Вселенная расширяется и, если мы экстраполируем назад во времени, что Вселенная изначально была бесконечно мала и бесконечно плотна. Это одно из многих доказательств теории большого взрыва . Пространство-время возникло около 13,8 миллиарда лет назад, было заполнено всей массой-энергией, которая существует сейчас и когда-либо будет существовать, а затем быстро расширилось от области, намного меньшей, чем протон, до области размером с грейпфрут в невероятно малое время 10 −32 секунд.Этот первоначальный выброс пространства-времени, наполненного массой-энергией, переносился собственным «импульсом» (из-за отсутствия лучшего слова), пока наблюдаемая Вселенная не выросла до размеров, которые мы видим сейчас, — примерно 13,8 миллиарда световых лет во всех направлениях.
постоянная Хаббла
Расстояния в астрономии настолько велики, что метр настолько уморительно мал, что бесполезен. (Префиксы, обозначающие кратные метры, достаточно большие, чтобы их можно было использовать для постоянной Хаббла, были изобретены только спустя десятилетия.) Чтобы обойти это, астрономы изобрели две единицы измерения: световой год и парсек. Из этих двух наиболее интуитивно понятным для меня является световых лет , то есть расстояние, которое луч света пройдет за один год (9,46 × 10 15 м).
Другая единица, парсек, является геометрической, а не физической единицей. Ближайшие к нам астрономические тела (ну, близкие в астрономических терминах) будут казаться смещающими свое положение в небе по мере того, как Земля движется по своей орбите. Слово парсек означает «параллакс в одну угловую секунду».Таким образом, объект, который кажется смещенным на одну угловую секунду ( 1 3600 °) по мере того, как Земля перемещается от одной стороны Солнца к другой через шесть месяцев, считается удаленным на парсек . Для астрономов-наблюдателей девятнадцатого и начала двадцатого веков парсек был более удобной единицей для профессионального использования, чем световой год. Один парсек [пк] равен примерно 3,26 световых года или 3,09 × 10 16 м. Ближайшие к Земле звезды, кроме Солнца, находятся на расстоянии чуть более одного парсека.Край Млечного Пути находится на расстоянии нескольких тысяч парсеков — нескольких килопарсеков [кпк]. Космические расстояния, как и расстояния между галактиками, измеряются в миллионах парсеков или мегапарсеков [Мпк]. Это единица, которую Хаббл использовал в своей работе.
Для астрономов-наблюдателей девятнадцатого и начала двадцатого веков парсек был более удобной единицей для профессионального использования, чем световой год. Один парсек [пк] равен примерно 3,26 световых года или 3,09 × 10 16 м. Ближайшие к Земле звезды, кроме Солнца, находятся на расстоянии чуть более одного парсека.Край Млечного Пути находится на расстоянии нескольких тысяч парсеков — нескольких килопарсеков [кпк]. Космические расстояния, как и расстояния между галактиками, измеряются в миллионах парсеков или мегапарсеков [Мпк]. Это единица, которую Хаббл использовал в своей работе.
В оригинальной статье Хаббла 1929 года он сообщил значение своей постоянной примерно 500 км/с/Мпк. Я включил его исходные данные в раздел этой книги, озаглавленный «Подгонка кривой». При желании вы можете проанализировать данные самостоятельно. Используя стандартный линейный регрессионный анализ, я получил значение H = 463 км/с/Мпк.Что интересно в этом значении, так это то, что теперь оно повсеместно признано ужасно неправильным. Позже было обнаружено, что измерения расстояний до внегалактических тел в эпоху Хаббла серьезно ошибочны. Тем не менее, теория оказалась верной, даже несмотря на то, что все данные, использованные для ее вывода, были занижены.
Позже было обнаружено, что измерения расстояний до внегалактических тел в эпоху Хаббла серьезно ошибочны. Тем не менее, теория оказалась верной, даже несмотря на то, что все данные, использованные для ее вывода, были занижены.
Определение H продвигалось медленно, но верно с начала 20-го века, и константа претерпела несколько изменений. Текущее наиболее точное значение получено с помощью микроволнового зонда анизотропии Уилкинсона НАСА (WMAP).По состоянию на 2014 год ученые WMAP получили значение 90 271 H 90 272 90 147 0 90 148 = 69,3 ± 0,8 км/с/Мпк. Давайте для перспективы переведем это значение в единицы СИ…
| Н 0 = | 2,25 × 10 −18 | 1 |
| с |
Постоянная Хаббла в обратной второй форме делает ее немного более доступной. Пространство вокруг нас расширяется со скоростью примерно одна часть из 10 18 каждую секунду. Учитывая, что диаметр протона или нейтрона составляет примерно 10 −15 м и что на 18 порядков больше, чем эти 1000 метров, хорошей фразой, которую можно сказать своей семье, друзьям и соседям, будет то, что один километр пространства расширяется на скорость, эквивалентная диаметру одного протона в секунду. Если хотите, мы можем немного увеличить масштаб по времени.
Учитывая, что диаметр протона или нейтрона составляет примерно 10 −15 м и что на 18 порядков больше, чем эти 1000 метров, хорошей фразой, которую можно сказать своей семье, друзьям и соседям, будет то, что один километр пространства расширяется на скорость, эквивалентная диаметру одного протона в секунду. Если хотите, мы можем немного увеличить масштаб по времени.
| Н 0 = | 2,25 × 10 −18 | 10 × 365.25 × 24 × 3600 с 90 530 | |
| с | десятилетие |
| Н 0 = | 7,09 × 10 −10 | 1 |
| десятилетие |
Это немного больше диаметра обычного атома. Таким образом, один метр пространства расширяется со скоростью, эквивалентной диаметру атома, каждое десятилетие. Такое медленное расширение незаметно в тех масштабах, к которым привыкли люди. Наша жизнь слишком коротка, а размеры, с которыми нам приходится иметь дело ежедневно, слишком малы.
Наша жизнь слишком коротка, а размеры, с которыми нам приходится иметь дело ежедневно, слишком малы.
Чтобы начать понимать постоянную Хаббла, нам нужно немного увеличить масштаб — огромный бит — на 23 порядка и выше. Нам нужно смотреть на вселенную как на набор галактик; ближайшие из которых находятся на расстоянии нескольких миллионов световых лет (10 23 м), а самые дальние — на расстоянии десяти миллиардов световых лет (10 26 м). В настоящее время наиболее удаленными известными объектами являются квазары. Квазар — это галактика со сверхмассивной черной дырой в ядре, которая активно поглощает звезды.Самый далекий квазар удаляется от нас со скоростью 90% скорости света. Используя закон Хаббла, это дает нам расстояние в 12,7 миллиарда световых лет.
| r = | против | = | 0,90 с | |
| Н 0 | 2,25 × 10 −18 с −1 | |||
| r = | 4,01 × 10 17 световые секунды | |||
| r = | 4. 01 × 10 17 световых секунд 01 × 10 17 световых секунд | |||
| 365,25 × 24 × 3600 с | ||||
| r = | 12,7 × 10 9 световых лет | |||
Конечная судьба вселенной
Вселенная началась с большого взрыва и продолжает расти, хотя и гораздо медленнее, чем в начале своего существования. Инфляционный период, когда пространство росло в геометрической прогрессии, был довольно коротким.Подавляющая часть истории Вселенной была историей почти постоянного роста в целом, разбавленного очагами локального сжатия. Звезды сжимаются, галактики сталкиваются и сливаются, но расстояние между скоплениями галактик становится все больше и больше. Увеличение общего размера Вселенной означает, что гравитационное притяжение в космическом масштабе становится все слабее и слабее.
У нас есть достаточно доказательств, подтверждающих рождение Вселенной в результате большого взрыва, но окончательная судьба Вселенной все еще остается открытым вопросом. Унесет ли расширение галактики так далеко друг от друга, что они перестанут оказывать существенное гравитационное притяжение друг на друга? Этот возможный результат известен как тепловая смерть — несколько неподходящее название, поскольку впоследствии изолированные галактики не будут содержать ничего, кроме холодных мертвых звезд. Или же победит гравитация, и все рухнет само на себя? (Будь проклято расширение.) Это космическое обращение Большого взрыва известно как большое сжатие .
Унесет ли расширение галактики так далеко друг от друга, что они перестанут оказывать существенное гравитационное притяжение друг на друга? Этот возможный результат известен как тепловая смерть — несколько неподходящее название, поскольку впоследствии изолированные галактики не будут содержать ничего, кроме холодных мертвых звезд. Или же победит гравитация, и все рухнет само на себя? (Будь проклято расширение.) Это космическое обращение Большого взрыва известно как большое сжатие .
Ответ на этот вопрос можно найти, объединив закон Хаббла с формулой для космической скорости.Вселенная, которая расширяется вечно, будет иметь плотность, обеспечивающую меньшую скорость убегания, чем скорость ее наблюдаемого расширения. Вселенная, которая врезается в саму себя, будет иметь более высокую скорость убегания.
Начните с установки формулы скорости убегания равной скорости из закона Хаббла.
Возведите в квадрат обе стороны, чтобы исключить квадратный корень.
А вот и сложная часть. Какова масса Вселенной? Определить это число довольно сложно, но, взглянув на большую часть Вселенной, мы можем определить ее плотность.Плотность, умноженная на объемы, дает нам массу. Глядя с нашей точки зрения на Млечный Путь, мы можем одинаково хорошо видеть практически во всех направлениях. (Млечный Путь довольно перегружен, что не позволяет нам видеть те части Вселенной, которые лежат вдоль его плоскости, но это не сильно вредит делу.) Геометрическое место всех точек, равноудаленных от фиксированной точки, порождает сферу в пространстве. Умножение плотности наблюдаемой Вселенной на объем содержащей ее сферы дает нам ее массу.
м = ρ = ρ v = ρ ( 4 3 π R 3 ) = 4 7 3 πρ R 3
Подставьте это выражение в производное от него…
| H 0 2 r 2 = | 2 Г | 4πρ р 3 | |
| р | 3 |
и решить для плотности.
Это критическая плотность, отделяющая вечное расширение от возможного коллапса. Давайте вычислим его значение, используя текущую наилучшую оценку постоянной Хаббла в единицах СИ.
| |||
|
Все, что выше этой плотности, будет сопротивляться расширению пространства. Вы, я и все, что мы видим в нашей обычной жизни, имеет гораздо большую плотность, чем эта, и будет сохранять свою форму и размер до тех пор, пока все остальные вещи остаются неизменными. Люди и другие животные имеют плотность примерно такую же, как вода — 10 3 кг/м 3 или на 30 порядков больше критической плотности.
Однако, глядя на вселенную в целом, ситуация несколько иная. Учитывая, что большая часть Вселенной состоит из водорода и что масса одного атома водорода составляет 1,67 × 10 –27 кг, это соответствует плотности в полдюжины атомов водорода на кубический метр.
| ||||
|
Наша галактика и, вероятно, любая другая видимая галактика имеет плотность примерно один атом водорода на кубический сантиметр. Поскольку в кубическом метре содержится миллион кубических сантиметров, плотность галактик более чем достаточна. Единственное, что не может противостоять расширению пространства, — это пространство между галактиками, где плотность, по-видимому, составляет порядка одного атома водорода на каждые четыре кубических метра.
Третий возможный исход
Постоянная Хаббла кажется , а не постоянной. Наблюдения, впервые сделанные в 1998 году, показывают, что скорость расширения Вселенной увеличивается. Если Вселенная началась с большого взрыва 13,8 миллиардов лет назад, она может закончиться большим разрывом , через 20 миллиардов лет в будущем. Причина в том, что во Вселенной есть нечто большее, чем кажется на первый взгляд. Намного больше.
То, что вы видите, не то, что вы получаете.
Фрэнк Вильчек, 2006 г.
Считается, что только 4% Вселенной состоит из обычных веществ — атомов, ядер, электронов, фотонов и нейтрино.Еще 23% составляет темной материи — «темная», потому что она взаимодействует гравитационно, как обычная материя, но не электромагнитно. Таким образом, его нельзя «увидеть» с помощью электромагнитного излучения, такого как свет, рентгеновские лучи или радиоволны. (Темная материя обсуждается более подробно в предыдущем разделе этой книги.) Остальные 73% Вселенной — подавляющее большинство — представлены в виде темной энергии . Темная энергия действительно странная не только потому, что ее нельзя увидеть, но и потому, что она во многом похожа на отрицательную массу.То есть стремится расширить пространство, а не сжать его. Несмотря на свое превосходство, темная энергия оказывает лишь самое слабое влияние на локальное пространство вокруг нас. (В этом контексте «местный» относится ко всему в пределах нашей галактики и почти ко всему отсюда до ближайшей тысячи галактик.) Каким бы маленьким он ни был, этот крошечный эффект суммируется до тех пор, пока не начинает доминировать над поведением пространства во Вселенной в целом. Темная энергия может быть крошечной, но она повсюду. Подобно стае комаров на летнем пикнике, темная энергия способна испортить всю вечеринку.
(Темная материя обсуждается более подробно в предыдущем разделе этой книги.) Остальные 73% Вселенной — подавляющее большинство — представлены в виде темной энергии . Темная энергия действительно странная не только потому, что ее нельзя увидеть, но и потому, что она во многом похожа на отрицательную массу.То есть стремится расширить пространство, а не сжать его. Несмотря на свое превосходство, темная энергия оказывает лишь самое слабое влияние на локальное пространство вокруг нас. (В этом контексте «местный» относится ко всему в пределах нашей галактики и почти ко всему отсюда до ближайшей тысячи галактик.) Каким бы маленьким он ни был, этот крошечный эффект суммируется до тех пор, пока не начинает доминировать над поведением пространства во Вселенной в целом. Темная энергия может быть крошечной, но она повсюду. Подобно стае комаров на летнем пикнике, темная энергия способна испортить всю вечеринку.
При таком развитии событий примерно через десять миллиардов лет расстояние между галактиками увеличится до такой степени, что свет не сможет достаточно быстро пересекать пространство между ними. Пространство будет расширяться так быстро, что каждая галактика станет независимой и невидимой для любой другой галактики. Тогда наша видимая Вселенная сократится с нынешних 100 000 галактик до одной — нашего Млечного Пути.
Пространство будет расширяться так быстро, что каждая галактика станет независимой и невидимой для любой другой галактики. Тогда наша видимая Вселенная сократится с нынешних 100 000 галактик до одной — нашего Млечного Пути.
Вот это действительно странно. Если ничто не остановит ускорение расширения, в конце концов сами галактики начнут разрушаться.(Это так называемый сценарий фантомной энергии .) Во-первых, 100 миллиардов звезд Млечного Пути разделятся, чтобы сформировать изолированные вселенные Солнечной системы. Тогда пространство внутри этих солнечных систем начнет заметно увеличиваться. Земля и другие планеты удалятся друг от друга в нашей Солнечной системе. Солнце будет становиться все меньше в небе, пока не исчезнет. В этот момент жизнь на Земле станет совсем плохой. (Если предположить, что Земля все еще существовала.) Мысль о потере связи с Солнцем хуже, чем мысль об изоляции от остальной вселенной.Это будет нашим эффективным концом. Если бы кто-нибудь вокруг стал свидетелем того, что произошло дальше, он в конечном итоге увидел бы, что скорость расширения увеличилась до такой степени, что Земля взорвалась, затем все на Земле превратилось бы в пар, затем молекулы потеряли бы когерентность, а затем атомы и ядра. Окончательный конец всего этого наступит, когда сами фундаментальные частицы будут разорваны в клочья и от Вселенной не останется ничего, что говорило бы о ее существовании.
Окончательный конец всего этого наступит, когда сами фундаментальные частицы будут разорваны в клочья и от Вселенной не останется ничего, что говорило бы о ее существовании.
Я скажу вам, что мне нравится в этой штуке.Это заставляет вас думать не только о себе. Как будет выглядеть мир, когда ты умрешь? Ответ культурно совершенно другой (такова природа времени, в котором мы живем), но физически почти такой же. Умножьте это на десять, на сто, на тысячу, на миллион жизней! Хотите сделать прогноз? Продолжать. Миллиард. Триллион жизней. Теперь временные масштабы стали настолько обширными, что лишь немногие будут строить догадки. Это область теоретической физики, и, что удивительно, это , а не за пределами нашего понимания.
Ускорение под действием силы тяжести — Frega Physics
Ускорение под действием силы тяжести — это скорость изменения скорости объекта под действием силы тяжести. Все объекты, упавшие из одного места, упадут на землю за одинаковое время, независимо от массы.
 На Земле среднее ускорение свободного падения составляет -9,81 м/с 2 *. Объекты, которые не ударяются о землю одновременно, испытывают сопротивление воздуха, силу трения, которая замедляет движение объектов.Этого можно добиться, уменьшив сопротивление воздуха путем изменения формы объекта.
На Земле среднее ускорение свободного падения составляет -9,81 м/с 2 *. Объекты, которые не ударяются о землю одновременно, испытывают сопротивление воздуха, силу трения, которая замедляет движение объектов.Этого можно добиться, уменьшив сопротивление воздуха путем изменения формы объекта.Ускорение свободного падения ВСЕГДА отрицательное. Любой объект, на который действует только сила тяжести (снаряд или объект в свободном падении), имеет ускорение -9,81 м/с 2 независимо от направления. Ускорение отрицательно при движении вверх, потому что скорость уменьшается. Ускорение отрицательное при движении вниз, потому что оно движется в отрицательном направлении, вниз. Даже в верхней части пути, где мгновенная скорость равна 0 м/с, ускорение равно -9.81 м/с 2 .
Всякий раз, когда в задаче упоминается объект, находящийся в состоянии “свободного падения”, “падающий”, “брошенный”, “брошенный” или любой другой синоним, предполагается постоянное значение ускорения свободного падения. Если уравнение имеет a в нем, например, v = v 0 + at , ускорение отрицательно . Если в уравнении есть g , например W = mg, подразумевается направление, а ускорение положительное .
Если уравнение имеет a в нем, например, v = v 0 + at , ускорение отрицательно . Если в уравнении есть g , например W = mg, подразумевается направление, а ускорение положительное .
*-10 м/с 2 является приемлемым числом для большинства расчетов в задачах, но -9.81 – более точное число.
| Переменный символ | Si Unit | A | Ускорение | метров в секунду в секунду (м/с/с) или метров в секунду в квадрате (м/с 2 ) | миль/ч/с, км/ч/с | Ускорение – это скорость, при которой скорость
изменения; это изменение скорости в единицу времени.На этом уровне
считать ускорение равномерным или постоянным.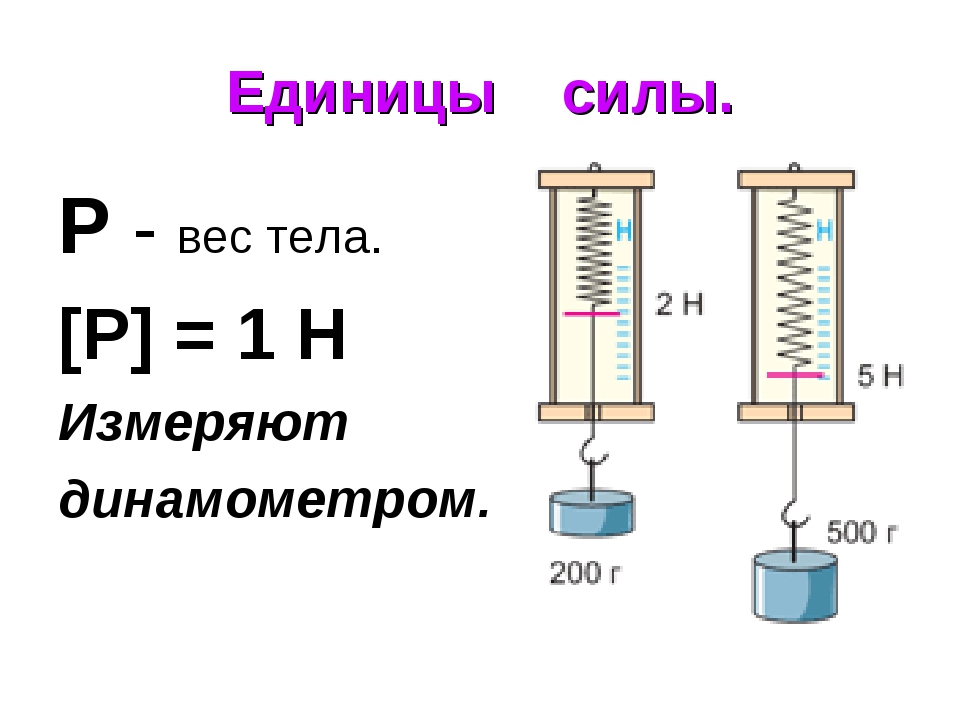 Поскольку это вектор, берется направление
в учетную запись. Будьте осторожны со своими негативами и позитивами. Положительный
ускорение может означать ускорение, движение вперед или замедление,
двигаться назад. Отрицательное ускорение может означать замедление,
двигаться вперед или ускоряться, двигаться назад. Поскольку это вектор, берется направление
в учетную запись. Будьте осторожны со своими негативами и позитивами. Положительный
ускорение может означать ускорение, движение вперед или замедление,
двигаться назад. Отрицательное ускорение может означать замедление,
двигаться вперед или ускоряться, двигаться назад. | ||||||
| г | GУскорение из-за гравитации | метров в секунду в секунду (м / с / с) или метров на второй квадрат (м / с 2 ) | MPH / с, км/ч/с | При отсутствии сопротивления воздуха все предметы при свободном падении ударятся о
землю одновременно при падении с одной и той же высоты, независимо от
масса.Ускорение под действием силы тяжести
это установленный номер для определенного места, обычно по планете (но это
число может незначительно варьироваться на поверхности планеты в зависимости от расстояния
от ядра планеты). На Земле среднее ускорение из-за
сила тяжести равна -9,81 м/с 2 (хотя -10 м/с 2 допустимо для использования в большинстве расчетов).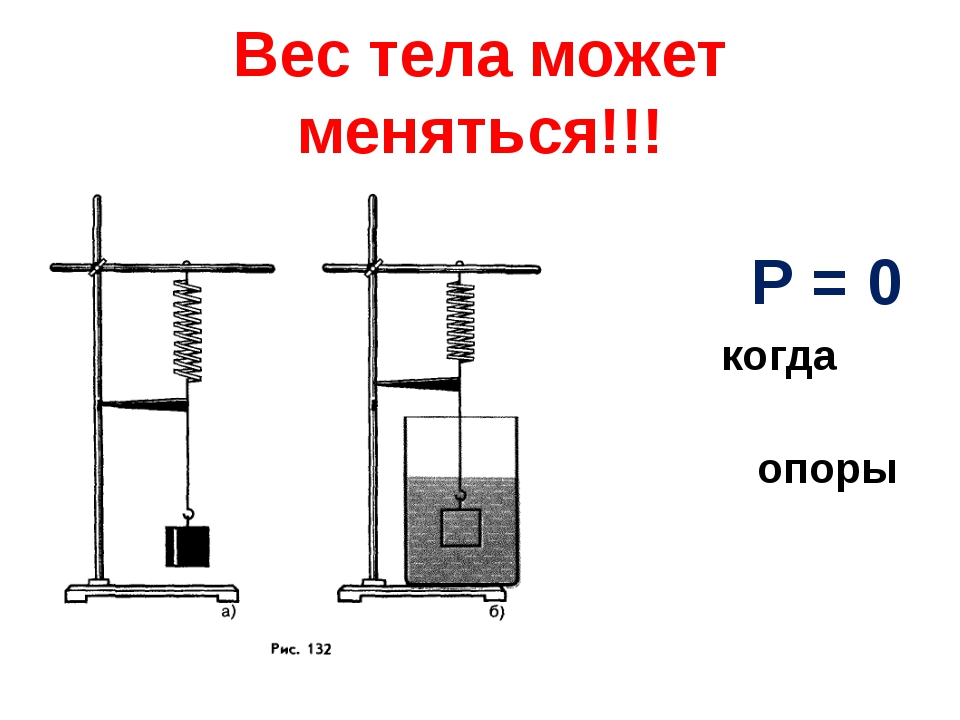 |

 Физика 104
Физика 104 3b выше:
3b выше:
 ноль
точки гравитационной потенциальной энергии для двух точек
частиц бесконечность.
ноль
точки гравитационной потенциальной энергии для двух точек
частиц бесконечность. 4а, площадь под графиком a в зависимости от t,
изменение скорости = 3,0 м/с 2 (4,0
с) = 12 м/с. Работа, совершаемая чистой силой = изменение кинетической
энергия = 1/2 мВ f 2 – 1/2 мВ o 2
4а, площадь под графиком a в зависимости от t,
изменение скорости = 3,0 м/с 2 (4,0
с) = 12 м/с. Работа, совершаемая чистой силой = изменение кинетической
энергия = 1/2 мВ f 2 – 1/2 мВ o 2  0 кг высвобождается из
отдых на вершине наклона без трения высотой 3
м и длиной 5 м. Принимая
0 кг высвобождается из
отдых на вершине наклона без трения высотой 3
м и длиной 5 м. Принимая 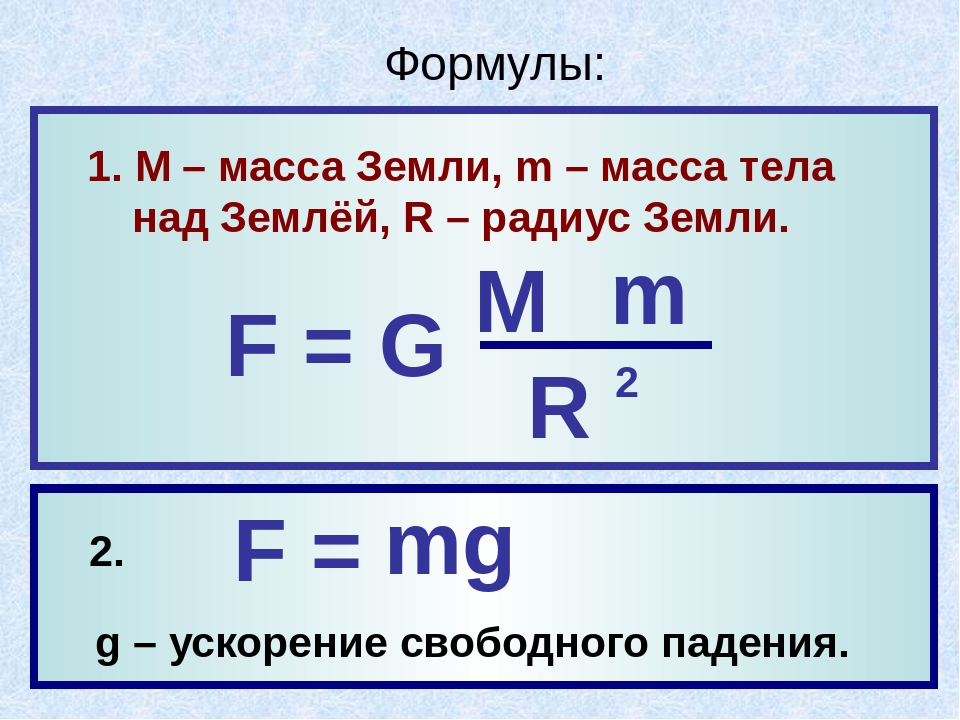 Объект, являющийся
выпущенный из верхней части наклона означает, что его
начальная скорость v i равна нулю, так что K i = 1/2 мв i 2 = 0.Из консервации
энергии, U i + K i = U f + K f
Объект, являющийся
выпущенный из верхней части наклона означает, что его
начальная скорость v i равна нулю, так что K i = 1/2 мв i 2 = 0.Из консервации
энергии, U i + K i = U f + K f 

 – ISO 31-3 «Количества и единицы.
Часть 3, Механика”, 1992 2
– ISO 31-3 «Количества и единицы.
Часть 3, Механика”, 1992 2  ан
объект на
Луна весит около одной шестой своего веса на Земле, но
его масса
без изменений.
ан
объект на
Луна весит около одной шестой своего веса на Земле, но
его масса
без изменений.
 От
это определение, нормальные силы, силы натяжения и трения
применяемый
силы, но мы
обычно выделяют их отдельно. В нашем случае применяется
силы
включать такие
явления, такие как толкание объекта или сила, приложенная
весна на
объект.
От
это определение, нормальные силы, силы натяжения и трения
применяемый
силы, но мы
обычно выделяют их отдельно. В нашем случае применяется
силы
включать такие
явления, такие как толкание объекта или сила, приложенная
весна на
объект.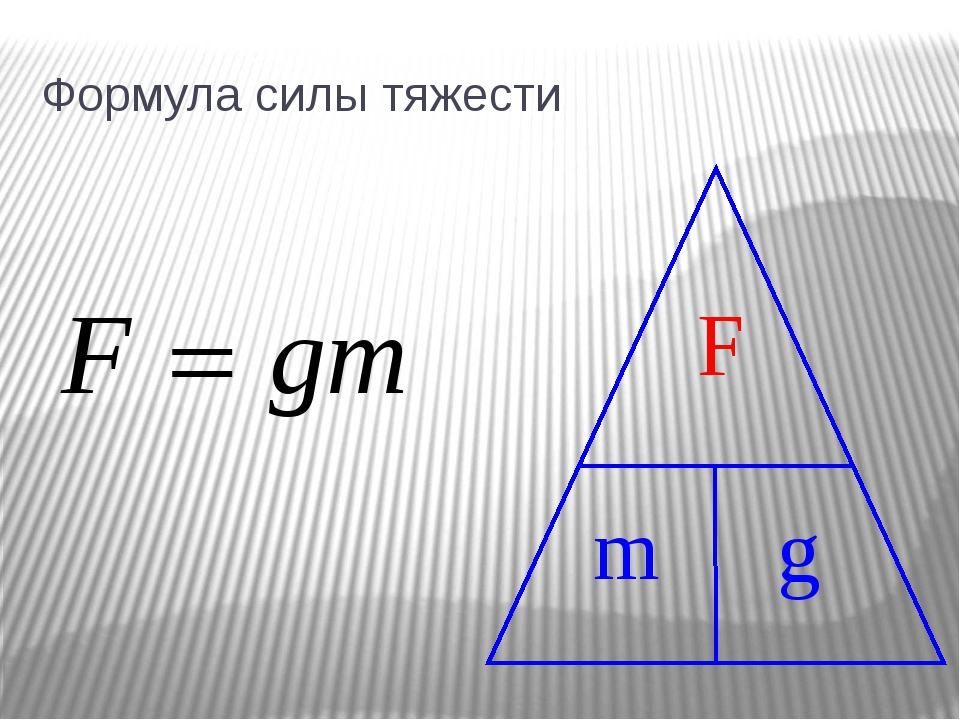
 Изолировать
в
тело. Это
шаг требует
что вы отделяете тело (блок,
колесо, тележка и т. д.), которые вы исследуете из
все остальное и
Нарисуй это.
Изолировать
в
тело. Это
шаг требует
что вы отделяете тело (блок,
колесо, тележка и т. д.), которые вы исследуете из
все остальное и
Нарисуй это.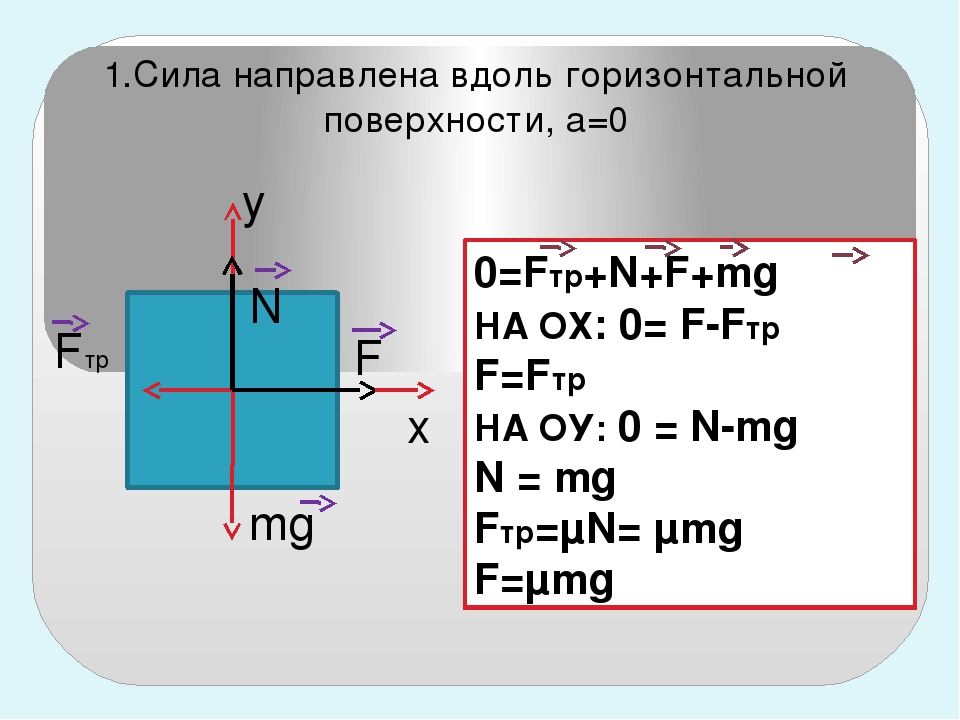

 Используйте следующие правила:
Используйте следующие правила: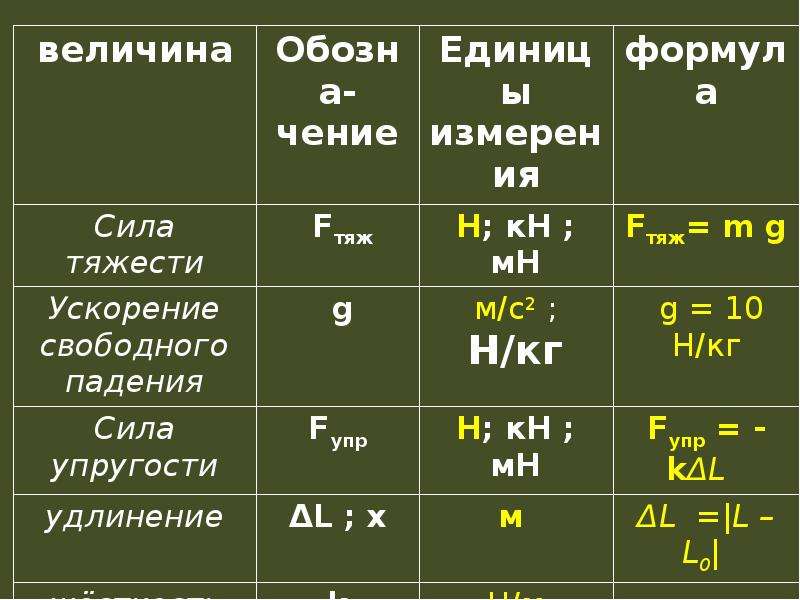
 Выберите одну ось
по направлению ускорения. Выберите другую ось
перпендикулярно
первый.
Выберите одну ось
по направлению ускорения. Выберите другую ось
перпендикулярно
первый.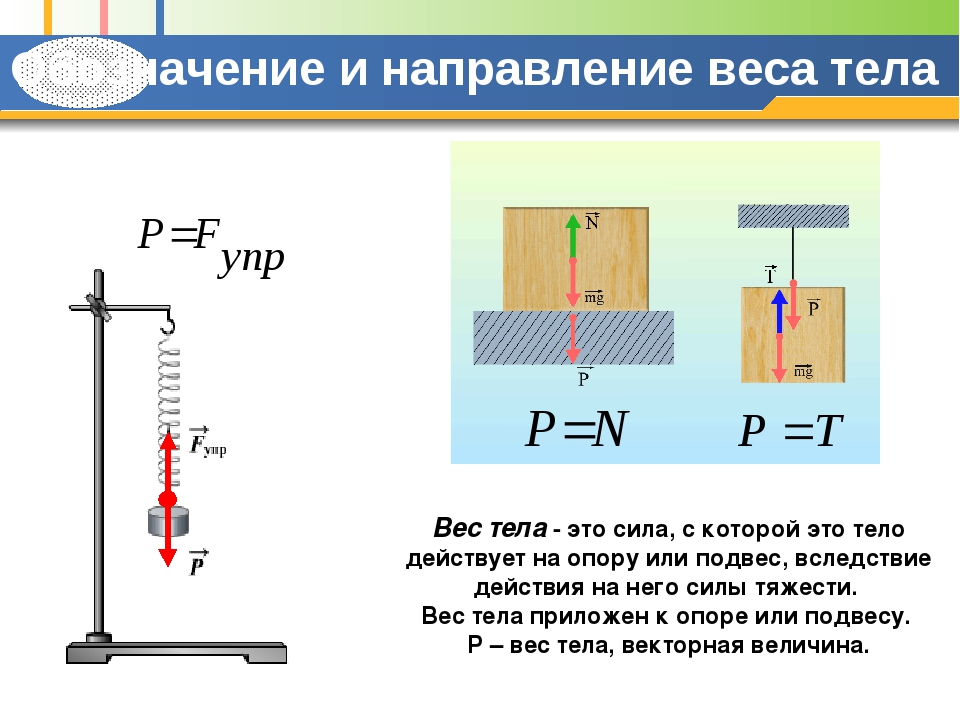 На данном этапе курса нам не нужно
себя с
крутящий момент.
На данном этапе курса нам не нужно
себя с
крутящий момент. Этот шаг является критическим.
Разве что можно выявить и правильно сложить все силы
воздействуя на каждый объект, вы не сможете решить
проблема.
Этот шаг является критическим.
Разве что можно выявить и правильно сложить все силы
воздействуя на каждый объект, вы не сможете решить
проблема. Один раз
у вас есть уравнения движения, в
принципе, вы можете решить их для желаемых неизвестных.
Один раз
у вас есть уравнения движения, в
принципе, вы можете решить их для желаемых неизвестных.