Мгновенная скорость материальной точки при криволинейном движении: Криволинейное движение – формула, примеры, признаки - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Материальная точка движется равномерно по криволинейной траектории. Неравномерное движение. Скорость при неравномерном движении

В зависимости от формы траектории, движение делится на прямолинейное и криволинейное. В реальном мире мы чаще всего имеем дело с криволинейным движением, когда траектория представляет собой кривую линию. Примерами такого движения является траектория тела, брошенного под углом к горизонту, движение Земли вокруг Солнца движение планет, конца стрелки часов по циферблату и т.д.

Рисунок 1. Траектория и перемещение при криволинейном движении

Определение

Криволинейное движение — это движение, траектория которого представляет собой кривую линию (например, окружность, эллипс, гиперболу, параболу). При движении по криволинейной траектории вектор перемещения $\overrightarrow{s}$ направлен по хорде (рис. 1), а l — длина траектории. Мгновенная скорость движения тела (то есть скорость тела в данной точке траектории) направлена по касательной в той точке траектории, где в данный момент находится движущееся тело (рис.

2).

Рисунок 2. Мгновенная скорость при криволинейном движении

Однако более удобным является следующий подход. Можно представить это движение как совокупность нескольких движений по дугам окружностей (см. рис. 4.). Таких разбиений получится меньше, чем в предыдущем случае, кроме того, движение по окружности само является криволинейным.

Рисунок 4. Разбиение криволинейного движения на движения по дугам окружностей

Вывод

Для того, чтобы описывать криволинейное движение, нужно научиться описывать движение по окружности, а потом произвольное движение представлять в виде совокупностей движений по дугам окружностей.

Задачей исследования криволинейного движения материальной точки является составление кинематического уравнения, описывающего это движение и позволяющего по заданным начальным условиям определить все характеристики этого движения.

Рисунок 1. Траектория и перемещение при криволинейном движении

Определение

Рисунок 2. Мгновенная скорость при криволинейном движении

Рисунок 4. Разбиение криволинейного движения на движения по дугам окружностей

Вывод

Кинематика изучает движение без выявления причин, вызывающих это движение. Кинематика является разделом механики. Главной задачей кинематики является математическое определение положения и характеристик движения точек или тел во времени.

Основные кинематические величины:

– Перемещение() – вектор, соединяющий начальную и конечную точки.

r – радиус-вектор, определяет положение МТ в пространстве.

– Скорость – отношение пути ко времени.

– Путь – множество точек через которое прошло тело.

– Ускорение – скорость изменения скорости, то есть первая производная от скорости.

2.Ускорение при криволинейном движении: нормальное и тангенциальное ускорение. Плоское вращение. Угловая скорость, ускорение.

Криволинейное движение – это движение, траектория которого представляет собой кривую линию. Примером криволинейного движения является движение планет, конца стрелки часов по циферблату и т.д.

Криволинейное движение – это всегда ускоренное движение. То есть ускорение при криволинейном движении присутствует всегда, даже если модуль скорости не изменяется, а изменяется только направление скорости.

Изменение величины скорости за единицу времени – это тангенциальное ускорение :

Где 𝛖 τ , 𝛖 0 – величины скоростей в момент времени t 0 + Δt и t 0 соответственно. Тангенциальное ускорение

в данной точке траектории по направлению совпадает с направлением скорости движения тела или противоположно ему.

Нормальное ускорение – это изменение скорости по направлению за единицу времени:

Нормальное ускорение направлено по радиусу кривизны траектории (к оси вращения). Нормальное ускорение перпендикулярно направлению скорости.

Полное ускорение при равнопеременном криволинейном движении тела равно:

–угловая скорость показывает, на какой угол поворачивается точка при равномерном движении по окружности за единицу времени. Единица измерения в СИ – рад/с.

Плоское вращение – это вращение всех векторов скоростей точек тела в одной плоскости.

3.Связь между векторами скорости и угловой скорости материальной точки. Нормальное, тангенциальное и полное ускорение.

Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.

Нормальное (центростремительное) ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой n. Вектор нормального ускорения направлен по радиусу кривизны траектории.

Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой.

Кинематика точки. Путь. Перемещение. Скорость и ускорение. Их проекции на координатные оси. Вычисление пройденного пути. Средние значения.

Кинематика точки – раздел кинематики, изучающий математическое описание движения материальных точек. Основной задачей кинематики является описание движения при помощи математического аппарата без выяснения причин, вызывающих это движение.

Путь и перемещение. Линия, по которой движется точка тела, называется траекторией движения . Длина траектории называется пройденным путём . Вектор, соединяющий начальную и конечную точки траектории называется перемещением. Скорость – векторная физическая величина, характеризующая быстроту перемещения тела, численно равная отношению перемещения за малый промежуток времени к величине этого промежутка. Промежуток времени считается достаточно малым, если скорость при неравномерном движении в течение этого промежутка не менялась. Определяющая формула скорости имеет вид v = s/t. Единица скорости – м/с. На практике используют единицу измерения скорости км/ч (36 км/ч = 10 м/с). Измеряют скорость спидометром.

Ускорение – векторная физическая величина, характеризующая быстроту изменения скорости, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло. Если скорость изменяется одинаково в течение всего времени движения, то ускорение можно рассчитать по формуле a=Δv/Δt. Единица ускорения – м/с 2

Скорость и ускорение при криволинейном движении. Тангенциальное и нормальное ускорения.

Криволинейные движения – движения, траектории которых представляют собой не прямые, а кривые линии.

Криволинейное движение – это всегда движение с ускорением, даже если по модулю скорость постоянна. Криволинейное движение с постоянным ускорением всегда происходит в той плоскости, в которой находятся векторы ускорения и начальные скорости точки. В случае криволинейного движения с постоянным ускорением в плоскости xOy проекции v x и v y ее скорости на оси Ox и Oy и координаты x и y точки в любой момент времени t определяется по формулам

v x =v 0 x +a x t, x=x 0 +v 0 x t+a x t+a x t 2 /2; v y =v 0 y +a y t, y=y 0 +v 0 y t+a y t 2 /2

Частным случаем криволинейного движения – является движение по окружности. Движение по окружности, даже равномерное, всегда есть движение ускоренное: модуль скорости все время направлен по касательной к траектории, постоянно меняет направление, поэтому движение по окружности всегда происходит с центростремительным ускорением |a|=v 2 /r где r – радиус окружности.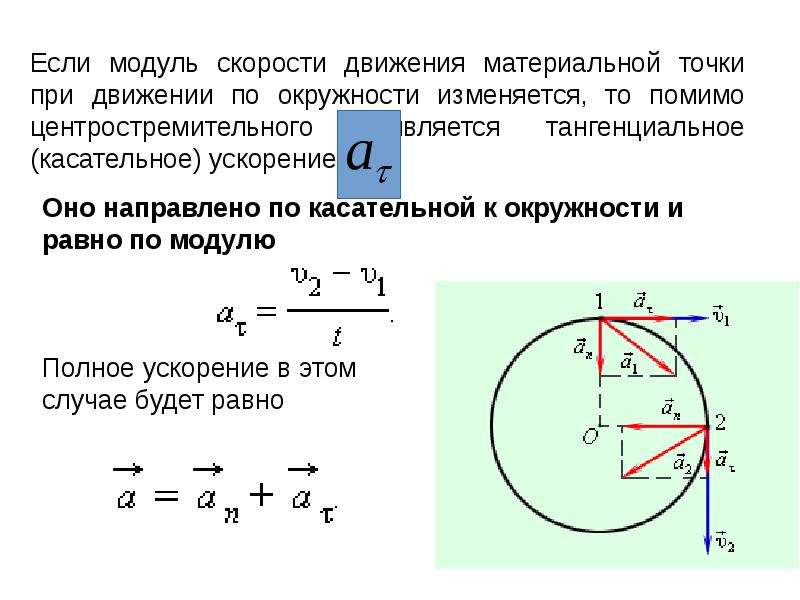

Вектор ускорения при движении по окружности направлен к центру окружности и перпендикулярно вектору скорости.

При криволинейном движении ускорение можно представить как сумму нормальной и тангенциальной составляющих: ,

Нормальное (центростремительное) ускорение, направлено к центру кривизны траектории и характеризует изменение скорости по направлению:

v – мгновенное значение скорости, r – радиус кривизна траектории в данной точке.

Тангенциальное (касательное) ускорение, направлено по касательной к траектории и характеризует изменение скорости по модулю.

Полное ускорение, с которым движется материальная точка, равно:

Тангенциальное ускорение характеризует быстроту изменения скорости движения по численному значению и направлена по касательной к траектории.

Следовательно

Нормальное ускорение характеризует быстроту изменения скорости по направлению. Вычислим вектор:

4.Кинематика твёрдого тела. Вращение вокруг неподвижной оси. Угловые скорость и ускорения. Связь между угловыми и линейными скоростями и ускорениями.

Кинематика вращательного движения.

Движение тела может быть как поступательным, так и вращательным. В этом случае тело представляется в виде системы жестко связанных между собой материальных точек.

При поступательном движение любая прямая, проведенная в теле, перемещается параллельно самой себе. По форме траектории поступательное движение может быть прямолинейным и криволинейным. При поступательном движении все точки твердого тела за один и тот же промежуток времени совершают равные по величине и направлению перемещения. Следовательно,скорости и ускорения всех точек тела в любой момент времени также одинаковы. Для описания поступательного движения достаточно определить движение одной точки.

Вращательным движением твёрдого тела вокруг неподвижной оси называется такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой (ось вращения).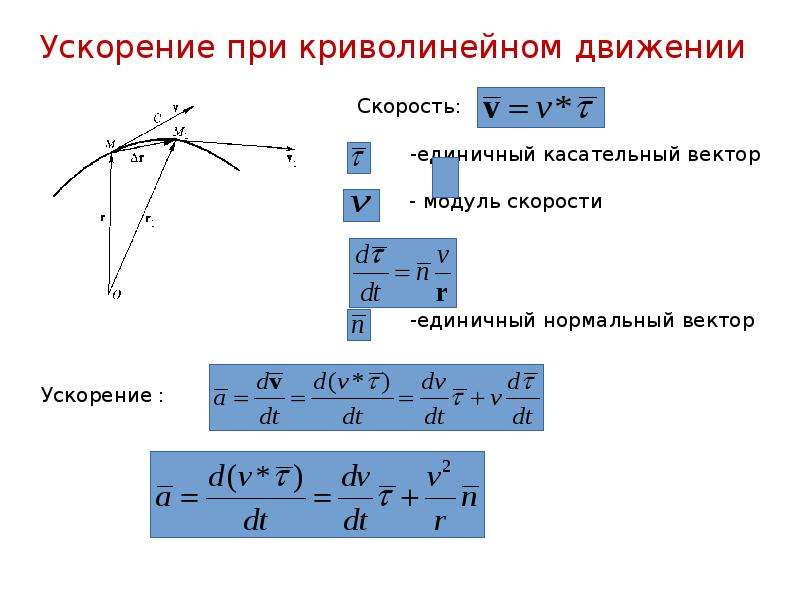

Ось вращения может проходить через тело или лежать за его пределами. Если ось вращения проходит сквозь тело, то точки, лежащие на оси, при вращении тела остаются в покое. Точки твёрдого тела, находящиеся на разных расстояниях от оси вращения за одинаковые промежутки времени проходят различные расстояния и, следовательно, имеют различные линейные скорости.

При вращении тела вокруг неподвижной оси точки тела за один и тот же промежуток времени совершают одно и тоже угловое перемещение . Модуль равен углу поворота тела вокруг оси за время , направления вектора углового перемещения с направлением вращения тела связано правилом винта: если совместить направления вращения винта с направлением вращения тела, то вектор будет совпадать с поступательным движением винта. Вектор направлен вдоль оси вращения.

Быстроту изменения углового перемещения определяет угловая скорость – ω. По аналогии с линейной скоростью вводят понятия средней и мгновенной угловой скорости :

Угловая скорость – величина векторная.

Быстроту изменения угловой скорости характеризует среднее и мгновенное

угловое ускорение .

Вектор и может совпадать с вектором , и быть противоположным ему

С прямолинейным движением мы более или менее научились работать на предыдущих уроках, а именно, решать главную задачу механики для такого вида движения.

Однако ясно, что в реальном мире мы чаще всего имеем дело с криволинейным движением, когда траектория представляет собой кривую линию. Примерами такого движения является траектория тела, брошенного под углом к горизонту, движение Земли вокруг Солнца, и даже траектория движения ваших глаз, следящих сейчас за этим конспектом.

Вопросу о том, как решается главная задача механики в случае криволинейного движения, и будет посвящен этот урок.

Для начала определимся, какие принципиальные отличия есть у криволинейного движения (Рис. 1) относительно прямолинейного, и к чему эти отличия приводят.

Рис.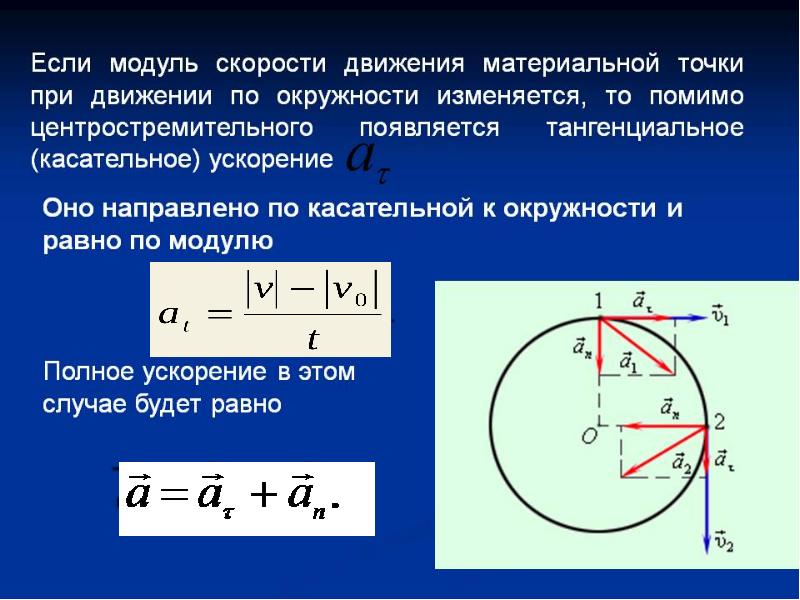 1. Траектория криволинейного движения

Поговорим о том, как удобно описывать движение тела при криволинейном движении.

Можно разбить движение на отдельные участки, на каждом из которых движение можно считать прямолинейным (Рис. 2).

Рис. 2. Разбиение криволинейного движения на поступательные движения

Однако более удобным является следующий подход. Мы представим это движение как совокупность нескольких движений по дугам окружностей (см. Рис. 3.). Обратите внимание, что таких разбиений меньше, чем в предыдущем случае, кроме того, движение по окружности является криволинейным. Кроме того, примеров движения по окружности в природе встречается очень часто. Из этого можно сделать вывод:

Для того чтобы описывать криволинейное движение, нужно научиться описывать движение по окружности, а потом произвольное движение представлять в виде совокупностей движений по дугам окружностей.

Рис. 3. Разбиение криволинейного движения на движения по дугам окружностей

Итак, начнем изучение криволинейного движения с изучения равномерного движения по окружности. Давайте разберемся, каковы принципиальные отличия криволинейного движения от прямолинейного. Для начала вспомним, что в девятом классе мы изучили тот факт, что скорость тела при движении по окружности направлена по касательной к траектории. Кстати, этот факт вы можете пронаблюдать на опыте, если посмотрите, как движутся искры при использовании точильного камня.

Рассмотрим движение тела по окружности (Рис. 4).

Рис. 4. Скорость тела при движении по окружности

Обратите внимание, что в данном случае модуль скорости тела в точке А равен модулю скорости тела в точке B.

Однако, вектор не равен вектору . Итак, у нас появляется вектор разности скоростей (см. Рис. 5).

Рис. 5. Разность скоростей в точках A и B.

Причем изменение скорости произошло через некоторое время . Таким образом, мы получаем знакомую комбинацию:

это не что иное, как изменение скорости за промежуток времени, или ускорение тела. Можно сделать очень важный вывод:

Движение по криволинейной траектории является ускоренным. Природа этого ускорения – непрерывное изменение направление вектора скорости.

Еще раз отметим, что даже если говорится, что тело равномерно движется по окружности, имеется в виду, что модуль скорости тела не изменяется, однако такое движение всегда является ускоренным, поскольку изменяется направление скорости.

В девятом классе вы изучали, чему равно такое ускорение и как оно направлено (см. Рис. 6). Центростремительное ускорение всегда направлено к центру окружности, по которой движется тело.

Рис. 6.Центростремительное ускорение

Модуль центростремительного ускорения может быть рассчитан по формуле

Переходим к описанию равномерного движения тела по окружности. Договоримся, что скорость , которой вы пользовались по время описания поступательного движения, теперь будет называться линейной скоростью. И под линейной скоростью мы будем понимать мгновенную скорость в точке траектории вращающегося тела.

Рис. 7. Движение точек диска

Рассмотрим диск, который для определенности вращается по часовой стрелке. На его радиусе отметим две точки A и B. И рассмотрим их движение. За некоторое время эти точки переместятся по дугам окружности и станут точками A’ и B’. Очевидно, что точка А совершила большее перемещение, чем точка B. Из этого можно сделать вывод, что чем дальше от оси вращения находится точка, тем с большей линейной скоростью она движется.

Однако, если внимательно посмотреть на точки А и В, можно сказать, что неизменным остался угол , на который они повернулись относительно оси вращения О. Именно угловые характеристики мы и будем использовать для описания движения по окружности. Отметим, что для описания движения по окружности, можно использовать угловые характеристики. Прежде всего, напомним понятие о радианной мере углов.

Угол в 1 радиан – это такой центральный угол, длина дуги которого равна радиусу окружности.

Таким образом, легко заметить, что например угол в равен радиан. И, соответственно, можно перевести любой угол, заданный в градусах, в радианы, умножив его на и поделив на .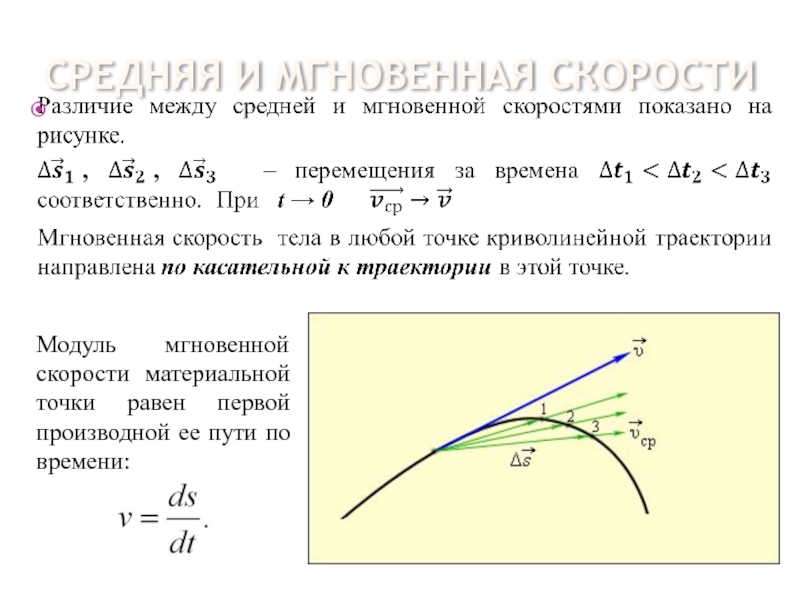 Угол поворота при вращательном движении аналогичен перемещению при поступательном движении. Заметим, что радиан – это безразмерная величина:

поэтому обозначение «рад» часто опускают.

Начнем рассмотрение движения по окружности с самого простого случая – равномерного движения по окружности. Напомним, что равномерным поступательным движением называется движение, при котором за любые равные промежутки времени тело совершает одинаковые перемещения. Аналогично,

Равномерным движением по окружности называется движение, при котором за любые равные промежутки времени тело поворачивается на одинаковые углы.

Аналогично понятию линейной скорости вводится понятие угловой скорости.

Угловой скоростью называется физическая величина, равная отношению угла, на который повернулось тело ко времени, за которое произошел этот поворот.

Измеряется угловая скорость в радианах в секунду, или просто в обратных секундах.

Найдем связь между угловой скоростью вращения точки и линейной скоростью этой точки.

Рис. 9. Связь между угловой и линейной скоростью

Точка А проходит при вращении дугу длиной S, поворачиваясь при этом на угол φ. Из определения радианной меры угла можно записать, что

Разделим левую и правую части равенства на промежуток времени , за который было совершено перемещение, затем воспользуемся определением угловой и линейной скоростей

Обратим внимание, что чем дальше точка находится от оси вращения, тем выше ее угловая и линейная скорость. А точки, расположенные на самой оси вращения, неподвижны. Примером этого может служить карусель: чем ближе вы находитесь к центру карусели, тем легче вам на ней удержаться.

Вспомним, что ранее мы вводили понятия периода и частоты вращения.

Период вращения – время одного полного оборота. Период вращения обозначается буквой и измеряется в секундах в системе СИ:

Частота вращения – число оборотов в единицу времени. Частота обозначается буквой и измеряется в обратных секундах:

Они связаны соотношением:

Существует связь между угловой скоростью и частотой вращения тела. Если вспомнить, что полный оборот равен , легко увидеть, что угловая скорость:

Кроме того, если вспомнить, каким образом мы определили понятие радиана, станет ясно, как связать линейную скорость тела с угловой:

Запишем также связь между центростремительным ускорением и этими величинами:

Таким образом, мы знаем связь между всеми характеристиками равномерного движения по окружности.

Подытожим. На этом уроке мы начали описывать криволинейное движение. Мы поняли, каким образом можно связать криволинейное движение с движением по окружности. Движение по окружности всегда является ускоренным, а наличие ускорения обуславливает тот факт, что скорость всегда меняет свое направление. Такое ускорение называется центростремительным. Наконец, мы вспомнили некоторые характеристики движения по окружности (линейную скорость, угловую скорость, период и частоту вращения), и нашли соотношения между ними.

Список литературы:

Г. Я. Мякишев, Б. Б. Буховцев, Н. Н. Сотский. Физика 10. – М.: Просвещение, 2008.
А. П. Рымкевич. Физика. Задачник 10-11. – М.: Дрофа, 2006.
О. Я. Савченко. Задачи по физике. – М.: Наука, 1988.
А. В. Пёрышкин, В. В. Крауклис. Курс физики. Т. 1. – М.: Гос. уч.-пед. изд. мин. просвещения РСФСР, 1957.

Энциклопедия ().
Аyp.ru ().
Википедия ().

Домашнее задание:

Решив задачи к данному уроку, вы сможете подготовиться к вопросам 1 ГИА и вопросам А1, А2 ЕГЭ.

Задачи 92, 94, 98, 106, 110 сб. задач А. П. Рымкевич изд. 10 ()
Вычислите угловую скорость движения минутной, секундной и часовой стрелок часов. Вычислите центростремительное ускорение, действующее на кончики этих стрелок, если радиус каждой из них равен одному метру.
Рассмотрите следующие вопросы и ответы на них:

Вопрос: Есть ли на поверхности Земли точки, в которых угловая скорость, связанная с суточным вращением Земли, равна нулю?

Ответ: Есть. Такими точками являются географические полюсы Земли. Скорость в этих точках равна нулю, потому что в этих точках вы будете находиться на оси вращения.

Тесты для педагогов по всем школьным предметам с ответами

Тест по теме “Имя существительное”

Тест на проверку знаний по теме “Имя существительное” в 4 классе (Определение морфологических признаков имени существительного, правописание имен существительных).

Мировоззрение, его виды и формы.

При составлении теста опора делалась на Краткий справочник по обществознанию Дениса Юрьевича Алексеева. Питер; Санкт-Петербург; 2016

Экономика и государство.

Тест составлен для 11-го класса и включает в себя такие темы, как “Экономические функции государства”, “Какой инструмент регулирования экономики выбрать?”, “Налоговая система РФ”, “Нужна ли рынку помощь государства?”

Налоги

Spotlight 5 module 1

Проверочный тест по английскому языку Spotlight 5 module 1

Германские земли в XVIII в.

Тест составлен для 8-го класса и включает в себя такие темы, как “Раздробленность Германии”, “Политическое развитие германских земель”, “Бранденбургско-Прусское государство”, “Два аграрных мира”, “Ремесло и торговля”, “Демографическое и социальное развитие”, “Фридрих II. Австро-прусский дуализм и реформы”, “Германские земли на рубеже XVIII-XIX вв.”

Экономика и её основные участники.

Тест по обществознанию составлен для учащихся 7-го класса и включил в себя следующие темы: “Что такое экономика”, “Натуральное и товарное хозяйство” и “Основные участники экономики”.

Англия на пути к индустриальной эре.

Тест по истории Нового времени составлен для 8-го класса и составлен с учётом следующих тем: “Ганноверы на троне”, “Власть у парламента. Тори и виги”, “Аграрная революция в Англии”, “Условия промышленного переворота”, “Промышленный переворот” и “Положение рабочих”.

Мир художественной культуры Возрождения

Тест для учащихся 7-го класса составлен в соответствии с УМК Юдовская А.Я. Всеобщая история. История Нового времени. 7 класс: учеб. для общеобразоват. организаций / А.Я. Юдовская, П.А. Баранов, Л.М. Ванюшкина; под ред. А.А. Искендерова. – 3-е изд. – М.: Просвещение, 2021. – 239 с.

Краткое содержание прямолинейное и криволинейное движение. Криволинейное

Понятия скорости и ускорения естественным образом обобщаются на случай движения материальной точки по криволинейной траектории . Положение движущейся точки на траектории задается радиус-вектором r , проведенным в эту точку из какой-либо неподвижной точки О , например, начала координат (рис. 1.2). Пусть в момент времени t материальная точка находится в положении М с радиус-вектором r = r (t ). Спустя короткое время Dt , она переместится в положение М 1 с радиусом – вектором r 1 = r (t + Dt ).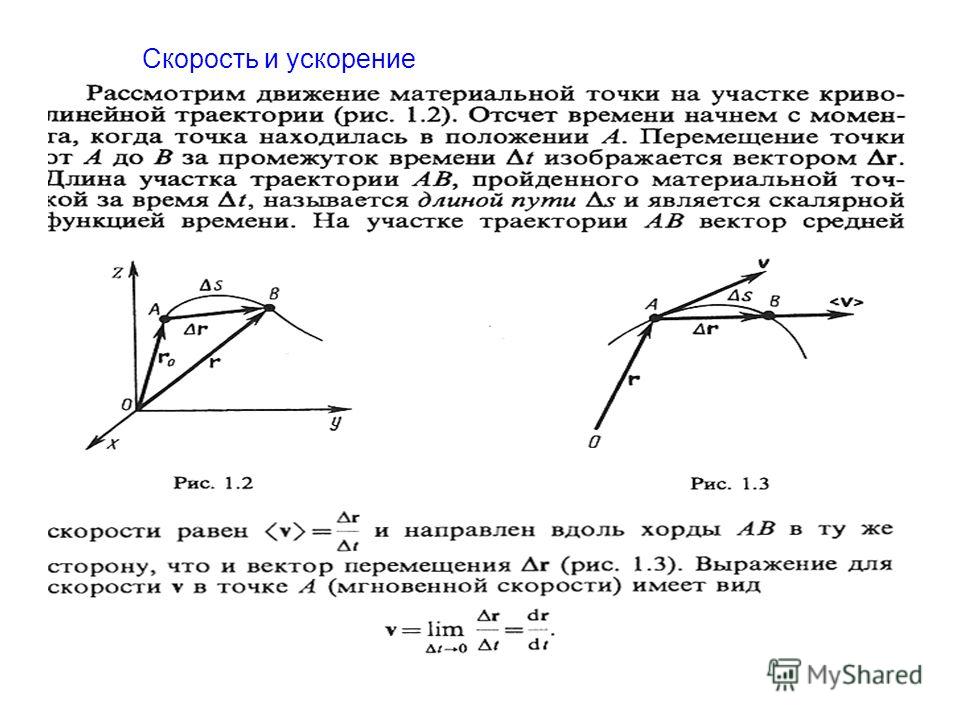 Радиус – вектор материальной точки получит приращение, определяемое геометрической разностью Dr = r 1 – r . Средней скоростью движения за время Dt называется величина

Направление средней скорости V ср совпадает с направлением вектора Dr .

Предел средней скорости при Dt ® 0, т. е. производная радиуса – вектора r по времени

(1.9)

называется истинной или мгновенной скоростью материальной точки. Вектор V направлен по касательной к траектории движущейся точки.

Ускорением а называется вектор, равный первой производной вектора скорости V или второй производной радиуса – вектора r по времени:

(1.10)

(1.11)

Отметим следующую формальную аналогию между скоростью и ускорением. Из произвольной неподвижной точки О 1 будем откладывать вектор скорости V движущейся точки во всевозможные моменты времени (рис. 1.3).

Конец вектора V называется скоростной точкой . Геометрическое место скоростных точек есть кривая, называемая годографом скорости. Когда материальная точка описывает траекторию, соответствующая ей скоростная точка движется по годографу.

Рис. 1.2 отличается от рис. 1.3 только обозначениями. Радиус – вектор r заменен на вектор скорости V , материальная точка – на скоростную точку, траектория – на годограф. Математические операции над вектором r при нахождении скорости и над вектором V при нахождении ускорения совершенно тождественны.

Скорость V направлена по касательной траектории. Поэтому ускорение a будет направлено по касательной к годографу скорости. Можно сказать, что ускорение есть скорость движения скоростной точки по годографу . Следовательно,

При криволинейном движении у вектора скорости изменяется направление. При этом может меняться и его модуль, т. е. длина. В этом случае вектор ускорения раскладывается на две составляющие: касательную к траектории и перпендикулярную к траектории (рис. 10). Составляющая называется тангенциальным (касательным) ускорением, составляющая –нормальным (центростремительным) ускорением.

Ускорение при криволинейном движении

Тангенциальное ускорение характеризует быстроту изменения линейной скорости, а нормальное ускорение характеризует быстроту изменения направления движения.

Полное ускорение равно векторной сумме тангенциального и нормального ускорений:

(15)

Модуль полного ускорения равен:

Рассмотрим равномерное движение точки по окружности. При этом и . Пусть в рассматриваемый момент времени t точка находится в положении 1 (рис. 11). Спустя время Δt точка окажется в положении 2, пройдя путь Δs , равный дуге 1-2. При этом скорость точки v получает приращение Δv , в результате чего вектор скорости, оставаясь неизменным по величине, повернется на угол Δφ , совпадающий по величине с центральным углом, опирающимся на дугу длиной Δs :

(16)

где R-радиус окружности, по которой движется точка. Найдем приращение вектора скорости Для этого перенесем вектор так, чтобы его начало совпадало с началом вектора . Тогда вектор изобразится отрезком, проведенным из конца вектора в конец вектора . Этот отрезок служит основанием равнобедренного треугольника со сторонами и и углом Δφ при вершине. Если угол Δφ невелик (что выполняется для малых Δt), для сторон этого треугольника можно приближенно написать:

Подставляя сюда Δφ из (16), получаем выражение для модуля вектора :

Разделив обе части уравнения на Δt и сделав предельный переход, получим величину центростремительного ускорения:

Здесь величины v и R постоянные, поэтому их можно вынести за знак предела. Предел отношения – это модуль скорости Его также называют линейной скоростью.

Радиус кривизны

Радиус окружности R называется радиусом кривизны траектории. Величина, обратная R, называется кривизной траектории:

где R – радиус рассматриваемой окружности. Если α есть центральный угол, соответствующий дуге окружности s, то, как известно, между R, α и s имеет место соотношение:

s = Rα . (18)

Понятие радиуса кривизны применимо не только к окружности, но и любой кривой линии. Радиус кривизны (или обратная ему величина – кривизна) характеризует степень изогнутости линии. Чем меньше радиус кривизны (соответственно, чем больше кривизна), тем сильнее изогнута линия. Рассмотрим это понятие подробнее.

Кругом кривизны плоской линии в некоторой точке A называется предельное положение окружности, проходящей через точку А и две другие точки В 1 и В 2 при их бесконечном приближении к точке А (на рис. 12 кривая проведена сплошной линией, а круг кривизны – пунктирной). Радиус круга кривизны дает радиус кривизны рассматриваемой кривой в точке A, а центр этого круга – центр кривизны кривой для той же точки А.

Проведем в точках B 1 и В 2 касательные B 1 D и В 2 Е к окружности, проходящей через точки В 1 , А и B 2 . Нормали к этим касательным B 1 С и В 2 С представят собой радиусы R окружности и пересекутся в ее центре С. Введем угол Δα между нормалями В1С и В 2 С; очевидно, он равен углу между касательными В 1 D и В 2 E. Обозначим участок кривой между точками B 1 и В 2 как Δs. Тогда по формуле (18):

Круг кривизны плоской кривой линии

Определение кривизны плоской кривой в разных точках

На рис. 13 изображены круги кривизны плоской линии в разных точках. В точке A 1 , где кривая является более пологой, радиус кривизны больше, чем в точке A 2 , соответственно, кривизна линии в точке A 1 будет меньше, чем в точке A 2 . В точке A 3 кривая является еще более пологой, чем в точках A 1 и A 2 , поэтому радиус кривизны в этой точке будет больше, а кривизна меньше. Кроме того, круг кривизны в точке A 3 лежит по другую сторону кривой. Поэтому величине кривизны в этой точке приписывают знак, противоположный знаку кривизны в точках A 1 и A 2: если кривизну в точках A 1 и A 2 будем считать положительной, то кривизна в точке A 3 будет отрицательной.

Криволинейные движения – движения, траектории которых представляют собой не прямые, а кривые линии. По криволинейным траекториям движутся планеты, воды рек.

Криволинейное движение – это всегда движение с ускорением, даже если по модулю скорость постоянна. Криволинейное движение с постоянным ускорением всегда происходит в той плоскости, в которой находятся векторы ускорения и начальные скорости точки. В случае криволинейного движения с постоянным ускорением в плоскости xOy проекции vxи vy ее скорости на оси Ox и Oy и координаты x и y точки в любой момент времени t определяется по формулам

Ни одно тело не движется все время с постоянной скоростью. Начиная движение, автомобиль движется быстрее и быстрее. Некоторое время он может двигаться равномерно, но потом он тормозит и останавливается. При этом автомобиль проходит разные расстояния за один и то же время.

Движение, при котором тело за равные промежутки времени проходит неодинаковые отрезки пути, называется неравномерным. При таком движении величина скорости не остается неизменной. В таком случае можно говорить лишь о средней скорости.

Средняя скорость показывает, чему равно перемещение, которое тело проходит за единицу времени. Она равна отношению перемещения тела до времени движения. Средняя скорость, как и скорость тела при равномерном движении, измеряется в метрах, разделенных на секунду. Для того, чтобы характеризовать движение точнее, в физике применяют мгновенную скорость.

Скорость тела в данный момент времени или в данной точке траектории называется мгновенной скоростью. Мгновенная скорость является векторной величиной и направлена так же, как вектор перемещения. Измерить мгновенную скорость можно с помощью спидометра. В Системе Интернациональной мгновенная скорость измеряется в метрах, разделенных на секунду.

точка движение скорость неравномерный

В природе и технике очень часто встречается криволинейное движение. Оно сложнее прямолинейного, так как существует множество криволинейных траекторий; это движение всегда ускоренное, даже когда модуль скорости не меняется.

Но движение по любой криволинейной траектории можно приблизительно представить как движение по дугам круга.

При движении тела по окружности направление вектора скорости меняется от точки к точке. Поэтому когда говорят о скорости такого движения, подразумевают мгновенную скорость. Вектор скорости направлен по касательной к окружности, а вектор перемещения – по хордам.

Равномерное движение по окружности – это движение, во время которого модуль скорости движения не изменяется, изменяется только ее направление. Ускорение такого движения всегда направлено к центру окружности и называется центростремительным. Для того чтобы найти ускорение тела, которое движется по кругу, необходимо квадрат скорости разделить на радиус окружности.

Помимо ускорения, движение тела по кругу характеризуют следующие величины:

Период вращения тела – это время, за которое тело совершает один полный оборот. Период вращения обозначается буквой Т и измеряется в секундах.

Частота вращения тела – это число оборотов в единицу времени. Частота вращения обозначается буквой? и измеряется в герцах. Для того чтобы найти частоту, надо единицу разделить на период.

Линейная скорость – отношение перемещения тела до времени. Для того чтобы найти линейную скорость тела по окружности, необходимо длину окружности разделить на период (длина окружности равна 2? умножить на радиус).

Угловая скорость – физическая величина, равная отношению угла поворота радиуса окружности, по которой движется тело, до времени движения. Угловая скорость обозначается буквой? и измеряется в радианах, разделенных на секунду. Найти угловую скорость можно, разделив 2? на период. Угловая скорость и линейная между собой. Для того чтобы найти линейную скорость, необходимо угловую скорость умножить на радиус окружности.

Рисунок 6. Движение по окружности, формулы.

Скорость и ускорение при криволинейном движении. Тангенциальное и нормальное ускорения.

Криволинейные движения – движения, траектории которых представляют собой не прямые, а кривые линии.

v x =v 0 x +a x t, x=x 0 +v 0 x t+a x t+a x t 2 /2; v y =v 0 y +a y t, y=y 0 +v 0 y t+a y t 2 /2

v – мгновенное значение скорости, r – радиус кривизна траектории в данной точке.

Полное ускорение, с которым движется материальная точка, равно:

Следовательно

Нормальное ускорение характеризует быстроту изменения скорости по направлению. Вычислим вектор:

Кинематика вращательного движения.

Угловая скорость – величина векторная.

Быстроту изменения угловой скорости характеризует среднее и мгновенное

угловое ускорение .

Вектор и может совпадать с вектором , и быть противоположным ему

Вам хорошо известно, что в зависимости от формы траектории движение делится на прямолинейное и криволинейное . С прямолинейным движением мы научились работать на предыдущих уроках, а именно решать главную задачу механики для такого вида движения.

Однако ясно, что в реальном мире мы чаще всего имеем дело с криволинейным движением, когда траектория представляет собой кривую линию. Примерами такого движения является траектория тела, брошенного под углом к горизонту, движение Земли вокруг Солнца и даже траектория движения ваших глаз, следящих сейчас за этим конспектом.

Для начала определимся, какие принципиальные отличия есть у криволинейного движения (рис. 1) относительно прямолинейного и к чему эти отличия приводят.

Рис. 1. Траектория криволинейного движения

Поговорим о том, как удобно описывать движение тела при криволинейном движении.

Можно разбить движение на отдельные участки, на каждом из которых движение можно считать прямолинейным (рис. 2).

Рис. 2. Разбиение криволинейного движения на участки прямолинейного движения

Однако более удобным является следующий подход. Мы представим это движение как совокупность нескольких движений по дугам окружностей (рис. 3). Обратите внимание, что таких разбиений меньше, чем в предыдущем случае, кроме того, движение по окружности является криволинейным. К тому же примеры движения по окружности в природе встречается очень часто. Из этого можно сделать вывод:

Рис. 3. Разбиение криволинейного движения на движения по дугам окружностей

Итак, начнем изучение криволинейного движения с изучения равномерного движения по окружности. Давайте разберемся, каковы принципиальные отличия криволинейного движения от прямолинейного. Для начала вспомним, что в девятом классе мы изучили тот факт, что скорость тела при движении по окружности направлена по касательной к траектории (рис. 4). Кстати, этот факт вы можете пронаблюдать на опыте, если посмотрите, как движутся искры при использовании точильного камня.

Рассмотрим движение тела по дуге окружности (рис. 5).

Рис. 5. Скорость тела при движении по окружности

Обратите внимание, что в данном случае модуль скорости тела в точке равен модулю скорости тела в точке :

Однако вектор не равен вектору . Итак, у нас появляется вектор разности скоростей (рис. 6):

Рис. 6. Вектор разности скоростей

Причем изменение скорости произошло через некоторое время . Таким образом, мы получаем знакомую комбинацию:

Это не что иное, как изменение скорости за промежуток времени, или ускорение тела. Можно сделать очень важный вывод:

Еще раз отметим, что, даже если говорится, что тело равномерно движется по окружности, имеется в виду, что модуль скорости тела не изменяется. Однако такое движение всегда является ускоренным, поскольку изменяется направление скорости.

В девятом классе вы изучали, чему равно такое ускорение и как оно направлено (рис. 7). Центростремительное ускорение всегда направлено к центру окружности, по которой движется тело.

Рис. 7. Центростремительное ускорение

Модуль центростремительного ускорения может быть рассчитан по формуле:

Рис. 8. Движение точек диска

Рассмотрим диск, который для определенности вращается по часовой стрелке. На его радиусе отметим две точки и (рис. 8). Рассмотрим их движение. За некоторое время эти точки переместятся по дугам окружности и станут точками и . Очевидно, что точка совершила большее перемещение, чем точка . Из этого можно сделать вывод, что чем дальше от оси вращения находится точка, тем с большей линейной скоростью она движется

Однако если внимательно посмотреть на точки и , можно сказать, что неизменным остался угол , на который они повернулись относительно оси вращения . Именно угловые характеристики мы и будем использовать для описания движения по окружности. Отметим, что для описания движения по окружности можно использовать угловые характеристики.

Аналогично понятию линейной скорости вводится понятие угловой скорости.

Угловой скоростью равномерного движения ( называется физическая величина, равная отношению угла, на который повернулось тело, ко времени, за которое произошел этот поворот.

В физике чаще всего используется радианная мера угла. Например, угол в равен радиан. Измеряется угловая скорость в радианах в секунду:

Найдем связь между угловой скоростью вращения точки и линейной скоростью этой точки.

Рис. 9. Связь между угловой и линейной скоростью

Точка проходит при вращении дугу длиной , поворачиваясь при этом на угол . Из определения радианной меры угла можно записать:

Разделим левую и правую части равенства на промежуток времени , за который было совершено перемещение, затем воспользуемся определением угловой и линейной скоростей:

Обратим внимание, что чем дальше точка находится от оси вращения, тем выше ее линейная скорость. А точки, расположенные на самой оси вращения, неподвижны. Примером этого может служить карусель: чем ближе вы находитесь к центру карусели, тем легче вам на ней удержаться.

Такая зависимость линейной и угловой скоростей используется в геостационарных спутниках (спутники, которые всегда находятся над одной и той же точкой земной поверхности). Благодаря таким спутникам мы имеем возможность получать телевизионные сигналы.

Вспомним, что ранее мы вводили понятия периода и частоты вращения.

Период вращения – время одного полного оборота. Период вращения обозначается буквой и измеряется в секундах в СИ:

Частота вращения – физическая величина, равная количеству оборотов, которое тело совершает за единицу времени.

Частота обозначается буквой и измеряется в обратных секундах:

Они связаны соотношением:

Подставляя эти выражения в зависимость между угловой и линейной скоростью, можно получить зависимость линейной скорости от периода или частоты:

Запишем также связь между центростремительным ускорением и этими величинами:

Таким образом, мы знаем связь между всеми характеристиками равномерного движения по окружности.

Подытожим. На этом уроке мы начали описывать криволинейное движение. Мы поняли, каким образом можно связать криволинейное движение с движением по окружности. Движение по окружности всегда является ускоренным, а наличие ускорения обуславливает тот факт, что скорость всегда меняет свое направление. Такое ускорение называется центростремительным. Наконец, мы вспомнили некоторые характеристики движения по окружности (линейную скорость, угловую скорость, период и частоту вращения) и нашли соотношения между ними.

Список литературы

Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский. Физика 10. – М.: Просвещение, 2008.
А.П. Рымкевич. Физика. Задачник 10-11. – М.: Дрофа, 2006.
О.Я. Савченко. Задачи по физике. – М.: Наука, 1988.
А.В. Перышкин, В.В. Крауклис. Курс физики. Т. 1. – М.: Гос. уч.-пед. изд. мин. просвещения РСФСР, 1957.

Аyp.ru ().
Википедия ().

Домашнее задание

Решив задачи к данному уроку, вы сможете подготовиться к вопросам 1 ГИА и вопросам А1, А2 ЕГЭ.

Задачи 92, 94, 98, 106, 110 – сб. задач А.П. Рымкевич, изд. 10
Вычислите угловую скорость движения минутной, секундной и часовой стрелок часов. Вычислите центростремительное ускорение, действующее на кончики этих стрелок, если радиус каждой из них равен одному метру.

Кинематика криволинейного движения. Конспект урока “Прямолинейное и криволинейное движение

Направление средней скорости V ср совпадает с направлением вектора Dr .

Предел средней скорости при Dt ® 0, т. е. производная радиуса – вектора r по времени

(1.9)

(1.10)

(1.11)

Эта тема будет посвящена более сложному виду движения – КРИВОЛИНЕЙНОМУ . Как несложно догадаться, криволинейным называется движение, траектория которого представляет собой кривую линию . И, поскольку это движение сложнее прямолинейного, то для его описания уже не хватает тех физических величин, которые были перечислены в предыдущей главе.

Для математического описания криволинейного движения имеются 2 группы величин: линейные и угловые.

ЛИНЕЙНЫЕ ВЕЛИЧИНЫ.

1. Перемещение . В разделе 1.1 мы не стали уточнять различие между понятием

Рис.1.3 пути (расстояния) и понятием перемещения,

поскольку в прямолинейном движении эти

различия не играют принципиальной роли, да и

Обозначаются эти величины одной и той же бук-

вой S . Но, имея дело с криволинейным движением,

этот вопрос нужно прояснить. Итак, что такое путь

(или расстояние)? – Это длина траектории

движения. То есть, если Вы отследите траекторию

движения тела и измерите ее (в метрах, километрах и т.д.), вы получите величину, которая называется путем (или расстоянием) S (см. рис.1.3). Таким образом, путь – это скалярная величина, которая характеризуется только числом.

Рис.1.4 А перемещение – это кратчайшее расстояние между

точкой начала пути и точкой конца пути. И, поскольку

перемещение имеет строгую направленность из начала

Пути в его конец, то оно является величиной векторной

и характеризуется не только численным значением, но и

направлением (рис.1.3). Нетрудно догадаться, что, если

тело совершает движение по замкнутой траектории, то к

моменту его возвращения в начальное положение перемещение будет равно нулю (см. рис.1.4).

2 . Линейная скорость . В разделе 1.1 мы давали определение этой величины, и оно остается в силе, хотя тогда мы не уточняли, что эта скорость линейная. Как же направлен вектор линейной скорости? Обратимся к рис.1.5. Здесь изображен фрагмент

криволинейной траектории тела. Любая кривая линия представляет собой соединение между собой дуг разных окружностей. На рис.1.5 изображены только две из них: окружность (О 1 , r 1) и окружность (О 2 , r 2). На момент прохождения тела по дуге данной окружности ее центр становится временным центром поворота с радиусом, равным радиусу этой окружности.

Вектор, проведенный из центра поворота в точку, где в данный момент находится тело, называется радиусом-вектором. На рис.1.5 радиусы-векторы представлены векторами и . Также на этом рисунке изображены и вектора линейной скорости: вектор линейной скорости всегда направлен по касательной к траектории в сторону движения. Следовательно, угол между вектором и радиусом-вектором, проведенным в данную точку траектории, всегда равен 90°. Если тело движется с постоянной линейной скоростью, то модуль вектора изменяться не будет, тогда как его направление все время меняется в зависимости от формы траектории. В случае, изображенном на рис.1.5, движение осуществляется с переменной линейной скоростью, поэтому у вектора изменяется модуль. Но, поскольку при криволинейном движении направление вектора изменяется всегда, то отсюда следует очень важный вывод:

при криволинейном движении всегда есть ускорение ! (Даже если движение осуществляется с постоянной линейной скоростью.) Причем, ускорение, о котором идет речь в данном случае, в дальнейшем мы будем называть линейным ускорением.

3 . Линейное ускорение . Напомню, что ускорение возникает тогда, когда изменяется скорость. Соответственно, линейное ускорение появляется в случае изменения линейной скорости. А линейная скорость при криволинейном движении может изменяться кок по модулю, так и по направлению. Таким образом, полное линейное ускорение раскладывается на две составляющие, одна из которых влияет на направление вектора , а вторая на его модуль. Рассмотрим эти ускорения (рис. 1.6). На этом рисунке

рис. 1.6

изображено тело, движущееся по круговой траектории с центром поворота в точке О.

Ускорение, которое изменяет направление вектора , называется нормальным и обозначается . Нормальным оно называется потому, что направлено перпендикулярно (нормально) к касательной, т.е. вдоль радиуса к центру поворота . Его еще называют центростремительным ускорением.

Ускорение, которое изменяет модуль вектора , называется тангенциальным и обозначается . Оно лежит на касательной и может быть направлено как в сторону направления вектора , так и противоположно ему :

Если линейная скорость увеличивается, то > 0 и их вектора сонаправлены;

Если линейная скорость уменьшается, то

направлены.

Таким образом, эти два ускорения всегда образуют между собой прямой угол (90º) и являются составляющими полного линейного ускорения , т.е. полное линейное ускорение есть векторная сумма нормального и тангенциального ускорения:

Замечу, что в данном случае речь идет именно о векторной сумме, но ни в коем случае не о скалярной. Чтобы найти численное значение , зная и , необходимо воспользоваться теоремой Пифагора (квадрат гипотенузы треугольника численно равен сумме квадратов катетов этого треугольника):

(1.8).

Отсюда следует:

(1.9).

По каким формулам рассчитывать и рассмотрим чуть позже.

УГЛОВЫЕ ВЕЛИЧИНЫ.

1 . Угол поворота φ . При криволинейном движении тело не только проходит какой-то путь и совершает какое-то перемещение, но и поворачивается на определенный угол (см. рис. 1.7(а)). Поэтому для описания такого движения вводится величина, которая называется углом поворота, обозначается греческой буквой φ (читается «фи»). В системе СИ угол поворота измеряется в радианах (обозначается «рад»). Напомню, что один полный оборот равен 2π радианам, а число π есть константа: π ≈ 3,14. на рис. 1.7(а) изображена траектория движения тела по окружности радиуса r с цетром в точке О. Сам угол поворота – это угол между радиус-векторами тела в некоторые моменты времени.

2 . Угловая скорость ω – это величина, показывающая, как изменяется угол поворота за единицу времени. (ω – греческая буква, читается «омега».) На рис. 1.7(б) изображено положение материальной точки, движущейся по круговой траектории с центром в точке О, через промежутки времени Δt . Если углы, на которые поворачивается тело в течение этих промежутков, одинаковы, то угловая скорость постоянна, и это движение можно считать равномерным. А если углы поворота разные – то движение неравномерное. И, поскольку угловая скорость показывает, на сколько радиан

повернулось тело за одну секунду, то ее единица измерения – радиан в секунду

(обозначается «рад/с »).

рис. 1.7

а). б). Δt

Δt

О φ О Δt

3 . Угловое ускорение ε – это величина, показывающая, как изменяется за единицу времени. И, поскольку угловое ускорение ε появляется тогда, когда изменяется, угловая скорость ω , то можно сделать вывод, что угловое ускорение имеет место только в случае неравномерного криволинейного движения. Единица измерения углового ускорения – «рад/с 2 » (радиан за секунду в квадрате).

Таким образом, таблицу 1.1 можно дополнить еще тремя величинами:

Табл.1.2

№	физическая величина	определение величины	обозначение величины	единица измерения
1.	путь	это расстояние, которое преодолевает тело в процессе своего движения	S	м (метр)
2.	скорость	это расстояние, которое проходит тело за единицу времени (например, за 1 секунду)	υ	м/с (метр в секунду)
3.	ускорение	это величина, на которую изменяется скорость тела за единицу времени	a	м/с 2 (метр за секунду в квадрате)
4.	время		t	с (секунда)
5.	угол поворота	это угол, на который поворачивается тело в процессе криволинейного движения	φ	рад (радиан)
6.	угловая скорость	это угол, на который поворачивается тело за единицу времени (например, за 1 сек.)	ω	рад/с (радиан в секунду)
7.	угловое ускорение	это величина, на которую изменяется угловая скорость за единицу времени	ε	рад/с 2 (радиан за секунду в квадрате)

Теперь можно перейти непосредственно к рассмотрению всех видов криволинейного движения, а их всего лишь три.

точка движение скорость неравномерный

Но движение по любой криволинейной траектории можно приблизительно представить как движение по дугам круга.

Помимо ускорения, движение тела по кругу характеризуют следующие величины:

Рисунок 6. Движение по окружности, формулы.

6. Криволинейное движение. Угловое перемещение, угловые скорость и ускорение тела. Путь и перемещение при криволинейном движении тела.

Криволинейное движение – это движение, траектория которого представляет собой кривую линию (например, окружность, эллипс, гиперболу, параболу). Примером криволинейного движения является движение планет, конца стрелки часов по циферблату и т.д. В общем случае скорость при криволинейном движении изменяется по величине и по направлению.

Криволинейное движение материальной точки считается равномерным движением, если модульскорости постоянен (например, равномерное движение по окружности), и равноускоренным, если модуль и направление скорости изменяется (например, движение тела, брошенного под углом к горизонту).

Рис. 1.19. Траектория и вектор перемещения при криволинейном движении.

При движении по криволинейной траектории вектор перемещения направлен по хорде (рис. 1.19), аl – длина траектории . Мгновенная скорость движения тела (то есть скорость тела в данной точке траектории) направлена по касательной в той точке траектории, где в данный момент находится движущееся тело (рис. 1.20).

Рис. 1.20. Мгновенная скорость при криволинейном движении.

Криволинейное движение – это всегда ускоренное движение. То есть ускорение при криволинейном движении присутствует всегда, даже если модуль скорости не изменяется, а изменяется только направление скорости. Изменение величины скорости за единицу времени – это тангенциальное ускорение :

или

Где v τ , v 0 – величины скоростей в момент времени t 0 + Δt и t 0 соответственно.

Тангенциальное ускорение в данной точке траектории по направлению совпадает с направлением скорости движения тела или противоположно ему.

Нормальное ускорение – это изменение скорости по направлению за единицу времени:

Центростремительное ускорение – это нормальное ускорение при равномерном движении по окружности.

Полное ускорение при равнопеременном криволинейном движении тела равно:

Движение тела по криволинейной траектории можно приближённо представить как движение по дугам некоторых окружностей (рис. 1.21).

Рис. 1.21. Движение тела при криволинейном движении.

Криволинейное движение

Криволинейные движения – движения, траектории которых представляют собой не прямые, а кривые линии. По криволинейным траекториям движутся планеты, воды рек.

Криволинейное движение – это всегда движение с ускорением, даже если по модулю скорость постоянна. Криволинейное движение с постоянным ускорением всегда происходит в той плоскости, в которой находятся векторы ускорения и начальные скорости точки. В случае криволинейного движения с постоянным ускорением в плоскости xOy проекции v x и v y ее скорости на оси Ox и Oy и координаты x и y точки в любой момент времениt определяется по формулам

При криволинейном движении ускорение можно представить как сумму нормальной и тангенциальной составляющих:

v – мгновенное значение скорости, r – радиус кривизна траектории в данной точке.

Полное ускорение, с которым движется материальная точка, равно:

Кроме центростремительного ускорения, важнейшими характеристиками равномерного движения по окружности являются период и частота обращения.

Период обращения – это время, за которое тело совершается один оборот.

Обозначается период буквой Т (с) и определяется по формуле:

где t – время обращения, п – число оборотов, совершенных за это время.

Частота обращения – это величина, численно равная числу оборотов, совершенных за единицу времени.

Обозначается частота греческой буквой (ню) и находится по формуле:

Измеряется частота в 1/с.

Период и частота – величины взаимно обратные:

Если тело, двигаясь по окружности со скоростью v, делает один оборот, то пройденный этим телом путь можно найти, умножив скорость v на время одного оборота:

l = vT. С другой стороны, этот путь равен длине окружности 2πr . Поэтому

vT = 2πr,

где w (с -1) – угловая скорость.

При неизменной частоте обращения центростремительное ускорение прямо пропорционально расстоянию от движущейся частицы до центра вращения.

Угловая скорость (w ) – величина, равная отношению угла поворота радиуса, на котором находится вращающаяся точка, к промежутку времени, за который произошел этот поворот:

Связь между линейной и угловой скоростями:

Движение тела можно считать известным лишь тогда, когда известно, как движется каждая его точка. Самое простое движение твердых тел – поступательное. Поступательным называется движение твердого тела, при котором любая прямая, проведенная в этом теле, перемещается параллельно самой себе.

Нам известно, что всякое криволинейное движение происходит под действием силы, направленной под углом к скорости. В случае равномерного движения по окружности этот угол будет прямым. В самом деле, если, например, вращать шарик, привязанный к верёвке, то направление скорости шарика в любой момент времени перпендикулярно верёвке.

Сила же натяжения верёвки, удерживающая шарик на окружности, направлена вдоль верёвки к центру вращения.

По второму закону Ньютона эта сила будет вызывать ускорение тела в том же направлении. Ускорение, направленное по радиусу к центру вращения, называется центростремительным ускорением .

Выведем формулу для определения величины центростремительного ускорения.

Прежде всего, заметим, что движение по окружности – сложное движение. Под действием центростремительной силы тело движется к центру вращения и одновременно по инерции удаляется от этого центра по касательной к окружности.

Пусть за время t тело, двигаясь равномерно со скоростью v, переместилось из D в Е. Допустим, что в тот момент, когда тело находилось в точке D, на него перестала бы действовать центростремительная сила. Тогда за время t оно переместилось бы в точку К, лежащую на касательной DL. Если же в начальный момент тело оказалось бы под действием только одной центростремительной силы (не двигалось по инерции), то оно за время t, двигаясь равноускоренно, переместилось бы в точку F, лежащую на прямой DC. В результате сложения этих двух движений за время t получается результирующее движение по дуге DE.

Сила, удерживающая вращающееся тело на окружности и направленная к центру вращения, называется центростремительной силой .

Чтобы получить формулу для расчёта величины центростремительной силы, надо воспользоваться вторым законом Ньютона, который применим и к любому криволинейному движению.

Подставляя в формулу F = ma значение центростремительного ускорения a = v 2 / R , получим формулу центростремительной силы:

F = mv 2 / R

Величина центростремительной силы равна произведению массы тела на квадрат линейной скорости , делённому на радиус .

Если дана угловая скорость тела, то центростремительную силу удобнее рассчитывать по формуле: F = m? 2 R, где? 2 R – центростремительное ускорение.

Из первой формулы видно, что при одной и той же скорости чем меньше радиус окружности, тем больше центростремительная сила. Так, на поворотах дороги на движущееся тело (поезд, автомобиль, велосипед) должна действовать по направлению к центру закругления тем большая сила, чем круче поворот, т. е. чем меньше радиус закругления.

Центростремительная сила зависит от линейной скорости: с увеличением скорости она увеличивается. Это хорошо известно всем конькобежцам, лыжникам и велосипедистам: чем с большей скоростью движешься, тем труднее сделать поворот. Шофёры очень хорошо знают, как опасно круто поворачивать автомобиль на большой скорости.

Бросим какое-нибудь тело л од углом к горизонту. Следя за его движением, мы заметим, что тело сначала поднимается, двигаясь по кривой, потом также по кривой падает вниз.

Если направлять струю воды под разными углами к горизонту, то можно видеть, что сначала с увеличением угла струя бьёт всё дальше и дальше. При угле в 45° к горизонту (если не учитывать сопротивления воздуха) дальность наибольшая. При дальнейшем увеличении угла дальность уменьшается.

Для построения траектории движения тела, брошенного под углом к горизонту, проведём горизонтальную прямую OA и к ней под заданным углом – прямую ОС.

На линии ОС в выбранном масштабе откладываем отрезки, численно равные путям, пройденным в направлении бросания (0–1, 1–2, 2–3, 3–4). Из точек 1, 2, 3 и т. д. опускаем перпендикуляры на ОА и на них откладываем отрезки, численно равные путям, проходимым свободно падающим телом в течение 1 сек (1–I), 2 сек (2–II), 3 сек (3–III) и т. д. Точки 0, I, II, III, IV и т. д. соединяем плавной кривой.

Траектория тела симметрична относительно вертикальной прямой, проходящей через точку IV.

Сопротивление воздуха уменьшает как дальность полёта, так и наибольшую высоту полёта, и траектория становится несимметричной. Таковы, например, траектории снарядов и пуль. На рисунке сплошная кривая показывает схематически траекторию снаряда в воздухе, а пунктирная – в безвоздушном пространстве. Насколько сопротивление воздуха изменяет дальность полёта, видно из следующего примера. При отсутствии сопротивления воздуха снаряд 76-миллиметрового орудия, выпущенный под углом 20° к горизонту, пролетел бы 24 км. В воздухе же этот снаряд пролетает около 7 км.

Независимость движений

Всякое криволинейное движение является сложным движением, состоящим из движения по инерции и движения под действием силы, направленной под углом к скорости тела. Это можно показать на следующем примере.

Допустим, что шарик движется по столу равномерно и прямолинейно. Когда шарик скатывается со стола, вес его больше уже не уравновешивается силой давления стола и он, по инерции сохраняя равномерное и прямолинейное движение, одновременно начинает падать. В результате сложения движений – равномерного прямолинейного по инерции и равноускоренного под действием силы тяжести – шарик перемещается по кривой линии.

Можно на опыте показать, что эти движения независимы одно от другого.

На рисунке изображена пружина, которая, выгибаясь под ударом молотка, может привести один из шариков в движение в горизонтальном направлении и одновременно освободить другой шарик, так что оба они начнут движение в один и тот же момент: первый – по кривой, второй – по вертикали вниз. Оба шарика ударятся о пол одновременно; следовательно, время падения обоих шариков одинаково. Отсюда можно заключить, что движение шарика под действием силы тяжести не зависит от того, покоился ли шарик в начальный момент или двигался в горизонтальном направлении.

Этот опыт иллюстрирует очень важное положение механики, называемое принципом независимости движений .

Одним из простейших и весьма распространённых видов криволинейного движения является равномерное движение тела по окружности. По окружности, например, движутся части маховиков, точки земной поверхности при суточном вращении Земли и т. д.

Введём величины, характеризующие это движение. Обратимся к рисунку. Пусть при вращении тела одна из его точек за время t перешла из A в В. Радиус, соединяющий точку А с центром окружности, повернулся при этом на угол? (греч. «фи»). Быстроту вращения точки можно характеризовать величиной отношения угла? ко времени t, т. е. ? / t .

Угловая скорость

Отношение угла поворота радиуса, соединяющего движущуюся точку с центром вращения, к промежутку времени, за который происходит этот поворот, называется угловой скоростью .

Обозначая угловую скорость греческой буквой? («омега»), можно написать:

? = ? / t

Угловая скорость численно равна углу поворота в единицу времени.

При равномерном движении по окружности угловая скорость есть величина постоянная.

При вычислении угловой скорости угол поворота принято измерять в радианах. Радиан есть центральный угол, длина дуги которого равна радиусу этой дуги.

При рассмотрении прямолинейного движения стало известно, что если на тело действует сила в направлении движения, то движение тела будет оставаться прямолинейным. Изменяться будет только величина скорости. При этом если направление силы совпадает с направлением скорости, движение будет прямолинейным и ускоренным. В случае же противоположного направления силы движение окажется прямолинейным и замедленным. Таковы, например, движение тела, брошенного вертикально вниз, и движение тела, брошенного вертикально вверх.

Рассмотрим теперь, как будет двигаться тело под действием силы, направленной под углом к направлению скорости.

Обратимся сначала к опыту. Создадим траекторию движения стального шарика около магнита. Сразу замечаем, что вдали от магнита шарик двигался прямолинейно, при приближении же к магниту траектория шарика искривлялась и шарик двигался по кривой. Направление скорости его при этом непрерывно менялось. Причиной этого было действие магнита на шарик.

Мы можем заставить двигаться по кривой прямолинейно перемещающееся тело, если будем толкать его, тянуть за привязанную к нему нить и так далее, лишь бы сила была направлена под углом к скорости перемещения тела.

Итак, криволинейное движение тела происходит под действием силы, направленной под углом к направлению скорости тела .

В зависимости от направления и величины силы, действующей на тело, криволинейные движения могут быть самыми разнообразными. Наиболее простыми видами криволинейных движений являются движения по окружности, параболе и эллипсу.

В некоторых случаях центростремительная сила является равнодействующей двух сил, действующих на движущееся по окружности тело.

Рассмотрим несколько таких примеров.

1. По вогнутому мосту движется автомобиль со скоростью v, масса автомобиля т, радиус кривизны моста R. Чему равна сила давления, производимого автомобилем на мост, в низшей его точке?

Установим прежде всего, какие силы действуют на автомобиль. Таких сил две: вес автомобиля и сила давления моста на автомобиль. (Силу трения в этом и во всех последующих призерах мы исключаем из рассмотрения).

Когда автомобиль неподвижен, то эти силы, будучи равными по величине и направленными в противоположные стороны» уравновешивают друг друга.

Когда же автомобиль движется по мосту, то на него, как и на всякое тело, движущееся по окружности, действует центростремительная сила. Что является источником этой силы? Источником этой силы может быть только действие моста на автомобиль. Сила Q, с которой мост давит на движущийся автомобиль, должна не только уравновешивать вес автомобиля Р, но и вынуждать его двигаться по окружности, создавая необходимую для этого центростремительную силу F. Сила F может быть только равнодействующей сил Р и Q, так как она является результатом взаимодействия движущегося автомобиля и моста.

кинематика

на главную

Официальный сайт АНО ДО Центра “Логос”, г.Глазов

http://logos-glz.ucoz.net/

ГОТОВИМСЯ К УРОКУ

Кинематика

Динамика

МКТ

Термодинамика

Электростатика

Электрический ток

Электрический ток в средах

Магнитное поле Электромагнитная индукция

Оптика

Методы познания

Кинематика немного о физике:

Кинематика – раздел механики, в котором изучается механическое движение, без учета масс тел и причин, которые обеспечивают это движение.

Основная задача кинематики – описать движение тела в пространстве в зависимости от времени, не выясняя причин движения.

Основные понятия.

Механическим движением называют изменение положения тела в пространстве относительно других тел с течением времени.

Рассмотрение любого движения начинают с выбора системы отсчета, включающей в себя: тело отсчета, систему координат и приборы для исследования движения.

Материальная точка – модель тела, размерами которого в рассматриваемых условиях можно пренебречь.

Траектория – линия, вдоль которой движется тело.

Путь – длина траектории.

Перемещение – вектор, соединяющий начальное и конечное положения тела.

Положение тела в пространстве задается радиус – вектором или тремя его проекциями на оси координат.

Следовательно закон движения – это зависимость радиус-вектора от времени или зависимость координат во времени.

где -радиус-вектор, x, y, z – координаты тела.

Скорость тела – векторная физическая величина, характеризующая изменение положения тела в пространстве с течением времени.

Средняя скорость перемещения равна отношению полного перемещения к промежутку времени, за которое это перемещение совершено.

где_ср-средняя скорость перемещения, – перемещение, ∆ t – интервал времени.

Средняя путевая скорость равна отношению полного пути к промежутку времени, за который этот путь пройден.

где υ_ср – средняя путевая скорость , l – путь.

Мгновенная скорость – скорость в заданный момент времени.

Модуль мгновенной скорости определяется равенством:

где υ_x , υ_y , υ_z – проекции вектора скорости на оси,

Мгновенная скорость в каждой точке всегда направлена по касательной к траектории. Направление вектора скорости задается косинусами:

где α , β , γ –углы между вектором скорости и осями x, y, z соответственно.

Ускорение – векторная физическая величина, характеризующая быстроту изменения скорости.

где а– ускорение, -изменение скорости, ,₀ – конечная и начальная скорости.

Модуль ускорения определяется равенством:

где – _x_, _y , _z – проекции вектора ускорения на оси x, y, z соответственно.

Равномерное прямолинейное движение.

Равномерное движение – движение при котором материальная точка за любые равные промежутки времени совершает равные перемещения.

При равномерном прямолинейном движении скорость тела постоянна, ускорение равно нулю. Траектория равномерного прямолинейного движения – прямая линия.

Для физических величин характеризующих движение имеем:

= 0

υ = const

S_x = υ_x· t

x = x₀ + υ_x· t

Графики зависимости физических величин от времени

при равномерном прямолинейном движении.

1. график зависимости проекции скорости от времени.

2. график зависимости проекции перемещения от времени

3. график зависимости координаты от времени.

Равноускоренное прямолинейное движение.

Равноускоренным движением называют движение с ускорением, постоянным по модулю и направлению. При равноускоренном движении скорость тела изменяется, ускорение остается постоянным. Траектория равноускоренного прямолинейного движения – прямая линия.

Для физических величин характеризующих движение имеем:

Графики зависимости физических величин от времени

при равноускоренном прямолинейном движении.

1. график зависимости проекции ускорения от времени.

2. график зависимости проекции скорости от времени.

3. график зависимости проекции перемещения от времени.

4. график зависимости координаты от времени.

Равномерное движение по окружности.

Скорость движения тела по окружности называют линейной скоростью. При равномерном движении по окружности модуль линейной скорости материальной точки со временем не изменяется, но изменяется ее направление.

Модуль линейной скорости равен отношению пройденного пути к промежутку времени. Учитывая. что при равномерном движении по окружности путь равен длине дуги, то для линейной скорости имеет место равенство:

где l – длина дуги, R – радиус описанной окружности, φ – угол поворота радиус-вектора, t- время движения.

Еще одной характеристикой движения по окружности является угловая скорость. Угловая скорость равна отношению угла поворота радиус-вектора к промежутку времени, за который этот угол пройден.

где ω – угловая скорость.

Связь между линейной и угловой скоростью определяется следующим равенством: υ = ω·R

При равномерном движении по окружности линейная скорость изменяется по направлению, поэтому движение по окружности – это движение с ускорением. При равномерном движении по окружности ускорение направлено к центру окружности и называется нормальным или центростремительным ускорением. Модуль ускорения не меняется:

где n -нормальное (центростремительное) ускорение.

Период вращения – промежуток времени, за который тело совершает один полный оборот.

где Т – период обращения.

Частота обращения – число оборотов, совершаемых телом в единицу времени. Частота обращения – величина , обратная периоду.

где ν – частота обращения.

Криволинейное движение.

Любое криволинейное движение можно представить как движение по дугам окружностей.

При произвольном криволинейном движении скорость может меняться как по модулю, так и по направлению. Ускорение так же является величиной переменной:

При криволинейном движении ускорение можно разложить на две составляющие:

где первое слагаемое – нормальная составляющая ускорения, второе слагаемое – тангенсальная составляющая ускорения.

Модуль полного ускорения равен:

Модули нормального и тангенсального ускорений соответственно равны:

где – производная модуля скорости по времени.

Материальной точки по окружности. Линейная и угловая скорости

Изучение новой темы

Просмотреть видеоролик и обсудить следующие вопросы с учащимися:

https://www.youtube.com/watch?v=Wk5Ff6LCgwg

1. Как направлена мгновенная скорость при криволинейном движении?

2. Что называется линейной скоростью тела при его движении по окружности? (вывести формулу расчета линейной скорости)

Движение по окружности часто характеризуют не скоростью движения, а промежутком времени, за который тело совершает один полный оборот. Это величина называется периодом обращения и обозначается буквой Т. Найдем связь между периодом обращения Т и модулем скорости при равномерном движении по окружности радиуса R. Т. к. а путь S равен длине окружности: S = 2πR , то

Движение тела по окружности можно охарактеризовать еще одной величиной – числом оборотов в единицу времени. Ее называют частотой обращения ν. Единицей измерения частоты [ν] = с^-1 = Гц.

3. Что называется периодом и частотой обращения? Как эти величины связаны между собой?

https://compendium.su/physics/9klas/16.html

Тренировочные задания

1. Маховик швейной машины радиусом 8 см делает 120 об/мин. Найдите:

а) период вращения.
b) угловую и линейную скорости.

2. Колесо диаметром 30 см делает 600 об за 30 с. Найдите:

a) период вращения колеса

b) частоту вращения колеса

c) угловую и линейную скорости точек на окружности колеса.

3. Колесо велосипеда делает 120 об/мин. С какой скоростью едет велосипедист, если радиус колеса 40 см ?

4. Сколько оборотов в секунду делают колеса тепловоза диаметром 1,5 м при скорости 72 км/час?

5. Диск совершает 600 об/мин. Найдите:

a) частоту вращения диска.

b) период вращения диска.

6. Лопасть вертолета длиной 5 м делает 300 об/мин. Найти линейную скорость концов лопастей.

В конце урока учащиеся проводят рефлексию:

– что узнал, чему научился

– что осталось непонятным

– над чем необходимо работать

Определение равномерного криволинейного движения. Прямолинейное и криволинейное движение

точка движение скорость неравномерный

Но движение по любой криволинейной траектории можно приблизительно представить как движение по дугам круга.

Помимо ускорения, движение тела по кругу характеризуют следующие величины:

Рисунок 6. Движение по окружности, формулы.

При помощи данного урока вы сможете самостоятельно изучить тему «Прямолинейное и криволинейное движение. Движение тела по окружности с постоянной по модулю скоростью». Вначале мы охарактеризуем прямолинейное и криволинейное движение, рассмотрев, как при этих видах движения связаны вектор скорости и приложенная к телу сила. Далее рассмотрим частный случай, когда происходит движение тела по окружности с постоянной по модулю скоростью.

На предыдущем уроке мы рассмотрели вопросы, связанные с законом всемирного тяготения. Тема сегодняшнего урока тесно связана с этим законом, мы обратимся к равномерному движению тела по окружности.

Ранее мы говорили, что движение – это изменение положения тела в пространстве относительно других тел с течением времени. Движение и направление движения характеризуются в том числе и скоростью. Изменение скорости и сам вид движения связаны с действием силы. Если на тело действует сила, то тело изменяет свою скорость.

Если сила направлена параллельно движению тела, то такое движение будет прямолинейным (рис. 1).

Рис. 1. Прямолинейное движение

Криволинейным будет такое движение, когда скорость тела и сила, приложенная к этому телу, направлены друг относительно друга под некоторым углом (рис. 2). В этом случае скорость будет изменять свое направление.

Рис. 2. Криволинейное движение

Итак, при прямолинейном движении вектор скорости направлен в ту же сторону, что и сила, приложенная к телу. А криволинейным движением является такое движение, когда вектор скорости и сила, приложенная к телу, расположены под некоторым углом друг к другу.

Рассмотрим частный случай криволинейного движения, когда тело движется по окружности с постоянной по модулю скоростью. Когда тело движется по окружности с постоянной скоростью, то меняется только направление скорости. По модулю она остается постоянной, а направление скорости изменяется. Такое изменение скорости приводит к наличию у тела ускорения, которое называется центростремительным .

Рис. 6. Движение по криволинейной траектории

Если траектория движения тела является кривой, то ее можно представить как совокупность движений по дугам окружностей, как это изображено на рис. 6.

На рис. 7 показано, как изменяется направление вектора скорости. Скорость при таком движении направлена по касательной к окружности, по дуге которой движется тело. Таким образом, ее направление непрерывно меняется. Даже если скорость по модулю остается величиной постоянной, изменение скорости приводит к появлению ускорения:

В данном случае ускорение будет направлено к центру окружности. Поэтому оно называется центростремительным.

Почему центростремительное ускорение направлено к центру?

Вспомним, что если тело движется по криволинейной траектории, то его скорость направлена по касательной. Скорость является векторной величиной. У вектора есть численное значение и направление. Скорость по мере движения тела непрерывно меняет свое направление. То есть разность скоростей в различные моменты времени не будет равна нулю (), в отличие от прямолинейного равномерного движения.

Итак, у нас есть изменение скорости за какой-то промежуток времени . Отношение к – это ускорение. Мы приходим к выводу, что, даже если скорость не меняется по модулю, у тела, совершающего равномерное движение по окружности, есть ускорение.

Куда же направлено данное ускорение? Рассмотрим рис. 3. Некоторое тело движется криволинейно (по дуге). Скорость тела в точках 1 и 2 направлена по касательной. Тело движется равномерно, то есть модули скоростей равны: , но направления скоростей не совпадают.

Рис. 3. Движение тела по окружности

Вычтем из скорость и получим вектор . Для этого необходимо соединить начала обоих векторов. Параллельно перенесем вектор в начало вектора . Достраиваем до треугольника. Третья сторона треугольника будет вектором разности скоростей (рис. 4).

Рис. 4. Вектор разности скоростей

Вектор направлен в сторону окружности.

Рассмотрим треугольник, образованный векторами скоростей и вектором разности (рис. 5).

Рис. 5. Треугольник, образованный векторами скоростей

Данный треугольник является равнобедренным (модули скоростей равны). Значит, углы при основании равны. Запишем равенство для суммы углов треугольника:

Выясним, куда направлено ускорение в данной точке траектории. Для этого начнем приближать точку 2 к точке 1. При таком неограниченном прилежании угол будет стремиться к 0, а угол – к . Угол между вектором изменения скорости и вектором самой скорости составляет . Скорость направлена по касательной, а вектор изменения скорости направлен к центру окружности. Значит, ускорение тоже направлено к центру окружности . Именно поэтому данное ускорение носит название центростремительное .

Как найти центростремительное ускорение?

Рассмотрим траекторию, по которой движется тело. В данном случае это дуга окружности (рис. 8).

Рис. 8. Движение тела по окружности

На рисунке представлены два треугольника: треугольник, образованный скоростями, и треугольник, образованный радиусами и вектором перемещения. Если точки 1 и 2 очень близки, то вектор перемещения будет совпадать с вектором пути. Оба треугольника являются равнобедренными с одинаковыми углами при вершине. Таким образом, треугольники подобны. Это значит, что соответствующие стороны треугольников относятся одинаково:

Перемещение равно произведению скорости на время: . Подставив данную формулу, можно получить следующее выражение для центростремительного ускорения:

Угловая скорость обозначается греческой буквой омега (ω), она говорит о том, на какой угол поворачивается тело за единицу времени (рис. 9). Это величина дуги в градусной мере, пройденной телом за некоторое время.

Рис. 9. Угловая скорость

Обратим внимание, что если твердое тело вращается, то угловая скорость для любых точек на этом теле будет величиной постоянной. Ближе точка располагается к центру вращения или дальше – это не важно, т. е. от радиуса не зависит.

Единицей измерения в этом случае будет либо градус в секунду (), либо радиан в секунду (). Часто слово «радиан» не пишут, а пишут просто . Для примера найдем, чему равна угловая скорость Земли. Земля делает полный поворот на за ч, и в этом случае можно говорить о том, что угловая скорость равна:

Также обратите внимание на взаимосвязь угловой и линейной скоростей:

Линейная скорость прямо пропорциональна радиусу. Чем больше радиус, тем больше линейная скорость. Тем самым, удаляясь от центра вращения, мы увеличиваем свою линейную скорость.

Необходимо отметить, что движение по окружности с постоянной скоростью – это частный случай движения. Однако движение по окружности может быть и неравномерным. Скорость может изменяться не только по направлению и оставаться одинаковой по модулю, но и меняться по своему значению, т. е., кроме изменения направления, существует еще изменение модуля скорости. В этом случае мы говорим о так называемом ускоренном движении по окружности.

Что такое радиан?

Существует две единицы измерения углов: градусы и радианы. В физике, как правило, радианная мера угла является основной.

Построим центральный угол , который опирается на дугу длиной .

Для математического описания криволинейного движения имеются 2 группы величин: линейные и угловые.

ЛИНЕЙНЫЕ ВЕЛИЧИНЫ.

1. Перемещение . В разделе 1.1 мы не стали уточнять различие между понятием

Рис.1.3 пути (расстояния) и понятием перемещения,

поскольку в прямолинейном движении эти

различия не играют принципиальной роли, да и

Обозначаются эти величины одной и той же бук-

вой S . Но, имея дело с криволинейным движением,

этот вопрос нужно прояснить. Итак, что такое путь

(или расстояние)? – Это длина траектории

движения. То есть, если Вы отследите траекторию

Рис.1.4 А перемещение – это кратчайшее расстояние между

точкой начала пути и точкой конца пути. И, поскольку

перемещение имеет строгую направленность из начала

Пути в его конец, то оно является величиной векторной

и характеризуется не только численным значением, но и

направлением (рис.1.3). Нетрудно догадаться, что, если

тело совершает движение по замкнутой траектории, то к

моменту его возвращения в начальное положение перемещение будет равно нулю (см. рис.1.4).

рис. 1.6

изображено тело, движущееся по круговой траектории с центром поворота в точке О.

Если линейная скорость увеличивается, то > 0 и их вектора сонаправлены;

Если линейная скорость уменьшается, то

направлены.

(1.8).

Отсюда следует:

(1.9).

По каким формулам рассчитывать и рассмотрим чуть позже.

УГЛОВЫЕ ВЕЛИЧИНЫ.

повернулось тело за одну секунду, то ее единица измерения – радиан в секунду

(обозначается «рад/с »).

рис. 1.7

а). б). Δt

Δt

О φ О Δt

Таким образом, таблицу 1.1 можно дополнить еще тремя величинами:

Табл.1.2

№	физическая величина	определение величины	обозначение величины	единица измерения
1.	путь	это расстояние, которое преодолевает тело в процессе своего движения	S	м (метр)
2.	скорость	это расстояние, которое проходит тело за единицу времени (например, за 1 секунду)	υ	м/с (метр в секунду)
3.	ускорение	это величина, на которую изменяется скорость тела за единицу времени	a	м/с 2 (метр за секунду в квадрате)
4.	время		t	с (секунда)
5.	угол поворота	это угол, на который поворачивается тело в процессе криволинейного движения	φ	рад (радиан)
6.	угловая скорость	это угол, на который поворачивается тело за единицу времени (например, за 1 сек.)	ω	рад/с (радиан в секунду)
7.	угловое ускорение	это величина, на которую изменяется угловая скорость за единицу времени	ε	рад/с 2 (радиан за секунду в квадрате)

Теперь можно перейти непосредственно к рассмотрению всех видов криволинейного движения, а их всего лишь три.

Ускорение при криволинейном движении

Полное ускорение равно векторной сумме тангенциального и нормального ускорений:

(15)

Модуль полного ускорения равен:

(16)

Подставляя сюда Δφ из (16), получаем выражение для модуля вектора :

Радиус кривизны

s = Rα . (18)

Круг кривизны плоской кривой линии

Определение кривизны плоской кривой в разных точках

Рисунок 1. Траектория и перемещение при криволинейном движении

Определение

Рисунок 2. Мгновенная скорость при криволинейном движении

Рисунок 4. Разбиение криволинейного движения на движения по дугам окружностей

Вывод

Мгновенная и равномерная угловая скорость кругового движения

Вращающийся карнавал

Вывод угловой скорости

Мы собираемся вывести уравнение для мгновенной угловой скорости объекта, совершающего круговое движение. На диаграмме 1 изображена красная точка, изображающая человека на карнавальном аттракционе, движущегося с угловой скоростью ω.

Диаграмма 1.Вид сверху.

Красная точка покрывает угол θ за определенный промежуток времени, t . Если мы определим мгновенное изменение угла dθ и разделим его на мгновенное изменение во времени dt , мы получим мгновенную угловую скорость dω . Если разделить dω на dt , мы получим мгновенное угловое ускорение dα . Если угловое ускорение постоянно, мы можем сказать, что dα = α .Теперь мы можем начать вычисление мгновенной угловой скорости объекта с помощью выражения, показанного в уравнении 1.

Уравнение 1

Следующий шаг – умножить обе стороны на dt . Это показано на шаге 1.

Шаг 1

Теперь мы можем интегрировать обе части уравнения, как показано на шаге 2.

Шаг 2

Мы рассмотрим обе стороны уравнения по отдельности.Результат интегрирования левой части уравнения показан на шаге 3.

Шаг 3

Шаг 4 показывает интегрирование правой части уравнения.

Шаг 4

Теперь мы полагаем обе стороны равными друг другу, что дает окончательное уравнение для угловой скорости в любой момент времени: t . Это показано в уравнении 2.

Уравнение 2

Решая для ω, мы получаем окончательное уравнение для угловой скорости в любое время, как показано в уравнении 3.

Уравнение 3

Если угловая скорость постоянна из-за отсутствия углового ускорения (α равно 0), это уравнение говорит нам, что ω = ω0. Это бесполезно для расчета угловой скорости. Нам нужно разработать другое уравнение для постоянной угловой скорости на основе угла поворота объекта: θ .

Постоянная угловая скорость

Вывод уравнения для постоянной угловой скорости начинается с мгновенного изменения углового положения, dθ , деленного на мгновенное изменение во времени dt , которое представляет собой мгновенную угловую скорость, ω. Это выражение показано в уравнении 4.

Уравнение 4

Умножение обеих сторон на dt и запись символа интеграла с обеих сторон уравнения дает нам Шаг 1.

Шаг 1

Разобьем этот вывод на левую и правую части. Начиная с левой стороны, интеграция дает нам Шаг 2.

Шаг 2

Теперь интегрируем правую часть. Тройные точки в левой части уравнения используются как заполнитель для левой части. Шаг 3 показывает интеграл правой части.

Шаг 3

Уравнивание правой и левой сторон – шаг 4.

Шаг 4

Разделение обеих сторон на t – последний шаг, который приводит к уравнению 5.

Уравнение 5

Уравнение 5 дает нам угловую скорость, которая постоянна, потому что угловое ускорение равно нулю.Мы можем записать (θ – θ0) как Δθ, что означает «изменение» θ. Сформулируем уравнение тангенциальной скорости объекта, совершающего круговое движение.

Расчет тангенциальной скорости

На диаграмме 2 показаны угловая скорость ω и тангенциальная скорость vT.

Диаграмма 2

Касательная скорость – это линейная скорость на краю круговой траектории. Основа этого уравнения начинается с выражения, включающего длину дуги, с , которое выделено на Диаграмме 3.

Диаграмма 3

Желтая дуга – это линейная длина, с . Длина дуги равна внутреннему углу, умноженному на радиус в θ. Это показано в уравнении 1.

Уравнение 1

Давайте разделим обе стороны на время, необходимое для поворота на угол, θ . Это дает нам уравнение 2.

Уравнение 2

Вы заметили, что мы имеем в левой части уравнения? Это линейное расстояние во времени, то есть линейная скорость, vT .Правую часть уравнения можно упростить, поскольку (θ / t) – угловая скорость ω. Уравнение 3 является окончательным выражением тангенциальной скорости объекта, совершающего круговое движение.

Уравнение 3

Давайте применим наши уравнения, проработав пример задачи.

Пример задачи

Подсказка: человек весом 60 кг проходит через 2π радиан по кругу радиусом 10 метров за 2,4 секунды.Какова их угловая скорость и тангенциальная скорость?

Решение: Угловая скорость равна ω = Δθ / t.

Это дает нам ω = 2π рад / 2,4 с.

ω ≈ 2,6 рад / с.

Тангенциальная скорость vT = rω.

Это дает нам vT = (10 м) (2,6 рад / с).

vT ≈ 26 м / с.

Резюме урока

Объект, совершающий круговое движение, имеет две скорости. Один из них – угловая скорость (ω) . Если угловое ускорение α отсутствует, выражение для угловой скорости показано в уравнении 1.

Уравнение 1

Другая скорость – тангенциальная скорость, vT . Это линейная скорость, которая зависит от угловой скорости и радиуса круговой траектории. Уравнение тангенциальной скорости приведено в уравнении 2.

Уравнение 2

Примечания по криволинейному движению | Инженерная механика II | ЕМ 2433

12.4 Общее криволинейное движение Частица, движущаяся по криволинейной траектории, совершает криволинейное движение. Поскольку движение часто бывает трехмерным, для описания движения используются векторы. Частица движется по кривой, определяемой функцией пути s. Положение частицы в любой момент обозначается вектором r = r (t). И величина, и направление r могут изменяться со временем. Если частица перемещается на расстояние ∆s по кривой в течение интервала времени ∆t, смещение определяется вычитанием вектора: _____________ Скорость представляет собой скорость изменения положения частицы.Средняя скорость частицы за время ∆t составляет ______________. Мгновенная скорость – это производная по времени от положения _____________. Вектор скорости v всегда касается траектории движения. Величина v называется скоростью. Поскольку длина дуги ∆s приближается к величине ∆r при t → 0, скорость может быть получена путем дифференцирования функции пути (_______). Учтите, что это не вектор! Ускорение представляет собой скорость изменения скорости частицы.Если скорость частицы изменяется с v на v ‘с интервалом времени ∆t, среднее ускорение в течение этого приращения равно: ____________________________ Мгновенное ускорение является производной от скорости по времени: __________________ График геометрического места точек, обозначенный стрелкой на вектор скорости называется годографом. Вектор ускорения касается годографа, но, как правило, не касается функции пути. Раздел 12.5 Криволинейное движение: прямоугольные компоненты Часто удобно описывать движение частицы в терминах ее x, y, z или прямоугольных компонентов относительно фиксированной системы отсчета.Положение частицы может быть определено в любой момент вектором положения ____________________. Компоненты x, y, z могут быть функциями времени, то есть: x = x (t), y = y (t) и z = z (t). Величина вектора положения равна: ___________________ Направление r определяется единичным вектором: ur = (1 / r) r 1. Если положение частицы определяется как r = [(1.5t2 + 1) i + (4t – 1) j] (м), его скорость при t = 1 с равна A) 2 м / с B) 3 м / с C) 5 м / с D) 7 м / с 2. Путь частицы определяется как y = 0.5×2. Если составляющая его скорости по оси x при x = 2 м равна vx = 1 м / с, его составляющая скорости вдоль оси y в этом положении будет A) 0,25 м / с B) 0,5 м / с C) 1 м / с D) 2 м / с Дано: частица движется по траектории, описываемой параболой y = 0,5×2. X-компонента скорости определяется как vx = (5t) ft / s. Когда t = 0, x = y = 0. Найти: расстояние частицы от начала координат и величину ее ускорения при t = 1 с. План: обратите внимание, что vx задается как функция времени. 1) Определите x-компонент положения и ускорения путем интегрирования и дифференцирования vx соответственно.2) Определите y-компонент положения из параболического уравнения и дифференцируйте, чтобы получить ay. 3) Определите величины векторов положения и ускорения. 1. При криволинейном движении направление A) касательное к годографу. Б) перпендикулярно годографу. В) касательная к пути. Г) перпендикулярно пути. 2. При криволинейном движении направление мгновенного ускорения всегда А) касается годографа. Б) перпендикулярно годографу. В) касательная к пути.Г) перпендикулярно пути. 3. Если частица переместилась из точки A в точку B по круговой траектории за 4 секунды, какова средняя скорость частицы? A) 2,5 мкм / с B) 2,5 i + 1,25 мкм / с C) 1,25 π im / с D) 1,25 π jm / s 4. Положение частицы задается как A) (4 i +8 j) m / s2 B) (8 C) (8 i) m / s2 D) (8 мгновенная скорость всегда r = (4t2 i – 2t j) m. Определите ускорение частицы. i -16 j) m / s2 j) m / s2 12.6 Движение снаряда Для иллюстрации рассмотрим два шара слева. Красный шар падает из состояния покоя, а желтый шар получает горизонтальную скорость.Каждый снимок в этой последовательности сделан через один и тот же интервал времени. Обратите внимание, что оба шара подвергаются одинаковому ускорению вниз, поскольку они остаются на одной высоте в любой момент. Также обратите внимание, что расстояние по горизонтали между последовательными фотографиями желтого шара постоянно, поскольку скорость в горизонтальном направлении постоянна. Кинематические уравнения для горизонтального движения снаряда Поскольку ax = 0, скорость в горизонтальном направлении остается постоянной (vx = vox), а положение в направлении x может быть определено следующим образом: _____________________________ ax равно нулю при незначительном сопротивлении воздуха! Кинематические уравнения для вертикального движения снаряда Поскольку положительная ось y направлена вверх, ay = -g.Применение уравнений постоянного ускорения дает: _____________________________ _____________________________ _____________________________ Для любой данной задачи можно использовать только два из этих трех уравнений. Почему? Дано: лыжник покидает рампу при θA = 25 o и попадает на склон в точке B. Найти: начальная скорость лыжника vA. 1. Снаряду придается начальная скорость v снаряд, когда он ударяется о склон, ____________ начальная скорость v A) меньше B) равна C) больше D) Ничего из вышеперечисленного.2. Частица имеет начальную скорость v, которую может достичь, когда A) Φ = 30 ° B) Φ C) Φ = 60 ° D) Φ o под углом Φ над горизонтом. Скорость о. o под углом Φ к горизонту. Максимальная высота it = 45 ° = 90 °

Криволинейный ход. Криволинейный

Вам хорошо известно, что в зависимости от формы траектории движение делится на прямолинейное и криволинейное … Мы научились работать с прямолинейным движением на предыдущих уроках, а именно, чтобы решить главную задачу: механика для этого типа движения.

Однако ясно, что в реальном мире мы чаще всего имеем дело с криволинейным движением, когда траектория представляет собой кривую линию. Примерами такого движения являются траектория тела, брошенного под углом к горизонту, движение Земли вокруг Солнца и даже траектория движения ваших глаз, которые теперь следуют этому контуру.

Этот урок будет посвящен вопросу о том, как решается основная задача механики в случае криволинейного движения.

Для начала определимся, какие принципиальные отличия криволинейного движения (рис. 1) от прямолинейного и к чему эти отличия приводят.

Рис. 1. Траектория криволинейного движения

Давайте поговорим о том, как удобно описывать движение тела криволинейным движением.

Вы можете разделить движение на отдельные участки, на каждом из которых движение можно считать прямолинейным (рис. 2).

Рис.2. Разделение криволинейного движения на участки прямолинейного движения

Однако более удобен следующий подход. Представим это движение как комбинацию нескольких движений по дугам окружностей (рис. 3). Обратите внимание, что таких подразделений меньше, чем в предыдущем случае; кроме того, движение по окружности криволинейно. К тому же примеры движения по кругу в природе очень распространены. Из этого можно сделать вывод:

Чтобы описать криволинейное движение, вам нужно научиться описывать движение по окружности, а затем представлять произвольное движение в виде набора движений по дугам окружностей.

Рис. 3. Разделение криволинейного движения на движение по дугам окружностей

Итак, начнем изучение криволинейного движения с изучения равномерного движения по окружности. Давайте посмотрим, в чем принципиальные различия между криволинейным движением и прямолинейным движением. Для начала напомним, что в девятом классе мы изучали тот факт, что скорость тела при движении по окружности направлена по касательной к траектории (рис. 4). Кстати, вы можете наблюдать этот факт на собственном опыте, если посмотрите, как движутся искры при использовании точильного камня.

Рассмотрим движение тела по дуге окружности (рис. 5).

Рис. 5. Скорость тела при движении по кругу

Обратите внимание, что в этом случае модуль скорости тела в точке равен модулю скорости тела в точке:

Однако вектор не равен вектору. Итак, у нас есть вектор разницы скоростей (рис.6):

Рис. 6. Вектор разности скоростей

Причем изменение скорости произошло через некоторое время.Таким образом, мы получаем знакомую комбинацию:

Это не что иное, как изменение скорости с течением времени или ускорение тела. Можно сделать очень важный вывод:

Движение по кривой траектории ускорено. Природа этого ускорения – непрерывное изменение направления вектора скорости.

Еще раз отметим, что даже если говорится, что тело движется равномерно по окружности, это означает, что модуль скорости тела не изменяется.Однако такое движение всегда ускоряется, так как направление скорости меняется.

В девятом классе вы изучали, что такое ускорение и как оно направлено (рис. 7). Центростремительное ускорение всегда направлено к центру круга, по которому движется тело.

Рис. 7. Центростремительное ускорение

Модуль центростремительного ускорения можно рассчитать по формуле:

Переходим к описанию равномерного движения тела по окружности.Согласитесь, что скорость, которую вы использовали при описании поступательного движения, теперь будем называть линейной скоростью. Под линейной скоростью мы понимаем мгновенную скорость в точке траектории вращающегося тела.

Рис. 8. Движение точек по диску

Рассмотрим диск, который вращается по часовой стрелке для определенности. На его радиусе отмечаем две точки и (рис. 8). Рассмотрим их движение. Некоторое время эти точки будут перемещаться по дугам окружности и станут точками и.Очевидно, точка переместилась больше, чем точка. Из этого можно сделать вывод, что чем дальше от оси вращения находится точка, тем с большей линейной скоростью она движется.

Однако, если присмотреться к точкам и, можно сказать, что угол, на который они повернулись относительно оси вращения, остался неизменным. Именно угловые характеристики мы будем использовать для описания движения по окружности. Обратите внимание, что для описания движения по окружности можно использовать спецификации угол .

Начнем рассмотрение движения по окружности с простейшего случая – равномерного движения по окружности. Напомним, что равномерное поступательное движение – это движение, при котором за любые равные промежутки времени тело совершает одни и те же движения. По аналогии можно дать определение равномерного движения по окружности.

Равномерное движение по окружности – это движение, при котором тело вращается на одинаковые углы в течение любых равных интервалов времени.

Аналогично понятию линейной скорости вводится понятие угловой скорости.

Угловая скорость равномерного движения ( называется физической величиной, равной отношению угла, на который повернулось тело, ко времени, в которое этот поворот произошел.

В физике чаще всего используется радианная мера угла. Например, угол равен радианам. Угловая скорость измеряется в радианах в секунду:

Найдем связь между угловой скоростью вращения точки и линейной скоростью этой точки.

Рис. 9. Связь между угловой и линейной скоростью

При вращении острие проходит дугу длины, поворачиваясь на угол. Из определения радианной меры угла можно написать:

Разделим левую и правую части равенства на интервал времени, в течение которого было совершено движение, затем воспользуемся определением угловой и линейной скоростей:

Обратите внимание, что чем дальше точка от оси вращения, тем выше ее линейная скорость.А точки, расположенные на самой оси вращения, неподвижны. Примером этого является карусель: чем ближе вы находитесь к центру карусели, тем легче вам оставаться на ней.

Эта зависимость линейной и угловой скоростей используется в геостационарных спутниках (спутники, которые всегда находятся над одной и той же точкой на земной поверхности). Благодаря таким спутникам мы можем принимать телевизионные сигналы.

Напомним, что ранее мы ввели понятия периода и частоты вращения.

Период вращения – это время одного полного оборота. Период вращения обозначается буквой и измеряется в секундах в системе СИ:

Частота вращения – это физическая величина, равная количеству оборотов, которые тело совершает за единицу времени.

Частота обозначается буквой и измеряется в секундах обратного направления:

Они связаны соотношением:

Существует взаимосвязь между угловой скоростью и частотой вращения тела.Если вспомнить, что полный оборот равен, легко увидеть, что угловая скорость равна:

Подставляя эти выражения в соотношение между угловой и линейной скоростью, можно получить зависимость линейной скорости от периода или частоты:

Мы также записываем соотношение между центростремительным ускорением и этими величинами:

Таким образом, мы знаем взаимосвязь между всеми характеристиками равномерного движения по окружности.

Подведем итоги. В этом уроке мы начали описывать криволинейное движение. Мы разобрались, как криволинейное движение может быть связано с круговым движением. Круговое движение всегда ускоряется, и наличие ускорения определяет тот факт, что скорость всегда меняет свое направление. Это ускорение называется центростремительным. Наконец, мы вспомнили некоторые характеристики кругового движения (линейная скорость, угловая скорость, период и частота вращения) и обнаружили связь между ними.

Библиография

Г.Я. Мякишев, Б.Б. Буховцев, Н. Сотский. Физика 10. – М .: Просвещение, 2008.
А.П. Рымкевич. Физика. Проблемная книга 10-11. – М .: Дрофа, 2006.
О.Я. Савченко. Физические задачи. – М .: Наука, 1988.
А.В. Перышкин, В. Крауклис. Курс физики. Т. 1. – М .: Гос. уч.-пед. изд. мин. образование РСФСР, 1957.

Айп.ру ().
Википедия ().

Домашнее задание

Решив задачи этого урока, вы сможете подготовиться к вопросам 1 GIA и вопросам A1, A2 экзамена.

Задачи 92, 94, 98, 106, 110 – Сб. задачи А.П. Рымкевича, под ред. десять
Рассчитайте угловую скорость минутной, секундной и часовой стрелок часов. Вычислите центростремительное ускорение, действующее на кончики этих стрелок, если радиус каждой из них равен одному метру.

Криволинейные движения – это движения, траектории которых представляют собой не прямые, а изогнутые линии. Планеты и речные воды движутся по криволинейным траекториям.

Криволинейное движение – это всегда движение с ускорением, даже если модуль скорости постоянен. Криволинейное движение с постоянным ускорением всегда происходит в плоскости, в которой расположены векторы ускорения и начальные скорости точки. В случае криволинейного движения с постоянным ускорением в плоскости xOy проекции vx и vy его скоростей на оси Ox и Oy и координаты x и y точки в любой момент времени t определяются по формулам

Ни одно тело не движется все время с постоянной скорости… Начиная движение, машина движется все быстрее и быстрее. Некоторое время он может двигаться равномерно, но затем замедляется и останавливается. В этом случае автомобиль преодолевает разные расстояния за одно и то же время.

Движение, при котором тело проходит неравные отрезки пути через равные промежутки времени, называется неравномерным. При таком движении величина скорости не остается неизменной. В данном случае можно говорить только о средней скорости.

Средняя скорость показывает, чему равно смещение, которое тело проходит за единицу времени.Он равен отношению движения тела ко времени движения. Средняя скорость, как и скорость равномерного движения тела, измеряется в метрах, разделенных на секунду. Для более точной характеристики движения в физике используется мгновенная скорость.

Скорость тела в этот момент времени или в заданной точке траектории называется мгновенной скоростью. Мгновенная скорость является векторной величиной и направлена так же, как вектор смещения. Вы можете измерить мгновенную скорость с помощью спидометра.В Международной системе мгновенная скорость измеряется в метрах, разделенных на секунду.

скорость движения точки неравномерная

Криволинейное движение очень распространено в природе и технике. Это сложнее прямолинейного, так как криволинейных траекторий много; это движение всегда ускоряется, даже если модуль скорости не изменяется.

Но движение по любой кривой пути можно грубо представить как движение по дугам окружности.

Когда тело движется по кругу, направление вектора скорости меняется от точки к точке.Поэтому, когда говорят о скорости такого движения, имеют в виду мгновенную скорость. Вектор скорости направлен по касательной к окружности, а вектор смещения – по хордам.

Равномерное движение по окружности – это движение, при котором модуль скорости движения не изменяется, изменяется только его направление. Ускорение такого движения всегда направлено к центру круга и называется центростремительным. Чтобы найти ускорение тела, движущегося по кругу, необходимо квадрат скорости разделить на радиус круга.

Движение тела по окружности, кроме ускорения, характеризуется следующими величинами:

Период вращения тела – это время, в течение которого тело совершает один полный оборот. Период вращения обозначается буквой Т и измеряется в секундах.

Скорость вращения тела – это количество оборотов в единицу времени. Скорость вращения обозначается буквой? и измеряется в герцах. Чтобы найти частоту, необходимо разделить единицу на период.

Линейная скорость – это отношение движения тела ко времени. Чтобы найти линейную скорость тела в окружности, необходимо разделить длину окружности на период (длина окружности равна двукратному радиусу).

Угловая скорость – это физическая величина, равная отношению угла поворота радиуса окружности, по которой движется тело, ко времени движения. Угловая скорость обозначается буквой? и измеряется в радианах, деленных на секунду.Вы можете найти угловую скорость, разделив 2? на срок. Угловая скорость и линейная скорость между собой. Чтобы найти линейную скорость, угловую скорость нужно умножить на радиус окружности.

Рисунок 6. Круговое движение, формулы.

В этой теме основное внимание будет уделено более сложному движению разума – КРИВОЛИНЕЙНОЕ … Как вы могли догадаться, криволинейное движение – это движение, траектория которого представляет собой кривую линию … И, поскольку это движение сложнее, чем прямолинейное, тогда тех физических величин, которые были перечислены в предыдущей главе, уже недостаточно для его описания.

Для математического описания криволинейного движения существует 2 группы величин: линейные и угловые.

ЛИНЕЙНЫЕ ЗНАЧЕНИЯ.

1. Перемещение … В разделе 1.1 мы не вдавались в подробности о различиях между концепцией

Рисунок 1.3 Пути (расстояния) и концепция смещения,

, так как в прямом движении эти

Отличия

не играют принципиальной роли, а

Эти значения обозначаются той же буквой

вой S … Но когда мы имеем дело с криволинейным движением,

, этот вопрос требует уточнения. Так в чем же способ

(или расстояние)? – Это длина траектории

движение. То есть, если отслеживать траекторию

движения тела и измерив его (в метрах, километрах и т. Д.), Вы получите значение, называемое путем (или расстоянием) S (см. Рисунок 1.3). Таким образом, путь – это скаляр, который характеризуется только числом.

Рисунок 1.4 Смещение – это кратчайшее расстояние между

начальная точка пути и конечная точка пути.А с

г.

Moving уделяет большое внимание с самого начала

Путь до его конца, тогда это значение вектора

и характеризуется не только числовым значением, но и

направление (рисунок 1.3). Нетрудно догадаться, что если

тело движется по замкнутой траектории, затем до

в момент возврата в исходное положение движение будет равно нулю (см. Рис. 1.4).

2 . Линейная скорость … В разделе 1.1 мы дали определение этой величины, и оно остается в силе, хотя в то время мы не указали, что эта скорость является линейной. Как направлен вектор линейной скорости? Обратимся к рисунку 1.5. Вот фрагмент

криволинейная траектория тела. Любая изогнутая линия – это соединение дуг разных окружностей. На рис. 1.5 показаны только два из них: круг (O 1, r 1) и круг (O 2, r 2). В момент прохождения тела по дуге данного круга его центр становится временным центром вращения с радиусом, равным радиусу этого круга.

Вектор, проведенный от центра вращения к точке, где в настоящее время находится тело, называется радиус-вектором. На рисунке 1.5 радиус-векторы представлены векторами и. На этом рисунке также показаны векторы линейной скорости: вектор линейной скорости всегда направлен по касательной к траектории в направлении движения. Следовательно, угол между вектором и радиус-вектором, проведенным к данной точке на пути, всегда равен 90 °. Если тело движется с постоянной линейной скоростью, то модуль вектора не изменится, а его направление все время меняется в зависимости от формы траектории.В случае, показанном на рис. 1.5, движение осуществляется с переменной линейной скоростью, следовательно, модуль вектора изменяется. Но, поскольку направление вектора всегда меняется при криволинейном движении, отсюда следует очень важный вывод:

всегда есть ускорение при криволинейном движении ! (Даже если движение осуществляется с постоянной линейной скоростью.) Более того, ускорение, о котором идет речь в этом случае, в дальнейшем мы будем называть линейным ускорением.

3 . Линейное ускорение … Напомню, что ускорение происходит при изменении скорости. Соответственно, линейное ускорение возникает при изменении линейной скорости. А линейная скорость при криволинейном движении может изменять вращение по модулю и по направлению. Таким образом, общее линейное ускорение раскладывается на две составляющие, одна из которых влияет на направление вектора, а вторая – на его модуль. Рассмотрим эти ускорения (рис.1.6). На этом рисунке

рис. 1,6

изображает тело, движущееся по круговой траектории с центром вращения в точке О.

Ускорение, изменяющее направление вектора, называется нормальное и обозначается значком. Нормальным он называется потому, что направлен перпендикулярно (нормально) к касательной, т.е. по радиусу до центра вращения … Его еще называют центростремительным ускорением.

Ускорение, изменяющее модуль вектора, называется тангенциальным и обозначается значком. Он лежит на касательной и может быть направлен как по направлению вектора, так и против него :

Если линейная скорость увеличивается, то> 0 и их векторы сонаправлены;

Если линейная скорость убывает, затем

направлено.

Таким образом, эти два ускорения всегда образуют прямой угол друг с другом (90º) и являются составляющими общего линейного ускорения, т.е. полное линейное ускорение представляет собой векторную сумму нормального и тангенциального ускорений:

Обратите внимание, что в данном случае речь идет именно о векторной сумме, но ни в коем случае не о скалярной сумме. Чтобы найти числовое значение, зная и, необходимо воспользоваться теоремой Пифагора (квадрат гипотенузы треугольника численно равен сумме квадратов катетов этого треугольника):

(1.8).

Это означает:

(1,9).

Какие формулы рассчитать и рассмотрим чуть позже.

УГЛОВЫЕ ЗНАЧЕНИЯ.

1 . Угол поворота φ … При криволинейном движении тело не только проходит какой-то путь и совершает какое-то движение, но и поворачивается на определенный угол (см. Рис. 1.7 (a)). Поэтому для описания такого движения вводится величина, которая называется углом поворота и обозначается греческой буквой φ. (читать «фи»).В системе СИ угол поворота измеряется в радианах (обозначается «рад»). Напомню, что один полный оборот равен 2π радиан, а число π является постоянной величиной: π ≈ 3,14. на рис. 1.7 (а) показана траектория тела по окружности радиуса r с центром в точке O. Сам угол поворота – это угол между радиус-векторами тела в некоторые моменты времени.

2 . Угловая скорость ω – это значение, которое показывает, как угол поворота изменяется в единицу времени. ( ω – греческая буква, читается «омега») На рис. 1.7 (b) показывает положение материальной точки, движущейся по круговой траектории с центром в точке O, с интервалами Δt … Если углы, на которые поворачивается тело в эти промежутки времени, одинаковы, то угловая скорость постоянна, и это движение можно считать равномерным. А если углы поворота разные, то движение неравномерное. И, поскольку угловая скорость показывает, сколько радианов

тело повернулось за одну секунду, то его единица измерения – радианы в секунду.

(обозначается « рад / с »).

рис. 1,7

а). б). Δt

Δt

О φ O Δt

3 . Угловое ускорение ε Количество, показывающее, как оно изменяется в единицу времени. А поскольку угловое ускорение ε появляется при изменении угловой скорости ω , то можно сделать вывод, что угловое ускорение возникает только в случае неравномерного криволинейного движения.Блок углового ускорения – « рад / с 2 “(Радиан на секунду в квадрате).

Таким образом, таблицу 1.1 можно дополнить еще тремя значениями:

Таблица 1.2

№	физическая величина	определение величины	обозначение количества	единица
1.	путь	это расстояние, которое проходит тело в процессе своего движения	S	м (метр)
2.	скорость	это расстояние, которое проходит тело за единицу времени (например, за 1 секунду)	υ	м / с (метр в секунду)
3.	ускорение	это величина, на которую скорость тела изменяется в единицу времени	a	м / с 2 (метр на секунду в квадрате)
4.	время		т	с (секунда)
5.	угол поворота	это угол, на который тело поворачивается при криволинейном движении	φ	рад (радиан)
6.	угловая скорость	это угол, на который тело поворачивается за единицу времени (например, за 1 секунду)	ω	рад / с (радиан в секунду)
7.	угловое ускорение	это величина, на которую угловая скорость изменяется в единицу времени	ε	рад / с 2 (радиан на секунду в квадрате)

Теперь можно перейти непосредственно к рассмотрению всех видов криволинейных движений, а их всего три.

Понятия скорости и ускорения естественным образом обобщаются на случай движения материальной точки по криволинейной траектории … Положение движущейся точки на траектории задается радиус-вектором r проведено в эту точку из некоторой фиксированной точки O , например начала координат (рис. 1.2). Пусть в момент времени t материальная точка находится в позиции M с радиус-вектором r = r ( т, ).Спустя короткое время D t он переместится в позицию M 1 с радиусом-вектором r 1 = r ( т + D т ). Радиус – вектор материальной точки получит приращение, определяемое геометрической разностью D r = r 1 – r . Средняя скорость движения за время D т называется количество

Средняя скорость в направлении В ср совпадает с направлением вектора D r .

Предел средней скорости при D t ® 0, т.е. производная от радиус-вектора r по времени

(1,9)

называется истинной или мгновенной скоростью материальной точки. Вектор В направлен по касательной к траектории движущейся точки.

Разгон a называется вектором, равным первой производной вектора скорости V или вторая производная радиуса – вектор r по времени:

(1.10)

(1.11)

Отметим следующую формальную аналогию между скоростью и ускорением. От произвольной фиксированной точки O 1 отложим вектор скорости V – это движущаяся точка во все возможные моменты времени (рис. 1.3).

Конец вектора В называется точкой скорости … Геометрическое место точек скорости – это кривая, называемая годографом скорости . Когда материальная точка описывает траекторию, соответствующая точка скорости перемещается по годографу.

Рис. 1.2 отличается от рис. 1.3 только условными обозначениями. Радиус – вектор r заменяется вектором скорости V , материальная точка – к точке скорости, траектория – к годографу. Векторные математические операции r при нахождении скорости и по вектору В при нахождении ускорения полностью идентичны.

Скорость В направлен по касательной.Вот почему ускорение a будет направлено по касательной к годографу скорости. Можно сказать, что ускорение – это скорость точки скорости вдоль годографа … Следовательно,

В зависимости от формы траектории движение делится на прямолинейное и криволинейное. В реальном мире мы чаще всего имеем дело с криволинейным движением, когда траектория представляет собой кривую линию. Примерами такого движения являются траектория тела, брошенного под углом к горизонту, движение Земли вокруг Солнца, движение планет, конец часовой стрелки на циферблате и т. Д.

Рисунок 1. Траектория и смещение при криволинейном движении

Определение

Криволинейное движение – это движение, траектория которого представляет собой кривую линию (например, окружность, эллипс, гипербола, парабола). При движении по криволинейной траектории вектор смещения $ \ overrightarrow (s) $ направлен по хорде (рис. 1), l – длина траектории. Мгновенная скорость движения тела (то есть скорость тела в данной точке траектории) направлена по касательной в той точке траектории, где в данный момент находится движущееся тело (рис.2).

Рисунок 2. Мгновенная скорость при криволинейном движении

Однако более удобен следующий подход. Вы можете представить это движение как комбинацию нескольких движений по дугам окружностей (см. Рис. 4.). Таких перегородок будет меньше, чем в предыдущем случае, к тому же движение по окружности само по себе криволинейно.

Рисунок 4. Разделение криволинейного движения на движения по дугам окружностей

Выход

Задача изучения криволинейного движения материальной точки состоит в том, чтобы составить кинематическое уравнение, которое описывает это движение и позволяет при заданных начальных условиях определить все характеристики этого движения.

Пример сферического движения: качение конуса по плоскости (x y). …

Контекст 1

… еще один компонент, связанный с переходом на ISA. Также указано, что последняя часть перпендикулярна общей касательной плоскости подвижной и неподвижной осей.Однако доказательство этого утверждения относится к решению плоской задачи качения, когда точка контакта с телом проходит через острие его траектории (см. Рис. 8), из чего следует, что ее ускорение перпендикулярно касательной плоскости. Это, безусловно, верно, но точное обобщение пространственных движений не дается явно в …

Контекст 2

… действительно для пространственных вращательных движений (v P = 0), как и в случае плоского кейс. Таким образом, во время вращения скорость смены полюсов перпендикулярна угловой скорости и ускорению точки P, как это показано на рис….

Контекст 3

… можно выделить: -Если α ω, ускорение точек и скорость изменения полюса постоянны вдоль IAR. Это движение соответствует качению цилиндра, т.е. плоскому движению. -Если P1 α × ω, должна быть точка P 2 вдоль IAR с нулевым ускорением. Этот случай соответствует качению конуса, т. Е. Сферическому движению (рис. 8). Напомним, что если ускорение равно нулю в точке IAR, соответствующая скорость изменения полюса [см.(13)] также равен нулю. Таким образом, мы снова переходим к анализу скорости смены полюсов. Выражая скорости смены полюсов, соответствующие точкам P 1 и P 2 в (19), через (12), получаем …

Контекст 4

… через u и ω во всех точках IAR то же направление u и вдоль IAR. Согласно (20), величина скорости смены полюсов линейно изменяется вдоль ИАР. Таким образом, геометрическая точка с нулевой скоростью изменения полюса (совпадающая с материальной точкой с нулевым ускорением) может быть найдена простым способом, как показано на рис.8. Однако есть и более общие случаи, когда разные касательные плоскости могут быть найдены для разных точек вдоль IAR, как показано на рис. 4. Для дальнейшего анализа мы разложим векторное тройное произведение в …

Круговое движение – Полный инструментарий

Цели

Чтобы описать направление скорости, ускорения и результирующей силы для объекта, который движется по кругу с постоянной скоростью.
Использовать закон инерции для объяснения того, почему человек, движущийся по кругу, испытывает ощущение, что его выталкивают наружу, и для определения причин, по которым внешняя чистая сила является фиктивной силой.
Математически связать скорость, ускорение, радиус, массу и чистую силу для объекта, движущегося по кругу, и использовать такие отношения для решения физических задач.
Построить диаграмму свободного тела для любой ситуации, когда объект движется по кругу.
Объединить второй закон движения Ньютона, диаграммы свободного тела и уравнения кругового движения для определения значения ускорения или индивидуальной силы для любой ситуации, когда объект движется по кругу.

Чтения из Учебника по физике

Учебное пособие по физике, круговое движение и движение спутников, урок 1
Учебник по физике, Круговое движение и движение спутников, Урок 2

Интерактивное моделирование

Модель простого кругового движения
Хорошая модель для начинающих, чтобы изучить силы, действующие на человека, едущего на карусели.Форматирование 3D очень полезно для просмотра движения с разных точек зрения. Используя ползунки, учащиеся сами узнают, как взаимодействуют скорость вращения и радиальное расстояние, создавая более захватывающую поездку. Учителя: исходный код этого моделирования находится в открытом доступе, что делает его настраиваемым ресурсом.
Веселая поездка на миксере, модель
Любой, кто катался на аттракционе «Скремблер» в парке развлечений, будет знаком с системой, изображенной в этой симуляции.Он показывает взаимодействие двух наложенных друг на друга круговых движений. Основная рама аттракциона вращается в одном направлении, в то время как второе вращение на концах рычагов рамы переносит гонщиков дополнительным круговым движением, обычно в противоположном направлении. Студенты могут управлять двумя скоростями вращения и радиусами двух орбит. Могут отображаться векторы горизонтальной силы, а также график перегрузки на всадника в зависимости от времени. Учителя: эта модель также предоставляет открытый доступ к исходному коду Java, что делает его настраиваемым ресурсом.
Моделирование PhET: Ladybug Revolution
Присоединяйтесь к божьей коровке в исследовании вращательного движения. Вращайте карусель, чтобы изменить ее угол, или выберите постоянную угловую скорость или угловое ускорение. Изучите, как круговое движение связано с положением, скоростью и ускорением жука, используя векторы или графики.
Дополнительные материалы для PhET : См. Ссылку ниже для краткого задания, разработанного группой учителей старших классов для обучения учащихся в использовании имитационного моделирования PhET «Ladybug Revolution».Студенты будут составлять таблицы данных, чтобы способствовать пониманию взаимосвязи между ускорением, скоростью и радиусом круговой траектории. Он также предоставляет подробные инструкции по изучению векторов скорости и ускорения. Включает план урока и руководство для студентов. http://phet.colorado.edu/en/contributions/view/3234
Класс физики: равномерное круговое движение
Это моделирование позволяет пользователю изменять радиус и скорость объекта, движущегося равномерно по кругу, чтобы увидеть эффект от ускорения и силы.Направление скорости и силы отображаются в виде векторных стрелок. Это моделирование сопровождается списком занятий с указаниями и исследовательскими вопросами.
http://www.physicsclassroom.com/shwave/ucmdirns.cfm

Видео и анимация

PBS Learning Media: Центростремительная сила на американских горках
Это 5-минутное видео замечательно объясняет, почему вы чувствуете, что вас отбрасывает от центра во время кругового движения, хотя нет никакой внешней чистой силы.Это поможет студентам отличить центростремительную силу от вымышленной «центробежной силы».
Круговое движение
В этом учебном цикле представлены 11 коротких видеороликов, подготовленных исследовательской группой по физике и астрономии Рутгерса, последовательно организованных для введения кругового движения во вводные курсы физики. Каждое видео включает в себя цель обучения, предварительную информацию, необходимую для понимания материала, и вопросы-подсказки. Разработанный для совместного обучения, учащиеся будут участвовать в мысленных экспериментах, наблюдении и применении.Эти материалы были разработаны, чтобы отражать деятельность ученых, когда они конструируют и применяют знания. Зарегистрированные пользователи-учителя имеют доступ к дополнительным инструкциям и справочным материалам.
Наука скорости: поворот
Это 5-минутное видео исследует центростремительную силу в контексте NASCAR. Как можно спроектировать гусеницы и шины для гоночных автомобилей, чтобы помочь водителям быстрее совершать повороты? И как угол (крен) трека влияет на центростремительное ускорение (это имеет огромное значение).Узнайте от инженеров, физиков и водителей NASCAR о компонентах, которые обеспечивают центростремительную силу, необходимую для движения гоночного автомобиля по кривой.
Физика цирка: центростремительное ускорение
В этом видео-уроке используется верховая езда, чтобы показать студентам основы кругового движения и центростремительного ускорения. Видео может помочь студентам понять, что неуравновешенная сила может изменить направление вектора скорости, но не его величину.Он включает советы о том, как включить видео в инструкции, вопросы для обсуждения и сопутствующие занятия в классе. (Видео длится 2 минуты; дайте 25-30 минут для полной активности.)

Лаборатории и исследования

Демонстрационные идеи

Обучение из космоса: центростремительная сила
Посмотрите, как астронавт НАСА на борту Международной космической станции демонстрирует центростремительную силу таким образом, чтобы пролить новый свет на студентов.Видео было снято в условиях невесомости – космонавт вращает привязанный инструмент вокруг шнура, вращает пакет с чаем, чтобы показать, как пузырьки воздуха выталкиваются к центру, и вращает каплю воды, чтобы показать деформацию, вызванную центростремительной силой.

Интернет-модули Minds On Physics

Интернет-модули Minds On Physics представляют собой набор модулей интерактивных вопросов, нацеленных на концептуальное понимание учащегося.Каждый вопрос сопровождается подробной справкой, в которой рассматриваются различные компоненты вопроса.

Круговое движение и гравитация, Ass’t CG1 – Speed and Velocity
Круговое движение и гравитация, Ass’t CG2 – Acceleration and Net Force
Круговое движение и гравитация, Ass’t CG3 – Центростремительная сила и инерция
Круговое движение и гравитация, Ass’t CG4 – Требование центростремительной силы
Круговое движение и гравитация, Ass’t CG5 – Математический анализ кругового движения

Ссылка: http: // www.Physicsclassroom.com/mop

Упражнения по построению концепции

Угол учебной программы, круговое движение, скорость и скорость
Угол учебной программы, круговое движение, ускорение и круговое движение
Угол учебной программы, круговое движение, круговое движение и инерция
Уголок учебной программы, круговое движение, требование центростремительной силы
Уголок учебной программы, круговое движение, математика кругового движения

Ссылка: http: // www.Physicsclassroom.com/curriculum/circles

Упражнения по решению проблем

Блокнот калькулятора, круговое движение и гравитация, задачи № 1-15

Ссылка: http://www.physicsclassroom.com/calcpad/circgrav

Научное рассуждение

Центр научных рассуждений, Петли для американских горок,

Ссылка: http://www.physicsclassroom.com/reasoning/circularmotion

Связи в реальной жизни

Проектирование проблемного учебного модуля
съезда с автомагистрали http: // pbl.ccdmd.qc.ca/resultat.php?action=clicFiche&he=1050&afficheRecherche=-1&IDFiche=141&endroitRetour=0
Двухдневное экспериментальное упражнение для вводного курса физики, относящейся к круговому движению и трению. В этом сценарии учащиеся проектируют плоский круговой съезд с шоссе и определяют в пределах набора заданных ограничений, каким должно быть ограничение скорости на съезде. Студенты будут применять концепции кинематики вращения, статического и кинетического трения и изучат динамику объекта, движущегося по круговой траектории.Следуя методу PBL, учащиеся будут просеивать информацию, чтобы отделить полезные от нерелевантных данных, самостоятельно находить недостающую информацию, а затем применять физику для поиска решений.

Общие заблуждения

Скорость, сила и инерционный путь
Объект, который движется по криволинейной траектории, испытывает скорость, направленную по касательной к траектории. Во всех точках окружности или изогнутой траектории скорость объекта направлена прямо вперед .Таким образом, это касательное направление или прямое направление описывает инерционный путь объекта . Если бы все силы были уравновешены, то объект продолжил бы свой путь по инерции. Движение по кругу – это отклонение от этого прямого направления и, следовательно, требует неуравновешенной силы. Движение по кругу требует чистой силы, направленной к центру круга, чтобы объект отклонился от инерционного пути. Но если в любой момент убрать эту чистую внутреннюю силу, то объект будет двигаться по инерционной траектории, касательной к окружности.
Ускорение
Среди студентов очень распространено мнение, что объект, движущийся по кругу с постоянной скоростью, не ускоряется. Но это совершенно неверно. Движение по кругу предполагает ускорение… даже если это движение с постоянной скоростью. Ускоряющиеся объекты меняют свою скорость. Как вектор, скорость объекта описывает скорость и направление объекта. Итак, объекты, которые меняют скорость или направление, ускоряются.Таким образом, объект, который движется по кругу с постоянной скоростью, ускоряется из-за изменения направления. Полезно напомнить учащимся, какие три элемента управления на автомобиле позволяют ему ускоряться: педаль тормоза для замедления, педаль газа для ускорения и рулевое колесо для изменения направления.
Понятие внешней или центробежной силы
Любой, кто был на машине с американскими горками, или совершал круговую поездку в парке развлечений, или просто круто повернул налево, когда пассажир в машине испытал то, что казалось сильный толчок или сила, направленная от центра круга.Это чувство выталкивания наружу неоспоримо; однако реальность не всегда согласуется с чувствами. Ощущение внешней силы приписывается инерции – тенденции объекта продолжать движение в том же направлении, в котором он движется, когда на него не действует неуравновешенная сила. В этих случаях – американские горки, аттракционы, поворотная машина – вы продолжаете движение по прямой, пока ваш инерционный путь не встретится с дверью машины, стеной или каким-либо другим препятствием. Встретившись с дверью или стеной машины, вы начинаете толкать ее наружу.Между тем дверь или стена толкают вас внутрь – в соответствии с третьим законом Ньютона.
Многие писали об этом опыте, ссылаясь на понятие центробежной или внешней силы. Те, кто обычно делятся на две категории – те, кто не знает, о чем они пишут и не должны писать об этом, и те, кто действительно знает, о чем они пишут, и должны быть осторожны, чтобы не вводить своих читателей в заблуждение. . В последнем случае обсуждение центробежной силы почти всегда сопровождается некоторым заключительным замечанием, которое звучит примерно так: «Такая сила является фиктивной силой.Его не существует, несмотря на то, что представление о нем может помочь объяснить ощущение выталкивания наружу ». Если читатель не осознает важность этой короткой фразы, то читатель вводится в заблуждение, полагая, что движение по кругу сопровождается центробежной или внешней силой. Это трагично.

В другом месте в Интернете

Physlet Physics: вращение вокруг фиксированной оси
Этот исчерпывающий набор задач на основе анимации разработан, чтобы помочь учащимся понять силы, действующие при вращении объекта вокруг фиксированной оси (круговое движение).Вы найдете 3 концептуальных иллюстрации, математические вычисления, исследования, дополненные рабочими листами для учащихся, и более десятка концептуальных вопросов, которые можно гибко использовать в совместных группах или с помощью полнофункциональных систем ответа (кликеров). Теперь в свободном доступе в цифровой библиотеке ComPADRE. (подходит для AP или с отличием по физике)
Physlet Physics: Анимация кругового движения
Этот Physlet задуман как предварительный вопрос для изучения кругового движения.Его можно гибко использовать в качестве анимированной демонстрации, концептуального вопроса для систем ответов учащихся или в качестве упражнения для выявления предшествующих представлений.

Стандарты A. Научные стандарты нового поколения (NGSS) – Средняя школа
Ожидаемые результаты
HS-PS2.1 : Проанализируйте данные, чтобы подтвердить утверждение о том, что второй закон движения Ньютона описывает математическое соотношение между результирующей силой, действующей на макроскопический объект, его массой и его ускорением.

Основные дисциплинарные идеи
HS-PS2.A.i : Второй закон Ньютона точно предсказывает изменения в движении макроскопических объектов

Общие концепции
Комплексная концепция № 4: Системы и системные модели
Разрабатывать и использовать модели (физические, математические и компьютерные) для прогнозирования поведения системы и проектирования систем для решения конкретных задач.

Наука и инженерная практика
Практика № 2: Разработка и использование моделей
Используйте модель для механистического объяснения явлений.

Практика № 4: Анализ и интерпретация данных
Анализируйте данные с помощью инструментов, технологий и / или моделей (например, вычислительных, математических), чтобы сделать обоснованные и надежные научные утверждения или определить оптимальное проектное решение.
Анализируйте данные с помощью вычислительных моделей, чтобы делать обоснованные и надежные научные утверждения.

Практика № 5: Использование математики и вычислительного мышления
Используйте математические представления явлений для описания объяснений.
Создайте вычислительную модель или симуляцию явления, спроектированного устройства, процесса или системы.

Практика № 6: Разработка решений (проектирование)
Разработайте, оцените и / или доработайте решение реальной проблемы, основанное на научных знаниях, источниках доказательств, созданных студентами, приоритетных критериях и компромиссных решениях.

Практика № 8: Получение, оценка и передача информации
Передавать техническую информацию или идеи (например, о явлениях и / или процессе разработки, а также о проектировании и исполнении предлагаемого процесса или системы) в различных форматах (включая устную, графическую, текстовую и математическую)

B. Общие основные стандарты по математике (CC) – 9–12 классы

Стандарты математической практики
МП.1 – Разбирать проблемы и настойчиво решать их
MP.2 – Размышляйте абстрактно и количественно
MP.4 – Математическая модель

Алгебра старших классов: видение структуры в выражениях
A-SSE.1.a : Интерпретация частей выражения, таких как термины, множители и коэффициенты
A-SSE.2 : Используйте структуру выражения, чтобы определить способы его переписывания.

Алгебра для старших классов: создание уравнений
A-CED.2 Создание уравнений в двух или более переменных для представления взаимосвязей между величинами, графические уравнения на осях координат с метками и шкалами
A-CED.4 Перегруппируйте формулы, чтобы выделить интересующее количество, используя те же рассуждения, что и при решении уравнений

High School Algebra: тригонометрические функции – High School
Ф-ТФ.1 Под углом в радианах понимается длина дуги единичной окружности, образуемой углом

Высшая школа алгебры: линейные, квадратичные и экспоненциальные модели – высшая школа
F-LE.5 Интерпретировать параметры линейной или экспоненциальной функции в терминах контекста

Геометрия средней школы: круги – средняя школа
G-C.4 Постройте касательную линию от точки за пределами данной окружности до окружности

C. Общие основные стандарты английского языка / языковых навыков (ELA) – 9–12 классы

Стандарты чтения: научные и технические предметы – основные идеи и подробности
RST.11-12.2 Определяет центральные идеи или выводы текста; резюмировать сложные концепции, процессы или информацию, представленную в тексте, перефразируя их в более простых, но все же точных терминах.
РСТ.11-12.3 Четкое соблюдение сложной многоступенчатой процедуры при проведении экспериментов, измерений или выполнении технических задач; проанализировать конкретные результаты на основе пояснений в тексте.

Научно-технические предметы – интеграция знаний и идей
RST.11-12.9 Синтезировать информацию из ряда источников (например, тексты, эксперименты, моделирование) в согласованное понимание процесса, явления или концепции, разрешая противоречивую информацию, когда это возможно.

Научно-технические дисциплины – диапазон чтения и уровень сложности текста
РСТ.11-12.10 К концу 12 класса самостоятельно и умело читать и понимать научно-технические тексты из диапазона сложности текста 11-CCR.

D. Физические стандарты для колледжей (Хеллер и Стюарт)

Стандарт 3: Законы движения Ньютона – 9–12 классы
Цель 3.1: Постоянное и изменяющееся движение
H-3.1.1 – Смещение или изменение положения объекта – это векторная величина, которая может быть вычислена путем вычитания начального положения из конечного положения, где начальное и конечное положения могут иметь положительные и отрицательные значения. Перемещение не всегда равно пройденному расстоянию.

Результат обучения:
Переводите между различными представлениями движения объектов: устные и / или письменные описания, диаграммы движения, таблицы данных, графические представления (графики положения в зависимости от времени и графики мгновенной скорости в зависимости от времени) и математические представления.

Цель 3.2: Силы и изменения в движении – Средняя школа
Объектив M-3.2.2d – Сила постоянной величины, действующая под прямым углом к направлению движения объекта, заставляет объект двигаться по кругу с постоянной скоростью.
Объектив M-3.2.3 – Силы, действующие на объект, могут быть представлены стрелками (векторами), нарисованными на изолированном изображении объекта, называемом диаграммой сил.Направление каждой стрелки показывает направление толчка или тяги. Силы обозначены: «(тип взаимодействия) толкание или притяжение (взаимодействующего объекта) на (интересующий объект).

Цель 3.2: Силы и изменения в движении – Средняя школа
Цель H.3.2.2c – Объект движется по кругу, когда сумма векторов всех сил (результирующая сила) постоянна по величине, всегда направлена под прямым углом к направлению движения и всегда направлена к одной и той же точке в пространство, центр круга.Скорость объекта не меняется; ускорение вызывает постоянное изменение направления вектора изменения скорости.

Результаты обучения:
Анализируйте диаграммы сил, чтобы определить, точно ли они представляют различные ситуации, включающие множественные контактные, гравитационные и / или электрические взаимодействия. При необходимости определите одномерную векторную сумму всех сил (чистую силу) и интерпретируйте значение векторной суммы всех сил (чистая сила).
Изобразите силы, действующие на интересующий объект, на диаграмме сил, показывающей как вертикальные, так и горизонтальные силы. При необходимости используйте сложение векторов, чтобы определить относительный размер и направление суммы всех сил (чистая сила) и интерпретировать значение чистой силы.
Выясните и объясните, почему объект, движущийся с постоянной скоростью по кругу, ускоряется. Обоснуйте объяснение, построив диаграмму движения и используя знание ускорения и второго закона Ньютона.
Траектория и уравнение положения
Траектория – это геометрическая линия или путь, описываемый движущимся телом. В этом разделе мы собираемся изучить:
Понятие траектории и уравнение положения
Когда тело перемещается из одной точки в другую, оно делает это, описывая геометрическую линию в пространстве. Эта геометрическая линия называется траекторией , и она образована последовательными позициями конца вектора позиции во времени. Следовательно, мы часто находим координаты x, y и z вектора положения, записанные как функцию времени , например x (t), y (t) и z (t), чтобы представить эволюцию положения тел. с течением времени.
Траектория тела – это геометрическая линия , описываемая движущимся телом.
Уравнение положения или уравнение траектории представляет вектор положения как функцию времени. Его выражение в декартовых координатах и в трех измерениях:
г → т = xti → + ytj → + ztk →
Где:
r → (t): уравнение положения или уравнение траектории
x (t) , y (t), z (t) : координаты как функция времени
i →, j →, k →: единичные векторы в направлениях осей OX, OY и OZ соответственно
Для тех задач, где вы работаете с меньшим количеством измерений, вы можете упростить предыдущую формулу, исключив ненужные термины.Таким образом, уравнение положения:
В двух измерениях становится r → t = xti → + ytj → + ztk → = xti → + ytj →, поскольку z = 0
В двух измерениях становится r → t = xti → + ytj → + ztk → = xti →, поскольку y = 0 и z = 0
Следующая анимация иллюстрирует концепцию уравнения положения или уравнения траектории .
Экспериментируй и учись
Данные
r → (t) = t + 1 · i → + 0.05 · t2 + 0,1 · t + 0,05 · j →
r → =
r → =
Траектория
На графике показана траектория (серая линия), по которой тело, представленное красной точкой, следует во времени. В нашем примере эта траектория задается уравнением траектории r⃗ (t) = (t + 1) · i⃗ + (0,05 · t ² + 0,1 · t + 0,05) · j⃗ m, которое определяет в каждый момент времени t, который является вектором положения тела.
Перетащите ползунок времени и проверьте, как тело и его вектор положения изменяются при его перемещении. Вектор положения в каждый момент времени t получается путем подстановки значения t, которое вы выбрали в уравнение траектории.
Типы уравнения траектории
Помимо вышеприведенного выражения, существуют и другие способы выражения траектории движения тела. Ниже мы показываем другие типов уравнений положения или траектории :
Параметрические уравнения траектории : Каждая из координат устанавливается как функция времени в форме x = x (t), y = y (t), z = z (t). Например, параметрические координаты тела, которое движется в плоскости x-y, могут быть:
Явное уравнение траектории : оно получается путем удаления параметра t из предыдущих выражений и решения одной переменной в зависимости от другой.В нашем примере это будет:
x = t + 2 ⇒t = x-2
у = t2⇒y = (х-2) 2
Неявное уравнение траектории : получается, если f (x, y) = 0 .
Рассмотрим следующий пример. Представьте, что поезд движется на восток 50 метров каждую секунду. После первой секунды поезд находится в 50 метрах от отправной точки. После второй второй поезд находится в 100 м от отправной точки и так далее. Следовательно, мы могли написать:
Движение x координата как функция времени: x = 50t m
Уравнение положения : r → = 50ti → m
Расстояние до начала координат , заданное величиной вектора положения: r → = 50t
Пример
S.H.S. Мадрид-Барселона на первом этапе своего путешествия движется на восток со скоростью 50 метров в секунду и на север со скоростью 30 метров в секунду. Вычислить:
Координата x движения как функция времени
Координата движения по оси Y как функция времени
Уравнение положения поезда на исследуемом участке
Расстояние до начала отсчета сечения как функция времени
Прямолинейное и криволинейное движение по окружности.Прямолинейное и криволинейное движение. Движение тела по кругу с постоянным модулем скорости. Почему решили не рассматривать возможность переезда
Сегодня продолжим изучение движения. Мы рассматривали случаи, когда тела двигались только по прямой линии, то есть по прямой. Но не слишком ли часто такое движение мы встречаем в жизни? Конечно, нет. Тела обычно движутся по криволинейным траекториям. Движение планет, поездов, животных – все это будет примером криволинейного движения. Такое движение описать сложнее.Смена координат будет происходить как минимум по двум осям, например, OX и OY. Сравним направление векторов скорости и смещения при прямолинейном и криволинейном движении. Когда тело движется по прямой, то направление вектора скорости и вектора смещения всегда совпадают. Чтобы ответить на тот же вопрос в случае криволинейного движения, рассмотрим рисунок. Предположим, что тело движется из точки M1 в точку M2 по дуге. Путь – это длина дуги, движение – это вектор M1M2.В геометрии такой отрезок называется хордой. Мы видим, что направление скорости и движения не совпадают. В криволинейном движении мы будем говорить о мгновенной скорости. Мгновенная скорость тела в каждой точке изогнутой траектории направлена по касательной к траектории в этой точке. В этом можно убедиться, наблюдая за брызгами из-под колес авто, они тоже вылетают по касательной к окружности колеса. Обратите внимание, что скорость имеет разное направление в каждой точке изогнутой траектории, поэтому, даже если модуль скорости остается прежним, если направление движения изменилось, необходимо рассмотреть новый вектор.Из того, что скорость постоянно меняется, следует, что и ускорение изменится. Следовательно, криволинейное движение – это ускоренное движение. Предположим, что тело движется по кривой. Таких траекторий может быть бесчисленное количество, неужели каждая из них должна описывать свои законы движения? Оказывается, отдельные участки траектории можно приблизительно представить в виде дуг окружностей. А само криволинейное движение в большинстве случаев можно представить как набор движений по дугам окружностей разного радиуса.Изучив движение по кругу, мы можем описать более сложные случаи движения. Помните, если скорость тела и действующая на него сила направлены по одной прямой, то тело движется по прямой линии, а если они направлены по пересекающимся линиям, то тело движется по кривой. Определите, по какой траектории полетит летящий по нитке камень, если нить вдруг порвется? Мгновенная скорость камня направлена по касательной к изогнутой линии, поэтому в момент прекращения по закону инерции тело будет двигаться, сохраняя ту же скорость, то есть по той же касательной.Грузовик движется по кривой траектории. Скорость движения по модулю постоянного значения. Можно ли утверждать, что ускорение грузовика равно нулю? Невозможно сказать, что ускорение грузовика равно нулю, поскольку скорость имеет разное направление в каждой точке криволинейного пути, поэтому даже если модуль скорости остается прежним, вам необходимо рассмотреть новый вектор. Из того, что скорость постоянно меняется, следует, что и ускорение изменится. Мы уже знаем, что причина ускорения – сила.Укажите, на каких участках криволинейного движения действовала сила?
Обоснуйте ответ. На траектории через равные промежутки времени делаются отметки положения тела. Сила действовала на площадке 0: 3. Тело двигалось по прямой, но скорость тела изменялась (тело двигалось с ускорением), то есть под действием силы. Сила действовала на участке 7-8 человек. Величина скорости не изменилась, но изменилось направление (тело двигалось с ускорением), то есть под действием силы.
Сила, действующая на тело, может изменять его скорость как по абсолютной величине, так и по направлению.
Пример силы регулирования скорости – сила ветра, давящая на парус.
Такая сила вызывает прямолинейное движение тела .
Пример силы, изменяющей скорость в направлении центростремительная сила раскрученного груза на канате
Эта сила приводит к криволинейному перемещению .
Если тело движется по окружности с постоянной скоростью по модулю, его ускорение называется центростремительным, направленным к центру окружности и вычисляется по формуле:
a = v 2 / r, где v – скорость, r – радиус окружности
a = ω 2 * r, где w – угловая скорость тела по окружности в радианах в секунду.
В общем случае силы, действующие на тело, изменяют свою скорость как по направлению, так и по модулю. Пример представлен на рисунке – сила тяжести одновременно замедляет спутник и искривляет его траекторию:
В таких случаях говорят, что сила имеет тангенциальную и нормальную составляющие. Составляющая касательной силы – это та, которая направлена вдоль (или против) скорости и ускоряет (или замедляет) тело.
Нормальная составляющая силы – это та, которая действует перпендикулярно движению и изменяет направление скорости.
Для криволинейной траектории в любой точке можно рассчитать радиус кривизны по формуле:
R = v 2 / an, где v – скорость тела, а an – нормальная (нормальная к скорости) составляющая ускорения.
Отредактируйте этот урок и / или добавьте задание Добавьте свой урок и / или задание
МБОУ «Чубаевская общеобразовательная школа» Урмарского района Чехии
УРОК ФИЗИКИ КЛАССА 9
«Прямолинейное и криволинейное движение.
Движение тела по кругу. “
Учитель: Степанова Е.А.
Чубаево – 2013

Тема: Прямолинейное и криволинейное движение. Движение тела по кругу с постоянным модулем скорости.
Задачи урока: дать учащимся представление о прямолинейном и криволинейном движении, частоте, периоде. Введите формулы для нахождения этих величин и единиц.
Учебные задания: сформировать понятие прямолинейного и криволинейного движения, характеризующие его величины, единицы измерения этих величин и формулы для расчета.
Развивающие задания: продолжить формирование умений применять теоретические знания для решения практических задач, развивать интерес к предмету и логическое мышление.
Учебные задачи: продолжить развитие кругозора учащихся; умение вести записи в тетрадях, наблюдать, замечать закономерности явлений, аргументировать свои выводы.
Оборудование: Презентационное. Компьютер. Мультимедийный проектор Мяч, мяч на нитке, наклонный желоб, мяч, машинка, юле, модель часов со стрелками, секундомер
На занятиях
I. Организация времени. Вступительное слово учителя. Здравствуйте, юные друзья! Начнем наш урок сегодня со следующих строк: «Тайны – страшные натуры повсюду в воздухе» (Н. Заболоцкий, стихотворение «Бешеный волк») (слайд 1)
2. Обновление знаний
– Какие типы движения вы знаете? – В чем разница между прямолинейными и криволинейными движениями? – Сравните траекторию и путь для прямолинейных и криволинейных перемещений. Уч:. Мы знаем, что все тела тянутся друг к другу. В частности, Луна, например, притягивается к Земле. Но возникает вопрос: если Луна притягивается к Земле, почему она вращается вокруг нее, а не падает на Землю? (w-)
Чтобы ответить на этот вопрос, необходимо рассмотреть типы движения тел. Мы уже знаем, что движение может быть равномерным и неравномерным, но есть и другие характеристики движения. (слайд)
3.Проблемная ситуация: Чем отличаются следующие движения?
Демонстрации : Бросьте мяч по прямой линии, катите мяч по прямой канавке. А по круговой траектории, вращение шарика на нитке, перемещение игрушечной машинки на столе, перемещение брошенного под углом к горизонту мяча … ( по типу траектории )
Уч: По типу траектории, эти движения могут быть разделены на на движения по прямой и по изогнутой линии .(слайд)
Попробуем дать определения криволинейных и прямолинейных движений. (Запись в тетрадь) прямолинейное движение – движение по прямой траектории. Криволинейное движение – движение по непрямой (кривой) траектории.
4. Итак, тема урока
Прямолинейное и криволинейное движение. Круговое движение (слайд)
Уч: Рассмотрим два примера криволинейного движения: по ломаной и по кривой (рисовать).В чем разница между этими траекториями?
Ученики: В первом случае траекторию можно разбить на прямые участки и рассматривать каждый участок отдельно. Во втором случае вы можете разделить кривую на дуги окружностей и прямые участки. T.ob. это движение можно рассматривать как последовательность движений, происходящих по дугам окружностей разного радиуса. Следовательно, чтобы изучить криволинейное движение, вам необходимо изучить круговых движений. (слайд 15)
Сообщение 1 Движение тела по окружности
В природе и технике очень часто встречаются движения, траектории которых представляют собой не прямые, а кривые линии.Это криволинейное движение. Искусственные спутники Земли движутся по криволинейным траекториям в космическом пространстве планеты, а на Земле находятся все виды транспортных средств, части машин и механизмов, речная вода, атмосферный воздух и т. Д.
Если конец стальной стержень прижимается к вращающемуся точильному камню, тогда раскаленные частицы, выходящие из камня, будут видны в виде искр. Эти частицы летят со скоростью, которая была у них во время отделения от камня.Хорошо видно, что направление движения искры совпадает с касательной к окружности в точке соприкосновения бруса с камнем. Tangent Распылитель с колес застрявшего автомобиля. (Рисовать.)
Модуль направления и скорости
Уч: Таким образом, мгновенная скорость тела в разных точках криволинейной траектории имеет разное направление. По модулю скорость может быть везде одинаковой или варьироваться от точки к точке. (Слайд)
Но даже если модуль скорости не меняется, его нельзя считать постоянным.Скорость – это векторная величина. Для векторной величины одинаково важны модуль и направление. А время изменения скорости означает, что есть ускорение. Следовательно, криволинейное движение всегда является ускоренным движением , даже если по модулю скорость постоянна. (слайд) (видео1)
Ускорение тела, равномерно движущегося по окружности в любой точке центростремительно , т.е. направленного по радиусу окружности к его центру. В любой точке вектор ускорения перпендикулярен вектору скорости.(Нарисовать)
Модуль центростремительного ускорения: и c = V 2 / R (напишите формулу), где V – линейная скорость тела, а R – радиус окружности. (слайд)
Центростремительная сила – сила, действующая на тело при криволинейном движении в любой момент времени, всегда направлена по радиусу окружности к центру (как центростремительное ускорение). И сила, действующая на тело, пропорциональна ускорению. F = ma тогда
Обхват тела
Движение по окружности часто характеризуется не скоростью движения, а периодом времени, в течение которого тело совершает один полный оборот.Эта величина называется период обращения и обозначается буквой T. (Определение периода записи) При движении по кругу тело в течение определенного периода времени вернется в исходную точку. Следовательно, круговое движение является периодическим.
Период – время одного полного поворота.
Если тело совершает N оборотов за время t, то как найти период? (формула)
Найдем связь между периодом обращения T и модулем скорости при равномерном движении по окружности радиуса R.Так как V = S / t = 2πR / T. (Запишите формулу в тетрадь)
Message2 Точка – это величина, довольно распространенная в природе и технике . Итак, мы знаем. Что Земля вращается вокруг своей оси, а средний период вращения составляет 24 часа. Полный оборот Земли вокруг Солнца происходит примерно за 365,26 суток. Рабочие колеса гидротурбины совершают один полный оборот за время, равное 1 секунде. Период обращения винта вертолета равен 0.От 15 до 0,3 секунды. Кровообращение у человека составляет примерно 21-22 секунды.
Уч: Движение тела по кругу можно охарактеризовать другой величиной – количеством оборотов в единицу времени. Ее называют частотой циркуляции: ν = 1 / Т. Единица частоты: с -1 = Гц. (Запишите определение, единицу измерения и формулу) (слайд)
Как найти частоту, если тело совершает N оборотов за время t (формула)
Уч: Какой вывод можно сделать о связи между этими величинами? (период и частота являются обратными значениями)
Message3 Коленчатые валы двигателей тракторов имеют частоту вращения от 60 до 100 оборотов в секунду.Ротор газовой турбины вращается с частотой от 200 до 300 об / с. Пуля. Вылет из автомата Калашникова вращается с частотой 3000 об / с. Для измерения частоты существуют приборы, так называемые круги для измерения частоты, основанные на оптических иллюзиях. На этом круге нанесены черные полосы и указаны частоты. Когда такой круг вращается, черные полосы образуют круг с частотой, соответствующей этому кругу. Также тахометры используются для измерения частоты. (слайд)
Связь Скорости вращения и периоды вращения
ℓ – окружность
ℓ = 2πr V = 2πr / T
Дополнительные характеристики кругового движения.(слайд)
Уч: Напомним, для каких величин характерно прямолинейное движение?
Движение, скорость, ускорение.
Уч: по аналогии круговое движение – с теми же значениями – угловое перемещение, угловая скорость и угловое ускорение.
Угловое перемещение: (скольжение) Это угол между двумя радиусами. Обозначается – Измеряется в рад. Или град.
Уч: Вспомните из курса алгебры, как радиан соотносится с градусом?
2pi рад.= 360 градусов Пи = 3,14, затем 1 рад. = 360 / 6,28 = 57 градусов.
Угловая скорость w =
Единица измерения угловой скорости – рад / с
Уч:. Подумайте, какой будет угловая скорость, если тело совершит один полный оборот?
Студент. Поскольку тело совершило полный оборот, время его движения равно периоду, а угловое смещение равно 360 ° или 2. Следовательно, угловая скорость равна.
Учитель: Так о чем мы сегодня говорили? (про криволинейный ход)
5. Вопросы по установке.
Какой механизм называется изогнутым?
Какое движение является частным случаем криволинейного движения?
Как направлена мгновенная скорость движения по кривой?
Почему ускорение называется центростремительным?
Что называется периодом и частотой? В каких единицах измерения?
Как обозначены эти значения?
Как описать криволинейное движение?
Как направлено ускорение тела, движущегося по окружности с постоянным модулем скорости?
6.Экспериментальная работа
Измерьте период и частоту тела, подвешенного на нити и вращающегося в горизонтальной плоскости.
(на столах подвешены тела на нитке, секундомер. Равномерно повернуть тело по горизонтали и измерить время 10 полных оборотов. Вычислить период и частоту)
7. Крепление. Решение проблем. (слайд)
A.S. Пушкин. “Руслан и Людмила”
Дуб зеленый у берега моря,
Золотая цепочка на дубе
День и ночь, кот ученый
Все идет по цепочке.
Q: Как называется это движение кошек? Определите частоту, период и угловую скорость, если через 2 мин. Он делает 12 кругов. (ответ: 0,1 1 / с, T = 10s, w = 0,628рад / с)
P.P. Ершов “Конек-Горбунок”
Ну так наш Иван идет
За кольцом на окияне
Горбун летит как ветер
И стартуют в первый вечер
Верста на сто тысяч махнул
И ни разу не отдыхал.
Q: Сколько раз в первый вечер Конек-Горбунок огибал Землю? Земля имеет форму шара, а одна миля составляет примерно 1066 м. (Ответ: 2,5 раза)
8. Тест Проверка усвоения нового материала (бумажные тесты)
Тест 1
1. Пример криволинейного движения …
а) падение камня ;
б) поворот автомобиля направо;
в) спринтер, бегущий на 100 метров.
2.Минутная стрелка часов совершает один полный оборот. Чему равен период обращения?
а) 60 с; б) 1/3600 с; в) 3600 с.
3. Велосипедное колесо делает один оборот за 4 с. Определите скорость.
а) 0,25 1 / с; б) 4 л / с; в) 2 1 / с.
4. Винт катера совершает 25 оборотов за 1 с. Чему равна скорость вращения винта?
а) 25 рад / с; б) / 25 рад / с; в) 50 рад / с
5. Определить частоту вращения дрели электродрели, если ее угловая скорость равна 400 .
а) 800 1 / с; б) 400 л / с; в) 200 1 / с.
Ответы: б; в; а; в; дюймы
Тест 2
1. Пример криволинейного движения …
а) движение лифта;
б) лыжный прыжок с трамплина;
в) падающие шишки с нижней ветви ели в безветренную погоду.
Секундная стрелка часов делает один полный оборот. Чему равна его частота обращения?
а) 1/60 с; б) 60 с; в) 1 с.
3. Колесо станка делает 20 оборотов за 10 с. Определите период вращения колеса?
а) 5 с; б) 10 с; в) 0,5 с.
4. Ротор мощной паровой турбины совершает 50 оборотов за 1 с. Рассчитайте угловую скорость.
а) 50 рад / с; б) / 50 рад / с; в) 10 рад / с.
5. Определите период вращения звездочки велосипеда, если угловая скорость равна.
а) 1 с; б) 2 с; в) 0,5 с.
Ответы: б; а; в; в; б.
Самопроверка
9. Отражение.
Залейте вам механизм ЗУХ (знаю, знаю, хочу знать)
10. Подведение итогов, оценок за занятие
11 . Домашнее задание 18.19,
домашнее исследование: по возможности вычислить все характеристики любого вращающегося тела (велосипедное колесо, минутная стрелка часов)
J.I. Перельман. Занимательная физика. Князь 1 и 2 – М.: Наука, 1979.
С. А. Тихомирова. Дидактический материал по физике. Физика в художественной литературе. 7-11 классы. – М .: Просвещение. 1996.
В ходе урока мы рассмотрим криволинейное движение, круговое движение и некоторые другие примеры. Мы также обсуждаем случаи, в которых необходимо применять различные модели для описания движения тела.
Неужели прямые линии? Кажется, они нас окружают повсюду. Но давайте внимательнее посмотрим на край стола, корпус или экран монитора: на них всегда есть выемка, материал шероховатости.Посмотрим в микроскоп, и сомнения в кривизне этих линий исчезнут.
Оказывается, прямое – действительно абстракция, нечто идеальное и несуществующее. Но с помощью этой абстракции можно описать многие реальные объекты, если при их рассмотрении для нас не важны их незначительные отклонения и мы можем рассматривать их прямо.
Мы рассмотрели простейшее движение – равномерное прямолинейное движение. Это такая же идеализация, как и сама прямая линия.Реальные объекты движутся в реальном мире, и их путь не может быть идеально прямым. Автомобиль движется из города A в город B: между городами не может быть абсолютно ровной дороги и не получится поддерживать постоянную скорость. Тем не менее, используя модель равномерного прямолинейного движения, мы можем даже описать такое движение.
Эта модель не всегда применима для описания движения.
1) Движение может быть неравномерным.
2) Например, карусель крутится – движение есть, но не по прямой.То же самое можно сказать и о мяче, по которому бьет футболист. Или о движении Луны вокруг Земли. В этих примерах движение происходит по кривой.
Итак, раз уж такие задачи есть, нужен удобный инструмент для описания движения по кривой.
Прямые и изогнутые
Мы можем рассматривать одну и ту же траекторию движения в одной задаче как прямую, а в другой – нет. Это условность, в зависимости от того, что нас интересует в этой задаче.
Если задача машина, которая едет из Москвы в Санкт-Петербург, то дорога не прямая, но на этих расстояниях все эти повороты нам не интересны – то, что на них происходит, ничтожно мало. Более того, речь идет о средней скорости, которая учитывает все эти заминки в поворотах, из-за них как раз средняя скорость станет меньше. Следовательно, мы можем перейти к эквивалентной задаче – мы можем «выпрямить» траекторию, сохранив длину и скорость – мы получим тот же результат.Поэтому здесь подходит модель прямолинейного движения. Если проблема заключается в движении автомобиля на конкретном повороте или во время обгона, то кривизна траектории может быть для нас важна, и мы будем использовать другую модель.
Мы разделяем движение по кривой на участки, достаточно маленькие, чтобы их можно было считать прямыми участками. Представьте себе пешехода, который движется по сложной тропе, объезжает препятствия, но идет и делает шаги. Нет криволинейных ступеней; это сегменты от посадочного места до посадочного места.
Рис. 1. Криволинейная траектория
Мы разделили движение на небольшие сегменты, и мы можем описать движение в каждом таком сегменте как прямолинейное. Чем короче эти прямые линии, тем точнее будут приближения.
Рис. 2. Аппроксимация криволинейного движения
Мы использовали такой математический инструмент, как деление на небольшие промежутки, когда мы обнаружили движение в прямолинейном равномерно ускоренном движении: мы разделили движение на участки настолько малые, что изменение скорости на этом участке было незначительным и движение можно было считать равномерным.Рассчитать смещение в каждом таком сечении было несложно, осталось сложить смещение в каждом сечении и получить итог.
Рис. 3. Движение при прямолинейном равноускоренном движении
Начнем описывать криволинейное движение с простейшей модели – окружности, которая описывается одним параметром – радиусом.
Рис. 4. Окружность как модель криволинейного движения
Конец стрелки часов перемещается на одинаковое расстояние длины стрелки от точки ее крепления.Точки обода колеса все время остаются на одинаковом расстоянии от оси – на расстоянии длины спиц. Мы продолжаем изучать движение материальной точки и работаем в рамках этой модели.
Поступательное и вращательное движение
Поступательное движение – это движение, при котором все точки тела движутся одинаково: с одинаковой скоростью, совершая одно и то же движение. Помашите рукой и следите: видно, что ладонь и плечо двигались по-разному.Посмотрите на колесо обозрения: точки около оси почти не двигаются, а кабины движутся с разной скоростью и по разным траекториям. Посмотрите на прямолинейно движущуюся машину: если не учитывать вращение колес и движение частей двигателя, все точки машины движутся одинаково, мы считаем движение машины поступательным. Тогда нет смысла описывать движение каждой точки, можно описать движение одной. Мы считаем машину материальной точкой.Обратите внимание, что при поступательном движении линия, соединяющая любые две точки тела во время движения, остается параллельной самой себе.
Второй тип движения согласно этой классификации – вращательное движение. Во время вращательного движения все точки тела движутся по кругу вокруг одной оси. Эта ось может пересекать тело, как в случае колеса обозрения, но не может пересекаться, как в случае автомобиля в повороте.
Рис. 5. Вращательное движение
Но не каждое движение можно отнести к одному из двух видов.Как описать движение педалей велосипеда относительно Земли – это какой-то третий тип? Наша модель удобна тем, что мы можем рассматривать движение как комбинацию поступательного и вращательного движений: педали вращаются вокруг своей оси, а ось вместе со всем велосипедом поступательно перемещается относительно Земли.
Конец стрелок часов для равных интервалов времени пойдет таким же образом. То есть можно говорить о равномерности его движения. Скорость – векторная величина, поэтому для того, чтобы она была постоянной, не должны изменяться и ее модуль, и направление.И если модуль скорости не меняется при движении по окружности, то направление будет постоянно меняться.
Рассмотрим равномерное движение по кругу.
Почему решили не рассматривать переезд
Рассмотрим, как меняется движение при движении по кругу. Точка находилась в одном месте (см. Рис. 6) и прошла четверть круга.
Мы следим за движением во время дальнейшего движения – сложно описать закономерность, по которой оно меняется, и такое рассмотрение малоинформативно.Имеет смысл рассматривать перемещение с достаточно маленькими интервалами, чтобы их можно было считать приблизительно равными.
Мы вводим некоторые удобные характеристики кругового движения.
Неважно, какого размера часы, за 15 минут конец минутной стрелки всегда пройдет четверть окружности циферблата. И через час совершит революцию. Путь будет зависеть от радиуса круга, а вот угол поворота – нет. То есть угол тоже будет меняться равномерно.Поэтому, помимо пройденного расстояния, мы поговорим еще об изменении угла. Как известно, угол пропорционален дуге, на которой он опирается:
Рис. 7. Изменение угла стрелки
Поскольку угол изменяется равномерно, можно по аналогии с путевой скоростью, показывая путь, который проходит тело за единицу времени, ввести угловую скорость: угол, на который тело вращается (или который проходит тело). в единицу времени ,.
То есть на сколько радиан поворачивается точка в секунду.Он будет измеряться, соответственно, в рад / с.
Равномерное круговое движение – это повторяющийся процесс, или, по-другому, периодический . Когда острие совершает полный оборот, оно снова возвращается в исходное положение, и движение повторяется.
Примеры периодических явлений в природе
Многие явления периодичны: смена дня и ночи, смена времен года. Здесь понятно, какой именно период: день и год соответственно.
Есть и другие периоды: пространственные (узор с периодически повторяющимися элементами, серия деревьев, расположенных через равные интервалы), периоды в записи чисел.Периоды в музыке, стихах.
Периодические явления описываются тем, что происходит в течение периода и продолжительностью этого периода. Например, суточный цикл – восход-закат и период – время, за которое все повторяется – 24 часа. Пространственный узор – это отдельный элемент узора и частота его повторений (или его длина). В десятичной системе счисления обыкновенная дробь – это последовательность цифр в периоде (в скобках), а длина / период – это количество цифр: в 1/3 – одна цифра, в 1/17 – 16 цифр.
Рассмотрим несколько периодов времени.
Период обращения Земли вокруг своей оси = день + ночь = 24 часа
Период обращения Земли вокруг Солнца = 365 периодов обращения день + ночь.
Период вращения на циферблате по часовой стрелке – 12 часов, минуты – 1 час.
Период колебаний маятника 1 с.
Период измеряется в общепринятых единицах времени (секунда в системе СИ, минута, час и т. Д.).).
Период узора измеряется в единицах длины (м, см), период в десятичной дроби – в количестве цифр в периоде.
Период – это время, в течение которого точка при равномерном движении по окружности совершает один полный оборот. Обозначим его заглавной буквой.
Если революции происходят во времени, то один оборот, очевидно, происходит во времени.
Чтобы судить, как часто повторяется процесс, введем величину, которую мы назовем частотой.
Частота появления Солнца за год – 365 раз. Частота полнолуния в году 12, иногда 13 раз. Периодичность прихода весны в год – 1 раз.
Для равномерного кругового движения частота – это количество полных оборотов, которые точка делает за единицу времени. Если обороты совершаются за t секунд, то обороты совершаются за каждую секунду. Обозначим частоту, иногда ее также обозначают или. Частота измеряется в оборотах в секунду, эта величина получила название Герц, по имени ученого Герца.
Частота и период являются взаимно обратными величинами: чем чаще что-то происходит, тем короче должен длиться период. И наоборот: чем дольше длится один период, тем реже происходит событие.
Математически мы можем написать обратную пропорциональность: или.
Итак, период – это время, в течение которого тело совершает полный оборот. Понятно, что это должно быть связано с угловой скоростью: чем быстрее изменится угол, тем быстрее тело вернется в исходную точку, то есть совершит оборот.
Рассмотрим один полный оборот. Угловая скорость – это угол, под которым тело вращается за единицу времени. На какой угол должно поворачиваться тело при полном вращении? 3600, или в радианах. Полный оборот – это период. Итак, по определению, угловая скорость равна :.
Мы также находим путевую скорость – ее еще называют линейной – проверив один оборот. Момент времени, один период, тело совершает полный оборот, то есть проходит путь, равный окружности. Отсюда мы выражаем скорость по определению как путь, разделенный во времени:
Если учесть, что это угловая скорость, то получим соотношение между линейной и угловой скоростью:
Задача
С какой частотой нужно повернуть затвор колодца, чтобы ковш поднимался со скоростью 1 м / с, если радиус поперечного сечения затвора равен?
Задание описывает вращение ворот – к нему применяем модель вращательного движения с учетом точек его поверхности.
Фиг.8. Ворота поворотные модели
Речь также идет о движении ковша. Ведро прикрепляется веревкой к воротнику, и эта веревка наматывается. Это означает, что любая часть веревки, в том числе намотанная на воротник, движется с той же скоростью, что и ведро. Таким образом, мы задали линейную скорость точек на поверхности ворот.
Физическая часть решения . Речь идет о линейной скорости движения по окружности, она равна :.
Период и частота являются взаимно обратными величинами, мы пишем :.
Мы получили систему уравнений, которую можно только решить – это будет математическая часть решения. Мы подставляем частоту в первое уравнение вместо:.
Мы выражаем частоту отсюда :.
Рассчитываем переводом радиуса в метры:
Получили ответ: нужно вращать вентиль с частотой 1,06 Гц, то есть делать примерно один оборот за одну секунду.
Представьте, что у нас движутся два одинаковых тела.Один находится на окружности, а другой (в тех же условиях и с теми же характеристиками), но вдоль правильного многоугольника. Чем больше сторон у такого многоугольника, тем меньше для нас будут отличаться движения этих двух тел.
Рис. 9. Криволинейное движение по окружности и многоугольнику
Разница в том, что второе тело в каждой секции (сторона многоугольника) движется по прямой линии.
На каждом таком отрезке обозначаем движение тела. Движение здесь – двумерный вектор на плоскости.
Рис. 10. Движение тела при криволинейном движении по многоугольнику
На этой небольшой территории движение было завершено вовремя. Разделите и получите вектор скорости в этом разделе.
При увеличении количества сторон многоугольника длина его стороны будет уменьшаться :. Поскольку модуль скорости тела постоянен, то время преодоления этого отрезка будет стремиться к 0 :.
Соответственно, скорость тела на такой небольшой площади будет называться , мгновенная скорость .
Чем меньше сторона многоугольника, тем ближе он будет к касательной к окружности. Поэтому в предельном, идеальном случае () можно считать, что мгновенная скорость в данной точке направлена по касательной к окружности.
И сумма модулей смещения будет все меньше и меньше отличаться от пути, который точка проходит по дуге. Следовательно, мгновенная скорость по модулю будет совпадать с путевой скоростью, и все те соотношения, которые мы получили ранее, будут верны для модуля мгновенной скорости в смещении.Вы даже можете обозначить это, имея в виду.
Скорость направлена по касательной, также можем найти ее модуль. Найдите скорость в другой точке. Его модуль такой же, так как движение равномерное, и оно направлено по касательной к окружности уже в этой точке.
Рис. 11. Скорость тела по касательной
Это не один и тот же вектор, они равны по модулю, но имеют разные направления. Скорость изменилась, и поскольку она изменилась, то это изменение можно рассчитать:
Изменение скорости в единицу времени, по определению, является ускорением:
Рассчитываем ускорение при движении по окружности.Изменение скорости.
Рис. 12. Графическое вычитание векторов
Получил вектор. Ускорение направлено туда, куда (эти векторы связаны соотношением, что означает, что они сонаправлены).
Чем меньше отрезок AB, тем больше будут совпадать векторы скорости и, и он будет ближе к перпендикуляру к ним обоим.
Рис. 13. Зависимость скорости от размера участка
То есть он будет лежать по перпендикуляру к касательной (скорость направлена по касательной), а значит, ускорение будет направлено в центр окружности, по радиусу.Помните из курса математики: радиус, проведенный до точки касания, перпендикулярен касательной.
Когда тело проходит небольшой угол, вектор скорости, касательный к радиусу, также поворачивается на угол.
Доказательство равенства углов
Рассмотрим четырехугольник АСВО. Сумма углов четырехугольника равна 360 °. (как углы между радиусами в точках касания и касательными).
Угол между направлениями скорости в точках A и B () и – рядом с линией AC, тогда
Ранее получал, отсюда.
На небольшом участке AB движение точки по модулю практически совпадает с траекторией, то есть с длиной дуги :.
Треугольники ABO и треугольник, составленный из векторов скорости в точках A и B, подобны (из точки A вектор был перенесен параллельно себе в точку B).
Эти треугольники равнобедренные (OA = OV – радиусы, так как движение равномерное), у них равные углы между сторонами (только что доказано в ветке). Значит, равные друг другу углы у основания будут равны.Равенства углов достаточно, чтобы утверждать, что треугольники подобны.
Из подобия треугольников запишем: сторона AB (а она равна) относится к радиусу круга, так как модуль изменения скорости относится к модулю скорости :.
Мы пишем без векторов, потому что нас интересуют длины сторон треугольников. Все мы приводим к ускорению, это связано с изменением скорости, или. Подставляем, получаем:
Вывод формулы оказался довольно сложным, но вы можете запомнить готовый результат и использовать его при решении задач.
В любой точке мы находим ускорение при равномерном движении по окружности, оно равно по модулю и в любой точке направлено к центру окружности. Поэтому его еще называют центростремительного ускорения .
Задача 2. Центростремительное ускорение
Давайте решим проблему.
Найдите, с какой скоростью машина движется в повороте, если вы рассматриваете поворот как часть окружности с радиусом 40 м, и центростремительное ускорение равно.
Анализ состояния. Задача описывает движение по кругу, речь идет о центростремительном ускорении. Запишем формулу центростремительного ускорения:
Даны ускорение и радиус круга, осталось только выразить и вычислить скорость:
Или, если перевести в км / ч, то это примерно 32 км / ч.
Чтобы изменить скорость тела, другое тело должно воздействовать на него с некоторой силой, или, проще говоря, сила должна действовать.Чтобы тело двигалось по кругу с центростремительным ускорением, сила, создающая это ускорение, также должна действовать на него. В случае с автомобилем в повороте это сила трения, поэтому нас дрейфует в поворотах, когда на дорогах гололед. Если мы что-то разматываем на веревке, это сила натяжения веревки – и мы чувствуем, как она тянет сильнее. Как только эта сила исчезает, например, обрывается нить, тело в отсутствие сил по инерции сохраняет скорость – ту скорость, которая касательна к окружности, которая была в момент отрыва.И в этом можно убедиться, проследив за направлением движения этого тела (рисунок). По той же причине мы прижимаемся к стенке транспортного средства в повороте: мы движемся по инерции таким образом, чтобы сохранять скорость, его как бы выбрасывает из круга, пока мы не ударяемся о стену, и возникает сила, которая передаст центростремительное ускорение.
Раньше у нас был только один инструмент – модель прямолинейного движения. Нам удалось описать другую модель – круговое движение.
Это распространенный тип движения (повороты, транспортные колеса, планеты и т. Д.).), поэтому понадобился отдельный инструмент (рисовать траекторию каждый раз маленькими прямыми отрезками не очень удобно).
Теперь у нас есть два «кирпича», а это значит, что с их помощью мы сможем строить здания более сложной формы – решать более сложные задачи с комбинированными типами движений.
Этих двух моделей нам хватит для решения большинства кинематических задач.
Например, такое движение можно представить как движение по дугам трех окружностей.Или пример: машина ехала прямо по улице и набирала скорость, затем повернула и поехала с постоянной скоростью по другой улице.
Рис. 14. Разбиение на участки траектории движения автомобиля
Мы рассмотрим три раздела и применим к каждому по одной из простых моделей.
Список литературы
Соколович Ю.А., Богданова Г.С. Физика: справочник с примерами решения задач. – 2-е изд., Распространение.- X .: Веста: Издательство «Ранок», 2005. – 464 с.
Перышкин А.В., Гутник Е.М. Физика. 9 кл .: учебник для общеобразовательных. учреждений / А.В. Перышкин, Э.М.Гутник. – 14-е изд., Стереотип. – М .: Дрофа, 2009. – 300.
.
Веб-сайт внеклассных занятий ()
Класс! Веб-сайт по физике ()
Домашнее задание
Приведите примеры криволинейного движения в повседневной жизни. Может ли это движение быть простым при построении состояния?
Определите центростремительное ускорение, с которым Земля движется вокруг Солнца.
Два велосипедиста с постоянной скоростью стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой дорожки. Через 10 минут после старта один из велосипедистов впервые догнал другого. Через какое время после старта первый велосипедист второй раз догонит другого?
Кинематика изучает движения тел без учета причин, определяющих это движение.
1. Материальная точка – – тело с массой, размерами которой в данной задаче можно пренебречь.
Материальная точка – это абстракция, но ее введение облегчает решение практических задач (например, планеты, движущиеся вокруг Солнца, в расчетах можно принять за материальные точки).
Система № № – комплект эталонного тела, системы координат, измерителя времени.
Простейшими видами механического движения тел являются поступательное и вращательное движение. Движение тела называется прогрессивное , г. , если все его точки перемещаются одинаково.
Траектория – линия, по которой движется тело (материальная точка).
Путь – длина траектории, скалярная величина.
Переезд – направленный отрезок прямой, соединяющий начальное положение точки с ее конечным положением. Значение вектора.
Виды механического движения (прямолинейное и криволинейное).
Равномерное прямолинейное движение называется движение, при котором тело в течение любых равных промежутков времени совершает одно и то же движение.
Скорость равномерным прямолинейным движением тела называется величина, равная отношению движения тела к периоду времени, в течение которого это движение произошло :.
Движение, при котором скорость в течение любых равных интервалов времени изменяется одинаково, называется равнопеременным движением .
Величина характеризует скорость изменения скорости. Это называется ускорением: a =.
Разгон движущимся телом называется величина, равная отношению изменения скорости тела к периоду времени, в течение которого это изменение произошло.
В положении вращающемся Движение тела его острия описывается концентрическими окружностями, расположенными в параллельных плоскостях.
Изгиб – движение тела, траектория которого представляет собой кривую линию.
Примеры.

ЛЕКЦИЯ 2
Динамика
Dynamics изучает законы движения тел и причины, вызывающие или изменяющие это движение.
1. Первый закон Ньютона .
Существуют такие системы отсчета, относительно которых движущиеся тела сохраняют свою скорость постоянной, если на них не действуют другие тела (или влияние других тел компенсируется).Такие системы отсчета называются инерционными (ISO).
Термин «сила» означает меру воздействия одного тела на другое. Force – векторное количество; он характеризуется модулем (абсолютным значением), направлением и точкой приложения. За единицу силы в СИ берется сила, которая сообщает телу массой 1 кг ускорение 1 м / с 2. Эта единица называется ньютон , 1Н = 1 кг ∙ 1 м / с 2 = 1 кг ∙ м / с 2.
Второй закон Ньютона .
Ускорение, получаемое телом, прямо пропорционально равнодействующей всех сил и обратно пропорционально массе тела:
Запишем следствия второго закона Ньютона:
а) если на два тела разной массы действуют силы, равные по величине, то отношение ускорений тел обратно пропорционально их массам. Делаем вывод:
Так как тогда или по модулю
b) если на два тела разной массы действуют силы, равные по величине, то ускорения, приобретаемые телами, прямо пропорциональны действующим силам.Делаем вывод:
; с тех пор
Третий закон Ньютона сформулирован следующим образом: при взаимодействии двух тел они действуют друг на друга с силами, направленными вдоль одной прямой, равной по модулю и противоположной по направлению:
Эти силы применяются к различным телам, взаимодействующим друг с другом.
2. Закон всемирного тяготения был открыт Исааком Ньютоном; закон формулируется следующим образом: сила взаимного притяжения двух тел прямо пропорциональна произведению масс этих тел и обратно пропорциональна квадрату расстояния между ними:
где G = 6.67 ∙ 10 -11 – гравитационная постоянная.
Физический смысл гравитационной постоянной таков: она показывает, что два тела массой 1 кг на расстоянии 1 м друг от друга притягиваются с силой 6,67 ∙ 10 -11 Н .
Пример : сила тяжести . Если на тело действует только сила тяжести, оно совершает свободное падение.
Масса тела называется силой, с которой тело, притягиваемое к Земле, действует на горизонтальную опору или подвес.
В общем, во всех инерциальных системах отсчета вес тела равен по величине силе тяжести. Масса тела Это сила, приложенная к опоре, и сила тяжести, приложенная к телу.

Материальная точка движется равномерно по криволинейной траектории. Неравномерное движение. Скорость при неравномерном движении

2.Ускорение при криволинейном движении: нормальное и тангенциальное ускорение. Плоское вращение. Угловая скорость, ускорение.

3.Связь между векторами скорости и угловой скорости материальной точки. Нормальное, тангенциальное и полное ускорение.

Тесты для педагогов по всем школьным предметам с ответами

Краткое содержание прямолинейное и криволинейное движение. Криволинейное

Кинематика криволинейного движения. Конспект урока “Прямолинейное и криволинейное движение

Независимость движений

Угловая скорость

кинематика

Материальной точки по окружности. Линейная и угловая скорости

Определение равномерного криволинейного движения. Прямолинейное и криволинейное движение

Мгновенная и равномерная угловая скорость кругового движения

Вывод угловой скорости

Постоянная угловая скорость

Расчет тангенциальной скорости

Пример задачи

Резюме урока

Примечания по криволинейному движению | Инженерная механика II | ЕМ 2433

Криволинейный ход. Криволинейный

Пример сферического движения: качение конуса по плоскости (x y). …

Круговое движение – Полный инструментарий

Круговое движение – Полный инструментарий

Чтения из Учебника по физике

Интерактивное моделирование

Видео и анимация

Лаборатории и исследования

Демонстрационные идеи

Интернет-модули Minds On Physics

Упражнения по построению концепции

Упражнения по решению проблем

Научное рассуждение

Связи в реальной жизни

Общие заблуждения

В другом месте в Интернете

Траектория и уравнение положения

Понятие траектории и уравнение положения

Типы уравнения траектории

Почему решили не рассматривать переезд

Оставить комментарий Отменить ответ