Прямолинейное равноускоренное движение: мгновенная скорость, ускорение, перемещение.
Прямолинейное равноускоренное движение: мгновенная скорость, ускорение, перемещение.| 9 класс | Прямолинейное равноускоренное движение: мгновенная скорость, ускорение, перемещение.основные понятия и определения:Равномерным движением является механическое движение тел, происходящие с постоянной скоростью. Из всех видов неравномерного движения самое простое – прямолинейное равноускоренное, при котором тело движется вдоль простой линии, а проекция вектора скорости тела за любые равные промежутки времени меняются одинаково (при этом модуль вектора скорости может, как увеличивается, так и уменьшаться) Мгновенная скорость-скорость в каждой конкретной точке траектории в соответствующий момент времени. Мгновенная скорость тел, движущихся равноускоренно, может меняться по-разному: в одних случаях быстрее, в других – медленнее.  В таких случаях говорят, что тела движутся с разным ускорением.
Рассмотрим, какая физическая величина называется ускорением. В таких случаях говорят, что тела движутся с разным ускорением.
Рассмотрим, какая физическая величина называется ускорением.Ускорение – векторная величина, которая характеризуется не только модулем, но и направление. Модуль вектора ускорения показывает, насколько меняется модуль вектора скорости в каждую единицу времени. Чем большее ускорение, тем быстрее меняется скорость тела. Если векторы скорости и ускорения движущегося тела направлены в одну и ту же сторону, то модуль вектора скорости тела увеличивается, а если в противоположенные – уменьшается скорость прямолинейного равноускоренного движения. перемещение прямолинейного равноускоренного движения. Задачи:Первый уровень1. Автомобиль начинает движение с ускорением 0,5 м\с2. Определите скорость и путь автомобиля за первые 2 секунды движения.2. Материальная точка движется по закону х = 2 + 2t – t2 Определите начальную координату, начальную скорость и ускорение точки.  Запишите уравнение скорости и постройте график. Запишите уравнение скорости и постройте график.3. В момент начала наблюдения расстояние между двумя телами было равно 6 м. Первое тело движется из состояния покоя с ускорением 2 м/с3. Второе движется вслед за ним, имея начальную скорость 2 м/с и ускорение 4 м/с2. Написать уравнения x(t) и найти место и время встречи тел. Второй уровень5. Тормозная система автомобиля обеспечивает торможение с максимальным ускорением -6м\с2. Определите, какое время потребуется автомобилю, движущемуся со скоростью 72 км\ч, для экстренной остановки и определите тормозной путь автомобиля.6. В результате торможения скорость автомобиля за 3 секунды уменьшилась с 72 км /ч до 7,2 км\ч. Определите ускорение автомобиля. 7. Материальная точка движется по закону х = 4t + 2t2 .Определите начальную координату, начальную скорость и ускорение точки.  8. Движение двух мотоциклистов заданы уравнениями x1=15+t2, X2=8t. Описать движение каждого мотоциклиста; найти место и время встречи. 9. За 10 секунд до финиша скорость велосипедиста равнялась 36 км\ч. а на финише – 72 км\ч. С каким ускорением финишировал велосипедист. 10. Тело, начавшее двигаться равноускорено из состояния покоя, за 4 секунды проходит путь 80 м. С каким ускорением двигается тело? 11. Велосипед съехал с горки за 5с,двигаясь с постоянным ускорением 0.5м/с.Определите длину горки,если известно,что в начале спуска скорость велосипедиста была равна 18км/ч |
Мгновенная скорость движения. Неравномерное движение
Скорость в физике означает быстроту перемещения какого-либо объекта в пространстве. Эта величина бывает разной: линейной, угловой, средней, космической и даже сверхсветовой. В число всех существующих разновидностей входит также и мгновенная скорость. Что это за величина, какова ее формула и какие действия необходимы для ее расчета – об этом как раз и пойдет речь в нашей статье.
Что это за величина, какова ее формула и какие действия необходимы для ее расчета – об этом как раз и пойдет речь в нашей статье.
Мгновенная скорость: сущность и понятие
О том, как определить быстроту перемещения объекта по прямой, известно даже ученику начальных классов: достаточно пройденное расстояние разделить на время, которое было затрачено на такое перемещение. Однако стоит помнить, что результат, полученный таким способом, позволяет судить о Если объект движется неравномерно, то на определенных участках его пути быстрота перемещения может заметно варьироваться. Поэтому порой требуется такая величина как мгновенная скорость. Она позволяет судить о быстроте перемещения материальной точки в любой момент движения.
Мгновенная скорость: формула расчета
Данный параметр равен пределу (обозначается limit, сокращенно lim) отношения перемещения (разнице координат) к промежутку времени, за которое это изменение произошло, при условии, что этот промежуток времени стремится достичь нуля.
v = Δs/Δt при Δt → 0 либо так v = lim Δt→0 (Δs/Δt)
Отметим, что мгновенная скорость есть Если движение происходит по прямой линии, то она меняется лишь по величине, а направление остается постоянным. В противном случае вектор скорости мгновенной направлен по касательной по отношению к траектории перемещения в каждой рассматриваемой точке. Какой смысл несет данный показатель? Мгновенная скорость позволяет выяснить, какое перемещение осуществит объект за единицу времени, если с рассматриваемого момента он движется равномерно и прямолинейно.
В случае никаких сложностей нет: нужно просто найти отношение расстояния к времени, за которое оно было объектом преодолено. В этом случае средняя и мгновенная скорость тела равны. Если же движение происходит непостоянно, то в этом случае следует узнать величину ускорения и определять мгновенную скорость в каждый определенный момент времени. При вертикальном перемещении следует учитывать влияние Мгновенную скорость автомобиля можно определить с помощью радара или спидометра. Следует иметь в виду, что перемещение в некоторых участках пути может принимать отрицательное значение.
Следует иметь в виду, что перемещение в некоторых участках пути может принимать отрицательное значение.
Для того чтобы найти ускорение, можно воспользоваться акселерометром либо составить функцию движения и воспользоваться формулой v=v0+a.t. Если перемещение начинается из состояния покоя, то v0 = 0. При расчетах нужно учитывать тот факт, что при торможении тела (уменьшении скорости) величина ускорения будет со знаком “минус”. Если объект совершает мгновенная быстрота его перемещения рассчитывается по формуле v= g.t. В этом случае начальная скорость также равна 0.
Для того, чтобы охарактеризовать насколько быстро изменяется в пространстве положение движущегося тела, используют специальное понятие скорость.
Средней скоростью
(3.1)
Если на всех участках траектории средняя скорость одинакова, то движение называется равномерным.
Вопрос о скорости бега является важным в спортивной биомеханике. Известно, что скорость бега на определенную дистанцию зависит от величины этой дистанции. Бегун может поддерживать максимальную скорость только в течение ограниченного времени. Средняя скорость стайеров обычно меньше, чем спринтеров. На рис. 3.8. показана зависимость средней скорости (V) от длины дистанции (S).
Рис. 3.8.
График зависимости проведен через точки, соответствующие средним скоростям для всех рекордных результатов у мужчин на дистанциях от 50 до 2000 м. Средняя скорость растет с увеличением дистанции до 200 м, а затем убывает.
В табл. 3.1 приведены мировые рекорды скорости.
Для удобства проведения вычислений среднюю скорость можно записать и через изменение координат тела. При прямолинейном движении пройденный путь равен разности координат конечной и начальной точек. Так, если в момент времени t 0 тело находилось в точке с координатой x 0 , а в момент времени t 1 – в точке с координатой
 Таблица 3.1
Таблица 3.1 Мировые спортивные рекорды
| Вид состязаний и дистанция | Мужчины | Женщины | ||
| | средняя скорость, м/с | время, показанное на дистанции | средняя скорость, м/с | |
| Бег 100 м | 9,83с | 10,16 | 10,49 с | 9,53 |
| 200 м | 19,72 с | 10,14 | 21,34 с | 9,37 |
| 400м | 43,29 с | 9,24 | 47,60 с | 8,40 |
| 800м | 1 мин 41,73 с | 7,86 | 1 мин 53,28 с | 7,06 |
| 1500м | 3 мин 29,46 с | 7,16 | 3 мин 52,47 с | 6,46 |
| 5000 м | 12 мин 58,39 с | 6,42 | 14 мин 37,33 с | 5,70 |
| 10000 м | 27 мин 13,81 с | 6,12 | 30 мин 13,75 с | 5,51 |
| Марафон (42 км 195 м) | 2 ч 6 мин 50 с | 5,5 | 2 ч 21 мин 0,6 с | 5,0 |
| Бег на коньках | 36,45 с | 13,72 | 39,10 с | 12,78 |
| 1500м | 1 мин 52,06 с | 13,39 | 1 мин 59,30 с | 12,57 |
| 5000м | 6 мин 43,59 с | 12,38 | 7 мин 14,13 с | 11,35 |
| 10000 м | 13 мин 48,20 с | 12,07 | ||
| Плавание 100 м (вольный стиль) | 48,74 с | 2,05 | 54,79 с | 1,83 |
| 200 м (вольный стиль) | 1 мин 47,25 с | 1,86 | 1 мин 57,55 с | 1,70 |
| 400 м (вольный стиль) | 3 мин 46,95 с | 1,76 | 4 мин 3,85 с | 1,64 |
| 100 м (брасс) | 1 мин 1,65 с | 1,62 | 1 мин 7,91 с | 1,47 |
| 200 м (брасс) | 2 мин 13,34 с | 1,50 | 2 мин 26,71 с | 1,36 |
| 100 м (баттерфляй) | 52,84 с | 1,89 | 57,93 с | 1,73 |
| 200 м (баттерфляй) | 1 мин 56,24 с | 1,72 | 2 мин 5,96 с | 1,59 |
В общем случае средние скорости на различных участках пути могут отличаться. На рис. 3.9 представлены координаты падающего тела, моменты времени, в которые тело проходит через эти точки, а также средние скорости для выделенных интервалов.
На рис. 3.9 представлены координаты падающего тела, моменты времени, в которые тело проходит через эти точки, а также средние скорости для выделенных интервалов.
Рис. 3.9. Зависимость средней скорости от участка пути
Из данных, приведенных на рис. 3.9 видно, что средняя скорость на всем пути (от 0 м до 5 м) равна
Средняя скорость на интервале от 2 м до 3 м равна
Движение, при котором средняя скорость изменяется, называется неравномерным.
Мы вычисляли среднюю скорость в окрестности одной и той же точки х = 2,5 м. На рис. 3.9 видно, что по мере уменьшения интервала, по которому проводятся вычисления, средняя скорость стремится к некоторому пределу (в нашем случае это 7 м/с). Этот предел называется мгновенной скоростью или скоростью в данной точке траектории.
Мгновенной скоростью движения, или скоростью в данной точке траектории называется предел, к которому стремится отношение перемещения тела в окрестности этой точки ко времени при неограниченном уменьшении интервала:
Размерность скорости в СИ – м/с.
Часто скорость указывают в других единицах (например, в км/ч). При необходимости такие значения можно перевести в СИ. Например, 54 км/ч = 54000 м/3600 с =15 м/с.
Для одномерного случая мгновенная скорость равна производной от координаты тела по времени:
При равномерном движении величины средней и мгновенной скорости совпадают и остаются неизменными.
Мгновенная скорость – величина векторная. Направление вектора мгновенной скорости показано на рис. 3.10.
Рис. 3.10. Направление вектора мгновенной скорости
Во время забега мгновенная скорость бегуна меняется. Особенно существенны такие изменения в спринте. На рис. 3.11 приводится пример такого изменения для дистанции 200 м.
Бегун начинает движение из состояния покоя и разгоняется, пока не достигнет максимальной скорости. Для бегуна-мужчины время ускорения приблизительно 2 с, а максимальная скорость приближается к 10,5 м/с. Средняя скорость на всей дистанции меньше этого значения.
Рис. 3.11. Зависимость мгновенной скорости от времени бега для дистанции 200 м, мужчины
3.11. Зависимость мгновенной скорости от времени бега для дистанции 200 м, мужчины
Причина того, что бегун не может долго поддерживать свою максимальную скорость движения, состоит в том, что он начинает испытывать недостаток кислорода. Тело содержит кислород, запасенный в мышцах, а в дальнейшем получает его при дыхании. Поэтому спринтер может поддерживать свою максимальную скорость только до тех пор, пока не израсходует запас кислорода. Это кислородное истощение наступает на дистанции около 300 м. Следовательно, для больших дистанций бегун должен ограничивать себя скоростью меньше максимальной. Чем длиннее дистанция, тем меньше должна быть скорость, чтобы кислорода хватило на весь забег. Только спринтеры бегут на максимальной скорости всю дистанцию.
На соревнованиях бегун обычно стремиться либо победить соперника, либо установить рекорд. От этого зависит стратегия забега. При установлении рекорда оптимальной стратегией будет та, при которой выбирается скорость, соответствующая полному истощению запаса кислорода к моменту пересечения финиша.
В спорте используются специальные временные характеристики.
Момент времени (t) – это временная мера положения точки, тела или системы. Момент времени определяют промежутком времени до него от начала отсчета.
Моментами времени обозначают, например, начало и окончание движения или какой-либо его части (фазы). По моментам времени определяют длительность движения.
Длительность движения (Δt) – это его временная мера, которая измеряется разностью моментов времени окончания и начала движения:
Δt = t кон – t нач .
Длительность движения представляет собой количество времени, прошедшее между двумя ограничивающими его моментами времени. Сами моменты длительности не имеют. Зная путь точки и длительность ее движения, можно определять ее среднюю скорость.
Темп движения (N) – это временная мера повторности движений. Он измеряется количеством движений, повторяющихся в единицу времени (частота движений):
Он измеряется количеством движений, повторяющихся в единицу времени (частота движений):
В повторных движениях одинаковой длительности темп характеризует их протекание во времени. Темп – величина, обратная длительности движений. Чем больше длительность каждого движения, тем меньше темп, и наоборот.
Ритм движений – это временная мера соотношения частей движений. Он определяется по соотношению промежутков времени – длительностей частей движений: Δt 2-1: Δt 2-3: Δt 4- 3 …
Различный ритм движений для лыжников при скользящем шаге (для пяти фаз шага) показан на рис. 3.12.
Рис. 3.12. Различный ритм в скользящем шаге на лыжах: а) у высококвалифицированных лыжников;
б) у сильнейших лыжников мира;
фазы /-/// – скольжение, фазы скольжения,
фазы IV- V – стояние лыжи
Быстрота – это темп, в котором преодолевается расстояние без учета направления.
Быстрота – скалярная величина. Пусть между двумя пунктами при движении по одному шоссе одновременно движутся автомобилист, мотоциклист, велосипедист, бегун. У всех четверых одинаковы траектории, пути, перемещения. Однако их движение отличается быстротой (стремительностью), для характеристики которой и вводится понятие «скорость».
Пусть между двумя пунктами при движении по одному шоссе одновременно движутся автомобилист, мотоциклист, велосипедист, бегун. У всех четверых одинаковы траектории, пути, перемещения. Однако их движение отличается быстротой (стремительностью), для характеристики которой и вводится понятие «скорость».
Развивать мыслительные способности учащихся, умение анализировать, выделять общие и отличительные свойства; развивать умение применять теоретические знания на практике при решении задач на нахождение средней скорости неравномерного движения.
Скачать:
Предварительный просмотр:
Урок в 9 классе по теме: «Средняя и мгновенная скорости неравномерного движения»
Учитель – Малышев М.Е.
Дата -17.10.2013
Цели урока:
Образовательная цель:
- Повторить понятие – средняя и мгновенная скорости,
- научиться находить среднюю скорость при различных условиях, используя задачи из материалов ГИА и ЕГЭ прошлых лет.
Развивающая цель:
- развивать мыслительные способности учащихся, умение анализировать, выделять общие и отличительные свойства; развивать умение применять теоретические знания на практике; развивать память, внимание, наблюдательность.

Воспитательная цель:
- воспитывать устойчивый интерес к изучению математики и физики через реализацию межпредметных связей;
Тип урока:
- урок обобщения и систематизации знаний, умений по данной теме.
Оборудование:
- компьютер, мультимедийный проектор;
- тетради;
- набор оборудования L- микро по разделу «Механика»
Ход урока
1. Организационный момент
Взаимное приветствие; проверка готовности учащихся к уроку, организация внимания.
2. Сообщение темы и целей урока
Слайд на экране : “ Практика рождается только из тесного соединения физики и математики ” Бэкон Ф.
Сообщается тема и цели урока.
3. Входной контроль (повторение теоретического материала) (10 мин)
Организация устной фронтальной работы с классом по повторению.
Учитель физики:
1. Какой простейший вид движения вам известен? (равномерное движение)
2. Как найти скорость при равномерном движении? (перемещение разделить на время v
=
s /
t
)? Равномерное движение встречается нечасто.
Обычно механическое движение – это движение с изменяющейся скоростью. Движение, при котором скорость тела с течением времени изменяется, называют неравномерным. Например, неравномерно движется транспорт. Автобус, начиная движение, увеличивает свою скорость; при торможении его скорость уменьшается. Падающие на поверхность Земли тела также движутся неравномерно: их скорость с течением времени возрастает.
3. Как найти скорость при неравномерном движении? Как она называется? (Средняя скорость, v ср = s/ t)
На практике при определении средней скорости пользуются величиной, равной отношению пути s ко времени t, за которое этот путь пройден: v ср = s/t . Ее часто называют средней путевой скоростью .
4. Какие особенности есть у средней скорости? (Средняя скорость является векторной величиной. Для определения модуля средней скорости в практических целях этой формулой можно воспользоваться лишь в том случае, когда тело движется вдоль прямой в одну сторону. Во всех остальных случаях эта формула непригодна).
5. Что такое мгновенная скорость? Как направлен вектор мгновенной скорости? (Мгновенная скорость – это скорость тела в данный момент времени или в данной точке траектории. Вектор мгновенной скорости в каждой точке совпадает с направлением движения в данной точке.)
6. Чем отличается мгновенная скорость при равномерном прямолинейном движении от мгновенной скорости при неравномерном движении? (В случае равномерного прямолинейного движения мгновенная скорость в любой точке и в любой момент времени одинакова; в случае неравномерного прямолинейного движения мгновенная скорость различна).
7. Можно ли определить положение тела в любой момент времени зная среднюю скорость его движения на каком-либо участке траектории? (нельзя определить его положение в любой момент времени).
Предположим, что автомобиль проехал путь 300 км за 6 ч. Чему равна средняя скорость движения? Средняя скорость движения автомобиля равна 50 км/ч. Однако при этом он мог какое-то время стоять, какое – то время двигаться со скоростью 70 км/ч, какое – то время – со скоростью 20 км/ч и т. п.
п.
Очевидно, что, зная среднюю скорость движения автомобиля за 6 ч, мы не можем определить его положение через 1 ч, через 2 ч, через 3 ч и т. д. времени”.
1. Устно найдите скорость автомобиля, если путь в 180 км он проехал за 3 часа.
2. Автомобиль ехал 1 час со скоростью 80 км /ч и 1 час со скоростью 60 км/ч. Найдите среднюю скорость. Действительно, средняя скорость равна(80+60)/2=70 км/ч. В данном случае средняя скорость равна среднему арифметическому скоростей.
3. Изменим условие. Автомобиль ехал 2 часа со скоростью 60 км /ч и 3 часа со скоростью 80 км/ч. Какова средняя скорость на всем пути?
(60 2+80 3)/5=72 км /ч. Скажите, а сейчас средняя скорость равна среднему арифметическому скоростей? Нет.
Самое главное, что нужно помнить, при нахождении средней скорости – это то, что она средняя, а не средняя арифметическая скорость. Конечно, услышав задачу, сразу хочется сложить скорости и разделить на 2.Это самая распространенная ошибка.
Средняя скорость равна среднему арифметическому от скоростей тела во время движения только в том случае, когда тело с этими скоростями проходит весь путь за одинаковые промежутки времени.
4. Решение задач (15 мин)
Задача №1. Скорость лодки по течению 24 км в час, против течения 16 км в час. Найти среднюю скорость. (Проверка выполнения заданий у доски.)
Решение. Пусть S – путь от начального до конечного пунктов, тогда время, затраченное на путь по течению S/24, а против течения – S/16, общее время движения – 5S/48. Так как весь путь, туда и обратно составляет 2S, следовательно, средняя скорость равна2S/(5S/48)=19,2 км в час.
Экспериментальное исследование “Равноускоренное движение, начальная скорость равна нолю” (Эксперимент проводится учащимися)
Прежде чем приступить к выполнению практической работы вспомним правила ТБ:
- Перед началом работы : внимательно изучить содержание и порядок проведения лабораторного практикума, подготовить рабочее место и убрать посторонние предметы, приборы и оборудование разместить таким образом, чтобы исключить их падение и опрокидывание, проверить исправность оборудования и приборов.
- Во время работы
: точно выполнять все указания учителя, без его разрешения не выполнять самостоятельно никаких работ, следить за исправностью всех креплений в приборах и приспособлениях.

- По окончании работы : привести в порядок рабочее место, сдать учителю приборы и оборудование.
Исследование зависимости скорости от времени при равноускоренном движении (начальная скорость равна нулю).
Цель: изучение равноускоренного движения, построение графика зависимости v=at на основе экспериментальных данных.
Из определения ускорения следует, что скорость тела v , двигающегося прямолинейно с постоянным ускорением, спустя некоторое время t после начала движения может быть определена из уравнения: v = v 0 +аt . Если тело начало двигаться, не имея начальной скорости, то есть при v 0 = 0, это уравнение становится более простым: v = а t. (1)
Скорость в заданной точке траектории можно определить, зная перемещение тела из состояния покоя до этой точки и время движения. Действительно, при движении из состояния покоя ( v 0 = 0 ) с постоянным ускорением перемещение определяется по формуле S= at 2 /2, откуда, а=2S/ t 2 (2). После подстановки формулы (2) в (1):v=2 S/t (3)
Для выполнения работы направляющую рейки устанавливают с помощью штатива в наклонном положении.
Её верхний край должен находиться на высоте 18-20 см от поверхности стола. Под нижний край подкладывают пластиковый коврик. Каретку устанавливают на направляющей в крайнем верхнем положении, причём её выступ с магнитом должен быть обращен в сторону датчиков. Первый датчик размещают вблизи магнита каретки так, чтобы он запускал секундомер, как только каретка начнёт двигаться. Второй датчик устанавливают на удалении 20-25 см от первого. Далее работу выполняют в таком порядке:
- Измеряют перемещение, которое каретка совершит, двигаясь между датчиками – S 1
- Производят пуск каретки и измеряют время её движения между датчиками t 1
- По формуле (3) определяют скорость, с которой двигалась каретка в конце первого участка v 1 =2S 1 /t 1
- Увеличивают расстояние между датчиками на 5см и повторяют серию опытов для измерения скорости тела в конце второго участка: v
2
=2 S
2
/t
2
Каретку в этой серии опытов, как и в первой, пускают из крайнего верхнего положения.

- Проводят ещё две серии опытов, увеличивая в каждой серии расстояние между датчиками на 5 см. Так находят значения скорости v з и v 4
- По полученным данным строят график зависимости скорости от времени движения.
- Подведение итогов урока
Домашнее задание с комментариями: Выберите любые три задачи:
1. Велосипедист, проехав 4 км со скоростью 12 км/ч, остановился и отдыхал в течении 40 мин. Оставшиеся 8 км пути он проехал со скоростью 8 км/ч. Найдите среднюю скорость (в км/ч) велосипедиста на всем пути?
2.Велосипедист за первые 5 с проехал 35 м, за последующие 10 с-100 м и за последние 5 с-25 м. Найдите среднюю скорость движения на всем пути.
3. Первые 3/4 времени своего движения поезд шел со скоростью 80 км/ч, остальное время – со скоростью 40 км/ч. Какова средняя скорость (в км/ч) движения поезда на всем пути?
4. Первую половину пути автомобиль прошел со скоростью 40 км/ч, вторую – со скоростью 60 км/ч. Найдите среднюю скорость(в км/ч) автомобиля на всем пути?
5. Автомобиль проехал первую половину пути со скоростью 60 км/ч. Оставшуюся часть пути он ехал со скоростью 35 км/ч, а последний участок – со скоростью 45 км/ч. Найдите среднюю скорость (в км/ч) автомобиля на всем пути.
Автомобиль проехал первую половину пути со скоростью 60 км/ч. Оставшуюся часть пути он ехал со скоростью 35 км/ч, а последний участок – со скоростью 45 км/ч. Найдите среднюю скорость (в км/ч) автомобиля на всем пути.
“ Практика рождается только из тесного соединения физики и математики ” Бэкон Ф.
а) “Разгон” (начальная скорость меньше конечной) б) “Торможение” (конечная скорость меньше начальной)
Устно 1. Найдите скорость автомобиля, если путь в 180 км он проехал за 3 часа. 2. Автомобиль ехал 1 час со скоростью 80 км /ч и 1 час со скоростью 60 км/ч. Найдите среднюю скорость. Действительно, средняя скорость равна(80+60)/2=70 км/ч. В данном случае средняя скорость равна среднему арифметическому скоростей. 3. Изменим условие. Автомобиль ехал 2 часа со скоростью 60 км /ч и 3 часа со скоростью 80 км/ч. Какова средняя скорость на всем пути?
(60* 2+80* 3)/5=72 км /ч. Скажите, а сейчас средняя скорость равна среднему арифметическому скоростей?
Задача Скорость лодки по течению 24 км в час, против течения 16 км в час. Найти среднюю скорость лодки.
Найти среднюю скорость лодки.
Решение. Пусть S- путь от начального до конечного пунктов, тогда время, затраченное на путь по течению S/24, а против течения – S/16, общее время движения – 5S/48. Так как весь путь, туда и обратно составляет 2S, следовательно, средняя скорость равна2S/(5S/48)=19,2 км в час.
Решение. V ср = 2s / t 1 + t 2 t 1 = s / V 1 и t 2 = s / V 2 V ср = 2s / V 1 + s / V 2 = 2 V 1 V 2 / V 1 + V 2 V ср = 19,2 км/ч
На дом: Первую треть трассы велосипедист ехал со скоростью 12 км в час, вторую треть – со скоростью 16 км в час, а последнюю треть – со скоростью 24 км в час. Найдите среднюю скорость велосипеда на протяжении всего пути. Ответ дайте в км в час.
К примеру, автомобиль, который трогается с места, движется ускоренно, так как наращивает скорость движения. В точке начала движения скорость автомобиля равняется нулю. Начав движение, автомобиль разгоняется до некоторой скорости. При необходимости затормозить, автомобиль не сможет остановиться мгновенно, а за какое-то время.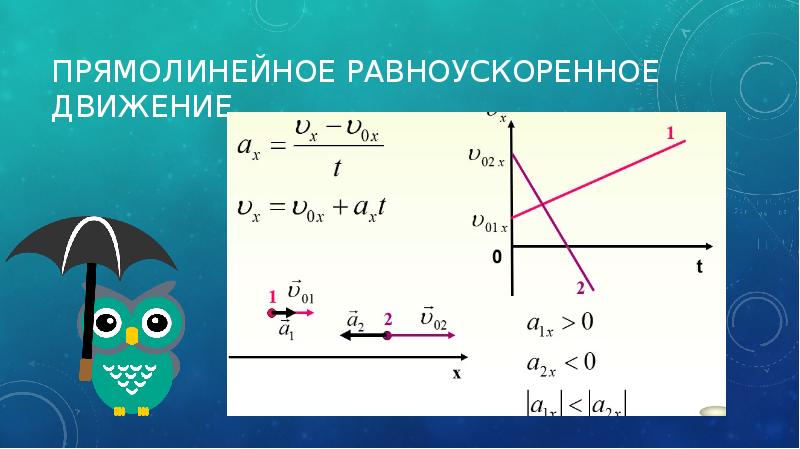 То есть скорость автомобиля будет стремиться к нулю – автомобиль начнет двигаться замедленно до тех пор, пока не остановится полностью. Но физика не имеет термина «замедление». Если тело двигается, уменьшая скорость, этот процесс тоже называется ускорением , но со знаком «-».
То есть скорость автомобиля будет стремиться к нулю – автомобиль начнет двигаться замедленно до тех пор, пока не остановится полностью. Но физика не имеет термина «замедление». Если тело двигается, уменьшая скорость, этот процесс тоже называется ускорением , но со знаком «-».
Средним ускорением называется отношение изменения скорости к промежутку времени, за который это изменении произошло. Вычисляют среднее ускорение при помощи формулы:
где – это . Направление вектора ускорения такое же, как у направления изменения скорости Δ = – 0
где 0 является начальной скоростью. В момент времени t 1 (см. рис. ниже) у тела 0 . В момент времени t 2 тело имеет скорость . Исходя из правила вычитания векторов, определим вектор изменения скорости Δ = – 0 . Отсюда вычисляем ускорение:
.
В системе СИ единицей ускорения называется 1 метр в секунду за секунду (либо метр на секунду в квадрате):
.
Метр на секунду в квадрате – это ускорение прямолинейно движущейся точки, при котором за 1 с скорость этой точки растет на 1 м/с. Другими словами, ускорение определяет степень изменения скорости тела за 1 с. К примеру, если ускорение составляет 5 м/с 2 , значит, скорость тела ежесекундно растет на 5 м/с.
Другими словами, ускорение определяет степень изменения скорости тела за 1 с. К примеру, если ускорение составляет 5 м/с 2 , значит, скорость тела ежесекундно растет на 5 м/с.
Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина , которая равна пределу, к которому стремится среднее ускорение при стремлении промежутка времени к 0. Другими словами – это ускорение, развиваемое телом за очень маленький отрезок времени:
.
Ускорение имеет такое же направление, как и изменение скорости Δ в крайне маленьких промежутках времени, за которые скорость изменяется. Вектор ускорения можно задать при помощи проекций на соответствующие оси координат в заданной системе отсчета (проекциями а Х, a Y , a Z).
При ускоренном прямолинейном движении скорость тела увеличивается по модулю, т.е. v 2 > v 1 , а вектор ускорения имеет такое же направление, как и у вектора скорости 2 .
Если скорость тела по модулю уменьшается (v 2 замедление движения (ускорение отрицательно, а
Если происходит движение по криволинейной траектории, то изменяется модуль и направление скорости. Значит, вектор ускорения изображают в виде 2х составляющих.
Значит, вектор ускорения изображают в виде 2х составляющих.
Тангенциальным (касательным) ускорением называют ту составляющую вектора ускорения, которая направлена по касательной к траектории в данной точке траектории движения. Тангенциальное ускорение описывает степень изменения скорости по модулю при совершении криволинейного движения.
У вектора тангенциального ускорения τ (см. рис. выше) направление такое же, как и у линейной скорости либо противоположно ему. Т.е. вектор тангенциального ускорения находится в одной оси с касательной окружности, являющейся траекторией движения тела.
Если материальная точка находится в движении, то ее координаты подвергаются изменениям. Этот процесс может происходить быстро или медленно.
Определение 1
Величина, которая характеризует быстроту изменения положения координаты, называется скоростью .
Определение 2
Средняя скорость – это векторная величина, численно равная перемещению в единицу времени, и сонаправленная с вектором перемещения υ = ∆ r ∆ t ; υ ∆ r .
Рисунок 1 . Средняя скорость сонаправлена перемещению
Модуль средней скорости по пути равняется υ = S ∆ t .
Мгновенная скорость характеризует движение в определенный момент времени. Выражение «скорость тела в данный момент времени» считается не корректным, но применимым при математических расчетах.
Определение 3
Мгновенной скоростью называют предел, к которому стремится средняя скорость υ при стремлении промежутка времени ∆ t к 0:
υ = l i m ∆ t ∆ r ∆ t = d r d t = r ˙ .
Направление вектора υ идет по касательной к криволинейной траектории, потому как бесконечно малое перемещение d r совпадает с бесконечно малым элементом траектории d s .
Рисунок 2 . Вектор мгновенной скорости υ
Имеющееся выражение υ = l i m ∆ t ∆ r ∆ t = d r d t = r ˙ в декартовых координатах идентично ниже предложенным уравнениям:
υ x = d x d t = x ˙ υ y = d y d t = y ˙ υ z = d z d t = z ˙ .
Запись модуля вектора υ примет вид:
υ = υ = υ x 2 + υ y 2 + υ z 2 = x 2 + y 2 + z 2 .
Чтобы перейти от декартовых прямоугольных координат к криволинейным, применяют правила дифференцирования сложных функций. Если радиус-вектор r является функцией криволинейных координат r = r q 1 , q 2 , q 3 , тогда значение скорости запишется как:
υ = d r d t = ∑ i = 1 3 ∂ r ∂ q i ∂ q i ∂ r = ∑ i = 1 3 ∂ r ∂ q i q ˙ i .
Рисунок 3 . Перемещение и мгновенная скорость в системах криволинейных координат
При сферических координатах предположим, что q 1 = r ; q 2 = φ ; q 3 = θ , то получим υ , представленную в такой форме:
υ = υ r e r + υ φ e φ + υ θ φ θ , где υ r = r ˙ ; υ φ = r φ ˙ sin θ ; υ θ = r θ ˙ ; r ˙ = d r d t ; φ ˙ = d φ d t ; θ ˙ = d θ d t ; υ = r 1 + φ 2 sin 2 θ + θ 2 .
Определение 4
Мгновенной скоростью называют значение производной от функции перемещения по времени в заданный момент, связанной с элементарным перемещением соотношением d r = υ (t) d t
Пример 1
Дан закон прямолинейного движения точки x (t) = 0 , 15 t 2 – 2 t + 8 . Определить ее мгновенную скорость через 10 секунд после начала движения.
Определить ее мгновенную скорость через 10 секунд после начала движения.
Решение
Мгновенной скоростью принято называть первую производную радиус-вектора по времени. Тогда ее запись примет вид:
υ (t) = x ˙ (t) = 0 . 3 t – 2 ; υ (10) = 0 . 3 × 10 – 2 = 1 м / с.
Ответ : 1 м / с.
Пример 2
Движение материальной точки задается уравнением x = 4 t – 0 , 05 t 2 . Вычислить момент времени t о с т, когда точка прекратит движение, и ее среднюю путевую скорость υ .
Решение
Вычислим уравнение мгновенной скорости, подставим числовые выражения:
υ (t) = x ˙ (t) = 4 – 0 , 1 t .
4 – 0 , 1 t = 0 ; t о с т = 40 с; υ 0 = υ (0) = 4 ; υ = ∆ υ ∆ t = 0 – 4 40 – 0 = 0 , 1 м / с.
Ответ: заданная точка остановится по прошествии 40 секунд; значение средней скорости равняется 0 , 1 м / с.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Скорость при равноускоренном движении ❤️
Теория равноускоренного движения была разработана знаменитым итальянским ученым Галилео Галилеем. В своей книге «Беседы и математические доказательства, касающиеся двух новых отраслей науки, относящихся к Механике и Местному движению», вышедшей в 1638 г., Галилей впервые дал определение равноускоренного движения и доказал ряд теорем, в которых описывались его закономерности.
В своей книге «Беседы и математические доказательства, касающиеся двух новых отраслей науки, относящихся к Механике и Местному движению», вышедшей в 1638 г., Галилей впервые дал определение равноускоренного движения и доказал ряд теорем, в которых описывались его закономерности.
Приступая к изучению равноускоренного прямолинейного движения, выясним сначала, как находится скорость
тела, если известны ускорение этого тела и время движения.Из формулы (2.1) следует, что при начальной скорости, равной нулю (v0 = 0), Эта формула показывает, что для нахождения скорости тела через время t после начала движения надо ускорение тела умножить на время движения.
В противоположном случае, когда тело совершает замедленное движение и в конце концов останавливается (v = 0), формула ускорения (2.2) позволяет найти начальную скорость тела: Наглядную картину
того, как изменяется скорость тела в процессе равноускоренного движения, можно получить, построив График скорости.Графики скорости впервые были введены в середине XIV в. францисканским ученым-монахом Джиованни ди Казалисом и архидьяконом Руанского собора Никола Оремом, ставшим впоследствии советником французского короля Карла V. По горизонтальной оси они предложили откладывать время, а по вертикальной оси — скорость. В такой системе координат графики скорости при равноускоренном движении имеют вид прямых линий, наклон которых показывает, как быстро изменяется скорость с течением времени.
францисканским ученым-монахом Джиованни ди Казалисом и архидьяконом Руанского собора Никола Оремом, ставшим впоследствии советником французского короля Карла V. По горизонтальной оси они предложили откладывать время, а по вертикальной оси — скорость. В такой системе координат графики скорости при равноускоренном движении имеют вид прямых линий, наклон которых показывает, как быстро изменяется скорость с течением времени.
Формуле (3.1), описывающей движение с возрастающей скоростью, соответствует, например, график скорости, изображенный на рисунке 5. График, изображенный на рисунке 6, соответствует движению с уменьшающейся скоростью. При равноускоренном движении скорость тела непрерывно изменяется.
Графики скорости позволяют определить скорость тела в различные моменты времени. Но иногда бывает нужно знать не скорость в тот или иной конкретный момент времени (такую скорость называют мгновенной), а среднюю скорость движения на всем пути.
Задачу о нахождении средней скорости при равноускоренном движении впервые удалось решить Галилею. В своих исследованиях он использовал графический метод описания движения.
В своих исследованиях он использовал графический метод описания движения.
Согласно теории Галилея, если скорость тела при равноускоренном движении увеличивается от 0 до некоторого значения v, то средняя скорость движения будет равна половине достигнутой скорости: Аналогичная формула справедлива и для движения с уменьшающейся скоростью. Если она уменьшается от некоторого начального значения v0 до 0, то средняя скорость такого движения оказывается равной
Полученные результаты можно проиллюстрировать с помощью графика скорости. Так, например, для нахождения средней скорости движения, которому соответствует график на рисунке 5, мы должны найти половину от 6 м/с. В результате получаем 3 м/с. Это и есть средняя скорость рассматриваемого движения.
1.
Кто является автором первой теории равноускоренного движения? 2. Как находится скорость тела при равноускоренном движении из состояния покоя? 3. Используя график, изображенный на рисунке 5, определите скорость тела через 2 с после начала движения.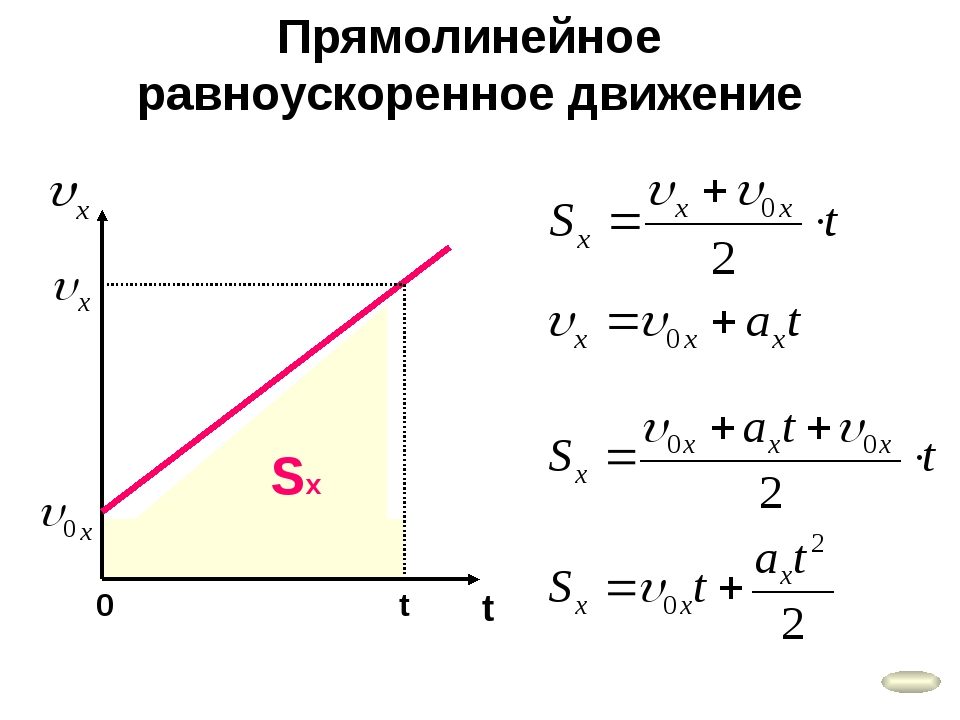
4. Используя график, изображенный на рисунке 6, определите среднюю скорость движения тела.
Примечание: в случае равномерного движения средняя и мгновенная скорость совпадают.
Кинематика материальной точки.
Кинематика материальной точки. : Скорость материальной точки…. Ускорение материальной точки…. 3 Тангенциальное и нормальное ускорение…. 4 Проекции скорости и ускорения… 5 График скорости… 6 Вращательное
ПодробнееКИНЕМАТИКА ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ
КИНЕМАТИКА ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ 2.1. Понятие механики, модели в механике 2.2. Система отсчета, тело отсчета 2.3. Кинематика материальной точки 2. 3.1. Путь, перемещение 2.3.2. Скорость 2.3.3. Проекция
3.1. Путь, перемещение 2.3.2. Скорость 2.3.3. Проекция
1. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
1. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА 1.. Кинематика. Кинематика это часть теоретической механики, в которой изучается механическое движение материальных точек и твердых тел. Механическое движение это перемещение
ПодробнееТема 1.1. Элементы кинематики
Тема 11 Элементы кинематики План 1 Предмет физики Физические законы, величины, их измерение 2 Модели в механике Система отсчёта Траектория, длина пути, вектор перемещения 3 Скорость 4 Ускорение и его составляющие
Подробнеедостаточно близко, то участок BB
Лекция 3 Криволинейное движение. Тангенциальная и нормальная составляющие ускорения. Движение точки по окружности. Угловое перемещение, векторы угловой скорости и углового ускорения. Связь между векторами
Связь между векторами
Кинематика материальной точки
Кинематика материальной точки Виды механических движений. Скорость и ускорение Прямолинейное движение Криволинейное движение Вращательное движение Преобразование Галилея. Инерциальные системы отсчета .
Подробнее2.3 Ускорение материальной точки
2.3 Ускорение материальной точки При неравномерном движении скорость частицы в общем случае меняется как по величине, так и по направлению. Быстрота изменения скорости определяется ускорением, которое
ПодробнееСПРАВОЧНИК ПО ФИЗИКЕ классы
СПРАВОЧНИК ПО ФИЗИКЕ 7 11 классы МОСКВА «ВАКО» 017 УДК 37853 ББК 746 С74 6+ Издание допущено к использованию в образовательном процессе на основании приказа Министерства образования и науки РФ от 0906016
Подробнее1.
 КИНЕМАТИКА. Кинематика точки
КИНЕМАТИКА. Кинематика точки1 КИНЕМАТИКА Кинематика точки Вектор скорости, модуль вектора скорости, вектор ускорения, модуль вектора ускорения dx v x = – проекция вектора скорости на координатную ось X может быть найдена dt как производная
ПодробнееОсновные законы и формулы
1.1. Кинематика материальной точки Основные законы и формулы При движении материальной точки в пространстве радиус-вектор, проведённый из начала координат к точке, и координаты этой точки, представляющие
ПодробнееРаздел I Физические основы механики
Раздел I Физические основы механики Механика часть физики, которая изучает закономерности механического движения и причины, вызывающие или изменяющие это движение Механическое движение это изменение с
ПодробнееМЕТОДИЧЕСКИЕ УКАЗАНИЯ
Министерство общего и профессионального образования Российской Федерации ОРЕНБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Кафедра физики Т. М. Чмерева М.Р. Ишмеев МЕТОДИЧЕСКИЕ УКАЗАНИЯ к лабораторной работе 104
М. Чмерева М.Р. Ишмеев МЕТОДИЧЕСКИЕ УКАЗАНИЯ к лабораторной работе 104
= const. r r. 1 m Законы Ньютона
5.3. Законы Ньютона При рассмотрении движении материальной точки в рамках динамики решаются две основные задачи. Первая или прямая задача динамики заключается в определении системы действующих сил по заданным
ПодробнееТема 2 Кинематика движений человека
Тема 2 Кинематика движений человека Механика занимается рассмотрением простейшей формы движения материи механической. Такое движение состоит в изменении взаимного расположения тел или их частей в пространстве
Подробнее/ /15
1. Задание 1 7777 Вариант 3580273 Небольшое тело движется в пространстве. На рисунке показаны графики зависимости от времени t проекций V x, V y и V z скорости этого тела на оси OX, OY и OZ от времени
ПодробнееОБЩАЯ ФИЗИКА.
 МЕХАНИКА
МЕХАНИКАИ.Л. Касаткина, Д.Г. Барсегов, А.А. Греков, З.П. Мастропас Готовимся к сессии ОБЩАЯ ФИЗИКА. МЕХАНИКА Тестовые задания с решениями и методическими указаниями УДК ББК К К ISBN Касаткина И.Л. Готовимся к
ПодробнееТЕОРЕТИЧЕСКАЯ МЕХАНИКА
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Теоретическая механика наука об общих законах движения и равновесия материальных тел и о возникающих при этом механических взаимодействиях между телами Движение (механическое движение)
ПодробнееКИНЕМАТИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
КИНЕМАТИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ Физика является одной из тех наук, знание которой необходимо для успешного изучения общенаучных и специальных дисциплин При изучении курса физики студенты должны прочно
ПодробнееМеханические колебания
Механические колебания Гармонические колебания Общие определения Колебаниями называют периодическое или почти периодическое движение или процесс Если колебания происходят при отклонения системы от устойчивого
ПодробнееЧАСТЬ 2.
 ОСНОВЫ КЛАССИЧЕСКОЙ МЕХАНИКИ
ОСНОВЫ КЛАССИЧЕСКОЙ МЕХАНИКИЧАСТЬ ОСНОВЫ КЛАССИЧЕСКОЙ МЕХАНИКИ Механика часть физики, изучающая движение и взаимодействие физических тел в пространстве и времени При этом физика имеет дело не с реальными телами: автомобилями, поездами,
Подробнее1, 3 10 км ), движущийся по круговой орби-
Лекция Кинематика материальной точки Система отсчета Радиус-вектор, векторы перемещения, скорости, ускорения Траектория движения и пройденный путь Перемещение и путь при равномерном и равнопеременном прямолинейном
ПодробнееЛекция К1. КИНЕМАТИКА ТОЧКИ
Лекция К1. 1 КИНЕМАТИКА ТОЧКИ 1. Способы задания движения точки в заданной системе отсчета 2. Скорость и ускорение точки 3. Определение скорости и ускорения точки при координатном способе задания движения
ПодробнееФИЗИКА И ПОЗНАНИЕ МИРА.

1 Введение. Физика фундаментальная наука о природе. Естественно-научный метод познания, его возможности и границы применимости. Эксперимент и теория в процессе познания природы. Моделирование физических
ПодробнееПРОБНЫЙ ЭКЗАМЕН по теме 1. КИНЕМАТИКА
ПРОБНЫЙ ЭКЗАМЕН по теме. КИНЕМАТИКА Внимание: сначала попытайтесь ответить на вопросы и решить задачи самостоятельно, а потом проверьте свои ответы. Указание: ускорение свободного падения принимать равным
ПодробнееИТОГО: Б А Итоговый контроль
ФИЗИКА Часть 1 Лекции Практические занятия: Б А Лаб. занятия Всего аудиторной работы: Б А СРС ИТОГО: Б А Итоговый контроль 40 час. 16 час. 32 час. 24 час. 80 час. 104 час. 80 час. 6 кредитов 160 час. 192
Подробнее), движется равномерно
РАВНОВЕСИЕ ТЕЛ Раздел механики, в котором изучается равновесие тел, называется статикой Равновесным называется состояние тела, неизменное во времени, т е равновесие это такое состояние тела, при котором
Подробнееt точки M за малый промежуток
006-07 уч. год. 6, 9 кл. Физика. Движение материальной точки по окружности.. Кинематика движения точки по окружности. Линейная и угловая скорости Важным частным случаем движения материальной точки по заданной
год. 6, 9 кл. Физика. Движение материальной точки по окружности.. Кинематика движения точки по окружности. Линейная и угловая скорости Важным частным случаем движения материальной точки по заданной
КИНЕМАТИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ
КИНЕМАТИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ ПРЕДИСЛОВИЕ Физика является одной из тех наук, знание которой необходимо для успешного изучения общенаучных и специальных дисциплин При изучении курса физики студенты
ПодробнееСписок литературы.
Список литературы 1. Ремизов А.Н., Максина А.Г., Потапенко А.Я. Медицинская и биологическая физика. 2. Федорова В.Н., Фаустов Е.В. Медицинская и биологическая физика. Курс лекций с задачами. 3. Огурцов
ПодробнееКИНЕМАТИКА задания типа В Стр. 1 из 5
КИНЕМТИК задания типа В Стр. 1 из 5 1. Тело начало движение вдоль оси OX из точки x = 0 с начальной скоростью v0х = 10 м/с и с постоянным ускорением a х = 1 м/c 2. Как будут меняться физические величины,
1 из 5 1. Тело начало движение вдоль оси OX из точки x = 0 с начальной скоростью v0х = 10 м/с и с постоянным ускорением a х = 1 м/c 2. Как будут меняться физические величины,
Лабораторная работа 2. Равномерно ускоренное движение
Введение
Все объекты на земной поверхности движутся к центру Земли с ускорением 9,81 м/с 2 . Это означает, что если вы поднимете объект над поверхностью земли, а затем бросите его, объект начнет движение из состояния покоя, и его скорость будет увеличиваться на 9,81 метра в секунду за каждую секунду, пока он падает к поверхности земли, пока не упадет на поверхность. .Обсуждение принципов
В этом эксперименте вы будете измерять с помощью компьютерных приборов положение падающего тела в зависимости от времени, прошедшего с момента его освобождения.Мы принимаем направление вниз как положительное и обозначаем смещения в этом направлении какy
. Если пренебречь сопротивлением воздуха, говорят, что тело находится в свободном падении, а его ускорение
Если пренебречь сопротивлением воздуха, говорят, что тело находится в свободном падении, а его ускорениеa
постоянно. Рассмотрим объект в позицииy 1
в некоторый начальный момент времениt 1
. В более позднее времяt 2
объект находится в местоположенииy 2
. Средняя скоростьv 12
для этого объекта при его перемещении между этими двумя точками будет Аналогично средняя скоростьv 23
в течение следующего интервала времени (то есть между моментамиt 2
иt 3
) равна Если ускорение равномерное или постоянное, скорость точно в середине временного интервала является средней скоростью.Это означает, что если ускорение постоянно, мгновенная скорость точно равна средней скорости в середине исследуемого интервала времени. Даже если бы ускорение было неравномерным, это было бы близким приближением, если бы интервал времени был коротким. Таким образом,
Таким образом,v 23
произойдет в середине временного интервала, заданного выражением С этими двумя средними скоростями и временем мы можем вычислить среднее ускорениечерез
как( 4 )
а = =| (v 23 − v 12 ) | |
| (t 23 − t 12 ) |
Чтобы быстро напомнить, сначала я определю каждую из переменных.
Символ дельта (Δ) означает «изменение».
x = Окончательная позиция
x 0 = начальная позиция
V = Final Velocity
V 0 = начальная скорость
V с баром над ним = Средняя скорость
a = ускорение
t = время
Вопросы о равномерно ускоренном движении предоставят вам некоторые из этих фрагментов информации и попросят вас найти неизвестную величину.Суть в том, чтобы вытащить значения и определить, какие из них у вас есть, какие вам нужно определить, а какие вообще не включены в вопрос. Затем просто подставьте их в соответствующее уравнение. Это может звучать как простое «заполни пробелы и посчитай», но это может быть немного сложнее. Извините, но вы должны запомнить эти пять уравнений. Ни один из вопросов с несколькими вариантами ответов, с которыми вы столкнетесь, не даст их вам.
Здесь нужно сделать еще одно замечание.В некоторых вопросах может показаться, что вы упускаете ключевую информацию, особенно начальную позицию. Если вы ищете изменение положения в течение определенного периода времени, и вопрос не дает вам начальное положение, вы можете предположить, что оно равно 0 метров. Не забывайте всегда перепроверять свои переменные и уравнения и будьте очень осторожны, делая какие-либо предположения.
Если вы ищете изменение положения в течение определенного периода времени, и вопрос не дает вам начальное положение, вы можете предположить, что оно равно 0 метров. Не забывайте всегда перепроверять свои переменные и уравнения и будьте очень осторожны, делая какие-либо предположения.
Работа с уравнениями
Давайте рассмотрим типичную задачу, чтобы вы поняли, как ее решать.
Гоночный автомобиль, стоящий на стартовой линии прямой трассы, равномерно ускоряется в течение 3.6 секунд при скорости 4,5 м/с2. Какой путь проедет автомобиль за это время, если начальная скорость равна 0 м/с?
Во-первых, давайте запишем переменные, данные нам в уравнении.
t = 3,6 с
a = 4,5 м/с2
v 0 = 0 м/с
x 0 = 0 м. Это не дано, но вы можете предположить, что это 0 м, чтобы рассчитать изменение положения.
x = то, что проблема просит вас решить.
Теперь взгляните на уравнения большой пятерки. Только у одного будут ровно эти пять переменных. В этом случае нам нужно Уравнение 3: x = x 0 + v 0 * t + ½ на 2. Теперь начните заполнять пробелы и вычислить ответ.
Только у одного будут ровно эти пять переменных. В этом случае нам нужно Уравнение 3: x = x 0 + v 0 * t + ½ на 2. Теперь начните заполнять пробелы и вычислить ответ.
Итак, в этой задаче гонщик проезжает около 29 метров за 3,6 секунды. Вы должны включить единицы измерения, то есть метры.
Если в какой-то момент во время таких вопросов вы не уверены, что у вас есть правильное уравнение, попробуйте подставить числа в несколько уравнений.Вы быстро обнаружите, что у вас есть неиспользуемые значения или что уравнению нужно значение, которого у вас нет.
Краткое содержание урока
Давайте кратко повторим.
Чтобы упростить решение задач с различными комбинациями переменных положения, смещения, скорости и ускорения, мы упростим пару аспектов этих задач. Во-первых, мы предполагаем, что все ускорения равномерны, то есть они происходят с одинаковой скоростью от начала до конца. Во-вторых, мы рассматриваем движение только по прямой линии, поэтому направление, связанное с векторными величинами, может быть только положительным или отрицательным.
Во-вторых, мы рассматриваем движение только по прямой линии, поэтому направление, связанное с векторными величинами, может быть только положительным или отрицательным.
Есть пять уравнений, которые вам нужно запомнить для решения задач равномерно ускоренного движения. Лучший способ начать — определить все переменные, включая ту, которую нужно рассчитать, и найти уравнение, в котором они все есть. Затем просто подключите их и посчитайте. Помните, чтобы правильно ответить на вопрос, вам нужно включить правильные единицы измерения.
Результаты обучения
После завершения этого урока вы должны уметь:
- Вспомнить уравнения большой пятерки для равноускоренного движения
- Определите переменные в уравнении равномерно ускоренного движения
- Решить задачу равномерно ускоренного движения
3.3 Среднее и мгновенное ускорение – University Physics Volume 1
Цели обучения
К концу этого раздела вы сможете:
- Вычислите среднее ускорение между двумя моментами времени.

- Рассчитайте мгновенное ускорение, зная функциональную форму скорости.
- Объясните векторную природу мгновенного ускорения и скорости.
- Объясните разницу между средним ускорением и мгновенным ускорением.
- Найдите мгновенное ускорение в указанное время на графике зависимости скорости от времени.
Важность понимания ускорения охватывает наш повседневный опыт, а также обширные пространства космического пространства и крошечный мир субатомной физики. В повседневном разговоре ускорить означает ускорить; при нажатии на педаль тормоза автомобиль замедляется. Например, мы знакомы с ускорением нашего автомобиля. Чем больше ускорение, тем больше изменение скорости за данное время.Ускорение широко используется в экспериментальной физике. В экспериментах с линейным ускорителем частиц, например, субатомные частицы разгоняются до очень высоких скоростей в экспериментах по столкновению, которые сообщают нам информацию о структуре субатомного мира, а также о происхождении Вселенной. В космосе космические лучи — это субатомные частицы, которые были ускорены до очень высоких энергий в сверхновых (взрывах массивных звезд) и активных ядрах галактик. Важно понимать процессы, которые ускоряют космические лучи, потому что эти лучи содержат сильно проникающее излучение, которое может повредить электронику, например, на космическом корабле.
В космосе космические лучи — это субатомные частицы, которые были ускорены до очень высоких энергий в сверхновых (взрывах массивных звезд) и активных ядрах галактик. Важно понимать процессы, которые ускоряют космические лучи, потому что эти лучи содержат сильно проникающее излучение, которое может повредить электронику, например, на космическом корабле.
Среднее ускорение
Формальное определение ускорения согласуется с только что описанными понятиями, но является более всеобъемлющим.
Среднее ускорение
Среднее ускорение — скорость изменения скорости:
где
— среднее ускорение, v — скорость, t — время. (Полоса над и означает , среднее ускорение .)
Поскольку ускорение — это скорость в метрах, деленная на время в секундах, единицы измерения ускорения в системе СИ часто обозначаются аббревиатурой м/с 2 , то есть метры в секунду в квадрате или метры в секунду в секунду. Это буквально означает, на сколько метров в секунду скорость изменяется каждую секунду. Напомним, что скорость — это вектор — она имеет как величину, так и направление — это означает, что изменение скорости может быть изменением величины (или скорости), но также может быть и изменением направления.Например, если бегун, движущийся со скоростью 10 км/ч строго на восток, замедляется до остановки, меняет направление и продолжает свой бег со скоростью 10 км/ч строго на запад, его скорость изменилась в результате изменения направления, хотя магнитуда скорости одинакова в обоих направлениях. Таким образом, ускорение возникает, когда скорость изменяется по величине (увеличение или уменьшение скорости) или по направлению, или по тому и другому.
Это буквально означает, на сколько метров в секунду скорость изменяется каждую секунду. Напомним, что скорость — это вектор — она имеет как величину, так и направление — это означает, что изменение скорости может быть изменением величины (или скорости), но также может быть и изменением направления.Например, если бегун, движущийся со скоростью 10 км/ч строго на восток, замедляется до остановки, меняет направление и продолжает свой бег со скоростью 10 км/ч строго на запад, его скорость изменилась в результате изменения направления, хотя магнитуда скорости одинакова в обоих направлениях. Таким образом, ускорение возникает, когда скорость изменяется по величине (увеличение или уменьшение скорости) или по направлению, или по тому и другому.
Ускорение как вектор
Ускорение является вектором в том же направлении, что и изменение скорости,
.Поскольку скорость является вектором, она может изменяться по величине или по направлению, или по обоим направлениям. Таким образом, ускорение — это изменение скорости или направления, или и того, и другого.
Таким образом, ускорение — это изменение скорости или направления, или и того, и другого.
Имейте в виду, что хотя ускорение происходит в направлении изменения скорости, оно не всегда совпадает с направлением движения. Когда объект замедляется, его ускорение противоположно направлению его движения. Хотя это обычно называют замедлением (рисунок), мы говорим, что поезд ускоряется в направлении, противоположном направлению его движения.
Рис. 3.10 Поезд метро в Сан-Паулу, Бразилия, замедляет скорость, приближаясь к станции. Он ускоряется в направлении, противоположном направлению его движения. (кредит: Юсуке Кавасаки) Термин замедление может вызвать путаницу в нашем анализе, поскольку он не является вектором и не указывает на определенное направление относительно системы координат, поэтому мы его не используем. Ускорение — это вектор, поэтому мы должны выбрать для него соответствующий знак в выбранной нами системе координат.В случае поезда на (рисунке) ускорение составляет в отрицательном направлении в выбранной системе координат , поэтому мы говорим, что поезд испытывает отрицательное ускорение.
Если объект в движении имеет скорость в положительном направлении относительно выбранного начала координат и приобретает постоянное отрицательное ускорение, объект в конце концов приходит в состояние покоя и меняет направление. Если мы подождем достаточно долго, объект пройдет через начало координат в противоположном направлении. Это показано на (рис.).
Рисунок 3.11 Объект, движущийся с вектором скорости на восток с отрицательным ускорением, останавливается и меняет направление. Он проходит начало координат, двигаясь в противоположном направлении через достаточно долгое время.Пример
Расчет среднего ускорения: скаковая лошадь покидает ворота
Скаковая лошадь, выходящая из ворот, разгоняется из состояния покоя до скорости 15,0 м/с строго на запад за 1,80 с. Каково его среднее ускорение?
Рис. 3.12 Скаковые лошади разгоняются за воротами. (кредит: Джон Салливан)Стратегия
Сначала рисуем эскиз и присваиваем задаче систему координат (Рисунок). Это простая задача, но ее всегда полезно визуализировать. Обратите внимание, что мы назначаем восток как положительный, а запад как отрицательный. Таким образом, в этом случае мы имеем отрицательную скорость.
Это простая задача, но ее всегда полезно визуализировать. Обратите внимание, что мы назначаем восток как положительный, а запад как отрицательный. Таким образом, в этом случае мы имеем отрицательную скорость.
Мы можем решить эту проблему, идентифицируя
из предоставленной информации, а затем рассчитать среднее ускорение непосредственно из уравнения
.
Решение
Во-первых, определите известные:
(знак минус указывает направление на запад), Δ t = 1,80 с.
Во-вторых, найдите изменение скорости. Поскольку лошадь движется от нуля до –15,0 м/с, изменение ее скорости равно ее конечной скорости:
.
Наконец, подставьте известные значения (
) и найти неизвестное
:
Значение
Отрицательный знак ускорения указывает на то, что ускорение направлено на запад. Ускорение 8,33 м/с 2 строго на запад означает, что лошадь увеличивает свою скорость на 8,33 м/с строго на запад каждую секунду; то есть 8,33 метра в секунду за секунду, что мы запишем как 8,33 м/с 2 . Это действительно среднее ускорение, потому что езда не плавная. Позже мы увидим, что ускорение такой величины потребовало бы от всадника удержания силы, почти равной его весу.
Ускорение 8,33 м/с 2 строго на запад означает, что лошадь увеличивает свою скорость на 8,33 м/с строго на запад каждую секунду; то есть 8,33 метра в секунду за секунду, что мы запишем как 8,33 м/с 2 . Это действительно среднее ускорение, потому что езда не плавная. Позже мы увидим, что ускорение такой величины потребовало бы от всадника удержания силы, почти равной его весу.
Проверьте свое понимание
протонов в линейном ускорителе разгоняются из состояния покоя до
через 10 –4 с.Каково среднее ускорение протонов?
[reveal-answer q=”fs-id1168327875120″]Показать решение[/reveal-answer]
[скрытый ответ a=”fs-id1168327875120″]
Подставляем известные, имеем
[/скрытый ответ]
Мгновенное ускорение
Мгновенное ускорение a или ускорение в конкретный момент времени получается с использованием того же процесса, который обсуждался для мгновенной скорости. То есть мы вычисляем среднюю скорость между двумя моментами времени, разделенными
То есть мы вычисляем среднюю скорость между двумя моментами времени, разделенными
и пусть
приближаются к нулю. Результатом является производная функции скорости v ( t ), которая равна мгновенному ускорению и математически выражается как
Таким образом, аналогично тому, как скорость является производной функции положения, мгновенное ускорение является производной функции скорости.Мы можем показать это графически так же, как мгновенную скорость. На (рисунке) мгновенное ускорение в момент времени t 0 представляет собой наклон касательной к графику зависимости скорости от времени в момент времени t 0 . Мы видим, что среднее ускорение
приближается к мгновенному ускорению как
приближается к нулю. Также в части (а) рисунка мы видим, что скорость имеет максимум, когда ее наклон равен нулю. Это время соответствует нулю функции ускорения. В части (b) показано мгновенное ускорение при минимальной скорости, которая также равна нулю, так как наклон кривой и там равен нулю. Таким образом, для данной функции скорости нули функции ускорения дают либо минимальную, либо максимальную скорость.
Это время соответствует нулю функции ускорения. В части (b) показано мгновенное ускорение при минимальной скорости, которая также равна нулю, так как наклон кривой и там равен нулю. Таким образом, для данной функции скорости нули функции ускорения дают либо минимальную, либо максимальную скорость.
между временами
и
.Когда
, среднее ускорение приближается к мгновенному ускорению в момент времени t0. На виде (а) показано мгновенное ускорение для точки на кривой скорости при максимальной скорости. В этой точке мгновенное ускорение представляет собой наклон касательной, который равен нулю. В любой другой момент времени наклон касательной и, следовательно, мгновенное ускорение не были бы равны нулю. (b) То же, что и (a), но показано для мгновенного ускорения при минимальной скорости.
Чтобы проиллюстрировать эту концепцию, рассмотрим два примера.Во-первых, показан простой пример с использованием (Рисунок)(b), графика зависимости скорости от времени (Рисунок), для графического определения ускорения. Этот график изображен на (Рисунок)(а) и представляет собой прямую линию. Соответствующий график зависимости ускорения от времени находится по наклону скорости и показан на (Рисунок)(б). В этом примере функция скорости представляет собой прямую линию с постоянным наклоном, поэтому ускорение является постоянным. В следующем примере функция скорости имеет более сложную функциональную зависимость от времени.
Рисунок 3.15 (a, b) График зависимости скорости от времени является линейным и имеет отрицательный постоянный наклон (a), равный ускорению, показанному на (b). Если мы знаем функциональную форму скорости, v ( t ), мы можем рассчитать мгновенное ускорение a ( t ) в любой момент времени в движении, используя (рисунок).
Пример
Расчет мгновенного ускорения
Частица движется и ускоряется.Функциональная форма скорости равна
.
.
- Найдите функциональную форму ускорения.
- Найти мгновенную скорость в момент времени t = 1, 2, 3 и 5 с.
- Найти мгновенное ускорение в точке т = 1, 2, 3 и 5 с.
- Интерпретируйте результаты (c) с точки зрения направлений векторов ускорения и скорости.
Стратегия
Мы находим функциональную форму ускорения, взяв производную функции скорости.Затем вычисляем значения мгновенной скорости и ускорения по заданным функциям для каждого. Для части (d) нам нужно каждый раз сравнивать направления скорости и ускорения.
Решение
,
,
,
,
,
,
- При t = 1 с, скорость
положительна, а ускорение положительно, поэтому и скорость, и ускорение имеют одинаковое направление.
 Частица движется быстрее.
Частица движется быстрее.
При t = 2 с скорость возросла до
, где оно максимальное, что соответствует времени, когда ускорение равно нулю. Мы видим, что максимальная скорость возникает, когда наклон функции скорости равен нулю, что равно нулю функции ускорения.
При t = 3 с, скорость
и ускорение отрицательное. Частица уменьшила свою скорость, и вектор ускорения отрицателен.Частица замедляется.
При t = 5 с, скорость
и ускорение становится все более отрицательным. Между моментами времени t = 3 с и t = 5 с скорость частицы уменьшилась до нуля, а затем стала отрицательной, тем самым изменив свое направление. Теперь частица снова ускоряется, но в противоположном направлении.
Мы можем увидеть эти результаты графически на (Рисунок).
Рисунок 3.16 (a) Скорость в зависимости от времени.Касательные линии указаны в моменты времени 1, 2 и 3 с. Наклоны касательных линий являются ускорениями. При t = 3 с скорость положительна. При t = 5 с скорость отрицательна, что указывает на то, что частица изменила направление. (b) Ускорение в зависимости от времени. Сравнивая значения ускорений, заданные черными точками, с соответствующими наклонами касательных (наклоны линий, проведенных через черные точки) на (а), мы видим, что они идентичны.
Наклоны касательных линий являются ускорениями. При t = 3 с скорость положительна. При t = 5 с скорость отрицательна, что указывает на то, что частица изменила направление. (b) Ускорение в зависимости от времени. Сравнивая значения ускорений, заданные черными точками, с соответствующими наклонами касательных (наклоны линий, проведенных через черные точки) на (а), мы видим, что они идентичны.Значение
Проводя численный и графический анализ скорости и ускорения частицы, мы можем многое узнать о ее движении.Численный анализ дополняет графический анализ, давая общее представление о движении. Ноль функции ускорения соответствует максимуму скорости в этом примере. Также в этом примере, когда ускорение положительно и в том же направлении, что и скорость, скорость увеличивается. По мере того, как ускорение стремится к нулю, со временем становясь отрицательным, скорость достигает максимума, после чего начинает уменьшаться. Если мы подождем достаточно долго, скорость также станет отрицательной, указывая на изменение направления. Реальным примером такого движения является автомобиль, скорость которого увеличивается до максимума, после чего он начинает замедляться, останавливается, а затем меняет направление.
Реальным примером такого движения является автомобиль, скорость которого увеличивается до максимума, после чего он начинает замедляться, останавливается, а затем меняет направление.
Проверьте свое понимание
Самолет приземляется на взлетно-посадочной полосе, направляясь на восток. Опишите его ускорение.
[reveal-answer q=”fs-id1168327963777″]Показать решение[/reveal-answer]
[скрытый ответ a=”fs-id1168327963777″]
Если принять восток за положительное значение, то ускорение самолета будет отрицательным, поскольку он движется на запад.Он также замедляется; его ускорение противоположно направлению его скорости.
[/скрытый ответ]
Почувствуйте ускорение
Вы, наверное, привыкли ощущать ускорение, когда входите в лифт или нажимаете на педаль газа в машине. Однако ускорение происходит и со многими другими объектами в нашей Вселенной, с которыми у нас нет прямого контакта. (Рисунок) представлены ускорения различных объектов. Мы можем видеть, что величины ускорений простираются на многие порядки.
Мы можем видеть, что величины ускорений простираются на многие порядки.
| Ускорение | Значение (м/с 2 ) |
|---|---|
| Скоростной поезд | 0,25 |
| Лифт | 2 |
| Гепард | 5 |
| Объект в свободном падении без сопротивления воздуха у поверхности Земли | 9,8 |
| Максимум космического корабля во время запуска | 29 |
| Пик парашютиста при нормальном раскрытии парашюта | 59 |
| Выход самолета F16 из пикирования | 79 |
| Катапультирование кресла взрывом из самолета | 147 |
| Спринт ракета | 982 |
| Самое быстрое пиковое ускорение ракетных саней | 1540 |
| Прыгающая блоха | 3200 |
| Удар битой по бейсбольному мячу | 30 000 |
| Замыкающие челюсти муравья-ловушки | 1 000 000 |
| Протон в большом адронном коллайдере |
|
В этой таблице мы видим, что типичные ускорения сильно различаются для разных объектов и не имеют ничего общего с размером объекта или его массой. Ускорение также может сильно меняться со временем во время движения объекта. Дрэг-рейсер имеет большое ускорение сразу после старта, но затем оно уменьшается, когда транспортное средство достигает постоянной скорости. Его среднее ускорение может сильно отличаться от его мгновенного ускорения в определенный момент времени во время его движения. (Рисунок) графически сравнивает среднее ускорение с мгновенным ускорением для двух очень разных движений.
Ускорение также может сильно меняться со временем во время движения объекта. Дрэг-рейсер имеет большое ускорение сразу после старта, но затем оно уменьшается, когда транспортное средство достигает постоянной скорости. Его среднее ускорение может сильно отличаться от его мгновенного ускорения в определенный момент времени во время его движения. (Рисунок) графически сравнивает среднее ускорение с мгновенным ускорением для двух очень разных движений.

Резюме
- Ускорение — это скорость изменения скорости.Ускорение — это вектор; оно имеет как величину, так и направление. Единицей ускорения в системе СИ является метр в секунду в квадрате.
- Ускорение может быть вызвано изменением величины или направления скорости, или и тем, и другим.
- Мгновенное ускорение a ( t ) является непрерывной функцией времени и дает ускорение в любой конкретный момент времени во время движения. Он рассчитывается из производной функции скорости. Мгновенное ускорение — это наклон графика зависимости скорости от времени.
- Отрицательное ускорение (иногда называемое замедлением) — это ускорение в отрицательном направлении в выбранной системе координат.
Концептуальные вопросы
Возможно ли, чтобы скорость была постоянной, а ускорение не равно нулю?
[reveal-answer q=”fs-id1168328025381″]Показать решение[/reveal-answer]
[скрытый ответ a = “fs-id1168328025381”]
Нет, в одном измерении постоянная скорость требует нулевого ускорения.
[/скрытый ответ]
Возможно ли, чтобы скорость была постоянной, а ускорение не равно нулю? Объяснять.
Приведите пример, в котором скорость равна нулю, а ускорение — нет.
[reveal-answer q=”fs-id1168328292164″]Показать решение[/reveal-answer]
[скрытый ответ a=”fs-id1168328292164″]
Мяч подброшен в воздух, и его скорость равна нулю в точке броска, но ускорение не равно нулю.
[/скрытый ответ]
Если поезд метро движется влево (имеет отрицательную скорость), а затем останавливается, как направлено его ускорение? Ускорение положительное или отрицательное?
Знаки плюс и минус используются в одномерном движении для указания направления.Каков знак ускорения, уменьшающего модуль отрицательной скорости? положительной скорости?
[reveal-answer q=”fs-id1168328228855″]Показать решение[/reveal-answer]
[скрытый ответ a=”fs-id1168328228855″]
Плюс, минус
[/скрытый ответ]
Гепард может разогнаться из состояния покоя до скорости 30,0 м/с за 7,00 с. Каково его ускорение?
Каково его ускорение?
[reveal-answer q=”fs-id1168328195958″]Показать решение[/reveal-answer]
[скрытый ответ a=”fs-id1168328195958″]
[/скрытый ответ]
Др.Джон Пол Стэпп был офицером ВВС США, изучавшим влияние экстремального ускорения на организм человека. 10 декабря 1954 года Стэпп проехал на ракетных санях, разогнавшись из состояния покоя до максимальной скорости 282 м/с (1015 км/ч) за 5,00 с и резко остановившись всего за 1,40 с. Вычислите его (а) ускорение в направлении его движения и (б) ускорение, противоположное направлению его движения. Выразите каждое из них кратным г (9,80 м/с 2 ), взяв его отношение к ускорению свободного падения.
Нарисуйте график зависимости ускорения от времени, используя следующий график зависимости скорости от времени.
[reveal-answer q=”1811″]Показать ответ[/reveal-answer]
[hidden-answer a=”1811″] [/hidden-answer]
Пассажирка выезжает из гаража задним ходом с ускорением 1,40 м/с 2 . а) За какое время она достигнет скорости 2,00 м/с? б) Если она затем затормозит до остановки через 0,800 с, каково ее ускорение?
а) За какое время она достигнет скорости 2,00 м/с? б) Если она затем затормозит до остановки через 0,800 с, каково ее ускорение?
Предположим, что межконтинентальная баллистическая ракета выходит из состояния покоя до суборбитальной скорости 6.50 км/с за 60,0 с (фактическая скорость и время засекречены). Каково его среднее ускорение в метрах в секунду и кратно g (9,80 м/с 2 )?
[reveal-answer q=”fs-id1168325667515″]Показать решение[/reveal-answer]
[скрытый ответ a=”fs-id1168325667515″]
[/скрытый ответ]
Самолет, стартовав из состояния покоя, движется по взлетно-посадочной полосе с постоянным ускорением в течение 18 с, а затем взлетает со скоростью 60 м/с.Каково среднее ускорение самолета?
Глоссарий
- среднее ускорение
- скорость изменения скорости; изменение скорости во времени
- мгновенное ускорение
- ускорение в определенный момент времени
Веб-сайт класса физики
Равномерное круговое движение
Равномерное круговое движение можно описать как движение объекта по окружности с постоянной скоростью. Когда объект движется по кругу, он постоянно меняет свое направление. Во всех случаях объект движется по касательной к окружности. Поскольку направление вектора скорости совпадает с направлением движения объекта, вектор скорости также направлен по касательной к окружности. Анимация справа изображает это с помощью векторной стрелки.
Когда объект движется по кругу, он постоянно меняет свое направление. Во всех случаях объект движется по касательной к окружности. Поскольку направление вектора скорости совпадает с направлением движения объекта, вектор скорости также направлен по касательной к окружности. Анимация справа изображает это с помощью векторной стрелки.
Объект, движущийся по кругу, ускоряется. Ускоряющиеся объекты — это объекты, которые изменяют свою скорость — либо скорость (т.е., модуль вектора скорости) или направление. Объект, совершающий равномерное круговое движение, движется с постоянной скоростью. Тем не менее, он ускоряется из-за изменения направления. Направление ускорения внутрь. Анимация справа изображает это с помощью векторной стрелки.
Окончательной характеристикой движения объекта, совершающего равномерное круговое движение, является результирующая сила. Суммарная сила, действующая на такой объект, направлена к центру окружности.Чистая сила называется направленной внутрь или центростремительной силой. Без такой внутренней силы объект продолжал бы движение по прямой линии, никогда не отклоняясь от своего направления. Тем не менее, с внутренней результирующей силой, направленной перпендикулярно вектору скорости, объект всегда меняет свое направление и испытывает внутреннее ускорение.
Без такой внутренней силы объект продолжал бы движение по прямой линии, никогда не отклоняясь от своего направления. Тем не менее, с внутренней результирующей силой, направленной перпендикулярно вектору скорости, объект всегда меняет свое направление и испытывает внутреннее ускорение.
Для получения дополнительной информации о физических описаниях движения посетите Учебное пособие по физике. Подробная информация доступна по следующим темам:
СкоростьУскорение
Суммарная сила и ускорение
Круговое движение и тангенциальная скорость
Круговое движение и ускорение
Требование к центростремительной силе
Равномерное ускорение — определение, уравнение, примеры и часто задаваемые вопросы
Чтобы определить законы, управляющие различными изменениями, происходящими в телах по отношению ко времени, мы должны уметь описывать эти изменения и каким-то образом записывать их на будущее. использованная литература.Самый простой способ наблюдения за телом — это кажущиеся изменения его положения по отношению ко времени, которые известны как Движение наблюдаемого объекта. Скорость изменения смещения объекта известна как скорость объекта.
использованная литература.Самый простой способ наблюдения за телом — это кажущиеся изменения его положения по отношению ко времени, которые известны как Движение наблюдаемого объекта. Скорость изменения смещения объекта известна как скорость объекта.
Следующим шагом в разработке уравнений Движения является введение еще одного важного понятия, которое выходит за рамки понятия Скорости к понятию изменения Скорости. Скорость изменения скорости известна как ускорение частицы.В этой статье мы подробно узнаем о том, что такое равномерно ускоренное движение.
Что такое равномерное ускорение
Мы знаем, что ускорение — это скорость изменения скорости во времени. Ускорение является векторной величиной, и направление ускорения будет таким же, как направление скорости изменения скорости. Единица СИ для Ускорения — м/с2, а размеры Ускорения — M0 L1T -2 .
Мы знакомы с концепцией Равномерного Движения, если объект проходит одинаковое Перемещение за равный интервал времени, говорят, что он подвергается Равномерному Движению. Теперь вопрос в том, что подразумевается под равномерным ускорением?
Теперь вопрос в том, что подразумевается под равномерным ускорением?
Определить равноускоренное движение
Чтобы ответить на определение равноускоренного движения, давайте сначала подробно разберемся, что такое равноускоренное движение. Как следует из самого названия, равномерно ускоренное движение означает, что объект или тело обладают постоянным ускорением. Постоянное ускорение не означает нулевую скорость. Таким образом, определение равномерного ускорения или определения равномерного ускорения гласит, что если тело движется так, что величина изменения его скорости за равные промежутки времени будет постоянной.
Другими словами, определение движения с равномерным ускорением — это когда объект движется по прямой линии, а изменение его скорости в течение периода времени или интервала остается постоянным. Из определения равномерно ускоренного движения мы понимаем, что равномерное ускорение можно наблюдать в прямолинейном движении.
Для Ускорения является Единым примером Движение свободно падающего тела Ускорение тела будет единственным Ускорением за счет силы тяжести.Если мы построим график зависимости скорости от времени, мы получим прямую линию, весь наклон даст необходимое ускорение.
(ImageWill будет загружены в ближайшее время)
(ImageWill будет загружено в ближайшее время)
сейчас, еще несколько примеров единого ускорения, как указано ниже:
шарик с поворотом наклона .
Когда велосипедист едет на велосипеде по склону, где задействованы обе педали.2\]
Где,
u – Начальная скорость тела
a – Ускорение тела
t – Интервал времени
2.
 Уравнение скорости:
Уравнение скорости:⇒ v = u + at
Где,
v – Конечная скорость тела
u – Начальная скорость тела
a – Ускорение тела
t – Интервал времени
И, у нас также есть другое уравнение для скорости в слагаемое Перемещения:
⇒ v2 = u2 + 2as
Где,
v – Конечная скорость тела
u – Начальная скорость тела
а – Ускорение тела
с – Расстояние покрыто
Характеристики равномерно ускоренного движения:
Если направление ускорения и изменения скорости одинаково, то это приведет к положительному ускорению.
В то же время, если направление Ускорения и изменения Скорости различны или противоположны, то это приведет к отрицательному Ускорению, известному как замедление или замедление.

При положительном Ускорении скорость объекта будет либо увеличиваться, либо уменьшаться, а при отрицательном Ускорении скорость объекта будет замедляться, поэтому это известно как замедление.
Примечание:
Теперь, чтобы понять равномерное ускорение в деталях, необходимо ответить на вопрос: является ли равномерно ускоренное движение равномерным? Равномерное ускорение и равномерное движение — одно и то же?
Ответ на этот вопрос: Равномерное движение и Равномерное ускорение полностью отличаются друг от друга.Мы знаем, что когда объект проходит одинаковое Смещение за равный интервал времени, говорят, что он совершает Равномерное Движение, в то время как Равномерное Ускорение возникает, когда объект движется по прямой линии и его Скорость не изменяется за период времени. изменяться или оставаться постоянными.
Поэтому мы всегда должны помнить, что Равномерное Ускорение — это не то же самое, что Равномерное Движение.

Неравномерное ускорение
Неравномерное ускорение относится к противоположному равномерному ускорению.Мы знаем, что равномерное ускорение означает, что ускорение остается постоянным, его изменение скорости будет постоянным в течение определенного периода времени. В то время как при неравномерном ускорении изменение скорости не будет таким же. Направление скорости и величина ускорения будут меняться со временем.
Например, в повседневной жизни мы видим, что при вождении автомобиля или велосипеда по криволинейной дороге или в плотном потоке скорость автомобиля постоянно меняется. Если мы построим график зависимости скорости от времени, мы получим неравномерную кривую.
(изображение будет загружено в ближайшее время)
(изображение будет загружено в ближайшее время)
примеры:
1.
 Человек, начиная с отдыха, путешествует 30 м с постоянным ускорением 10 м / с2 Сколько времени это занимает?
Человек, начиная с отдыха, путешествует 30 м с постоянным ускорением 10 м / с2 Сколько времени это занимает?Сол: Человек начинает свой путь с отдыха, тогда начальная скорость человека будет равна нулю. Дано, что человек проходит расстояние 30 м с постоянным ускорением 10 м/с2
Теперь нас просят рассчитать время, необходимое для преодоления этого расстояния.2\]
⇒ 5t2 = 30
⇒ t2 = 6
⇒ t = 2,45 с
Следовательно, для преодоления этого расстояния требуется 2,45 с.
2. Автомобиль, стартовавший с места, разогнался со скоростью 9 м/с2 в течение 9 секунд.
а. Каково будет положение автомобиля по истечении 9 секунд?
б. Какой будет скорость автомобиля через 9 секунд?
Sol: Учитывая, что автомобиль движется с постоянным ускорением 9 м/с2 в течение 9 секунд.
а. Нас просят рассчитать положение автомобиля по истечении 9 секунд.
 2\]
2\]⇒ X = 364,5 м
Следовательно, положение автомобиля в конце 9 секунд будет на расстоянии 364,5 м от начального положения.
б. Вторая часть вопроса требует скорости автомобиля в конце 9 секунд. Дано, что начальная скорость автомобиля равна нулю, так как дано, что он стартует с места. Предположим, что его начальное положение равно нулю.
Теперь из уравнения Движения имеем:
⇒ v = u + at ….(1)
Где,
v – конечная скорость тела
u – начальная скорость тела
а – Ускорение тела
t – Интервал времени
Подставляя данные значения в уравнение (1) получаем,
⇒ v = 0 + (9)(9) = 81 м/с
Следовательно, Скорость автомобиля по истечении 9 секунд равна 81 м/с.
Введение:
Задумывались ли вы когда-нибудь, что даже после того, как Земля движется вокруг Солнца по круговой орбите, вы никогда не чувствовали движения, оставаясь здесь, на Земле? Что ж, в этом есть логика.
 Движение, которое вы не можете почувствовать, происходит из-за возникающего равномерного ускорения. Ускорение — это Движение, при котором объект, получая силу, движется вперед. Это ускорение может быть разных типов. Здесь, в этом руководстве через Vedantu, студенты смогут узнать больше об равномерном ускорении — определении, уравнении, примерах и часто задаваемых вопросах, а также о том, как они влияют на движение определенных объектов во вселенной.
Движение, которое вы не можете почувствовать, происходит из-за возникающего равномерного ускорения. Ускорение — это Движение, при котором объект, получая силу, движется вперед. Это ускорение может быть разных типов. Здесь, в этом руководстве через Vedantu, студенты смогут узнать больше об равномерном ускорении — определении, уравнении, примерах и часто задаваемых вопросах, а также о том, как они влияют на движение определенных объектов во вселенной.Типы ускорения, основанные на увеличении или уменьшении:
Положительное ускорение:
Говорят, что тело испытывает положительное ускорение, когда скорость тела увеличивается с течением времени. Это означает, что график, построенный для данного Ускорения, будет иметь положительный наклон.
Отрицательное ускорение:
Говорят, что тело испытывает отрицательное ускорение, когда скорость тела уменьшается с течением времени.
 Это означает, что при построении графика скорость-время будет присутствовать отрицательный наклон.
Это означает, что при построении графика скорость-время будет присутствовать отрицательный наклон.Нулевое ускорение:
Говорят, что тело имеет нулевое ускорение, когда оно испытывает постоянную во времени скорость или находится в состоянии покоя. В этом случае график будет иметь наклон, равный нулю.
Что такое равноускоренное движение?
Равномерно ускоренное движение или постоянное ускорение — это движение с постоянной и неизменной скоростью.Равномерно ускоренное движение может включать или не включать разницу в скорости объекта.
Ускорение объекта означает, что в направлении ускорения этого объекта действует результирующая сила. Кроме того, объект иногда, но не всегда, имеет изменение скорости. Например, говорят, что объект, который падает в вакууме под действием силы тяжести, имеет равномерное ускорение и изменение скорости. Напротив, планета, которая вращается вокруг Солнца по круговой траектории без изменения скорости, по-прежнему имеет равномерное ускорение, но без сопутствующего изменения скорости.

Ускорение и скорость В физике ускорение — это тип векторной величины. Ученые описывают его как скорость или скорость, с которой изменяется скорость объекта. Изменение скорости означает, что объект ускоряется. Например, автомобиль, который разгоняется от 60 миль в час до 80 миль в час, ускоряется. Изменение скорости необходимо для изменения скорости. Например, автомобиль, движущийся с постоянной скоростью 70 миль в час, не имеет изменения скорости.Скорость измеряется как скорость, с которой объект изменяет скорость, но не является мерой самой скорости. Например, объект, движущийся со скоростью 80 миль в час, не обязательно имеет другую скорость, чем объект, движущийся со скоростью 30 миль в час. Автомобиль, движущийся со скоростью 80 миль в час, движется быстро, но не ускоряется, пока его скорость не изменится. Всякий раз, когда скорость автомобиля изменяется, говорят, что он ускоряется.
Ускоренное движение Ускоренное движение называется постоянным ускорением.
 Он определяется как изменение, когда объект изменяет свою скорость на одну и ту же величину каждую секунду. Однако объект с постоянным ускорением не обязательно имеет постоянную скорость. Объект ускоряется или ускоряется, если он меняет свою скорость каждую секунду, независимо от того, является ли его изменение скорости постоянным или переменным. Автомобиль, который разгоняется от 80 миль в час до 90 миль в час в течение 10 секунд, например, имеет постоянную скорость, в то время как автомобиль, который разгоняется от 80 миль в час до 90 миль в час с различной скоростью в течение курса 10 секунд имеет переменную скорость.Объект с постоянной скоростью, напротив, не ускоряется, даже если он движется со скоростью 80 миль в час.
Он определяется как изменение, когда объект изменяет свою скорость на одну и ту же величину каждую секунду. Однако объект с постоянным ускорением не обязательно имеет постоянную скорость. Объект ускоряется или ускоряется, если он меняет свою скорость каждую секунду, независимо от того, является ли его изменение скорости постоянным или переменным. Автомобиль, который разгоняется от 80 миль в час до 90 миль в час в течение 10 секунд, например, имеет постоянную скорость, в то время как автомобиль, который разгоняется от 80 миль в час до 90 миль в час с различной скоростью в течение курса 10 секунд имеет переменную скорость.Объект с постоянной скоростью, напротив, не ускоряется, даже если он движется со скоростью 80 миль в час.Расчет ускоренного движения Поскольку объекты всегда меняют свою скорость, редко когда объект падает с действительно постоянной скоростью ускорения. Объект в свободном падении, например, обычно ускоряется при падении. Пока он преодолевает определенное расстояние, чтобы добраться из одной точки в другую, он может менять свою скорость, путешествуя по воздуху.




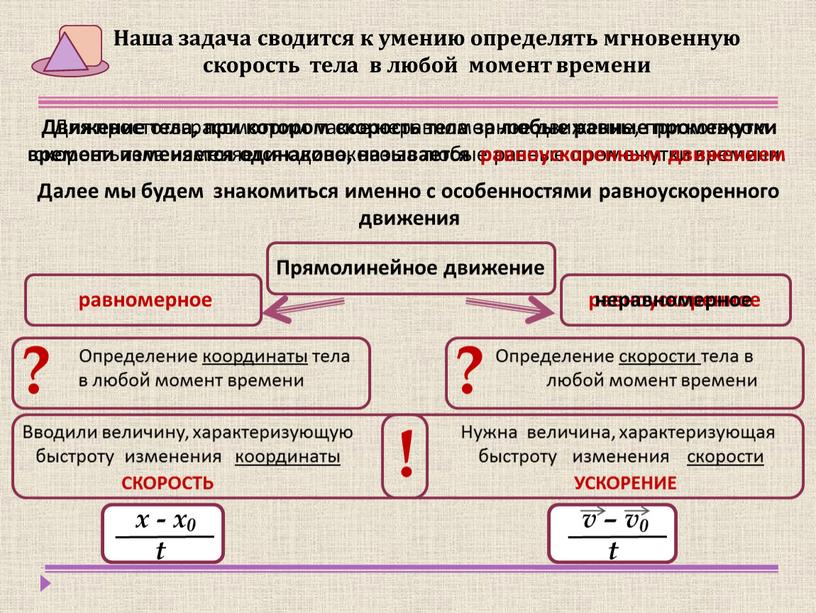
 1b показан график зависимости положения от времени для объекта, движущегося с возрастающей скоростью.Здесь мы можем нарисовать график, в котором мы соединяем точки сплошными линиями, обозначенными красными линиями на рис. 1б. Если бы мы измеряли положение объекта за меньшие промежутки времени, мы бы увидели более гладкую кривую, как показано синей кривой. Средняя скорость между двумя точками
1b показан график зависимости положения от времени для объекта, движущегося с возрастающей скоростью.Здесь мы можем нарисовать график, в котором мы соединяем точки сплошными линиями, обозначенными красными линиями на рис. 1б. Если бы мы измеряли положение объекта за меньшие промежутки времени, мы бы увидели более гладкую кривую, как показано синей кривой. Средняя скорость между двумя точками 2, мгновенная скорость и рассчитанная средняя скорость имеют одно и то же значение в это среднее время,
2, мгновенная скорость и рассчитанная средняя скорость имеют одно и то же значение в это среднее время, Таким образом, вы можете найти ускорение, рассматривая данные за два последовательных интервала времени:
Таким образом, вы можете найти ускорение, рассматривая данные за два последовательных интервала времени:

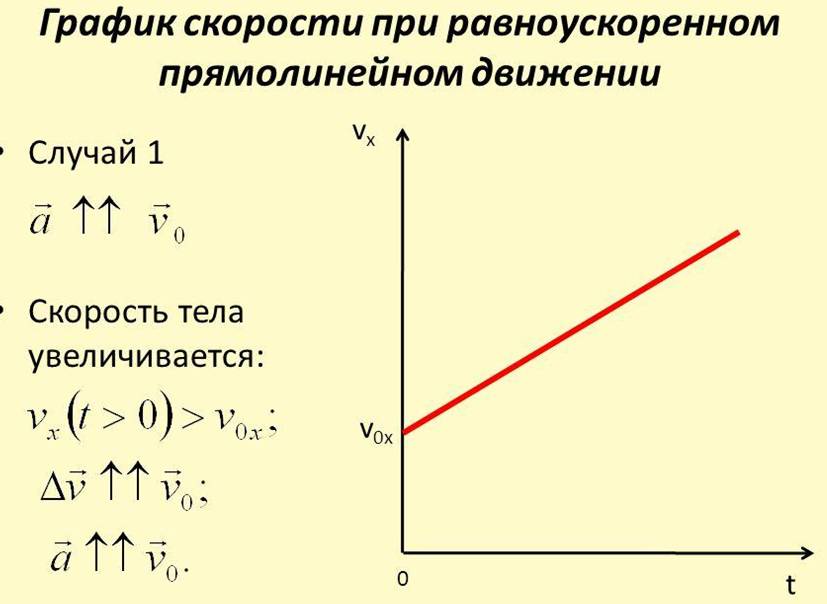
 Таблица, которая была пустой на рис. 6, теперь будет заполнена данными, содержащими два столбца. В первом столбце указаны моменты времени (измеряемые в секундах), когда передние фронты темных полос прошли через фотозатвор, а во втором столбце приведены отсчеты, т. е. количество прерываний луча. См. рис. 8.
Таблица, которая была пустой на рис. 6, теперь будет заполнена данными, содержащими два столбца. В первом столбце указаны моменты времени (измеряемые в секундах), когда передние фронты темных полос прошли через фотозатвор, а во втором столбце приведены отсчеты, т. е. количество прерываний луча. См. рис. 8. Принятое значение этого ускорения составляет 9,81 м/с 2 . Поскольку единственной силой, действующей на штакетник во время его свободного падения, была сила тяжести, найденное вами ускорение должно быть ускорением свободного падения.
Принятое значение этого ускорения составляет 9,81 м/с 2 . Поскольку единственной силой, действующей на штакетник во время его свободного падения, была сила тяжести, найденное вами ускорение должно быть ускорением свободного падения. Введите это значение в рабочий лист.
Введите это значение в рабочий лист.
 Этот вид движения называется равноускоренным движением .Объект, падающий под действием силы тяжести вблизи поверхности Земли, например яблоко на рис. 24, дает приблизительную реализацию такого движения. (Сопротивление воздуха, увеличивающееся со скоростью, препятствует тому, чтобы ускорение в таких случаях было действительно постоянным.) Более точную реализацию равноускоренного движения дает объект, падающий под действием силы тяжести вблизи поверхности безвоздушного тела, такого как Луна ( см. рис. 38) или падающим предметом в вакуумной (т.е. безвоздушной) градирне или шахте, описанной в разделе 1 этого курса.
Этот вид движения называется равноускоренным движением .Объект, падающий под действием силы тяжести вблизи поверхности Земли, например яблоко на рис. 24, дает приблизительную реализацию такого движения. (Сопротивление воздуха, увеличивающееся со скоростью, препятствует тому, чтобы ускорение в таких случаях было действительно постоянным.) Более точную реализацию равноускоренного движения дает объект, падающий под действием силы тяжести вблизи поверхности безвоздушного тела, такого как Луна ( см. рис. 38) или падающим предметом в вакуумной (т.е. безвоздушной) градирне или шахте, описанной в разделе 1 этого курса. Из этого следует, что график зависимости скорости от времени должен иметь одинаковый градиент во всех точках и, следовательно, должен представлять собой прямую линию, как показано на рисунке 39.Обратите внимание, что знак ускорения определяет, имеет ли график скорость-время наклон вверх или вниз, а значение ускорения определяет точное значение градиента. Однако ускорение не определяет начальное значение v x , поэтому мы произвольно выбрали точку на оси v x для представления этого значения и обозначили ее u х . От рисунка 38, вывод, что если
Из этого следует, что график зависимости скорости от времени должен иметь одинаковый градиент во всех точках и, следовательно, должен представлять собой прямую линию, как показано на рисунке 39.Обратите внимание, что знак ускорения определяет, имеет ли график скорость-время наклон вверх или вниз, а значение ускорения определяет точное значение градиента. Однако ускорение не определяет начальное значение v x , поэтому мы произвольно выбрали точку на оси v x для представления этого значения и обозначили ее u х . От рисунка 38, вывод, что если На самом деле, при таком графике скорость-время, как на рис. 39, соответствующий график координаты-времени будет иметь общую форму, показанную на рис. 40.
На самом деле, при таком графике скорость-время, как на рис. 39, соответствующий график координаты-времени будет иметь общую форму, показанную на рис. 40. Поскольку площадь треугольника равна половине произведения его высоты на длину основания, отсюда следует, что смещение от x 0 в момент времени T будет равно
Поскольку площадь треугольника равна половине произведения его высоты на длину основания, отсюда следует, что смещение от x 0 в момент времени T будет равно
 Это редко достигается в реальном мире из-за дополнительных внешних сил, создающих вариативность того, насколько быстро или медленно объект ускоряется во время всего своего движения.Чтобы упростить задачу, мы пока не будем заморачиваться ни с одним из них.
Это редко достигается в реальном мире из-за дополнительных внешних сил, создающих вариативность того, насколько быстро или медленно объект ускоряется во время всего своего движения.Чтобы упростить задачу, мы пока не будем заморачиваться ни с одним из них.
 Частица движется быстрее.
Частица движется быстрее.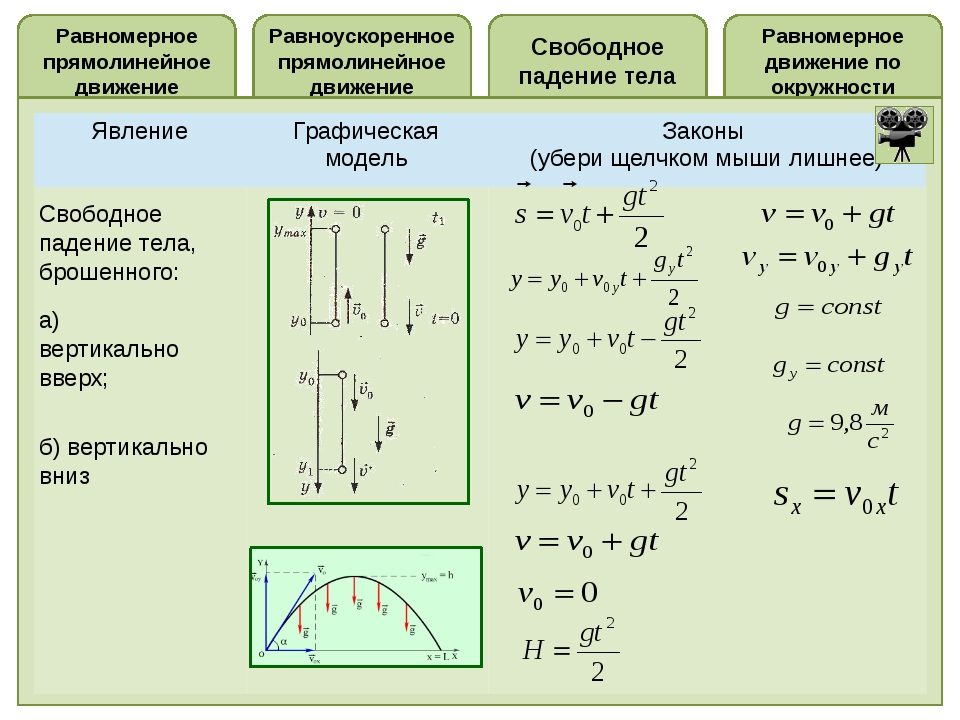 Уравнение скорости:
Уравнение скорости:

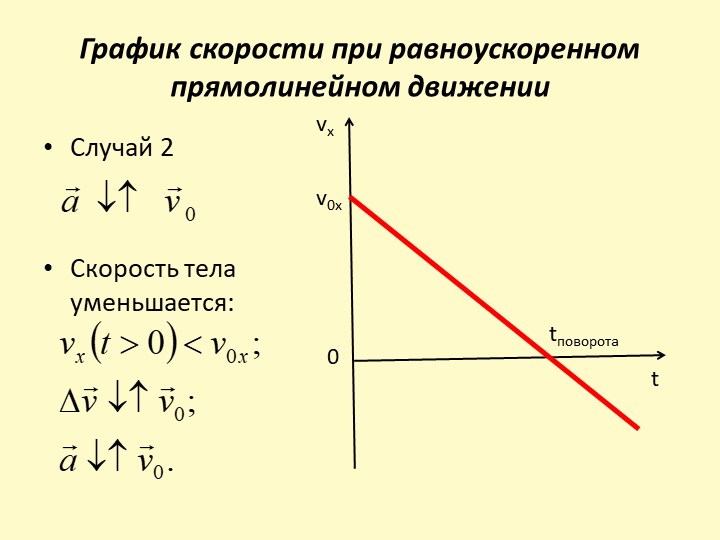 Человек, начиная с отдыха, путешествует 30 м с постоянным ускорением 10 м / с2 Сколько времени это занимает?
Человек, начиная с отдыха, путешествует 30 м с постоянным ускорением 10 м / с2 Сколько времени это занимает? 2\]
2\] Движение, которое вы не можете почувствовать, происходит из-за возникающего равномерного ускорения. Ускорение — это Движение, при котором объект, получая силу, движется вперед. Это ускорение может быть разных типов. Здесь, в этом руководстве через Vedantu, студенты смогут узнать больше об равномерном ускорении — определении, уравнении, примерах и часто задаваемых вопросах, а также о том, как они влияют на движение определенных объектов во вселенной.
Движение, которое вы не можете почувствовать, происходит из-за возникающего равномерного ускорения. Ускорение — это Движение, при котором объект, получая силу, движется вперед. Это ускорение может быть разных типов. Здесь, в этом руководстве через Vedantu, студенты смогут узнать больше об равномерном ускорении — определении, уравнении, примерах и часто задаваемых вопросах, а также о том, как они влияют на движение определенных объектов во вселенной. Это означает, что при построении графика скорость-время будет присутствовать отрицательный наклон.
Это означает, что при построении графика скорость-время будет присутствовать отрицательный наклон.
 Он определяется как изменение, когда объект изменяет свою скорость на одну и ту же величину каждую секунду. Однако объект с постоянным ускорением не обязательно имеет постоянную скорость. Объект ускоряется или ускоряется, если он меняет свою скорость каждую секунду, независимо от того, является ли его изменение скорости постоянным или переменным. Автомобиль, который разгоняется от 80 миль в час до 90 миль в час в течение 10 секунд, например, имеет постоянную скорость, в то время как автомобиль, который разгоняется от 80 миль в час до 90 миль в час с различной скоростью в течение курса 10 секунд имеет переменную скорость.Объект с постоянной скоростью, напротив, не ускоряется, даже если он движется со скоростью 80 миль в час.
Он определяется как изменение, когда объект изменяет свою скорость на одну и ту же величину каждую секунду. Однако объект с постоянным ускорением не обязательно имеет постоянную скорость. Объект ускоряется или ускоряется, если он меняет свою скорость каждую секунду, независимо от того, является ли его изменение скорости постоянным или переменным. Автомобиль, который разгоняется от 80 миль в час до 90 миль в час в течение 10 секунд, например, имеет постоянную скорость, в то время как автомобиль, который разгоняется от 80 миль в час до 90 миль в час с различной скоростью в течение курса 10 секунд имеет переменную скорость.Объект с постоянной скоростью, напротив, не ускоряется, даже если он движется со скоростью 80 миль в час.