Мгновенная скорость ускорение 9 класс: Конспект и презентация урока “Мгновенная скорость ускорение” (9 класс)

9 класс. Конспект урока №05/05. Прямолинейное равноускоренное движение. Ускорение.

Физика.

9 класс.

Урок №05/05.

Прямолинейное равноускоренное движение. Ускорение.

Цель урока. Рассмотреть прямолинейное равноускоренное движение и его характеристики; ввести физические понятия «мгновенная скорость», «ускорение»; научить решать задачи на расчёт ускорения, времени движения, начальной и конечной скоростей движения.

Демонстрации. Определение ускорения прямолинейного равноускоренного движения.

Содержание нового материала. Мгновенная скорость. Равноускоренное движение. Ускорение.

Планируемые результаты обучения.

Метапредметные: овладеть навыками самостоятельного приобретения знаний о прямолинейном равноускоренном движении тел, регулятивными УУД при решении расчетных задач.

Личностные: сформировать познавательный интерес и творческую инициативу, самостоятельность в приобретении новых знаний об ускорении тела при прямолинейном неравномерном движении, ценностное отношение друг к другу, к учителю, к результатам обучения; уметь принимать самостоятельные решения, обосновывать и оценивать результаты своих действий.

Общие предметные: проводить наблюдения, планировать и проводить эксперимент по изучению прямолинейного равноускоренного движения; объяснять полученные результаты и делать выводы; применять теоретические знания на практике; решать расчетные задачи по определению ускорения, времени, начальной и конечной скоростей движения.

Частные предметные: объяснять физический смысл понятий: мгновенная скорость, ускорение; приводить примеры равноускоренного движения; записывать формулу для определения ускорения в векторном виде и в виде проекций на выбранную ось; применять формулу для расчёта ускорения при решении расчётных задач.

Ход урока.

1. Проверка домашнего задания.

Упражнение 4.

1. Может ли график зависимости модуля вектора скорости от времени располагаться под осью Оt (то есть в области отрицательных значений оси скорости)?

(Да.)

2. Постройте графики зависимости проекций векторов скорости от времени для трёх автомобилей, движущихся прямолинейно и равномерно, если два из них едут в одном направлении, а третий — навстречу им. Скорость первого автомобиля равна 60км/ч, второго — 80км/ч, а третьего — 90км/ч.

2. Опрос.

1. Что называется скоростью равномерного прямолинейного движения?

(Скорость равномерного прямолинейного движения – это постоянная векторная величина, равная отношению перемещения тела за любой промежуток времени к значению этого промежутка.

)

2. Как найти проекцию вектора перемещения тела?

(

3. Что представляет собой график скорости?

(График скорости – график зависимости скорости от времени.)

4. Как найти модуль проекции перемещения по графику скорости?

(

При прямолинейном равномерном движении тела модуль вектора его перемещения численно равен площади прямоугольника, заключённого между графиком скорости, осью Оt и перпендикулярами к этой оси, восставленными из точек, соответствующих моментам начала и конца наблюдения (в данном случае из точек О и t₁). Часто эту площадь называют площадью под графиком скорости.)

3. Изучение нового материала.

1. Простейший вид неравномерного движения – прямолинейное равноускоренное движение, при котором тело движется вдоль прямой линии, а проекция вектора скорости за любые равные промежутки времени меняется одинаково (при этом модуль вектора скорости может как увеличиваться, так и уменьшаться).

2. Определение: «Мгновенная скорость – скорость в каждой конкретной точке траектории в соответствующий момент времени.»

3. Определение: «Ускорением тела при его равноускоренном движении называется векторная физическая величина, равная отношению изменения скорости к промежутку времени, за который это изменение произошло.»

– ускорение

– изменение скорости

t – промежуток времени, за который произошло изменение скорости

– ускорение

– начальная скорость тела

– конечная скорость тела

t – промежуток времени, за который произошло изменение скорости

a_x – проекция вектора ускорения на ось OX

v_x – проекция вектора конечной скорости на ось OX

v_0x – проекция вектора начальной скорости на ось OX

t – промежуток времени, за который произошло изменение скорости

Равноускоренное движение – это движение с постоянным ускорением.

4. Модуль вектора ускорения показывает, на сколько меняется модуль вектора скорости в каждую единицу времени.

5. В СИ единицей ускорения является метр на секунду в квадрате

[a]=1м/с²

6.

Если векторы скорости и ускорения движущегося тела направлены в одну сторону, то модуль вектора скорости тела увеличивается.

Если векторы скорости и ускорения движущегося тела направлены в противоположные стороны, то модуль вектора скорости тела уменьшается.

4. Решение задач.

М.1424(46). Может ли тело иметь постоянную по модулю скорость при изменении вектора скорости?

(Да. Например, при равномерном движении по окружности.)

М.1430(52).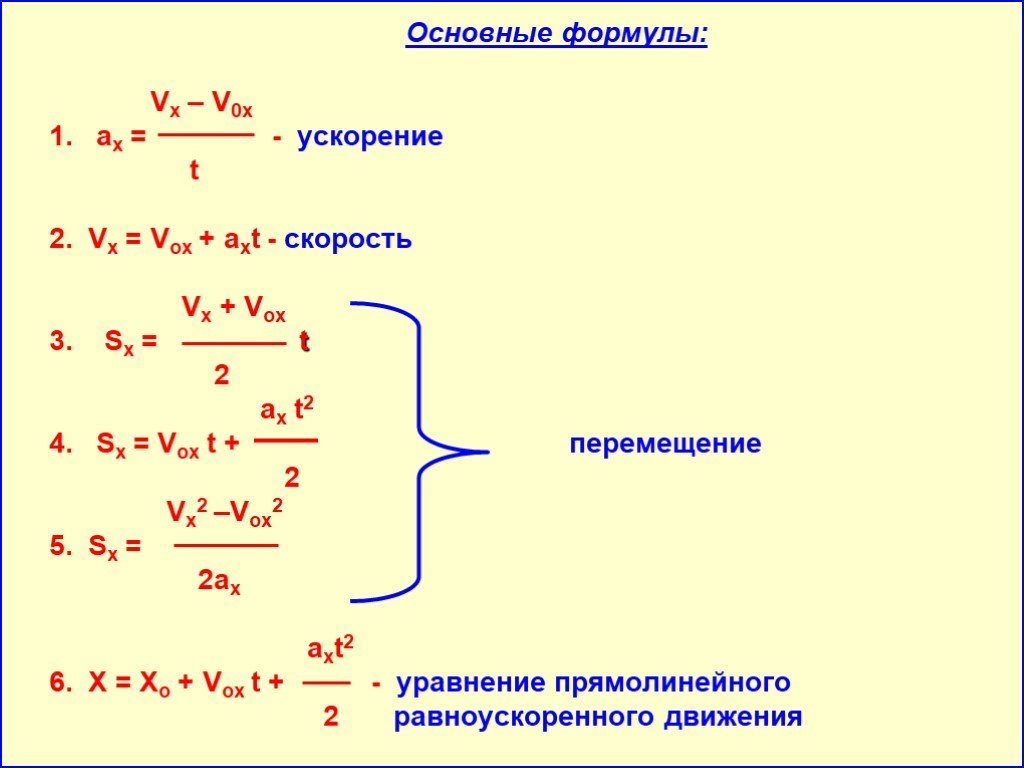 С каким ускорением движется гоночный автомобиль, если его скорость за 6с увеличивается от 144км/ч до 216км/ч?

5. Самостоятельная работа.

9 класс.

К уроку №5.

Самостоятельная работа.

Вариант 1.

1. Имеет ли материальная точка размеры?

2. Стул передвинули сначала на 6м, а затем ещё на 8м. Чему равен пройденный путь?

3. Тело переместилось из точки А с координатой x_A=26м в точку В с координатой х_B=-4м. Определите проекцию перемещения тела на ось ОХ.

4. Скорость акулы равна 8,3м/с, а скорость дельфина — 72км/ч. Кто из них имеет бóльшую скорость?

——————————————————————————————————-

9 класс.

К уроку №5.

Самостоятельная работа.

Вариант 2.

1. Обладает ли материальная точка массой?

2. Стрела, выпущенная вертикально вверх, достигла максимальной высоты 15м и упала на то же место, откуда была выпущена. Чему равен модуль её перемещения?

3. Тело переместилось из точки А с координатой x_A=-24м в точку B с координатой х_B=14м. Определите проекцию перемещения тела на ось ОХ.

4. Скорость иглохвостого стрижа равна 180км/ч, а скорость сокола-сапсана — 4800м/мин. Кто из них имеет бóльшую скорость?

——————————————————————————————————-

9 класс.

К уроку №5.

Самостоятельная работа.

Вариант 3.

1. Имеет ли материальная точка размеры?

2. Самолёт пролетел по прямой 300км, затем повернул под прямым углом и пролетел ещё 400км. Чему равен модуль вектора перемещения?

3. Материальная точка движется из пункта А в пункт В с координатой х_B=5м. Определите координату пункта А, если проекция перемещения точки на ось ОХ равна s_x=9м.

4. Гоночный автомобиль может достигать скорости 360км/ч. За какое время такой автомобиль преодолеет 500м?

9 класс.

К уроку №5.

Самостоятельная работа.

Вариант 4.

1. Обладает ли материальная точка массой?

2. Самолёт пролетел по прямой 600км, затем повернул под прямым углом и пролетел 800км. Определите путь самолёта.

3. Поезд движется из пункта А с координатой x_A=-435км в пункт В. Определите координату пункта В, если проекция перемещения точки на ось ОХ равна s_х=165км.

4. Вертолёт Ми-8 достигает скорости 250км/ч. Сколько минут он затратит на перелёт между двумя населёнными пунктами, расположенными на расстоянии 50км?

——————————————————————————————————-

9 класс.

К уроку №5.

Самостоятельная работа.

Вариант 5.

1. Имеет ли материальная точка размеры?

2. Определите проекцию вектора перемещения на ось ОХ.

3. От автостанции с интервалом 0,5мин в одном направлении выехали автобус, а затем автомобиль, скорости которых соответственно 10м/с и 20м/с. На каком расстоянии от автостанции автомобиль догонит автобус?

4. Тело движется вдоль оси ОХ. Проекция его скорости v_х(t) меняется по закону, приведённому на графике. Определите путь, пройденный телом за 2с.

9 класс.

К уроку №5.

Самостоятельная работа.

Вариант 6.

1. Обладает ли материальная точка массой?

2. Определите проекцию вектора перемещения на ось ОУ.

3. Мимо светофора проследовал товарный поезд со скоростью 10м/с. Через полчаса мимо того же светофора в том же направлении проследовал экспресс, скорость которого в 1,5 раза больше, чем у товарного поезда. На каком расстоянии от светофора экспресс нагонит товарный поезд?

4. Тело движется вдоль оси ОХ. Проекция его скорости v_х(t) меняется по закону, приведённому на графике. Определите путь, пройденный телом за 2с.

Ответы.

	1	2	3	4
Вариант 1	Нет, не имеет	14м	-30м	Дельфин
Вариант 2	Да, обладает	0м	38м	Сокол-сапсан
Вариант 3	Нет, не имеет	500км	-4м	5с
Вариант 4	Да, обладает	1400км	-270м	12мин
Вариант 5	Нет, не имеет	-4м	600м	30м
Вариант 6	Да, обладает	-3м	54000м	20м

6.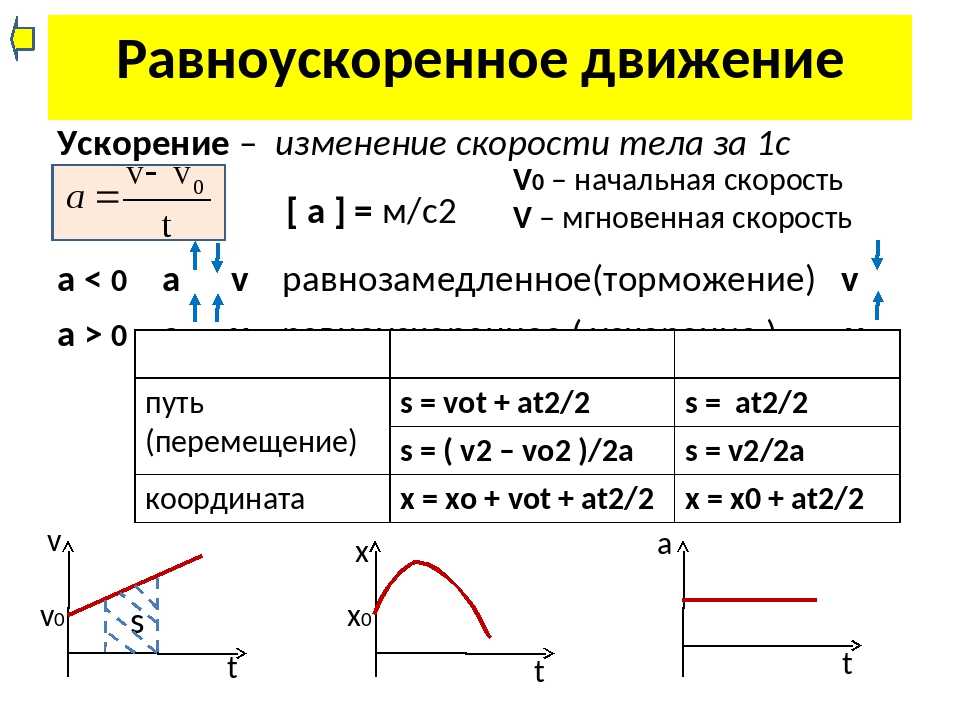 Закрепление материала.

Вопросы после §5.

1. К какому виду движения — равномерному или неравномерному — относится прямолинейное равноускоренное движение?

(Прямолинейное равноускоренное движение – вид неравномерного движения.)

2. Что понимают под мгновенной скоростью неравномерного движения?

(Мгновенная скорость – скорость в каждой конкретной точке траектории в соответствующий момент времени.)

3. Дайте определение ускорения равноускоренного движения. Какова единица ускорения?

(Ускорением тела при прямолинейном равноускоренном движении называется векторная физическая величина, равная отношению изменения скорости к промежутку времени, за который это изменение произошло.

За единицу ускорения в СИ принимается ускорение такого равноускоренного движения, при котором за 1с скорость тела меняется на 1м/с.

В СИ единицей ускорения является метр на секунду в квадрате (1м/с²).)

4. Что такое равноускоренное движение?

(Равноускоренное движение – это движение с постоянным ускорением.)

5. Что показывает модуль вектора ускорения?

(Модуль вектора ускорения показывает, на сколько меняется модуль вектора скорости в каждую единицу времени.)

6. При каком условии модуль вектора скорости движущегося тела увеличивается; уменьшается?

(Если векторы скорости и ускорения движущегося тела направлены в одну сторону, то модуль вектора скорости тела увеличивается, а если в противоположные — уменьшается.)

7. Домашнее задание.

§5.

Упражнение 5(2,3).

100 ballov.kz образовательный портал для подготовки к ЕНТ и КТА

  

Хотите купить новую квартиру и уже нашли несколько подходящих под ваш бюджет вариантов? Не забудьте добавить к стоимости жилья ряд дополнительных расходов, которые вам придется оплатить при покупке недвижимости в Казахстане. Квартиры в Астане и квартиры в Алматы можно посмотреть на korter.kz, где с помощью фильтров можно максимально точно подобрать желаемые варианты.

Что оплачивает покупатель?

Договор купли-продажи недвижимости включает в себя ряд обязательных платежей, независимо от того, где было куплено жилье — на вторичном рынке или в новостройке. Определенную часть расходов должен погасить покупатель. Сумма платежей рассчитывается в зависимости от особенностей сделки и может достигать значительных размеров, поэтому важно перед покупкой подсчитать все расходы.

Дополнительные платежи покупателя при оформлении права собственности:

• услуги нотариуса;
• оплата госпошлины за регистрацию.

Нотариальное оформление договора

Нотариальное оформление договора купли-продажи не является обязательной процедурой, но специалисты рынка недвижимости советуют не пренебрегать услугами нотариуса. Нотариус проверяет стороны сделки, контролирует процесс заключения договора и выступает гарантом безопасности.

Нотариальные услуги имеют фиксированную стоимость. Средняя стоимость нотариального оформления объекта недвижимости в 2023 году составляет 12 МРП, т.е. около 37000 тг. Следует обращать внимание на то, что сумма платы зависит от того, кто является участниками сделки. Если сделка заключается с близким родственником – сумма уменьшается, если с юридическим лицом – увеличивается. 

Как правило, участники сделки делят расходы на оформление поровну. Однако, лучше заранее согласовать этот момент с продавцом недвижимости.

Прямые сделки также предусматривают дополнительные расходы, например, оформление задатка.

Регистрация прав на имущество

При покупке недвижимости покупатель обязуется оплатить государственную пошлину за регистрацию своих прав на имущество в ЦОН. Процедура оформления занимает до 3 рабочих дней. Стоимость данной услуги — 1 073,7 тг. 

Покупатель может заказать услугу ускоренной регистрации права собственности. Процесс внесения информации в реестр займет 1 день. Стоимость ускоренной регистрации — 5000 тг.

Дополнительные расходы

Зачастую дополнительных трат требуют услуги опытных специалистов: риелторов, оценщиков, юристов. Однако в зависимости от типа сделки могут появиться и другие дополнительные издержки:

• Ипотечный налог. Если вы покупаете квартиру в ипотеку, вы должны совершить платеж, размер которого зависит от условий кредитования, налоговых вычетов и т.д.
• Банковские услуги. Плата за совершение операций, использование банковской ячейки, аренда сейфа, страховка и т.д.
• Увеличение фактической площади. Это относится к покупке квартиры в новостройке. Когда конечная площадь жилья превышает предусмотренную проектом.
• Оплата коммунальных. Управляющая компания жилого комплекса может взимать оплату своих услуги наперед.

Следовательно, в понятие конечной стоимости жилья входит не только цена квадратных метров, но ряд дополнительных расходов, сумма которых может составлять около 10% стоимости самого объекта.

Speed ​​and Velocity – GeeksforGeeks

Механику можно назвать разделом физики, изучающим понятия энергии и сил и их влияние на тела. Он регулирует отношения, связанные с движением объектов, то есть между материей, силой и связанной с ними энергией. Она отвечает за движение тел и действие сил на эти тела. На практике механика включает в себя проектирование, строительство или эксплуатацию машин или инструментов. Например, расстояние, пройденное автомобилем до остановки со скоростью 30 км/ч.

Раздел классической механики, занимающийся движением точек, групп объектов, а также их систем, не имеющий отношения к движению этих объектов, называется Кинематика , часто называемая « Геометрия движения». »

Подраздел физической науки, который связан с движением материальных объектов под действием воздействующих на них физических факторов, то есть силы, массы, импульса, энергии, называется Динамика .

Отдых

Говорят, что кто-либо находится в состоянии покоя, если его положение (расстояние, смещение) не меняется со временем относительно его окружения или точки отсчета.

Движение

Изменение положения кого-либо во времени можно назвать движением. Любой движущийся объект можно визуализировать невооруженным глазом, определив изменение позиционных координат и затем связав его через глаз произвольного наблюдателя. Движение может быть вычислено как с точки зрения векторов положения, то есть смещения, расстояния, так и с учетом факторов скорости, то есть скорости, ускорения, скорости и времени.

Например, можно предположить, что пружинный шарик, прикрепленный к одному концу стержня, качающегося в разные промежутки времени, находится в движении.

A rubber ball undergoing displacement under the influence of motion

Difference in Scalar and Vector:

	Scalar	Vector
Definition	Физическое количество с величиной	Физическая величина с величиной и направлением
заглавная буква или стрелка вверху и единица измерения.
Направление	Нет	Да
Примеры	Масса и скорость	Velocity and Acceleration

Расстояние

Расстояние. Расстояние — это скалярная величина, имеющая только величину и не связанное с ней направление. Расстояние обозначается символом «d». Расстояние любого объекта считается положительным товаром. Расстояния можно измерять как по прямой, так и по зигзагообразной траектории. Расстояние тела дает подробную информацию о маршруте, по которому следуют при путешествии из одной точки в другую.

Расстояние = скорость x время

Расстояние от точки A до точки B равно 5 см

Перемещение

Перемещение — это прямая длина минимального пути между любыми двумя последовательными точками. Смещение является векторной величиной, имеющей как соответствующую величину, так и направление. Обозначается буквой «с». Смещение объекта между любыми двумя точками считается положительным, отрицательным и даже нулевым. Перемещение не зависит от пути и зависит только от начального и конечного положения тела. Поэтому он не дает полной информации о маршруте. Смещение всегда указывается стрелкой.

Перемещение = Скорость x Время

Скорость

Скорость можно определить как скорость изменения положения объекта, движущегося в любом направлении. Скорость измеряется как отношение расстояния, пройденного объектом, ко времени, за которое это расстояние было пройдено. Скорость любого тела считается скалярной величиной, имеющей только величину и не связанную с направлением.

 

где «s» — скорость в м/с, «d» — пройденное расстояние в м, а t — время в секундах.

CGS system	cm/s
SI system	m/s

Dimensional formula for Speed ​​

Mathematically, 

Dimensional formula for Distance = M ⁰ L ¹ T ⁰

Размерная формула для времени = M ⁰ L ⁰ T ¹

Следовательно, размерная формула для расстояния деления на размерную формулу времени;

Следовательно,

Dimensional Formula для скорости = ML ¹ T ^-1

Скорость

Скорость объекта может быть определен в качестве изменения позиции объекта с точки зрения объекта с точки зрения объекта с точки зрения объекта с точки зрения объекта. система отсчета и время. Смещение является векторной величиной, имеющей как соответствующую величину, так и направление. Единицей СИ является метр в секунду (м/с). Скорость объекта может быть положительной, отрицательной или даже нулевой. Если происходит изменение величины или направления скорости тела, говорят, что тело ускоряется.

Начальная скорость описывает скорость, с которой движется любой объект, когда гравитация впервые воздействует на объект, тогда как конечная скорость является векторной величиной, которая описывает товары скорости и направления движения тела после того, как оно достигло своего максимума ускорение.

Постоянная скорость 

Постоянную скорость можно назвать движением по прямой линии с постоянной скоростью. Алгебраически

x = x ₀ + vt

, где

x ₀ представляет положение объекта при

t = 0, а наклон линии указывает на скорость объекта.

Скорость может быть положительной или отрицательной и обозначается знаком нашего наклона. Это говорит нам, в каком направлении движется объект.

График постоянной скорости

Единицы скорости

Единицей скорости в системе СИ является м/с (м/с).

Единицы и размеры скорости следующие: 

Units of velocity
SI unit	m/s
Other units	mph, ft/s
Dimension	LT -1

Разница между скоростью и скоростью

0042

Скорость
Количественная мера того, насколько быстро что-то движется	Направление движения тела или объекта.
Скалярное количество	Векторная Количество
Это скорость изменения дистанции	. Это скорость изменения смещения 9000	.0002 Скорость движущегося объекта никогда не может быть отрицательной	Скорость движущегося объекта может быть равна нулю.
Указывает скорость объекта.	Указывает положение, а также скорость объекта.
Расстояние, пройденное объектом в единицу времени.	Перемещение объекта в единицу времени.

Скорость против скорости

Единая скорость и однородная скорость

Единая скорость	Единая скорость
. время может быть.	Если объект совершает равные перемещения за равные промежутки времени, какими бы малыми ни были эти промежутки времени.
Движение с постоянной скоростью может или не может быть движением с постоянной скоростью.	Движение с постоянной скоростью также является движением с постоянной скоростью.
Скалярное количество	Переменная Количество

СВОЙСТВА И ВАРИТАЯ ВАР. времени, даже в случае пренебрежимо малых промежутков времени. Любое тело, совершающее неравные перемещения за равные промежутки времени, даже в случае пренебрежимо малых промежутков времени. Скалярная величина Векторная величина

Мгновенная скорость и Мгновенная скорость

Мгновенная скорость всегда больше или равна нулю, то есть это положительный товар. Мгновенная скорость — это скалярная величина, связанная с величиной, а не с направлением. Она постоянна при равномерном движении. Это предел средней скорости для бесконечно малого интервала времени.

Мгновенная скорость — это показатель скорости движения объекта в разные моменты времени в пределах заданного интервала времени. Также называется средней скоростью за пренебрежимо малый интервал времени. Подводя итог, мгновенная скорость в любой заданный интервал времени эквивалентна величине мгновенной скорости в это время.

У нас есть, 

Здесь lim выполняет операцию ограничения со временем, стремящимся к 0 или бесконечно малому. И,   – это дифференциальный коэффициент – скорость изменения положения по отношению ко времени в данный момент.

P-T График для мгновенных скоростей

Из графика мы имеем

Наклон P ₁ P ₂ -скорость в мгновенном 3 с

Слейп Q ₁ Q ₂ -VELOCE Q ₁ Q ₂ -SLOPE Q ₁ Q ₂ -VELOCTION. момент 1 с

Где as,

Мгновенная скорость называется величиной скорости. Мгновенная скорость в любой момент времени эквивалентна величине мгновенной скорости в этот конкретный момент. Это скорость изменения расстояния до любого объекта во времени.

Единицей измерения скорости является метр в секунду (м/с).

Теперь у нас есть

Мгновенная скорость (v) =

v = ограничение при приближении изменения во времени к нулю

Где

v = мгновенная скорость (м/с)

Δ = изменение значений

x = перемещение (м)

t = время (с)

Средняя скорость

Средняя скорость объекта представляет собой отношение общего расстояния, пройденного объектом, к общему затраченному времени.

Average speed = 

If a particle travels distances s ₁ , s ₂ , s ₃ , … with speeds v ₁ , v ₂ , v ₃ , … respectively then,

Средняя скорость = 

Если какой-либо объект проходит равные расстояния в разные моменты времени (с ₁ = с ₂ = с) со скоростями v ₁ и v ₂ , то

Средняя скорость0 = 2 9002 Если какой-либо объект движется со скоростью v ₁ , v ₂ , v ₃ , …, в промежутках времени t ₁ , t ₂ , t ₃ , t ₃ ,…, то, скорости v ₁ и v ₂ за равные промежутки времени, т. е. t ₁ = t ₂ = t ₃ , тогда

v ₁ и v ₂ средняя скорость, которая является гармоническим средним значением двух скоростей, определяется выражением

Расчет средней скорости

Общая длина пути, пройденного в единицу времени, называется средней скоростью.

Средняя скорость = 

Средняя скорость

Средняя скорость любого тела – это отношение полного перемещения ко всему затраченному времени. Это векторная величина с той же единицей, что и скорость. Это скорость, с которой объект меняет свое положение из одного места в другое за определенный период времени. Его стандартной единицей измерения является метр в секунду, но его также можно преобразовать в другие единицы, такие как мили в час (миль в час) или километр в час (км в час).

Вычисление средней скорости

Это та единственная скорость, с которой объект может пройти одно и то же расстояние за то же время, как это обычно происходит с различной скоростью. Средняя скорость тела в любой момент времени строго больше чем величина средней скорости.

Средняя скорость = 

Разница между средней скоростью и средней скоростью

Средняя скорость	Средняя скорость
Общая пройденная длина пути, деленная на общий интервал времени, независимо от направления.	Изменение положения или перемещения, разделенное на временной интервал.
Средняя скорость =	Средняя скорость =
Скаляр
Всегда положительный	может быть отрицательным или положительным
м/с	м/с

1 70003 9000. объекта по отношению к другому объекту в том же временном интервале называется относительной скоростью.

Предположим, что относительная скорость объекта A относительно объекта B равна

V _AB = V _A – V _B  

Если два объекта движутся в одном направлении, то 

Если два объекта движутся в противоположном направлении, то

Когда два объекта движутся в угол, затем

и

Примеры;

Пример 1. Если автомобиль проедет расстояние 900 м на запад за 90 секунд. Найдите скорость и скорость автомобиля?

Решение:

Здесь

Расстояние = 900 м

Время = 90 с

Скорость =

Скорость = 10 м/с на запад

м за 6 секунд. Найдите скорость автомобиля и время, за которое он проедет расстояние 480 м.

Решение:

Здесь

Расстояние = 240 м

Время = 6 с

Скорость поезда v = ?

Время, за которое поезд преодолевает расстояние 480 м ‘t’ = ?

Скорость = 

Время, затрачиваемое автомобилем на преодоление 480 м пути =  

Вопрос 3.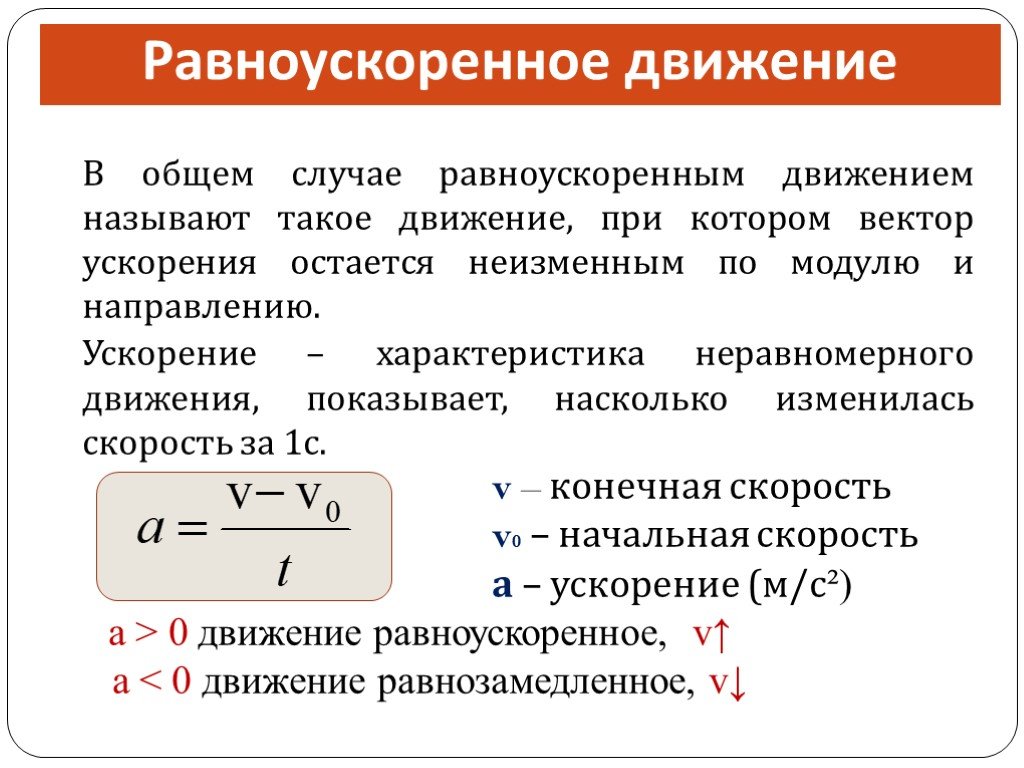 Если поезд едет из Дели в Джайпур со скоростью 120 км/ч и едет 3 часа. Рассчитать расстояние между городами?

Решение:

Здесь

Скорость поезда v = 120 км/ч

Время t = 3 часа

Расстояние = Скорость × Время

= 120 × 3

= 360 км

Вопрос 4. Мальчик подбрасывает мяч вверх, мяч поднимается вертикально примерно на 50 м за 2,5 секунды, возвращается к мальчику в том же положении еще через 2,5 секунды. Рассчитайте

(i) Расстояние, пройденное

(II) Смещение

(III) Средняя скорость

(IV) Средняя скорость

Райство:

ЗДЕСЬ

Райство:

ЗДЕСЬ,

. пройдено вверх = 50 м

Затраченное время = 2,5 секунды

(i) Общее пройденное расстояние = расстояние, пройденное вверх + расстояние, пройденное вниз

= 50 + 50

= 100 м

(ii) перемещение = когда мяч достигает своей начальной точки, следовательно будет нулевое смещение

= 0

(iii) Средняя скорость =

(iv) Средняя скорость = 0 {Поскольку смещение равно 0, значит, скорость также равна 0}.

Пример 5. Если машине требуется 4 часа, чтобы добраться из Шимлы в Чандигарх, который находится на расстоянии 153 км от Шимлы. Если на обратном пути машина занимает 5 часов, то есть из Чандигарха в Шимлу. Рассчитать среднюю скорость и среднюю скорость автомобиля?

Решение:

Здесь,

Расстояние, пройденное в обоих поездках S ₁ , S ₂ = 153 км

Время. из Чандигарха в Шимлу t ₂ = 5 часов

Нам нужно найти среднюю скорость = ?

и средняя скорость = ?

Общее пройденное расстояние = с ₁ + с ₂ = 153 км + 153 км = 306 км

Общее затраченное время = t + t = 4 часа + 5 часов = 9 часов

Средняя скорость =

Средняя скорость =

Когда автомобиль возвращается в Шимлу, т.е. в исходную точку, таким образом, перемещение равно нулю.

Таким образом,

Средняя скорость = 0

Пример 6. Если машинист поезда имеет время реакции 0,4 с между тем, как он увидел препятствие и нажал на тормоз. Предположим, что поезд движется со скоростью 72 км/ч, и машинист замечает препятствие. Рассчитайте пройденное расстояние до торможения?

Решение:

Здесь

Время реакции ‘t’ = 0,4 с

Скорость поезда ‘v’ = 72 км/ч или 

Нужно найти пройденное расстояние ‘s’ = ?

Расстояние = скорость × время

Расстояние = 20 × 0,4

Расстояние = 8 м

Пример 7. Предположим, что мяч движется со скоростью v в направлении зеркала, а зеркало движется со скоростью v в направлении мяч, так вычислить относительную скорость изображения мяча в соответствии с мячом?

Решение:

Скорость мяча относительно земли = v

Скорость зеркала относительно земли = v

Скорость отражения мяча в зеркале согласно = v движутся навстречу друг другу, поэтому относительная скорость будет = v + v = 2v.

21.4 Ускорение | Движение в одном измерении

Предыдущий 21.3 Скорость и скорость

Следующий 21,5 Мгновенная скорость и скорость

21.4 Ускорение (ESAGY)

Среднее ускорение

Среднее ускорение — это изменение средней скорости, деленное на затраченное время. 9{-1}$} \text{)}}{\text{изменение во времени (в } \text{s} \text{)}} \\ \vec{a}_{av} & = \frac{\Delta \vec{v}}{\Delta t} \конец{выравнивание*}

Мы занимаемся только проблемами с постоянным ускорением. Это означает, что среднее ускорение и мгновенное ускорение одинаково. Для простоты мы будем говорить только об ускорении, а не среднее или мгновенное.

Это представлено как \(\vec{a}\). Мы также можем иметь величину ускорения. Это:

\[a = \frac{\Delta \vec{v}}{\Delta t}\]

Ускорение является вектором. Ускорение не дает никакой информации о движении, а только о том, как изменения движения. Невозможно сказать, как быстро движется объект или в каком направлении от разгон один.

Как и скорость, ускорение может быть отрицательным или положительным. Мы видим, что когда знак ускорения и скорости одинаковы, объект ускоряется. Если и скорость, и ускорение положительны, объект ускорение в положительную сторону. Если и скорость, и ускорение отрицательны, то объект ускоряется в негативное направление.

Избегайте использования слова замедление для обозначения отрицательного ускорения. Это слово обычно означает замедляет , и объект может замедляться как с положительным, так и с отрицательным ускорение, так как для определения необходимо учитывать и знак скорости тела.

замедляется тело или нет.

Мы можем увидеть это на следующей диаграмме:

Если скорость положительна, а ускорение отрицательно, то объект замедляется. Аналогично, если скорость отрицателен, а ускорение положительно, объект замедляется. Это показано в следующем отработанный пример. 9{-1}$}\) за \(\text{6}\) секунд. Рассчитать ускорение автомобиля в течение первых \(\text{8}\) секунд и в течение последних \(\text{6}\) секунд.

Выбираем систему отсчета

Мы выбираем точку, в которой автомобиль начинает ускоряться, в качестве начала координат и направления, в котором движется автомобиль уже движется в позитивном направлении.

Определите, какая информация предоставляется и какая запрашивается

Рассмотрим движение автомобиля в двух частях: первые \(\text{8}\) секунды и последние \(\text{6}\) секунды секунды. 9{-2}$} \конец{выравнивание*}

Первые \(\text{8}\) секунд автомобиль имел положительное ускорение.