что это такое, единица измерения, формула и определение
Мгновенная скорость в физике
ОпределениеМгновенной скоростью называется скорость объекта в данный момент времени в конкретной точке. Это векторная физическая величина, которая обозначается символом \vec v и определяется по формуле:
\(\vec v=\frac{\Delta\vec S}{\Delta t}\)
Где \(\Delta\vec S\) — перемещение, а \(\Delta t \) — промежуток времени.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Величина измеряется в м/с.
Мгновенное ускорение в физике
ОпределениеМгновенное ускорение — это векторная физическая величина, численно равная изменению скорости в единицу времени.
Обозначается \(\vec a\).
Единицами измерения мгновенного ускорения являются м/с2.
Как направлены мгновенная скорость и ускорение
Вектор мгновенной скорости всегда направлен по касательной к траектории движения объекта в любой момент времени. Графически это выглядит так:
У вектора \vec a две составляющие: \(\vec a_tg\) (касательное или тангенциальное \(\vec a\)) и \(\vec a_n\) (нормальное \(\vec a\)). Каждая из них имеет свое направление вектора.
Как найти мгновенное ускорение, формула
Ускорение определяется по формуле:
\(\vec a=\lim_{t\rightarrow0}\frac{\Delta\vec V}{\Delta t}\)
Где \(\Delta\vec V\) — изменение скорости, \(\Delta t\) — промежуток времени, когда происходило изменение скорости.
Составляющими данной векторной величины являются:
- касательное или тангенциальное ускорение;
- нормальное ускорение.
Касательное — указывает, насколько быстро изменяется скорость объекта по модулю. 2}r \)
2}r \)
Задача на определение мгновенного ускорения
Для усвоения теоретического материала важно закрепить знания на практике. Решим задачу на определение мгновенного ускорения.
Задача
С каким ускорением движется гоночный болид, если его скорость изменилась со 144 км/ч до 216 км/ч за 6 секунд?
Решение:
Записываем все известные вводные:
\(V_0\)=144 км/ч, \(V\)=216 км/ч, t=6 с, a=?
Переводим км/ч в м/с, получаем:
\(V_0\)=40 м/с, \(V\)=60 м/с.
Формула:
\(\vec a=\frac{\Delta\vec V}{\Delta t}\)
Где \(\Delta\vec V=V-V_0\)
Получаем значение ускорения, равное 3,33 м/с2.
Мгновенный ускорений – Энциклопедия по машиностроению XXL
Из этой формулы следует, что вектор мгновенного углового ускорения направлен перпендикулярно к плоскости 22 (рис. а предыдущей задачи), т. е. по линии узлов.
Сохранив условие задачи 329, определить мгновенное ускорение е конуса. [c.61]
Во всякое мгновение ускорения всех точек поступательно движущегося тела одинаковы. В этой теореме, как и в предыдущей, одинаковость не надо понимать как неизменяемость с течением времени. [c.164]
При i = 4 сек угол поворота трубки ф = 4л и ось Ох совпадала с осью Ох. Следовательно, в это мгновение ускорение Кориолиса направлено по положительной оси Оу.
Направление относительной скорости точки не меняется, так как по свойству поступательного движения прямая передвигается параллельно самой себе. Напротив, направление относительной скорости точки В2 непрерывно изменяется по мере вращения О А . Даже при прямолинейном относительном движении направление относительной скорости изменяется (вследствие переносного вращения). Изменение вектора скорости точки в данное мгновение (ускорение), вызванное этой причиной, тоже пропорционально угловой и относительной скоростям. В этом заключается другой фактор, порождающий ускорение Кориолиса. Ускорение Кориолиса как бы поворачивает вектор относительной скорости в направлении переносного вращения. По этой причине его иногда называют поворотным ускорением .
Даже при прямолинейном относительном движении направление относительной скорости изменяется (вследствие переносного вращения). Изменение вектора скорости точки в данное мгновение (ускорение), вызванное этой причиной, тоже пропорционально угловой и относительной скоростям. В этом заключается другой фактор, порождающий ускорение Кориолиса. Ускорение Кориолиса как бы поворачивает вектор относительной скорости в направлении переносного вращения. По этой причине его иногда называют поворотным ускорением .
Чтобы определить направление ускорения Кориолиса, надо повернуть вектор относительной скорости на 90 ” в сторону вращения трубки, т. е. против хода часовой стрелки. При i = 4 с угол поворота трубки ф = 4я и ось Ох совпадала с осью Ох. Следовательно, в это мгновение ускорение Кориолиса направлено по положительной оси Оу. [c.186]
В общем случае при движении материальной точки может изменяться не только значение, но и направление ее скорости.
Это уравнение в рассматриваемом здесь случае постоянной силы Р выражает постоянство среднего ускорения движущегося тела за какой угодно промежуток времени М и его пропорциональность силе. Приближая Дтела, мы получим [c.303]
При изучении механики мы встречались с выражением механическая работа в виде произведения силы, приложенной к телу, и расстояния, на которое тело перемещается под действием этой силы в том же направлении. Согласно второму закону Ньютона, сила Р, необходимая для придания телу массой т мгновенного ускорения
Мгновенное ускорение. Опираясь на определение ускорения, можно показать, что при равнопеременном движении ускорение ja] не зависит от того, какой выбирается промежуток времени At большой или малый (рассуждения подобны тем, которые проводились при рассмотрении мгновенной скорости равномерного движения).

Предел, к которому стремится отношение вектора Аи изменения скорости к промежутку времени А , за которое произошло это изменение при неограниченном уменьшении At, называют вектором мгновенного ускорения или просто ускорением) [c.25]
Что называют вектором мгновенного ускорения точки и каков его физический смысл Как направлен этот вектор Почему его направление не совпадает при криволинейном движении с направлением скорости
Что называют угловым ускорением равнопеременного движения по окружности Дайте определение единицы измерения углового ускорения. Что называют мгновенным ускорением Как угловое ускорение связано с угловой скоростью и углом поворота
[c. 41]
41]
Отсюда следует, что мгновенное ускорение имеет наибольшее значение для тех точек, смещение которых в данный момент наибольшее. Однако, если смещение положительно, ускорение отрицательно, и наоборот (ускорение точки всегда направлено к положению равновесия). Графики мгновенных смещений н ускорений сдвинуты в пространстве на -g- (рис. 12.8).
Для конкретности рассмотрим (рис. 40) цилиндрическую трубу бесконечной длины, вдоль которой может перемещаться поршень. Пусть вначале газ неподвижен, а затем внезапно поршень получает мгновенное ускорение влево, и достигнув скорости V, продолжает двигаться равномерно с этой скоростью. Возникает вопрос, как произойдет передача движения поршня находящемуся перед ним газу. [c.174]
Мгновенное ускорение по формуле (76) [c.132]
Мгновенное ускорение (прн переключении ступеней реостата) [c.430]
Пример 3. Определить среднее и максимальное мгновенные ускорения груза при подъеме, если известны рабочая скорость 12
 435]
435]
Максимальное мгновенное ускорение [c.435]
Ш мин-, Ъ сек 60-1,5 Максимальное мгновенное ускорение стрелы [c.436]
Ускорение жидкой сферы. Рассмотрим начальное движение жидкой сферы плотности р, вызванное мгновенным ускорением из состояния покоя в окружающей жидкости плотности р или же мгновенным появлением однородного гравитационного поля д. Если А и А — потенциалы ускорения обеих жидкостей, то, очевидно, VM = = 0. На границе раздела жидкостей 5 из условия несжимаемости получим
Если д — мгновенное ускорение, то мы также имеем Ит (х) = [c.317]
Из соотношений (IV) следует, что мгновенное ускорение точек твердого тела складывается из трех составляющих [c.95]
Испытание на вибро- и ударопрочность. Под вибрацией понимается простое гармоническое колебание изделия, характеризуемое частотой и амплитудой. Под тряской понимаются колебания изделия, при которых мгновенные ускорения достигают заданных значений за период времени, не превышающий 1 % времени от одного удара до другого. [c.388]
[c.388]
Если мгновенное ускорение желоба меньше или равно /макс, то груз движется вместе с желобом. Если упомянутое ускорение превысит эту величину, произойдет скольжение груза по желобу под действием накопленной живой силы. [c.355]
Мгновенное ускорение поршня / в зависимости от угла поворота коленчатого вала [c.86]
Значения мгновенных ускорений могут значительно превосходить приведенные в табл. 1-2 значения средних ускорений. [c.179]
При скачкообразном режиме трения салазки металлорежущего станка то неподвижны, то получают мгновенное ускорение, быстро замедляют движение и опять становятся неподвижными. Неравномерность движения в большой степени зависит от конструкции и материала направляющих. Например, применением направляющих с поверхностями, пропитанными политетрафторэтиленом (РТРЕ), можно избежать возникновения скачкообразного движения. Низкие характеристики трения, присущие РТРЕ, создают возможность устойчивого однородного движения при низких скоростях. Однако наиболее часто изготовляют направляющие из стали или чугуна.
[c.43]
Однако наиболее часто изготовляют направляющие из стали или чугуна.
[c.43]
Соответственно находим компоненты тензора мгновенных ускорений деформаций [c.24]
Незначительность мгновенных ускорений и замедлений в числах оборотов, благодаря хорошему распыливанию на всех режимах работы мотора. [c.71]
Ускорение мгновенное ускорение) а определяется как [c.8]
Ускорением (мгновенным ускорением) материальной точки в момент времени t называется физическая величина а, равная пределу, к которому стремится среднее ускорение (п. Г) за промежуток времени от t до при неограниченном уменьшении А/ [c.20]
Таким образом, если мгновенное ускорение желоба меньше или равно /max. то обеспечено совместное движение груза и желоба В случае превышения мгновенным ускорением желоба этой величины происхо-
[c. 509]
509]
Плавность pa oTia нарушается мгновенными резкими изменещиями углов поворота зубчатых колес. При таком режиме работы появляются систематически возникающие мгновенные ускорения ведомых зубчатых колес, дополнительные инерционные наг )узки и удары в зацеплении, а также вибрации машин и повышенный шум. Все это неблагоприятно влияет на надежность передач, особенно работающих с большими скоростями и нагрузками. [c.198]
Для построения (фиг. 7) откладывают АМ= =Р, проводят MN параллельно 02 и получают MN=K. Силы инерции К. м. обыкновенно находят приближенно по весу звеньев, движущихся прямолинейно – поступательно (поршня, штока, ползуна), причем для обобщения результата и сложения с давлениями пара относят вес к 1 см площади поршня кроме того к найденному выше весу прибавляют еще 0,3—0,45 веса шатуна, разделенного также на площадь поршня в см умножая полученный вес д кг1см на мгновенное ускорение поршня / и изменяя направление на обратное, получают силу инерции возвратно движущихся частей
[c. 295]
295]
Таким образом, если мгновенное ускорение желоба меньше или равно /max. то обеспечено совместное движение груза и желоба, В случае превышения мгновенным ускорением желоба этой величины происходит скольжение груза по желобу под действием силы инерции. При этом между грузом и желобом действует постоянная сила трения Qrpgf. где / — коэффициент трения скольжения в движении. [c.230]
Произвольный элемент М матрицы масс представляет собой усилие типа /, необходимое для создания единичного (мгновенного) ускорения типа /. Это определение совпадает с тем, что было дано для коэффициента влияния жесткости при этом вычисление элементов столбцов матрицы М проводится так же, как было описано применительно к элементам столбцов матрицы 8. На рис. 3.10, в я г показан процесс, при котором в качестве характерной точки для описания движений абсолютно жесткостного стержня взята точка А. На рис. 3.10, в представлены моменты Мц и УИ21, необходимые для создания единичного ускорения Уа = 1 при 0а = О, а также моменты М-хч, и М22 (см. рис. 3.10, г), необходимые для создания единичного ускорения 0А = 1 при ул = 0. Для наглядности ускорения изображены так, как будто они являются перемещениями, а двой-
[c.210]
рис. 3.10, г), необходимые для создания единичного ускорения 0А = 1 при ул = 0. Для наглядности ускорения изображены так, как будто они являются перемещениями, а двой-
[c.210]
Г. Равнопеременное прямолинейное движение является частным случаем неравномерного движения, при котором ускорение остается постоянным и по модулю и по направлению (а=сопз1). При этом среднее ускорение Яср равно мгновенному ускорению а(аср=а). Направлено ускорение а вдоль траектории точки. Нормальное ускорение (1.1.4.3°) при этом отсутствует (а =0). [c.23]
При равнопеременном вращателыюм движении (п. 6°) мгновенное ускорение тела остается неизменным и совпадает со средним угловым ускорением e=e(.p= onst. [c.37]
Первый член выражения описывает электростатическое ку-лоновское поле (в ближней зоне). Оно зависит голько от знака и величины заряда и расстояния от заряда до точки наблюдения. Второй член описывает поле в волновой зоне, обусловленное ускоренным движением заряда. На больших расстояниях (г А,/2зг) значение имеет только второй член, который и отображает поле излучения. Следует заметить, что значение выражения в скобках берется с задержкой по времени, т. е. в момент времени (/ — г/с). Как и ранее, волновой вектор к тождествен к2л/> , через и обозначено значение мгновенного ускорения электрона в момент времени I — г/с.
[c.40]
На больших расстояниях (г А,/2зг) значение имеет только второй член, который и отображает поле излучения. Следует заметить, что значение выражения в скобках берется с задержкой по времени, т. е. в момент времени (/ — г/с). Как и ранее, волновой вектор к тождествен к2л/> , через и обозначено значение мгновенного ускорения электрона в момент времени I — г/с.
[c.40]
Для улучшения технологических свойств дуги применяют периодическое изменение ее мгновенной мощности — импульсно-дуговая сварка (рис. 48). Теплота, выделяемая основной дугой, недостаточна для плавления электродной проволоки со скоростью, равной скорости ее подачи. Вследствие этого длина дугового промежутка уменьшается. Под действием импульса тока происходит ускоренное раснлавлепиэ электрода, обеспечивающее формирование капли на его конпе. Резкое увеличение электродинамических сил сужает шейку канли и сбрасывает ее в направлении сварочной ванны в любом пространственном по-ло5кении.
[c. 56]
56]
Ускорение и его составляющие
Механика Ускорение и его составляющие
просмотров – 265
Чаще всего приходится иметь дело с движением, в котором вектор скорости не остается постоянным, а меняется как по модулю, так и по направлению.
Физической величиной, характеризующей быстроту изменения скорости по модулю и направлению, является ускорение.
Пусть вектор задает скорость материальной точки в положении А в момент времени . За время движущаяся точка перешла в положение B и приобрела скорость , отличающуюся от как по модулю, так и по направлению (рис. 1.3.1). Перенесем вектор в точку А и найдем вектор изменения скорости .
Средним ускорением неравномерного движения принято называть векторная величина, равная отношению изменения скорости к тому интервалу времени, за который это изменение произошло:
. (1.3.1)
(1.3.1)
Вектор совпадает по направлению с вектором изменения скорости.
Мгновенным ускорением принято называть величина, равная пределу, к которому стремится среднее ускорение материальной точки:
. (1.3.2)
Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, мгновенное ускорение – векторная величина, равная первой производной скорости по времени.
Пример 1.3.1. Уравнение движения точки по прямой имеет вид: . Найти: 1) среднюю путевую скорость за промежуток времени от до ; 2) мгновенную скорость и модуль мгновенной скорости в указанные моменты времени; 3) среднее ускорение за промежуток времени от до ; 4) мгновенное ускорение и модуль мгновенного ускорения в указанные моменты времени.
Решение:
1) Средняя путевая скорость находится по формуле 1.2.2:
.
Найдем положения движущейся точки в указанные моменты времени: (м),
(м).
Тогда .
2) При прямолинейном движении мгновенная скорость в любой момент времени (формула 1.2.4): .
Модуль мгновенной скорости в указанные моменты времени:
, .
3) Модуль среднего ускорения (формула 1.3.1):
.
4) Мгновенное ускорение в любой момент времени (формула 1.3.2):
.
Модуль мгновенного ускорения в указанные моменты времени:
, .
Ответ:, , , , , , , .
Разложим вектор изменения скорости на две составляющие: вдоль направления мгновенной скорости и перпендикулярно этому направлению , то есть по касательной к траектории движения и нормали к траектории:
.
Тогда ,
где вектор направлен по касательной к траектории, характеризует быстроту изменения скорости по модулю и принято называть тангенциальным ускорением; вектор направлен к центру кривизны траектории, характеризует быстроту изменения скорости по направлению и принято называть нормальным ускорением.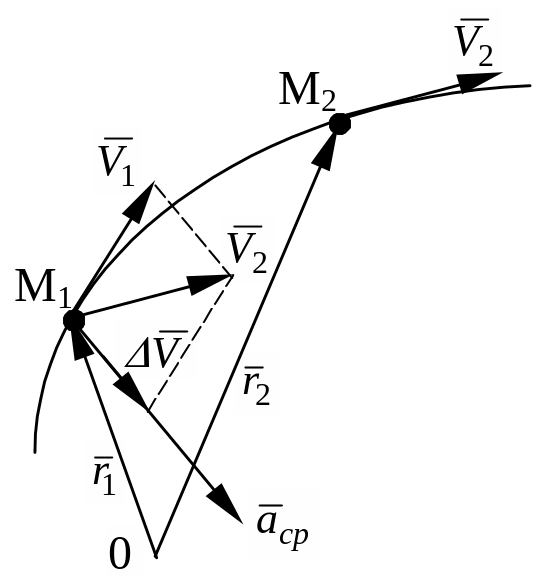
Численные значения тангенциального и нормального ускорений соответственно равны:
, , (1.3.3)
где радиус окружности, которая в окрестности данной точки совпадает с траекторией.
Мгновенное ускорение также называют полным ускорением. Численное значение полного ускорения:
. (1.3.4)
Зная зависимость ускорения от времени , можно найти зависимость скорости от времени
.
Пример 1.3.2. Машина идет по закругленному шоссе. Зависимость радиуса-вектора от времени задана уравнением: . Найти:1) мгновенную скорость машины и значение скорости в момент времени ; 2) тангенциальное и нормальное ускорение в указанный момент времени; 3) радиус кривизны шоссе.
Дано: Решение:
1) Мгновенная скорость .
Учитывая, что , а ; ; и , подставив , получим значение скорости .
2) Полное ускорение – ускорение постоянно по величине, а знак «–» указывает, что движение машины замедленное (модуль скорости уменьшается).
Тангенциальное ускорение .
При , .
По 1.3.4 , получим в момент времени .
3) Радиус кривизны окружности по 1.3.3 .
Ответ:, , , ,
В случае если ускорение тела не зависит от времени и остается постоянным в процессе движения , то движение принято называть равнопеременным (при этом и траектория движения не обязательно прямолинейная).
При равнопеременном движении скорость тела изменяется с течением времени по закону
, (1.3.5)
где скорость в начальный момент времени.
В свою очередь, зависимость имеет вид:
, (1.3.6)
где начальный радиус-вектор тела.
Величины и представляют собой начальные условия, позволяющие в любой момент времени однозначно определить векторы и .
При координатном способе описания равнопеременного движения векторным уравнениям 1.3.5 и 1.3.6 соответствуют следующие системы уравнений для проекций скорости и радиус-вектора тела на оси выбранной системы координат:
(1. 3.7) (1.3.8)
3.7) (1.3.8)
где и начальные абсцисса и ордината тела при , и проекции
начальной скорости тела на координатные оси, и проекции вектора ускорения на оси и соответственно. В принципе, формулы 1.3.5 и 1.3.6 или равносильные им системы 1.3.7 и 1.3.8 позволяют решить любую задачу на движение тела с постоянным ускорением.
Наглядным примером равнопеременного движения является движение тела в поле тяготения Земли. Для решения задач в этом случае нужно заменить в формулах 1.3.7 и 1.3.8 ускорение на ускорение свободного падения , сообщаемое силой гравитационного притяжения всякому телу, движущемуся в поле тяготения Земли.
Примечание: во всех примерах, если в условиях не оговорено иное, будем считать ускорение свободного падения равным .
Пример 1.3.3. Стрела выпущена из лука вертикально вверх с башни высотой со скоростью . У основания башни находится ров глубиной . Пренебрегая сопротивлением воздуха, определить: время подъема на максимальную высоту и максимальную высоту подъема ; время полета стрелы до падения на дно рва, скорость стрелы в момент падения и путь, который пролетела стрела за это время.
Пренебрегая сопротивлением воздуха, определить: время подъема на максимальную высоту и максимальную высоту подъема ; время полета стрелы до падения на дно рва, скорость стрелы в момент падения и путь, который пролетела стрела за это время.
Решение:
Поскольку движение происходит только в вертикальном направлении, то достаточно одной координатной оси .
Совместим начало отсчета с точкой нахождения лука (рис. 1.3.2).
Начальные условия движения стрелы:
, .
Проекция ускорения стрелы на ось в отсутствии сопротивления воздуха равна , т.к. вектор направлен вертикально вниз противоположно направлению координатной оси.
Вторые уравнения систем 1.3.7 и 1.3.8 с учетом начальных условий имеют вид: и .
Пусть при стрела находится в наивысшей точке подъема. Это значит, что и (стрела из точки 0 будет подниматься вверх до тех пор, пока ее скорость не станет равной нулю).
Получаем откуда и .
Пусть при стрела упала в ров. В данный момент и уравнение движения имеет вид:
.
Откуда для получаем , где первое слагаемое – время подъема, второе – время падения. Отрицательный корень физического смысла не имеет, следовательно, время полета стрелы
.
Уравнение с учетом найденного значения имеет вид
,
ᴛ.ᴇ. скорость стрелы в момент падения направлена вертикально вниз – ее проекция на отрицательна.
Путь , пройденный стрелой за время полета͵ складывается из двух участков: подъема до высшей точки траектории и падения с высшей точки траектории в ров:
.
Ответ: ; ; ; ; .
Пример 1.3.4. Два тела брошены вертикально вверх с поверхности земли из одной точки вслед друг за другом с интервалом времени , с одинаковыми начальными скоростями . Пренебрегая сопротивлением воздуха, определить, через сколько времени они
«встретятся»? Прокомментировать решение для .
Дано: Решение:
Направим ось вертикально вверх, начало отсчета поместим в точку бросания. Отсчет времени будем вести с момента бросания первого тела. Начальные условия движения тел: 1) , , ; 2) , , . Проекции ускорений тел при отсутствии сопротивления воздуха равны: . Уравнения движения тел в проекциях на ось с учетом начальных условий имеют вид: , .
Условие «встречи»: , то есть .
Решая это уравнение относительно , находим .
Проанализируем полученное выражение при .
Время полета тела, брошенного вертикально (пример 1.3.3) вверх, до наивысшей точки подъема равно , ᴛ.ᴇ. общее время полета равно . В случае если , то . Это означает, что сначала упадет на землю первое тело, а только затем будет брошено вверх второе. Иными словами, тела «встретятся» в точке бросания.
Ответ:.
Пример 1.3.5. Мяч бросили с башни высотой над поверхностью земли, сообщив ему начальную скорость , направленную горизонтально. Пренебрегая сопротивлением воздуха, определить 1) время полета мяча до его падения на землю; 2) дальность полета мяча; 3) скорость мяча в момент падения; 4) радиус кривизны траектории мяча через после начала движения.
Пренебрегая сопротивлением воздуха, определить 1) время полета мяча до его падения на землю; 2) дальность полета мяча; 3) скорость мяча в момент падения; 4) радиус кривизны траектории мяча через после начала движения.
Дано: Решение:
Направим оси прямоугольной системы координат так, как показано на рис. 1.3.3. Начало отсчета поместим на поверхности земли под точкой бросания. Начальные условия:
, , , .
Проекции ускорения мяча на оси координат при отсутствии сопротивления воздуха равны:
,.
Запишем системы уравнений 1.3.7 и 1.3.8 с учетом этих значений:
(1) (2)
Пусть при мяч упал на землю. Это означает, что , и уравнения системы (2) принимают вид: Решая их, находим
В момент падения на землю система уравнений (1) принимает вид:
С учетом найденного значения получим , следовательно, скорость мяча в момент падения на землю будет равна:
.
Направление вектора скорости в любой момент времени определяется углом , который вектор составляет с горизонтом, причем
.
Полное ускорение при движении мяча в поле тяготения Земли всегда равно и направлено вертикально вниз. По этой причине .
Из рис. 1.3.3 видно, что . Учитывая, что , а полная скорость , находим радиус кривизны траектории в любой момент времени: .
В момент времени после начала движения .
Ответ:, , .
Пример 1.3.6.Снаряд выпущен из пушки с начальной скоростью под углом к горизонту. Пренебрегая сопротивлением воздуха, определить: 1) время подъема снаряда на максимальную высоту ; 2) наибольшую высоту подъема снаряда ; 3) дальность полета снаряда ; 4) время полета до момента падения снаряда на землю; 5) скорость в момент его падения на землю; 6) радиус кривизны траектории снаряда в ее наивысшей точке; 7) уравнение траектории снаряда.
Решение:
Направим оси прямоугольной системы координат так, как показано на рис. 1.3.4. Начало отсчета поместим в точку бросания. Начальные условия движения снаряда таковы:
, , , .
При отсутствии сопротивления воздуха , . С учетом этих значений системы уравнений 1.3.7 и 1.3.8 примут вид:
(1) (2)
Пусть при снаряд достиг максимальной высоты. В данный момент , .
Тогда вторые уравнения обеих систем примут вид:
откуда ,
.
Пусть при снаряд упал на землю. В данный момент , .
Тогда система (2) будет иметь вид: откуда
и .
Скорость снаряда в любой момент времени равна . Учитывая, что в момент падения на землю система (1) примет вид
подставим в нее найденное значение :
Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, скорость снаряда в момент падения его на землю будет равна
.
Радиус кривизны траектории снаряда в наивысшей точке траектории , где скорость в наивысшей точке траектории. Учитывая, что в наивысшей точке траектории и , получаем и
.
Уравнение траектории можно получить, исключив из системы (2) время :
.
График траектории представляет собой участок параболы, ветви которой направлены вниз.
Ответ:, , , , , , .
Читайте также
В случае неравномерного движения важно знать, как быстро изменяется скорость с течением времени. Физической величиной, характеризующей быстроту изменения скорости по модулю и направлению, является ускорение. Пусть вектор задает скорость точки А в момент времени . За… [читать подробенее]
Векторную функцию в виде графика изобразить нельзя. Рис.4.3. Площадь заштрихованной полоски приближенно равна Vi&… [читать подробенее]
Векторную функцию в виде графика изобразить нельзя. Рис.4.3. Площадь заштрихованной полоски приближенно равна Vi&… [читать подробенее]
Ускорение – это векторная величина, характеризующая быстроту изменения скорости материальной точки по модулю и направлению. Вектор среднего ускорения точки за время определяется отношением изменения скорости к промежутку времени : (1.1.10) Единица ускорения – . … [читать подробенее]
Чаще всего приходится иметь дело с движением, в котором вектор скорости не остается постоянным, а меняется как по модулю, так и по направлению. Физической величиной, характеризующей быстроту изменения скорости по модулю и направлению, является ускорение. Пусть вектор… [читать подробенее]
В случае неравномерного движения важно знать, как быстро изменяется скорость с течением времени. Физической величиной, характеризующей быстроту изменения скорости по модулю и направлению, является ускорение. Рассмотрим плоское движение,т. е. такое, при котором все… [читать подробенее]
В случае неравномерного движения важно знать, как быстро изменяется скорость с течением времени. Физической величиной, характеризующей быстроту изменения скорости по модулю и направлению, является ускорение. Рассмотрим плоское движение, т. е. движение, при котором все… [читать подробенее]
Ускорение – физическая величина, характеризующей быстроту изменения скорости по модулю и направлению. Средним ускорением неравномерного движения в интервале от t до t + &… [читать подробенее]
Мгновенный центр ускорений (МЦУ). Способы нахождения.
Мгновенный центр ускорений (МЦУ). Способы нахождения.16) Мгновенный центр ускорений (МЦУ). Способы нахождения.
При определении скоростей точек плоской фигуры было установлено, что в каждый момент времени существует такая точка Р фигуры (МЦС), скорость которой равна нулю. Покажем, что в каждый момент времени существует точка фигуры, ускорение которой равно нулю. Такая точка называется мгновенным центром ускорений (МЦУ). Обозначим ее через Q.
Рассмотрим плоскую фигуру, совершающую движение в плоскости рисунка (рис.). Примем за полюс какую-либо точку А, модуль и направление ускорения аА которой известны в рассматриваемый момент времени. Пусть в этот момент времени известны угловая скорость и угловое ускорение фигуры. Из формулы следует, что точка Q будет МЦУ, если , т. е. когда . Так как вектор aQA составляет с линией AQ угол “альфа” , то параллельный ему вектор аА направлен к линии, соединяющей полюс А с точкой Q, также под углом “альфа” (см. рис.).
Проведем через полюс А прямую MN, составляющую с вектором его ускорения угол “альфа”, откладываемый от вектора аА в направлении дуговой стрелки углового ускорения. Тогда на луче AN найдется точка Q, для которой . Поскольку, согласно , , точка Q (МЦУ) будет отстоять от полюса А на расстоянии .
Таким образом, в каждый момент движения плоской фигуры, если угловая скорость и угловое ускорение не равны нулю одновременно, имеется единственная точка этой фигуры, ускорение которой равно нулю. В каждый последующий момент времени МЦУ плоской фигуры будет находиться в различных ее точках.
Если МЦУ — точку Q выбрать за полюс, то ускорение любой точки А плоской фигуры
, так как aQ = 0. Тогда . Ускорение аА составляет с отрезком QA, соединяющим эту точку с МЦУ, угол “альфа”, откладываемый от QA в сторону, противоположную направлению дуговой стрелки углового ускорения. Ускорения точек фигуры при плоском движении пропорциональны расстояниям от МЦУ до этих точек.
Таким образом, ускорение всякой точки фигуры при ее плоском движении определяется в данный момент времени так же, как и при вращательном движении фигуры вокруг МЦУ.
Рассмотрим случаи, когда положение МЦУ можно определить с помощью геометрических построений.
1) Пусть известны направления ускорений двух точек плоской фигуры, ее угловые скорость и ускорение. Тогда МЦУ лежит на пересечении прямых линий, проведенных к векторам ускорений точек фигуры под одним и тем же острым углом:, отложенным от векторов ускорений точек в направлении дуговой стрелки углового ускорения.
2) Пусть известны направления ускорений хотя бы двух точек плоской фигуры, ее угловое ускорение = 0, а угловая скорость не равна 0.
3) Угловая скорость= 0, угловое ускорение не равно 0. Угол прямой.
Используются технологии uCozМгновенный центр скоростей в теоретической механике
Содержание:
Мгновенный центр скоростей:
В каждый момент времени при плоском движении фигуры в ее плоскости, если Обозначим ее
Для доказательства этой теоремы достаточно указать способ нахождения мгновенного центра скоростей, если известны по модулю и направлению скорость какой-либо точки плоской фигуры и угловая скорость этой фигуры в рассматриваемый момент времени. Пусть вращение происходит по часовой стрелке ( и ) (рис. 46). Скорость точки плоской фигуры равна нулю, если скорость полюса и скорость от вращения вокруг полюса в этой точке равны по модулю, но противоположны по направлению. Эти точки лежат на перпендикуляре к скорости в точке . В других точках векторная сумма двух векторов не может быть равна нулю.
Рис. 46
Итак, если , то .
Ho
следовательно,
Таким образом, мгновенный центр скоростей находится на перпендикуляре к скорости , проведенном из точки , на расстоянии .
Мгновенный центр скоростей является единственной точкой плоской фигуры для данного момента времени. В другой момент времени мгновенным центром является уже другая точка плоской фигуры.
Если мгновенный центр известен, то, приняв его за полюс и учитывая, что скорость его в этом случае равна нулю, согласно (3) и (4), для точки фигуры имеем
где —расстояние от точки до мгновенного центра скоростей.
По направлению скорость в этом случае перпендикулярна отрезку . Для точки , аналогично,
причем скорость перпендикулярна отрезку .
Из (5) и (6) имеем
и
Следовательно, если мгновенный центр скоростей известен, то скорости точек плоской фигуры при ее движении в своей плоскости вычисляют так же, как и в случае вращения фигуры в рассматриваемый момент вокруг своего мгновенного центра скоростей с угловой скоростью .
Для нахождения скоростей точек тела при его плоском движении обычно предварительно находят мгновенный центр скоростей. Но можно применить формулу, выражающую зависимость между скоростями двух точек тела.
Рассмотрим способы нахождения мгновенного центра скоростей. Существует два основных способа его нахождения: из механических условий задачи и по скоростям точек плоской фигуры.
В некоторых случаях удается сразу указать точку плоской фигуры, скорость которой в рассматриваемый момент равна нулю. Эти точки в таких задачах и являются мгновенными центрами скоростей. Так, в случае качения без скольжения одного тела по поверхности другого неподвижного тела точка соприкосновения поверхностей тел и является мгновенным центром скоростей.
Рис. 47
Рис. 48
Например, при качении без скольжения колеса по неподвижной прямой линии (см. рис. 52) и одного колеса по неподвижному другому колесу (см. рис. 61) мгновенный центр скоростей находится в точках соприкосновения колеса с прямой и соответственно колеса с колесом. В общем случае, если известны скорости двух точек плоской фигуры (рис. 47), мгновенный центр скоростей находится на пересечении перпендикуляров к скоростям этих точек.
В том случае, когда точки лежат на общем перпендикуляре к скоростям этих точек, скорости точек параллельны и концы их лежат на одной прямой, проведенной через мгновенный центр скоростей (рис. 48 и 49), так как скорости точек пропорциональны расстояниям от этих точек до мгновенного центра скоростей. Если скорости двух точек, расположенных на общем перпендикуляре к этим скоростям, еще и равны (рис. 50), то имеем мгновенное поступательное движение плоской фигуры, при котором скорости всех точек фигуры одинаковы по модулю и направлению. Угловая скорость плоской фигуры при мгновенном поступательном движении равна нулю, и в этом случае, согласно формуле (7), мгновенный центр скоростей находится в бесконечности.
Рис. 49
Рис. 50
Рис. 51
Рис. 52
Заметим, что при мгновенном поступательном движении только скорости точек одинаковы, а их ускорения в общем случае различны. Невозможен случай, когда скорости двух точек, не лежащих на общем перпендикуляре к скоростям, не равны друг другу по модулю, но параллельны (рис. 51), так как для него не выполняется теорема о проекциях скоростей двух точек тела на прямую, соединяющую эти точки.
Пример:
Колесо радиусом (рис. 52) катится без скольжения по неподвижной прямой, имея скорость центра . Определить скорости точек , и обода колеса в данный момент времени.
Решение. Мгновенный центр скоростей в этом случае находится в точке соприкосновения колеса с прямой. Угловая скорость колеса определяется по формуле (7):
По формуле (5) для скоростей указанных точек имеем
так как
Скорости точек колеса направлены по перпендикулярам к отрезкам прямых, соединяющих мгновенный центр скоростей с рассматриваемыми точками.
Вычисление угловой скорости при плоском движенииУгловую скорость плоской фигуры при плоском движении можно вычислить, согласно ее определению, как
Затем ее можно определить по формуле (7):
Чтобы определить угловую скорость, надо скорость какой-либо точки плоской фигуры разделить на расстояние от этой точки до мгновенного центра скоростей. Направление вращения определяем по направлению скорости какой-либо точки, считая, что плоская фигура в данный момент вращается вокруг мгновенного центра скоростей с угловой скоростью .
Рис. 53
Угловую скорость при плоском движении можно вычислить путем предварительного нахождения скорости какой-либо точки плоской фигуры от вращения фигуры вокруг другой ее точки, принятой за полюс, например или . Тогда угловая скорость, согласно формуле (4),
Знак угловой скорости определяют по направлению относительной скорости какой-либо точки фигуры от вращения фигуры вокруг другой ее точки, выбранной за полюс.
Применяют и другие способы определения угловой скорости. Так, если предварительно установить зависимость угла поворота плоской фигуры от линейных и угловых величин других плоских фигур тождественным соотношением, то, дифференцируя его по времени, получаем соотношение, из которого иногда удается определить искомую угловую скорость. Этот способ используют часто для нахождения зависимости угловых скоростей отдельных звеньев плоских механизмов.
Пример:
В кривошипно-шатунном механизме (рис. 53) даны длины кривошипа , шатуна и расстояние от оси вращения кривошипа до направляющей ползуна . Установить зависимость между угловыми скоростями кривошипа и шатуна при любом положении механизма.
Решение. Положение кривошипа определяется углом , а шатуна — углом . До тех пор пока , справедливо тождество
Дифференцируя это тождество по времени, получим
Но ; следовательно,
Полученное соотношение и является искомой зависимостью между угловыми скоростями кривошипа и шатуна. При имеем частный случай кривошипно-шатунного механизма. Если дополнительно , то и .
Направления вращений кривошипа и шатуна противоположны. При вращении кривошипа против часовой стрелки шатун вращается по часовой стрелке.
Ускорения точек тела при плоском движенииРассматривая плоское движение плоской фигуры как сложное, состоящее из переносного поступательного вместе с полюсом и относительного вращательного вокруг , по теореме о сложении ускорений для точки имеем
Рис. 54
Так как переносное движение является поступательным вместе с точкой фигуры, то переносное ускорение
Относительное ускорение точки от вращения вокруг полюса обозначим . После этого формула (9) принимает вид
т. е. ускорение какой-либо точки плоской фигуры при плоском движении равно векторной сумме ускорения полюса и ускорения этой точки от вращательного движения плоской фигуры вокруг полюса.
Ускорение от относительного вращательного движения вокруг полюса, как и в случае вращения тела вокруг неподвижной оси, состоит из касательной и нормальной составляющих и :
причем
и _________
Касательное относительное ускорение направлено по перпендикуляру к отрезку в сторону дуговой стрелки углового ускорения (рис. 54, а). Нормальное относительное ускорение соответственно направлено по линии от точки к полюсу . Наконец, полное относительное ускорение составляет с отрезком угол , тангенс которого можно определить по формуле
Из формулы (15) следует, что угол для всех точек плоской фигуры одинаков. При угол от ускорения к отрезку надо откладывать против часовой стрелки. При его надо откладывать по часовой стрелке, т. е. во всех случаях, независимо от направления вращения фигуры, угол всегда надо откладывать в направлении дуговой стрелки углового ускорения. В соответствии с (10) и (11) можно построить в выбранном масштабе многоугольник ускорений для точки (рис. 54, б).
Формулу (10), определяющую зависимость ускорений двух точек плоской фигуры, можно получить непосредственным дифференцированием векторного равенства для скоростей, справедливого в любой момент времени. Имеем
Продифференцируем по времени обе части этого равенства, учитывая изменения векторных величин относительно неподвижной системы координат (полные производные). Получаем
Здесь — ускорения точек и относительно неподвижной системы координат; — угловое ускорение плоской фигуры. У вектора постоянный модуль; следовательно, его производная по времени выражается в форме
Объединяя полученные результаты, получаем
Рассуждения, аналогичные тем, которые проведены для скорости , позволяют сделать вывод о том, что
т. е. являются соответственно касательным и нормальным ускорениями от вращения плоской фигуры вокруг точки . Следовательно,
Пример:
Колесо радиусом катится со скольжением по неподвижной прямой, совершая плоское движение (рис. 55). Ускорение центра колеса в рассматриваемый момент времени , а угловая скорость и угловое ускорение колеса и . Дуговые стрелки для и направлены по часовой стрелке, т. е. и . Определить в этот момент времени ускорения точек , и , расположенных на концах вертикального и горизонтального диаметров обода колеса.
Решение. Ускорение точки , приняв за полюс точку , определим по формуле
и аналогичным формулам для точек и . Для касательного и нормального ускорений точки от вращения колеса вокруг точки имеем
Рис. 55
Ускорение перпендикулярно отрезку и направлено в сторону, указываемую дуговой стрелкой , а ускорение направлено от точки к точке , принятой за полюс. Аналогично направлены ускорения для точек и .
Так как для точки ускорения и направлены по одной прямой, то, предварительно их сложив, получим две перпендикулярные составляющие ускорения и, следовательно,
Для точки
так как
Окончательно для точки имеем
Для точки соответственно
В том случае, когда колесо катится без скольжения, точка является мгновенным центром скоростей и скорость точки в любой момент времени равна нулю. Скорость точки в этом случае можно определить по формуле
Дифференцируя по времени обе части этого тождества и приравнивая результат дифференцирования, получим
или
так как точка движется прямолинейно, и
Учитывая, что
имеем
Следовательно, при качении колеса по прямой без скольжения
т. е. ускорение мгновенного центра скоростей, скорость которого равна нулю, не равно нулю.
Если угловое ускорение не задано, то при отсутствии скольжения колеса по прямой его можно определить по формуле
Скорость при движении с постоянным ускорением. Прямолинейное движение с постоянным ускорением
На данном уроке, тема которого: «Уравнение движения с постоянным ускорением. Поступательное движение», мы вспомним, что такое движение, каким оно бывает. Также вспомним, что такое ускорение, рассмотрим уравнение движения с постоянным ускорением и как им пользоваться для определения координаты движущегося тела. Рассмотрим пример задачи для закрепления материала.
Главная задача кинематики – определить положение тела в любой момент времени. Тело может покоиться, тогда его положение меняться не будет (см. рис. 1).
Рис. 1. Покоящееся тело
Тело может двигаться прямолинейно с постоянной скоростью. Тогда его перемещение будет изменяться равномерно, то есть одинаково за равные промежутки времени (см. рис. 2).
Рис. 2. Перемещение тела при движении с постоянной скоростью
Перемещение , скорость, умноженная на время, это мы давно умеем делать. Тело может двигаться с постоянным ускорением, рассмотрим такой случай (см. рис. 3).
Рис. 3. Движение тела с постоянным ускорением
Ускорение
Ускорение – это изменение скорости за единицу времени (см. рис. 4): Рис. 4. Ускорение Скорость – векторная величина, поэтому и изменение скорости, т. е. разность векторов конечной и начальной скорости, является вектором. Ускорение – тоже вектор, направленный туда же, куда и вектор разности скоростей (см. рис. 5). Мы рассматриваем прямолинейное движение, поэтому можно выбрать координатную ось вдоль прямой, вдоль которой происходит движение, и рассматривать проекции векторов скорости и ускорения на эту ось: |
Тогда равномерно изменяется его скорость: (если его начальная скорость была равна нулю). Как теперь найти перемещение? Скорость умножить на время – нельзя : скорость постоянно менялась; какую брать? Как определить, где при таком движении будет находиться тело в любой момент времени – сегодня мы эту проблему решим.
Сразу определимся с моделью: мы рассматриваем прямолинейное поступательное движение тела. В таком случае можем применять модель материальной точки. Ускорение направлено вдоль той же прямой, вдоль которой материальная точка движется (см. рис. 6).
Поступательное движение
Поступательное движение – это такое движение, при котором все точки тела движутся одинаково: с одинаковой скоростью, совершая одинаковое перемещение (см. рис. 7). Рис. 7. Поступательное движение А как еще может быть? Взмахните рукой и проследите: понятно, что ладонь и плечо двигались по-разному. Посмотрите на колесо обозрения: точки вблизи оси почти не движутся, а кабинки движутся с другой скоростью и по другим траекториям (см. рис. 8). Рис. 8. Движение выбранных точек на колесе обозрения Посмотрите на движущийся автомобиль: если не учитывать вращение колес и движение частей мотора, все точки автомобиля движутся одинаково, движение автомобиля считаем поступательным (см. рис. 9). Рис. 9. Движение автомобиля Тогда нет смысла описывать движение каждой точки, можно описать движение одной. Автомобиль считаем материальной точкой. Обратите внимание, что при поступательном движении линия, соединяющая любые две точки тела при движении, остается параллельной сама себе (см. рис. 10). Рис. 10. Положение линии, соединяющей две точки |
Автомобиль ехал прямолинейно в течение часа. В начале часа его скорость была 10 км/ч, а в конце – 100 км/ч (см. рис. 11).
Рис. 11. Рисунок к задаче
Скорость изменялась равномерно. Сколько километров проехал автомобиль?
Проанализируем условие задачи.
Скорость автомобиля изменялась равномерно, то есть всё время пути его ускорение было постоянным. Ускорение по определению равно:
Автомобиль ехал прямолинейно, поэтому мы можем рассматривать его движение в проекции на одну ось координат:
Найдем перемещение.
Пример возрастающей скорости
На стол кладут орехи, по одному ореху в минуту. Понятно: сколько минут пройдет, столько орехов на столе окажется. А теперь представим, что скорость накладывания орехов равномерно возрастает с нуля: первую минуту орехов не кладут, во вторую кладут один орех, потом два, три и так далее. Сколько орехов окажется на столе через какое-то время? Понятно, что меньше, чем если бы максимальная скорость поддерживалась всегда. Причем хорошо видно, что меньше в 2 раза (см. рис. 12). Рис. 12. Количество орехов при разной их скорости выкладывании Так же и с равноускоренным движением: допустим, сначала скорость была равна нулю, в конце стала равна (см. рис. 13). Рис. 13. Изменение скорости Если бы тело постоянно двигалось с такой скоростью, его перемещение было бы равно , но поскольку скорость равномерно возрастала – то в 2 раза меньше. |
Мы умеем находить перемещение при РАВНОМЕРНОМ движении: . Как обойти эту проблему? Если скорость изменяется не на много, то движение можно приближенно считать равномерным. Изменение скорости будет небольшим за небольшой интервал времени (см. рис. 14).
Рис. 14. Изменение скорости
Поэтому разобьем время в пути T на N небольших отрезков длительностью (см. рис. 15).
Рис. 15. Разбиение отрезка времени
Подсчитаем перемещение на каждом отрезке времени. Скорость прирастает на каждом интервале на:
На каждом отрезке мы будем считать движение равномерным и скорость приближенно равной начальной скорости на данном отрезке времени. Посмотрим, не приведет ли к ошибке наше приближение, если на небольшом промежутке движение будем считать равномерным. Максимальная ошибка будет равна:
и суммарная ошибка за всё время пути -> . При больших N принимаем ошибка близка к нулю. Это мы увидим и на графике (см. рис. 16): на каждом интервале будет ошибка, но суммарная ошибка при достаточно большом количестве интервалов будет пренебрежимо мала.
Рис. 16. Ошибка на интервалах
Итак, каждое следующее значение скорости на одну и ту же величину больше предыдущего. Из алгебры мы знаем, что это арифметическая прогрессия с разностью прогрессии :
Путь на участках (при равномерном прямолинейном движении (см. рис. 17) равен:
Рис. 17. Рассмотрение участков движения тела
На втором участке:
На n-м участке путь равен:
Арифметическая прогрессия
Просуммируем все пути. Это будет сумма первых N членов арифметической прогрессии:
Т. к. мы разбили движение на много интервалов, то можно считать, что , тогда:
У нас было множество формул, и, чтобы не запутаться, мы не писали каждый раз индексы х, но рассматривали всё в проекции на координатную ось.
Итак, мы получили главную формулу равноускоренного движения: перемещение при равноускоренном движении за время T, которую мы наряду с определением ускорения (изменение скорости за единицу времени) будем использовать для решения задач:
Мы занимались решением задачи об автомобиле. Подставим в решение числа и получим ответ: автомобиль проехал 55,4 км.
Математическая часть решения задачи
С перемещением мы разобрались. А как определить координату тела в любой момент времени?
По определению перемещение тела за время – это вектор, начало которого находится в начальной точке движения, а конец – в конечной точке, в которой тело будет через время . Нам нужно найти координату тела, поэтому запишем выражение для проекции перемещения на ось координат (см. рис. 18):
Рис. 18. Проекция перемещения
Выразим координату :
То есть координата тела в момент времени равна начальной координате плюс проекция перемещения, которое совершило тело за время . Проекцию перемещения при равноускоренном движении мы уже нашли, осталось подставить и записать:
Это и есть уравнение движения с постоянным ускорением. Оно позволяет узнать координату движущейся материальной точки в любой момент времени. Понятно, что момент времени мы выбираем в пределах промежутка, когда работает модель: ускорение постоянное, движение прямолинейное.
Почему уравнение движения нельзя применять для нахождения пути
В каких случаях мы можем считать перемещение по модулю равным пути? Когда тело движется вдоль прямой и не меняет направления. Например, при равномерном прямолинейном движении мы не всегда четко оговариваем, путь мы находим или перемещение, всё равно они совпадают. При равноускоренном движении скорость изменяется. Если скорость и ускорение направлены в противоположные стороны (см. рис. 19), то модуль скорости убывает, и в какой-то момент он станет равен нулю и скорость поменяет направление, то есть тело начнет двигаться в противоположную сторону. Рис. 19. Модуль скорости убывает И тогда, если в данный момент времени тело находится на расстоянии 3 м от начала наблюдения, то его перемещение равно 3 м, но если тело сначала прошло 5 м, затем развернулось и прошло еще 2 м, то путь будет равен 7 м. И как же его найти, если не знать этих чисел? Просто надо найти момент, когда скорость равна нулю, то есть когда тело развернется, и найти путь к этой точке и от нее (см. рис. 20). Рис. 20. Момент, когда скорость равна 0 |
Список литературы
- Соколович Ю.А., Богданова Г.С Физика: Справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.
- Ландсберг Г.С. Элементарный учебник физики; т.1. Механика. Теплота. Молекулярная физика – М.: Издательство «Наука», 1985.
- Интернет портал «kaf-fiz-1586.narod.ru» ()
- Интернет портал «Учеба – Легко» ()
- Интернет портал «Гипермаркет знаний» ()
Домашнее задание
- Что такое арифметическая прогрессия?
- Какое движение называется поступательным?
- Чем характеризуется векторная величина?
- Запишите формулу для ускорения через изменение скорости.
- Какой вид имеет уравнение движения с постоянным ускорением?
- Вектор ускорения направлен в сторону движения тела. Как будет изменять свою скорость тело?
Среди разнообразных движений с постоянным уско-рением наиболее простым является прямолинейное движение. Если при этом модуль скорости возрастает, то движение иногда называют равноускоренным, а при уменьшении модуля скорости – равнозамедленным. Подобного рода движения совершает поезд, отходящий от станции или приближающийся к ней. Равно-ускоренно движется камень, брошенный вертикально вниз, а равнозамедленно – камень, брошенный вертикально вверх.
Для описания прямолинейного движения с постоянным ускорением можно обойтись одной осью координат (например, осью X), которую целесообразно направить вдоль траектории движения. В этом случае любая задача решается при помощи двух уравнений:
(1.20.1)
и
2? Проекция перемещения и путь при прямолинейном движении с постоянным ускорением Проекцию на ось X перемещения, равную Ах = х – х0, найдем из уравнения (1.20.2):
М2
Ax = v0xt +(1.20.3)
Если скорость тела (точки) не меняет своего направления, то путь равен модулю проекции перемещения
.2
s = |Ax| =
(1.20.4)
axt
VoJ + -о
Если же скорость меняет свое направление, то путь вычисляется сложнее. = v. Следовательно, при прямолинейном движении с по- t
стоянным ускорением проекция средней скорости на ось X равна:
!)аг + Vr
vx= 0х2 . (1.20.5)
Можно доказать, что если какая-нибудь другая физическая величина находится в линейной зависимости от времени, то среднее по времени значение этой величины равно полусумме ее наименьшего и наибольшего значений в течение данного промежутка времени.
Если при прямолинейном движении с постоянным ускорением направление скорости не меняется, то средний модуль скорости равен полусумме модулей начальной и конечной скоростей, т. е.
К* + vx\ v0 + v
Связь между проекциями начальной и конечной скоростей, ускорения и перемещения
Согласно формуле (1.19.1)
Лх= °*2 xt. (1.20.7)
Время t выразим из формулы (1.20.1)
Vx~V0x ах
и подставим в (1.20.7). Получим:
Vx + V0x Vx – v0x V2X – i>jj
= 2 ST” –257-
Отсюда
v2x = v Іх+2а3Лх. (1.20.8)
Полезно запомнить формулу (1.20.8) и выражение (1.20.6) для средней скорости. Эти формулы могут по-надобиться для решения многих задач.
? 1. Как направлено ускорение при отправлении поезда от станции (разгон)? При подходе к станции (торможение)?
Начертите график пути при разгоне и при торможении.
Докажите самостоятельно, что при равноускоренном прямолинейном движении без начальной скорости пути, проходимые телом за равные последовательные промежутки времени, пропорциональны последовательным нечетным числам:
Sj: S2* Sg … = 1: 3: 5: … . Впервые это было доказано Галилеем.
Еще по теме §1.20. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ С ПОСТОЯННЫМ УСКОРЕНИЕМ:
- § 4.3. НЕИНЕРЦИАЛЬНЫЕ СИСТЕМЫ ОТСЧЕТА, ДВИЖУЩИЕСЯ ПРЯМОЛИНЕЙНО С ПОСТОЯННЫМ УСКОРЕНИЕМ
- §1.18. ГРАФИКИ ЗАВИСИМОСТИ МОДУЛЯ И ПРОЕКЦИИ УСКОРЕНИЯ И МОДУЛЯ И ПРОЕКЦИИ СКОРОСТИ ОТ ВРЕМЕНИ ПРИ ДВИЖЕНИИ С ПОСТОЯННЫМ УСКОРЕНИЕМ
Ускорение. Прямолинейное движение с постоянным ускорением. Мгновеннная скорость.
Ускорение показывает, как быстро меняется скорость тела.
t 0 = 0c v 0 = 0 м/с Скорость изменилась на v = v 2 – v 1 в течение
t 1 = 5c v 1 = 2 м/ с промежутка времени = t 2 – t 1 . Значит за 1 с скорость
t 2 = 10c v 2 = 4 м/с тела увеличится на = .
t 3 = 15c v 3 = 6 м/с = или = . (1 м/с 2)
Ускорение – векторная величина, равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.
Физический смысл : а = 3 м/с 2 – это значит, что за 1 с модуль скорости меняется на 3 м/с.
Если тело разгоняется а>0, если тормозит а
Аt = ; = + аt мгновенная скорость тела в любой момент времени. (Функция v(t)).
Перемещение при равноускоренном движении. Уравнение движения
Д
ля
равномерного движения S=v*t,
где v
и t
являются сторонами прямоугольника под
графиком скорости. Т.е. перемещение =
площади фигуры под графиком скорости.
Аналогично
можно найти перемещение при равноускоренном
движении. Нужно всего лишь найти отдельно
площадь прямоугольника, треугольника
и сложить их. Площадь прямоугольника
v 0 t,
площадь треугольника (v-v 0)t/2,
где мы делаем замену v
– v 0 =
аt . Получим s
= v 0 t
+ аt 2 /2
s = v 0 t + аt 2 /2
Формула перемещения при равноускоренном движении
Учитывая, что вектор s = х-х 0 , получим х-х 0 = v 0 t + аt 2 /2 или вынесем начальную координату вправо х = х 0 + v 0 t + аt 2 /2
х = х 0 + v 0 t + аt 2 /2
По этой формуле можно найти координату ускоренно движущегося тела в любой момент времени
При равнозамедленном движении перед буквой «а» в формулах знак + можно заменить на –
Движение с постоянным ускорением–это такое движение, при котором вектор ускорения остается постоянным как по величине, так и по направлению. Примером такого типа движения может служить движения точки в поле силы тяжести (как вертикально, так и под углом к горизонту).
Используя определение ускорения получим следующее соотношение
После интегрирования
имеем равенство
.
С учетом того, что
вектор мгновенной скорости есть
,
будем иметь следующее выражение
Интегрирование последнего выражение дает следующее соотношение
. Откуда имеем получаем уравнение движения точки с постоянным ускорением
.
Примеры векторных уравнений движения материальной точки
Равномерное
прямолинейное движение (
):
. (1.7)
Движение с постоянным
ускорением (
):
. (1.8)
Зависимость скорости от времени при движении точки с постоянным ускорением имеет вид:
. (1.9)
Вопросы для самоконтроля.
Сформулируйте определение механического движения.
Дайте определение материальной точки.
Каким образом определяется положение материальной точки в пространстве в векторном способе описания движения?
В чем сущность векторного метода описания механического движения? Какие характеристики используются для описания этого движения?
Дайте определения векторов средней и мгновенной скорости. Как определяется направление этих векторов?
Дайте определение векторов среднего и мгновенного ускорений.
Какое из соотношений является уравнением движения точки с постоянным ускорением? Какое соотношение определяет зависимость вектора скорости от времени?
§1.2. Координатный способ описания движения
В координатном
способе для описания движения выбирают
систему координат (например, декартову).
Начало отсчета жестко закрепляют с
выбранным телом (телом
отсчета ).
Пусть
единичные орты, направленные в
положительные стороны осейOX,
OY
и OZ
соответственно. Положение точки задается
координатами
.
Вектор мгновенной скорости определяется следующим образом:
где
проекции
вектора скорости на оси координат, а
производные от координат по времени.
Длина вектора скорости связана с его проекциями соотношением:
. (1.11)
Для вектора мгновенного ускорения справедливо соотношение:
где
проекции
вектора ускорения на оси координат, а
производные по времени от проекций
вектора скорости.
Длина вектора мгновенного ускорения находится по формуле:
. (1.13)
Примеры уравнений движения точки в декартовой системе координат
. (1.14)
Уравнения
движения:
. (1.15)
Зависимости проекций вектора скорости на оси координат от времени:
(1.16)
Вопросы для самоконтроля.
В чем сущность координатного способа описания движения?
Каким соотношением определяется вектор мгновенной скорости? По какой формуле вычисляется величина вектора скорости?
Каким соотношением определяется вектор мгновенного ускорения? По какой формуле вычисляется величина вектора мгновенного ускорения?
Какие соотношения называют уравнениями равномерного движения точки?
Какие соотношения называют уравнениями движения с постоянным ускорением? По каким формулам рассчитывают проекции мгновенной скорости точки на оси координат?
Мгновенное ускорение
В физике мы говорим, что тело имеет ускорение, когда происходит изменение вектора скорости, либо по величине, либо по направлению, что мы уже видели в разделе, посвященном концепции ускорения. В этом разделе мы собираемся изучить мгновенное ускорение, которое представляет собой изменение скорости, имеющее место в определенное время.
Мгновенное ускорение
Мгновенное ускорение тела – это ускорение тела в конкретный момент времени, в определенной точке его траектории.Чтобы точно определить понятие мгновенного ускорения , мы должны начать со среднего ускорения в интервале и сделать его бесконечно малым (∆t → 0). Этот процесс похож на тот, который мы использовали для вычисления мгновенной скорости из средней скорости.
Мгновенное ускорение , или просто ускорение , определяется как предел среднего ускорения, когда рассматриваемый интервал времени приближается к 0.Он также определяется аналогично производной скорости по времени . Это дается выражением:
a → = lim∆t → 0a → a = lim∆t → 0∆v → ∆ t = dv → dt
где:
- a →: Разгон кузова
- a → a: Вектор среднего ускорения
- ∆v →: вектор изменения скорости
- ∆ t: интервал времени, который приближается к нулю, то есть бесконечно малый интервал
Ускорение – это величина вектора.Размерное уравнение мгновенного ускорения имеет вид [a] = [L] [T] -2 и, следовательно, его единица измерения в Международной системе (СИ) – это метров в секунду. в квадрате [м / с 2 ] .
Вы можете найти вектор ускорения , выраженный его декартовыми компонентами, таким образом:
Вектор ускорения в 3-х мерных декартовых координатах:
a → = axi → + ayj → + azj → = lim∆t → 0∆vx∆ti → + lim∆t → 0∆vy∆tj → + lim∆t → 0∆vz∆tj → = dvxdti → + dvydtj → + dvxdtj →
Вектор ускорения в двумерных декартовых координатах:
a → = axi → + ayj → = lim∆t → 0∆vx∆ti → + lim∆t → 0∆vy∆tj → = dvxdti → + dvydtj →
Как видите, мгновенное ускорение – это величина вектора, удовлетворяющая следующему:
- Ее звездная величина может быть выражена:
- Его направление , в целом , не совпадает с вектором скорости, но зависит от изменения, которое он испытывает.
Вектор скорости и вектор ускорения
Не путайте декартовы компоненты ускорения с внутренними компонентами, которые мы изучим в следующих разделах. Проще говоря, декартовы компоненты представляют собой разложение вектора ускорения на его соответствующие компоненты в декартовых осях. Внутренние компоненты возникают в результате нарушения вектора ускорения в системе отсчета, присущего движению.
И, наконец, чтобы указать вам, что, как и в случае с любым другим вектором, вы можете иногда найти вектор ускорения , записанный как в терминах его величины .Для этого просто умножьте величину вектора ускорения на единичный вектор с тем же направлением, что и a →, и который мы назовем u → a, потому что это единичный вектор в направлении ускорения.
а → = а⋅у → а
Пример
Метеорит движется в космосе со скоростью v⃗ (t) = (1 + 4 · t) i⃗ + t 2 Дж⃗ м . Рассчитать
a) Его среднее ускорение между моментами времени t 1 = 2 с и t 2 = 4 с.
б) Его ускорение при t 3 = 6 с.
– Мгновенная скорость и ускорение
Мы обсудили смещение и скорость . Напомним, что мы определили скорость как изменение смещения в единицу времени. Это могло произойти в результате изменения скорости объекта, направление или и то, и другое. Теперь определим новый термин: ускорение . Среднее ускорение (символ ‘ a ‘) – это изменение скорости на единицу time, или
Ускорение является векторной величиной – оно имеет как величину, так и направление.Мы может ускорять объект, изменяя его скорость в течение определенного промежутка времени, например ускоряя или замедляя движение вашего автомобиля. Нам знакома правая педаль газа на автомобилях – мы называем ее «ускоритель». Но педаль тормоза может нас замедлить, поэтому ее также можно назвать «акселератором». Мы также можем изменить скорость объекта, изменив направление движения объекта. Так что в У автомобиля руль тоже разновидность «акселератора».
Единицы ускорения – это единицы скорости в единицу времени.Обычно мы будет использовать наши стандартные единицы СИ, поэтому у нас будет (метров в секунду) в секунду или м / с / с. Обычно мы пишем это как м / с 2 . Например, если автомобиль разгоняется из состояния покоя до 20 м / с за 5 секунд, то его ускорение определяется как
. Направление ускорения обычно задается знаком смещение и скорость. Опять же, мы будем использовать положительные и отрицательные знаки, чтобы показать направление нашего ускорения. То, что мы выбираем в качестве положительного (левое, правое, верхнее, нижнее и т. Д.), В основном вопрос личных предпочтений, но в некоторых более поздних примерах решения проблем мы увидим, что иногда имеет смысл выбирать наши обозначения определенным образом.Мы можем сделать некоторые интересные наблюдения, которые могут концептуально помочь нам понять знаки. Объект может двигаться в прямом направлении (+ скорость) и иметь отрицательное ускорение. Примером этого является автомобиль с включенными тормозами. Объект может находиться в состоянии покоя (нулевая скорость) и иметь положительный ускорение (например, автомобиль, только трогающийся с места; именно ускорение автомобиля вызывает изменение скорости). Есть и другие примеры, которые мы обсудим в будущих уроках.
Движение с равномерным ускорением
Следующее, что нужно рассмотреть, – это специальный случай ускорения, который мы Буду изучать довольно долго: движение по прямой (направление не меняется) с равномерным изменением скорости.Мы иногда называем это равноускоренным движением . Вот предположения для наших следующих шагов:
- Объект движется по прямой
- Скорость изменения скорости одинакова (одинакова).
Пусть наше начальное время t o = 0, так что в любом случае D t = t f = t. Наше начальное положение и скорость будут обозначаться как x o и v или . Наконец, пусть x = конечное положение (x f ) и v = конечная скорость (v f ).Теперь мы готовы разработать основные уравнения линейного движения.
Из определения ускорения:
Если мы хотим найти скорость в любое время, мы можем переставить термины так, чтобы that
Это наше первое уравнение. Теперь вспомним из нашего урока по скорости, что средняя скорость (используя термины, которые мы определили выше и действительна только для равномерного ускорения) может быть выражена как
Второе уравнение может быть переписано как x = x o + в пр. т.В дальнейшем это можно переписать как
, что является невероятно полезным уравнением для определения положения как функция времени. Наконец, если мы возьмем уравнение v = v o + at и решим для t, мы получим
Подставив это уравнение в
и решая относительно v 2 , мы получаем еще одно уравнение для движение:
Так же, как мы построили график зависимости смещения от времени и скорости от времени, давайте также Рассмотрим график зависимости ускорения от времени для представления о равномерном ускорении.Данные для этого графика обычно начинаются с графика зависимости скорости от времени, поэтому давайте рассмотрим следующее. пример:
- На нашем графике выше (область 1) мы начинаем со скорости 0 м / с (при отдых) и разгонитесь до 10 м / с за 10 секунд.
- В районе 2 мы остаемся на скорости 10 метров в секунду еще 10 секунд.
- В районе 3 мы разгоняемся до 20 метров в секунду за 4 секунд.
- В районе 4 отрицательно разгоняемся до -10 м / с за 10 секунд.
- В районе 5 мы держимся на отметке -10 м / с.
Аналогично нашему уроку по графикам скоростей, мы рассмотрим наклон линии в каждом регионе. Здесь наш наклон (подъем за пробегом) – это изменение скорости, деленное на изменение во времени, или D v / D t. Это наше определение ускорения. Итак, – наклон графика зависимости скорости от времени. – ускорение объекта на этом интервале. Какие у нас трассы?
Номер интервала | Наклон = ускорение |
1 | D = 10 м / с за 10 секунд = 1 м / с 2 |
2 | D = 0 м / с на дюйм |
3 | D = 10 м / с в |
4 | D = -30 м / с |
5 | D = 0 м / с на дюйм |
Так как же выглядит график?
Обратите внимание, что каждая из вышеперечисленных линий является горизонтальной линией (или линией с нулевым уклоном). Это означает, что ускорение не меняется во время интервалов.Кажется, что от одного интервала к другому происходит изменение шага, но на самом деле между ними должна быть какая-то линия. интервал, так как действительно сложно получить мгновенное изменение ускорения от одного числа к другому.
Проверка, прочитали ли вы: Дополнительный балл в классе, на лист бумаги, нарисуйте приведенные выше графики и покажите мне времена, когда скорость этого объекта равна нулю, и вычислите для меня полное смещение объекта.
Часто бывает полезно узнать, что говорят другие тема.Попробуйте http://www.physicsclassroom.com/Class/1DKin/U1L1e.html для больше информации об ускорении.
Для практических задач попробуйте: От Университета Орегона, любой из этих:
Джанколи Практические вопросы с множественным выбором (вопросы 1-12)
Ускорение Рона Куртуса – Уроки физики: Школа чемпионов
SfC Home> Физика> Движение>
от Рона Куртуса
Ускорение объекта – это изменение его скорости с течением времени.Поскольку скорость является вектором (указывающим величину и направление), ускорение также является вектором.
Если величина и / или направление скорости изменяется, изменяется и ускорение. Если скорость замедляется, говорят, что объект замедляется или имеет отрицательное ускорение.
Единицы ускорения могут выражаться в метрах на секунду в квадрате (м / с 2 ) или в футах на секунду в квадрате (фут / с 2 ).
Ускорение учитывается при вычислении среднего и мгновенного ускорения, а также при рассмотрении равномерного ускорения при прямолинейном и круговом движении.
Вот некоторые вопросы, которые могут у вас возникнуть:
- Что такое среднее ускорение?
- Что такое мгновенное ускорение?
- Какие бывают примеры постоянного ускорения?
Этот урок ответит на эти вопросы. Полезный инструмент: Конвертация единиц
Среднее ускорение
Среднее ускорение – это изменение скорости за период времени.
Когда движущийся автомобиль ускоряется по прямой, он переходит с одной скорости на другую.Его среднее ускорение – это изменение скорости, деленное на время, необходимое для этого изменения:
a ср. = Δv / Δt
где
- a av – среднее ускорение (м / с 2 или фут / с 2 )
- Δv = v 2 – v 1 – изменение скорости ( Δ – дельта заглавной греческой буквы)
- Δt = t 2 – t 1 – временной интервал для Δv
Торможение – это замедление движущегося объекта.Его еще называют отрицательным ускорением.
Ускорение по прямой
Если объект движется по прямой линии, его ускорение – это разница его скорости или скорости вдоль этой линии, деленная на приращение времени.
Ускорение смены направления
Когда движущийся объект меняет направление, он ускоряется.
Если v 1 – начальная скорость в направлении x , а v 2 – скорость после изменения направления, ускорение определяется путем разрушения v 2 на x и y составляющие и деление на приращение времени.
Пусть v x будет компонентом v 2 вдоль той же оси, что и v 1 , и пусть v y будет компонентом на перпендикулярной оси. Тогда результирующие ускорения в двух направлениях равны:
a x = (v x – v 1 ) / Δt и a y = v y / Δt
Возведите компоненты в квадрат, сложите их и извлеките квадратный корень.Результирующее ускорение из-за изменения направления:
a = √ (a x 2 + a y 2 )
Мгновенное ускорение
Мгновенное ускорение – это изменение скорости с течением времени.
Мгновенное ускорение определяется как предел среднего ускорения, когда рассматриваемый интервал времени приближается к нулю. Оно также определяется аналогично производной скорости по времени.Это скорость изменения скорости в определенный момент времени.
Уравнение мгновенного ускорения:
a дюйм = lim (Δt = 0) Δv / Δt
, где lim (Δt = 0) Δv / Δt – это предел Δv / Δt , поскольку Δt приближается к 0
Обычно записывается как:
а = дв / дт
где
- dv является производным от v
- dt является производной от t
Производная v является пределом, поскольку Δv приближается к 0 .Аналогично для dt является пределом, поскольку Δt приближается к 0 . Производные обычно используются в математическом анализе.
Постоянное ускорение
Постоянное или равномерное ускорение – это когда скорость изменяется на одинаковую величину в каждый равный период времени.
Один из примеров равномерного ускорения касается ускорения свободного падения для падающих предметов. В таком случае величина скорости увеличивается с постоянной скоростью, но ее направление остается постоянным.
Другой пример постоянного ускорения – это когда величина скорости постоянна, но направление изменяется с постоянной скоростью. Это можно увидеть, качая груз, прикрепленный к тетиве, равномерным круговым движением.
Сводка
Ускорение объекта – это изменение его скорости с течением времени. Это может означать изменение скорости или направления объекта
Среднее ускорение – это изменение скорости за период времени.Мгновенное ускорение – это изменение скорости с течением времени.
Ускорение свободного падения и равномерное круговое движение являются примерами постоянного или равномерного ускорения.
Старайтесь делать все возможное
Ресурсы и ссылки
Полномочия Рона Куртуса
Сайтов
Acceleration – Physics Hypertextbook
Acceleration – Физический класс
Ускорение – Википедия
Физические ресурсы
Книги
(Примечание: Школа чемпионов может получать комиссионные от покупки книг)
Книги по физике движения с самым высоким рейтингом
Поделиться страницей
Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:
Студенты и исследователи
Веб-адрес этой страницы:
www.school-for-champions.com/science/
motion_acceleration. 2 м / с.2? почему мы не можем увидеть это изменение в таблице? Возможно, я звучу глупо или глупо, но я не знаю, что здесь происходит. Надеюсь, вы уловили то, о чем я прошу. Спасибо.
Ускорение (расчет): определение, как его найти (среднее или мгновенное)
Ускорение – это мера изменения скорости объекта. В математике это можно найти с помощью производных.
Содержание (щелкните, чтобы перейти к этому разделу):
- Постоянное ускорение
- Мгновенное ускорение
- Найти с помощью исчисления
Ускорение – важное понятие в физике: это скорость изменения скорости с течением времени .Другими словами, он сообщает вам, насколько скорость увеличивается или уменьшается. Объект ускоряется? Замедление? Двигаетесь с постоянной скоростью по прямой? Если вы когда-нибудь были в движущемся лифте, вы, вероятно, ощущали эффект ускорения: ускоряющийся лифт толкает вас на пол, а лифт, который замедляется, заставляет вас чувствовать себя немного невесомым.
Постоянное ускорение – это когда скорость изменяется с постоянной скоростью .
Пример : Представьте, что вы подбрасываете мешок с фасолью в воздух.Мешок поднимается в воздух, останавливаясь наверху своего пути. Затем он начинает быстро опускаться, пока не упадет в вашу ладонь. Легко представить и другие примеры, связанные с гравитацией: грузовик, катящийся с холма, или яблоко, падающее с дерева.
Примеры
Когда объект находится в состоянии покоя, его ускорение постоянно (и равно нулю). Это верно, потому что его положение не меняется, поэтому его скорость всегда равна нулю.
x (t) = 0
v (t) = x ′ (t) = 0
a (t) = v ′ (t) = 0
Даже если скорость может изменяться, ускорение может быть постоянным.Однако он должен меняться с постоянной скоростью .
Уравнения, описывающие объект, движущийся из-за постоянного ускорения, называются кинематическими уравнениями . Четыре кинематических уравнения выглядят следующим образом:
Δ x = v i t + ½ при 2
Δx = ½ ( v f + v i ) t
v f 2 = v i 2 + 2 a Δ x
v f = v i + at
где:
- t: время (секунды)
- Δx: изменение положения (метры)
- v i : начальная скорость (метры в секунду)
- v f : конечная скорость (метры в секунду)
- a: ускорение (метры на секунду в квадрате)
Пример вопроса: Если вы уроните бейсбольный мяч из большого каньона, сколько времени потребуется, чтобы мяч пролетел 100 метров?
В данном случае ускорение равно 9.8 метров в секунду в квадрате, а смена позиции составляет 100 метров. Поскольку мяч падает из состояния покоя, начальная скорость равна нулю. Зная эти переменные, мы можем использовать уравнение №1, чтобы найти время.
Δx = v i t + ½ при 2
100 = 0 + ½ (9,8) т 2
20,408 = т 2
т = 4,52 секунды
Постоянное ускорение иногда сложно представить, но, надеюсь, в этой статье были предложены несколько реальных примеров, которые делают идею более конкретной.
Открытие закона всемирного тяготения, основанного на постоянном ускорении.
Наиболее частая ситуация, характеризующаяся постоянным ускорением, – это объект, притягиваемый силой тяжести . Гравитация – это относительно постоянная сила у поверхности планеты, что означает, что она оказывает постоянное ускорение всем объектам. Например, значение ускорения свободного падения на Земле составляет 9,8 м / с 2 .
Другой частый случай постоянного ускорения – замедление кузова из-за трения. Трение прямо пропорционально весу объекта, поэтому оно будет оставаться постоянным с течением времени. Помните из нашего примера с гравитацией, что постоянная сила подразумевает постоянное ускорение.
Примеры, связанные с трением, немного сложнее визуализировать, но некоторые распространенные сценарии включают:
- Шар для боулинга катится по аллее,
- Фигуристка, планирующая остановиться.
В Calculus мгновенное ускорение – это ускорение объекта в определенный момент времени.Это скорость, с которой объект изменяет свою скорость.
В качестве примера предположим, что автомобиль меняет свою скорость от одной минуты к другой – возможно, от 4 метров в секунду при t = 4 до 5 метров в секунду при t = 5, тогда вы можете сказать, что автомобиль ускоряется. Единица СИ для a – метры на секунду в квадрате (м / с 2 .
Ноль и униформа
Объект, который просто быстро движется с постоянной скоростью (например, 60 миль в час), имеет ускорение , а не – и имеет мгновенное ускорение , равное нулю .Например, предположим, что автомобиль движется со следующей скоростью:
- 60 м / с при t = 10 секунд,
- 60 м / с при t = 11 секунд,
- 60 м / с при t = 12 секунд.
Хотя машина движется, ее скорость не меняется от 60 м / с; У него нулевое ускорение. Это также может означать, что скорость находится на максимальном или минимальном значении.
Не следует путать с с постоянным ускорением (иногда называемым равномерным), когда ускоряется с постоянной скоростью.Например, предположим, что машина едет по адресу:
.- 10 м / с при t = 10 секунд,
- 15 м / с при t = 11 секунд,
- 20 м / с при t = 12 секунд.
За каждое изменение времени в одну минуту автомобиль увеличивает свою скорость на 5 м / с. Автомобиль имеет постоянное ускорение 5 м / с 2 .
Графический образ
Если вы изобразите скорость как функцию времени, мгновенное ускорение будет наклоном касательной.
Это означает, что если функция скорости представляет собой прямую линию, мгновенное ускорение будет постоянным (касательная всегда будет прямой линией).
Если мгновенное ускорение изменяется, скорость соответствует кривой.
Отрицательное мгновенное ускорение означает, что скорость уменьшается. Если он положительный, наша скорость увеличивается.
Ускорение измеряется как изменение скорости с течением времени (ΔV / Δt), где Δ сокращенно от «изменения».Например, давайте вычислим a , используя приведенный выше пример для константы a . Скорость при t = 10 составляет 10 м / с, а скорость при t = 11 составляет 15 м / с. Среднее ускорение будет:
Изменение скорости / изменение во времени = (15 м / с – 10 м / с) / (11-10) = 5/1 = 5 м / с 2.
Вы не можете рассчитать мгновенное ускорение таким же образом, потому что у вас нет времени начала и времени окончания. Вместо этого представьте, что вы находите такое же частное – разность скорости в зависимости от разницы во времени – за бесконечно малый период времени.Вы можете написать это как:
По-английски это означает, что a – это производная скорости (dv / dt).
Чтобы получить ускорение объекта в расчетах, мы должны взять производную от его скорости по времени:
a ( т ) = v ′ ( т )
Мы также можем думать об ускорении с точки зрения положения объекта. Поскольку скорость представляет собой изменение положения во времени, то ускорение будет второй производной положения по времени:
a (t) = x ′ ′ (t)
Ускорение – это вторая производная функции положения.
Как вы найдете ускорение ( a ) в расчетах, зависит от того, какая информация вам предоставлена.
Если вам дали функцию и попросили найти a , следуйте диаграмме выше, чтобы выяснить, что вам нужно сделать. Например,
- Если у вас есть функция скорости , диаграмма показывает, что a на один шаг ниже скорости. А стрелка вниз показывает «Деривативы». Следовательно, возьмите первую производную , чтобы найти a .«Взять первую производную» означает просто взять производную один раз.
- Если вам дана функция положения (то есть положение объекта во времени), вы находитесь в двух шагах от вас, поэтому возьмите вторую производную , чтобы найти a .
Вы также можете перебрать назад , чтобы найти и . Когда я говорю «наоборот», я имею в виду интегралы, которые, по сути, «отменяют» производную. Если вам дается толчок (третья производная функции положения), вам нужно выполнить интегрирование один раз.
Примечание: Вы можете найти «a» , если дано либо:
- функция расстояния объект перемещается во времени, или
- – функция скорости объекта во времени.
Если вам задано расстояние, начните с шага 1. Если вам задана скорость, переходите к шагу 3.
Шаг 1: Составьте уравнение . Имея функцию для расстояния объект перемещается во времени, установите производную функции по времени равной скорости объекта.Например:
Запись « d / dt » предназначена для производной. Я мог бы просто использовать D или другие обозначения.
Разделив слагаемые (чтобы упростить дифференцирование), уравнение изменится на:
Шаг 2: Найдите скорость , выполнив дифференцирование. Это можно сделать несколькими способами, в зависимости от формата вашей функции. Эта конкретная функция вызывает правило мощности:
Шаг 3: Снова найдите производную (здесь вы в основном находите вторую производную функции положения).
Это означает, что ускорение объекта имеет постоянное значение 2.
Совет: если в формуле есть оставшиеся переменные, это означает, что ускорение не является постоянным во времени. Обязательно укажите в своем ответе любые единицы измерения, чтобы он был правильным.
Список литературы
Линг, Санни и Мобс. Среднее и мгновенное. Ускорение. Физика Университета OpenStax. Получено с веб-сайта
https://phys.libretexts.org/TextBooks_and_TextMaps/University_Physics/Book%3A_University_Physics_(OpenStax)/Map%3A_University_Physics_I_-_Mechanics%2C_Sound%2C_oscillations_Sound_I_-_Mechanics%2C_Sound%2C_oscillations_Sound%2C_Oscillations_Sound_S2C_Oscill_a3% 3A_Average_and_Instantaneous_Acceleration 7 октября 2018 г.
Стоунер, Рон. Мгновенный. Ускорение. Получено с http://physics.bgsu.edu/~stoner/p201/kin2d/sld008.htm, 7 октября 2018 г.
Изображение шара для боулинга: Orderinchaos | Wikimedia Commons. CC-Sharealike.
Чувствуете себя “обманом” в Calculus? Ознакомьтесь с нашим Руководством по практическому исчислению мошенничества, которое дает вам сотни простых ответов в удобной электронной книге.
Руководство по расчету ускорения: среднее и мгновенное
Что такое ускорение?
Скорее всего, вы слышали о термине «ускорение», когда слушали спортивные комментарии, такие как автогонки, или когда видели новости о космическом корабле, запускаемом в космос. Это даст вам смутное представление об ускорении как о форме движения. Однако существует точное определение ускорения в его физическом смысле, и оно также может быть представлено математическими уравнениями.
Чтобы понять ускорение, вы должны сначала знать скорость. Так же, как скорость описывает скорость изменения положения относительно времени, ускорение описывает скорость изменения скорости относительно времени . Важно не путать эти два понятия. Если у вас возникли проблемы с различением этих двух параметров, может быть полезно запомнить фразу «ускорение зависит от скорости, а скорость зависит от положения». Ускорение, как и скорость, является векторной величиной.Это означает, что направление рассматривается с величиной.
Ниже я расскажу, как рассчитать ускорение для двух случаев: среднего и мгновенного ускорения.
Среднее ускорение
Самый простой и распространенный тип ускорения, с которым вы столкнетесь, – это среднее ускорение. Это описывает ускорение объекта на рассматриваемой длине пути. Например, давайте рассмотрим автомобиль, едущий по прямой дороге, и водитель нажимает на педаль газа.При рассмотрении среднего ускорения мы всегда будем учитывать два момента времени. Итак, мы возьмем произвольные точки A и B на пути, по которому машина едет через A в B. Предположим, что в точке A прошло 10 секунд, и машина движется со скоростью 20 м / с, а в точке B 30 секунд имеют проехал и машина едет 50 м / с. Для расчета его средней скорости воспользуемся следующим стандартным уравнением:
Если мы подставим наши предполагаемые значения в переменные, мы получим:
Следовательно, среднее ускорение автомобиля равно 1.5 м / с2. Обратите внимание, что для получения единиц ускорения мы берем (м / с) / с, что дает нам м / с2.
Мгновенное ускорение
В зависимости от того, на каком уровне вы изучаете ускорение, вы можете рассчитывать или не рассчитывать мгновенное ускорение, поскольку для этого требуются базовые знания математики. Тем не менее, я кратко определю мгновенное ускорение.
Термин «мгновенный» определяется как происходящий в мгновение ока. Следовательно, мгновенное ускорение – это просто мгновенное ускорение объекта.Хотя может показаться, что это противоречит концепции среднего ускорения, которая всегда учитывает два момента времени, на самом деле это не так. И здесь на помощь приходит расчет.
Одно из первых понятий, которое вы изучаете в математике, – это пределы. Что касается ускорения, если мы рассмотрим точку A, как было сказано ранее, а затем возьмем точку B, чтобы она была все ближе и ближе к A, чтобы среднее ускорение вычислялось за все более и более короткие интервалы времени, мы получим предел среднее ускорение на временном интервале приближается к нулю .И это именно мгновенное ускорение.
Однако более практичный подход к вычислению мгновенного ускорения – использование производных. Это также требует некоторых базовых знаний в области математического анализа. При этом очевидно, что мгновенное ускорение равно скорости изменения мгновенной скорости относительно времени .
Эти результаты показаны следующим образом:
До сих пор я объяснил два конкретных типа ускорения, среднее и мгновенное, и рассмотрел, как рассчитать ускорение в этих двух случаях.Лучший способ понять эти концепции – задавать практические вопросы. Если у вас есть учебник физики, вы можете перейти к соответствующей главе и ответить на некоторые вопросы, которые у них есть в конце.
Если вы хотите увидеть другой пример, в котором используются формулы ускорения, вы можете взглянуть на Учебное пособие по формулам ускорения.
Список литературы
- Университетская физика с современной физикой, 12-е изд. / Хью Д. Янг… [и др.].
Формула мгновенной скорости
Скорость – это мера того, насколько быстро объект перемещается из одного положения в другое.Если объект ускоряется или замедляется, скорость объекта изменяется со временем. Мгновенная скорость объекта – это скорость в определенный момент времени. Скорость – это изменение положения, деленное на изменение во времени, а мгновенная скорость – это предел скорости, когда изменение во времени приближается к нулю. Это эквивалентно производной позиции по времени. Мгновенная скорость – это вектор, поэтому он имеет величину (значение) и направление. Единица измерения мгновенной скорости – метры в секунду (м / с).
= мгновенная скорость (м / с)
= изменение вектора положения (м)
Δt = изменение во времени (с)
= производная положения вектора по времени (м / с)
Формула мгновенной скорости Вопросы:
1) Кошка, идущая к дому по вершине забора, движется с разной скоростью. Положение кота на заборе такое. Позиция x указывается в метрах, а время t – в секундах. Какова мгновенная скорость кошки в момент времени t = 10.0 с?
Ответ: Скорость кошки можно найти по формуле:
Поза кошки состоит только из одного компонента, так как она движется по прямой линии вдоль забора. Положительное направление x выбрано так, чтобы оно было направлено к дому. Величина скорости в направлении x:
.Эта производная может быть решена с использованием скалярного правила множественности и правила мощности для производных:
Величина мгновенной скорости:
Величина мгновенной скорости кошки при t = 10.0 с это:
Мгновенная скорость кошки при t = 10,0 с составляет 0,05 м / с в направлении -x (от дома).
2) Ребенок отбивает мяч горизонтально, от края обрыва. Горизонтальное положение мяча задается функцией x (t) = bt, где b = 6,0 м / с. Вертикальное положение мяча задается функцией y (t) = ct 2 , где c = -4,90 м / с 2 . Каковы горизонтальная и вертикальная составляющие мгновенной скорости при t = 4,0 с?
Ответ: Компоненты мгновенной скорости можно найти по формуле:
Если горизонтальное направление мяча определено как положительное направление x, а вертикальное направление вверх определено как положительное направление y, то величины компонент x и y мгновенной скорости равны:
и
Их можно решить с помощью скалярного правила множественности и правила мощности для производных:
Мгновенная горизонтальная скорость:
Горизонтальная скорость мяча имеет постоянное значение 6.0 м / с в направлении + x.
Мгновенная вертикальная скорость:
v y = c (2t)
v y = 2ct
При t = 4,0 с мгновенная вертикальная скорость составляет:
v y = 2ct
v y = 2 (-4,90 м / с 2 ) (4,0 с)
Мгновенная вертикальная скорость при t = 4,0 с составляет 39,2 м / с в направлении -y.
