Як перемножити матриці в Excel
Однією з частих операцій, яку виконують при роботі з матрицями, є множення однієї з них на іншу. Програма Excel є потужним табличним процесором, який призначений, в тому числі і для роботи над матрицями. Тому у нього є інструменти, які дозволяють перемножити їх між собою. Давайте дізнаємося, як це можна виконати різними способами.
зміст
- Процедура множення матриць
- Спосіб 1: функція МУМНОЖ
- Спосіб 2: використання складовою формули
- Питання та відповіді
Відразу потрібно сказати, що перемножити між собою можна далеко не все матриці, а тільки ті, які відповідають певній умові: число стовпців однієї матриці має дорівнювати кількості держав рядків інший і навпаки. Крім того, виключається наявність в складі матриць порожніх елементів. У цьому випадку теж виконати необхідну операцію не вийде.
Способів перемножити матриці в Ексель все-таки не так вже й багато – всього два. І обидва вони пов’язані із застосуванням вбудованих функцій Excel. Розберемо в деталях кожен з цих видів.
І обидва вони пов’язані із застосуванням вбудованих функцій Excel. Розберемо в деталях кожен з цих видів.
Спосіб 1: функція МУМНОЖ
Найбільш простим і популярним варіантом серед користувачів є застосування функції МУМНОЖ. Оператор МУМНОЖ відноситься до математичної групі функцій. Якраз його безпосереднім завданням і є знаходження добутку двох матричних масивів. Синтаксис МУМНОЖ має такий вигляд:
=МУМНОЖ(массив1;массив2)
Таким чином цей оператор має два аргументи, які представляють собою посилання на діапазони двох перемножуєте матриць.
Тепер давайте подивимося, як використовується функція МУМНОЖ на конкретному прикладі. Є дві матриці, число рядків однієї з яких, відповідає кількості стовпців в інший і навпаки. Нам потрібно перемножити два цих елементу.
- Виділяємо діапазон, де буде відображатися результат множення, починаючи з його верхньої лівої комірки. Розмір даного діапазону повинен відповідати числу рядків у першій матриці і числу стовпців у другій.
 Клацають по піктограмі «Вставити функцію».
Клацають по піктограмі «Вставити функцію». - Активується Майстер функцій. Подорожуємо у блок «Математичні», натискаємо по найменуванню «МУМНОЖ» і клацають по кнопці «OK» в нижній частині вікна.
- Буде виконаний запуск вікна аргументів необхідної функції. У цьому вікні є два поля для введення адрес матричних масивів. Ставимо курсор в поле «массів1» і, затиснувши ліву кнопку миші, виділяємо на аркуші всю область першою матриці. Після цього її координати відобразяться в поле. Ставимо курсор в поле «массів2» і аналогічним чином виділяємо діапазон другуматриці.
Після того, як обидва аргументи внесені, чи не поспішаємо тиснути на кнопку «OK», так як ми маємо справу з функцією масиву, а це значить, що для отримання коректного результату звичайний варіант завершення роботи з оператором не підійде. Даний оператор призначений не для того, щоб виводити результат в одну клітинку, так як виводить його в цілий діапазон на аркуші.
 Отже, замість натискання кнопки «OK» тиснемо комбінацію кнопок Ctrl + Shift + Enter.
Отже, замість натискання кнопки «OK» тиснемо комбінацію кнопок Ctrl + Shift + Enter. - Як бачимо, після цього попередньо виділений діапазон був заповнений даними. Це і є результат множення матричних масивів. Якщо поглянути на рядок формул, після виділення будь-якого з елементів даного діапазону, то ми побачимо, що сама формула обгорнута в фігурні дужки. Це і є ознака функції масиву, який додається після натискання клавіш Ctrl + Shift + Enter перед виведенням результат на лист.
урок: Функція МУМНОЖ в Ексель
Спосіб 2: використання складовою формули
Крім того, існує ще один спосіб множення двох матриць. Він складніший, ніж попередній, але теж заслуговує на увагу, як альтернативний варіант. Даний спосіб передбачає використання складовою формули масиву, яка буде складатися з функції СУММПРОИЗВ і вкладеного в неї в якості аргументу оператора ТРАНСП.
- На цей раз виділяємо на аркуші тільки лівий верхній елемент масиву порожніх клітинок, який розраховуємо використовувати для виведення результату.
 Клацаємо по значку «Вставити функцію».
Клацаємо по значку «Вставити функцію». - Майстер функцій запускається. Переміщаємося в блок операторів «Математичні», але на цей раз обираємо найменування СУММПРОИЗВ. Клацають по кнопці «OK».
- Відбувається відкриття вікна аргументів вищевказаної функції. Даний оператор призначений для перемноження різних масивів між собою. Його синтаксис наступний:
=СУММПРОИЗВ(массив1;массив2;…)В якості аргументів з групи «Масив» використовується посилання на конкретний діапазон, який потрібно перемножити. Всього може бути використано від двох до 255 таких аргументів. Але в нашому випадку, так як ми маємо справу з двома матрицями, нам знадобиться як раз два аргументи.
Ставимо курсор в поле «массів1». Тут нам потрібно буде ввести адресу першого рядка першої матриці. Для цього, затиснувши ліву кнопку миші, потрібно просто виділити її на аркуші курсором. Тут же координати даного діапазону будуть відображені у відповідному полі вікна аргументів.

- Після цього встановлюємо курсор в поле «массів2». З цим аргументом буде складніше, тому що за правилами множення матриць, другу матрицю потрібно «перевернути». Для цього використовуємо вкладену функцію
Щоб перейти до неї, клацають по значку у вигляді трикутника, спрямованого гострим кутом вниз, який розміщений зліва від рядка формул. Відкривається список недавно використовуваних формул. Якщо ви в ньому знайдете найменування «ТРАНСП», то клацайте по ньому. Якщо ж ви давно використовували даний оператор або взагалі ніколи не застосовували його, то в цьому списку вказане найменування ви не знайдете.
 В цьому випадку потрібно натиснути по пункту «Інші функції …».
В цьому випадку потрібно натиснути по пункту «Інші функції …». - Відкривається вже добре знайоме нам вікно Майстра функцій. На цей раз подорожуємо у категорію «Посилання та масиви» і вибираємо найменування «ТРАНСП». Клацаємо по кнопці «OK».
- Виробляється запуск вікна аргументів функції ТРАНСП. Даний оператор призначений для транспонування таблиць. Тобто, попросту кажучи, він міняє місцями стовпчики та рядки. Це нам і потрібно зробити для другого аргументу оператора СУММПРОИЗВ. Синтаксис функції ТРАНСП гранично простий:
=ТРАНСП(массив)Тобто, єдиним аргументом даного оператора є посилання на той масив, який слід «перевернути». Вірніше, в нашому випадку навіть не на весь масив, а тільки на його перший стовпець.
Отже, встановлюємо курсор в поле «Масив» і виділяємо перший стовпець другуматриці на аркуші з затиснутою лівою кнопкою миші.
 Адреса відобразиться в поле. Як і в попередньому випадку, тут теж потрібно зробити певні координати абсолютними, але на цей раз не координати стовпців, а адреси рядків. Тому ставимо знак долара перед цифрами на засланні, яка відображається в полі. Можна також виділити все вираз і двічі клікнути по клавіші F4. Після того, як необхідні елементи стали мати абсолютні властивості, які не тиснемо на кнопку
Адреса відобразиться в поле. Як і в попередньому випадку, тут теж потрібно зробити певні координати абсолютними, але на цей раз не координати стовпців, а адреси рядків. Тому ставимо знак долара перед цифрами на засланні, яка відображається в полі. Можна також виділити все вираз і двічі клікнути по клавіші F4. Після того, як необхідні елементи стали мати абсолютні властивості, які не тиснемо на кнопку - Але на цей раз у нас заповнені не масив, а тільки одна комірка, яку ми раніше виділили при виклику Майстра функцій.
- Нам потрібно заповнити даними такий же за розміром масив, як і в першому способі. Для цього слід скопіювати формулу, отриману в осередку, на рівнозначний діапазон, який буде дорівнює кількості рядків першої матриці і кількістю стовпців другий. У конкретно нашому випадку виходить три рядки і три стовпці.

Для копіювання вдамося до використання маркера заповнення. Наводимо курсор на нижній правий кут комірки, в якій розташована формула. Курсор перетвориться в чорний хрестик. Це і є маркер заповнення. Затискаємо ліву кнопку миші і простягаємо курсор по всьому вищезазначеному діапазону. Сама початкова осередок з формулою повинна стати лівим верхнім елементом даного масиву.
- Як бачимо, виділений діапазон заповнений даними. Якщо їх порівняти з тим результатом, який ми отримали завдяки застосуванню оператора МУМНОЖ, то побачимо, що значення повністю ідентичні. Це означає, що множення двох матриць виконано вірно.
урок: Робота з масивами в Ексель
Як бачимо, незважаючи на те, що був отриманий рівнозначний результат, використовувати функцію для множення матриць 
Множення матриць – що це таке, визначення та поняття – 2021
Зміст
- Множення матриць
- Властивості
- Схема комутативних властивостей
- Процес
- Теоретичний приклад
- Вправа
Множення матриць складається з лінійного об’єднання двох або більше матриць шляхом додавання їх елементів залежно від їх розташування в матриці початку, дотримуючись порядку факторів.
Іншими словами, множення двох матриць полягає у об’єднанні матриць в одній матриці шляхом множення та додавання елементів рядків і стовпців вихідних матриць, беручи до уваги порядок факторів.
Рекомендовані статті: операції з матрицями, квадратна матриця.
Множення матриць
Дано дві матриці Z Y Y з n рядків і m стовпців:
Властивості
- Розмірність матриці результатів – це поєднання розмірності матриць. Іншими словами, розмірністю матриці результатів будуть стовпці першої матриці та рядки другої матриці.

У цьому випадку ми це знайдемо Zп (рядки Z) дорівнює Yм(стовпці Y), щоб мати можливість їх множити. Отже, якщо вони рівні, матриця результату буде такою:
Приклади
- Помножимо матриці два на два.
Ми множимо матриці два на два, щоб зберегти розміри вихідних матриць та полегшити процес.
- Множення матриць не є комутативним.
Схема комутативних властивостей
Комутативна властивість являє собою добре відому фразу: порядок факторів не змінює результат.
Ми знаходимо цю властивість у звичайному додаванні та множенні, тобто коли додаємо та множимо будь-який об’єкт, який не є матрицею.
З огляду на наведену вище схему, комутативна властивість говорить нам, що якщо спочатку помножити синє сонце, а потім жовте сонце, ми отримаємо той самий результат (зелене сонце), як ніби помножимо спочатку жовте, а потім синє сонце.
Отже, якщо множення матриць не поважає комутативну властивість, це означає, що порядок факторів Так впливає на результат. Іншими словами, ми не отримаємо зеленого сонця, якщо змінимо порядок жовтого та синього сонечок.
Іншими словами, ми не отримаємо зеленого сонця, якщо змінимо порядок жовтого та синього сонечок.
Процес
Ми можемо помножити попередні матриці, якщо кількість рядків у матриці Z дорівнює кількості стовпців у матриці Y. А саме Zп
Після того, як буде визначено, що ми можемо множити матриці, ми множимо елементи кожного рядка на кожен стовпець і додаємо їх таким чином, щоб залишилося лише одне число в точці, де попередні сині овали збігаються.
Спочатку ми знаходимо, де збігаються сині овали, а потім робимо суму множення елементів.
- Для першого елемента матриці результатів ми бачимо, що овали збігаються там, де знаходиться елемент z11.
- Для останнього елемента матриці результатів ми бачимо, що овали збігаються в елементі інм.
Теоретичний приклад
Дано дві квадратні матриці D Y І,
Помножте попередні матриці.
Почнемо з множення першого рядка матриці D з першим стовпцем матриці І. Потім ми робимо те саме, але зберігаємо рядок або стовпець кожної матриці залежно від того, чи хочемо ми помножити деякі елементи чи інші. Повторюємо процедуру, поки не заповнимо всі прогалини.
Вправа
Доведіть, що комутативна властивість не виконується у добутку матриць.
numpy.matmul — Руководство NumPy v1.24
- Numpy.matmul ( x1 , x2 , /, out = none , * , Casting = ‘Some_kind’
Произведение матриц двух массивов.
- Параметры:
- x1, x2 array_like
Входные массивы, скаляры не допускаются.
- out ndarray, необязательный
Местоположение, в котором сохраняется результат.
 Если он предусмотрен, он должен иметь
форма, соответствующая подписи
Если он предусмотрен, он должен иметь
форма, соответствующая подписи - **kwargs
Другие аргументы, содержащие только ключевые слова, см. документы ufunc.
Новое в версии 1.16: теперь обрабатывает ufunc kwargs
- Возвращает:
- y ndarray
Матричный продукт входных данных. Это скаляр только тогда, когда оба x1, x2 являются одномерными векторами.
- Повышение:
- ValueError
Если последний размер x1 не совпадает с размером предпоследнее измерение x2 .
Если передается скалярное значение.
См. также
-
vdot Комплексно-сопряженное скалярное произведение.
-
тензордот Суммирование произведений по произвольным осям.

-
einsum Соглашение Эйнштейна о суммировании.
-
точка альтернативный матричный продукт с другими правилами вещания.
Примечания
Поведение зависит от аргументов следующим образом.
Если оба аргумента являются двумерными, они умножаются, как обычно матрицы.
Если любой из аргументов имеет значение N-D, N > 2, он рассматривается как стек матрицы, находящиеся в последних двух индексах, и транслируются соответственно.
Если первый аргумент одномерный, он преобразуется в матрицу с помощью добавляя 1 к своим размерам. После умножения матриц предшествующая 1 удаляется.
Если второй аргумент одномерный, он преобразуется в матрицу с помощью добавление 1 к его размерам. После умножения матриц добавленная 1 удаляется.
матмулотличается отточкапо двум важным параметрам:Умножение на скаляры не допускается, вместо этого используйте
*.
Стеки матриц передаются вместе, как если бы матрицы были элементы, соблюдающие подпись
(н,к),(к,м)->(н,м):>>> a = np.ones([9, 5, 7, 4]) >>> c = np.ones([9, 5, 4, 3]) >>> np.dot(a, c).shape (9, 5, 7, 9, 5, 3) >>> np.matmul(a, c).shape (9, 5, 7, 3) >>> # n равно 7, k равно 4, m равно 3
Функция matmul реализует семантику оператора
@введен в Python 3.5 после PEP 465 .По возможности использует оптимизированную библиотеку BLAS (см.
numpy.linalg).Примеры
Для двумерных массивов это матричное произведение:
>>> a = np.array([[1, 0], ... [0, 1]]) >>> b = np.array([[4, 1], ... [2, 2]]) >>> np.matmul(а, б) массив([[4, 1], [2, 2]])Для 2-D, смешанного с 1-D, результат обычный.
>>> a = np.array([[1, 0], ... [0, 1]]) >>> b = np.массив ([1, 2]) >>> np.matmul(а, б) массив ([1, 2]) >>> np.matmul(б, а) массив ([1, 2])
Вещание обычное для стеков массивов
>>> a = np.
 arange(2 * 2 * 4).reshape((2, 2, 4))
>>> b = np.arange(2 * 2 * 4).reshape((2, 4, 2))
>>> np.matmul(a,b).shape
(2, 2, 2)
>>> np.matmul(a, b)[0, 1, 1]
98
>>> сумма(а[0, 1, :] * b[0, :, 1])
98
arange(2 * 2 * 4).reshape((2, 2, 4))
>>> b = np.arange(2 * 2 * 4).reshape((2, 4, 2))
>>> np.matmul(a,b).shape
(2, 2, 2)
>>> np.matmul(a, b)[0, 1, 1]
98
>>> сумма(а[0, 1, :] * b[0, :, 1])
98
Вектор, вектор возвращает скалярное скалярное произведение, но ни один аргумент комплексно-сопряженный:
>>> np.matmul([2j, 3j], [2j, 3j]) (-13+0j)
Скалярное умножение вызывает ошибку.
>>> np.matmul([1,2], 3) Traceback (последний последний вызов): ... ValueError: matmul: входному операнду 1 не хватает размеров...
Оператор
@может использоваться как сокращение дляnp.matmulна ндаррейс.>>> x1 = np.массив([2j, 3j]) >>> x2 = np.array([2j, 3j]) >>> х1 @ х2 (-13+0j)
Новое в версии 1.10.0.
Использование матрицы для ваших заданий
Создайте матрицу для определения вариантов для каждого задания.
О матричных стратегиях
Матричная стратегия позволяет использовать переменные в одном определении задания для автоматического создания нескольких запусков задания на основе комбинаций переменных. Например, вы можете использовать матричную стратегию для тестирования своего кода в нескольких версиях языка или в нескольких операционных системах.
Например, вы можете использовать матричную стратегию для тестирования своего кода в нескольких версиях языка или в нескольких операционных системах.
Использование матричной стратегии
Использование заданий. для определения матрицы различных конфигураций заданий. В вашей матрице определите одну или несколько переменных, за которыми следует массив значений. Например, в следующей матрице есть переменная с именем версия со значением [10, 12, 14] и переменная с именем os со значением [ubuntu-latest, windows-latest] :
jobs :
пример_матрицы:
стратегия:
матрица:
версия: [10, 12, 14]
ОС: [ubuntu-последняя, Windows-последняя]
Задание будет выполняться для каждой возможной комбинации переменных. В этом примере рабочий процесс будет выполнять шесть заданий, по одному для каждой комбинации переменных os и версии .
По умолчанию GitHub максимизирует количество заданий, выполняемых параллельно, в зависимости от доступности исполнителя. Порядок переменных в матрице определяет порядок создания заданий. Первая переменная, которую вы определите, будет первым заданием, созданным в ходе вашего рабочего процесса. Например, приведенная выше матрица создаст задания в следующем порядке:
-
{версия: 10, ОС: ubuntu-последняя} -
{версия: 10, ОС: последняя версия Windows} -
{версия: 12, ОС: ubuntu-последняя} -
{версия: 12, ОС: последняя версия Windows} -
{версия: 14, ОС: ubuntu-последняя} -
{версия: 14, ОС: последняя версия Windows}
Матрица создает не более 256 заданий за один запуск рабочего процесса. Это ограничение распространяется как на исполнителей, размещенных на GitHub, так и на собственных.
Переменные, которые вы определяете, становятся свойствами в контексте матрицы , и вы можете ссылаться на свойство в других областях вашего файла рабочего процесса. В этом примере можно использовать
В этом примере можно использовать matrix.version и matrix.os для доступа к текущему значению version и os , которое использует задание. Дополнительные сведения см. в разделе «Контексты».
Пример: Использование одномерной матрицы
Вы можете указать одну переменную для создания одномерной матрицы.
Например, следующий рабочий процесс определяет переменную версии со значениями [10, 12, 14] . Рабочий процесс запустит три задания, по одному для каждого значения переменной. Каждое задание будет получать доступ к значению версии через контекст matrix.version и передавать значение как node-version в действие action/setup-node .
вакансии:
пример_матрицы:
стратегия:
матрица:
версия: [10, 12, 14]
шаги:
- использует: action/setup-node@v3
с:
версия узла: ${{ matrix.version }}
Пример: использование многомерной матрицы
Можно указать несколько переменных для создания многомерной матрицы. Задание будет выполняться для каждой возможной комбинации переменных.
Задание будет выполняться для каждой возможной комбинации переменных.
Например, в следующем рабочем процессе указаны две переменные:
- Две операционные системы, указанные в переменной
os - Три версии Node.js, указанные в переменной
версии
Рабочий процесс будет выполнять шесть заданий, по одному для каждой комбинации из os и версия переменные. Каждое задание установит значение run-on в текущее значение os и передаст текущее значение версии в действие action/setup-node .
вакансии:
пример_матрицы:
стратегия:
матрица:
ОС: [убунту-22.04, убунту-20.04]
версия: [10, 12, 14]
запуски: ${{ matrix.os }}
шаги:
- использует: action/setup-node@v3
с:
версия узла: ${{ matrix.version }}
Пример: использование контекстов для создания матриц
Вы можете использовать контексты для создания матриц. Дополнительные сведения о контекстах см. в разделе «Контексты».
Дополнительные сведения о контекстах см. в разделе «Контексты».
Например, следующий рабочий процесс запускается по событию relay_dispatch и использует информацию из полезной нагрузки события для построения матрицы. Когда событие отправки репозитория создается с полезной нагрузкой, подобной приведенной ниже, переменная matrix version будет иметь значение [12, 14, 16] . Для получения дополнительной информации о репозиторий_диспетч триггер, см. «События, запускающие рабочие процессы».
{
"тип_события": "тест",
"client_payload": {
"версии": [12, 14, 16]
}
}
на:
репозиторий_отправка:
типы:
- тест
вакансии:
пример_матрицы:
запуски: ubuntu-последняя
стратегия:
матрица:
версия: ${{ github.event.client_payload.versions }}
шаги:
- использует: action/setup-node@v3
с:
версия узла: ${{ matrix.version }}
Расширение или добавление конфигураций матрицы
Используйте задания . для расширения существующих конфигураций матриц или добавления новых конфигураций. Значение 
включает — список объектов.
Для каждого объекта в списке include пары ключ:значение в объекте будут добавлены к каждой из комбинаций матриц, если ни одна из пар ключ:значение не перезапишет какие-либо исходные значения матрицы. Если объект не может быть добавлен ни к одной из комбинаций матриц, вместо нее будет создана новая комбинация матриц. Обратите внимание, что исходные значения матрицы не будут перезаписаны, но добавленные значения матрицы могут быть перезаписаны.
Например, эта матрица:
стратегия:
матрица:
фрукты: [яблоко, груша]
животное: [кошка, собака]
включать:
- цвет: зеленый
- цвет: розовый
животное: кошка
- фрукты: яблоко
форма: круг
- фрукты: банан
- фрукты: банан
животное: кошка
приведет к шести заданиям со следующими комбинациями матриц:
-
{фрукт: яблоко, животное: кошка, цвет: розовый, форма: круг} -
{фрукт: яблоко, животное: собака, цвет: зеленый, форма: круг} -
{фрукт: груша, животное: кошка, цвет: розовый} -
{фрукт: груша, животное: собака, цвет: зеленый} -
{фрукты: банан} -
{фрукт: банан, животное: кошка}
, следуя следующей логике:
-
{цвет: зеленый}добавляется ко всем исходным матричным комбинациям, поскольку его можно добавлять без перезаписи какой-либо части исходных комбинаций.
-
{цвет: розовый, животное: кошка}добавляетцвет:розовыйтолько к исходным матричным комбинациям, включающимживотное: кошка. Это перезаписывает цвет: зеленый, который был добавлен предыдущей записьюinclude. -
{фрукт: яблоко, форма: круг}добавляетформа: кругтолько к исходным матричным комбинациям, которые включаютфрукт: яблоко. -
{фрукт: банан}нельзя добавить ни к одной исходной комбинации матриц без перезаписи значения, поэтому он добавляется как дополнительная комбинация матриц. -
{фрукт: банан, животное: кошка}нельзя добавить ни к какой исходной комбинации матриц без перезаписи значения, поэтому она добавляется как дополнительная комбинация матриц. Он не добавляется к матричной комбинации{фрукты: банан}, потому что эта комбинация не была одной из исходных матричных комбинаций.
Пример: расширение конфигураций
Например, следующий рабочий процесс будет выполнять шесть заданий, по одному для каждой комбинации os и узел . При выполнении задания для os со значением windows-latest и node со значением 16 в задание будет включена дополнительная переменная с именем npm со значением 6 .
вакансии:
пример_матрицы:
стратегия:
матрица:
ОС: [Windows-последняя, Ubuntu-последняя]
узел: [12, 14, 16]
включать:
- ОС: windows-последняя
узел: 16
нпм: 6
запуски: ${{ matrix.os }}
шаги:
- использует: action/setup-node@v3
с:
версия узла: ${{ matrix.node }}
- если: ${{ matrix.npm }}
выполнить: npm install -g npm@${{ matrix.npm }}
- запустить: npm --версия
Пример: добавление конфигураций
Например, эта матрица будет запускать 10 заданий, по одному для каждой комбинации os и версии в матрице, а также задание для os со значением windows-latest и версия значение 17 .
вакансии:
пример_матрицы:
стратегия:
матрица:
os: [macos-последние, windows-последние, ubuntu-последние]
версия: [12, 14, 16]
включать:
- ОС: windows-последняя
версия: 17
Если вы не укажете какие-либо матричные переменные, все конфигурации под включают . Например, следующий рабочий процесс будет запускать два задания, по одному для каждой записи , включая . Это позволяет вам воспользоваться матричной стратегией, не имея полностью заполненной матрицы.
вакансии:
include_only:
запуски: ubuntu-последняя
стратегия:
матрица:
включать:
- сайт: "производство"
центр обработки данных: "site-a"
- сайт: "постановка"
центр обработки данных: "site-b"
Исключение конфигураций матрицы
Чтобы удалить определенные конфигурации, определенные в матрице, используйте задания . . Исключенная конфигурация должна иметь только частичное совпадение, чтобы ее можно было исключить. Например, следующий рабочий процесс будет выполнять девять заданий: по одному заданию для каждой из 12 конфигураций минус одно исключенное задание, соответствующее  exclude
exclude {os: macos-latest, version: 12, environment: production} , и два исключенных задания. что соответствует {ОС: последняя версия Windows, версия: 16} .
стратегия:
матрица:
os: [macos-последние, windows-последние]
версия: [12, 14, 16]
среда: [постановка, производство]
исключать:
- os: macos-последняя
версия: 12
среда: производство
- ОС: windows-последняя
версия: 16
запуски: ${{ matrix.os }}
Примечание: Все комбинации включают и обрабатываются после исключают . Это позволяет использовать , включая , чтобы добавить обратные комбинации, которые ранее были исключены.
Обработка сбоев
Вы можете управлять обработкой сбоев заданий с помощью заданий . и заданий. .
jobs. применяется ко всей матрице. Если для jobs. установлено значение true , GitHub отменит все выполняемые и поставленные в очередь задания в матрице, если какое-либо задание в матрице завершится неудачно. Это свойство по умолчанию равно верно .
заданий. относится к одному заданию. Если заданий. равно true , другие задания в матрице будут продолжать выполняться, даже если задание с заданиями. завершится ошибкой.
Вы можете использовать задания . и . вместе. Например, следующий рабочий процесс запустит четыре задания. За каждую работу  continue-on-error
continue-on-error продолжение при ошибке определяется значением matrix.experimental . Если какое-либо из заданий с ошибкой продолжения : false завершится ошибкой, все задания, которые выполняются или находятся в очереди, будут отменены. Если задание с continue-on-error: true завершится ошибкой, это не повлияет на другие задания.
вакансии:
тест:
запуски: ubuntu-последняя
продолжение при ошибке: ${{ matrix.experimental }}
стратегия:
безотказный: правда
матрица:
версия: [6, 7, 8]
экспериментальный: [ложь]
включать:
- версия: 9экспериментальный: правда
Определение максимального количества одновременных заданий
По умолчанию GitHub максимизирует количество заданий, выполняемых параллельно, в зависимости от доступности исполнителя. Чтобы установить максимальное количество заданий, которые могут выполняться одновременно при использовании стратегии заданий matrix , используйте jobs.

 Клацають по піктограмі «Вставити функцію».
Клацають по піктограмі «Вставити функцію». Отже, замість натискання кнопки «OK» тиснемо комбінацію кнопок Ctrl + Shift + Enter.
Отже, замість натискання кнопки «OK» тиснемо комбінацію кнопок Ctrl + Shift + Enter. Клацаємо по значку «Вставити функцію».
Клацаємо по значку «Вставити функцію».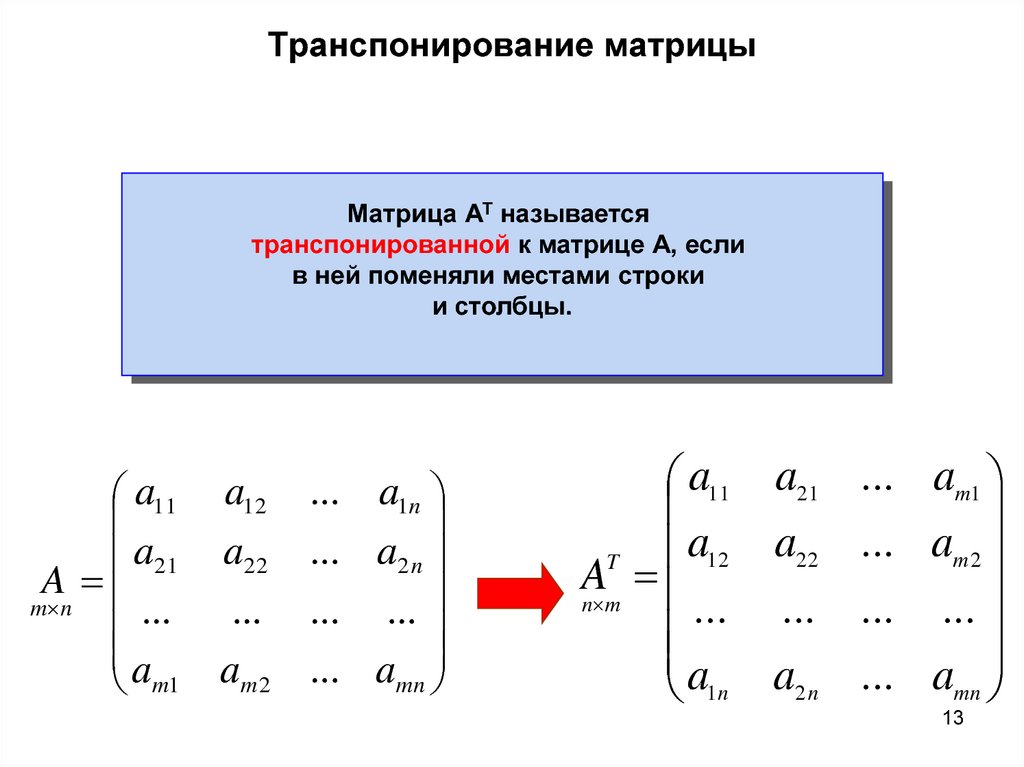
 В цьому випадку потрібно натиснути по пункту «Інші функції …».
В цьому випадку потрібно натиснути по пункту «Інші функції …». Адреса відобразиться в поле. Як і в попередньому випадку, тут теж потрібно зробити певні координати абсолютними, але на цей раз не координати стовпців, а адреси рядків. Тому ставимо знак долара перед цифрами на засланні, яка відображається в полі. Можна також виділити все вираз і двічі клікнути по клавіші F4. Після того, як необхідні елементи стали мати абсолютні властивості, які не тиснемо на кнопку
Адреса відобразиться в поле. Як і в попередньому випадку, тут теж потрібно зробити певні координати абсолютними, але на цей раз не координати стовпців, а адреси рядків. Тому ставимо знак долара перед цифрами на засланні, яка відображається в полі. Можна також виділити все вираз і двічі клікнути по клавіші F4. Після того, як необхідні елементи стали мати абсолютні властивості, які не тиснемо на кнопку 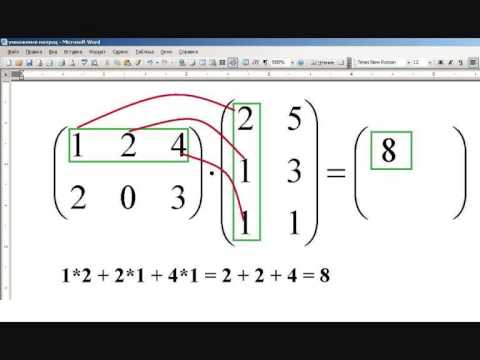

 Если он предусмотрен, он должен иметь
форма, соответствующая подписи
Если он предусмотрен, он должен иметь
форма, соответствующая подписи 

 arange(2 * 2 * 4).reshape((2, 2, 4))
>>> b = np.arange(2 * 2 * 4).reshape((2, 4, 2))
>>> np.matmul(a,b).shape
(2, 2, 2)
>>> np.matmul(a, b)[0, 1, 1]
98
>>> сумма(а[0, 1, :] * b[0, :, 1])
98
arange(2 * 2 * 4).reshape((2, 2, 4))
>>> b = np.arange(2 * 2 * 4).reshape((2, 4, 2))
>>> np.matmul(a,b).shape
(2, 2, 2)
>>> np.matmul(a, b)[0, 1, 1]
98
>>> сумма(а[0, 1, :] * b[0, :, 1])
98

