Модуль средней скорости формула: Формула средней скорости в физике

Дайте определение средней скорости. Средняя скорость перемещения. Средняя путевая скорость

Понятие скорости − одно из главных понятий в кинематике.
 Многим наверняка известно, что скорость − это физическая величина, показывающая насколько быстро (или насколько медленно) перемещается в пространстве движущееся тело. Разумеется, речь идет о перемещении в выбранной системе отсчета. Известно ли, однако, Вам, что используются не одно, а три понятия скорости? Есть скорость в данный момент времени, называемая мгновенной скоростью, и есть два понятия средней скорости за данный промежуток времени − средняя путевая скорость (по английски speed) и средняя скорость по перемещению (по-английски velocity).
 Будем рассматривать материальную точку в системе координат x , y , z (рис. а).

Положение A точки в момент времени t характеризуем координатами x(t) , y(t) , z(t) , представляющими три составляющих радиуса-вектора (t ).

Точка движется, ее положение в выбранной системе координат с течением времени изменяется − конец радиуса-вектора (t ) описывает кривую, называемую траекторией движущейся точки.
 Траектория, описанная за промежуток времени от t до t + Δt , показана на рисунке б.

 Через B обозначено положение точки в момент t + Δt (его фиксирует радиус-вектор (t + Δt )). Пусть Δs − длина рассматриваемой криволинейной траектории, т. е. путь, пройденный точкой за время от t до t + Δt .
 Среднюю путевую скорость точки за данный промежуток времени определяют соотношением

 Очевидно, что v п − скалярная величина; она характеризуется только числовым значением.

 Показанный на рисунке б вектор

называют перемещением материальной точки за время от t до t + Δt .
 Среднюю скорость по перемещению за данный промежуток времени определяют соотношением

 Очевидно, что v ср − векторная величина. Направление вектора v ср совпадает с направлением перемещения Δr .
 Заметим, что в случае прямолинейного движения средняя путевая скорость движущейся точки совпадает с модулем средней скорости по перемещению.
 Движение точки по прямолинейной либо криволинейной траектории называют равномерным, если в соотношении (1) величина vп не зависит от

Δt . Если, например, уменьшить Δt в 2 раза, то и длина пройденного точкой пути Δs уменьшится в 2 раза. При равномерном движении точка проходит за равные промежутки времени пути равной длины.
 Вопрос :
 Можно ли считать, что при равномерном движении точки от Δt не зависит также вектор ср средней скорости по перемещению?

 Ответ :
 Так можно считать только в случае прямолинейного движения (при этом, напомним, модуль средней скорости по перемещению равен средней путевой скорости). Если же равномерное движение совершается по криволинейной траектории, то с изменением промежутка усреднения

Δt будут изменяться как модуль, так и направление вектора средней скорости по перемещению. При равномерном криволинейном движении равным промежуткам времени Δt будут соответствовать разные векторы перемещения Δr (а значит, и разные векторы v ср ).
 Правда, в случае равномерного движения по окружности равным промежуткам времени будут соответствовать равные значения модуля перемещения |r| (а значит, и равные |v ср | ). Но направления перемещений (а значит, и векторов v ср ) и в данном случае будут различными для одинаковых Δt . Это видно на рисунке,

 Где равномерно движущаяся по окружности точка описывает за равные промежутки времени равные дуги AB , BC , CD . Хотя векторы перемещений 1 , 2 , 3 имеют одинаковые модули, однако направления у них различны, так что о равенстве этих векторов говорить не приходится.
 Примечание
 Из двух средних скоростей в задачах обычно рассматривают среднюю путевую скорость, а среднюю скорость по перемещению используют довольно редко. 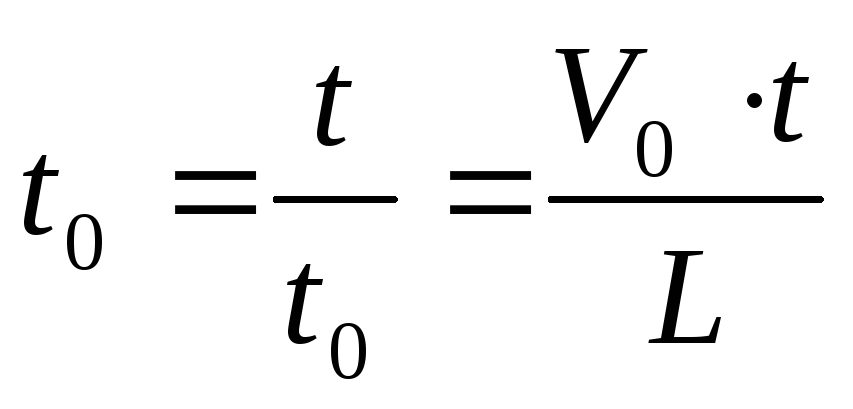Однако она заслуживает внимания, так как позволяет ввести понятие мгновенной скорости.

Средней скоростью называется скорость, которая получается, если весь путь поделить на время, за которое объект преодолел этот путь. Формула средней скорости:

• S = S1 + S2 + S3 = v1*t1 + v2*t2 + v3*t3
• V ср = S/t = (v1*t1 + v2*t2 + v3*t3) / (t1 + t2 + t3)

Чтобы не путаться с часами и минутами, переводим все минуты в часы: 15 мин. = 0,4 час, 36 мин. = 0,6 час. Подставляем числовые значения в последнюю формулу:

• V ср = (20*0,4 + 0,5*6 + 0,6*15) / (0,4 + 0,5 + 0,6) = (8 + 3 + 9) / (0,4 + 0,5 + 0,6) = 20 / 1,5 = 13,3 км/час

Ответ: средняя скорость V ср = 13,3 км/час.

Как найти среднюю скорость движения с ускорением

Если скорость в начале движения отличается от скорости в его конце, такое движение называют ускоренным. Причём далеко не всегда тело действительно двигается всё быстрее и быстрее. Если движение замедляется, всё равно говорят, что оно движется с ускорением, только ускорение будет уже отрицательным.

Иными словами, если автомобиль, трогаясь с места, через секунду разогнался до скорости 10 м/сек, то его ускорение а равно 10 м в секунду за секунду а = 10 м/сек². Если в следующую секунду автомобиль остановился, то его ускорение тоже равно 10 м/сек², только уже со знаком минус: а = -10 м/сек².

Скорость движения с ускорением в конце временного отрезка вычисляется по формуле:

где V0 – начальная скорость движения, a – ускорение, t – время, за которое наблюдалось данное ускорение. Плюс или минус в формуле ставится в зависимости от того, увеличивалась скорость или уменьшалась.

Средняя скорость за отрезок времени t вычисляется как среднее арифметическое начальной и конечной скорости:

Находим среднюю скорость: задача

Шарик толкнули по ровной плоскости с начальной скоростью V0 = 5 м/сек. Через 5 сек. шарик остановился. Чему равны ускорение и средняя скорость?

Конечная скорость шарика V = 0 м/сек. Ускорение из первой формулы равно

• а = (V – V0)/ t = (0 – 5)/ 5 = – 1 м/сек².

Средняя скорость V ср = (V0 + V) / 2= 5 /2 = 2,5 м/сек.

Задачи на среднюю скорость (далее СК). Мы уже рассматривали задания на прямолинейное движение. Рекомендую посмотреть статьи ” ” и ” ” . Типовые задания на среднюю скорость это группа задач на движение, они включены в ЕГЭ по математике и такая задача вполне вероятно может оказаться перед вами в момент самого экзамена. Задачки простые, решаются быстро.

Смысл таков: представьте объект передвижения, например автомобиль. Он проходит определённые участки пути с разной скоростью. На весь путь затрачивается какое-то определённое время. Так вот: средняя скорость это такая постоянная скорость с которой автомобиль преодолел бы данный весть путь за это же время То есть формула средней скорости такова:

Если участков пути было два, тогда

Если три, то соответственно:

*В знаменателе суммируем время, а в числителе расстояния пройденные за соответствующие им отрезки времени.

Первую треть трассы автомобиль ехал со скоростью 90 км/ч, вторую треть – со скоростью 60 км/ч, а последнюю – со скоростью 45 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Как уже сказано необходимо весь путь разделить на всё время движения. В условии сказано о трёх участках пути. Формула:

Обозначим весь пусть S. Тогда первую треть пути автомобиль ехал:

Вторую треть пути автомобиль ехал:

Последнюю треть пути автомобиль ехал:

Таким образом

Решите самостоятельно:

Первую треть трассы автомобиль ехал со скоростью 60 км/ч, вторую треть – со скоростью 120 км/ч, а последнюю – со скоростью 110 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Первый час автомобиль ехал со скоростью 100 км/ч, следующие два часа – со скоростью 90 км/ч, а затем два часа – со скоростью 80 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

В условии сказано о трёх участках пути. СК будем искать по формуле:

Участки пути нам не даны, но мы можем без труда их вычислить:

Первый участок пути составил 1∙100 = 100 километров.

Второй участок пути составил 2∙90 = 180 километров.

Третий участок пути составил 2∙80 = 160 километров.

Вычисляем скорость:

Решите самостоятельно:

Первые два часа автомобиль ехал со скоростью 50 км/ч, следующий час – со скоростью 100 км/ч, а затем два часа – со скоростью 75 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Первые 120 км автомобиль ехал со скоростью 60 км/ч, следующие 120 км – со скоростью 80 км/ч, а затем 150 км – со скоростью 100 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Сказано о трёх участках пути. Формула:

Протяжённость участков дана. Определим время, которое автомобиль затратил на каждый участок: на первый затрачено 120/60 часов, на второй участок 120/80 часов, на третий 150/100 часов. Вычисляем скорость:

Решите самостоятельно:

Первые 190 км автомобиль ехал со скоростью 50 км/ч, следующие 180 км – со скоростью 90 км/ч, а затем 170 км – со скоростью 100 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 74 км/ч, а вторую половину времени – со скоростью 66 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

*Есть задача про путешественника, который пересёк море. С решением у ребят возникают проблемы. Если вы не видите его, то пройдите регистрацию на сайте! Кнопка регистрации (входа) находится в ГЛАВНОМ МЕНЮ сайта. После регистрации войдите на сайт и обновите данную страницу.

Путешественник переплыл море на яхте со средней скоростью 17 км/ч. Обратно он летел на спортивном самолете со скоростью 323 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч.

С уважением, Александр.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Все задачи, в которых присутствует движение объектов, их перемещение или вращение, так или иначе связаны со скоростью.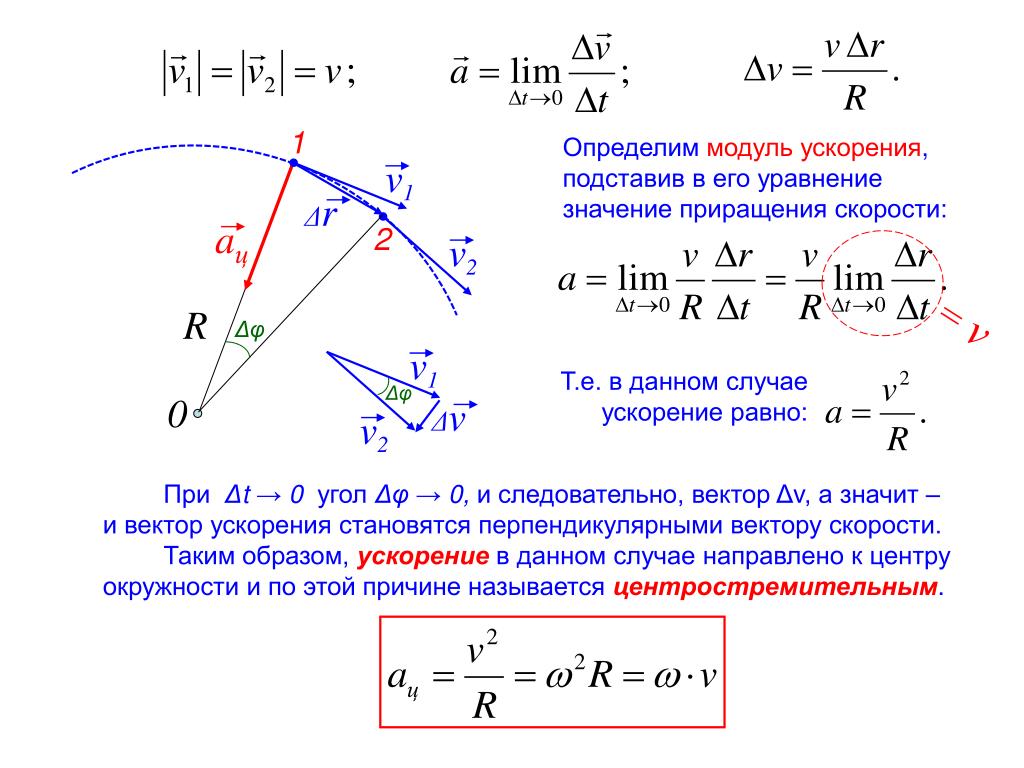

Данный термин характеризует перемещение объекта в пространстве за определенный отрезок времени – число единиц расстояния за единицу времени. Он является частым «гостем» как разделов математики, так и физики. Исходное тело может менять свое расположение как равномерно, так и с ускорением. В первом случае величина скорости статична и в ходе движения не меняется, во втором наоборот – увеличивается или уменьшается.

Как найти скорость – равномерное движение

Если скорость движения тела оставалась неизменной от начала перемещения и до окончания пути, то речь идет о перемещении с постоянным ускорением – равномерном движении. Оно может быть прямолинейным или же криволинейным. В первом случае траекторией перемещения тела является прямая.

Тогда V=S/t, где:

• V – искомая скорость,
• S – пройденное расстояние (общий путь),
• t – общее время движения.

Как найти скорость – ускорение постоянно

Если объект двигался с ускорением, то его скорость по мере движения менялась. В таком случае найти искомую величину поможет выражение:

V=V (нач) + at, где:

• V (нач) – первоначальная скорость движения объекта,
• a – ускорение тела,
• t – общее время пути.

Как найти скорость – неравномерное движение

В данном случае имеет место ситуация, когда разные участки пути тело проходило за разное время.
S(1) – за t(1),
S(2) – за t(2) и т.д.

На первом участке движение происходило в “темпе” V(1), на втором – V(2) и т.д.

Чтобы узнать скорость перемещения объекта на всем пути (ее среднее значение) воспользуйтесь выражением:

Как найти скорость – вращение объекта

В случае вращения речь идет об угловой скорости, определяющей угол, на который поворачивается элемент за единицу времени. Обозначается искомая величина символом ω (рад/с).

Δφ – пройденный угол (приращение угла),
Δt – прошедшее время (время движения – приращение времени).

• В случае, если вращение равномерное, искомая величина (ω) связана с таким понятием как период вращения – за какое время наш объект совершит 1 полный оборот. В таком случае:

ω = 2π/T, где:
π – константа ≈3,14,
T – период.

Или ω = 2πn, где:
π – константа ≈3,14,
n – частота обращения.

• При известной линейной скорости объекта для каждой точки на пути движения и радиусе окружности, по которой она перемещается, для нахождения скорости ω потребуется следующее выражение:

ω = V/R, где:
V – численное значение векторной величины (линейной скорости),
R – радиус траектории следования тела.

Как найти скорость – сближение и отдаление точек

В подобного рода задачах уместным будет использование терминов скорость сближения и скорость отдаления.

Если объекты направляются друг к другу, то скорость сближения (отдаления) будет следующей:
V (сближ) = V(1) + V(2), где V(1) и V(2) – скорости соответствующих объектов.

Если одно из тел догоняет другое, то V (сближ) = V(1) – V(2), V(1) больше V(2).

Как найти скорость – движение по водоему

Если события разворачиваются на воде, то к собственной скорости объекта (движение тела относительно воды) добавляется еще и скорость течения (т. е. движение воды относительно неподвижного берега). Как взаимосвязаны эти понятия?

В случае перемещения по течению V=V(собст) + V(теч).
Если против течения – V=V(собств) – V(теч.).

Неравномерным считается движение с изменяющейся скоростью. Скорость может изменяться по направлению. Можно заключить, что любое движение НЕ по прямой траектории является неравномерным. Например, движение тела по окружности, движение тела брошенного вдаль и др.

Скорость может изменяться по численному значению. Такое движение тоже будет неравномерным. Особенный случай такого движения – равноускоренное движение.

Иногда встречается неравномерное движение, которое состоит из чередования различного вида движений, например, сначала автобус разгоняется (движение равноускоренное), потом какое-то время движется равномерно, а потом останавливается.

Мгновенная скорость

Охарактеризовать неравномерное движение можно лишь скоростью. Но скорость всегда изменяется! Поэтому можно говорить лишь о скорости в данное мгновение времени.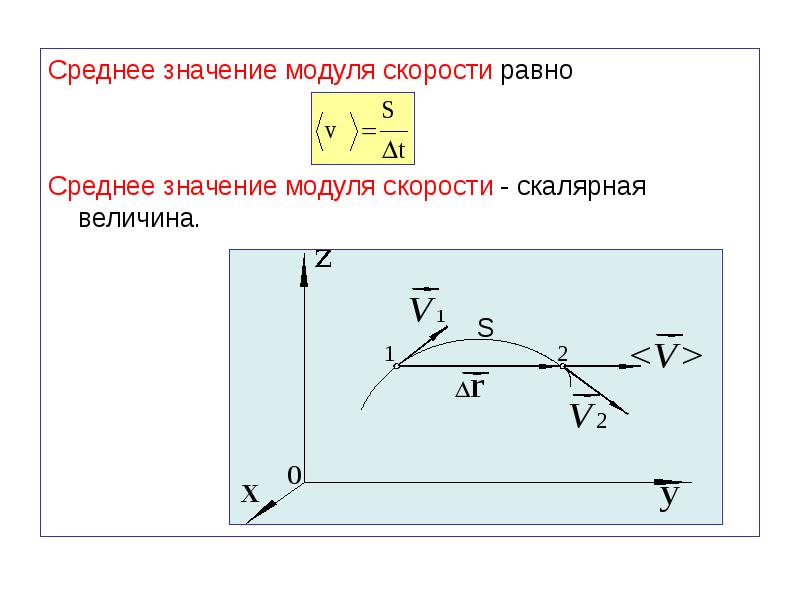 Путешествуя на машине спидометр ежесекундно демонстрирует вам мгновенную скорость движения. Но время при этом надо уменьшить не до секунды, а рассматривать гораздо меньший промежуток времени!

Средняя скорость

Что же такое средняя скорость? Неверно думать, что необходимо сложить все мгновенные скорости и разделить на их количество. Это самое распространенное заблуждение о средней скорости! Средняя скорость – это весь путь разделить на затраченное время . И никакими другими способами она не определяется. Если рассмотреть движение автомобиля, можно оценить его средние скорости на первой половине пути, на второй, на всем пути. Средние скорости могут быть одинаковыми, а могут быть различными на этих участках.

У средних величин рисуют сверху горизонтальную черту.

Средняя скорость перемещения. Средняя путевая скорость

Если движение тела не является прямолинейным, то пройденный телом путь будет больше, чем его перемещение. В этом случае средняя скорость перемещения отличается от средней путевой скорости. Путевая скорость – скаляр .

Главное запомнить

1) Определение и виды неравномерного движения;
2) Различие средней и мгновенной скоростей;
3) Правило нахождения средней скорости движения

Часто требуется решить задачу, где весь путь разбит на равные участки, даны средние скорости на каждом участке, требуется найти среднюю скорость движения на всем пути. Неверное решение будет, если сложить средние скорости и разделить на их количество. Ниже выводится формула, которую можно использовать при решении подобных задач.

Мгновенную скорость можно определить с помощью графика движения. Мгновенная скорость тела в любой точке на графике определяется наклоном касательной к кривой в соответствующей точке. Мгновенная скорость – тангенс угла наклона касательной к графику функции.

Упражнения

Во время езды на автомобиле через каждую минуту снимались показания спидометра. Можно ли по этим данным определить среднюю скорость движения автомобиля?

Нельзя, так как в общем случае величина средней скорости не равна среднему арифметическому значению величин мгновенных скоростей. А путь и время не даны.

Какую скорость переменного движения показывает спидометр автомобиля?

Близкую к мгновенной. Близкую, так как промежуток времени должен быть бесконечно мал, а при снятии показаний со спидометра так о времени судить нельзя.

В каком случае мгновенная и средняя скорости равны между собой? Почему?

При равномерном движении. Потому что скорость не изменяется.

Скорость движения молотка при ударе равна 8м/с. Какая это скорость: средняя или мгновенная?

Средняя скорость с остановками. Перемещение, путь, средняя скорость примеры решения задач

Задачи на среднюю скорость (далее СК). Мы уже рассматривали задания на прямолинейное движение. Рекомендую посмотреть статьи ” ” и ” ” . Типовые задания на среднюю скорость это группа задач на движение, они включены в ЕГЭ по математике и такая задача вполне вероятно может оказаться перед вами в момент самого экзамена. Задачки простые, решаются быстро.

Смысл таков: представьте объект передвижения, например автомобиль. Он проходит определённые участки пути с разной скоростью. На весь путь затрачивается какое-то определённое время. Так вот: средняя скорость это такая постоянная скорость с которой автомобиль преодолел бы данный весть путь за это же время То есть формула средней скорости такова:

Если участков пути было два, тогда

Если три, то соответственно:

*В знаменателе суммируем время, а в числителе расстояния пройденные за соответствующие им отрезки времени.

Первую треть трассы автомобиль ехал со скоростью 90 км/ч, вторую треть – со скоростью 60 км/ч, а последнюю – со скоростью 45 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Как уже сказано необходимо весь путь разделить на всё время движения. В условии сказано о трёх участках пути. Формула:

Обозначим весь пусть S. Тогда первую треть пути автомобиль ехал:

Вторую треть пути автомобиль ехал:

Последнюю треть пути автомобиль ехал:

Таким образом

Решите самостоятельно:

Первую треть трассы автомобиль ехал со скоростью 60 км/ч, вторую треть – со скоростью 120 км/ч, а последнюю – со скоростью 110 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Первый час автомобиль ехал со скоростью 100 км/ч, следующие два часа – со скоростью 90 км/ч, а затем два часа – со скоростью 80 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

В условии сказано о трёх участках пути. СК будем искать по формуле:

Участки пути нам не даны, но мы можем без труда их вычислить:

Первый участок пути составил 1∙100 = 100 километров.

Второй участок пути составил 2∙90 = 180 километров.

Третий участок пути составил 2∙80 = 160 километров.

Вычисляем скорость:

Решите самостоятельно:

Первые два часа автомобиль ехал со скоростью 50 км/ч, следующий час – со скоростью 100 км/ч, а затем два часа – со скоростью 75 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Первые 120 км автомобиль ехал со скоростью 60 км/ч, следующие 120 км – со скоростью 80 км/ч, а затем 150 км – со скоростью 100 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Сказано о трёх участках пути. Формула:

Протяжённость участков дана. Определим время, которое автомобиль затратил на каждый участок: на первый затрачено 120/60 часов, на второй участок 120/80 часов, на третий 150/100 часов. Вычисляем скорость:

Решите самостоятельно:

Первые 190 км автомобиль ехал со скоростью 50 км/ч, следующие 180 км – со скоростью 90 км/ч, а затем 170 км – со скоростью 100 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 74 км/ч, а вторую половину времени – со скоростью 66 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

*Есть задача про путешественника, который пересёк море. С решением у ребят возникают проблемы. Если вы не видите его, то пройдите регистрацию на сайте! Кнопка регистрации (входа) находится в ГЛАВНОМ МЕНЮ сайта. После регистрации войдите на сайт и обновите данную страницу.

Путешественник переплыл море на яхте со средней скоростью 17 км/ч. Обратно он летел на спортивном самолете со скоростью 323 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч.

С уважением, Александр.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Понятие скорости − одно из главных понятий в кинематике.
 Многим наверняка известно, что скорость − это физическая величина, показывающая насколько быстро (или насколько медленно) перемещается в пространстве движущееся тело. Разумеется, речь идет о перемещении в выбранной системе отсчета. Известно ли, однако, Вам, что используются не одно, а три понятия скорости? Есть скорость в данный момент времени, называемая мгновенной скоростью, и есть два понятия средней скорости за данный промежуток времени − средняя путевая скорость (по английски speed) и средняя скорость по перемещению (по-английски velocity).
 Будем рассматривать материальную точку в системе координат x , y , z (рис. а).

Положение A точки в момент времени t характеризуем координатами x(t) , y(t) , z(t) , представляющими три составляющих радиуса-вектора (t ). Точка движется, ее положение в выбранной системе координат с течением времени изменяется − конец радиуса-вектора (t ) описывает кривую, называемую траекторией движущейся точки.
 Траектория, описанная за промежуток времени от t до t + Δt , показана на рисунке б.

 Через B обозначено положение точки в момент t + Δt (его фиксирует радиус-вектор (t + Δt )). Пусть Δs − длина рассматриваемой криволинейной траектории, т. е. путь, пройденный точкой за время от t до t + Δt .
 Среднюю путевую скорость точки за данный промежуток времени определяют соотношением

 Очевидно, что v п − скалярная величина; она характеризуется только числовым значением.
 Показанный на рисунке б вектор

называют перемещением материальной точки за время от t до t + Δt .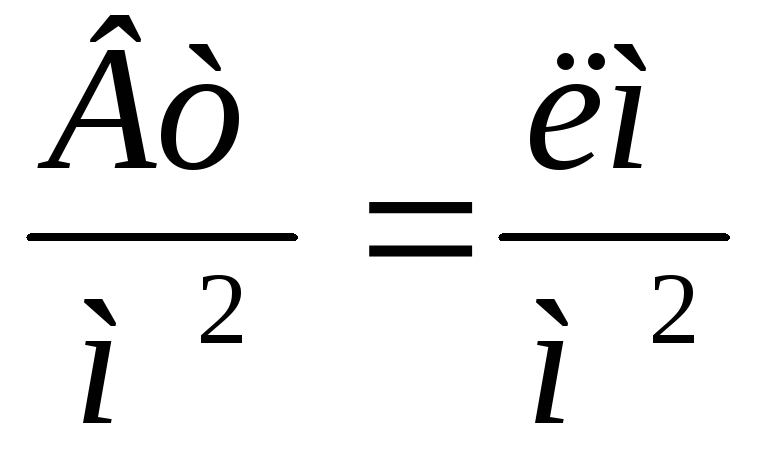
 Среднюю скорость по перемещению за данный промежуток времени определяют соотношением

 Очевидно, что v ср − векторная величина. Направление вектора v ср совпадает с направлением перемещения Δr .
 Заметим, что в случае прямолинейного движения средняя путевая скорость движущейся точки совпадает с модулем средней скорости по перемещению.
 Движение точки по прямолинейной либо криволинейной траектории называют равномерным, если в соотношении (1) величина vп не зависит от Δt . Если, например, уменьшить Δt в 2 раза, то и длина пройденного точкой пути Δs уменьшится в 2 раза. При равномерном движении точка проходит за равные промежутки времени пути равной длины.
 Вопрос :
 Можно ли считать, что при равномерном движении точки от Δt не зависит также вектор ср средней скорости по перемещению?

 Ответ :
 Так можно считать только в случае прямолинейного движения (при этом, напомним, модуль средней скорости по перемещению равен средней путевой скорости). Если же равномерное движение совершается по криволинейной траектории, то с изменением промежутка усреднения Δt будут изменяться как модуль, так и направление вектора средней скорости по перемещению. При равномерном криволинейном движении равным промежуткам времени Δt будут соответствовать разные векторы перемещения Δr (а значит, и разные векторы v ср ).
 Правда, в случае равномерного движения по окружности равным промежуткам времени будут соответствовать равные значения модуля перемещения |r| (а значит, и равные |v ср | ). Но направления перемещений (а значит, и векторов v ср ) и в данном случае будут различными для одинаковых Δt . Это видно на рисунке,

 Где равномерно движущаяся по окружности точка описывает за равные промежутки времени равные дуги AB , BC , CD . Хотя векторы перемещений 1 , 2 , 3 имеют одинаковые модули, однако направления у них различны, так что о равенстве этих векторов говорить не приходится.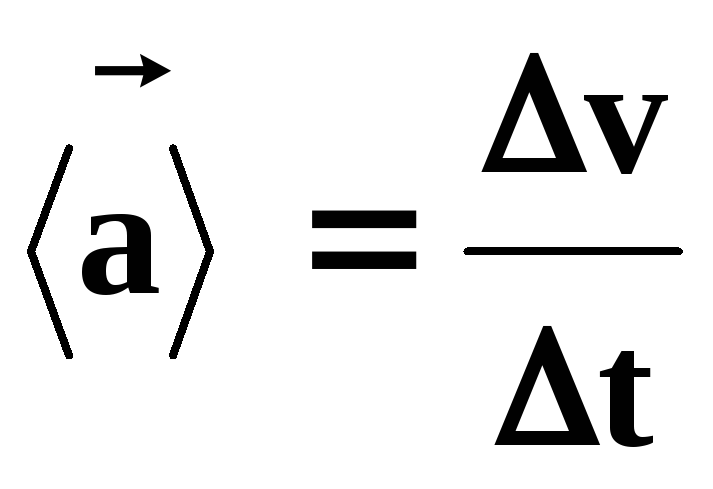
 Примечание
 Из двух средних скоростей в задачах обычно рассматривают среднюю путевую скорость, а среднюю скорость по перемещению используют довольно редко. Однако она заслуживает внимания, так как позволяет ввести понятие мгновенной скорости.

Средней скоростью называется скорость, которая получается, если весь путь поделить на время, за которое объект преодолел этот путь. Формула средней скорости:

• S = S1 + S2 + S3 = v1*t1 + v2*t2 + v3*t3
• V ср = S/t = (v1*t1 + v2*t2 + v3*t3) / (t1 + t2 + t3)

Чтобы не путаться с часами и минутами, переводим все минуты в часы: 15 мин. = 0,4 час, 36 мин. = 0,6 час. Подставляем числовые значения в последнюю формулу:

• V ср = (20*0,4 + 0,5*6 + 0,6*15) / (0,4 + 0,5 + 0,6) = (8 + 3 + 9) / (0,4 + 0,5 + 0,6) = 20 / 1,5 = 13,3 км/час

Ответ: средняя скорость V ср = 13,3 км/час.

Как найти среднюю скорость движения с ускорением

Если скорость в начале движения отличается от скорости в его конце, такое движение называют ускоренным. Причём далеко не всегда тело действительно двигается всё быстрее и быстрее. Если движение замедляется, всё равно говорят, что оно движется с ускорением, только ускорение будет уже отрицательным.

Иными словами, если автомобиль, трогаясь с места, через секунду разогнался до скорости 10 м/сек, то его ускорение а равно 10 м в секунду за секунду а = 10 м/сек². Если в следующую секунду автомобиль остановился, то его ускорение тоже равно 10 м/сек², только уже со знаком минус: а = -10 м/сек².

Скорость движения с ускорением в конце временного отрезка вычисляется по формуле:

где V0 – начальная скорость движения, a – ускорение, t – время, за которое наблюдалось данное ускорение. Плюс или минус в формуле ставится в зависимости от того, увеличивалась скорость или уменьшалась.

Средняя скорость за отрезок времени t вычисляется как среднее арифметическое начальной и конечной скорости:

Находим среднюю скорость: задача

Шарик толкнули по ровной плоскости с начальной скоростью V0 = 5 м/сек. Через 5 сек. шарик остановился. Чему равны ускорение и средняя скорость?

Конечная скорость шарика V = 0 м/сек. Ускорение из первой формулы равно

• а = (V – V0)/ t = (0 – 5)/ 5 = – 1 м/сек².

Средняя скорость V ср = (V0 + V) / 2= 5 /2 = 2,5 м/сек.

Неравномерным считается движение с изменяющейся скоростью. Скорость может изменяться по направлению. Можно заключить, что любое движение НЕ по прямой траектории является неравномерным. Например, движение тела по окружности, движение тела брошенного вдаль и др.

Скорость может изменяться по численному значению. Такое движение тоже будет неравномерным. Особенный случай такого движения – равноускоренное движение.

Иногда встречается неравномерное движение, которое состоит из чередования различного вида движений, например, сначала автобус разгоняется (движение равноускоренное), потом какое-то время движется равномерно, а потом останавливается.

Мгновенная скорость

Охарактеризовать неравномерное движение можно лишь скоростью. Но скорость всегда изменяется! Поэтому можно говорить лишь о скорости в данное мгновение времени. Путешествуя на машине спидометр ежесекундно демонстрирует вам мгновенную скорость движения. Но время при этом надо уменьшить не до секунды, а рассматривать гораздо меньший промежуток времени!

Средняя скорость

Что же такое средняя скорость? Неверно думать, что необходимо сложить все мгновенные скорости и разделить на их количество. Это самое распространенное заблуждение о средней скорости! Средняя скорость – это весь путь разделить на затраченное время . И никакими другими способами она не определяется. Если рассмотреть движение автомобиля, можно оценить его средние скорости на первой половине пути, на второй, на всем пути. Средние скорости могут быть одинаковыми, а могут быть различными на этих участках.

У средних величин рисуют сверху горизонтальную черту.

Средняя скорость перемещения. Средняя путевая скорость

Если движение тела не является прямолинейным, то пройденный телом путь будет больше, чем его перемещение. В этом случае средняя скорость перемещения отличается от средней путевой скорости. Путевая скорость – скаляр .

Главное запомнить

1) Определение и виды неравномерного движения;
2) Различие средней и мгновенной скоростей;
3) Правило нахождения средней скорости движения

Часто требуется решить задачу, где весь путь разбит на равные участки, даны средние скорости на каждом участке, требуется найти среднюю скорость движения на всем пути. Неверное решение будет, если сложить средние скорости и разделить на их количество. Ниже выводится формула, которую можно использовать при решении подобных задач.

Мгновенную скорость можно определить с помощью графика движения. Мгновенная скорость тела в любой точке на графике определяется наклоном касательной к кривой в соответствующей точке. Мгновенная скорость – тангенс угла наклона касательной к графику функции.

Упражнения

Во время езды на автомобиле через каждую минуту снимались показания спидометра. Можно ли по этим данным определить среднюю скорость движения автомобиля?

Нельзя, так как в общем случае величина средней скорости не равна среднему арифметическому значению величин мгновенных скоростей. А путь и время не даны.

Какую скорость переменного движения показывает спидометр автомобиля?

Близкую к мгновенной. Близкую, так как промежуток времени должен быть бесконечно мал, а при снятии показаний со спидометра так о времени судить нельзя.

В каком случае мгновенная и средняя скорости равны между собой? Почему?

При равномерном движении. Потому что скорость не изменяется.

Скорость движения молотка при ударе равна 8м/с. Какая это скорость: средняя или мгновенная?

В данной статье рассказано о том, как найти среднюю скорость. Дано определение этого понятия, а также рассмотрено два важных частных случая нахождения средней скорости. Представлен подробный разбор задач на нахождение средней скорости тела от репетитора по математике и физике.

Определение средней скорости

Средней скоростью движения тела называется отношение пути , пройденного телом, ко времени , в течение которого двигалось тело:

Научимся ее находить на примере следующей задачи:

Обратите внимание, что в данном случае это значение не совпало со средним арифметическим скоростей и , которое равно:
м/с.

Частные случаи нахождения средней скорости

1. Два одинаковых участка пути. Пусть первую половину пути тело двигалось со скоростью , а вторую половину пути — со скоростью . Требуется найти среднюю скорость движения тела.

2. Два одинаковых интервала движения. Пусть тело двигалось со скоростью в течение некоторого промежутка времени, а затем стало двигаться со скоростью в течение такого же промежутка времени. Требуется найти среднюю скорость движения тела.

Здесь мы получили единственный случай, когда средняя скорость движения совпала со средним арифметическим скоростей и на двух участках пути.

Решим напоследок задачу из Всероссийской олимпиады школьников по физике, прошедшей в прошлом году, которая связана с темой нашего сегодняшнего занятия.

Тело двигалось с, и средняя скорость движения составила 4 м/с. Известно, что за последние с движения средняя скорость этого же тела составила 10 м/с. Определите среднюю скорость тела за первые с движения.

Пройденный телом путь составляет: м. Можно найти также путь, который прошло тело за последние с своего движения: м. Тогда за первые с своего движения тело преодолело путь в м. Следовательно, средняя скорость на этом участке пути составила:
м/с.

Задачи на нахождение средней скорости движения очень любят предлагать на ЕГЭ и ОГЭ по физике, вступительных экзаменах, а также олимпиадах. Научиться решать эти задачи должен каждый школьник, если он планирует продолжить свое обучение в вузе. Помочь справиться с этой задачей может знающий товарищ, школьный учитель или репетитор по математике и физике. Удачи вам в изучении физики!

Сергей Валерьевич

Как определяют среднюю скорость неравномерном движение. Неравномерное движение

Равномерное движение, это вдвижение спостоянной скоростью. То есть другимим словами, тело за одинаковые промежутки времени должно проходить одинаковое расстояние. Например, если машина будет за каждый час своего пути проезжать расстояние в 50 километров, то такое движение будет являться равномерным.

Обычно равномерное движение очень редко можно встретить в реальной жизни. За примеры равномерного движения в природе, можно считать вращение Земли вокруг Солнца. Или например, конец секундной стрелки часов, тоже будет двигаться равномерно.

Расчет скорости при равномерном движении

Скорость тела при равномерном движении будет вычисляться по следующей формуле.

• Скорость = путь / время.

Если обозначить скорость движения буквой V, время движения буквой t, а путь пройденный телом буквой S, то получим следующую формулу.

Единица измерения скорости 1 м/с. То есть тело проходит расстояние в один метр, за время равное одной секунде.

Движения с переменной скоростью называется неравномерным движением. Чаще всего, все тела в природе двигаются именно неравномерно. Например, человек, когда куда-либо идет, двигается неравномерно, то есть его скорость в течении всего пути будет изменяться.

Расчет скорости при неравномерном движении

При неравномерном движении, скорость все время изменяется, и в этом случае говорят о средней скорости движения.

Средняя скорость неравномерного движения вычисляется по формуле

Из формулы для определения скорости, мы можем получить и другие формулы, например, для расчета пройденного пути или времени, которое двигалось тело.

Расчет пути при равномерном движении

Чтобы определить путь, который прошло тело при равномерном движении, необходимо скорость движения тела умножить на время которое это тело двигалось.

То есть, зная скорость и время движения, мы всегда сможем найти путь.

Теперь, получим формулу для расчета времени движения, при известных: скорости движения и пройденном пути.

Расчет времени при равномерном движении

Для того чтобы определить время равномерного движения, необходимо путь пройденный телом, поделить на скорость, с которой это тело двигалось.

Полученные выше формулы будут справедливы, если тело совершало равномерное движение.

При расчете средней скорости неравномерного движения, полагают, что движение было равномерным. Исходя из этого, для вычисления по средней скорости неравномерного движения, пути или времени движения используют те же самые формулы, что и при равномерном движении.

Расчет пути при неравномерном движении

Получаем, что путь пройденный телом при неравномерном движении, равен произведению средней скорости на время которое тело двигалось.

Расчет времени при неравномерном движении

Время необходимое для прохождения некоторого пути при неравномерном движении, равняется частному от деления пути на среднюю скорость неравномерного движения.

Графиком равномерного движения, в координатах S(t) будет являться прямая линия.

План-конспект урока по теме « »

Дата:

Тема: Неравномерное (переменное) движение. Средняя скорость

Цели:

Образовательная: формирование знаний и представлений о неравномерном (переменном) движении, а также о средней скорости;

Развивающая: развитие и формирование практических умений пользоваться физическими понятиями и величинами для описания равномерного прямолинейного движения; развивать познавательный интерес;

Воспитательная: прививать культуру умственного труда, аккуратность, учить видеть практическую пользу знаний, продолжить формирование коммуникативных умений, воспитывать внимательность, наблюдательность.

Тип урока: урок усвоения новых знаний

Оборудование и источники информации:

Исаченкова, Л. А. Физика: учеб. для 7 кл. учреждений общ. сред. образования с рус. яз. обучения / Л. А. Исаченкова, Г. В. Пальчик, А. А. Сокольский; под ред. А. А. Сокольского. Минск: Народная асвета, 2017.

Структура урока:

Организационный момент(5 мин)

Актуализация опорных знаний(5мин)

Изучение нового материала (14 мин)

Физкультминутка (1 мин)

Закрепление знаний (15 мин)

Итоги урока(5 мин)

Содержание урока

Организационный момент (проверка присутствующих в классе, проверка выполнения домашнего задания, озвучивание темы и основных целей урока)

Актуализация опорных знаний

Что выражает график пути?

Для какого движения график пути представляет собой прямую?

Как по графику скорости определить пройденный путь?

Изучение нового материала

Проанализируйте движение автобуса. Он уменьшает скорость перед остановкой. Затем в течение ка кого-то промежутка времени стоит на остановке, т. е. его скорость равна нулю, после чего скорость увеличивается. Значит, скорость автобуса в процессе движения изменяется, т. е. является переменной величиной.

Движение, при котором скорость изменяется, называется неравномерным (переменным).

Практически все движения, наблюдаемые в природе и технике, – неравномерные. С изменяющейся скоростью движутся, например, люди, птицы (рис. 103), дельфины (рис. 104), поезда, падают предметы (рис. 105). Но как же тогда характеризовать это движение?

Неравномерное движение характеризуется средней скоростью. Как определить среднюю скорость? Рассмотрим пример. Вы едете на экскурсию в Брест поездом. Поезд проходит от Минска до Бреста путь s = 330 км. На прохождение этого пути затрачивается время t = 4,5 ч. В течение данного времени поезд стоит на станциях, движется то с увеличивающейся, то с уменьшающейся скоростью.

Обозначим среднюю скорость ( v ) и запишем формулу:

Тогда поезд «Минск – Брест» движется со средней скоростью

Вас не удивило, что мы использовали формулу равномерного движения? Да, действительно, формально мы нашли среднюю скорость так, как будто поезд весь путь s = 330 км двигался равномерно с постоянной скоростью v = 73 Это, конечно же, не означает, что он на самом деле двигался равномерно. На отдельных участках пути скорость движения поезда была как значительно

большей (120 , так и меньшей, чем 73 , и даже равной нулю (рис. 106).

Средняя скорость дает лишь приблизительное представление о быстроте движения тела. Описание переменного движения более сложно по сравнению с описанием равномерного.

Например, если скорость поезда на участке разгона возрастает от 0 до 90 то в различных точках траектории она принимает различные значения из этого промежутка. Таким образом, можно говорить не только о средней скорости на данном участке траектории, но и о скорости в данной точке траектории. Такую скорость называют в физике мгновенной скоростью.

Рассмотрим пример решения задачи со стр. 66

Физкультминутка

Закрепление знаний

А сейчас поработаем с карточками по теме «Неравномерное (переменное) движение. Средняя скорость» (приложение 1)

Заполните таблицу.

Ответ:

Движение, при кото-ром скорость изменя-ется, называется неравномерным (переменным).

Среднюю скорость находят путем деления всего пути на весь промежуток времени, за который этот путь пройден.

Ответ: при равномерном движении тело за равное время проходит равное расстояние, а при неравномерном – разное.

Ответ: по формуле

Ответ: «всего» – это весь путь, который прошло тело, «весь» – все время, за который этот путь пройден

Яблоко падало с высоты h = 2,2 м в течение времени t

Ответ:

Ответ: сначала мотоциклист за 3 секунды разогнался до скорости 6 м/с, затем 6 секунд ехал с постоянной скоростью равной 6 м/с, а после начал тормозить и через 3,5 секунды остановился.

Итоги урока

Итак, подведем итоги:

Характеристикой неравномерного движения является средняя скорость.

Для вычисления средней скорости нужно путь разделить на весь промежуток времени, затраченный на прохождение этого пути.

Организация домашнего задания

§18,ответить на контрольные вопросы.

Решить задачу:

Определите среднюю скорость своего движения от дома до школы. Оцените полученный результат.

Рефлексия

Продолжите фразы:

Сегодня на уроке я узнал…

Было интересно…

Знания, которые я получил на уроке, пригодятся.

Приложение 1

Карточка по теме «Неравномерное (переменное) движение. Средняя скорость»

Выполните задания и решите задачи

Заполните таблицу, ответьте устно на контрольные вопросы, решите задачи.

Заполните таблицу.

1. Чем отличается неравномерное движение тела от равномерного?

   Как найти среднюю скорость неравномерного движения?

   Какое физическое значение имеют слова «всего» и «весь» в определении средней скорости

   Яблоко падало с высоты h = 2,2 м в течение времени t = 0,67 с. Найдите среднее значение скорости падения яблока.

   По данным графика (см. рисунок) опишите движение мотоциклиста.

В реальной жизни очень сложно встретить равномерное движения, так как с такой большой точностью объекты материального мира не могут передвигаться, да еще и долгий промежуток времени, поэтому обычно на практике используются более реальное физическое понятие, характеризующее движение определенного тела в пространстве и времени.

Замечание 1

Неравномерное движение характеризуется тем, что тело может проходить одинаковый или разный путь за равные промежутки времени.

Для полного понимания этого вида механического движения вводится дополнительное понятие средней скорости.

Средняя скорость

Определение 1

Средняя скорость представляет собой физическую величину, которая равна отношению всего пути, пройденного телом, к полному времени движения.

Этот показатель рассматривается на определенном участке:

$\upsilon = \frac{\Delta S}{\Delta t}$

По данному определению средняя скорость является скалярной величиной, так как время и путь – скалярные величины.

Средняя скорость можно определять по уравнению перемещения:

Средняя скорость в подобных случаях считается векторной величиной, так как она ее можно определить через отношение векторной величины к скалярной.

Средняя скорость перемещения и средняя скорость прохождения пути характеризуют одинаковое движение, однако являются различными величинами.

В процессе расчета средней скорости обычно допускается ошибка. Она состоит в том, что понятие средней скорости иногда заменяется средней арифметической скоростью тела. Этот недочет допускается на разных участках движения тела.

Средняя скорость тела не может определяться через среднее арифметическое значение. Для решения задач используется уравнение для средней скорости. По нему можно найти среднюю скорость тела на определенном участке. Для этого весь путь, который пройден телом, разделить на общее время движения.

Неизвестную величину $\upsilon$ можно выразить через другие. Их обозначают:

$L_0$ и $\Delta t_0$.

Получается формула, согласно которой идет поиск неизвестной величины:

$L_0 = 2 ∙ L$, а $\Delta t_0 = \Delta t_1 + \Delta t_2$.

При решении длинной цепочки уравнений можно прийти к изначальной версии поиска средней скорости тела на определенном участке.

При непрерывном движении также непрерывно изменяется скорость тела. Подобное движение рождает закономерность, при которой скорость в любой последующих точках траектории отличается от скорости объекта в предыдущей точке.

Мгновенная скорость

Мгновенной скоростью называют скорость в данный отрезок времени в определенной точке траектории.

Средняя скорость тела будет сильнее отличаться от мгновенной скорости в случаях, когда:

• она больше промежутка времени $\Delta t$;
• она меньше промежутка времени.

Определение 2

Мгновенная скорость – это физическая величина, которая равна отношению небольшого перемещения на определенном участке траектории или пройденного пути телом, к небольшому промежутку времени, за которое это перемещение совершалось.

Мгновенная скорость становится векторной величиной, когда речь идет о средней скорости перемещения.

Мгновенная скорость становится скалярной величиной, когда говорят о средней скорости прохождения пути.

При неравномерном движении изменение скорости тела происходит за равные промежутки времени на равную величину.

Равнопеременное движение тела возникает в момент, когда скорость объекта за любые равные промежутки времени изменяется на равную величину.

Виды неравномерного движения

При неравномерном движении постоянно меняется скорость тела. Различают основные виды неравномерного движения :

• движение по окружности;
• движение тела, брошенного вдаль;
• равноускоренное движение;
• равнозамедленное движение;
• равнопеременное движение
• неравнопеременное движение.

Скорость может изменяться по численному значению. Подобное движение также считают неравномерным. Особенным случаем неравномерного движения считают равноускоренное движение.

Определение 3

Неравнопеременным движением называют такое движение тела, когда скорость объекта за любые неравные промежутки времени не меняется на определенную величину.

Равнопеременное движение характеризуется возможностью увеличения или уменьшения скорости тела.

Равнозамедленным называют движение, когда скорость тела уменьшается. Равноускоренным называют движение, при котором скорость тела увеличивается.

Ускорение

Для неравномерного движения введена еще одна характеристика. Эта физическая величина называется ускорением.

Ускорением называют векторную физическую величину, равная отношению изменения скорости тела ко времени, когда это изменение происходило.

$a=\frac{\upsilon }{t}$

При равнопеременном движении нет зависимости ускорения от изменения скорости тела, а также от времени изменения этой скорости.

Ускорение показывает на количественное изменение скорости тела за определенную единицу времени.

Для того, чтобы получить единицу ускорения, необходимо в классическую формулу для ускорения подставить единицы скорости и времени.

В проекции на координатную ось 0X уравнение примет следующий вид:

$υx = υ0x + ax ∙ \Delta t$.

Если знать ускорение тела и его начальную скорость, можно заранее найти скорость в любой заданный момент времени.

Физическая величина, которая равна отношению пути, пройденного телом за конкретный промежуток времени, к длительности подобного промежутка, является средней путевой скоростью. Средняя путевая скорость выражается в виде:

• скалярной величины;
• неотрицательной величины.

Средняя скорость представлена в форме вектора. Она направлена туда, куда направлено перемещение тела за определенный промежуток времени.

Модуль средней скорости равняется средней путевой скорости в случаях, если тело все это время движется в одном направлении. Модуль средней скорости уменьшается к средней путевой скорости, если в процессе движения тело изменяет направление своего движения.

Основные положения:

Неравномерное движение – это движение с переменной скоростью.

Мгновенная скорость – это векторная физическая величина, равная пределу отношения перемещения тела к промежутку времени, стремящимся к нулю.

Если за произвольные равные промежутки времени точка проходит пути разной длины, то численное значение ее скорости с течением времени изменяется. Такое движение называется неравномерным . В этом случае пользуются скалярной величиной, называемой средней путевой скоростью неравномерного движения на данном участке траектории. Она равна отношению пройденного пути к промежутку времени, за который этот путь пройден:

Средняя скорость при неравномерном движении – отношение вектора перемещения тела к промежутку времени, за который это перемещение произошло.

Для характеристики изменения скорости движения вводится понятие ускорения .

Средним ускорением неравномерного движения в интервале времени от t до называется векторная величина, равная отношению изменения скорости к интервалу времени :

Мгновенным ускорением, или ускорением материальной точки в момент времени t, будет предел среднего ускорения:

Движение, происходящее с постоянным ускорением, называется равнопеременным.

Уравнение равнопеременного движения : .

Вектор ускорения принято раскладывать на две составляющие: тангенциальное и центростремительное ускорение.

Тангенциальное ускорение показывает быстроту изменения модуля скорости, а нормальное ускорение характеризует быстроту изменения направления скорости при криволинейном движении.

Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих:

;

.

Контрольные вопросы:

1. Дать определение неравномерного движения.

2. Что называют равнопеременным движением?

3. Дайте определение мгновенной скорости.

4. Как направлен вектор мгновенной скорости?

5. Дайте определение мгновенного ускорения. В каких единицах измеряется?

6. Как направлены тангенциальное и центростремительное ускорение относительно кривизны траектории?

7. Дайте определение угловой скорости. Ее единицы измерения.

Выполните задания:

1. Напишите формулы зависимости:

а) частоты вращения от периода;

б) угловой скорости от периода;

в) угловой и линейной скорости;

г) угловой скорости от частоты;

д) центростремительного ускорения от скорости;

е) линейной скорости от частоты вращения;

ж) линейной скорости от периода.

Средняя скорость. В § 9 мы говорили, что утверждение о равномерности данного движения справедливо только с той степенью точности, с которой произведены измерения. Например, применив секундомер, можно обнаружить, что движение поезда, представлявшееся при грубом измерении равномерным, оказывается неравномерным при более тонком измерении.

Но когда поезд подходит к станции, мы обнаружим неравномерность его движения даже без секундомера. Даже грубые измерения покажут нам, что промежутки времени, за которые поезд проходит расстояния от одного телеграфного столба до другого, становятся все больше и больше. С той малой степенью точности, которую дает измерение времени по часам, движение поезда на перегоне равномерно, а при подходе к станции – неравномерно. Поместим на игрушечный заводной автомобиль капельницу, заведем его и пустим катиться по столу. В середине движения расстояния между каплями оказываются одинаковыми (движение равномерно), но затем, когда завод приблизится к концу, будет заметно, что капли ложатся все ближе одна к другой – движение неравномерно (рис. 25).

При неравномерном движении нельзя говорить о какой-то определенной скорости, так как отношение пройденного пути к соответственному промежутку времени не одинаково для разных участков , как это имело место для равномерного движения. Если, однако, нас интересует движение только на каком-либо определенном участке пути, то это движение в целом можно охарактеризовать, введя понятие средней скорости движения :средней скоростью неравномерного движения на данном участке пути называют отношение длины этого участка к промежутку времени, за который этот участок пройден :

Отсюда видно, что средняя скорость равна скорости такого равномерного движения, при котором тело прошло бы данный участок пути за тот же промежуток времени, что и при действительном движении.

Как и в случае равномерного движения, можно пользоваться формулой для определения пути, пройденного за данный промежуток времени при определенной средней скорости, и формулой для определения времени, за которое пройден данный путь с данной средней скоростью. Но пользоваться этими формулами можно только для того участка пути и для того промежутка времени, для которых эта средняя скорость была рассчитана. Например, зная среднюю скорость на участке пути АВ и зная длину АВ, можно определить время, за которое был пройден этот участок, но нельзя найти время, за которое была пройдена половина участка АВ, так как средняя скорость на половине участка при неравномерном движении, вообще говоря, не будет равна средней скорости на всем участке.

Если для любых участков пути средняя скорость оказалась одинаковой, то это значит, что движение равномерное и средняя скорость равна скорости этого равномерного движения.

Если средняя скорость известна за отдельные последовательные промежутки времени, то можно найти среднюю скорость и за суммарное время движения. Пусть, например, поезд двигался в течение двух часов, причем его средняя скорость за первые 10 мин равнялась 18 км/ч, за следующие полтора часа – 50 км/ч и за остальное время – 30 км/ч. Найдем пути, пройденные за отдельные промежутки времени. Они будут равны км; км; км. Значит, общий путь, пройденный поездом, есть км. Поскольку весь этот путь был пройден за два часа, искомая средняя скорость км/ч.

Из этого примера видно, как вычислять среднюю скорость и в общем случае, когда известны средние скорости движения с которыми тело двигалось в течение последовательных промежутков времени . Средняя скорость всего движения выразится формулой

Средняя путевая скорость формула. Как найти среднюю скорость

В данной статье рассказано о том, как найти среднюю скорость. Дано определение этого понятия, а также рассмотрено два важных частных случая нахождения средней скорости. Представлен подробный разбор задач на нахождение средней скорости тела от репетитора по математике и физике.

Определение средней скорости

Средней скоростью движения тела называется отношение пути , пройденного телом, ко времени , в течение которого двигалось тело:

Научимся ее находить на примере следующей задачи:

Обратите внимание, что в данном случае это значение не совпало со средним арифметическим скоростей и , которое равно:
м/с.

Частные случаи нахождения средней скорости

1. Два одинаковых участка пути. Пусть первую половину пути тело двигалось со скоростью , а вторую половину пути — со скоростью . Требуется найти среднюю скорость движения тела.

2. Два одинаковых интервала движения. Пусть тело двигалось со скоростью в течение некоторого промежутка времени, а затем стало двигаться со скоростью в течение такого же промежутка времени. Требуется найти среднюю скорость движения тела.

Здесь мы получили единственный случай, когда средняя скорость движения совпала со средним арифметическим скоростей и на двух участках пути.

Решим напоследок задачу из Всероссийской олимпиады школьников по физике, прошедшей в прошлом году, которая связана с темой нашего сегодняшнего занятия.

Тело двигалось с, и средняя скорость движения составила 4 м/с. Известно, что за последние с движения средняя скорость этого же тела составила 10 м/с. Определите среднюю скорость тела за первые с движения.

Пройденный телом путь составляет: м. Можно найти также путь, который прошло тело за последние с своего движения: м. Тогда за первые с своего движения тело преодолело путь в м. Следовательно, средняя скорость на этом участке пути составила:
м/с.

Задачи на нахождение средней скорости движения очень любят предлагать на ЕГЭ и ОГЭ по физике, вступительных экзаменах, а также олимпиадах. Научиться решать эти задачи должен каждый школьник, если он планирует продолжить свое обучение в вузе. Помочь справиться с этой задачей может знающий товарищ, школьный учитель или репетитор по математике и физике. Удачи вам в изучении физики!

Сергей Валерьевич

Механическим движением тела называется изменение его положения в пространстве относительно других тел с течением времени. При этом тела взаимодействуют по законам механики.

Раздел механики, описывающий геометрические свойства движения без учета причин, его вызывающих, называется кинематикой.

В более общем значении движением называется любое пространственное или временное изменение состояния физической системы. Например, можно говорить о движении волны в среде.

Относительность движения

Относительность – зависимость механического движения тела от системы отсчёта Не указав систему отсчёта, не имеет смысла говорить о движении.

Траектория материальной точки – линия в трёхмерном пространстве, представляющая собой множество точек, в которых находилась, находится или будет находиться материальная точка при своём перемещении в пространстве. Существенно, что понятие о траектории имеет физический смысл даже при отсутствии какого-либо по ней движения. Кроме того, и при наличии движущегося по ней объекта, траектория сама по себе не может ничего дать в отношении причин движения, то есть о действующих силах.

Путь – длина участка траектории материальной точки, пройденного ею за определённое время.

Скорость (часто обозначается , от англ. velocity или фр. vitesse) – векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта (например, угловая скорость). Этим же словом может называться скалярная величина, точнее модуль производной радиус-вектора.

В науке используется также скорость в широком смысле, как быстрота изменения какой-либо величины (не обязательно радиус-вектора) в зависимости от другой (чаще изменения во времени, но также в пространстве или любой другой). Так, например, говорят о скорости изменения температуры, скорости химической реакции, групповой скорости, скорости соединения, угловой скорости и т. д. Математически характеризуется производной функции.

Единицы измерения скорости

Метр в секунду, (м/с), производная единица системы СИ

Километр в час, (км/ч)

узел (морская миля в час)

Число Маха, 1 Мах равен скорости звука в данной среде; Max n в n раз быстрее.

Как единица, зависящая от конкретных условий среды, должна дополнительно определяться.

Скорость света в вакууме (обозначается c )

В современной механике движение тела подразделяется на виды, и существует следующая классификация видов движения тела :

Поступательное движение, при котором любая прямая линия, связанная с телом, остаётся при движении параллельной самой себе

Вращательное движение или вращение тела вокруг своей оси, считающейся неподвижной.

Сложное движение тела, состоящее из поступательного и вращательного движений.

Каждое из этих видов может быть неравномерным и равномерным (с не постоянной и постоянной скоростью соответственно).

Средняя скорость неравномерного движения

Средняя путевая скорость – это отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден:

Средняя путевая скорость, в отличие от мгновенной скорости не является векторной величиной.

Средняя скорость равна среднему арифметическому от скоростей тела во время движения только в том случае, когда тело двигалось с этими скоростями одинаковые промежутки времени.

В то же время если, например, половину пути автомобиль двигался со скоростью 180 км/ч, а вторую половину со скоростью 20 км/ч, то средняя скорость будет 36 км/ч. В примерах, подобных этому, средняя скорость равна среднему гармоническому всех скоростей на отдельных, равных между собой, участках пути.

Средняя скорость по перемещению

Можно также ввести среднюю скорость по перемещению, которая будет вектором, равным отношению перемещения ко времени, за которое оно совершено:

Средняя скорость, определённая таким образом, может равняться нулю даже в том случае, если точка (тело) реально двигалась (но в конце промежутка времени вернулась в исходное положение).

Если перемещение происходило по прямой (причём в одном направлении), то средняя путевая скорость равна модулю средней скорости по перемещению.

Прямолинейное равномерное движение – это движение, при котором тело (точка) за любые равные промежутки времени совершает одинаковые перемещения. Вектор скорости точки остаётся неизменным, а её перемещение есть произведение вектора скорости на время:

Если направить координатную ось вдоль прямой, по которой движется точка, то зависимость координаты точки от времени является линейной: , где – начальная координата точки, – проекция вектора скорости на координатную ось x.

Точка, рассматриваемая в инерциальной системе отсчёта, находится в состоянии равномерного прямолинейного движения, если равнодействующая всех сил, приложенных к точке, равна нулю.

Вращательное движение – вид механического движения. При вращательном движении абсолютно твердого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землей, ось вращения ротора генератора на электростанции неподвижна.

Характеристики вращения тела

При равномерном вращении (N оборотов в секунду),

Частота вращения – число оборотов тела в единицу времени,

Период вращения – время одного полного оборота. Период вращения T и его частота v связаны соотношением T = 1 / v.

Линейная скорость точки, находящейся на расстоянии R от оси вращения

,
Угловая скорость вращения тела.

Кинетическая энергия вращательного движения

Где I z – момент инерции тела относительно оси вращения. w – угловая скорость.

Гармонический осциллятор (в классической механике) – это система, которая при смещении из положения равновесия испытывает действие возвращающей силы, пропорциональной смещению.

Если возвращающая сила – единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором. Свободные колебания такой системы представляют собой периодическое движение около положения равновесия (гармонические колебания). Частота и амплитуда при этом постоянны, причём частота не зависит от амплитуды.

Если имеется ещё и сила трения (затухание), пропорциональная скорости движения (вязкое трение), то такую систему называют затухающим или диссипативным осциллятором. Если трение не слишком велико, то система совершает почти периодическое движение – синусоидальные колебания с постоянной частотой и экспоненциально убывающей амплитудой. Частота свободных колебаний затухающего осциллятора оказывается несколько ниже, чем у аналогичного осциллятора без трения.

Если осциллятор предоставлен сам себе, то говорят, что он совершает свободные колебания. Если же присутствует внешняя сила (зависящая от времени), то говорят, что осциллятор испытывает вынужденные колебания.

Механическими примерами гармонического осциллятора являются математический маятник (с малыми углами смещения), груз на пружине, торсионный маятник и акустические системы. Среди других аналогов гармонического осциллятора стоит выделить электрический гармонический осциллятор (см. LC-цепь).

Звук , в широком смысле – упругие волны, продольно распространяющиеся в среде и создающие в ней механические колебания; в узком смысле – субъективное восприятие этих колебаний специальными органами чувств животных или человека.

Как и любая волна, звук характеризуется амплитудой и спектром частот. Обычно человек слышит звуки, передаваемые по воздуху, в диапазоне частот от 16 Гц до 20 кГц. Звук ниже диапазона слышимости человека называют инфразвуком; выше: до 1 ГГц, – ультразвуком, более 1 ГГц – гиперзвуком. Среди слышимых звуков следует также особо выделить фонетические, речевые звуки и фонемы (из которых состоит устная речь) и музыкальные звуки (из которых состоит музыка).

Физические параметры звука

Колебательная скорость – величина, равная произведению амплитуды колебаний А частиц среды, через которую проходит периодическая звуковая волна, на угловую частоту w :

где В – адиабатическая сжимаемость среды; р – плотность.

Как и световые волны, звуковые тоже могут отражаться, преломляться и т.д.

Если Вам понравилась эта страница, и Вам захотелось, чтобы Ваши друзья тоже её увидели, то выберите внизу значок социальной сети, где вы имеете свою страницу, и выразите своё мнение о содержании.

Ваши друзья и случайные посетители благодаря этому добавят Вам и моему сайту рейтинг

Неравномерным считается движение с изменяющейся скоростью. Скорость может изменяться по направлению. Можно заключить, что любое движение НЕ по прямой траектории является неравномерным. Например, движение тела по окружности, движение тела брошенного вдаль и др.

Скорость может изменяться по численному значению. Такое движение тоже будет неравномерным. Особенный случай такого движения – равноускоренное движение.

Иногда встречается неравномерное движение, которое состоит из чередования различного вида движений, например, сначала автобус разгоняется (движение равноускоренное), потом какое-то время движется равномерно, а потом останавливается.

Мгновенная скорость

Охарактеризовать неравномерное движение можно лишь скоростью. Но скорость всегда изменяется! Поэтому можно говорить лишь о скорости в данное мгновение времени. Путешествуя на машине спидометр ежесекундно демонстрирует вам мгновенную скорость движения. Но время при этом надо уменьшить не до секунды, а рассматривать гораздо меньший промежуток времени!

Средняя скорость

Что же такое средняя скорость? Неверно думать, что необходимо сложить все мгновенные скорости и разделить на их количество. Это самое распространенное заблуждение о средней скорости! Средняя скорость – это весь путь разделить на затраченное время . И никакими другими способами она не определяется. Если рассмотреть движение автомобиля, можно оценить его средние скорости на первой половине пути, на второй, на всем пути. Средние скорости могут быть одинаковыми, а могут быть различными на этих участках.

У средних величин рисуют сверху горизонтальную черту.

Средняя скорость перемещения. Средняя путевая скорость

Если движение тела не является прямолинейным, то пройденный телом путь будет больше, чем его перемещение. В этом случае средняя скорость перемещения отличается от средней путевой скорости. Путевая скорость – скаляр .

Главное запомнить

1) Определение и виды неравномерного движения;
2) Различие средней и мгновенной скоростей;
3) Правило нахождения средней скорости движения

Часто требуется решить задачу, где весь путь разбит на равные участки, даны средние скорости на каждом участке, требуется найти среднюю скорость движения на всем пути. Неверное решение будет, если сложить средние скорости и разделить на их количество. Ниже выводится формула, которую можно использовать при решении подобных задач.

Мгновенную скорость можно определить с помощью графика движения. Мгновенная скорость тела в любой точке на графике определяется наклоном касательной к кривой в соответствующей точке. Мгновенная скорость – тангенс угла наклона касательной к графику функции.

Упражнения

Во время езды на автомобиле через каждую минуту снимались показания спидометра. Можно ли по этим данным определить среднюю скорость движения автомобиля?

Нельзя, так как в общем случае величина средней скорости не равна среднему арифметическому значению величин мгновенных скоростей. А путь и время не даны.

Какую скорость переменного движения показывает спидометр автомобиля?

Близкую к мгновенной. Близкую, так как промежуток времени должен быть бесконечно мал, а при снятии показаний со спидометра так о времени судить нельзя.

В каком случае мгновенная и средняя скорости равны между собой? Почему?

При равномерном движении. Потому что скорость не изменяется.

Скорость движения молотка при ударе равна 8м/с. Какая это скорость: средняя или мгновенная?

Понятие скорости − одно из главных понятий в кинематике.
 Многим наверняка известно, что скорость − это физическая величина, показывающая насколько быстро (или насколько медленно) перемещается в пространстве движущееся тело. Разумеется, речь идет о перемещении в выбранной системе отсчета. Известно ли, однако, Вам, что используются не одно, а три понятия скорости? Есть скорость в данный момент времени, называемая мгновенной скоростью, и есть два понятия средней скорости за данный промежуток времени − средняя путевая скорость (по английски speed) и средняя скорость по перемещению (по-английски velocity).
 Будем рассматривать материальную точку в системе координат x , y , z (рис. а).

Положение A точки в момент времени t характеризуем координатами x(t) , y(t) , z(t) , представляющими три составляющих радиуса-вектора (t ). Точка движется, ее положение в выбранной системе координат с течением времени изменяется − конец радиуса-вектора (t ) описывает кривую, называемую траекторией движущейся точки.
 Траектория, описанная за промежуток времени от t до t + Δt , показана на рисунке б.

 Через B обозначено положение точки в момент t + Δt (его фиксирует радиус-вектор (t + Δt )). Пусть Δs − длина рассматриваемой криволинейной траектории, т. е. путь, пройденный точкой за время от t до t + Δt .
 Среднюю путевую скорость точки за данный промежуток времени определяют соотношением

 Очевидно, что v п − скалярная величина; она характеризуется только числовым значением.
 Показанный на рисунке б вектор

называют перемещением материальной точки за время от t до t + Δt .
 Среднюю скорость по перемещению за данный промежуток времени определяют соотношением

 Очевидно, что v ср − векторная величина. Направление вектора v ср совпадает с направлением перемещения Δr .
 Заметим, что в случае прямолинейного движения средняя путевая скорость движущейся точки совпадает с модулем средней скорости по перемещению.
 Движение точки по прямолинейной либо криволинейной траектории называют равномерным, если в соотношении (1) величина vп не зависит от Δt . Если, например, уменьшить Δt в 2 раза, то и длина пройденного точкой пути Δs уменьшится в 2 раза. При равномерном движении точка проходит за равные промежутки времени пути равной длины.
 Вопрос :
 Можно ли считать, что при равномерном движении точки от Δt не зависит также вектор ср средней скорости по перемещению?

 Ответ :
 Так можно считать только в случае прямолинейного движения (при этом, напомним, модуль средней скорости по перемещению равен средней путевой скорости). Если же равномерное движение совершается по криволинейной траектории, то с изменением промежутка усреднения Δt будут изменяться как модуль, так и направление вектора средней скорости по перемещению. При равномерном криволинейном движении равным промежуткам времени Δt будут соответствовать разные векторы перемещения Δr (а значит, и разные векторы v ср ).
 Правда, в случае равномерного движения по окружности равным промежуткам времени будут соответствовать равные значения модуля перемещения |r| (а значит, и равные |v ср | ). Но направления перемещений (а значит, и векторов v ср ) и в данном случае будут различными для одинаковых Δt . Это видно на рисунке,

 Где равномерно движущаяся по окружности точка описывает за равные промежутки времени равные дуги AB , BC , CD . Хотя векторы перемещений 1 , 2 , 3 имеют одинаковые модули, однако направления у них различны, так что о равенстве этих векторов говорить не приходится.
 Примечание
 Из двух средних скоростей в задачах обычно рассматривают среднюю путевую скорость, а среднюю скорость по перемещению используют довольно редко. Однако она заслуживает внимания, так как позволяет ввести понятие мгновенной скорости.

Задачи на среднюю скорость (далее СК). Мы уже рассматривали задания на прямолинейное движение. Рекомендую посмотреть статьи ” ” и ” ” . Типовые задания на среднюю скорость это группа задач на движение, они включены в ЕГЭ по математике и такая задача вполне вероятно может оказаться перед вами в момент самого экзамена. Задачки простые, решаются быстро.

Смысл таков: представьте объект передвижения, например автомобиль. Он проходит определённые участки пути с разной скоростью. На весь путь затрачивается какое-то определённое время. Так вот: средняя скорость это такая постоянная скорость с которой автомобиль преодолел бы данный весть путь за это же время То есть формула средней скорости такова:

Если участков пути было два, тогда

Если три, то соответственно:

*В знаменателе суммируем время, а в числителе расстояния пройденные за соответствующие им отрезки времени.

Первую треть трассы автомобиль ехал со скоростью 90 км/ч, вторую треть – со скоростью 60 км/ч, а последнюю – со скоростью 45 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Как уже сказано необходимо весь путь разделить на всё время движения. В условии сказано о трёх участках пути. Формула:

Обозначим весь пусть S. Тогда первую треть пути автомобиль ехал:

Вторую треть пути автомобиль ехал:

Последнюю треть пути автомобиль ехал:

Таким образом

Решите самостоятельно:

Первую треть трассы автомобиль ехал со скоростью 60 км/ч, вторую треть – со скоростью 120 км/ч, а последнюю – со скоростью 110 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Первый час автомобиль ехал со скоростью 100 км/ч, следующие два часа – со скоростью 90 км/ч, а затем два часа – со скоростью 80 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

В условии сказано о трёх участках пути. СК будем искать по формуле:

Участки пути нам не даны, но мы можем без труда их вычислить:

Первый участок пути составил 1∙100 = 100 километров.

Второй участок пути составил 2∙90 = 180 километров.

Третий участок пути составил 2∙80 = 160 километров.

Вычисляем скорость:

Решите самостоятельно:

Первые два часа автомобиль ехал со скоростью 50 км/ч, следующий час – со скоростью 100 км/ч, а затем два часа – со скоростью 75 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Первые 120 км автомобиль ехал со скоростью 60 км/ч, следующие 120 км – со скоростью 80 км/ч, а затем 150 км – со скоростью 100 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Сказано о трёх участках пути. Формула:

Протяжённость участков дана. Определим время, которое автомобиль затратил на каждый участок: на первый затрачено 120/60 часов, на второй участок 120/80 часов, на третий 150/100 часов. Вычисляем скорость:

Решите самостоятельно:

Первые 190 км автомобиль ехал со скоростью 50 км/ч, следующие 180 км – со скоростью 90 км/ч, а затем 170 км – со скоростью 100 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 74 км/ч, а вторую половину времени – со скоростью 66 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

*Есть задача про путешественника, который пересёк море. С решением у ребят возникают проблемы. Если вы не видите его, то пройдите регистрацию на сайте! Кнопка регистрации (входа) находится в ГЛАВНОМ МЕНЮ сайта. После регистрации войдите на сайт и обновите данную страницу.

Путешественник переплыл море на яхте со средней скоростью 17 км/ч. Обратно он летел на спортивном самолете со скоростью 323 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч.

С уважением, Александр.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Как определить среднюю скорость автомобиля. По какой формуле рассчитывается средняя скорость

Инструкция

Рассмотрим функцию f(x) = |x|. Для начала этой без знака модуля, то есть график функции g(x) = x. Этот график является прямой, проходящей через начало координат и угол между этой прямой и положительным направлением оси абсцисс составляет 45 градусов.

Так как модуль величина неотрицательная, то ту часть , которая находится ниже оси абсцисс необходимо зеркально отобразить относительно нее. Для функции g(x) = x получим, что график после такого отображения станет похож на V. Этот новый график и будет являться графической интерпретацией функции f(x) = |x|.

Видео по теме

Обратите внимание

График модуля функции никогда не будет находится в 3 и 4 четверти, так как модуль не может принимать отрицательных значений.

Полезный совет

Если в функции присутствуют несколько модулей, то их нужно раскрывать последовательно, а затем накладывать друг на друга. Результат и будет искомым графиком.

Источники:

• как построить график функции с модулями

Задачи на кинематику, в которых необходимо вычислить скорость , время или путь равномерно и прямолинейно движущихся тел, встречаются в школьном курсе алгебры и физики. Для их решения найдите в условии величины, которые можно между собой уравнять. Если в условии требуется определить время при известной скорости, воспользуйтесь следующей инструкцией.

Вам понадобится

• – ручка;
• – бумага для записей.

Инструкция

Самый простой случай – движение одного тела с заданной равномерной скорость ю. Известно расстояние, которое тело прошло. Найдите в пути: t = S/v, час, где S – расстояние, v – средняя скорость тела.

Второй – на встречное движение тел. Из пункта А в пункт В движется автомобиль со скорость ю 50 км/ч. Навстречу ему из пункта B одновременно выехал мопед со скорость ю 30 км/час. Расстояние между пунктами А и В 100 км. Требуется найти время , через которое они встретятся.

Обозначьте точку встречи К. Пусть расстояние АК, которое автомобиль, будет х км. Тогда путь мотоциклиста составит 100-х км. Из условия задачи следует, что время в пути у автомобиля и мопеда одинаково. Составьте уравнение: х/v = (S-x)/v’, где v, v’ – и мопеда. Подставив данные, решите уравнение: x = 62,5 км. Теперь время : t = 62,5/50 = 1,25 часа или 1 час 15 минут.

Третий пример – даны те же условия, но автомобиль выехал на 20 минут позже мопеда. Определить, времени в пути будет автомобиль до встречи с мопедом.

Составьте уравнение, аналогично предыдущему. Но в этом случае время мопеда в пути будет на 20 минут , чем у автомобиля. Для уравнивания частей, вычтите одну треть часа из правой части выражения: х/v = (S-x)/v’-1/3. Найдите х – 56,25. Вычислите время : t = 56,25/50 = 1,125 часа или 1 час 7 минут 30секунд.

Четвертый пример – задача на движение тел в одном направлении. Автомобиль и мопед с теми же скоростями двигаются из точки А. Известно, что автомобиль выехал на полчаса позже. Через какое время он догонит мопед?

В этом случае одинаковым будет расстояние, которое проехали транспортные средства. Пусть время в пути автомобиля будет x часов, тогда время в пути мопеда будет x+0,5 часов. У вас получилось уравнение: vx = v’(x+0,5). Решите уравнение, подставив значение , и найдите x – 0,75 часа или 45 минут.

Пятый пример – автомобиль и мопед с теми же скоростями двигаются в одном направлении, но мопед выехал из точки В, находящейся на расстоянии 10 км от точки А, на полчаса раньше. Вычислить, через какое время после старта автомобиль догонит мопед.

Расстояние, которое проехал автомобиль, на 10 км больше. Прибавьте эту разницу к пути мотоциклиста и уравняйте части выражения: vx = v’(x+0,5)-10. Подставив значения скорости и решив его, вы получите : t = 1,25 часа или 1 час 15 минут.

Источники:

• какая скорость машины времени

Инструкция

Рассчитайте среднюю тела, движущегося равномерно на протяжении участка пути. Такая скорость вычисляется проще всего, поскольку она не изменяется на всем отрезке движения и равняется средней . Можно это в виде : Vрд = Vср, где Vрд – скорость равномерного движения , а Vср – средняя скорость .

Вычислите среднюю скорость равнозамедленного (равноускоренного) движения на данном участке, для чего необходимо сложить начальную и конечную скорость . Разделите на два полученный результат, который и

1. Материальная точка прошла половину окружности. Найти отношение средней путевой скорости к модулю средней векторной скорости.

Решение . Из определения средних значений путевой и векторной скоростей с учетом того, что путь, пройденный материальной точкой за время движенияt , равенR , а величина перемещения 2R , гдеR – радиус окружности, получим:

2. Автомобиль проехал первую треть пути со скоростью v 1 = 30 км/ч, а оставшуюся часть пути – со скоростью v 2 = 40 км/ч. Найти среднюю скорость на всем пройденном пути.

Решение . По определению =гдеS – путь, пройденный за времяt . Очевидно, что
Поэтому искомая средняя скорость равна

3. Студент проехал половину пути на велосипеде со скоростьюv 1 = 12 км/ч. Далее половину оставшегося времени он ехал со скоростьюv 2 = 10 км/ч, а оставшуюся часть пути шел пешком со скоростьюv 3 = 6 км/ч. Определить среднюю скорость движения студента на всем пути.

Решение . По определению
гдеS – путь, аt – время движения. Ясно, чтоt =t 1 +t 2 +t 3 . Здесь
– время движения на первой половине пути,t 2 – время движения на втором участке пути иt 3 – на третьем. По условию задачиt 2 =t 3 . Кроме того,S /2 =v 2 t 2 + v 3 t 3 = (v 2 +v 3)t 2 . Отсюда следует:

Подставив t 1 и t 2 +t 3 = 2t 2 в выражение для средней скорости, получим:

4. Расстояние между двумя станциями поезд прошел за времяt 1 = 30 мин. Разгон и торможение длилисьt 2 = 8 мин, а остальное время поезд двигался равномерно со скоростью v = 90 км/ч. Определить среднюю скорость поезда , считая, что при разгоне скорость увеличивалась с течением времени по линейному закону, а при торможении уменьшалась тоже по линейному закону.

Р

ешение . Построим график зависимости скорости поезда от времени (см. рис.). Этот график описывает трапецию с длинами оснований, равнымиt 1 иt 1 –t 2 и высотой, равной v. Площадь этой трапеции численно равна пути, пройденному поездом от начала движения до остановки. Поэтому средняя скорость равна:

Задачи и упражнения

1.1. Мяч упал с высотыh 1 = 4 м, отскочил от пола и был пойман на высотеh 2 = 1 м. Чему равен путьS и величина перемещения
?

1.2. Материальная точка переместилась на плоскости из точки с координатамиx 1 = 1 см иy 1 = 4cм в точку с координатамиx 2 = 5 см иy 2 = 1 см. Построить вектор перемещения и с помощью линейки определить модуль вектора перемещения и проекции вектора перемещения на осиx иy . Найти эти же величины аналитически и сравнить результаты.

1.3. Первую половину пути поезд шел со скоростью вn = 1,5 раза большей, чем вторую половину пути. Средняя скорость поезда на всем пути = 43,2 км/ч. Каковы скорости поезда на первой и второй половинах пути?

1.4. Первую половину времени своего движения велосипедист проехал со скоростью v 1 = 18 км/ч, а вторую половину времени – со скоростью v 2 = 12 км/ч. Определить среднюю скорость движения велосипедиста.

1.5. Движение двух автомобилей описывается уравнениями
и
, где все величины измеряются в системе СИ. Запишите закон изменения расстояния
между автомобилями от времени и найдите
через время
с. после начала движения.

Чтобы вычислить среднюю скорость, воспользуйтесь простой формулой: Скорость = Пройденный путь Время {\displaystyle {\text{Скорость}}={\frac {\text{Пройденный путь}}{\text{Время}}}} . Но в некоторых задачах даются два значения скорости – на разных участках пройденного пути или в различные промежутки времени. В этих случаях нужно пользоваться другими формулами для вычисления средней скорости. Навыки решения подобных задач могут пригодиться в реальной жизни, а сами задачи могут встретиться на экзаменах, поэтому запомните формулы и уясните принципы решения задач.

Шаги

По одному значению пути и одному значению времени

• длина пути, пройденного телом;
• время, за которое тело прошло этот путь.
• Например: автомобиль проехал 150 км за 3 ч. Найдите среднюю скорость автомобиля.

1. Формула: , где v {\displaystyle v} – средняя скорость, s {\displaystyle s} – пройденный путь, t {\displaystyle t} – время, за которое пройден путь.

   В формулу подставьте пройденный путь. Значение пути подставьте вместо s {\displaystyle s} .

   • В нашем примере автомобиль проехал 150 км. Формула запишется так: v = 150 t {\displaystyle v={\frac {150}{t}}} .

2. В формулу подставьте время. Значение времени подставьте вместо t {\displaystyle t} .

   • В нашем примере автомобиль ехал в течение 3 ч. Формула запишется так: .

3. Разделите путь на время. Вы найдете среднюю скорость (как правило, она измеряется в километрах в час).

   • В нашем примере:
     v = 150 3 {\displaystyle v={\frac {150}{3}}}

     Таким образом, если автомобиль проехал 150 км за 3 ч, то он двигался со средней скоростью 50 км/ч.

4. Вычислите общий пройденный путь. Для этого сложите значения пройденных участков пути. В формулу подставьте общий пройденный путь (вместо s {\displaystyle s} ).

   • В нашем примере автомобиль проехал 150 км, 120 км и 70 км. Общий пройденный путь: .

5. T {\displaystyle t} ).

   • . Таким образом, формула запишется так: .
6. • В нашем примере:
     v = 340 6 {\displaystyle v={\frac {340}{6}}}

     Таким образом, если автомобиль проехал 150 км за 3 ч, 120 км за 2 ч, 70 км за 1 ч, то он двигался со средней скоростью 57 км/ч (округленно).

По нескольким значениям скоростей и нескольким значениям времени

1. Посмотрите на данные величины. Воспользуйтесь этим методом, если даны следующие величины:

   Запишите формулу для вычисления средней скорости. Формула: v = s t {\displaystyle v={\frac {s}{t}}} , где v {\displaystyle v} – средняя скорость, s {\displaystyle s} – общий пройденный путь, t {\displaystyle t} – общее время, за которое пройден путь.

2. Вычислите общий путь. Для этого умножьте каждую скорость на соответствующее время. Так вы найдете длину каждого участка пути. Чтобы вычислить общий путь, сложите значения пройденных участков пути. В формулу подставьте общий пройденный путь (вместо s {\displaystyle s} ).

   • Например:
     50 км/ч в течение 3 ч = 50 × 3 = 150 {\displaystyle 50\times 3=150} км
     60 км/ч в течение 2 ч = 60 × 2 = 120 {\displaystyle 60\times 2=120} км
     70 км/ч в течение 1 ч = 70 × 1 = 70 {\displaystyle 70\times 1=70} км
     Общий пройденный путь: 150 + 120 + 70 = 340 {\displaystyle 150+120+70=340} км. Таким образом, формула запишется так: v = 340 t {\displaystyle v={\frac {340}{t}}} .

3. Вычислите общее время в пути. Для этого сложите значения времени, за которые был пройден каждый участок пути. В формулу подставьте общее время (вместо t {\displaystyle t} ).

   • В нашем примере автомобиль ехал в течение 3 ч, 2 ч и 1 ч. Общее время в пути: 3 + 2 + 1 = 6 {\displaystyle 3+2+1=6} . Таким образом, формула запишется так: v = 340 6 {\displaystyle v={\frac {340}{6}}} .

4. Разделите общий путь на общее время. Вы найдете среднюю скорость.

   • В нашем примере:
     v = 340 6 {\displaystyle v={\frac {340}{6}}}
     v = 56 , 67 {\displaystyle v=56,67}
     Таким образом, если автомобиль двигался со скоростью 50 км/ч в течение 3 ч, со скоростью 60 км/ч в течение 2 ч, со скоростью 70 км/ч в течение 1 ч, то он двигался со средней скоростью 57 км/ч (округленно).

По двум значениям скоростей и двум одинаковым значениям времени

1. Посмотрите на данные величины. Воспользуйтесь этим методом, если даны следующие величины и условия:

   • два или несколько значений скоростей, с которыми двигалось тело;
   • тело двигалось с определенными скоростями в течение равных промежутков времени.
   • Например: автомобиль двигался со скоростью 40 км/ч в течение 2 ч и со скоростью 60 км/ч в течение других 2 ч. Найдите среднюю скорость автомобиля на всем протяжении пути.

2. Запишите формулу для вычисления средней скорости, если даны две скорости, с которыми тело движется в течение равных промежутков времени. Формула: v = a + b 2 {\displaystyle v={\frac {a+b}{2}}} , где v {\displaystyle v} – средняя скорость, a {\displaystyle a} – скорость тела в течение первого промежутка времени, b {\displaystyle b} – скорость тела в течение второго (такого же, как первый) промежутка времени.

   • В таких задачах значения промежутков времени не важны – главное, чтобы они были равны.
   • Если дано несколько значений скоростей и равные промежутки времени, перепишите формулу так: v = a + b + c 3 {\displaystyle v={\frac {a+b+c}{3}}} или v = a + b + c + d 4 {\displaystyle v={\frac {a+b+c+d}{4}}} . Если промежутки времени равны, сложите все значения скоростей и разделите их на количество таких значений.

3. В формулу подставьте значения скоростей. Неважно, какое значение подставить вместо a {\displaystyle a} , а какое – вместо b {\displaystyle b} .

   • Например, если первая скорость равна 40 км/ч, а вторая скорость равна 60 км/ч, формула запишется так: .

4. Сложите значения двух скоростей. Затем сумму разделите на два. Вы найдете среднюю скорость на всем протяжении пути.

   • Например:
     v = 40 + 60 2 {\displaystyle v={\frac {40+60}{2}}}
     v = 100 2 {\displaystyle v={\frac {100}{2}}}
     v = 50 {\displaystyle v=50}
     Таким образом, если автомобиль двигался со скоростью 40 км/ч в течение 2 ч и со скоростью 60 км/ч в течение других 2 ч, средняя скорость автомобиля на всем протяжении пути составила 50 км/ч.

Средней скоростью называется скорость, которая получается, если весь путь поделить на время, за которое объект преодолел этот путь. Формула средней скорости:

• S = S1 + S2 + S3 = v1*t1 + v2*t2 + v3*t3
• V ср = S/t = (v1*t1 + v2*t2 + v3*t3) / (t1 + t2 + t3)

Чтобы не путаться с часами и минутами, переводим все минуты в часы: 15 мин. = 0,4 час, 36 мин. = 0,6 час. Подставляем числовые значения в последнюю формулу:

• V ср = (20*0,4 + 0,5*6 + 0,6*15) / (0,4 + 0,5 + 0,6) = (8 + 3 + 9) / (0,4 + 0,5 + 0,6) = 20 / 1,5 = 13,3 км/час

Ответ: средняя скорость V ср = 13,3 км/час.

Как найти среднюю скорость движения с ускорением

Если скорость в начале движения отличается от скорости в его конце, такое движение называют ускоренным. Причём далеко не всегда тело действительно двигается всё быстрее и быстрее. Если движение замедляется, всё равно говорят, что оно движется с ускорением, только ускорение будет уже отрицательным.

Иными словами, если автомобиль, трогаясь с места, через секунду разогнался до скорости 10 м/сек, то его ускорение а равно 10 м в секунду за секунду а = 10 м/сек². Если в следующую секунду автомобиль остановился, то его ускорение тоже равно 10 м/сек², только уже со знаком минус: а = -10 м/сек².

Скорость движения с ускорением в конце временного отрезка вычисляется по формуле:

где V0 – начальная скорость движения, a – ускорение, t – время, за которое наблюдалось данное ускорение. Плюс или минус в формуле ставится в зависимости от того, увеличивалась скорость или уменьшалась.

Средняя скорость за отрезок времени t вычисляется как среднее арифметическое начальной и конечной скорости:

Находим среднюю скорость: задача

Шарик толкнули по ровной плоскости с начальной скоростью V0 = 5 м/сек. Через 5 сек. шарик остановился. Чему равны ускорение и средняя скорость?

Конечная скорость шарика V = 0 м/сек. Ускорение из первой формулы равно

• а = (V – V0)/ t = (0 – 5)/ 5 = – 1 м/сек².

Средняя скорость V ср = (V0 + V) / 2= 5 /2 = 2,5 м/сек.

Помните, что скорость задается как численным значением, так и направлением. Скорость описывает быстроту изменения положения тела, а также направление, в котором движется это тело. Например, 100 м/с (на юг).

7. Найдите общее перемещение, то есть расстояние и направление между начальной и конечной точками пути. В качестве примера рассмотрим тело, движущееся с постоянной скоростью в одном направлении.

   • Например, ракета была запущена в северном направлении и двигалась в течение 5 минут с постоянной скоростью 120 метров в минуту. Чтобы вычислить общее перемещение, воспользуйтесь формулой s = vt: (5 минут) (120 м/мин) = 600 м (на север) .
   • Если в задаче дано постоянное ускорение, воспользуйтесь формулой s = vt + ½at 2 (в следующем разделе описывается упрощенный способ работы с постоянным ускорением).

8. Найдите общее время в пути. В нашем примере ракета перемещается в течение 5 минут. Среднюю скорость можно выразить в любых единицах измерения, но в международной системе единиц скорость измеряется в метрах в секунду (м/с). Конвертируйте минуты в секунды: (5 минут) х (60 секунд/минута) = 300 секунд .

   • Если даже в научной задаче время дано в часах или других единицах измерения, лучше сначала вычислить скорость, а затем преобразовать ее в м/с.

9. Вычислите среднюю скорость. Если вы знаете значение перемещения и общее время в пути, вычислить среднюю скорость можно по формуле v ср = Δs/Δt. В нашем примере средняя скорость ракеты равна 600 м (на север) / (300 секунд) = 2 м/с (на север) .

   • Не забудьте указать направление движения (например, «вперед» или «на север»).
   • В формуле v ср = Δs/Δt символ «дельта» (Δ) означает «изменение величины», то есть Δs/Δt означает «изменение положения к изменению времени».
   • Средняя скорость может быть записана как v ср или как v с горизонтальной чертой сверху.

10. Решение более сложных задач, например, если тело вращается или ускорение не является постоянным. В этих случаях средняя скорость по-прежнему вычисляется как отношение общего перемещения к общему времени. Не имеет значения, что происходит с телом между начальной и конечной точками пути. Вот несколько примеров задач с одинаковым общим перемещением и общим временем (а, следовательно, и одинаковой средней скоростью).

    • Анна идет на запад со скоростью 1 м/с в течение 2 секунд, затем мгновенно ускоряется до 3 м/с и продолжает идти на запад в течение 2 секунд. Ее общее перемещение составляет (1 м/с)(2 с) + (3 м/с)(2 с) = 8 м (на запад). Общее время в пути: 2 с + 2 с = 4 с. Ее средняя скорость: 8 м / 4 с = 2 м/с (на запад) .
    • Борис идет на запад со скоростью 5 м/с в течение 3 секунд, затем разворачивается и идет на восток со скоростью 7 м/с в течение 1 секунды. Мы можем рассматривать движение на восток как «отрицательное движение» на запад, поэтому общее перемещение равно (5 м/с)(3 с) + (-7 м/с)(1 с) = 8 метров. Общее время равно 4 с. Средняя скорость равна 8 м (на запад) / 4 с = 2 м/с (на запад) .
    • Юля проходит 1 метр на север, затем проходит 8 метров на запад, а затем проходит 1 метр на юг. Общее время в пути составляет 4 секунды. Нарисуйте схему этого движения на бумаге, и вы увидите, что оно заканчивается в 8 метрах к западу от начальной точки, то есть общее перемещение равно 8 м. Общее время в пути составило 4 секунды. Средняя скорость равна 8 м (на запад) / 4 с = 2 м/с (на запад) .

Мгновенная и средняя скорости. Неравномерное движение

Если материальная точка находится в движении, то ее координаты подвергаются изменениям. Этот процесс может происходить быстро или медленно.

Определение 1

Величина, которая характеризует быстроту изменения положения координаты, называется скоростью .

Определение 2

Средняя скорость – это векторная величина, численно равная перемещению в единицу времени, и сонаправленная с вектором перемещения υ = ∆ r ∆ t ; υ ∆ r .

Рисунок 1 . Средняя скорость сонаправлена перемещению

Модуль средней скорости по пути равняется υ = S ∆ t .

Мгновенная скорость характеризует движение в определенный момент времени. Выражение «скорость тела в данный момент времени» считается не корректным, но применимым при математических расчетах.

Определение 3

Мгновенной скоростью называют предел, к которому стремится средняя скорость υ при стремлении промежутка времени ∆ t к 0:

υ = l i m ∆ t ∆ r ∆ t = d r d t = r ˙ .

Направление вектора υ идет по касательной к криволинейной траектории, потому как бесконечно малое перемещение d r совпадает с бесконечно малым элементом траектории d s .

Рисунок 2 . Вектор мгновенной скорости υ

Имеющееся выражение υ = l i m ∆ t ∆ r ∆ t = d r d t = r ˙ в декартовых координатах идентично ниже предложенным уравнениям:

υ x = d x d t = x ˙ υ y = d y d t = y ˙ υ z = d z d t = z ˙ .

Запись модуля вектора υ примет вид:

υ = υ = υ x 2 + υ y 2 + υ z 2 = x 2 + y 2 + z 2 .

Чтобы перейти от декартовых прямоугольных координат к криволинейным, применяют правила дифференцирования сложных функций. Если радиус-вектор r является функцией криволинейных координат r = r q 1 , q 2 , q 3 , тогда значение скорости запишется как:

υ = d r d t = ∑ i = 1 3 ∂ r ∂ q i ∂ q i ∂ r = ∑ i = 1 3 ∂ r ∂ q i q ˙ i .

Рисунок 3 . Перемещение и мгновенная скорость в системах криволинейных координат

При сферических координатах предположим, что q 1 = r ; q 2 = φ ; q 3 = θ , то получим υ , представленную в такой форме:

υ = υ r e r + υ φ e φ + υ θ φ θ , где υ r = r ˙ ; υ φ = r φ ˙ sin θ ; υ θ = r θ ˙ ; r ˙ = d r d t ; φ ˙ = d φ d t ; θ ˙ = d θ d t ; υ = r 1 + φ 2 sin 2 θ + θ 2 .

Определение 4

Мгновенной скоростью называют значение производной от функции перемещения по времени в заданный момент, связанной с элементарным перемещением соотношением d r = υ (t) d t

Пример 1

Дан закон прямолинейного движения точки x (t) = 0 , 15 t 2 – 2 t + 8 . Определить ее мгновенную скорость через 10 секунд после начала движения.

Решение

Мгновенной скоростью принято называть первую производную радиус-вектора по времени. Тогда ее запись примет вид:

υ (t) = x ˙ (t) = 0 . 3 t – 2 ; υ (10) = 0 . 3 × 10 – 2 = 1 м / с.

Ответ : 1 м / с.

Пример 2

Движение материальной точки задается уравнением x = 4 t – 0 , 05 t 2 . Вычислить момент времени t о с т, когда точка прекратит движение, и ее среднюю путевую скорость υ .

Решение

Вычислим уравнение мгновенной скорости, подставим числовые выражения:

υ (t) = x ˙ (t) = 4 – 0 , 1 t .

4 – 0 , 1 t = 0 ; t о с т = 40 с; υ 0 = υ (0) = 4 ; υ = ∆ υ ∆ t = 0 – 4 40 – 0 = 0 , 1 м / с.

Ответ: заданная точка остановится по прошествии 40 секунд; значение средней скорости равняется 0 , 1 м / с.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Для того, чтобы охарактеризовать насколько быстро изменяется в пространстве положение движущегося тела, используют специальное понятие скорость.

Средней скоростью тела на данном участке траектории называется отношение пройденного пути ко времени движения:

(3.1)
Если на всех участках траектории средняя скорость одинакова, то движение называется равномерным.

Вопрос о скорости бега является важным в спортивной биомеханике. Известно, что скорость бега на определенную дистанцию зависит от величины этой дистанции. Бегун может поддерживать максимальную скорость только в течение ограниченного времени. Средняя скорость стайеров обычно меньше, чем спринтеров. На рис. 3.8. показана зависимость средней скорости (V) от длины дистанции (S).

Рис. 3.8. Зависимость средней скорости бега от длины дистанции
График зависимости проведен через точки, соответствующие средним скоростям для всех рекордных результатов у мужчин на дистанциях от 50 до 2000 м. Средняя скорость растет с увеличением дистанции до 200 м, а затем убывает.

В табл. 3.1 приведены мировые рекорды скорости.

Для удобства проведения вычислений среднюю скорость можно записать и через изменение координат тела. При прямолинейном движении пройденный путь равен разности координат конечной и начальной точек. Так, если в момент времени t 0 тело находилось в точке с координатой x 0 , а в момент времени t 1 – в точке с координатой x 1 , то пройденный путь Δх = х 1 – х 0 , а время движения Δ t = t 1 – t 0 (в физике и математике принято использовать символ Δ для обозначения разности однотипных величин или для обозначения очень маленьких интервалов). Таблица 3.1

Мировые спортивные рекорды


Вид состязаний и дистанция	Мужчины		Женщины
		средняя скорость, м/с	время, показанное на дистанции	средняя скорость, м/с
Бег 100 м	9,83с	10,16	10,49 с	9,53
200 м	19,72 с	10,14	21,34 с	9,37
400м	43,29 с	9,24	47,60 с	8,40
800м	1 мин 41,73 с	7,86	1 мин 53,28 с	7,06
1500м	3 мин 29,46 с	7,16	3 мин 52,47 с	6,46
5000 м	12 мин 58,39 с	6,42	14 мин 37,33 с	5,70
10000 м	27 мин 13,81 с	6,12	30 мин 13,75 с	5,51
Марафон (42 км 195 м)	2 ч 6 мин 50 с	5,5	2 ч 21 мин 0,6 с	5,0
Бег на коньках	36,45 с	13,72	39,10 с	12,78
1500м	1 мин 52,06 с	13,39	1 мин 59,30 с	12,57
5000м	6 мин 43,59 с	12,38	7 мин 14,13 с	11,35
10000 м	13 мин 48,20 с	12,07
Плавание 100 м (вольный стиль)	48,74 с	2,05	54,79 с	1,83
200 м (вольный стиль)	1 мин 47,25 с	1,86	1 мин 57,55 с	1,70
400 м (вольный стиль)	3 мин 46,95 с	1,76	4 мин 3,85 с	1,64
100 м (брасс)	1 мин 1,65 с	1,62	1 мин 7,91 с	1,47
200 м (брасс)	2 мин 13,34 с	1,50	2 мин 26,71 с	1,36
100 м (баттерфляй)	52,84 с	1,89	57,93 с	1,73
200 м (баттерфляй)	1 мин 56,24 с	1,72	2 мин 5,96 с	1,59

В общем случае средние скорости на различных участках пути могут отличаться. На рис. 3.9 представлены координаты падающего тела, моменты времени, в которые тело проходит через эти точки, а также средние скорости для выделенных интервалов.

Рис. 3.9. Зависимость средней скорости от участка пути
Из данных, приведенных на рис. 3.9 видно, что средняя скорость на всем пути (от 0 м до 5 м) равна

Средняя скорость на интервале от 2 м до 3 м равна

Движение, при котором средняя скорость изменяется, называется неравномерным.

Мы вычисляли среднюю скорость в окрестности одной и той же точки х = 2,5 м. На рис. 3.9 видно, что по мере уменьшения интервала, по которому проводятся вычисления, средняя скорость стремится к некоторому пределу (в нашем случае это 7 м/с). Этот предел называется мгновенной скоростью или скоростью в данной точке траектории.

Мгновенной скоростью движения, или скоростью в данной точке траектории называется предел, к которому стремится отношение перемещения тела в окрестности этой точки ко времени при неограниченном уменьшении интервала:

Размерность скорости в СИ – м/с.

Часто скорость указывают в других единицах (например, в км/ч). При необходимости такие значения можно перевести в СИ. Например, 54 км/ч = 54000 м/3600 с =15 м/с.

Для одномерного случая мгновенная скорость равна производной от координаты тела по времени:

При равномерном движении величины средней и мгновенной скорости совпадают и остаются неизменными.

Мгновенная скорость – величина векторная. Направление вектора мгновенной скорости показано на рис. 3.10.

Рис. 3.10. Направление вектора мгновенной скорости
Во время забега мгновенная скорость бегуна меняется. Особенно существенны такие изменения в спринте. На рис. 3.11 приводится пример такого изменения для дистанции 200 м.

Бегун начинает движение из состояния покоя и разгоняется, пока не достигнет максимальной скорости. Для бегуна-мужчины время ускорения приблизительно 2 с, а максимальная скорость приближается к 10,5 м/с. Средняя скорость на всей дистанции меньше этого значения.


Рис. 3.11. Зависимость мгновенной скорости от времени бега для дистанции 200 м, мужчины
Причина того, что бегун не может долго поддерживать свою максимальную скорость движения, состоит в том, что он начинает испытывать недостаток кислорода. Тело содержит кислород, запасенный в мышцах, а в дальнейшем получает его при дыхании. Поэтому спринтер может поддерживать свою максимальную скорость только до тех пор, пока не израсходует запас кислорода. Это кислородное истощение наступает на дистанции около 300 м. Следовательно, для больших дистанций бегун должен ограничивать себя скоростью меньше максимальной. Чем длиннее дистанция, тем меньше должна быть скорость, чтобы кислорода хватило на весь забег. Только спринтеры бегут на максимальной скорости всю дистанцию.

На соревнованиях бегун обычно стремиться либо победить соперника, либо установить рекорд. От этого зависит стратегия забега. При установлении рекорда оптимальной стратегией будет та, при которой выбирается скорость, соответствующая полному истощению запаса кислорода к моменту пересечения финиша.

В спорте используются специальные временные характеристики.

Момент времени (t) – это временная мера положения точки, тела или системы. Момент времени определяют промежутком времени до него от начала отсчета.

Моментами времени обозначают, например, начало и окончание движения или какой-либо его части (фазы). По моментам времени определяют длительность движения.

Длительность движения (Δt) – это его временная мера, которая измеряется разностью моментов времени окончания и начала движения:

Δt = t кон – t нач .

Длительность движения представляет собой количество времени, прошедшее между двумя ограничивающими его моментами времени. Сами моменты длительности не имеют. Зная путь точки и длительность ее движения, можно определять ее среднюю скорость.

Темп движения (N) – это временная мера повторности движений. Он измеряется количеством движений, повторяющихся в единицу времени (частота движений):

В повторных движениях одинаковой длительности темп характеризует их протекание во времени. Темп – величина, обратная длительности движений. Чем больше длительность каждого движения, тем меньше темп, и наоборот.

Ритм движений – это временная мера соотношения частей движений. Он определяется по соотношению промежутков времени – длительностей частей движений: Δt 2-1: Δt 2-3: Δt 4- 3 …

Различный ритм движений для лыжников при скользящем шаге (для пяти фаз шага) показан на рис. 3.12.

Рис. 3.12. Различный ритм в скользящем шаге на лыжах: а) у высококвалифицированных лыжников;

б) у сильнейших лыжников мира;

фазы /-/// – скольжение, фазы скольжения,

фазы IV- V – стояние лыжи

Быстрота – это темп, в котором преодолевается расстояние без учета направления.

Быстрота – скалярная величина. Пусть между двумя пунктами при движении по одному шоссе одновременно движутся автомобилист, мотоциклист, велосипедист, бегун. У всех четверых одинаковы траектории, пути, перемещения. Однако их движение отличается быстротой (стремительностью), для характеристики которой и вводится понятие «скорость».

К примеру, автомобиль, который трогается с места, движется ускоренно, так как наращивает скорость движения. В точке начала движения скорость автомобиля равняется нулю. Начав движение, автомобиль разгоняется до некоторой скорости. При необходимости затормозить, автомобиль не сможет остановиться мгновенно, а за какое-то время. То есть скорость автомобиля будет стремиться к нулю – автомобиль начнет двигаться замедленно до тех пор, пока не остановится полностью. Но физика не имеет термина «замедление». Если тело двигается, уменьшая скорость, этот процесс тоже называется ускорением , но со знаком «-».

Средним ускорением называется отношение изменения скорости к промежутку времени, за который это изменении произошло. Вычисляют среднее ускорение при помощи формулы:

где – это . Направление вектора ускорения такое же, как у направления изменения скорости Δ = – 0

где 0 является начальной скоростью. В момент времени t 1 (см. рис. ниже) у тела 0 . В момент времени t 2 тело имеет скорость . Исходя из правила вычитания векторов, определим вектор изменения скорости Δ = – 0 . Отсюда вычисляем ускорение:

.

В системе СИ единицей ускорения называется 1 метр в секунду за секунду (либо метр на секунду в квадрате):

.

Метр на секунду в квадрате – это ускорение прямолинейно движущейся точки, при котором за 1 с скорость этой точки растет на 1 м/с. Другими словами, ускорение определяет степень изменения скорости тела за 1 с. К примеру, если ускорение составляет 5 м/с 2 , значит, скорость тела ежесекундно растет на 5 м/с.

Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина , которая равна пределу, к которому стремится среднее ускорение при стремлении промежутка времени к 0. Другими словами – это ускорение, развиваемое телом за очень маленький отрезок времени:

.

Ускорение имеет такое же направление, как и изменение скорости Δ в крайне маленьких промежутках времени, за которые скорость изменяется. Вектор ускорения можно задать при помощи проекций на соответствующие оси координат в заданной системе отсчета (проекциями а Х, a Y , a Z).

При ускоренном прямолинейном движении скорость тела увеличивается по модулю, т.е. v 2 > v 1 , а вектор ускорения имеет такое же направление, как и у вектора скорости 2 .

Если скорость тела по модулю уменьшается (v 2 замедление движения (ускорение отрицательно, а

Если происходит движение по криволинейной траектории, то изменяется модуль и направление скорости. Значит, вектор ускорения изображают в виде 2х составляющих.

Тангенциальным (касательным) ускорением называют ту составляющую вектора ускорения, которая направлена по касательной к траектории в данной точке траектории движения. Тангенциальное ускорение описывает степень изменения скорости по модулю при совершении криволинейного движения.




У вектора тангенциального ускорения τ (см. рис. выше) направление такое же, как и у линейной скорости либо противоположно ему. Т.е. вектор тангенциального ускорения находится в одной оси с касательной окружности, являющейся траекторией движения тела.

Скорость в физике означает быстроту перемещения какого-либо объекта в пространстве. Эта величина бывает разной: линейной, угловой, средней, космической и даже сверхсветовой. В число всех существующих разновидностей входит также и мгновенная скорость. Что это за величина, какова ее формула и какие действия необходимы для ее расчета – об этом как раз и пойдет речь в нашей статье.

Мгновенная скорость: сущность и понятие

О том, как определить быстроту перемещения объекта по прямой, известно даже ученику начальных классов: достаточно пройденное расстояние разделить на время, которое было затрачено на такое перемещение. Однако стоит помнить, что результат, полученный таким способом, позволяет судить о Если объект движется неравномерно, то на определенных участках его пути быстрота перемещения может заметно варьироваться. Поэтому порой требуется такая величина как мгновенная скорость. Она позволяет судить о быстроте перемещения материальной точки в любой момент движения.

Мгновенная скорость: формула расчета

Данный параметр равен пределу (обозначается limit, сокращенно lim) отношения перемещения (разнице координат) к промежутку времени, за которое это изменение произошло, при условии, что этот промежуток времени стремится достичь нуля. Это определение можно записать в виде следующей формулы:

v = Δs/Δt при Δt → 0 либо так v = lim Δt→0 (Δs/Δt)

Отметим, что мгновенная скорость есть Если движение происходит по прямой линии, то она меняется лишь по величине, а направление остается постоянным. В противном случае вектор скорости мгновенной направлен по касательной по отношению к траектории перемещения в каждой рассматриваемой точке. Какой смысл несет данный показатель? Мгновенная скорость позволяет выяснить, какое перемещение осуществит объект за единицу времени, если с рассматриваемого момента он движется равномерно и прямолинейно.

В случае никаких сложностей нет: нужно просто найти отношение расстояния к времени, за которое оно было объектом преодолено. В этом случае средняя и мгновенная скорость тела равны. Если же движение происходит непостоянно, то в этом случае следует узнать величину ускорения и определять мгновенную скорость в каждый определенный момент времени. При вертикальном перемещении следует учитывать влияние Мгновенную скорость автомобиля можно определить с помощью радара или спидометра. Следует иметь в виду, что перемещение в некоторых участках пути может принимать отрицательное значение.

Для того чтобы найти ускорение, можно воспользоваться акселерометром либо составить функцию движения и воспользоваться формулой v=v0+a.t. Если перемещение начинается из состояния покоя, то v0 = 0. При расчетах нужно учитывать тот факт, что при торможении тела (уменьшении скорости) величина ускорения будет со знаком “минус”. Если объект совершает мгновенная быстрота его перемещения рассчитывается по формуле v= g.t. В этом случае начальная скорость также равна 0.

СЛОБОДСКОВ БОРИС АНАТОЛЬЕВИЧ – ФИЗИКА (КУРС ЛЕКЦИЙ)

§ 17. Переменное движение. Средняя скорость. Средний модуль скорости

1. Переменное движение.

Определение 1. Движение называется переменным, если за любые равные промежутки времени точка совершает различные перемещения.

   Перемещение – вектор. Он может изменяться по модулю и направлению. При переменном движении за любые равные промежутки времени перемещения могут отличаться либо модулями, либо направлениями, либо и модулями и направлениями.

2. Средняя скорость.

Определение 2а. Средней скоростью переменного движения называется отношение перемещения ко времени, за которое это перемещение произошло.

   Запишем формулу скорости равномерного движения и средней скорости переменного движения.

   Если посмотреть на правые части этих равенств, заметим, что они одинаковы. В этом заключается смысл средней скорости.

Определение 2б. Под средней скоростью переменного движения понимают скорость некоторого воображаемого равномерного прямолинейного движения, у которого перемещение и время одинаковы с переменным движением.

   Согласно рисунку, представленному выше, это понимать надо так. Если бы точка двигалась не переменно по криволинейной траектории, а равномерно и прямолинейно прямо по вектору перемещения , то она за время попала бы в точку A из точки , если бы скорость этого воображаемого равномерного движения была бы одинаковой со средней скоростью переменного движения.

   Модуль вектора средней скорости, или модуль средней скорости:

.

3. Средний модуль скорости.

   На практике при составлении расписания движения поездов, автобусов используют ещё одно понятие средней скорости, которое называют средним модулем скорости, то есть средним по времени модулем всех скоростей, которые имела точка на различных участках траектории.

Определение 3а. Средним модулем скорости переменного движения называется отношение пути S ко времени t, за которое этот путь пройден.

– средний модуль скорости

   Не надо путать средний модуль скорости с модулем вектора средней скорости.

   Например, если автобус вышел на маршрут в начале дня и к концу дня возвратился в гараж, то перемещение за всё время движения равно нулю . Поэтому равны нулю средняя скорость и её модуль:

,     .

   Но средний модуль скорости отличен от нуля, так как не равен нулю путь, пройденный автобусом:

.

   Аналогично для бумеранга.

   За время полёта бумеранга средняя скорость его движения и модуль средней скорости равны нулю, так как равно нулю перемещение бумеранга относительно точки А (см. рис.). Но так как путь, который проделал бумеранг, не равен нулю, то и средний модуль скорости движения бумеранга отличен от нуля.

   Если посмотреть на правые части формул модуля скорости равномерного движения и среднего модуля скорости переменного движения, то увидим, что правые части равенств одинаковы.

   В этом заключается смысл среднего модуля скорости.

Определение 3б. Средний модуль скорости переменного движения равен модулю скорости такого воображаемого равномерного прямолинейного движения, у которого путь и время одинаковы с переменным движением.

Скорость звука Уравнения

Возмущение, внесенное в какую-либо точку вещества – твердого или жидкого, – будет распространяться через вещество как волна с конечной скоростью.

Акустическая скорость и скорость звука

Скорость, с которой небольшое возмущение будет распространяться в среде, называется Акустическая скорость или Скорость звука.

Обратите внимание, что скорость – это скалярная величина. Скорость – это векторная величина с направлением.

Скорость звука связана с изменением давления и плотности вещества и может быть выражена как

c = (dp / dρ) ^1/2 (1)

где

c = скорость звука (м / с, фут / с)

dp = изменение давления (Па, фунт / кв. дюйм)

dρ = изменение плотности (кг / м ³ , фунт / фут ³ )

Скорость звука в газах, жидкостях и твердых телах

Акустическая скорость также может быть выражена с помощью закона Хука как

c = (K / ρ) ^1/2 (2)

где

K = объемный модуль упругости (Па, фунт / кв. Дюйм)

ρ = плотность (кг / м ³ , фунт / фут ³ )

Это уравнение действительно для жидкостей, твердые вещества и газы.Звук быстрее распространяется через среды с более высокой эластичностью и / или меньшей плотностью. Если среда вообще несжимаема – несжимаема – скорость звука бесконечна ( c ≈ ∞).

• свойства при 1 бар и 0 ^o C

Скорость звука – скорость звука – в идеальных газах

Поскольку акустические возмущения, вносимые в точку, очень малы, теплопередачей можно пренебречь и для газов предполагается изэнтропический. Для изоэнтропического процесса можно использовать закон идеального газа, а скорость звука можно выразить как

c = (kp / ρ) ^1/2

= (k RT) ^1/2 (3)

, где

k = отношение удельных теплоемкостей (индекс адиабаты)

p = давление (Па, фунт / кв. Дюйм)

R = индивидуальная газовая постоянная (Дж / кг · K, фут-фунт / оторочка ^o R)

T = абсолютная температура ( ^o K, ^o R)

Для идеального газа скорость звука пропорциональна корень квадратный из абсолютной температуры.

Пример – Скорость звука в воздухе

Скорость звука в воздухе при 0 ^o C (273,15 K) и абсолютном давлении 1 бар можно рассчитать как

c = (1,4 (286,9 Дж / К кг) (273,15 K)) ^1/2

= 331,2 (м / с)

где

k = 1,4

и

R = 286.9 (Дж / К кг)

Скорость звука в воздухе при 20 ^o C (293,15 K) и абсолютном давлении 1 бар можно рассчитать как

c = (1,4 (286,9 Дж / K кг) (293,15 K)) ^1/2

= 343,1 (м / с)

Пример – Скорость звука в воде

Скорость звука в воде при 0 ^o C можно рассчитать как

c = ((2.06 10 ⁹ Н / м ² ) / (999,8 кг / м ³ )) ^1/2

= 1435,4 (м / с)

где

E _v = 2,06 10 ⁹ (Н / м ² )

и

ρ = 999,8 (кг / м ³ )

Скорость звука в Твердые тела

Дозвуковая и сверхзвуковая скорость

• Если число Маха ниже 1 , скорость потока ниже скорости звука – и скорость дозвуковая .
• Если число Маха 1 – скорость околозвуковая .
• Если число Маха выше 1 , скорость потока выше скорости звука – и скорость равна сверхзвуковой.

12.3 Напряжение, деформация и модуль упругости – Университетская физика, Том 1

Цели обучения

К концу этого раздела вы сможете:

• Объясните концепции напряжения и деформации при описании упругих деформаций материалов
• Описать виды упругого деформирования предметов и материалов

Модель твердого тела – идеализированный пример объекта, не деформирующегося под действием внешних сил.Это очень полезно при анализе механических систем, а многие физические объекты действительно в значительной степени жесткие. Степень, в которой объект может восприниматься как жесткий, зависит от физических свойств материала, из которого он сделан. Например, мяч для пинг-понга, сделанный из пластика, является хрупким, а теннисный мяч, сделанный из резины, эластичен, когда на него воздействуют сжимающие силы. Однако при других обстоятельствах и мяч для пинг-понга, и теннисный мяч могут хорошо отскакивать как твердые тела.Точно так же тот, кто проектирует протезы конечностей, может приблизиться к механике человеческих конечностей, моделируя их как твердые тела; однако фактическая комбинация костей и тканей представляет собой эластичную среду.

В оставшейся части этой главы мы переходим от рассмотрения сил, влияющих на движение объекта, к тем, которые влияют на форму объекта. Изменение формы из-за приложения силы называется деформацией. Известно, что даже очень небольшие силы вызывают некоторую деформацию.Деформация испытывается объектами или физическими средами под действием внешних сил – например, это может быть сжатие, сжатие, разрыв, скручивание, срезание или растяжение объектов. На языке физики два термина описывают силы, действующие на объекты, подвергающиеся деформации: напряжение и деформация .

Напряжение – это величина, которая описывает величину сил, вызывающих деформацию. Напряжение обычно определяется как силы на единицу площади .Когда силы притягивают объект и вызывают его удлинение, как при растяжении эластичной ленты, мы называем такое напряжение растягивающим напряжением. Когда силы вызывают сжатие объекта, мы называем это напряжением сжатия. Когда объект сжимается со всех сторон, как подводная лодка в глубинах океана, мы называем этот вид напряжения объемным напряжением (или объемным напряжением). В других ситуациях действующие силы могут быть ни растягивающими, ни сжимающими, и все же вызывать заметную деформацию. Например, предположим, что вы держите книгу в ладонях, затем одной рукой вы нажимаете и тянете переднюю обложку от себя, а другой рукой вы нажимаете и тянете заднюю обложку в направлении ты.В таком случае, когда деформирующие силы действуют по касательной к поверхности объекта, мы называем их «поперечными» силами, а вызываемое ими напряжение – поперечным напряжением.

Единицей измерения напряжения в системе СИ является паскаль (Па). Когда сила в один ньютон давит на единицу площади квадратного метра, результирующее напряжение составляет один паскаль:

один паскаль = 1.0Па = 1.0N1.0м2. один паскаль = 1.0Па = 1.0N1.0м2.

В британской системе единиц измерения напряжения используется «фунт на квадратный дюйм», что означает «фунт на квадратный дюйм» (фунт / дюйм2).(фунт / дюйм2). Еще одна единица измерения объемного напряжения – это атм (атмосфера). Коэффициенты пересчета:

. 1 фунт / кв. Дюйм = 6895 Па и 1 Па = 1,450 × 10–4 фунт / кв. Дюйм · атм = 1,013 × 105 Па = 14,7 фунт / кв. Дюйм. 1 фунт / кв. Дюйм = 6895 Па и 1 Па = 1,450 × 10–4 фунт / кв.

Объект или среда под напряжением деформируются. Величина, описывающая эту деформацию, называется деформацией. Деформация задается как частичное изменение длины (при растягивающем напряжении), объема (при объемном напряжении) или геометрии (при напряжении сдвига). Следовательно, деформация – это безразмерное число.Деформация под действием растягивающего напряжения называется деформацией растяжения, деформация под действием объемного напряжения называется объемной деформацией (или объемной деформацией), а деформация, вызванная напряжением сдвига, называется деформацией сдвига.

Чем больше напряжение, тем больше напряжение; однако связь между деформацией и напряжением не обязательно должна быть линейной. Только когда напряжение достаточно низкое, вызываемая им деформация прямо пропорциональна величине напряжения. Константа пропорциональности в этом отношении называется модулем упругости.В линейном пределе низких значений напряжения общее соотношение между напряжением и деформацией составляет

. напряжение = (модуль упругости) × деформация. напряжение = (модуль упругости) × деформация.

12,33

Как видно из анализа размеров этого соотношения, модуль упругости имеет ту же физическую единицу, что и напряжение, поскольку деформация безразмерна.

Из уравнения 12.33 также видно, что, когда объект характеризуется большим значением модуля упругости, влияние напряжения невелико.С другой стороны, небольшой модуль упругости означает, что напряжение вызывает большую деформацию и заметную деформацию. Например, напряжение на резиновой ленте вызывает большую деформацию (деформацию), чем такое же напряжение на стальной ленте тех же размеров, потому что модуль упругости резины на два порядка меньше модуля упругости стали.

Модуль упругости при растяжении называется модулем Юнга; то, что для объемного напряжения называется объемным модулем упругости; а напряжение сдвига называется модулем сдвига.Обратите внимание, что соотношение между напряжением и деформацией – это наблюдаемое соотношение , измеренное в лаборатории. Модули упругости для различных материалов измеряются при различных физических условиях, таких как изменяющаяся температура, и собираются в таблицах технических данных для справки (таблица 12.1). Эти таблицы являются ценными справочными материалами для промышленности и для всех, кто занимается проектированием или строительством. В следующем разделе мы обсудим зависимости деформации от напряжения за пределами линейного предела, представленного уравнением 12.33, в полном диапазоне значений напряжений до точки разрушения. В оставшейся части этого раздела мы изучаем линейный предел, выражаемый уравнением 12.33.

Материал	Модуль Юнга × 1010 Па × 1010 Па	Объемный модуль × 1010 Па × 1010 Па	Модуль сдвига × 1010 Па × 1010 Па
Алюминий	7,0	7,5	2,5
Кость (напряжение)	1.6	0,8	8,0
Кость (компрессия)	0,9
Латунь	9,0	6,0	3,5
Кирпич	1,5
Бетон	2,0 ​​
Медь	11,0	14,0	4,4
Коронное стекло	6.0	5,0	2,5
Гранит	4,5	4,5	2,0 ​​
Волосы (человеческие)	1,0
Твердая древесина	1,5		1,0
Утюг	21,0	16,0	7,7
Свинец	1,6	4,1	0,6
Мрамор	6.0	7,0	2,0 ​​
Никель	21,0	17,0	7,8
Полистирол	3,0
шелк	6,0
Паутинка	3,0
Сталь	20,0	16,0	7,5
Ацетон		0.07
Этанол		0,09
Глицерин		0,45
Меркурий		2,5
Вода		0,22

Стол 12.1 Приблизительные модули упругости для выбранных материалов

Напряжение при растяжении или сжатии, деформация и модуль Юнга

Напряжение или сжатие возникает, когда две антипараллельные силы равной величины действуют на объект только вдоль одного из его измерений таким образом, что объект не перемещается.Один из способов представить себе такую ​​ситуацию показан на рисунке 12.18. Сегмент стержня либо растягивается, либо сжимается парой сил, действующих по его длине и перпендикулярно его поперечному сечению. Общий эффект таких сил состоит в том, что стержень изменяет свою длину от исходной длины L0L0, которая была у него до появления сил, на новую длину L , которую он имеет под действием сил. Это изменение длины ΔL = L-L0ΔL = L-L0 может быть либо удлинением (когда L больше исходной длины L0) L0), либо сокращением (когда L меньше исходной длины L0).L0). Напряжение растяжения и деформация возникают, когда силы растягивают объект, вызывая его удлинение, и изменение длины ΔLΔL является положительным. Напряжение сжатия и деформация возникают, когда силы сжимают объект, вызывая его сокращение, а изменение длины ΔLΔL отрицательно.

В любой из этих ситуаций мы определяем напряжение как отношение деформирующей силы F⊥F⊥ к площади A поперечного сечения деформируемого объекта. Символ F⊥F⊥, который мы оставляем для деформирующей силы, означает, что эта сила действует перпендикулярно поперечному сечению объекта.Силы, действующие параллельно поперечному сечению, не изменяют длину объекта. Определение растягивающего напряжения –

. растягивающее напряжение = F⊥A. растягивающее напряжение = F⊥A.

12,34

Деформация растяжения – это мера деформации объекта при растягивающем напряжении и определяется как частичное изменение длины объекта, когда объект испытывает растягивающее напряжение.

деформация растяжения = ΔLL0. деформация растяжения = ΔLL0.

12,35

Напряжение сжатия и деформация определяются по той же формуле, уравнение 12.34 и уравнение 12.35 соответственно. Единственное отличие от ситуации с растяжением состоит в том, что для сжимающего напряжения и деформации мы берем абсолютные значения правых частей в уравнениях 12.34 и 12.35.

Фигура 12,18 Когда объект находится в состоянии растяжения или сжатия, результирующая сила, действующая на него, равна нулю, но объект деформируется, изменяя свою исходную длину L0.L0. (a) Натяжение: стержень удлинен на ΔL.ΔL. (b) Сжатие: стержень сжимается на ΔL.ΔL. В обоих случаях деформирующая сила действует по длине стержня и перпендикулярно его поперечному сечению.В линейном диапазоне малых напряжений площадь поперечного сечения стержня не изменяется.

Модуль Юнга Y – это модуль упругости, когда деформация вызвана либо растягивающим, либо сжимающим напряжением, и определяется уравнением 12.33. Разделив это уравнение на деформацию растяжения, мы получим выражение для модуля Юнга:

Y = растягивающая деформация растяжения = F⊥ / A∆L / L0 = F⊥AL0∆L.Y = растягивающая деформация растяжения = F⊥ / A∆L / L0 = F⊥AL0∆L.

12,36

Пример 12,7

Напряжение сжатия в опоре

Скульптура весом 10 000 Н покоится на горизонтальной поверхности на вершине 6.Вертикальный столб высотой 0 м Рис. 12.19. Площадь поперечного сечения столба 0,20 м 20,20 м 2, он выполнен из гранита с удельной массой 2700 кг / м3. 2700 кг / м3. Найдите сжимающее напряжение в поперечном сечении, расположенном на 3,0 м ниже верха столба, и значение сжимающей деформации верхнего 3,0-метрового сегмента столба.

Фигура 12,19 Колонна Нельсона на Трафальгарской площади, Лондон, Англия. (кредит: модификация работы Кристиана Бортеса)

Стратегия

Сначала мы находим вес 3.Верхняя часть столба длиной 0 м. Нормальная сила, действующая на поперечное сечение, расположенное на 3,0 м ниже вершины, складывается из веса столба и веса скульптуры. Когда у нас есть нормальная сила, мы используем уравнение 12.34, чтобы найти напряжение. Чтобы найти деформацию сжатия, мы находим значение модуля Юнга для гранита в таблице 12.1 и инвертируем уравнение 12.36.

Решение

Объем сегмента колонны высотой h = 3,0мh = 3,0м и площадью поперечного сечения A = 0,20м2A = 0,20м2 составляет V = Ah = (0.20м2) (3,0м) = 0,60м3. V = Ah = (0,20м2) (3,0м) = 0,60м3.

При плотности гранита ρ = 2,7 × 103 кг / м3, ρ = 2,7 × 103 кг / м3 масса сегмента столба составляет

m = ρV = (2,7 × 103 кг / м3) (0,60 м3) = 1,60 × 103 кг. m = ρV = (2,7 × 103 кг / м3) (0,60 м3) = 1,60 × 103 кг.

Вес сегмента стойки

wp = mg = (1,60 × 103 кг) (9,80 м / с2) = 1,568 × 104 Н. wp = mg = (1,60 × 103 кг) (9,80 м / с2) = 1,568 × 104 Н.

Вес скульптуры составляет ws = 1,0 × 104 Н, ws = 1,0 × 104 Н, поэтому нормальная сила на поверхности поперечного сечения, расположенной на 3,0 м ниже скульптуры, составляет

F⊥ = wp + ws = (1.568 + 1.0) × 104N = 2.568 × 104N. F⊥ = wp + ws = (1.568 + 1.0) × 104N = 2.568 × 104N.

Следовательно, напряжение

напряжение = F⊥A = 2,568 × 104N0,20м2 = 1,284 × 105Па = 128,4 кПа. напряжение = F⊥A = 2,568 × 104N0,20м2 = 1,284 × 105Па = 128,4 кПа.

Модуль Юнга для гранита составляет Y = 4,5 × 1010 Па = 4,5 × 107 кПа. Y = 4,5 × 1010 Па = 4,5 × 107 кПа. Следовательно, деформация сжатия в этом положении равна

. деформация = напряжение Y = 128,4 кПа 4,5 × 107 кПа = 2,85 × 10-6. деформация = напряжение Y = 128,4 кПа 4,5 × 107 кПа = 2,85 × 10-6.

Значение

Обратите внимание, что нормальная сила, действующая на площадь поперечного сечения колонны, не является постоянной по всей ее длине, а изменяется от наименьшего значения вверху до наибольшего значения внизу колонны.Таким образом, если опора имеет равномерную площадь поперечного сечения по всей длине, наибольшее напряжение у ее основания.

Проверьте свое понимание 12,9

Найдите сжимающее напряжение и деформацию в основании колонны Нельсона.

Пример 12,8

Растяжка стержня

Стальной стержень длиной 2,0 м имеет площадь поперечного сечения 0,30 см2 0,30 см2. Штанга является частью вертикальной опоры, которая удерживает тяжелую платформу массой 550 кг, которая подвешена к нижнему концу штанги.Пренебрегая весом стержня, каково растягивающее напряжение стержня и удлинение стержня под действием напряжения?

Стратегия

Сначала мы вычисляем растягивающее напряжение в стержне под весом платформы в соответствии с уравнением 12.34. Затем мы обращаем уравнение 12.36, чтобы найти удлинение стержня, используя L0 = 2,0 м. L0 = 2,0 м. Из таблицы 12.1 модуль Юнга для стали равен Y = 2,0 × 1011 Па. Y = 2,0 × 1011 Па.

Решение

Подстановка числовых значений в уравнения дает нам F⊥A = (550 кг) (9.8 м / с2) 3,0 × 10–5 м2 = 1,8 × 108 Па ΔL = F⊥AL0Y = (1,8 × 108 Па) 2,0 × 1011 Па = 1,8 × 10–3 м = 1,8 мм. F⊥A = (550 кг) (9,8 м / s2) 3,0 × 10–5 м2 = 1,8 × 108 Па ΔL = F⊥AL0Y = (1,8 × 108 Па) 2,0 × 1011 Па = 1,8 × 10–3 м = 1,8 мм.

Значение

Как и в примере с колонной, растягивающее напряжение в этом примере неоднородно по длине стержня. Однако, в отличие от предыдущего примера, если принять во внимание вес штанги, напряжение в штанге будет наибольшим в верхней части и наименьшим в нижней части штанги, к которой прикреплено оборудование.

Проверьте свое понимание 12.10

Проволока длиной 2,0 м растягивается на 1,0 мм под действием нагрузки. Какова деформация растяжения в проволоке?

Объекты часто могут одновременно испытывать напряжение сжатия и растяжения. Рис. 12.20. Один из примеров – длинная полка, загруженная тяжелыми книгами, которая провисает между концевыми опорами под весом книг. Верхняя поверхность полки испытывает напряжение сжатия, а нижняя поверхность полки – растягивающее напряжение.Точно так же длинные и тяжелые балки провисают под собственным весом. В современном строительстве такие деформации изгиба можно практически исключить с помощью двутавровых балок. Рисунок 12.21.

Фигура 12.20 (a) Объект, изгибающийся вниз, испытывает растягивающее напряжение (растяжение) в верхней части и сжимающее напряжение (сжатие) в нижней части. (b) Элитные тяжелоатлеты часто временно сгибают железные прутья во время подъема, как на Олимпийских играх 2012 года. (кредит б: модификация работы Александра Кочерженко)

Фигура 12.21 год Стальные двутавры используются в строительстве для уменьшения деформаций изгиба. (Источник: модификация работы «Инженерный корпус армии США в Европе» / Flickr)

Объемное напряжение, деформация и модуль

Когда вы ныряете в воду, вы чувствуете силу, давящую на каждую часть вашего тела со всех сторон. Тогда вы испытываете объемный стресс или, другими словами, давление. Объемное напряжение всегда имеет тенденцию к уменьшению объема, заключенного на поверхности погружаемого объекта.Силы этого «сжатия» всегда перпендикулярны погружаемой поверхности. Рис. 12.22. Эффект этих сил заключается в уменьшении объема погруженного объекта на величину ΔVΔV по сравнению с объемом V0V0 объекта при отсутствии объемного напряжения. Этот вид деформации называется объемной деформацией и описывается изменением объема по сравнению с исходным объемом:

объемная деформация = ΔVV0. объемная деформация = ΔVV0.

12,37

Фигура 12,22 Объект при увеличении объемного напряжения всегда претерпевает уменьшение своего объема.Равные силы, перпендикулярные поверхности, действуют со всех сторон. Эффект этих сил заключается в уменьшении объема на величину ΔVΔV по сравнению с исходным объемом V0.V0.

Объемная деформация возникает в результате объемного напряжения, которое представляет собой силу F⊥F⊥, нормальную к поверхности, которая оказывает давление на единицу площади A погруженного объекта. Такая физическая величина или давление p определяется как

давление = p≡F⊥A. давление = p≡F⊥A.

12,38

Мы будем изучать давление в жидкостях более подробно в Гидромеханике.Важной характеристикой давления является то, что оно является скалярной величиной и не имеет определенного направления; то есть давление действует одинаково во всех возможных направлениях. Когда вы погружаете руку в воду, вы чувствуете такое же давление, действующее на верхнюю поверхность руки, как на нижнюю, или на боковую, так и на поверхность кожи между пальцами. В этом случае вы ощущаете увеличение давления ΔpΔp по сравнению с тем, что вы привыкли ощущать, когда ваша рука не погружена в воду.Когда ваша рука не погружена в воду, вы чувствуете нормальное давление p0p0 в одну атмосферу, которое служит точкой отсчета. Объемное напряжение – это увеличение давления, или Δp, Δp, по сравнению с нормальным уровнем, p0.p0.

Когда объемное напряжение увеличивается, объемная деформация увеличивается в соответствии с уравнением 12.33. Константа пропорциональности в этом отношении называется модулем объемного сжатия, B или

. B = объемное напряжение, объемная деформация = −ΔpΔV / V0 = −ΔpV0ΔV. B = объемное напряжение, объемная деформация = −ΔpΔV / V0 = −ΔpV0ΔV.

12,39

Знак минус, который появляется в уравнении 12.39, предназначен для согласованности, чтобы гарантировать, что B является положительной величиной. Обратите внимание, что знак минус (-) (-) необходим, потому что увеличение ΔpΔp давления (положительная величина) всегда вызывает уменьшение ΔVΔV в объеме, а уменьшение объема является отрицательной величиной. Величина, обратная модулю объемного сжатия, называется сжимаемостью k, k или

. k = 1B = −ΔV / V0Δp.k = 1B = −ΔV / V0Δp.

12,40

Термин «сжимаемость» используется в отношении жидкостей (газов и жидкостей).Сжимаемость описывает изменение объема жидкости на единицу увеличения давления. Жидкости, характеризующиеся большой сжимаемостью, относительно легко сжимаются. Например, сжимаемость воды составляет 4,64 × 10–5 / атм. 4,64 × 10–5 / атм, а сжимаемость ацетона составляет 1,45 × 10–4 / атм. 1,45 × 10–4 / атм. Это означает, что при повышении давления на 1,0 атм относительное уменьшение объема для ацетона примерно в три раза больше, чем для воды.

Пример 12.9

Гидравлический пресс

В гидравлическом прессе, рис. 12.23, 250-литровый объем масла подвергается повышению давления на 2300 фунтов на квадратный дюйм. Если сжимаемость масла составляет 2,0 × 10–5 / атм, 2,0 × 10–5 / атм, найдите объемную деформацию и абсолютное уменьшение объема масла при работе пресса.

Фигура 12,23 В гидравлическом прессе, когда маленький поршень смещается вниз, давление в масле передается по маслу на большой поршень, заставляя большой поршень двигаться вверх.Небольшая сила, приложенная к маленькому поршню, вызывает большую прижимающую силу, которую большой поршень оказывает на объект, который либо поднимается, либо сжимается. Устройство действует как механический рычаг.

Стратегия

Мы должны обратить уравнение 12.40, чтобы найти объемную деформацию. Во-первых, мы преобразуем увеличение давления из фунтов на квадратный дюйм в атм, Δp = 2300psi = 2300 / 14,7atm≈160atm, Δp = 2300psi = 2300 / 14.7atm≈160atm, и определяем V0 = 250L.V0 = 250L.

Решение

Подставляя значения в уравнение, имеем объемная деформация = ΔVV0 = ΔpB = kΔp = (2.0 × 10-5 / атм) (160атм) = 0,0032 ответ: ΔV = 0,0032V0 = 0,0032 (250L) = 0,78L. Объемная деформация = ΔVV0 = ΔpB = kΔp = (2,0 × 10-5 / атм) (160атм) = 0,0032 ответ: ΔV = 0,0032V0 = 0,0032 (250 л) = 0,78 л.

Значение

Обратите внимание, что, поскольку сжимаемость воды в 2,32 раза больше, чем у масла, если бы рабочее вещество в гидравлическом прессе этой задачи было заменено на воду, объемная деформация, а также изменение объема были бы в 2,32 раза больше.

Проверьте свое понимание 12.11

Если нормальная сила действует на каждую грань кубической 1.Стальной кусок 0-м31,0-м3 заменяют на 1,0 × 107 Н, 1,0 × 107 Н, находят результирующее изменение объема стального куска.

Напряжение сдвига, деформация и модуль

Понятия напряжения сдвига и деформации относятся только к твердым объектам или материалам. Здания и тектонические плиты являются примерами объектов, которые могут подвергаться сдвиговым напряжениям. В общем, эти концепции не применимы к жидкостям.

Деформация сдвига возникает, когда две антипараллельные силы равной величины прикладываются по касательной к противоположным поверхностям твердого объекта, не вызывая деформации в поперечном направлении к силовой линии, как в типичном примере напряжения сдвига, показанном на рисунке 12.24. Сдвиговая деформация характеризуется постепенным сдвигом ΔxΔx слоев в направлении, касательном к действующим силам. Эта градация ΔxΔx происходит в поперечном направлении на некотором расстоянии L0.L0. Деформация сдвига определяется отношением наибольшего смещения ΔxΔx к поперечному расстоянию L0L0

деформация сдвига = ΔxL0. деформация сдвига = ΔxL0.

12,41

Деформация сдвига вызвана напряжением сдвига. Напряжение сдвига возникает из-за сил, действующих на параллель к поверхности. Для таких сил мы используем символ F∥F∥.Величина F∥F∥ на площадь поверхности A , где применяется сила сдвига, является мерой напряжения сдвига

напряжение сдвига = F∥A. напряжение сдвига = F∥A.

12,42

Модуль сдвига является константой пропорциональности в уравнении 12.33 и определяется отношением напряжения к деформации. Модуль сдвига обычно обозначается как S :

. S = напряжение сдвига деформация сдвига = F∥ / AΔx / L0 = F∥AL0Δx.S = напряжение сдвига деформация сдвига = F∥ / AΔx / L0 = F∥AL0Δx.

12,43

Фигура 12.24 Объект под напряжением сдвига: две антипараллельные силы равной величины прикладываются по касательной к противоположным параллельным поверхностям объекта. Контур пунктирной линией показывает результирующую деформацию. Направление, перпендикулярное действующим силам, не изменяется, и поперечная длина L0L0 не изменяется. Сдвиговая деформация характеризуется постепенным смещением ΔxΔx слоев в направлении, касательном к силам.

Пример 12.10

Старая книжная полка

Уборщик пытается переместить тяжелый старый книжный шкаф по ковровому покрытию, тангенциально толкая поверхность самой верхней полки.Однако единственный заметный эффект от этого усилия аналогичен эффекту, показанному на рисунке 12.24, и он исчезает, когда человек перестает толкать. Книжный шкаф высотой 180 см и шириной 90 см с четырьмя полками глубиной 30 см, частично заполненными книгами. Общий вес книжного шкафа и книг составляет 600,0 Н. Если человек толкает верхнюю полку с силой 50,0 Н, которая смещает верхнюю полку по горизонтали на 15,0 см относительно неподвижной нижней полки, найдите модуль сдвига книжного шкафа.

Стратегия

Единственная важная информация – это физические размеры книжного шкафа, величина тангенциальной силы и смещение, вызываемое этой силой.Мы определяем F∥ = 50.0N, Δx = 15.0cm, F∥ = 50.0N, Δx = 15.0cm, L0 = 180.0cm, L0 = 180.0cm и A = (30.0 cm) (90.0 cm) = 2700.0 cm2, A = (30,0 см) (90,0 см) = 2700,0 см2, и мы используем уравнение 12.43 для вычисления модуля сдвига.

Решение

Подставляя числа в уравнения, получаем для модуля сдвига S = F∥AL0Δx = 50.0N2700.0cm2180.0cm.15.0cm. = 29Ncm2 = 29 × 104Nm2 = 209 × 103Pa = 2.222 кПа S = F∥AL0Δx = 50.0N2700.0cm2180.0cm.15.0cm. = 29Ncm2 = 29 × 104Нм2 = 209 × 103Па = 2,222 кПа.

Мы также можем найти напряжение сдвига и деформацию соответственно:

F∥A = 50.0N2700,0 см2 = 527 кПа = 185,2 Па ΔxL0 = 15,0 см 180,0 см = 112 = 0,083.F∥A = 50,0N2700,0 см2 = 527 кПа = 185,2 Па ΔxL0 = 15,0 см 180,0 см = 112 = 0,083.

Значение

Если человек в этом примере толкнет полку здоровым движением, может случиться так, что индуцированный сдвиг превратит ее в груду мусора. Примерно тот же механизм сдвига ответственен за разрушения засыпанных землей дамб и дамб; и в целом по оползням.

Проверьте свое понимание 12,12

Объясните, почему концепции модуля Юнга и модуля сдвига неприменимы к жидкостям.

Учебник по физике: Скорость звука

Звуковая волна – это возмущение давления, которое распространяется через среду посредством межчастичного взаимодействия. Когда одна частица становится возмущенной, она оказывает силу на следующую соседнюю частицу, таким образом выводя эту частицу из состояния покоя и передавая энергию через среду. Как и любая волна, скорость звуковой волны означает, насколько быстро возмущение передается от частицы к частице. В то время как частота относится к количеству колебаний, которые отдельная частица совершает за единицу времени, скорость относится к расстоянию, которое возмущение проходит за единицу времени.Всегда будьте осторожны, чтобы различать две часто путаемые величины: скорость (, как быстро … ) и частоту (, как часто … ).

Поскольку скорость волны определяется как расстояние, которое точка на волне (например, сжатие или разрежение) проходит за единицу времени, она часто выражается в метрах в секунду (сокращенно м / с). В форме уравнения это

скорость = расстояние / время

Чем быстрее распространяется звуковая волна, тем большее расстояние она преодолеет за тот же период времени.Если бы звуковая волна прошла расстояние 700 метров за 2 секунды, то скорость волны составила бы 350 м / с. Более медленная волна преодолеет меньшее расстояние – возможно, 660 метров – за тот же период времени в 2 секунды и, таким образом, будет иметь скорость 330 м / с. Более быстрые волны преодолевают большее расстояние за тот же период времени.

Факторы, влияющие на скорость волны

Скорость любой волны зависит от свойств среды, в которой она распространяется.Обычно существует два основных типа свойств, которые влияют на скорость волны – инерционные свойства и упругие свойства. Упругие свойства – это свойства, связанные со склонностью материала сохранять свою форму и не деформироваться при приложении к нему силы или напряжения. Такой материал, как сталь, будет испытывать очень небольшую деформацию формы (и размеров) при приложении к нему напряжения. Сталь – жесткий материал, обладающий высокой эластичностью. С другой стороны, такой материал, как резинка, очень гибкий; когда к резиновой ленте прилагается сила, она легко деформируется или меняет свою форму.Небольшая нагрузка на резиновую ленту вызывает большую деформацию. Сталь считается жестким или жестким материалом, а резинка – гибким материалом. На уровне частиц жесткий или жесткий материал характеризуется атомами и / или молекулами с сильным притяжением друг к другу. Когда сила прилагается в попытке растянуть или деформировать материал, его сильные взаимодействия с частицами предотвращают эту деформацию и помогают материалу сохранять свою форму. Считается, что твердые материалы, такие как сталь, обладают высокой эластичностью.(Модуль упругости – это технический термин). Фаза вещества оказывает огромное влияние на упругие свойства среды. В общем, твердые тела имеют самое сильное взаимодействие между частицами, за ними следуют жидкости, а затем газы. По этой причине продольные звуковые волны в твердых телах распространяются быстрее, чем в жидкостях, чем в газах. Несмотря на то, что инерционный фактор может благоприятствовать газам, фактор упругости имеет большее влияние на скорость ( v ) волны, таким образом давая общую картину:

v _{твердые вещества} > v _{жидкости} > v _газы

Инерционные свойства – это свойства, связанные с тенденцией материала быть вялым при изменении состояния его движения.Плотность среды является примером инерционного свойства . Чем больше инерция (то есть массовая плотность) отдельных частиц среды, тем меньше они будут реагировать на взаимодействия между соседними частицами и тем медленнее будет волна. Как указывалось выше, звуковые волны в твердых телах распространяются быстрее, чем в жидкостях, чем в газах. Однако в пределах одной фазы вещества инерционное свойство плотности имеет тенденцию быть тем свойством, которое оказывает наибольшее влияние на скорость звука.Звуковая волна будет распространяться быстрее в менее плотном материале, чем в более плотном. Таким образом, звуковая волна в гелии распространяется почти в три раза быстрее, чем в воздухе. В основном это связано с меньшей массой частиц гелия по сравнению с частицами воздуха.


Скорость звука в воздухе

Скорость звуковой волны в воздухе зависит от свойств воздуха, в основном от температуры и, в меньшей степени, от влажности.Влажность – это результат присутствия водяного пара в воздухе. Как и любая жидкость, вода имеет свойство испаряться. При этом частицы газообразной воды смешиваются с воздухом. Это дополнительное вещество будет влиять на массовую плотность воздуха (инерционное свойство). Температура влияет на силу взаимодействия частиц (упругое свойство). При нормальном атмосферном давлении температурная зависимость скорости звуковой волны через сухой воздух аппроксимируется следующим уравнением:

v = 331 м / с + (0.6 м / с / C) • T

где T – температура воздуха в градусах Цельсия. Использование этого уравнения для определения скорости звуковой волны в воздухе при температуре 20 градусов Цельсия дает следующее решение.

v = 331 м / с + (0,6 м / с / C) • T

v = 331 м / с + (0,6 м / с / C) • (20 C)

v = 331 м / с + 12 м / с

v = 343 м / с

(Приведенное выше уравнение, связывающее скорость звуковой волны в воздухе с температурой, дает достаточно точные значения скорости для температур от 0 до 100 по Цельсию.Само уравнение не имеет теоретической основы; это просто результат проверки данных температура-скорость для этого диапазона температур. Существуют и другие уравнения, основанные на теоретических рассуждениях и обеспечивающие точные данные для всех температур. Тем не менее приведенного выше уравнения будет достаточно для использования нами в качестве студентов, изучающих физику на начальном этапе.)

Посмотрите!
Приведенный ниже виджет Speed ​​of Sound позволяет узнать скорость распространения звуковых волн в различных материалах.Просто введите название материала. Например, введите воду, гелий, воздух, воздух с температурой 45 ° C (или любой другой материал и условия) в заготовку; затем нажмите кнопку «Отправить ».

Использование скорости волны для определения расстояний

При нормальном атмосферном давлении и температуре 20 градусов Цельсия звуковая волна будет распространяться со скоростью примерно 343 м / с; это примерно равно 750 милям в час. Хотя эта скорость может показаться высокой по человеческим меркам (самые быстрые люди могут бежать со скоростью примерно 11 м / с, а скорость на шоссе – примерно 30 м / с), скорость звуковой волны меньше по сравнению со скоростью световой волны.Свет распространяется по воздуху со скоростью примерно 300 000 000 м / с; это почти в 900 000 раз больше скорости звука. По этой причине люди могут наблюдать заметную задержку во времени между громом и молнией во время шторма. Прибытие световой волны от места удара молнии происходит за столь короткое время, что им можно пренебречь. Однако приход звуковой волны от места удара молнии происходит намного позже. Временная задержка между приходом световой волны (молнии) и приходом звуковой волны (грома) позволяет человеку приблизительно определить его / ее расстояние от места шторма.Например, если гром слышен через 3 секунды после появления молнии, значит звук (скорость которого приблизительно равна 345 м / с) прошел расстояние

. расстояние = v • t = 345 м / с • 3 s = 1035 м

Если это значение преобразовать в мили (разделить на 1600 м / 1 милю), то шторм находится на расстоянии 0,65 мили.

Еще одно явление, связанное с восприятием временных задержек между двумя событиями, – это эхо. Человек часто может ощущать временную задержку между воспроизведением звука и появлением отражения этого звука от удаленного барьера.Если вы когда-либо издали крик в каньоне, возможно, вы слышали эхо вашего крика от далекой стены каньона. Временная задержка между криком и эхом соответствует времени, за которое кричащий сигнал проходит расстояние туда и обратно до стены каньона и обратно. Измерение этого времени позволило бы человеку оценить расстояние до стены каньона в одну сторону. Например, если эхо слышно через 1,40 секунды после того, как кричит , то расстояние до стены каньона можно найти следующим образом:

расстояние = v • t = 345 м / с • 0.70 с = 242 м

Стена каньона находится в 242 метрах от отеля. Вы могли заметить, что в уравнении используется время 0,70 секунды. Так как временная задержка соответствует времени прохождения орбитального аппарата holler туда и обратно до стены каньона и обратно, одностороннее расстояние до стены каньона соответствует половине временной задержки.

В то время как эхо имеет относительно минимальное значение для людей, эхолокация является важным трюком торговли с летучими мышами.Поскольку летучие мыши ведут ночной образ жизни, они должны использовать звуковые волны для навигации и охоты. Они производят короткие всплески ультразвуковых звуковых волн, которые отражаются от окружающих предметов и возвращаются обратно. Их обнаружение временной задержки между отправкой и получением импульсов позволяет летучей мыши приблизительно определять расстояние до окружающих объектов. Некоторые летучие мыши, известные как летучие мыши Доплера, способны определять скорость и направление любых движущихся объектов, отслеживая изменения частоты отраженных импульсов.Эти летучие мыши используют физику эффекта Доплера, рассмотренную в предыдущем разделе (и также будут обсуждаться позже в Уроке 3). Этот метод эхолокации позволяет летучей мыши ориентироваться и охотиться.




Новый взгляд на волновое уравнение

Как и любая волна, звуковая волна имеет скорость, которая математически связана с частотой и длиной волны. Как обсуждалось в предыдущем разделе, математическая взаимосвязь между скоростью, частотой и длиной волны определяется следующим уравнением.

Скорость = Длина волны • Частота

Используя символы v , λ и f , уравнение можно переписать как

v = f • λ

Приведенное выше уравнение полезно для решения математических задач, связанных с соотношением скорости, частоты и длины волны. Однако это уравнение может передать одно важное заблуждение. Несмотря на то, что скорость волны вычисляется с использованием частоты и длины волны, скорость волны составляет , а не , в зависимости от этих величин.Изменение длины волны не влияет (т. Е. На изменение) скорости волны. Скорее изменение длины волны влияет на частоту обратным образом. Удвоение длины волны приводит к уменьшению частоты вдвое; пока скорость волны не изменилась. Скорость звуковой волны зависит от свойств среды, в которой она движется, и единственный способ изменить скорость – это изменить свойства среды.

Проверьте свое понимание

1.Камера с автоматической фокусировкой может фокусироваться на объектах с помощью ультразвуковой звуковой волны. Камера излучает звуковые волны, которые отражаются от удаленных объектов и возвращаются в камеру. Датчик определяет время, необходимое для возвращения волн, а затем определяет расстояние, на котором объект находится от камеры. Если звуковая волна (скорость = 340 м / с) возвращается к камере через 0,150 секунды после выхода из камеры, как далеко находится объект?




2.В жаркий летний день надоедливый маленький комар издал предупреждающий звук возле вашего уха. Звук возникает при взмахе крыльев со скоростью около 600 ударов крыльев в секунду.

а. Какая частота звуковой волны в Герцах?

г. Если предположить, что звуковая волна движется со скоростью 350 м / с, какова длина волны?

3. Увеличение частоты источника волн вдвое увеличивает их скорость вдвое.

4. При игре в середине C на клавиатуре фортепиано получается звук с частотой 256 Гц. Предполагая, что скорость звука в воздухе составляет 345 м / с, определите длину волны звука, соответствующую ноте средней C.




5. Большинство людей может определять частоты до 20 000 Гц.Предполагая, что скорость звука в воздухе составляет 345 м / с, определите длину волны звука, соответствующую этому верхнему диапазону слышимости.

6. Слон издает звуковую волну 10 Гц. Предполагая, что скорость звука в воздухе составляет 345 м / с, определите длину волны этой инфразвуковой звуковой волны.




7.Определите скорость звука в холодный зимний день (T = 3 градуса C).




8. Майлз Туго находится в кемпинге в национальном парке Глейшер. Посреди ледникового каньона он громко кричит. Через 1,22 секунды он слышит эхо. Температура воздуха 20 градусов по Цельсию. Как далеко стены каньона?




9.Две звуковые волны проходят через контейнер с неизвестным газом. Волна А имеет длину 1,2 м. Волна B имеет длину волны 3,6 м. Скорость волны B должна быть __________ скорости волны A.

а. одна девятая	г. одна треть
г. то же, что	г. в три раза больше, чем




10.Две звуковые волны проходят через контейнер с неизвестным газом. Волна А имеет длину 1,2 м. Волна B имеет длину волны 3,6 м. Частота волны B должна быть __________ частоты волны A.

а. одна девятая	г. одна треть
г. то же, что	г. в три раза больше, чем

Модуль объемной упругости

– обзор

6.3.3 Модули петроупругой модели IFM

Модуль объемной упругости при насыщении K * моделируется как форма уравнения Гассмана (Gassmann, 1951), а именно

(6.3.9) K * = KIFM + [1 − KIFMKm] 2ϕKf + 1− ϕKm − KIFMKm2

, где

K _IFM = объемный модуль упругости в сухой раме

K _м

3

3 9104 9104

6 f = модуль объемной упругости жидкости

Уравнение Гассмана представляет собой идеальную связь между поровой жидкостью и твердым каркасом пористой среды (Schön, 1996).Это соотношение строго справедливо только для изотропной однородной породы, состоящей из одного минерала. Уравнение Гассмана широко используется в физике горных пород из-за его относительной простоты и ограниченных требований к данным. Уравнение (6.3.9) имеет форму уравнения Гассмана, но параметры в уравнении (6.3.9), включая модули, могут изменяться при изменении пластовых условий.

Модуль объемной упругости жидкости является обратной величиной сжимаемости жидкости C _f :

(6.3.10) Kf = 1 / Cf

Сжимаемость жидкости – это средневзвешенная по насыщению сжимаемость фаз, то есть

(6.3.11) Cf = coSo + cwSw + cgSg

Модули K _IFM и K _м моделируются с использованием следующих уравнений:

(6.3.12) KIFM = A0 + A1Pee1 + A2ϕ + A3ϕ2 + A4ϕPee2 + A5C

и

(6.3.13) Km = A0 + A1Pee1 + A5C

, где

A ₀ , A ₁ , A ₂ , A ₃ , A _{4 9024 , e 1 и e 2 = коэффициенты модели}

P _e = эффективное давление

C = 9102 9102 9102 объемная доля содержания глины Модуль сдвига рассчитывается с использованием

(6.3.14) μ * = B0 + B1Peɛ1 + B2ϕ + B3ϕ2 + B4ϕPeɛ2 + B5C

, где B ₀ , B ₁ , B ₂ , B 9024 ₄ , B ₅ , ɛ ₁ и ɛ ₂ – коэффициенты модели.

Коэффициенты в уравнениях. (6.3.12) и (6.3.14) определяются путем подгонки уравнений к измерениям модулей. Если модули являются линейными функциями пористости и не зависят от эффективного давления или содержания глины, коэффициенты A ₀ , B ₀ положительны; A ₁ , B ₁ отрицательны; а остальные коэффициенты равны нулю.В общем, значение каждого коэффициента модели зависит от набора данных, которым соответствует модель. Например, Мерфи и его коллеги (1993) представляют объемные модули и модули сдвига для кварцевого песчаника, которые имеют линейную зависимость от пористости, а Кастанья и его коллеги (1985) представляют объемные модули и модули сдвига для обломочных силикатных пород, которые имеют квадратичную зависимость от пористости. . В этих случаях многие коэффициенты устанавливаются равными нулю. Более сложным примером, который зависит от пористости, эффективного давления и содержания глины, является набор данных, представленный Ханом (1986) для хорошо консолидированных песчаников побережья Мексиканского залива.Соответствие данных Хана Эберхарту-Филлипсу (1989) было преобразовано в формат петроупругой модели, описанный здесь (Fanchi, 2003).

Уравнения (6.3.1) и (6.3.2) можно преобразовать, чтобы выразить модули в терминах измеренных акустических скоростей; таким образом, объемный модуль упругости породы, насыщенной поровой жидкостью, составляет

(6.3.15) K * = ρB [VP2-43VS2]

, а эффективный модуль сдвига составляет

(6.3.16) μ * = ρBVS2

Измерения скорости сдвига и скорость сжатия при нулевой пористости дают эффективный модуль объемной упругости, равный модулю зерен K _м , таким образом,

(6.3.17) Km = Kdry = Ksat = K * atϕ = 0

Этот результат может быть получен с использованием уравнения Гассмана и признания того, что объемный модуль упругости равен модулю зерна, когда пористость стремится к нулю.

Модуль объемной упругости сухой рамы может быть рассчитан на основе измеренных скоростей звука, свойств жидкости, плотности матрицы и модуля упругости зерна с использованием уравнения

(6.3.18) Kdry = Ksat (ϕKf + 1 − ϕKm) −1ϕKf + 1 − ϕKm− 2Km + KsatKm2

где мы запишем модуль объемной упругости в насыщенном состоянии как K _sat = K * и модуль объемной упругости сухой рамы как K _сухой = K _{IFM подчеркнуть, чтобы подчеркнуть IFM их физическое содержание.Уравнение (6.3.18) было получено путем решения уравнения Гассмана для модуля объемного сжатия сухого каркаса и расчета модуля объемного сжатия в насыщенном состоянии с использованием уравнения. (6.3.9).}

Упражнение 7

Упражнение 7.

Землетрясения

Для этого упражнения вам понадобится карта, показывающая границ пластин , которая является маленькой картой, или , эта , которая больше [если вы печатаете из браузера, переверните изображение на бок и уменьшите размер примерно до 75% для лучший эффект), или вы можете использовать другую фигуру, которую вы найдете.

Это упражнение оценивается в 30 баллов и будет сдано 28 апреля 2001 г., когда вы будете сдавать экзамен 3.

Фон

Скорость продольной или поперечной волны зависит от физических свойств породы, через которую проходит волна. Различные породы имеют разные физические характеристики (например, насколько они сжимаемы и как реагируют на напряжения сдвига) и разные скорости продольных и поперечных волн. Фактически, если скорость волны можно измерить, можно будет предсказать тип породы, через которую прошла волна – косвенное определение типа породы!

Скорость волны P может быть выражена как:

1. Скорость волны P = ((B + 1.3G) / Плотность) ^1/2 , где:
   • B = модуль объемной упругости – сопротивление изменению объема
     
   • G = модуль сдвига – сопротивление изменению формы
     
   • Плотность = масса / объем

   По мере увеличения давления (увеличения глубины перемещения) величина (B + G) увеличивается быстрее, чем плотность. Следовательно, с увеличением глубины мы ожидаем увеличения скорости продольной волны.

   ОДНАКО, если волна переходит от одного материала к другому, волна может ускоряться, замедляться или не менять скорость или направление, в зависимости от контраста свойств двух типов материала.

2. Скорость волны S = (G / плотность) ^1/2

   Вопросы

   1. Если вы поместите каменный куб в аквариум, изменит ли камень форму? Следовательно, G для твердых тел – большое число. (Помните, однако, что некоторые породы могут течь при высоких температурах). Если вы возьмете молоко из прямоугольной емкости и нальете его в аквариум, будет ли молоко сопротивляться изменению формы? Следовательно, G для жидкости составляет 0,0.
   2. Если зубец P перейдет из твердого тела в жидкость – что произойдет с его скорость (используйте уравнение)?
   3. Если S-волна перейдет из твердого тела в жидкость – что произойдет с ее скоростью (используйте уравнение)?
   4. Опишите границу на Земле, где продольные и поперечные волны переходят от твердого тела к жидкости.

   Каждый день новые землетрясения наносятся на карту Earthquake Locator . Еще один хороший источник информации о недавних землетрясениях – это IRIS

   . Начиная с 27 марта 2001 г., выберите 20 самых последних землетрясений с магнитудой 5,0 и выше. Подготовьте таблицу со столбцами для:

   Местоположение Эпицентра	Фокусная глубина	Звездная величина	Примечания

   На трясущейся земле – это аналогичное упражнение, которое может дать вам некоторые идеи.

   Подготовьте копию карты границ плит и найдите эпицентры этих 20 последних событий с магнитудой 5 или выше в области , красного цвета . Запишите величину и глубину фокуса (если он указан) для каждого события в вашей таблице.

   1. В примечаниях укажите, находился ли эпицентр вблизи границы плиты; если это так, кратко опишите характер границы пластины и ощущение движения. Если эпицентр находился внутри плиты, дайте название плите и ее общее направление движения.
   2. С сегодняшнего дня и до 21 апреля запишите новые землетрясения (магнитудой 5,0 и выше) в вашу таблицу, выделив ее синим цветом .
   3. Используйте свои быстро улучшающиеся способности и поищите в Интернете список из десяти землетрясений с сильнейшей магнитудой на Земле. Добавьте эти землетрясения в свою таблицу и нанесите эпицентры оранжевым цветом
   4. На основе этой очень ограниченной выборки прокомментирует взаимосвязь между эпицентрами землетрясений и краями плит .

   Тектоника плит – причина землетрясений – очень хорошее введение в землетрясения и тектонику плит. Прочтите этот раздел для общего обзора. Прочтите следующий раздел о Seismic Waves . Завершите чтение, быстро пройдя через раздел о звездной величине Рихтера . Не увязайте в математике. Сосредоточьтесь на различиях между шкалой Рихтера и старой шкалой Меркалли.

   Письмо в редакцию

   Вы живете в районе Каскадов.В последних редакционных статьях региональные планировщики написали статьи о том, насколько новый конференц-центр Cascades Convention Center добавит региональной экономике. Вы полагаете, что эти авторы сбили общественность с толку относительно частоты и масштабов событий в Каскадах. Напишите письмо (или около того) из 300 слов редактору, в котором вы изложите свое мнение о безопасности такого объекта. Насколько вероятны землетрясения в этом районе? Используйте собранную вами информацию, чтобы сформулировать свое письмо.

   Своими словами опишите шкалу Рихтера и шкалу Меркалли для описания землетрясений.Включите различие между интенсивностью и величиной.

   Какие проблемы возникают при использовании шкалы Меркалли? Как пользователи этой шкалы противостоят этой критике?

   Таблица и карта и редакционная статья , которые вы заполните для этого упражнения, будут переданы в день экзамена 3.

   _________________________________________________________________________________________________

   | jbutler @ эээ.edu | Отправить по электронной почте ClassListserv | Прочтите ClassListserv |
   | Домашняя страница учебника | Глоссарий геологических терминов | Искать на этих страницах |
   | Другие курсы | Ресурсы | Зачётная книжка |

   _________________________________________________________________________________________________

   Вернуться на главную страницу Physical Geology

   Авторские права принадлежат Джону К.Батлер, 29 июля 1995 г.

   Упругие свойства и плоская акустическая скорость кубических Sr2CaMoO6 и Sr2CaWO6 из расчетов из первых принципов

   Ссылки

   [1] Шарма Г., Нарула А.К., Eu ³⁺ Yb ³⁺ и Eu ³⁺ -Yb ³⁺ Комплексы с салициловой кислотой и 1,10-фенантролином, синтез, фотолюминесцентные свойства и передача энергии, J. Fluorescence, 2015, 25 (2), 355-360.10.1007 / s10895 -015-1517-1Поиск в Google Scholar

   [2] Li Y., Лю Т., Е С. Специальное преобразование эмиссии Eu в SrCa (W, Mo) O, Yb, Eu с помощью лазера с электронным поляризационным механизмом, J. Mat. Chem. C, 2015, 3 (19), 4997-5003.10.1039 / C5TC00340G Искать в Google Scholar

   [3] Шарма К.Г., Сингх Н.Р., Синтез и люминесцентные свойства наночастиц CaMO4, Dy ³⁺ (M = W, Mo) получены с использованием этиленгликоля, New J. Chem., 2013, 37 (9), 2784-2791.10.1039 / c3nj00155e Поиск в Google Scholar

   [4] Guo J., Zhou D., Wang L.Инфракрасные спектры, спектры комбинационного рассеяния света, микроволновые диэлектрические свойства и моделирование эффективной диэлектрической проницаемости термостабильной керамики AMoO ₄ -TiO ₂ (A = Ca, Sr)., Dalton Transactions, 2013, 42 (5), 1483-91.10. 1039 / C2DT31878D Искать в Google Scholar

   [5] Ильхан С., Калпакли А.О., Кахруман К. Исследование поведения растворения пустой породы при растворении шеелитового концентрата в растворе щавелевой кислоты, Гидрометаллургия, 2013, 136 (4), 15 -26.10.1016 / j.hydromet.2013.02.013Поиск в Google Scholar

   [6] Goel A., Mccloy J.S., Jr C.F.W. Структура боросиликатного стекла, содержащего рений, Международный журнал прикладной науки о стекле, 2013 г., 4 (1), 42-52.10.1111 / ijag.12003 Поиск в Google Scholar

   [7] Кан Ф., Пэн М., Ян X Широкая настройка излучения Bi ³⁺ посредством модуляции кристаллического поля в соединениях твердых растворов (Y, Lu, Sc) VO4, Bi для белых светодиодов с преобразованием в ультрафиолетовое излучение, J. Mat. Chem. С, 2014, 2 (30), 6068-6076.10.1039 / C4TC00238ES Искать в Google Scholar

   [8] Ансари А.А., Парчур А.К., Алам М. Влияние поверхностного покрытия на структурные и фотолюминесцентные свойства CaMoO 4, Pr Nanoparticles, J. Fluorescence, 2014, 24 (4), 1253-1262.10 .1007 / s10895-014-1409-9 Искать в Google Scholar

   [9] Chen Y., Park SW, Moon BK Влияние цитрата натрия на форму и фотолюминесцентные свойства сверхструктур CaWO4, Eu3 +, синтезированных гидротермальным методом, Crystengcomm, 2013, 15 (41), 8255-8261.10.1039 / c3ce40872hПоиск в Google Scholar

   [10] Chouard N., Caurant D., Majérus O. Влияние MoO ₃ Nd2O ₃ и RuO ₂ на кристаллизацию алюмоборосиликатных содово-известковых стекол, J. Mat . Sci., 2015, 50 (1), 219-241.10.1007 / s10853-014-8581-9 Искать в Google Scholar

   [11] Сараф Р., Шивакумара К., Дхананджая Н. Фотолюминесцентные свойства Eu ³⁺ активированный CaMoO ₄ люминофор для приложений WLED и его анализ Джадда-Офельта, J.Мат. Sci., 2015, 50 (1), 287-298.10.1007 / s10853-014-8587-3 Искать в Google Scholar

   [12] Wang M., Chen Z., Chen D. Структурные, упругие и термодинамические свойства A15 соединения типа V3X (X = Ir, Pt и Au) из расчетов из первых принципов, Modern Phys. Lett. B, 2016, 30 (35), 165041410.1142 / S0217984916504145 Искать в Google Scholar

   [13] Гуо З.К., Луо Ф., Ченг Й., Фазовый переход и термодинамические свойства бериллия на основе расчетов из первых принципов, Comp. Мат.Sci., 2014, 84 (1), 139-144.10.1016 / j.commatsci.2013.12.013 Искать в Google Scholar

   [14] Лю С., Чжан Ю., Понимание структурных, механических и термодинамических свойств борида циркония из первопринципных расчетов, Comp. Мат. Sci., 2015, 103, 111-115.10.1016 / j.commatsci.2015.03.027 Искать в Google Scholar

   [15] Niu Z.W., Cheng Y., Zhang H.Y. Первопринципные исследования структурных, фононных и термодинамических свойств кубического $$ \ text {CeO_ {2 $$ CeO 2, Int.J. Thermophys., 2014, 35 (8), 1601-1612.10.1007 / s10765-014-1689-y Искать в Google Scholar

   [16] Tao X., Zhu J., Guo H. Фазовая стабильность, термодинамическая и механическая свойства AlZr 2, FeZr 2 и Al 2 FeZr 6, исходя из расчетов из первых принципов, J. Nucl. Матем., 2013, 440 (1-3), 6-10.10.1016 / j.jnucmat.2013.04.037 Искать в Google Scholar

   [17] Pu CY, Wang L., Lin-Xia L. Структурный переход, вызванный давлением и термодинамические свойства NbSi_2 из расчетов из первых принципов, Acta Physica Sinica, 2015, 64 (8), 1-2.Искать в Google Scholar

   [18] Ян Т., Лю Д., Джи Дж. Расчеты из первых принципов для переходной фазы, механических и термодинамических свойств ZnS в экстремальных условиях, Int. J. Modern Phys. B, 2017, 31 (5), 175002810.1142 / S021797921750028XПоиск в Google Scholar

   [19] Пу К., Чжоу Д., Сонг Й. Фазовый переход и термодинамические свойства сплава YAg на основе расчетов из первых принципов, Comp. Мат. Sci., 2015, 102 (8), 21-26.10.1016 / j.commatsci.2015.02.011 Искать в Google Scholar

   [20] Zhang X., Чжао X., Чжэн Б. и др .. Исследование первых принципов термодинамических и упругих свойств η ′ – (Cu, Co) 6 Sn 5, тройные сплавы, J. Electr. Mat., 2016, 45 (10), 4919-4927.10.1007 / s11664-016-4654-7 Искать в Google Scholar

   [21] Yan HY, Zhang MG, Huang DH Изучение первых принципов упругих и термодинамических свойств орторомбического OsB 4, под высоким давлением, Solid State Sci., 2013, 18 (22), 17-23.10.1016 / j.solidstatesciences.2012.12.015 Искать в Google Scholar

   [22] Юань Дж., Ю. Н., Сюэ К. Стабильность, электронные и термодинамические свойства алюминия на основе расчетов из первых принципов, Прил. Прибой. Sci., 2017, 409, 85-90.10.1016 / j.apsusc.2017.02.238 Искать в Google Scholar

   [23] Чжан Б., Исследования магнитных, механических и термодинамических свойств кубической фазы LaMO3 (M = Ti ~ Fe), Фил. Mag. Lett., 2017, 97 (5), 169-179.10.1080 / 09500839.2017.1304657 Поиск в Google Scholar

   [24] Xu C., Li Q., ​​Liu C.M. Структурная устойчивость, упругие и электронные свойства тетраборида хрома из первых принципов расчетов, Int.J. Modern Phys. B, 2016, 30 (17), 1650098.10.1142 / S0217979216500983 Поиск в Google Scholar

   [25] Планас М.И.Г., Климчук Т., Анализ возмущений матричного дифференциального уравнения x = ABx, Прил. Математика. Nonlinear Sci., 2018, 3, 97-104.10.21042 / AMNS.2018.1.00007Поиск в Google Scholar

   [26] Baig AQ, Naeem M., Gao W., индексы Ревана и гипер-Ревана октаэдрических и икосаэдрических сетей. Прил. Математика. Нелинейные науки, 2018, 3 (1), 33-40.10.21042 / AMNS.2018.1.00004 Искать в Google Scholar

   Physclips: Уравнение звуковой волны

   Волновое уравнение и скорость звука

   Уравнение (2) дало нам, поэтому, объединив это с уравнением выше, мы имеем

   (3)

   Если вы вспомните волну в струне, вы заметите, что это одномерное волновое уравнение .Когда мы вывели его для струны с натяжением T и линейной плотностью μ, у нас было

   Тогда мы показали, что это волновое решение со скоростью

   Давайте сделаем это еще раз: если мы будем искать решение

   y = y _м sin (kx – ωt)

   и возьмем производные, имеем

   Итак, это решение при условии, что (ω / k) ² = / ρ.Теперь ω / k – это скорость волны (см. Travelling_sine_wave для уточнения), так что для скорости звука у нас есть:

   Давайте посмотрим на аналогии: натяжение струны обеспечивает возвращающую силу; здесь также эластичность среды. Инерция обеспечивалась массой единицы длины струны μ, в данном случае массой единицы объема среды ρ.

   Хотя мы предполагали, что наша стихия – воздух, мы до сих пор предполагали только, что она упругая.Таким образом, это уравнение справедливо для продольных волн в любой упругой среде. Для воздуха мы можем указать значение модуля упругости.

   На странице об идеальном газе мы показываем, что во время адиабатического расширения и сжатия давление P и объем V связаны

   PV ^γ = постоянная,

   , где γ – адиабатическая постоянная или отношение удельной теплоемкости при постоянном давлении к удельной теплоемкости при постоянном объеме, равное примерно 1.4 для воздуха. (Попутно заметим, что это нелинейное уравнение.) Принимая натуральные логарифмы с обеих сторон, получаем

   ln P + γ ln V = постоянная.

   Теперь d ( ln x) = dx / x (исправьте здесь), поэтому взятие производных дает нам

   т.

   (Хотя мы отметили выше, что уравнение P (V) является нелинейным, теперь мы видим, что изменения давления и объема ΔP и ΔV пропорциональны, если ΔP / P мало.Паскаль уже является очень громким звуком на нормальных частотах, а атмосферное давление составляет около 100000 Па, поэтому звуковые волны в воздухе обычно линейны в превосходном приближении.)

   Определение модуля объемной упругости (см. Выше), выраженное как дифференциал, равно

   .

   , поэтому, объединив два приведенных выше уравнения, мы получим

   Итак, скорость звука в идеальном газе равна

   .

   Для воздуха при атмосферном давлении (P = 101 кПа) и при T = 20 ° C плотность равна 1.20 кг.м ⁻³ . Принимая γ = 1,4, получаем скорость звука 343 мс ⁻¹ .

   Удельное акустическое сопротивление

   Давайте свяжем скорость и давление, используя решение выше:

   y = y _м sin (kx – ωt)

   Скорость частицы

   Используя уравнение (2), имеем

   Удельный акустический импеданс z среды определяется как p / u, поэтому, используя уравнения выше

   z = κk / ω.