Модуль ускорения тела формула: Модуль ускорения равен 2 м/с2 как это понимать выберите правильное утверждение а) за 1 с…

Формулы модуля ускорения для прямолинейного и криволинейного движения. Пример решения задачи

В физике существует несколько видов ускорения, которые используются для описания того или иного типа механического перемещения тел в пространстве. Все эти виды являются векторными величинами. В данной статье не будем рассматривать вопрос, куда направлено ускорение, а сосредоточим свое внимание на формулах модуля ускорения.

Что такое ускорение?

Максимально полное определение этой кинематической характеристики можно привести следующее: ускорение – это величина, показывающая быстроту изменения скорости во времени. Речь идет об изменении как модуля, так и направления. Математически ускорение вычисляют так:

a = dv/dt.

Оно называется мгновенным, то есть справедливым для конкретного момента времени t. Чтобы найти среднее значение модуля ускорения, формулу такую необходимо использовать:

a = (v₂ – v₁)/(t₂ – t₁).

Где v₂ и v₁ – скорости в моменты времени t₂ и t₁ соответственно.

Единицами измерения изучаемой физической величины являются метры в квадратную секунду (м/с²). Многих может смутить возведение во вторую степень единиц времени, тем не менее, понять смысл единицы м/с² несложно, если ее представить в виде [м/с]/с. Последняя запись означает изменение скорости на одну единицу за одну единицу времени.

Движение по прямой и ускорение

Самой простой траекторией для перемещения тел в пространстве является прямая линия. Если скорость при движении по такой траектории не изменяется, то говорить об ускорении не приходится, поскольку оно будет равно нулю.

Линейная скорость: формула расчета нахождения

С точки зрения физики абсолютного покоя не существует. Каждое тело и частицы, которые его…

В технике широко распространено прямолинейное равноускоренное (равнозамедленное) движение.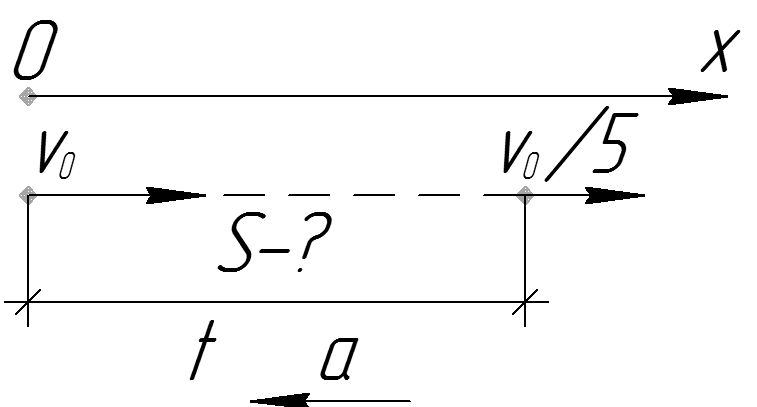 Например, при старте автомобиля или при его торможении мы имеем именно этот вид движения. Для его математического описания пользуются следующими равенствами:

v = v₀±a*t;

l = v₀*t±a*t²/2.

Здесь v₀ – некоторая начальная скорость тела, которая может быть также равна нулю, l – пройденный телом путь к моменту времени t. Знак + говорит об ускорении тела, знак – – о его торможении. Важно запомнить, что время t при использовании записанных формул начинает отсчитываться от момента появления у тела постоянного ускорения a. С учетом записанных равенств, формулы модуля ускорения тела принимают вид:

±a = (v – v₀)/t;

±a = 2*(l – v₀*t)/t².

Как правило, если тело ускоряется, то говорят о положительном ускорении, если же оно замедляет свое движение, то говорят об отрицательной величине a. Нетрудно проверить, что обе формулы приводят к одной и той же единице измерения ускорения (м/с²).

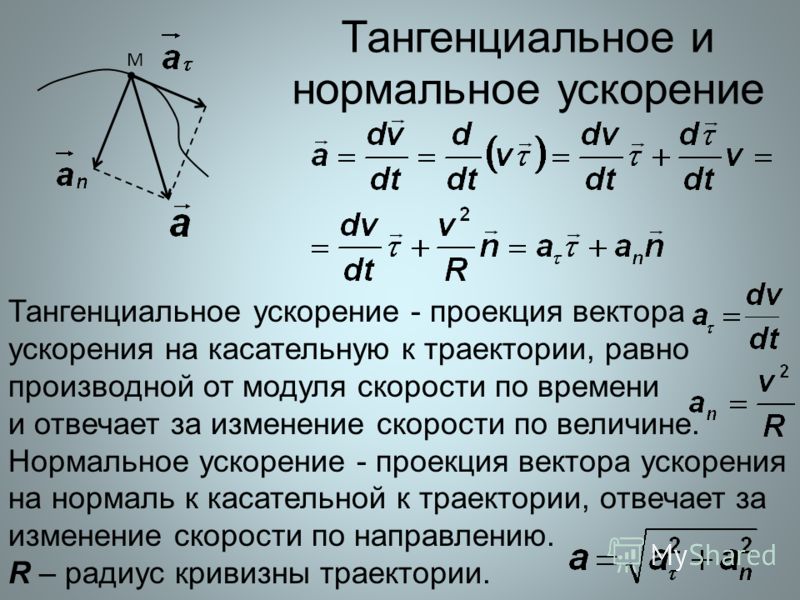
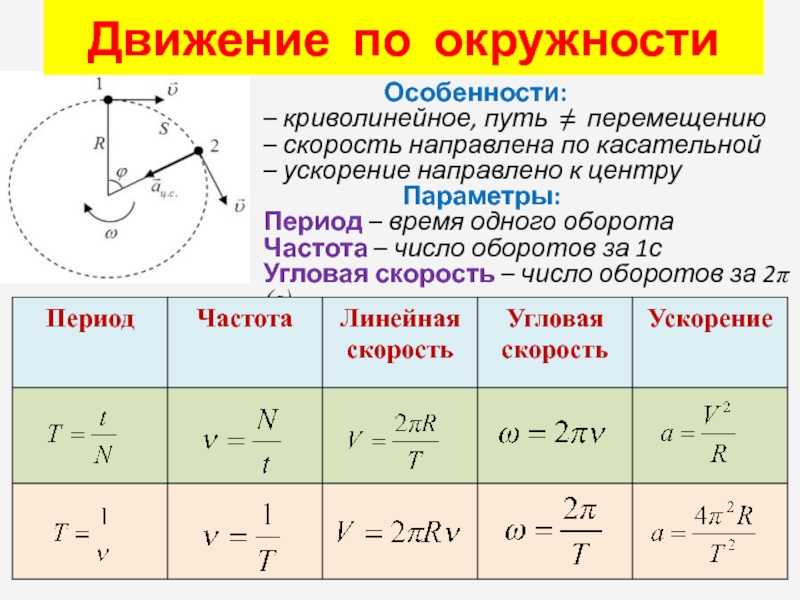
Полное ускорение и его компоненты при движении тела по кривой

В случае перемещения тела по криволинейной траектории, величину a удобно представить в виде двух взаимно перпендикулярных составляющих. Они называются тангенциальным a_t и нормальным a_n ускорениями. Для такого случая формула модуля ускорения точки принимает вид:

Линейная скорость: формула расчета нахождения

С точки зрения физики абсолютного покоя не существует. Каждое тело и частицы, которые его…

a = √(a_t² + a_n²).

Тангенциальную компоненту следует рассчитывать через производную функции v(t) по времени. Нормальная же компонента определяется не изменением модуля скорости, а самой ее величиной. Для ее расчета пользуются таким выражением:

a_n = v²/r.

Здесь r – радиус кривизны траектории, который в случае вращения по окружности совпадает с радиусом последней.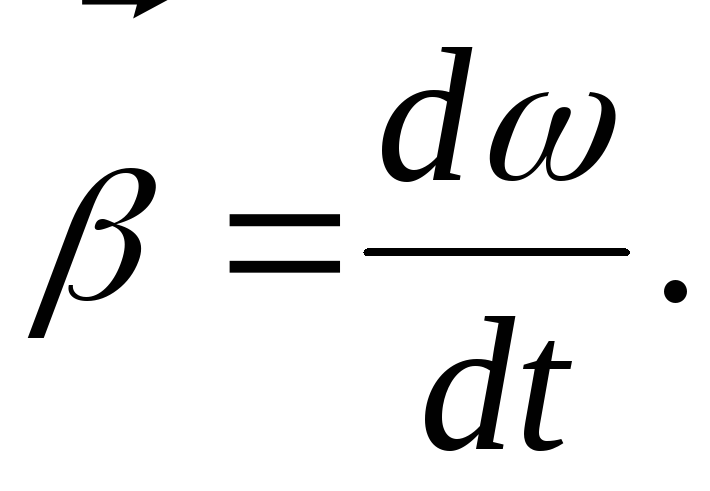

Для полноты информации отметим, что криволинейность траектории перемещения тела является достаточным признаком присутствия ненулевой нормальной составляющей ускорения. При этом величина a_t может быть равна нулю, что является справедливым для равномерного вращения тел.

Угловое ускорение

Как было отмечено во введении, существуют несколько видов ускорения. Одним из них является угловая кинематическая величина. Обозначим ее α. По аналогии с линейным ускорением, формула модуля ускорения углового имеет вид:

α = dω/dt.

Где греческой буквой ω (омега) обозначена скорость угловая, единицами измерения которой являются радианы в секунду. Величина α показывает, как быстро тело увеличивает или замедляет скорость своего вращения.

Ускорение угловое можно связать с линейной величиной. Делается это с помощью такой формулы:

α = a_t/r.

Важно понимать, что угловое ускорение является удобным способом представления тангенциальной составляющей полного ускорения в случае вращательного движения. Удобство здесь заключается в независимости величины α от расстояния до оси вращения r. В свою очередь, компонента a_t линейно возрастает при увеличении радиуса кривизны r.

Пример решения задачи

Известно, что тело вращается по окружности, радиус которой составляет 0,2 метра. Вращение является ускоренным, при этом скорость изменяется во времени по следующему закону:

v = 2 + 3*t² + 2*t³.

Необходимо определить тангенциальное, нормальное, полное и угловое ускорения в момент времени 3 секунды.

Начнем решать эту задачу по порядку. Тангенциальная компонента определяется через производную скорости. Имеем:

a_t = dv/dt = 6*t + 6*t² = 6*3 + 6*9 = 76 м/с².

Отметим, что это очень большое ускорение по сравнению с ускорением свободного падения (9,81 м/с²).

Нормальная компонента вычисляется так:

a_n = v²/r = 1/r*(2 + 3*t² + 2*t³)² = 1/0,2*(2+27+54)² = 34445 м/c².

Теперь можно рассчитать полное ускорение. Оно будет равно:

a = √(a_t² + a_n²) = √(76 ² + 34445 ²) = 34445,1 м/с².

То есть, полное ускорение практически полностью образовано нормальной компонентой.

Наконец, ускорение угловое определяется по формуле:

α = a_t/r = 76/0,2 = 380 рад/с².

Полученное значение соответствует увеличению скорости угловой приблизительно на 60 оборотов за каждую секунду.

Модуль ускорения определяется выражением

. (2.21)

Выше было отмечено, что вектор ускорения материальной точки характеризует изменение скорости по модулю и направлению. Оказывается, что векторможно разложить на две составляющие, одна из которых характеризует изменение только модуля скорости, а другая – только его направления. Такое разложение возможно при любом виде движения материальной точки. В качестве примера покажем это для случая плоского движения точки по произвольной криволинейной траектории.

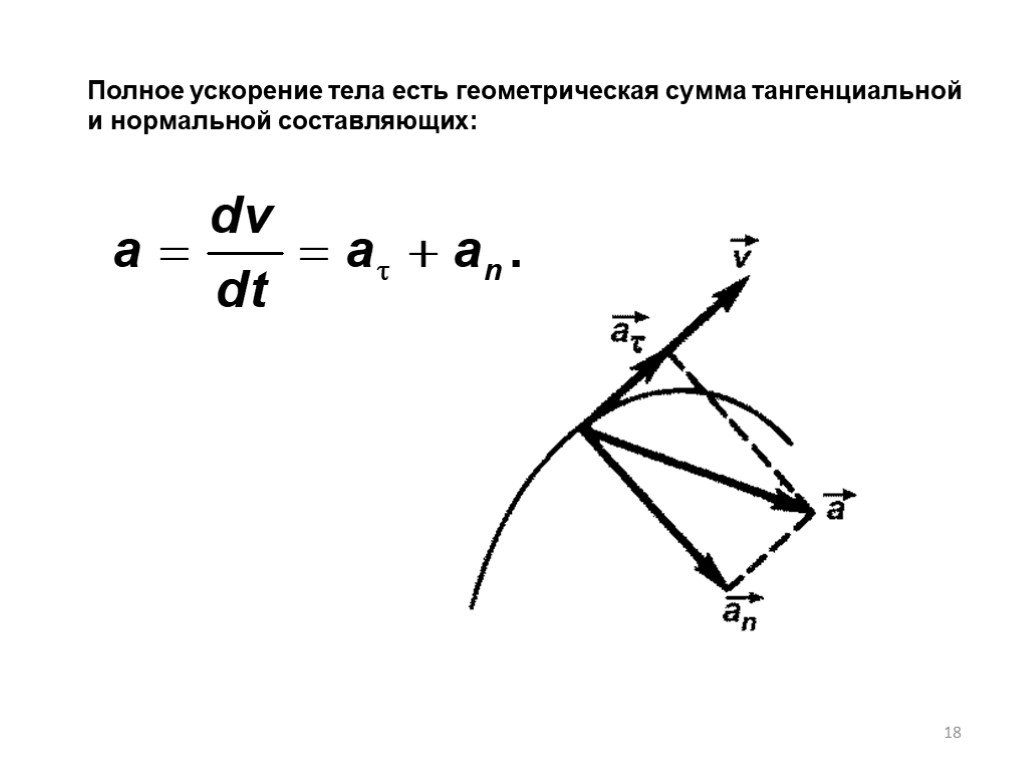
Пусть материальная точка M совершает неравномерное плоское движение по криволинейной траектории (рис. 2.6). Проведем в точке М два взаимно перпендикулярных единичных вектора (орта) илежащих в плоскости траектории. Векторнаправлен по касательной к траектории в сторону движения материальной точки, то есть в направлении ее скорости. Вектор, проведен в сторону вогнутости траектории по линии, соединяющей точку

M с центром О кривизны траектории для данной ее точки.

В этих условиях ускорение может быть разложено на две следующие составляющие:

. (2.22)

В

Рис. 2.7

качестве примера рассмотрим неравномерное движение точки М по окружности (рис 2.7). В момент времени t точка М находится в положении 1 и имеет скорость. Через малый промежуток времениt точка переместится в положение 2 и будет иметь скорость . Найдем приращение вектора скоростиза времяt. Для этого перенесем вектор без изменения его направления так, чтобы его начало совпало с началом вектора(рис. 2.8). Векторизображен направленным отрезком, проведенным из конца векторав конец вектора. Разложим векторна две составляющие

n и _. Составляющую _n выберем так, чтобы расстояние от точки 1 до конца вектора было равно. При таком выборе_n, составляющая _ будет иметь модуль равный приращению модуля (величины) скорости за время t, то есть

|_|=||. (2.27)

Введем единичный вектор , совпадающий по направлению с вектором_, тогда его можно будет представить в виде

_=. (2.28)

Вектор _n также можно представить в виде произведения его модуля на единичный вектор , задающий его направление

_n =|_n |. (2.29)

Угол между векторами и () равен, то есть углу между векторами и () (рис 2.7 и 2.8). При малыхt модуль вектора _n можно приближенно заменить дугой окружности радиуса || (рис. 2.8):

_n. (2.30)

Угол  можно выразить через радиус окружности и пройденный точкой М путь S за время t (рис. 2.7) с помощью известного из геометрии соотношения

=^. (2.31)

С учетом (2.31) формула (2.30) принимает вид:

_n . (2.32)

Найдем ускорение точки М в положении 1 (рис. 2.7). Для этого учтем, что =_n +_, и воспользуемся формулой (2.21)

(2.33)

С учетом выражения (2.32) первый предел справа принимает вид:

^. (2.34)

В точке 1 траектории V и имеют фиксированные значения, а. Кроме того, приt0 вектор переходит в вектор- вектор главной нормали к траектории в точке 1 (рис.

2.8). Таким образом, вычисляя предел в (2.34) и обозначая его через, получим

^. (2.35)

Второй предел в выражении (2.33) обозначим через и учтем выражение (2.28), тогда можем записать:

^. (2.36)

При вычислении предела в (2.36) учтено, что при t0 вектор переходит в вектор- единичный вектор касательной к траектории в точке 1 (рис. 2.8).

Таким образом, вектор ускорения точки в любой момент времени может быть представлен в виде суммы двух векторов:

. (2.37)

Вектор – называется нормальным ускорением и характеризует изменение скорости по направлению.

Вектор – называется тангенциальным (касательным) ускорением и характеризует изменение скорости по величине.

Модуль полного ускорения в соответствии с выражениями (2.35), (2.36) и (2.37) равен:

^. (2.38)

Если траектория не окружность, а произвольная кривая, то в формуле (2. 38) представляет собой радиус кривизны траектории в точке, для которой определяется полное ускорение.

Модуль Юнга: формула, эксперимент, единица измерения, график

Модуль Юнга или модуль упругости описывает способность материалов сопротивляться изменению длины при растяжении или сжатии. Этот модуль очень полезен в инженерии, поскольку он предоставляет подробную информацию об упругих свойствах материалов, таких как их прочность на растяжение и жесткость.

Определение модуля Юнга

Модуль Юнга равен приложенному продольному напряжению, деленному на деформацию. Напряжение и деформация объекта, подвергающегося растяжению, также могут быть выражены следующим образом: когда металлический объект тянут с силой F за каждый конец, объект будет растягиваться от первоначальной длины L ₀ на новую длину в растянутом состоянии L _n .

Поскольку объект растягивается, площадь поперечного сечения уменьшается. Напряжение может быть выражено как приложенная растягивающая сила (F), измеренная в ньютонах (Н), деленная на площадь поперечного сечения (A), измеренную в м ² , , как показано в приведенном ниже уравнении. Полученная единица напряжения равна Н/м ² .

Деформация, также известная как относительная деформация, представляет собой изменение длины, вызванное растяжением или сжатием, деленное на исходную длину л ₀ . Деформация безразмерна, так как оба члена дроби измеряются в метрах и могут быть рассчитаны по следующему уравнению.

Формула модуля Юнга

Модуль упругости E можно выразить как напряжение, деленное на деформацию, как показано в формуле ниже.

Единицы модуля Юнга такие же, как и напряжение, Н/м ² , что эквивалентно Па (паскаль). Так как модуль упругости обычно очень большое число величины 10 ⁹ часто выражается в гигапаскалях, показанных как ГПа.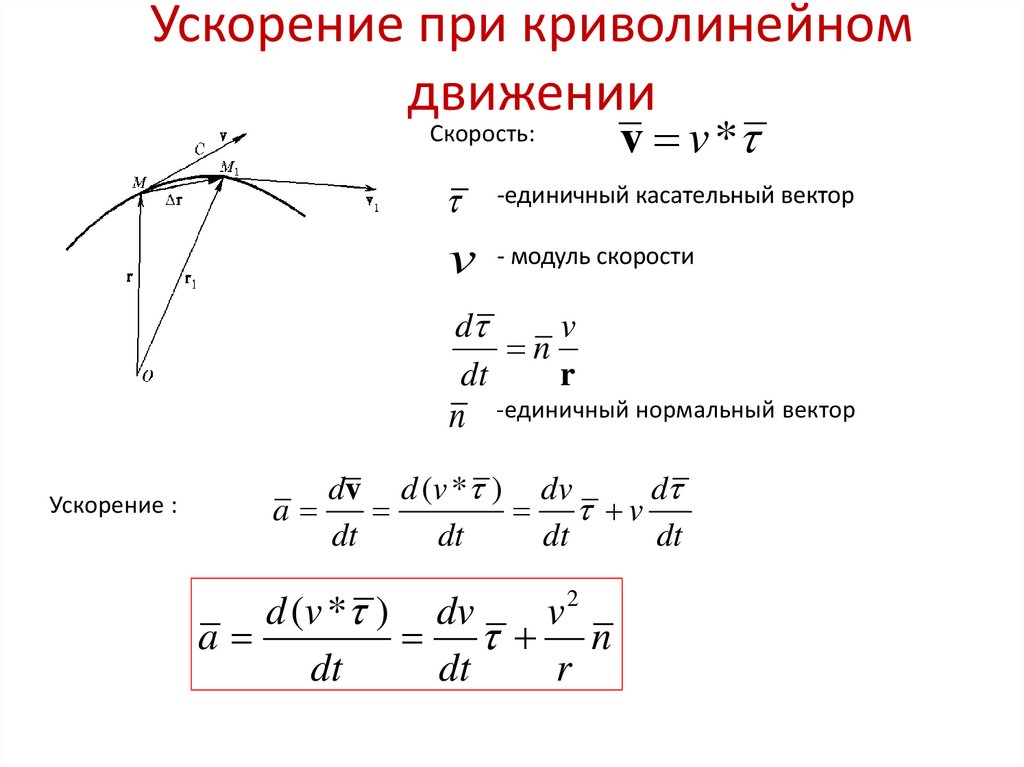

Металлический стержень испытывает нагрузку 60 Н , приложенную к концу. Металлический стержень имеет цилиндрическую форму и площадь поперечного сечения 0,02 мм ² . Длина полосы увеличивается на 0,30 процента. Найдите модуль упругости стержня.

Решение:

Поскольку требуется модуль Юнга, нам нужно сначала найти напряжение и деформацию (помните, модуль Юнга – это отношение напряжения к деформации). Применим формулу напряжения, чтобы найти напряжение.

Затем мы применяем формулу деформации, чтобы найти деформацию:

Затем, наконец, мы делим напряжение на деформацию, чтобы найти модуль Юнга.

Как модуль Юнга связан с законом Гука?

Закон Гука гласит, что сила, действующая на тело или пружину, создающая смещение Δx, линейна по отношению к смещению, создаваемому в соответствии с приведенным ниже уравнением, где k — константа, относящаяся к жесткости пружины. Закон Гука можно применить к ситуациям, когда тело упруго деформируется.

Аналогично закону Гука, где растяжение или сжатие пружины линейно пропорционально приложенной силе; напряжение, приложенное к телу, линейно пропорционально модулю Юнга E, как показано в приведенном ниже преобразованном уравнении.

Графический расчет модуля Юнга

Поскольку модуль упругости материала линейно пропорционален приложенному напряжению, деленному на деформацию, модуль Юнга также можно рассчитать по графику напряжение-деформация, который описывает линейную деформацию, как показано по закону Гука. Модуль Юнга равен наклону линейного участка кривой зависимости напряжения от деформации, как показано на рисунке ниже.

Расчет модуля Юнга по графику напряжения-деформации

Эксперименты для определения модуля Юнга

Чтобы измерить модуль Юнга металла, можно провести несколько экспериментов. К медному проводу будут прикладываться различные нагрузки — полученное удлинение будет измерено для построения графика напряжения-деформации. В соответствии с уравнениями напряжений и деформаций требуемые параметры будут измеряться с помощью следующего оборудования.

• Провод

• Micrometre

• Pulley

• Metre ruler

• Caliper

• Weights

• Clamp

• Wooden block

• Bench

Methodology

1. С помощью линейки измеряем начальную длину провода. Мы используем микрометр для измерения диаметра проволоки в трех точках по ее длине. Это для среднего диаметра, который будет использоваться в расчете площади.

2. Один конец провода присоединяем к шкиву, который зажат к скамье, а другой конец к зажатому деревянному бруску.

3. Удлинение проволоки под действием веса измеряется и регистрируется. Разница между новой длиной и исходной длиной до удлинения используется при расчете деформации.

4. Повторите процесс, чтобы получить еще от 5 до 10 показаний. Для уменьшения ошибок рекомендуется проводить различные измерения с различными весами.

5. Затем постройте график зависимости напряжения от деформации и найдите модуль упругости, взяв градиент линии.

Анализ результатов

Целью эксперимента является оценка модуля Юнга. Это можно найти, оценив напряжение и деформацию. Следующие шаги необходимы, чтобы найти напряжение и деформацию.

1. Найдите площадь провода, используя измеренный диаметр и уравнение A=πr ² , где r=R/2.

2. Переформулируйте формулу модуля Юнга и решите ее для F. Это даст нам F=((E⋅A)/L)⋅ΔL.

3. Перестроенное уравнение аналогично уравнению прямой вида y = ax, , где y равно F , а наклон является коэффициентом ΔL.

4. График зависимости силы от ΔL строится по зарегистрированным точкам силы и растяжения, чтобы можно было найти наклон. Уклон ΔF/ΔL находится и умножается на исходную длину L ₀ и делится на площадь A, для оценки значения модуля Юнга.

График напряжения-деформации и характеристики материалов

Некоторые важные характеристики материалов показаны на рисунке ниже.

• Красная область указывает на упругую область, где она деформируется в соответствии с законом Гука, а напряжение и деформация пропорциональны друг другу. Красная точка указывает предел упругости или предел текучести. Это точка, в которой материал может сохранять свою первоначальную длину после приложения нагрузки.

• Зеленая область указывает на область пластичности, в которой материал не может вернуться в исходное состояние и подвергся необратимой деформации. Зеленая точка указывает предел прочности при растяжении, до которого материал может выдерживать максимальную нагрузку на единицу без разрушения.

• Синяя точка указывает точку разрыва или предел прочности при разрыве материала.

График напряжения-деформации предела упругости материала, области пластичности и точек разрыва

Модуль Юнга — основные выводы

• Модуль Юнга — это способность материала сопротивляться изменению длины при растяжении или сжатии.

• Модуль Юнга можно рассчитать графически с помощью графика напряжения-деформации.

• Экспериментальный расчет модуля Юнга возможен путем построения разности длины груза.

• Используя график напряжений и деформаций, можно определить прочность материала на растяжение и предел прочности.

Эластичность и простое гармоническое движение

Твердое тело — это идеализация, потому что даже самый прочный материал слегка деформируется при приложении силы. Упругость — это область физики, изучающая отношения между деформациями твердого тела и силами, которые их вызывают.

Эластичные модули

В общем, модуль упругости представляет собой отношение напряжения к деформации. Модуль Юнга, объемный модуль и модуль сдвига описывают реакцию объекта на растягивающие, сжимающие и сдвигающие напряжения соответственно. Когда объект, такой как проволока или стержень, подвергается натяжению, длина объекта увеличивается.

Модуль Юнга определяется как отношение напряжения растяжения к деформации растяжения. Напряжение растяжения — это мера деформации, вызывающей напряжение. Его определение представляет собой отношение силы растяжения (F) и площади поперечного сечения, нормального к направлению силы (A) . Единицами напряжения являются ньютоны на квадратный метр (Н/м ² ). Деформация растяжения определяется как отношение изменения длины ( l _o − l ) до исходной длины ( l _o ). Штамм – это число без единиц измерения; следовательно, выражение для модуля Юнга равно

.

Если к объекту кубической формы приложена сила, толкающая каждую грань внутрь, возникает сжимающее напряжение. Давление определяется как сила на единицу площади P = F/A . Единицей давления в СИ является паскаль, который равен 1 ньютон/метр ² или Н/м ² . При равномерном давлении тело сожмется, и его относительное изменение объема (V) – деформация сжатия . Соответствующий модуль упругости называется объемным модулем и определяется как

B = − P / (Δ V / V _o ). Отрицательный знак гарантирует, что B всегда будет положительным числом, поскольку увеличение давления вызывает уменьшение объема.

Приложение силы к верхней части объекта параллельно поверхности, на которой он стоит, вызывает деформацию. Например, толкните верхнюю часть книги, лежащей на столешнице, так, чтобы сила была параллельна поверхности. Форма поперечного сечения изменится с прямоугольника на параллелограмм из-за напряжение сдвига (см. рис. 1). Напряжение сдвига определяется как отношение тангенциальной силы к площади

(A) нагруженной поверхности. Деформация сдвига представляет собой отношение горизонтального расстояния, на которое перемещается сдвигаемая поверхность (Δ x ) и высоты объекта (h) , что приводит к модулю сдвига :

Рисунок 1

Напряжение сдвига деформирует книгу.

Закон Гука

Прямая зависимость между приложенной силой и изменением длины пружины, называемая законом Гука, равна F = − kx , где x — растяжение пружины, а k определяется как жесткость пружины . Единицами для k являются ньютоны на метр. Когда груз подвешен на конце пружины, при равновесии нисходящая сила тяжести, действующая на массу, должна быть уравновешена направленной вверх силой пружины.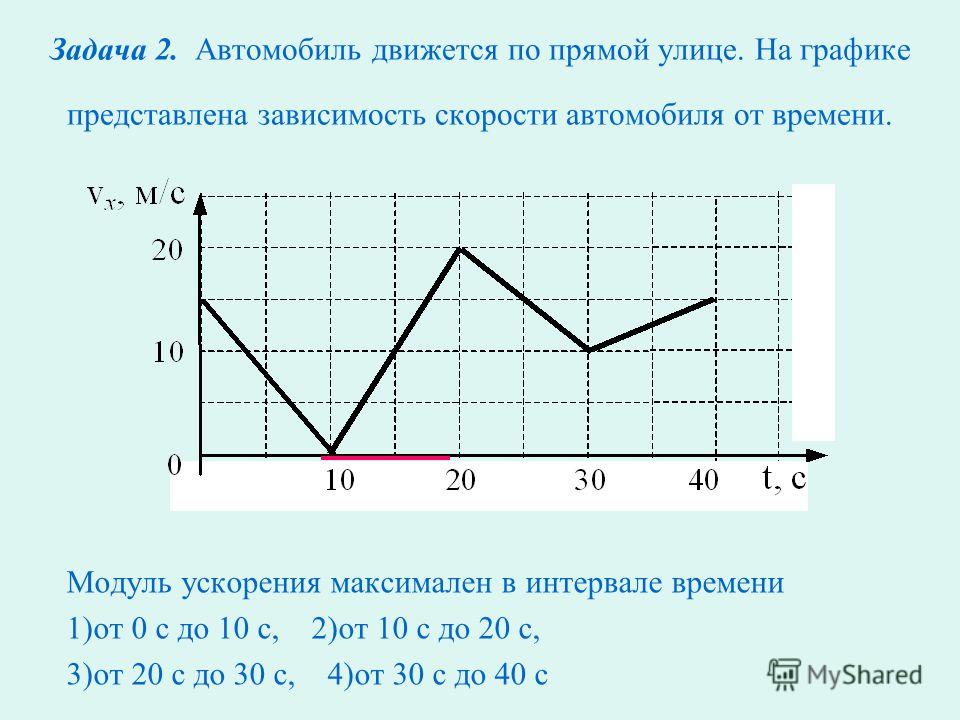

Эта сила называется восстанавливающая сила. Знак минус указывает, что направление восстанавливающей силы пружины противоположно направлению растяжения или смещения пружины.

Простое гармоническое движение

Масса, подпрыгивающая на конце пружины, совершает колебательное движение. Движение любой системы, ускорение которой пропорционально отрицательной величине смещения, называется простым гармоническим движением (SHM), т. е.

F = ma = – kx . Некоторые определения относятся к SHM:

• Полная вибрация — это одно движение вниз и вверх.

• Время одного полного колебания составляет период, измеряемый в секундах.

• Частота представляет собой число полных колебаний в секунду и определяется как величина, обратная периоду. Его единицами являются циклы в секунду или герц (Гц).

• Амплитуда является абсолютной величиной расстояния от максимального вертикального смещения до центральной точки движения, то есть наибольшего расстояния вверх или вниз перемещается масса от своего начального положения.

Уравнение, относящееся к периоду, массе и жесткости пружины: T = 2π√ m / k . Это отношение дает период в секундах.

Отношение СГМ к круговому движению

Аспекты SHM можно визуализировать, взглянув на его отношение к равномерному круговому движению. Представьте себе карандаш, приклеенный вертикально к горизонтальному поворотному столу. Посмотрите на вращающийся карандаш со стороны поворотного стола. Поскольку поворотный стол вращается с равномерным круговым движением, карандаш движется вперед и назад с простым гармоническим движением. Рисунок (а) иллюстрирует P как точка на ободе поворотного стола — положение карандаша. Точка P ′ указывает видимое положение карандаша при просмотре только компонента x . Вектор ускорения и компоненты вектора показаны на рисунке 2(b).

Рисунок 2

Связь между круговым движением и СГМ.

Ниже приводится доказательство связи между SHM и одной составляющей равномерного кругового движения. Этот компонент движения наблюдается при взгляде на круговое движение со стороны. Максимальное перемещение составляющей равномерного кругового движения равно радиусу окружности (А) . Подставим радиус окружности (А) в уравнения для угловой скорости и углового ускорения, чтобы получить = r ω ² = А ω ² . Горизонтальная составляющая этого ускорения равна a = − A ω ^o sin θ = −ω ² x , используя x = A , как показано на рисунке . Поскольку ускорение пропорционально смещению, точка, вращающаяся с равномерным круговым движением, подвергается SHM, когда рассматривается только одна составляющая движения.

Простой маятник

Простой маятник представляет собой идеализированную модель массы, качающейся на конце безмассовой струны. Для малых дуг качания менее 15 градусов движение маятника приближается к SHM. Период маятника равен T = 2π√ l / g , где l — длина маятника, а g — ускорение свободного падения.