Физика. 8 класс
Физика. 8 класс
ОглавлениеГлава 1. Общие сведения о движении§ 1. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ. МАТЕРИАЛЬНАЯ ТОЧКА § 2. ПОЛОЖЕНИЕ ТОЧКИ (ТЕЛА) В ПРОСТРАНСТВЕ § 3. ПЕРЕМЕЩЕНИЕ § 4.  § 5. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: СЛОЖЕНИЕ ВЕКТОРОВ § 6. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: ВЫЧИТАНИЕ ВЕКТОРОВ § 7. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: УМНОЖЕНИЕ ВЕКТОРА НА СКАЛЯР § 8. ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ § 9. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДВИЖЕНИЯ § 10. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ § 11. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ (ПРОДОЛЖЕНИЕ) § 12. ЕДИНИЦЫ ИЗМЕРЕНИЙ ДЛИНЫ И ВРЕМЕНИ Глава 2. Прямолинейное неравномерное движение § 13. СРЕДНЯЯ СКОРОСТЬ § 14. МГНОВЕННАЯ СКОРОСТЬ § 15. УСКОРЕНИЕ. РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ § 16. НАПРАВЛЕНИЕ УСКОРЕНИЯ § 17. ПЕРЕМЕЩЕНИЕ ПРИ РАВНОУСКОРЕННОМ ДВИЖЕНИИ § 18. СРЕДНЯЯ СКОРОСТЬ ПРИ ПРЯМОЛИНЕЙНОМ РАВНОУСКОРЕННОМ ДВИЖЕНИИ. СВЯЗЬ МЕЖДУ ПЕРЕМЕЩЕНИЕМ И СКОРОСТЬЮ § 20. СВОБОДНОЕ ПАДЕНИЕ ТЕЛ § 21. ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ВЕРТИКАЛЬНО ВВЕРХ Глава 3. Криволинейное движение § 22. ПЕРЕМЕЩЕНИЕ И СКОРОСТЬ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ § 23. 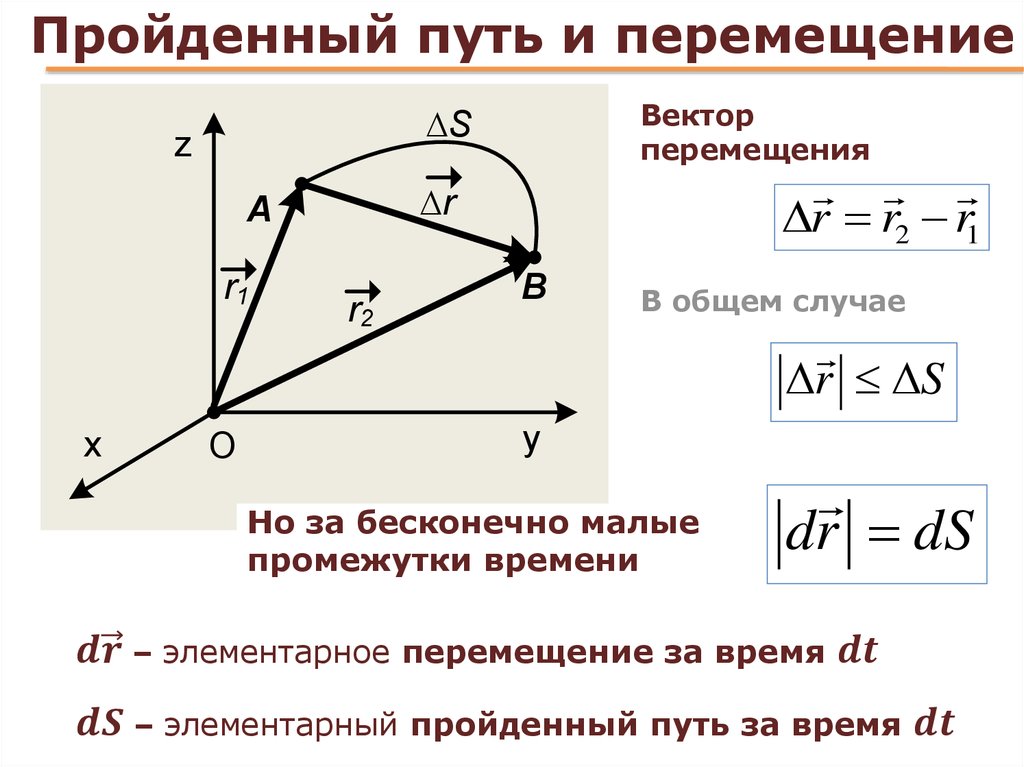 УСКОРЕНИЕ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ§ 24. ДВИЖЕНИЕ ПО ОКРУЖНОСТИ. УГОЛ ПОВОРОТА И УГЛОВАЯ СКОРОСТЬ § 25. УСКОРЕНИЕ ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ ТЕЛА ПО ОКРУЖНОСТИ § 26. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА § 27. ОБ ОТНОСИТЕЛЬНОСТИ ДВИЖЕНИЯ ТЕЛА ПРИ ВРАЩЕНИИ СИСТЕМЫ ОТСЧЕТА Динамика Глава 4. Законы движения § 29. ПОЧЕМУ ВОЗНИКАЮТ УСКОРЕНИЯ § 30. ВЗАИМОДЕЙСТВИЕ TEЛ. УСКОРЕНИЯ ТЕЛ ПРИ ИХ ВЗАИМОДЕЙСТВИИ § 31. ИНЕРТНОСТЬ ТЕЛ § 32. МАССА ТЕЛ § 33. МАССА ЛУНЫ § 34. СИЛА § 35. ВТОРОЙ ЗАКОН НЬЮТОНА § 36. ВТОРОЙ ЗАКОН НЬЮТОНА (продолжение) § 37. ИЗМЕРЕНИЕ СИЛ. ДИНАМОМЕТР § 38. ТРЕТИЙ ЗАКОН НЬЮТОНА § 39. ЗНАЧЕНИЕ ЗАКОНОВ НЬЮТОНА Глава 5. Силы природы § 40. ЭЛЕКТРОМАГНИТНЫЕ СИЛЫ § 41. СИЛА УПРУГОСТИ § 42. СИЛА ВСЕМИРНОГО ТЯГОТЕНИЯ § 43. ПОСТОЯННАЯ ВСЕМИРНОГО ТЯГОТЕНИЯ § 44. СИЛА ТЯЖЕСТИ § 45. ВЕС ТЕЛ § 46. ИЗМЕРЕНИЕ МАССЫ ТЕЛ ВЗВЕШИВАНИЕМ § 47. МАССА ЗЕМЛИ  СИЛА ТРЕНИЯ. ТРЕНИЕ ПОКОЯ§ 49. СИЛА ТРЕНИЯ СКОЛЬЖЕНИЯ § 50. СИЛА СОПРОТИВЛЕНИЯ, ВОЗНИКАЮЩАЯ ПРИ ДВИЖЕНИИ ТЕЛА В ЖИДКОСТИ ИЛИ В ГАЗЕ Глава 6. Применение законов движения § 51. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ УПРУГОСТИ § 52. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: НАЧАЛЬНАЯ СКОРОСТЬ ТЕЛА РАВНА НУЛЮ ИЛИ ПАРАЛЛЕЛЬНА СИЛЕ ТЯЖЕСТИ § 53. ВЕС ТЕЛА, ДВИЖУЩЕГОСЯ С УСКОРЕНИЕМ § 54. НЕВЕСОМОСТЬ § 55. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ПОД УГЛОМ К ГОРИЗОНТУ § 56. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ГОРИЗОНТАЛЬНО § 57. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ПЕРВАЯ КОСМИЧЕСКАЯ СКОРОСТЬ § 59. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ ТРЕНИЯ § 60. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ НЕСКОЛЬКИХ СИЛ § 61. ПАДЕНИЕ ТЕЛА В ГАЗЕ ИЛИ В ЖИДКОСТИ § 62. НАКЛОН ТЕЛ ПРИ ДВИЖЕНИИ НА ПОВОРОТАХ § 63. ПРИ КАКИХ УСЛОВИЯХ ТЕЛА ДВИЖУТСЯ ПОСТУПАТЕЛЬНО? ЦЕНТР МАСС И ЦЕНТР ТЯЖЕСТИ § 64. ВСЕГДА ЛИ ВЕРНЫ ЗАКОНЫ МЕХАНИКИ НЬЮТОНА Равновесие тел Глава 7.  Элементы статики§ 65. РАВНОВЕСИЕ ТЕЛ ПРИ ОТСУТСТВИИ ВРАЩЕНИЯ § 66. РАВНОВЕСИЕ ТЕЛА С ЗАКРЕПЛЕННОЙ ОСЬЮ. МОМЕНТ СИЛЫ § 67. ПРАВИЛО МОМЕНТОВ § 68. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ ТЕЛ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ § 69. РАВНОВЕСИЕ ТЕЛ НА ОПОРАХ Глава 8. Закон сохранения импульса § 70. СИЛА И ИМПУЛЬС § 71. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА § 72. РЕАКТИВНОЕ ДВИЖЕНИЕ Глава 9. Механическая работа и мощность § 74. ПОЧЕМУ РАБОТА ОПРЕДЕЛЯЕТСЯ КАК ПРОИЗВЕДЕНИЕ § 75. БОЛЕЕ ОБЩЕЕ ОПРЕДЕЛЕНИЕ РАБОТЫ § 76. РАБОТА, СОВЕРШАЕМАЯ СИЛАМИ, РАВНОДЕЙСТВУЮЩАЯ КОТОРЫХ НЕ РАВНА НУЛЮ. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ § 77. РАБОТА СИЛЫ ТЯЖЕСТИ § 78. РАБОТА СИЛЫ УПРУГОСТИ § 79. РАБОТА СИЛЫ ТРЕНИЯ § 80. МОЩНОСТЬ Глава 10. Закон сохранения энергии § 82. РАБОТА ТЕЛА И ИЗМЕНЕНИЕ ЕГО СОСТОЯНИЯ. ПОНЯТИЕ ОБ ЭНЕРГИИ § 83. ПОТЕНЦИАЛЬНАЯ И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ § 84. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГО ДЕФОРМИРОВАННОГО ТЕЛА § 36.  КИНЕТИЧЕСКАЯ ЭНЕРГИЯ§ 87. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ § 88. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ И СИЛА ТРЕНИЯ § 89. ПРЕВРАЩЕНИЕ ЭНЕРГИИ И ИСПОЛЬЗОВАНИЕ МАШИН § 90. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ § 91. СТОЛКНОВЕНИЕ ТЕЛ § 92. ДВИЖЕНИЕ ЖИДКОСТИ ПО ТРУБАМ. ЗАКОН БЕРНУЛЛИ § 93. О ЗНАЧЕНИИ ЗАКОНОВ СОХРАНЕНИЯ Заключение Лабораторные работы 1. Определение ускорения тела при равноускоренном движении 2. Определение коэффициента трения скольжения 3. Изучение движения тела по параболе 5. Определение центра тяжести плоской пластины Ответы к упражнениям |
7. Перемещением точки за промежуток времени называется вектор, проведенный из начального положения точки (в момент времени) в ее конечное положение ( в момент времени).
Если
точка совершает последовательно два
перемещения
и,
торезультирующее
перемещение равно векторной сумме (рис.
1.3):
Вектор перемещения направлен вдоль хорды, стягивающей соответствующий участок траектории точки, из положения движущейся точки в момент времени в её положение в момент времени. Поэтому во всех случаях, кроме прямолинейного движения точки, модуль вектора перемещения меньше длины пути точки за тот же самый промежуток времени.
1.2.Скорость
1. В физике под скоростью понимают векторную величину, характеризующую быстроту перемещения материальной точки по траектории и направление движения в каждый момент времени.
Разобьем траекторию на бесконечно малые участки длины(рис.1.4), каждому из этих участков сопоставим бесконечно малое перемещение.
Разделив это перемещение на соответствующий промежуток времени , получиммгновенную скорость в данной точке траектории:
. (1.3)
Таким
образом,
скорость есть первая производная
радиус-вектора точки по времени.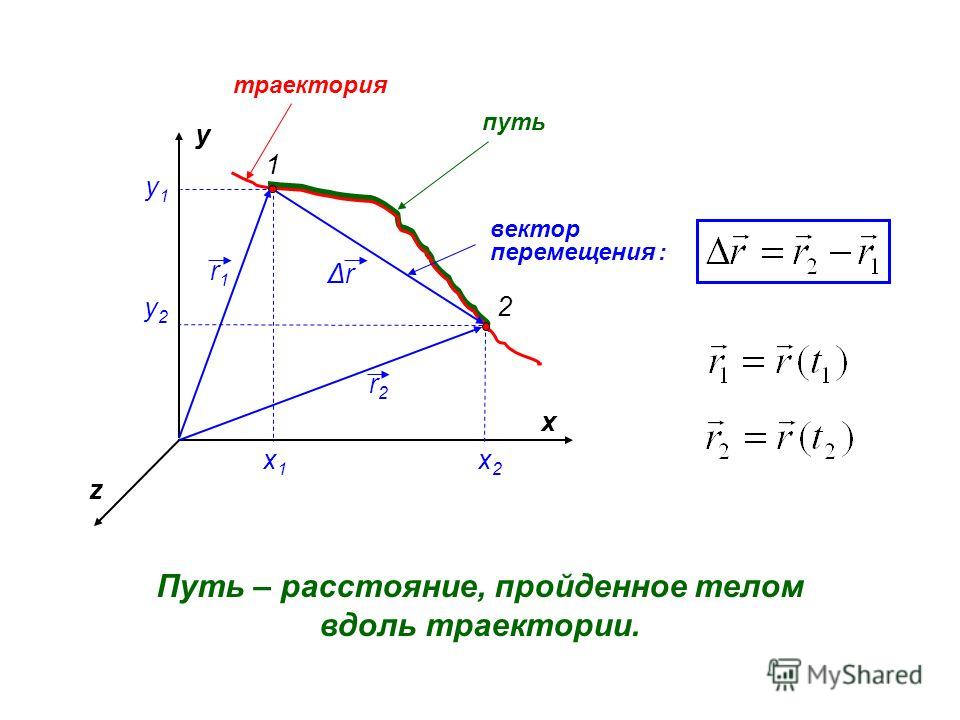
Перемещение совпадает с бесконечно малым элементом траектории, следовательно вектор направлен по касательной к траектории ( рис.1.4).
Разложив вектор скорости по базису системы координат, получаем:
,
где проекции вектора на координатные оси :
Модуль вектора скорости равен:
.
Средней скоростью точки в промежутке времени от t до t +Δt называется вектор , равный отношению приращения Δr радиуса-вектора точки за этот промежуток времени к его продолжительности Δt:
Средняя скорость направлена также как и вектор перемещения , т. е. вдоль хорды, стягивающей соответствующий участок траектории.
2.
Движение называется равномерным, если вектор
скорости остается постоянным по величине
и направлению.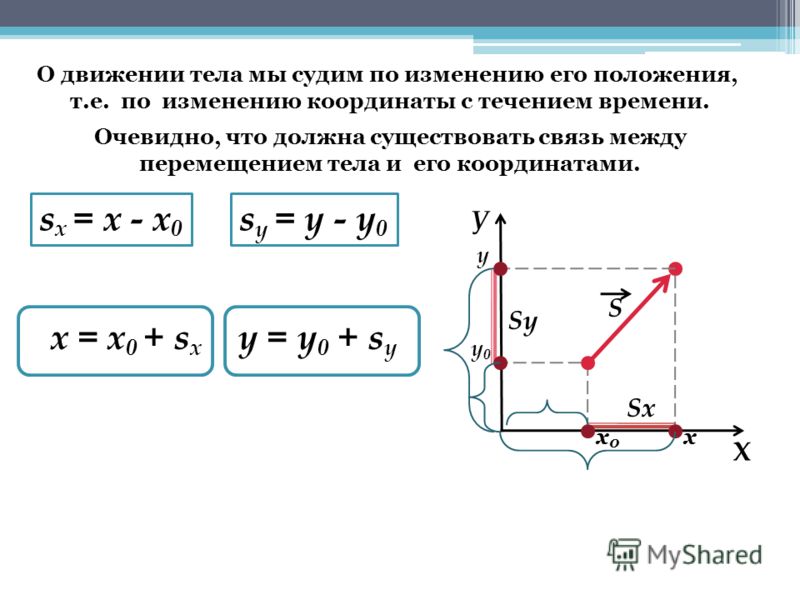
В противном случае говорят о переменном движении.
В соответствии с формулой (1.3), элементарное перемещение материальной точки :
.
Тогда перемещение из положения 1 в положение 2 (рис.1.2) равно интегралу:
Пройденный путь определяется выражением:
.
Если точка движется равномерно и прямолинейно со скоростью вдоль оси ОХ, то зависимость координаты от времени имеет вид:
3. Если модуль вектора скорости точки изменяется с течением времени, то такое движение точки называется неравномерным.
Среднее значение модуля скорости за время от до равно:
Средний вектор скорости : .
1.3.Ускорение
1. Быстрота изменения вектора скорости называетсяускорением материальной точки и определяется производной вектора по времени:
.
Cпроектируем это выражение на координатные оси:
.
Подставив в формулу (1.5) выражение (1.4), получаем:
.
Продифференцировав, имеем:
.
Следовательно, вектор можно представить в виде суммы двух взаимно перпендикулярных составляющих(рис.1.6).
Первая направлена по касательной к траекториии называетсятангенциальным или касательным ускорением:
. (1.6)
Вторая составляющая направлена по , т.е. перпендикулярно касательной, по нормали к траектории, и называется нормальным ускорением:
.
Исследуем
свойства обеих составляющих, ограничившись
случаем плоского движения.
1) тангенциальное ускорение точки характеризует быстроту изменения модуля её скорости
Модуль тангенциального ускорения, как следует из (1.6), равен .
Если (скорость растет по величине), вектор направлен в ту же сторону, что и( т.е. в ту же сторону, что и), проекция ускорения на направление скорости положительная величина – ускоренное движение.
Если (скорость со временем уменьшается), векторы инаправлены противоположно, проекция ускорения на направление скорости отрицательная величина – замедленное движение.
При равнопеременном движении .
Равноускоренное движение >0, равнозамедленное – <0
2) Нормальное
ускорение определяется величиной
,
характеризует быстроту изменения
направления вектора скорости точек.
Эта быстрота будет тем больше, чем сильнее искривлена траектория и чем быстрее перемещается частица по траектории.
Направлено всегда к центру кривизны траектории.
При равномерном движении точки по окружности , но векторизменяется, так как направление векторовв разных точках окружности разные.
2.Степень искривления плоской кривой характеризуется кривизной С, которая определяется выражением
где –угол между касательными к кривой в точках, отстоящих друг от друга на расстояние(рис.1.7).
Таким образом, кривизна определяет скорость поворота касательной при перемещении вдоль кривой.
Величина, обратная кривизне С, называется радиусом кривизны в данной точке
Радиус
кривизныпредставляет
собой радиус окружности, которая
сливается в данном месте с кривой на
бесконечно малом ее участке.
Центр такой окружности называется центром кривизны для данной точки кривой.
Радиус и центр кривизны в точке 1 (рис.1.7) определим следующим образом.
– Возьмем вблизи точки 1 точку 1.
– Построим в этих точках касательные и, перпендикуляры к которым пересекутся в некоторой точкеО. При этом для кривой, не являющейся окружностью, расстояния и несколько отличаются друг от друга.
– Если точку 1 приближать к точке 1, пересечение перпендикуляров O будет перемещаться вдоль прямой и в пределе окажется в некоторой точке О. Эта точка и будет центром кривизны для точки 1.
– Расстояния R и R будут стремиться к общему пределу , равному радиусу кривизны.
Как известно из математики, (1.7)
Здесь
– орт нормали к траектории, направленный
в сторону поворота векторапри движении частицы по траектории.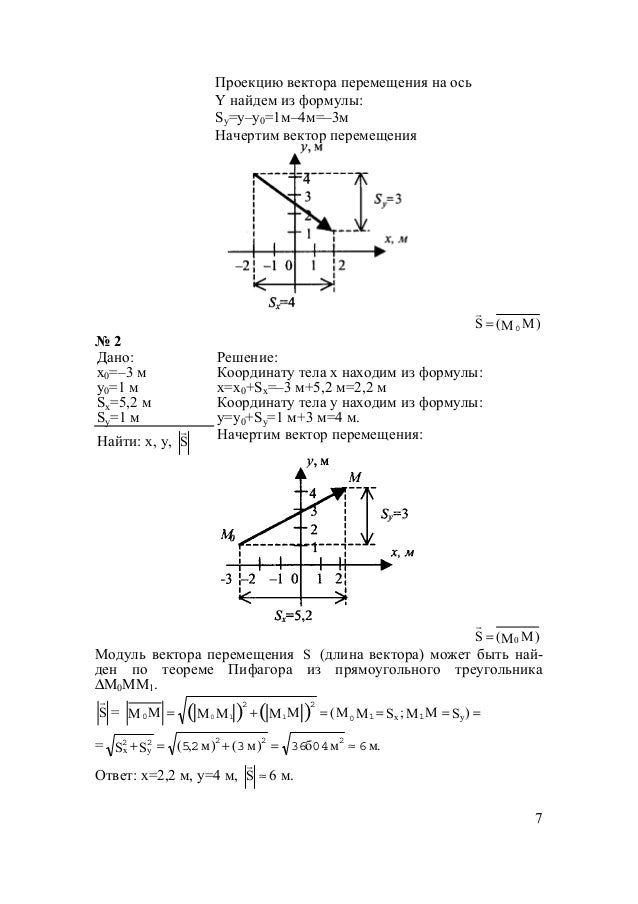
Величину можно связать с радиусом кривизны траектории и скоростью частицы.
Из рис. 1.7 следует, что
где – угол поворота вектораза время(совпадающий с углом между перпендикулярами и ),
– средняя скорость на пути .
Отсюда .
В пределе при 0 приближенное равенство станет строгим, средняя скорость превратится в мгновенную скоростьв точке 1,- в радиус кривизны .
В результате получится равенство (1.8)
– быстрота поворота вектора скорости пропорциональна кривизне траектории и скорости перемещения частицы по траектории.
Подставив (1.7) в формулу (1.8), получим ,
тогда нормальное ускорение равно .
Видео: Векторы смещения | Nagwa
Стенограмма видео
В этом видео мы узнаем
о векторах смещения.
Что это такое и как рассчитать
их как графически, так и алгебраически. Для начала представьте, что вы
участие в охоте на соседей. Где, имея список подсказок, вы
перемещайтесь из одного места в другое, пока не доберетесь до последней подсказки и последней
место, где заканчивается игра. Каждый участник начинает с базы
дерева в юго-западном углу города. И подсказка за подсказкой, вы перемещаетесь по
конечно, пока, наконец, в конце вы не получите самую последнюю подсказку и не сможете найти
последнее место. Так же, как вы завершаете
конечно, ваш друг говорит вам, что они начинают на курсе
начало. Если вы хотите подарить им
направление, в котором они могли бы идти прямо к конечной точке, где вы сейчас находитесь, что
ты бы им сказал? Это векторы смещения, которые
помогите нам понять эту мысль более ясно.
Первое, что мы можем захотеть
понять с этой темы, что такое вектор смещения? И чтобы понять это, давайте посмотрим
в одном на графике. Давайте представим, что эта 𝑥𝑦 пара
осей кладется на столешницу. А потом муравей сидит на этом
столешницу в исходное заданное положение. Исходя из этой системы отсчета,
Начальная позиция муравья, которую мы можем назвать 𝑝 sub one, задается вектором
от источника до местонахождения муравья. Скажите, что затем муравей начинает
двигаться. И пройдя путь за
какое-то время оказывается во второй позиции, которую мы можем назвать 𝑝 sub two. Если бы мы взяли эти два
векторы положения и вычесть первое из второго, тогда результатом будет
вектор, который мы можем назвать 𝑑. Это смещение,
муравей. Графически 𝑑 представляет собой вектор, который
начинается в конце нашего первого вектора положения и заканчивается в точке или кончике
наш последний вектор положения.
Отсюда мы понимаем, что векторы смещения соединяют векторы начального положения с конечным положением векторы. Он показывает изменение в позиция. В этом примере мы нашли вектор смещения 𝑑 с использованием графического подхода. Мы соединили кончик вектор начального положения с вершиной вектора конечного положения. Также можно решить для 𝑑 используя алгебраический подход, где 𝑝 второстепенные два и 𝑝 второстепенные даны в их компонентная форма. Чтобы получить некоторую практику с этим метод решения для смещения, давайте рассмотрим пример.
F-35B укороченный взлет и
истребитель с вертикальной посадкой. F-35B взлетает вертикально
вверх на высоту 20,00 метров, все еще глядя горизонтально. Затем истребитель следует за полетом
путь под углом 30,00 градусов над линией, параллельной земле, 20,00
метров по вертикали над землей.
Истребитель летит на расстояние
20,00 километров по этой траектории. Что такое финал бойца
смещение?
Мы можем назвать смещение
истребитель после этих маневров 𝑑, где мы понимаем, что 𝑑 вектор с обоими
величину и направление. Чтобы начать с нашего решения, давайте
нарисуйте эскиз движения этого F-35B. Нам говорят, что реактивный истребитель
поднимается вертикально на расстояние, которое мы назвали ℎ в 20,00 метров. А потом начинает двигаться под углом
30,00 градусов к горизонту на пути длиной 20,00 километров. Водоизмещение истребителя 𝑑 составляет
вектор, который соединяет его начальное местоположение на земле с его конечным местоположением
в конце своего 20-километрового этапа. Это тот вектор, который мы хотим
решить на основе этой данной информации. Мы можем начать с ориентации
движение нашего истребителя относительно множества координатных осей.
Разместим пару 𝑥- и
𝑦-оси координат так, чтобы их начало, место их пересечения, было местом
где наш реактивный истребитель начал свой путь. Это означает, что мы можем написать наш
вектор смещения 𝑑 в следующем виде. Компонент, назовем его 𝑑 sub
𝑥, в 𝑖-направлении плюс компонент, назовем его 𝑑 sub 𝑦, в
𝑗-направление.
Итак, теперь наша задача состоит в том, чтобы установить и
решить для 𝑑 sub 𝑥 и 𝑑 sub 𝑦. Глядя сначала на 𝑑 sub 𝑥, мы видим
что эта величина, 𝑥-составляющая движения реактивного истребителя, будет равна 𝑙
умножить на cos 30,00 градусов. Мы знаем, что 𝑙 задается как 20.00
километров или 20,00 умножить на 10 до третьего метра. Когда мы умножаем это на cos
30,00 градусов, мы находим значение 1,732 умножить на 10 до четвертого метра. Это 𝑑 саб 𝑥. Теперь мы хотим решить для 𝑑 sub 𝑦,
вертикальное перемещение реактивного истребителя.
Глядя на нашу схему, мы видим, что
𝑑 sub 𝑦 равно ℎ плюс 𝑙, умноженное на грех 30,00 градусов. Подключив ℎ и 𝑙, мы однажды
снова используйте значение 20,00 умножить на 10 до третьего метра для 𝑙. И ℎ, мы даны как 20.00
метров. С этими значениями, введенными на нашем
калькулятор, мы находим, что 𝑑 sub 𝑦 с точностью до четырех значащих цифр равно 1,002 умножить на 10.
до четвертого метра. Мы вставляем это значение для 𝑑 sub 𝑦
в нашем выражении для смещения, 𝑑. И это дает нам окончательную форму
для водоизмещения реактивного истребителя, 1,732 раза 10 до четвертого метра в
𝑖-направлении и 1,002 умножить на 10 до четвертого метра в 𝑗-направлении.
Теперь посмотрим на другой пример вектора смещения, где мы найдем величину смещения, а также направление.
Курьер начинает на почте
офис, проехать 40 км на север, затем 20 км на запад, затем 60 км
северо-восток и, наконец, 50 километров на север, чтобы остановиться на обед.
Найдите величину доставки
вектор смещения человека. Дайте ответ с точностью до
три значащие цифры. Найдите угол к северу от востока, сделанный
по вектору чистого смещения курьера. Дайте ответ с точностью до
две значащие цифры.
В этом упражнении, состоящем из двух частей, мы хотим
решить сначала для величины чистого вектора смещения доставки
мужчина. Мы назовем эту величину
𝑑. Мы также хотим найти угол
к северу от востока, сделанному этим чистым вектором смещения. Обозначим этот угол 𝜃. Начнем с рисования эскиза
движения курьера. Начиная с наших четырех компасов
направлений — север, юг, восток и запад — мы можем позволить курьеру начать с
пересечение этих двух осей. Нам говорят, что первый этап
Путь курьера составляет 40 км на север, затем 20 км на запад, затем 60 км.
километров на северо-восток.
И, наконец, 50 километров к северу от
конечная точка пути курьера на это утро.
С намеченным путешествием
графически, как это, мы можем нарисовать наш вектор смещения 𝑑, который показывает из
от начала до конца этих четырех этапов путешествия. Мы видим, что этот вектор 𝑑 имеет
оба компонента севернее, мы можем назвать его 𝑑 суб 𝑁 на севере
направление. И компонент на восток, мы можем
назовите это 𝑑 sub 𝐸 в восточном направлении. Для решения величины
вектора смещения, мы хотим найти сам вектор смещения
первый. А для этого решим на 𝑑
суб 𝑁 и 𝑑 суб 𝐸. Начиная с 𝑑 под 𝑁, 𝑑 под 𝑁
равно сумме всех северных компонентов каждого этапа нашего путешествия. Отметив, что третья часть нашего
путешествие, в котором мы проезжаем 60 километров на северо-восток, предполагает движение на 45 градусов выше
горизонтальный.
Мы можем записать 𝑑 sub 𝑁 как 40
километров плюс 60 километров умножить на грех 45 градусов плюс 50 километров. Когда мы добавляем эти три члена
вместе мы находим значение с точностью до четырех значащих цифр 132,4 километра.
Теперь переходим к решению
восточная составляющая смещения 𝑑 sub 𝐸. Глядя на нашу схему
движения курьера, мы можем записать условия 𝑑 sub 𝐸 как отрицательные 20
км, это когда мы движемся на запад, плюс 60 км умножить на стоимость
45 градусов. Сложив эти термины вместе,
четыре значащие цифры, они равны 22,46 километра. Теперь у нас есть вектор смещения
𝑑, выписанный по его северной и восточной компонентам. Чтобы найти величину этого
вектор смещения, мы возьмем квадратный корень из 𝑑 sub 𝑁 в квадрате плюс 𝑑 sub 𝐸
в квадрате. Ввод этих значений в наш
калькулятор, до трех значащих цифр величина 𝑑 составляет 134 километра.
Это чистое водоизмещение
курьер.
Далее мы хотим найти 𝜃, который, Глядя на нашу диаграмму, это угол к северу от востока, под которым вектор смещения точки. Тангенс этого угла 𝜃 равен равно 𝑑 sub 𝑁, северной составляющей смещения, деленной на 𝑑 sub 𝐸, восточная составляющая. Если мы возьмем арктангенс обоих стороны уравнения, подставьте значения для 𝑑 sub 𝑁 и 𝑑 sub 𝐸, а затем введите это выражение на нашем калькуляторе. Мы находим, что до двух существенных цифры, 𝜃 составляет 80 градусов. Это угол к северу от востока в на которую указывает вектор смещения.
Давайте теперь подведем итог тому, что мы
узнали о векторах смещения. Векторы смещения имеют длину
или величина равна кратчайшему расстоянию между начальной точкой и концом
точка. Добавление векторов для получения сети
смещение требует разделения их по размерам, 𝑥 и 𝑦.
И векторы смещения, как и все
векторы имеют как величину или длину, так и направление. Так что в следующий раз, когда вы будете искать
кратчайший путь из 𝐴 в 𝐵, рассмотрите возможность использования вектора смещения.
Величина вектора — определение, формула
Величина векторной формулы помогает обобщить числовое значение данного вектора. Вектор имеет направление и величину. Отдельные меры вектора вдоль оси x, оси y и оси z суммируются с использованием этой величины векторной формулы. Обозначается | против |. Величина вектора всегда является положительным числом или нулем, т. е. не может быть отрицательным числом. Давайте поймем величину векторной формулы, используя несколько решенных примеров в конце.
Какова величина вектора?
Величина вектора A равна длине вектора и обозначается | А |. Это квадратный корень из суммы квадратов компонентов вектора.
Для заданного вектора с отношениями направлений по осям x, y и z величина вектора равна квадратному корню из суммы квадратов его отношений направлений. Это можно ясно понять из приведенной ниже величины векторной формулы.
Величина векторной формулы
- для вектора A = x 1 I + Y 1 J + Z 1 K , A Magnity AS AS AS AS . =√(x 1 2 + y 1 2 + z 1 2 )
- Для вектора v , когда одна из его конечных точек находится в начале координат (0,0), а другая конечная точка находится в (x, y), его величина равна: | против | =√(х 2 + у 2 )
- Для вектора v с концами в точках (x 1 , y 1 ) и (x 2 , y 2 ) его величина равна: | против | =√((х 2 – х 1 ) 2 + (у 2 – у 1 ) 2 )
Как найти модуль вектора?
Чтобы определить величину двумерного вектора по его координатам,
- Шаг 1: Определите его компоненты.
- Шаг 2: Найдите сумму квадратов каждой из его составляющих.
- Шаг 3: Извлеките квадратный корень из полученной суммы.
Таким образом,
- формула для определения величины вектора (в двумерном пространстве) v = (x, y): | против | =√(х 2 + у 2 ). Эта формула выводится из теоремы Пифагора.
- формула для определения величины вектора (в трехмерном пространстве) V = (х, у, г) это: | В | = √(х 2 + у 2 + z 2 )
Давайте посмотрим на применение формулы величины в следующем разделе.
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Запись на бесплатный пробный урок
Примеры использования формулы вектора величины
Пример 1: Используя формулу величины, найдите величину вектора с u = (2, 5)?
Решение:
Найти: Модуль данного вектора
Дано:
Вектор u = (2,5)
Используя формулу модуля,
| и | = √(x 2 + y 2 )
= √(2 2 + 5 2 )
= √(4 + 25)
4 |
и | = 5,385Ответ: Величина заданного вектора = 5,385
Пример 2: Найти модуль вектора 3 i + 4 j – 5 k .
Решение:
Найти: Модуль данного вектора
Данного вектора A = 3 i + 4 j – 5 k , 90| = √(3 2 + 4 2 + (-5) 2 ) = √(9 + 16 + 25) =√50 =5√2 Ответ: Величина заданного вектора = 5√2 Пример 3: Найти модуль вектора к
Решение:
Найти: Модуль данного вектора
Данного вектора A = 5 i – 4 j + 2 k | 90| =√(5 2 + (-4) 2 + 2 2 ) = √(25 + 16 + 4) = √45 = 3√ 5 Ответ: Величина заданного вектора = 3√5 Величина векторной формулы суммирует числовое значение для данного вектора. Часто задаваемые вопросы о2 Что такое величина векторной формулы
Величина векторной формулы?
Обозначается | против |. Величины векторных формул следующие:
Как использовать модуль векторной формулы?
Чтобы использовать величину векторной формулы, выполните шаги, указанные ниже.
- Шаг 1: Проверьте заданные параметры.
- Шаг 2: Подставьте значения в соответствующую формулу
Для вектора A = x i + y j + z k его величина равна |A| =√(х 2 + у 2 + z 2 )
Величина вектора, когда его конечная точка находится в начале координат (0,0), тогда | против | =√(x 2 + y 2 )
Начальная и конечная точки вектора находятся в определенных точках (x 1 , y 1 ) и (x 2 , y 290506) 5 затем | против | =√((x 2 – x 1 ) 2 + (y 2 – y 1 ) 2 )
Какое понятие величины вектора лежит в основе формулы?
Величина вектора относится к длине или размеру вектора.