Молекулярная физика формулы: Молекулярная физика в формулах - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Молекулярная физика и термодинамика – Формулы, теоремы, определения

Нет нужного материала?

Укажите материал, который Вы не нашли, и он будет добавлен в самое ближайшее время!

Название*:

Раздел науки:

———Математика > АрифметикаМатематика > Арифметика > Арифметические действияМатематика > Арифметика > Рациональные числаФизика > Атомная и ядерная физикаМатематика > Квадратные уравненияФизика > Колебания и волныФизика > Колебания и волны > Механические волныФизика > Колебания и волны > Механические колебанияФизика > Колебания и волны > Электромагнитные волныМатематика > ЛогарифмыФизика > МеханикаФизика > Механика > ДинамикаФизика > Механика > Импульс, энергияФизика > Механика > КинематикаФизика > Механика > Механика жидкостиФизика > Молекулярная физика и термодинамикаФизика > ОптикаГеометрия > ПланиметрияМатематика > ПределыМатематика > ПрогрессииМатематика > Прогрессии > Арифметическая прогрессияМатематика > Прогрессии > Геометрическая прогрессияМатематика > Производная функцииФизика > Специальная теория относительностиГеометрия > СтереометрияМатематика > Теория группМатематика > Теория чиселМатематика > ТригонометрияМатематика > Формулы сокращенного умноженияФизика > ЭлектричествоФизика > Электричество > МагнетизмФизика > Электричество > Переменный электрический токФизика > Электричество > Постоянный электрический токФизика > Электричество > Электрическое полеФизика > Электричество > Электронные и ионные явленияМатематика > Элементарная математика

Что такое h3O*:

Данное поле ОБЯЗАТЕЛЬНО к заполнению, чтобы убедиться, что Вы человек

показать все на одной странице

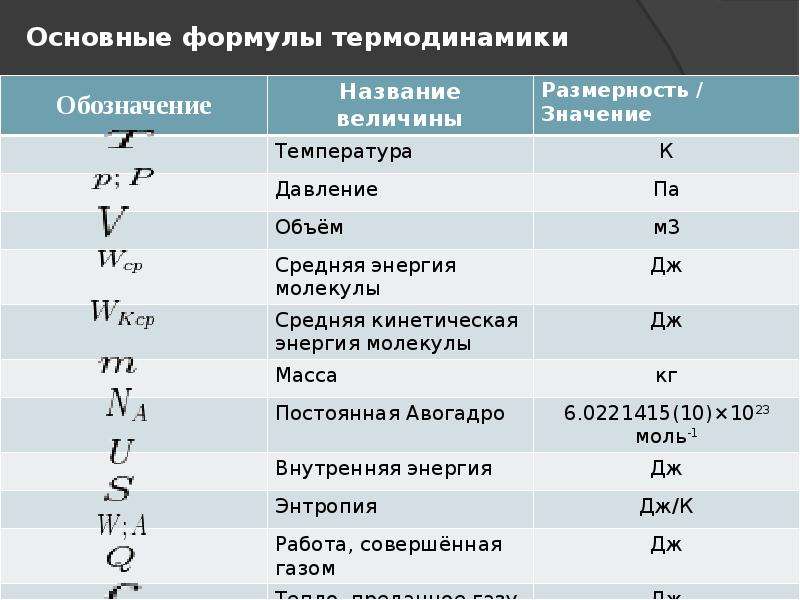
Молекулярная физика и термодинамика

Формула Первое начало термодинамики

Формула Средняя квадратичная скорость молекул

Формула Уравнение состояния идеального газа

Формула Теплоёмкость газа при постоянном объёме

Формула Теплоёмкость газа при постоянном давлении

Формула Уравнение Ван-дер-Ваальса

Формула Средняя квадратичная скорость одной молекулы

Формула Количество вещества

Формула Концентрация частиц

Формула Масса одной молекулы

Формула Внутренняя энергия идеального газа

Формула Коэффициент полезного действия теплового двигателя

Формула Коэффициент полезного действия тепловой машины Карно

Формула Основное уравнение кинетической теории газов

Формула Средняя кинетическая энергия молекулы идеального газа

Формула Универсальная газовая постоянная

Формула Суммарное давление смеси газов

Формула Работа газа в изобарном процессе

Формула Теплоемкость тела

Формула Молярная теплоемкость

Формула Удельная теплоемкость

Формула Уравнение Пуассона

Формула Относительная влажность

Формула Закон Гука

Формула Увеличение линейного размера твердого тела при нагревании

Формула Работа газа в изохорном процессе

Формула Работа газа в изотермическом процессе

Формула Работа газа в адиабатическом процессе

Формула Закон Гей-Люссака

Формула Закон Шарля

Формула Закон Бойля-Мариотта

Определение Внутренняя энергия идеального газа

Статья Определение числа степеней свободны

Определение Молярная масса

Формула Молярная масса

Определение Количество вещества

Молекулярная физика (расчетная задача) | ЕГЭ по физике

Основные положения молекулярно-кинетической теории (МКТ) заключаются в следующем.
1. Вещества состоят из атомов и молекул.
2. Атомы и молекулы находятся в непрерывном хаотическом движении.
3. Атомы и молекулы взаимодействуют между собой с силами притяжения и отталкивания
Характер движения и взаимодействия молекул может быть разным, в связи с этим принято различать 3 агрегатных состояния вещества: твёрдое, жидкое и газообразное. Наиболее сильно взаимодействие между молекулами в твёрдых телах. В них молекулы расположены в так называемых узлах кристаллической решётки, т.е. в положениях, при которых равны силы притяжения и отталкивания между молекулами. Движение молекул в твёрдых телах сводится к колебательному около этих положений равновесия. В жидкостях ситуация отличается тем, что, поколебавшись около каких-то положений равновесия, молекулы часто их меняют. В газах молекулы далеки друг от друга, поэтому силы взаимодействия между ними очень малы и молекулы движутся поступательно, изредка сталкиваясь между собой и со стенками сосуда, в котором они находятся.
Относительной молекулярной массой M_r называют отношение массы m_o молекулы к 1/12 массы атома углерода m_oc:

Количество вещества в молекулярной физике принято измерять в молях.
Молем ν называется количество вещества, в котором содержится столько же атомов или молекул (структурных единиц), сколько их содержится в 12 г углерода. Это число атомов в 12 г углерода называется числом Авогадро:

Молярная масса M = M_r · 10⁻³ кг/моль — это масса одного моля вещества. Количество молей в веществе можно рассчитать по формуле

Основное уравнение молекулярно-кинетической теории идеального газа:

где m₀ — масса молекулы; n — концентрация молекул; Ṽ — средняя квадратичная скорость движения молекул.

2.1. Газовые законы

Уравнение состояния идеального газа — уравнение Менделеева-Клапейрона:

Изотермический процесс (закон Бойля-Мариотта):
Для данной массы газа при неизменной температуре произведение давления на его объём есть величина постоянная:

В координатах p − V изотерма — гипербола, а в координатах V − T и p − T — прямые (см. рис. 4)

Изохорный процесс (закон Шарля):
Для данной массы газа при неизменном объёме отношение давления к температуре в градусах Кельвина есть величина постоянная (см. рис. 5).

Изобарный процесс (закон Гей-Люссака):
Для данной массы газа при неизменном давлении отношение объёма газа к температуре в градусах Кельвина есть величина постоянная (см. рис. 6).

Закон Дальтона:
Если в сосуде находится смесь нескольких газов, то давление смеси равно сумме парциальных давлений, т.е. тех давлений, которые каждый газ создавал бы в отсутствии остальных.

2.2. Элементы термодинамики

Внутренняя энергия тела равна сумме кинетических энергий беспорядочного движения всех молекул относительно центра масс тела и потенциальных энергий взаимодействия всех молекул друг с другом.
Внутренняя энергия идеального газа представляет собой сумму кинетических энергий беспорядочного движения его молекул; так как молекулы идеального газа не взаимодействуют друг с другом, то их потенциальная энергия обращается в нуль.
Для идеального одноатомного газа внутренняя энергия

Количеством теплоты Q называют количественную меру изменения внутренней энергии при теплообмене без совершения работы.
Удельная теплоёмкость — это количество теплоты, которое получает или отдаёт 1 кг вещества при изменении его температуры на 1 К

Работа в термодинамике:
работа при изобарном расширении газа равна произведению давления газа на изменение его объёма:

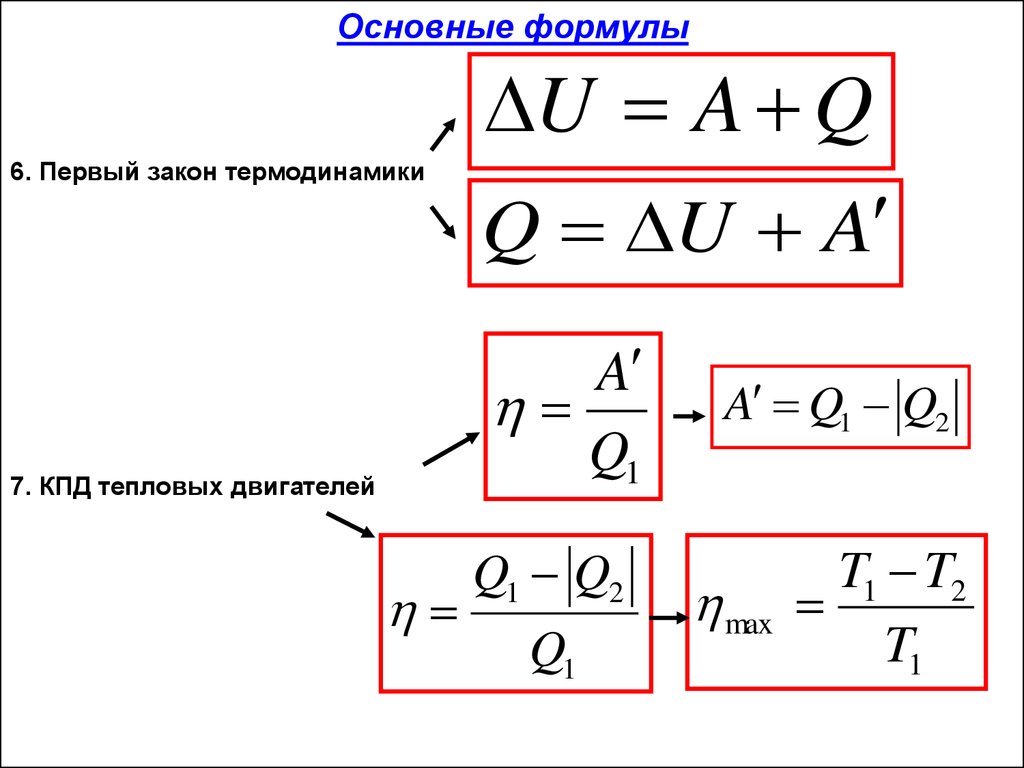
Закон сохранения энергии в тепловых процессах (первый закон термодинамики):
изменение внутренней энергии системы при переходе её из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе:

Применение первого закона термодинамики к изопроцессам:
а) изотермический процесс T = const ⇒ ∆T = 0.
В этом случае изменение внутренней энергии идеального газа

Следовательно: Q = A.
Всё переданное газу тепло расходуется на совершение им работы против внешних сил;

б) изохорный процесс V = const ⇒ ∆V = 0.
В этом случае работа газа

Следовательно, ∆U = Q.
Всё переданное газу тепло расходуется на увеличение его внутренней энергии;

в) изобарный процесс p = const ⇒ ∆p = 0.
В этом случае:

Адиабатным называется процесс, происходящий без теплообмена с окружающей средой:

В этом случае A = −∆U, т.е. изменение внутренней энергии газа происходит за счёт совершения работы газа над внешними телами.
При расширении газ совершает положительную работу. Работа A, совершаемая внешними телами над газом, отличается от работы газа только знаком:

Количество теплоты, необходимое для нагревания тела в твёрдом или жидком состоянии в пределах одного агрегатного состояния, рассчитывается по формуле

где c — удельная теплоёмкость тела, m — масса тела, t₁ — начальная температура, t₂ — конечная температура.
Количество теплоты, необходимое для плавления тела при температуре плавления, рассчитывается по формуле

где λ — удельная теплота плавления, m — масса тела.
Количество теплоты, необходимое для испарения, рассчитывается по формуле

где r — удельная теплота парообразования, m — масса тела.

Для того чтобы превратить часть этой энергии в механическую, чаще всего пользуются тепловыми двигателями. Коэффициентом полезного действия теплового двигателя называют отношение работы A, совершаемой двигателем, к количеству теплоты, полученному от нагревателя:

Французский инженер С. Карно придумал идеальную тепловую машину с идеальным газом в качестве рабочего тела. КПД такой машины

В воздухе, представляющем из себя смесь газов, наряду с другими газами находятся водяные пары. Их содержание принято характеризовать термином «влажность». Различают абсолютную и относительную влажность.
Абсолютной влажностью называют плотность водяных паров в воздухе — ρ ([ρ] = г/м³ ). Можно характеризовать абсолютную влажность парциальным давлением водяных паров — p ([p] = мм. рт. столба; Па).
Относительная влажность (ϕ) — отношение плотности водяного пара, имеющегося в воздухе, к плотности того водяного пара, который должен был бы содержаться в воздухе при этой температуре, чтобы пар был насыщенным. Можно измерять относительную влажность как отношение парциального давления водяного пара (p) к тому парциальному давлению (p₀), которое имеет насыщенный пар при этой температуре:

2.S: Кинетическая теория газов (краткое содержание)

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 10271

OpenStax
OpenStax

Ключевые термины 9{−23}Дж/К\)

критическая температура \(T_c\), в которой изотерма имеет точку с нулевым наклоном

Закон Дальтона для парциальных давлений физический закон, утверждающий, что полное давление газа равно сумме парциальных давлений составных газов

степень свободы

независимый вид движения, обладающий энергией, такой как кинетическая энергия движения в одном из трех ортогональных пространственных направлений теорема о равнораспределении Теорема о том, что энергия классической термодинамической системы распределяется поровну между ее степенями свободы идеальный газ газ на пределе низкой плотности и высокой температуры закон идеального газа физический закон, связывающий давление и объем газа вдали от сжижения с числом молекул газа или числом молей газа и температурой газа внутренняя энергия сумма механических энергий всех молекул в нем кинетическая теория газов теория, которая выводит макроскопические свойства газов из движения молекул, из которых они состоят Распределение Максвелла-Больцмана Функция, которую можно интегрировать, чтобы дать вероятность нахождения молекул идеального газа со скоростями в диапазоне между пределами интегрирования средний свободный пробег среднее расстояние между столкновениями частицы среднее свободное время среднее время между столкновениями частицы моль количество вещества, масса которого (в граммах) равна его молекулярной массе наиболее вероятная скорость скорость, вблизи которой находятся скорости большинства молекул, пик функции распределения скоростей парциальное давление давление, которое создал бы газ, если бы он занимал весь доступный объем пространства пиковая скорость то же, что и «наиболее вероятная скорость» pV-диаграмма график зависимости давления от объема среднеквадратичное значение скорости квадратный корень из среднего квадрата (количества) сверхкритические состояние жидкости при такой высокой температуре и давлении, что жидкая фаза не может существовать универсальная газовая постоянная R , постоянная, которая появляется в законе об идеальном газе, выраженная в молях, определяемая как \(R=N_Ak_B\) уравнение состояния Ван-дер-Ваальса уравнение, обычно приближенное, которое связывает давление и объем газа с числом молекул газа или числом молей газа и температурой газа

давление пара парциальное давление пара, при котором он находится в равновесии с жидкой (или твердой в случае сублимации) фазой того же вещества

Ключевые уравнения

Закон идеального газа в терминах молекул 92pv_{rms}}\)

Следующие два уравнения применимы только к одноатомному идеальному газу:

92/2k_BT}\)

Средняя кинетическая энергия молекулы	\(\bar{K}=\frac{3}{2}k_BT\)
Внутренняя энергия	\(E_{int}=\frac{3}{2}Nk_BT\).
Теплота в пересчете на молярную теплоемкость при постоянном объеме	\(Q=nCVΔT\)
Средняя скорость молекулы	\(\ bar {v} = \ sqrt {\ frac {8} {π} \ frac {k_BT} {m}} = \ sqrt {\ frac {8} {π} \ frac {RT} {M}} \)
Пиковая скорость молекулы	\(v_p=\sqrt{\frac{2k_BT}{m}}=\sqrt{\frac{2RT}{M}}\)

Резюме

2.2 Молекулярная модель идеального газа

Закон идеального газа связывает давление и объем газа с числом молекул газа и температурой газа. 9{−1}\).
- Моль любого вещества имеет массу в граммах, численно равную его молекулярной массе в единых единицах массы, которую можно определить из периодической таблицы элементов. Закон идеального газа также можно записать и решить в единицах количества молей газа:
\(pV=nRT\),
, где n число молей и R универсальная газовая постоянная,
\(R=8,31 Дж/моль⋅K\).
- Закон идеального газа, как правило, справедлив при температурах значительно выше температуры кипения.
- Уравнение состояния Ван-дер-Ваальса для газов справедливо ближе к температуре кипения, чем закон идеального газа.
- Выше критической температуры и давления для данного вещества жидкая фаза не существует, и образец является «сверхкритическим».
2.3 Давление, температура и среднеквадратичная скорость
- Кинетическая теория — это атомарное описание газов, а также жидкостей и твердых тел. Он моделирует свойства материи в терминах непрерывного случайного движения молекул. 92}\), среднее квадрата молекулярной скорости вместо температуры.
- Температура газов пропорциональна средней поступательной кинетической энергии молекул. Следовательно, типичная скорость молекул газа \(v_{rms}\) пропорциональна квадратному корню из температуры и обратно пропорциональна квадратному корню из молекулярной массы.
- В смеси газов каждый газ оказывает давление, равное общему давлению, умноженному на долю смеси, которую составляет этот газ.
- Длина свободного пробега (среднее расстояние между столкновениями) и среднее время свободного пробега молекул газа пропорциональны температуре и обратно пропорциональны молярной плотности и площади поперечного сечения молекул.
2.4 Теплоемкость и равнораспределение энергии
- Каждая степень свободы идеального газа вносит вклад \(\frac{1}{2}k_BT\) на атом или молекулу в изменения его внутренней энергии.
- Каждая степень свободы вносит вклад \(\frac{1}{2}R\) в его молярную теплоемкость при постоянном объеме \(C_V\).
- Степени свободы не вносят вклад, если температура слишком низка для возбуждения минимальной энергии степени свободы, заданной квантовой механикой. Следовательно, при обычных температурах d=3 для одноатомных газов, d=5 для двухатомных газов и d≈6 для многоатомных газов.
2.5 Распределение молекулярных скоростей
- Движение отдельных молекул в газе является случайным по величине и направлению. Однако газ из многих молекул имеет предсказуемое распределение молекулярных скоростей, известное как распределение Максвелла-Больцмана.
- Средние и наиболее вероятные скорости молекул, имеющих распределение скорости Максвелла-Больцмана, а также среднеквадратичная скорость могут быть рассчитаны по температуре и молекулярной массе.
Авторы и авторство
Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойолы Мэримаунт) и Билл Моебс со многими сотрудничающими авторами. Эта работа находится под лицензией OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Эта страница под названием 2.S: The Kinetic Theory of Gases (Summary) распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами Платформа LibreTexts; подробная история редактирования доступна по запросу.
1. Наверх
- Была ли эта статья полезной?
1. Тип изделия
  Раздел или Страница
  Автор
  ОпенСтакс
  Лицензия
  СС BY
  Версия лицензии
  4,0
  Программа OER или Publisher
  ОпенСтакс
  Показать оглавление
  нет
2. Теги
  1. source@https://openstax. org/details/books/university-physics-volume-2
Эмпирическая и молекулярная формула | Bioprofe
Эмпирическая формула является простейшим выражением для представления химического соединения. Он говорит нам о присутствующих элементах и минимальной пропорции целых чисел между их атомами. Эта формула также известна как «минимальная формула», представленная «fe».

Например:
Биопрофе | Эмпирическая и молекулярная формула | 01

Для его получения необходимо знать молекулярную массу каждого химического элемента.
Например:
- Рассчитайте эмпирическую формулу вещества, сотенный состав которого: 0,8% H; 36,5% натрия; 24,6% Р и 38,1% О.
С учетом молекулярной массы каждого вещества рассчитывается число относительных атомов каждого химического элемента:
Биопроф | Эмпирическая и молекулярная формула | 02
Если мы посмотрим, что наименьшее из всех, и приведем их к единице, мы получим:
Bioprofe | Эмпирическая и молекулярная формула | 03
Таким образом, эмпирическая формула нашего продукта: Na ₂ HPO ₃ .
Молекулярная формула – это реальная формула молекулы, состоящая из символов, обозначающих химические элементы, и некоторых индексов, указывающих на число атомов, участвующих в образовании молекулы. Он представлен «FM».
Например:
Биопрофе | Эмпирическая и молекулярная формула | 04
Когда мы хотим рассчитать молекулярную формулу (fm), помимо нахождения эмпирической формулы (fe) и его молекулярной массы (PMfe), нам необходимо знать молекулярную массу конечного соединения (PMc) и в Таким образом, мы можем применить следующие уравнения и получить молекулярную формулу.
Биопроф | Эмпирическая и молекулярная формула | 05
Например:
- Дибутилсукцинат — репеллент, используемый в домах для борьбы с насекомыми. Его состав составляет 62,58% углерода, 9,63% водорода и 27,79% кислорода. Если ваша экспериментально определенная молекулярная масса составляет 239 г/моль, рассчитайте молекулярную формулу.
Прежде всего мы должны рассчитать эмпирическую формулу, получив количество атомов каждого химического элемента:
Bioprofe | Эмпирическая и молекулярная формула | 06
Приводим все к единице и получаем количество атомов каждого элемента:
Bioprofe | Эмпирическая и молекулярная формула | 07
Эмпирическая формула соединения топа C ₃ H _5,5 O _1. Округляем нижние индексы, умножая все элементы на 2 и окончательно остается эмпирическая формула: C _{688 Н ₁₁ О ₂}
Чтобы получить молекулярную формулу, мы должны связать молекулярную массу этого (PMc) с молекулярной массой эмпирической формулы (PMfe).
Биопроф | Эмпирическая и молекулярная формула | 08
С вышеупомянутым уравнением мы связываем две молекулярные массы:
Bioprofe | Эмпирическая и молекулярная формула | 09
Наша молекулярная формула: C ₁₂ H ₂₂ O ₄ .

Как только мы определили формулу молекулы, мы можем изучить ее структуру , которая представляет собой расположение или распределение различных атомов, соединенных вместе, чтобы дать начало конечной молекуле.

Мы должны иметь в виду, что молекулы имеют пространственное расположение, они представляют собой трехмерные структуры и для их представления мы должны прибегать к молекулярным моделям, из которых наиболее известны:
- Проекция Фишера. Своим названием он обязан немецкому химику Герману Эмилю Фишеру, и в этой проекции молекула изображена в виде креста, где заместители, идущие в нижнюю часть плоскости, расположены по вертикали, а группы, идущие к нам расположены в горизонтальной линии. Точка пересечения обеих линий представляет собой атом углерода. В каждой молекуле, когда атом углерода присоединен к четырем различным заместителям, ему присваивается имя 9.0478 «Хиральный или асимметричный углерод» , и каждый хиральный углерод образует две изомерные зеркальные молекулы или энантиомеры.
  Биопроф | Эмпирическая и молекулярная формула | 10
  Эта проекция приводит к двум пространственно различным конфигурациям, которые являются «зеркальными изображениями». Это симметричные изображения относительно плоскости, но они не накладываются друг на друга, как наши правая и левая руки.
  Например, мы можем изучить случай ГЛЮКОЗЫ , молекула которой также имеет 6 атомов углерода, а четыре центральных атома представляют собой хиральный углерод.
  Биопроф | Эмпирическая и молекулярная формула | 11
- Проекция Ньюмана. Представление получается при взгляде на молекулу вдоль оси углерод-углерод, где ближайший к наблюдателю углерод нарисован точкой, от которой отходят три связи, соединяющие каждый заместитель, а углерод позади него отражен кружком из которого выходят три его заместителя.
  Биопроф | Эмпирическая и молекулярная формула | 12
  Биопроф | Эмпирическая и молекулярная формула | 13
- Проекция Хаворта. Своим названием он обязан английскому химику Уолтеру Норману Хауорту и чаще всего используется для представления углеводов с пятиугольной или гексагональной химической структурой в трехмерной перспективе.
  Наиболее часто используемыми углеводами для визуализации с помощью этой проекции являются глюкоза, галактоза или фруктоза.
  
  Биопроф | Эмпирическая и молекулярная формула | 14
Наконец, мы должны помнить, что атомы и молекулы могут быть представлены в трехмерном виде для лучшего понимания их структуры.
Если мы сравним молекулы, упомянутые выше, в нескольких уже изученных проекциях, мы увидим, какие большие изменения они претерпевают, когда мы видим их трехмерную структуру. Поэтому, чтобы действительно понять строение молекулы, лучше всего наблюдать ее со всех сторон и во всех возможных проекциях.