МОМЕНТ ИНЕРЦИИ • Большая российская энциклопедия
В книжной версии
Том 20. Москва, 2012, стр. 707
Скопировать библиографическую ссылку:
Авторы: В. А. Самсонов
МОМЕ́НТ ИНЕ́РЦИИ тела, скалярная величина, мера инертности тела при его непоступательном (вращательном) движении. Величина М. и. зависит от распределения масс в теле. В механике различают осевые и центробежные М. и. Осевым М. и. тела называется величина, определяемая формулой $J=\sum_i M_ih_i^2$, где $M_i$ – массы точек тела, $h_i$ – их расстояния от оси.
Центробежными М. и. в системе координат $Oxyz$ называются величины $$J_{xy}=\sum_iM_ix_iy_i, \quad J_{yz}=\sum_iM_iy_iz_i, \quad J_{zx}=\sum_iM_iz_ix_i,$$ служащие характеристиками динамич. неуравновешенности вращающегося тела. Напр., при вращении вокруг оси $z$ силы давления на подшипники, в которых закреплена эта ось, пропорциональны значениям $J_{yz}$ и $J_{zx}$.
Если координатные оси системы $Oxyz$ связаны с самим телом, то величины $J_x, J_y, J_z, J_{xy}, J_{yz}, J_{zx}$ постоянны. Они образуют т. н. тензор инерции тела в точке $O$. Для каждой точки тела, выбранной за начало отсчёта системы $Oxyz$, можно указать взаимно перпендикулярные оси $x,y,z$, для которых $J_{xy}=J_{yz}=J_{zx}= 0$. Такие оси называют главными осями инерции.
В динамике твёрдого тела существует спец. раздел, называемый геометрией масс, в котором рассматриваются М. 2$. М. и. тел сложной конфигурации определяются, как правило, экспериментально.
2$. М. и. тел сложной конфигурации определяются, как правило, экспериментально.
Понятие М. и. широко используется при решении мн. задач механики и техники (см. Вращающий момент, Кинетический момент, Динамика, Кинетическая энергия).
Шаговый двигатель в системе с вращающимся цилиндром
Система состоит из вертикально закрепленного на валу двигателя цилиндра массой m и моментом инерции J. Момент трения в подшипниках М тр . Определить величину вращающего момента М, который нужно приложить к цилиндрй, чтобы его угловое ускорение было равно ε.
Используемые обозначения:
r – радиус цилиндра (наружный)
r0 – радиус цилиндра (внутренний)
L – длина
m – масса цилиндра
J – момент инерции цилиндра
Jдв – момент инерции двигателя
ω – угловая скорость
Для определения крутящего момента в системе с вращающимся цилиндром, необходимо знать момент инерции цилиндра:
- Сплошной цилиндр, относительно оси a: J = 1/2 m * r

- Полый цилиндр, относительно оси a: J = 1/2 * m * (r2+r02)
Кинетическая энергия системы:
E=1/2(J+Jдв)ω2
Производная от кинетической энергии по времени:
dE/dt = (J+Jдв) ω ε
Мощности внешних сил в системе:
- мощность момента трения: Pтр=Mтрω
- сумма мощностей всех сил: ∑Pi=Mω – Mтрω
Производная кинетической энергии по времени определяется мощностями внешних сил:
- dE/dt=∑Pi или
- (J+Jдв) ω ε = Mω – Mтрω
Величина вращающего момента M:
M=(J+Jдв) ε + Mтр
определение, законы, формулы для чайников
Часто мы слышим выражения: «он инертный», «двигаться по инерции», «момент инерции».
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Что такое инерция
Согласно определению инерция в физике – это способность тел сохранять состояние покоя или движения в отсутствие действия внешних сил.
Если с самим понятием инерции все понятно на интуитивном уровне, то момент инерции – отдельный вопрос. Согласитесь, сложно представить в уме, что это такое. В этой статье Вы научитесь решать базовые задачи на тему
Определение момента инерции
Из школьного курса известно, что масса – мера инертности тела. Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.
Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.
По аналогии с массой и поступательным движением момент инерции – это мера инертности тела при вращательном движении вокруг оси.
Момент инерции
– скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр.
Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.
Это общая формула для момента инерции в физике. Для материальной точки массы m, вращающейся вокруг оси на расстоянии
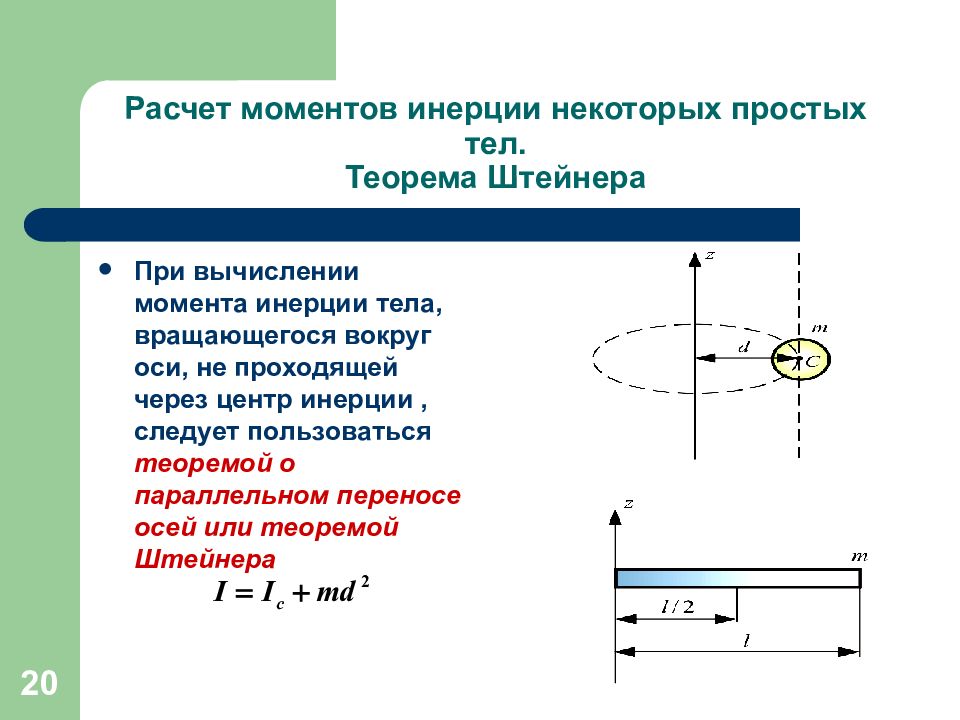
Теорема Штейнера
От чего зависит момент инерции? От массы, положения оси вращения, формы и размеров тела.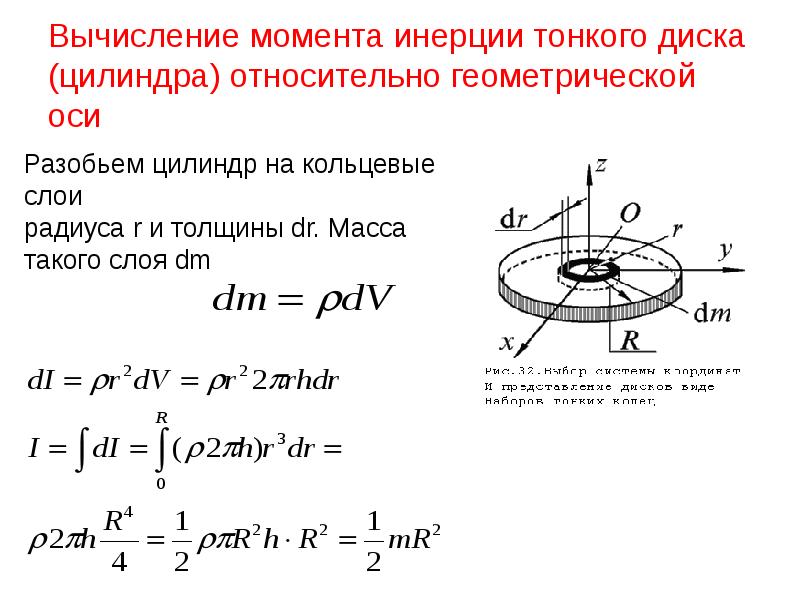
Теорема Гюйгенса-Штейнера – очень важная теорема, которую часто используют при решении задач.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Теорема Гюйгенса-Штейнера гласит:
Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.
Для тех, кто не хочет постоянно интегрировать при решении задач на нахождение момента инерции, приведем рисунок с указанием моментов инерции некоторых однородных тел, которые часто встречаются в задачах:
Пример решения задачи на нахождение момента инерции
Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.
Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.
Ось вращения проходит через центр диска.
Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от 0 до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:
Массу кольца можно представить в виде:
Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:
В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.
Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.
Решение:
Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:
Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.
Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.
Физические основы механики
Движение материальной точки характеризуется перемещением, скоростью, ускорением. Но при вращении твердого тела все его элементы имеют разные перемещения, различные скорости. Удобно найти переменные, одинаковые для всех элементов твердого тела. Мы их, собственно, уже знаем — угол поворота, угловая скорость, угловое ускорение. Соответственно, изучая динамику вращения, вместо импульса и силы мы будем оперировать их угловыми аналогами — моментом импульса и моментом силы.
Уравнение движения. В теме 4.8 было выведено уравнение движения системы материальных точек в виде
где моменты импульса и силы определялись как
Внутренние силы между телами системы, напомним, выпали из уравнений движения.
Рис. 7.1. Момент импульса L двух шаров массы m, соединенных стержнем. Вся система вращается вокруг оси z c угловой скоростью ω
Направим ось z вдоль оси вращения и выделим в твердом теле элемент массой , положение которого характеризуется радиус-вектором (рис. 7.2).
Рис. 7.2 Вращение твердого тела вокруг неподвижной оси 0z
Момент импульса этого элемента есть
Рис. 7.3. Момент импульса системы направлен вдоль оси вращения.
7.3. Момент импульса системы направлен вдоль оси вращения.
Радиус-вектор можно представить как сумму его проекций на ось z и плоскость ху :
где вектор лежит в плоскости вращения и направлен от оси к выделенному элементу (см. рис. 7.1). Имеем:
Первое слагаемое — вектор, направленный противоположно Поэтому оно не дает вклада в z-компоненту момента импульса. Второе слагаемое — вектор, направленный вдоль оси z. Так как
и
можем написать:
Суммируя по всем элементам тела, получаем
где
Величина называется моментом инерции тела.
Говоря о моменте инерции, всегда указывают, относительно какой именно оси вращения он определен (в данном случае — это ось z). Момент инерции того же тела относительно какой-то другой оси примет иное значение. Сохраняется только общее правило его вычисления: берется сумма по элементам массы, составляющим тело, умноженным на квадраты расстояний этих элементов массы до оси вращения.
В случае непрерывного распределения масс с плотностью сумма заменится на интеграл по всему объему тела:
Если тело однородно, то его плотность во всех точках постоянна и можно вынести из-под знака интеграла.
Записываем теперь уравнение движения в проекции на ось z :
Если момент инерции не зависит от времени, то дифференцировать нужно только угловую скорость, в результате получаем основное уравнение динамики вращательного движения твердого тела в виде
Производная угловой скорости по времени — это угловое ускорение
Видео 7.1. Основное уравнение динамики вращательного движения. Демонстрация, вытекающей из него связи между угловым ускорением, моментом силы и моментом инерции
Рассмотрим теперь момент внешних сил. Разложим силу на вектор в направлении оси z и вектор, ей ортогональный:
Используя снова аналогичное разложение радиус-вектора
получаем для момента внешних сил :
Первое слагаемое равно нулю. Два следующих содержат единичный орт — вектор k, направленный вдоль оси 0z и, следовательно, не дают вклада в проекцию . Оба вектора
Два следующих содержат единичный орт — вектор k, направленный вдоль оси 0z и, следовательно, не дают вклада в проекцию . Оба вектора
лежат в плоскости xy и, следовательно, последнее слагаемое направлено параллельно оси 0z. Если — угол между этими векторами, то
где — плечо силы (см. тему. 4.8). Силу
надо здесь понимать в алгебраическом смысле: она входит со знаком минус, если сила тормозит вращение.
Момент инерции. Найдем моменты инерции для простейших (геометрически правильных) форм твердого тела, масса которого равномерно распределена по объему.
Рис. 7.4. Моменты инерции различных тел
1. Момент инерции обруча относительно оси, перпендикулярной к его плоскости и проходящей через его центр.
Обруч считается бесконечно тонким, то есть толщиной обода можно пренебречь по сравнению с радиусом . Поскольку в этой системе все массы находятся на одинаковом расстоянии от оси вращения, можно вынести из-под знака интеграла:
где — полная масса обруча.
2. Момент инерции диска относительно оси, перпендикулярной его плоскости и проходящей через центр.
Диск считается бесконечно тонким, если его толщина много меньше радиуса . Момент инерции, согласно определению, величина аддитивная: момент инерции целого тела равен сумме моментов инерции его частей. Разобьем диск на бесконечно тонкие обручи радиусом и шириной (рис. 7.5).
Рис. 7.5 Вычисление момента инерции диска относительно оси z, перпендикулярной его плоскости и проходящей через центр
Площадь поверхности обруча равна произведению его длины окружности на ширину: . Поскольку масса m диска распределена равномерно, масса единицы площади равна , так что масса обруча равна
Момент инерции обруча мы уже знаем:
Осталось просуммировать моменты инерции всех таких обручей:
Такой же результат получится и для момента инерции цилиндра конечной длины относительно его продольной оси.
3. Момент инерции шара относительно его диаметра.
Поступим аналогичным образом: «нарежем» шар на бесконечно тонкие диски толщиной , находящиеся на расстоянии z от центра (рис. 7.6).
Рис. 7.6. Момент инерции шара относительно его диаметра
Радиус такого диска
Объем диска равен его площади, умноженной на толщину:
Массу диска находим, разделив массу шара на его объем и умножив на объем диска:
Момент инерции диска был найден выше. В применении к данному случаю он равен
Момент инерции шара находится интегрированием по всем таким дискам:
4. Момент инерции тонкого стержня относительно оси, проходящей через его середину перпендикулярно стержню.
Пусть стержень имеет длину . Направим ось x вдоль стержня. Начало координат по условию находится в центре стержня (рис. 7.7).
Рис. 7.7. Момент инерции тонкого стержня относительно оси, проходящей через его середину перпендикулярно стержню
7.7. Момент инерции тонкого стержня относительно оси, проходящей через его середину перпендикулярно стержню
Возьмем элемент стержня длиной , находящийся на расстоянии x от оси вращения. Его масса равна
а момент инерции
Отсюда находим момент инерции стержня:
Теорема Штейнера. В приведенных примерах оси проходят через центр масс (центр инерции) тела. Момент инерции относительно других осей вращения определяется в соответствии с теоремой Штейнера:
Рис. 7.8. К выводу теоремы Штейнера
Момент инерции тела относительно произвольной оси равен сумме момента инерции JC относительно параллельной оси, проходящей через центр инерции тела, и величины ma2 — произведения массы тела на квадрат расстояния от центра инерции тела до выбранной оси, то есть
Продемонстрируем сначала применение теоремы Штейнера. Вычислим момент инерции тонкого стержня относительно оси, проходящей через его край перпендикулярно стержню. Прямое вычисление сводится к тому же интегралу, возникшему при вычислении момента инерции стержня относительно оси, проходящей через его середину, но взятому в других пределах:
Вычислим момент инерции тонкого стержня относительно оси, проходящей через его край перпендикулярно стержню. Прямое вычисление сводится к тому же интегралу, возникшему при вычислении момента инерции стержня относительно оси, проходящей через его середину, но взятому в других пределах:
Расстояние до оси, проходящей через центр масс, равно a = l/2. По теореме Штейнера получаем тот же результат:
Вывод теоремы Штейнера иллюстрируется рис. 7.8, 7.9
Рис. 7.9. К выводу теоремы Штейнера
Пусть одна ось проходит в направлении единичного вектора n через центр масс С твердого тела (системы тел), а другая — параллельно ей через некоторую точку 0. Из центра масс в направлении второй оси проводим ортогональный осям вектор a, который определяет положение точки 0. Радиус-векторы некоторого элемента системы массой относительно точек С и 0 обозначаем и , соответственно. Момент инерции этого элемента относительно оси С есть
Момент инерции этого элемента относительно оси С есть
где — расстояние элемента от оси. По теореме Пифагора (см. рис. 7.9).
Катет равен проекции векторов и на ось вращения, то есть
Используя эти выражения и суммируя по всем элементам системы, находим момент инерции относительно оси, проходящей через точку С, и, аналогичным образом, момент инерции относительно параллельной оси, проходящей через точку 0 :
Здесь выражение для получено из простой заменой на .
Как видно из рис. 7.9, векторы и связаны между собой:
причем
так как векторы n и а ортогональны и их скалярное произведение
Тогда мы можем преобразовать выражение для :
Первое слагаемое в правой части — момент инерции относительно оси, проходящей через точку C. Третье слагаемое равно , где
— полная масса системы.
Второе слагаемое равно нулю, так как оно пропорционально радиус-вектору центра инерции относительно самого центра инерции. Окончательно:
что и требовалось доказать.
Теорема Штейнера связывает моменты инерции относительно параллельных осей. Иногда оказывается полезной другая теорема, связывающая моменты инерции относительно трех взаимно перпендикулярных осей. Однако эта теорема относится только к плоским фигурам, толщиной которых можно пренебречь по сравнению с размерами в двух других направлениях. Итак, теорема о моментах инерции плоских фигур:
Если через произвольную точку 0 плоской фигуры приведена ортогональная к фигуре ось, то момент инерции относительно этой оси равен сумме моментов инерции относительно двух взаимно перпендикулярных осей, лежащих в плоскости фигуры и проходящих через эту же точку 0.
Иными словами, берем на фигуре произвольную точку 0 и проводим координатные оси так, чтобы 0x и 0y лежали в плоскости фигуры. Тогда, согласно теореме, момент инерции относительно оси 0z равен сумме моментов инерции относительно осей 0x и 0y:
Тогда, согласно теореме, момент инерции относительно оси 0z равен сумме моментов инерции относительно осей 0x и 0y:
При этом расположение осей 0x, 0y может быть произвольным; главное, чтобы они лежали в плоскости фигуры (рис. 7.10).
Рис. 7.10. Моменты инерции плоской фигуры относительно взаимно перпендикулярных осей
Из рисунка видно, что
что и требовалось доказать.
Найдем, например, момент инерции диска относительно его диаметра. Два ортогональных диаметра диска равноправны, поэтому
Согласно теореме о плоской фигуре
откуда
Теперь можно применить теорему Штейнера, чтобы найти, например, момент инерции относительно оси , параллельной диаметру и проходящей через край диска (см. рис. 7.10):
Не удается найти страницу | Autodesk Knowledge Network
(* {{l10n_strings. REQUIRED_FIELD}})
REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}}*
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}}/500 {{l10n_strings.TAGS}} {{$item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings. LANGUAGE}}
{{$select.selected.display}}
LANGUAGE}}
{{$select.selected.display}}{{article.content_lang.display}}
{{l10n_strings.AUTHOR}}{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}III Момент инерции и момент силы.
 Момент импульса системы, закон сохранения момента импульса замкнутой системы
Момент импульса системы, закон сохранения момента импульса замкнутой системыМоментом инерции твёрдого тела относительно оси называется сумма произведений массы каждой материальной точки тела на квадрат её расстояния до оси.
Момент силы относительно оси называется скалярная физическая величина, численно равная проекции на эту ось момента силы относительно произвольной точки взятой на данной оси.
Моментом импульса относительно оси называется скалярная величина, численно равная проекции на эту ось момента импульса, относительно произвольной точки, взятой на этой оси.
Момент считается положительным, если, глядя с конца оси, мы видим поворот против часовой стрелки.
Парой
сил называются две силы равные по модулю и
противоположные по направлению, силы,
приложенные к телу.
Рассмотрим возможные случаи приложения сил:
1. Действие всех сил эквивалентно одной равнодействующей – поступательное движение.
2. Действие всех сил эквивалентно паре сил – вращательное движение.
3. Действие всех сил эквивалентно совокупности равнодействующих и паре сил – сложное движение.
Найдём момент импульса твёрдого тела.
Из основного уравнения динамики для вращательного движения.
, если
– закон сохранения момента импульса для твердого тела. Если момент внешних сил относительно неподвижной оси вращения тела тождественно равен нулю, то момент импульса тела относительно этой оси не изменяется в процессе движения.
Изменяя момент инерции можно изменить угловую скорость вращающегося тела.
Кинетическая энергия вращающегося тела.
–
кинетическая энергия вращающегося
тела.
В случае плоского движения необходимо кроме вращательного движения учитывать поступательное движение.
– кинетическая энергия плоского движения.
– скорость центра масс тела.
– момент инерции тела относительно оси проходящей через центр масс тела.
Лекция 7 Оси вращения. Условие равновесия тела
План лекции
Мгновенные оси вращения. Главные оси вращения
Условие равновесия твёрдого тела. Виды равновесия
Мгновенные оси вращения. Главные оси вращения
Плоское движение твердого тела можно представить как сумму двух движений: поступательного, со скоростью , и вращательного с угловой скоростью(цилиндр катится по плоскости без скольжения).
Систему отчета связанную с плоскостью назовем неподвижной.
Движение можно представить, как вращение с угловой скоростьюв системе отсчета, которая движется относительно неподвижной системы, поступательно со скоростью, тогда скорость произвольной точки тела при сложном движении.
Рассмотрим куб.
Элементарные перемещения твердого тела при плоском движении всегда можно представить, как поворот вокруг неподвижной оси называемой мгновенной осью вращения. Мгновенная ось вращения перемещается по боковой поверхности цилиндра со скоростью равной скорости поступательного движения его оси.
Ось, положения которой остается в пространстве неизменной при вращении вокруг нее тела в отсутствии внешних сил называется свободной осью тела.
Для тела любой формы и с произвольным распределением массы существует три взаимноперпендикулярных и проходящих через центр масс тел оси, которые могут служить свободными осями. Они называются главными осями инерции тела.
1. Моменты инерции относительно главной оси называют главными моментами инерции. В общем случае: .
2. В случае осевой симметрии: .
3. В случае центральной симметрии: .
Момент инерции и момент сопротивления
05-12-2012: Адольф СталинБыло бы неплохо объяснить на наглядном примере для особо одаренных, типа меня, что такое момент инерции и с чем его едят. На специализированных сайтах как-то всё очень запутанно, а у Дока есть явный талант довести информацию, быть может не самую сложную, но очень грамотно и понятно
05-12-2012: Доктор Лом
В принципе, что такое момент инерции и откуда он взялся, достаточно подробно объяснено в статье “Основы сопромата, расчетные формулы”, здесь лишь повторюсь: “W – это момент сопротивления поперечного сечения балки, другими словами, площадь сжимаемой или растягиваемой части сечения балки, умноженная на плечо действия равнодействующей силы”. Момент сопротивления необходимо знать для расчетов конструкции на прочность, т.е. по предельным напряжениям. Момент инерции необходимо знать для определения углов поворота поперечного сечения и прогиба (смещения) центра тяжести поперечного сечения, так как максимальные деформации возникают в самом верхнем и в самом нижнем слое изгибаемой конструкции, то определить момент инерции можно, умножив момент сопротивления на расстояние от центра тяжести сечения до верхнего или нижнего слоя, поэтому для прямоугольных сечений I=Wh/2. При определении момента инерции сечений сложных геометрических форм сначала сложная фигура разбивается на простейшие, затем определяются площади сечения этих фигур и моменты инерции простейших фигур, затем площади простейших фигур умножаются на квадрат расстояния от общего центра тяжести сечения до центра тяжести простейшей фигуры. Момент инерции простейшей фигуры в составе сложного сечения равен моменту инерции фигуры + квадрат расстояния умноженный на площадь. Затем полученные моменты инерции суммируются и получается момент инерции сложного сечения. Но это максимально упрощенные формулировки (хотя, соглашусь, все равно выглядит достаточно мудрено). Со временем напишу отдельную статью.
05-12-2012: Гиви
В принципе все предельно ясно, но здесь проще www.kataltim.ru
20-04-2013: Petr
Не нужно полностью доверять поданной в сайтах информации. Её никто по-хорошему не проверяет. И ссылки на неё не даются. Так в Таблице 1. “Формы сечения, площади сечений, моменты инерции и моменты сопротивления для конструкций достаточно простых геометрических форм” для тонкостенной трубы дается определение, что отношение диаметра к толщине оболочки должно быть больше 10. По другим источникам – должно быть больше 20!!! (Н.М. Беляев. Сопротивление материалов. М.1996. стр.160. или Н.И.Безухов. Основы теории упругости, пластичности и ползучести.М.1961.стр.390)
21-04-2013: Доктор Лом
Верно. Доверять нельзя. Но логическое мышление пока никто не отменял. Самый правильный вариант – рассчитывать момент инерции или момент сопротивления для любой трубы по формулам, приведенным для обычной трубы (на 1 пункт выше). Формулы, приводимые для тонкостенной трубы, в любом случае будут приближенными и годятся только для первичного расчета и об этом забывать нельзя.
Впрочем параметры максимально допустимой толщины стенки исправил.
25-06-2013: Саня
требуется определить момент инерции для сложного нестандартного сечения. сечение: прямоугольник с двумя пазами. внешне похоже на букву “Ш”. не получается найти какую либо информацию. буду признателен за какую нибудь информацию
25-06-2013: Доктор Лом
Посмотрите статью “Расчет прочности потолочного профиля для гипсокартона” (http://doctorlom.3)*3,14/32.
Объясните, пожалуйста, правильность этой формулы (или неправильность).
04-11-2014: Доктор Лом
Формула из приведенного вами источника неправильная (ею можно пользоваться только для приблизительных вычислений) и проверить это легко.
Чтобы определить момент инерции сечения трубы, достаточно вычесть из момента инерции стержня круглого сечения (тут при вычислениях используется наружный диаметр трубы) момент инерции отверстия (внутренний диаметр, ведь внутри трубы никакого материала нет, на то она и труба). После простейших математических преобразований мы получим формулу момента инерции трубы, приведенную в таблице.
А для того, чтобы определить момент сопротивления, нужно момент инерции разделить на максимальное расстояние от центра тяжести до самой дальней точки сечения, соответственно на D/2, или умножить на 2/D.
В итоге получить указанную вами формулу невозможно и чем толще будет стенка трубы, тем больше будет погрешность при использовании этой формулы.
04-11-2014: Радик
Спасибо, док!
11-11-2014: Ильгам
Не смог найти инфо о том в каких единицах (мм, см, м) все значения в формулах.
Попробовал посчитать Wz для уголка 210х90мм (если у швел.24П срезать верхнюю полку), получилось 667,5 см3, при условии что все значения в см.
Для примера, у швел.24П (до срезания полки) Wx(Wz)=243 см3.
11-11-2014: Доктор Лом
Это общие формулы. В каких единицах подставите значения, в таких и получите результат, только само собой уже в кубических. Но если начали подставлять, например, в сантиметрах, то так и нужно продолжать.
У швеллера без полки момент сопротивления по умолчанию не может быть больше чем у целого швеллера. Для приблизительного определения момента сопротивления швеллера без полки вы можете воспользоваться формулами для неравнополочного уголка (только для определения Wz, для Wy эти формулы не подойдут).
04-01-2015: Valerij
Если сечение трубы ослаблено несколькими значительными отверстиями, как учесть это при расчёте момента инерции и момента сопротивления? Труба 32.39см и в ней 9 отв. диам.2.8см в сечении(шаг отвермтий 10см. по длине трубы).
05-01-2015: Доктор Лом
Для определения момента инерции вам нужно вычесть из момента инерции трубы момент инерции вашего отверстия. Для этого нужно определить площадь сечения отверстия и затем умножить ее на квадрат расстояния до центра трубы плюс собственный момент инерции отверстия. Больше подробностей в статье “Моменты инерции поперечных сечений”.
Если расчет не требует особой точности и диаметр отверстия в 5 и более раз меньше диаметра трубы (вроде ваш случай, если 32.39 – это наружный диаметр), то сегмент отверстия можно привести к прямоугольнику. Если отверстие не сквозное, то следует дополнительно определить положение центра тяжести трубы с отверстием для того, чтобы потом вычислить новое значение момента сопротивления.
Но и это еще не все. Вам следует учесть, что возле отверстий возникают значительные локальные напряжения.
09-10-2015: Борис
Неравноплечий уголок.При вычислении Wy не y,а H-y
09-10-2015: Доктор Лом
Не пойму, о чем вы. Определение момента сопротивления относительно оси у в таблицах вообще не приводится.
09-10-2015: Борс
Для треугольников при вычислении Wzп h в квадрате.
09-10-2015: Борис
Пардон,Wz
09-10-2015: Доктор Лом
Все верно. Теперь понял, о чем вы. Более корректно было бы указать момент сопротивления для верхней и для нижней части сечения, а я указал только для нижней. Ну а при определении момента сопротивления треугольников банально пропущен квадрат.
Исправил. Спасибо за внимательность.
28-04-2016: Jama
Здравствуете! Кто может помочь о правильности расчета http://ej.kubagro.ru/2011/02/pdf/19.pdf
я не могу понят откуда значение берется момент сопротивления. Помогите пожалуйста!
28-04-2016: Доктор Лом
Что именно вам не понятно (вычитывать весь документ у меня нет времени). Если речь о балке, лежащей на упругом основании, то скорее всего балка эта имеет прямоугольное сечение (см. таблицу 1).
29-08-2016: Максим
Здравствуйте ! Имеется швеллер № 12. В верхний пояс будут вкручиваться саморезы и винты для крепления кровли. Как учесть ослабление швеллера, т.е как определить W ослабленного сечения.
29-08-2016: Доктор Лом
Если максимально упростить, то:
Сначала определяете момент инерции отверстия (для упрощения расчетов его можно принимать прямоугольным). Затем из момента инерции швеллера вычитаете момент инерции отверстия, затем делите полученный момент инерции на половину высоты швеллера и получаете момент сопротивления.
21-03-2017: игорь
здравствуйте,Сергей. я прочитал некоторые ваши статьи,очень интересно и понятно(в основном).я хотел бы рассчитать балку двутаврового сечения,но не могу найти Ix и Wx. дело в том что она не стандартная,я её буду делать сам,из дерева.можете ли вы мне помочь? я оплачу.только я не смогу оплатить электронными средствами т.к. не знаю как этим пользоваться.
21-03-2017: Доктор Лом
Игорь, я отправил вам письмо.
30-08-2017: Али
Уважаемый доктор, желаю вам всего найлучшего. Помогите пожалуйста, какими формулами нужны для подбора и проверки на прочность балку следующих сечений,:Швеллер,уголок и бульбовый профиль, имея допускаемый момент сопротивления W=58,58cm3. спасибо большое и жду вашу помощь.
31-08-2017: Доктор Лом
Посмотрите статью “Расчет стальных однопролетных балок с шарнирными опорами при изгибе согласно СП 16.2/8 почему деленная на 8 и почему иногда делим на 6 и 24 итд подскажите пожалуйста только это не понял
момент инерции | Определение, уравнение, единицы измерения и факты
Момент инерции , в физике, количественная мера инерции вращения тела, т. Е. Сопротивление тела изменению скорости вращения вокруг оси приложением. крутящего момента (крутящего момента). Ось может быть внутренней или внешней и может быть или не быть фиксированной. Момент инерции ( I ), однако, всегда указывается относительно этой оси и определяется как сумма произведений, полученных путем умножения массы каждой частицы вещества в данном теле на квадрат расстояния до нее. ось.При вычислении момента количества движения твердого тела момент инерции аналогичен массе в импульсе. Для количества движения импульс p равен массе m, умноженной на , и умноженной на скорость v ; тогда как для углового момента угловой момент L равен моменту инерции I , умноженному на угловую скорость ω.
На рисунке показаны два стальных шарика, приваренных к стержню AB , который прикреплен к стержню OQ при C .Пренебрегая массой AB и предполагая, что все частицы массой м каждого шара сосредоточены на расстоянии r от OQ , момент инерции определяется как I = 2 mr 2 .
Encyclopædia Britannica, Inc.Момент инерции является составной единицей измерения. В Международной системе (СИ) м выражается в килограммах и r в метрах, причем I (момент инерции) имеет размерность килограмм-метр квадрат.В общепринятой системе США м выражается в образцах (1 пуля = 32,2 фунта) и r в футах, при этом I выражается в единицах квадратного метра на фут.
Момент инерции любого тела, форма которого может быть описана математической формулой, обычно вычисляется с помощью интегрального исчисления. Момент инерции диска на рисунке около OQ можно аппроксимировать, разрезав его на несколько тонких концентрических колец, определив их массы, умножив массы на квадраты их расстояний от OQ и сложив их. продукты.При использовании интегрального исчисления процесс суммирования выполняется автоматически; ответ: I = ( mR 2 ) / 2. (См. Механику; крутящий момент.)
Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчасДля тела математически неописуемой формы момент инерции может быть получен экспериментально. В одной из экспериментальных процедур используется связь между периодом (временем) колебания торсионного маятника и моментом инерции подвешенной массы.Если диск на рисунке подвешен на тросе OC , закрепленном на O , он будет колебаться примерно на OC , если его скрутить и отпустить. Время одного полного колебания будет зависеть от жесткости проволоки и момента инерции диска; чем больше инерция, тем больше время.
Моменты инерции – обзор
§ 51. Многоатомные газы
Свободная энергия многоатомного газа, как и энергия двухатомного газа, может быть записана как сумма поступательной, вращательной и колебательной частей.Поступательная часть по-прежнему характеризуется значениями теплоемкости и химической постоянной
(51,1) ctr = 32, ζtr = 32log (m / 2πℏ2).
Из-за больших моментов инерции многоатомных молекул (и соответствующей малости их вращательных квантов) их вращение всегда можно трактовать классически. † Многоатомная молекула имеет три степени свободы вращения и три главных момента инерции I 1 , I 2 , I 3 , которые в целом различны; поэтому его кинетическая энергия вращения равна
(51.2) εrot = Mξ22I1 + Mη22I2 + Mζ22I3,
где ξ, η, ζ – координаты во вращающейся системе, оси которой совпадают с главными осями инерции молекулы; пока мы не будем рассматривать частный случай молекул, состоящих из коллинеарных атомов. Это выражение необходимо подставить в статистическую сумму
(51.3) Zrot = ∫′e − εrot / Tdτrot,
, где
dτrot = 1 (2πℏ) 3dMξdMηdMζdϕξdϕηdϕζ,
, а штрих, как обычно, означает, что интегрирование должно производиться только по физически различным ориентациям молекулы.
Если молекула имеет оси симметрии, вращения вокруг этих осей оставляют молекулу неизменной и сводятся к обмену идентичными атомами. Понятно, что количество физически неразличимых ориентаций молекулы равно количеству возможных различных поворотов вокруг осей симметрии, включая поворот на 360 ° (тождественное преобразование). Обозначив это число † через σ, мы можем взять интегрирование в (51.3) просто по всем ориентациям и разделить на σ.
В продукте d ϕ ξ d ϕ η d ϕ ζ трех бесконечно малых углов поворота, d ϕ ξ d ϕ η можно рассматривать как элемент телесного угла d o ζ для направлений оси ζ. Интегрирование по o ζ не зависит от интегрирования при вращениях d ϕ ζ вокруг оси ζ и дает 4π. Интегрирование по ϕ ζ дает еще 2π.Интегрируя также более M ξ , M η , M ζ от –∞ до ∞, в итоге получаем
Zrot = 8π2σ (2πℏ) 3 (2πT) 3/2 (I1I2I3) 1/2 = (2T) 3/2 (πI1I2I3) 1/2 / σℏ3.
Следовательно, свободная энергия равна
(51,4) F = −32NTlogT − NTlog (8πI1I2I3) 1 / 2σℏ3.
Таким образом, для удельной теплоемкости вращения в соответствии с § 44 мы имеем
(51,5) crot = 32,
, а химическая постоянная равна
(51,6) ζrot = log (8πI1I2I3) 1 / 2σℏ3.
Для линейной молекулы , то есть такой, в которой все атомы коллинеарны, есть, как и в двухатомной молекуле, только две вращательные степени свободы и один момент инерции I . Удельная теплоемкость вращения и химическая постоянная, как и в двухатомном газе, равны
(51,7) crot = 1, ζrot = log (2I / σℏ2),
, где σ = 1 для асимметричной молекулы (такой как NNO) и σ = 2 для молекулы, симметричной относительно ее средней точки (такой как ОСО).
Колебательная часть свободной энергии многоатомного газа вычисляется аналогично тому, как это было для двухатомного газа, приведенному выше.Единственное отличие состоит в том, что многоатомная молекула имеет не одну, а несколько колебательных степеней свободы: нелинейная молекула из n атомов явно имеет r виб = 3 n –6 колебательных степеней свободы, в то время как для линейная молекула из n атомов r виб = 3 n –5 (см. § 44). Число колебательных степеней свободы определяет количество нормальных мод колебаний молекулы, каждой из которых соответствует частота ω α (суффикс α, обозначающий нормальные моды).Следует помнить, что некоторые из частот ω α могут быть равными, и в этом случае рассматриваемая частота называется вырожденной .
В гармоническом приближении, где колебания предполагаются малыми (будут рассматриваться только температуры, для которых это так), все нормальные моды независимы, а энергия колебаний является суммой энергий отдельных мод. Таким образом, колебательная статистическая сумма представляет собой произведение статистических сумм отдельных мод, а свободная энергия F vib является суммой выражений типа (49.1):
(51,8) Fvib = NT∑αlog (1 − e − ℏωα / T).
Каждая частота появляется в этой сумме количество раз, равное ее вырождению. Аналогичные суммы получены для колебательных частей других термодинамических величин.
Каждый из нормальных режимов дает в своем собственном классическом пределе ( T ħω α ) вклад cvib (α) = 1 в удельную теплоемкость; для T больше наибольшего ħω α мы должны получить
(51.9) cvib = rvib.
Однако на практике этот предел не достигается, поскольку многоатомные молекулы обычно разлагаются при значительно более низких температурах.
Различные частоты ω α для многоатомной молекулы обычно находятся в очень широком интервале. По мере увеличения температуры различные нормальные режимы последовательно вносят вклад в удельную теплоемкость. Вследствие этого удельную теплоемкость многоатомных газов часто можно рассматривать как приблизительно постоянную в довольно широких интервалах температур.
Мы можем упомянуть возможность любопытного перехода от вибрации к вращению, примером которого является молекула этана C 2 H 6 . Эта молекула состоит из двух групп CH 3 , расположенных на определенном расстоянии друг от друга и определенным образом ориентированных друг к другу. Одно из нормальных колебаний молекулы – это «крутильное» колебание, при котором одна из групп CH 3 закручена относительно другой. По мере увеличения энергии колебаний увеличивается их амплитуда и, в конечном итоге, при достаточно высоких температурах колебание превращается в свободное вращение.Вклад этой степени свободы в удельную теплоемкость, которая составляет приблизительно 1, когда колебания полностью возбуждены, поэтому начинает уменьшаться при дальнейшем повышении температуры, асимптотически приближаясь к значению 12, типичному для вращения.
Наконец, можно упомянуть, что если молекула имеет ненулевой спин S (например, молекулы NO 2 и ClO 2 ), химическая константа включает член
(51.10) ζS = журнал (2S + 1).
ПРОБЛЕМА
Определите вращательную статистическую сумму для метана при низких температурах.
РЕШЕНИЕ
Как уже упоминалось в первом примечании к этому разделу, квантовый расчет Z rot для метана требуется при достаточно низких температурах.
Молекула CH 4 является тетраэдром типа сферической вершины, поэтому ее уровни вращения составляют are 2 J ( J + 1) / 2 I , где I – общее значение трех главных моментов инерции, а Дж – квантовое число вращения.Поскольку спин i ядра H равен 12, а спин ядра C 12 равен нулю, полный ядерный спин молекулы CH 4 может быть равен 0, 1 или 2, при этом соответствующие ядерные статистические веса равны 1, 3 или 5; см. Quantum Mechanics , § 105, Problem 5. Для любого заданного значения J существует определенное количество состояний, соответствующих значениям полного ядерного спина. В следующей таблице приведены эти числа для первых пяти значений Дж .
| Ядерное вращение | 0 | 1 | 2 |
| J = 0 | – | – | 1 |
| 1 | |||
| 2 | 2 | 1 | – |
| 3 | – | 2 | 1 |
| 4 | 2 | 2 |
Zrot = 516 + 916e − ℏ2 / IT + 2516e − 3ℏ2 / IT + 7716e − 6ℏ2 / IT + 11716e − 10ℏ2 / IT +….
Момент инерции: площадь или масса?
Момент инерции является важным параметром при определении размеров и выборе линейной системы. Но очень важно знать, какой тип инерции – планарный момент инерции или момент инерции массы – задан и как он влияет на производительность системы.
Планарный момент инерции
Планарный момент инерции (также называемый вторым моментом площади или моментом инерции площади) определяет, как точки области распределяются относительно базовой оси (обычно центральной оси) и, следовательно, ее сопротивление изгибу.Терминология для плоского момента и момента инерции массы варьируется, а иногда и перекрывается. Если неясно, какой тип момента указан, просто посмотрите на единицы измерения. Планарный момент инерции выражается длиной в четвертой степени (фут 4 , м 4 ).
I = ∫∫ x 2 d A
I = планарный момент инерции
x = расстояние до оси отсчета
d A = элемент площади
Второй момент площади может быть плоским или полярным.Полярный момент инерции описывает сопротивление объекта крутящему моменту или кручению и используется только для цилиндрических объектов. Уравнение для полярного момента инерции по существу такое же, как и для плоского момента инерции, но используемое расстояние – это расстояние до оси, параллельной поперечному сечению области.
I = ∫∫ r 2 d A
I = полярный момент инерции
r = расстояние до оси отсчета
d A = элемент площади
Планарный момент инерции поперечного сечения балки является важным фактором при расчетах прогиба балки, а также используется для расчета напряжения, вызываемого моментом в балке.В линейных системах модели отклонения балки используются для определения отклонения консольных осей в многокоординатных системах. Вал без опоры также анализируется с помощью расчетов прогиба балки.
Консольная балка с сосредоточенной нагрузкой на свободном концеP = нагрузка
l = длина балки (расстояние до груза)
E = модуль упругости
I = планарный момент инерции
Момент инерции массы
Момент инерции массы (также называемый вторым моментом массы, угловой массой или инерцией вращения) определяет крутящий момент, необходимый для создания желаемого углового ускорения вокруг оси вращения, и зависит от распределения массы объекта (т. Е.е. его форма) вокруг оси. У него такое же отношение к угловому ускорению, как у массы к линейному ускорению. Момент инерции массы, как и планарный момент, обычно обозначается «I», но в отличие от плоского момента, единицы для массового момента инерции – это квадрат массы-расстояния (снаряд-фут 2 , кгм 2 ).
Уравнение массового момента инерции для точечной массы просто:
I = mr 2
I = момент инерции массы
м = точечная масса
r = расстояние до оси вращения
Для твердого тела момент инерции массы рассчитывается путем интегрирования момента массы каждого элемента массы тела:
I = ∫ r 2 d м
I = момент инерции массы
d м = элемент массы
r = расстояние до оси вращения
При определении размеров линейных систем наиболее важным использованием момента инерции массы, вероятно, является выбор двигателя, где соотношение между инерцией нагрузки и инерцией двигателя является критическим фактором производительности.
Изображение предоставлено: wikipedia.org
5.4: Момент инерции – Physics LibreTexts
Предположим, у нас есть масса m на конце безмассовой палки длиной \ (r \), вращающейся вокруг другого конца палки. Если мы хотим увеличить скорость вращения, нам нужно применить тангенциальное ускорение на
\ [\ boldsymbol {a} _ {\ mathrm {t}} = r \ boldsymbol {\ alpha} \ nonumber \]
, для которого по второму закону движения Ньютона нам нужна сила
\ [\ boldsymbol {F} = m \ boldsymbol {a} _ {\ mathrm {t}} = \ operatorname {mr} \ boldsymbol {\ alpha}.2 \). По аналогии с массой, представляющей инерцию тела, испытывающего линейное ускорение, мы будем идентифицировать эту величину как инерцию тела, испытывающего вращательное ускорение, которое мы назовем моментом инерции и обозначим как \ (I \):
\ [\ boldsymbol {\ tau} = I \ boldsymbol {\ alpha} \ label {крутящий момент} \]
Уравнение \ ref {крутящий момент} – вращательный аналог второго закона движения Ньютона. {2} \ sigma \ mathrm {d} A = I_ {y} + I_ {x} \]
Обратите внимание, что последние две строки таблицы 5.1 (моменты инерции тонкого плоского прямоугольника) удовлетворяют теореме о параллельных осях.
2 Подобно одномерному и двумерному аналогам центра масс сплошного объекта (4.1.3), существуют одно- и двумерные аналоги \ ref {интеграл}, которые вы получаете заменой \ (\ rho \) с \ (\ lambda \) или \ (\ sigma \) и dV на dx или dA, соответственно.
Что такое момент инерции в физике?
Момент инерции объекта – это расчетная мера для твердого тела, которое совершает вращательное движение вокруг фиксированной оси: то есть, он измеряет, насколько сложно было бы изменить текущую скорость вращения объекта.Это измерение рассчитывается на основе распределения массы внутри объекта и положения оси, что означает, что один и тот же объект может иметь очень разные значения момента инерции в зависимости от местоположения и ориентации оси вращения.
Концептуально момент инерции можно рассматривать как представление сопротивления объекта изменению угловой скорости, аналогично тому, как масса представляет сопротивление изменению скорости при невращающемся движении согласно законам движения Ньютона.Расчет момента инерции определяет силу, необходимую для замедления, ускорения или остановки вращения объекта.
В Международной системе единиц (единица СИ) момент инерции равен одному килограмму на квадратный метр (кг-м 2 ). В уравнениях он обычно представлен переменной I или I P (как в показанном уравнении).
Простые примеры момента инерции
Насколько сложно повернуть конкретный объект (перемещать его по кругу относительно точки поворота)? Ответ зависит от формы объекта и от того, где сосредоточена масса объекта.Так, например, величина инерции (сопротивления изменению) довольно мала в колесе с осью посередине. Вся масса равномерно распределена вокруг точки поворота, поэтому небольшой крутящий момент на колесе в правильном направлении заставит его изменить свою скорость. Однако это намного сложнее, и измеренный момент инерции будет больше, если вы попытаетесь перевернуть то же колесо против его оси или повернуть телефонный столб.
Использование момента инерции
Момент инерции объекта, вращающегося вокруг неподвижного объекта, полезен при вычислении двух ключевых величин во вращательном движении:
Вы можете заметить, что приведенные выше уравнения очень похожи на формулы для линейной кинетической энергии и количества движения, с моментом инерции « I» вместо массы « м» и угловой скоростью « ω» вместо скорости “ v “, что еще раз демонстрирует сходство между различными концепциями вращательного движения и в более традиционных случаях линейного движения.
Расчет момента инерции
На рисунке на этой странице показано уравнение для расчета момента инерции в самом общем виде. В основном он состоит из следующих шагов:
- Измерьте расстояние r от любой частицы в объекте до оси симметрии
- Квадратное расстояние
- Умножьте этот квадрат расстояния на массу частицы
- Повторить для каждой частицы в объекте
- Сложите все эти значения
Для очень простого объекта с четко определенным количеством частиц (или компонентов, которые могут быть обработаны как частицы), можно просто выполнить вычисление этого значения методом грубой силы, как описано выше.В действительности, однако, большинство объектов настолько сложны, что это практически невозможно (хотя некоторые умные компьютерные коды могут сделать метод грубой силы довольно простым).
Вместо этого существует множество методов расчета момента инерции, которые особенно полезны. Ряд обычных объектов, таких как вращающиеся цилиндры или сферы, имеют очень четко определенные формулы момента инерции. Существуют математические средства решения проблемы и расчета момента инерции для тех объектов, которые более необычны и нерегулярны и, следовательно, представляют большую проблему.
Момент инерции | Квинтик Спортс
Q4 E Пример 14 – Момент инерции
Предлагаемое использование темы:
Математика / физика (уровень A / AS), спортивные науки (степень 1/2)
Введение
Момент инерции объекта – это показатель уровня силы, которая должна быть приложена, чтобы заставить объект или удерживать объект в движении вокруг определенной оси вращения.Момент инерции, который является производной от второго закона Ньютона, иногда называют вторым моментом массы и может быть вычислен с помощью уравнения:
I = mr²
Где:
I = момент инерции (кг м²)
m = масса (кг)
r = радиус (м) (кратчайшее расстояние от оси вращения до частицы)
Более высокие моменты инерции указывают на то, что необходимо приложить больше силы, чтобы вызвать вращение, тогда как более низкие моменты инерции означают, что необходимы только небольшие силы.Массы, находящиеся дальше от оси вращения, обладают наибольшим моментом инерции.
Угловой момент объекта, вращающегося вокруг оси, является мерой количества вращения этого объекта, когда на него не действуют внешние крутящие моменты, при этом крутящий момент определяется как момент силы и является мерой того, сколько силы необходимо, чтобы вызвать вращение объекта. Угловой момент – это постоянная величина, что означает, что он остается постоянным, если на него не действуют внешние крутящие моменты, и является произведением момента инерции, умноженного на угловую скорость.Когда тело имеет увеличенный радиус, то есть во время начальной и конечной фаз погружения, момент инерции велик, а угловая скорость мала. В положении пики радиус тела уменьшается по мере приближения каждого сегмента к оси вращения, что приводит к увеличению угловой скорости и уменьшению момента инерции. Таким образом, во время погружения угловой момент постоянен, что означает, что момент инерции обратно пропорционален угловой скорости.
Объективы
- Для поиска и анализа Момента инерции прямого и обратного пикирования.
- Для сравнения различий моментов инерции обоих погружений.
Методы
- Видео были оцифрованы и откалиброваны с помощью
Quintic
- программное обеспечение.
- Для сглаживания данных использовался фильтр Баттерворта.
- Данные были экспортированы в файл Excel, где они использовались для расчета момента инерции. Графики были подготовлены с использованием этой информации.
- Снимки сделаны.
Используемые функции программного обеспечения Quintic:
- Модуль многоточечной оцифровки
- Фильтр Баттерворта
- Калибровка
- Интерактивный график и дисплеи данных
- Экспорт данных
- Захват нескольких изображений
Результаты
моментов инерции были найдены для прыжков согнувшись назад и вперед путем вычисления суммы инерций для каждого сегмента тела.Оба погружения были выполнены одним и тем же дайвером, но моменты инерции различаются из-за расстояния каждого сегмента от оси вращения, т. Е. Бедра, различного для обоих погружений и разницы в угловой скорости во время погружений.
Дайверы всегда стремятся выполнить необходимое количество сальто и / или поворотов как можно быстрее, оставляя больше времени для подготовки к входу в воду. Для этого они должны увеличить свою угловую скорость, следовательно, уменьшить момент инерции.Это достигается путем изменения конфигурации их тела, чтобы уменьшить расстояние между центром масс каждого сегмента тела и осью вращения, таким образом, более плотное положение пикинга дает дайверу меньший момент инерции и большую угловую скорость. Когда дайвер покидает доску, на тело не действует крутящий момент. Это означает, что угловой момент сохраняется, когда на него не действует внешний крутящий момент, таким образом, когда момент инерции уменьшается, угловая скорость увеличивается, и наоборот.
Погружение разделено на 3 фазы.Первая фаза – от момента, когда ныряльщик покидает доску, до перехода в положение полной пикинга. Фаза 2 – это выполнение сальто в положении согнувшись, а заключительная фаза – выход из положения согнувшись и подготовка к входу в воду. В фазе 1, когда дайвер покидает доску, на него не действует внешний крутящий момент, поэтому угловой момент сохраняется и остается им на протяжении всего погружения. Когда ныряльщик впервые покидает доску, момент инерции велик из-за конечностей i.е. руки вытянуты и дальше от оси вращения. К концу фазы 1 дайвер принимает положение согнувшись, что означает, что все сегменты тела подтягиваются как можно ближе к оси вращения, уменьшая момент инерции и увеличивая угловую скорость. Момент инерции во второй фазе изменяется в соответствии с угловой скоростью, чтобы сохранить угловой момент. К третьей фазе момент инерции увеличивается, когда дайвер готовится войти в воду и выходит из положения согнувшись.Это связано с тем, что руки вытянуты над головой и, таким образом, находятся дальше от оси вращения, как и в исходном положении. Увеличенный момент инерции снижает угловую скорость и позволяет дайверу подготовиться к входу в воду по как можно более прямой линии, чтобы произвести минимальный всплеск.
График 1: Момент инерции во время прямого пикирования
График 1 показывает расчетный момент инерции дайвера во время пикирования вперед.График разделен на 3 фазы. На этапе 1, когда дайвер покидает доску, инерция составляет 10,25 кгм². После небольшого увеличения инерция быстро уменьшается, когда дайвер принимает положение согнувшись. В конце этой фазы момент инерции составляет 6,86 кгм². Теперь ныряльщик находится в положении полной пикировки и начинает сальто. Во время погружения инерция постоянно изменяется от 6,86 до 9,36 кгм²; это связано с различной угловой скоростью во время каждого сальто. По мере увеличения угловой скорости момент инерции уменьшается, и наоборот, следовательно, угловой момент остается постоянным на протяжении всего погружения.На заключительном этапе инерция сначала уменьшается, но когда дайвер выпрямляется; готовясь войти в воду, момент инерции начинает расти.
Рисунок 1: Пайка вперед
График 2: Момент инерции обратного пикирования
График 2 показывает момент инерции для пикирования назад. График снова разделен на 3 фазы.Первоначально на этапе 1 момент инерции составляет 11,41 кгм². Когда дайвер покинул доску, момент инерции уменьшается и продолжает уменьшаться до тех пор, пока дайвер не займет положение согнувшись в конце фазы 1. Во время второй фазы момент инерции колеблется в соответствии с уменьшающейся угловой скоростью, сохраняя угловой момент постоянная. На кадре 222 дайвер начинает готовиться к входу в воду и, таким образом, начинает выход из положения согнувшись. По мере того, как он это делает, момент инерции увеличивается и продолжает увеличиваться, поскольку дайвер полностью вытягивается, чтобы войти в воду по прямой линии.
Рисунок 2: Пика назад
График 3: Сравнение моментов инерции
График 3 показывает сравнение моментов инерции как для прямого, так и для обратного погружения согнувшись. Погружения сравнивались от кадра последнего контакта с доской до момента входа дайвера в воду. Момент инерции согнувшись вперед более изменчив в течение всего погружения, но оба прыжка по-прежнему следуют схожей схеме.Когда дайвер покидает доску, момент инерции уменьшается для обоих погружений. Прыжок назад согнувшись занимает немного больше времени, чтобы полностью снизиться, так как для достижения положения согнувшись во время пикирования назад требуется немного больше времени. Тем не менее, прыжок согнувшись назад уменьшается до более низкого момента инерции, что означает, что угловая скорость больше и что дайвер находится в более узком положении согнувшись во время согнувшись назад. В конце погружения инерция увеличивается с уменьшением угловой скорости. Пикирование согнувшись назад имеет большее увеличение инерции из-за уменьшения угловой скорости.Поскольку у ныряющего сучкой вперед была меньшая угловая скорость, при входе в воду увеличение инерции меньше.
Заключение
Момент инерции – это расчет силы, необходимой для вращения объекта. Этим значением можно управлять для увеличения или уменьшения инерции. В таких видах спорта, как катание на коньках, прыжки в воду и гимнастика, спортсмены постоянно меняют конфигурацию тела. При увеличении радиуса от оси вращения момент инерции увеличивается, тем самым замедляя скорость вращения.В качестве альтернативы, если спортсмен хочет увеличить скорость вращения, он должен уменьшить радиус, приближая сегменты тела к оси вращения, таким образом уменьшая радиус и момент инерции.
Загрузки
Письменный пример использования | Видео avi. файлы | |
| 3м назад Pike.avi ~ 3,10 МБ | 3м вперед Щука.avi ~ 3,03 МБ | |
Моменты инерции
Чтобы легко вычислить моменты инерции относительно осей через $ P $ и $ C $ проще всего выбрать система координат, выровненная с осью вращения направление $ \ hat {a} $. 2, \ конец {выровнено} \] где $ P $ имеет позицию $ (x_P, y_P, z_P) $ в этих координаты.2. \ конец {выровнено} \] Здесь мы использовали координатное представление центра массы, чтобы понять, что координата $ x $ точки $ C $ равна $ x_C = \ frac {1} {m} \ int _ {\ mathcal {B}} \ rho x \, dV $, но поскольку наши координаты отсчитываются от $ C $, мы должны имеет $ x_C = 0 $ и поэтому $ \ int _ {\ mathcal {B}} \ rho x \, dV = 0 $. Интеграл от $ \ rho y $ аналогично равен нулю.
.
