Момент инерции это в физике: Национальный исследовательский университет «Высшая школа экономики»

§21.Момент инерции.

Определение: Моментом инерции материальной точки относительно неподвижной оси называется скалярная физическая величина, являющаяся мерой инертности этой точки при вращательном движении и, равная произведению её массы на квадрат расстояния до оси, т.е. , а также, где- угловая скорость тела относительно данной оси.

Определение: Моментом инерции системы материальных точек относительно неподвижной оси называется скалярная физическая величина, являющаяся мерой инертности этой системы при вращательном движении и, равная алгебраической сумме произведений масс всех материальных точек системы на квадрат их расстояний до оси, т.е. .

Момент инерции определен только относительно оси.

В случае непрерывного распределения масс с плотностью сумма за­менится на интеграл по всему объему тела: (Интегрирование производится по всему объёму; пределы интегрирования устанавливаются исходя из конфигурации тела и его размеров).

Если тело однородно, то его плотность во всех точках постоянна и можно вынести из-под знака интеграла.

Найдем моменты инерции для простейших (геометрически правильных) форм твердого тела, масса которого равномерно распределена по объему, т.е. .

1. Момент инерции обручаотносительно оси, перпендикулярной к его плоскости и проходящей через его центр.

Обруч считается бесконечно тонким, т.е. толщиной обода можно пре­небречь по сравнению с радиусом R.. Поскольку в этой системе все массы находятся на одинаковом расстоянии от оси вращения, R²можно вынести из-под знака интеграла:, где

m— полная масса обруча.

2. Момент инерции дискаотносительно оси, перпендикулярной его плоскости и проходящей через центр. Диск считается бесконечно тонким, т.е. его толщина много меньше ра­диуса R.Момент инерции, согласно определению, величина аддитивная: момент инерции целого тела равен сумме моментов инерции его частей. Разобьем диск на бесконечно тонкие обручи радиусомsи толщинойds (См.рис.).

Момент инерции диска относительно перпендикулярной оси, проходящей через центр.

Площадь поверхности обруча равна произведению его длины на толщину:

2  s ds.Поскольку массатдиска распределена равномерна, масса обручаdmпропорциональна площади его поверхности:

.

Момент инерции обруча мы уже знаем: . Осталось просуммировать моменты инерции всех таких обручей:.

Такой же результат получится и для момента инерции цилиндра конеч­ной длины относительно его продольной оси.

3. Момент инерции шараотносительно его диаметра. Поступим аналогичным образом: “нарежем” шар на бесконечно тон­кие диски толщинойdz.находящиеся на расстоянииzот центра (См.рис.).

Момент инерции шара относительно диаметра.

Радиус такого диска равен . Объем дискаdV_z равен произведению его площади на толщину:

. Массу дискаdmнаходим, разде­лив массу шаратна его объем, умножив на объем диска:

.

Момент инерции диска был найден выше. В применении к данному слу­чаю, он равен:

.

Момент инерции шара находится интегрированием по всем таким дискам:

4.Момент инерции тонкого стержняотносительно оси, проходящей через его середину перпендикулярно стержню.

Пусть стержень имеет длину

ℓ.Направим осьxвдоль стержня. Начало координат по условию находится в центре стрежня. Возьмем эле­мент стержня длинойdx.находящийся на расстоянииxот оси враще­ния. Его масса равна

dm = (m/ℓ) dx,а момент инерцииdJ=(m/ℓ) x²  dx. Отсюда находим момент инерции стрежня:

(*).

Момент инерции величина аддитивная, т.е. суммарный момент инерции системы тел относительно какой-либо оси, равен сумме моментов инерции каждого из тел данной системы относительно той же оси:

Физический смысл момента инерции:Инерционные свойства при поступательном движении характеризуются только массой тела, т.е. зависит только от массы. Инерционные свойства при вращательном движении характеризуются моментом инерции, т.е. зависят от его массы, расстояния до оси вращения и расположению теда по отношению к этой оси. Последнее означает, что относительно двух разных осей инерционные свойства вращательного движения одного и того же движения тела будут разными. Пример.

Курс общей физики, Т.1

Курс общей физики, Т.1

Савельев И. В. Курс общей физики, т. 1. Механика. Молекулярная физика: Учебное пособие.— 2-е изд., перераб.—М.: Наука. Главная редакция физико-математической литературы, 1982.— 432 с. Книга представляет собой первый том трехтомного курса общей физики, созданного заведующим кафедрой общей физики Московского инженерно-физического института, заслуженным деятелем науки и техники РСФСР, лауреатом Государственной премии, профессором И. В. Савельевым. Главная цель книги—познакомить студентов с основными идеями и методами физики. Особое внимание обращено на разъяснение смысла физических законов и на сознательное применение их. Данный курс предназначен в первую очередь для втузов с расширенной программой по физике. Однако изложение построено так, что, опустив отдельные места, эту книгу можно использовать в качестве учебного пособия для втузов с обычной программой. Оглавление ПРЕДИСЛОВИЕ МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ВВЕДЕНИЕ ЧАСТЬ 1. ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ § 1. Механическое движение § 2. Некоторые сведения о векторах § 3. Скорость § 4. Ускорение § 5. Кинематика вращательного движения ГЛАВА II. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ § 6. Классическая механика. Границы ее применимости § 7. Первый закон Ньютона. Инерциальные системы отсчета § 8. Масса и импульс тела § 9. Второй закон Ньютона § 10. Единицы и размерности физических величин § 11. Третий закон Ньютона § 12. Принцип относительности Галилея § 13. Силы § 14. Упругие силы § 15. Силы трения. § 16, Сила тяжести и вес § 17. Практическое применение законов Ньютона ГЛАВА III. ЗАКОНЫ СОХРАНЕНИЯ § 18. Сохраняющиеся величины § 19. Кинетическая энергия § 20. Работа § 21. Консервативные силы § 22. Потенциальная энергия во внешнем поле сил § 23. Потенциальная энергия взаимодействия § 24. Закон сохранения энергии § 25. Энергия упругой деформации § 26. Условия равновесия механической системы § 27. Закон сохранения импульса § 28. Соударение двух тел § 29. Закон сохранения момента импульса § 30. Движение в центральном поле сил § 31. Задача двух тел ГЛАВА IV. НЕИНЕРЦИАЛЬНЫЕ СИСТЕМЫ ОТСЧЕТА § 32. Силы инерции § 33. Центробежная сила инерции § 34. Сила Кориолиса § 35. Законы сохранения в неинерциальных системах отсчета ГЛАВА V. МЕХАНИКА ТВЕРДОГО ТЁЛА § 36. Движение твердого тела § 37. Движение центра масс твердого тела § 38. Вращение тела вокруг неподвижной оси § 39. Момент инерции § 40. Понятие о тензоре инерции § 41. Кинетическая энергия вращающегося твердого тела § 42. Кинетическая энергия тела при плоском движении § 43. Применение закона динамики твердого тела § 44. Гироскопы ГЛАВА VI. ВСЕМИРНОЕ ТЯГОТЕНИЕ § 45. Закон всемирного тяготения § 46. Гравитационное поле § 47. Принцип эквивалентности § 48. Космические скорости ГЛАВА VII. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ § 49. Общие сведения о колебаниях § 50. Малые колебания § 51. Комплексные числа § 52. Линейные дифференциальные уравнения § 53. Гармонические колебания § 54. Маятник § 55. Векторная диаграмма § 56. Биения § 57. Сложение взаимно перпендикулярных колебаний § 58. Затухающие колебания § 59. Автоколебания § 60. Вынужденные колебания § 61. Параметрический резонанс ГЛАВА VIII. РЕЛЯТИВИСТСКАЯ МЕХАНИКА § 62. Специальная теория относительности § 63. Преобразования Лоренца § 64. Следствия из преобразований Лоренца § 65. Интервал § 66. Преобразование и сложение скоростей § 67. Релятивистское выражение для импульса § 68. Релятивистское выражение для энергии § 69. Преобразования импульса и энергии § 70. Взаимосвязь массы и энергии § 71. Частицы с нулевой массой покоя ГЛАВА IX. ГИДРОДИНАМИКА § 72. Линии и трубки тока. Неразрывность струи § 73. Уравнение Бернулли § 74. Истечение жидкости из отверстия § 75. Силы внутреннего трения § 76. 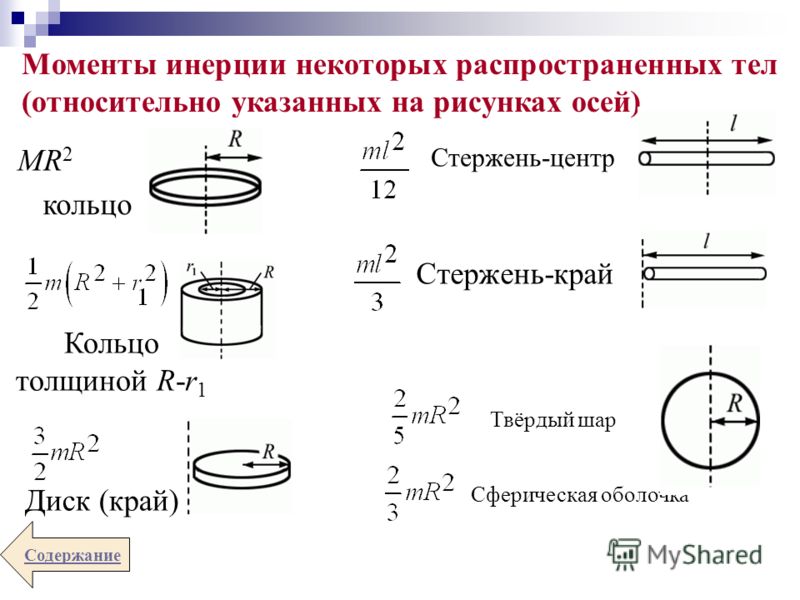Ламинарное и турбулентное течения § 77. Течение жидкости в круглой трубе § 78. Движение тел в жидкостях и газах ЧАСТЬ 2. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА § 79. Статистическая физика и термодинамика § 80. Масса и размеры молекул § 81. Состояние системы. Процесс § 82. Внутренняя энергия системы § 83. Первое начало термодинамики § 84. Работа, совершаемая телом при изменениях объема § 85. Температура § 86. Уравнение состояния идеального газа § 87. Внутренняя энергия и теплоемкость идеального газа § 88. Уравнение адиабаты идеального газа § 89. Политропические процессы § 90. Работа, совершаемая идеальным газом при различных процессах § 91. Ван-дер-ваальсовский газ § 92. Барометрическая формула ГЛАВА XI. СТАТИСТИЧЕСКАЯ ФИЗИКА § 93. Некоторые сведения из теории вероятностей § 94. Характер теплового движения молекул § 95. Число ударов молекул о стенку § 96. Давление газа на стенку § 97. Средняя энергия молекул § 98. Распределение Максвелла § 99. Экспериментальная проверка закона распределения Максвелла § 100. Распределение Больцмана § 101. Определение Перреном числа Авогадро § 102. Макро- и микросостояния. Статистический вес § 103. Энтропия ГЛАВА XII. ТЕРМОДИНАМИКА § 104. Основные законы термодинамики § 105. Цикл Карно § 106. Термодинамическая шкала температур § 107. Примеры на вычисление энтропии § 108. Некоторые применения энтропии § 109. Термодинамические потенциалы ГЛАВА XIII. КРИСТАЛЛИЧЕСКОЕ СОСТОЯНИЕ § 110. Отличительные черты кристаллического состояния § 111. Классификация кристаллов § 112. Физические типы кристаллических решеток § 113. Дефекты в кристаллах § 114. Теплоемкость кристаллов ГЛАВА XIV. ЖИДКОЕ СОСТОЯНИЕ § 115. Строение жидкостей § 116. Поверхностное натяжение § 117. Давление под изогнутой поверхностью жидкости § 118. Явления на границе жидкости и твердого тела § 119. Капиллярные явления ГЛАВА XV. ФАЗОВЫЕ РАВНОВЕСИЯ И ПРЕВРАЩЕНИЯ § 121. Испарение и конденсация § 122. Равновесие жидкости и насыщенного пара § 123. Критическое состояние § 124. Пересыщенный пар и перегретая жидкость § 125. Плавление и кристаллизация § 126. Уравнение Клапейрона—Клаузиуса § 127. Тройная точка. Диаграмма состояния ГЛАВА XVI. ФИЗИЧЕСКАЯ КИНЕТИКА § 128. Явления переноса § 129. Средняя длина свободного пробега § 130. Диффузия в газах § 131. Теплопроводность газов § 132. Вязкость газов § 133. Ультраразреженные газы § 134. Эффузия ПРИЛОЖЕНИЯ I. Вычисление некоторых интегралов II. Формула Стирлинга III. Симметричные тензоры второго ранга

2: Моменты инерции – Физика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

6938

• Джереми Татум
• Университет Виктории

В этой главе мы рассмотрим, как вычислить (секундный) момент инерции для различных размеров и форм тела, а также некоторые связанные с этим теоремы. Но следует задать вопрос: «Какова цель вычисления квадратов расстояний множества частиц от оси, умножения этих квадратов на массу каждой и сложения их всех вместе?

• 2.1: Определение момента инерции

• 2.2: Значение инерции вращения

  Если на тело действует сила, тело будет ускоряться. Отношение приложенной силы к полученному ускорению есть инерция (или масса) тела.

• 2.3: Моменты инерции некоторых простых форм

  “Для скольких различных форм тел я должен запомнить формулы для их моментов инерции?” У меня возникло бы искушение сказать: «Ничего». Однако, если какие-то из них нужно запомнить, я бы посоветовал ограничить список для запоминания теми немногими телами, которые, вероятно, будут встречаться очень часто (особенно если их можно использовать для быстрого определения моментов инерции тел). другие тела) и для которых легче запомнить формулы, чем их вывести.

• 2.4: Радиус вращения

  Второй момент инерции любого тела можно записать в виде mk², где k – радиус вращения. Если бы вся масса тела была сосредоточена на радиусе его вращения, его момент инерции остался бы прежним.

• 2.5: Плоские слои и точки массы, распределенные в плоскости

• 2.6: Трехмерные объемные фигуры. Сферы, цилиндры, конусы.

• 2.7: Трехмерные полые фигуры. Сферы, цилиндры, конусы

• 2.8: Тор

  Вращательная инерция сплошных и полых торов (большой радиус a , малый радиус b ) приведены ниже для справки и без выведения. Их можно вывести с помощью интегрального исчисления, и их вывод рекомендуется читателю в качестве задачи.

• 2.9: Линейная трехатомная молекула

• 2. 10: Маятники

  Мы знакомы с уравнением движения массы, колеблющейся на конце пружины с постоянной силой – это простое гармоническое движение. Механизм крутильного маятника аналогичен.

• 2.11: Плоские пластины. Момент продукта. Перемещение осей (Теорема о параллельных осях)

• 2.12: Вращение осей

• 2.13: Momental Ellipse

• 2,14: Собственные векторы и собственные значения

• 2.15: Сплошное тело

• 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 :15: 3. найти набор осей, относительно которых все моменты произведения F, G и H равны нулю, эти оси называются главными осями тела, а моменты инерции относительно этих осей являются главными моментами инерции.

• 2.17: Вращение твердого тела и тензор инерции

  Предполагается, что эта глава должна быть ограничена расчетом моментов инерции тел различной формы, а не огромным предметом динамики вращения твердых тел, которая требует отдельной главы. В этом разделе я упоминаю только для интереса две небольшие темы, связанные с главными осями.

• 2.18: Определение главных осей

  Главные оси — это три взаимно перпендикулярные оси тела, относительно которых момент инерции максимален.

• 2.19: Момент инерции относительно точки

  Под «моментом инерции» мы до сих пор подразумевали второй момент массы относительно оси. Мы легко смогли отождествить его с инерцией вращения относительно оси, а именно с отношением приложенного крутящего момента к результирующему угловому ускорению.

• 2.20: Эллипсы и эллипсоиды

• 2.21: Тетраэдры

  Твердые правильные тетраэдры и эллипсоиды являются точками вращения относительно одной и той же оси молекулы метана, масса.

Миниатюра: Момент инерции тонкого стержня относительно оси, перпендикулярной длине стержня и проходящей через его центр. (Общественное достояние; Кришнаведала).

---

Эта страница под названием 2: Moments of Inertia распространяется под лицензией CC BY-NC 4.0 и была создана, изменена и/или курирована Джереми Татумом посредством исходного контента, отредактированного в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Глава

   Автор

   Джереми Татум

   Лицензия

   CC BY-NC

   Версия лицензии

   4,0

   Показать оглавление

   нет

2. Теги

   1. источник@http://orca. phys.uvic.ca/~tatum/classmechs.html

Демонстрация инерции вращения (или момента инерции)

Предыдущее видео

Конспект лекций

Поддерживать

Следующее видео

Спасибо Arbor Scientific за то, что позволили мне одолжить демонстратор инерции вращения, чтобы… ммм… продемонстрировать инерцию вращения. Это тема AP Physics 1. Содержание Время: 0:22 Демонстратор инерции вращения 0:58 Инерция вращения 1:40 Демонстрация #1 2:00 Демонстрация #2 2:55 Почему всегда сбалансирован? 4:30 Демонстрация №3 5:27 Демонстрация №4

Многоязычный? Пожалуйста, помогите перевести видео Flipping Physics! Пожалуйста, поддержите меня на Патреоне! Спасибо Скотту Картеру, Кристоферу Бекке, Джонатану Эверетту и Файазу Рахману за участие в моей команде контроля качества для этого видео. Спасибо Джонатану Салливану-Вуду за расшифровку английских субтитров к этому видео.

Вы когда-нибудь пытались описать своим ученикам вращательную инерцию? Хуже того, вы когда-нибудь пытались понять вращательную инерцию самостоятельно. (Я знаю, что знаю. 😇) Знаете ли вы, что инерция вращения — это то же самое, что и момент инерции? Да, я с тобой там. Я не знал, что имя было изменено до недавнего времени. Тем не менее, я думаю, что «Инерция вращения» — более логичная фраза, чем «Момент инерции». Что ж, если вам нужна помощь с концепцией инерции вращения, то я настоятельно рекомендую Демонстратор инерции вращения от Arbor Scientific, потому что это простой способ продемонстрировать концепцию инерции вращения. Демонстратор состоит из трех шкивов разного размера, центрированных вокруг одной оси. К шкивам прикреплены четыре спицы, на которых можно разместить четыре груза. Расстояние от оси или оси вращения четырех масс на спицах можно регулировать.

Чтобы понять инерцию вращения, мы должны сначала рассмотреть уравнение для инерции вращения системы частиц:

Вращательная инерция системы частиц равна сумме количества массы каждой частицы, умноженной на квадрат расстояния, на котором каждая частица находится от оси вращения. Хотя демонстратор инерции вращения не является системой частиц, уравнение для инерции вращения системы частиц помогает нам понять, как изменяется инерция вращения демонстратора, когда мы корректируем положение четырех регулируемых масс. Чем ближе четыре регулируемые массы находятся к оси или оси вращения, тем меньше значение «r» в уравнении инерции вращения и тем меньше инерция вращения демонстратора.
 
Нам также необходимо рассмотреть форму вращения второго закона Ньютона, чтобы лучше понять инерцию вращения. Чистый крутящий момент, действующий на объект, равен произведению инерции вращения объекта на угловое ускорение объекта. Пожалуйста, помните, что крутящий момент и угловое ускорение являются векторами.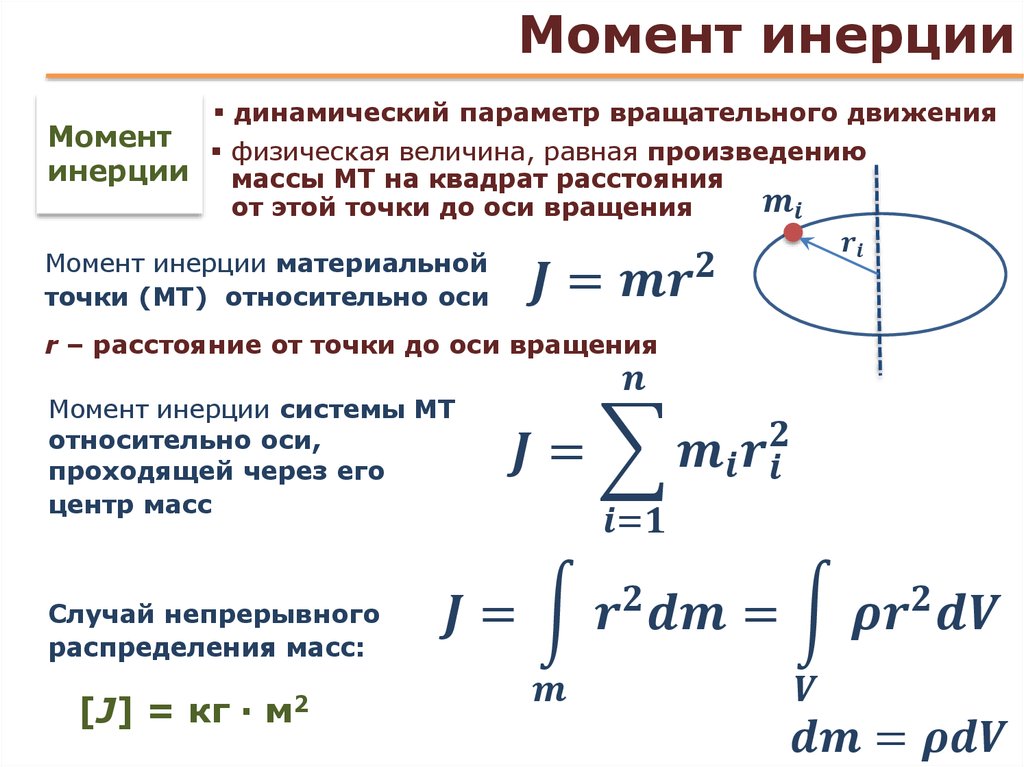

Обратите внимание на сходство с поступательной формой второго закона движения Ньютона. Суммарная сила, действующая на объект, равна произведению инерционной массы объекта на линейное ускорение объекта. Опять же, помните, что сила и линейное ускорение являются векторами.

Сила — это способность вызывать линейное ускорение объекта.
Крутящий момент — это способность силы вызывать угловое ускорение объекта.
 
Крутящий момент — это вращательный эквивалент силы.
Инерция вращения является вращательным эквивалентом инерционной массы.
Угловое ускорение является вращательным эквивалентом линейного ускорения.
 
Но что означает, что инерция вращения является вращательным эквивалентом инертной массы? Инерционная масса — это измерение сопротивления объекта линейному ускорению . Следовательно, инерция вращения является мерой сопротивления объекта угловому ускорению . Другими словами, чем больше инерция вращения объекта, тем больше этот объект будет сопротивляться угловому ускорению. Возвращаясь к демонстратору инерции вращения, чем дальше четыре регулируемые массы от оси вращения, тем больше значение «r» в уравнении для инерции вращения системы частиц, следовательно, тем больше инерция вращения демонстратора. . Чем больше инерция вращения демонстратора, тем больше сопротивление демонстратора угловому ускорению. Таким образом, чем больше расстояние между четырьмя регулируемыми массами и осью, тем больше инерция вращения и, следовательно, больше сопротивление демонстратора угловому ускорению.
 
Это демонстрируется ниже путем подвешивания 100-граммового груза к самому большому шкиву в двух одновременных демонстрациях. На демонстрации слева четыре регулируемые массы расположены близко к оси вращения, поэтому инерция вращения системы меньше. На демонстрации справа четыре регулируемые массы находятся дальше от оси вращения, поэтому инерция вращения системы больше. Когда оба демонстратора одновременно выходят из состояния покоя, поскольку чистый крутящий момент, создаваемый 100-граммовыми массами, примерно одинаков, демонстратор с большей инерцией вращения справа имеет меньшее угловое ускорение.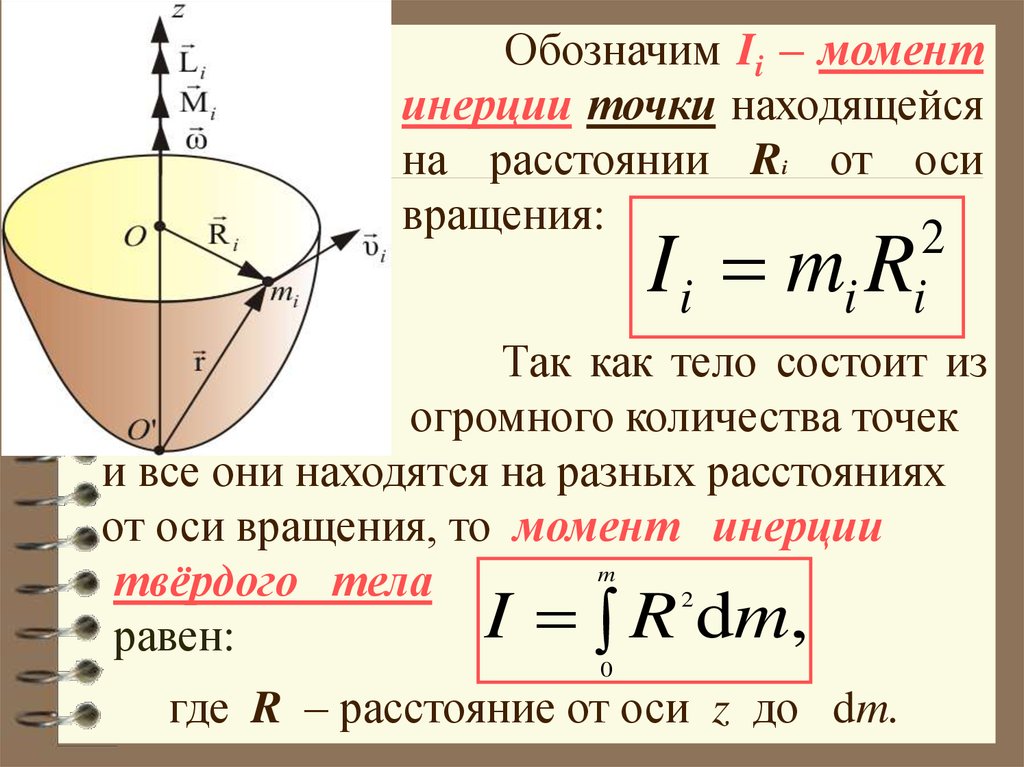 Другими словами, демонстратор с большей инерцией вращения ускоряется с меньшей скоростью. Возвращаясь к вращательной форме второго закона Ньютона, поскольку чистый крутящий момент почти одинаков, большая инерция вращения приводит к меньшему угловому ускорению.

Обратите внимание, что мы всегда держим четыре регулируемые массы на одинаковом расстоянии от оси или оси вращения. Это необходимо для того, чтобы центр масс системы находился на оси вращения системы. Когда четыре массы не находятся на равном расстоянии от оси вращения, центр масс системы смещен от оси вращения, и сила тяжести, действующая на систему, вызывает крутящий момент в системе. Сила гравитации, вызывающая крутящий момент в системе, значительно усложняет понимание демонстрации. В примерах, показанных ниже, демонстратор слева с четырьмя массами, расположенными на равном расстоянии от оси, вращается с почти постоянной угловой скоростью. Демонстратор справа имеет на одну массу дальше от оси вращения, и поэтому вся система фактически становится физическим маятником. Система колеблется вперед и назад в простом гармоническом движении. Хотя это интересно, это не дает очевидного способа узнать об инерции вращения. Таким образом, гораздо легче узнать об инерции вращения от демонстратора, если все четыре массы находятся на одинаковом расстоянии от оси вращения.

Давайте посмотрим на другой набор демонстраций ниже, чтобы узнать об инерции вращения. Как и в предыдущей демонстрации, справа у нас есть 100-граммовая масса, подвешенная к самому большому шкиву, и все четыре регулируемые массы далеко от оси вращения. Слева все четыре регулируемые массы все еще далеки от оси вращения, однако вместо них на самом маленьком шкиве висит 100-граммовая масса. Другими словами, оба демонстратора вращательной инерции имеют одинаковую вращательную инерцию, и сила тяжести, действующая на струну, одинакова, однако сеть крутящий момент действующий на каждый демонстратор различен. Напомним, что крутящий момент равен вектору «r», умноженному на силу, вызывающую крутящий момент, умноженной на угол между направлением вектора «r» и направлением силы. Величина вектора «r» — это расстояние от оси вращения до точки приложения силы к объекту:

Поскольку 100-граммовая масса висит на маленьком шкиве слева и на большом шкиве справа, вектор «r» для малого шкива меньше, и, следовательно, чистый крутящий момент, действующий на демонстратор через малый шкив, меньше . Следовательно, согласно вращательной форме второго закона движения Ньютона, угловое ускорение демонстратора слева меньше углового ускорения демонстратора справа.

В нашем последнем наборе демонстраций оба демонстратора имеют одинаковую инерцию вращения и массы, свисающие с самых маленьких шкивов. Кроме того, у обоих демонстраторов над левой стороной шкива висит 100-граммовый груз. Однако у демонстратора справа есть вторая масса, масса 200 граммов, висящая над правой стороной шкива. Это означает, что демонстратор справа имеет две разные массы, свисающие с самого маленького шкива.

Чтобы определить, что произойдет, помните, что вращательная форма второго закона движения Ньютона включает чистый крутящий момент не просто крутящий момент. В этом примере чистый крутящий момент от двух масс на демонстраторе справа фактически имеет примерно ту же величину , что и чистый крутящий момент, действующий на демонстратор слева, однако направления противоположны друг другу.
 
Опять же, оба демонстратора имеют одинаковую инерцию вращения, используют один и тот же шкив и груз массой 100 грамм висит над левой стороной шкива. Шкив справа добавляет 200-граммовую массу, нависающую над правой стороной шкива. Для демонстратора справа 100-граммовая масса, висящая над левой стороной шкива, по существу уравновешивает 100 граммов 200-граммовой массы, висящей над правой стороной шкива. Это фактически означает, что правый демонстратор имеет 100-граммовую массу, нависающую над правой стороной шкива. Следовательно, чистые крутящие моменты на обоих демонстраторах имеют по существу одинаковую величину и противоположные направления. Следовательно, угловые ускорения обоих демонстраторов должны иметь примерно одинаковую величину и противоположные направления. Вы можете видеть, что это правда в демонстрации.

Но почему два демонстратора имеют «примерно» одинаковые угловые ускорения? Добавление 200-граммовой массы к демонстратору справа увеличивает общую массу системы. Поскольку инерционная масса является сопротивлением ускорению, увеличение общей массы системы фактически немного уменьшает угловое ускорение системы, даже если чистый крутящий момент должен быть примерно таким же. Доказательство этого требует рисования диаграмм свободного тела, суммирования крутящих моментов на колесе и суммирования сил, воздействующих на каждую подвешенную массу, поэтому я не собираюсь доходить до этого решения здесь.
 
Существует много других способов настройки демонстратора инерции вращения для лучшего понимания инерции вращения. Например, спросите себя, что произойдет с угловым ускорением демонстратора, если единственное изменение, которое мы внесем в него, — это увеличение массы, подвешенной к демонстратору? Увеличение массы, подвешенной к демонстратору, увеличивает чистый крутящий момент, действующий на демонстратор. Вращательная инерция остается прежней. Следовательно, согласно вращательной форме второго закона движения Ньютона, угловое ускорение демонстратора будет увеличиваться.
 
Что, если единственное изменение, которое мы вносим, ​​заключается в том, чтобы изменить расположение четырех регулируемых масс не в самых дальних крайних положениях, а на расположение двух регулируемых масс вблизи оси вращения и двух регулируемых масс вдали от оси вращения? Приведение двух регулируемых масс к оси вращения уменьшает инерцию вращения системы и, следовательно, согласно вращательной форме второго закона Ньютона, угловое ускорение демонстратора будет увеличиваться. Обратите внимание, это будет работать только тогда, когда две близкие регулируемые массы расположены друг напротив друга, а две дальние регулируемые массы также расположены друг напротив друга. Если это не так, центр масс демонстратора вращательной инерции не будет находиться на оси или оси вращения, что является проблемой, которую мы рассматривали ранее.
 
Размеры шкива демонстратора инерции вращения предоставлены Arbor Scientific. Они составляют 20,22 мм для малого шкива, 28,65 мм для среднего шкива и 38,52 мм для большого шкива. Имея эту информацию, мы можем даже предсказать, в какую сторону будет вращаться демонстратор инерции вращения, если мы повесим 100 граммов на одну сторону большого шкива и 200 граммов на другую сторону маленького шкива. Перед выпуском демонстратора угловое ускорение демонстратора равно нулю, поскольку он находится в состоянии покоя. Следовательно, крутящий момент, вызванный массой 100 граммов, будет равен 0,3852 метра, умноженному на 0,100 килограмма, умноженному на 9.В 2 раза больше синуса 90 градусов, что примерно равно 0,40 Н.

Таким образом, чистый крутящий момент, вызванный обеими массами, действующими на демонстратор до того, как он начнет ускоряться , представляет собой разницу между этими двумя крутящими моментами, поскольку они действуют в противоположных направлениях.