Используя формулы (10) и (11), находим
(12)
После соприкосновения груза со столом сила упругости Т обращается в нуль (нить должна в момент соприкосновения соскользнуть со шкива). Дальнейшее вращение маятника под действием сил трения в опоре становиться замедленным и описывается уравнением
(13)
Предполагая, что в течении всего времени вращения маятника момент сил трения в опоре не изменяется, т.е. , уравнение (13)можно проинтегрировать следующим образом
, (14)
где – угловая скорость в момент соприкосновения груза со столом, – промежуток времени от момента соприкосновения груза со столом до остановки маятника. Это время измеряется секундомером ЭС-2. Элементарное интегрирование приводит уравнение (14) к виду
. (15) Учитывая теперь, что, из (10) с помощью (11) находим
(16)
(17)
Принимая во внимание соотношения (11), (12), (17) и вводя диаметр шкива , систему уравнений (8), (9) можно представить в виде
(18)
(19)
Уравнения
(18) и (19) образуют систему двух уравнений
с двумя неизвестными I и Т. Все остальные входящие в них величины,
за исключением g=9,8
м/с2,
определяются экспериментально в прямых
измерениях.
Все остальные входящие в них величины,
за исключением g=9,8
м/с2,
определяются экспериментально в прямых
измерениях.
Исключая из (19) с помощью (18) неизвестную Т, получаем формулу для измерения момента инерции крестообразного маятника относительно оси вращения
Изменяя массу подвешенного к нити груза, можно изменять силы упругости нити и трения в опоре (а, следовательно, и их моменты). Однако при этом, как следует из уравнения движения (9), при заданном расположении грузов m на стержнях маятника или при их отсутствии отношение модулей суммарного момента сил и углового ускорения маятника должно оставаться неизменным, т.е.
Это следует из определения момента инерции как физической величины. Следовательно, если, проделав опыт с различными грузами m1,m2,m3…, мы получим в результате расчетов по формуле (20) одинаковые значения моментов инерции маятника I1
 При этом результаты косвенных
измерений считаются одинаковыми в
пределах погрешностей, т.е. I1=I2=I3=…,
если пересекаются их доверительные
интервалы. Практически это легко
установить, отложив на вещественной
оси в выбранном масштабе средние значения
,
окруженные соответствующими доверительными
интервалами,,…,
При этом результаты косвенных
измерений считаются одинаковыми в
пределах погрешностей, т.е. I1=I2=I3=…,
если пересекаются их доверительные
интервалы. Практически это легко
установить, отложив на вещественной
оси в выбранном масштабе средние значения
,
окруженные соответствующими доверительными
интервалами,,…,При проверки свойства аддитивности момента инерции (т.е. того, что момент инерции тела относительно некоторой оси равен сумме моментов инерций любых частей этого тела относительно той же оси) и изучении характера зависимости момента инерции крестообразного маятника от распределения масс относительно оси вращения, будем обозначать момент инерции маятника без грузов m на стержнях (рис.1.3.2) через , а с закрепленными на них четырьмя грузами – через. Тогда, пренебрегая размерами грузов по сравнению с размерами стержней, в соответствии со свойством аддитивности момента инерции можно записать
(21)
где
l
– расстояние от центра закрепленного
на стержне груза до оси вращения, m
– масса одного груза.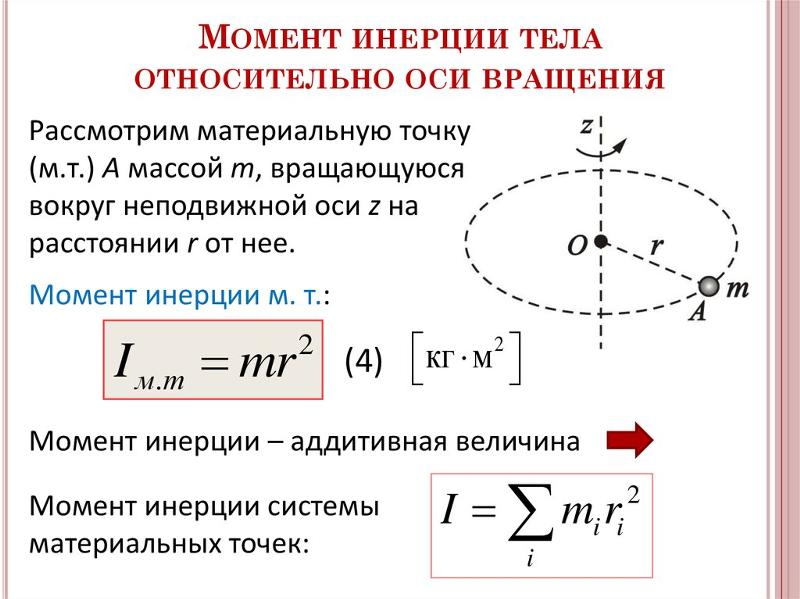
(22)
где d –диаметр шкива, х – длина закрепленного груза, S – расстояние до ближайшего торца этого груза.
Порядок выполнения работы
Упражнение 1. Измерение момента инерции крестообразного маятника без грузов и проверки уравнения динамики вращательного движения твердого тела вокруг неподвижной оси.
Снять со стержней маятника цилиндрические грузы.
Измерить диаметр шкива d штангенциркулем.
Измерить массу m1 груза, подвешенного к нити.
Намотать на шкив нить с грузом так чтобы находясь на площадке, груз натягивал нить.
Включить секундомер с помощью тумблера “Сеть” на панелях и установить их на нуль.
Привести груз в движение, освободив площадку. Время движения груза до касания со столом измерить секундомером ЭС-1.
В момент касания грузом стола нажать кнопку “Пуск” секундомера ЭС-2 и измерить время вращения маятника до остановки.

Замечание. В момент касания нить должна соскользнуть со шкива.
Вычислить момент инерции крестообразного маятника без грузов m по формуле (20).
Повторить действия по пунктам 1-8 для груза m2 , а затем – m3 .
Убедиться в равенстве (в пределах погрешностей) моментов инерции I1, I2 , I3 , измеренных при проведении опытов с массами m1 ,m2 , m3 соответственно.
Упражнение 2. Изучение зависимости момента инерции крестообразного маятника от распределения его массы относительно оси вращения и проверка свойства аддитивности момента инерции.
Надеть грузы m на стержни и расположить их на одинаковом расстоянии l от оси вращения. После закрепления убедиться, что маятник находиться в состоянии безразличного равновесия (сбалансирован).
Подвесить к нити какой – либо груз m и провести все измерения, необходимые для определения момента инерции маятника, как в упражнении 1 (п.
 п. 1-8), не
менее чем для трех различных расстояний l1, l2, l3.
п. 1-8), не
менее чем для трех различных расстояний l1, l2, l3.Рассчитать по формуле (20) момент инерции маятника с закрепленными на стержнях грузами m для всех установленных расстояний.
Выбрав какое – либо измеренное значение момента инерции маятника без грузов
Изобразить на плоскости графика I(l) точки, соответствующие результатам расчета момента инерции маятника по формуле (20) для всех установленных расстояний, и по их расположению относительно построенной кривой сделать вывод о справедливости соотношения (21).
Контрольные вопросы
С какими физическими величинами вы познакомились при изучении теории и в процессе выполнения работы? Дайте определение этих величин.

Какие физические законы необходимо знать для понимания настоящей лабораторной работы? Сформулируйте эти законы в математической и словесной формах.
Обоснуйте вывод расчетной формулы (20), сформулировав все необходимые для него упрощающие предположения.
Каким образом на приборе Обербека можно проверить уравнение динамики вращательного движения твердого тела вокруг неподвижной оси? Какие экспериментальные данные подтверждают справедливость этого уравнения.
Являются ли момент инерции аддитивной величиной. Ответ подтвердите с помощью полученных экспериментальных данных.
Как зависит момент инерции тела от характера распределения его массы относительно оси? Как эта зависимость устанавливается в настоящей работе?
Литература
Савельев И.В. Курс общей физики – М. Наука, 1988. т.1. – §§ 2,5, 36-43.
Савельев И.В. Курс общей физики – М. Наука, 1989.
 т.1.
– §§ 5–8, 11-14, 28-34.
т.1.
– §§ 5–8, 11-14, 28-34.
Лабораторная работа № 1.4.
ИЗМЕРЕНИЕ МОМЕНТОВ ИНЕРЦИИ И МОДУЛЯ СДВИГА ТВЕРДЫХ ТЕЛ
МЕТОДОМ КРУТИЛЬНЫХ КОЛЕБАНИЙ
Момент инерции абсолютно твердого тела. Урок №14
Похожие презентации:
Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов
Газовая хроматография
Геофизические исследования скважин
Искусственные алмазы
Трансформаторы тока и напряжения
Транзисторы
Воздушные и кабельные линии электропередач
Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса
Магнитные аномалии
Нанотехнологии
Физика. 10 класс. Урок №14.
«Недостаточно только получить знания, надо
найти им применение. Недостаточно только
Гёте
© Фокина Лидия Петровна
Знаешь ли ты?
Почему вместо обычных колес на
велосипедах гонщиков устанавливают
сплошные диски?
Если ты затрудняешься ответить на данный вопрос
сейчас, то я уверенн, что ты на него сможешь ответить
в конце этого урока.

© Фокина Лидия Петровна
Физика. 10 класс. Урок №14.
Тема урока:
Момент инерции
абсолютно твердого тела
Цели обучения:
10.2.2.5 – использовать теорему Штейнера для
расчета момента инерции материальных тел
© Фокина Лидия Петровна
Давайте вспомним!
1. Что такое инерция?
Инерция – это физическое явление. Оно
состоит в том, что любое тело, на которое не
действуют другие тела (или действие других
тел скомпенсировано), сохраняет состояние
покоя или движется равномерно и
прямолинейно
2. Какое тело в физике называют абсолютно
твердым телом?
Абсолютно твердое тело – это тело,
расстояние между частями которого не
меняется при действии на него любых сил.
© Фокина Лидия Петровна
Рассмотрим вращение материальной точки
массой m вокруг неподвижного центра О.
Докажем, что инерциальные свойства данной
точки зависят не только от массы, но и от
радиуса вращения.
Запишем второй закон
Ньютона для точки массой m,
движущейся по окружности
под действием силы ,
тангенциальное ускорение
будет создавать касательная
к траектории составляющая
© Фокина Лидия Петровна
Тангенциальное ускорение связано с угловым
ускорением формулой
Учитывая это получим:
Умножим обе части данного уравнения на радиус
окружности, по которой двигалась
рассматриваемая точка, получим:
, где
M – момент силы
– момент инерции
© Фокина Лидия Петровна
Величину, равную произведению массы на
квадрат радиуса окружности, по которой
движется тело, называют моментом
инерции.
Момент инерцииобозначают
буквой I.
Единица измерения момента
инерции [I] = 1 кг м2
-второй закон Ньютона для
вращающегося тела
© Фокина Лидия Петровна
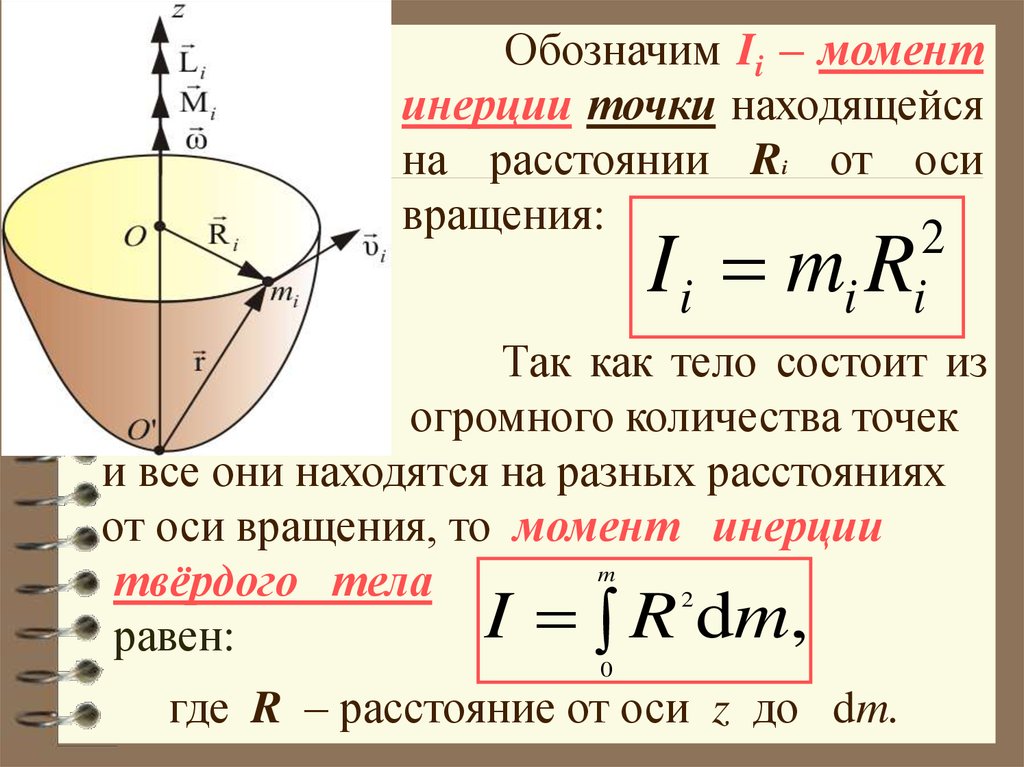
Мы нашли момент инерции материальной точки,
вращающейся вокруг неподвижного центра.
А как найти момент инерции абсолютно твердого тела?
Момент инерции твердого тела равен сумме
моментов инерций материальных точек, из
которых состоит это тело:
Инертные свойства вращающихся тел зависят
не только от массы, но и от ее распределения
по объему тела и радиуса вращения.
© Фокина Лидия Петровна
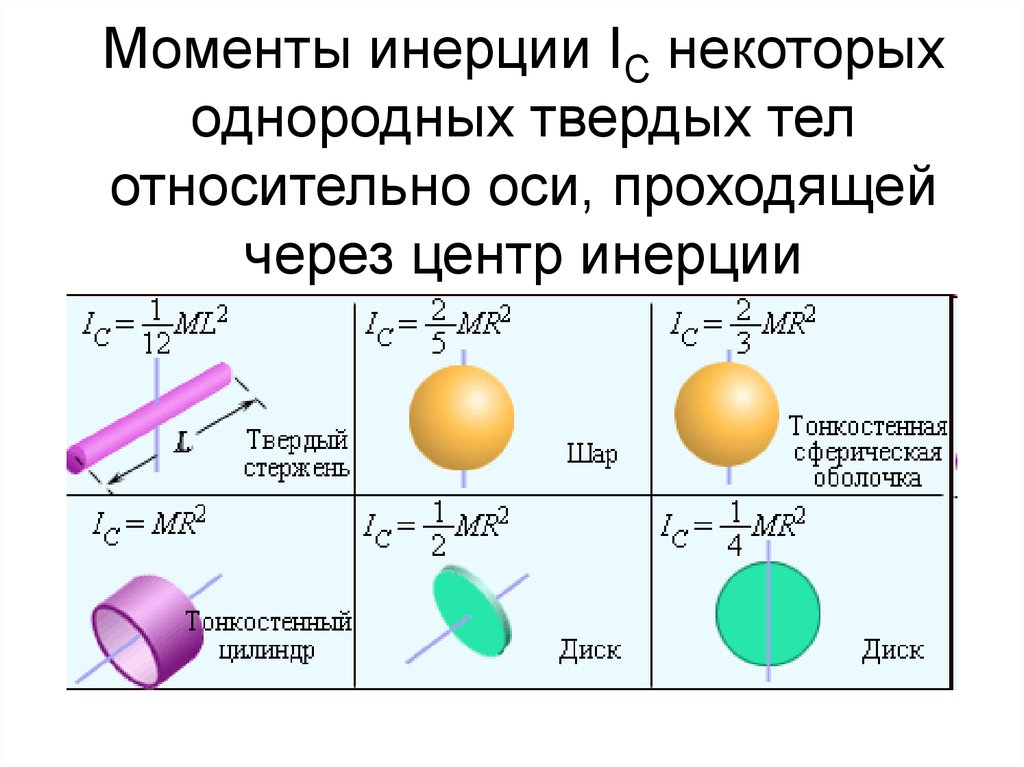
стр 49-50 Таблица 6. Моменты инерции тел
© Фокина Лидия Петровна
Теорема Штейнера
Если для тела известен момент инерции I0
относительно оси, проходящей через центр
масс, то момент инерции относительно любой
оси, параллельной центральной, можно найти
по формуле, полученной швейцарским ученымматематиком Штейнером:
d – расстояние от центра масс до оси вращения
© Фокина Лидия Петровна
Задача №1
Определите момент инерции I тонкого однородного стержня
длиной l=30 см и m=100 г относительно оси, перпендикулярной
стержню и проходящей через: 1) его конец; 2) его середину; 3)
точку отстоящую от конца стержня на 1/3 его длины
Дано: CИ
Решение:
(из таблицы)
l= 30 см 0,3 м
m = 100 г 0,1 кг
I-?
1) расстояние от центра масс до
конца стержня
© Фокина Лидия Петровна
2) ось вращения проходит через центр масс
3) Расстояние от центра масс до оси, отстоящей
от конца стержня на 1/3 его длины
Ответ:
© Фокина Лидия Петровна
Выполни самостоятельно!
1.

Определите момент инерции стержня длиной l,
вращающегося вокруг своего конца. Во сколько раз
увеличился момент инерции в сравнении с моментом
инерции стержня, вращающегося вокруг центра масс?
2.
Определите момент инерции материальной точки, масса
которой 50 г, относительно оси, отстоящей от точки на
расстоянии 20 см.
3.
Найти момент инерции обруча массой и
радиусом относительно оси, проходящей через его край
перпендикулярно обручу.
§9 стр 48-51
© Фокина Лидия Петровна
Итоги урока
Момент инерции – скалярная физическая величина, мера
инертности во вращательном движении вокруг оси,
подобно тому, как масса тела является мерой его
инертности в поступательном движении.
© Фокина Лидия Петровна
Момент инерции материальной точки,
вращающейся по окружности радиуса R,
можно рассчитать по формуле …
I=mR2
Момент инерции тела измеряется в …
кг м2
Момент инерции тела относительно
любой оси, параллельной центральной,
можно вычислить применяя …
теорему
Штейнера
Формула, полученная Штейнером …
I=I0+ md2
© Фокина Лидия Петровна
English Русский Правила
2~\mathrm dm$ пришло на ум. Так что я не буду писать то же самое снова. Тем не менее, поскольку ОП заинтересован в «логическом развитии» идеи, я считаю целесообразным добавить краткое обсуждение момента инерции как тензора второго ранга в более общем случае, чтобы ОП мог получить представление о короче вся тема.
Так что я не буду писать то же самое снова. Тем не менее, поскольку ОП заинтересован в «логическом развитии» идеи, я считаю целесообразным добавить краткое обсуждение момента инерции как тензора второго ранга в более общем случае, чтобы ОП мог получить представление о короче вся тема.Введение:
Момент импульса $\mathbf L$ твердого тела относительно некоторой стационарной точки выражается как:
$$\begin{align}\mathbf L &= \sum_i \mathbf r_i\ раз (m_i\mathbf v_i)\\ & =\sum_i \mathbf r_i \times m_i (\boldsymbol \omega \times \mathbf r_i)\end{align}$$, где $\mathbf r_i$ — расстояние от $i $-я частица из неподвижной точки. 92)~\omega_x – m_ix_iy_i~\omega_y- m_ix_iz_i~\omega_z\right]$$
Итак, $L_z$ является линейной функцией каждой компоненты угловой скорости.
Таким образом, $\mathbf L$ линейно преобразуется из $\boldsymbol \omega\,.$
Это можно выразить как $$\mathbf L = \mathsf I\boldsymbol\omega\tag{II}$$
, где $\sf I$ — оператор, линейно переводящий $\boldsymbol\omega$ в $\mathbf L\,. 2 ~\delta_{ij} – r_ir_j)\tag{III}$$ и $\mathbf L$ и $\boldsymbol\omega$ являются матрицами-столбцами.
2 ~\delta_{ij} – r_ir_j)\tag{III}$$ и $\mathbf L$ и $\boldsymbol\omega$ являются матрицами-столбцами.
Эллипсоид инерции:
Из $\rm(III),$ можно заключить, что $I_{xy} = I_{yx};$ это означает, что $\sf I$ является симметричной матрицей.
Любой симметричный линейный оператор может быть представлен в единственной диагональной форме (диагональные элементы уникальны, но порядок элементов может быть разным) путем ортогонального преобразования координат. Соответствующий принцип осей будет уникальным и ортогональным.
Теперь кинетическая энергия $\textrm{KE}$ твердого тела равна $$\begin{align}\textrm{KE}&=\frac12 \sum_i m_i (\boldsymbol \omega \times\mathbf r_i)\cdot (\boldsymbol \omega \times\mathbf r_i)\\ &=\frac12\sum_i m_i \boldsymbol\omega\cdot (\mathbf r_i\times (\boldsymbol \omega \times\mathbf r_i))\\&= \frac12 \boldsymbol\omega\cdot \mathbf L\\ &= \frac12 \boldsymbol\omega\cdot \mathsf I\boldsymbol \omega~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~(\textrm{using}~\mathrm{II})\end{align}$$, что при расширении дает $$\begin{align}T &=\frac12( I_{xx}\omega_x^2 + I_{ yy}\omega_y^2 + I_{zz}\omega_z^2) + \frac12\sum_i\sum_j(I_{ij}\omega_i\omega_j) \\ &= \frac12\sum_{i}I_{ii}~\ omega_i^2 + (I_{xy}\omega_x\omega_y + I_{yz}\omega_y\omega_z + I_{zx}\omega_z\omega_x)~~~~~~~~~~~~~(I_{xy} = I_{yx}) \end{align}\,. $$ 92\,.$$
$$ 92\,.$$
Литература:
$\bullet$ Классическая механика by Гольдштейн .
Вращательная инерция — физика Колледжа Дугласа 1104 Пользовательский учебник — зима и лето 2020 г.
Глава 9 Вращательное движение и угловой момент
Резюме
- Поймите взаимосвязь между силой, массой и ускорением.
- Изучите вращающее действие силы.
- Изучите аналогию между силой и крутящим моментом, массой и моментом инерции, линейным ускорением и угловым ускорением.
Если вы когда-либо крутили велосипедное колесо или толкали карусель, вы знаете, что для изменения угловой скорости необходима сила, как показано на рис. 1. На самом деле ваша интуиция надежно предсказывает многие из задействованных факторов . Например, мы знаем, что дверь открывается медленно, если мы прислоняем ее слишком близко к петлям. Кроме того, мы знаем, что чем массивнее дверь, тем медленнее она открывается.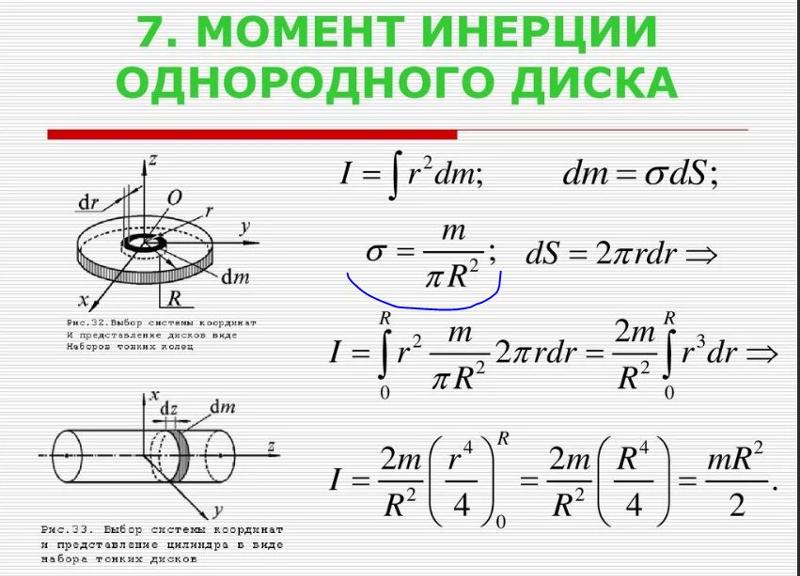 Первый пример подразумевает, что чем дальше приложена сила от оси вращения, тем больше угловое ускорение; другое следствие состоит в том, что угловое ускорение обратно пропорционально массе. Эти отношения должны казаться очень похожими на знакомые отношения между силой, массой и ускорением, воплощенные во втором законе движения Ньютона. На самом деле существуют точные вращательные аналоги как силы, так и массы.
Первый пример подразумевает, что чем дальше приложена сила от оси вращения, тем больше угловое ускорение; другое следствие состоит в том, что угловое ускорение обратно пропорционально массе. Эти отношения должны казаться очень похожими на знакомые отношения между силой, массой и ускорением, воплощенные во втором законе движения Ньютона. На самом деле существуют точные вращательные аналоги как силы, так и массы.
Чтобы установить точное соотношение между силой, массой, радиусом и угловым ускорением, рассмотрим, что произойдет, если мы приложим силу F к точке массой м , находящейся на расстоянии r от точки вращения, как показано на рисунке 2. Поскольку сила перпендикулярна r , ускорение [латекс]\boldsymbol{a=\frac{F}{m}}[/latex ] получается по направлению F . 2\alpha}[/латекс] 92\альфа}.[/латекс]
2\alpha}[/латекс] 92\альфа}.[/латекс]
Это последнее уравнение является вращательным аналогом второго закона Ньютона ( F = ma ), где крутящий момент аналогичен силе, угловое ускорение аналогично поступательному ускорению, а mr 2 аналогично к массе (или инерции). Величина mr 2 называется инерцией вращения или моментом инерции точечной массы м расстояние r от центра вращения.
Рисунок 2. Объект поддерживается горизонтальным столом без трения и прикреплен к точке поворота шнуром, создающим центростремительную силу. Сила F приложена к объекту перпендикулярно радиусу r , заставляя его ускоряться относительно точки вращения. Сила удерживается перпендикулярно r .
ВЫПОЛНЕНИЕ СОЕДИНЕНИЙ: ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Динамика вращательного движения полностью аналогична линейной или поступательной динамике. Динамика занимается силой и массой и их влиянием на движение. Для вращательного движения мы найдем прямые аналоги силы и массы, которые ведут себя именно так, как мы и ожидали, исходя из нашего предыдущего опыта.
Прежде чем мы сможем рассмотреть вращение чего-либо, кроме точечной массы, подобной той, что изображена на рис. 2, мы должны распространить идею инерции вращения на все типы объектов. Чтобы расширить наше понятие инерции вращения, мы определяем момент инерции I объекта должен быть суммой mr 2 для всех точечных масс, из которых он состоит. То есть I =∑ мр 2 . Здесь I аналогичны m в поступательном движении. Из-за расстояния r момент инерции любого объекта зависит от выбранной оси.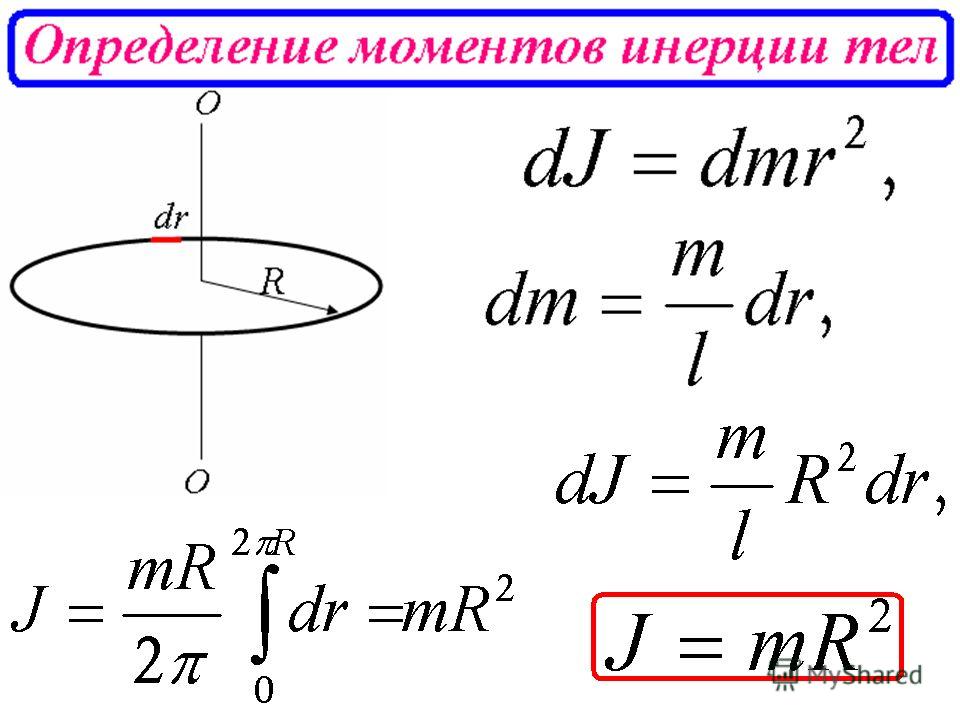 На самом деле, вычисляя I выходит за рамки этого текста, за исключением одного простого случая — обруча, вся масса которого находится на одинаковом расстоянии от его оси. Таким образом, момент инерции кольца вокруг его оси равен MR 2 , где M — его полная масса, а R — его радиус. (Мы используем M и R для всего объекта, чтобы отличить их от m и r для точечных масс.) Во всех других случаях мы должны обращаться к рисунку 3 (обратите внимание, что таблица представляет собой произведение искусства, имеющее формы, а также формулы) для формул для I , которые имеют получена интегрированием по непрерывному телу. Обратите внимание, что I имеет единицы массы, умноженные на квадрат расстояния ( кг⋅м 2 ), как и следовало ожидать из его определения.
На самом деле, вычисляя I выходит за рамки этого текста, за исключением одного простого случая — обруча, вся масса которого находится на одинаковом расстоянии от его оси. Таким образом, момент инерции кольца вокруг его оси равен MR 2 , где M — его полная масса, а R — его радиус. (Мы используем M и R для всего объекта, чтобы отличить их от m и r для точечных масс.) Во всех других случаях мы должны обращаться к рисунку 3 (обратите внимание, что таблица представляет собой произведение искусства, имеющее формы, а также формулы) для формул для I , которые имеют получена интегрированием по непрерывному телу. Обратите внимание, что I имеет единицы массы, умноженные на квадрат расстояния ( кг⋅м 2 ), как и следовало ожидать из его определения.
Общее соотношение между крутящим моментом, моментом инерции и угловым ускорением составляет
[латекс] \boldsymbol{\textbf{net}\tau=I\alpha}[/латекс]
или
[латекс]\boldsymbol{\alpha\:=}[/латекс][латекс]\boldsymbol{\frac{\textbf{net}\tau}{I}},[/latex]
, где net τ — это суммарный крутящий момент от всех сил относительно выбранной оси. Для простоты мы будем рассматривать только крутящие моменты, создаваемые силами в плоскости вращения. Такие крутящие моменты бывают положительными или отрицательными и складываются как обычные числа. Соотношение в [латекс]\boldsymbol{\tau=I\alpha},\:\boldsymbol{\alpha=\frac{\textbf{net}\tau}{I}}[/latex] является аналогом вращения Ньютона. второй закон и очень широко применимы. Это уравнение действительно справедливо для любой крутящий момент, примененный к любому объекту относительно любой оси .
Как и следовало ожидать, чем больше крутящий момент, тем больше угловое ускорение. Например, чем сильнее ребенок толкает карусель, тем быстрее она разгоняется. Кроме того, чем массивнее карусель, тем медленнее она разгоняется при том же крутящем моменте. Основное соотношение между моментом инерции и угловым ускорением заключается в том, что чем больше момент инерции, тем меньше угловое ускорение. Но есть дополнительный нюанс. Момент инерции зависит не только от массы тела, но и от его распределение массы относительно оси, вокруг которой она вращается. Например, будет намного легче разогнать карусель, полную детей, если они будут стоять близко к ее оси, чем если все они будут стоять на внешнем краю. Масса одинакова в обоих случаях; но момент инерции намного больше, когда дети находятся на краю.
Например, чем сильнее ребенок толкает карусель, тем быстрее она разгоняется. Кроме того, чем массивнее карусель, тем медленнее она разгоняется при том же крутящем моменте. Основное соотношение между моментом инерции и угловым ускорением заключается в том, что чем больше момент инерции, тем меньше угловое ускорение. Но есть дополнительный нюанс. Момент инерции зависит не только от массы тела, но и от его распределение массы относительно оси, вокруг которой она вращается. Например, будет намного легче разогнать карусель, полную детей, если они будут стоять близко к ее оси, чем если все они будут стоять на внешнем краю. Масса одинакова в обоих случаях; но момент инерции намного больше, когда дети находятся на краю.
ЭКСПЕРИМЕНТ ДЛЯ ДОМА
Вырежьте круг радиусом около 10 см из плотного картона. Рядом с краем круга напишите числа от 1 до 12, как часы на циферблате. Расположите круг так, чтобы он мог свободно вращаться вокруг горизонтальной оси, проходящей через его центр, как колесо.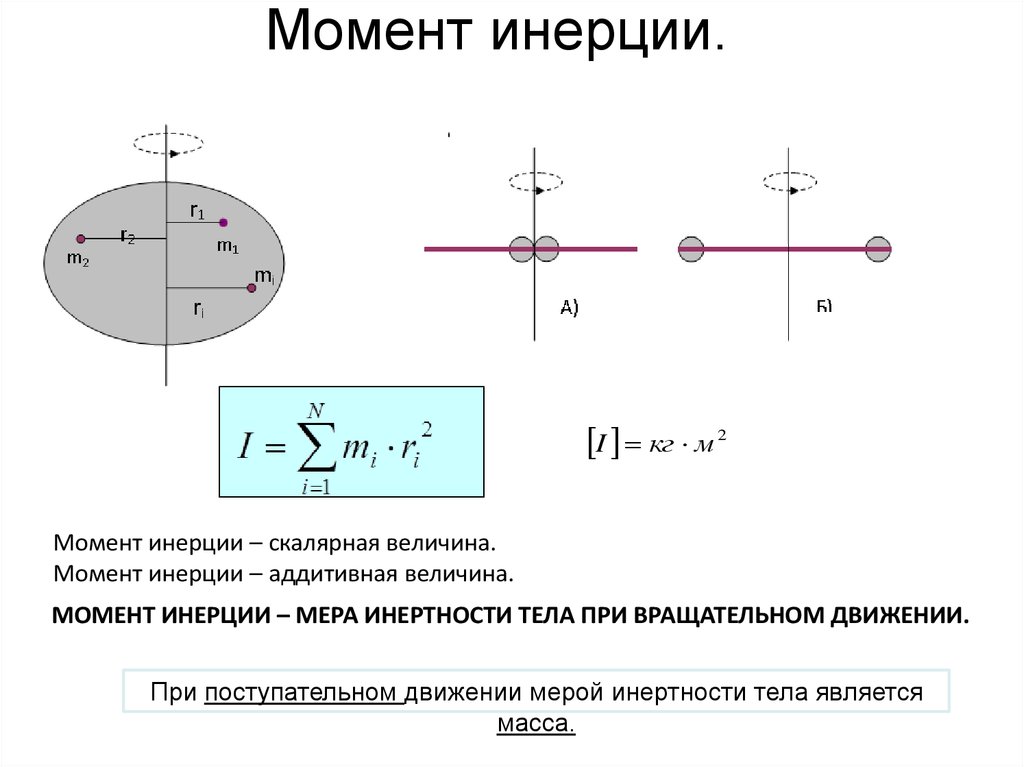 (Вы можете свободно прибить круг к стене.) Держите круг неподвижно и, расположив цифру 12 вверху, прикрепите кусок синей замазки (клейкий материал, используемый для крепления постеров к стенам) к цифре 3. Какого размера глыба должна быть, чтобы просто вращать круг? Опишите, как можно изменить момент инерции окружности. Как это изменение повлияет на количество синей замазки, необходимое под номером 3, чтобы просто повернуть круг? Измените момент инерции круга, а затем попробуйте повернуть круг, используя разное количество синей замазки. Повторите этот процесс несколько раз.
(Вы можете свободно прибить круг к стене.) Держите круг неподвижно и, расположив цифру 12 вверху, прикрепите кусок синей замазки (клейкий материал, используемый для крепления постеров к стенам) к цифре 3. Какого размера глыба должна быть, чтобы просто вращать круг? Опишите, как можно изменить момент инерции окружности. Как это изменение повлияет на количество синей замазки, необходимое под номером 3, чтобы просто повернуть круг? Измените момент инерции круга, а затем попробуйте повернуть круг, используя разное количество синей замазки. Повторите этот процесс несколько раз.
СТРАТЕГИЯ РЕШЕНИЯ ЗАДАЧ ДЛЯ ДИНАМИКИ ВРАЩЕНИЯ
- Изучите ситуацию, чтобы определить, что крутящий момент и масса участвуют во вращении . Нарисуйте тщательный набросок ситуации.
- Определить интересующую систему .
- Нарисуйте диаграмму свободного тела . То есть нарисуйте и обозначьте все внешние силы, действующие на интересующую вас систему.
- Применить [латекс]\boldsymbol{\textbf{net}\tau=I\alpha},\:\boldsymbol{\alpha=\frac{\textbf{net}\tau}{I}},[/latex ] вращательный эквивалент второго закона Ньютона, чтобы решить задачу .
 Необходимо соблюдать осторожность, чтобы использовать правильный момент инерции и учитывать крутящий момент вокруг точки вращения.
Необходимо соблюдать осторожность, чтобы использовать правильный момент инерции и учитывать крутящий момент вокруг точки вращения. - Как всегда, проверьте правильность решения .
ВЫПОЛНЕНИЕ СОЕДИНЕНИЙ
В статике чистый крутящий момент равен нулю, а угловое ускорение отсутствует. При вращательном движении чистый крутящий момент является причиной углового ускорения, точно так же, как во втором законе движения Ньютона для вращения.
Рисунок 3. Некоторые инерции вращения.Пример 1. Расчет влияния распределения масс на карусель
Рассмотрим отца, толкающего игровую карусель на рис. 4. Он прикладывает силу 250 Н к краю карусели весом 50,0 кг. круговой, который имеет радиус 1,50 м. Вычислите угловое ускорение, создаваемое (а), когда на карусели никого нет, и (б), когда ребенок массой 18,0 кг сидит на расстоянии 1,25 м от центра. Считайте саму карусель однородным диском с пренебрежимо малым тормозящим трением.
Стратегия
Угловое ускорение задается непосредственно выражением [латекс]\boldsymbol{\alpha=\frac{\textbf{net}\tau}{I}}:[/latex]
[латекс]\boldsymbol {\alpha\:=}[/latex][latex]\boldsymbol{\frac{\tau}{I}}.[/latex]
Чтобы найти [латекс]\boldsymbol{\alpha},[/latex ] мы должны сначала рассчитать крутящий момент τ (одинаковый в обоих случаях) и момент инерции I (во втором случае больше). Чтобы найти крутящий момент, заметим, что приложенная сила перпендикулярна радиусу, а трение незначительно, так что
[латекс]\boldsymbol{\tau=rF\:\sin\:\theta=(1,50\textbf{ m })(250\textbf{ N})=375\textbf{ N}\cdotp\textbf{m}.}[/latex]
Решение задачи (a)
Момент инерции твердого диска около эта ось указана на рисунке 3 как 92}}. 2}.[/латекс] 92}}.[/latex]
2}.[/латекс] 92}}.[/latex]
Обсуждение
Угловое ускорение меньше, когда ребенок находится на карусели, чем когда карусель пуста, как и ожидалось. Найденные угловые ускорения довольно велики, отчасти из-за того, что трение считалось пренебрежимо малым. Если бы, например, отец продолжал толкать перпендикулярно в течение 2,00 с, он придал бы карусели угловую скорость 13,3 рад/с, когда она пуста, и только 8,89 рад/с, когда на ней находится ребенок. В пересчете на обороты в секунду эти угловые скорости составляют 2,12 об/с и 1,41 об/с соответственно. В первом случае отец будет бежать со скоростью около 50 км/ч. Летние Олимпийские игры, вот и он! Подтверждение этих цифр оставлено читателю в качестве упражнения.
- Чем дальше сила приложена от оси вращения, тем больше угловое ускорение; угловое ускорение обратно пропорционально массе.
- Если мы приложим силу F к точке массой m , которая находится на расстоянии r от точки вращения, и поскольку сила перпендикулярна r r
6 ускорению a = F / m
получается в направлении Ф .

 п. 1-8), не
менее чем для трех различных расстояний l1, l2, l3.
п. 1-8), не
менее чем для трех различных расстояний l1, l2, l3.
 т.1.
– §§ 5–8, 11-14, 28-34.
т.1.
– §§ 5–8, 11-14, 28-34.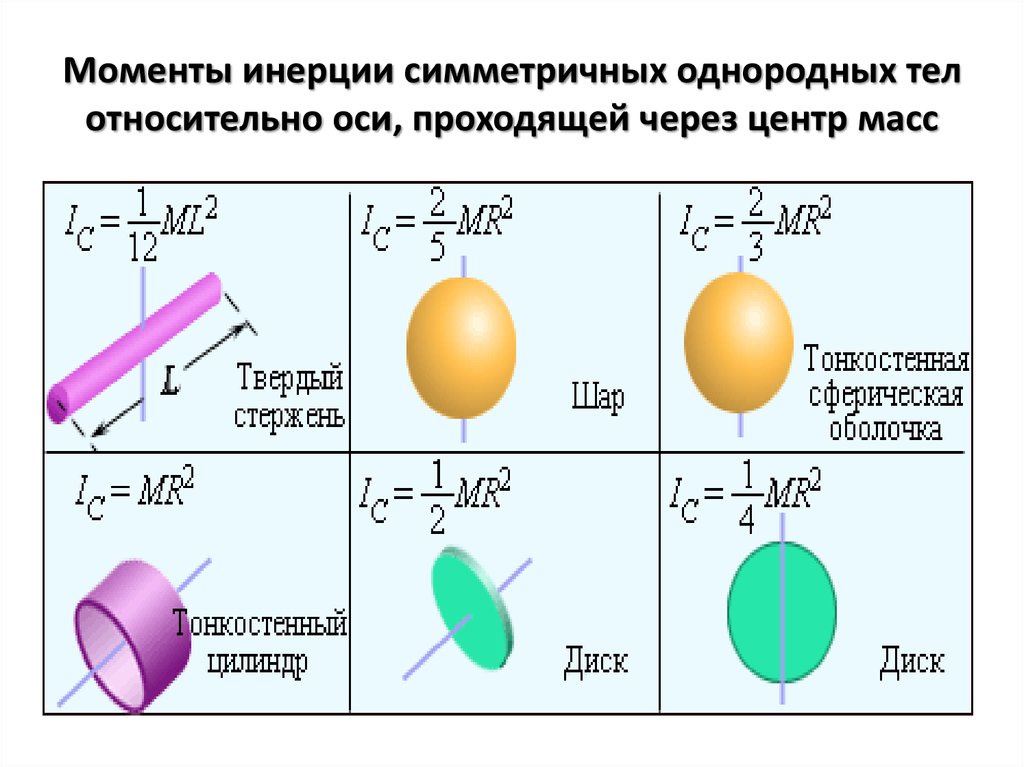 Необходимо соблюдать осторожность, чтобы использовать правильный момент инерции и учитывать крутящий момент вокруг точки вращения.
Необходимо соблюдать осторожность, чтобы использовать правильный момент инерции и учитывать крутящий момент вокруг точки вращения.