Сопротивление материалов
Сопротивление материалов
ОглавлениеПРЕДИСЛОВИЕГлава 1. ОСНОВНЫЕ ПОНЯТИЯ § 2.1. РАСЧЕТНАЯ СХЕМА. НАГРУЗКИ § 3.1. ВНУТРЕННИЕ СИЛЫ. МЕТОД СЕЧЕНИЙ § 4.1. НАПРЯЖЕНИЯ § 5.1. ДЕФОРМАЦИИ И ПЕРЕМЕЩЕНИЯ § 6.1. ОСНОВНЫЕ ПРЕДПОСЫЛКИ НАУКИ О СОПРОТИВЛЕНИИ МАТЕРИАЛОВ Вопросы для самопроверки Глава 2. РАСТЯЖЕНИЕ И СЖАТИЕ § 1.  § 2.2. НАПРЯЖЕНИЯ В ПОПЕРЕЧНЫХ И НАКЛОННЫХ СЕЧЕНИЯХ БРУСА § 3.2. ПРОДОЛЬНЫЕ И ПОПЕРЕЧНЫЕ ДЕФОРМАЦИИ § 4.2. ДИАГРАММЫ РАСТЯЖЕНИЯ И СЖАТИЯ § 5.2. ПЕРЕМЕЩЕНИЯ ПОПЕРЕЧНЫХ СЕЧЕНИЙ БРУСЬЕВ § 6.2. РАБОТА СИЛЫ ПРИ ЕЕ СТАТИЧЕСКОМ ДЕЙСТВИИ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ § 7.2. СОБСТВЕННЫЙ ВЕС БРУСА § 8.2. ДОПУСКАЕМЫЕ НАПРЯЖЕНИЯ. РАСЧЕТЫ НА ПРОЧНОСТЬ § 9.2. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ § 10.2. МЕСТНЫЕ НАПРЯЖЕНИЯ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 3. ТЕОРИЯ НАПРЯЖЕННОГО СОСТОЯНИЯ § 1.3. ВИДЫ НАПРЯЖЕННОГО СОСТОЯНИЯ § 2.3. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ § 3.3. ГЛАВНЫЕ НАПРЯЖЕНИЯ. ГЛАВНЫЕ ПЛОЩАДКИ § 4.3. ЭКСТРЕМАЛЬНЫЕ КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ § 6.3. ПОНЯТИЕ О ПРОСТРАНСТВЕННОМ НАПРЯЖЕННОМ СОСТОЯНИИ § 7.3. ОБОБЩЕННЫЙ ЗАКОН ГУКА § 8.3. ОБЪЕМНАЯ ДЕФОРМАЦИЯ § 9.3. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 4.  СДВИГ СДВИГ§ 1.4. ЧИСТЫЙ СДВИГ § 2.4. ДЕФОРМАЦИЯ ПРИ СДВИГЕ. ЗАКОН ГУКА ПРИ СДВИГЕ § 3.4. ОБЪЕМНАЯ ДЕФОРМАЦИЯ И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ПРИ ЧИСТОМ СДВИГЕ. ЗАВИСИМОСТЬ МЕЖДУ E, G и «мю» § 4.4. ПРАКТИЧЕСКИЕ РАСЧЕТЫ НЕКОТОРЫХ ПРОСТЕЙШИХ КОНСТРУКЦИЙ, РАБОТАЮЩИХ НА СДВИГ Расчет сварных соединений Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 5. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ § 2.5. СТАТИЧЕСКИЕ МОМЕНТЫ СЕЧЕНИЙ § 3.5. МОМЕНТЫ ИНЕРЦИИ СЕЧЕНИЙ § 4.5. ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ СЕЧЕНИЙ ПРОСТОЙ ФОРМЫ § 5.5. ИЗМЕНЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПРИ ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ ОСЕЙ § 6.5. ИЗМЕНЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПРИ ПОВОРОТЕ ОСЕЙ § 7.5. ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ. ГЛАВНЫЕ ОСИ ИНЕРЦИИ § 8.5. ИССЛЕДОВАНИЕ МОМЕНТОВ ИНЕРЦИИ ПЛОСКИХ СЕЧЕНИЙ С ПОМОЩЬЮ КРУГА МОРА § 9.5. ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ СЛОЖНЫХ СЕЧЕНИЙ Задачи для самостоятельного решения Вопросы для самопроверки Глава 6.  КРУЧЕНИЕ КРУЧЕНИЕ§ 1.6. ОСНОВНЫЕ ПОНЯТИЯ. КРУТЯЩИЙ МОМЕНТ § 2.6. КРУЧЕНИЕ ПРЯМОГО БРУСА КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ § 3.6. ГЛАВНЫЕ НАПРЯЖЕНИЯ И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ ПРИ КРУЧЕНИИ БРУСА КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ § 4.6. РАСЧЕТ БРУСА КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ ПРИ КРУЧЕНИИ § 5.6. РАСЧЕТ ЦИЛИНДРИЧЕСКИХ ВИНТОВЫХ ПРУЖИН § 6.6. КРУЧЕНИЕ ПРЯМОГО БРУСА НЕКРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ § 7.6. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ ЗАДАЧИ ПРИ КРУЧЕНИИ Задачи для самостоятельного решения Вопросы для самопроверки Глава 7. ПРЯМОЙ ИЗГИБ § 1.7. ВНУТРЕННИЕ УСИЛИЯ § 3.7. ОПОРЫ И ОПОРНЫЕ РЕАКЦИИ § 4.7. ЭПЮРЫ ВНУТРЕННИХ УСИЛИЙ § 5.7. ДИФФЕРЕНЦИАЛЬНЫЕ ЗАВИСИМОСТИ МЕЖДУ ИЗГИБАЮЩИМ МОМЕНТОМ, ПОПЕРЕЧНОЙ СИЛОЙ И ИНТЕНСИВНОСТЬЮ РАСПРЕДЕЛЕННОЙ НАГРУЗКИ § 6.7. ПРИМЕРЫ ПОСТРОЕНИЯ ЭПЮР ВНУТРЕННИХ УСИЛИЙ § 7.7. ПРЯМОЙ ЧИСТЫЙ ИЗГИБ § 8.7. ПРЯМОЙ ПОПЕРЕЧНЫЙ ИЗГИБ § 9.7. ГЛАВНЫЕ НАПРЯЖЕНИЯ ПРИ ПРЯМОМ ПОПЕРЕЧНОМ ИЗГИБЕ § 10.  7. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ ПРИ ИЗГИБЕ 7. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ ПРИ ИЗГИБЕ§ 11.7. РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ ИЗГИБЕ § 12.7. ПОНЯТИЕ О ЦЕНТРЕ ИЗГИБА § 14.7. ПОНЯТИЕ О БАЛКАХ РАЗНОРОДНОЙ УПРУГОСТИ § 15.7. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В БАЛКАХ ПОСТОЯННОГО СЕЧЕНИЯ МЕТОДОМ НЕПОСРЕДСТВЕННОГО ИНТЕГРИРОВАНИЯ § 16.7. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В БАЛКАХ ПОСТОЯННОГО СЕЧЕНИЯ МЕТОДОМ НАЧАЛЬНЫХ ПАРАМЕТРОВ § 17.7. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЯ В БАЛКАХ ГРАФО-АНАЛИТИЧЕСКИМ МЕТОДОМ § 18.7. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ БАЛОК Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 8. ТЕОРИИ ПРОЧНОСТИ § 1.8. КЛАССИЧЕСКИЕ И ЭНЕРГЕТИЧЕСКАЯ ТЕОРИИ ПРОЧНОСТИ § 2.8. ТЕОРИЯ ПРОЧНОСТИ МОРА § 3.8. ЕДИНАЯ ТЕОРИЯ ПРОЧНОСТИ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки § 1.9. КОСОЙ ИЗГИБ § 2.9. ВНЕЦЕНТРЕННОЕ РАСТЯЖЕНИЕ И СЖАТИЕ БРУСЬЕВ БОЛЬШОЙ ЖЕСТКОСТИ § 3.  9. ЯДРО СЕЧЕНИЯ 9. ЯДРО СЕЧЕНИЯ§ 4.9. ИЗГИБ С КРУЧЕНИЕМ БРУСЬЕВ КРУГЛОГО СЕЧЕНИЯ § 5.9. ОБЩИЙ СЛУЧАЙ ДЕЙСТВИЯ СИЛ НА БРУС КРУГЛОГО СЕЧЕНИЯ § 6.9. ПОСТРОЕНИЕ ЭПЮР ВНУТРЕННИХ УСИЛИЙ ДЛЯ ПРОСТРАНСТВЕННЫХ БРУСЬЕВ С ЛОМАНОЙ ОСЬЮ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 10. РАСЧЕТ КРИВЫХ БРУСЬЕВ § 2.10. ЭПЮРЫ ВНУТРЕННИХ УСИЛИЙ § 3.10. НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ В ПОПЕРЕЧНЫХ СЕЧЕНИЯХ БРУСА БОЛЬШОЙ КРИВИЗНЫ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 11. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЯ В УПРУГИХ СИСТЕМАХ § 1.11. РАБОТА ВНЕШНИХ СИЛ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ § 2.11. ТЕОРЕМА О ВЗАИМНОСТИ РАБОТ § 3.11. ТЕОРЕМА О ВЗАИМНОСТИ ПЕРЕМЕЩЕНИЯ 4.11. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЯ. ИНТЕГРАЛ МОРА § 5.11. ПРАВИЛО ВЕРЕЩАГИНА Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 12. РАСЧЕТ ПРОСТЕЙШИХ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СТЕРЖНЕВЫХ СИСТЕМ § 1.  § 2.12. КАНОНИЧЕСКИЕ УРАВНЕНИЯ МЕТОДА СИЛ § 3.12. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ § 4.12. ИСПОЛЬЗОВАНИЕ СИММЕТРИИ § 5.12. ПОСТРОЕНИЕ ЭПЮР ПОПЕРЕЧНЫХ И ПРОДОЛЬНЫХ СИЛ § 6.12. ПРОВЕРКА ПРАВИЛЬНОСТИ ЭПЮР М, Q И N § 7.12. НЕРАЗРЕЗНЫЕ БАЛКИ ПРИМЕРЫ РАСЧЕТА Вопросы для самопроверки Глава 13. ПРОДОЛЬНЫЙ ИЗГИБ ПРЯМОГО СТЕРЖНЯ § 1.13. ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ РАВНОВЕСИЯ УПРУГИХ ТЕЛ § 2.13. ПРОДОЛЬНЫЙ ИЗГИБ § 3.13. ПОТЕРЯ УСТОЙЧИВОСТИ ПРИ НАПРЯЖЕНИЯХ, ПРЕВЫШАЮЩИХ ПРЕДЕЛ ПРОПОРЦИОНАЛЬНОСТИ § 4.13. ПРАКТИЧЕСКИЕ РАСЧЕТЫ СТЕРЖНЕЙ НА УСТОЙЧИВОСТЬ § 5.13. ПРОДОЛЬНО-ПОПЕРЕЧНЫЙ ИЗГИБ Задачи для самостоятельного решения Вопросы для самопроверки Глава 14. ДИНАМИЧЕСКАЯ НАГРУЗКА § 2.14. ДИНАМИЧЕСКИЕ ЗАДАЧИ, ПРИВОДИМЫЕ К ЗАДАЧАМ СТАТИЧЕСКОГО РАСЧЕТА СИСТЕМ § 3.14. УДАР § 4.14. ЧАСТНЫЕ СЛУЧАИ УДАРНОГО ДЕЙСТВИЯ НАГРУЗКИ § 5.14. КОЛЕБАНИЯ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 15.  НАПРЯЖЕНИЯ, ПЕРЕМЕННЫЕ ВО ВРЕМЕНИ НАПРЯЖЕНИЯ, ПЕРЕМЕННЫЕ ВО ВРЕМЕНИ§ 1.15. ПЕРЕМЕННЫЕ НАПРЯЖЕНИЯ. УСТАЛОСТЬ § 2.15. ПРЕДЕЛ ВЫНОСЛИВОСТИ § 3.15. ДИАГРАММЫ ПРЕДЕЛЬНЫХ АМПЛИТУД И ПРЕДЕЛЬНЫХ НАПРЯЖЕНИИ § 5.15. РАСЧЕТ НА ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАПРЯЖЕНИЯХ Примеры расчета Вопросы для самопроверки Глава 16. ТОНКОСТЕННЫЕ ОСЕСИММЕТРИЧНЫЕ ОБОЛОЧКИ И ТОЛСТОСТЕННЫЕ ЦИЛИНДРЫ § 1.16. РАСЧЕТ ТОНКОСТЕННЫХ ОСЕСИММЕТРИЧНЫХ ОБОЛОЧЕК § 2.16. РАСЧЕТ ТОЛСТОСТЕННЫХ ЦИЛИНДРОВ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 17. РАСЧЕТ КОНСТРУКЦИЙ ПО НЕСУЩЕЙ СПОСОБНОСТИ § 2.17. РАСТЯЖЕНИЕ И СЖАТИЕ § 3.17. КРУЧЕНИЕ ПРЯМОГО БРУСА КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ § 4.17. ИЗГИБ БАЛОК § 5.17. МЕТОД РАСЧЕТА КОНСТРУКЦИЙ ПО РАСЧЕТНЫМ ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ Примеры расчета Вопросы для самопроверки ПРИЛОЖЕНИЯ |
1.
 Вывод формул для моментов инерции простейших фигур (прямоугольник, треугольник, круг)
Вывод формул для моментов инерции простейших фигур (прямоугольник, треугольник, круг)Прямоугольное сечение.
Прямоугольное сечение имеет две оси симметрии, а главные центральные оси Сx и Cy проходят через середины параллельных сторон.
Главный центральный момент инерции относительно оси x
Элементарную площадку dA в этом случае можно представить в виде полоски во всю ширину сечения и толщиной dy, значит dA=b*dy. Подставим под знак интеграла значение dA и проинтегрировав по всей площади, т.е. в пределах изменения ординаты y от –h/2 до +h/2, получим
Окончательно
Аналогично получим формулу главного центрального момента инерции прямоугольника относительно оси y:
Круглое сечение
Для круга главные центральные моменты инерции относительно осей x и y равны между собой.
Поэтому из равенства
Треугольник
2.
 Изменение моментов инерции при переходе от центральных осей к параллельным:
Изменение моментов инерции при переходе от центральных осей к параллельным:Jx1=Jx + a2А;
Jy1=Jy + b2А;
момент инерции относительно любой оси равен моменту инерции относительно центральной оси, параллельной данной, плюс произведение площади фигуры на квадрат расстояния между осями. Jy1x1=Jyx + abF; (“a” и “b” подставляют в формулу с учетом их знака).
3.Изменение моментов инерции при повороте осей
Jx1=Jxcos2 + Jysin2 — Jxysin2; Jy1=Jycos2 + Jxsin2 + Jxysin2;
Jx1y1=(Jx — Jy)sin2 + Jxycos2 ;
Угол
>0,
если переход от старой системы координат
к новой происходит против час. стр. Jy1 + Jx1=
Jy + Jx
стр. Jy1 + Jx1=
Jy + Jx
Экстремальные (максимальное и минимальное) значения моментов инерции называются главными моментами инерции. Оси, относительно которых осевые моменты инерции имеют экстремальные значения, называются главными осями инерции. Главные оси инерции взаимно перпендикулярны. Центробежные моменты инерции относительно главных осей = 0, т.е. главные оси инерции — оси, относительно которых центробежный момент инерции = 0. Если одна из осей совпадает или обе совпадают с осью симметрии, то они главные. Угол, определяющий положение главных осей: , если
0>0 оси поворачиваются против час.стр. Ось максимума всегда составляет меньший угол с той из осей, относительно которой момент инерции имеет большее значение. Главные оси, проходящие через центр тяжести, называются главными центральными осями инерции. Моменты инерции относительно этих осей:
Jmax + Jmin=
Jx + Jy. Центробежный момент инерции относительно
главных центральных осей инерции равен
0. Если известны главные моменты инерции,
то формулы перехода к повернутым осям:
Центробежный момент инерции относительно
главных центральных осей инерции равен
0. Если известны главные моменты инерции,
то формулы перехода к повернутым осям:
Jx1=Jmaxcos2 + Jminsin2; Jy1=Jmaxcos2 + Jminsin2; Jx1y1=(Jmax — Jmin)sin2;
4.Классификация элементов конструкций
Стержнем наз. Геом тела у которых один из размеров много больше других.
Пластины или оболочки – это геом тела у которых один из размеров << других
Массивные тела– все размеры одного порядка
5.Основные допущения о свойствах материала
Однородные – в люб. точке материалы имеют одинак. физико-химич. св-ва;
Сплошная среда – кристаллич. строение и микроскопич. дефекты не учитываются;
Изотропны
– механич. св-ва не зависят от направления
нагружения;
св-ва не зависят от направления
нагружения;
Идеальная упругость – полностью восстанавливают форму и размеры после снятия нагрузки.
6.Типы опор
а) Шарнирно – неподвижная (двухсвязная) опора: Воспринимает как вертикальные, так и горизонтальные усилия (усилия под углом).
б) Шарнирно – подвижная опора – воспринимает только вертикальные нагрузки. Реакция опоры всегда направлена вдоль опорного стержня, перпендикулярно опорной поверхности
в) Жесткая заделка (трехсвязная)
Реакции в опорах определяют из условия равновесия (уравнение статики).
7.Классификация нагрузок
По месту действия
Поверхностные и объемные
а) сосредоточенная сила
б) распределенная сила
прямоугольная Rq= qa
треугольная Rq= ½ qa
в) сосредоточенный момент
изгибающий
скручивающий
г) распределенный момент
Rmz= mz a –равнодейств распр мом
По времени действия
Постоянные и временные
По характеру действия
Статические и динамические
По характеру возникновения
Активная(известны) и реактивная (неизвестны)
8. Основные
принципы изучаемого курса
Основные
принципы изучаемого курса
При расчете сложного сопротивления используется принцип независимости действия сил. Сложный вид нагружения представляется как система простых видов нагружения действующих независимо друг от друга. Решение при сложном сопротивлении получается в результате сложения решений полученных при простых видах нагружения.
принцип Сен-Венана
на достаточном удалении от места приложения нагрузки характер её воздействия не зависит от способа её приложения, а зависит от величины равнодействующей.
9.Внутренние усилия. Метод сечений (Метод РОЗУ)
Nz=∑z (pi) нормальная с
Qx=∑x (pi) поперечная с
Qy=∑y (pi)
Mz=∑mz (pi) крутящий момент
Mx=∑mx (pi) изгибающий
My=∑my (pi)
Разрезаем мысл тело плоск
Отбрасываем одну из г внутр усил
Заменяем внутр усилиями
Уравновешив внутр ус внеш нагр
10. Правило
знаков внутренних усилий
Правило
знаков внутренних усилий
Правило знаков поперечных сил при изгибе:
Крутящий момент
Против ЧС при взгляде со стороны сеч то +
Правило знаков изгибающих моментов:
Правило проверки правильности построения эпюр нагружения:
В сечениях балки, где приложены внешние сосредоточенные нагрузки на эпюре д.б. скачёк на величину этой нагрузки.
11.Эпюры внутренних усилий
ПРИ РАСТЯЖЕНИИ-СЖАТИИ
ПРИ КРУЧЕНИИ
при прямом изгибе
12.Дифференциальные зависимости при изгибе
; ;
13.Следствия из дифференциальных зависимостей
Если на участке нет распр нагр (q=0) то поперечная сила на этом участке имеет пост вел.
 , а эпюры изгиб мом
меняются по лин закону
, а эпюры изгиб мом
меняются по лин законуНа уч на котором присутст распр нагр пост интенсивн. Поперечная сила меняется по лин зак , а эпюры по закону квадр параболы. Причем эпюра мх всегда напр навстречу распр нагрузке. Где Qy равно 0 эпюра мх имеет экстремум. Если Qy равно 0 на всем участке, то мх постоян величину
4. На участке где Qy>0 эпюра мх возрастает слева направо
5. В том сеч. где приложена сосред сила эпюра Qy имеет скачок на вел этой силы. В сеч где сосред момент эпюра мх имеет скачок на величену этого момента
Момент инерции окружности – объяснение, формула и часто задаваемые вопросы
Дата последнего обновления: 20 апреля 2023 г. Обсудите основную концепцию момента инерции простыми словами. Можно сделать вывод, что инерция связана с массой тела. Когда тело начинает двигаться во вращательном движении вокруг постоянной оси, каждый элемент тела движется по петле с линейной скоростью, т.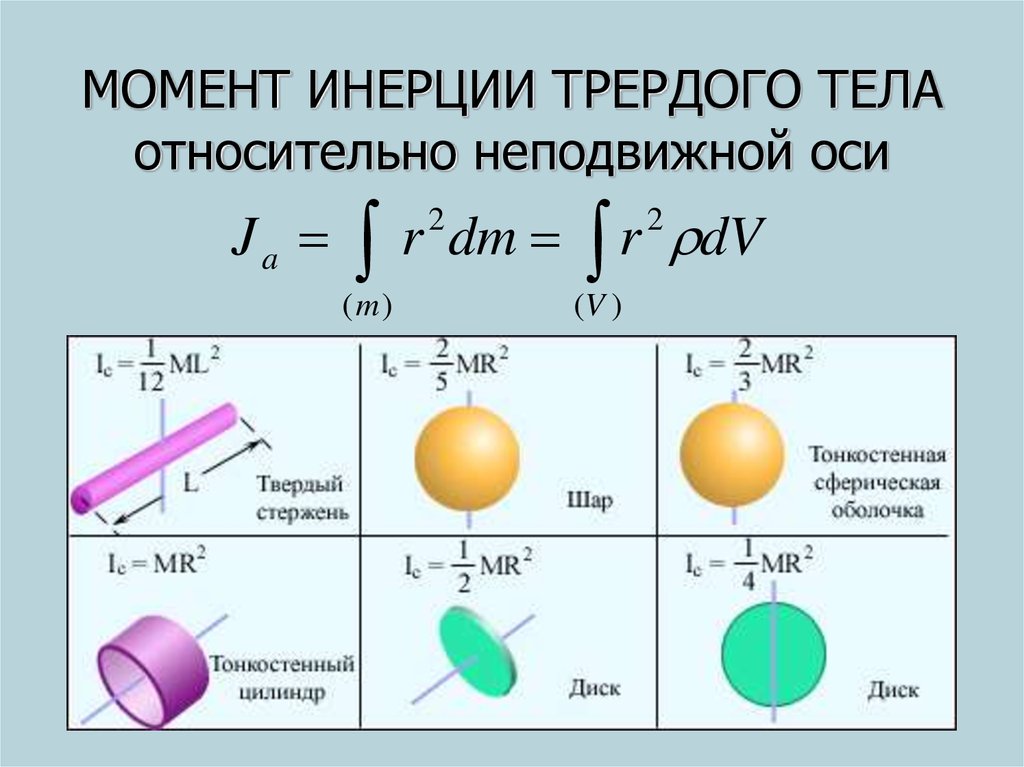 е. каждая частица движется с угловым ускорением. Да, правильное определение момента инерции состоит в том, что тело стремится бороться с угловым ускорением. Математически это сумма произведения массы каждой частицы в теле на квадрат ее длины от оси вращения.
е. каждая частица движется с угловым ускорением. Да, правильное определение момента инерции состоит в том, что тело стремится бороться с угловым ускорением. Математически это сумма произведения массы каждой частицы в теле на квадрат ее длины от оси вращения.
Формула момента инерции может быть представлена следующим образом:
I = момент инерции = Σ miri2
Здесь m = масса тела
r = радиус окружности
(изображение будет загружено в ближайшее время)
Момент инерции = I = πR4/4
(Изображение скоро будет загружено)
Момент инерции = I = 5πR4/4
Момент инерции = I = 5πR4/2
инерция = I = πR4/8
Момент инерции = I = πR4/16
Момент инерции окружности относительно ее диаметра
Если мы рассматриваем диаметр окружности D, то мы также должны принять «r» радиус как D/2.
Ось проходит через центр.
Это выражение для момента инерции окружности относительно ее диаметра можно представить как
I = π D4/64.
Момент инерции окружности Вывод
Вы знаете, как найти момент инерции окружности? Чтобы узнать об этом, нам нужно понять вывод момента инерции окружности, как объясняется ниже. По такому выводу проще будет понять, как найти момент инерции окружности.
Формула момента инерции окружности, в соответствии с выводом, круглое поперечное сечение будет рассчитываться с радиусом и осью, проходящей точно через центр. Это объяснение будет следовать определенным шагам, таким как:
Описать систему координат.
Откройте для себя дифференциальную зону.
Наконец, интегрируйте его.

Шаг: 1
Начнем с того, что вспомним уравнение для площади второго момента. Это уравнение выражено ниже:
∫A∫ z2 по DZ = Iy
∫ z2 da = Iy
Это составляющая MOI по оси y.
Теперь давайте просто опишем координаты, применяя полярную систему.
После подачи заявки приобретаем;
r sin θ = z
r cos θ = y
Шаг: 2
После завершения шага-1 нам необходимо вычислить дифференциальную площадь, что может быть достигнуто путем объявления площади сектора.
На изображении площадь сектора может быть выражена как;
A = ½r2dθ
Теперь после дифференцирования выражение будет получено как;
dA = rdrdθ
Шаг: 3
Теперь просто запишем интеграл для момента инерции окружности.
Выражение будет;
o∫2πo∫r(r sin θ)2rdrdθ = Iy
Просто упростим это интегрирование с соответствующими шагами: ] dθ = Iy
o∫2π sin2θ [r4/4]ordθ = Iy
r4/4o∫2πsin2θ = Iy
Как мы знаем о тригонометрическом тождестве, т. е.
е.
sin2θ = 1 – cos2θ/2 ——-eq(1)
Подставим значение в интеграл . Выражение будет иметь вид: )
½θ–½sin(2θ)o2π = Iy
r4/4
½(2π)–¼sin(4π)–½(0)+¼sin(0)
½(2π)–¼sin(4π)– ½(0)+¼sin(0)o2π = Iy
r4/4 (π – 0 – 0 + 0) = Iy
πr4/4 = Iy
В некоторых случаях существует возможность рассчитать M.O.I круга относительно его оси, касательной к периметру, тогда попрактиковаться в теореме о параллельных осях.
По теореме;
I + Ad2 = II
Итак, нам нужно учесть некоторые факторы, такие как
d = r
I = πR4/4
A = πR2
Давайте просто подставим значение в уравнение ( 1):
πR4/4 + πR2/4= II
5πR4/4 = II
Момент инерции окружности Формула
I = πR4/4 – МВД круга
I = πD4/64 – МВД кругового сечения, перпендикулярного оси сечение
I = 5πR4/4 – МВД окружности относительно оси, касательной к периметру (окружности)
I = 5πR4/2 – полярный момент инерции
I = πR4/2 – Корпус полукруга
I = πR4/16 – Случай четверти окружности
Закон инерции-применения в механике.

Согласно первому закону движения Ньютона никто сам по себе не может изменить свое состояние покоя или равномерного прямолинейного движения. Эта инертность или инертность тела называется инерцией. Очевидно, что для изменения состояния покоя или равномерного движения тела по прямой требуется внешняя сила. Чем больше сила, необходимая для изменения состояния тела, тем больше его инерция. следовательно, чтобы создать или разрушить заданную равномерную силу ускорения, требуется прямо пропорционально массе тела. Ясно, что чем тяжелее тело, тем больше сила, необходимая для изменения его состояния, и, следовательно, больше его инерция. Верно и обратное. Масса Поэтому тело является мерой его инерции при поступательном движении. Инерция тела зависит только от его массы, момент инерции тела относительно данной оси зависит от его массы, положения и направления оси вращения. также зависит от формы тела. Это связано с тем, что два тела, имеющие одинаковую массу, но разную форму, будут иметь разные моменты инерции относительно данной оси вращения.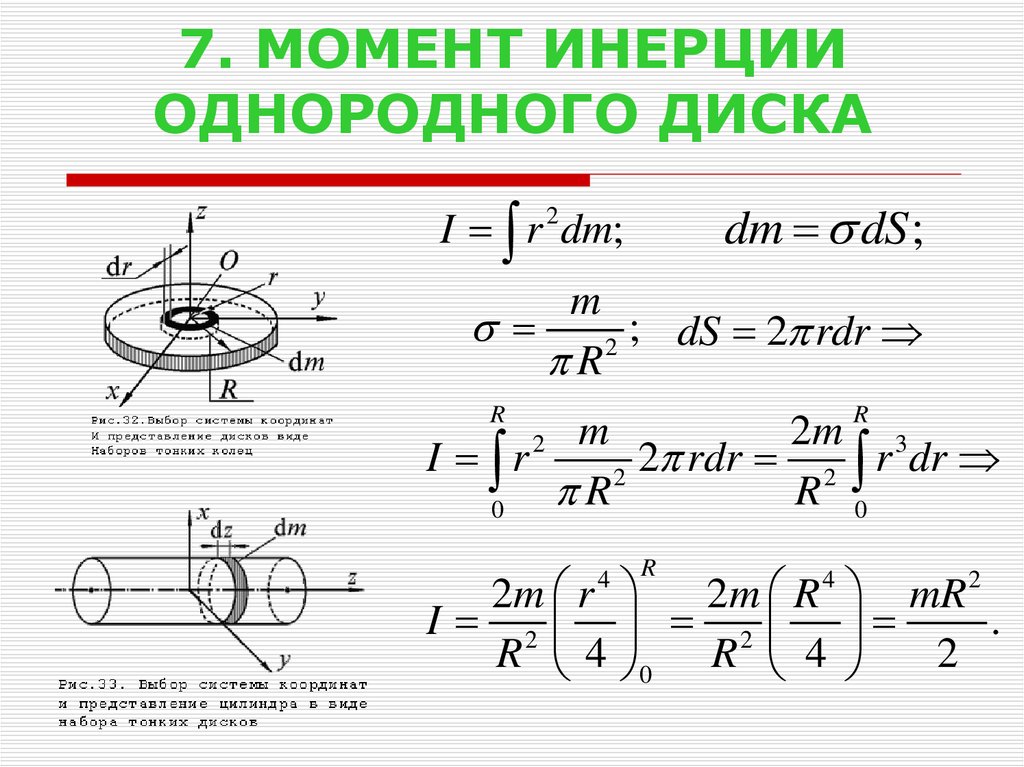 2 дА
2 дА
, где A — площадь фигуры, а y — расстояние от любой точки внутри области A до заданной оси вращения.
Из этого определения становится ясно, что момент инерции не является свойством только формы, но всегда связан с осью вращения. Однако часто можно использовать термин «момент инерции окружности», отсутствующий для указания оси. В зависимости от контекста может подразумеваться ось, проходящая через центр, однако для более сложных форм не гарантируется, что подразумеваемая ось будет очевидна.
Из определения также видно, что момент инерции всегда должен иметь положительное значение, так как внутри интеграла есть только квадратный член.
Нахождение уравнения для момента инерции окружности
Используя приведенное выше определение, применимое для любой замкнутой формы, мы попробуем прийти к окончательному уравнению для момента инерции окружности вокруг оси x, проходящей через его центр. Сначала мы должны определить систему координат. Поскольку у нас есть круглая область, декартова система x,y не лучший вариант. Вместо этого мы выбираем полярную систему с полюсом O, совпадающим с центром окружности, и полярной осью L, совпадающей с осью вращения x, как показано на рисунке ниже. Независимыми переменными являются r и φ. В частности, для любой точки плоскости r — это расстояние от полюса, а φ — это угол от полярной оси L, измеренный против часовой стрелки.
Вместо этого мы выбираем полярную систему с полюсом O, совпадающим с центром окружности, и полярной осью L, совпадающей с осью вращения x, как показано на рисунке ниже. Независимыми переменными являются r и φ. В частности, для любой точки плоскости r — это расстояние от полюса, а φ — это угол от полярной оси L, измеренный против часовой стрелки.
В этой системе координат дифференциальная площадь dA теперь принимает вид: dA=dr\: ds = dr \:(rd\varphi)=r\:dr \:d\varphi, где ds — дифференциальная длина дуги для дифференциального угла дφ.
Кроме того, область, заключенная в круг, должна иметь следующие границы:
- r\in [0,R]
- \varphi \in [0,2\pi]
Кроме того, координата y точки любая точка может быть выражена через полярные координаты r и φ. Для этого рассмотрим для произвольной точки P (см. рисунок) прямоугольный треугольник синего цвета и с помощью простой тригонометрии найдем: y=r \sin\varphi 94}{4}
Получается, что новый момент инерции резко увеличен по сравнению с центроидальным. Это более общая характеристика. Поскольку расстояние от центра тяжести квадратично, оно влияет на момент инерции гораздо больше, чем площадь A.
Это более общая характеристика. Поскольку расстояние от центра тяжести квадратично, оно влияет на момент инерции гораздо больше, чем площадь A.
Массовый момент инерции
В физике термин момент инерции имеет другое значение. Это связано с распределением массы объекта (или нескольких объектов) вокруг оси. Это отличается от определения, которое обычно дается в инженерных дисциплинах (также на этой странице) как свойство площади формы, обычно поперечного сечения, вокруг оси. Срок 903:43 второй момент области кажется более точным в этом отношении.
Применение
Момент инерции (второй момент или площадь) используется в теории балок для описания жесткости балки на изгиб (см. теорию изгиба балки). Изгибающий момент M, приложенный к поперечному сечению, связан с его моментом инерции следующим уравнением:
M = E\times I \times \kappa
где E – модуль Юнга, свойство материала, и κ искривление балки из-за приложенной нагрузки. Кривизна балки κ описывает степень изгиба в балке и может быть выражена через прогиб балки w(x) вдоль продольной оси балки x, как: \kappa = \frac{d^2 w(x)}{dx^2 } .

 , а эпюры изгиб мом
меняются по лин закону
, а эпюры изгиб мом
меняются по лин закону