Помогите решить / разобраться (Ф)
Сообщения без ответов | Активные темы | Избранное
| fronnya |
| ||
27/03/14 |
| ||
| |||
| melnikoff |
| ||
02/04/13 |
| ||
| |||
| fronnya |
| ||
27/03/14 |
| ||
| |||
| melnikoff |
| ||
02/04/13 |
| ||
| |||
| fronnya |
| ||
27/03/14 |
| ||
| |||
| Ms-dos4 |
| |||
25/02/08 |
| |||
| ||||
| fronnya |
| ||
27/03/14 |
| ||
| |||
| Munin |
| |||
30/01/06 |
| |||
| ||||
| fronnya |
| ||
27/03/14 |
| ||
| |||
| Munin |
| |||
30/01/06 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 10 ] |
Модераторы: photon, whiterussian, profrotter, Jnrty, Aer, Парджеттер, Eule_A, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
|
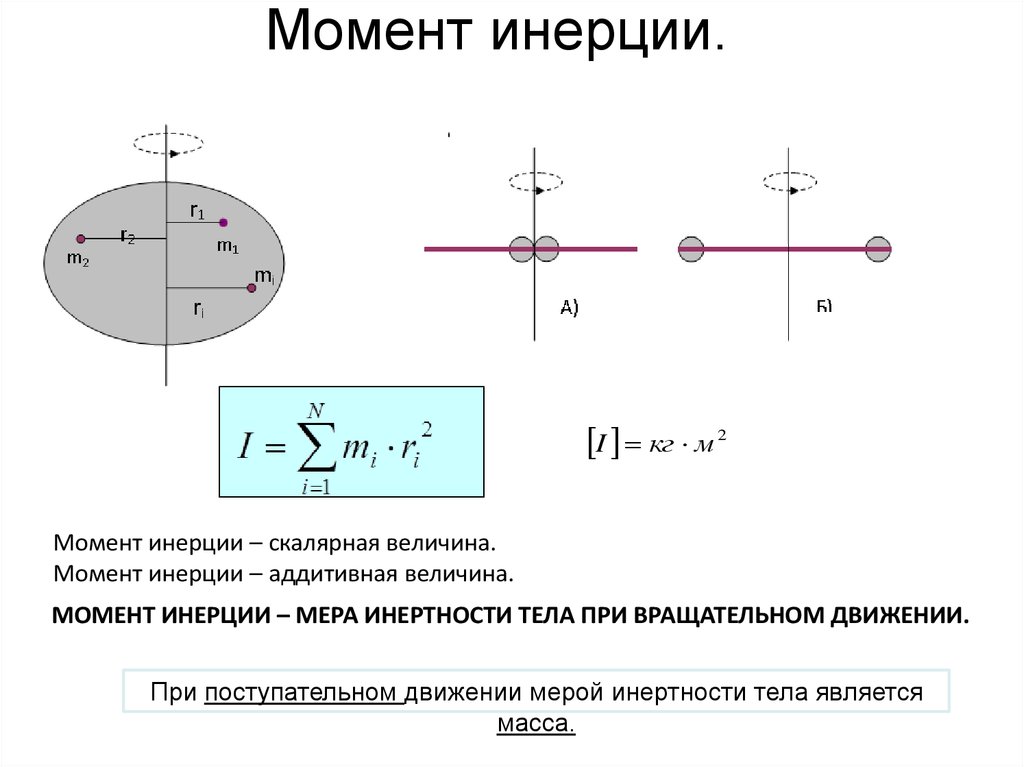
ЦЕЛЬ РАБОТЫ 1. 2. Определить экспериментальные значения моментов инерции тел различной формы. 3. Рассчитать теоретические значения моментов инерции тех же тел.
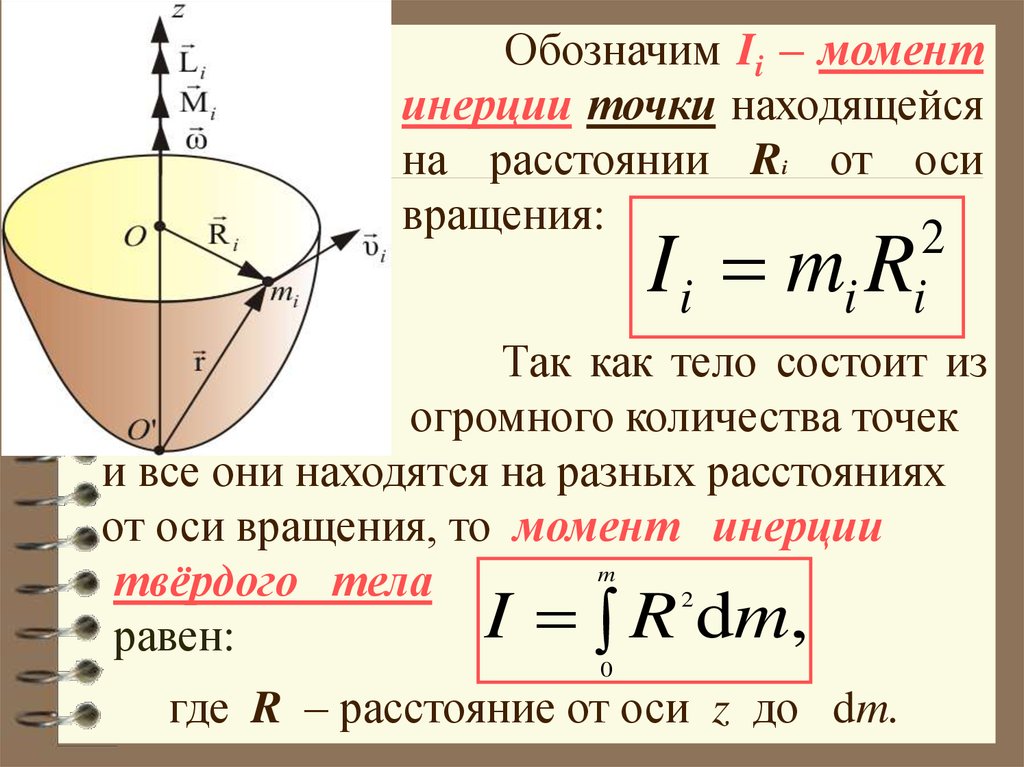
КРАТКАЯ ТЕОРИЯ Момент инерции I является мерой инертности тел при вращательном движении. Для тела или системы тел эта величина равна сумме моментов инерции всех точек Ii этого тела или системы тел: (127) где mi – масса материальной точки (частицы тела), ri – расстояние от этой точки до оси вращения. Следовательно, значение момента инерции зависит от размеров, формы, массы тела, а также от расположения тела относительно оси вращения. Исследуемыми телами в данной работе являются стальные образцы в форме куба и параллелепипедов. Схема установки дана на рисунке 25. Рис. 25
Рамка 1 закреплена на натянутых стальных проволоках 2 и 6, проходящих по ее геометрической оси. Из формулы (124) для циклической частоты колебаний период Т0 колебаний пустой рамки равен: (128) Если к рамке добавить два цилиндра 3 (рис.), находящихся на расстоянии а от оси рамки, то период Т крутильных колебаний такой системы тел увеличится: (129) Здесь I – момент инерции цилиндров, который можно определить по теореме Штейнера: (130) где m – масса одного цилиндра, r – его радиус, a – расстояние между осью проволоки и осью цилиндра (рис. 25). Решая систему двух уравнений (128) и (129), можно исключить неизвестную величину модуля кручения с проволоки и найти значение момента инерции Ip рамки: (131) Чтобы найти момент инерции куба или параллелепипеда, цилиндры 3 снимают с рамки и закрепляют в ней исследуемое тело 5 (рис. Определив период крутильных колебаний Т1 рамки с данным телом с помощью электронного блока, можно рассчитать момент его инерции I1 по формуле: (132) Эти же значения моментов инерции можно рассчитать теоретически по формулам, которые выводят из определения (127): (133) где m1 – масса куба (или параллелепипеда), b и d – длины сторон образца, расположенных в горизонтальной плоскости.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 1. Установить рамку так, чтобы при ее вращении флажок рамки 8 (рис. 25) свободно перемещался между окнами фотодатчика 7. 2. Включить электропитание нажатием клавиши «СЕТЬ» на задней стенке электронного блока ФМ 1/1. 3. Повернуть пустую рамку так, чтобы она удерживалась в исходном положении электромагнитом. 4. Нажав кнопку «ПУСК» на электронном блоке, измеряют t0 время N полных колебаний рамки. 5. Установить цилиндры 3 на рамку. Определить t время N полных колебаний. Повторить измерения 3 – 5 раз. 6. Снять цилиндры 3 с рамки. Установить в рамке куб с помощью винтов на перекладине 4. Определить t1 время N полных колебаний. Повторить измерения 3 – 5 раз. 7. Заменить куб в рамке на параллелепипед. Определить t2 время N полных колебаний, повторив измерения 3 – 5 раз. 8. Поменять положение параллелепипеда в рамке и определить t3 время N полных колебаний. 9. Рассчитать момент инерции Ip пустой рамки по формуле (131). 10. Рассчитать экспериментальные значения моментов инерции куба и параллелепипеда по формуле (132). 11. Оценить погрешности экспериментальных значений моментов инерции. 12. Рассчитать теоретические значения моментов инерции тел по формуле (133). 13. Сравнить экспериментальные значения с теоретическими. Сделать вывод о зависимости момента инерции тела от его массы, формы, размеров и положения тела относительно оси вращения.
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Что собой представляет деформация кручения? Как записывается закон Гука для кручения? 2. Сформулируйте основной закон динамики для вращательного движения. 3. Какой вид имеет динамическое уравнение крутильных колебаний? Какой вид имеет кинематическое уравнение этого движения? 4. От чего зависит период крутильных колебаний? 5. Что такое момент инерции материальной точки (частицы)? Момент инерции тела или системы тел? От чего зависит значения момента инерции? 6. Сформулируйте теорему Штейнера. Выведите формулу (130). 7. Выведите формулы (131) и (132).
ЛИТЕРАТУРА 1. Трофимова Т.И. Курс общей физики. – М.: Высшая школа. 2004 г. 2. Савельев И.В. Курс общей физики. 3. Бордовский Г.А., Бурсиан Э.В. Общая физика. Курс лекций. – М.: Изд-во ВЛАДОС – ПРЕСС, 2001. – Т.1 123456 Читайте также: |
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ. Моментом инерции материальной точки называют скалярную физическую величину, равную произведению массы точки на квадрат расстояния от оси ее вращения
Поделись
КРАТКАЯ ТЕОРИЯ.
Моментом инерции материальной точки называют скалярную физическую величину, равную произведению массы точки на квадрат расстояния от оси ее вращения
I = mr2.
Всякое тело можно рассматривать как совокупность некоторого числа материальных точек. Поэтому момент инерции тела определяется суммой моментов инерции всех его материальных точек
.
Момент инерции характеризует инертность тела при вращательном движении. Он входит в ряд важных физических соотношений, определяющих момент импульса и кинетическую энергию твердых тел, вращающихся вокруг неподвижной оси
С помощью момента инерции удобно представлять второй закон Ньютона для вращающихся тел.
`M = I `b
Определение момента инерции тел является довольно сложной математической задачей. Поэтому весьма часто момент инерции тела определяют экспериментально с помощью крутильного маятника.
Известно, что при небольших углах закручивания крутильный маятник совершает гармонические колебания, период которых определяется по формуле
, (1)
где I – момент инерции маятника, D– некоторая постоянная, характеризующая упругие свойства подвеса.
Увеличим момент инерции крутильного маятника, закрепив на нем тело с моментом инерции I1. Период колебаний маятника также увеличится и станет равным
. (2)
(2)
Если закрепить другое тело с моментом инерции I2, период колебаний маятника станет
. (3)
Исключая из формул (2) и (3) неизвестные величины I0 и D, получим простую формулу, с помощью которой можно сравнивать моменты инерции двух тел
. (4)
Здесь T0 – период колебаний ненагруженного маятника, T1 – период колебаний маятника, когда на нем закреплено тело с моментом инерции I1 , T2 – период колебаний маятника, когда на нем закреплено тело с моментом инерции I2.
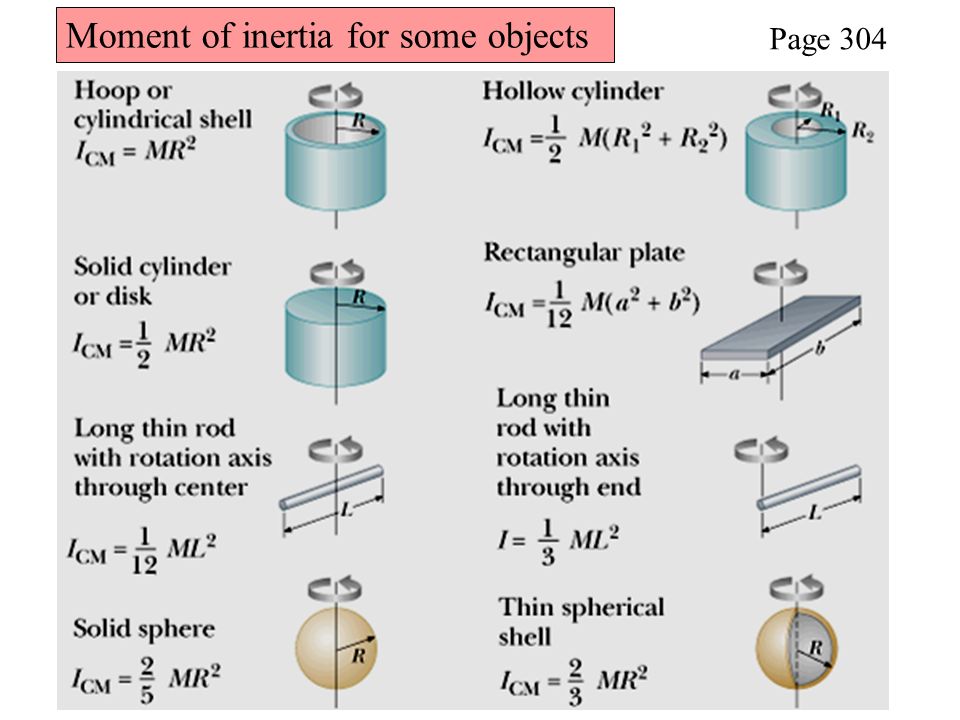
В случае однородных тел правильной формы момент инерции легко вычислить. В результате можно получить формулы, связывающие моменты инерции тел с их массой и размерами.
Момент инерции прямого кругового цилиндра с радиусом основания R относительно оси, проходящий через центр масс, параллельно образующей, будет равен
. (5)
(5)
Момент инерции однородного шара с радиусом R относительно оси, проходящей через его центр масс, будет равен
. (6)
Момент инерции однородного куба с ребром a относительно оси, проходящей через его центр масс перпендикулярно одной из граней, будет равен
(7)
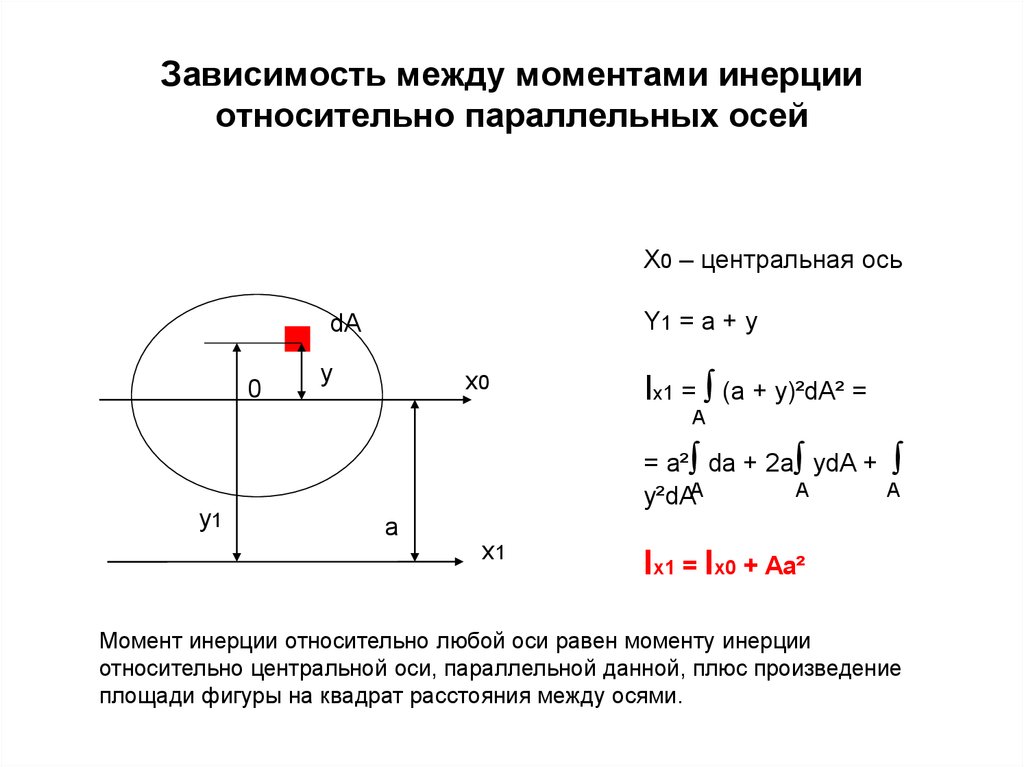
Момент инерции тела относительно оси, не проходящей через центр масс, можно определить по теореме Штейнера.
Согласно теореме Штейнера момент инерции тела относительно произвольной оси I (рис.1) превосходит его момент инерции относительно оси, проходящей через центр масс Ic параллельно данной, на величину ml2, т.е.
|
I = Ic + mℓ2 (8) Здесь m – масса тела, ℓ – расстояние между параллельными осями.
Лабораторная работа предусматривает проверку теоремы Штейнера и формул, определяющих моменты инерции тел различной формы.
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ.
Экспериментальная установка /крутильный маятник/ представлена на рис. 2. Она состоит из основания 1, на котором закреплена стойка 2 с двумя кронштейнами. На нижней части основания имеются опорные винты 3, с помощью которых производится необходимая регулировка. В зажимах 4 и 5 крепятся концы двух отрезков стальной проволоки 6. Другие концы проволоки жестко связаны с прямоугольной рамой 7, которая способна совершать крутильные колебания относительно вертикальной оси. На вертикальных гладких стержнях рамы находится горизонтальная пластинка 8 с винтом 9 для фиксации в раме исследуемых тел. Пластинка может перемещаться вдоль стержней и крепиться в нужном положении гайками 10.
Отклоненную от положения равновесия раму можно удерживать электромагнитом 11. Включение и выключение электромагнита производится тумблером 12.
На основании смонтирован пульт управления, который имеет электронный секундомер 13 и счетчик числа колебаний 14. Включение секундомера и счетчика колебаний производится автоматически с помощью фотодатчика 15 после нажатия кнопки “СБРОС”, а выключение – после нажатия кнопки “СТОП”.
ВЫПОЛНЕНИЕ РАБОТЫ.
ЗАДАНИЕ 1. Проверить теорему Штейнера I = Ic + mℓ2.
Для проверки теоремы Штейнера исследуют стальной брусок прямоугольного (квадратного) сечения. Размеры бруска L = 2a позволяют представить его в виде сложенных вместе двух однородных кубов с ребром a
.
Очевидно, что момент инерции бруска относительно продольной оси равен удвоенному моменту инерции куба
I1 = 2Ic
Здесь I1 – момент инерции бруска относительно продольной оси, Ic – момент инерции куба относительно оси, проходящей через центр масс, перпендикулярно одной из его граней.
Момент инерции бруска относительно поперечной оси, проходящей через центр бруска можно рассчитать по теореме Штейнера
I2 = 2Ic + 2mℓ2.
Здесь I2– момент инерции бруска относительно поперечной оси, Ic– момент инерции куба относительно оси, проходящей через его центр масс, m– масса куба, ℓ– расстояние между поперечной осью бруска и параллельными ей осями, проходящими через центр масс кубов.
Замечая, что , а для I1и I2получим
; ,
отношение этих моментов будет равно 2,5:
I2 /I1 = 2,5
Это необходимо проверить экспериментально.
домашних заданий и упражнений – Как рассчитать момент инерции твердого куба?
Спросил
Изменено 4 года, 2 месяца назад
Просмотрено 50 тысяч раз
$\begingroup$
Закрыто. Этот вопрос не по теме. В настоящее время ответы не принимаются.
Этот вопрос не по теме. В настоящее время ответы не принимаются.
Вопросы, похожие на домашнее задание, и вопросы проверки моей работы считаются здесь не по теме, особенно когда спрашивают о конкретных вычислениях, а не об основных понятиях физики. Домашнее задание могут быть по теме , когда они полезны для более широкой аудитории. Если вы намерены изменить свой вопрос, , пожалуйста, внимательно прочитайте приведенные выше ссылки перед редактированием. Обратите внимание, что ответы с полными решениями могут быть удалены!
Закрыт 2 года назад.
Улучшить этот вопрос
Как рассчитать момент инерции однородного сплошного куба относительно оси, проходящей через его центр масс?
Я также хотел узнать, не зависит ли момент инерции тела от его формы. Кроме того, недавно я где-то читал, что момент инерции однородного сплошного куба составляет минимум относительно оси , проходящей через его COM , потому что масса больше сосредоточена в его центре. Имеет ли это заявление какой-либо смысл?
Имеет ли это заявление какой-либо смысл?
- домашние задания и упражнения
- ньютоновская механика
- геометрия
- интеграция
- момент инерции 9\intercal$
Пример:
Один оборот $\theta$ вокруг мировой оси $z$ равен
$$E = \begin{pmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{pmatrix} $$
Если массовый момент инерции матрицы относительно главных осей $(x,y,z)$ равно
$$I_{body} = \begin{vmatrix} I_{xx} & & \\ & I_{yy} & \\ & & I_{zz} \end{vmatrix} $$
тогда массовый момент инерции относительно мировых координат 92 $$ где $r$ обозначает расстояние от центра масс объекта до оси вращения, а $I_{cm}$ — нормальный момент инерции объекта (например, приведенные выше).
$\endgroup$
$\begingroup$
Две теоремы, о которых стоит знать, когда дело доходит до вычислений, подобных этому:
1) Теорема о параллельных осях.
 2 + I_C$$ 92$ всегда будет >0 для любого ненулевого значения $x$ (смещение).
2 + I_C$$ 92$ всегда будет >0 для любого ненулевого значения $x$ (смещение).2) Теорема о перпендикулярной оси. Для пластинки (тонкого листа) момент инерции относительно оси, перпендикулярной листу, равен сумме моментов инерции относительно двух перпендикулярных осей листа.
Эта теорема удобна для вычисления момента инерции квадратной пластины массой $m$ и стороной $s$. Легко вычислить момент инерции относительно оси, лежащей в плоскости пластины и параллельной сторонам квадрата — относительно этой оси распределение массы объекта ничем не отличается от распределения стержня, для которого имеем результат 92$$
Если рассматривать куб, состоящий из пакета пластин, то момент инерции куба относительно оси, проходящей через центр масс (и через грань куба), равен выше.
Вы можете увидеть довольно полный список других моментов инерции для различных форм по этой ссылке
$\endgroup$
Очень активный вопрос .
 Заработайте 10 репутации (не считая бонуса ассоциации), чтобы ответить на этот вопрос. Требование к репутации помогает защитить этот вопрос от спама и отсутствия ответа.
Заработайте 10 репутации (не считая бонуса ассоциации), чтобы ответить на этот вопрос. Требование к репутации помогает защитить этот вопрос от спама и отсутствия ответа.куб, сфера и цилиндр · GitHub
#/usr/bin/env Python # На основе: # http://mathworld.wolfram.com/MomentofInertia.html по определению get_cube_inertia_matrix (масса, x, y, z): “””Заданные масса и размеры куба возвращают интерциальную матрицу. :возврат: ixx, ixy, ixz, ixy, iyy, iyz, ixz, iyz, izz Из https://www.  wolframalpha.com/input/?i=moment+of+inertia+cube”””
wolframalpha.com/input/?i=moment+of+inertia+cube”””ixx = (1,0 / 12,0) * (y**2 + z**2) * масса iyy = (1,0 / 12,0) * (x**2 + z**2) * масса izz = (1,0 / 12,0) * (x**2 + y**2) * масса иксу = 0,0 ixz = 0,0 iyz = 0,0 возврат [[ixx, ixy, ixz], [ixy, iyy, iyz], [ixz, iyz, izz]] def get_sphere_inertia_matrix (масса, радиус): “””Заданные масса и радиус сферы возвращают матрицу инерции. 
:возврат: ixx, ixy, ixz, ixy, iyy, iyz, ixz, iyz, izz Из https://www.wolframalpha.com/input/?i=inertia+matrix+sphere “”” ixx = iyy = izz = (2,0 / 5,0) * радиус**2 * масса иксу = 0,0 ixz = 0,0 iyz = 0,0 возврат [[ixx, ixy, ixz], [ixy, iyy, iyz], [ixz, iyz, izz]] def get_cylinder_inertia_matrix (масса, радиус, высота): “””Заданные масса и радиус и высота цилиндра возвращают матрицу инерции. 
:возврат: ixx, ixy, ixz, ixy, iyy, iyz, ixz, iyz, izz https://www.wolframalpha.com/input/?i=inertia+matrix+cylinder&rawformassumption=%7B%22C%22,+%22cylinder%22%7D+-%3E+%7B%22Solid%22%7D “”” ixx = (1,0 / 12,0) * (3,0 * радиус**2 + высота**2) * масса iyy = (1,0 / 12,0) * (3,0 * радиус**2 + высота**2) * масса izz = (1,0 / 2,0) * радиус**2 * масса иксу = 0,0 ixz = 0,0 iyz = 0,0 возврат [[ixx, ixy, ixz], [ixy, iyy, iyz], [ixz, iyz, izz]] , если __name__ == ‘__main__’: система импорта , если len(sys.  argv) < 2:
argv) < 2:print “Матрица инерции как:” print “[[ixx, ixy, ixz], [ixy, iyy, iyz], [ixz, iyz, izz]]” print “Инерция куба с массой куба 1,0 и всеми измерениями 1,0:” печать get_cube_inertia_matrix(1.0, 1.0, 1.0, 1.0) print “Сфера инерции массой 1,0 и радиусом 1,0:” печать get_sphere_inertia_matrix(1.0, 1.0) print “Цилиндр инерции массой 1,0, радиусом 1,0 и высотой 1,0:” печать get_cylinder_inertia_matrix(1.0, 1.0, 1.0) Элиф Лен (sys.  argv) == 3:
argv) == 3:печать get_sphere_inertia_matrix(float(sys.argv[1]), с плавающей запятой (sys.argv [2])) Элиф Лен (sys.argv) == 4: печать get_cylinder_inertia_matrix(float(sys.argv[1]), число с плавающей точкой (sys.argv[2]), с плавающей точкой (sys.argv[3])) Элиф Лен (sys.argv) == 5: print “Кубическая матрица инерции:” печать get_cube_inertia_matrix(float(sys.argv[1]), число с плавающей точкой (sys.  argv[2]),
argv[2]),с плавающей запятой (sys.argv [3]), с плавающей запятой (sys.argv [4])) иначе: print “Получите матрицу инерции простых фигур.” print “Использование:” печать “Для шара:” print sys.argv[0] + “массовый радиус” print “Для цилиндра:” print sys.argv[0] + “масса радиус высота” печать “Для куба:” печать sys.  argv[0] + “масса x y z”
argv[0] + “масса x y z”print “\nНапример:\n” + sys.argv[0] + “1.0 1.0 1.0 1.0” print “[[0.16666666666666666, 0.0, 0.0], [0.0, 0.166666666666666666, 0.0], [0.0, 0.0, 0.16666666666666666]]” Момент инерции куба массы m и стороны a относительно одного из его ребер равен равно 1,23ma2 2,43ma2 3,3ma2 4,83ma2 Система частиц и физика вращательного движения Практические вопросы NEET, MCQ, вопросы прошлого года (PYQ), вопросы NCERT, банк вопросов, вопросы класса 11 и класса 12 и PDF-файл, решенный с ответами
Select Question Set:
Recommended MCQs – 130 Questions Recommended PYQs (STRICTLY NCERT Based) NCERT Solved Examples Based MCQs NCERT Exercise Based MCQs MCQ AR и других типов Padma Shri HC Verma (целевые упражнения) MCQ на основе Прошлый год (2019)далее – NTA Papers) MCQ Прошлый год (2016 – 2018) MCQ Прошлый год (2006 – 2015) MCQ 8 Один из его краев равен1.
 23 MA2
23 MA22. 43 MA2
3. 3 MA2
4. 83 MA2
Q24:
52
%
- 9000
52
%
9000
52
%.0002 (1)
(2)
(3)
(4)
52
%
Подтема: Момент инерции |
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс, описанный ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Пожалуйста, сначала попробуйте ответить на этот вопрос.
Предпочитаете книги для практики вопросов? Получите уникальные книги MCQ от NEETprep с онлайн-решениями для видео/текста через Telegram Bot
High Yield NEET MCQ Books for 11 th Physics & Chemistry
Если суммарные внешние силы, действующие на систему частиц, равны нулю, то что из следующего может меняться?
1.
 Импульс системы
Импульс системы2. Скорость центра масс
3. Положение центра масс
4. Ничего из перечисленного
Q25:
Из NCERT 502
8 - 9000
(2)
(3)
(4)
Подтема: Центр масс |
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс, описанный ниже.
NEET 2023 – Целевая партия – Арьян Радж Сингх
Чтобы просмотреть объяснение, пожалуйста, пройдите пробную версию в курсе ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Пожалуйста, сначала попробуйте ответить на этот вопрос.
Предпочитаете книги для практики вопросов? Получите уникальных книг MCQ от NEETprep с онлайн Видео/текстовые решения через Telegram Bot
High Yield NEET MCQ Books for 11 th Физика и химия
Постоянный крутящий момент 1000 Н·м вращает колесо с моментом инерции 200 кг·м2 вокруг оси, проходящей через его центр . Его угловая скорость после 3 с составляет
Его угловая скорость после 3 с составляет
1. 1 рад/с
2. 5 рад/с
3. 10 рад/с
4. 15 рад/с
Q26:
83
% От НЦЭРТ
(1)
(2)
(3)
(4)
Подтема: Крутящий момент |
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс, описанный ниже.
NEET 2023 – Целевая партия – Арьян Радж Сингх
Чтобы просмотреть объяснение, пожалуйста, пройдите пробную версию в курсе ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Пожалуйста, сначала попробуйте ответить на этот вопрос.
Предпочитаете книги для практики вопросов? Получить NEETprep Уникальные книги MCQ с онлайн-версией Видео/текстовые решения через Telegram Bot
Книги NEET MCQ High Yield для 11 th Физика и химия
Точечные массы m1 и m2 размещены на противоположных концах твердой поверхности л и пренебрежимо малая масса. Стержень должен вращаться вокруг оси, перпендикулярной ему. Положение точки P на этом стержне, через которую должна проходить ось, чтобы работа, необходимая для приведения стержня во вращение с угловой скоростью ω0, была минимальной, определяется выражением
Стержень должен вращаться вокруг оси, перпендикулярной ему. Положение точки P на этом стержне, через которую должна проходить ось, чтобы работа, необходимая для приведения стержня во вращение с угловой скоростью ω0, была минимальной, определяется выражением
1. x =m1m2L2. х = m2m1L3. х = m2Lm1+ m24. x = m1Lm1+ m2
Q27:
79
% From NCERT AIPMT – 2015
(1)
(2)
(3)
(4)
Подтема: Вращательное движение: динамика |
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс, описанный ниже.
NEET 2023 – Целевая партия – Арьян Радж Сингх
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Пожалуйста, сначала попробуйте ответить на этот вопрос.
Предпочитаете книги для практики вопросов? Получите уникальных книг MCQ от NEETprep с онлайн-решениями для видео/текста через Telegram Bot
Высокодоходные книги NEET MCQ для 11 th Физика и химия
Круглый диск радиусом r имеет одинаковую толщину. Круглое отверстие диаметром, равным радиусу диска, было вырезано, как показано на рисунке. Центр тяжести оставшегося диска лежит на диаметре диска на расстоянии x левее центра исходного диска. Значение х равно
1. r
2. R2
3. R4
4. R6
Q28:
64
%
(1)
99990 %(1)
99999.%
(1) 9000
99999999999928(1)
99%9005
(1)
9999.
. )
(3)
(4)
Подтема: Центр масс |
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс, описанный ниже.
NEET 2023 – Целевая партия – Арьян Радж Сингх
Сначала попробуйте ответить на этот вопрос.
Предпочитаете книги для практики вопросов? Получите уникальные книги NEETprep MCQ с онлайн-решениями для видео/текста через Telegram Bot
High Yield NEET MCQ Books for 11 th Physics & Chemistry
Т-образный объект, размеры которого показаны на рисунке. лежа на гладком полу. В точке P, параллельной AB, приложена сила F→, так что объект совершает только поступательное движение без вращения. Найдите расположение P относительно C
1. 43L
2. I
3. 23L
4. 32L
Q29:
от NCERT
(1)
(2)
- 88999928
(2)
- 8888888899928
(2)
- 888888999928
(2)
- 8889999928
(2)
- 88899
.
 )
)(4)
Подтема: Центр масс |
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс, описанный ниже.
NEET 2023 – Целевая партия – Арьян Радж Сингх
Чтобы просмотреть объяснение, пожалуйста, пройдите пробную версию в курсе ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Пожалуйста, сначала попробуйте ответить на этот вопрос.
Предпочитаете книги для практики вопросов? Получите уникальных книг MCQ от NEETprep с онлайн-решениями для видео/текста через Telegram Bot
High Yield NEET MCQ Books for 11 th Physics & Chemistry
Колесо вращается вокруг оси2, проходящей через его центр. На него воздействует постоянный крутящий момент, противодействующий его движению в течение 8 секунд, чтобы окончательно остановить его. Значение крутящего момента в Нм составляет: (при l = 24π кг м2)
1. 48
2.
 72
723. 96
4. 120
Q30:
84
%от NCERT
(1)
(1)
- (1)
(2)
(1)
(2)
(1)(1)
9003(1)
9003(1)
9005(1).
(3)
(4)
(1)
(2)
(3)
(4)
0039
(1)
(2)
(3)
(4)
Подтема: Вращательное движение: Динамика |
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс, описанный ниже.
NEET 2023 – Целевая партия – Арьян Радж Сингх
Чтобы просмотреть объяснение, пожалуйста, пройдите пробную версию в курсе ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Пожалуйста, сначала попробуйте ответить на этот вопрос.
Предпочитаете книги для практики вопросов? Получите уникальных книг MCQ от NEETprep с онлайн-решениями для видео/текста через Telegram Bot
High Yield NEET MCQ Books for 11 th Physics & Chemistry
Утверждение: скорость вихря тревожно высока.

Причина : Если на тело не действует внешний крутящий момент, его угловая скорость сохраняется.
1. Если и утверждение, и причина верны и причина является правильным объяснением утверждения.
2. Если и утверждение, и причина верны, но причина не является правильным объяснением утверждения.
3. Если утверждение истинно, но причина ложна.
4. Если и утверждение, и причина ложны.
Q31:
от NCERT
Подтема: Угловой момент |
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс, описанный ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Пожалуйста, сначала попробуйте ответить на этот вопрос.
Предпочитаете книги для практики вопросов? Получите уникальные книги NEETprep MCQ с онлайн-решениями для видео/текста через Telegram Bot
High Yield NEET MCQ Books for 11 th Physics & Chemistry
Круглый диск A радиусом r сделан из железной пластины r толщиной t и еще один круглый диск B радиуса 2r и толщины t4.
 Отношение между моментами инерции IA и IB равно
Отношение между моментами инерции IA и IB равно1. IA> IB
2. IA = IB
3. IA
4. В зависимости от фактических значений T и R
Q32:
68
%от NCERT
|
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс, описанный ниже.
NEET 2023 – Целевая партия – Арьян Радж Сингх 9) РС. Его угловой момент относительно оси Z в кг-м2/с составляет:
1. +4
2. +8
3. -4
4. -8
Q33:
- 85
(1)
(2)
(3)
(4)
Подтема: Угловой момент |
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс, описанный ниже.
NEET 2023 – Целевая партия – Арьян Радж Сингх
Чтобы просмотреть объяснение, пожалуйста, пройдите пробную версию в курсе ниже.







 10.2014, 23:58 —
10.2014, 23:58 —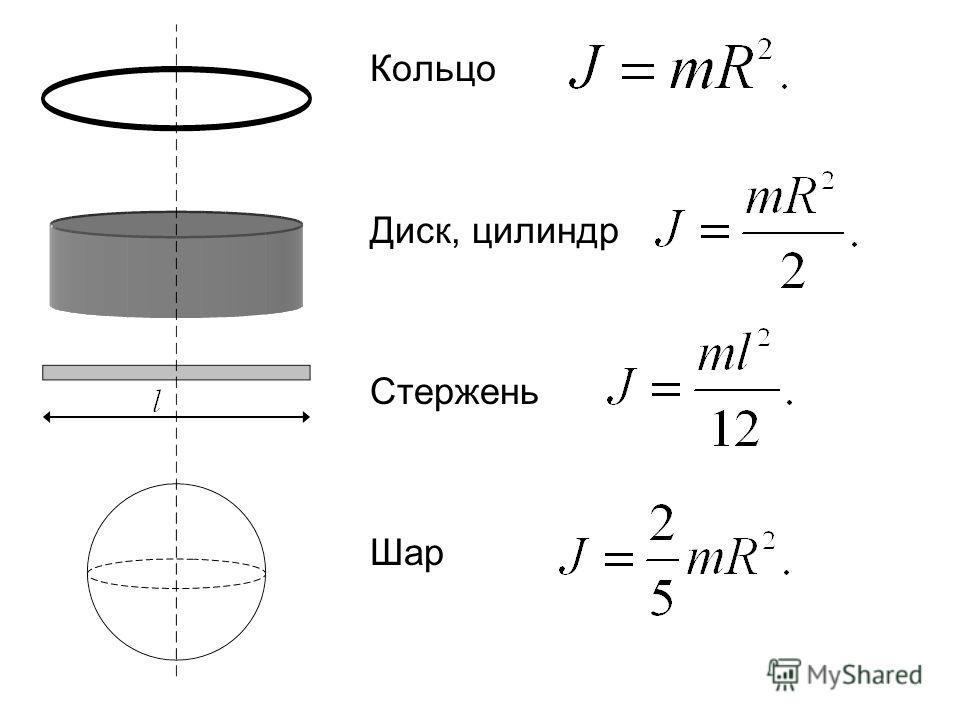

 Получается куча произведений второй степени с разными коэффициентами, матрица как раз задаёт эти коэффициенты. Так что, квадратичная форма – это однородный полином второй степени от переменных, но его свойства – удобнее всего анализировать аналогично свойствам матрицы.
Получается куча произведений второй степени с разными коэффициентами, матрица как раз задаёт эти коэффициенты. Так что, квадратичная форма – это однородный полином второй степени от переменных, но его свойства – удобнее всего анализировать аналогично свойствам матрицы.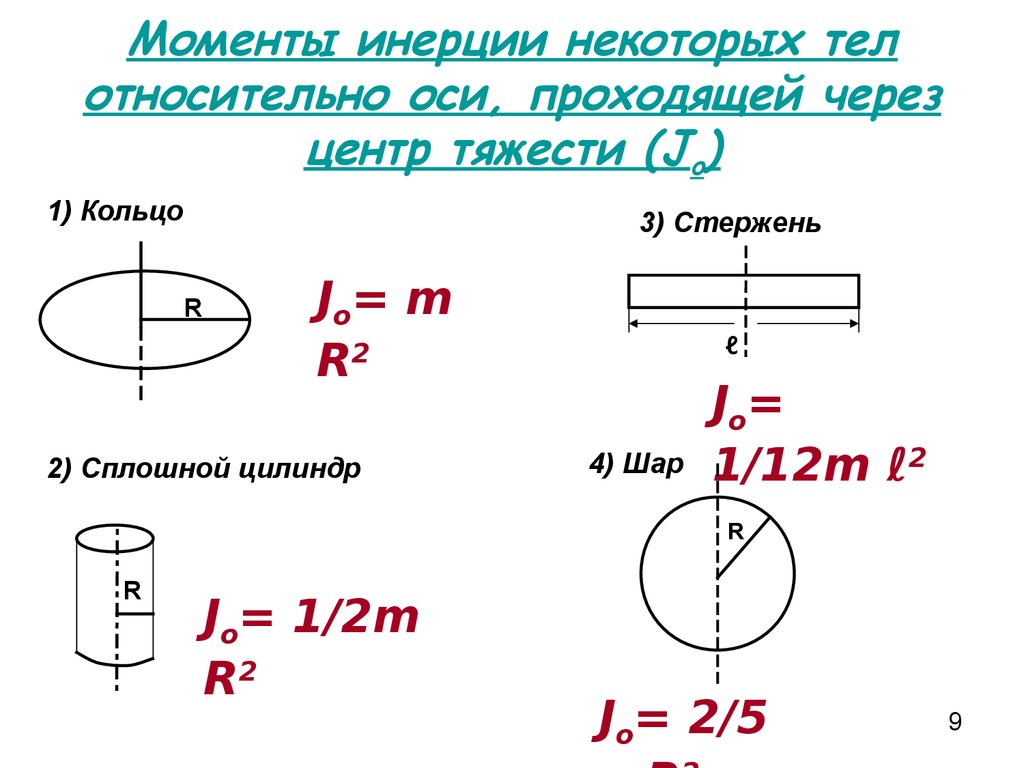 Ознакомиться с методом крутильных колебаний.
Ознакомиться с методом крутильных колебаний. Если рамку повернуть на некоторый угол , то произойдет закручивание проволоки. Возникающие силы упругости в проволоке создают вращающий момент М и заставляют рамку возвращаться в положение равновесия. Рамка совершает крутильные колебания согласно уравнению (123) (см. описание лаб. раб. № 25)
Если рамку повернуть на некоторый угол , то произойдет закручивание проволоки. Возникающие силы упругости в проволоке создают вращающий момент М и заставляют рамку возвращаться в положение равновесия. Рамка совершает крутильные колебания согласно уравнению (123) (см. описание лаб. раб. № 25) ) с помощью винтов на перекладине 4.
) с помощью винтов на перекладине 4.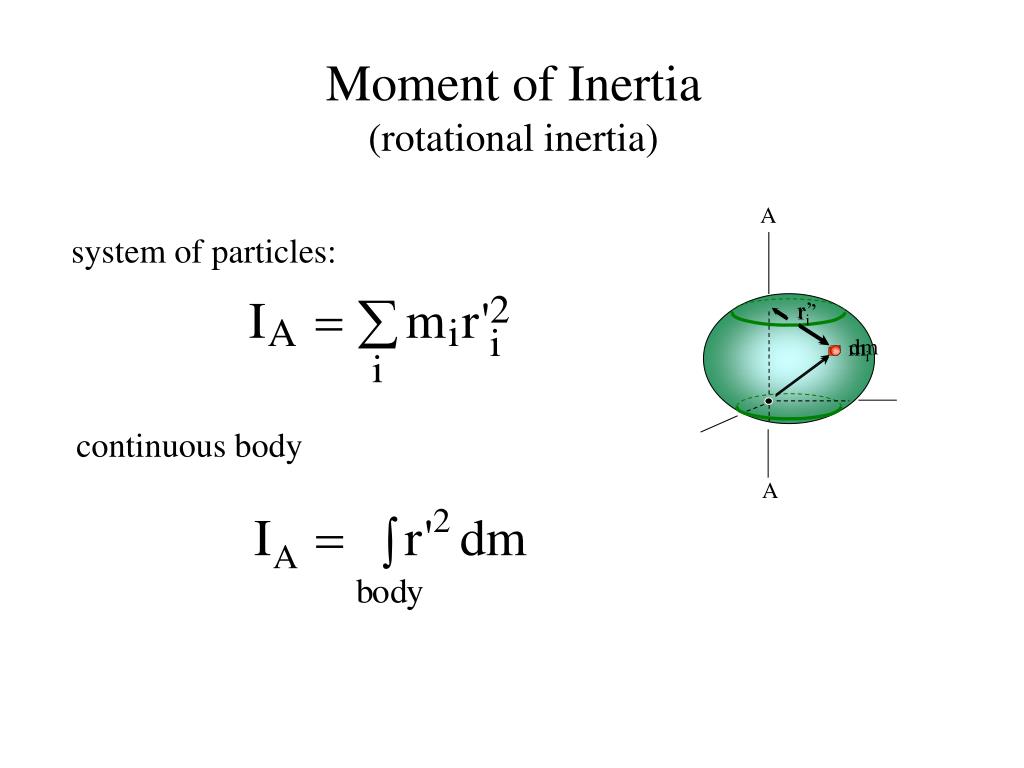 Кнопку «СТОП» нажать, когда число полных колебаний будет равно N-1. Повторить измерения 3 – 5 раз.
Кнопку «СТОП» нажать, когда число полных колебаний будет равно N-1. Повторить измерения 3 – 5 раз.
 Учебное пособие для втузов 5кн. Т.1. /Игорь Савельев – М.: АСТ Астрель/
Учебное пособие для втузов 5кн. Т.1. /Игорь Савельев – М.: АСТ Астрель/ 2 + I_C$$ 92$ всегда будет >0 для любого ненулевого значения $x$ (смещение).
2 + I_C$$ 92$ всегда будет >0 для любого ненулевого значения $x$ (смещение). Заработайте 10 репутации (не считая бонуса ассоциации), чтобы ответить на этот вопрос. Требование к репутации помогает защитить этот вопрос от спама и отсутствия ответа.
Заработайте 10 репутации (не считая бонуса ассоциации), чтобы ответить на этот вопрос. Требование к репутации помогает защитить этот вопрос от спама и отсутствия ответа. wolframalpha.com/input/?i=moment+of+inertia+cube”””
wolframalpha.com/input/?i=moment+of+inertia+cube”””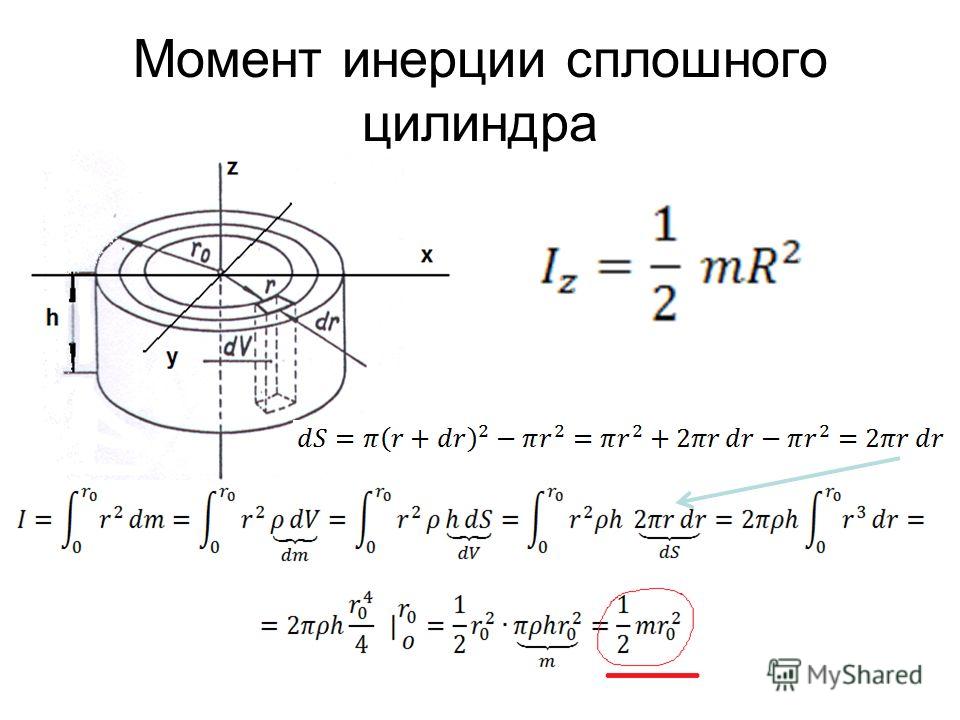
 argv) < 2:
argv) < 2: argv) == 3:
argv) == 3: argv[2]),
argv[2]), argv[0] + “масса x y z”
argv[0] + “масса x y z” 23 MA2
23 MA2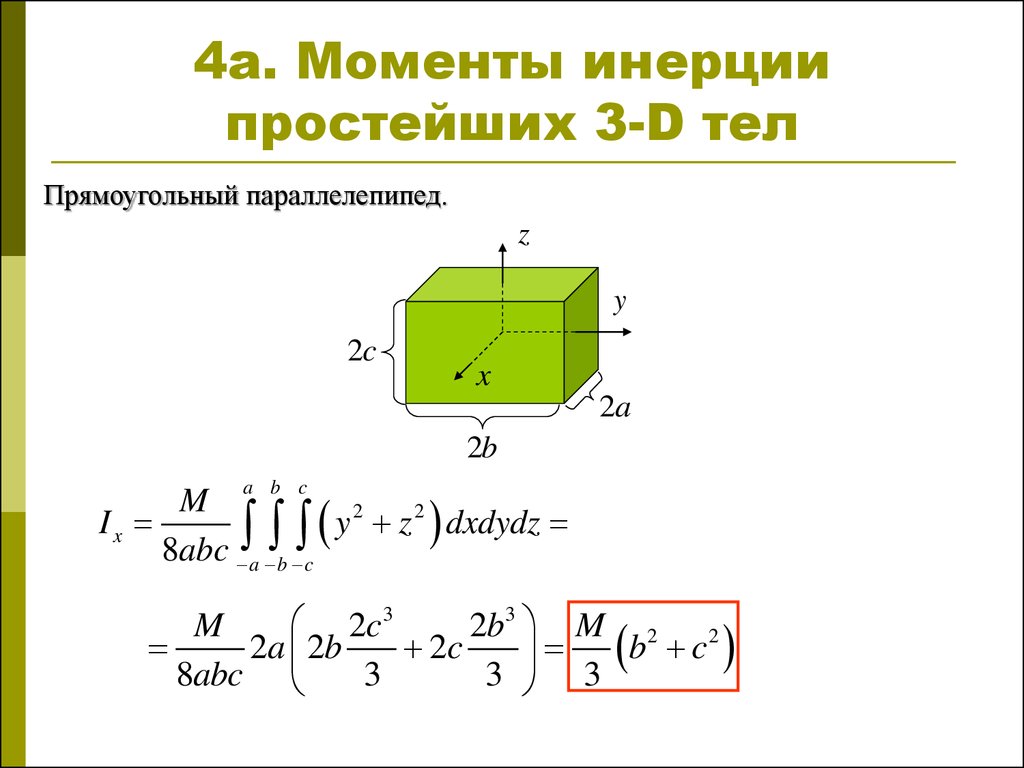 Импульс системы
Импульс системы
 )
) 72
72
 Отношение между моментами инерции IA и IB равно
Отношение между моментами инерции IA и IB равно