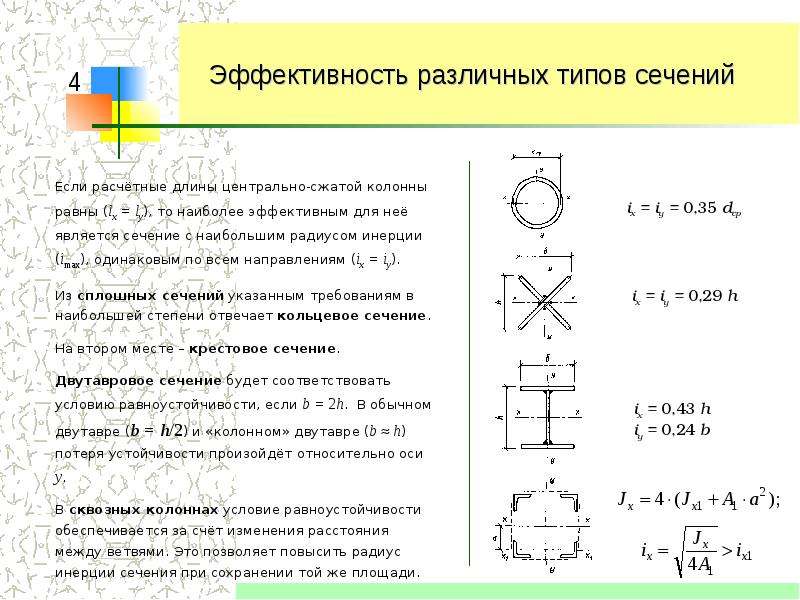
Момент инерции и момент сопротивления
05-12-2012: Адольф СталинБыло бы неплохо объяснить на наглядном примере для особо одаренных, типа меня, что такое момент инерции и с чем его едят. На специализированных сайтах как-то всё очень запутанно, а у Дока есть явный талант довести информацию, быть может не самую сложную, но очень грамотно и понятно
05-12-2012: Доктор Лом
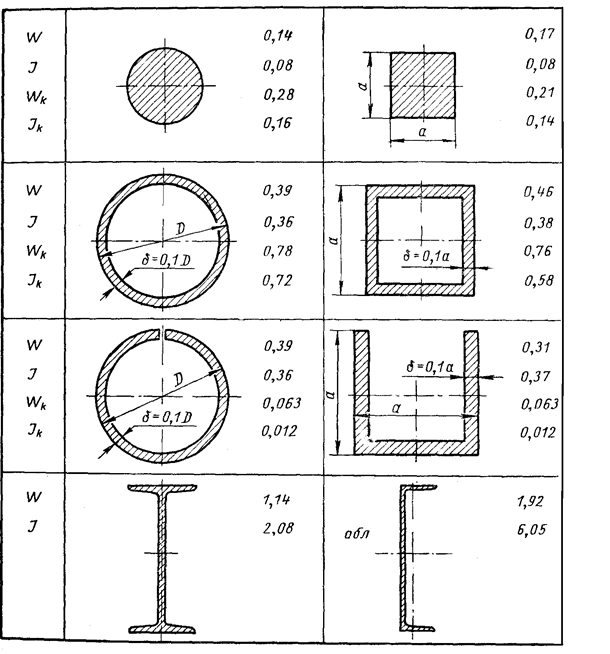
В принципе, что такое момент инерции и откуда он взялся, достаточно подробно объяснено в статье “Основы сопромата, расчетные формулы”, здесь лишь повторюсь: “W – это момент сопротивления поперечного сечения балки, другими словами, площадь сжимаемой или растягиваемой части сечения балки, умноженная на плечо действия равнодействующей силы”. Момент сопротивления необходимо знать для расчетов конструкции на прочность, т.е. по предельным напряжениям.
05-12-2012: Гиви
В принципе все предельно ясно, но здесь проще www.kataltim.ru
20-04-2013: Petr
Не нужно полностью доверять поданной в сайтах информации. Её никто по-хорошему не проверяет. И ссылки на неё не даются. Так в Таблице 1. “Формы сечения, площади сечений, моменты инерции и моменты сопротивления для конструкций достаточно простых геометрических форм” для тонкостенной трубы дается определение, что отношение диаметра к толщине оболочки должно быть больше 10. По другим источникам – должно быть больше 20!!! (Н.М. Беляев. Сопротивление материалов. М.1996. стр.160. или Н.И.Безухов. Основы теории упругости, пластичности и ползучести.М.1961.стр.390)
21-04-2013: Доктор Лом
Верно. Доверять нельзя. Но логическое мышление пока никто не отменял. Самый правильный вариант – рассчитывать момент инерции или момент сопротивления для любой трубы по формулам, приведенным для обычной трубы (на 1 пункт выше). Формулы, приводимые для тонкостенной трубы, в любом случае будут приближенными и годятся только для первичного расчета и об этом забывать нельзя.
Впрочем параметры максимально допустимой толщины стенки исправил.
25-06-2013: Саня
требуется определить момент инерции для сложного нестандартного сечения. сечение: прямоугольник с двумя пазами. внешне похоже на букву “Ш”. не получается найти какую либо информацию. буду признателен за какую нибудь информацию
25-06-2013: Доктор Лом
Посмотрите статью “Расчет прочности потолочного профиля для гипсокартона” (http://doctorlom. 3)*3,14/32.
3)*3,14/32.
Объясните, пожалуйста, правильность этой формулы (или неправильность).
04-11-2014: Доктор Лом
Формула из приведенного вами источника неправильная (ею можно пользоваться только для приблизительных вычислений) и проверить это легко.
Чтобы определить момент инерции сечения трубы, достаточно вычесть из момента инерции стержня круглого сечения (тут при вычислениях используется наружный диаметр трубы) момент инерции отверстия (внутренний диаметр, ведь внутри трубы никакого материала нет, на то она и труба). После простейших математических преобразований мы получим формулу момента инерции трубы, приведенную в таблице.
А для того, чтобы определить момент сопротивления, нужно момент инерции разделить на максимальное расстояние от центра тяжести до самой дальней точки сечения, соответственно на D/2, или умножить на 2/D.

04-11-2014: Радик
Спасибо, док!
11-11-2014: Ильгам
Не смог найти инфо о том в каких единицах (мм, см, м) все значения в формулах.
Для примера, у швел.24П (до срезания полки) Wx(Wz)=243 см3.
11-11-2014: Доктор Лом
Это общие формулы. В каких единицах подставите значения, в таких и получите результат, только само собой уже в кубических. Но если начали подставлять, например, в сантиметрах, то так и нужно продолжать.
У швеллера без полки момент сопротивления по умолчанию не может быть больше чем у целого швеллера.
04-01-2015: Valerij
Если сечение трубы ослаблено несколькими значительными отверстиями, как учесть это при расчёте момента инерции и момента сопротивления? Труба 32.39см и в ней 9 отв. диам.2.8см в сечении(шаг отвермтий 10см. по длине трубы).
Для определения момента инерции вам нужно вычесть из момента инерции трубы момент инерции вашего отверстия. Для этого нужно определить площадь сечения отверстия и затем умножить ее на квадрат расстояния до центра трубы плюс собственный момент инерции отверстия. Больше подробностей в статье “Моменты инерции поперечных сечений”.
Если расчет не требует особой точности и диаметр отверстия в 5 и более раз меньше диаметра трубы (вроде ваш случай, если 32.39 – это наружный диаметр), то сегмент отверстия можно привести к прямоугольнику. Если отверстие не сквозное, то следует дополнительно определить положение центра тяжести трубы с отверстием для того, чтобы потом вычислить новое значение момента сопротивления.
09-10-2015: Борис
Неравноплечий уголок.При вычислении Wy не y,а H-y
09-10-2015: Доктор Лом
Не пойму, о чем вы. Определение момента сопротивления относительно оси у в таблицах вообще не приводится.
Для треугольников при вычислении Wzп h в квадрате.
09-10-2015: Борис
Пардон,Wz
09-10-2015: Доктор Лом
Все верно. Теперь понял, о чем вы. Более корректно было бы указать момент сопротивления для верхней и для нижней части сечения, а я указал только для нижней. Ну а при определении момента сопротивления треугольников банально пропущен квадрат.
28-04-2016: Jama
Здравствуете! Кто может помочь о правильности расчета http://ej.kubagro.ru/2011/02/pdf/19.pdf
я не могу понят откуда значение берется момент сопротивления. Помогите пожалуйста!
28-04-2016: Доктор Лом
Что именно вам не понятно (вычитывать весь документ у меня нет времени). Если речь о балке, лежащей на упругом основании, то скорее всего балка эта имеет прямоугольное сечение (см. таблицу 1).
Если речь о балке, лежащей на упругом основании, то скорее всего балка эта имеет прямоугольное сечение (см. таблицу 1).
29-08-2016: Максим
Здравствуйте ! Имеется швеллер № 12. В верхний пояс будут вкручиваться саморезы и винты для крепления кровли. Как учесть ослабление швеллера, т.е как определить W ослабленного сечения.
29-08-2016: Доктор Лом
Если максимально упростить, то:
Сначала определяете момент инерции отверстия (для упрощения расчетов его можно принимать прямоугольным). Затем из момента инерции швеллера вычитаете момент инерции отверстия, затем делите полученный момент инерции на половину высоты швеллера и получаете момент сопротивления.
21-03-2017: игорь
здравствуйте,Сергей. я прочитал некоторые ваши статьи,очень интересно и понятно(в основном).я хотел бы рассчитать балку двутаврового сечения,но не могу найти Ix и Wx. дело в том что она не стандартная,я её буду делать сам,из дерева.можете ли вы мне помочь? я оплачу.только я не смогу оплатить электронными средствами т.к. не знаю как этим пользоваться.
я прочитал некоторые ваши статьи,очень интересно и понятно(в основном).я хотел бы рассчитать балку двутаврового сечения,но не могу найти Ix и Wx. дело в том что она не стандартная,я её буду делать сам,из дерева.можете ли вы мне помочь? я оплачу.только я не смогу оплатить электронными средствами т.к. не знаю как этим пользоваться.
21-03-2017: Доктор Лом
Игорь, я отправил вам письмо.
30-08-2017: Али
Уважаемый доктор, желаю вам всего найлучшего. Помогите пожалуйста, какими формулами нужны для подбора и проверки на прочность балку следующих сечений,:Швеллер,уголок и бульбовый профиль, имея допускаемый момент сопротивления W=58,58cm3. спасибо большое и жду вашу помощь.
31-08-2017: Доктор Лом
Посмотрите статью “Расчет стальных однопролетных балок с шарнирными опорами при изгибе согласно СП 16. 2/8 почему деленная на 8 и почему иногда делим на 6 и 24 итд подскажите пожалуйста только это не понял
2/8 почему деленная на 8 и почему иногда делим на 6 и 24 итд подскажите пожалуйста только это не понял
Легенда:
|
Легенда:
|
||
|
Форма поперечного сечения |
Осевой момент инерции, J, см4 |
Момент сопротивления W, см3 |
Радиус инерции i, см |
| Круг |
|||
| Кольцо c=d1/d |
|||
| Тонкостенное кольцо s≤(D/10) |
|||
| Полукруг Vo=2d/3π=0,2122d=0,4244r |
|||
| Круговой сегмент |
|||
| Круговой сектор |
— | ||
| Круговое полукольцо |
|||
| Сектор кругового кольца |
— | ||
| Профиль с симметричными закруглениями |
— | ||
|
Эллипс |
|||
|
Квадрат |
|||
|
Полый квадрат
|
|||
|
Полый тонкостенный квадрат s<(B/15) |
|||
| Квадрат, поставленный на ребро |
Срез верхнего и нижнего углов увеличивает Wx; при срезе углов на С=1/18 диагонали с каждой стороны момент сопротивления увеличивается до Wx=0,124b3 |
||
| Полый квадрат, поставленный на ребро |
|||
|
Прямоугольник
|
|||
| Прямоугольник повернутый |
|||
|
Полый прямоугольник |
|||
|
Полый тонкостенный прямоугольник |
|||
|
Сечение из двух равных прямоугольников |
|||
|
Треугольник |
При вычислении напряжения в вершине треугольника |
||
|
Поставленный на ребро треугольник |
|||
|
Трапеция |
При вычислении напряжений в точках верхнего основания |
||
|
Трапеция |
|||
|
Тавр |
Для нижних волокон Для верхних волокон |
||
|
Корытное сечение |
|||
|
Крестообразное сечение |
|||
|
Правильный шестиугольник |
|||
|
Правильный восьмиугольник |
|||
4.
 3. Моменты инерции простых фигур
3. Моменты инерции простых фигурКак уже отмечалось выше, к числу простых плоских фигур относятся три фигуры: прямоугольник, треугольник и круг. Простыми эти фигуры считаются потому, что положение центра тяжести этих фигур заранее известно. Все остальные фигуры могут быть составлены из этих простых фигур и считаются сложными. Вычислим осевые моменты инерции простых фигур относительно их центральных осей.
1. Прямоугольник.Рассмотрим сечение прямоугольного профиля размерами(Рис.4.6). Выделим элемент сечения двумя бесконечно близко расположенными сечениями на расстоянииот центральной оси.
Рис.4.6
Вычислим момент инерции прямоугольного сечения относительно оси :
.
(4. 10)
10)
Момент инерции прямоугольного сечения относительно оси найдем аналогично. Здесь вывод не приводится.
. (4.11)
Центробежный момент инерции относительно осей иравен нулю, так как осииявляются осями симметрии, а, следовательно, главными осями.
2. Равнобедренный треугольник.Рассмотрим сечение треугольного профиля размерами(Рис.4.7). Выделим элемент сечения двумя бесконечно близко расположенными сечениями на расстоянииот центральной оси. Центр тяжести треугольника находится на расстояниот основания. Треугольник принимается равнобедренным, так что осьсечения является осью симметрии.
Рис.4.7
Вычислим момент инерции сечения относительно оси :
.
(4. 12)
12)
Величину определим из подобия треугольников:
; откуда .
Подставляя выражения для в (4.12) и интегрируя, получим:
. (4.13)
Момент инерции для равнобедренного треугольника относительно оси находится аналогичным образом и равен:
(4.14)
Центробежный момент инерции относительно осей иравен нулю, так как осьявляется осью симметрии сечения.
3. Круг. Рассмотрим сечение круглого профиля диаметром(Рис.4.8). Выделим элемент сечения двумя бесконечно близко расположенными концентрическими окружностями, расположенными на расстоянииот центра тяжести круга.
Рис.4.8
Вычислим полярный момент инерции круга,
воспользовавшись выражением (4. 5):
5):
. (4.15)
Используя условие инвариантности для суммы осевых моментов инерции относительно двух взаимно перпендикулярных осей (4.6) и учитывая, что для круга в силу симметрии , определяем величину осевых моментов инерции:
. (4.16)
Откуда:
. (4.17)
Центробежный момент инерции относительно осей иравен нулю, так как осииявляются осями симметрии сечения.
4.4. Зависимости между моментами инерции относительно параллельных осей
При
вычислении моментов инерции для сложных
фигур следует запомнить одно правило:
значения для моментов инерции можно
складывать, если
они вычислены относительно одной и той
же оси. Для
сложных фигур чаще всего центры тяжести
отдельных простых фигур и всей фигуры
не совпадают. Не совпадают, соответственно,
и центральные оси для отдельных простых
фигур и всей фигуры. В связи с этим
существуют приемы приведения моментов
инерции к одной оси, например, центральной
оси всей фигуры. Это может быть связано
с параллельным переносом осей инерции
и дополнительными вычислениями.
Не совпадают, соответственно,
и центральные оси для отдельных простых
фигур и всей фигуры. В связи с этим
существуют приемы приведения моментов
инерции к одной оси, например, центральной
оси всей фигуры. Это может быть связано
с параллельным переносом осей инерции
и дополнительными вычислениями.
Рассмотрим определение моментов инерции относительно параллельных осей инерции, изображенных на рис.4.9.
Рис.4.9
Пусть осевые и центробежный моменты инерции изображенной на рис.4.9. фигуры относительно произвольно выбранных осей ис началом координат в точкеизвестны. Требуется вычислить осевые и центробежный моменты инерции фигуры относительно произвольных параллельных осейис началом координат в точке. Осиипроведены на расстоянияхисоответственно от осейи.
Воспользуемся
выражениями для осевых моментов инерции
(4. 4) и для центробежного момента инерции
(4.7). Подставим в эти выражения вместо
текущих координат
иэлемента с бесконечно малой площадью
координатыив новой системе координат. Получим:
4) и для центробежного момента инерции
(4.7). Подставим в эти выражения вместо
текущих координат
иэлемента с бесконечно малой площадью
координатыив новой системе координат. Получим:
. (4.18)
. (4.19)
.
(4.20)
Анализируя полученные выражения, приходим к выводу, что при вычислении моментов инерции относительно параллельных осей к моментам инерции, вычисленных относительно исходных осей инерции, следует призводить добавки в виде дополнительных членов, которые могут оказаться намного больше значений для моментов инерции относительно исходных осей. Поэтому пренебрегать этими дополнительными членами ни в коем случае нельзя.
Рассмотренный случай представляет
собой самый общий случай параллельного
переноса осей, когда в качестве исходных
были взяты произвольные оси инерции. В
большинстве расчетов встречаются
частные случаи определения моментов
инерции.
Первый частный случай. Исходные оси являются центральными осями инерции фигуры. Тогда, используя основное свойство для статического момента площади, можно исключить из уравнений (4.18)(4.20) члены уравнений, в которые входит статический момент площади фигуры. В результате получим:
. (4.21)
. (4.22)
. (4.23)
Здесь оси ицентральные оси инерции.
Второй частный случай. Исходные оси являются главными осями инерции. Тогда, учитывая, что относительно главных осей инерции центробежный момент инерции равен нулю, получим:
. (4.24)
. (4.25)
. (4.26)
(4.26)
Здесь оси иглавные оси инерции.
Воспользуемся полученными выражениями и рассмотрим несколько примеров вычисления моментов инерции для плоских фигур.
Пример 4.2.Определить осевые моменты инерции фигуры, приведенной на рис. 4.10, относительно центральных осейи.
Рис.4.10
Решение:
В предыдущем примере 4.1 для изображенной
на рис.4.10 фигуры было определено положение
центра тяжести С. Координата центра
тяжести откладывалась от оси
и составила.
Вычислим расстоянияимежду осямиии осямии.
Эти расстояния составили соответственнои.
Так как исходные осииявляются центральными осями для простых
фигур в виде прямоугольников, для
определения момента инерции фигуры
относительно осивоспользуемся выводами для первого
частного случая, в частности, формулой
(4. 21).
21).
см4.
Момент инерции относительно оси получим путем сложения моментов инерции простых фигур относительно этой же оси, так как осьявляется общей центральной осью для простых фигур и для всей фигуры.
см4.
Центробежный момент инерции относительно осей иравен нулю, так как ось инерцииявляется главной осью (осью симметрии фигуры).
Пример 4.3. Чему равен размер b (в см) фигуры, изображенной на рис. 4.11, если момент инерции фигуры относительно оси равен 1000 см4?
Рис.4.11
Решение:
Выразим момент инерции относительно оси через неизвестный размер сечения, воспользовавшись формулой (4.21), учитывая, что расстояние между осямииравно 7см:
см4. (а)
(а)
Решая выражение (а) относительно размера сечения , получим:
см.
Пример.4.4. Какая из фигур, изображенных на рис.4.12 , имеет больший момент инерции относительно оси , если обе фигуры имеют одинаковую площадьсм2?
Рис.4.12
Решение:
1. Выразим площади фигур через их размеры и определим:
а) диаметр сечения для круглого сечения:
см2; Откудасм.
б) размер стороны квадрата:
; Откудасм.
2. Вычисляем момент инерции для круглого сечения:
см4.
3. Вычисляем момент инерции для сечения квадратной формы:
см4.
Сравнивая полученные результаты, приходим к выводу, что наибольшим моментом инерции будет обладать сечение квадратной формы по сравнению с сечение круглой формы при одинаковой у них площади.
Пример 4.5.Определить полярный момент инерции (в см4) сечения прямоугольной формы относительно его центра тяжести, если ширина сечения см, высота сечениясм.
Решение:
1. Найдем моменты инерции сечения относительно горизонтальной и вертикальнойцентральных осей инерции:
см4;см4.
2. Определяем полярный момент инерции сечения как сумму осевых моментов инерции:
см4.
Пример
4.6. Определить
момент инерции фигуры треугольной формы
изображенной на рис.4.13, относительно
центральной оси
,
если момент инерции фигуры относительно
осиравен 2400 см4.
Определить
момент инерции фигуры треугольной формы
изображенной на рис.4.13, относительно
центральной оси
,
если момент инерции фигуры относительно
осиравен 2400 см4.
Рис.4.13
Решение:
Момент инерции сечения треугольной формы относительно главной оси инерции будет меньше по сравнению с моментом инерции относительно осина величину. Поэтому присм момент инерции сечения относительно осинайдем следующим образом:
см4.
Геометрические характеристики сплошных сечений 017
Внимание! Размер “с” игнорируется!
Внимание! Размер “a” игнорируется!
Ошибка! Проверьте правильность построения треугольника и формат ввода данных.
Площадь треугольника:
Центр тяжести треугольника:
Размеры треугольника:
Моменты инерции треугольника:
Полярные моменты инерции треугольника:
Радиусы инерции треугольника:
Моменты сопротивления треугольника:
Верхние волокна:
Нижние волокна:
Левые волокна:
Правые волокна:
определение, формулы, примеры решения задач.
 Расчет винтовых цилиндрических пружин
Расчет винтовых цилиндрических пружинБазовый курс лекций по сопромату, теория, практика, задачи.
1. Геометрические характеристики сечений.1.3. Моменты инерции простых сечений.
1. Прямоугольник (рис. 1.5,а). Вычислим момент инерции сечения относительно оси Х0 , проходящей через центр тяжести параллельно основанию.
За dA примем площадь бесконечно тонкого слоя dA = bdy.
Тогда
Итак,
(1.11)
Аналогично, получим
(1.12)
2. Круг (рис. 1.5,б). Сначала определим полярный момент инерции относительно центра круга
За dA принимаем площадь бесконечно тонкого кольца толщиной dp
тогда
Следовательно,
(1.13)
Теперь легко найдем Ixo
. Действительно, для круга согласно формуле (1.9.), имеем Iр
= 2Iхо
= 2Iуо
, откуда
(1.14)
2. Кольцо (рис. 1.5,в). Осевой момент инерции в этом случае равен разности моментов инерции внешнего и внутреннего кругов
(1. 15)
15)
где c = d/D.
Аналогично полярный момент инерции
(1.16)
2. Треугольник (рис. 1.5,г). Определим момент инерции относительно оси x1
, параллельной основанию и проходящей через вершину треугольника
За dA примем площадь бесконечно тонкой трапеции KBDE, площадь которой можно считать равной площади прямоугольника:
DA = by dy,
Где by – длина прямоугольника.
ОПРЕДЕЛЕНИЕ
Осевым (или экваториальным) моментом инерции сечения относительно оси называется величина, которую определяют как:
Выражение (1) обозначает, для вычисления осевого момента инерции берется по всей площади S сумма произведений бесконечно малых площадок () умноженных на квадраты расстояний от них до оси вращения:
Сумма осевых моментов инерции сечения относительно взаимно перпендикулярных осей (например, относительно осей X и Y в декартовой системе координат) дают полярный момент инерции () относительно точки пересечения этих осей:
ОПРЕДЕЛЕНИЕ
Полярным моментом инерции называют момент инерции сечением по отношению к некоторой точке.
Осевые моменты инерции всегда больше нуля, так как в их определениях (1) под знаком интеграла стоят величина площади элементарной площадки (), всегда положительная и квадрат расстояния от этой площадки до оси.
Если мы имеем дело с сечением сложной формы, то часто при расчетах используют то, что осевой момент инерции сложного сечения по отношению к оси равен сумме осевых моментов инерции частей этого сечения относительно той же оси. Однако следует помнить, что нельзя суммировать моменты инерции, которые найдены относительно разных осей и точек.
Осевой момент инерции относительно оси проходящей через центр тяжести сечения имеет наименьшее значение из всех моментов относительно параллельных с ней осей. Момент инерции относительно любой оси () при условии ее параллельности с осью, проходящей через центр тяжести равен:
где – момент инерции сечения относительно оси проходящей через центр тяжести сечения; – площадь сечения; – расстояние между осями.
Примеры решения задач
ПРИМЕР 1
| Задание | Чему равен осевой момент инерции равнобедренного треугольного сечения относительно оси Z, проходящей через центр тяжести () треугольника, параллельно его основанию? Высота треугольника равна . |
| Решение | Выделим на треугольном сечении прямоугольную элементарную площадку (см. рис.1). Она находится на расстоянии от оси вращения, длина одной ее стороны , другая сторона . Из рис.1 следует, что: Площадь выделенного прямоугольника с учетом (1.1) равна: Для нахождения осевого момента инерции используем его определение в виде: |
| Ответ |
ПРИМЕР 2
| Задание | Найдите осевые моменты инерции относительно перпендикулярных осей X и Y (рис.2) сечения в виде круга диаметр которого равен d. |
| Решение | Для решения задачи удобнее начать с нахождения полярного момента относительно центра сечения (). Все сечение разобьем на бесконечно тонкие кольца толщиной , радиус которых обозначим . Тогда элементарную площадь найдем как: |
Рассматривая в предыдущих разделах простейшие виды деформаций – осевое растяжение и сжатие, смятие, скалывание – мы выяснили, что их сопротивление действующей силе пропорционально только размерам площади поперечного сечения элемента, на который действует сила.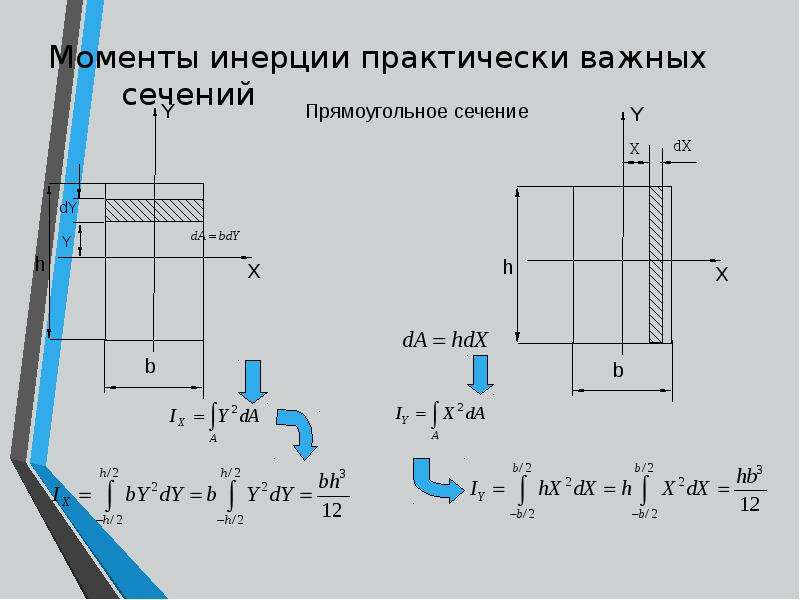 Так, при одинаковой площади сечения, одном и том же материале и одинаковой силе, действующей на каждый из стержней, изображенный на рис. 9.14, в них возникнут равные напряжения.
Так, при одинаковой площади сечения, одном и том же материале и одинаковой силе, действующей на каждый из стержней, изображенный на рис. 9.14, в них возникнут равные напряжения.
Переходя далее к изучению других более сложных видов деформаций (кручение, изгиб, внецентренное сжатие и др.) мы увидим, что в этих случаях сопротивление элемента конструкции
внешним силам зависит не только от площади его поперечного сечения, но и от распределения этой площади в плоскости сечения, т. е. от формы сечения.
Из обыденного опыта ясно, что согнуть стержень 4 в вертикальном направлении труднее, чем стержень 5, а стержень 6 имеет еще большую жесткость, хотя площади сечений всех этих стержней одинаковые (рис. 9.14).
Параметрами,
характеризующими геометрические свойства различных плоских фигур,
кроме площади, являются: статические моменты, моменты инерции, моменты
сопротивления и радиусы инерции.
Статический момент
площади . Представим брус с произвольной формой поперечного сечения
площадью F , в плоскости которого проведена ось х (рис. 9.15). Выделим элемент площади dF , расположенный на расстоянии у от оси х .. Статическим моментом элементарной площадки
, относительно
оси х называют произведение этой площадки на ее расстояние до оси:
9.15). Выделим элемент площади dF , расположенный на расстоянии у от оси х .. Статическим моментом элементарной площадки
, относительно
оси х называют произведение этой площадки на ее расстояние до оси:
Статический момент всей площади F относительно оси х равен сумме статических моментов всех элементарных площадок, которые
могут быть выделены на рассматриваемой площади:
Из теоретической механики известно, что координаты центра тяжести
площади фигуры определяют по формулам:
Следовательно, статический момент фигуры площадью F относительно какой-нибудь оси равен произведению площади на расстояние центра тяжести фигуры до этой оси. Размерность статического момента – единица длины в кубе ( , ).
Оси, проходящие через центр тяжести сечения, называют центральными.Если фигура имеет ось симметрии, то последняя всегда проходит через центр тяжести фигуры, т.
 е. оси симметрии одновременно являются и центральными осями.
е. оси симметрии одновременно являются и центральными осями. Будем также иметь в виду, что статический момент сложной фигуры относительно некоторой оси равен сумме статических моментов относительно той же оси простых фигур, на которые может быть разбита исходная сложная фигура:
Рис. 9.16. Схема к определению координат центра тяжести сложной фигуры.
Для решения этой задачи выберем две оси координат х и у , совпадающие со сторонами фигуры. Разобьем фигуру, все размеры которой должны быть известны, на элементарные части – прямоугольники – координаты центров тяжести которых очевидны, так как эти части симметричны. Составим теперь выражения для вычисления статического момента всей площади, например относительно оси у . Это можно сделать двумя способами:
а) взять сумму статических моментов отдельных площадей
В этих выражениях F – площадь всей фигуры; – координата ее центра тяжести; – площади отдельных частей фигуры, а – координаты их центров тяжести.

Приравнивая друг к другу написанные выше формулы, получим уравнение с одной неизвестной :
Аналогично этому расстояние центра тяжести фигуры от оси х может быть выражено так:
Составляя интеграл, в котором подынтегральное выражение представляет собой произведение элемента площади на квадрат расстояния до начала координат (рис. 9.17), получим полярный момент инерции :
Отметим еще одну характеристику, в которой площадка dF умножается на произведение координат
Эту величину называют центробежным моментом инерции . Приведенные моменты инерции измеряются в единицах длины” взятой в четвертой степени (, ).
Осевые и полярные моменты инерции фигуры – величины положительные и не могут быть равными нулю. Центробежный момент инерции в зависимости от положения осей может быть положительным или отрицательным, а также равным нулю. Две взаимно перпендикулярные оси, относительно которых центробежный момент инерции равен нулю, называют главными осями инерции и обозначаются .
 Для симметричной
фигуры ось симметрии является и главной осью.
Для симметричной
фигуры ось симметрии является и главной осью. Осевые моменты инерции, определенные относительно главных осей, имеют максимальное и минимальное значения.
Так же как и для статического момента, момент инерции сложной фигуры равен сумме моментов инерции образующих ее фигур. Подчеркнем, что сказанное справедливо в том случае, когда все моменты инерции вычисляются относительно одной и той же оси.
Для моментов инерции существует еще одно правило, часто используемое в расчетах. Применительно к осевым моментам оно “формулируется следующим образом: момент инерции фигуры относительно оси, параллельной центральной, равен моменту инерции относительно центральной оси плюс произведение площади фигуры, на квадрат расстояния между осями (рис. 9.18):
Для центробежных моментов инерции соответствующее правило в аналитическом виде выглядит так:
Для получения значения момента инерции конкретной фигуры в принципе надо решить соответствующий интеграл по площади этой фигуры.
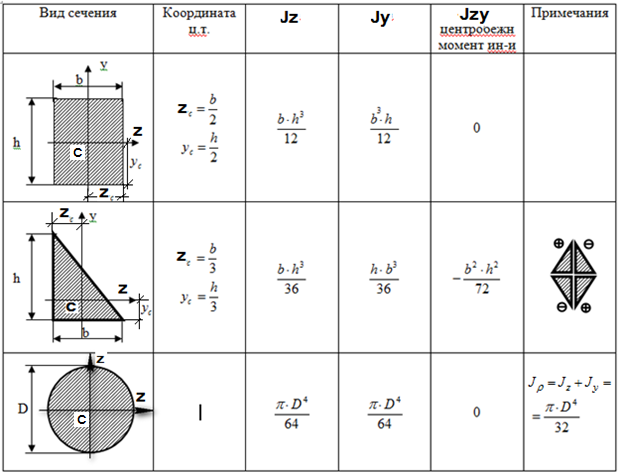 Однако с целью облегчения инженерных
расчетов такие интегралы для наиболее распространенных форм поперечных
сечений строительных элементов уже решены и результаты решений в
виде формул представлены в таблицах, одна из которых помещена в
приложении 3.
Однако с целью облегчения инженерных
расчетов такие интегралы для наиболее распространенных форм поперечных
сечений строительных элементов уже решены и результаты решений в
виде формул представлены в таблицах, одна из которых помещена в
приложении 3. Кроме того, в ГОСТах на все стандартные профили проката, выпускаемые в нашей стране (уголки, двутавры и др.), даются значения осевых моментов инерции и других геометрических характеристик для каждого типоразмера проката (см. приложение 4).
Наконец, для сложных по форме сечений моменты инерции определяют, используя изложенные выше два правила: о сложении моментов инерции и о пересчете моментов инерции относительно одних осей на другие оси.
Момент сопротивления . Осевым моментом сопротивления плоской фигуры относительно какой-либо оси, лежащей в плоскости фигуры, называется частное от деления момента инерции относительно той же оси на расстояние до наиболее удаленной точки фигуры (см. рис. 9.17):
Моменты сопротивления имеют размерность длины в кубе (, ).

Формулы для расчетов осевых моментов сопротивлений наиболее часто встречающихся фигур приведены в приложении 3, а конкретные значения этой характеристики для профилей стального проката даны в ГОСТах (приложение 4). Отметим, что в отличие от моментов инерции моменты сопротивления складывать нельзя.
Радиус инерции . Радиусом инерции называется величина, получаемая по формуле
а для круга диаметром d радиус инерции относительно оси, проходящей через центр круга, равен
Сфера применения рассмотренных выше геометрических характеристик сечений будет раскрыта при изучении видов деформаций, которым посвящены следующие подразделы настоящей главы.
I = ∑r i 2 dF i =∫r 2 dF (1.1)
В принципе и определение и формула, его описывающая, не сложные и запомнить их намного легче, чем вникнуть в суть. Но все-таки попробуем разобраться, что же такое момент инерции и откуда он взялся.
Понятие момент инерции пришло в сопромат и строительную механику из другого раздела физики, изучающего кинематику движения, в частности вращательное движение. Но все равно начнем издалека.
Но все равно начнем издалека.
Я точно не знаю, упало ли Исааку Ньютону на голову яблоко, упало оно рядом, или вообще не падало, теория вероятности допускает все эти варианты (к тому же в этом яблоке слишком много от библейской легенды о древе познания), однако я уверен, что Ньютон был наблюдательным человеком, способным делать выводы из своих наблюдений. Так наблюдательность и воображение позволили Ньютону сформулировать основной закон динамики (второй закон Ньютона), согласно которому масса тела m , умноженная на ускорение a , равна действующей силе Q (вообще-то более привычным для силы является обозначение F, но так как дальше мы будем иметь дело с площадью, которая также часто обозначается как F, то я использую для внешней силы, рассматриваемой в теоретической механике как сосредоточенная нагрузка, обозначение Q, сути дела это не меняет):
Q = ma (1.2)
По мне величие Ньютона именно в простоте и понятности данного определения. А еще, если учесть, что при равноускоренном движении ускорение а равно отношению приращения скорости ΔV к периоду времени Δt , за который скорость изменилась:
a = Δv/Δt = (v – v о)/t (1.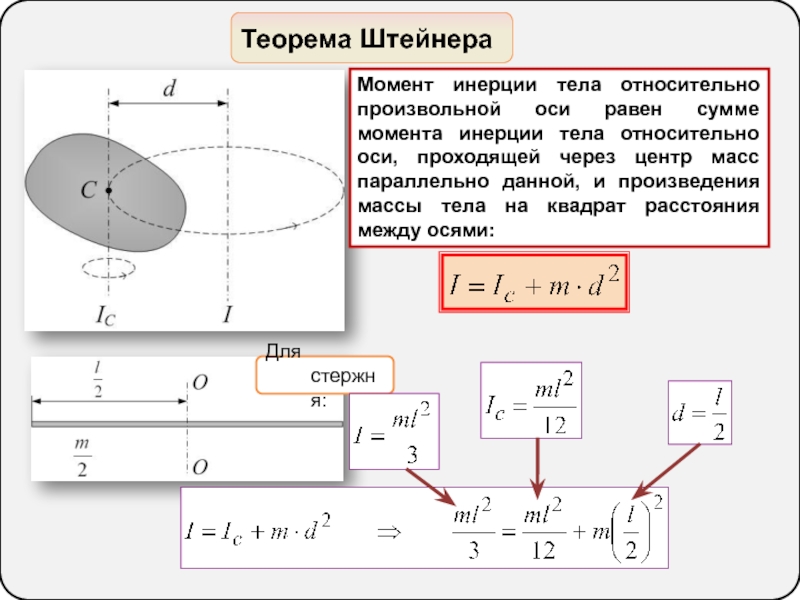 3.1)
3.1)
при V о = 0 a = v/t (1.3.2)
то можно определить основные параметры движения, такие как расстояние, скорость, время и даже импульс р , характеризующий количество движения:
p = mv (1.4)
Например, яблоко, падающее с разной высоты под действием только силы тяжести, будет падать до земли разное время, иметь разную скорость в момент приземления и соответственно разный импульс. Другими словами, яблоко, падающее с бóльшей высоты, будет дольше лететь и сильнее треснет по лбу незадачливого наблюдателя. И все это Ньютон свел к простой и понятной формуле.
А еще Ньютон сформулировал закон инерции (первый закон Ньютона): если ускорение а = 0 , то в инерциальной системе отсчета невозможно определить, находится ли наблюдаемое тело, на которое не действуют внешние силы, в состоянии покоя или движется прямолинейно с постоянной скоростью. Это свойство материальных тел сохранять свою скорость, пусть даже и нулевую, называется инертностью.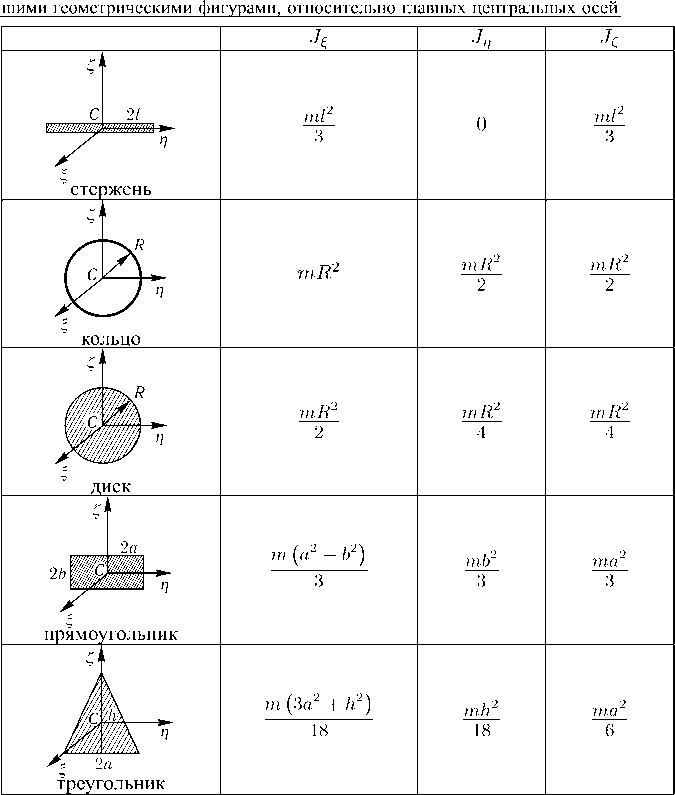 Мерой инертности является инерционная масса тела. Иногда инерционная масса называется инертной, но сути дела это не меняет. Считается, что инерционная масса равна гравитационной массе и потому часто не уточняется, какая именно масса имеется в виду, а упоминается просто масса тела.
Мерой инертности является инерционная масса тела. Иногда инерционная масса называется инертной, но сути дела это не меняет. Считается, что инерционная масса равна гравитационной массе и потому часто не уточняется, какая именно масса имеется в виду, а упоминается просто масса тела.
Не менее важным и значимым является и третий закон Ньютона, согласно которому сила действия равна силе противодействия, если силы направлены по одной прямой, но при этом в противоположные стороны . Не смотря, на кажущуюся простоту, и этот вывод Ньютона гениален и значение этого закона трудно переоценить. Об одном из применений этого закона чуть ниже.
Однако данные положения справедливы только для тел, движущихся поступательно, т.е. по прямолинейной траектории и при этом все материальные точки таких тел двигаются с одинаковой скоростью или одинаковым ускорением. При криволинейном движении и в частности при вращательном движении, например, когда тело вращается вокруг своей оси симметрии, материальные точки такого тела перемещаются в пространстве с одинаковой угловой скоростью w , но при этом линейная скорость v у различных точек будет разная и эта линейная скорость прямо пропорциональна расстоянию r от оси вращения до этой точки:
v = wr (1. 5)
5)
при этом угловая скорость равна отношению приращения угла поворота Δφ к периоду времени Δt , за который угол поворота изменился:
w = Δφ/Δt = (φ – φ о)/t (1.6.1)
при φ о = 0 w = φ/t (1.7.2)
соответственно нормальное ускорение а n при вращательном движении равно:
a n = v 2 /r = w 2 r (1.8)
И получается, что для вращательного движения мы не можем прямо использовать формулу (1.2), так как при вращательном движении одного только значения массы тела недостаточно, требуется еще знать распределение этой массы в теле. Получается, что чем ближе материальные точки тела к оси вращения, тем меньшую силу требуется приложить, чтобы заставить тело вращаться и наоборот, чем дальше материальные точки тела от оси вращения, тем большую силу нужно приложить, чтобы заставить тело вращаться (в данном случае речь идет о приложении силы в одной и той же точке). К тому же при вращении тела более удобно рассматривать не действующую силу, а вращающий момент, так как при вращательном движении точка приложения силы также имеет большое значение.
Поразительные свойства момента нам известны со времен Архимеда и если применить понятие момента к вращательному движению, то значение момента М будет тем больше, чем больше расстояние r от оси вращения до точки приложения силы F (в строительной механике внешняя сила часто обозначается как Р или Q ):
М = Qr (1.9)
Из этой также не очень сложной формулы выходит, что если сила будет приложена по оси вращения, то никакого вращения не будет, так как r = 0, а если сила будет приложена на максимальном удалении от оси вращения, то и значение момента будет максимальным. А если мы подставим в формулу (1.9) значение силы из формулы (1.2) и значение нормального ускорения и формулы (1.8), то получим следующее уравнение:
М = mw 2 r·r = mw 2 r 2 (1.10)
В частном случае когда тело является материальной точкой, имеющей размеры намного меньше, чем расстояние от этой точки до оси вращения, уравнение (1.10) применимо в чистом виде. Однако для тела, вращающегося вокруг одной из своих осей симметрии, расстояние от каждой материальной точки составляющей данное тело, всегда меньше одного из геометрических размеров тела и потому распределение массы тела имеет большое значение, в этом случае требуется учесть эти расстояния отдельно для каждой точки:
Однако для тела, вращающегося вокруг одной из своих осей симметрии, расстояние от каждой материальной точки составляющей данное тело, всегда меньше одного из геометрических размеров тела и потому распределение массы тела имеет большое значение, в этом случае требуется учесть эти расстояния отдельно для каждой точки:
M = ∑r i 2 w 2 m i (1.11.1)
М с = w 2 ∫r 2 dm
И тогда получается, что согласно третьему закону Ньютона в ответ на действие вращающего момента будет возникать так называемый момент инерции I . При этом значения вращающего момента и момента инерции будут равны, а сами моменты направлены в противоположные стороны. При постоянной угловой скорости вращения, например w = 1, основными величинами, характеризующими вращающий момент или момент инерции будут масса материальных точек, составляющих тело, и расстояния от этих точек до оси вращения. В итоге формула момента инерции примет следующий вид:
[- М] = I = ∑r i 2 m i (1. 12.1)
12.1)
I c = ∫r 2 dm (1.11.2) – при вращении тела вокруг оси симметрии
где I – общепринятое обозначение момента инерции, I c – обозначение осевого момента инерции тела, кг/м 2 . Для однородного тела, имеющего одинаковую плотность ρ по всему объему тела V формулу осевого момента инерции тела можно записать так:
I c = ∫ρr 2 dV (1.13)
Таким образом момент инерции является мерой инертности тела при вращательном движении, подобно тому как масса является мерой инертности тела при поступательном прямолинейном движении .
Все круг замкнулся. И тут может возникнуть вопрос, какое отношение все эти законы динамики и кинематики имеют к расчету статических строительных конструкций? Оказывается, что ни на есть самое прямое и непосредственное. Во-первых потому, что все эти формулы выводились физиками и математиками в те далекие времена, когда таких дисциплин, как “Теоретическая механика” или “Теория сопротивления материалов” попросту не существовало. А во-вторых потому, что весь расчет строительных конструкций и построен на основе указанных законов и формулировок и пока ни кем не опровергнутом утвержении о равенстве гравитационной и инертой масс. Вот только в теории сопротивления материалов все еще проще, как ни парадоксально это звучит.
А во-вторых потому, что весь расчет строительных конструкций и построен на основе указанных законов и формулировок и пока ни кем не опровергнутом утвержении о равенстве гравитационной и инертой масс. Вот только в теории сопротивления материалов все еще проще, как ни парадоксально это звучит.
А проще потому, что при решении определенных задач может рассматриваться не все тело, а только его поперечное сечение, а при необходимости несколько поперечных сечений. Но в этих сечениях действуют такие же физические силы, правда имеющие несколько иную природу. Таким образом, если рассматривать некое тело, длина которого постоянна, а само тело является однородным, то если не учитывать постоянные параметры – длину и плотность (l = const, ρ = const ) – мы получим модель поперечного сечения. Для такого поперечного сечения с математической точки зрения будет справедливым уравнение:
I р = ∫r 2 dF (2.1) → (1.1)
где I p – полярный момент инерции поперечного сечения, м 4 .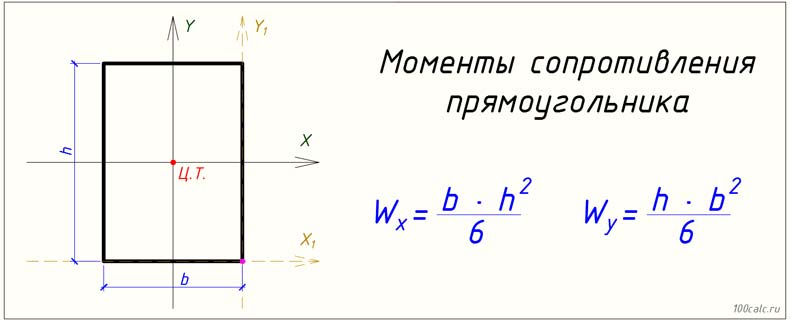 В итоге мы получили формулу, с которой начинали (а вот стало ли понятнее, что такое момент инерции сечения, не знаю).
В итоге мы получили формулу, с которой начинали (а вот стало ли понятнее, что такое момент инерции сечения, не знаю).
Так как в теории сопротивления материалов часто рассматриваются прямоугольные сечения, да и прямоугольная система координат более удобна, то при решении задач обычно рассматриваются два осевых момента инерции поперечного сечения:
I z = ∫y 2 dF (2.2.1)
I y = ∫z 2 dF (2.2.2)
Рисунок 1 . Значения координат при определении осевых моментов инерции.
Тут может возникнуть вопрос, почему использованы оси z и у , а не более привычные х и у ? Так уж сложилось, что определение усилий в поперечном сечении и подбор сечения, выдерживающего действующие напряжения, равные приложенным усилиям – две разные задачи. Первую задачу – определение усилий – решает строительная механика, вторую задачу – подбор сечения – теория сопротивления материалов. При этом в строительной механике рассматривается при решении простых задач достаточно часто стержень (для прямолинейных конструкций), имеющий определенную длину l , а высота и ширина сечения не учитываются, при этом считается, что ось х как раз и проходит через центры тяжести всех поперечных сечений и таким образом при построении эпюр (порой достаточно сложных) длина l как раз и откладывается по оси х , а по оси у откладываются значения эпюр. В то же время теория сопротивления материалов рассматривает именно поперечное сечение, для которого важны ширина и высота, а длина не учитывается. Само собой при решении задач теории сопротивления материалов, также порой достаточно сложных используются все те же привычные оси х и у . Мне такое положение дел кажется не совсем правильным, так как не смотря на разницу, это все же смежные задачи и потому будет более целесообразным использование единых осей для рассчитываемой конструкции.
В то же время теория сопротивления материалов рассматривает именно поперечное сечение, для которого важны ширина и высота, а длина не учитывается. Само собой при решении задач теории сопротивления материалов, также порой достаточно сложных используются все те же привычные оси х и у . Мне такое положение дел кажется не совсем правильным, так как не смотря на разницу, это все же смежные задачи и потому будет более целесообразным использование единых осей для рассчитываемой конструкции.
Значение полярного момента инерции в прямоугольной системе координат будет:
I р = ∫r 2 dF = ∫y 2 dF + ∫z 2 dF (2.3)
Так как в прямоугольной системе координат радиус – это гипотенуза прямоугольного треугольника, а как известно квадрат гипотенузы равен сумме квадратов катетов. А еще существует понятие центробежного момента инерции поперечного сечения:
I xz = ∫xzdF (2.4)
Среди осей прямоугольной системы координат, проходящих через центр тяжести поперечного сечения, есть две взаимно-перпендикулярные оси, относительно которых осевые моменты инерции принимают максимальное и минимальное значение, при этом центробежный момент инерции сечения I zy = 0 . Такие оси называют главными центральными осями поперечного сечения, а моменты инерции относительно таких осей – главными центральными моментами инерции
Такие оси называют главными центральными осями поперечного сечения, а моменты инерции относительно таких осей – главными центральными моментами инерции
Когда в теории сопротивления материалов речь заходит о моментах инерции, то как правило в виду имеются именно главные центральные моменты инерции поперечного сечения. Для квадратных, прямоугольных, круглых сечений главные оси будут совпадать с осями симметрии. Моменты инерции поперечного сечения также называют геометрическими моментами инерции или моментами инерции площади, но суть от этого не изменяется.
В принципе самому определять значения главных центральных моментов инерции для поперечных сечений наиболее распространенных геометрических форм – квадрата, прямоугольника, круга, трубы, треугольника и некоторых других – большой необходимости нет. Такие моменты инерции давно определены и широко известны. А при расчете осевых моментов инерции для сечений сложной геометрической формы справедлива теорема Гюйгенса-Штейнера:
I = I c + r 2 F (2.5)
таким образом, если известны площади и центры тяжести простых геометрических фигур, составляющих сложное сечение, то определить значение осевого момента инерции всего сечения не составит труда. А для того, чтобы определить центр тяжести сложного сечения, используются статические моменты поперечного сечения. Более подробно статические моменты рассматриваются в другой статье, здесь лишь добавлю. Физический смысл статического момента следующий: статический момент тела – это сумма моментов для материальных точек, составляющих тело, относительно некоторой точки (полярный статический момент) или относительно оси (осевой статический момент), а так как момент – это произведение силы на плечо (1.9), то и определяется статический момент тела соответственно:
S = ∑M = ∑r i m i = ∫rdm (2.6)
и тогда полярный статический момент поперечного сечения будет:
S р = ∫rdF (2.7)
Как видим, определение статического момента сходно с определением момента инерции. Но есть и принципиальная разница. Статический момент потому и называется статическим, что для тела, на которое действует сила тяжести, статический момент равен нулю относительно центра тяжести. Другими словами такое тело находится в состоянии равновесия, если опора приложена к центру тяжести тела. А согласно первому закону Ньютона такое тело или находится в состоянии покоя или движется с постоянной скоростью, т.е. ускорение = 0. А еще с чисто математической точки зрения статический момент может быть равен нулю по той простой причине, что при определении статического момента необходимо учитывать направление действия момента. Например относительно осей координат, проходящих через центр тяжести прямоугольника, площади верхней части и нижней части прямоугольника будут положительными так как символизируют силу тяжести, действующую в одном направлении. При этом расстояние от оси до центра тяжести можно рассматривать как положительное (условно: момент от силы тяжести верхней части прямоугольника пытается вращать сечение по часовой стрелке), а до центра тяжести нижней части – как отрицательное (условно: момент от силы тяжести нижней части прямоугольника пытается вращать сечение против часовой стрелки). А так как такие площади численно равны и равны расстояния от центров тяжести верхней части прямоугольника и нижней части прямоугольника, то сумма действующих моментов и составит искомый 0.
S z = ∫ydF = 0 (2.8)
А еще этот великий ноль позволяет определять опорные реакции строительных конструкций. Если рассматривать строительную конструкцию, к которой приложена например сосредоточенная нагрузка Q в некоторой точке, то такую строительную конструкцию можно рассматривать, как тело с центром тяжести в точке приложения силы, а опорные реакции в этом случае рассматриваются, как силы приложенные в точках опор. Таким образом зная значение сосредоточенной нагрузки Q и расстояния от точки приложения нагрузки до опор строительной конструкции, можно определить опорные реакции. Например для шарнирно опертой балки на двух опорах значение опорных реакций будет пропорционально расстоянию до точки приложения силы, а сумма реакций опор будет равна приложенной нагрузке. Но как правило при определении опорных реакций поступают еще проще: за центр тяжести принимается одна из опор и тогда сумма моментов от приложенной нагрузки и от остальных опорных реакций все равно равна нулю. В этом случае момент от опорной реакции относительно которой составляется уравнение моментов, равен нулю, так как плечо действия силы = 0, а значит в сумме моментов остаются только две силы: приложенная нагрузка и неизвестная опорная реакция (для статически определимых конструкций).
Таким образом принципиальная разница между статическим моментом и моментом инерции в том, что статический момент характеризует сечение, которое сила тяжести как бы пытается сломать пополам относительно центра тяжести или оси симметрии, а момент инерции характеризует тело, все материальные точки которого перемещаются (или пытаются переместиться в одном направлении). Возможно, более наглядно представить себе эту разницу помогут следующие достаточно условные расчетные схемы для прямоугольного сечения:
Рисунок 2 . Наглядная разница между статическим моментом и моментом инерции.
А теперь вернемся еще раз к кинематике движения. Если проводить аналогии между напряжениями, возникающими в поперечных сечениях строительных конструкций, и различными видами движения, то в центрально растягиваемых и центрально сжатых элементах возникают напряжения равномерные по всей площади сечения. Эти напряжения можно сравнить с действием некоторой силы на тело, при котором тело будет двигаться прямолинейно и поступательно. А самое интересное, это то, что поперечные сечения центрально-растянутых или центрально сжатых элементов действительно движутся, так как действующие напряжения вызывают деформации. И величину таких деформаций можно определить для любого поперечного сечения конструкции. Для этого достаточно знать значение действующих напряжений, длину элемента, площадь сечения и модуль упругости материала, из которого изготовлена конструкция.
У изгибаемых элементов поперечные сечения также не остаются на месте, а перемещаются, при этом перемещение поперечных сечений изгибаемых элементов подобно вращению некоего тела относительно некоторой оси. Как вы уже наверное догадались, момент инерции позволяет определить и угол наклона поперечного сечения и перемещение Δl для крайних точек сечения. Эти крайние точки для прямоугольного сечения находятся на расстоянии, равном половине высоты сечения (почему – достаточно подробно описано в статье “Основы сопромата. Определенение прогиба “). А это в свою очередь позволяет определить прогиб конструкции.
А еще момент инерции позволяет определить момент сопротивления сечения . Для этого момент инерции нужно просто разделить на расстояние от центра тяжести сечения до наиболее удаленной точки сечения, для прямоугольного сечения на h/2. А так как исследуемые сечения не всегда симметричны, то значение момента сопротивления может быть разным для разных частей сечения.
А началось все с банального яблока… хотя нет, начиналось все со слова.
Результат расчетов зависит не только от площади сечения, поэтому при решении задач по сопромату не обойтись без определения геометрических характеристик фигур : статических, осевых, полярного и центробежного моментов инерции. Обязательно необходимо уметь определять положение центра тяжести сечения (от положения центра тяжести зависят перечисленные геометрические характеристики). К дополнению к геометрическим характеристикам простых фигур: прямоугольника, квадрата, равнобедренного и прямоугольного треугольников, круга, полукруга . Указаны центр тяжести и положение главных центральных осей, и определены относительно них геометрические характеристики при условии, что материал балки однородный.
Геометрические характеристики прямоугольника и квадрата
Осевые моменты инерции прямоугольника (квадрата)
Геометрические характеристики прямоугольного треугольника
Осевые моменты инерции прямоугольного треугольника
Геометрические характеристики равнобедренного треугольника
Осевые моменты инерции равнобедренного треугольника
MYsopromat.ru: Моменты инерции простейших фигур
В расчетной практике часто встречаются сечения в виде простейших фигур (прямоугольников, кругов, треугольников и т. п.) или их комбинаций. При вычислении моментов инерции таких фигур обычно пользуются заранее выведенными расчетными формулами. Рассмотрим некоторые из фигур.
Прямоугольник и параллелограмм (рис. 6.4). Выделим элементарную полоску площадью dF=bdy и подставим это значение dF под знак интеграла (6.5):
|
Рис. 6.4 |
Рис. 6.5 |
.
Следовательно, момент инерции прямоугольника и параллелограмма с основанием b и высотой h относительно центральной оси, параллельной основанию,
|
. |
(6.16) |
Моменты инерции этих фигур относительно осей, проходящих через основание, находим по формуле (6.13):
|
. |
(6.17) |
Моменты инерции прямоугольника относительно осей yc и y вычисляются по формулам (6.16) и (6.17), где b заменяется на h, а h на b:
|
. |
(6.18) |
|
. |
(6.19) |
Треугольник с основанием b и высотой h (рис. 6.5).
Разобьем треугольник на элементарные полоски, параллельные его основанию. Площадь такой полоски
.
Тогда момент инерции треугольника относительно оси, проходящей через основание,
|
. |
(6.20) |
Подсчитывая по формулам переноса момент инерции треугольника относительно центральной оси, параллельной основанию, получаем
|
. |
(6.21) |
Круг и полукруг диаметра d (рис. 6.6). Подсчитываем сначала полярный момент инерции круга. Для этого выделим в сечении окружностями радиуса ρ и ρ+dρ элементарное кольцо площадью dF=2πρdρ и вычислим Iy по формуле (6.7):
|
. |
(6.22) |
Рис. 6.6.
Обычно размеры круглого сечения выражают через диаметр d и подсчитывают Ip по формуле
|
. |
(6.23) |
Осевые моменты инерции круга найдем с помощью соотношения (6.8). Замечая, что в силу симметрии круга Iz=Iy, получаем для осевых моментов инерции круга выражение
|
. |
(6.24) |
Центральные оси y и z делят круг на четыре совершенно одинаковые части с равными моментами инерции относительно этих осей. Следовательно, моменты инерции круга и полукруга относительно осей y и z должны быть равны соответственно учетверенным и удвоенным моментам инерции относительно тех же осей одной четверти круга. Из сказанного следует, что моменты инерции полукруга относительно оси симметрии y и оси z, проходящей через его основание (рис. 6.2), будут одинаковы и равны половине момента инерции круга,
|
, |
(6.25) |
а моменты инерции четверти круга
|
. |
(6.26) |
График зависимости момента инерции от квадрата расстояний
Кафедра общей и технической физики
Отчет по лабораторной работе №6.
По дисциплине Физика
Тема: Определение момента инерции с помощью маятника Оберкека
Автор: студент гр. ГС-16-1 /Галомзик В.А./
(подпись) (Ф.И.О.)
ПРОВЕРИЛдоцент _____________ /Фицак В.В./
(должность) (подпись)(Ф.И.О.)
Санкт-Петербург
Цель работы – исследовать зависимость момента инерции крестовины с надетыми на нее грузиками от распределения массы относительно оси вращения, проходящей через центр масс крестовины.
Явление изученное в процессе работе:
Вращательным движением твердого тела – явление(((Фицак сказал, что бред))), когда при вращении твердого тела все его точки движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения.
Основные определения физических величин, явлений, процессов:
Момент инерции телаявляется мерой инертности тела при вращательном движении. Момент инерции тела зависит от размеров и формы тел и от распределения массы тела относительно оси вращения.
Моментом инерции материальной точки относительно некоторой оси называется величина J,равная произведению массmматериальной точки на квадраты её расстояния от оси. ,где m-масса материальной точки, r-расстояние от материальной точки до оси.
Момент инерции твердого тела (сплошного)называется величинаJ, равная произведениюмассытела-m на радиус-R относительно оси, проходящей через центры оснований.
Моментом инерции системы материальной точки относительно осиназывается величина J,равная сумме произведений массвсех материальных точек, образующихмеханическуюсистему, на квадраты их расстояний от данной оси.
***Эту страницу выучить(еще он спросил про основное уравнение вращательного движения)
Закон и соотношения
1) Основное уравнение динамика вращательного движение твердого тела:
где: – суммарный момент внешних сил; J -момент инерции тела относительно той же оси; -угловое ускорение
[M]=Н*м
,
2) Закон Ньютона:
; m=const. где a – ускорение тела, m – масса тела. F – сила натяжения
[M]=кг [F]=H [a]=
-изменение импульса тела
F-сила натяжения
[P]=Н*с
[F]=Н
Теоретические ожидания. Результат.
1. Расчётные формулы:
. где – радиус шкива, m- масса груза, h – путь, пройденный грузом
где J0 – момент инерции тела при r = 0.
Исходные данные:h=0,43м
=0,042м; m=0,083кг
Формулы погрешности: .
Таблица 1(Расчет момента инерции тела)
| № | r, м | t, c | , c | Jэ кг*м2 | Jр кг*м2 |
| 0,25 | 8.633 | 8.632 | 0.127 | 0,124235 | |
| 8.638 | |||||
| 8.625 | |||||
| 0,22 | 7.836 | 7.706 | 0,0985 | 0,096176 | |
| 7.700 | |||||
| 7.581 | |||||
| 0,19 | 6.144 | 6.176 | 0,0632 | 0,071699 | |
| 6.010 | |||||
| 6.375 | |||||
| 0,16 | 5.066 | 5.092 | 0.0429 | 0,050804 | |
| 5.084 | |||||
| 5.126 | |||||
| 0,13 | 4.068 | 4.05 | 0,0271 | 0,033491 | |
| 4.048 | |||||
| 4,033 | |||||
| 0,10 | 3.541 | 3,444 | 0,0195 | 0,01976 | |
| 3,405 | |||||
| 3,386 | |||||
| 0,07 | 2.859 | 2.809 | 0,0129 | 0,009611 | |
| 2.770 | |||||
| 2.798 |
Таблица 2(Обработка результатов эксперимента)
| № | r, м | xi | Ji | xiJi | |
| 0,25 | 0,0625 | 0,12671 | 0,00391 | 0,00792 | |
| 0,22 | 0,0484 | 0,101 | 0,00234 | 0,004885 | |
| 0,19 | 0,0361 | 0,06479 | 0,0013 | 0,00233 | |
| 0,16 | 0,0256 | 0,0440 | 0,0007 | 0,00113 | |
| 0,13 | 0,0169 | 0,0278 | 0,0003 | 0,00046 | |
| 0,1 | 0,01 | 0,02004 | 0,0001 | 0,0002 | |
| 0,07 | 0,0049 | 0,01328 | 0,00002 | 0,00007 | |
| 0,0292 | 0,0568 | 0,00123 | 0,00243 |
Примеры расчётов:
m – масса груза, кг;
r0 – радиус шкива, м;
g – ускорение свободного падения;
t – время движения груза;
h – путь, пройденный грузом
Среднее квадратичное отклонение:
Окончательный результат:
График зависимости момента инерции от квадрата расстояний.
Вывод: После проведения опытов и произведения расчётов был определён момент инерции с помощью м
аятника Обербека. При уменьшении радиуса вращения время вращения уменьшается. Чем больше радиус шкива, тем больше момент инерции системы
Процент погрешности:
Вычисление момента инерции квадратной пластины
Авторские права © Майкл Ричмонд. Эта работа находится под лицензией Creative Commons License.Теорема о параллельных осях позволяет использовать ПРОСТЫЕ части. создать момент инерции СЛОЖНОГО тела. Давайте сделаем пример, чтобы увидеть, как это работает.
Начните с очень простого предмета: длинного тонкого стержня. массой м и длиной L , закрутился вокруг его центра.
Какой момент инерции этого стержня?
Теперь предположим, что я отодвинул стержень от ось вращения на небольшое расстояние x , как это:
Какой момент инерции у этого смещенного стержня, если я продолжу вращать его вокруг той же оси?
Итак, что, если я объединю два стержня, чтобы получился составной объект? Предположим, я помещаю первый стержень по центру оси, а вторая штанга смещена на расстояние х .Какой бы суммарный момент инерции этого двухстержневого комбинация быть?
Но зачем останавливаться на двух стержнях? Я могу использовать ту же технику, чтобы построить большую конструкцию. из множества стержней, а также вычислить его момент инерции.
Например, я мог бы разместить целую кучу стержней рядом с друг друга, чтобы получилась квадратная тарелка.
Назовем общую массу всей этой прямоугольной пластины M . Он имеет площадь поверхности A = L x L = L 2 .Мы можем определить массу на единицу площади как
Теперь, чтобы выяснить момент инерции этого сложная структура, я рассматриваю только одну деталь за раз. Позвольте мне взять один тонкий стержень, расстояние x от оси и шириной dx .
Масса этого кусочка дМ составляет
и вклад этой детали в момент инерции должен быть
Ладно, теперь твоя очередь: вычислить момент инерции всей квадратной пластины, суммируя вклады от всех маленьких стержней.
- Выразите момент инерции через общая масса M и длина стороны L
- Соответствует ли это значение тому, что указано в вашем учебнике?
Вы можете проверить свои ответы, посмотрев на мое собственное решение.
Авторские права © Майкл Ричмонд. Эта работа находится под лицензией Creative Commons License.
Момент инерции площади – типичные поперечные сечения I
Момент инерции площади или Момент инерции площади – , также известный как секундный момент площади – I , это свойство формы, которое используется для прогнозирования прогиба, изгиба и напряжения в балках.
Момент инерции площади – Британские единицы Момент инерции площади – Метрические единицыПреобразование между единицами измерения
- 1 см 4 = 10 -8 м 4 = 10 4 мм 4
- 1 дюйм 4 = 4,16×10 5 мм 4 = 41,6 см 4
9240 см 4 можно преобразовать в мм 4 умножением на 10 4
(9240 см 4 ) 10 4 = 9.24 10 7 мм 4
Момент инерции площади (момент инерции площади или второй момент площади)для изгиба вокруг оси x можно выразить как
I x = ∫ y 2 dA (1)
где
I x = момент инерции площади относительно оси x ( м 4 , мм 4 , дюймы 4 )
y = перпендикулярное расстояние от оси x до элемента dA (м, мм, дюймов )
dA = площадь элемента ( м 2 , мм 2 , дюймов 2 )
Момент инерции изгиба вокруг оси y можно выразить как
90 094 I y = ∫ x 2 dA (2)
где
I y = момент инерции площади относительно оси y ( м 4 , мм 4 , дюймы 4 )
x = перпендикулярное расстояние от оси y до элемента dA (м, мм, дюймов )
Площадь Момент инерции для типичного поперечного сечения I
Сплошное квадратное поперечное сечение
Момент инерции площади для сплошного квадратного сечения можно рассчитать как
I x = a 4 /12 (2)
где
a = сторона (мм, м, дюйм..)
I y = a 4 /12 (2b)
Сплошное прямоугольное сечение
Момент площади Ineria для прямоугольного сечения можно рассчитать как
I x = bh 3 /12 (3)
где
b = ширина
h = высота
I y = b 3 h / 12 (3b)
Сплошное круглое сечение
Момент инерции площади для сплошного цилиндрического сечения можно рассчитать как
I x = π r 4 /4
= π d 4 /64 (4)
где
9 0094 r = радиус
d = диаметр
I y = π r 4 /4
= π d 4 /64 (4b)
полый Цилиндрическое поперечное сечение
Момент инерции площади для полого цилиндрического профиля можно рассчитать как
I x = π (d o 4 – d i 4 ) / 64 ( 5)
, где
d o = внешний диаметр цилиндра
d i = внутренний диаметр цилиндра
I y = π (d o 9017 4 – d i 4 ) / 64 (5b)
Квадратное сечение – диагональные моменты
90 002 Моменты инерции диагональной площади для квадратного сечения можно рассчитать какI x = I y = a 4 /12 (6)
Прямоугольное сечение – Моменты площади на любой линии, проходящей через центр силы тяжести
Прямоугольное сечение и площадь момента на линии, проходящей через центр тяжести, можно рассчитать как
I x = (bh / 12) (h 2 cos 2 a + b 2 sin 2 a) (7)
Симметричная форма
Момент инерции площади для сечения симметричной формы можно рассчитать как
I x = (ah 3 /12) + (b / 12) (H 3 – h 3 ) (8)
I y = (a 3 h / 12) + (b 3 /12) (H – h) ( 8b)
Не симметричная форма
Площадь Момент инерции для несимметричного профиля можно рассчитать как
I x = (1/3) (B y b 3 – B 1 h b 3 + by t 3 – b1 h t 3 ) (9)
Площадь Момент инерции в зависимости отЗависимость полярного момента инерции от момента инерции
- «Момент инерции площади» – это свойство формы, которое используется для прогнозирования прогиба, изгиба и напряжения в балках. 2 $, а не от $ r $? (физическая причина)
Это частично основано на ответе TZDZ.{net} \ tau_i = \ alpha I
долл. СШАможно отобразить тем же способом.
С этим связаны большие вопросы: почему крутящий момент важен и почему он так сильно отличается от всего, о чем узнали ранее? Кроме того, когда следует использовать крутящий момент, в отличие от законов Ньютона и кинематических уравнений?
Ответ на первый вопрос:
В большинстве вводных курсов физики инерция вводится сразу после главы о центре масс, которая следует за несколькими главами о движении твердых тел, в которых каждая частица движется с одинаковым общим движением.Уравнения кинематики могут быть применены к твердым объектам в этих предыдущих главах, потому что каждая частица в объекте движется примерно с той же скоростью, что и любая другая частица в объекте. Когда вы дойдете до глав, посвященных центру масс, это уже не так, но из-за природы центра масс кинематические уравнения все еще могут применяться. Затем, в главах о вращении, становятся необходимыми понятия крутящего момента, инерции и углового момента, потому что не каждая частица в объектах, с которыми вы имеете дело, движется с одной и той же поступательной скоростью.Тем не менее, они по-прежнему движутся с регулярным движением, поэтому их можно моделировать, но для этого требуются другие модели.
Ответ на второй вопрос:
Torque следует использовать, когда отдельные частицы в системе частиц, которую вы моделируете, не все движутся примерно с одинаковой скоростью. IOW, его следует использовать, когда не все частицы в системе движутся одинаково. Более конкретно, однако, его следует использовать, когда система не имеет равномерного поступательного движения, но имеет равномерное угловое движение.2 $ объясняется тем, что одна из $ r $ проистекает из того факта, что $ a_T = r \ alpha $, где $ a_T $ – тангенциальное ускорение. Другой связан с тем, что $ s = r \ theta $. Поскольку крутящий момент является производной $ W_R $ по $ \ theta $, а не по $ s $, $ r $ из $ s = r \ theta $ остается в уравнении. Инерция также становится для нас вдвойне полезной, потому что она также присутствует в расчете кинетической энергии вращения, и поэтому теперь это полноценная концепция со своим собственным названием и страницей в википедии.2 dA
, где A – площадь формы, а y – расстояние любой точки внутри области A от заданной оси вращения. Из определения очевидно, что момент инерции всегда должен иметь положительное значение, поскольку внутри интеграла есть только квадратный член.
Концептуально второй момент площади связан с распределением площади фигуры. В частности, более высокий момент указывает на то, что площадь формы распределена далеко от оси. Напротив, более низкий момент указывает на более компактную форму, площадь которой расположена ближе к оси.Например, на следующем рисунке обе формы имеют равные площади, тогда как правая форма имеет более высокий второй момент площади вокруг красной оси, поскольку, по сравнению с левой, ее площадь распределена значительно дальше от оси. .
Терминология
Чаще всего термин момент инерции используется для второго момента площади, особенно в инженерных дисциплинах. Однако в физике момент инерции связан с распределением массы вокруг оси и, как таковой, является свойством объемных объектов, в отличие от второго момента площади, который является свойством плоских областей.На практике для описания второго момента площади можно использовать следующие термины:
- момент инерции
- момент инерции площади
- момент инерции площади
- момент инерции поперечного сечения
- момент инерции балка
Второй момент площади (момент инерции) имеет значение только тогда, когда определена ось вращения. Тем не менее, часто можно использовать термин «момент инерции окружности», отсутствующий для обозначения оси.В таких случаях, вероятно, подразумевается ось, проходящая через центр тяжести формы.
Произведение инерции
Произведение инерции плоской замкнутой области определяется как интеграл по площади произведения расстояний от пары осей x и y:
I_ {xy} = \ iint_A xy dA
, где A – площадь формы, а x, y – расстояния любой точки внутри области A от соответствующих осей.
Если одна из двух осей также является осью симметрии, то I_ {xy} = 0.
Также обратите внимание, что в отличие от второго момента площади, произведение инерции может принимать отрицательные значения.
Дополнительная информация
Понравилась страница? Поделись с друзьями!
Как рассчитать момент инерции балки?
размер шрифта: 15 пикселей;
}
]]> Как рассчитать момент инерции секции балки
(второй момент площади)Прежде чем мы найдем момент инерции (или второй момент площади) сечения балки, необходимо знать ее центроид (или центр масс).Например, если требуется момент инерции секции относительно ее горизонтальной (XX) оси, тогда сначала потребуется вертикальный (y) центроид (пожалуйста, просмотрите наше Учебное пособие о том, как рассчитать центроид секции балки).
Прежде чем мы начнем, если вы искали наш калькулятор свободного момента инерции, щелкните ссылку, чтобы узнать больше. Это вычислит центроид, moi и другие результаты и даже покажет вам пошаговые вычисления! А пока давайте посмотрим на пошаговое руководство и пример того, как рассчитать момент инерции:
Шаг 1. Разделите секцию балки на частиПри вычислении момента инерции площади мы должны вычислить момент инерции меньших сегментов.Попробуйте разбить их на простые прямоугольные секции. Например, рассмотрим секцию двутавровой балки ниже, которая также была представлена в нашем руководстве по центроидам. Мы решили разделить эту секцию на 3 прямоугольных сегмента:
Шаг 2: Расчет нейтральной оси (NA)Нейтральная ось (NA) или горизонтальная ось XX расположена в центре тяжести или центре масс. В нашем руководстве по центроидам центр тяжести этой секции ранее находился на расстоянии 216,29 мм от нижней части секции.
Шаг 3: Расчет момента инерцииДля расчета полного момента инерции секции нам необходимо использовать «Теорему о параллельности оси»:
Поскольку мы разделили его на три прямоугольные части, мы должны вычислить момент инерции каждой из этих частей. Широко известно, что уравнение момента инерции прямоугольника относительно его центральной оси имеет простой вид:
Момент инерции других форм часто указывается на лицевой / оборотной стороне учебников или в этом руководстве по формам момента инерции.Однако прямоугольная форма очень характерна для сечений балок, поэтому, наверное, стоит запомнить.
Теперь у нас есть вся информация, необходимая для использования «Теоремы о параллельной оси» и определения полного момента инерции двутавровой балки. В нашем примере момента инерции:
Итак, у вас есть руководство по расчету площади момента для секций балки. Этот результат имеет решающее значение при проектировании конструкций и является важным фактором отклонения балки.Мы надеемся, что вам понравилось это руководство, и с нетерпением ждем ваших комментариев.
БОНУС: Использование нашего калькулятора момента инерции Учетная записьSkyCiv показывает полные расчеты момента инерции. Этот интерактивный модуль покажет вам пошаговые расчеты того, как найти момент инерции:
Вы также можете посмотреть результаты нашего калькулятора свободного момента инерции, чтобы проверить свою работу. Это вычислит все свойства вашего поперечного сечения и является полезным справочным материалом для расчета центроида, площади и момента инерции сечений вашей балки!
Калькулятор свободного момента инерции
Формула момента инерции и другие физические формулы
Момент инерции объекта – это числовое значение, которое может быть вычислено для любого твердого тела, которое совершает физическое вращение вокруг фиксированной оси.Он основан не только на физической форме объекта и его распределении массы, но и на конкретной конфигурации того, как объект вращается. Таким образом, один и тот же объект, вращающийся по-разному, будет иметь разный момент инерции в каждой ситуации.
Общая формула
Общая формула для определения момента инерции. Эндрю Циммерман ДжонсОбщая формула представляет собой самое основное концептуальное понимание момента инерции. В принципе, для любого вращающегося объекта момент инерции можно рассчитать, взяв расстояние каждой частицы от оси вращения ( r в уравнении), возведя это значение в квадрат (это член r 2 ), и умножая его на массу этой частицы.Вы делаете это для всех частиц, составляющих вращающийся объект, а затем складываете эти значения вместе, и это дает момент инерции.
Следствием этой формулы является то, что один и тот же объект получает разное значение момента инерции в зависимости от того, как он вращается. Новая ось вращения заканчивается другой формулой, даже если физическая форма объекта остается прежней.
Эта формула представляет собой наиболее грубый подход к вычислению момента инерции.Другие приведенные формулы обычно более полезны и представляют собой наиболее распространенные ситуации, с которыми сталкиваются физики.
Интегральная формула
Общая формула полезна, если объект можно рассматривать как набор дискретных точек, которые можно складывать. Однако для более сложного объекта может потребоваться применить исчисление, чтобы взять интеграл по всему объему. Переменная r – это радиус-вектор от точки до оси вращения.Формула p ( r ) представляет собой функцию плотности массы в каждой точке r:
I-sub-P равно сумме i от 1 до N количества m-sub-i, умноженного на r-sub-i в квадрате.
Твердая сфера
Твердая сфера, вращающаяся вокруг оси, проходящей через центр сферы, с массой M и радиусом R , имеет момент инерции, определяемый по формуле:
I = (2/5) MR 2
Полая тонкостенная сфера
Полая сфера с тонкой незначительной стенкой, вращающейся вокруг оси, проходящей через центр сферы, с массой M и радиусом R , имеет момент инерции, определяемый по формуле:
I = (2/3) MR 2
Цельный цилиндр
Сплошной цилиндр, вращающийся вокруг оси, проходящей через центр цилиндра, с массой M и радиусом R , имеет момент инерции, определяемый по формуле:
I = (1/2) MR 2
Полый тонкостенный цилиндр
Полый цилиндр с тонкой незначительной стенкой, вращающейся вокруг оси, проходящей через центр цилиндра, с массой M и радиусом R , имеет момент инерции, определяемый по формуле:
Я = MR 2
Полый цилиндр
Полый цилиндр с вращающейся вокруг оси, проходящей через центр цилиндра, с массой M , внутренним радиусом R 1 и внешним радиусом R 2 , имеет момент инерции, определяемый формула:
I = (1/2) M ( R 1 2 + R 2 2 )
Примечание: Если вы взяли эту формулу и установили R 1 = R 2 = R (или, что более уместно, взяли математический предел как R 1 и R 2 с общим радиусом R ), вы получите формулу для момента инерции полого тонкостенного цилиндра.
Прямоугольная пластина, центральная ось
Тонкая прямоугольная пластина, вращающаяся вокруг оси, перпендикулярной центру пластины, с массой M и длинами сторон a и b , имеет момент инерции, определяемый по формуле:
I = (1/12) M ( a 2 + б 2 )
Прямоугольная пластина, ось вдоль кромки
Тонкая прямоугольная пластина, вращающаяся вокруг оси вдоль одного края пластины, с массой M и длинами сторон a и b , где a – расстояние, перпендикулярное оси вращения, имеет момент инерция определяется по формуле:
I = (1/3) млн лет 2
Тонкая штанга, центральная ось
Тонкий стержень, вращающийся вокруг оси, проходящей через центр стержня (перпендикулярно его длине), с массой M и длиной L , имеет момент инерции, определяемый по формуле:
I = (1/12) мл 2
Тонкая штанга, сквозная ось с одного конца
Тонкий стержень, вращающийся на оси, проходящей через конец стержня (перпендикулярно его длине), с массой M и длиной L , имеет момент инерции, определяемый по формуле:
I = (1/3) мл 2
(момент инерции – TotalConstructionHelp)
Центроиды и момент инерцииЦентроид двумерной поверхности (например, поперечное сечение структурной формы) – это точка, которая соответствует центру тяжести очень тонкой однородной пластины той же площади и формы.Плоская поверхность (или рисунок) может представлять фактическую площадь (например, площадь притока или поперечное сечение балки) или образную диаграмму (например, диаграмму нагрузки или изгибающего момента). В любом случае часто бывает полезно определить центр тяжести области.
Симметрия может быть очень полезной для определения местоположения центра тяжести области. Если область (или сечение, или тело) имеет одну линию симметрии, центр тяжести будет лежать где-то вдоль линии симметрии. Это означает, что если бы требовалось уравновесить область (или тело, или секцию) в горизонтальном положении, подложив под нее карандаш или край, то карандаш лучше всего положить прямо под линией симметрии.
Если тело (или область, или сечение) имеет две (или более) линии симметрии, центр тяжести должен лежать где-то вдоль каждой из этих линий. Таким образом, центр тяжести находится в точке пересечения линий. Это означает, что если бы требовалось уравновесить область (или тело, или секцию) в горизонтальном положении, поместив под нее гвоздь, то кончик гвоздя лучше всего расположить непосредственно под точкой, где встречаются линии симметрии. Это может показаться очевидным, но понятие центроида очень важно понимать как графически, так и численно.Положение центра тяжести некоторых простых форм легко определяется при осмотре. Известно, что центр тяжести круга находится в его центре, а центр тяжести квадрата находится на пересечении двух линий, соединяющих середины параллельных сторон. У круга бесконечное количество линий симметрии, а у квадрата – четыре.
Центроид сечения не всегда находится в пределах площади или материала сечения. Полые трубы, L-образные и некоторые секции неправильной формы имеют центроид, расположенный вне материала секции.Это не проблема, поскольку центроид на самом деле используется только как точка отсчета, от которой измеряются расстояния. Точное положение центроида можно определить, как описано выше, с помощью графической статики или численно.
Центроид любой области можно найти, взяв моменты идентифицируемых областей (например, прямоугольников или треугольников) вокруг любой оси. Это делается так же, как центр тяжести можно найти, взяв моменты веса. Момент большой площади относительно любой оси равен алгебраической сумме моментов составляющих ее площадей.Это выражается следующим уравнением:
Сумма MAtotal = MA1 + MA2 + MA3 + …
Момент любой области определяется как произведение площади и перпендикулярного расстояния от центра тяжести площади до оси момента. С помощью этого принципа мы можем найти центр тяжести любой простой или составной области.
Центр тяжести:
Дано: пластина, показанная на схеме, имеет вес 1 # / дюйм 2 (1 фунт на квадратный дюйм) горизонтальной поверхности.
Определить:
центр тяжести пластины, зная, что она симметрична относительно оси X-X.
Решение: Принцип моментов гласит, что общий вес вокруг оси равен сумме моментов весов компонентов относительно этой же оси. Таким образом, первое, что нужно сделать, – это разделить тарелку на несколько простых частей. Затем определите площадь и центр тяжести (или центроид) для каждой из составных частей. После этого измерьте моменты каждой из частей вокруг удобной оси (в этом случае выберите ось Z-Z, вокруг которой будут измеряться эти моменты).Ось Z-Z здесь обозначена как Ref Axis.
Сумма MAtotal = MA1 + MA2 + MA3Это простое уравнение можно переписать следующим образом, в котором описана каждая из составных частей:
(Atotal) (расстояние от исходной оси до центральной оси) = (A1) (расстояние от центра тяжести A1 до исходной оси) + (A2) (расстояние от центра тяжести A2 до исходной оси) + (A3) (расстояние от центроида от A3 до оси отсчета)
, а затем решить относительно y…. центральная ось находится на расстоянии 7,3 дюйма от исходной оси.
Фактический центр тяжести находится на полпути по глубине пластины в точке, рассчитанной выше. При уменьшении толщины пластины линия действия центра тяжести останется, в то время как центр тяжести перемещается пропорционально этой линии действия, всегда действующей в средней точке глубины пластины. Если толщина пластины уменьшается до нуля, она не имеет веса, и прежнее положение центра тяжести теперь называется центроидом площади.
Момент инерции (I) – это термин, используемый для описания способности поперечного сечения сопротивляться изгибу. Он всегда учитывается относительно базовой оси, такой как X-X или Y-Y. Это математическое свойство сечения, связанное с площадью поверхности и тем, как эта площадь распределяется относительно базовой оси. Базовой осью обычно является центральная ось.
Момент инерции также известен как Второй момент области и математически выражается как:
Ixx = Сумма (A) (y 2 )
В котором:
Ixx = момент инерции вокруг оси x
A = площадь плоскости объекта
y = расстояние между центром тяжести объекта и осью xМомент инерции – это важное значение, которое используется для определения напряженного состояния в сечении, расчета сопротивления продольному изгибу и определения величины прогиба балки.
Например, если проектировщику дается определенный набор ограничений для структурной проблемы (т.е. нагрузки, пролеты и конечные условия), может быть определено «требуемое» значение момента инерции. Тогда любой структурный элемент, который имеет хотя бы этот конкретный момент инерции, можно будет использовать в конструкции. Другой пример может быть, если верно обратное; конкретный элемент дается в дизайне. Затем можно было определить несущую способность элемента.Давайте посмотрим на две доски, чтобы интуитивно определить, какая из них будет отклоняться больше и почему.Если две доски с фактическими размерами 2 дюйма на 10 дюймов были уложены рядом – одна со стороны двух дюймов, а другая – со стороны восьми дюймов, то плата, которая опирается на ее 2-дюймовый край, будет значительно жестче, чем та, которая поддерживается вдоль. его 10-дюймовый край. Обе платы имеют одинаковую площадь поперечного сечения, но по-разному распределены относительно горизонтальной центральной оси.
Ixx = (1/12) (b) (h 3 ) = (1/12) x (b) x (h x h x h)В котором значение b всегда принимается равным стороне, параллельной базовой оси, а h – высотой секции.Это очень важно отметить! Если принять неправильное значение для значения b, вычисления будут совершенно неверными.
Момент инерции
Дано: поперечное сечение.
Определите: моменты инерции, Ixx и Iyy этого раздела.Решение:
Момент инерции прямоугольной формы, такой как эта, легко вычисляется с помощью уравнения I = 1/12 bh4. Однако очень важно, чтобы b и h были присвоены правильные значения.Вы можете просто повернуть элемент на 90 градусов и произвести пересчет, всегда запоминая исходное положение элемента.
Ixx = 1/12 (4 дюйма) (10 дюймов) 3 = 333,2 дюйма 4
Iyy = 1/12 (10 дюймов) (4 дюйма) 3 = 53,312 дюйм 4В этом случае наблюдение подтвердит выбор для b и h. Логично, что Ixx больше, чем Iyy, потому что большая часть прямоугольной области находится дальше от оси x-x, чем ось y-y. Это приводит к тому, что форма имеет большее сопротивление вращению вокруг оси x-x и, следовательно, больший момент инерции вокруг этой оси.
Важность распределения площади вокруг его центральной оси становится очевидной при сравнении значений момента инерции ряда типичных конфигураций балки. Все элементы, показанные ниже, имеют размер 2 x 10 дюймов; в поперечном сечении, равной длины и одинаковой нагрузки.
НАСТРОЕННЫЕ РАЗДЕЛЫ Часто бывает выгодно объединить несколько элементов меньшего размера, чтобы создать балку или колонну большей прочности. Момент инерции такой сборной секции определяется сложением моментов инерции составных частей.Это может быть сделано, если и только если моменты инерции каждой составляющей области взяты относительно общей оси, и тогда и только тогда, когда результирующее сечение действует как единое целое.
Застроенные секции
Дано:
следующие поперечные сечения
Определить:
Ix каждого раздела с учетом его составных частей.Решение:
В этом примере Box разбит на 4 отдельных элемента, и показана процедура вычисления Ixx.Расчет вручную с помощью компьютерного расчета, приведенного ниже.
Пример результатов компьютерной программы, доступной в нашем разделе бесплатного программного обеспечения
ФОРМУЛА ПЕРЕДАЧИСуществует много составных секций, в которых составные части не распределены симметрично относительно центральной оси. Самый простой способ определить момент инерции такого участка – найти момент инерции составных частей относительно их собственной центральной оси, а затем применить формулу переноса.Формула переноса переносит момент инерции сечения или площади с его собственной центральной оси на другую параллельную ось. Из математического анализа известно, что это:
Ix = Ic + Ad 2
Где:
Ix = момент инерции относительно оси x-x (в 4 )
Ic = момент инерции относительно центральной оси c-c, параллельной x-x (в 4 )
A = площадь сечения (в 2 )
d = расстояние по перпендикуляру между параллельными осями x-x и c-c (дюймы)Формула передачи
Дано:
приклеенный асимметричный нарост внизу.
