1.13.2.5. Момент инерции однородного стержня
Найдем момент инерции тонкого однородного стержня относительно оси , проходящей через один из его концов перпендикулярно продольной геометрической оси симметрии (см. рис. 1.61). Разобьем стержень на элементарные массыdm бесконечно малой длины , удаленные от оси вращения на расстояние. Введем понятие линейной плотности массы стержня, гдеm – масса стержня, – его длина, тогда элементарная масса , а момент инерции стержня будет равен
Рис. 1.61.
.
Учитывая, что , получим момент инерции однородного стержня относительно оси:
.
1.13.2.6. Теорема Штейнера
Как правило, путем интегрирования легко вычислить момент инерции I0 симметричного тела относительно оси, проходящей через центр масс. Теорема Штейнера позволяет найти момент инерции относительно произвольной параллельной оси. Она формулируется следующим образом:
Момент
инерции относительно произвольной оси
вращения равен сумме момента инерции
тела относительно параллельной оси
вращения, проходящей через центр инерции
тела, и произведения массы этого тела
на квадрат расстояния между осями.
.
Найдем момент инерции диска относительно оси, проходящей через его край перпендикулярно плоскости диска (рис. 1.62). В этом случае a = R и, согласно теореме Штейнера,
Рис. 1.62.
.
Теперь рассчитаем момент инерции стержня относительно оси, проходящей через центр инерции (середину) стержня. Для оси, проходящей через конец стержня . Расстояние между осями(рис. 1.63). Тогда по теореме Штейнера. Отсюда.
Рис. 1.63
Видим, что в любом случае момент инерции тела представляется в виде I = kmr2, где r – какой-либо характерный размер тела, а k – коэффициент пропорциональности, зависящий от формы тела. Единица измерения момента инерции – кг∙м2.
Свободная ось вращения. Главные оси инерции
Рассмотрим
твёрдое тело, которое может вращаться
вокруг неподвижной вертикальной оси. Чтобы удержать ось от перемещений в
пространстве, заключим ее в подшипники.
При вращении тела возникают силы
взаимодействия между осью и подшипниками,
удерживающие ось вращения в заданном
положении. В случае вращения однородного
симметричного тела вокруг оси симметрии
силы бокового давления подшипников на
ось не возникают. В отсутствие силы
тяжести подшипники можно было бы убрать
– ось и без них сохраняла бы своё
положение в пространстве. Ось
вращения, положение которой в пространстве
остается неизменным в отсутствие внешних
сил, называется
Чтобы удержать ось от перемещений в
пространстве, заключим ее в подшипники.
При вращении тела возникают силы
взаимодействия между осью и подшипниками,
удерживающие ось вращения в заданном
положении. В случае вращения однородного
симметричного тела вокруг оси симметрии
силы бокового давления подшипников на
ось не возникают. В отсутствие силы
тяжести подшипники можно было бы убрать
– ось и без них сохраняла бы своё
положение в пространстве. Ось
вращения, положение которой в пространстве
остается неизменным в отсутствие внешних
сил, называется
Для тела любой формы и с произвольным распределением массы существуют три взаимно перпендикулярные, проходящие через центр инерции тела оси, которые могут служить свободными осями. Они называются главными осями инерции тела. Моменты инерции относительно главных осей называются главными моментами инерции тела.
Так, для
прямоугольного параллелепипеда главные
оси инерции
проходят так,
как показано на рис. 1.63, а моменты инерции
относительно этих осей в общем случае
не равны.
1.63, а моменты инерции
относительно этих осей в общем случае
не равны.
У тел с осевой симметрией одной главной осью инерции служит ось симметрии, а остальными – любые две взаимно перпендикулярные оси, проходящие через центр инерции, и перпендикулярные оси симметрии (рис. 1.64). Для этих осей в общем случае . Такое тело называется симметричным волчком. Примером симметричного волчка может служить тело цилиндрической формы или юла.
Рис. 1.63.
У тела с центральной симметрией ни одна из главных осей не фиксирована, ими могут служить любые три взаимно перпендикулярные оси, проходящие через центр симметрии. Для этих осей моменты инерции равны . Такое тело называется шаровым волчком. Примером шарового волчка может служить тело в форме шараили в форме куба.
Если
тело вращается в условиях, когда
какое-либо воздействие извне отсутствует,
то устойчивым оказывается только
вращение вокруг главных осей,
соответствующих максимальному и
минимальному значениям момента инерции.
Рис. 1.64.
Под действием внешней силы устойчивым является вращение тела вокруг главной оси, соответствующей максимальному моменту инерции .
Понятие о тензоре инерции тела
Определим, в каком соотношении находятся моменты инерции тела, вычисленные относительно различных координатных осей. Для этого разобьем тело на совокупность материальных точек массой
Рис. 1.65.
Как
видно из рис. 1.65,
это квадраты
расстояний от материальной точки до
осей координат.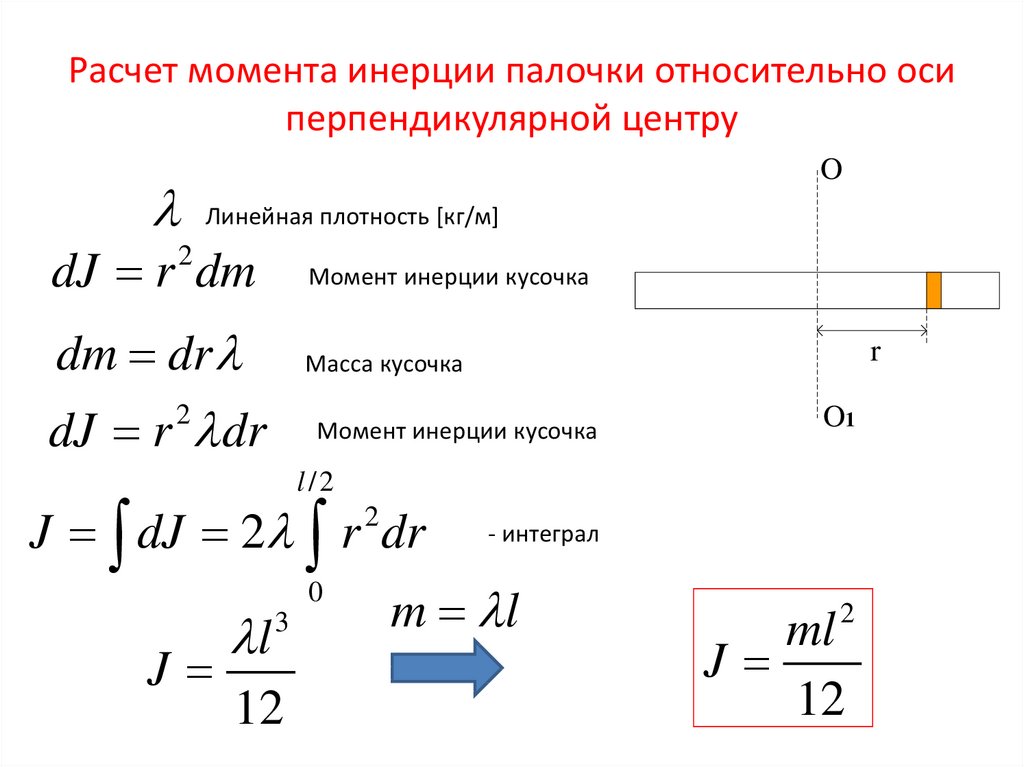 Тогда
Тогда
момент инерции тела относительно оси х;
момент инерции тела относительно оси у;
момент инерции тела относительно оси z, и
Для плоских тел, лежащих в плоскости
Для тела в форме шара, если ось вращения проходит через центр масс, то все три момента инерции равны:. Найдем, например,.
Разобьем шар на очень тонкие сферические слои (рис. 1.66) массой , где плотность вещества шара. .
dV объем сферического слоя.
Масса сферического слоя
Подставляя в формулу для момента инерции, получим:
Рис. 1.66.
Теперь
рассмотрим тело произвольной формы,
вращающееся с угловой скоростью
вокруг некоторой
оси, проходящей через центр масс.
Совместим с центром масс начало координат.
Момент импульса теласкладывается
из моментов импульсовматериальных
точек, составляющих это тело.
Учитывая, что , и применяя свойство двойного векторного произведения (см. ПриложениеI), получим
Используя разложения векторов ипо осям координат, их скалярное произведение можно представить как. Тогда проекции векторана оси координат запишутся как
Как видно из рис. 1.65, это квадраты расстояний от материальной точки до осейИнтегрирование полученной системы уравнений, придем к выражениям для проекций вектора момента импульса всего тела:
Величины есть моменты инерции тела относительно осейа величины
называют центробежными моментами инерции.
Совокупность всех этих величин, записанную в виде матрицы, называют тензором инерции тела
.
Компоненты являются диагональными элементами тензора, остальные недиагональными. Величины, расположенные симметрично относительно диагонали, попарно равны: . Такой тензор называется симметричным.
Матрицу-столбец вектора можно записать как произведение матрицы момента инерции на матрицу-столбец вектора:
или
Момент
импульса тела
весьма сложно
зависит от распределения масс в теле. Его направление в общем случае не
совпадает с направлением угловой
скорости вращения.
Его направление в общем случае не
совпадает с направлением угловой
скорости вращения.
Если оси координат направить вдоль главных осей инерции тела, то центробежные моменты инерции будут равны нулю, и тензор инерции приводится к диагональному виду:
.
Момент импульса в этом случае .
При вращении тела вокруг главной оси векторы момента импульса и угловой скорости совпадают по направлению.
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов. Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации – обмен информацией между организацией и её внешней средой… Интересное: Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы… Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории… Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 10 из 10
14.
14.2 .Найти момент инерции тонкого однородного стержня массы М и длины L относительно оси, перпендикулярной стержню и проходящей: 1.через один из его концов; 2.через середину стержня; 3. Через точку А, лежащую на продолжении стержня на расстоянии L от одного из его концов.
14.3 .Найти момент инерции тонкого обода радиуса 0,2 м и массы 3 кг относительно оси, перпендикулярной плоскости обода и проходящей: 1.через центр тяжести обода; 2.через конец диаметра.
14.4 .Определить момент инерции диска массы m, радиуса R относительно оси, перпендикулярной плоскости диска и проходящей через край диска.
14.5 .Определить момент инерции сплошного шара радиуса R и массы m относительно оси, проходящей: 1.через центр тяжести; 2.по касательной к шару.
14.6 .Определить момент инерции полого шара массы m относительно оси, проходящей через центр тяжести. Внешний радиус шара R, внутренний – r.
14.7 .Определить момент инерции тонкого кольца радиуса R и массы m относительно оси, проходящей через центр тяжести и лежащей в плоскости обода.
14.8 .Определить момент инерции шайбы, радиусы которой r и R, относительно оси, перпендикулярной плоскости шайбы и проходящей через ее центр масс.
14.9 .Определить момент инерции сплошного цилиндра радиуса R, массы m относительно оси цилиндра.
14.10 .Определить момент инерции полого цилиндра массы m, внутренний радиус которого r, внешний R.
14.11 .Определить момент инерции фигур, изготовленных из тонких стержней массы m, длины L относительно осей, перпендикулярных плоскости рисунка и проходящих через указанные точки (рис. 51).
а) б) в)
Рис. 51
14.12 .Определить момент инерции тонкой прямоугольной пластинки (масса m, стороны и ) относительно оси, проходящей через центр тяжести параллельно одной из сторон.
14.13 . Определить момент инерции тонкой прямоугольной пластинки (масса m, стороны и b) относительно оси, проходящей через центр тяжести перпендикулярно плоскости пластинки.
14.14 .В тонком диске массой m и радиусом R вырезают n круглых отверстий радиуса r на равных расстояниях a от центра диска. Определить момент инерции диска относительно оси, проходящей через его центр масс.
14.15 .Цилиндр массы 3 кг, диаметр которого 12 см, лежит на горизонтальной плоскости. Определить момент инерции цилиндра относительно оси, проходящей по линии контакта его боковой поверхности с плоскостью.
14.16 .Кинолента наматывается на бобину со скоростью V. Момент инерции бобины без ленты Iо, радиус rо. Определить зависимость момента инерции катушки с лентой от времени. Ширина ленты , плотность , толщина b.
14.17 .Две частицы с одинаковой массой m соединены жестким однородным стержнем длины L и массы m1.
14.18 .Поверхностная плотность тонкого диска радиуса R изменяется по закону . Найти момент инерции диска относительно оси, проходящей через центр диска перпендикулярно его плоскости.
14.19 .Прямой круглый однородный конус имеет массы m и радиус основания R. Найти момент инерции конуса относительно его оси.
14.20 .Найти момент инерции однородного куба относительно оси, проходящей через центры противолежащий граней. Масса куба m, длина ребра L.
14.21 .Вычислить момент инерции однородного круглого прямого цилиндра относительно оси, перпендикулярной к оси симметрии цилиндра и проходящей через его центр. Масса цилиндра m, радиус R, высота h. Рассмотреть предельные случаи: R << h, h << R.
14.22 .Найти момент инерции однородной пирамиды, основанием которой является квадрат со стороной , относительно оси, проходящей через вершину и центр основания.
15.ДИНАМИКА ТВЕРДОГО ТЕЛА ,ВРАЩАЮЩЕГОСЯ ВОКРУГ НЕПОДВИЖНОЙ ОСИ
15.1 . Найти ускорение грузов и натяжение нитей на машине, изображенной на рис. 52, учитывая момент инерции I блока, при условии, что нить не скользит по блоку. Определить натяжение подвеса А.
А
I, r
m2 m1
Рис. 52
15.2 . На однородный сплошной цилиндр массы М и радиуса R плотно намотана легкая нить, к концу которой прикреплен груз массы m (рис. 54). В момент времени t=0 система пришла в движение. Пренебрегая трением в оси цилиндра, найти:1. Зависимость угловой скорости от времени; 2.
М
m
Рис. 54
15.3 .Через блок радиуса 10 см, масса которого m=100 г, перекинута тонкая гибкая нерастяжимая нить, к концам которой подвешены два груза массами m1=200 г и m2=300 г (рис. 55). Определить: 1. Ускорения грузов; 2. Угловое ускорение; 3. Силы натяжения нитей.
m2
m1
Рис. 55
15.
Р
Р
Рис. 56
15.5 . На ступенчатый блок намотаны в противоположных направлениях две нити (рис 57). На конец одной нити действуют постоянной силой F, а к концу другой нити прикреплен груз массы m. Известны радиусы R1 и R2 блока и его момент инерции I относительно оси вращения. Найти угловое ускорение блока.
Рис. 57 15.6 . На горизонтальном столе лежат два тела, которые могут скользить по столу без трения. Тела связаны невесомой нерастяжимой нитью (рис. 58). Такая же нить, переброшенная через блок, связывает тело 2 с грузом массы m=0,5 кг. 1 2 М F1 М F2 М
Fm m
Рис. 58 15.7 . Однородный сплошной цилиндр массы m=1 кг висит в горизонтальном положении на двух намотанных на него невесомых нитях (рис. 59). Цилиндр опускается без толчка. А). За сколько времени t цилиндр опустится на расстояние h=50 см? б) Какое натяжение F испытывает при этом каждая из нитей?
Рис. 59
15.8 . Система, состоящая из цилиндрического катка радиуса R и гири, связанных нитью, перекинутой через блок (рис.
М
m
Рис. 60
15.9 . Из колодца с помощью ворота поднималось ведро с водой массы m. В момент, когда ведро находилось на высоте h от поверхности воды, рукоятка освободилась, и ведро стало двигаться вниз. Определить линейную скорость рукоятки в момент удара ведро о поверхность воды в колодце, если радиус рукоятки R, радиус вала ворота r, его масса m1. Трением и весом торса пренебречь.
15.
m1 m2
Рис. 61
15.11 . По наклонной плоскости, образующей угол с горизонтом, скатывается без скольжения сплошной однородный диск. Найти линейное ускорение центра диска.
15.12 . Какой путь пройдет катящийся без скольжения диск, поднимаясь вверх по наклонной плоскости с углом наклона 300,если ему сообщена начальная скорость 7 м/с, параллельная наклонной плоскости.
15.13 . Найти ускорение центра однородного шара, скатывающегося по наклонной плоскости, образующей угол с горизонтом. Чему равна сила трения шара о плоскость?
15.14 . Шар скатывается по наклонной плоскости с углом наклона 300. Какую скорость будет иметь центр шара относительно наклонной плоскости через 1,5 с, если его начальная скорость была равна нулю?
15.15 . По наклонной плоскости, составляющей с горизонтом угол 300, скатывается без скольжения сплошной цилиндр, масса которого равна 300 г. Найти величину силы трения цилиндра о плоскость.
15.16 . С одного уровня наклонной плоскости одновременно начинают скатываться сплошной цилиндр и шар одинаковых радиусов. 1)Какое тело будет иметь скорость на данном уровне? 2)Во сколько раз? 3)Во сколько раз скорость одного будет больше скорости другого в данный момент времени?
⇐ Предыдущая12345678910 Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства. Папиллярные узоры пальцев рук – маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… |
11.6: Расчет моментов инерции
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 18253
- OpenStax
- OpenStax
Цели обучения
- Расчет момента инерции твердых тел однородной формы
- Применить теорему о параллельных осях, чтобы найти момент инерции относительно любой оси, параллельной уже известной
- Расчет момента инерции для составных объектов
В предыдущем подразделе мы определили момент инерции, но не показали, как его вычислить. В этом подразделе мы покажем, как рассчитать момент инерции для нескольких стандартных типов объектов, а также как использовать известные моменты инерции, чтобы найти момент инерции для смещенной оси или для составного объекта. Этот раздел очень полезен для того, чтобы увидеть, как применять общее уравнение к сложным объектам (навык, который имеет решающее значение для более продвинутых курсов физики и инженерии). 92 \]
В этом подразделе мы покажем, как рассчитать момент инерции для нескольких стандартных типов объектов, а также как использовать известные моменты инерции, чтобы найти момент инерции для смещенной оси или для составного объекта. Этот раздел очень полезен для того, чтобы увидеть, как применять общее уравнение к сложным объектам (навык, который имеет решающее значение для более продвинутых курсов физики и инженерии). 92 \]
для всех точечных масс, составляющих объект. Поскольку \(r\) — это расстояние до оси вращения от каждой части массы, из которой состоит объект, момент инерции любого объекта зависит от выбранной оси. Чтобы убедиться в этом, давайте возьмем простой пример двух масс на конце безмассового (пренебрежимо малой массы) стержня (рис. \(\PageIndex{1}\)) и рассчитаем момент инерции относительно двух разных осей. В этом случае суммирование по массам простое, потому что две массы на конце штанги можно аппроксимировать как точечные массы, и поэтому сумма состоит только из двух членов. 9{2} \ldotp\]
9{2} \ldotp\]
Из этого результата можно сделать вывод, что вращать штангу вокруг конца в два раза труднее, чем вокруг ее центра.
Рисунок \(\PageIndex{1}\): (a) Штанга с осью вращения, проходящей через ее центр; (b) штанга с осью вращения через один конец.В этом примере у нас было две точечные массы, и их сумму было просто вычислить. Однако, чтобы иметь дело с объектами, которые не являются точечными, нам нужно тщательно продумать каждый член уравнения. Уравнение просит нас просуммировать по каждой «части массы» на определенном расстоянии от оси вращения. Но что именно означает каждый «кусок массы»? Напомним, что в нашем выводе этого уравнения каждая часть массы имела одинаковую величину скорости, что означает, что вся часть должна была иметь единственное расстояние r до оси вращения. Однако это невозможно, если мы не возьмем бесконечно малый кусок массы dm, как показано на рисунке \(\PageIndex{2}\). 9{2} dm \ldotp \label{10.19}\]
Фактически это та форма, которая нам нужна для обобщения уравнения для сложных форм. Лучше всего детально проработать конкретные примеры, чтобы понять, как рассчитать момент инерции для конкретных форм. Это основное внимание в остальной части этого раздела.
Лучше всего детально проработать конкретные примеры, чтобы понять, как рассчитать момент инерции для конкретных форм. Это основное внимание в остальной части этого раздела.
Однородный тонкий стержень с осью, проходящей через центр
Рассмотрим однородный (по плотности и форме) тонкий стержень массы M и длины L, как показано на рисунке \(\PageIndex{3}\). Нам нужен тонкий стержень, так что мы можем предположить, что площадь поперечного сечения стержня мала, и стержень можно рассматривать как цепочку масс вдоль одномерной прямой линии. В этом примере ось вращения перпендикулярна стержню и для простоты проходит через его середину. Наша задача — вычислить момент инерции относительно этой оси. Ориентируем оси так, чтобы ось z была осью вращения, а ось x проходила по длине стержня, как показано на рисунке. Это удобный выбор, потому что тогда мы можем интегрировать по оси x.
Рисунок \(\PageIndex{3}\): Расчет момента инерции I для однородного тонкого стержня относительно оси, проходящей через центр стержня.
Мы определяем dm как небольшой элемент массы, из которого состоит стержень. Интеграл момента инерции представляет собой интеграл по распределению масс. Однако мы умеем интегрировать по пространству, а не по массе. Поэтому нам нужно найти способ связать массу с пространственными переменными. Мы делаем это, используя линейную плотность массы \(\лямбда\) объекта, которая является массой на единицу длины. Поскольку массовая плотность этого объекта однородна, мы можем написать
\[\lambda = \frac{m}{l}\; или же\; m = \lambda l \ldotp\]
Если мы возьмем дифференциал каждой части этого уравнения, мы найдем
\[dm = d(\lambda l) = \lambda (dl)\]
, так как \( \лямбда\) постоянна. Мы решили сориентировать стержень вдоль оси x для удобства — именно здесь этот выбор становится очень полезным. Заметим, что кусок стержня dl полностью лежит вдоль оси x и имеет длину dx; на самом деле в этой ситуации dl = dx. Поэтому мы можем записать dm = \(\lambda\)(dx), что дает нам переменную интегрирования, с которой мы знаем, как работать.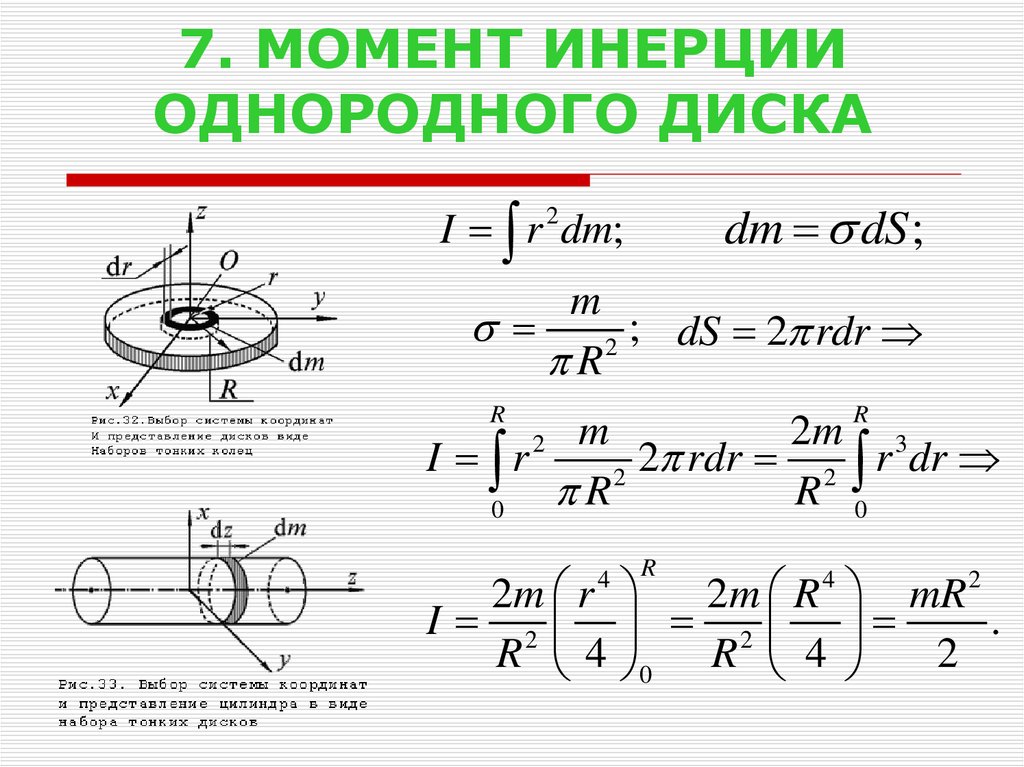 Расстояние каждого куска массы dm от оси задается переменной x, как показано на рисунке. Складываем все вместе, получаем 9{2} \ldotp \end{split}\]
Расстояние каждого куска массы dm от оси задается переменной x, как показано на рисунке. Складываем все вместе, получаем 9{2} \ldotp \end{split}\]
Далее мы вычисляем момент инерции для того же однородного тонкого стержня, но с другим выбором оси, чтобы можно было сравнить результаты. Мы ожидаем, что момент инерции будет меньше относительно оси, проходящей через центр масс, чем ось конечной точки, как это было в примере со штангой в начале этого раздела. Это происходит потому, что больше массы распределено дальше от оси вращения.
Однородный тонкий стержень с осью на конце
Теперь рассмотрим тот же однородный тонкий стержень массой \(M\) и длиной \(L\), но на этот раз мы перенесем ось вращения на конец стержня. Мы хотим найти момент инерции относительно этой новой оси (рисунок \(\PageIndex{4}\)).
Рисунок \(\PageIndex{4}\): Расчет момента инерции \(I\) однородного тонкого стержня относительно оси, проходящей через конец стержня. Величина \(dm\) снова определяется как малый элемент массы, из которого состоит стержень. {2} \lambda dx \ldotp\] 9{2} \ldotp \label{ThinRod} \end{align} \]
{2} \lambda dx \ldotp\] 9{2} \ldotp \label{ThinRod} \end{align} \]
Обратите внимание, что инерция вращения стержня относительно его конечной точки больше, чем инерция вращения вокруг его центра (в соответствии с примером со штангой) в четыре раза .
Теорема о параллельной оси
Сходство между процессом нахождения момента инерции стержня относительно оси, проходящей через его середину, и относительно оси, проходящей через его конец, поразительно и предполагает, что может существовать более простой метод определения момент инерции стержня относительно любой оси, параллельной оси, проходящей через центр масс. Такая ось называется 9{2} \ldotp\]
Этот результат согласуется с нашим более длинным расчетом (уравнение \ref{ThinRod}). Уравнение \ref{10.20} — полезное уравнение, которое мы применяем в некоторых примерах и задачах.
Exrecise \(\PageIndex{1}\)
Чему равен момент инерции цилиндра радиуса \(R\) и массы \(m\) относительно оси, проходящей через точку на поверхности, как показано ниже ?
- Ответить
\[I_{параллельная ось} = I_{центр\; из\; масса} + md^{2} = mR^{2} + mR^{2} = 2mR^{2} \nonumber \]
Однородный тонкий диск вокруг оси, проходящей через центр ось через его центр (рис.
 \(\PageIndex{5}\)). Рисунок \(\PageIndex{5}\): Расчет момента инерции тонкого диска относительно оси, проходящей через его центр.
\(\PageIndex{5}\)). Рисунок \(\PageIndex{5}\): Расчет момента инерции тонкого диска относительно оси, проходящей через его центр.Поскольку диск тонкий, мы можем считать, что масса полностью распределена в плоскости xy. Мы снова начинаем с отношения для поверхностная массовая плотность , которая представляет собой массу на единицу площади поверхности. Поскольку она однородна, поверхностная массовая плотность \(\sigma\) постоянна:
\[\sigma = \frac{m}{A}\] или \[\sigma A = m\], поэтому \[dm = \sigma (dA)\]
Теперь используем упрощение площади. Площадь можно представить как состоящую из ряда тонких колец, где каждое кольцо представляет собой приращение массы dm радиуса \(r\), равноудаленное от оси, как показано в части (b) рисунка. Таким образом, бесконечно малая площадь каждого кольца \(dA\) определяется как длина каждого кольца (\(2 \pi r\)) умноженная на бесконечно малую ширину каждого кольца \(dr\): 9{2} \ldotp \end{split}\]
Обратите внимание, что это соответствует значению, указанному на рис. 10.5.4.
10.5.4.
Расчет момента инерции для составных объектов
Теперь рассмотрим составной объект, подобный показанному на рисунке \(\PageIndex{6}\), на котором изображен тонкий диск на конце тонкого стержня. Это не может быть легко интегрировано, чтобы найти момент инерции, потому что это объект неоднородной формы. Однако, если мы вернемся к первоначальному определению момента инерции как суммы, мы можем сделать вывод, что момент инерции составного объекта может быть найден из суммы каждой части объекта:
\[I_{total} = \sum_{i} I_{i} \ldotp \label{10.21}\]
Важно отметить, что моменты инерции объектов в уравнении \(\PageIndex{6 }\) вокруг общей оси . В случае этого объекта это будет стержень длиной L, вращающийся вокруг своего конца, и тонкий диск радиуса \(R\), вращающийся вокруг оси, смещенной от центра на расстояние \(L + R\) , где \(R\) — радиус диска. Определим массу стержня как m r , а массу диска как \(m_d\). 9{2} \ldotp\]
Применение расчета момента инерции для решения задач
Теперь давайте рассмотрим некоторые практические применения расчета момента инерции.
Пример \(\PageIndex{1}\): Человек на карусели
Ребенок массой 25 кг стоит на расстоянии \(r = 1,0\, м\) от оси вращающейся карусели. обход (Рисунок \(\PageIndex{7}\)). Карусель можно представить как однородный сплошной диск массой 500 кг и радиусом 2,0 м. Найдите момент инерции этой системы.
Рисунок \(\PageIndex{7}\): Расчет момента инерции ребенка на карусели.Стратегия
Эта задача включает расчет момента инерции. Нам даны масса и расстояние до оси вращения ребенка, а также масса и радиус карусели. Поскольку масса и размер ребенка намного меньше карусели, мы можем аппроксимировать ребенка как точечную массу. Используемые обозначения: m c = 25 кг, r 9{2} \ldotp \nonumber \]
Значимость
Значение должно быть близко к моменту инерции самой карусели, потому что она имеет гораздо большую массу, распределенную от оси, чем ребенок .
Пример \(\PageIndex{2}\): Стержень и твердая сфера
Найдите момент инерции комбинации стержня и сплошной сферы относительно двух осей, как показано ниже.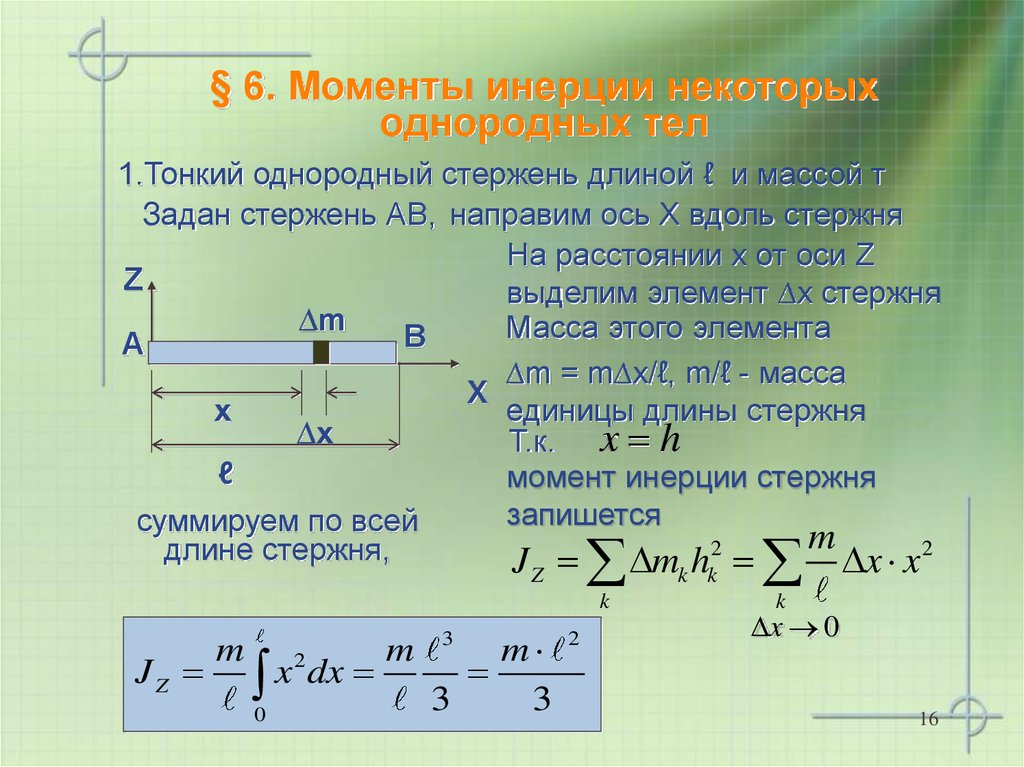 Стержень имеет длину 0,5 м и массу 2,0 кг. Радиус шара 20 см, масса 1 кг.
Стержень имеет длину 0,5 м и массу 2,0 кг. Радиус шара 20 см, масса 1 кг.
Стратегия
Поскольку в обоих случаях у нас есть составной объект, мы можем использовать теорему о параллельных осях, чтобы найти момент инерции относительно каждой оси. В (а) центр масс сферы расположен на расстоянии \(L + R\) от оси вращения. В (б) центр масс сферы расположен на расстоянии \(R\) от оси вращения. В обоих случаях момент инерции стержня направлен вокруг оси на одном конце. Обратитесь к Таблице 10.4 для моментов инерции для отдельных объектов. 9{2} \ldotp \end{split}\]
Значение
Использование теоремы о параллельных осях упрощает вычисление момента инерции составных объектов. Мы видим, что момент инерции больше в (а), чем в (б). Это связано с тем, что ось вращения ближе к центру масс системы в (б). Простая аналогия — стержень. Момент инерции относительно одного конца равен \(\frac{1}{3}\)mL 2 , а момент инерции через центр масс по его длине равен \(\frac{1}{12}\ )мл 2 .
Пример \(\PageIndex{3}\): угловая скорость маятника
Маятник в форме стержня (рисунок \(\PageIndex{8}\)) выходит из состояния покоя под углом 30° . Имеет длину 30 см и массу 300 г. Какова его угловая скорость в нижней точке?
Рисунок \(\PageIndex{8}\): Маятник в виде стержня выпущен из состояния покоя под углом 30°.Стратегия
Используйте сохранение энергии для решения проблемы. В момент выпуска маятник обладает гравитационной потенциальной энергией, которая определяется по высоте центра масс над его нижней точкой при качании. В нижней части качелей вся гравитационная потенциальная энергия преобразуется во вращательную кинетическую энергию. 9{2}) \left(\dfrac{3}{0,3\; m}\right) (1 – \cos 30)} = 3,6\; рад/с \ldotp \nonumber\]
Значение
Обратите внимание, что угловая скорость маятника не зависит от его массы.
- Наверх
- Была ли эта статья полезной?
- Тип артикула
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Показать оглавление
- нет
- Включено
- да
- Теги
- линейная массовая плотность
- параллельная ось
- теорема о параллельных осях
- источник-физ-4031
- поверхностная массовая плотность
МОМЕНТ ИНЕРЦИИ РАВНОГО ШТОКА
Сегодня мы увидим здесь решимость
момента инерции одного однородного тонкого стержня; мы выведем здесь уравнение
выразить момент инерции тонкого стержня.
Прежде чем идти вперед, мы должны найти несколько основных постов, которые будут связаны с определением момента инерция для различных случаев, таких как упомянутые здесь.
Момент инерции для прямоугольного сечения Момент инерции для полого прямоугольного сечения Момент инерции для круглого сечения Момент инерции для полого круглого сечения Район момент инерции Радиус вращения Базовый принцип дополнительных касательных напряженийТеперь мы пойдем дальше начать наше обсуждение, чтобы понять метод определения момент инерции одного однородного тонкого стержня с помощи этого поста.
Рассмотрим один равномерный
тонкий стержень, как показано на следующем рисунке. Рассмотрим одну небольшую полоску
длине dx и на расстоянии x от оси YY, как показано на рисунке.
L = длина однородной тонкой стержень
m = масса однородной тонкой стержень на единицу длины
M = общая масса униформы тонкий стержень
М = м.л
dx= длина небольшой полосы
x= расстояние небольшой полосы от оси YY
Теперь определим момент инерция однородного тонкого стержня относительно оси YYОпределим массу маленькая полоска, и мы можем легко написать здесь как
Масса маленькой полоски = (Масса однородного тонкого стержня на единицу длины) x (длина полоски)
Масса маленькой полоски = м.дх
Момент инерции этого
небольшая полоска вокруг оси YY может быть легко определена, и мы можем написать здесь
Следующее уравнение для представления момента инерции этой небольшой полоски о
ось YY.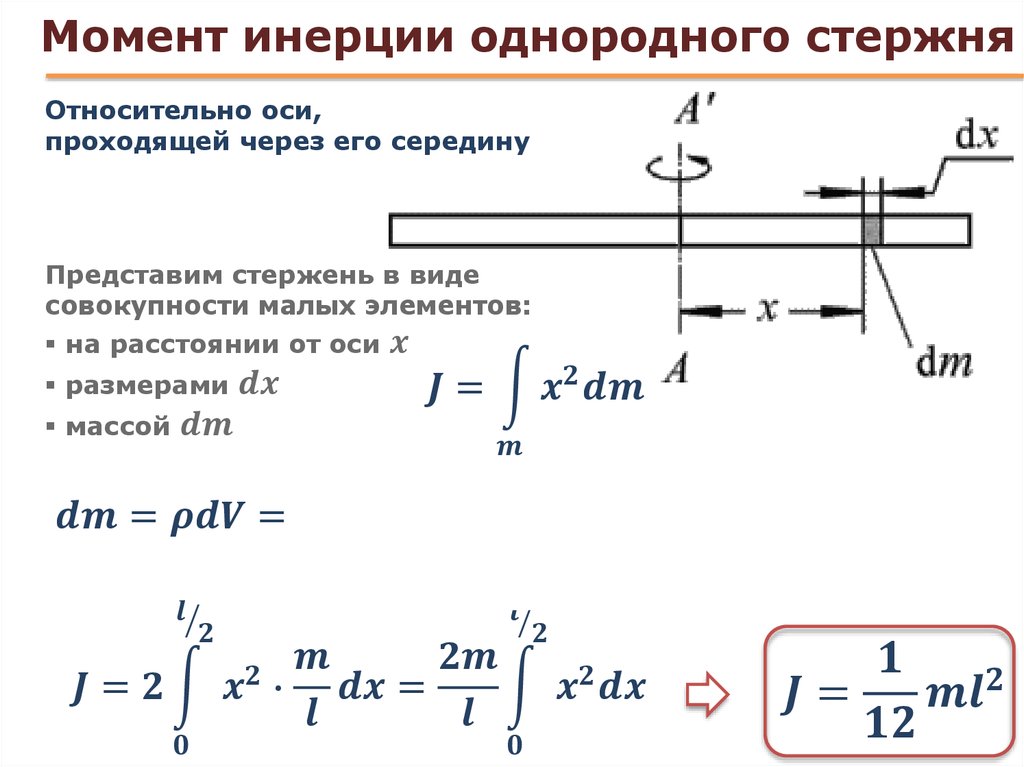
Момент инерции малого полоса вокруг оси YY = (m. dx). х 2
Момент инерции малого полоса вокруг оси YY = mx 2 dx
Теперь мы будем интегрировать
приведенное выше уравнение от 0 до L, чтобы обеспечить значение момента инерции
весь однородный тонкий стержень вокруг оси YY.
Наконец, мы можем сделать вывод, что момент инерции всего однородного тонкого стержня относительно оси YY легко записать как упоминалось здесь.
I ГГ =ML 2 /3Где, M = m.L
Есть ли у вас какие-либо предложения или какие-либо нужна поправка в этом посте? Пожалуйста, напишите в поле для комментариев.
Артикул:Прочность материала, Р. К. Бансал
Изображение предоставлено: Google
Мы увидим еще одну статью в нашем следующем
пост т.

 ..
..
 1 .Найти момент инерции математическго маятника относительно точки подвеса.
1 .Найти момент инерции математическго маятника относительно точки подвеса.

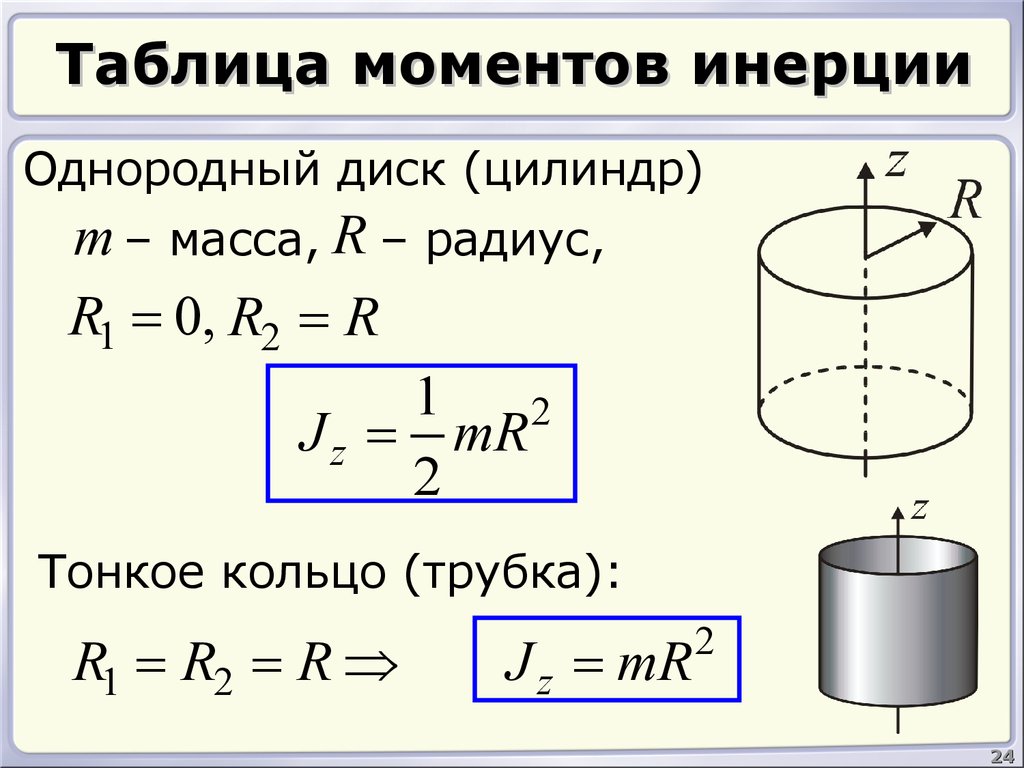 Найти момент инерции этой системы относительно оси, перпендикулярной стержню и проходящей через: 1.центр масс системы; 2.одну из частиц.
Найти момент инерции этой системы относительно оси, перпендикулярной стержню и проходящей через: 1.центр масс системы; 2.одну из частиц. Масса пирамиды равна m.
Масса пирамиды равна m. Направление векторов и ; 3. Ускорение груза; 4. Силу натяжения нити; 5. Для системы блок-груз зависимость от времени момента импульса относительно оси блока и кинетической энергии; 6. Углы поворота блока в зависимости от времени.
Направление векторов и ; 3. Ускорение груза; 4. Силу натяжения нити; 5. Для системы блок-груз зависимость от времени момента импульса относительно оси блока и кинетической энергии; 6. Углы поворота блока в зависимости от времени. 4 . Однородный цилиндр массы М и радиуса R вращается вокруг горизонтальной оси, проходящей через его центр масс, под действием грузов весом Р каждый. Найти силу натяжения нити на участках и (рис. 56).
4 . Однородный цилиндр массы М и радиуса R вращается вокруг горизонтальной оси, проходящей через его центр масс, под действием грузов весом Р каждый. Найти силу натяжения нити на участках и (рис. 56).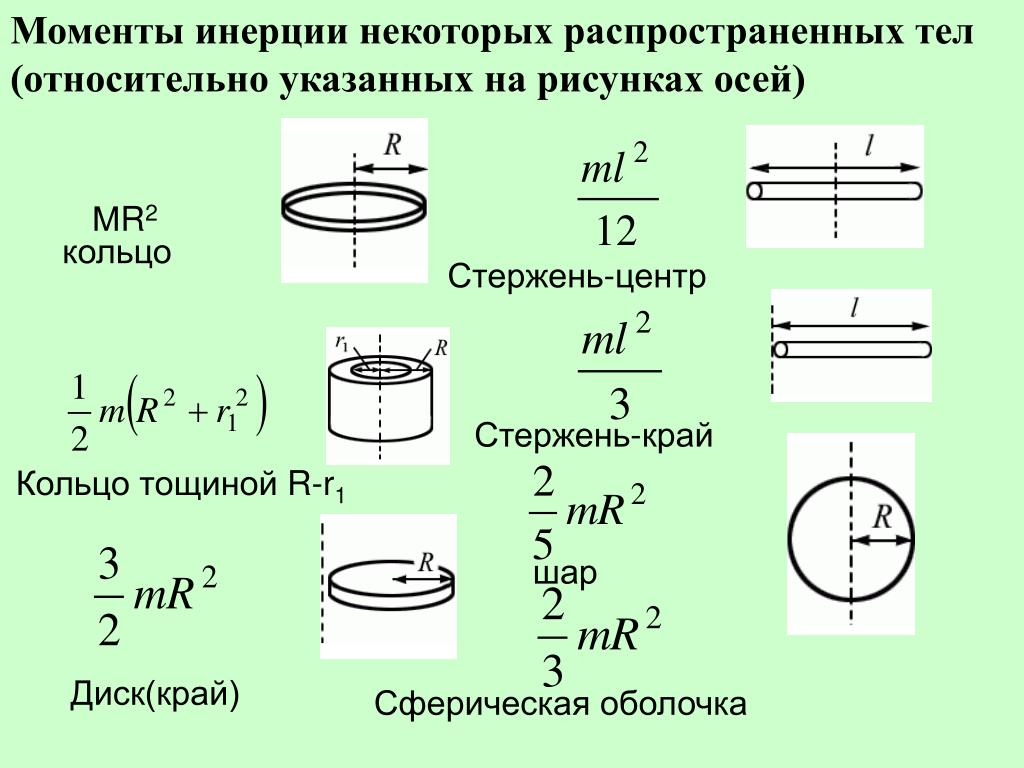 Блок представляет собой однородный сплошной цилиндр. Масса тел и блока одинакова и равна М=1 кг. Считая, что блок вращается без трения, а нить не проскальзывает по блоку, найти ускорение тел, натяжение F12 нити, связывающей оба тела, натяжение нити F2 на участке от тела 2 до блока, натяжение нити Fm на участке от блока до груза m.
Блок представляет собой однородный сплошной цилиндр. Масса тел и блока одинакова и равна М=1 кг. Считая, что блок вращается без трения, а нить не проскальзывает по блоку, найти ускорение тел, натяжение F12 нити, связывающей оба тела, натяжение нити F2 на участке от тела 2 до блока, натяжение нити Fm на участке от блока до груза m. 60) под действием силы тяжести приходит в движение из состояния покоя. Определить ускорение a центра масс катка и силу натяжения нити. Какую скорость приобретет гиря, если она опускается с высоты h? Масса цилиндра М, масса гири m, массой блока пренебречь. Каток катится без скольжения.
60) под действием силы тяжести приходит в движение из состояния покоя. Определить ускорение a центра масс катка и силу натяжения нити. Какую скорость приобретет гиря, если она опускается с высоты h? Масса цилиндра М, масса гири m, массой блока пренебречь. Каток катится без скольжения.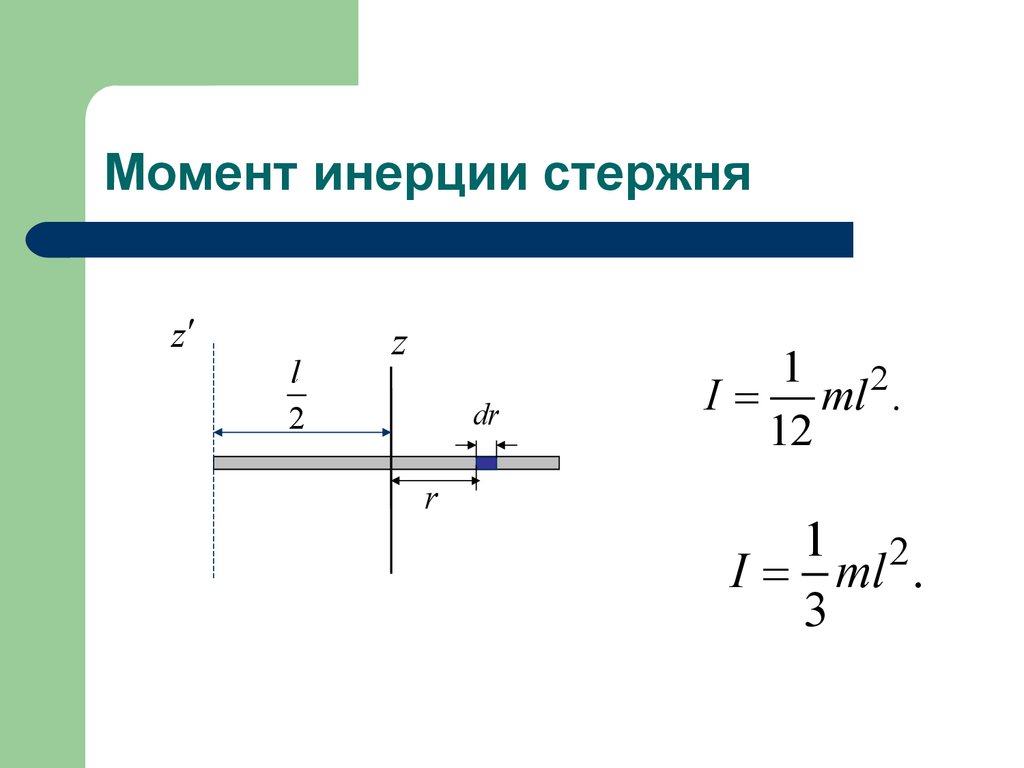 10 . К концу тонкой нерастяжимой нити, намотанной на цилиндрический сплошной блок массой m1=200 г, прикреплено тело массой m2=500 г, которое находится на наклонной плоскости с углом наклона 450 (рис. 61). Нить, удерживающая тело, параллельна наклонной плоскости. Какой путь пройдет тело по наклонной плоскости за t=1 с, если коэффициент трения скольжения по наклонной плоскости равен k=0,1?
10 . К концу тонкой нерастяжимой нити, намотанной на цилиндрический сплошной блок массой m1=200 г, прикреплено тело массой m2=500 г, которое находится на наклонной плоскости с углом наклона 450 (рис. 61). Нить, удерживающая тело, параллельна наклонной плоскости. Какой путь пройдет тело по наклонной плоскости за t=1 с, если коэффициент трения скольжения по наклонной плоскости равен k=0,1?
 ..
..