Момент – инерция – диск
Cтраница 2
Таким образом, момент инерции диска относительно диаметра в два раза меньше, чем относительно оси, перпендикулярной к плоскости диска и проходящей через ее центр. [16]
Считая, что момент инерции диска относительно оси вращения равен I, определить закон изменения его угловой скорости. [17]
Таким образом, момент инерции диска относительно указанной оси равен половине произведения массы диска на квадрат его радиуса. Понятно, что формулой (9.19) определяется и момент инерции сплошного цилиндра относительно его собственной оси. [18]
J – радиус и момент инерции диска относительно оси вращения. Наибольшее распространение получили вискозиметры 1 – й группы. Большая часть этих приборов служит для относит, измерений; они градуируются по эталонным жидкостям ( гли-церинововодные растворы, растворы тростникового сахара, минеральные масла и их смеси и др.
J – радиус и момент инерции диска относительно оси вращения. [20]
Выведите формулу для подсчета момента инерции диска относительно трех осей: перпендикулярной плоскости диска и проходящей через центр масс; совпадающей с диаметром; совпадающей с линией, параллельной диаметру и касательной к окружности диска. Как найти момент инерции диска относительно оси, проходящей через центр масс, но не перпендикулярной плоскости диска. [21]
Момент инерции нагрузки равен моменту инерции диска диаметром 457 и толщиной 34 3 мм, а упругость соответствует упругости стального вала диаметром 76 2 и длиной 660 мм. [22]
По данным задачи 34.24 вычислить момент инерции диска относительно оси г, лежащей в вертикальной плоскости xz и образующей с осью z угол ср. [23]
К – полярный и экваториальный моменты инерции диска; х0, их – постоянные коэффициенты линейной и нелинейной части в выражениях для внешнего трения; Е – модуль упругости; / – экваториальный момент инерции площади сечения вала; I – длина вала; оа – угловая скорость ротора. [24]
[24]
Мы видим, что изменение момента инерции диска
По данным условия задачи 34.25 вычислить момент инерции диска относительно оси z, лежащей в вертикальной плоскости xz и образующей с осью z угол ср. [26]
В цельнокованых роторах это увеличе – альный моменты инерции диска; знак ние менее значительно. [27]
Энергия, поглощаемая гасителем, зависит от момента инерции дисков и момента тре-кпя между элементами гасителя. При малом моменте трения гаситель не будет поглощать достаточного количества энергии, а при моменте трения, превышающем инерционный момент дисков, энергия вообще не поглощается, так как диски ие перемещаются относительно втулки 7, закрепленной на переднем конце вала. При расчете гасителя сухого трения необходимо выбрать оптимальное соотношение между инерционным моментом дисков 4 и моментом трения.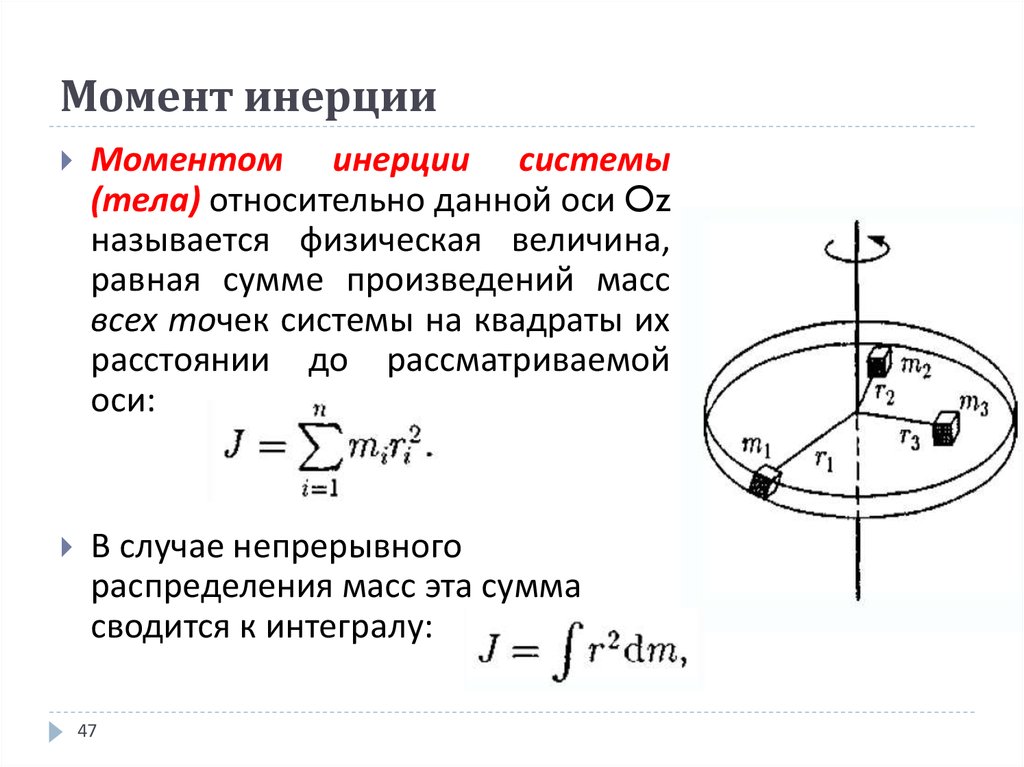
А и С – поперечный и осе вой моменты инерции диска, р, q, r – проекции мгновенной угло вой скорости диска на оси О г ], где ось Ох. [29]
Если моменты инерции зубчатых колес малы по сравнению с моментами инерции дисков и ими при расчете можно пренебречь, то новая динамически эквивалентная система представляет вал с двумя дисками ( фиг. [30]
Страницы: 1 2 3 4
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда… Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации – обмен информацией между организацией и её внешней средой. Эволюция кровеносной системы позвоночных животных: Биологическая эволюция – необратимый процесс исторического развития живой природы… Интересное: Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы… Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски… Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 5 из 9Следующая ⇒ Примеры решения задач 7. а) момент силы относительно начала системы координат; б) модуль момента силы M; в) проекцию Mz момента силы на ось z.
Следовательно, Mz = -1, Н×м. Ответ: , Н×м; M = 17,2 Н×м; Mz = –1 Н×м. 8. Во сколько раз уменьшится момент инерции однородного сплошного диска оносительно оси, проходящей через его центр инерции (точка О) и перпендикулярной к плоскости диска, если сделать круглый дисковый вырез, как показано на рисунке.
Момент инерции – величина аддитивная. Поэтому момент инерции I3 диска с вырезом относительно точки О равен разности момента инерции диска относительно точки О и момента инерции малого диска , соответствующего вырезанной части, также относительно точки О, т. е. . В задаче необходимо найти отношение . Обозначим массу диска через m, а радиус диска через R. Тогда масса вырезанной части , а радиус . Как известно, момент инерции диска относительно оси симметрии равен: . Для вычисления момента инерции используем теорему Штейнера: , где – момент инерции малого диска, соответствующего вырезанной части, относительно оси симметрии этого диска, походящей через точку О′. Ответ: момент инерции диска после сделанного выреза уменьшается в 1,2 раза.
9. Тонкий однородный обруч массой m = 2,0 кг и радиусом R = 1,0 м вращается вокруг оси симметрии, перпендикулярной к плоскости обруча, делая n0 = 120 об/мин. Под действием постоянной касательной к поверхности обруча силы Fт = 4,0 Н обруч тормозится и останавливается. Определить время торможения tт и число оборотов Nт, которое сделает обруч от начала торможения до остановки.
(2) где ω0 – начальная угловая скорость обруча. Знак «минус» в выражении (2) показывает, что вращение равнозамедленное. Число оборотов N связано с углом поворота обруча φ соотношением . (3) В конце времени торможения угловая скорость обруча равна нулю, и из формул (1) и (2) получим с с. Для числа оборотов Nт за время торможения из выражения (3) следует: об. Ответ: tт = 6,3 с; Nт = 13 об.
10. Небольшое тело массой m = 200 г брошено по углом α= 60° к горизонту со скоростью = 10 м/с. Выразить зависимость момента импульса тела от времени в системе координат, изображенной на рисунке, относительно точки О. Определить модуль изменения момента импульса для положения тела в точке наивысшего подъема О΄ и точке падения на землю А.
где , в котором mg – сила тяжести, l – плечо силы относительно точки О. Знак (-) обусловлен тем, что момент силы в соответствии с правилом правого винта направлен в сторону противоположную оси z. Плечо l найдем как l = , так как вдоль оси x силы не действуют и движение равномерное. Тогда момент импульса . (1) Время достижения телом точки наивысшего подъема определяется выражением с (так как ). Время достижения телом точки А в два раза больше времени (как известно, время подъема равно времени спуска тела). Окончательно производя необходимые вычисления, получим для (кг×м2)/с; для модуля изменения момента импульса из (*), учитывая, что в начальный момент времени (кг∙м²)/с. Ответ: (кг∙м²)/с; (кг∙м²)/с.
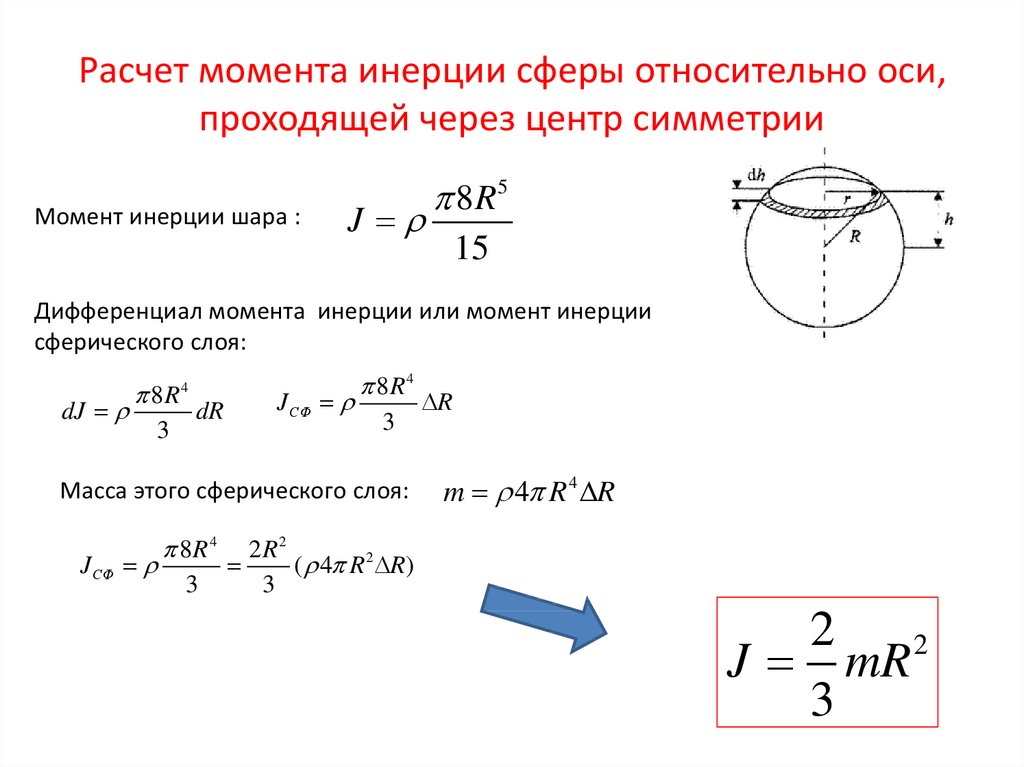
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ 1.24. Сфера радиусом R = 2,0 м равномерно вращается вокруг вертикальной оси симметрии, делая 30 об/мин. Внутри сферы находится шарик. Найти высоту h, соответствующую положению равновесия шарика. При какой наименьшей угловой скорости радиус вращения шарика будет 0,9 R? Шарик считать материальной точкой. (h = 1,0 м;ω = 3,4 рад/с) 1.25. Тело участвует в двух вращательных движениях, происходящих со скоростями и (a = 1,0 рад/с3). Определить: а) на какой угол j повернется тело за первые 3,0 с; б) какой угол составляет ось вращения, вокруг которой происходит поворот, с осью Х. (а) j = 20 рад, б) a = 63°) 1.26. Тело вращается вокруг неподвижной оси так, что угол его поворота меняется в зависимости от времени t по закону , где а>0; b>0. Найти момент времени t, в который тело остановится, а также число оборотов N тела до остановки. ( ; ) 1.27. Материальная точка движется по окружности радиусом R со скоростью u = kt, где k>0. Найдите зависимость от времени модуля полного ускорения точки; постройте графики зависимости тангенциального и нормального ускорений от времени. ( ) 1.28. Определить полное ускорение W в момент времени t = 3,0 c точки, находящейся на ободе колеса радиусом R = 0,50 м, вращающегося согласно уравнению j = Аt+Вt3, где А = 2,0 рад/с; В = 0,20 рад/c3. Изобразите графики нормального и полного ускорений Wn = f(t) и W = f(t) на интервале 0<t<3 с. (W = 27 м/с2) 1.29. Точка движется по окружности с постоянным тангенциальным ускорением. Через некоторый промежуток времени t после начала движения, угол между полным ускорением и радиусом окружности равен 45°. Чему равно угловое ускорение точки? (e ) 1.30. Материальная точка (частица) массой m брошена под углом a к горизонту с начальной скоростью . Траектория полета частицы лежит в плоскости Х, Y. Ось Z направлена “на нас”.
Найти зависимость от времени: а) момента силы , действующего на частицу; б) момента импульса частицы относительно начала координат. (а) ; б) ) . 1.31. Две материальные точки массами m1 и m2 соединены жестким невесомым стрежнем длиной L. Найти положение центра масс системы Хс и момент инерции I этой системы относительно перпендикулярной к стержню оси, проходящей через центр масс. ( ; ) 1.32. Тело массой m = 0,10 кг брошено с некоторой высоты в горизонтальном направлении со скоростью u0 = 20 м/с. Найти модуль приращения момента импульса тела относительно точки бросания за первые t = 5 с. ( = 2,5 ∙102 кгм2/с) 1.33. Сила с компонентами (3, 4, 5) Н приложена к точке с координатами (4, 2, 3) (м). Найти: а) момент силы относительно начала координат; б) модуль вектора ; в) проекцию на ось Z момента силы Мz. ( (Н×м), = 15 Н×м) 1.34. Найти момент инерции однородной прямоугольной пластинки массой m, длиной а и шириной b относительно перпендикулярной к ней оси, проходящей через одну из вершин пластинки. ( ) 1.35. Цилиндр, расположенный горизонтально, может вращаться вокруг оси, совпадающей с осью цилиндра. Масса цилиндра m1 = 12 кг. На цилиндр намотан шнур, к которому привязали гирю массой m2 = 1,0 кг. (W = 1,4 м/с2; T = 8,4 Н) 1.36. На обод маховика диаметром D = 60 cм намотан шнур, к концу которого привязан груз массой m = 2,0 кг. Определить момент инерции маховика, если он, вращаясь равноускоренно под действием силы тяжести груза, за время t = 3,0 с приобрел угловую скорость w = 9,0 рад/с. (J = 1,8 кг×м2) 1.37. Тонкий обруч радиусом R раскрутили вокруг его оси до угловой скорости и положили (опустили) на горизонтальный стол. Через какое время t обруч остановится, если коэффициент трения между столом и обручем равен m? Сколько оборотов N сделает обруч до полной остановки? ( ; ) 1.38. С какой угловой скоростью должен вращаться сосуд в виде усеченного конуса, чтобы шарик, лежащий на его дне, выкатился из него? Диаметр верхнего основания равен d. Стенки сосуда наклонены к горизонту под углом a. ( ) 1.39. Из сплошного однородного цилиндра радиусом R сделали полый, удалив внутреннюю часть радиусом R/2 от оси симметрии. Во сколько раз изменится момент инерции тела относительно указанной оси? ( ) 1.40. Из сплошного однородного цилиндра сделали полый, удалив половину его массы. Как изменится момент инерции J цилиндра относительно его оси и во сколько раз? Как и во сколько раз изменится момент импульса указанных цилиндров, если они вращаются с одинаковой угловой скоростью? ( ) 1.41. В сплошном однородном диске радиусом R просверлили сквозное отверстие радиусом R/2 от оси симметрии. Как изменится момент инерции тела относительно указанной оси по отношению к первоначальному? ( ) 1.42. Два однородных цилиндра с одинаковыми высотами h и равными массами m вращаются относительно своих осей симметрии. Соотношение плотностей материалов цилиндров r1 = (3/4)r2. Сравнить вращающие моменты сил, если угловые ускорения цилиндров одинаковы, а моменты сил трения Мтр равны. ( ) 1.43. Грузик массой 5,0 г, привязанный к нити длиной l = 50 см, вращается вокруг вертикальной оси и описывает окружность в горизонтальной плоскости. Какой угол j образует нить с вертикалью, если частота вращения n = 1,0 c-1. Чему равен модуль проекции момента импульса на ось вращения? (j = 60°; L = 5,9∙10-2 (кг∙м²)/с)
⇐ Предыдущая123456789Следующая ⇒ Папиллярные узоры пальцев рук – маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ – конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой. |
11.6: Расчет моментов инерции
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 18253
- OpenStax
- OpenStax
Цели обучения
- Расчет момента инерции твердых тел однородной формы
- Применить теорему о параллельных осях, чтобы найти момент инерции относительно любой оси, параллельной уже известной
- Расчет момента инерции для составных объектов
В предыдущем подразделе мы определили момент инерции, но не показали, как его вычислить. В этом подразделе мы покажем, как рассчитать момент инерции для нескольких стандартных типов объектов, а также как использовать известные моменты инерции, чтобы найти момент инерции для смещенной оси или для составного объекта. Этот раздел очень полезен для того, чтобы увидеть, как применять общее уравнение к сложным объектам (навык, который имеет решающее значение для более продвинутых курсов физики и инженерии). 92 \]
Этот раздел очень полезен для того, чтобы увидеть, как применять общее уравнение к сложным объектам (навык, который имеет решающее значение для более продвинутых курсов физики и инженерии). 92 \]
для всех точечных масс, составляющих объект. Поскольку \(r\) — это расстояние до оси вращения от каждой части массы, из которой состоит объект, момент инерции любого объекта зависит от выбранной оси. Чтобы убедиться в этом, давайте возьмем простой пример двух масс на конце безмассового (пренебрежимо малой массы) стержня (рис. \(\PageIndex{1}\)) и рассчитаем момент инерции относительно двух разных осей. В этом случае суммирование по массам простое, потому что две массы на конце штанги можно аппроксимировать как точечные массы, и поэтому сумма состоит только из двух членов. 9{2} \ldotp\]
Из этого результата можно сделать вывод, что вращать штангу вокруг конца в два раза труднее, чем вокруг ее центра.
Рисунок \(\PageIndex{1}\): (a) Штанга с осью вращения, проходящей через ее центр; (b) штанга с осью вращения через один конец.
В этом примере у нас было две точечные массы, и их сумму было просто вычислить. Однако, чтобы иметь дело с объектами, которые не являются точечными, нам нужно тщательно продумать каждый член уравнения. Уравнение просит нас просуммировать по каждой «части массы» на определенном расстоянии от оси вращения. Но что именно означает каждый «кусок массы»? Напомним, что в нашем выводе этого уравнения каждая часть массы имела одинаковую величину скорости, что означает, что вся часть должна была иметь единственное расстояние r до оси вращения. Однако это невозможно, если мы не возьмем бесконечно малый кусок массы dm, как показано на рисунке \(\PageIndex{2}\). 9{2} dm \ldotp \label{10.19}\]
Фактически это та форма, которая нам нужна для обобщения уравнения для сложных форм. Лучше всего детально проработать конкретные примеры, чтобы понять, как рассчитать момент инерции для конкретных форм. Это основное внимание в остальной части этого раздела.
Однородный тонкий стержень с осью, проходящей через центр
Рассмотрим однородный (по плотности и форме) тонкий стержень массы M и длины L, как показано на рисунке \(\PageIndex{3}\). Нам нужен тонкий стержень, так что мы можем предположить, что площадь поперечного сечения стержня мала, и стержень можно рассматривать как цепочку масс вдоль одномерной прямой линии. В этом примере ось вращения перпендикулярна стержню и для простоты проходит через его середину. Наша задача — вычислить момент инерции относительно этой оси. Ориентируем оси так, чтобы ось z была осью вращения, а ось x проходила по длине стержня, как показано на рисунке. Это удобный выбор, потому что тогда мы можем интегрировать по оси x.
Нам нужен тонкий стержень, так что мы можем предположить, что площадь поперечного сечения стержня мала, и стержень можно рассматривать как цепочку масс вдоль одномерной прямой линии. В этом примере ось вращения перпендикулярна стержню и для простоты проходит через его середину. Наша задача — вычислить момент инерции относительно этой оси. Ориентируем оси так, чтобы ось z была осью вращения, а ось x проходила по длине стержня, как показано на рисунке. Это удобный выбор, потому что тогда мы можем интегрировать по оси x.
Мы определяем dm как небольшой элемент массы, из которого состоит стержень. Интеграл момента инерции представляет собой интеграл по распределению масс. Однако мы умеем интегрировать по пространству, а не по массе. Поэтому нам нужно найти способ связать массу с пространственными переменными. Мы делаем это, используя линейную плотность массы \(\лямбда\) объекта, которая является массой на единицу длины. Поскольку массовая плотность этого объекта однородна, мы можем написать
Поскольку массовая плотность этого объекта однородна, мы можем написать
\[\lambda = \frac{m}{l}\; или же\; m = \lambda l \ldotp\]
Если мы возьмем дифференциал каждой части этого уравнения, мы найдем
\[dm = d(\lambda l) = \lambda (dl)\]
, так как \( \лямбда\) постоянна. Мы решили сориентировать стержень вдоль оси x для удобства — именно здесь этот выбор становится очень полезным. Заметим, что кусок стержня dl полностью лежит вдоль оси x и имеет длину dx; на самом деле в этой ситуации dl = dx. Поэтому мы можем записать dm = \(\lambda\)(dx), что дает нам переменную интегрирования, с которой мы знаем, как работать. Расстояние каждого куска массы dm от оси задается переменной x, как показано на рисунке. Складываем все вместе, получаем 9{2} \ldotp \end{split}\]
Далее мы вычисляем момент инерции для того же однородного тонкого стержня, но с другим выбором оси, чтобы можно было сравнить результаты. Мы ожидаем, что момент инерции будет меньше относительно оси, проходящей через центр масс, чем ось конечной точки, как это было в примере со штангой в начале этого раздела. {2} \lambda dx \ldotp\] 9{2} \ldotp \label{ThinRod} \end{align} \]
{2} \lambda dx \ldotp\] 9{2} \ldotp \label{ThinRod} \end{align} \]
Обратите внимание, что инерция вращения стержня относительно его конечной точки больше, чем инерция вращения вокруг его центра (в соответствии с примером со штангой) в четыре раза .
Теорема о параллельной оси
Сходство между процессом нахождения момента инерции стержня относительно оси, проходящей через его середину, и относительно оси, проходящей через его конец, поразительно и предполагает, что может существовать более простой метод определения момент инерции стержня относительно любой оси, параллельной оси, проходящей через центр масс. Такая ось называется 9{2} \ldotp\]
Этот результат согласуется с нашим более длинным расчетом (уравнение \ref{ThinRod}). Уравнение \ref{10.20} — полезное уравнение, которое мы применяем в некоторых примерах и задачах.
Exrecise \(\PageIndex{1}\)
Чему равен момент инерции цилиндра радиуса \(R\) и массы \(m\) относительно оси, проходящей через точку на поверхности, как показано ниже ?
- Ответить
\[I_{параллельная ось} = I_{центр\; из\; масса} + md^{2} = mR^{2} + mR^{2} = 2mR^{2} \nonumber \]
Однородный тонкий диск вокруг оси, проходящей через центр ось через его центр (рис.
 \(\PageIndex{5}\)). Рисунок \(\PageIndex{5}\): Расчет момента инерции тонкого диска относительно оси, проходящей через его центр.
\(\PageIndex{5}\)). Рисунок \(\PageIndex{5}\): Расчет момента инерции тонкого диска относительно оси, проходящей через его центр.Поскольку диск тонкий, мы можем считать, что масса полностью распределена в плоскости xy. Мы снова начинаем с отношения для поверхностная массовая плотность , которая представляет собой массу на единицу площади поверхности. Поскольку она однородна, поверхностная массовая плотность \(\sigma\) постоянна:
\[\sigma = \frac{m}{A}\] или \[\sigma A = m\], поэтому \[dm = \sigma (dA)\]
Теперь используем упрощение площади. Площадь можно представить как состоящую из ряда тонких колец, где каждое кольцо представляет собой приращение массы dm радиуса \(r\), равноудаленное от оси, как показано в части (b) рисунка. Таким образом, бесконечно малая площадь каждого кольца \(dA\) определяется как длина каждого кольца (\(2 \pi r\)) умноженная на бесконечно малую ширину каждого кольца \(dr\): 9{2} \ldotp \end{split}\]
Обратите внимание, что это соответствует значению, указанному на рис. 10.5.4.
10.5.4.
Расчет момента инерции для составных объектов
Теперь рассмотрим составной объект, подобный показанному на рисунке \(\PageIndex{6}\), на котором изображен тонкий диск на конце тонкого стержня. Это не может быть легко интегрировано, чтобы найти момент инерции, потому что это объект неоднородной формы. Однако, если мы вернемся к первоначальному определению момента инерции как суммы, мы можем сделать вывод, что момент инерции составного объекта может быть найден из суммы каждой части объекта:
\[I_{total} = \sum_{i} I_{i} \ldotp \label{10.21}\]
Важно отметить, что моменты инерции объектов в уравнении \(\PageIndex{6 }\) вокруг общей оси . В случае этого объекта это будет стержень длиной L, вращающийся вокруг своего конца, и тонкий диск радиуса \(R\), вращающийся вокруг оси, смещенной от центра на расстояние \(L + R\) , где \(R\) — радиус диска. Определим массу стержня как m r , а массу диска как \(m_d\). 9{2} \ldotp\]
Применение расчета момента инерции для решения задач
Теперь давайте рассмотрим некоторые практические применения расчета момента инерции.
Пример \(\PageIndex{1}\): Человек на карусели
Ребенок массой 25 кг стоит на расстоянии \(r = 1,0\, м\) от оси вращающейся карусели. обход (Рисунок \(\PageIndex{7}\)). Карусель можно представить как однородный сплошной диск массой 500 кг и радиусом 2,0 м. Найдите момент инерции этой системы.
Рисунок \(\PageIndex{7}\): Расчет момента инерции ребенка на карусели.Стратегия
Эта задача включает расчет момента инерции. Нам даны масса и расстояние до оси вращения ребенка, а также масса и радиус карусели. Поскольку масса и размер ребенка намного меньше карусели, мы можем аппроксимировать ребенка как точечную массу. Используемые обозначения: m c = 25 кг, r 9{2} \ldotp \nonumber \]
Значимость
Значение должно быть близко к моменту инерции самой карусели, потому что она имеет гораздо большую массу, распределенную от оси, чем ребенок .
Пример \(\PageIndex{2}\): Стержень и твердая сфера
Найдите момент инерции комбинации стержня и сплошной сферы относительно двух осей, как показано ниже. Стержень имеет длину 0,5 м и массу 2,0 кг. Радиус шара 20 см, масса 1 кг.
Стержень имеет длину 0,5 м и массу 2,0 кг. Радиус шара 20 см, масса 1 кг.
Стратегия
Поскольку в обоих случаях у нас есть составной объект, мы можем использовать теорему о параллельных осях, чтобы найти момент инерции относительно каждой оси. В (а) центр масс сферы расположен на расстоянии \(L + R\) от оси вращения. В (б) центр масс сферы расположен на расстоянии \(R\) от оси вращения. В обоих случаях момент инерции стержня направлен вокруг оси на одном конце. Обратитесь к Таблице 10.4 для моментов инерции для отдельных объектов. 9{2} \ldotp \end{split}\]
Значение
Использование теоремы о параллельных осях упрощает вычисление момента инерции составных объектов. Мы видим, что момент инерции больше в (а), чем в (б). Это связано с тем, что ось вращения ближе к центру масс системы в (б). Простая аналогия — стержень. Момент инерции относительно одного конца равен \(\frac{1}{3}\)mL 2 , а момент инерции через центр масс по его длине равен \(\frac{1}{12}\ )мл 2 .
Пример \(\PageIndex{3}\): угловая скорость маятника
Маятник в форме стержня (рисунок \(\PageIndex{8}\)) выходит из состояния покоя под углом 30° . Имеет длину 30 см и массу 300 г. Какова его угловая скорость в нижней точке?
Рисунок \(\PageIndex{8}\): Маятник в виде стержня выпущен из состояния покоя под углом 30°.Стратегия
Используйте сохранение энергии для решения проблемы. В момент выпуска маятник обладает гравитационной потенциальной энергией, которая определяется по высоте центра масс над его нижней точкой при качании. В нижней части качелей вся гравитационная потенциальная энергия преобразуется во вращательную кинетическую энергию. 9{2}) \left(\dfrac{3}{0,3\; m}\right) (1 – \cos 30)} = 3,6\; рад/с \ldotp \nonumber\]
Значение
Обратите внимание, что угловая скорость маятника не зависит от его массы.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Показать оглавление
- нет
- Включено
- да
- Теги
- линейная массовая плотность
- параллельная ось
- теорема о параллельных осях
- источник-физ-4031
- поверхностная массовая плотность
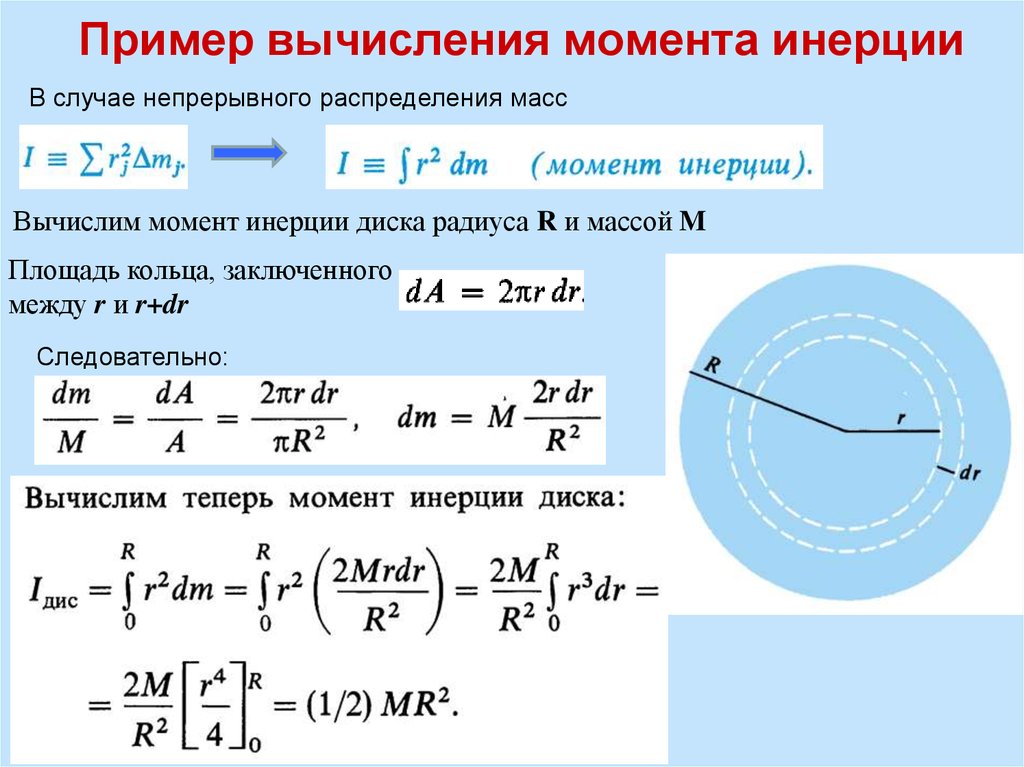
Вычисление момента инерции диска .
 Определение момента инерции элемента объема, имеющего массу, дается выражением 9.0374
Определение момента инерции элемента объема, имеющего массу, дается выражением 9.0374 где – расстояние по перпендикуляру от оси вращения до элемента объема. Чтобы найти общий момент инерции объекта, нужно просуммировать моменты инерции всех элементов объема объекта по всем значениям расстояния от оси вращения. Обычно мы рассматриваем момент инерции относительно вертикали (оси z) и обычно обозначаем его . Мы можем написать
Момент инерции относительно двух других основных осей обозначается и , но мы можем рассматривать момент инерции относительно любой удобной оси.
Вычисление момента инерции диска
В этом блоге я выведу момент инерции диска. В следующих блогах я выведу другие моменты инерции, например. для кольца, твердой сферы, сферической оболочки и полой сферы с очень тонкой оболочкой.
Для наших целей диск представляет собой сплошной круг с малой толщиной (, малой по сравнению с радиусом диска). Если он имеет толщину, сравнимую с его радиусом, он становится цилиндром, о чем мы поговорим в следующем блоге. Итак, наш диск выглядит примерно так.
Итак, наш диск выглядит примерно так.
Диск малой толщины с радиусом
Для расчета момента инерции этого диска относительно оси z суммируем момент инерции элемента объема от центра (где ) до внешнего радиуса .
Элемент массы связан с элементом объема уравнением
(где плотность элемента объема). Будем считать в этом примере, что плотность диска однородна; но в принципе, если бы мы знали его зависимость от , это не было бы проблемой.
Элемент объема можно рассчитать, рассматривая кольцо на радиусе шириной и толщиной . Объем этого кольца равен произведению окружности этого кольца на его ширину, умноженной на его толщину.
поэтому мы можем написать
и, следовательно, мы можем написать уравнение (1) как
Интегрируя между радиусом и , мы получаем
Если мы теперь определим полную массу диска как , где
и общий объем диска. Общий объем диска равен произведению его площади на толщину,
и, таким образом, общая масса равна
Используя это, мы можем переписать уравнение (2) как
Каковы моменты инерции относительно осей x и y?
Чтобы найти момент инерции относительно оси x или оси y, мы используем теорему о перпендикулярной оси . Это утверждает, что для объектов, которые лежат внутри плоскости, момент инерции относительно оси, параллельной этой плоскости, определяется выражением
Это утверждает, что для объектов, которые лежат внутри плоскости, момент инерции относительно оси, параллельной этой плоскости, определяется выражением
, где и — два момента инерции в плоскости и перпендикулярно друг другу.
Из симметрии диска видно, что момент инерции относительно осей x и y будет одинаковым, поэтому . Поэтому мы можем написать
Маховики
Маховики используются для накопления энергии вращения. Это полезно, когда источник энергии не является непрерывным, поскольку они могут помочь обеспечить непрерывный источник энергии. Они используются во многих типах двигателей, включая современные автомобили.
Именно из-за момента инерции диска он может накапливать энергию вращения таким образом. Как и в случае с массой в линейном случае, для изменения скорости вращения (угловой скорости) объекта требуется сила. Чем больше момент инерции, тем большая сила требуется для изменения его угловой скорости. Как мы видим выше из уравнения для момента инерции диска, для двух маховиков одинаковой массы более тонкий больший будет запасать больше энергии, чем более толстый меньший, потому что его момент инерции увеличивается пропорционально квадрату радиуса диск.


 Сила с компонентами (2, -1, 4), H приложена к точке с координатами (–3, 2, 1), м. Найти:
Сила с компонентами (2, -1, 4), H приложена к точке с координатами (–3, 2, 1), м. Найти: Модуль момента силы получится из выражения вышеприведенного: = , Н∙м.
Модуль момента силы получится из выражения вышеприведенного: = , Н∙м.
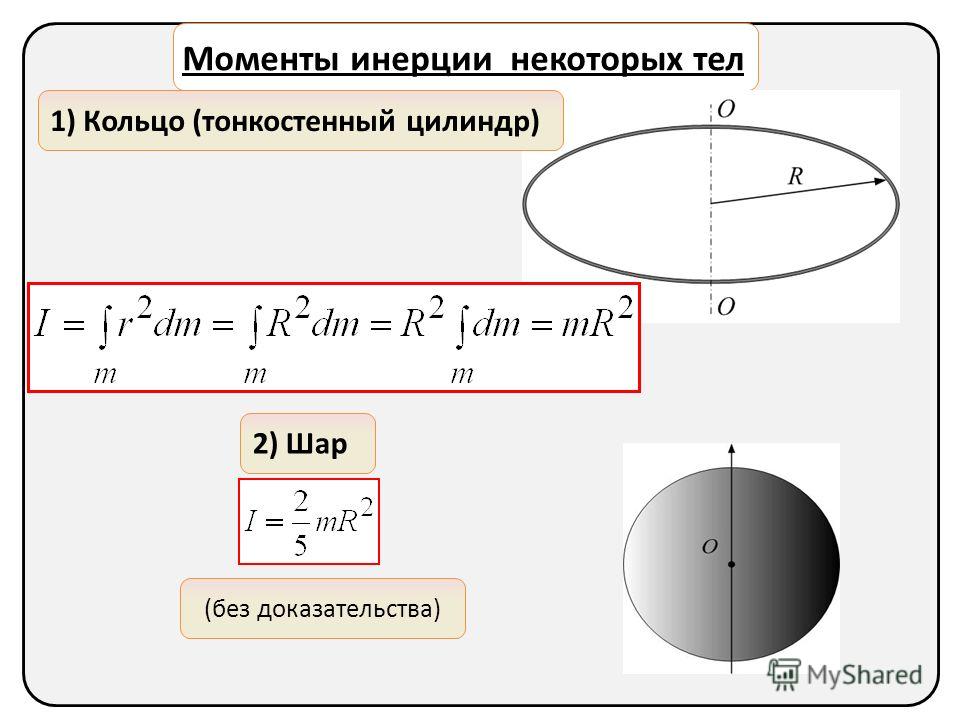
 Момент инерции тонкого однородного обруча I = mR². Угловое ускорение постоянно, так как тормозящий момент сил не изменяется. Следотельно, угловая скорость ωсвязана с угловым ускорением формулой
Момент инерции тонкого однородного обруча I = mR². Угловое ускорение постоянно, так как тормозящий момент сил не изменяется. Следотельно, угловая скорость ωсвязана с угловым ускорением формулой




 С каким ускорением будет опускаться гиря? Какова сила натяжения шнура во время движения гири?
С каким ускорением будет опускаться гиря? Какова сила натяжения шнура во время движения гири?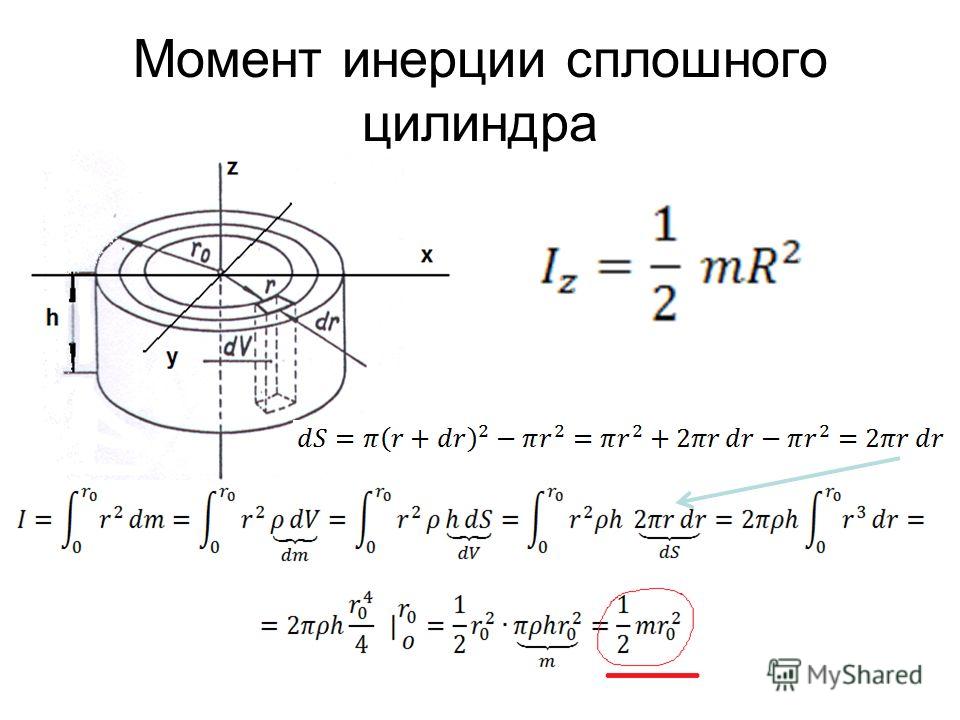
 ..
..