Кинематика и динамика вращательного движения
Контроль знаний(продолжение. См. № 1, 5, 9, 13, 17, 21, 25, 29/01)
Кинематика и динамика вращательного движения
38. (I) Найдите момент инерции велосипедного колеса диаметром 68 см и суммарной массой обода и шины 1,3 кг. Объясните, почему массой ступицы при расчете можно пренебречь.
Calculate the moment of inertia of a 68-cm-diameter bicycle wheel. The rim and tire together have a mass of 1.3 kg. Why can the mass of the hub be ignored?
Решение
Момент инерции обруча равен I = mR2. Подставляя m = 1,3 кг, R = 0,34 м, находим I = 1,3 • (0,34)2 = 0,15 (кг • м2).
39. (I) Молекула кислорода
состоит из двух атомов кислорода суммарной
массой 5,3 Ч 10–26 кг. Момент инерции молекулы
относительно оси, проходящей через ее центр масс
перпендикулярно соединяющему атомы отрезку,
равен 1,9 Ч 10 Оцените эффективное
расстояние между атомами.
Оцените эффективное
расстояние между атомами.
An oxygen molecule consists of two oxygen atoms whose total mass is 5.3 • 10–16 kg and whose moment of inertia about an axis at its center and perpendicular to the line joining them is 1.9 • 10–46 kg•m2. Estimate, from these data, the effective distance between the two atoms.
Решение
Момент инерции молекулы О2 равен моменту инерции гантели I = 2mR2, где m –
масса атома, M = 2m – суммарная масса. Отсюда
расстояние между атомами Подставляя заданные значения,
получаем d=1,2•10
40. (I) Используя теорему Штейнера, найдите момент инерции тонкого однородного стержня массой m и длиной L относительно оси, перпендикулярной стержню и проходящей через его конец. Известно, что момент инерции стержня относительно его центра масс равен
Use the parallel-axis theorem to show that the moment
of inertia of a thin rod about an axis perpendicular to the rod at one end is assuming that if the axis passes
through the center, .
Решение
Теорема Штейнера утверждает,
что если I0 – момент инерции тела (системы
тел) относительно оси, проходящей через центр
масс тела, то момент инерции относительно
параллельной оси, расположенной на расстоянии a
от нее, равен I = I
Разобьем мысленно тело на
отдельные материальные точки с массами mi и
радиус-векторами ri (относительно центра масс). По
определению, момент инерции
При параллельном смещении оси, относительно
которой рассчитывается момент инерции, на вектор
a, новый момент инерции запишется как
Мы использовали определение центра масс,
согласно которому в системе центра масс и возможность
выносить общий множитель (в том числе вектор) за
знак суммы.
41. (II) Используя связь между
моментами инерции относительно точки и
относительно трех взаимно перпендикулярных
осей, проходящих через эту точку, найдите момент
инерции тонкой плоской квадратной пластины со
стороной s относительно оси, проходящей через
центр пластины: а) вдоль ее диагонали; б)
параллельно одной из сторон.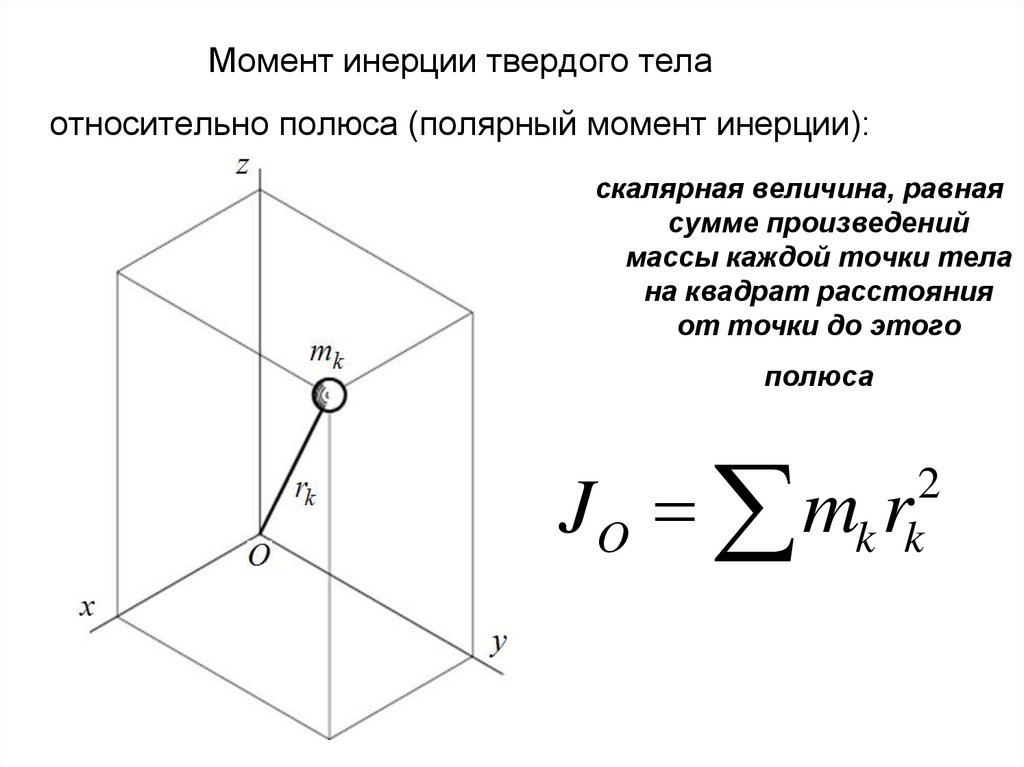
Use the perpendicular-axis theorem to determine a formula for the moment of inertia of a thin, square plate of side s about an axis (a) through its center and along a diagonal of the plate, (b) through the center and parallel to a side.
Решение
Три перпендикулярные оси образуют прямоугольную декартовую систему координат. Обозначим оси соответственно x, y, z. Тогда момент инерции относительно точки начала координат можно записать в виде (см. решение задачи 40):
где Ik – момент инерции относительно k-й оси.
Для плоских тел момент
инерции относительно точки (например центра
масс) совпадает с моментом инерции относительно
оси, проходящей через эту точку перпендикулярно
плоскости тела. Этот момент называется полярным
моментом инерции. Момент относительно оси,
лежащей в плоскости тела, называется
экваториальным. Из доказанного выше следует, что
полярный момент плоского тела равен сумме двух
экваториальных, оси которых взаимно
перпендикулярны.
Для квадратной пластины проще
всего находится момент инерции относительно
экваториальной оси, проходящей через центр
параллельно одной из сторон: он такой же, как для
однородного стержня длины s (относительно его
центра масс). Согласно условию задачи 40 он равен
Используя симметрию квадрата, отсюда легко найти
полярный момент инерции
42. (II) Найдите момент инерции тонкого обруча радиусом R и массой m относительно оси, направленной по касательной к обручу.
Determine a formula for the moment of inertia of a thin hoop of radius R and mass M about an axis tangent to its circular outline.
Решение
Используя решения задач 40 и 41, находим
43. (II) Два одинаковых
однородных шара массой m и радиусом r0 каждый соединены тонким невесомым стержнем
длиной r0, так что центры шаров находятся на
расстоянии 3r0 друг от друга.
Two uniform solid spheres of mass M and radius r0 are connected by a thin (massless) rod of length r0 so that the centers are 3r0 apart. (a) Determine the moment of inertia of this system about an axis perpendicular to the rod at its center. (b) What would be the percentage error if the masses of each sphere were assumed to be concentrated at their centers and a very simple calculation were made?
Решение
Момент инерции шара
относительно оси, проходящей через его центр,
равен
Действительно, момент инерции Ic относительно центра шара равен если учесть, что dm = r4pr2dr,
Согласно решению задачи 41:
Используя теорему Штейнера и
свойство аддитивности момента инерции, находим
искомую величину I = 5,3mr02. Этот
результат точный.
Этот
результат точный.
Если считать массу каждого
шара сосредоточенной в его центре, то искомый
момент равен
44. (II) Два однородных диска одинаковой толщины радиусами R1 и R2 соответственно касаются плоскими основаниями так, что их центры совпадают. Найдите момент инерции системы относительно оси, проходящей через центры дисков перпендикулярно их основанию. Плотности дисков одинаковы, суммарная масса дисков m.
The flat sides of two uniform solid cylindrical wheels
of radii R1 and R2 are placed next to each other with their centers
superposed. They are of equal thickness and are made of material of equal density. Find
the moment of inertia of the system in terms of R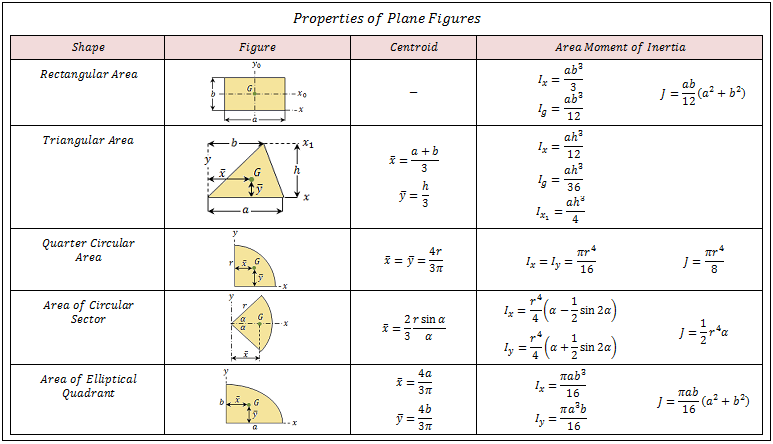
Решение
Момент инерции тела цилиндрической формы относительно оси симметрии равен (см. решение задачи 25). Из условия следует, что
Сумма масс равна m, отсюда
Момент инерции системы равен
45. (II) Шар массой m и радиусом r, закрепленный на конце тонкого невесомого стержня, вращается в горизонтальной плоскости вокруг оси АВ по окружности радиусом R. Расчитайте момент инерции системы относительно оси АВ точно и приближенно, считая, что вся масса шара сосредоточена в его центре. Найдите ошибку, возникающую во втором случае, для r = 10 см и R = 1 м.
A ball of mass M and radius r on the end of a thin
massless rod is rotated in a horizontal circle of radius R about an axis of rotation AB,
as shown in Figure. (a) Considering the mass of the ball to be concentrated at its center
of mass, calculate its moment of inertia about AB. (b) Using the parallel-axis theorem and
considering the finite radius of the ball, calculate the moment of inertia of the ball
about AB.
Решение
Задачи решены Ю.А.Кокшаровым и А.В.Берковым
Фейнмановские лекции по физике: Т.2 Пространство. Время. Движение
Фейнмановские лекции по физике: Т.2 Пространство. Время. Движение
ОглавлениеГлава 15. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ§ 1. Принцип относительности § 2. Преобразование Лоренца § 3. Опыт Майкельсона-Морли § 4. Преобразование времени § 5. Лоренцево сокращение § 6.  Одновременность Одновременность§ 7. Четырехвекторы § 8. Релятивистская динамика § 9. Связь массы и энергии Глава 16. РЕЛЯТИВИСТСКАЯ ЭНЕРГИЯ И РЕЛЯТИВИСТСКИЙ ИМПУЛЬС § 1. Относительность и «философы» § 2. Парадокс близнецов § 3. Преобразование скоростей § 4. Релятивистская масса § 5. Релятивистская энергия Глава 17. ПРОСТРАНСТВО-ВРЕМЯ § 1. Геометрия пространства-времени § 2. Пространственно-временные интервалы § 3. Прошедшее, настоящее, будущее § 4. Еще о четырехвекторах § 5. Алгебра четырехвекторов Глава 18. ДВУМЕРНЫЕ ВРАЩЕНИЯ § 1. Центр масс § 2. Вращение твердого тела § 3. Момент количества движения § 4. Закон сохранения момента количества движения Глава 19. ЦЕНТР МАСС; МОМЕНТ ИНЕРЦИИ § 1. Свойства центра масс § 2. Положение центра масс § 3. Вычисление момента инерции § 4. Кинетическая энергия вращения Глава 20. ВРАЩЕНИЕ В ПРОСТРАНСТВЕ § 1. Моменты сил в трехмерном пространстве § 2. Уравнения вращения в векторном виде § 3.  Гироскоп Гироскоп§ 4. Момент количества движения твердого тела Глава 21. ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР § 1. Линейные дифференциальные уравнения § 2. Гармонический осциллятор § 3. Гармоническое движение и движение по окружности § 4. Начальные условия § 5. Колебания под действием внешней силы Глава 22. АЛГЕБРА § 1. Сложение и умножение § 2. Обратные операции § 3. Шаг в сторону и обобщение § 4. Приближенное вычисление иррациональных чисел § 5. Комплексные числа § 6. Мнимые экспоненты Глава 23. РЕЗОНАНС § 1. Комплексные числа и гармоническое движение § 2. Вынужденные колебания с торможением § 3. Электрический резонанс § 4. Резонанс в природе Главa 24. ПЕРЕХОДНЫЕ РЕШЕНИЯ § 1. Энергия осциллятора § 2. Затухающие колебания § 3. Переходные колебания в электрических цепях Глава 25. ЛИНЕЙНЫЕ СИСТЕМЫ И ОБЗОР § 1. Линейные дифференциальные уравнения § 2. Суперпозиция решений § 3. Колебания в линейных системах § 4.  Аналогии в физике Аналогии в физике§ 5. Последовательные и параллельные сопротивления |
b = основание треугольника
h = высота треугольника
В этом случае b= ab=a 2 и h=\[\frac{a} {\ sqrt (2)} \].
Сумма второго момента площади двух треугольников относительно их общего основания вдвое больше второго момента площади одного из треугольников.
Момент инерции квадратной пластины
Чтобы определить момент инерции квадратной пластины, нам необходимо рассмотреть следующие вещи. 92}]\]
Применение интеграции;
Iplate = 1 / 6 M / L 2
Найдите момент инерции квадратной пластины вдоль оси
Определим МВД квадратной пластины, пересекающей ее центр и перпендикуляр. Возможно, вы не в курсе, но есть способ найти момент инерции. MOI остается неизменным, если масса, расстояние от оси и распределение массы вокруг этой оси остаются прежними».
MOI остается неизменным, если масса, расстояние от оси и распределение массы вокруг этой оси остаются прежними».
Итак, предположим, что у нас есть молекула массы m, расположенная вокруг оси на расстоянии d. Следовательно, его MOI относительно этой оси будет md 92)}\]
Решенный пример для момента инерции квадрата
Вопрос: МВД квадратной пластинки относительно перпендикулярной оси вдоль ее центра масс составляет 20 кг-м 2 . Найдите его момент инерции относительно оси, касающейся его стороны и в плоскости пластинки.
Решение:
Учитывая, что
Инерция в центре = 20 кг-м 2
Предположим, что
Масса квадратной пластины = m
Сторона квадрата = a
Инерция относительно перпендикулярной оси в центре квадрата = Ix + Iy= 2Ix(так как стороны квадрата равны)
Ix= 2Iz = 12ma2
Край квадрата находится на расстоянии 2a от центра.
Используя теорему о параллельных осях, мы имеем
Iedge = Ix+m2a 2
Iedge =12ma2+m2a 2
Iedge = 3MA 2 = 2 × 6MA 2 = 2IZ
IEDE = 2 × 20 = 40 кг -М 2
IEDES = 40KG -M 2
the Iedge = 40KG -M 2
The Eged Момент инерции является важным предметом, который рассматривается в большинстве задач физики, связанных с массой во вращательном движении. MOI обычно используется для вычисления углового момента. В следующих параграфах мы узнаем больше об этом предмете.
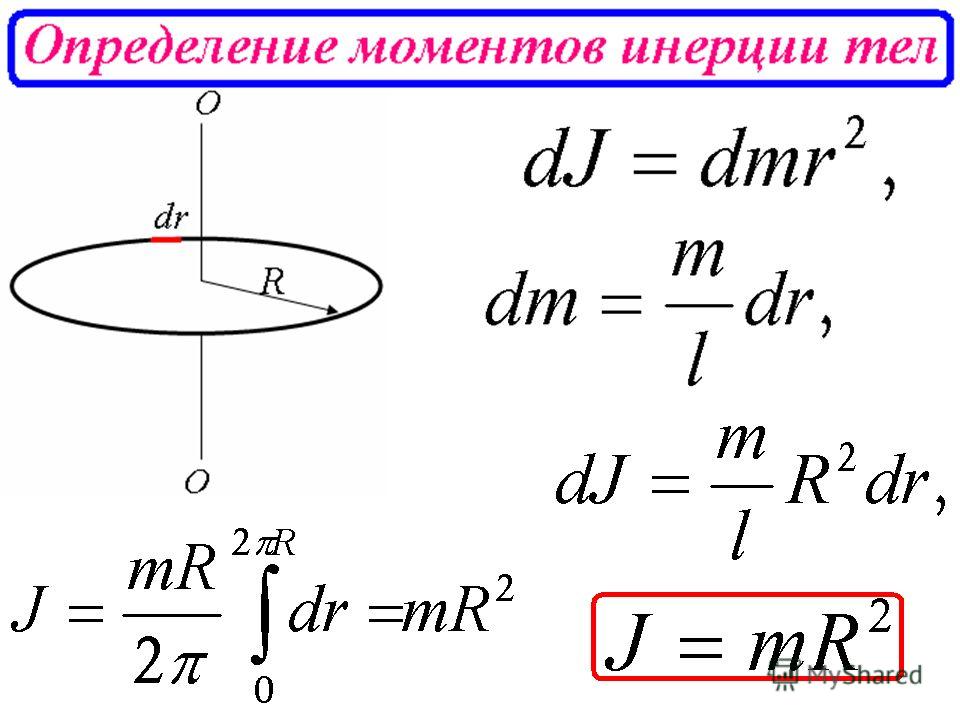
Что такое момент инерции?
Момент инерции определяется как величина сопротивления тела угловому ускорению, которая представляет собой сумму произведения массы каждой частицы на квадрат ее расстояния от оси вращения. Проще говоря, это число, определяющее величину крутящего момента, необходимого для определенного углового ускорения вращающейся оси. Угловая масса или инерция вращения — это другие названия момента инерции. кг м 2 – это единица СИ для Момент Инерции.
Угловая масса или инерция вращения — это другие названия момента инерции. кг м 2 – это единица СИ для Момент Инерции.
Момент инерции часто выражается относительно определенной оси вращения. В основном это определяется распределением массы вокруг оси вращения. MOI изменяется в зависимости от используемой оси.
Какие факторы влияют на момент инерции?
На момент инерции влияют следующие факторы:
Плотность материала
Форма и размер тела
Ось вращения (распределение массы относительно оси)
Системы вращающихся тел дополнительно классифицируются следующим образом:
Отдельные (система частиц)
Непротиворечивые (твердое тело)
Момент инерции площади, также известный как второй момент площади или 2-й момент площади, представляет собой особенность двумерной плоской формы, показывающая, как ее точки распределяются в плоскости поперечного сечения вдоль произвольной оси.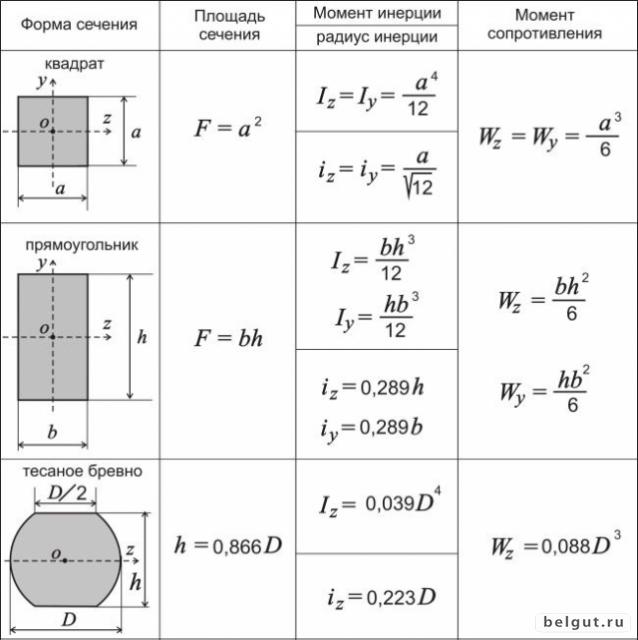 Эта характеристика по существу описывает отклонение плоской формы под действием силы.
Эта характеристика по существу описывает отклонение плоской формы под действием силы.
Для оси на плоскости момент инерции площади обычно обозначается символом I. Когда ось перпендикулярна плоскости, он также обозначается как J. Единицей измерения второго момента площади является L4 (длина в степени четыре). Если мы посмотрим на международную систему единиц, единицей измерения будет метр в четвертой степени, или м4. Это могут быть дюймы в четвертой степени, in4, если мы используем имперскую систему единиц.
Эта тема часто встречается в области проектирования конструкций. В этом контексте считается, что момент инерции площади является мерой жесткости балки на изгиб. Это важная характеристика, которая используется для расчета прогиба балки или для количественной оценки сопротивления балки изгибу. В этом случае мы должны рассмотреть два сценария.
Во-первых, плоский второй момент площади, где сила расположена перпендикулярно нейтральной оси, может просто характеризовать или количественно определять сопротивление балки изгибу.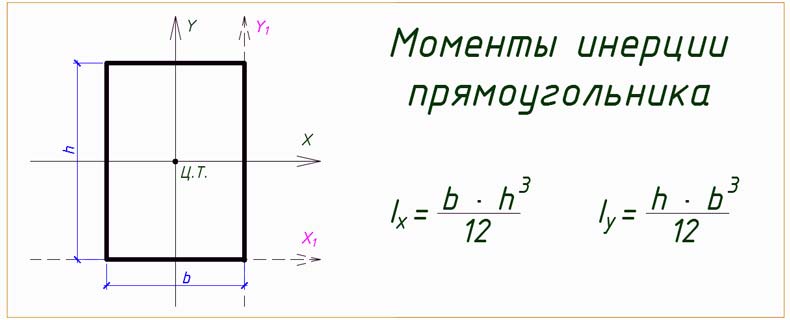
Во-вторых, когда приложенный момент параллелен поперечному сечению балки, можно использовать полярный секундный момент площади для расчета ее сопротивления. По сути, это сопротивление балки кручению.
Different Kinds of Moments of Inertia
The Moment of Inertia is classified into three types:
Moment of Inertia in mass
Moment of Inertia in the area
Moment of Inertia at the poles
Момент инерции массы
Момент инерции массы определяется как сопротивление вращению, создаваемое телом благодаря его массе. Потолочный вентилятор, крыльчатка и маховик — все это примеры моментов инерции масс. Для минимизации энергопотребления необходимо уменьшить момент инерции массы объектов. Для таких тел инерция измеряется относительно оси вращения.
Для таких тел инерция измеряется относительно оси вращения.
Момент инерции площади
Сопротивление, оказываемое объектом изгибу или отклонению, описывается как момент инерции площади. В этом случае инерция не зависит от массы и пропорциональна площади объекта. Луч иллюстрирует момент инерции площади.
Момент инерции на полюсах
Момент инерции на полюсах — это сопротивление, оказываемое предметом скручиванию. Полярный момент отличается от массового Момента инерции так же, как закручивание отличается от вращения. Полярный момент инерции представлен валом.
Момент инерции квадрата
Формула момента инерции квадрата:
I = a 4 / 12
Зарегистрируйтесь, чтобы получить бесплатный пробный тест и учебный материал
+91
Подтвердите OTP-код (обязательно)
Я согласен с условиями и политикой конфиденциальности.
В данном случае a = стороны квадратного сечения.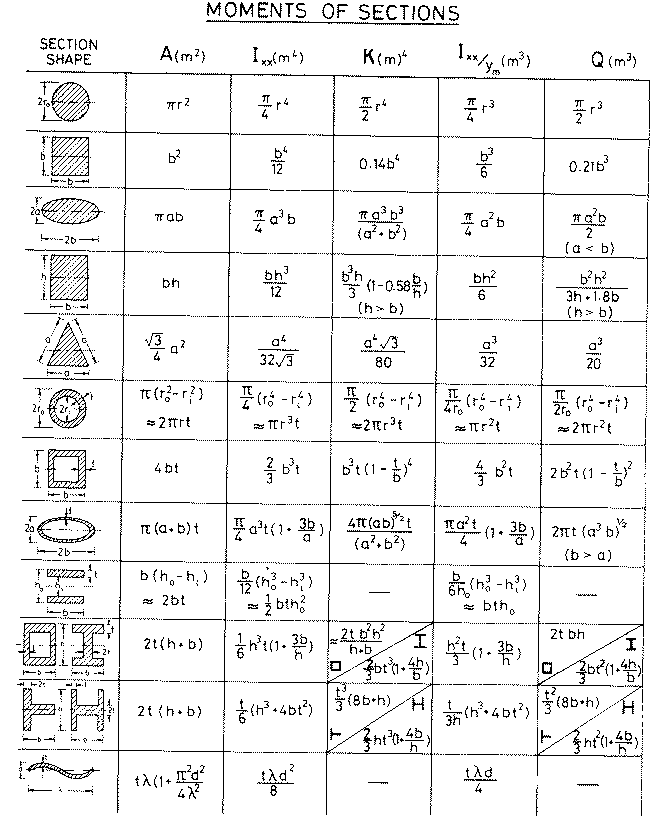 Это будет уравнение сплошного квадрата с центром масс вдоль оси x.
Это будет уравнение сплошного квадрата с центром масс вдоль оси x.
Диагональный момент инерции квадрата также можно рассчитать как;
I x = I y = a 4 / 12
используйте другое выражение для расчета момента инерции того же квадрата.
I = a 4 / 3
Теорема о параллельных осях утверждает, что момент инерции можно легко рассчитать.
I = I см + Ad 2
Icm = центр масс
Несмотря на это, в этом уроке мы заменим массу (M) площадью (A). В дополнение к интегрированию мы будем использовать прямоугольник в качестве эталона, чтобы найти M.O.I. во время выведения.
Помните, что момент инерции прямоугольника определяется как;
I X = ⅓ WH 3
W = width and H = height
I X = ⅓ (WH)H 2
I X = ⅓ ( A)H 2
(1) Когда мы смотрим на квадрат, центр масс которого проходит через ось x, мы видим, что он состоит из двух прямоугольников одинакового размера.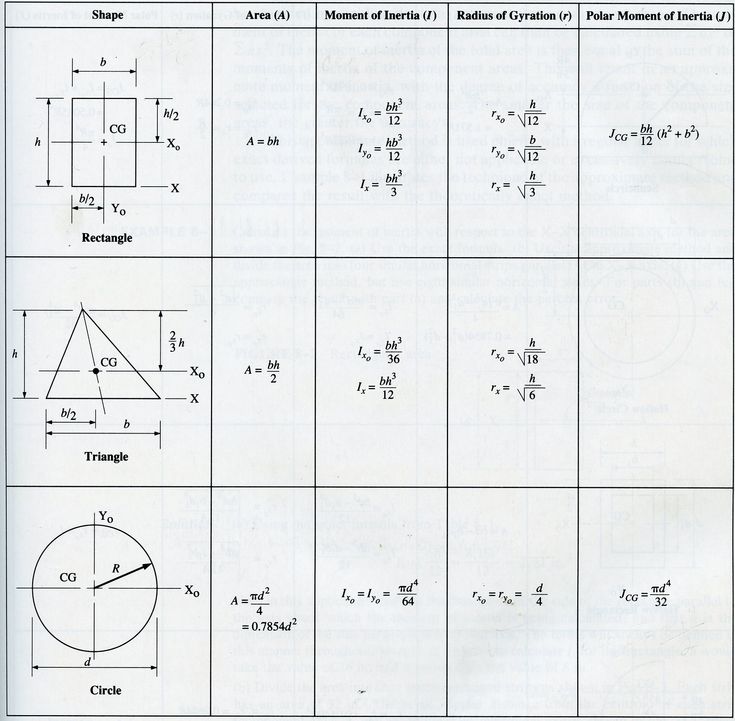
Теперь мы можем выразить это как;
I х = 2 [⅓ а (а / 2) 3 ]
I x = [⅔ a ( a 3 / 8) ]
I x = (1/12)a 4
I Xcm = a 4 / 12
(2) Следующий вывод для квадрата, когда центр масс перемещается на определенное расстояние (d).
Используя теорему о параллельных осях, мы можем теперь утверждать;
I x = I см + Ad 2
I x = (1/12) a 4 + a 2 (a / 2) 2
I x = (1/12) a 4 + (1/4) A 4
I x = (1/12) A 4 + (3/12) A 4
I x =) = (⅓ =) = (⅓ x =) ⅓ =) ⅓ =) =
7). a 4
a 4
При расчете момента инерции квадратной пластины необходимо учитывать несколько факторов.
Для начала предположим, что пластина имеет массу (M) и длину сторон (L).
То есть площадь поверхности A = L X L = L 2
Теперь мы определим массу на единицу площади как;
То есть поверхностная плотность, ρ = M / A = M / L 2
С помощью интегрирования;
I пластина = ∫ dI = ∫ (dI com + dI параллельная ось )
I пластина = x=-L/2 17=10248 10/90 ) р L 3 dx + ρ Lx 2 dx
I пластина = ρ (L 3 / 12) [x | -L/2 L/2 + ρ L [ ⅓ x 3 | -L/2 L/2
I пластина = ρ (L 3 / 12) [ L / 2 – (-L / 2)] + ρ L [(⅓ L 3 / 8) – (- ⅓ L 3 / 8)]
I пластина = ρ (L 3 / 12) (L) + ρ L (⅔ L 3 / 8)
I пластина = (ρ / 12) L 4 + (ρ / 12) L 4
I пластина = (1 / 6) ρ L 4
I пластина = (1 / 6) (M / L 07 8 ) L 90 4
I пластина = (1 / 6) M L 2
Часто задаваемые вопросыДля чего нужен момент инерции?
MOI объекта помогает определить, какой крутящий момент требуется для достижения заданного углового ускорения.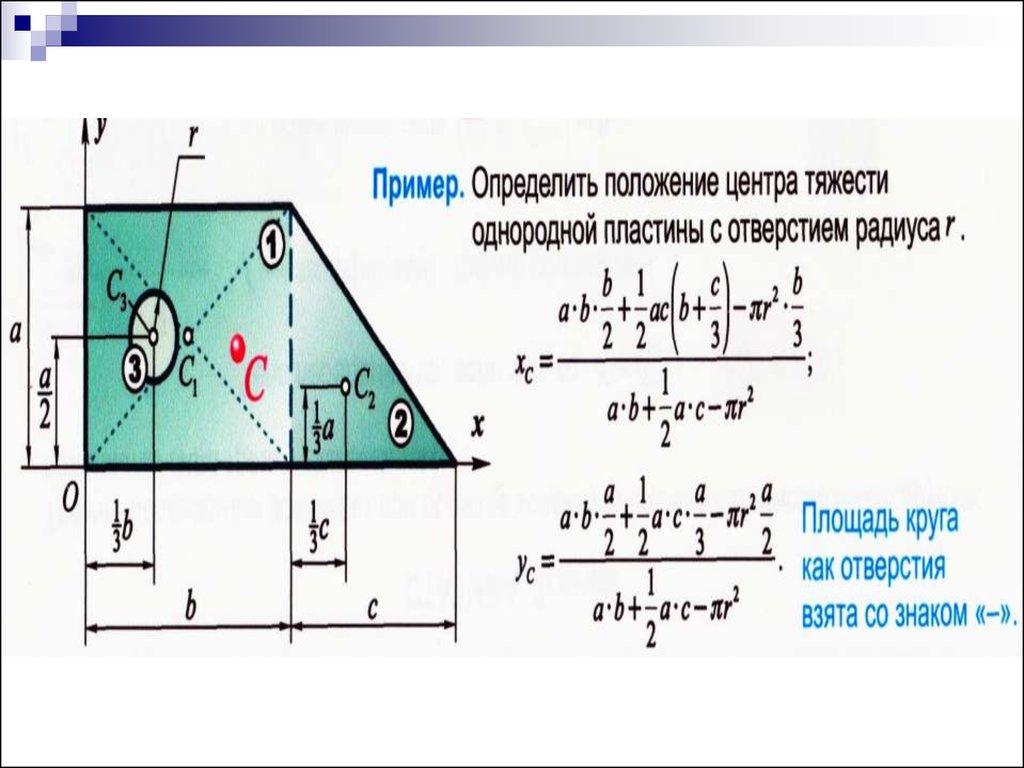

 Однако даже математики считают, что их науке надо учить по-другому. А уж о физике и говорить нечего: она столь интенсивно развивается, что даже лучшие педагоги все время сталкиваются с большими трудностями, когда им надо рассказывать студентам о современной пауке. Они жалуются, что им приходится ломать то, что принято называть старыми или привычными представлениями. Но откуда берутся привычные представления? Обычно они попадают в молодые головы в школе от таких же педагогов, которые потом будут говорить о недоступности идей современной науки. Поэтому прежде чем подойти к сути дела, приходится тратить много времени на то, чтобы убедить слушателей в ложности того, что было ранее внушено им как очевидная и непреложная истина.
Однако даже математики считают, что их науке надо учить по-другому. А уж о физике и говорить нечего: она столь интенсивно развивается, что даже лучшие педагоги все время сталкиваются с большими трудностями, когда им надо рассказывать студентам о современной пауке. Они жалуются, что им приходится ломать то, что принято называть старыми или привычными представлениями. Но откуда берутся привычные представления? Обычно они попадают в молодые головы в школе от таких же педагогов, которые потом будут говорить о недоступности идей современной науки. Поэтому прежде чем подойти к сути дела, приходится тратить много времени на то, чтобы убедить слушателей в ложности того, что было ранее внушено им как очевидная и непреложная истина.