|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Оснащения врачебно-сестринской бригады. Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов… Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие… Интересное: Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья… Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски. Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 11 из 15Следующая ⇒ При вращении материальной точки массой m вокруг фиксированной оси Z по окружности радиуса r, лежащей в плоскости, перпендикулярной оси Z, со скоростью v момент импульса равен . Если вокруг фиксированной оси вращается твердое тело, то его можно разбить на совокупность материальных точек с моментами инерции , вращающихся вокруг оси с одинаковой угловой скоростью и имеющих моменты импульса . Тогда момент импульса твердого тела относительно оси вращения будет равен , где величину называют моментом инерции твердого тела относительно выбранной оси вращения. Однако вычислить момент инерции твердого тела по этой формуле нельзя. Для тела с распределенной массой его вычисляют по формуле . Для сведения этого интеграла к математическому элемент массы тела в зависимости от характера ее распределения (по кривой, поверхности или объему тела) представляют в виде , где – линейная, поверхностная и объемная плотности тела, соответственно. В справочниках приводятся только моменты инерции тел относительно осей вращения, проходящих через их центр масс (ЦМ)C. Так, момент инерции стержня длиной l и массой m относительно оси вращения, перпендикулярной стержню и проходящей через его ЦМ, равен . Для кольца или цилиндра с внутренним и внешним радиусами и – или , где . В частных случаях обруча и полого цилиндра , диска и сплошного цилиндра опять придем к прежним формулам моментов инерции этих тел. Для сферы с толстыми стенками с внутренним и внешними радиусами стенок и – , где . Если ось вращения тела смещена от оси вращения, проходящей через его ЦМ, на расстояниеa и параллельна ей, то момент инерции тела относительно этой оси рассчитывают по теореме Штейнера: , где m – масса тела. Например, момент инерции круглых тел относительно оси вращения, касающейся их поверхности (a = R) и параллельной исходной оси вращения, проходящей через ЦМ тела, по теореме Штейнера равен . Пример 1. Рис.51 Дано: . Найти: Решение: Решение задачи построим в виде последовательного алгоритма. Расстояния ЦМ тел до оси цилиндра: . Моменты инерции тел относительно их ЦМ: . Моменты инерции тел относительно оси цилиндра, рассчитанные по теореме Штейнера: . Полный момент инерции системы тел: . Ответ: . Пример 2. Найти момент инерции каркаса равностороннего треугольника массой m со сторонами длиной l относительно оси вращения, проходящую через его ЦМ, перпендикулярную его плоскости (рис.52). Каким станет момент инерции треугольника, если ось вращения параллельно перенести в одну из его вершин. Рис.52 Дано: m, l. Решение: ЦМ С равностороннего треугольника находится в точке пересечения его высот. Масса одной стороны треугольника , расстояния от ЦМ сторон треугольника до оси вращения . Момент инерции одной стороны треугольника относительно оси вращения по теореме Штейнера: . Момент инерции треугольника . При параллельном переносе оси вращения в одну из вершин треугольника расстояние между ЦМ треугольника и новой осью вращения станет равным , а его новый момент инерции по теореме Штейнера – . Ответ: . Пример 3. Найти момент инерции каркаса квадрата массой m со сторонами длиной l относительно оси вращения, проходящей через его центр и перпендикулярной плоскости квадрата (рис.53). Рис. 53 Дано Решение: Масса одной стороны квадрата , расстояния от оси вращения до сторон квадрата . Момент инерции одной стороны квадрата относительно выбранной оси вращения по теореме Штейнера: . Ответ: . Пример 4. Найти момент инерции стержня длиной l и массой m, наклоненного под углом α к оси вращения, проходящей через его ЦМ. Рис.54 Дано: m, l, α.Найти: Решение Из полученного выражения следует, что вклад в момент инерции стержня дает его проекция на направление, перпендикулярное оси вращения. Ответ: . Пример 5. Найти момент инерции стержня длиной l и массой m, наклоненного под углом α к оси вращения, ближайший конец которого отстоит от оси вращения на расстояние a (рис.55). Ось вращения и стержень лежат в одной плоскости. Рис.55 Дано: . Найти: Решение: Для вычисления момента инерции выберем систему координат, как это показано на рис.56. Повторяя рассуждения примера 1 и изменяя пределы интегрирования, получим для момента инерции стержня . При a=0 получим . Откуда при . Выражение для можно записать в виде . Откуда при получим . Отсюда следует, что стержень, параллельный оси вращения, ведет себя как материальная точка. Пример 6. Найти момент инерции каркаса прямоугольника массой m со сторонами, равными a и b, относительно оси вращения, проходящей в его плоскости через его ЦМ параллельно стороне a (рис.56). Рис.56 Дано: m, a, b. Найти: Решение: Линейная плотность массы каркаса прямоугольника равна . Массы сторон длиной a и b равны соответственно и . Стороны прямоугольника с длиной равной a, параллельные оси вращения, ведут себя как материальные точки с моментом инерции , а стороны длиной b, перпендикулярные оси вращения, как стержни с моментом инерции . Полный момент инерции каркаса прямоугольника . Ответ: . Пример 7. Вывести формулу для момента инерции прямоугольника массой m со сторонами a и b относительно оси вращения, проходящей через его ЦМ, перпендикулярно его плоскости (рис.57). Рис.57 Дано: m, a, b. Найти: Решение: Выберем систему координат XYZ с началом О в ЦМ прямоугольника, ось Z которой перпендикулярна его плоскости. Оси X и Y направим перпендикулярно его сторонам a и b. Масса прямоугольника , где – поверхностная плотность его массы. В качестве элемента поверхности возьмем прямоугольник с координатами и ,со сторонами и и площадью , находящийся на расстоянии от начала О системы координат. Масса этого прямоугольника , а момент инерции . Полный момент инерции прямоугольника Если или , то придем к формуле момента инерции стержня относительно оси вращения, перпендикулярной стержню и проходящей через его ЦМ. Ответ: . Пример 8. Вывести формулу для момента инерции равнобедренного треугольника массой m, высотой h и длиной основания, равной a, относительно оси вращения, лежащей в плоскости треугольника и проходящей вдоль его высоты. Рис.58 Дано: m, a. Найти: Решение: Выберем систему координат с началом О в вершине треугольника. Ось Z направим вдоль высоты треугольника к его основанию (рис.58). Масса треугольника . В качестве элементарного тела выберем стержень, перпендикулярный к оси Z на расстоянии z от начала О шириной dz. Из подобия треугольников длина стержня , его площадь , масса , а момент инерции . Момент инерции треугольника относительно оси вращения, проходящей вдоль его высоты . Ответ: . Пример 9. Вывести формулу для момента инерции равнобедренного треугольника массой m, высотой h и длиной основания, равной a, относительно оси вращения, перпендикулярной плоскости треугольника и проходящей через его вершину. Дано: m, a,h. Найти: Решение: Выберем систему координат так же, как в примере 8 (рис.59). Масса треугольника . В качестве элементарного тела выберем стержень, перпендикулярный к оси X на расстоянии z от начала О шириной dz и длиной , его масса и момент инерции относительно его ЦМ . Момент инерции стержня относительно его вершины по теореме Штейнера . Полный момент инерции равнобедренного треугольника относительно оси вращения, проходящей через его вершину перпендикулярно его плоскости . Откуда . Для равностороннего треугольника , и . Ответ: ,для равностороннего треугольника– . Пример 10. Вывести формулу для момента инерции равнобедренного треугольника массой m, высотой h и длиной основания, равной a, относительно оси вращения, перпендикулярной плоскости треугольника и проходящей через его ЦМ. Дано: m, a,h. Найти: Решение: Согласно разделу Центр масс ЦМ треугольника находится от вершины треугольника на расстоянии . Тогда по теореме Штейнера с учетом примера 9получим Для равностороннего треугольника , , . Ответ: , для равностороннего треугольника – . Пример 11. Вывести формулу для момента инерции кольца (полого цилиндра) массой m с внутренним и внешним радиусами и относительно оси вращения, проходящей через центр кольца, перпендикулярно его плоскости (рис.59). Рис.59 Решение: Масса кольца , где – поверхностная плотность его массы. Выберем в качестве элементарного тела кольцо радиуса r и шириной dr, площадь которого , а масса равна . Момент инерции кольца . Тогда момент инерции большого кольца Ответ: . Пример 12.Вывести формулу для момента инерции кругового сектора диска массой m радиусом R относительно оси вращения, перпендикулярной его плоскости и проходящей через его вершину (рис. Дано: m, R. Найти: Решение:Задачу будем решать в полярной системе координат. Начало О системы координат выберем в центре кругового сектора. Масса сектора с углом при его вершине . В качестве элемента массы dm выберем площадку, находящуюся на расстоянии r от точки О под углом α к оси X, перпендикулярной оси симметрии сектора. Ее площадь , а масса . Момент инерции кругового сектора, боковые стороны которого составляют углы с осью X , равен Ответ: . Пример 13. Вывести формулу для момента инерции для половины диска массой m и радиусом R относительно оси вращения, перпендикулярной его плоскости и проходящей через его ЦМ. Дано: m, R. Найти: Решение: Положение ЦМ половины диска было найдено в разделе 7 – Центр масс и равно , а его момент инерции относительно его центра в О получен примере 12. . Ответ: .
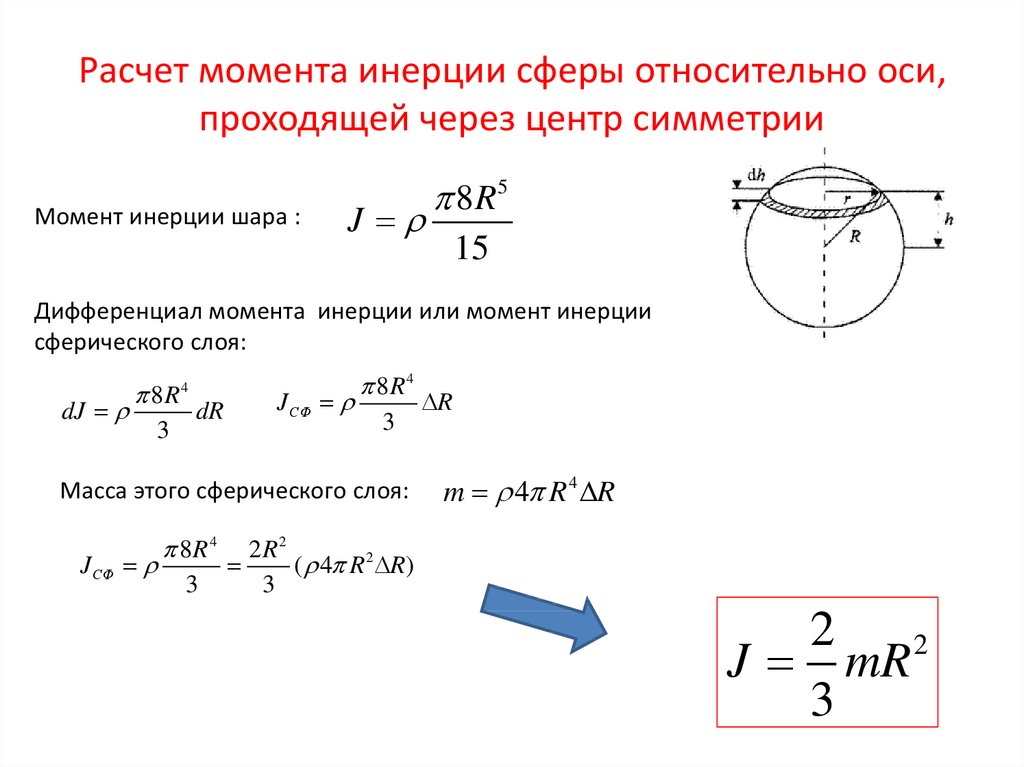
Пример 14. Вывести формулу для момента инерции диска массой m и радиусом R относительно оси вращения, лежащей в его плоскости и проходящей через его диаметр. Рис.60 Дано: m, R. Найти: Решение: Начало О системы координат возьмем в ЦМ диска, а его ось вращения Z направим по его диаметру (рис.60). Масса диска ,где – поверхностная плотность массы диска. Для расчета момента инерции диска выберем в качестве элементарного тела стержень, перпендикулярный оси вращения Z, находящийся на расстоянии z от точки О. Длина стержня , , его ширина dz, масса стержня . Элементарный момент инерции стержня . Тогда с учетом, что при – , откуда получим для полного момента инерции диска относительно оси вращения, проходящей через его диаметр . Ответ: . Пример 15. Вывести формулу для момента инерции кругового сектора массой m и радиусом R и углом при его вершине относительно оси вращения, лежащей в его плоскости и проходящей через его ось симметрии. Дано: . Найти: Решение:Начало О системы координат возьмем в центре кругового сектора, а его ось вращения Z направим вдоль его оси симметрии. Масса сектора ,где – поверхностная плотность его массы. Задачу будем решать в полярной системе координат. Начало О системы координат выберем в центре кругового сектора. В качестве элемента массы dmвыберем площадку, находящуюся на расстоянии rот точки О под углом α к оси X, перпендикулярной оси Z симметрии сектора (рис.21 раздела 7). Ее координата по оси Z равна , площадь , а масса . Момент инерции кругового сектора относительно оси Z, боковые стороны которого составляют углы с осью X, с учетом, что , равен . Откуда . При придем к моменту инерции диска и половины диска, полученному в предыдущем примере. Ответ: . Пример 16. Вывести формулу для момента инерции шара массой m и радиусом R относительно оси вращения, проходящей через его ЦМ (рис.60). Дано: m, R. Найти: Решение: Масса шара , где – объемная плотность массы шара. Выберем в качестве элементарного тела диск, лежащий в плоскости, перпендикулярной оси вращения, и отстоящий на расстояние z от ЦМ сферы. Радиус диска , его высота dz, а объем . Масса диска , его момент инерции . Полный момент инерции шара Ответ: . Пример 17. Вывести формулу для момента инерции шарового слоя массой m с внутренним и внешним радиусами, равными и относительно оси вращения, проходящей через его ЦМ. Рассмотреть момент инерции сферы массой m и радиусом R как частный случай.
Дано: . Решение: Масса шара с объемной плотностью массы ρравна , а масса полости в нем . Тогда масса шарового слоя . Откуда . Если момент инерции шара равен , а шаровой полости в нем , то момент инерции шарового слоя согласно примеру 16 . Откуда при и опять придем к формуле момента инерции шара . Используя преобразование , момент инерции шарового слоя можно представить в виде . Откуда при получим момент инерции сферы . Ответ: для шарового слоя , для сферы . Пример 18. Вывести формулу для момента инерции прямого конуса массой m с радиусом основания R и высотой h относительно оси вращения, проходящей через его ось симметрии. Рис.61 Дано: m, R. Найти: Решение: Выберем ось Z по направлению оси симметрии конуса с началом О в его вершине (рис.61). Масса конуса . Выберем в качестве элементарного тела диск, лежащий в плоскости, перпендикулярной оси вращения и отстоящий на расстояние z от вершины конуса. Из подобия треугольников , тогда радиус диска , его высота dz, а объем . Масса диска , его момент инерции . Полный момент инерции конуса . Ответ: .
⇐ Предыдущая6789101112131415Следующая ⇒ Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ – конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого. |
Момент инерции и крутильные колебания
Nach oben
Информация
- Контактное лицо
- Условия сотрудничества
- Декларация о конфиденциальности
- Вводные данные
Обслуживание
- Краткий обзор услуг
- Скачать
- Каталоги
- Вебинары и Видео
- Связаться со службой поддержки клиентов
Компания
- О нас
- Качественная политика
- Безопасность в классе
Please note
* Prices subject to VAT.
We only supply companies, institutions and educational facilities. No sales to private individuals.
Please note: To comply with EU regulation 1272/2008 CLP, PHYWE does not sell any chemicals to the general public. We only accept orders from resellers, professional users and research, study and educational institutions.
Пожалуйста, введите имя, под которым должна быть сохранена Ваша корзина.
Сохраненные корзины вы можете найти в разделе My Account.
Название корзины
2$$
Это явно не правильный ответ. Где я ошибся в своем методе? Является ли разделение сферы на полые оболочки концептуально неправильным в первую очередь?
- исчисление
- интеграция
- физика
$\endgroup$
$\begingroup$
Из других ответов не ясно, почему ваш подход неверен. Помните, что вы рассчитываете момент инерции для вращения 92\dr)$$
Помните, что вы рассчитываете момент инерции для вращения 92\dr)$$
Интеграция даст правильный ответ. Помните, что вы суммируете сферические оболочки, а не отдельные точечные массы, так что это меняет расчет.
$\endgroup$
5
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
определенные интегралы – Момент инерции n-мерного шара
ПЕРЕСТАНОВКА ЗАДАЧИ
Эта задача некорректна.

 ..
.. Величину называют моментом инерции материальной точки относительно оси Z.
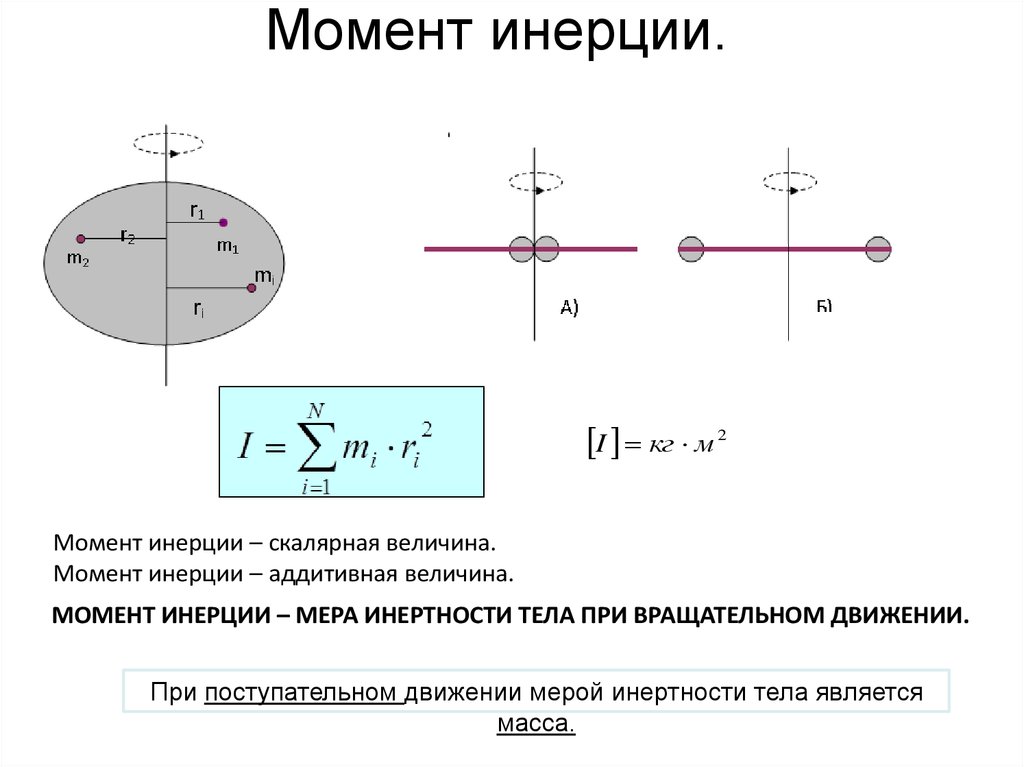
Величину называют моментом инерции материальной точки относительно оси Z. Момент инерции круглых тел массой m и радиусом R относительно оси вращения, проходящей через их ЦМ вдоль оси их симметрии – , где k – коэффициент инерции равный k = 1 для обруча и полого цилиндра, для диска и сплошного цилиндра, для шара, для сферы.
Момент инерции круглых тел массой m и радиусом R относительно оси вращения, проходящей через их ЦМ вдоль оси их симметрии – , где k – коэффициент инерции равный k = 1 для обруча и полого цилиндра, для диска и сплошного цилиндра, для шара, для сферы. Перпендикулярно к боковой поверхности прямого цилиндра массой и радиусом прикреплен стержень массой и длиной l. Ко второму концу стержня прикреплен шар массой и радиусом (рис.51). Найти момент инерции этой системы тел относительно оси цилиндра.
Перпендикулярно к боковой поверхности прямого цилиндра массой и радиусом прикреплен стержень массой и длиной l. Ко второму концу стержня прикреплен шар массой и радиусом (рис.51). Найти момент инерции этой системы тел относительно оси цилиндра. Найти:
Найти: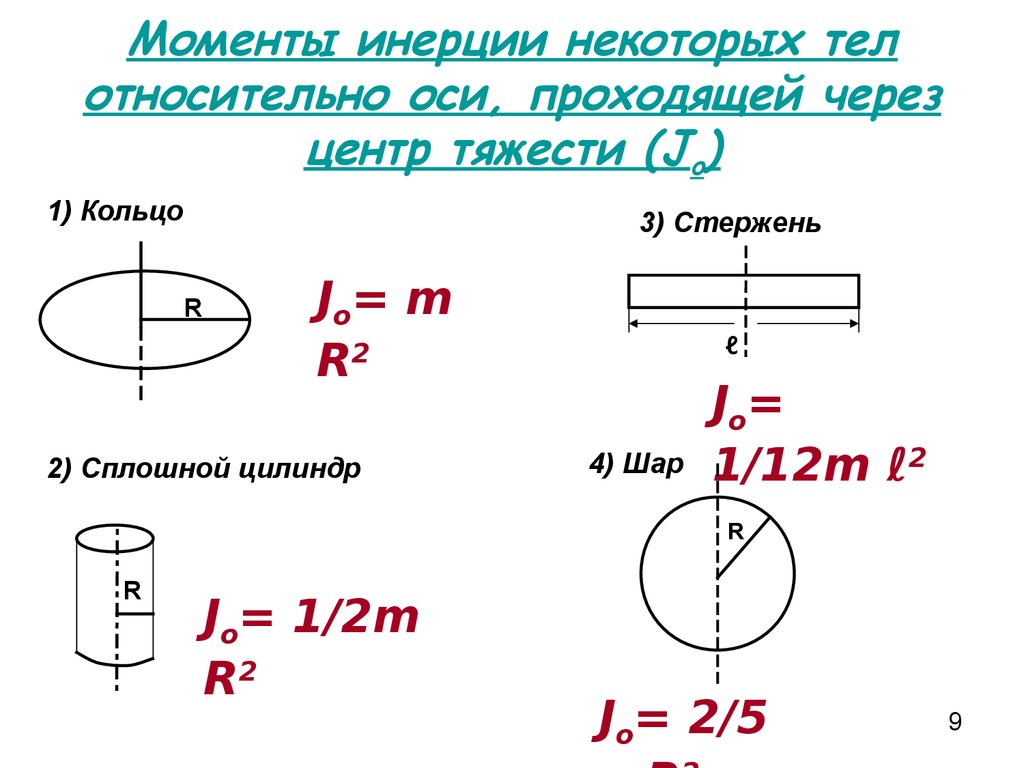 Момент инерции квадрата .
Момент инерции квадрата .



 21, раздел 7).
21, раздел 7). Тогда момент инерции половины диска относительно его ЦМ по теореме Штейнера будет равен
Тогда момент инерции половины диска относительно его ЦМ по теореме Штейнера будет равен

 Найти:
Найти:
 ..
..