Момент инерции шара: Момент инерции шара, теория и примеры

6.5. Момент инерции сплошного шара

Рис. 6.3

Сплошной однородный шар можно представить как сумму бесконечно тонких сферических слоев с массами dm = mdV/V (рис. 6.3). Объем сферического слоя dV представим в виде: dV = 4r²dr, где r – радиус сферического слоя. Объем шара V = 4/3R³, где R – радиус шара. Если шар полый, то момент инерции сферического слоя относительно его центра масс (точка С) ^I_c ^{= mR2, но ,} где из-за симметрии I_x = I_y = I_z. ^{Момент инерции сферического слоя относительно диаметра .}

Тогда момент инерции шара

6.5.1. Примеры моментов инерции некоторых тел

4. Тонкое кольцо радиусом R

и шириной d.

однородного состава относительно оси

3. Полый цилиндр с внутренним r и внешним R радиусами

.

2. Тонкое кольцо

радиуса R

1. Сплошной

цилиндр радиуса R

5. Тонкий параллелепипед

6.6. Работа, совершаемая телом

при вращательном движении

Если произвольная м. т. вращается по окружности и на нее действует сила (рис. 6.4), то при повороте на некоторый угол совершается элементарная работа

Рис. 6.4

А = F ds, где ds = r d.

Тогда А = (r F) d = M d. (6.8)

Полученное выражение остается справедливым и случае системы м.т. (твердых тел), совершающих вращательное движение относительно оси Z при  = сonst. В этом случае момент внутренних сил равен нулю и работа не совершается. Для нахождения полной работы необходимо вычислить интеграл:

, (6.9)

где  = ₂  _1.

Если действующая сила является потенциальной, то А =  dWp ,

где dWp  бесконечно малое изменение потенциальной энергии тела при повороте на малый угол dj, т. е.

dWp =  M_zd или M_{z =}  dWp/d .

6.7. Кинетическая энергия тела, совершающего

вращательное движение

Кинетическая энергия м. т. W_k = mv² / 2 . Тогда для системы м. т. или тела . Используя связь линейной скорости с угловой в видеv_i = r_i, получим . (6.10)

Замечание: При плоском движении тел (например, цилиндр скатывается по наклонной плоскости, рис. 6.5) полная скорость

, (6.11)

где С  центр инерции.

Полная кинетическая энергия тела равна сумме кинетической энергии поступательного движения его центра масс (центра инерции) и кинетической энергии вращательного движения тела относительно точки С, т. е.

. (6.12)

Замечание: При скатывании тела (без проскальзывания) на него действует сила трения покоя (рис. 6.5).

Рис. 6.5

Несмотря на наличие диссипативной силы (сила трения покоя) можно применять законы сохранения, так как сила трения покоя приложена к точкам (А) тела, которые лежат на мгновенной оси вращения. Скорость таких точек равна нулю. Поэтому сила трения сцепления работы не совершает и не влияет на величину полной кинетической энергии.Роль силы трения сцепления заключается в том, чтобы привести тело во вращательное движение для обеспечения чистого качения. При этом работа силы тяжести приводит к увеличению кинетической энергии как поступательного, так и вращательного движений.

Вычисление момента инерции однородного шара

Рассчитаем момент инерции шара радиусаR и плотности ρ относительно оси, проходящей через его центр. Введем декартову прямоугольную систему координат с началом в центре шара (рис. 18). Пусть осью вращения является ось

OZ. Разобьем мысленно шар на малые объемы , сумма которых равна объему шара:, а сумма массравна его массе. Будем считать их материальными точками. Момент инерции системы материальных точек относительно осиOZ равен сумме моментов:

. (25)

Шар однороден, это значит ρ=const, поэтому . Тогда формула (25) запишется в виде:

. (26)

Если элементы объема уменьшать так, что , то пределом суммы (26) будет интеграл

. (27)

Введем сферическую систему координат . Положение произвольной точкиM в ней характеризуется тремя числами: , гдеr– расстояние от M до начала координат, θ – угол между радиусом-вектором точки M и осью вращения OZ, φ – полярный угол. Они будут меняться в пределах:

(28)

Связь между декартовыми координатами любой точки пространства M(x, y, z) и сферическими Mэтой же точки имеет вид:

(29)

Элемент объема в сферических координатах .

Квадрат расстояния от произвольной точкиM до оси вращения равен:

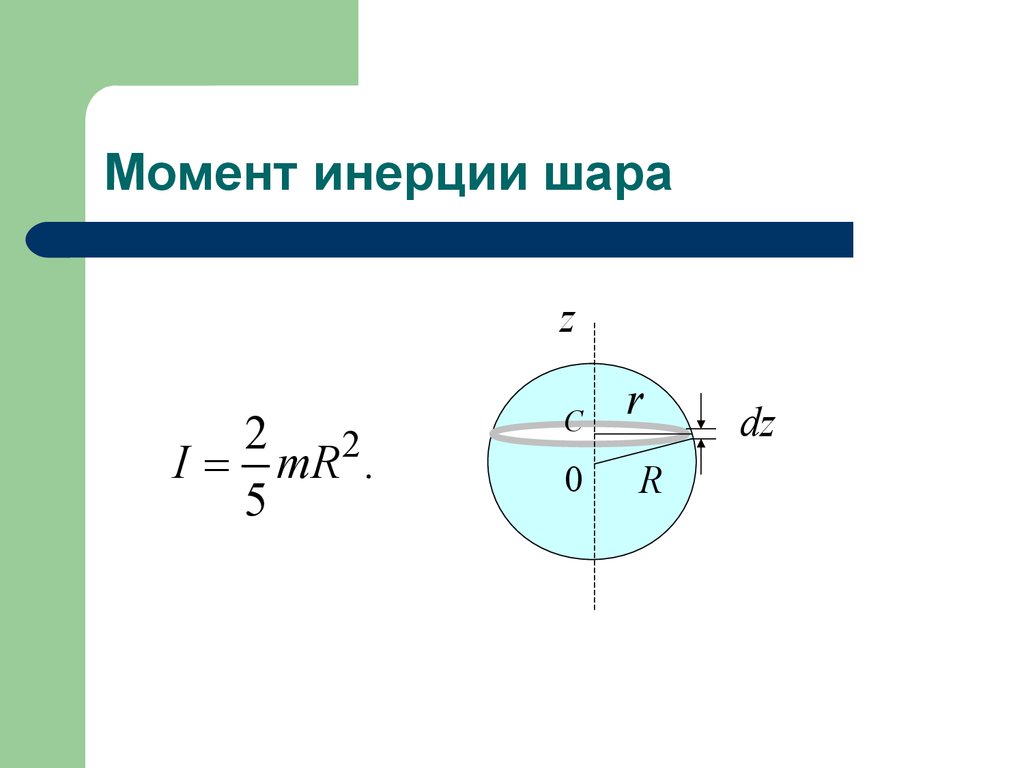
. (30)

Формула (27) для момента инерции в сферических координатах примет вид:

. (31)

Вычисление начнем с интеграла

(32)

Вычислим интеграл

. (33)

И, наконец, найдем последний интеграл:

. (34)

Масса шара равна . (35)

Тогда момент инерции шара относительно оси OZ запишется в виде:

. (36)

Аналогично можно рассчитать моменты инерции относительно осей OX и OY.

Ход работы

1. Определите диапазон углов, в пределах которого справедлива формула (10) и период колебаний не зависит от амплитуды. Измерьте период колебаний маятника для 10 различных значений максимального угла отклонения, в пределах от 15⁰до0⁰_,постепенно уменьшая угол отклонения, до тех пор, пока измеряемые периоды колебаний престанут отличаться друг от друга в пределах случайных ошибок эксперимента.

   Результаты занесите в таблицу 1. Сделайте вывод, в каком диапазоне амплитудных углов колебания можно считать изохронными, то есть не зависящими от амплитуды, с точностью до0,1; 0,5; 1%.

Таблица 1

θ	θ1	θ2	θ3	…	θ10
T(θ)	T(θ1)	T(θ2)	T(θ3)	…	T(θ10)

2. Определите добротность маятника.

3. Рассчитайте, при какой длине нити закрепленный на ней груз можно считать материальной точкой. Для этого измерьте при помощи штангенциркуля радиус шара, найдите массу шара и рассчитайте, в каких пределах длины нити момент инерции однородного шара будет составлять 5% от момента инерции

   МТ, закрепленной на невесомой нити длиныl. Используйте формулу (13)

4. Исследуйте зависимость периода колебаний Tи квадрата периодаT²от длины нитиl. Результаты занесите в таблицу.

l				…
T(l)				…
T2(l)				…

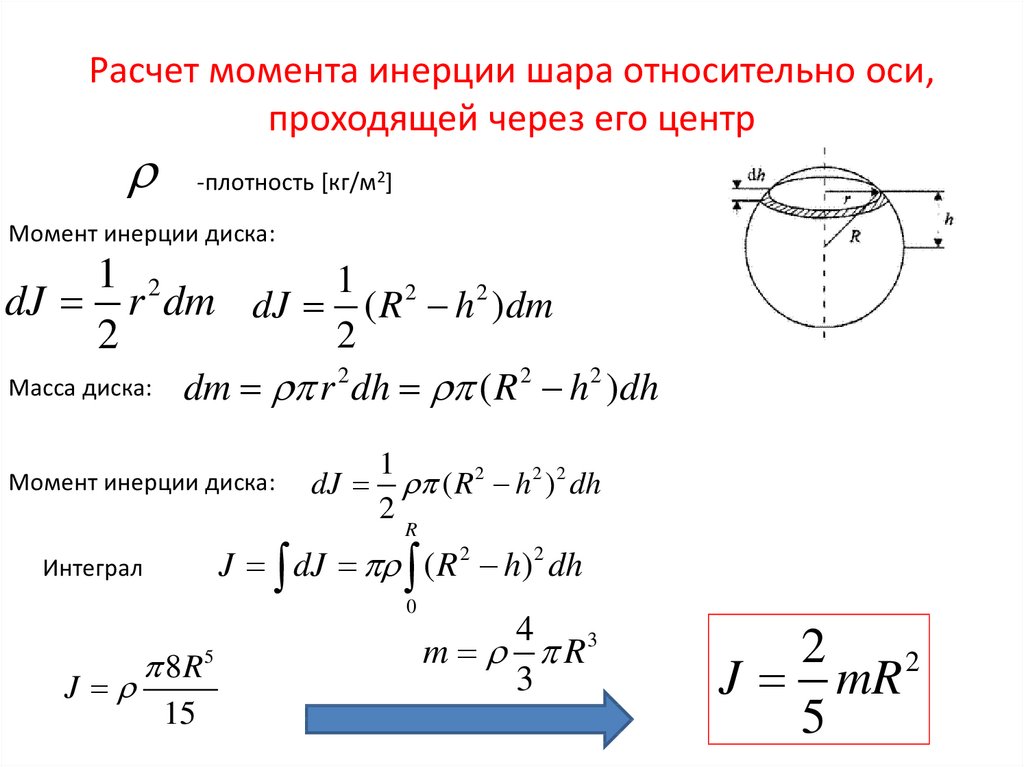
Постройте график экспериментальной зависимости .

Обработка результатов

5. Рассчитайте затухание маятника.

6. Оцените влияние затухания на период колебаний.

7. Методом наименьших квадратов найдите тангенс угла наклона зависимости и оцените погрешность метода.

8. По тангенсу угла наклона зависимости рассчитайтеg – ускорение свободного падения.

Контрольные вопросы

1. Что такое амплитуда, частота, фаза колебаний?

2. Как будут зависеть от времени кинетическая и потенциальная энергия математического маятника?

3. Какие функции являются решениями уравнения (9)? Проверить.

4. Как будут связаны между собой смещение, скорость и ускорение при гармоническом колебании?

5. Постройте график зависимости скорости осциллятора от его смещения при гармоническом колебании.

6. Что такое нелинейные колебания?

7. Что такое затухающие колебания? Запишите уравнение затухающих колебаний.

8. Начертите график зависимости затухающих колебаний от времени.

9. Рассчитайте логарифмический декремент затухания маятника.

10. Получите формулы для частоты и периода колебаний при наличии затухания.

11. Получите уравнение (14) для математического маятника, пользуясь законом сохранения энергии.

12. Убедитесь, что функция (18) является решением уравнения (17).

Литература: [1] – §34, [2] – § 39-41, [11] – глава 7.

домашнее задание и упражнения – Инерция вращения мяча

спросил 8 лет, 3 месяца назад

Изменено 8 лет, 3 месяца назад

Просмотрено 1к раз

$\begingroup$

Этот вопрос относится к решению задачи 12 здесь.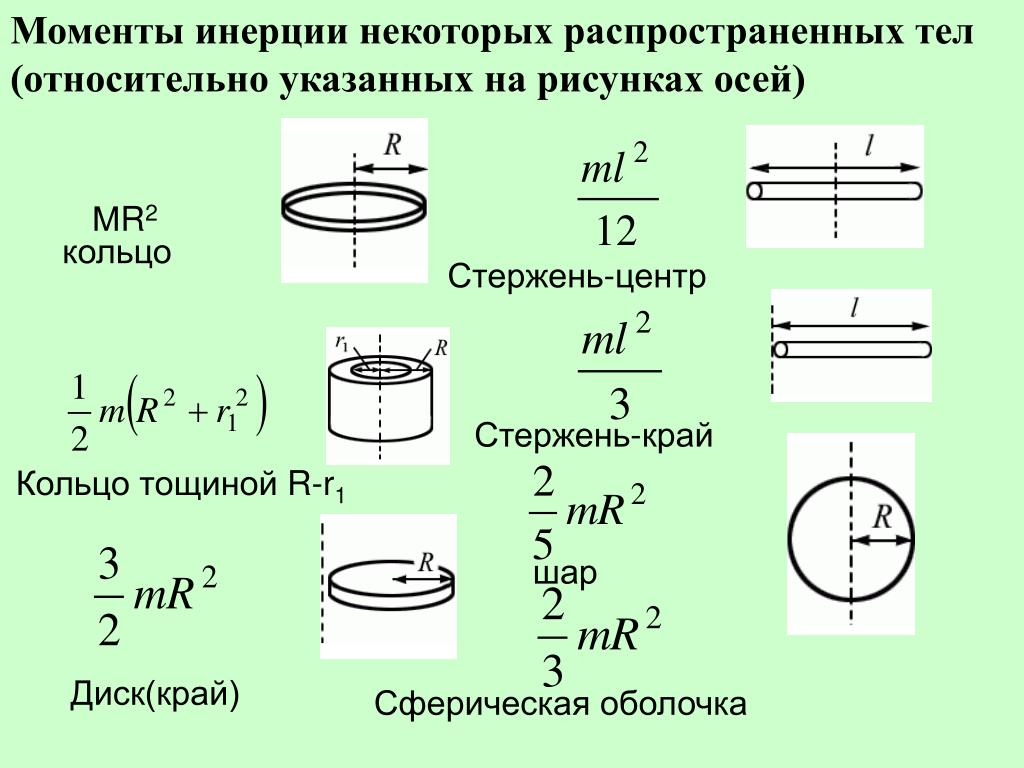 Он представляет собой сферическую оболочку массой $M$, заполненную без трения жидкостью массы $M$, катящуюся по наклонной плоскости. 92 достаточно).

$\endgroup$

$\begingroup$

Кажется, это приложение теоремы о параллельных осях. Из Википедии http://en.wikipedia.org/wiki/Parallel_axis_theorem:

Предположим, что тело массой $m$ вращается вокруг оси $z$, проходящей через центр масс тела. Тело имеет момент инерции $I_\textrm{cm}$ относительно этой оси. Теорема о параллельных осях утверждает, что если вместо этого тело заставить вращаться вокруг новой оси $z′$, которая параллельна первой оси и смещена от нее на расстояние $d$, то момент инерции $I$ относительно новой оси связан с $I_\textrm{cm}$ к 9Второй член соответствует моменту инерции жидкости без трения внутри оболочки, имеющей такую ​​же массу, как и сферическая оболочка, и вообще не вращающейся.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя адрес электронной почты и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

домашнее задание и упражнения – Расчет момента инерции твердого шара с использованием бесконечно малых толстых сфер

спросил 6 лет, 10 месяцев назад

Изменено 3 года, 11 месяцев назад

Просмотрено 16 тысяч раз 92$, правильный ответ.