Момент инерции стержня относительно оси вращения: Кафедра физики Физико-механический институт СПбПУ

Фейнмановские лекции по физике: Т.2 Пространство. Время. Движение

Фейнмановские лекции по физике: Т.2 Пространство. Время. Движение

Фейнмановские лекции по физике. Т. 2. Пространство. Время. Движение Это лекции по общей физике, которые читал физик-теоретик. Они совсем не похожи ни на один известный курс. Это может показаться странным: основные принципы классической физики, да и не только классической, но в квантовой, давно установлены, курс общей физики читается во всем мире в тысячах учебных заведений уже много лет и ему пора превратиться в стандартную последовательность известных фактов и теорий, подобно, например, элементарной геометрии в школе. Однако даже математики считают, что их науке надо учить по-другому. А уж о физике и говорить нечего: она столь интенсивно развивается, что даже лучшие педагоги все время сталкиваются с большими трудностями, когда им надо рассказывать студентам о современной пауке. Они жалуются, что им приходится ломать то, что принято называть старыми или привычными представлениями. Но откуда берутся привычные представления? Обычно они попадают в молодые головы в школе от таких же педагогов, которые потом будут говорить о недоступности идей современной науки. Поэтому прежде чем подойти к сути дела, приходится тратить много времени на то, чтобы убедить слушателей в ложности того, что было ранее внушено им как очевидная и непреложная истина. Оглавление Глава 15. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ § 1. Принцип относительности § 2. Преобразование Лоренца § 3. Опыт Майкельсона-Морли § 4. Преобразование времени § 5. Лоренцево сокращение § 6. Одновременность § 7. Четырехвекторы § 8. Релятивистская динамика § 9. Связь массы и энергии Глава 16. РЕЛЯТИВИСТСКАЯ ЭНЕРГИЯ И РЕЛЯТИВИСТСКИЙ ИМПУЛЬС § 1. Относительность и «философы» § 2. Парадокс близнецов § 3. 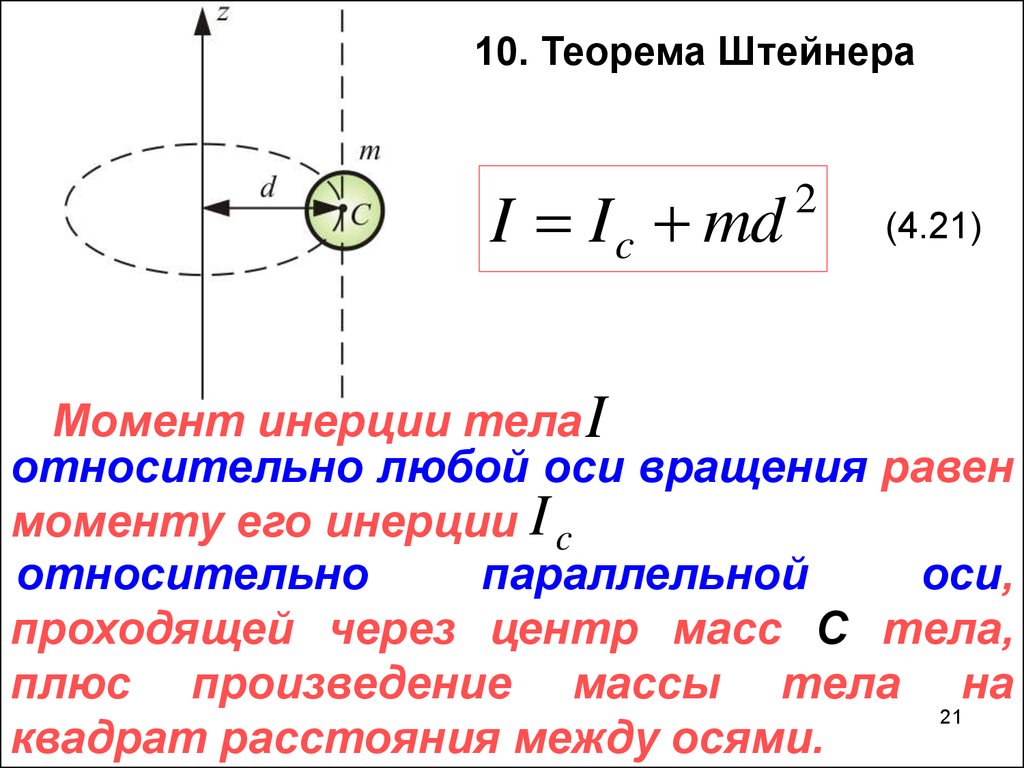Преобразование скоростей § 4. Релятивистская масса § 5. Релятивистская энергия Глава 17. ПРОСТРАНСТВО-ВРЕМЯ § 1. Геометрия пространства-времени § 2. Пространственно-временные интервалы § 3. Прошедшее, настоящее, будущее § 4. Еще о четырехвекторах § 5. Алгебра четырехвекторов Глава 18. ДВУМЕРНЫЕ ВРАЩЕНИЯ § 1. Центр масс § 2. Вращение твердого тела § 3. Момент количества движения § 4. Закон сохранения момента количества движения Глава 19. ЦЕНТР МАСС; МОМЕНТ ИНЕРЦИИ § 1. Свойства центра масс § 2. Положение центра масс § 3. Вычисление момента инерции § 4. Кинетическая энергия вращения Глава 20. ВРАЩЕНИЕ В ПРОСТРАНСТВЕ § 1. Моменты сил в трехмерном пространстве § 2. Уравнения вращения в векторном виде § 3. Гироскоп § 4. Момент количества движения твердого тела Глава 21. ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР § 1. Линейные дифференциальные уравнения § 2. Гармонический осциллятор § 3. Гармоническое движение и движение по окружности § 4. 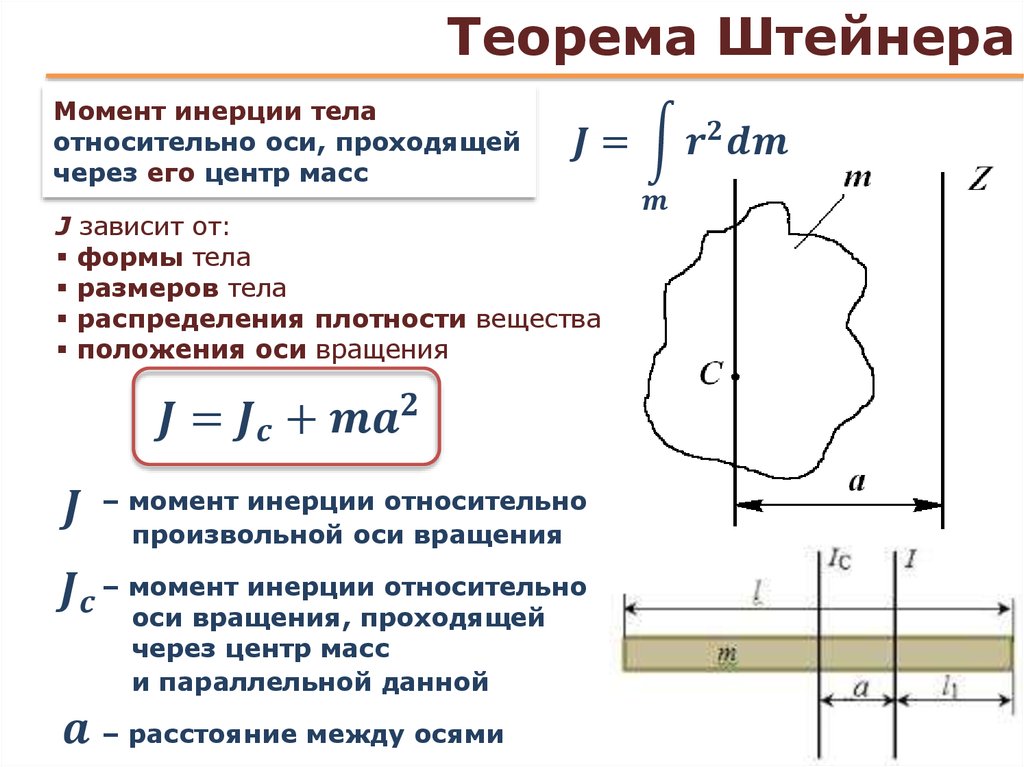Начальные условия § 5. Колебания под действием внешней силы Глава 22. АЛГЕБРА § 1. Сложение и умножение § 2. Обратные операции § 3. Шаг в сторону и обобщение § 4. Приближенное вычисление иррациональных чисел § 5. Комплексные числа § 6. Мнимые экспоненты Глава 23. РЕЗОНАНС § 1. Комплексные числа и гармоническое движение § 2. Вынужденные колебания с торможением § 3. Электрический резонанс § 4. Резонанс в природе Главa 24. ПЕРЕХОДНЫЕ РЕШЕНИЯ § 1. Энергия осциллятора § 2. Затухающие колебания § 3. Переходные колебания в электрических цепях Глава 25. ЛИНЕЙНЫЕ СИСТЕМЫ И ОБЗОР § 1. Линейные дифференциальные уравнения § 2. Суперпозиция решений § 3. Колебания в линейных системах § 4. Аналогии в физике § 5. Последовательные и параллельные сопротивления

Момент инерции стержня однородного и тонкого. Использование теоремы Штейнера.

Пример задачи

В физике для описания инерционных качеств поступательного или линейного движения пользуются понятием массы тела. Если же движение рассматривается вокруг некоторой оси вращения, то используют несколько иную физическую характеристику – момент инерции. В данной статье рассмотрим, что это за величина и как можно рассчитать момент инерции тонкого стержня.

Вращение и момент инерции

Инерции момент проще всего ввести для материальной точки. Когда она, обладая массой M, вращается вокруг оси, описывая окружность радиусом R, то момент инерции для нее определяется по формуле:

I = M*R².

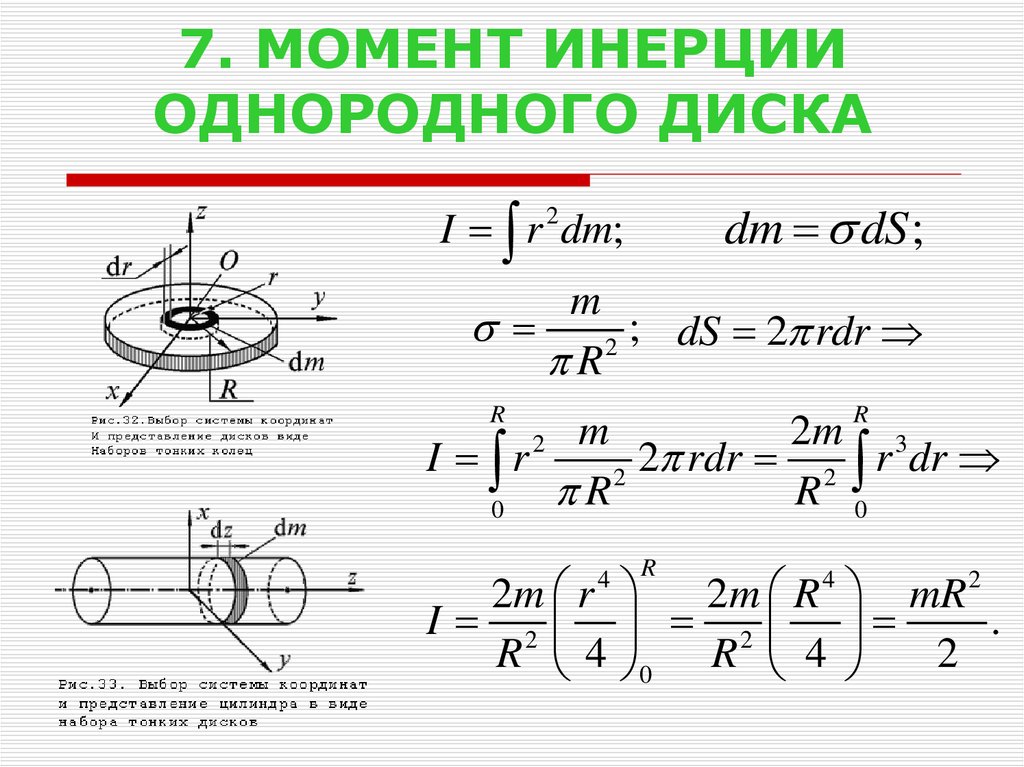
Любое реальное тело, какой бы сложной геометрической формой оно не обладало, можно представить как совокупность материальных точек. Это означает, что для всего тела или системы твердых тел величину I можно вычислить, если проинтегрировать по элементарным массам dm выражение выше. Общая формула для определения момента инерции имеет вид:

I = ∫_m(r²*dm).

Через объем и плотность это равенство записывается в таком виде:

I = ∫_V(ρ*r²*dV).

Его часто применяют для вычисления значений I конкретных геометрических объектов.

Физический смысл инерции момента I заключается в том, что он определяет, насколько “сложно” данной силе, создающей некоторый крутящий момент, раскрутить или остановить вращающуюся систему. Иными словами, I характеризует инерционные свойства изучаемой системы.

Вопрос на засыпку – это веселая игра или неловкая ситуация?

Зыбучий, ненадежный, неустойчивый песок – плохая опора, и об этом знает каждый из нас. Более того,…

Самым известным примером использования момента инерции является маховик двигателя внутреннего сгорания в автомобилях. Благодаря большому значению величины I, маховик обеспечивает плавность движения автомобиля, сглаживая любые резкие воздействия на коленчатый вал. Пример иного характера, где также важно знать момент инерции, – это закон сохранения момента импульса.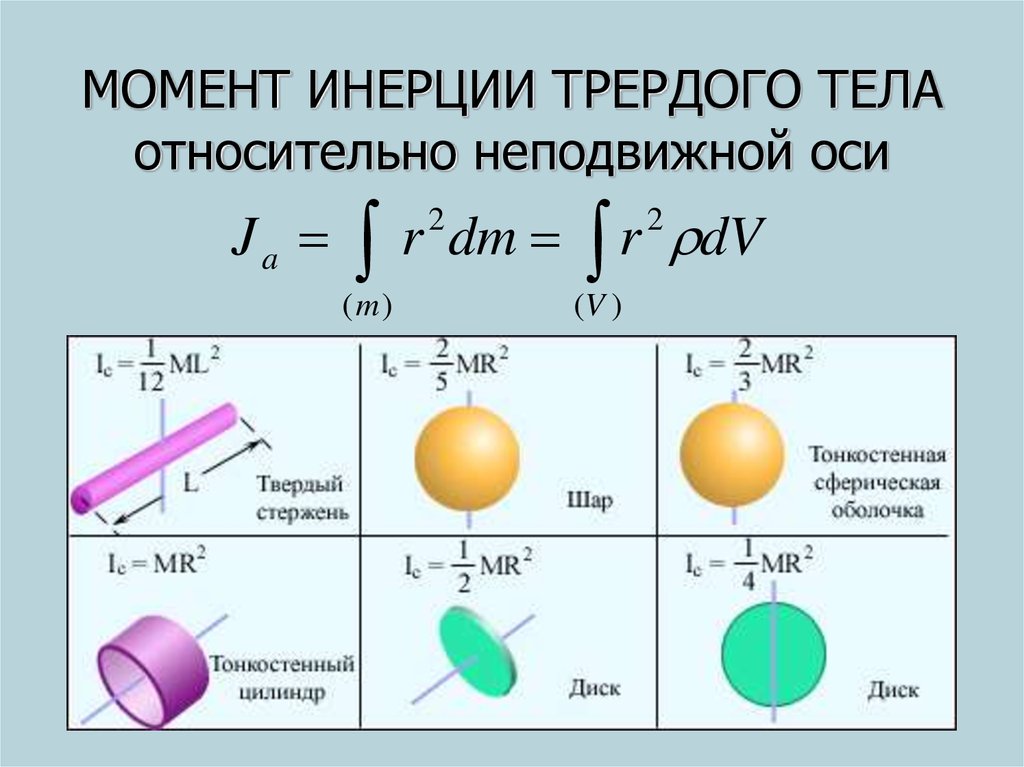 Применяется он для поворота вокруг оси искусственных спутников в космическом пространстве Земли.

Тонкий стержень и оси вращения

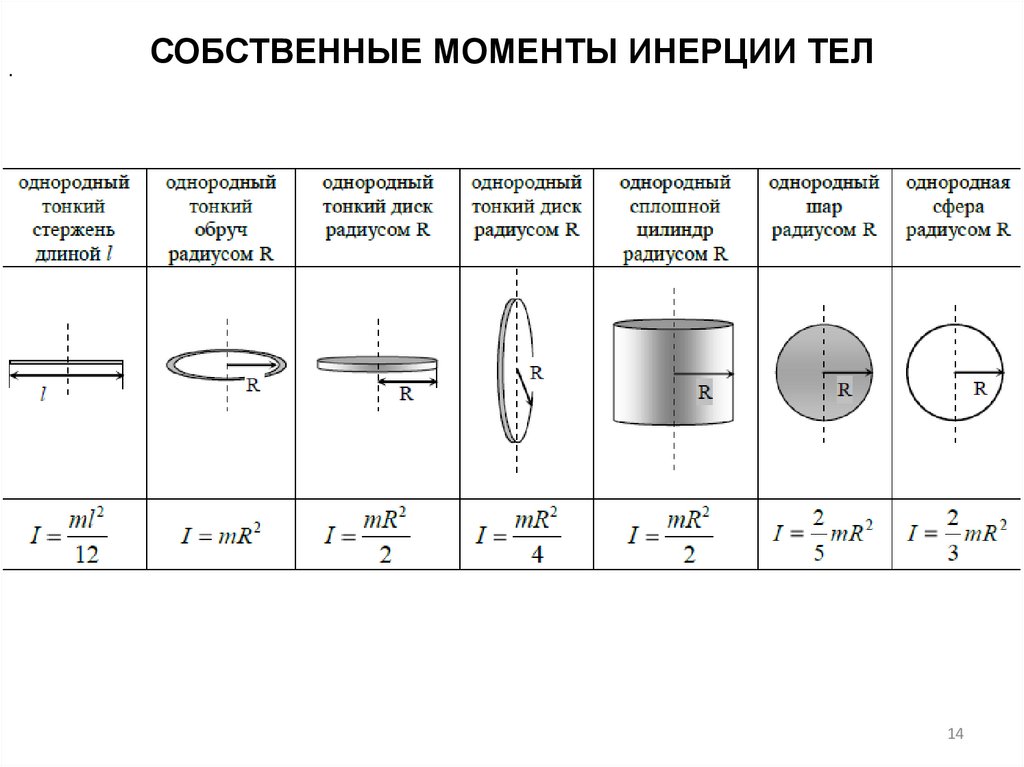
Далее будет рассмотрен момент инерции стержня относительно осей (разных). Вычисления будут проводиться для тонкого стержня, который обладает однородным распределением массы, то есть его плотность во всех точках является постоянной величиной. Под тонким понимают такой стержень, у которого ширина (толщина) намного меньше, чем его длина L. Для обозначения его массы будем использовать букву M.

Из приведенных выше формул следует, что величина I зависит от относительного положения тела и оси вращения. Для стержня можно выделить три основных оси. Одна из них проходит через длину всего стержня. Поскольку его толщина стремится к нулю, то момент инерции для такого положения тела также будет стремиться к этому значению.

Две другие оси перпендикулярны длине рассматриваемого тела. Одна из них проходит через центр масс, назовем ее O₁, вторая – через конец стержня, обозначим ее O₂.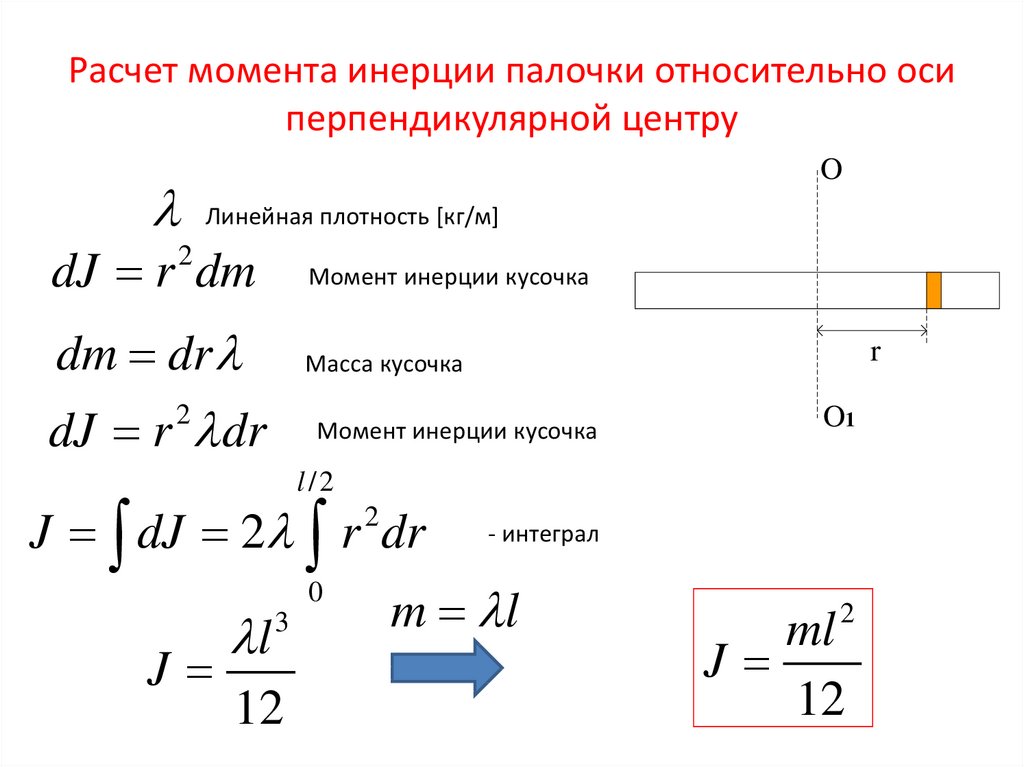 Относительно них и вычислим величину I.

Момент инерции относительно O1

В первую очередь выпишем общую формулу. Имеем:

Вопрос на засыпку – это веселая игра или неловкая ситуация?

Зыбучий, ненадежный, неустойчивый песок – плохая опора, и об этом знает каждый из нас. Более того,…

I = ∫_V(ρ*r²*dV).

Обозначим площадь сечения стержня буквой S. Очевидно, что она стремится к нулю, поскольку стержень тонкий. Но это обозначение удобно ввести для выполнения дальнейших расчетов.

Теперь мысленно разобьем стержень на бесконечное количество мелких кусочков, каждый из которых будет иметь сечение S и толщину dl. Заменяя r на l в формуле выше, получаем:

I = ∫_L(ρ*S*l²*dl).

Остается только подставить правильные пределы интегрирования и записать конечную формулу. Поскольку ось O₁ проходит через середину стержня, то пределы интегрирования будут следующими:

I = ∫_-L/2^L/2(ρ*S*l²*dl).

Результатом вычисления этого интеграла является следующая формула:

I = M*L²/12.

Таким образом, момент инерции тонкого стержня определяется его массой и длиной.

Инерции момент относительно O2

Теперь рассмотрим ситуацию, когда ось вращения будет проходить через любой из концов стержня и будет ему перпендикулярна. Соответствующую формулу можно получить из записанного выше интеграла, если правильно подставить пределы интегрирования. Однако мы пойдем несколько иным путем и определим инерции момент с помощью теоремы Штейнера.

Она говорит о том, что если две оси являются параллельными друг другу и одна из них (ось O) проходит через центр масс тела, то момент инерции относительно второй оси может быть вычислен с помощью такого равенства:

I = I₀ + M*h².

Здесь I₀ – момент инерции стержня относительно оси O, h – дистанция между осями.

Эту формулу можно с успехом применить для нашего случая. Поскольку I₀ мы рассчитали в предыдущем пункте статьи относительно оси O₁, и расстояние между O₁ и O₂ составляет L/2, то с использованием теоремы Штейнера получаем следующий результат:

I = I₀ + M*h² = M*L²/12 + M*L²/4 = M*L²/3.

Таким образом, для стержня величина I относительно оси O₂ в 4 раза больше, чем относительно оси O₁. Это означает, что для придания одинакового углового ускорения стержню в случае вращения вокруг оси O₂ следует приложить в 4 раза больший крутящий момент, чем в случае оси O₁.

Пример задачи

Дан тонкий стержень длиною 0,5 м и массой 5 кг. На расстоянии 2/5 от его конца расположена ось вращения, перпендикулярная стержню. Чему равен момент инерции системы?

Для решения задачи воспользуемся теоремой Штейнера. Расстояние между осями O₁ и заданной в задаче равно:

h = 0,25 – 0,2 = 0,05 м.

Тогда получаем момент инерции стержня (однородного):

I = I₀ + M*h² = 0,5²/12 + 0,05² = 0,117 кг*м².

В СИ момент инерции стержня измеряется в указанных единицах.

Видео с вопросом: Сравнение моментов инерции вокруг различных осей вращения асимметричного объекта

Стенограмма видео

Стержень и сфера объединены образуют систему. Длина стержня 𝐿 равна 0,50 метров. А его масса составляет 2,0 килограмма. Радиус сферы 𝑅 равен 20,0 сантиметры. А его масса составляет 1,0 килограмма. Система может вращаться вокруг точка 𝐴 на противоположном конце стержня к сфере или около точки 𝐵 где стержень и сфера соединяются, как показано на схеме. Найдите момент инерции система о точке 𝐴. Найдите момент инерции система о точке 𝐵.

Мы можем назвать эти два значения 𝐼 sub 𝐴 и 𝐼 под 𝐵. С учетом имеющейся у нас информации дано, что нам говорят длину стержня, его массу, радиус сфере и ее массе, мы можем начать вычисление 𝐼 sub 𝐴, выписав этот момент инерции как суммы компонентов этой системы стержня и сфера. 𝐼 sub 𝐴 равно моменту инерция стержня, вращающегося вокруг точки 𝐴, плюс момент инерции сферы вращается вокруг одной и той же точки.

Когда мы рассмотрим поиск моменты инерции двух частей нашей системы, мы знаем, что сможем найти момент инерции стержня, вращающегося вокруг своего конца, как в этом случае. Но для момента инерции сфере, мы сможем найти это значение для сферы, вращающейся вокруг своего центра. Но в этом случае сфера вращаться не вокруг своего центра, а вокруг точки 𝐴.

Чтобы помочь нам, мы можем вспомнить теорема о параллельных осях. Эта теорема говорит, что если мы имеем масса 𝑚 с осью вращения, смещенной на расстояние 𝑑 от центра масс 𝑚, то общий момент инерции этого объекта равен моменту инерции объекта относительно его центра масс плюс его масса, умноженная на расстояние 𝑑 в квадрате между двумя параллельными осями.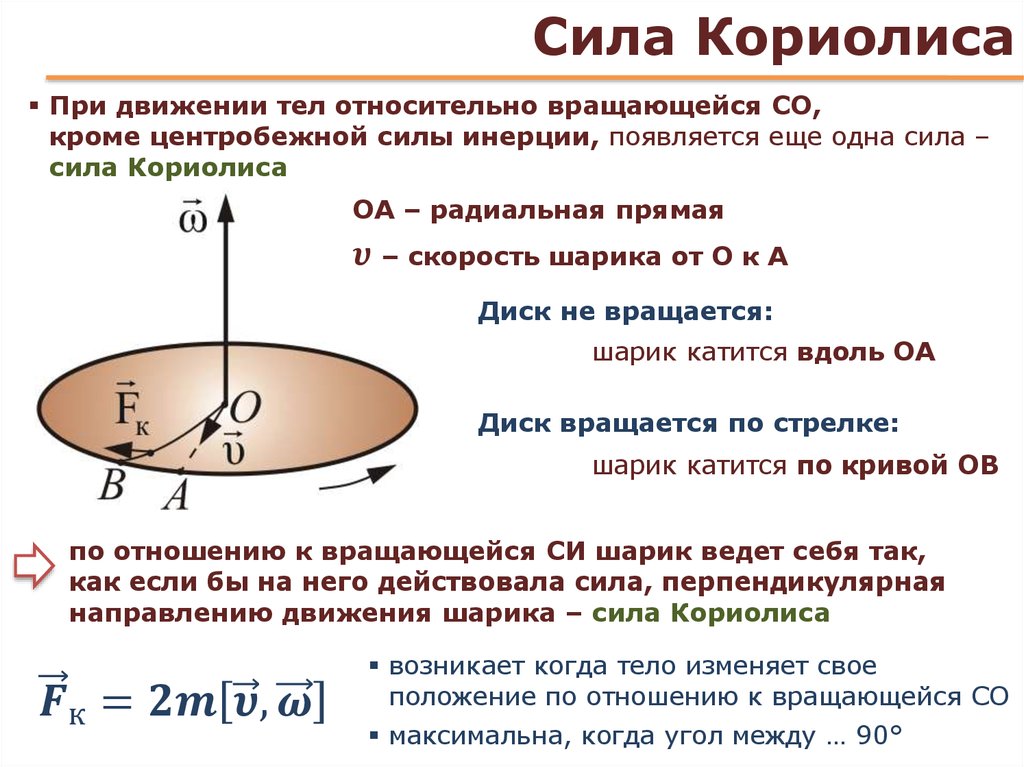

Это означает, что когда речь идет о момент инерции сферы, вращающейся вокруг точки 𝐴, этот момент инерции равен моменту инерции шара относительно его центра масс плюс его масса, умноженная на расстояние от оси вращения, в нашем случае 𝐿 плюс 𝑅, в квадрате.

Если мы пойдем и посмотрим в Из таблицы момент инерции стержня, вращающегося вокруг одного из своих концов, мы видим, что это одна треть массы стержня, умноженная на длину стержня в квадрате. Более того, когда мы ищем момента инерции шара, вращающегося вокруг своего центра, видим, что величина равна к двум пятым массы сферы, умноженной на квадрат ее радиуса. Все это означает, что мы можем переписать момент инерции нашей системы, вращающейся вокруг точки 𝐴, составляет одну треть масса стержня, умноженная на его длину в квадрате, плюс две пятых массы шара умножить на квадрат радиуса плюс, из-за теоремы о параллельных осях, массу сфера, умноженная на длину стержня плюс радиус сферы.

в квадрате.

Так как нам даны значения для все четыре из этих переменных в нашей постановке задачи, мы готовы подключить и решить для 𝐼 под 𝐴. Когда мы подключаемся ко всем этим значений, мы стараемся преобразовать радиус нашей сферы в сантиметры к единицам метров, чтобы согласоваться с единицами в остальной части нашего выражения. Сложив эти три термина вместе, мы находим результат с точностью до двух значащих цифр 0,67 килограмма на метр в квадрате. Это момент инерции эта система вращается вокруг точки 𝐴.

Далее мы хотим рассмотреть то же самое система, но другая ось вращения. Теперь наша ось вращения находится в место, где стержень и сфера соединяются. И снова момент инерции нашей системы равно стержню плюс шару для этого конкретная ось вращения. Так как стержень, еще раз, вращаясь вокруг одного из его концов, мы снова можем использовать соотношение для его момента инерция относительно такой оси.

Так же и сфера не вращается вокруг своего центра масс, момент инерции которого мы знаем, но вращается вокруг оси на расстоянии ее радиуса 𝑅 от этого центра.

Наше уравнение для 𝐼 sub 𝐵 таким же, как наше уравнение для 𝐼 sub 𝐴, за исключением одного члена. Вместо того, чтобы наше расстояние 𝑑 было 𝐿 плюс 𝑅, теперь это просто 𝑅, радиус нашей сферы. Когда мы подключаемся к этим значениям, снова переводя радиус нашей сферы в единицы метров, мы находим, что 𝐼 sub 𝐵, с точностью до двух значащих цифр, составляет 0,22 килограмма на метр в квадрате. Это момент инерции эта система вращается вокруг оси, проходящей через точку 𝐵.

ньютоновская механика – Момент инерции системы сферы, прикрепленной к стержню, вращающемуся вокруг показанной оси

спросил 2 года, 1 месяц назад

Изменено 2 года, 1 месяц назад

Просмотрено 1к раз

$\begingroup$

В этой системе задан момент инерции всей системы относительно оси, указанной в вопросе (сфера может свободно вращаться вокруг своей оси)

“я хочу знать, почему мы не рассматриваем сферу как точечную массу? почему мы рассматриваем его вращение вокруг своей оси и добавляем его момент инерции *поскольку все точки сферы движутся одинаково вокруг оси * .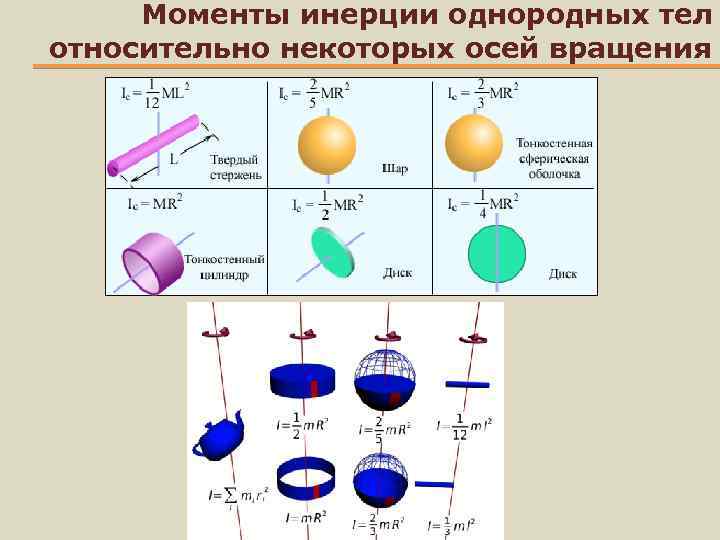 я не могу увидеть никакого вращательного движения сферы вокруг своей оси так почему рассматриваем ли мы его момент инерции относительно своей оси

Но по моему Момент инерции этой системы должен быть таким. рассматривая сферу как точечную массу, расположенную на расстоянии L+R от оси вращения

• ньютоновская механика
• динамика вращения
• кинематика вращения
• момент инерции

$\endgroup$

6

$\begingroup$

ОП – Почему мы не рассматриваем сферу как точечную массу?

Так как это не точечная масса . Сфера имеет распределение массы в конечном пространстве, которое мы должны учитывать. Момент инерции сферы отличается от точки массы. Если вы возьмете точку на сфере, то ее расстояние от оси вращения будет меняться при перемещении точки по поверхности сферы.