3. Моменты инерции тел различной формы.
Рассчитаем моменты инерции некоторых тел при различном расположении оси вращения.
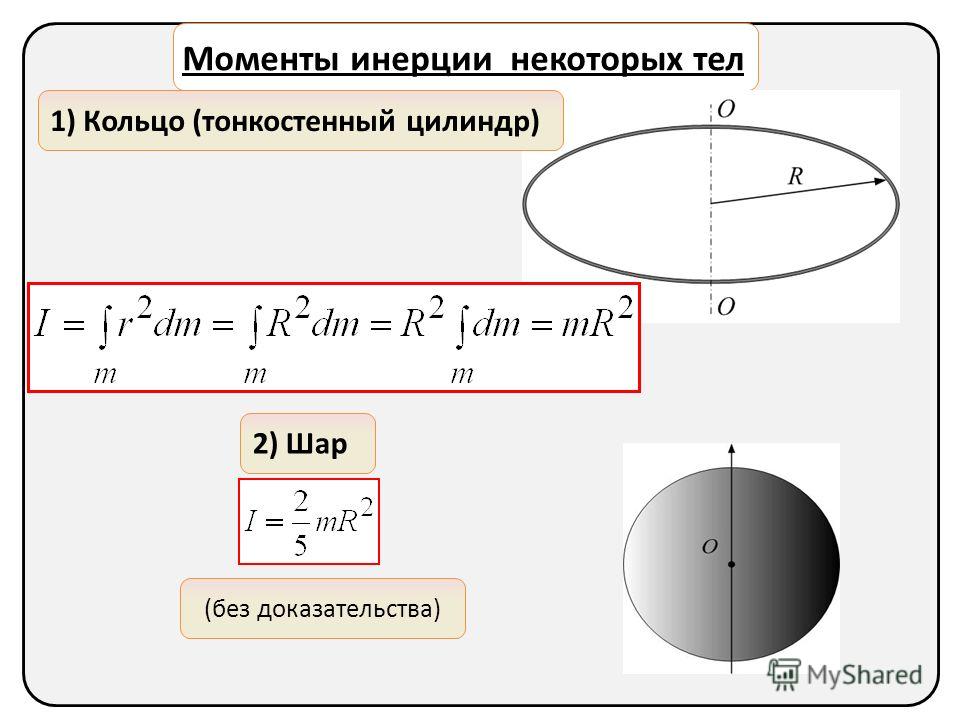
1.Кольцо (тонкостенный цилиндр), ось вращения проходит через центр масс. (рис.3).
Рис.3а. Рис.3б.
Пусть кольцо (цилиндр) имеет радиус и массу. Для расчета используем формулу. В этом случаедля всех элементарных масс. Поэтому.
2. Однородный стержень, ось вращения проходит через конец стержня.
Разобьем стержень на несколько частей длинойс массой, расположенных на разных расстоянияхот оси вращения. Чем больше разбиений, тем точнее можно сосчитать момент инерции (рис.4). Поэтому удобней сумму заменить интегрированием:
где
– масса всего стержня. Введем плотность
и выразим через нее массу.
Рис.4.
,
где – объем элемента стержня площадью поперечного сеченияи длины. Тогда,
где – длина стержня. После интегрирования получаем:
,
где – объем всего стержня. Таким образом
.
Если ось вращения стержня проходит через центр масс стержня, то
.
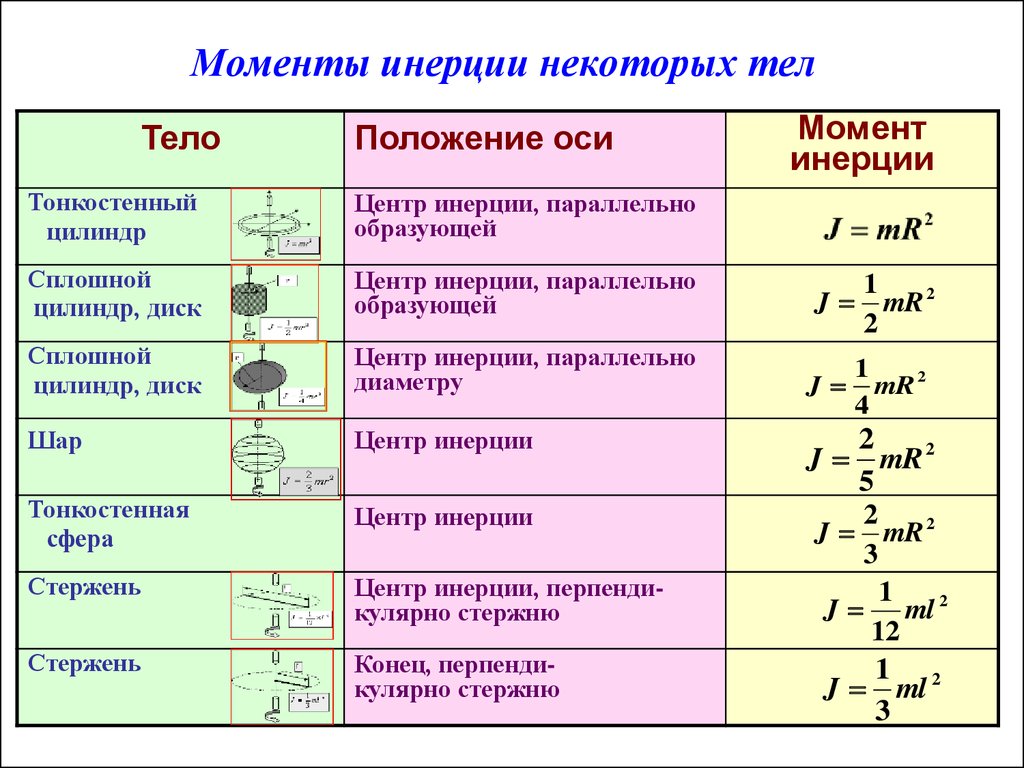
В таблице 1 приведены значения моментов инерции некоторых тел.
Таблица 1
Тело | Положение оси вращения | Момент инерции |
Полый тонкостенный цилиндр радиусом R | Ось симметрии | mR2 |
Сплошной цилиндр или диск радиусом R | Ось симметрии | (1/2)mR2 |
Прямой тонкий стержень длиной l | Ось перпендикулярна стержню и проходит через его середину | (1/12)ml2 |
Прямой тонкий стержень длиной l | Ось перпендикулярна стержню и проходит через его конец | (1/3)ml2 |
Шар радиусом R | Ось проходит через центр шара | (2/5)mR2 |
(15)
Момент инерции твердого тела относительно
любой оси равен моменту инерции
относительно оси параллельной данной
и проходящей через центр масс тела плюс
произведение массы тела на квадрат
расстояния между осями.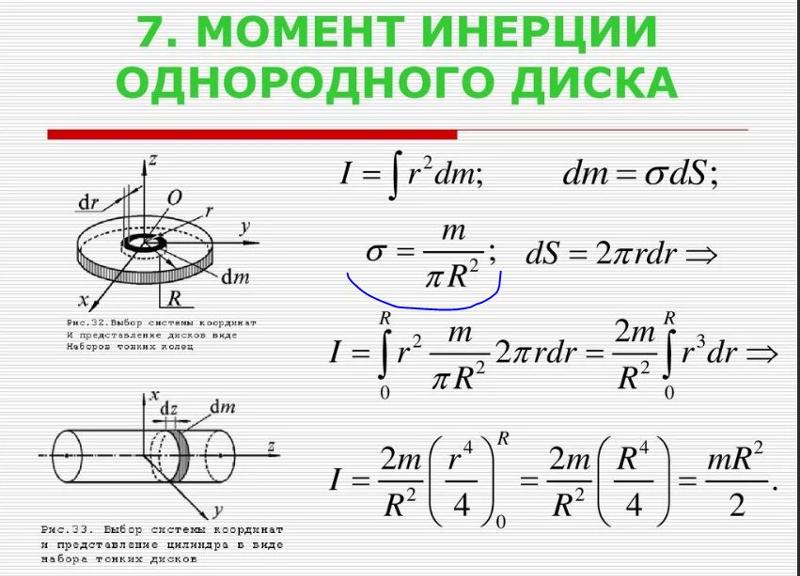
Рис.5.
Применим теорему Штейнера для определения момента инерции однородного стержня, длиной . Пусть. Величина( смотри таблицу). Тогда
Рис.6.
.
4. Момент силы относительно неподвижной точки.
Моментом силы относительно неподвижной точки 0 называется физическая величина, определяемая векторным произведением радиуса-вектора, проведенного из точки 0 в точкуаприложения силы, на силу
(16)
Рис.7.
Направление вектора совпадает с направлением поступательного движения правого винта при его вращении отк. Модуль момента силы равен
,
где – угол междуи, а- кратчайшее расстояние между линией действия силы и точкой 0 называется плечом силы.
5. Момент силы относительно неподвижной оси.

Моментом силы относительно неподвижной оси zназывается скалярная величина, равная проекции на эту ось вектора момента силы, определенного относительно произвольной точки 0 данной осиz. Значение моментане зависит от выбора точки 0 на осиz.
Рис. 8.
В частном случае, если ось zсовпадает с направлением вектора М, величина момента силы относительно точки, совпадает с моментом силы относительно оси.
Рассмотрим систему материальных точек, к которым приложены силы. Моментом всех сил, действующих на систему материальных точек относительно неподвижной точки, называется векторная сумма моментов отдельных сил относительно той же точки.
(18)
Моментом всех сил, действующих на систему материальных точек относительно неподвижной оси называется алгебраическая сумма моментов отдельных сил относительно той же оси,
(19)
|
Момент инерции твердого тела относительно некоторой оси вращения определяется выражением (15): . Суммирование распространяется на элементы всего твердого тела. Если разбиение тела проводить на все более и более мелкие элементы, то тогда сумма в пределе трансформируется в интеграл, и в результате чего получим: (16) (интегрирование ведется по всему объему твердого тела). Можно получить еще одну формулу полезную для расчета момента инерции. Для этого воспользуемся выражением для плотности вещества: . После подстановки dm = rdV в (16) получим: . (17) В качестве примера применения формулы (16) найдем момент инерции тонкого стержня относительно оси перпендикулярной к стержню и проходящей через его середину (рис.11). Длина стержня l, масса стержня т. Разобьем весь стержень на отрезки малой длины . Масса такого отрезка равна , а расстояние до оси вращения r = x.
.
Приведем, для справок, формулы для моментов инерции тел простейшей геометрической формы. Момент инерции однородного диска (рис.12) относительно оси, перпендикулярной к плоскости диска и проходящей через его центр равен: , где радиус диска R, масса т.
Эта же формула справедлива и для момента инерции сплошного цилиндра относительно оси совпадающей с осью цилиндра. Момент инерции тонкого обруча относительно оси, перпендикулярной к плоскости обруча и проходящей через его центр будет (рис.13): . где радиус обруча – R, масса обруча – т. Эта же формула справедлива для тонкостенного цилиндра. Момент инерции шара относительно оси проходящей через его центр. . Момент инерции тонкого диска массы m и радиуса R, (толщина диска b << R), относительно оси совпадающей с диаметром диска: : ,
Все приведенные формулы справедливы для моментов инерции относительно оси проходящей через центр масс (центр инерции) твердого тела. Момент инерции относительно произвольной оси можно найти с помощью теоремы Штейнера: Момент инерции относительно произвольной оси О1О1 равен сумме момента инерции I0, относительно оси OO, параллельной данной и проходящей через центр инерции тела (центр масс тела) и произведения массы тела на квадрат расстояния между осями. .
В качестве примера получим с помощью этой теоремы выражение для момента инерции стержня относительно оси перпендикулярной к стержню и проходящей через один из его концов (рис. Поэтому по теореме Штейнера получим: .
Главные оси инерции Момент инерции твердого тела произвольной формы и распределения масс зависит от ориентации оси вращения. Допустим, что ось проходит через центр масс тела (центр инерции). Найдем такую ориентацию оси, для которой момент инерции максимален. Далее, как доказывается в теоретической механике, существует также ось перпендикулярная найденной, и проходящая через центр масс, для которой момент импульса твердого тела будет минимален. Для третьей оси, ортоганальной к первым двум, момент импульса в общем случае имеет величину промежуточную между максимальным и минимальным значениями. Введенные таким образом оси вращения называются главными осями инерции. Моменты инерции относительно этих осей не обязательно отличаются друг от друга по величине. Действительно, если однородное по плотности твердое тело обладает той или иной симметрией, то некоторые главные моменты инерции могут равняться друг другу. Однородный куб с массой М и длиной ребра имеет также три равных момента инерции относительно главных осей инерции . Главные оси инерции перпендикулярны граням куба и проходят через центр куба.. Тонкий однородный по плотности диск имеет максимальный по величине момент инерции относительно оси, проходящей через центр диска перпендикулярно его плоскости, а также два других главных момента инерции равных друг другу. Приведем также пример тела, когда все три момента инерции относительно главных осей инерции различны – однородный по плотности параллелепипед с отличающимися по длине ребрами.
Предыдущая12345678910111213141516Следующая Читайте также: |
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 2 из 4Следующая ⇒
Цель работы – измерить моменты инерции различных тел. Проверить теорему Штейнера.
Теоретические основы лабораторной работы Момент инерции тела является мерой инертности тела при вращательном движении. Момент инерции тела зависит от размеров и формы тел и от распределения массы тела относительно оси вращения. Момент инерции сплошного твёрдого тела определяется по формуле , где – расстояние от элемента объема с массой dm до оси вращения, r – плотность вещества.
Рис. 5.1. Общий вид экспериментальной установки
Таким образом, момент инерции тел различной формы можно найти как результат интегрирования по соответствующему объёму тела. Частные случаи. 1. Момент инерции материальной точки массой m , находящейся на расстоянии R от оси вращения (5.1) 2. Момент инерции сплошного цилиндра относительно оси, перпендикулярной к плоскости основания цилиндра и проходящей через его центр масс (ось цилиндра) (5.2) здесь R, m – радиус и масса цилиндра. Так как момент инерции не зависит от высоты цилиндра, эта же формула справедлива для момента инерции однородного диска относительно оси перпендикулярной к плоскости диска. 3. Момент инерции полого цилиндра с внутренним радиусом R1 и внешним радиусом R2 относительно оси, совпадающей с осью цилиндра. (5.3) 4. Момент инерции шара массой m и радиуса R относительно оси проходящей через его центр масс (5.4) 5. Момент инерции тонкого стержня массой m и длиной l относительно оси проходящей через его середину перпендикулярно стержню. (5.5) Эти формулы справедливы для момента инерции относительно оси симметрии. Момент инерции относительно произвольной оси параллельной оси симметрии можно найти с помощью теоремы Штейнера. Момент инерции относительно произвольной оси О1О1 равен сумме момента инерции I0, относительно оси OO, параллельной данной и проходящей через центр масс тела и произведения массы тела на квадрат расстояния d между осями. (5.6) Например, с помощью теоремы Штейнера, зная момент инерции стержня относительно оси перпендикулярной к стержню и проходящей через его центр масс, можно получить формулу для вычисления момента инерции стержня относительно оси проходящей через его конец. (5.7) В общем случае расчет момента инерции представляет собой достаточно сложную задачу. В данной работе для экспериментального измерения моментов инерции различных тел используется метод крутильных колебаний. Исследуемые тела насаживаются на ось спиральной пружины. M=Dj (5.8) В этой формуле коэффициентом пропорциональности D является модуль кручения пружины. С другой стороны из определения момента силы следует, что это вектор, модуль которого определяется по формуле М=Fl (5.9) Крутящий момент стремится вернуть пружину в исходное (равновесное) состояние. В результате возникают крутильные колебания. В соответствии с теорией период крутильных колебаний определяется по формуле (5.10) Отсюда момент инерции тела (5.11) Таким образом, измеряя период крутильных колебаний и зная модуль кручения D пружины, можно вычислить момент инерции тела, насаженного на ось пружины. Методика лабораторной работы позволяет измерять моменты инерции стержня без грузов, стержня с грузами, сплошного цилиндра, полого цилиндра, диска и шара.
Порядок выполнения работы I. Определение модуля кручения пружины. 1. Возьмите стержень с грузами и насадите его на ось пружины. Грузы сдвиньте к центру. 2. Поверните стержень на 90о (p/2 радиан).
3. Прикрепите к стержню (у края грузов) динамометр и измерьте величину силы F, необходимую для удержания стержня в этом положении (динамометр держите перпендикулярно стержню и оси вращения). 4. Проделайте эти измерения для углов j, равных 180о, 270о, 360о. 5. Полученные данные занесите в таблицу 5.1. ⇐ Предыдущая1234Следующая ⇒ Читайте также: Где возникла философия и почему? Относительная высота сжатой зоны бетона Сущность проекции Гаусса-Крюгера и использование ее в геодезии Тарифы на перевозку пассажиров |
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 852; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. |
Момент инерции сплошных тел
Момент инерции является мерой сопротивления объекта изменениям его вращения. Это вращательный аналог массы, который количественно определяет сопротивление объекта изменениям его линейного движения. Момент инерции зависит от формы объекта и распределения его массы. Например, сфера имеет меньший момент инерции, чем цилиндр с той же массой и радиусом, потому что масса сферы более равномерно распределена вокруг ее центра.
Момент инерции важен во многих областях, включая инженерию, физику и астрономию. В машиностроении он используется для расчета прочности балок и колонн. В физике он используется для изучения динамики вращающихся объектов.
Формула момента инерции
Формула момента инерции (I) представляет собой сумму произведений массы (m) каждой частицы на квадрат ее расстояния (r) от оси вращения:
9{2}}$ Это уравнение получено из второго закона движения Ньютона, который гласит, что сумма сил, действующих на тело, равна его массе, умноженной на ускорение. Формулу можно использовать для расчета момента инерции любого объекта при условии, что известны массы и расстояния до всех частиц.
Формулу можно использовать для расчета момента инерции любого объекта при условии, что известны массы и расстояния до всех частиц.
Факторы, от которых зависит момент инерции
На момент инерции объекта влияют три основных фактора. Это:
Распределение массы внутри объекта. То, как распределяется масса, влияет на то, какая сила вращения требуется для ее перемещения.
Форма объекта – Более компактная форма будет иметь меньший момент инерции, чем менее компактная.
Размер объекта. Более крупный объект будет иметь более высокий момент инерции, чем меньший.
Момент инерции сплошных тел Зависит от
Момент инерции сплошного тела равен сумме моментов инерции всех его составных частей. Суммарный момент инерции является мерой сопротивления объекта изменениям его вращения. Тело с большим моментом инерции потребует большей силы для изменения направления вращения, чем тело с малым моментом инерции.
Суммарный момент инерции является мерой сопротивления объекта изменениям его вращения. Тело с большим моментом инерции потребует большей силы для изменения направления вращения, чем тело с малым моментом инерции.
Момент инерции сплошного тела зависит от распределения массы внутри этого тела. Если тело симметрично, то момент инерции будет меньше, чем если бы оно было несимметричным. Например, сфера имеет меньший момент инерции, чем эллипсоид. Причина этого в том, что масса сферы равномерно распределена по всему ее объему, а масса эллипсоида — нет.
Вторым фактором, влияющим на момент инерции сплошного тела, является форма этого тела. Стройное тело имеет меньший момент инерции, чем приземистое тело. Это связано с тем, что тонкое тело имеет меньшую массу по краям, где оно будет вращаться, если упадет.
Наконец, третьим фактором, влияющим на момент инерции сплошного тела, является расположение его центра тяжести. Тело с центром тяжести ближе к краям будет иметь больший момент инерции, чем тело с центром тяжести ближе к центру. Это потому, что когда тело вращается, вся его масса не вращается вокруг центра тяжести; только масса на его краях делает это.
Тело с центром тяжести ближе к краям будет иметь больший момент инерции, чем тело с центром тяжести ближе к центру. Это потому, что когда тело вращается, вся его масса не вращается вокруг центра тяжести; только масса на его краях делает это.
Теоремы для расчета момента инерции тел
Если мы будем наблюдать момент инерции различных тел, то мы узнаем, что положение оси вращения влияет на момент инерции тел. Чтобы найти момент инерции относительно любой заданной оси, у нас есть теоремы, которые идеально подходят для нашего случая использования.
Теорема о параллельной оси
Теорема о моменте инерции о параллельной оси утверждает, что момент инерции тела относительно любой оси равен сумме моментов инерции относительно параллельной оси, проходящей через центр масс, плюс произведение массы на квадрат расстояния между осями. Другими словами, эта теорема позволяет вычислить момент инерции тела относительно оси, не проходящей через его центр тяжести.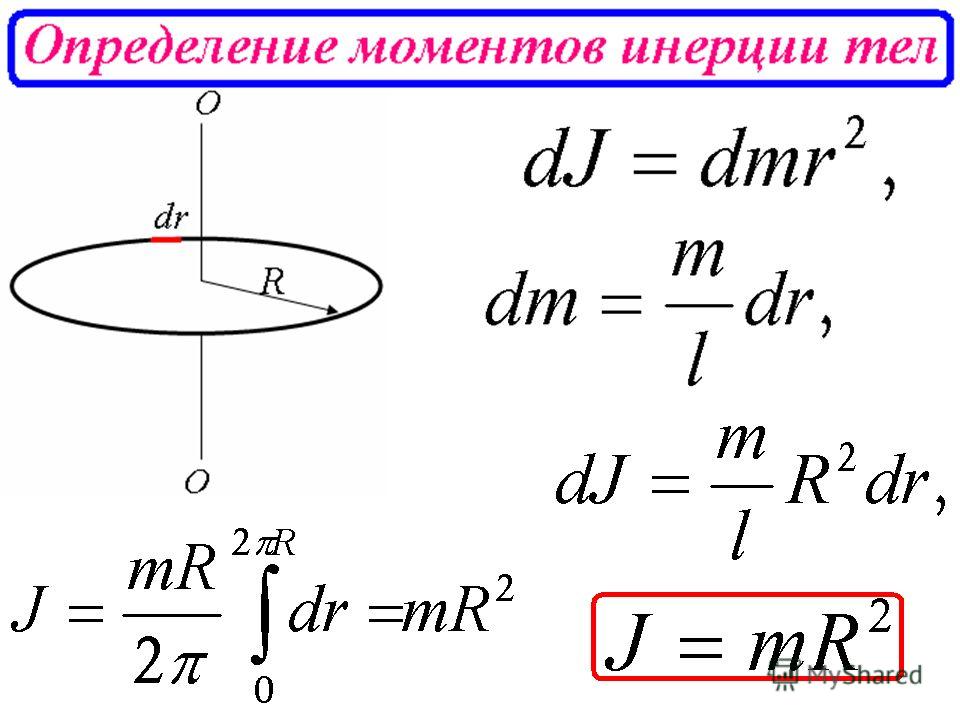 Это может быть очень полезно при работе с объектами неправильной формы или несимметричными. 9{2}}\]
Это может быть очень полезно при работе с объектами неправильной формы или несимметричными. 9{2}}\]
Где d — расстояние между двумя осями.
M — масса тела
${{l}_{cm}}$ — момент инерции относительно центра масс
Теорема о перпендикулярной оси момент инерции любого тела относительно оси, перпендикулярной его плоскости симметрии, равен сумме моментов инерции относительно любых двух других взаимно перпендикулярных осей, лежащих в этой плоскости, каждая из которых проходит через точку пересечения первой оси с плоскостью .
\[{{I}_{z}}\text{ }=~\text{ }{{I}_{x}}\text{ }+~\text{ }{{I}_{y} }\]
Теорема о перпендикулярной оси
Момент инерции для различных тел
Sl. No | Shape of Object | M.I along the Symmetry Axis | M. |
1. | Rod | 9{2}}}{2}$ |
Сводка
Момент инерции – это вращательный аналог массы, который количественно определяет сопротивление объекта изменениям его линейного движения. Это важно во многих областях, включая инженерию, физику и астрономию. Момент инерции зависит от формы, размера и распределения массы объекта. Большему или более компактному объекту потребуется больше силы для изменения своего вращения, чем меньшему. Момент инерции сплошного тела зависит от распределения массы внутри этого тела.
Если тело симметрично, то его инерция будет меньше, чем если бы оно не было симметричным. Это связано с тем, что масса сферического тела равномерно распределена по всему его объему, а эллипсоид имеет меньшую массу по краям. На расположение центра тяжести тела также влияет форма этого тела — стройное тело имеет меньший момент устойчивости, чем приземистое.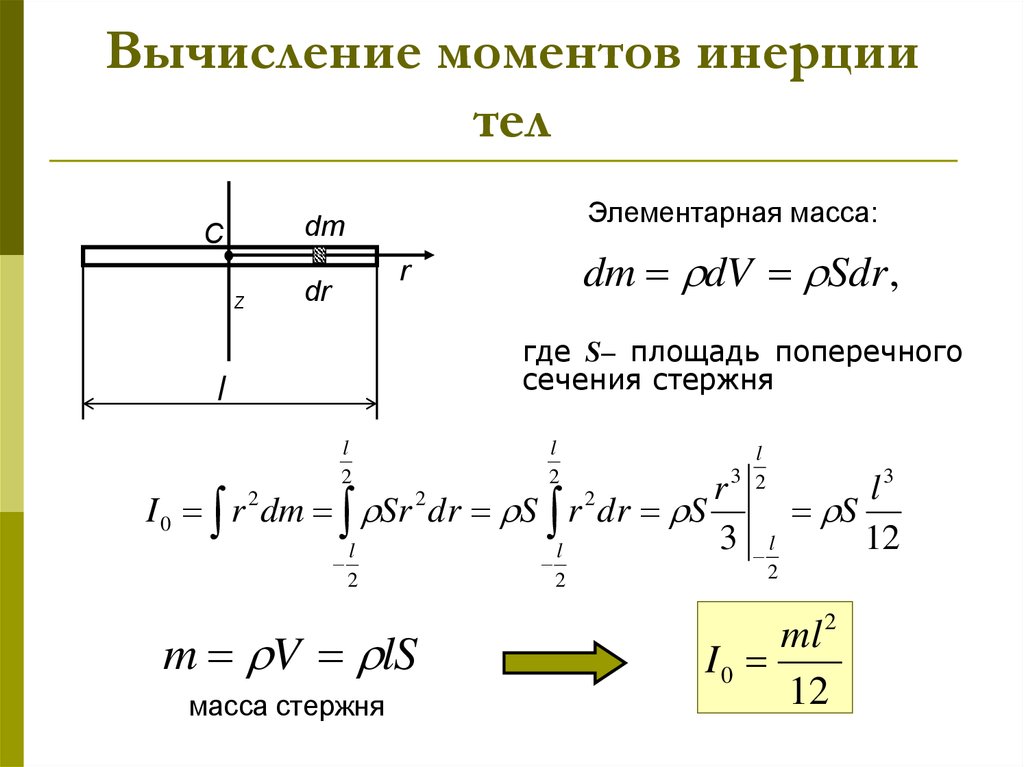
10.4 Момент инерции и кинетическая энергия вращения – University Physics Volume 1
10 Вращение с фиксированной осью
Цели обучения
К концу этого раздела вы сможете:
- Описывать различия между вращательной и поступательной кинетической энергией
- Дайте определение физической концепции момента инерции в терминах распределения массы относительно оси вращения
- Объясните, как момент инерции твердых тел влияет на их кинетическую энергию вращения
- Использование закона сохранения механической энергии для анализа систем, подвергающихся как вращению, так и поступательному перемещению
- Расчет угловой скорости вращающейся системы при наличии потерь энергии из-за неконсервативных сил
До сих пор в этой главе мы работали с кинематикой вращения: описанием движения вращающегося твердого тела с фиксированной осью вращения. В этом разделе мы определяем две новые величины, полезные для анализа свойств вращающихся объектов: момент инерции и кинетическую энергию вращения. Определив эти свойства, мы получим два важных инструмента, необходимых для анализа динамики вращения.
Определив эти свойства, мы получим два важных инструмента, необходимых для анализа динамики вращения.
Вращательная кинетическая энергия
Любой движущийся объект обладает кинетической энергией. Мы знаем, как вычислить это для тела, совершающего поступательное движение, но как насчет твердого тела, совершающего вращательное движение? Это может показаться сложным, потому что каждая точка твердого тела имеет разную скорость. Однако мы можем использовать угловую скорость, которая одинакова для всего твердого тела, чтобы выразить кинетическую энергию вращающегося объекта. На рисунке показан пример очень энергичного вращающегося тела: электрический точильный камень, приводимый в движение двигателем. Когда точильный камень выполняет свою работу, летят искры, возникают шум и вибрация. Эта система обладает значительной энергией, частично в виде тепла, света, звука и вибрации. Однако большая часть этой энергии находится в форме 9{2}[/latex], а скорость — это величина, разная для каждой точки тела, вращающегося вокруг оси, имеет смысл найти способ записать кинетическую энергию через переменную [latex]\omega[/ латекс], который одинаков для всех точек на твердом вращающемся теле. Для одиночной частицы, вращающейся вокруг фиксированной оси, это легко вычислить. Мы можем связать угловую скорость с величиной поступательной скорости, используя соотношение [latex]{v}_{\text{t}}=\omega r[/latex], где 9{2}.[/latex]
Для одиночной частицы, вращающейся вокруг фиксированной оси, это легко вычислить. Мы можем связать угловую скорость с величиной поступательной скорости, используя соотношение [latex]{v}_{\text{t}}=\omega r[/latex], где 9{2}.[/latex]
В случае твердого вращающегося тела мы можем разделить любое тело на большое количество меньших масс, каждая из которых имеет массу [latex]{m}_{j}[/latex ] и расстояние до оси вращения [латекс]{r}_{j}[/латекс], такое, чтобы общая масса тела была равна сумме отдельных масс: [латекс]М=\сумма _{ j}{m}_{j}[/латекс]. Каждая меньшая масса имеет тангенциальную скорость [латекс]{v}_{j}[/латекс], где мы временно опустили индекс t . Полная кинетическая энергия твердого вращающегося тела равна 9{2}[/latex], где r — расстояние от точечной частицы до оси вращения. В следующем разделе мы исследуем интегральную форму этого уравнения, которую можно использовать для расчета момента инерции некоторых твердых тел правильной формы.
Момент инерции есть количественная мера инерции вращения, как и в поступательном движении, а масса есть количественная мера линейной инерции, т. е. чем массивнее объект, тем больше у него инерция и тем больше его сопротивление изменению линейной скорости. Аналогично, чем больше момент инерции твердого тела или системы частиц, тем больше их сопротивление изменению угловой скорости относительно неподвижной оси вращения. Интересно посмотреть, как меняется момент инерции в зависимости от r, расстояние до оси вращения массы частицы на рис. Твердые тела и системы частиц с большей массой, сосредоточенные на большем расстоянии от оси вращения, обладают большими моментами инерции, чем тела и системы той же массы, но сосредоточенные вблизи оси вращения. Таким образом, мы можем видеть, что полый цилиндр имеет большую инерцию вращения, чем сплошной цилиндр той же массы при вращении вокруг оси, проходящей через центр. Подставляя рисунок в рисунок, выражение для кинетической энергии вращающегося твердого тела принимает вид 9{2}.[/latex]
е. чем массивнее объект, тем больше у него инерция и тем больше его сопротивление изменению линейной скорости. Аналогично, чем больше момент инерции твердого тела или системы частиц, тем больше их сопротивление изменению угловой скорости относительно неподвижной оси вращения. Интересно посмотреть, как меняется момент инерции в зависимости от r, расстояние до оси вращения массы частицы на рис. Твердые тела и системы частиц с большей массой, сосредоточенные на большем расстоянии от оси вращения, обладают большими моментами инерции, чем тела и системы той же массы, но сосредоточенные вблизи оси вращения. Таким образом, мы можем видеть, что полый цилиндр имеет большую инерцию вращения, чем сплошной цилиндр той же массы при вращении вокруг оси, проходящей через центр. Подставляя рисунок в рисунок, выражение для кинетической энергии вращающегося твердого тела принимает вид 9{2}.[/latex]
Из этого уравнения видно, что кинетическая энергия вращающегося твердого тела прямо пропорциональна моменту инерции и квадрату угловой скорости. Это используется в накопителях энергии маховика , которые предназначены для накопления большого количества вращательной кинетической энергии. Многие автопроизводители в настоящее время испытывают в своих автомобилях накопители энергии маховика, такие как маховик или система рекуперации кинетической энергии, показанные на рисунке.
Это используется в накопителях энергии маховика , которые предназначены для накопления большого количества вращательной кинетической энергии. Многие автопроизводители в настоящее время испытывают в своих автомобилях накопители энергии маховика, такие как маховик или система рекуперации кинетической энергии, показанные на рисунке.
Вращательные и поступательные величины для кинетической энергии и инерции представлены на рисунке. Столбец отношений не включен, потому что не существует константы, на которую мы могли бы умножить вращательную величину, чтобы получить поступательную величину, как это можно сделать для переменных на рисунке.
Пример
Момент инерции системы частиц
Шесть маленьких шайб расположены на расстоянии 10 см друг от друга на стержне незначительной массы и длиной 0,5 м. Масса каждой шайбы 20 г. Стержень вращается вокруг оси, расположенной на расстоянии 25 см, как показано на рис. а) Чему равен момент инерции системы? б) Если убрать две ближние к оси шайбы, каков будет момент инерции оставшихся четырех шайб? в) Если система с шестью шайбами вращается со скоростью 5 об/с, какова ее кинетическая энергия вращения?
Рисунок 10.19 Шесть шайб расположены на расстоянии 10 см друг от друга на стержне незначительной массы, вращающемся вокруг вертикальной оси.Стратегия
- Мы используем определение момента инерции для системы частиц и выполняем суммирование для оценки этой величины.
 Все массы одинаковы, поэтому мы можем поставить это количество перед символом суммирования.
Все массы одинаковы, поэтому мы можем поставить это количество перед символом суммирования. - Делаем аналогичный расчет.
- Подставим результат (а) в выражение для кинетической энергии вращения. 9{2}=1,73\,\text{J}[/латекс].
Значение
Мы можем видеть индивидуальные вклады в момент инерции. Массы вблизи оси вращения вносят очень небольшой вклад. Когда мы их убрали, это очень мало повлияло на момент инерции.
В следующем разделе мы обобщим уравнение суммирования для точечных частиц и разработаем метод расчета моментов инерции твердых тел. Однако пока на рисунке приведены значения инерции вращения для обычных форм объектов вокруг заданных осей.
Рисунок 10.20 Значения инерции вращения для обычных форм объектовПрименение кинетической энергии вращения
Теперь давайте применим идеи кинетической энергии вращения и таблицы моментов инерции, чтобы получить представление об энергии, связанной с несколькими вращающимися объектами. Следующие примеры также помогут вам освоиться с этими уравнениями. Во-первых, давайте рассмотрим общую стратегию решения проблем с вращательной энергией.
Следующие примеры также помогут вам освоиться с этими уравнениями. Во-первых, давайте рассмотрим общую стратегию решения проблем с вращательной энергией.
Стратегия решения проблем: энергия вращения
- Определите, какая энергия или работа связана с вращением.
- Определите интересующую систему. Эскиз обычно помогает.
- Проанализируйте ситуацию, чтобы определить виды работы и энергии.
- Если нет потерь энергии из-за трения и других неконсервативных сил, механическая энергия сохраняется, то есть [латекс] {K} _ {\ text {i}} + {U} _ {\ text {i}} ={K}_{\text{f}}+{U}_{\text{f}}[/латекс].
- Если присутствуют неконсервативные силы, механическая энергия не сохраняется, и другие формы энергии, такие как тепло и свет, могут входить в систему или выходить из нее. Определите, каковы они, и рассчитайте их по мере необходимости.
- Удалите термины везде, где это возможно, чтобы упростить алгебру.
- Оцените численное решение, чтобы увидеть, имеет ли оно смысл в физической ситуации, представленной в формулировке задачи.

Пример
Расчет энергии вертолета
Типичный небольшой спасательный вертолет имеет четыре лопасти: каждая имеет длину 4,00 м и массу 50,0 кг (рисунок). Лопасти можно представить как тонкие стержни, которые вращаются вокруг одного конца оси, перпендикулярной их длине. Вертолет имеет полную загруженную массу 1000 кг. а) Рассчитайте кинетическую энергию вращения лопастей, когда они вращаются со скоростью 300 об/мин. (b) Рассчитайте поступательную кинетическую энергию вертолета, когда он летит со скоростью 20,0 м/с, и сравните ее с энергией вращения лопастей.
Рисунок 10.21 (a) Эскиз четырехлопастного вертолета. b) спасательная операция на воде с участием вертолета Оклендской спасательной вертолетной службы Westpac. (кредит b: «111 Emergency»/Flickr)Стратегия
Кинетическая энергия вращения и поступательного движения может быть рассчитана по их определениям. Формулировка задачи дает все необходимые константы для вычисления выражений для вращательной и поступательной кинетических энергий.
Раствор
9{2}.[/латекс]Мы должны преобразовать угловую скорость в радианы в секунду и рассчитать момент инерции, прежде чем мы сможем найти K . Угловая скорость [латекс]\омега[/латекс] равна
[латекс]\omega =\frac{300\,\text{rev}}{1.00\,\text{min}}\,\frac{2\pi \,\text{rad}}{\text{1 rev}}\,\frac{1.00\,\text{min}}{60.0\,\text{s}}=\,31.4\,\frac{\text{rad}}{\text{s}}. [/латекс]
Момент инерции одной лопасти равен моменту инерции тонкого стержня, вращающегося вокруг своего конца, указанному на рис. Всего 9{2}=450,0\,\text{J}.[/latex]
Таким образом, полная энергия бумеранга равна
[латекс] {K} _ {\ text {Всего}} = {K} _ {\ text {R}} + {K} _ {\ text {T}} = 80,93 + 450,0 = 530,93 \, \ text { Дж}.[/латекс]
 {2}[/латекс]. Если погружной гребной винт имеет скорость вращения 4,0 об/с при выключенном двигателе, какова будет скорость вращения гребного винта через 5,0 с, когда сопротивление воды уберет из системы 50 000 Дж? 9{2}[/latex] момент инерции увеличивается как квадрат расстояния до фиксированной оси вращения. Момент инерции является вращательным аналогом массы в линейном движении.
{2}[/латекс]. Если погружной гребной винт имеет скорость вращения 4,0 об/с при выключенном двигателе, какова будет скорость вращения гребного винта через 5,0 с, когда сопротивление воды уберет из системы 50 000 Дж? 9{2}[/latex] момент инерции увеличивается как квадрат расстояния до фиксированной оси вращения. Момент инерции является вращательным аналогом массы в линейном движении.Концептуальные вопросы
Что, если бы другая планета размером с Землю была выведена на орбиту вокруг Солнца вместе с Землей. Момент инерции системы увеличится, уменьшится или останется прежним?
Твердый шар вращается вокруг оси, проходящей через его центр, с постоянной скоростью вращения. Другая полая сфера той же массы и радиуса вращается вокруг своей оси, проходящей через центр, с той же скоростью вращения. Какой шар имеет большую кинетическую энергию вращения?
Другая полая сфера той же массы и радиуса вращается вокруг своей оси, проходящей через центр, с той же скоростью вращения. Какой шар имеет большую кинетическую энергию вращения?
Полая сфера, так как масса распределена дальше от оси вращения.
Задачи
Система точечных частиц показана на следующем рисунке. Каждая частица имеет массу 0,3 кг и все они лежат в одной плоскости. а) Чему равен момент инерции системы относительно данной оси? б) Если система вращается со скоростью 5 об/с, какова ее кинетическая энергия вращения?
(a) Рассчитайте кинетическую энергию вращения Земли вокруг своей оси. б) Какова кинетическая энергия вращения Земли на ее орбите вокруг Солнца? 9{33}\,\text{J}[/латекс]
Рассчитайте кинетическую энергию вращения колеса мотоцикла массой 12 кг, если его угловая скорость равна 120 рад/с, внутренний радиус равен 0,280 м, а внешний радиус равен 0,330 м.
Бейсбольный питчер бросает мяч движением, при котором происходит вращение предплечья вокруг локтевого сустава, а также другие движения. {2}[/latex], какова кинетическая энергия вращения предплечья? 9{2}[/латекс] и массой 200 кг. Сопротивлением воздуха пренебречь. а) С какой поступательной скоростью гребной винт ударяется о землю? б) Какова скорость вращения пропеллера в момент удара?
{2}[/latex], какова кинетическая энергия вращения предплечья? 9{2}[/латекс] и массой 200 кг. Сопротивлением воздуха пренебречь. а) С какой поступательной скоростью гребной винт ударяется о землю? б) Какова скорость вращения пропеллера в момент удара?
а. [латекс] {v}_{\text{f}}=86,5\,\text{m}\text{/}\text{s}[/latex];
б. Скорость вращения винта остается прежней и составляет 20 об/с.
Если в предыдущей задаче присутствует сопротивление воздуха и оно снижает кинетическую энергию вращения пропеллера при ударе на 30 %, какова скорость вращения пропеллера при ударе? 9{42}\,\text{J}[/латекс]
Электрический шлифовальный станок, состоящий из вращающегося диска массой 0,7 кг и радиусом 10 см, вращается со скоростью 15 об/сек. При нанесении на грубую деревянную стену скорость вращения уменьшается на 20%. а) Чему равна конечная кинетическая энергия вращения вращающегося диска? б) Насколько уменьшилась его кинетическая энергия вращения?
Система состоит из диска массой 2,0 кг и радиусом 50 см, на котором закреплен кольцевой цилиндр массой 1,0 кг с внутренним радиусом 20 см и внешним радиусом 30 см (см. ниже). Система вращается вокруг оси, проходящей через центр диска и кольцевой цилиндр со скоростью 10 об/с. а) Чему равен момент инерции системы? б) Какова его кинетическая энергия вращения? 9{2}[/латекс]; б. [латекс]К=621,8\,\текст{J}[/латекс]
ниже). Система вращается вокруг оси, проходящей через центр диска и кольцевой цилиндр со скоростью 10 об/с. а) Чему равен момент инерции системы? б) Какова его кинетическая энергия вращения? 9{2}[/латекс]; б. [латекс]К=621,8\,\текст{J}[/латекс]
Глоссарий
- момент инерции
- вращающаяся масса твердых тел, которая относится к тому, насколько легко или сложно будет изменить угловую скорость вращающегося твердого тела
- вращательная кинетическая энергия
- кинетическая энергия за счет вращения объекта; это часть его полной кинетической энергии
Момент инерции и кинетическая энергия вращения – University Physics Volume 1
Вращение с фиксированной осью
Цели обучения
К концу этого раздела вы сможете:
- Описывать различия между вращательной и поступательной кинетической энергией
- Дайте определение физической концепции момента инерции в терминах распределения массы относительно оси вращения
- Объясните, как момент инерции твердых тел влияет на их кинетическую энергию вращения
- Использование закона сохранения механической энергии для анализа систем, подвергающихся как вращению, так и поступательному перемещению
- Расчет угловой скорости вращающейся системы при наличии потерь энергии из-за неконсервативных сил
До сих пор в этой главе мы работали с кинематикой вращения: описанием движения вращающегося твердого тела с фиксированной осью вращения.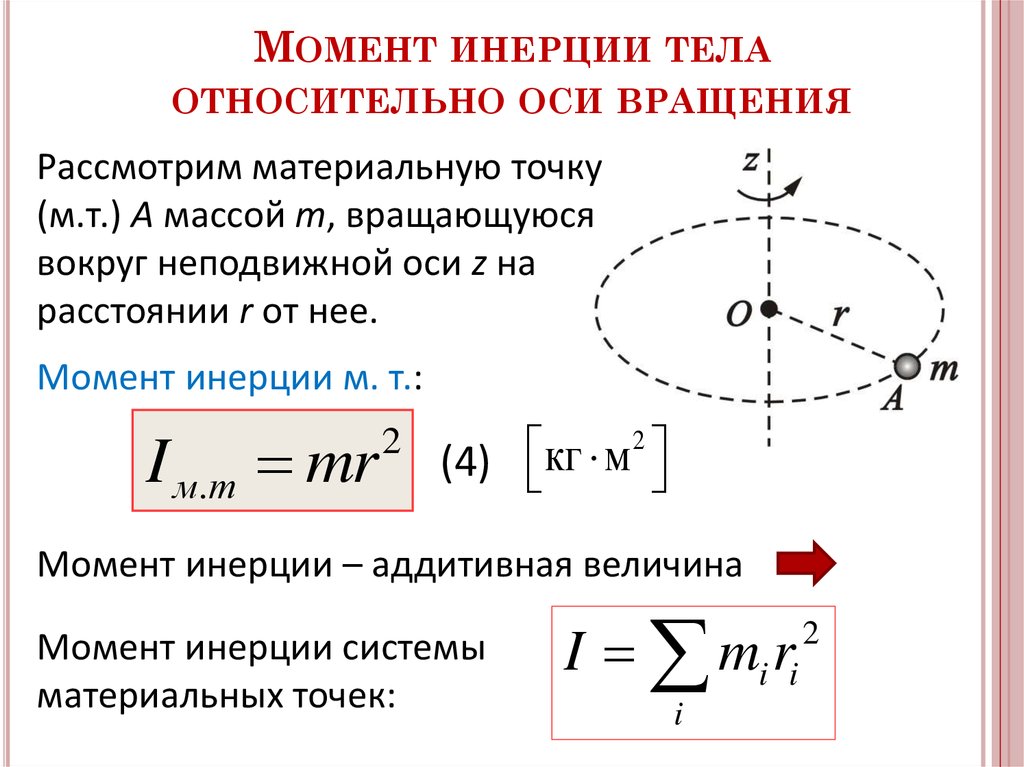 В этом разделе мы определяем две новые величины, полезные для анализа свойств вращающихся объектов: момент инерции и кинетическую энергию вращения. Определив эти свойства, мы получим два важных инструмента, необходимых для анализа динамики вращения.
В этом разделе мы определяем две новые величины, полезные для анализа свойств вращающихся объектов: момент инерции и кинетическую энергию вращения. Определив эти свойства, мы получим два важных инструмента, необходимых для анализа динамики вращения.
Вращательная кинетическая энергия
Любой движущийся объект обладает кинетической энергией. Мы знаем, как вычислить это для тела, совершающего поступательное движение, но как насчет твердого тела, совершающего вращательное движение? Это может показаться сложным, потому что каждая точка твердого тела имеет разную скорость. Однако мы можем использовать угловую скорость, которая одинакова для всего твердого тела, чтобы выразить кинетическую энергию вращающегося объекта. (Рисунок) показывает пример очень энергичного вращающегося тела: электрический точильный камень, приводимый в движение двигателем. Когда точильный камень выполняет свою работу, летят искры, возникают шум и вибрация. Эта система обладает значительной энергией, частично в виде тепла, света, звука и вибрации. Однако большая часть этой энергии находится в форме кинетической энергии вращения. 9{2}[/latex], а скорость — это величина, разная для каждой точки тела, вращающегося вокруг оси, имеет смысл найти способ записать кинетическую энергию через переменную [latex]\omega[/ латекс], который одинаков для всех точек на твердом вращающемся теле. Для одиночной частицы, вращающейся вокруг фиксированной оси, это легко вычислить. Мы можем связать угловую скорость с величиной поступательной скорости, используя соотношение [latex]{v}_{\text{t}}=\omega r[/latex], где 9{2}.[/latex]
Однако большая часть этой энергии находится в форме кинетической энергии вращения. 9{2}[/latex], а скорость — это величина, разная для каждой точки тела, вращающегося вокруг оси, имеет смысл найти способ записать кинетическую энергию через переменную [latex]\omega[/ латекс], который одинаков для всех точек на твердом вращающемся теле. Для одиночной частицы, вращающейся вокруг фиксированной оси, это легко вычислить. Мы можем связать угловую скорость с величиной поступательной скорости, используя соотношение [latex]{v}_{\text{t}}=\omega r[/latex], где 9{2}.[/latex]
В случае твердого вращающегося тела мы можем разделить любое тело на большое количество меньших масс, каждая из которых имеет массу [latex]{m}_{j}[/latex ] и расстояние до оси вращения [латекс]{r}_{j}[/латекс], такое, чтобы общая масса тела была равна сумме отдельных масс: [латекс]М=\сумма _{ j}{m}_{j}[/латекс]. Каждая меньшая масса имеет тангенциальную скорость [латекс]{v}_{j}[/латекс], где мы временно опустили индекс t .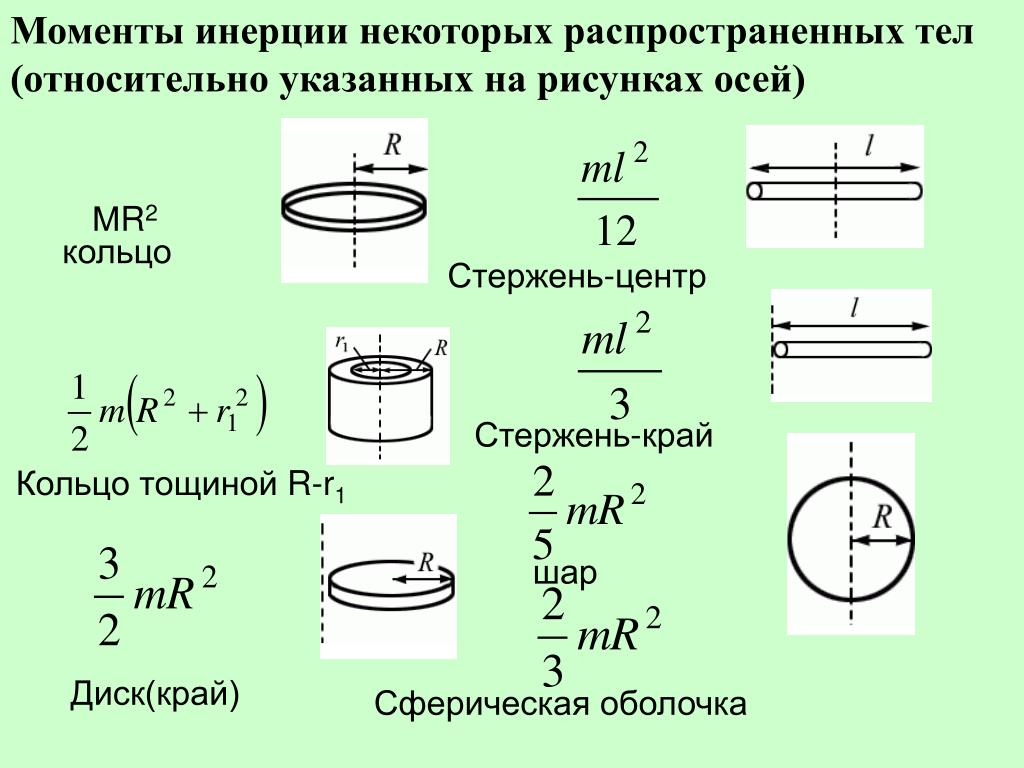 Полная кинетическая энергия твердого вращающегося тела равна 9{2}[/latex], где r — расстояние от точечной частицы до оси вращения. В следующем разделе мы исследуем интегральную форму этого уравнения, которую можно использовать для расчета момента инерции некоторых твердых тел правильной формы.
Полная кинетическая энергия твердого вращающегося тела равна 9{2}[/latex], где r — расстояние от точечной частицы до оси вращения. В следующем разделе мы исследуем интегральную форму этого уравнения, которую можно использовать для расчета момента инерции некоторых твердых тел правильной формы.
Момент инерции есть количественная мера инерции вращения, как и в поступательном движении, а масса есть количественная мера линейной инерции, т. е. чем массивнее объект, тем больше у него инерция и тем больше его сопротивление изменению линейной скорости. Аналогично, чем больше момент инерции твердого тела или системы частиц, тем больше их сопротивление изменению угловой скорости относительно неподвижной оси вращения. Интересно посмотреть, как меняется момент инерции в зависимости от r, расстояние до оси вращения массы частицы на (рис.). Твердые тела и системы частиц с большей массой, сосредоточенные на большем расстоянии от оси вращения, обладают большими моментами инерции, чем тела и системы той же массы, но сосредоточенные вблизи оси вращения. Таким образом, мы можем видеть, что полый цилиндр имеет большую инерцию вращения, чем сплошной цилиндр той же массы при вращении вокруг оси, проходящей через центр. Подставляя (Рисунок) в (Рисунок), выражение для кинетической энергии вращающегося твердого тела принимает вид 9{2}.[/latex]
Таким образом, мы можем видеть, что полый цилиндр имеет большую инерцию вращения, чем сплошной цилиндр той же массы при вращении вокруг оси, проходящей через центр. Подставляя (Рисунок) в (Рисунок), выражение для кинетической энергии вращающегося твердого тела принимает вид 9{2}.[/latex]
Из этого уравнения видно, что кинетическая энергия вращающегося твердого тела прямо пропорциональна моменту инерции и квадрату угловой скорости. Это используется в устройствах накопления энергии маховика, которые предназначены для накопления большого количества кинетической энергии вращения. Многие автопроизводители в настоящее время испытывают в своих автомобилях накопители энергии маховика, такие как маховик или система рекуперации кинетической энергии, показанные на (рис.).
A Маховик KERS (система рекуперации кинетической энергии), используемый в автомобилях. (кредит: «cmonville»/Flickr)
Вращательные и поступательные величины для кинетической энергии и инерции приведены на (Рисунок). Столбец отношения не включен, потому что не существует константы, на которую мы могли бы умножить вращательную величину, чтобы получить поступательную величину, как это можно сделать для переменных на (рис.).
Столбец отношения не включен, потому что не существует константы, на которую мы могли бы умножить вращательную величину, чтобы получить поступательную величину, как это можно сделать для переменных на (рис.).
| Ротационный | Трансляционное |
|---|
Момент инерции системы частиц
Шесть маленьких шайб расположены на расстоянии 10 см друг от друга на стержне ничтожной массы и длины 0,5 м. Масса каждой шайбы 20 г. Стержень вращается вокруг оси, расположенной на расстоянии 25 см, как показано на (рис. ). а) Чему равен момент инерции системы? б) Если убрать две ближние к оси шайбы, каков будет момент инерции оставшихся четырех шайб? в) Если система с шестью шайбами вращается со скоростью 5 об/с, какова ее кинетическая энергия вращения?
). а) Чему равен момент инерции системы? б) Если убрать две ближние к оси шайбы, каков будет момент инерции оставшихся четырех шайб? в) Если система с шестью шайбами вращается со скоростью 5 об/с, какова ее кинетическая энергия вращения?
Шесть шайб расположены на расстоянии 10 см друг от друга на стержне незначительной массы и вращаются вокруг вертикальной оси.
Стратегия
- Мы используем определение момента инерции для системы частиц и выполняем суммирование для оценки этой величины. Все массы одинаковы, поэтому мы можем поставить это количество перед символом суммирования.
- Делаем аналогичный расчет.
- Подставим результат (а) в выражение для кинетической энергии вращения. 9{2}=1,73\phantom{\rule{0.2em}{0ex}}\text{J}[/latex].
Значение
Мы можем видеть индивидуальные вклады в момент инерции. Массы вблизи оси вращения вносят очень небольшой вклад. Когда мы их убрали, это очень мало повлияло на момент инерции.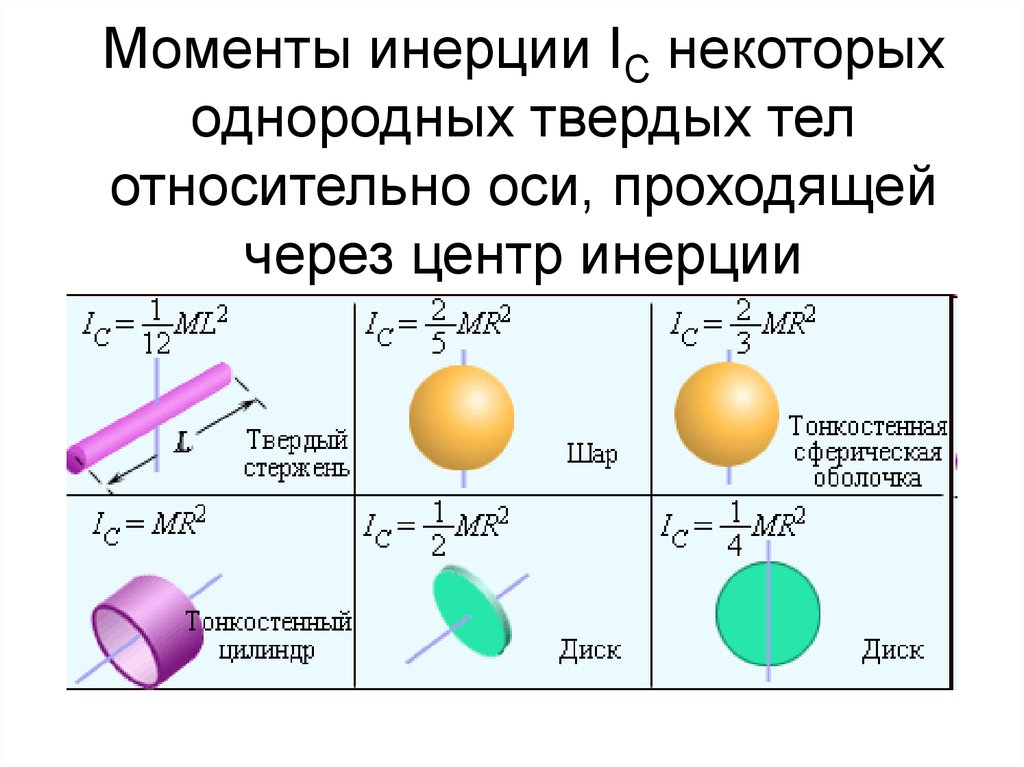
В следующем разделе мы обобщим уравнение суммирования для точечных частиц и разработаем метод расчета моментов инерции твердых тел. Однако на данный момент (Рисунок) дает значения инерции вращения для обычных форм объектов вокруг указанных осей.
Значения инерции вращения для обычных форм объектов.
Применение кинетической энергии вращения
Теперь давайте применим идеи кинетической энергии вращения и таблицы моментов инерции, чтобы получить представление об энергии, связанной с несколькими вращающимися объектами. Следующие примеры также помогут вам освоиться с этими уравнениями. Во-первых, давайте рассмотрим общую стратегию решения проблем с вращательной энергией.
Стратегия решения проблем: энергия вращения
- Определите, какая энергия или работа связана с вращением.
- Определите интересующую систему. Эскиз обычно помогает.
- Проанализируйте ситуацию, чтобы определить виды работы и энергии.
- Если нет потерь энергии из-за трения и других неконсервативных сил, механическая энергия сохраняется, то есть [латекс] {K} _ {\ text {i}} + {U} _ {\ text {i}} ={K}_{\text{f}}+{U}_{\text{f}}[/латекс].

- Если присутствуют неконсервативные силы, механическая энергия не сохраняется, и другие формы энергии, такие как тепло и свет, могут входить в систему или выходить из нее. Определите, каковы они, и рассчитайте их по мере необходимости.
- Удалите термины везде, где это возможно, чтобы упростить алгебру.
- Оцените численное решение, чтобы увидеть, имеет ли оно смысл в физической ситуации, представленной в формулировке задачи.
Расчет энергии вертолета
Типичный небольшой спасательный вертолет имеет четыре лопасти: каждая имеет длину 4,00 м и массу 50,0 кг ((Рисунок)). Лопасти можно представить как тонкие стержни, которые вращаются вокруг одного конца оси, перпендикулярной их длине. Вертолет имеет полную загруженную массу 1000 кг. а) Рассчитайте кинетическую энергию вращения лопастей, когда они вращаются со скоростью 300 об/мин. (b) Рассчитайте поступательную кинетическую энергию вертолета, когда он летит со скоростью 20,0 м/с, и сравните ее с энергией вращения лопастей.
(а) Эскиз четырехлопастного вертолета. b) спасательная операция на воде с участием вертолета Оклендской спасательной вертолетной службы Westpac. (кредит b: «111 Emergency»/Flickr)
Стратегия
Вращательная и поступательная кинетическая энергия может быть рассчитана по их определениям. Формулировка задачи дает все необходимые константы для вычисления выражений для вращательной и поступательной кинетических энергий.
Раствор
- 9{2}.[/латекс]
- Мы используем закон сохранения механической энергии. Поскольку бумеранг запускается под углом, нам нужно записать полную энергию системы через ее линейную кинетическую энергию, используя скорость в направлениях x и y . Полная энергия, когда бумеранг покидает руку, равна 9{2}\right)}=18,97\phantom{\rule{0.2em}{0ex}}\text{m}.[/latex]
Мы должны преобразовать угловую скорость в радианы в секунду и рассчитать момент инерции, прежде чем мы сможем найти K . Угловая скорость [латекс]\омега[/латекс] равна
[латекс]\omega =\frac{300\phantom{\rule{0.2em}{0ex}}\text{rev}}{1.00\phantom{\rule{0.2em}{0ex}}\text{min} }\phantom{\rule{0.2em}{0ex}}\frac{2\pi \phantom{\rule{0.2em}{0ex}}\text{rad}}{\text{1 rev}}\phantom{ \rule{0.2em}{0ex}}\frac{1.00\phantom{\rule{0.2em}{0ex}}\text{min}}{60.0\phantom{\rule{0.2em}{0ex}}\text {s}}=\phantom{\rule{0. {2}[/латекс].
9{2}=450.0\phantom{\rule{0.2em}{0ex}}\text{J}.[/latex]
{2}[/латекс].
9{2}=450.0\phantom{\rule{0.2em}{0ex}}\text{J}.[/latex]
Таким образом, полная энергия бумеранга равна
[латекс] {K} _ {\ text {Всего}} = {K} _ {\ text {R}} + {K} _ {\ text {T}} = 80,93 + 450,0 = 530,93 \ фантом {\ правило {0.2em}{0ex}}\text{J}.[/latex]
Значение
В части (b) решение демонстрирует, как сохранение энергии является альтернативным методом решения проблемы, которая обычно решается с использованием кинематики. При отсутствии сопротивления воздуха кинетическая энергия вращения не учитывалась в решении для максимальной высоты.
Проверьте правильность понимания Момент инерции винта атомной подводной лодки составляет [латекс]800,0\phantom{\rule{0. {2 }[/латекс]. Если погружной гребной винт имеет скорость вращения 4,0 об/с при выключенном двигателе, какова будет скорость вращения гребного винта через 5,0 с, когда сопротивление воды уберет из системы 50 000 Дж? 9{2}[/latex] момент инерции увеличивается как квадрат расстояния до фиксированной оси вращения. Момент инерции является вращательным аналогом массы в линейном движении.
{2 }[/латекс]. Если погружной гребной винт имеет скорость вращения 4,0 об/с при выключенном двигателе, какова будет скорость вращения гребного винта через 5,0 с, когда сопротивление воды уберет из системы 50 000 Дж? 9{2}[/latex] момент инерции увеличивается как квадрат расстояния до фиксированной оси вращения. Момент инерции является вращательным аналогом массы в линейном движении.
Концептуальные вопросы
Что, если бы другая планета размером с Землю была выведена на орбиту вокруг Солнца вместе с Землей. Момент инерции системы увеличится, уменьшится или останется прежним?
Твердый шар вращается вокруг оси, проходящей через его центр, с постоянной скоростью вращения. Другая полая сфера той же массы и радиуса вращается вокруг своей оси, проходящей через центр, с той же скоростью вращения. Какой шар имеет большую кинетическую энергию вращения?
Другая полая сфера той же массы и радиуса вращается вокруг своей оси, проходящей через центр, с той же скоростью вращения. Какой шар имеет большую кинетическую энергию вращения?
Полая сфера, так как масса распределена дальше от оси вращения.
Задачи
Система точечных частиц показана на следующем рисунке. Каждая частица имеет массу 0,3 кг и все они лежат в одной плоскости. а) Чему равен момент инерции системы относительно данной оси? б) Если система вращается со скоростью 5 об/с, какова ее кинетическая энергия вращения?
(a) Рассчитайте кинетическую энергию вращения Земли вокруг своей оси. б) Какова кинетическая энергия вращения Земли на ее орбите вокруг Солнца? 9{33}\phantom{\rule{0.2em}{0ex}}\text{J}[/latex]
Рассчитайте кинетическую энергию вращения колеса мотоцикла массой 12 кг, если его угловая скорость равна 120 рад/с, а внутренний радиус составляет 0,280 м, а внешний радиус 0,330 м.
Бейсбольный питчер бросает мяч движением, при котором происходит вращение предплечья вокруг локтевого сустава, а также другие движения. {2}[/latex], какова вращательная кинетическая энергия предплечья? 9{2}[/латекс] и массой 200 кг. Сопротивлением воздуха пренебречь. а) С какой поступательной скоростью гребной винт ударяется о землю? б) Какова скорость вращения пропеллера в момент удара?
{2}[/latex], какова вращательная кинетическая энергия предплечья? 9{2}[/латекс] и массой 200 кг. Сопротивлением воздуха пренебречь. а) С какой поступательной скоростью гребной винт ударяется о землю? б) Какова скорость вращения пропеллера в момент удара?
а. [латекс] {v} _ {\ text {f}} = 86,5 \ phantom {\ rule {0.2em} {0ex}} \ text {m} \ text{/} \ text {s} [/latex];
б. Скорость вращения винта остается прежней и составляет 20 об/с.
Если в предыдущей задаче присутствует сопротивление воздуха и оно уменьшает кинетическую энергию вращения пропеллера при ударе на 30 %, какова скорость вращения пропеллера при ударе? 9{42}\phantom{\rule{0.2em}{0ex}}\text{J}[/latex]
Электрическая шлифовальная машина, состоящая из вращающегося диска массой 0,7 кг и радиусом 10 см, вращается со скоростью 15 об/сек. При нанесении на грубую деревянную стену скорость вращения уменьшается на 20%. а) Чему равна конечная кинетическая энергия вращения вращающегося диска? б) Насколько уменьшилась его кинетическая энергия вращения?
Система состоит из диска массой 2,0 кг и радиусом 50 см, на котором закреплен кольцевой цилиндр массой 1,0 кг с внутренним радиусом 20 см и внешним радиусом 30 см (см.

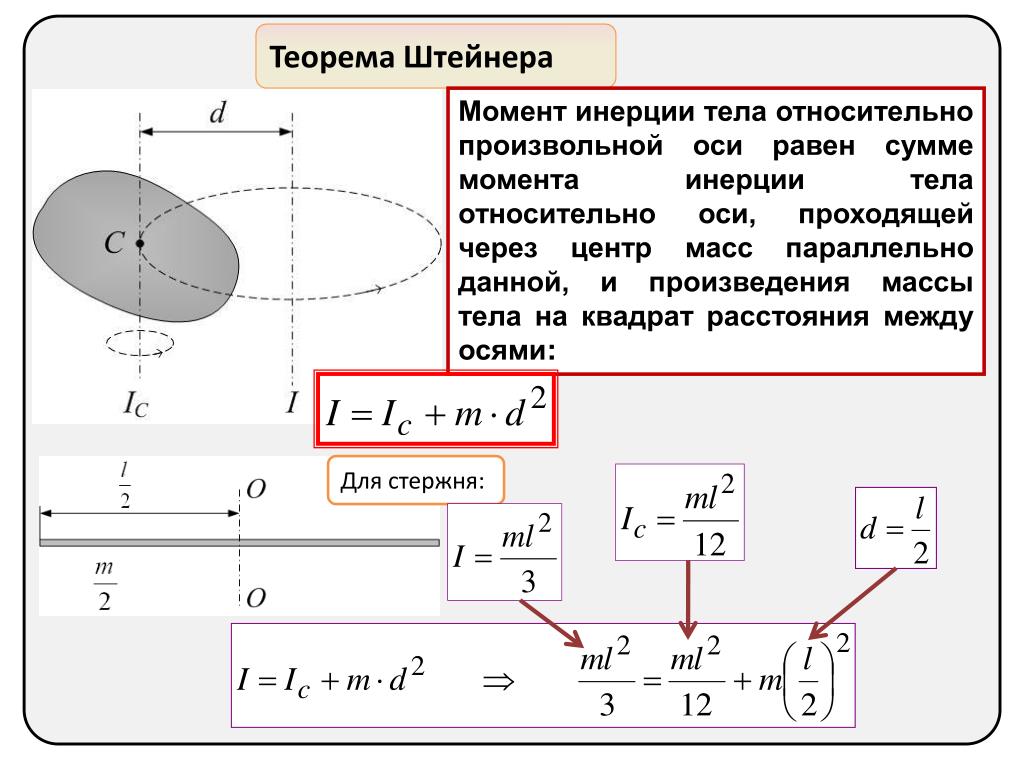
 12
12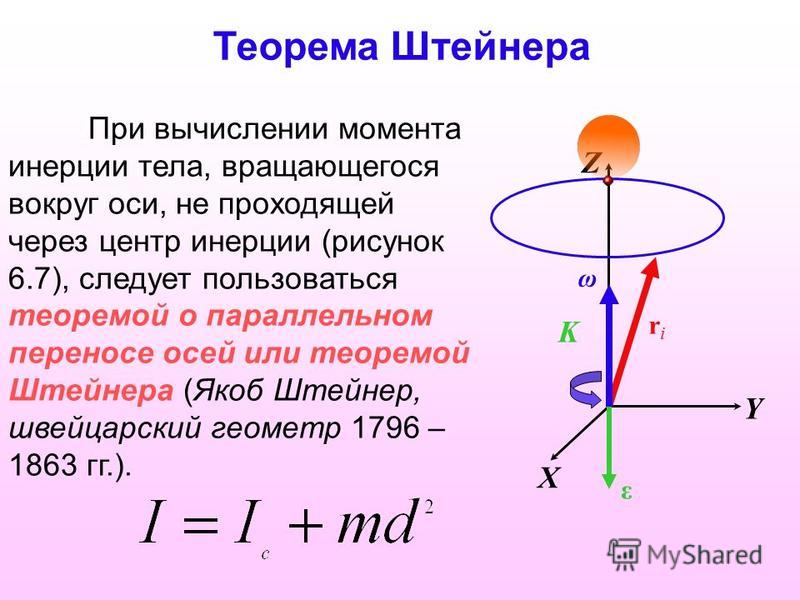 Радиус шара R, масса т:
Радиус шара R, масса т: 14). Из рисунка ясно, что а = , кроме этого момент инерции относительно оси, проходящей через центр масс равен:
14). Из рисунка ясно, что а = , кроме этого момент инерции относительно оси, проходящей через центр масс равен:
 МОМЕНТ ИНЕРЦИИ РАЗЛИЧНЫХ ТЕЛ. ТЕОРЕМА ШТЕЙНЕРА
МОМЕНТ ИНЕРЦИИ РАЗЛИЧНЫХ ТЕЛ. ТЕОРЕМА ШТЕЙНЕРА Все правила по сольфеджио
Все правила по сольфеджио


 В результате деформации пружины при её закручивании на угол j возникнет упругая сила. Эта сила создает крутящий момент (момент силы) . Модуль момента пропорционален углу закручивания пружины
В результате деформации пружины при её закручивании на угол j возникнет упругая сила. Эта сила создает крутящий момент (момент силы) . Модуль момента пропорционален углу закручивания пружины

 Обратная связь – 161.97.168.212 (0.012 с.)
Обратная связь – 161.97.168.212 (0.012 с.)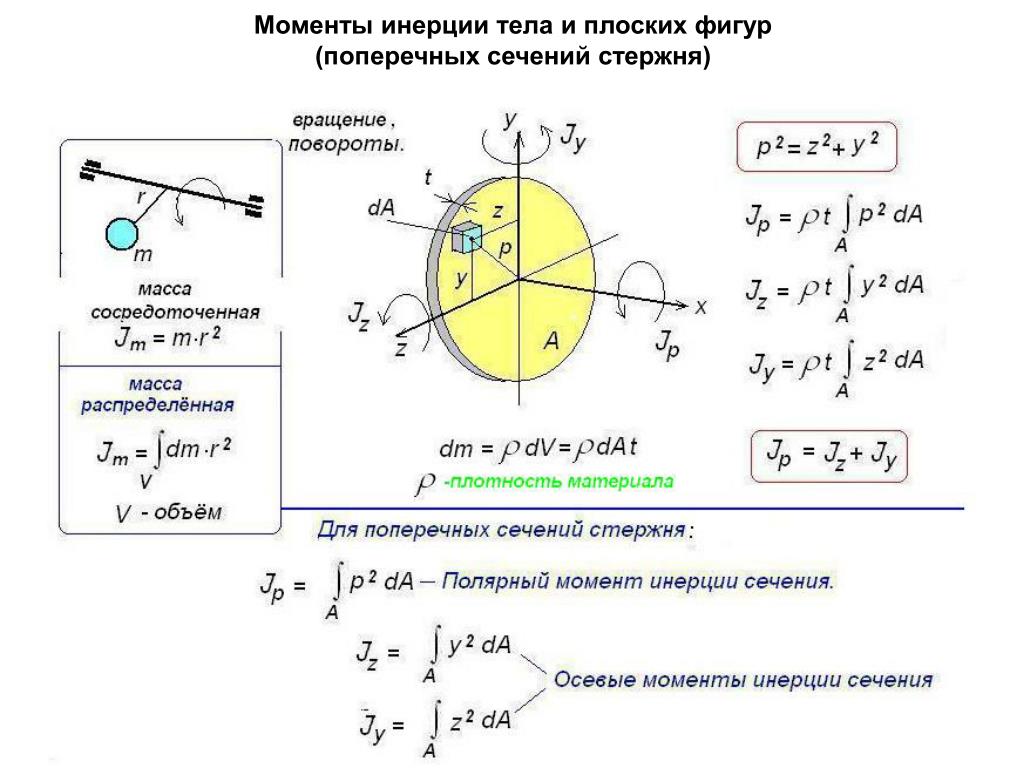 I about the Diameter
I about the Diameter Все массы одинаковы, поэтому мы можем поставить это количество перед символом суммирования.
Все массы одинаковы, поэтому мы можем поставить это количество перед символом суммирования.