Момент инерции тела формула. Момент инерции
Рассмотрим теперь проблему определения момента инерции различных тел. Общая формула для нахождения момента инерции объекта относительно оси имеет вид
,
Иными словами, нужно сложить все массы, умножив каждую из них на квадрат ее расстояния до оси . Заметьте, что это верно даже для трехмерного тела, несмотря на то, что расстояние имеет такой «двумерный вид». Впрочем, в большинстве случаев мы будем ограничиваться двумерными телами.
В
качестве простого примера рассмотрим стержень, вращающийся относительно оси,
проходящей через его конец и перпендикулярной к нему (фиг. 19.3). Нам нужно
просуммировать теперь все массы, умноженные на квадраты расстояния (в этом случае
все –
нулевые). Под суммой, разумеется, я имею в виду интеграл от , умноженный на
«элементики» массы. Если мы разделим стержень на кусочки длиной , то
соответствующий элемент массы будет пропорционален , а если бы составляло длину
всего стержня, то его масса была бы равна .
. (19.5)
Размерность момента инерции всегда равна массе, умноженной на квадрат длины, так что единственная существенная величина, которую мы вычислили, это множитель .
Фиг. 19.3. Прямой стержень, вращающийся вокруг оси, проходящей черед один из его концов.
А чему будет равен момент инерции , если ось вращения проходит через середину стержня? Чтобы найти его, нам снова нужно взять интеграл, но уже в пределах от до . Заметим, однако, одну особенность этого случая. Такой стержень с проходящей через центр осью можно представлять себе как два стержня с осью, проходящей через конец, причем масса каждого из них равна , а длина равна . Моменты инерции двух таких стержней равны друг другу и вычисляются по формуле (19.5). Поэтому момент инерции всего стержня равен
. (19.6)
Таким образом, стержень гораздо легче крутить за середину, чем за конец.
Можно,
конечно, продолжить вычисление моментов инерции других интересующих нас тел. Но
поскольку такие расчеты требуют большого опыта в вычислении интегралов (что
очень важно само по себе), они как таковые не представляют для нас большого
интереса. Впрочем, здесь имеются некоторые очень интересные и полезные теоремы.
Пусть имеется какое-то тело и мы хотим узнать его момент инерции относительно
какой-то оси. Это означает, что мы хотим найти его инертность при вращении
вокруг этой оси. Если мы будем двигать тело за стержень, подпирающий его центр
масс так, чтобы оно не поворачивалось при вращении вокруг оси (в этом случае на
него не действуют никакие моменты сил инерции, поэтому тело не будет поворачиваться,
когда мы начнем двигать его), то для того, чтобы повернуть его, понадобится
точно такая же сила, как если бы вся масса была сосредоточена в центре масс и
момент инерции был бы просто равен , где – расстояние от центра масс до оси
вращения. Однако формула эта, разумеется, неверна. Она не дает правильного
момента инерции тела. Ведь в действительности при повороте тело вращается.
Крутится не только центр масс (что давало бы величину ), само тело тоже должно
поворачиваться относительно центра масс. Таким образом, к моменту инерции нужно добавить – момент инерции
относительно центра масс.
Впрочем, здесь имеются некоторые очень интересные и полезные теоремы.
Пусть имеется какое-то тело и мы хотим узнать его момент инерции относительно
какой-то оси. Это означает, что мы хотим найти его инертность при вращении
вокруг этой оси. Если мы будем двигать тело за стержень, подпирающий его центр
масс так, чтобы оно не поворачивалось при вращении вокруг оси (в этом случае на
него не действуют никакие моменты сил инерции, поэтому тело не будет поворачиваться,
когда мы начнем двигать его), то для того, чтобы повернуть его, понадобится
точно такая же сила, как если бы вся масса была сосредоточена в центре масс и
момент инерции был бы просто равен , где – расстояние от центра масс до оси
вращения. Однако формула эта, разумеется, неверна. Она не дает правильного
момента инерции тела. Ведь в действительности при повороте тело вращается.
Крутится не только центр масс (что давало бы величину ), само тело тоже должно
поворачиваться относительно центра масс. Таким образом, к моменту инерции нужно добавить – момент инерции
относительно центра масс.
Эта теорема называется теоремой о параллельном переносе оси. Доказывается она очень легко. Момент инерции относительно любой оси равен сумме масс, умноженных на сумму квадратов и , т. е. . Мы сейчас сосредоточим наше внимание на , однако все в точности можно повторить и для . Пусть координата есть расстояние данной частной точки от начала координат; посмотрим, однако, как все изменится, если мы будем измерять расстояние от центра масс вместо от начала координат. Чтобы это выяснить, мы должны написать
Возводя это выражение в квадрат, находим
.
Что получится, если умножить его на и просуммировать по всем ? Вынося постоянные величины за знак суммирования, находим
.
Третью
сумму подсчитать легко; это просто . Второй член состоит из двух
сомножителей, один из которых ; он равен -координате центра масс. Но
это должно быть равно нулю, ведь отсчитывается от центра масс, а в
этой системе координат среднее положение всех частиц, взвешенное их массами,
равно нулю.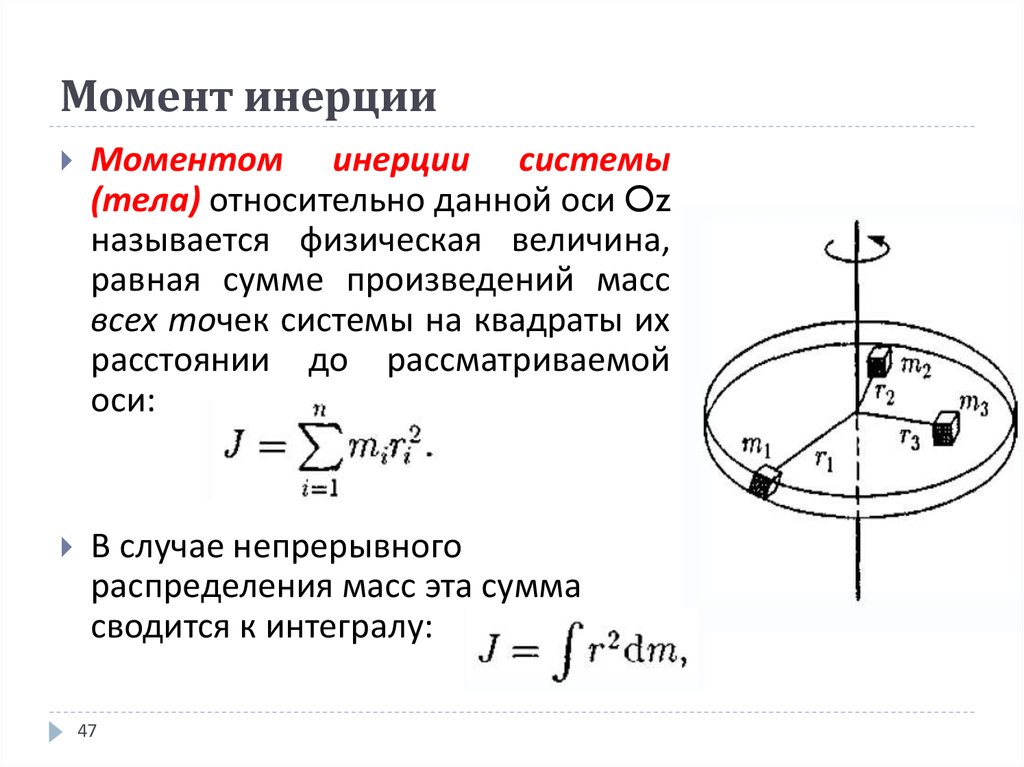
Давайте проверим формулу (19.7) на одном примере. Просто проверим, будет ли она применима для стержня. Мы уже нашли, что момент инерции стержня относительно его конца должен быть равен . А центр масс стержня, разумеется, находится на расстоянии . Таким образом, мы должны получить, что . Так как одна четвертая + одна двенадцатая = одной третьей, то мы не сделали никакой грубой ошибки.
Кстати, чтобы найти момент инерции (19.5), вовсе не обязательно вычислять интеграл. Можно просто предположить, что он равен величине , умноженной на некоторый неизвестный коэффициент . После этого можно использовать рассуждения о двух половинках и для момента инерции (19.6) получить коэффициент . Используя теперь теорему о параллельном переносе оси, докажем, что , откуда . Всегда можно найти какой-нибудь окольный путь!
При
применении теоремы о параллельных осях важно помнить, что ось должна быть
параллельна оси, относительно которой мы хотим вычислять момент инерции.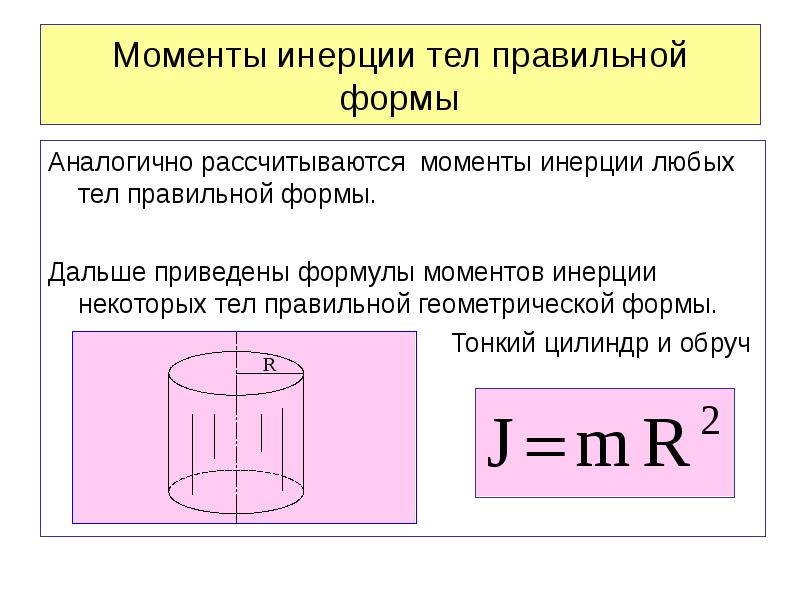
Стоит, пожалуй, упомянуть еще об одном свойстве, которое часто бывает очень полезно при нахождении момента инерции некоторых типов тел. Оно состоит в следующем: если у нас есть плоская фигура и тройка координатных осей с началом координат, расположенным в этой плоскости, и осью , направленной перпендикулярно к ней, то момент инерции этой фигуры относительно оси равен сумме моментов инерции относительно осей и . Доказывается это совсем просто. Заметим, что
(поскольку все ). Аналогично,
,
Момент инерции однородной прямоугольной пластинки, например с массой , шириной и длиной относительно оси, перпендикулярной к ней и проходящей через ее центр, равен просто
,
поскольку момент инерции относительно оси, лежащей в плоскости пластинки и параллельной ее длине, равен , т. е. точно такой же, как и для стержня длиной , а момент инерции относительно другой оси в той же плоскости равен , такой же, как и для стержня длиной .
Итак, перечислим свойства момента инерции относительно данной оси, которую мы назовем осью :
1. Момент инерции равен
Момент инерции равен
.
2. Если предмет состоит из нескольких частей, причем момент инерции каждой из них известен, то полный момент инерции равен сумме моментов инерции этих частей.
3. Момент инерции относительно любой данной оси равен моменту инерции относительно параллельной оси, проходящей через центр масс, плюс произведение полной массы на квадрат расстояния данной оси от центра масс.
4. Момент инерции плоской фигуры относительно оси, перпендикулярной к ее плоскости, равен сумме моментов инерций относительно любых двух других взаимно перпендикулярных осей, лежащих в плоскости фигуры и пересекающихся с перпендикулярной осью.
В табл. 19.1 приведены моменты инерции некоторых элементарных фигур, имеющих однородную плотность масс, а в табл. 19.2 – моменты инерции некоторых фигур, которые могут быть получены из табл. 19.1 с использованием перечисленных выше свойств.
Таблица 19.1 Простые примеры моментов инерции
Тонкий стержень длиной | Проходит через центр перпендикулярно к стержню | |
Тонкое концентрическое кольцо с радиусами и | Проходит через центр кольца перпендикулярно к плоскости кольца | |
Сфера радиуса | Проходит через центр |
Таблица
19. 2 Моменты инерции, полученные из табл. 19.1
2 Моменты инерции, полученные из табл. 19.1
Прямоугольник со сторонами и Прямоугольный параллелепипед со сторонами Проходит через центр параллельно |
| Значение | |
| Тема статьи: | Момент инерции |
| Рубрика (тематическая категория) | Механика |
Рассмотрим материальную точку массой m , которая находится на расстоянии r, от неподвижной оси (рис. 26). Моментом инерции J материальной точки относительно оси принято называть скалярная физическая величина, равная произведению массы m на квадрат расстояния r до этой оси:
J = mr 2 (75)
Момент инерции системы N материальных точек будет равен сумме моментов инерции отдельных точек
(76)
К определению момента инерции точки
В случае если масса распределена в пространстве непрерывно, то суммирование заменяется интегрированием. Тело разбивается на элементарные объёмы dv, каждый из которых обладает массой dm. В результате получается следующее выражение:
Тело разбивается на элементарные объёмы dv, каждый из которых обладает массой dm. В результате получается следующее выражение:
(77)
Для однородного по объёму тела плотность ρ постоянна, и записав элементарную массу в виде
dm = ρdv, преобразуем формулу (70) следующим образом:
(78)
Размерность момента инерции – кг*м 2 .
Момент инерции тела является мерой инертности тела во вращательном движении, подобно тому, как масса тела является мерой его инертности при поступательном движении.
Момент инерции – это мера инертных свойств твердого тела при вращательном движении, зависящая от распределения массы относительно оси вращения . Иными словами, момент инерции зависит от массы, формы, размеров тела и положения оси вращения.
Всякое тело, независимо от того, вращается оно или покоится, обладает моментом инерции относительно любой оси, подобно тому, как тело обладает массой независимо от того, движется оно или находиться в покое.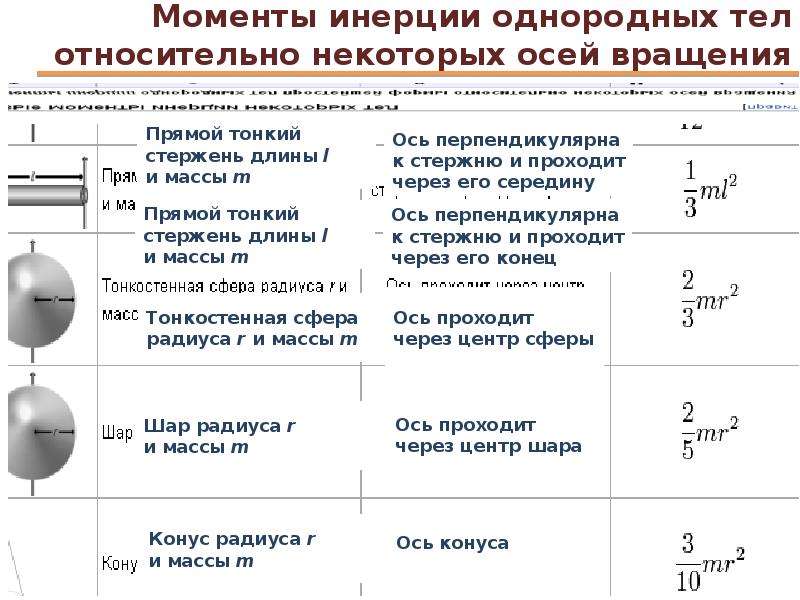 Аналогично массе момент инерции является величиной аддитивной.
Аналогично массе момент инерции является величиной аддитивной.
В некоторых случаях теоретический расчёт момента инерции достаточно прост. Ниже приведены моменты инерции некоторых сплошных тел правильной геометрической формы относительно оси, проходящей через центр тяжести.
Момент инерции бесконечно плоского диска радиуса R относительно оси, перпендикулярной плоскости диска:
Момент инерции шара радиуса R :
Момент инерции стержня длиной L относительно оси, проходящей через середину стержня перпендикулярно ему:
Момент инерции бесконечно тонкого обруча радиуса R относительно оси, перпендикулярной его плоскости:
Момент инерции тела относительно произвольной оси рассчитывается с помощью теоремы Штейнера:
Момент инерции тела относительно произвольной оси равен сумме момента инерции относительно оси, проходящей через центр масс параллельно данной, и произведения массы тела на квадрат расстояния между осями.
Рассчитаем при помощи теоремы Штейнера момент инерции стержня длиной L относительно оси, проходящей через конец перпендикулярно ему (рис. 27).
К расчету момента инерции стержня
Согласно теореме Штейнера, момент инерции стержня относительно оси O′O′ равен моменту инерции относительно оси OO плюс md 2 . Отсюда получаем:
Очевидно: момент инерции неодинаков относительно разных осей, и в связи с этим, решая задачи на динамику вращательного движения, момент инерции тела относительно интересующей нас оси каждый раз приходится искать отдельно. Так, к примеру, при конструировании технических устройств, содержащих вращающиеся детали (на железнодорожном транспорте, в самолетостроении, электротехнике и т. д.), требуется знание величин моментов инерции этих деталей. При сложной форме тела теоретический расчет его момента инерции может оказаться трудно выполнимым. В этих случаях предпочитают измерить момент инерции нестандартной детали опытным путем.
Момент силы F относительно точки O
Момент инерции – понятие и виды. Классификация и особенности категории “Момент инерции” 2017, 2018.
Рис.35 Проведем через центр масс С тела произвольные оси Cx”y”z”, а через любую точку О на оси Сх” – оси Oxyz, такие, что Оy½½Сy”, Oz½½Cz” (рис. 35). Расстояние между осями Cz” и Оz обозначим через d. Тогда но, как видно из рисунка, для любой точки тела или, а. Подставляя… .
Момент инерции тела – величина, определяющая его инертность во вращательном движении. В динамике поступательного движения инерцию тела полностью характеризует его масса. Влияние собственных свойств тела на динамику вращательного движения оказывается более сложным,… .

Лекция 3. Силы. Масса, импульс материальной точки и механической системы. Динамика поступательного движения в инерциальных системах отсчета. Закон изменения импульса механической системы. Закон сохранения импульса. Динамика изучает движение тел с учетом причин,… .
Проанализируем формулу для момента инерции твердого тела. Момент инерции зависит от 1) массы тела, 2) формы и размеров тела, 3) положения оси вращения относительно тела (рис 2) Рис. 2а Рис.2б Итак, момент инерции есть мера инертности тела при вращательном движении,… .
Момент инерции относительно любой оси равен моменту инерции относительно центральной оси, параллельной данной, плюс произведение площади фигуры на квадрат расстояния между осями. Из формулы видно, что момент инерции относительно центральной оси меньше, чем момент…
В динамике поступательного движения материальной точки кроме кинематических характеристик вводились понятия силы и массы. При изучении динамики вращательного движения вводятся физические величины – момент сил и момент инерции , физический смысл которых раскроем ниже.
При изучении динамики вращательного движения вводятся физические величины – момент сил и момент инерции , физический смысл которых раскроем ниже.
Пусть некоторое тело под действием силы , приложенной в точке А , приходит во вращение вокруг оси ОО” (рисунок 5.1).
Рисунок 5.1 – К выводу понятия момента силы
Сила действует в плоскости, перпендикулярной оси. Перпендикуляр р , опущенный из точки О (лежащей на оси) на направление силы, называют плечом силы . Произведение силы на плечо определяет модуль момента силы относительно точки О :
(5.1)
Момент силы есть вектор, определяемый векторным произведением радиуса-вектора точки приложения силы и вектора силы :
(5.2)
Единица момента силы – ньютон-метр (Н . м). Направление вектора момента силы находиться с помощью правила правого винта .
Мерой инертности тел при поступательном движении является масса. Инертность тел при вращательном движении зависит не только от массы, но и от ее распределения в пространстве относительно оси вращения. Мерой инертности при вращательном движении служит величина, называемая моментом инерции тела относительно оси вращения.
Инертность тел при вращательном движении зависит не только от массы, но и от ее распределения в пространстве относительно оси вращения. Мерой инертности при вращательном движении служит величина, называемая моментом инерции тела относительно оси вращения.
Момент инерции материальной точки относительно оси вращения – произведение массы этой точки на квадрат расстояния от оси :
Момент инерции тела относительно оси вращения – сумма моментов инерции материальных точек, из которых состоит это тело :
(5.4)
В общем случае, если тело сплошное и представляет собой совокупность точек с малыми массами dm , момент инерции определяется интегрированием:
, (5.5)
где r – расстояние от оси вращения до элемента массой dm .
Если тело однородно и его плотность ρ = m /V , то момент инерции тела
(5.6)
Момент инерции тела зависит от того, относительно какой оси оно вращается и как распределена масса тела по объему.
Наиболее просто определяется момент инерции тел, имеющих правильную геометрическую форму и равномерное распределение массы по объему.
Момент инерции однородного стержня относительно оси, проходящей через центр инерции и перпендикулярной стержню,
Момент инерции однородного цилиндра относительно оси, перпендикулярной его основанию и проходящей через центр инерции,
(5.8)
Момент инерции тонкостенного цилиндра или обруча относительно оси, перпендикулярной плоскости его основания и проходящей через его центр,
Момент инерции шара относительно диаметра
(5.10)
Определим момент инерции диска относительно оси, проходящей через центр инерции и перпендикулярной плоскости вращения. Пусть масса диска – m , а его радиус – R .
Площадь кольца (рисунок 5.2), заключенного между r и , равна .
Рисунок 5.2 – К выводу момента инерции диска
Площадь диска . При постоянной толщине кольца,
При постоянной толщине кольца,
откуда или .
Тогда момент инерции диска,
Для наглядности на рисунке 5.3 изображены однородные твердые тела различной формы и указаны моменты инерции этих тел относительно оси, проходящей через центр масс.
Рисунок 5.3 – Моменты инерции I C некоторых однородных твердых тел.
Теорема Штейнера
Приведенные выше формулы для моментов инерции тел даны при условии, что ось вращения проходит через центр инерции. Чтобы определить моменты инерции тела относительно произвольной оси, следует воспользоваться теоремой Штейнера : момент инерции тела относительно произвольной оси вращения равен сумме момента инерции J 0 относительно оси, параллельной данной и проходящей через центр инерции тела, и величины md 2:
(5.12)
где m – масса тела, d – расстояние от центра масс до выбранной оси вращения. Единица момента инерции – килограмм-метр в квадрате (кг . м 2).
м 2).
Так, момент инерции однородного стержня длиной l относительно оси, проходящей через его конец, по теореме Штейнера равен
Относительно неподвижной оси («осевой момент инерции») называется величина J a , равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
- m i – масса i -й точки,
- r i – расстояние от i -й точки до оси.
Осевой момент инерции тела J a является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении .
Если тело однородно, то есть его плотность всюду одинакова, то
Теорема Гюйгенса-Штейнера
Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы , формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J c относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:
где – полная масса тела.
Например, момент инерции стержня относительно оси, проходящей через его конец, равен:
Осевые моменты инерции некоторых тел
Вывод формул
Тонкостенный цилиндр (кольцо, обруч)
Вывод формулы
Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобъём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJ i . Тогда
Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду
Толстостенный цилиндр (кольцо, обруч)
Вывод формулы
Пусть имеется однородное кольцо с внешним радиусом R , внутренним радиусом R 1 , толщиной h и плотностью ρ. Разобьём его на тонкие кольца толщиной dr . Масса и момент инерции тонкого кольца радиуса r составит
Момент инерции толстого кольца найдём как интеграл
Поскольку объём и масса кольца равны
получаем окончательную формулу для момента инерции кольца
Однородный диск (сплошной цилиндр)
Вывод формулы
Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (R 1 = 0), получим формулу для момента инерции цилиндра (диска):
Сплошной конус
Вывод формулы
Разобьём конус на тонкие диски толщиной dh , перепендикулярные оси конуса.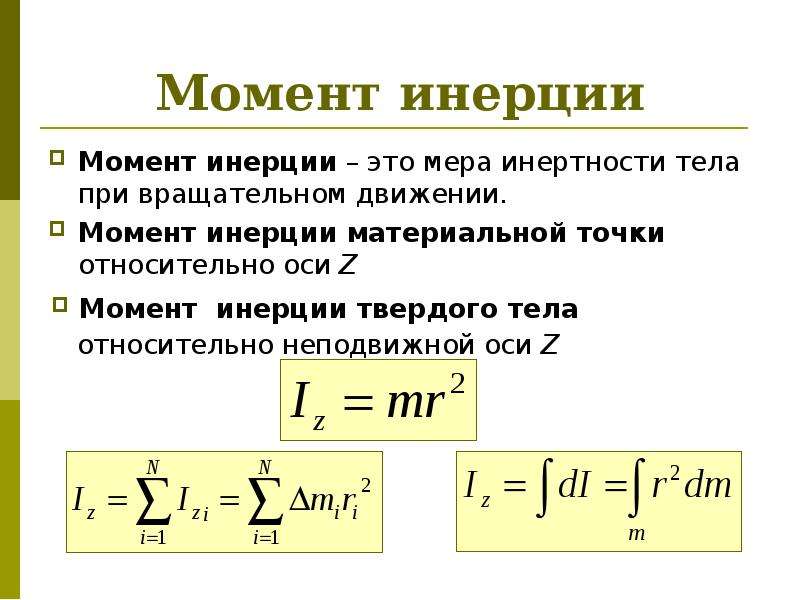 Радиус такого диска равен
Радиус такого диска равен
где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска. Масса и момент инерции такого диска составят
Интегрируя, получим
Сплошной однородный шар
Вывод формулы
Разобъём шар на тонкие диски толщиной dh , перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле
Масса и момент инерции такого диска составят
Момент инерции сферы найдём интегрированием:
Тонкостенная сфера
Вывод формулы
Для вывода воспользуемся формулой момента инерции однородного шара радиуса R :
Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину dR .
Тонкий стержень (ось проходит через центр)
Вывод формулы
Разобъём стержень на малые фрагменты длиной dr . Масса и момент инерции такого фрагмента равна
Интегрируя, получим
Тонкий стержень (ось проходит через конец)
Вывод формулы
При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние l /2. По теореме Штейнера новый момент инерции будет равен
По теореме Штейнера новый момент инерции будет равен
Безразмерные моменты инерции планет и их спутников
Большое значение для исследований внутренней структуры планет и их спутников имеют их безразмерные моменты инерции. Безразмерный момент инерции тела радиуса r и массы m равен отношению его момента инерции относительно оси вращения к моменту инерции материальной точки той же массы относительно неподвижной оси вращения, расположенной на расстоянии r (равному mr 2). Эта величина отражает распределение массы по глубине. Одним из методов её измерения у планет и спутников является определение допплеровского смещения радиосигнала, передаваемого АМС , пролетающей около данной планеты или спутника. Для тонкостенной сферы безразмерный момент инерции равен 2/3 (~0,67), для однородного шара – 0,4, и вообще тем меньше, чем большая масса тела сосредоточена у его центра. Например, у Луны безразмерный момент инерции близок к 0,4 (равен 0,391), поэтому предполагают, что она относительно однородна, её плотность с глубиной меняется мало. Безразмерный момент инерции Земли меньше, чем у однородного шара (равен 0,335), что является аргументом в пользу существования у неё плотного ядра.
Безразмерный момент инерции Земли меньше, чем у однородного шара (равен 0,335), что является аргументом в пользу существования у неё плотного ядра.
Центробежный момент инерции
Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются следующие величины:
где x , y и z – координаты малого элемента тела объёмом dV , плотностью ρ и массой dm .
Ось OX называется главной осью инерции тела , если центробежные моменты инерции J xy и J xz одновременно равны нулю. Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке O тела, называются главными моментами инерции тела .
Главные оси инерции, проходящие через центр масс тела, называются главными центральными осями инерции тела , а моменты инерции относительно этих осей – его главными центральными моментами инерции . Ось симметрии однородного тела всегда является одной из его главных центральных осей инерции.
Ось симметрии однородного тела всегда является одной из его главных центральных осей инерции.
Геометрический момент инерции
Геометрический момент инерции – геометрическая характеристика сечения вида
где – расстояние от центральной оси до любой элементарной площадки относительно нейтральной оси .
Геометрический момент инерции не связан с движением материала, он лишь отражает степень жесткости сечения. Используется для вычисления радиуса инерции, прогиба балки, подбора сечения балок, колонн и др.
Единица измерения СИ – м 4 . В строительных расчетах, литературе и сортаментах металлопроката в частности указывается в см 4 .
Из него выражается момент сопротивления сечения:
.| Геометрические моменты инерции некоторых фигур | |
|---|---|
| Прямоугольника высотой и шириной : | |
| Прямоугольного коробчатого сечения высотой и шириной по внешним контурам и , а по внутренним и соответственно | |
| Круга диаметром | |
Центральный момент инерции
Центральный момент инерции (или момент инерции относительно точки O) – это величина
Центральный момент инерции можно выразить через главные осевые или центробежные моменты инерции: .
Тензор инерции и эллипсоид инерции
Момент инерции тела относительно произвольной оси, проходящей через центр масс и имеющей направление, заданное единичным вектором , можно представить в виде квадратичной (билинейной) формы :
(1),где – тензор инерции . Матрица тензора инерции симметрична, имеет размеры и состоит из компонент центробежных моментов:
.
Выбором соответствующей системы координат матрица тензора инерции может быть приведена к диагональному виду. Для этого нужно решить задачу о собственных значениях для матрицы тензора :
,
где – ортогональная матрица перехода в собственный базис тензора инерции. В собственном базисе координатные оси направлены вдоль главных осей тензора инерции, а также совпадают с главными полуосями эллипсоида тензора инерции. Величины – главные моменты инерции. Выражение (1) в собственной системе координат имеет вид:
откуда получается уравнение
Пусть твёрдое тело вращается вокруг оси Z (рисунок 6). Его можно представить как неизменную с течением времени систему разных материальных точек m i , каждая из которых движется по окружности радиусом r i , лежащей в плоскости, перпендикулярной оси Z. Угловые скорости всех материальных точек одинаковы. Моментом инерции тела относительно оси Z называется величина:
Его можно представить как неизменную с течением времени систему разных материальных точек m i , каждая из которых движется по окружности радиусом r i , лежащей в плоскости, перпендикулярной оси Z. Угловые скорости всех материальных точек одинаковы. Моментом инерции тела относительно оси Z называется величина:
где – момент инерции отдельной материальной точки относительно оси ОZ. Из определения вытекает, что момент инерции – аддитивная величина , т. е. момент инерции тела, состоящего из отдельных частей, равен сумме моментов инерции частей.
Рисунок 6
Очевидно, [I ] = кг×м 2 . Важность понятия момента инерции выражается в трёх формулах:
; ; .
Первая из них выражает момент импульса тела, которое вращается вокруг неподвижной оси Z (полезно эту формулу сравнить с выражением для импульса тела P = mV c , где V c – скорость центра масс). Вторая формула носит название основного уравнения динамики вращательного движения тела вокруг неподвижной оси, т. е., иначе говоря, второго закона Ньютона для вращательного движения (сравним с законом движения центра масс: ). Третья формула выражает кинетическую энергию тела, вращающегося вокруг неподвижной оси (сравним с выражением для кинетической энергии частицы ). Сравнение формул позволяет сделать вывод о том, что момент инерции во вращательном движении играет роль, аналогичную массе в том смысле, что чем больше момент инерции тела, тем меньше угловое ускорение при прочих равных условиях оно приобретает (тело, образно говоря, труднее раскрутить). Реально вычисление моментов инерции сводится к вычислению тройного интеграла и может быть произведено лишь для ограниченного числа симметричных тел и лишь для осей симметрии. Количество осей, вокруг которых может вращаться тело, бесконечно велико. Среди всех осей выделяется та, которая проходит через замечательную точку тела – центр масс (точку, для описания движения которой достаточно представить, что вся масса системы сосредоточена в центре масс и к этой точке приложена сила, равная сумме всех сил).
е., иначе говоря, второго закона Ньютона для вращательного движения (сравним с законом движения центра масс: ). Третья формула выражает кинетическую энергию тела, вращающегося вокруг неподвижной оси (сравним с выражением для кинетической энергии частицы ). Сравнение формул позволяет сделать вывод о том, что момент инерции во вращательном движении играет роль, аналогичную массе в том смысле, что чем больше момент инерции тела, тем меньше угловое ускорение при прочих равных условиях оно приобретает (тело, образно говоря, труднее раскрутить). Реально вычисление моментов инерции сводится к вычислению тройного интеграла и может быть произведено лишь для ограниченного числа симметричных тел и лишь для осей симметрии. Количество осей, вокруг которых может вращаться тело, бесконечно велико. Среди всех осей выделяется та, которая проходит через замечательную точку тела – центр масс (точку, для описания движения которой достаточно представить, что вся масса системы сосредоточена в центре масс и к этой точке приложена сила, равная сумме всех сил). Но осей, проходящих через центр масс, также бесконечно много. Оказывается, что для любого твёрдого тела произвольной формы существуют три взаимно перпендикулярных оси С х, С у, С z , называемые осями свободного вращения , обладающие замечательным свойством: если тело закрутить вокруг любой из этих осей и подбросить вверх, то при последующем движении тела ось останется параллельной самой себе, т.е. не будет кувыркаться. Закручивание вокруг любой другой оси этим свойством не обладает. Значение моментов инерции типичных тел относительно указанных осей приведено ниже. Если ось проходит через центр масс, но составляет углы a, b, g с осями С х, С у, С z соответственно, то момент инерции относительно такой оси равен
Но осей, проходящих через центр масс, также бесконечно много. Оказывается, что для любого твёрдого тела произвольной формы существуют три взаимно перпендикулярных оси С х, С у, С z , называемые осями свободного вращения , обладающие замечательным свойством: если тело закрутить вокруг любой из этих осей и подбросить вверх, то при последующем движении тела ось останется параллельной самой себе, т.е. не будет кувыркаться. Закручивание вокруг любой другой оси этим свойством не обладает. Значение моментов инерции типичных тел относительно указанных осей приведено ниже. Если ось проходит через центр масс, но составляет углы a, b, g с осями С х, С у, С z соответственно, то момент инерции относительно такой оси равен
I c = I cx cos 2 a + I cy cos 2 b + I cz cos 2 g (*)
Рассмотрим кратко вычисление момента инерции для простейших тел.
1. Момент инерции длинного тонкого однородного стержня относительно оси, проходящей через центр масс стержня и ему перпендикулярной.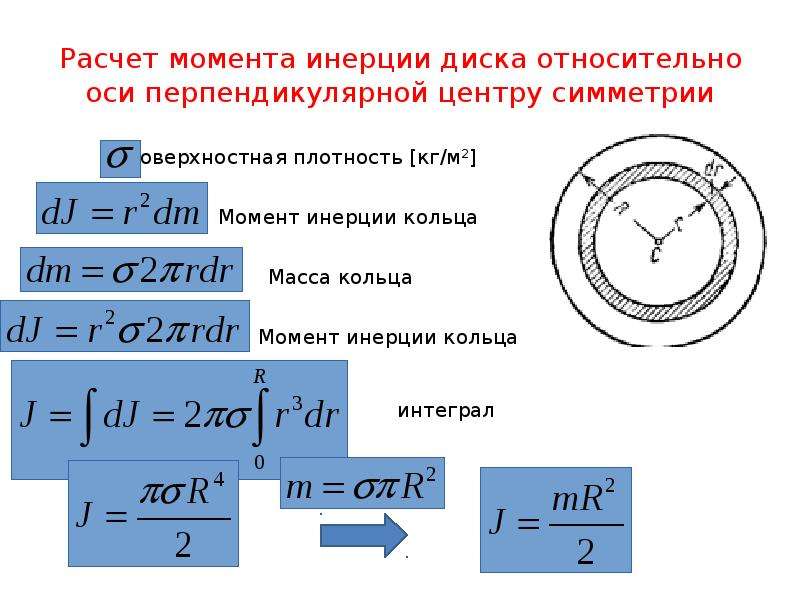
Пусть т – масса стержня, l – его длина.
,
Индекс «с » у момента инерции I c означает, что это момент инерции относительно оси, проходящий через точку центра масс (центр симметрии тела), C(0,0,0).
2. Момент инерции тонкой прямоугольной пластинки.
; ;
3. Момент инерции прямоугольного параллелепипеда.
, т. С(0,0,0)
4. Момент инерции тонкого кольца.
;
, т. С(0,0,0)
5. Момент инерции тонкого диска.
В силу симметрии
; ;
6. Момент инерции сплошного цилиндра.
;
В силу симметрии:
7. Момент инерции сплошного шара.
, т. С(0,0,0)
8. Момент инерции сплошного конуса.
, т. С(0,0,0)
где R – радиус основания, h – высота конуса.
Напомним, что cos 2 a + cos 2 b + cos 2 g = 1. 2$
2$
Момент инерции тела – Справочник химика 21
Пример 3.3. Рассчитать частоту собственных колебаний балки см. (рис. 3.11, а), состоящей из двух швеллеров № 12 с суммарным моментом инерции сечения У = = 608 см закрепленное тело — плои(адка с электродвигателем (Пцс = 980 об/мин 102 с 1) общей массой т = 160 кг момент инерции тела Jx = 3,5 кг-м /1 = 2 м 2 = к = 0,5 м. [c.60]Массы и моменты инерции тел [c.80]
Момент инерции тела представляет собой сумму моментов инерции материальных точек, составляющих данное тело, и определяется по уравнению [c.66]
Заметьте, что момент инерции тела, являющийся мерой инертности вращающегося твердого тела, зависит не только от его массы, но и от распределения массы в теле относительно оси вращения. Другими словами, размеры и форма тела оказывают значительное влияние на его вращательное движение.
 [c.193]
[c.193]Величина момента внешней силы (вращающего момента), приложенного к телу, вращающемуся вокруг неподвижной оси, равна моменту инерции тела относительно этой оси, умноженному на величину углового ускорения тела. [c.193]
Момент инерции тела [c.193]
Для решения практических задач о вращении твердых тел нужно знать, в каких единицах измеряется момент инерции тела, и уметь определить его численное значение. В соответствии с определением момента инерции тела и формулой [c.193]
Вычисление момента инерции произвольных тел представляет достаточно сложную задачу. Сравнительно просто вычислить моменты инерции тел вращения. Приведем без доказательства значение моментов инерции тел, эскизы которых показаны на рис. 121. [c.193]
Ус — момент инерции тела относительно оси, проходящей через центр тяжести (относительно центральной оси) [c.195]
Разность величин движущего вращающего момента и момента сил сопротивления представляет собой результирующий момент внешних сил, который в соответствии с основным уравнением динамики вращающегося тела равен произведению момента инерции тела на величину углового ускорения. Теперь нетрудно сделать практические выводы о вращении тела в зависимости от величины действующих моментов сил. [c.196]
Теперь нетрудно сделать практические выводы о вращении тела в зависимости от величины действующих моментов сил. [c.196]
Что такое момент инерции тела и в каких единицах он измеряется [c.199]
В табл. 23 даны формулы для вычисления моментов инерции тел, которые встречаются при расчете центрифуг. [c.263]
У — относительный момент инерции тела [c.6]
Примечание. и — моменты инерции тела относительно главных осей инерции тела соответственно хх а гг М — масса тела р — плотность материала I — расстояние от центра инерции С тела до его нижнего основания. [c.350]
Основной характеристикой всякого тела по отнощению к его способности совершать вращательные движения является момент инерции тела. Момент инерции жесткого ротатора, представляющего две материальные точки с массами тл и тв, находящиеся на неизменном [c.211]
Массовый момент инерции тела относительно оси — мера инертности тела во вращательном движении вокруг этой оси. Массовый момент инерции тела вычисляют по формуле [c.321]
Массовый момент инерции тела вычисляют по формуле [c.321]
Зависимость периода гармонических колебаний от параметров системы играет важную роль во многих технических и физических измерениях, например в определении моментов инерции тел, в измерении магнитных полей. Если известен момент инерции магнита, то из результатов исследования его колебаний в магнитном поле можно найти в отдельности произведение магнитного момента на поле и отношение магнитного момента к полю и вычислить по этим данным магнитное поле. Этим способом Гаусс определял напряжение магнитного поля Земли. [c.66]
Здесь в свою очередь А, В, С представляют собой моменты инерции тел относительно осей координат, определяемые из соотношений [c.560]
Проекции полного момента количества движения Ь выражаются через моменты инерции и центробежные моменты инерции тела [c.561]
В табл. 66 даны моменты инерции тел, встречающихся при проектировании центрифуг, сепараторов, пальцеврлх мельниц и подобных машин. [c.635]
66 даны моменты инерции тел, встречающихся при проектировании центрифуг, сепараторов, пальцеврлх мельниц и подобных машин. [c.635]
Величина I = тг называется моментом инерции. Урав1 ние (6.5) относится к материальной точке. Момент инерции тела представляе умму моментов материальных точек, составляющих данное тело [c.296]
Такие расчеты можно производить и в более сложных случаях. Напрнмер, мы можем изучить, как много энергии можгга ввести во вращающееся тело. В линейном случае линейный момент р связан с линейной скоростью v через p = mv в случае вращения угловой момент J связан с угловой скоростью и через J = Iw, где /—момент инерции тела. (Необходимо помнить об аналогичных ролях т и 1, V и (О II р и / в линейном случае и в случае вращения, по- [c.420]
Для большинства тел, применяемых в машиностроении соленчатых валов и шатунов двигателей внутреннего сгорания, роторов паровых и газовых турбин, винтов самолетов, хеталей часового механизма и многих других — математи- еские методы определения моментов инерции малопригодны, главным образом потому, что они оказываются недо- таточно точными. Поэтому моменты инерции тел обычно определяют опытным путем. [c.195]
Поэтому моменты инерции тел обычно определяют опытным путем. [c.195]
Здесь величина со вынесена за знак суммы как общий множитель. Величина 2т г нам уже известна. Она равна моменту инерции тела J Ът1гЬ Поэтому величина кинетической энергии вращающегося твердого тела равна [c.221]
Величина 1=тг называется моментом инерции. Уравнение (6.5) относится к материальной точке. Момент инерции тела представляет сумму моментов инерции материальных точек, составляющих данное телЪ [c.298]
Момент инерции тела относительно оси Х1Х1, не проходящей через центр инерции [c.350]
Наилучшее направление силы 2 во втором секторе определили с использованием математической модели, решив задачу на минимум суммарного момента поднимателей тела, выразив его как функцию направления силы 2. При этом мы учли еще один способ снижения суммарного момента поднимателей — за счет смещения точки пересечения сил 2 и 3 в сторону от прямой N (рис. 6,6). Правда, при этом векторы 1 и 1 образуют пару сил и сообщают телу вращательный момент, но, благодаря краткости его действия (при высокой частоте шагов) и значительному моменту инерции тела, эта пара сил не успевает вызвать существенного поворота тела. Повышению момента инерции тела способствует длинный хвост. Например, как показали наши измерения, момент инерции кавказской агамы без хвоста в 4 раза меньше, чем с хвостом. Отсюда ясно, что длинный хвост — важный элемент локомоторной адаптации низших тетрапод. [c.19]
6,6). Правда, при этом векторы 1 и 1 образуют пару сил и сообщают телу вращательный момент, но, благодаря краткости его действия (при высокой частоте шагов) и значительному моменту инерции тела, эта пара сил не успевает вызвать существенного поворота тела. Повышению момента инерции тела способствует длинный хвост. Например, как показали наши измерения, момент инерции кавказской агамы без хвоста в 4 раза меньше, чем с хвостом. Отсюда ясно, что длинный хвост — важный элемент локомоторной адаптации низших тетрапод. [c.19]
Лекция 5. Моменты инерции поперечного сечения
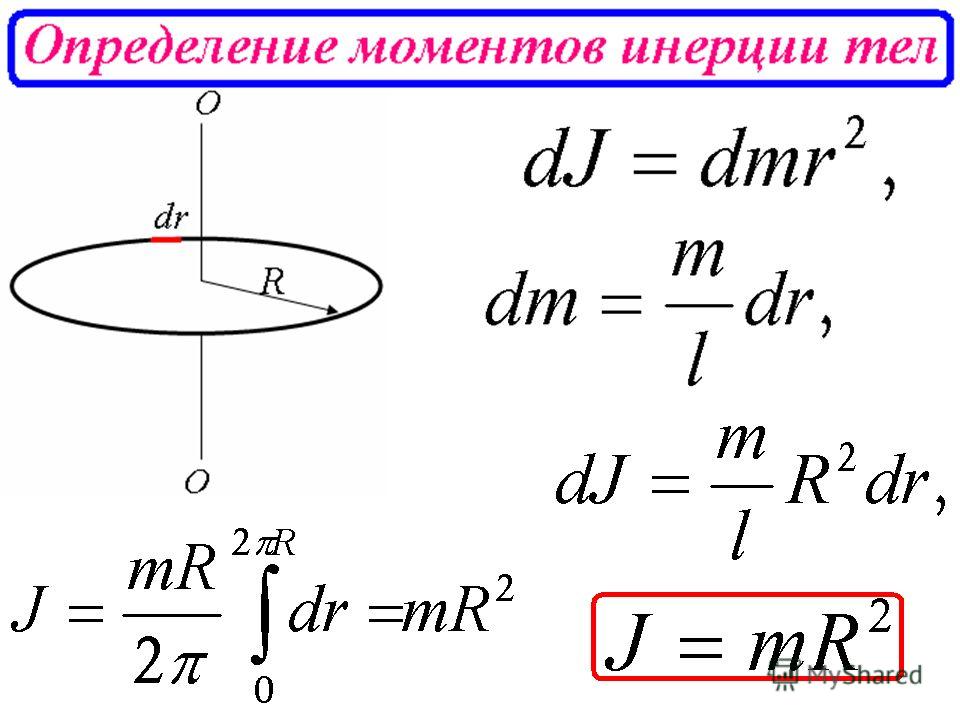
момент инерции сечения – это сумма всех элементарно малых площадей dF, составляющих это сечение, умноженных на квадрат расстояния от этих площадей до выбранной оси:
I = ∑ri2dFi =∫r2dF (1.1)
В принципе и определение и формула, его описывающая, не сложные и запомнить их намного легче, чем вникнуть в суть. Но все-таки попробуем разобраться, что же такое момент инерции и откуда он взялся.
Но все-таки попробуем разобраться, что же такое момент инерции и откуда он взялся.
Понятие момент инерции пришло в сопромат и строительную механику из другого раздела физики, изучающего кинематику движения, в частности вращательное движение. Но все равно начнем издалека.
Я точно не знаю, упало ли Исааку Ньютону на голову яблоко, упало оно рядом, или вообще не падало, теория вероятности допускает все эти варианты (к тому же в этом яблоке слишком много от библейской легенды о древе познания), однако я уверен, что Ньютон был наблюдательным человеком, способным делать выводы из своих наблюдений. Так наблюдательность и воображение позволили Ньютону сформулировать основной закон динамики (второй закон Ньютона), согласно которому масса тела m, умноженная на ускорение a, равна действующей силе Q (вообще-то более привычным для силы является обозначение F, но так как дальше мы будем иметь дело с площадью, которая также часто обозначается как F, то я использую для внешней силы, рассматриваемой в теоретической механике как сосредоточенная нагрузка, обозначение Q, сути дела это не меняет):
Q = ma (1. 2)
2)
По мне величие Ньютона именно в простоте и понятности данного определения. А еще, если учесть, что при равноускоренном движении ускорение а равно отношению приращения скорости ΔV к периоду времени Δt, за который скорость изменилась:
a = Δv/Δt = (v – vо)/t (1.3.1)
при Vо = 0 a = v/t (1.3.2)
то можно определить основные параметры движения, такие как расстояние, скорость, время и даже импульс р, характеризующий количество движения:
p = mv (1.4)
Например, яблоко, падающее с разной высоты под действием только силы тяжести, будет падать до земли разное время, иметь разную скорость в момент приземления и соответственно разный импульс. Другими словами, яблоко, падающее с бóльшей высоты, будет дольше лететь и сильнее треснет по лбу незадачливого наблюдателя. И все это Ньютон свел к простой и понятной формуле.
А еще Ньютон сформулировал закон инерции (первый закон Ньютона): если ускорение а = 0, то в инерциальной системе отсчета невозможно определить, находится ли наблюдаемое тело, на которое не действуют внешние силы, в состоянии покоя или движется прямолинейно с постоянной скоростью. Это свойство материальных тел сохранять свою скорость, пусть даже и нулевую, называется инертностью. Мерой инертности является инерционная масса тела. Иногда инерционная масса называется инертной, но сути дела это не меняет. Считается, что инерционная масса равна гравитационной массе и потому часто не уточняется, какая именно масса имеется в виду, а упоминается просто масса тела.
Не менее важным и значимым является и третий закон Ньютона, согласно которому сила действия равна силе противодействия, если силы направлены по одной прямой, но при этом в противоположные стороны. Не смотря, на кажущуюся простоту, и этот вывод Ньютона гениален и значение этого закона трудно переоценить. Об одном из применений этого закона чуть ниже.
Об одном из применений этого закона чуть ниже.
Однако данные положения справедливы только для тел, движущихся поступательно, т.е. по прямолинейной траектории и при этом все материальные точки таких тел двигаются с одинаковой скоростью или одинаковым ускорением. При криволинейном движении и в частности при вращательном движении, например, когда тело вращается вокруг своей оси симметрии, материальные точки такого тела перемещаются в пространстве с одинаковой угловой скоростью w, но при этом линейная скорость v у различных точек будет разная и эта линейная скорость прямо пропорциональна расстоянию r от оси вращения до этой точки:
v = wr (1.5)
при этом угловая скорость равна отношению приращения угла поворота Δφ к периоду времени Δt, за который угол поворота изменился:
w = Δφ/Δt = (φ – φо)/t (1.6.1)
при φо = 0 w = φ/t (1. 7.2)
7.2)
соответственно нормальное ускорение аn при вращательном движении равно:
an = v2/r = w2r (1.8)
И получается, что для вращательного движения мы не можем прямо использовать формулу (1.2), так как при вращательном движении одного только значения массы тела недостаточно, требуется еще знать распределение этой массы в теле. Получается, что чем ближе материальные точки тела к оси вращения, тем меньшую силу требуется приложить, чтобы заставить тело вращаться и наоборот, чем дальше материальные точки тела от оси вращения, тем большую силу нужно приложить, чтобы заставить тело вращаться (в данном случае речь идет о приложении силы в одной и той же точке). К тому же при вращении тела более удобно рассматривать не действующую силу, а вращающий момент, так как при вращательном движении точка приложения силы также имеет большое значение.
Поразительные свойства момента нам известны со времен Архимеда и если применить понятие момента к вращательному движению, то значение момента М будет тем больше, чем больше расстояние r от оси вращения до точки приложения силы F (в строительной механике внешняя сила часто обозначается как Р или Q):
М = Qr (1. 9)
9)
Из этой также не очень сложной формулы выходит, что если сила будет приложена по оси вращения, то никакого вращения не будет, так как r = 0, а если сила будет приложена на максимальном удалении от оси вращения, то и значение момента будет максимальным. А если мы подставим в формулу (1.9) значение силы из формулы (1.2) и значение нормального ускорения и формулы (1.8), то получим следующее уравнение:
М = mw2r·r = mw2r2 (1.10)
В частном случае когда тело является материальной точкой, имеющей размеры намного меньше, чем расстояние от этой точки до оси вращения, уравнение (1.10) применимо в чистом виде. Однако для тела, вращающегося вокруг одной из своих осей симметрии, расстояние от каждой материальной точки составляющей данное тело, всегда меньше одного из геометрических размеров тела и потому распределение массы тела имеет большое значение, в этом случае требуется учесть эти расстояния отдельно для каждой точки:
M = ∑ri2w2mi (1. 11.1)
11.1)
Мс= w2∫r2dm (1.11.2) – при вращении тела вокруг оси симметрии
И тогда получается, что согласно третьему закону Ньютона в ответ на действие вращающего момента будет возникать так называемый момент инерции I. При этом значения вращающего момента и момента инерции будут равны, а сами моменты направлены в противоположные стороны. При постоянной угловой скорости вращения, например w = 1, основными величинами, характеризующими вращающий момент или момент инерции будут масса материальных точек, составляющих тело, и расстояния от этих точек до оси вращения. В итоге формула момента инерции примет следующий вид:
[- М] = I = ∑ri2mi (1.12.1)
Ic = ∫r2dm (1.11.2) – при вращении тела вокруг оси симметрии
где I – общепринятое обозначение момента инерции, Ic – обозначение осевого момента инерции тела, кг/м2.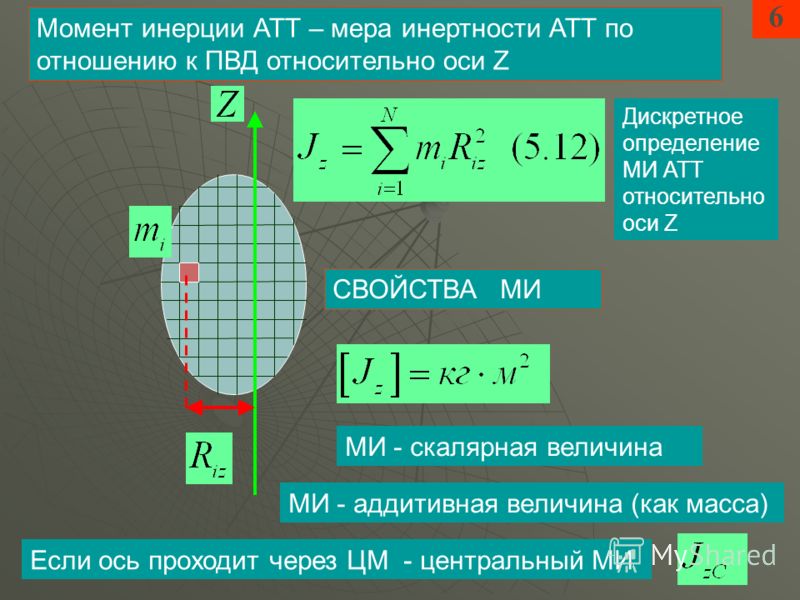 Для однородного тела, имеющего одинаковую плотность ρ по всему объему тела V формулу осевого момента инерции тела можно записать так:
Для однородного тела, имеющего одинаковую плотность ρ по всему объему тела V формулу осевого момента инерции тела можно записать так:
Ic = ∫ρr2dV (1.13)
Таким образом момент инерции является мерой инертности тела при вращательном движении, подобно тому как масса является мерой инертности тела при поступательном прямолинейном движении.
Все круг замкнулся. И тут может возникнуть вопрос, какое отношение все эти законы динамики и кинематики имеют к расчету статических строительных конструкций? Оказывается, что ни на есть самое прямое и непосредственное. Во-первых потому, что все эти формулы выводились физиками и математиками в те далекие времена, когда таких дисциплин, как “Теоретическая механика” или “Теория сопротивления материалов” попросту не существовало. А во-вторых потому, что весь расчет строительных конструкций и построен на основе указанных законов и формулировок и пока ни кем не опровергнутом утвержении о равенстве гравитационной и инертой масс. Вот только в теории сопротивления материалов все еще проще, как ни парадоксально это звучит.
Вот только в теории сопротивления материалов все еще проще, как ни парадоксально это звучит.
А проще потому, что при решении определенных задач может рассматриваться не все тело, а только его поперечное сечение, а при необходимости несколько поперечных сечений. Но в этих сечениях действуют такие же физические силы, правда имеющие несколько иную природу. Таким образом, если рассматривать некое тело, длина которого постоянна, а само тело является однородным, то если не учитывать постоянные параметры – длину и плотность (l = const, ρ = const) – мы получим модель поперечного сечения. Для такого поперечного сечения с математической точки зрения будет справедливым уравнение:
Iр = ∫r2dF (2.1) → (1.1)
где Ip – полярный момент инерции поперечного сечения, м4. В итоге мы получили формулу, с которой начинали (а вот стало ли понятнее, что такое момент инерции сечения, не знаю).
Так как в теории сопротивления материалов часто рассматриваются прямоугольные сечения, да и прямоугольная система координат более удобна, то при решении задач обычно рассматриваются два осевых момента инерции поперечного сечения:
Iz = ∫y2dF (2.2.1)
Iy = ∫z2dF (2.2.2)
Рисунок 1. Значения координат при определении осевых моментов инерции.
Тут может возникнуть вопрос, почему использованы оси z и у, а не более привычные х и у? Так уж сложилось, что определение усилий в поперечном сечении и подбор сечения, выдерживающего действующие напряжения, равные приложенным усилиям – две разные задачи. Первую задачу – определение усилий – решает строительная механика, вторую задачу – подбор сечения – теория сопротивления материалов. При этом в строительной механике рассматривается при решении простых задач достаточно часто стержень (для прямолинейных конструкций), имеющий определенную длину l, а высота и ширина сечения не учитываются, при этом считается, что ось х как раз и проходит через центры тяжести всех поперечных сечений и таким образом при построении эпюр (порой достаточно сложных) длина l как раз и откладывается по оси х, а по оси у откладываются значения эпюр.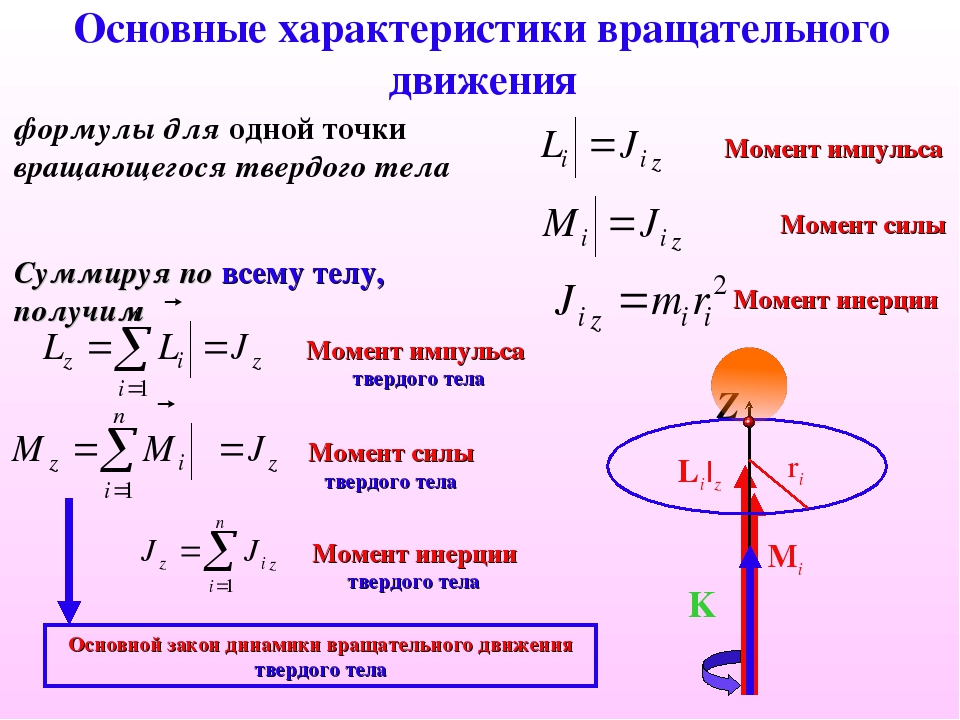
В то же время теория сопротивления материалов рассматривает именно поперечное сечение, для которого важны ширина и высота, а длина не учитывается. Само собой при решении задач теории сопротивления материалов, также порой достаточно сложных используются все те же привычные оси х и у. Мне такое положение дел кажется не совсем правильным, так как не смотря на разницу, это все же смежные задачи и потому будет более целесообразным использование единых осей для рассчитываемой конструкции.
Значение полярного момента инерции в прямоугольной системе координат будет:
Iр = ∫r2dF = ∫y2dF + ∫z2dF (2.3)
Так как в прямоугольной системе координат радиус – это гипотенуза прямоугольного треугольника, а как известно квадрат гипотенузы равен сумме квадратов катетов. А еще существует понятие центробежного момента инерции поперечного сечения:
Ixz = ∫xzdF (2. 4)
4)
Среди осей прямоугольной системы координат, проходящих через центр тяжести поперечного сечения, есть две взаимно-перпендикулярные оси, относительно которых осевые моменты инерции принимают максимальное и минимальное значение, при этом центробежный момент инерции сечения
Izy = 0. Такие оси называют главными центральными осями поперечного сечения, а моменты инерции относительно таких осей – главными центральными моментами инерцииКогда в теории сопротивления материалов речь заходит о моментах инерции, то как правило в виду имеются именно главные центральные моменты инерции поперечного сечения. Для квадратных, прямоугольных, круглых сечений главные оси будут совпадать с осями симметрии. Моменты инерции поперечного сечения также называют геометрическими моментами инерции или моментами инерции площади, но суть от этого не изменяется.
В принципе самому определять значения главных центральных моментов инерции для поперечных сечений наиболее распространенных геометрических форм – квадрата, прямоугольника, круга, трубы, треугольника и некоторых других – большой необходимости нет. Такие моменты инерции давно определены и широко известны. А при расчете осевых моментов инерции для сечений сложной геометрической формы справедлива теорема Гюйгенса-Штейнера:
Такие моменты инерции давно определены и широко известны. А при расчете осевых моментов инерции для сечений сложной геометрической формы справедлива теорема Гюйгенса-Штейнера:
I = Ic + r2F (2.5)
таким образом, если известны площади и центры тяжести простых геометрических фигур, составляющих сложное сечение, то определить значение осевого момента инерции всего сечения не составит труда. А для того, чтобы определить центр тяжести сложного сечения, используются статические моменты поперечного сечения. Более подробно статические моменты рассматриваются в другой статье, здесь лишь добавлю. Физический смысл статического момента следующий: статический момент тела – это сумма моментов для материальных точек, составляющих тело, относительно некоторой точки (полярный статический момент) или относительно оси (осевой статический момент), а так как момент – это произведение силы на плечо (1.9), то и определяется статический момент тела соответственно:
S = ∑M = ∑rimi = ∫rdm (2. 6)
6)
и тогда полярный статический момент поперечного сечения будет:
Sр = ∫rdF (2.7)
Как видим, определение статического момента сходно с определением момента инерции. Но есть и принципиальная разница. Статический момент потому и называется статическим, что для тела, на которое действует сила тяжести, статический момент равен нулю относительно центра тяжести. Другими словами такое тело находится в состоянии равновесия, если опора приложена к центру тяжести тела. А согласно первому закону Ньютона такое тело или находится в состоянии покоя или движется с постоянной скоростью, т.е. ускорение = 0. А еще с чисто математической точки зрения статический момент может быть равен нулю по той простой причине, что при определении статического момента необходимо учитывать направление действия момента.
Например относительно осей координат, проходящих через центр тяжести прямоугольника, площади верхней части и нижней части прямоугольника будут положительными так как символизируют силу тяжести, действующую в одном направлении.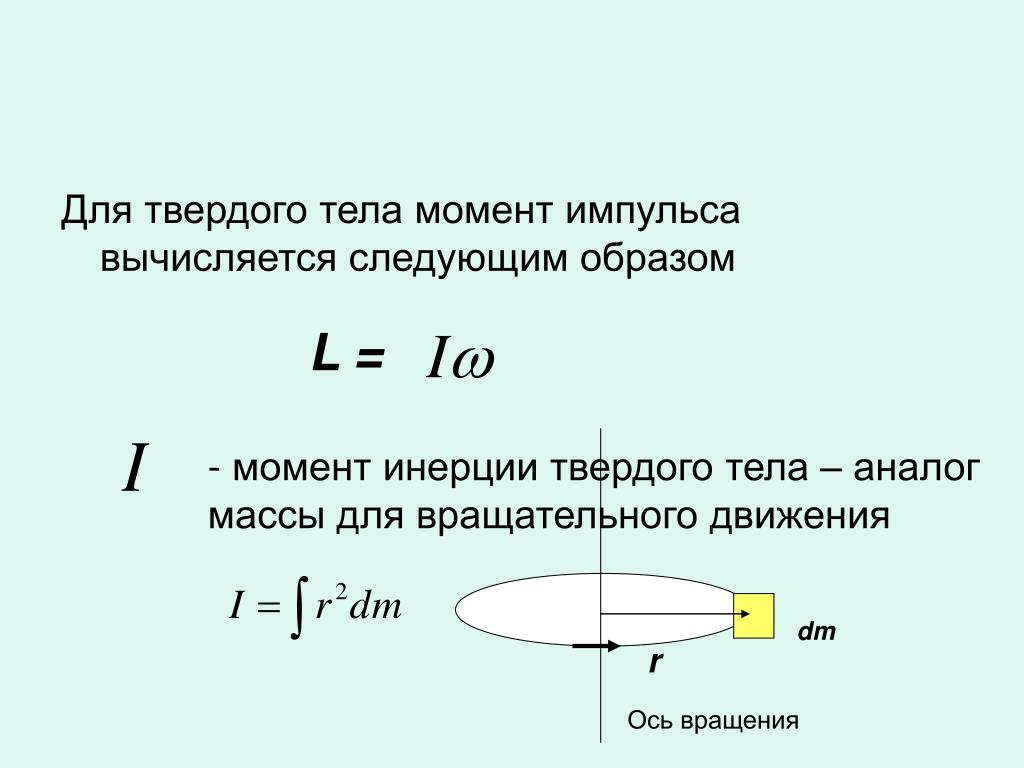 При этом расстояние от оси до центра тяжести можно рассматривать как положительное (условно: момент от силы тяжести верхней части прямоугольника пытается вращать сечение по часовой стрелке), а до центра тяжести нижней части – как отрицательное (условно: момент от силы тяжести нижней части прямоугольника пытается вращать сечение против часовой стрелки). А так как такие площади численно равны и равны расстояния от центров тяжести верхней части прямоугольника и нижней части прямоугольника, то сумма действующих моментов и составит искомый 0.
При этом расстояние от оси до центра тяжести можно рассматривать как положительное (условно: момент от силы тяжести верхней части прямоугольника пытается вращать сечение по часовой стрелке), а до центра тяжести нижней части – как отрицательное (условно: момент от силы тяжести нижней части прямоугольника пытается вращать сечение против часовой стрелки). А так как такие площади численно равны и равны расстояния от центров тяжести верхней части прямоугольника и нижней части прямоугольника, то сумма действующих моментов и составит искомый 0.
Sz = ∫ydF = 0 (2.8)
А еще этот великий ноль позволяет определять опорные реакции строительных конструкций. Если рассматривать строительную конструкцию, к которой приложена например сосредоточенная нагрузка Q в некоторой точке, то такую строительную конструкцию можно рассматривать, как тело с центром тяжести в точке приложения силы, а опорные реакции в этом случае рассматриваются, как силы приложенные в точках опор. Таким образом зная значение сосредоточенной нагрузки Q и расстояния от точки приложения нагрузки до опор строительной конструкции, можно определить опорные реакции.
Таким образом зная значение сосредоточенной нагрузки Q и расстояния от точки приложения нагрузки до опор строительной конструкции, можно определить опорные реакции.
Например для шарнирно опертой балки на двух опорах значение опорных реакций будет пропорционально расстоянию до точки приложения силы, а сумма реакций опор будет равна приложенной нагрузке. Но как правило при определении опорных реакций поступают еще проще: за центр тяжести принимается одна из опор и тогда сумма моментов от приложенной нагрузки и от остальных опорных реакций все равно равна нулю. В этом случае момент от опорной реакции относительно которой составляется уравнение моментов, равен нулю, так как плечо действия силы = 0, а значит в сумме моментов остаются только две силы: приложенная нагрузка и неизвестная опорная реакция (для статически определимых конструкций).
Таким образом принципиальная разница между статическим моментом и моментом инерции в том, что статический момент характеризует сечение, которое сила тяжести как бы пытается сломать пополам относительно центра тяжести или оси симметрии, а момент инерции характеризует тело, все материальные точки которого перемещаются (или пытаются переместиться в одном направлении). Возможно, более наглядно представить себе эту разницу помогут следующие достаточно условные расчетные схемы для прямоугольного сечения:
Возможно, более наглядно представить себе эту разницу помогут следующие достаточно условные расчетные схемы для прямоугольного сечения:
Рисунок 2. Наглядная разница между статическим моментом и моментом инерции.
А теперь вернемся еще раз к кинематике движения. Если проводить аналогии между напряжениями, возникающими в поперечных сечениях строительных конструкций, и различными видами движения, то в центрально растягиваемых и центрально сжатых элементах возникают напряжения равномерные по всей площади сечения. Эти напряжения можно сравнить с действием некоторой силы на тело, при котором тело будет двигаться прямолинейно и поступательно. А самое интересное, это то, что поперечные сечения центрально-растянутых или центрально сжатых элементов действительно движутся, так как действующие напряжения вызывают деформации. И величину таких деформаций можно определить для любого поперечного сечения конструкции. Для этого достаточно знать значение действующих напряжений, длину элемента, площадь сечения и модуль упругости материала, из которого изготовлена конструкция.
У изгибаемых элементов поперечные сечения также не остаются на месте, а перемещаются, при этом перемещение поперечных сечений изгибаемых элементов подобно вращению некоего тела относительно некоторой оси. Как вы уже наверное догадались, момент инерции позволяет определить и угол наклона поперечного сечения и перемещение Δl для крайних точек сечения. Эти крайние точки для прямоугольного сечения находятся на расстоянии, равном половине высоты сечения (почему – достаточно подробно описано в статье “Основы сопромата. Определенение прогиба” ). А это в свою очередь позволяет определить прогиб конструкции.
А еще момент инерции позволяет определить момент сопротивления сечения. Для этого момент инерции нужно просто разделить на расстояние от центра тяжести сечения до наиболее удаленной точки сечения, для прямоугольного сечения на h/2. А так как исследуемые сечения не всегда симметричны, то значение момента сопротивления может быть разным для разных частей сечения.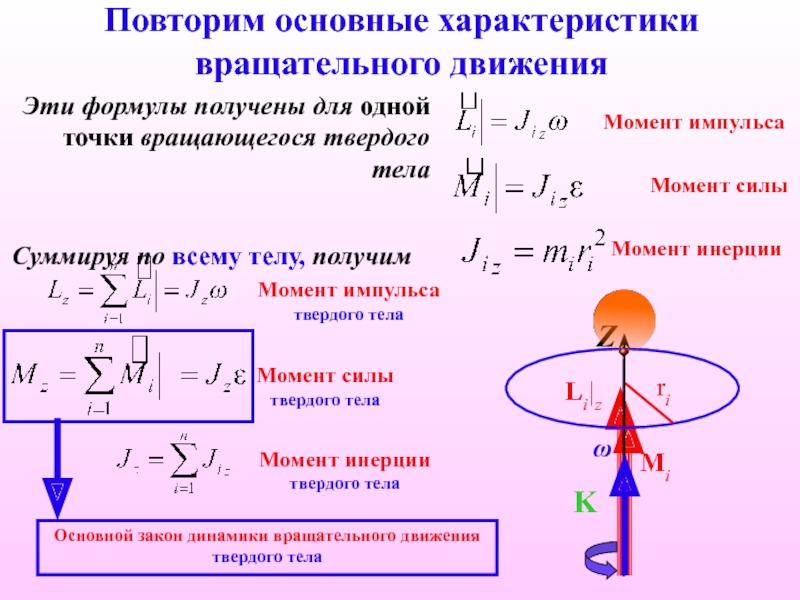
А началось все с банального яблока… хотя нет, начиналось все со слова.
Момент инерции тела и материальной точки. Формулы для цилиндра и стержня. Физический смысл величины
В школьном курсе физики большое внимание уделяется описанию кинематики и динамики поступательного движения тел в трехмерном пространстве. Но вращательное движение играет не менее важную роль в технике и природе. В данной статье рассмотрим, что понимают под моментом инерции тела при его вращении вокруг оси.
Динамика вращения
Прежде чем давать определение момента инерции тела, расскажем, для чего нужна эта величина и в каких уравнениях она появляется. В первую очередь, это главное уравнение динамики вращения – формула моментов. Записывается она так:
M = I*α.
Здесь M, α и I – это момент силы, ускорение угловое и инерции момент, соответственно. По сути, это уравнение можно назвать вторым ньютоновским законом для вращательного движения. Несложно догадаться, что величина I здесь играет ту же самую роль, что инерционная масса в случае поступательного движения.
Помимо приведенного уравнения, существует еще одна важная формула, которая применяется часто для решения задач на вращение тел – это закон сохранения момента импульса. Его, как правило, записывают в следующей удобной для практики форме:
I*ω = const.
Как видим, здесь инерции момент тоже является ключевой величиной, ω – это скорость угловая.
Момент инерции твердого тела
Теперь пришло время дать определение величине I. Сначала рассмотрим его для материальной точки. Ее моментом инерции называется произведение массы на квадрат расстояния до оси вращения. Если массу обозначить буквой m, а дистанцию до оси от точки буквой r, то формула для I запишется так:
I = m*r2.
Как видно, I выражается в кг*м2. Равенство для точки можно использовать для определения момента инерции тела относительно оси. В этом случае применяют следующее интегральное выражение:
I = ∫m(r2*dm).
Эта формула применяется для вычисления величин I абсолютно любых систем с разными геометрическими формами. Последнее равенство также используют при решении практических задач в следующем виде:
I = ∫V(ρ*r2*dV).
Где ρ – плотность вещества. Ниже в статье покажем, как использовать интегральное равенство для решения конкретных задач.
Величина I для цилиндра
Каждый школьник представляет себе фигуру “цилиндр”. По правде говоря, они бывают самыми разными (эллиптическими, гиперболическими, наклонными). Здесь рассмотрим самый простой случай. Это круговой прямой цилиндр, который ограничен цилиндрической поверхностью и двумя одинаковыми кругами. Ось вращения фигуры проходит через ее центр масс и через центры обоих оснований. Вычислим относительно нее инерции момент тела.
Запишем исходную формулу:
I = ∫V(ρ*r2*dV).
Чтобы ее применить, представим себе цилиндр в виде тонко нарезанных круглых одинаковых слоев. Обозначим их толщину dl, радиус фигуры равен R, а высота – L. Теперь каждый тонкий слой объемом pi*R2*dl разрежем на бесконечное множество колец, толщина каждого из которых равна dr. После выполнения всех описанных мысленных геометрических операций можно записать формулу для элементарного объема dV, то есть для объема одного кольца:
Обозначим их толщину dl, радиус фигуры равен R, а высота – L. Теперь каждый тонкий слой объемом pi*R2*dl разрежем на бесконечное множество колец, толщина каждого из которых равна dr. После выполнения всех описанных мысленных геометрических операций можно записать формулу для элементарного объема dV, то есть для объема одного кольца:
dV = 2*pi*r*dr*dl.
В результате этого представления исходное выражение для I преобразуется в формулу с двойным интегралом:
I = ∫L∫R(ρ*r2*2*pi*r*dr*dl) = 2*pi*ρ*L*R4/4 = M*R2/2.
Где буквой M обозначена масса всего цилиндра.
Таким образом, мы получили конечное выражение для инерции момента цилиндра. Как видно, он определяется только радиусом фигуры и ее массой и не зависит от длины (высоты). Последнее означает, что аналогичную формулу можно применять для определения величины I для диска любой толщины.
Величина I для стержня
Теперь применим формулу для определения момента инерции тонкого стержня. Принципиальным моментом здесь является тот факт, что его толщина должна быть намного меньше длины L. Массу стержня обозначим буквой M. Момент инерции рассчитаем для положения оси, которая проходит через центр масс тела и перпендикулярна ему.
Принципиальным моментом здесь является тот факт, что его толщина должна быть намного меньше длины L. Массу стержня обозначим буквой M. Момент инерции рассчитаем для положения оси, которая проходит через центр масс тела и перпендикулярна ему.
Начнем расчет все с той же формулы, что и в случае с цилиндром:
I = ∫V(ρ*r2*dV).
Мысленно разрежем весь стержень на тонкие слои. Обозначим площадь сечения каждого из них S, а его толщину – dl. Тогда получаем формулу для dV:
dV = S*dl.
Теперь можно вычислить инерции момент тела:
I = ∫-L/2+L/2(ρ*S*l2*dl).
Заметим, что каждый слой находится от оси вращения на расстоянии l, поэтому мы заменили букву r. Кроме того, обращаем внимание на пределы интегрирования, которые имеют такое значение потому, что ось проходит точно через середину стержня. В итоге получаем:
I = ∫-L/2+L/2(ρ*S*l2*dl) = ρ*S*l3/3|-L/2+L/2 = M*L2/12.
С помощью аналогичных рассуждений и вычислений можно показать, что если ось вращения проходит через какой-либо конец стержня, то его момент инерции будет в четыре раза больше, то есть:
I = M*L2/3.
Физический смысл величины
Выше мы уже сказали несколько слов о том, что означает момент инерции тела с физической точки зрения. Здесь остановимся несколько подробнее на этом вопросе.
Если внимательно посмотреть на формулу для I, то можно увидеть, что эта величина зависит не только от самой массы тела, но и от ее распределения, то есть от формы тела, а также от его положения относительно оси вращения.
Ярким примером являются обычная швабра или просто стержень. Каждый человек хоть раз в жизни раскручивал швабру вокруг оси, проходящей вдоль ее ручки или перпендикулярно ей. В первом случае легкого движения ладоней достаточно, чтобы придать угловое ускорение швабре, во втором же – приходится прилагать некоторую силу рук, чтобы раскрутить ее. Объяснить этот факт просто. В первом случае момент инерции практически равен нулю, во втором – он имеет некоторую конечную величину.
Объяснить этот факт просто. В первом случае момент инерции практически равен нулю, во втором – он имеет некоторую конечную величину.
Момент инерции простейших тел вращения формула. Момент инерции. Приложение. Момент инерции и его вычисление
Относительно неподвижной оси («осевой момент инерции») называется величина J a , равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
- m i – масса i -й точки,
- r i – расстояние от i -й точки до оси.
Осевой момент инерции тела J a является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении .
Если тело однородно, то есть его плотность всюду одинакова, то
Теорема Гюйгенса-Штейнера
Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы , формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J c относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:
Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J c относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:
где – полная масса тела.
Например, момент инерции стержня относительно оси, проходящей через его конец, равен:
Осевые моменты инерции некоторых тел
Вывод формул
Тонкостенный цилиндр (кольцо, обруч)
Вывод формулы
Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобъём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJ i . Тогда
Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду
Толстостенный цилиндр (кольцо, обруч)
Вывод формулы
Пусть имеется однородное кольцо с внешним радиусом R , внутренним радиусом R 1 , толщиной h и плотностью ρ.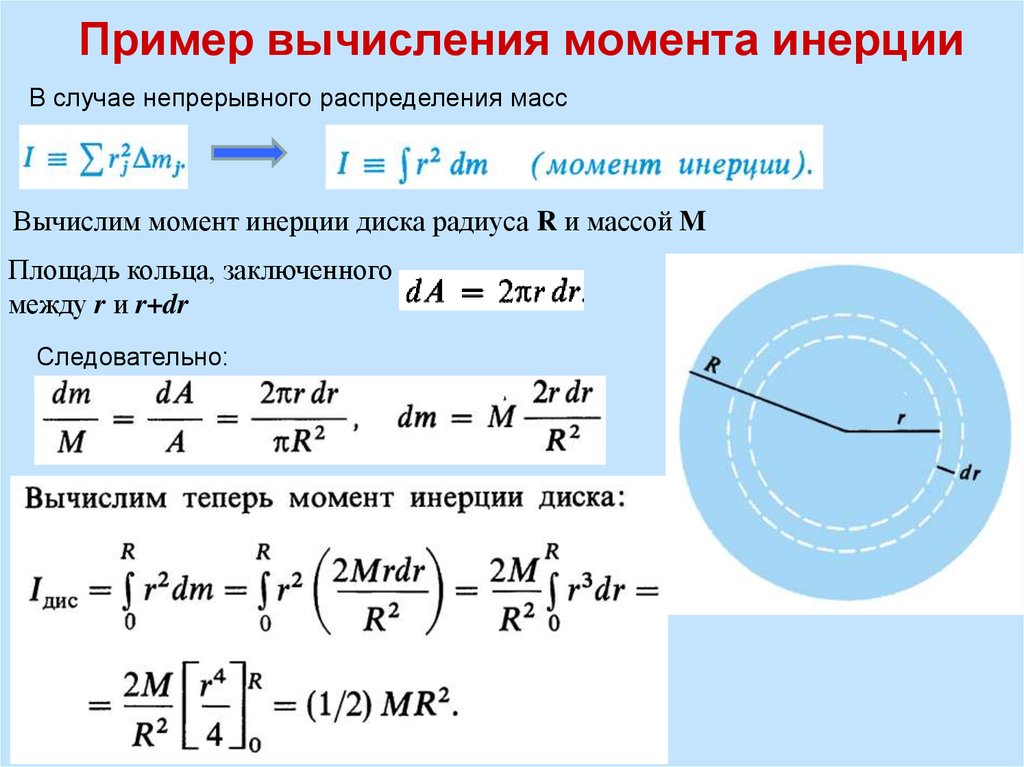 Разобьём его на тонкие кольца толщиной dr . Масса и момент инерции тонкого кольца радиуса r составит
Разобьём его на тонкие кольца толщиной dr . Масса и момент инерции тонкого кольца радиуса r составит
Момент инерции толстого кольца найдём как интеграл
Поскольку объём и масса кольца равны
получаем окончательную формулу для момента инерции кольца
Однородный диск (сплошной цилиндр)
Вывод формулы
Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (R 1 = 0), получим формулу для момента инерции цилиндра (диска):
Сплошной конус
Вывод формулы
Разобьём конус на тонкие диски толщиной dh , перепендикулярные оси конуса. Радиус такого диска равен
где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска. Масса и момент инерции такого диска составят
Интегрируя, получим
Сплошной однородный шар
Вывод формулы
Разобъём шар на тонкие диски толщиной dh , перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле
Масса и момент инерции такого диска составят
Момент инерции сферы найдём интегрированием:
Тонкостенная сфера
Вывод формулы
Для вывода воспользуемся формулой момента инерции однородного шара радиуса R :
Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину dR .
Тонкий стержень (ось проходит через центр)
Вывод формулы
Разобъём стержень на малые фрагменты длиной dr . Масса и момент инерции такого фрагмента равна
Интегрируя, получим
Тонкий стержень (ось проходит через конец)
Вывод формулы
При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние l /2. По теореме Штейнера новый момент инерции будет равен
Безразмерные моменты инерции планет и их спутников
Большое значение для исследований внутренней структуры планет и их спутников имеют их безразмерные моменты инерции. Безразмерный момент инерции тела радиуса r и массы m равен отношению его момента инерции относительно оси вращения к моменту инерции материальной точки той же массы относительно неподвижной оси вращения, расположенной на расстоянии r (равному mr 2). Эта величина отражает распределение массы по глубине. Одним из методов её измерения у планет и спутников является определение допплеровского смещения радиосигнала, передаваемого АМС , пролетающей около данной планеты или спутника. Для тонкостенной сферы безразмерный момент инерции равен 2/3 (~0,67), для однородного шара – 0,4, и вообще тем меньше, чем большая масса тела сосредоточена у его центра. Например, у Луны безразмерный момент инерции близок к 0,4 (равен 0,391), поэтому предполагают, что она относительно однородна, её плотность с глубиной меняется мало. Безразмерный момент инерции Земли меньше, чем у однородного шара (равен 0,335), что является аргументом в пользу существования у неё плотного ядра.
Одним из методов её измерения у планет и спутников является определение допплеровского смещения радиосигнала, передаваемого АМС , пролетающей около данной планеты или спутника. Для тонкостенной сферы безразмерный момент инерции равен 2/3 (~0,67), для однородного шара – 0,4, и вообще тем меньше, чем большая масса тела сосредоточена у его центра. Например, у Луны безразмерный момент инерции близок к 0,4 (равен 0,391), поэтому предполагают, что она относительно однородна, её плотность с глубиной меняется мало. Безразмерный момент инерции Земли меньше, чем у однородного шара (равен 0,335), что является аргументом в пользу существования у неё плотного ядра.
Центробежный момент инерции
Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются следующие величины:
где x , y и z – координаты малого элемента тела объёмом dV , плотностью ρ и массой dm .
Ось OX называется главной осью инерции тела , если центробежные моменты инерции J xy и J xz одновременно равны нулю. Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке O тела, называются главными моментами инерции тела .
Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке O тела, называются главными моментами инерции тела .
Главные оси инерции, проходящие через центр масс тела, называются главными центральными осями инерции тела , а моменты инерции относительно этих осей – его главными центральными моментами инерции . Ось симметрии однородного тела всегда является одной из его главных центральных осей инерции.
Геометрический момент инерции
Геометрический момент инерции – геометрическая характеристика сечения вида
где – расстояние от центральной оси до любой элементарной площадки относительно нейтральной оси .
Геометрический момент инерции не связан с движением материала, он лишь отражает степень жесткости сечения. Используется для вычисления радиуса инерции, прогиба балки, подбора сечения балок, колонн и др.
Единица измерения СИ – м 4 . В строительных расчетах, литературе и сортаментах металлопроката в частности указывается в см 4 .
Из него выражается момент сопротивления сечения:
.| Геометрические моменты инерции некоторых фигур | |
|---|---|
| Прямоугольника высотой и шириной : | |
| Прямоугольного коробчатого сечения высотой и шириной по внешним контурам и , а по внутренним и соответственно | |
| Круга диаметром | |
Центральный момент инерции
Центральный момент инерции (или момент инерции относительно точки O) – это величина
Центральный момент инерции можно выразить через главные осевые или центробежные моменты инерции: .
Тензор инерции и эллипсоид инерции
Момент инерции тела относительно произвольной оси, проходящей через центр масс и имеющей направление, заданное единичным вектором , можно представить в виде квадратичной (билинейной) формы :
(1),где – тензор инерции . Матрица тензора инерции симметрична, имеет размеры и состоит из компонент центробежных моментов:
Матрица тензора инерции симметрична, имеет размеры и состоит из компонент центробежных моментов:
.
Выбором соответствующей системы координат матрица тензора инерции может быть приведена к диагональному виду. Для этого нужно решить задачу о собственных значениях для матрицы тензора :
,
где – ортогональная матрица перехода в собственный базис тензора инерции. В собственном базисе координатные оси направлены вдоль главных осей тензора инерции, а также совпадают с главными полуосями эллипсоида тензора инерции. Величины – главные моменты инерции. Выражение (1) в собственной системе координат имеет вид:
откуда получается уравнение
Момент инерции
тела относительно оси и относительно
точки. Момент инерции материальной
точки относительно оси равен произведению
массы точки на квадрат расстояния точки
до оси. Чтобы найти момент инерции тела
(с непрерывным распределением вещества)
относительно оси, надо мысленно разбить
его на такие малые элементы, чтобы
каждый из них можно было считать
материальной точкой бесконечно малой
массыdm = dV . Тогда момент инерции тела относительно
оси равен интегралу по объёму тела:
Тогда момент инерции тела относительно
оси равен интегралу по объёму тела:
Вычисление момента инерции тела относительно оси часто упрощается, если предварительно вычислить его момент инерции относительно точки . Он вычисляется по формуле, аналогичной (1):
(2)
где r – расстояние элементаdm до выбранной точки (относительно которой вычисляется ). Пусть эта точка является началом системы координатX , Y , Z (рис. 1). Квадраты расстояний элементаdm до координатных осейX , Y , Z и до начала координат равны соответственноy 2 + z 2 , z 2 + x 2 , x 2 + y 2 , x 2 + y 2 + z 2 . Моменты инерции тела относительно осейX , Y , Z и относительно начала координат
Из этих соотношений следует, что
Таким образом, сумма моментов инерции тела относительно
трёх любых взаимно перпендикулярных
осей, проходящих через одну точку,
равна удвоенному моменту инерции тела
относительно этой точки.
Момент инерции тонкого кольца. Все элементы кольцаdm (рис. 2) находятся на одинаковом расстоянии, равном радиусу кольцаR , от его оси симметрии (осьY) и от его центра. Момент инерции кольца относительно осиY
(4)Момент инерции тонкого диска. Пусть тонкий однородный диск массыm с концентрическим отверстием (рис. 3) имеет внутренний и внешний радиусыR 1 иR 2 . Мысленно разобьём диск на тонкие кольца радиусаr , толщиныdr . Момент инерции такого кольца относительно осиY (рис. 3, она перпендикулярна рисунку и не показана), в соответствии с (4):
Момент инерции диска:
(6)
В частности, полагая в (6) R 1 = 0, R 2 = R , получим формулу для вычисления момента инерции тонкого сплошного однородного диска относительно его оси:
Момент инерции
диска относительно его оси симметрии
не зависит от толщины диска . Поэтому
по формулам (6) и (7) можно вычислять
моменты инерции соответствующих
цилиндров относительно их осей симметрии.
Поэтому
по формулам (6) и (7) можно вычислять
моменты инерции соответствующих
цилиндров относительно их осей симметрии.
Момент инерции тонкого диска относительно его центра также вычисляется по формуле (6), = J y , а моменты инерции относительно осейX иZ равны между собой,J x = J z . Поэтому, в соответствии с (3): 2 J x + J y = 2 J y , J x = J y /2, или
(8)
Момент инерции цилиндра. Пусть имеется полый симметричный цилиндр массыm , длины h , внутренний и внешний радиусы которого равныR 1 и R 2 . Найдём его момент инерции относительно осиZ , проведенной через центр масс перпендикулярно оси цилиндра (рис. 4). Для этого мысленно разобьём его на диски бесконечно малой толщиныdy . Один из таких дисков, массойdm = mdy / h , расположенный на расстоянииy от начала координат, показан на рис. 4. Его момент инерции относительно осиZ , в соответствии с (8) и теоремой Гюйгенса – ШтейнераМомент инерции всего цилиндра
Момент инерции цилиндра относительно оси Z (оси вращения маятника) найдём по теореме Гюйгенса – Штейнера
где d – расстояние от центра масс цилиндра до осиZ . В работе 16 этот момент инерции обозначен какJ ц
(11)
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
Нанесение экспериментальных точек и проведение по ним графика «на глаз», а также определение по графику абсцисс и ординат точек, не отличаются высокой точностью. Её можно повысить, если использовать аналитический метод. Математическое правило построения графика заключается в подборе таких значений параметров «а» и «в» в линейной зависимости вида у = ах + b , чтобы сумма квадратов отклонений у i (рис. 5) всех экспериментальных точек от линии графика была наименьшей (метод «наименьших квадратов» ), т.е. чтобы величина
(1)
Пусть твёрдое тело вращается вокруг оси Z (рисунок 6). Его можно представить как неизменную с течением времени систему разных материальных точек m i , каждая из которых движется по окружности радиусом r i , лежащей в плоскости, перпендикулярной оси Z. Угловые скорости всех материальных точек одинаковы. Моментом инерции тела относительно оси Z называется величина:
где – момент инерции отдельной материальной точки относительно оси ОZ. Из определения вытекает, что момент инерции – аддитивная величина , т. е. момент инерции тела, состоящего из отдельных частей, равен сумме моментов инерции частей.
Рисунок 6
Очевидно, [I ] = кг×м 2 . Важность понятия момента инерции выражается в трёх формулах:
; ; .
Первая из них выражает момент импульса тела, которое вращается вокруг неподвижной оси Z (полезно эту формулу сравнить с выражением для импульса тела P = mV c , где V c – скорость центра масс). Вторая формула носит название основного уравнения динамики вращательного движения тела вокруг неподвижной оси, т.е., иначе говоря, второго закона Ньютона для вращательного движения (сравним с законом движения центра масс: ). Третья формула выражает кинетическую энергию тела, вращающегося вокруг неподвижной оси (сравним с выражением для кинетической энергии частицы ). Сравнение формул позволяет сделать вывод о том, что момент инерции во вращательном движении играет роль, аналогичную массе в том смысле, что чем больше момент инерции тела, тем меньше угловое ускорение при прочих равных условиях оно приобретает (тело, образно говоря, труднее раскрутить). Реально вычисление моментов инерции сводится к вычислению тройного интеграла и может быть произведено лишь для ограниченного числа симметричных тел и лишь для осей симметрии. Количество осей, вокруг которых может вращаться тело, бесконечно велико. Среди всех осей выделяется та, которая проходит через замечательную точку тела – центр масс (точку, для описания движения которой достаточно представить, что вся масса системы сосредоточена в центре масс и к этой точке приложена сила, равная сумме всех сил). Но осей, проходящих через центр масс, также бесконечно много. Оказывается, что для любого твёрдого тела произвольной формы существуют три взаимно перпендикулярных оси С х, С у, С z , называемые осями свободного вращения , обладающие замечательным свойством: если тело закрутить вокруг любой из этих осей и подбросить вверх, то при последующем движении тела ось останется параллельной самой себе, т.е. не будет кувыркаться. Закручивание вокруг любой другой оси этим свойством не обладает. Значение моментов инерции типичных тел относительно указанных осей приведено ниже. Если ось проходит через центр масс, но составляет углы a, b, g с осями С х, С у, С z соответственно, то момент инерции относительно такой оси равен
I c = I cx cos 2 a + I cy cos 2 b + I cz cos 2 g (*)
Рассмотрим кратко вычисление момента инерции для простейших тел.
1. Момент инерции длинного тонкого однородного стержня относительно оси, проходящей через центр масс стержня и ему перпендикулярной.
Пусть т – масса стержня, l – его длина.
,
Индекс «с » у момента инерции I c означает, что это момент инерции относительно оси, проходящий через точку центра масс (центр симметрии тела), C(0,0,0).
2. Момент инерции тонкой прямоугольной пластинки.
; ;
3. Момент инерции прямоугольного параллелепипеда.
, т. С(0,0,0)
4. Момент инерции тонкого кольца.
;
, т. С(0,0,0)
5. Момент инерции тонкого диска.
В силу симметрии
; ;
6. Момент инерции сплошного цилиндра.
;
В силу симметрии:
7. Момент инерции сплошного шара.
, т. С(0,0,0)
8. Момент инерции сплошного конуса.
, т. С(0,0,0)
где R – радиус основания, h – высота конуса.
Напомним, что cos 2 a + cos 2 b + cos 2 g = 1. Наконец, если ось О не проходит через центр масс, то момент инерции тела может быть вычислен с помощью теоремы Гюйгенса Штейнера
I о = I с + md 2 , (**)
где I о – момент инерции тела относительно произвольной оси, I с – момент инерции относительно параллельной ей оси, проходящей через центр масс,
m – масса тела, d – расстояние между осями.
Процедура вычисления моментов инерции для тел стандартной формы относительно произвольной оси сводится к следующему.
Рассмотрим теперь проблему определения момента инерции различных тел. Общая формула для нахождения момента инерции объекта относительно оси имеет вид
,
Иными словами, нужно сложить все массы, умножив каждую из них на квадрат ее расстояния до оси . Заметьте, что это верно даже для трехмерного тела, несмотря на то, что расстояние имеет такой «двумерный вид». Впрочем, в большинстве случаев мы будем ограничиваться двумерными телами.
В качестве простого примера рассмотрим стержень, вращающийся относительно оси, проходящей через его конец и перпендикулярной к нему (фиг. 19.3). Нам нужно просуммировать теперь все массы, умноженные на квадраты расстояния (в этом случае все – нулевые). Под суммой, разумеется, я имею в виду интеграл от , умноженный на «элементики» массы. Если мы разделим стержень на кусочки длиной , то соответствующий элемент массы будет пропорционален , а если бы составляло длину всего стержня, то его масса была бы равна . Поэтому
. (19.5)
Размерность момента инерции всегда равна массе, умноженной на квадрат длины, так что единственная существенная величина, которую мы вычислили, это множитель .
Фиг. 19.3. Прямой стержень, вращающийся вокруг оси, проходящей черед один из его концов.
А чему будет равен момент инерции , если ось вращения проходит через середину стержня? Чтобы найти его, нам снова нужно взять интеграл, но уже в пределах от до . Заметим, однако, одну особенность этого случая. Такой стержень с проходящей через центр осью можно представлять себе как два стержня с осью, проходящей через конец, причем масса каждого из них равна , а длина равна . Моменты инерции двух таких стержней равны друг другу и вычисляются по формуле (19.5). Поэтому момент инерции всего стержня равен
. (19.6)
Таким образом, стержень гораздо легче крутить за середину, чем за конец.
Можно, конечно, продолжить вычисление моментов инерции других интересующих нас тел. Но поскольку такие расчеты требуют большого опыта в вычислении интегралов (что очень важно само по себе), они как таковые не представляют для нас большого интереса. Впрочем, здесь имеются некоторые очень интересные и полезные теоремы. Пусть имеется какое-то тело и мы хотим узнать его момент инерции относительно какой-то оси. Это означает, что мы хотим найти его инертность при вращении вокруг этой оси. Если мы будем двигать тело за стержень, подпирающий его центр масс так, чтобы оно не поворачивалось при вращении вокруг оси (в этом случае на него не действуют никакие моменты сил инерции, поэтому тело не будет поворачиваться, когда мы начнем двигать его), то для того, чтобы повернуть его, понадобится точно такая же сила, как если бы вся масса была сосредоточена в центре масс и момент инерции был бы просто равен , где – расстояние от центра масс до оси вращения. Однако формула эта, разумеется, неверна. Она не дает правильного момента инерции тела. Ведь в действительности при повороте тело вращается. Крутится не только центр масс (что давало бы величину ), само тело тоже должно поворачиваться относительно центра масс. Таким образом, к моменту инерции нужно добавить – момент инерции относительно центра масс. Правильный ответ состоит в том, что момент инерции относительно любой оси равен
Эта теорема называется теоремой о параллельном переносе оси. Доказывается она очень легко. Момент инерции относительно любой оси равен сумме масс, умноженных на сумму квадратов и , т. е. . Мы сейчас сосредоточим наше внимание на , однако все в точности можно повторить и для . Пусть координата есть расстояние данной частной точки от начала координат; посмотрим, однако, как все изменится, если мы будем измерять расстояние от центра масс вместо от начала координат. Чтобы это выяснить, мы должны написать
Возводя это выражение в квадрат, находим
.
Что получится, если умножить его на и просуммировать по всем ? Вынося постоянные величины за знак суммирования, находим
.
Третью сумму подсчитать легко; это просто . Второй член состоит из двух сомножителей, один из которых ; он равен -координате центра масс. Но это должно быть равно нулю, ведь отсчитывается от центра масс, а в этой системе координат среднее положение всех частиц, взвешенное их массами, равно нулю. Первый же член, очевидно, представляет собой часть от . Таким образом, мы и приходим к формуле (19.7).
Давайте проверим формулу (19.7) на одном примере. Просто проверим, будет ли она применима для стержня. Мы уже нашли, что момент инерции стержня относительно его конца должен быть равен . А центр масс стержня, разумеется, находится на расстоянии . Таким образом, мы должны получить, что . Так как одна четвертая + одна двенадцатая = одной третьей, то мы не сделали никакой грубой ошибки.
Кстати, чтобы найти момент инерции (19.5), вовсе не обязательно вычислять интеграл. Можно просто предположить, что он равен величине , умноженной на некоторый неизвестный коэффициент . После этого можно использовать рассуждения о двух половинках и для момента инерции (19.6) получить коэффициент . Используя теперь теорему о параллельном переносе оси, докажем, что , откуда . Всегда можно найти какой-нибудь окольный путь!
При применении теоремы о параллельных осях важно помнить, что ось должна быть параллельна оси, относительно которой мы хотим вычислять момент инерции.
Стоит, пожалуй, упомянуть еще об одном свойстве, которое часто бывает очень полезно при нахождении момента инерции некоторых типов тел. Оно состоит в следующем: если у нас есть плоская фигура и тройка координатных осей с началом координат, расположенным в этой плоскости, и осью , направленной перпендикулярно к ней, то момент инерции этой фигуры относительно оси равен сумме моментов инерции относительно осей и . Доказывается это совсем просто. Заметим, что
(поскольку все ). Аналогично,
,
Момент инерции однородной прямоугольной пластинки, например с массой , шириной и длиной относительно оси, перпендикулярной к ней и проходящей через ее центр, равен просто
,
поскольку момент инерции относительно оси, лежащей в плоскости пластинки и параллельной ее длине, равен , т. е. точно такой же, как и для стержня длиной , а момент инерции относительно другой оси в той же плоскости равен , такой же, как и для стержня длиной .
Итак, перечислим свойства момента инерции относительно данной оси, которую мы назовем осью :
1. Момент инерции равен
.
2. Если предмет состоит из нескольких частей, причем момент инерции каждой из них известен, то полный момент инерции равен сумме моментов инерции этих частей.
3. Момент инерции относительно любой данной оси равен моменту инерции относительно параллельной оси, проходящей через центр масс, плюс произведение полной массы на квадрат расстояния данной оси от центра масс.
4. Момент инерции плоской фигуры относительно оси, перпендикулярной к ее плоскости, равен сумме моментов инерций относительно любых двух других взаимно перпендикулярных осей, лежащих в плоскости фигуры и пересекающихся с перпендикулярной осью.
В табл. 19.1 приведены моменты инерции некоторых элементарных фигур, имеющих однородную плотность масс, а в табл. 19.2 – моменты инерции некоторых фигур, которые могут быть получены из табл. 19.1 с использованием перечисленных выше свойств.
Таблица 19.1 Простые примеры моментов инерции
Тонкий стержень длиной | Проходит через центр перпендикулярно к стержню | |
Тонкое концентрическое кольцо с радиусами и | Проходит через центр кольца перпендикулярно к плоскости кольца | |
Сфера радиуса | Проходит через центр |
Таблица 19.2 Моменты инерции, полученные из табл. 19.1
Прямоугольник со сторонами и Прямоугольный параллелепипед со сторонами Проходит через центр параллельно |
| Наименование параметра | Значение |
| Тема статьи: | Момент инерции |
| Рубрика (тематическая категория) | Механика |
Рассмотрим материальную точку массой m , которая находится на расстоянии r, от неподвижной оси (рис. 26). Моментом инерции J материальной точки относительно оси принято называть скалярная физическая величина, равная произведению массы m на квадрат расстояния r до этой оси:
J = mr 2 (75)
Момент инерции системы N материальных точек будет равен сумме моментов инерции отдельных точек
(76)
К определению момента инерции точки
В случае если масса распределена в пространстве непрерывно, то суммирование заменяется интегрированием. Тело разбивается на элементарные объёмы dv, каждый из которых обладает массой dm. В результате получается следующее выражение:
(77)
Для однородного по объёму тела плотность ρ постоянна, и записав элементарную массу в виде
dm = ρdv, преобразуем формулу (70) следующим образом:
(78)
Размерность момента инерции – кг*м 2 .
Момент инерции тела является мерой инертности тела во вращательном движении, подобно тому, как масса тела является мерой его инертности при поступательном движении.
Момент инерции – это мера инертных свойств твердого тела при вращательном движении, зависящая от распределения массы относительно оси вращения . Иными словами, момент инерции зависит от массы, формы, размеров тела и положения оси вращения.
Всякое тело, независимо от того, вращается оно или покоится, обладает моментом инерции относительно любой оси, подобно тому, как тело обладает массой независимо от того, движется оно или находиться в покое. Аналогично массе момент инерции является величиной аддитивной.
В некоторых случаях теоретический расчёт момента инерции достаточно прост. Ниже приведены моменты инерции некоторых сплошных тел правильной геометрической формы относительно оси, проходящей через центр тяжести.
Момент инерции бесконечно плоского диска радиуса R относительно оси, перпендикулярной плоскости диска:
Момент инерции шара радиуса R :
Момент инерции стержня длиной L относительно оси, проходящей через середину стержня перпендикулярно ему:
Момент инерции бесконечно тонкого обруча радиуса R относительно оси, перпендикулярной его плоскости:
Момент инерции тела относительно произвольной оси рассчитывается с помощью теоремы Штейнера:
Момент инерции тела относительно произвольной оси равен сумме момента инерции относительно оси, проходящей через центр масс параллельно данной, и произведения массы тела на квадрат расстояния между осями.
Рассчитаем при помощи теоремы Штейнера момент инерции стержня длиной L относительно оси, проходящей через конец перпендикулярно ему (рис. 27).
К расчету момента инерции стержня
Согласно теореме Штейнера, момент инерции стержня относительно оси O′O′ равен моменту инерции относительно оси OO плюс md 2 . Отсюда получаем:
Очевидно: момент инерции неодинаков относительно разных осей, и в связи с этим, решая задачи на динамику вращательного движения, момент инерции тела относительно интересующей нас оси каждый раз приходится искать отдельно. Так, к примеру, при конструировании технических устройств, содержащих вращающиеся детали (на железнодорожном транспорте, в самолетостроении, электротехнике и т. д.), требуется знание величин моментов инерции этих деталей. При сложной форме тела теоретический расчет его момента инерции может оказаться трудно выполнимым. В этих случаях предпочитают измерить момент инерции нестандартной детали опытным путем.
Момент силы F относительно точки O
Момент инерции – понятие и виды. Классификация и особенности категории “Момент инерции” 2017, 2018.
Рис.35 Проведем через центр масс С тела произвольные оси Cx”y”z”, а через любую точку О на оси Сх” – оси Oxyz, такие, что Оy½½Сy”, Oz½½Cz” (рис. 35). Расстояние между осями Cz” и Оz обозначим через d. Тогда но, как видно из рисунка, для любой точки тела или, а. Подставляя… .
Момент инерции тела – величина, определяющая его инертность во вращательном движении. В динамике поступательного движения инерцию тела полностью характеризует его масса. Влияние собственных свойств тела на динамику вращательного движения оказывается более сложным,… .
Лекция 3. Силы. Масса, импульс материальной точки и механической системы. Динамика поступательного движения в инерциальных системах отсчета. Закон изменения импульса механической системы. Закон сохранения импульса. Динамика изучает движение тел с учетом причин,… .
Проанализируем формулу для момента инерции твердого тела. Момент инерции зависит от 1) массы тела, 2) формы и размеров тела, 3) положения оси вращения относительно тела (рис 2) Рис. 2а Рис.2б Итак, момент инерции есть мера инертности тела при вращательном движении,… .
Момент инерции относительно любой оси равен моменту инерции относительно центральной оси, параллельной данной, плюс произведение площади фигуры на квадрат расстояния между осями. Из формулы видно, что момент инерции относительно центральной оси меньше, чем момент…
Момент инерции: формула. Момент инерции тела
Чтобы изменить скорость перемещения тела в пространстве, необходимо приложить некоторое усилие. Этот факт относится ко всем видам механического движения и связан с наличием инерционных свойств у объектов, имеющих массу. В данной статье рассматривается вращение тел и дается понятие об их моменте инерции.
Что такое вращение с точки зрения физики?
Ответ на этот вопрос может дать каждый человек, поскольку этот физический процесс ничем не отличается от его понятия в обиходе. Процесс вращения представляет собой перемещение объекта, обладающего конечной массой, по круговой траектории вокруг некоторой воображаемой оси. Можно привести следующие примеры вращения:
- Движение колеса автомобиля или велосипеда.
- Вращение лопастей вертолета или вентилятора.
- Движение нашей планеты вокруг оси и вокруг Солнца.
Какие физические величины характеризуют процесс вращения?
Перемещение по окружности описывается набором величин в физике, основные из которых перечислены ниже:
- r – расстояние до оси материальной точки массой m.
- ω и α – угловая скорость и ускорение, соответственно. Первая величина показывает, на сколько радиан (градусов) поворачивается тело вокруг оси за одну секунду, вторая величина описывает скорость изменения во времени первой.
- L – момент импульса, который подобен аналогичной характеристике при линейном движении.
- I – момент инерции тела. Эта величина рассматривается ниже в статье подробно.
- M – момент силы. Он характеризует степень изменения величины L, если приложена внешняя сила.
Перечисленные величины связаны друг с другом следующими формулами вращательного движения:
- L = I*ω
- M = I*α
Первая формула описывает круговое движение тела в отсутствие действия внешних моментов сил. В приведенном виде она отражает закон сохранения момента импульса L. Второе выражение описывает случай ускорения или замедления вращения тела в результате действия момента силы M. Оба выражения часто используются при решении задач динамики по круговой траектории.
Как видно из этих формул, момент инерции относительно оси (I) в них используется в качестве некоторого коэффициента. Рассмотрим подробнее эту величину.
Откуда появляется величина I?
В этом пункте рассмотрим самый простой пример вращения: круговое перемещение материальной точки массой m, дистанция которой от оси вращения составляет r. Эта ситуация приведена на рисунке.
Согласно определению, момент импульса L записывается, как произведение плеча r на линейный импульс p точки:
L = r*p = r*m*v, поскольку p = m*v
Учитывая, что линейная и угловая скорость связаны друг с другом через расстояние r, это равенство можно переписать так:
v = ω*r => L = m*r2*ω
Произведение массы материальной точки на квадрат расстояния до оси вращения принято называть моментом инерции. Формула выше перепишется в таком случае следующим образом:
I = m*r2 => L = I*ω
То есть мы получили выражение, которое было приведено в предыдущем пункте, и ввели в использование величину I.
Общая формула для величины I тела
Выражение для момента инерции массой m материальной точки является базовым, то есть оно позволяет рассчитать эту величину для любого тела, имеющего произвольную форму и неоднородное распределение массы в нем. Для этого необходимо разбить рассматриваемый объект на маленькие элементы массой mi (целое число i – номер элемента), затем, умножить каждый из них на квадрат расстояния ri2 до оси, вокруг которой рассматривают вращение, и сложить полученные результаты. Описанную методику нахождения величины I можно записать математически так:
I = ∑i(mi*ri2)
Если тело разбито таким образом, что i->∞, тогда приведенная сумма заменяется интегралом по массе тела m:
I = ∫m(ri2*dm)
Этот интеграл эквивалентен другому интегралу по объему тела V, поскольку dV=ρ*dm:
I = ρ*∫V(ri2*dV)
Все три формулы используются для вычисления момента инерции тела. При этом в случае дискретного распределения масс в системе предпочтительнее пользоваться 1-м выражением. При непрерывном распределении массы применяют 3-е выражение.
Свойства величины I и ее физический смысл
Описанная процедура получения общего выражения для I позволяет сделать некоторые выводы о свойствах этой физической величины:
- она является аддитивной, то есть полный момент инерции системы можно представить, как сумму моментов отдельных ее частей;
- она зависит от распределения массы внутри системы, а также от расстояния до оси вращения, чем больше последнее, тем больше I;
- она не зависит от действующих на систему моментов сил M и от скорости вращения ω.
Физический смысл I заключается в том, насколько сильно система препятствует любому изменению скорости ее вращения, то есть момент инерции характеризует степень “плавности” возникающих ускорений. Например, колесо велосипеда можно легко раскрутить до больших угловых скоростей и также легко его остановить, но чтобы изменить вращение маховика на коленвале автомобиля, понадобится приложить значительное усилие и некоторое время. В первом случае имеет место система с маленьким моментом инерции, во втором – с большим.
Значение I некоторых тел для оси вращения, проходящей через центр масс
Если применить интегрирование по объему для любых тел с произвольным распределением массы, то можно получить для них величину I. В случае однородных объектов, которые имеют идеальную геометрическую форму, эта задача уже решена. Ниже приводятся формулы момента инерции для стержня, диска и шара массой m, в которых составляющее их вещество распределено равномерно:
- Стержень. Ось вращения проходит перпендикулярно ему. I = m*L2/12, где L – длина стержня.
- Диск произвольной толщины. Момент инерции с осью вращения, проходящей перпендикулярно его плоскости через центр масс, вычисляется так: I = m*R2/2, где R – радиус диска.
- Шар. В виду высокой симметрии этой фигуры, для любого положения оси, проходящей через ее центр, I = 2/5*m*R2, здесь R – шара радиус.
Далее приведем два примера решения задач на применение общей формулы для расчета I и на использование свойства аддитивности этой величины.
Задача на расчет значения I для системы с дискретным распределением массы
Представим себе стержень длиною 0,5 метра, который сделан из твердого и легкого материала. Этот стержень закреплен на оси таким образом, что она проходит перпендикулярно ему точно посередине. На этот стержень подвешены 3-и груза следующим образом: с одной стороны оси имеются два груза массами 2 кг и 3 кг, находящиеся на расстояниях 10 см и 20 см от его конца, соответственно; с другой стороны подвешен один груз массой 1,5 кг к концу стержня. Для этой системы необходимо рассчитать момент инерции I и определить, с какой скоростью ω стержень будет вращаться, если к одному из его концов приложить силу 50 Н в течение 10 секунд.
Поскольку массой стержня можно пренебречь, тогда необходимо рассчитать момент I для каждого груза и сложить полученные результаты, чтобы получить полный момент системы. Согласно условию задачи от оси груз массой 2 кг находится на расстоянии 0,15 м (0,25-0,1), груз 3 кг – 0,05 м (0,25-0,20), груз 1,5 кг – 0,25 м. Воспользовавшись формулой для момента I материальной точки, получаем:
I = I1+I2+I3 = m1*r12 + m2*r22 + m3*r32 = 2*(0,15)2+3*(0,05)2+1,5*(0,25)2 = 0,14 625 кг*м2.
Обратим внимание, что при выполнении вычислений все единицы измерения были переведены в систему СИ.
Чтобы определить угловую скорость вращения стержня после действия силы, следует применить формулу с моментом силы, которая была приведена во втором пункте статьи:
M = I*α
Поскольку α = Δω/Δt и M = r*F, где r – длина плеча, получаем:
r*F = I*Δω/Δt => Δω = r*F*Δt/I
Учитывая, что r = 0,25 м, подставляем числа в формулу, получаем:
Δω = r*F*Δt/I = 0,25*50*10/0,14625 = 854,7 рад/с
Полученная величина является достаточно большой. Чтобы получить привычную частоту вращения, следует поделить Δω на 2*pi радиан:
f = Δω/(2*pi) = 854,7/(2*3,1416) = 136 с-1
Таким образом, приложенная сила F к концу стержня с грузами за 10 секунд раскрутит его до частоты 136 оборотов в секунду.
Расчет значения I для стержня, когда ось проходит через его конец
Пусть имеется однородный стержень массой m и длиной L. Необходимо определить момент инерции, если ось вращения расположена на конце стержня перпендикулярно ему.
Воспользуемся общим выражением для I:
I = ρ*∫V(ri2*dV)
Разбивая рассматриваемый объект на элементарные объемы, заметим, что dV может быть записано, как dr*S, где S – площадь сечения стержня, а dr – толщина элемента разбиения. Подставляя это выражение в формулу, имеем:
I = ρ*S*∫L(r2*dr)
Этот интеграл вычислить достаточно просто, получаем:
I = ρ*S* (r3/3)∣0L => I = ρ*S*L3/3
Поскольку объем стержня равен S*L, а масса – ρ*S*L, то получаем конечную формулу:
Любопытно отметить, что момент инерции для того же стержня, когда ось проходит через его центр масс, в 4 раза меньше полученной величины (m*L2/3/(m*L2/12)=4).
Вращательная инерция – гипертекст по физике
Обсуждение
введение и теория
Логика момента инерции: зачем нам это?
Определение для точечных тел
I = mr 2
Это скалярная величина (как и ее трансляционная родственница масса), но имеет необычно выглядящие единицы.
[кг м 2 ]
Скажите это, килограмм на метр в квадрате и не говорите это случайно.
Для коллекции объектов просто добавьте моменты. В этом отношении он работает как масса, если вы добавляете моменты, измеренные относительно одной и той же оси.
I = ∑ I = ∑ mr 2
Для протяженного тела замените суммирование на интеграл, а массу на бесконечно малую массу. Вы складываете (интегрируете) все моменты инерции, создаваемые крошечными массами ( дм ), расположенными на любом расстоянии ( × ) от оси, на которой они оказываются.
На практике для объектов с однородной плотностью (ρ = м / V ) вы делаете что-то вроде этого…
| I = | ⌠ ⌡ | r 2 дм = | ⌠ ⌡ | r 2 ρ dV = | ⌠ ⌡ | r 2 | м | ДВ |
| В |
Для объектов с неоднородной плотностью замените плотность функцией плотности ρ ( r ).
| Я = | ⌠ ⌡ | r 2 дм = | ⌠ ⌡ | r 2 ρ ( r ) dV |
Бесконечно малая величина dV – это крошечный кусочек всего тела. На практике это может принимать одну из двух форм (но не ограничивается этими двумя формами). Бесконечно малый ящик, вероятно, концептуально самый простой.Представьте, что объект нарезают кубиками.
[фото нарезанного кубиками картофеля]
Детали имеют размер dx ширину, dy высоту и dz глубину. Объем каждой бесконечно малой штуки…
dV = dx dy dz
Когда объект по существу прямоугольный, получается что-то вроде этого…
| I = | ⌠⌠⌠ ⌡⌡⌡ | ( x 2 + y 2 + z 2 ) | м | dx dy dz |
| В |
или это…
| Я = | ⌠⌠⌠ ⌡⌡⌡ | ( x 2 + y 2 + z 2 ) ρ ( x , y , z ) dx dy dz |
Это способ найти момент инерции кубов, коробок, тарелок, плиток, стержней и других прямоугольных предметов.Обратите внимание, что хотя строгое математическое описание требует тройного интеграла, для многих простых форм фактическое количество интегралов, вычисленных с помощью анализа методом грубой силы, может быть меньше. Иногда интегралы тривиальны.
Другой простой элемент объема – бесконечно малая трубка. Представьте себе лук-порей.
[фото лука-порея]
Каждый слой лука-порея имеет окружность 2π r , толщину dr и высоту h . Объем каждого бесконечно малого слоя тогда…
dV = 2π rh dr
Для многих цилиндрических объектов вы в основном начинаете с чего-то вроде этого…
| I = | ⌠ ⌡ | r 2 | м | 2π правая др. |
| В |
или это…
| Я = | ⌠ ⌡ | r 2 ρ ( r ) 2π rh dr |
Этот метод может применяться к дискам, трубкам, трубкам, цилиндрам, карандашам, рулонам бумаги и, возможно, даже к ветвям деревьев, вазам и настоящему луку-порею (если они имеют простое математическое описание).
Когда формы становятся более сложными, но все еще остаются геометрически простыми, разбейте их на части, напоминающие формы, над которыми уже работали, и сложите эти известные моменты инерции, чтобы получить итог.
I всего = I 1 + I 2 + I 3 +…
Для более сложных круглых форм вам, возможно, придется вернуться к интегралу, который я не знаю, как написать.Что-то вроде вложенных цилиндрических оболочек…
| Я = | ⌠ ⌡ | I цилиндрическая оболочка ( r ) dr |
или это для установленных друг на друга дисков и шайб
| Я = | ⌠ ⌡ | I диск или шайба ( r ) dr |
Эти методы можно использовать для определения момента инерции таких вещей, как сферы, полые сферы, тонкие сферические оболочки и другие более экзотические формы, такие как конусы, ведра и яйца – в основном, все, что может катиться и имеет довольно простой математическое описание.
Когда вы закончите со всем этим, вы часто получаете красивую маленькую формулу, которая выглядит примерно так…
I = α mr 2
, где α – простое рациональное число, такое как 1 для обруча, ½ для цилиндра или ⅖ для сферы.
Что делать, если объект не вращается вокруг оси, используемой для расчета момента инерции? Примените теорему о параллельности оси.
I = I см + мл 2
Что я могу сказать о теореме о перпендикулярной оси, кроме того, что это интересно.Это применимо только к ламинарным объектам. Мне не нужно было много его использовать.
I z = I x + I y
Лучший способ научиться этому – на собственном примере. Много примеров.
| концепция | перевод | соединение | вращение | |||
|---|---|---|---|---|---|---|
| причина ускорения | ∑ F | τ = | r × F | ∑ τ | ||
| сопротивление ускорению | м | I = | ∑ r i 2 м i = ∫ r 2 дм | I | ||
| второй закон Ньютона | ∑ F = | м а | ∑ τ = | I α | ||
Момент инерции куба – объяснение, вывод, формулы и часто задаваемые вопросы
Момент инерции играет во вращательном движении ту же роль, что и масса в поступательном движении.Другими словами, момент инерции – это измерение сопротивления тела изменению его вращательного движения. Например, если тело находится в состоянии покоя. Чем больше момент инерции тела, тем труднее привести тело во вращательное движение. Так же, чем больше момент инерции тела, тем труднее остановить его вращательное движение.
Момент инерции куба вычисляется по разным уравнениям в зависимости от положения его оси. Когда ось вращения находится в центре:
Понятие плотности площади (σ)
Плотность площади можно найти, выбрав и определив крошечную полосу массы с разной шириной.Теперь напишем выражение для плотности площади для всего куба, а затем для крошечных полос разной ширины. Сложите все отдельные полоски с помощью интегрального исчисления.
Из концепции поверхностной плотности, которая представляет собой массу, деленную на площадь, поверхностная плотность (σ) является интенсивным свойством, что означает, что она не зависит от количества материала, а также, пока масса однородна, ее Плотность площади одинакова, независимо от того, выбрали ли вы всю или небольшую полосу разницы ширины.
Плотность площади в макромасштабе задается следующим уравнением: dm / da = σ
Выведение момента инерции куба
Чтобы получить момент инерции куба, когда его ось проходит через центр, мы предположим, что твердый куб имеет массу m, высоту h, ширину w и глубину d.Теперь момент инерции куба подобен моменту инерции квадратного ламинара со стороной вокруг оси, проходящей через центр. Кроме того, мы будем предполагать, что поверхностная плотность пластинки равна ρ. Затем мы возьмем элемент пластинки с декартовыми координатами x, y на плоскости как dx -dy. Таким образом, его масса должна быть = ρdxdy.
Чтобы найти Момент инерции тела, воспользуемся ρ (x2 + y2) dx dy.
Теперь следующий шаг включает интеграцию, при которой мы интегрируем всю пластину.Мы получаем;
-a / 2∫a / 2 -a / 2∫a / 2 ρ (x2 + y2) dx dy = ρa4 / 6.
Затем нам нужно будет подставить значения массы пластинки, которая равна ρ = ma2.
И мы получаем, I = ma2 / 6
Теперь следующий случай, когда ось проходит через ребро, мы разберемся, как выполняется вывод ниже.
Уравнение для момента инерции записывается как:
I = ∫ r2dm
Теперь нам нужно найти MOI вокруг оси, проходящей через ребро, мы возьмем его за ось z.
Двигаясь дальше, нам придется рассматривать куб как разбиваемый на бесконечно малые массы. Таким образом, мы можем предположить, что их размеры равны dy, dx и dz. С этим мы получаем;
dm = ρdxdydz
Здесь ρ = плотность
Если мы посмотрим на формулу момента инерции, приведенную выше, у нас также будет r. Это расстояние от оси z до массы dm. Пусть координаты массы dm равны x, y и z). Теперь расстояние «r» будет;
r = √ (x2 + y2)
r2 = x2 + y2
Между тем, значения x, y и z будут варьироваться от O до b в зависимости от длины ребер.
Теперь нам нужно будет подставить значения, которые мы получили до сих пор, в уравнение момента инерции и, наконец, выполнить интегрирование.
I = ∫ r2dm
I = o∫b o∫b o∫b (x2 + y2) ρdxdydz
I = ρ 2b5 / 3
Масса куба, m = ρb3.
Наконец, подставив его в уравнение, мы получаем;
I = 2mb2 / 3
Нахождение момента инерции через диагональ грани куба
Из рисунка видно, что момент инерции квадратной пластины может быть задан как
I = 2 × (Момент инерции треугольной пластины)
Таким образом, момент инерции треугольной пластины равен
Itri = MR2 / 6
∴ I = 2 × Itri
I = 2 × (M r2 / 6 )
Из приведенного выше рисунка r = a / √2
Теперь мы можем считать, что куб состоит из квадратных пластин массой dm, уложенных друг на друга до высоты a.
Итак, суммарный момент инерции куба относительно диагонали равен
0I∫ dI = 1/12 (0M∫a2dm) /
I = Ma2 / 12
Формула крутящего момента (момент инерции и угловое ускорение)
При вращательном движении крутящий момент требуется для создания углового ускорения объекта. Величина крутящего момента, необходимого для создания углового ускорения, зависит от распределения массы объекта. Момент инерции – это величина, описывающая распределение.Его можно найти, интегрировав массу всех частей объекта и их расстояния до центра вращения, но также можно найти моменты инерции для общих форм. Крутящий момент на данной оси является произведением момента инерции и углового ускорения. Единицы крутящего момента – ньютон-метры (Н ∙ м).
крутящий момент = (момент инерции) (угловое ускорение)
τ = Iα
τ = крутящий момент вокруг определенной оси (Н ∙ м)
I = момент инерции (кг ∙ м 2 )
α = угловое ускорение (радиан / с 2 )
Формула крутящего момента Вопросы:
1) Момент инерции твердого диска равен, где M – масса диска, а R – радиус.Каждое колесо игрушечной машинки имеет массу 0,100 кг и радиус 20,0 см. Если угловое ускорение колеса составляет 1,00 радиан / с 2 , каков крутящий момент?
Ответ: Крутящий момент можно найти с помощью формулы крутящего момента и момента инерции твердого диска. Крутящий момент:
τ = Iα
τ = 0,0020 Н ∙ м
Крутящий момент, прилагаемый к одному колесу, составляет 0,0020 Н ∙ м.
2) Момент инерции тонкого стержня, вращающегося на оси, проходящей через его центр, равен, где M – масса, а L – длина стержня.Предположим, что лопасть вертолета представляет собой тонкий стержень массой 150,0 кг и длиной 8,00 м. Какой крутящий момент требуется для достижения углового ускорения 18,00 радиан / с 2 ?
Ответ: Крутящий момент можно найти, используя формулу крутящего момента и момент инерции тонкого стержня. Крутящий момент:
τ = Iα
τ = 14 400 Н ∙ м
Требуемый крутящий момент составляет 14 400 Н ∙ м.
(момент инерции – TotalConstructionHelp)
Центроиды и момент инерции
Центроид двумерной поверхности (например, поперечное сечение структурной формы) – это точка, которая соответствует центру тяжести очень тонкой однородной пластины той же площади и формы.Плоская поверхность (или рисунок) может представлять фактическую площадь (например, площадь перекрытия притока или поперечное сечение балки) или образную диаграмму (например, диаграмму нагрузки или изгибающего момента). В любом случае часто бывает полезно определить центр тяжести области.
Симметрия может быть очень полезной для определения местоположения центра тяжести области. Если область (или сечение, или тело) имеет одну линию симметрии, центр тяжести будет лежать где-то вдоль линии симметрии. Это означает, что если бы требовалось уравновесить область (или тело, или секцию) в горизонтальном положении, подложив под нее карандаш или край, то карандаш лучше всего положить прямо под линией симметрии.
Если тело (или область, или сечение) имеет две (или более) линии симметрии, центр тяжести должен лежать где-то вдоль каждой из этих линий. Таким образом, центр тяжести находится в точке пересечения линий. Это означает, что если бы требовалось уравновесить область (или тело, или секцию) в горизонтальном положении, поместив под нее гвоздь, острие гвоздя лучше всего расположить непосредственно под точкой, где встречаются линии симметрии. Это может показаться очевидным, но понятие центроида очень важно понимать как графически, так и численно.Положение центра тяжести некоторых простых форм легко определяется при осмотре. Известно, что центр тяжести круга находится в его центре, а центр тяжести квадрата находится на пересечении двух линий, соединяющих середины параллельных сторон. У круга бесконечное количество линий симметрии, а у квадрата – четыре.
Центроид сечения не всегда находится в пределах площади или материала сечения. Полые трубы, L-образные и некоторые секции неправильной формы имеют центроид, расположенный вне материала секции.Это не проблема, поскольку центроид на самом деле используется только как точка отсчета, от которой измеряются расстояния. Точное положение центроида можно определить, как описано выше, с помощью графической статики или численно.
Центроид любой области можно найти, взяв моменты идентифицируемых областей (например, прямоугольников или треугольников) вокруг любой оси. Это делается так же, как центр тяжести можно найти, взяв моменты веса. Момент большой площади относительно любой оси равен алгебраической сумме моментов составляющих ее площадей.Это выражается следующим уравнением:
Сумма MAtotal = MA1 + MA2 + MA3 + …
Момент любой области определяется как произведение площади и перпендикулярного расстояния от центра тяжести площади до оси момента. С помощью этого принципа мы можем найти центр тяжести любой простой или составной области.
Центр тяжести:
Дано: пластина, показанная на схеме, имеет вес 1 # / дюйм 2 (1 фунт на квадратный дюйм) горизонтальной поверхности.
Определить:
центр тяжести пластины, зная, что она симметрична относительно оси X-X.
Решение:
Принцип моментов гласит, что общий вес вокруг оси равен сумме моментов весов компонентов относительно этой же оси. Таким образом, первое, что нужно сделать, – это разделить тарелку на несколько простых частей. Затем определите площадь и центр тяжести (или центроид) для каждой из составных частей. После этого измерьте моменты каждой из частей вокруг удобной оси (в этом случае выберите ось Z-Z, вокруг которой будут измеряться эти моменты).Ось Z-Z здесь обозначена как Ref Axis.
Сумма MAtotal = MA1 + MA2 + MA3
Это простое уравнение можно переписать следующим образом, в котором описана каждая из составных частей:
(Atotal) (расстояние от исходной оси до центральной оси) = (A1) (расстояние от центра тяжести A1 до исходной оси) + (A2) (расстояние от центра тяжести A2 до исходной оси) + (A3) (расстояние от центроида от A3 до оси отсчета)
, а затем решить относительно y…. центральная ось находится на расстоянии 7,3 дюйма от исходной оси.
Фактический центр тяжести находится на полпути по глубине пластины в точке, рассчитанной выше. По мере уменьшения толщины пластины линия действия центра тяжести останется, в то время как центр тяжести перемещается пропорционально этой линии действия, всегда действующей в средней точке глубины пластины. Если толщина пластины уменьшается до нуля, она не имеет веса, и прежнее положение центра тяжести теперь называется центроидом площади.
Момент инерции (I) – это термин, используемый для описания способности поперечного сечения сопротивляться изгибу. Он всегда учитывается относительно базовой оси, такой как X-X или Y-Y. Это математическое свойство сечения, связанное с площадью поверхности и тем, как эта площадь распределена относительно базовой оси. Базовой осью обычно является центральная ось.
Момент инерции также известен как Второй момент области и математически выражается как:
Ixx = Сумма (A) (y 2 )
В котором:
Ixx = момент инерции вокруг оси x
A = площадь плоскости объекта
y = расстояние между центром тяжести объекта и осью x
Момент инерции – это важное значение, которое используется для определения напряженного состояния в сечении, расчета сопротивления продольному изгибу и определения величины прогиба балки.
Например, если проектировщику дается определенный набор ограничений для структурной проблемы (т.е. нагрузки, пролеты и конечные условия), может быть определено «требуемое» значение момента инерции. Тогда любой структурный элемент, который имеет хотя бы этот конкретный момент инерции, можно будет использовать в конструкции. Другой пример может быть, если верно обратное; конкретный элемент дается в дизайне. Затем можно было определить несущую способность элемента.
Давайте посмотрим на две доски, чтобы интуитивно определить, какая из них будет отклоняться больше и почему.Если две доски с фактическими размерами 2 дюйма на 10 дюймов были уложены рядом – одна со стороны двух дюймов, а другая – со стороны восьми дюймов, то плата, которая опирается на ее 2-дюймовый край, будет значительно жестче, чем та, которая поддерживается вдоль. его 10-дюймовый край. Обе платы имеют одинаковую площадь поперечного сечения, но по-разному распределены относительно горизонтальной центральной оси.
Ixx = (1/12) (b) (h 3 ) = (1/12) x (b) x (h x h x h)
В котором значение b всегда принимается равным стороне, параллельной базовой оси, а h – высотой секции.Это очень важно отметить! Если принять неправильное значение для значения b, вычисления будут совершенно неверными.
Момент инерции
Дано: поперечное сечение.
Определите: моменты инерции, Ixx и Iyy этого раздела.
Решение:
Момент инерции прямоугольной формы, такой как эта, легко вычисляется с помощью уравнения I = 1/12 bh4. Однако очень важно, чтобы b и h были присвоены правильные значения.
Вы можете просто повернуть элемент на 90 градусов и произвести пересчет, всегда запоминая исходное положение элемента.
Ixx = 1/12 (4 дюйма) (10 дюймов) 3 = 333,2 дюйма 4
Iyy = 1/12 (10 дюймов) (4 дюйма) 3 = 53,312 дюйм 4
В этом случае наблюдение подтвердит выбор для b и h. Логично, что Ixx больше, чем Iyy, потому что большая часть прямоугольной области находится дальше от оси x-x, чем ось y-y. Это приводит к тому, что форма имеет большее сопротивление вращению вокруг оси x-x и, следовательно, больший момент инерции вокруг этой оси.
Важность распределения площади вокруг его центральной оси становится очевидной при сравнении значений момента инерции ряда типичных конфигураций балки. Все элементы, показанные ниже, имеют размер 2 x 10 дюймов; в поперечном сечении, равной длины и одинаковой нагрузки.
НАСТРОЕННЫЕ РАЗДЕЛЫ Часто бывает выгодно объединить несколько элементов меньшего размера, чтобы создать балку или колонну большей прочности. Момент инерции такой сборной секции определяется сложением моментов инерции составных частей.Это может быть сделано, если и только если моменты инерции каждой составляющей области взяты относительно общей оси, и тогда и только тогда, когда результирующее сечение действует как единое целое.
Застроенные секции
Дано:
следующие сечения
Определить:
Ix каждого раздела с учетом его составных частей.
Решение:
В этом примере Box разбит на 4 отдельных элемента, и показана процедура вычисления Ixx.
Расчет вручную с помощью компьютерного расчета, приведенного ниже.
Пример результатов компьютерной программы, доступной в нашем разделе бесплатного программного обеспечения
ФОРМУЛА ПЕРЕДАЧИ
Есть много составных секций, в которых составные части не распределены симметрично относительно центральной оси. Самый простой способ определить момент инерции такого участка – найти момент инерции составных частей относительно их собственной центральной оси, а затем применить формулу переноса.Формула переноса переносит момент инерции сечения или площади с его собственной центральной оси на другую параллельную ось. Из математического анализа известно, что это:
Ix = Ic + Ad 2
Где:
Ix = момент инерции относительно оси x-x (в 4 )
Ic = момент инерции относительно центральной оси c-c, параллельной x-x (в 4 )
A = площадь сечения (в 2 )
d = расстояние по перпендикуляру между параллельными осями x-x и c-c (дюймы)
Формула передачи
Дано:
приклеенный асимметричный набивной разрез внизу.
Определить:
момент инерции составной области относительно оси x.
Центроидная ось и формула переноса
Пример результатов компьютерной программы, доступной в нашем разделе бесплатного программного обеспечения
Оценка момента инерции человеческого тела как единого …
ОЦЕНКА МОМЕНТА ИНЕРЦИИ ЧЕЛОВЕЧЕСКОГО ТЕЛА КАК МОДЕЛЬ ОДНОЗВЕННОГО ПЕРЕВЕРНУТОГО МАЯТНИКА Пилвон Хур и Элизабет Т.Иллинойсский университет механических наук и инженерии имени Сяо-Векслера в Урбана-Шампейн, Урбана, Иллинойс, США Эл. Почта: [email protected] Веб-сайт: www.mechse.uiuc.edu/research/hsiao-wecksler/ ВВЕДЕНИЕ Момент инерции человеческого тела – часто используемый параметр для понимания системы управления позой человека с помощью моделей управления, которые представляют вертикальное тело как перевернутый маятник с одним звеном. Однако единого способа вычисления момента инерции не существует. Наиболее часто используемый метод – рассматривать человеческое тело как точечную массу. n момент инерции может быть легко вычислен как J = mh 2, где m – масса тела, а h – высота точечной массы от лодыжки. Для получения более точных значений момента инерции можно использовать объединение всех моментов инерции каждого сегмента на основе антропометрических данных (Winter, 2005). В этой статье простая модель перевернутого маятника с одним звеном использовалась для вывода уравнений движения (EOM), связывающих центр масс (COM) и центр давления (COP). КПД был рассчитан непосредственно из данных силовой пластины.COM был вычислен с помощью метода проекции линии тяжести (GLP) (Зациорский и Дуарте, 2000), который является надежным и независимым от постоянных условий; кроме того, для этого требуются только данные силовой пластины. Определив значение момента инерции, которое наилучшим образом соответствует COM от EOM к COM из GLP, можно оценить момент инерции. МЕТОДЫ Рис. 1. Одиночный модель перевернутого маятника: схемы стопы и маятника всего тела и свободного тела. EOM стопы Предполагая, что стопа неподвижна, ∑ F x = F x0 + F mx x1 = ɺɺ foot foot = 0 (1) ∑ F z = F z0 + F mz z1 = footɺɺ foot = 0 (2) ∑ M голеностопный сустав = M + yFz 0 + ha Fx 0 = J ɺɺ θ = 0 (3) стопа стопа EOM маятника По приближению малого угла F x = – F mx x1 = ɺɺ com com (4) ∑ F z = – F mgmz z1 – com = comɺɺ com (5) ∑ M ankle = −M – mcom ghcom sinθ = −M – m gh θ = −J ɺɺ (6) θ com com
момент инерции – калькулятор.org
Что такое момент инерции?
Момент инерции, также известный как инерция вращения, аналогичен инерции линейного движения. Необходимо указать момент инерции относительно оси вращения. Согласно первому закону движения Ньютона «тело сохраняет текущее состояние движения, если только на него не действует какая-то внешняя сила». Момент инерции связан с распределением массы по всему телу, а не только с массой тела. Поэтому два тела одинаковой массы могут иметь разные моменты инерции.
Если мы рассматриваем твердое тело как систему частиц и взаимное положение этих частиц не меняется, то момент инерции точечной массы равен: I = mr 2 для каждой частицы, так что момент инерции равен массе, умноженной на квадрат расстояния, где m = масса частицы, а r = расстояние от оси вращения до частицы. Момент инерции также называют моментом второй массы.Первый момент массы равен массе, умноженной на расстояние, м.р. Центр масс системы частиц или твердого тела может быть получен с использованием концепции первого момента.
Момент инерции объекта – это мера того, насколько сложно изменить угловое движение этого объекта вокруг оси. Например, мы можем взять два диска одинаковой массы, но диаметр одного больше другого. В результате его масса будет распределена дальше от оси вращения, и для ускорения первого диска потребуется больше усилий, чем для второго.Это потому, что первый диск имеет больший момент инерции.
Если форма объекта изменится, то изменится и момент инерции этого объекта. Когда фигурист тянет вытянутые руки, ее вращение ускоряется, потому что ее момент инерции уменьшается, и, следовательно, увеличивается угловой момент. Эта инерция также отвечает за устойчивость гироскопа.
Кинетическая энергия вращения
Кинетическая энергия вращения тела может быть выражена через его момент инерции.Учитывая массы m, движущиеся со скоростью v, энергия вращения T для каждой равна массе T = 1 / 2mv 2 = 1 / 2m (wr) 2 = 1 / 2mr2w2 = 1 / 2Iw 2 где w – угловая скорость Когда вектор углового момента параллелен вектору угловой скорости, их можно связать с помощью уравнения L = wI , где угловой момент равен L, а угловая скорость ω. Если момент инерции постоянен, крутящий момент на объекте и его угловое ускорение связаны соотношением T = I α , где t – крутящий момент, а α – угловое ускорение.
Теорема о параллельной оси
После того, как момент инерции был вычислен для вращения вокруг центра масс твердого тела, можно также вычислить момент инерции для любых параллельных осей вращения, без необходимости возвращаться к формальному определению. Если ось вращения смещена на расстояние R от оси вращения центра масс (например, диск вращается вокруг точки около его края, а не центра), смещение и центральный момент инерции связаны следующим образом: можно легко вычислить момент инерции для параллельных осей вращения, если мы вычислили момент инерции для вращений вокруг центра масс.Если ось вращения находится на расстоянии R от центра масс, мы получаем следующее уравнение. I (смещенный) = I (центр) + M.R 2
Формулы момента инерции
Тонкая цилиндрическая оболочка с открытыми концами радиуса r и массы m: I = m.r 2
Толстостенная цилиндрическая труба с открытыми концами, внутренним радиусом r1, внешним радиусом r2 и массой m: I = 1 / 2м. (R1 2 + r2 2 )
Сплошной цилиндр радиуса r и массы m: I = m.р 2 /2
Тонкий сплошной диск радиуса r и массы m: I = m.r 2 /2
Тонкая круглая пяльца радиуса r и массы m: I = m.r 2
Твердая сфера радиуса r и массы m: I = 2m.r 2 /5
Добавьте эту страницу в закладки в своем браузере, используя Ctrl и d или используя одну из следующих служб: (открывается в новом окне)(PDF) Расчет центра масс и момента инерции движущегося тела человека с помощью матрицы трансформации
(, 12) (, 1) (1,3) (3) (, 1) (1,3) ( 3,4) (4) (, 1) (1,3) (3,4) (4,12) (12)
(, 1) (1,3) (3,4) (4,12) (12)
oo oo
o
GSS SSS SSSS
SSSS r
ξξ
= ⋅⋅ + ⋅⋅⋅ + ⋅⋅⋅ ⋅
+ ⋅⋅⋅ ⋅
(, 13) ( , 1) (1,5) (5) (, 1) (1,5) (5,6) (6) (, 1) (1,5) (5,6) (6,13) (13)
(, 1) (1,5) (5,6) (6,13) (13)
oo oo
o
GSS SSS SSSS
SSSS r
ξξ
= ⋅⋅ + ⋅ ⋅⋅ + ⋅⋅⋅ ⋅
+ ⋅⋅⋅ ⋅
(, 14) (, 1) (1,2) (2) (, 1) (1,2) (2,7) (7) ( , 1) (1,2) (2,7) (7,8) (8)
(, 1) (1,2) (2,7) (7,8) (8,14) (14) (, 1) (1,2) (2,7) (7,8) (8,14) (14)
oo oo
oo
G SS SSS SSS S
SSSSS SSSSS r
ξξ ξ
ξ
= ⋅ ⋅ + ⋅ ⋅ ⋅ + ⋅ ⋅ ⋅ ⋅
+ ⋅⋅⋅⋅ ⋅ + ⋅⋅⋅⋅ ⋅
(, 15) (, 1) (1,2) (2) (, 1) (1,2) (2,9) (9) (, 1) (1,2) (2,9) (9,10) (10)
(, 1) (1,2) (2,9) (9,10) (10,15) (15) (, 1) (1,2) (2,9 ) (9,10) (10,15) (15)
oo oo
oo
G SS SSS SSSS
SSSS S SSSS S r
ξξ ξ
ξ
= ⋅⋅ + ⋅⋅⋅ + ⋅⋅⋅ ⋅
+ ⋅⋅⋅ ⋅ ⋅ + ⋅⋅⋅ ⋅ ⋅
ССЫЛКИ
1.Бартер Дж. Т. «Оценка массы сегментов тела», Технический отчет AMRL, Центр разработки воздуха Райта,
База ВВС Райт-Паттерсон, TR-57-260 (1957).
2. Брауне В., Фишер О. «Центр тяжести человеческого тела по отношению к снаряжению немецкого пехотинца
», Тракт. математико-физ. Класс Королевской Акад. наук of Saxony, 26,138-452 (1989). (на немецком).
3. Чендлер Р.Ф., Клаузер К.Э., МакКонвилл Дж. Т., Янг Дж. У., “Исследование инерционных свойств человеческого тела
“, Технический отчет AMRL, База ВВС Райт-Паттерсон, TR-74-137 (1969).
4. Clauser CE, McConville JT, Young JW, “Вес, объем и центр масс сегментов человеческого тела”,
Технический отчет AMRL, База ВВС Райт-Паттерсон, TR-69-70 (1969) .
5. Демпстер В.Т., «Требования к пространству сидящего оператора», Технический отчет AMRL, Wright-Patterson Air Force
Base, TR-55-159 (1955).
6. Дуркин Дж. Л., Доулинг Дж., Эндрюс Д. М., «Измерение инерционных параметров сегментов тела с использованием двухэнергетической рентгеновской абсорбциометрии
», J. Biomechanics, 35: 1575–1580 (2002).
7. Ханаван Э.П., “Математическая модель человеческого тела”, Технический отчет AMRL, Аэрокосмические медицинские исследования
Лаборатория База ВВС Райт-Паттерсон, TR-64-102 (1964).
8. Хатце Х. «Новый метод одновременного измерения момента инерции, коэффициента демпфирования и
местоположения центра масс сегмента тела на месте», Europ Japp Physiol, 34, 217 -226 (1975).
9. Хатце Х., “Математическая модель для компьютерного определения значений параметров антропометрических
сегментов”, J. Biomechanics, 13, 833-843 (1980).
10. Хьюстон Р.Л., Пассерелло К.Э. Механика движения человеческого тела. В: Гиста Д. Н., редакторы. Человеческое тело
Dynamics, 1971.
11. Дженсен Р.К., «Оценка биомеханических свойств трех типов телосложения с использованием фотограмметрического метода», J.
Biomechanics, 11, 349-358 (1978).
12. Мартин П.Е., Мунгиоле М., Марцке М.В., Лонгхилл Дж.


