Краткий курс теоретической механики
Краткий курс теоретической механики
ОглавлениеПРЕДИСЛОВИЕ К ДЕСЯТОМУ ИЗДАНИЮВВЕДЕНИЕ Раздел первый. СТАТИКА ТВЕРДОГО ТЕЛА § 1. АБСОЛЮТНО ТВЕРДОЕ ТЕЛО; СИЛА. ЗАДАЧИ СТАТИКИ § 2. ИСХОДНЫЕ ПОЛОЖЕНИЯ СТАТИКИ § 3. СВЯЗИ И ИХ РЕАКЦИИ Глава II. СЛОЖЕНИЕ СИЛ. СИСТЕМА СХОДЯЩИХСЯ СИЛ § 4. ГЕОМЕТРИЧЕСКИЙ СПОСОБ СЛОЖЕНИЯ СИЛ. РАВНОДЕЙСТВУЮЩАЯ СХОДЯЩИХСЯ СИЛ; РАЗЛОЖЕНИЕ СИЛ § 5. ПРОЕКЦИЯ СИЛЫ НА ОСЬ И НА ПЛОСКОСТЬ. АНАЛИТИЧЕСКИЙ СПОСОБ ЗАДАНИЯ И СЛОЖЕНИЯ СИЛ § 6. РАВНОВЕСИЕ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ § 7. РЕШЕНИЕ ЗАДАЧ СТАТИКИ Глава III. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА. ПАРА СИЛ § 8. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА (ИЛИ ТОЧКИ) § 9. ПАРА СИЛ. МОМЕНТ ПАРЫ Глава IV. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ЦЕНТРУ. УСЛОВИЯ РАВНОВЕСИЯ § 11. ТЕОРЕМА О ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ СИЛЫ § 12. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ § 13. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛ. ТЕОРЕМА О МОМЕНТЕ РАВНОДЕЙСТВУЮЩЕЙ Глава V.  ПЛОСКАЯ СИСТЕМА СИЛ§ 14. АЛГЕБРАИЧЕСКИЕ МОМЕНТЫ СИЛЫ И ПАРЫ § 15. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ § 16. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ § 17. РЕШЕНИЕ ЗАДАЧ § 19. СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ И СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ ТЕЛ (КОНСТРУКЦИИ) § 21. РАСПРЕДЕЛЕННЫЕ СИЛЫ § 22. РАСЧЕТ ПЛОСКИХ ФЕРМ Глава VI. ТРЕНИЕ § 23. ЗАКОНЫ ТРЕНИЯ СКОЛЬЖЕНИЯ § 24. РЕАКЦИИ ШЕРОХОВАТЫХ СВЯЗЕЙ. УГОЛ ТРЕНИЯ § 25. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ § 26. ТРЕНИЕ НИТИ О ЦИЛИНДРИЧЕСКУЮ ПОВЕРХНОСТЬ § 27. ТРЕНИЕ КАЧЕНИЯ Глава VII. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ § 28. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ. ВЫЧИСЛЕНИЕ ГЛАВНОГО ВЕКТОРА И ГЛАВНОГО МОМЕНТА СИСТЕМЫ СИЛ § 29. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ § 30. РАВНОВЕСИЕ ПРОИЗВОЛЬНОЙ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ Глава VIII. ЦЕНТР ТЯЖЕСТИ § 31. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ  ЦЕНТР ТЯЖЕСТИ ТВЕРДОГО ТЕЛА§ 33. КООРДИНАТЫ ЦЕНТРОВ ТЯЖЕСТИ ОДНОРОДНЫХ ТЕЛ § 34. СПОСОБЫ ОПРЕДЕЛЕНИЯ КООРДИНАТ ЦЕНТРОВ ТЯЖЕСТИ ТЕЛ § 35. ЦЕНТРЫ ТЯЖЕСТИ НЕКОТОРЫХ ОДНОРОДНЫХ ТЕЛ Раздел второй. КИНЕМАТИКА ТОЧКИ И ТВЕРДОГО ТЕЛА § 36. ВВЕДЕНИЕ В КИНЕМАТИКУ § 37. СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ § 38. ВЕКТОР СКОРОСТИ ТОЧКИ § 39. ВЕКТОР УСКОРЕНИЯ ТОЧКИ § 40. ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ ПРИ КООРДИНАТНОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ § 41. РЕШЕНИЕ ЗАДАЧ КИНЕМАТИКИ ТОЧКИ § 42. ОСИ ЕСТЕСТВЕННОГО ТРЕХГРАННИКА. ЧИСЛОВОЕ ЗНАЧЕНИЕ СКОРОСТИ § 44. НЕКОТОРЫЕ ЧАСТНЫЕ СЛУЧАИ ДВИЖЕНИЯ ТОЧКИ § 45. ГРАФИКИ ДВИЖЕНИЯ, СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ § 46. РЕШЕНИЕ ЗАДАЧ § 47. СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ В ПОЛЯРНЫХ КООРДИНАТАХ Глава X. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА § 48. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ § 49. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ ОСИ, УГЛОВАЯ СКОРОСТЬ И УГЛОВОЕ УСКОРЕНИЕ § 50.  РАВНОМЕРНОЕ И РАВНОПЕРЕМЕННОЕ ВРАЩЕНИЯ§ 51. СКОРОСТИ И УСКОРЕНИЯ ТОЧЕК ВРАЩАЮЩЕГОСЯ ТЕЛА Глава XI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА § 53. ОПРЕДЕЛЕНИЕ ТРАЕКТОРИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ § 54. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ § 55. ТЕОРЕМА О ПРОЕКЦИЯХ СКОРОСТЕЙ ДВУХ ТОЧЕК ТЕЛА § 56. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ С ПОМОЩЬЮ МГНОВЕННОГО ЦЕНТРА СКОРОСТЕЙ. ПОНЯТИЕ О ЦЕНТРОИДАХ § 57. РЕШЕНИЕ ЗАДАЧ § 58. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ § 59. МГНОВЕННЫЙ ЦЕНТР УСКОРЕНИЙ ГЛАВА XII. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА § 60. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА, ИМЕЮЩЕГО ОДНУ НЕПОДВИЖНУЮ ТОЧКУ § 61. КИНЕМАТИЧЕСКИЕ УРАВНЕНИЯ ЭЙЛЕРА § 63. ОБЩИЙ СЛУЧАЙ ДВИЖЕНИЯ СВОБОДНОГО ТВЕРДОГО ТЕЛА Глава XIII. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ § 64.  ОТНОСИТЕЛЬНОЕ, ПЕРЕНОСНОЕ И АБСОЛЮТНОЕ ДВИЖЕНИЯ§ 65. ТЕОРЕМА О СЛОЖЕНИИ СКОРОСТЕЙ § 66. ТЕОРЕМА О СЛОЖЕНИИ УСКОРЕНИЙ (ТЕОРЕМА КОРИОЛИСА) § 67. РЕШЕНИЕ ЗАДАЧ Глава XIV. СЛОЖНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА § 68. СЛОЖЕНИЕ ПОСТУПАТЕЛЬНЫХ ДВИЖЕНИЙ § 69. СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ДВУХ ПАРАЛЛЕЛЬНЫХ ОСЕЙ § 70. ЦИЛИНДРИЧЕСКИЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ § 71. СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ § 72. СЛОЖЕНИЕ ПОСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЙ. ВИНТОВОЕ ДВИЖЕНИЕ Глава XV. ВВЕДЕНИЕ В ДИНАМИКУ. ЗАКОНЫ ДИНАМИКИ § 74. ЗАКОНЫ ДИНАМИКИ. ЗАДАЧИ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ § 75. СИСТЕМЫ ЕДИНИЦ § 76. ОСНОВНЫЕ ВИДЫ СИЛ Глава XVI. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ, РЕШЕНИЕ ЗАДАЧ ДИНАМИКИ ТОЧКИ § 77. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ § 78. РЕШЕНИЕ ПЕРВОЙ ЗАДАЧИ ДИНАМИКИ (ОПРЕДЕЛЕНИЕ СИЛ ПО ЗАДАННОМУ ДВИЖЕНИЮ) § 79. РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ДИНАМИКИ ПРИ ПРЯМОЛИНЕЙНОМ ДВИЖЕНИИ ТОЧКИ § 80.  ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ§ 81. ПАДЕНИЕ ТЕЛА В СОПРОТИВЛЯЮЩЕЙСЯ СРЕДЕ (В ВОЗДУХЕ) Глава XVII. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ § 83. КОЛИЧЕСТВО ДВИЖЕНИЯ ТОЧКИ. ИМПУЛЬС СИЛЫ § 84. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ § 85. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ (ТЕОРЕМА МОМЕНТОВ) § 86. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНОЙ СИЛЫ. ЗАКОН ПЛОЩАДЕЙ § 87. РАБОТА СИЛЫ. МОЩНОСТЬ § 88. ПРИМЕРЫ ВЫЧИСЛЕНИЯ РАБОТЫ § 89. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ТОЧКИ Глава XVIII. НЕСВОБОДНОЕ И ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЯ ТОЧКИ § 90. НЕСВОБОДНОЕ ДВИЖЕНИЕ ТОЧКИ § 91. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ § 92. ВЛИЯНИЕ ВРАЩЕНИЯ ЗЕМЛИ НА РАВНОВЕСИЕ И ДВИЖЕНИЕ ТЕЛ Глава XIX. ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ ТОЧКИ § 94. СВОБОДНЫЕ КОЛЕБАНИЯ БЕЗ УЧЕТА СИЛ СОПРОТИВЛЕНИЯ § 95. СВОБОДНЫЕ КОЛЕБАНИЯ ПРИ ВЯЗКОМ СОПРОТИВЛЕНИИ (ЗАТУХАЮЩИЕ КОЛЕБАНИЯ) § 96.  ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. РЕЗОНАНСГлава XX. ДВИЖЕНИЕ ТЕЛА В ПОЛЕ ЗЕМНОГО ТЯГОТЕНИЯ § 97. ДВИЖЕНИЕ БРОШЕННОГО ТЕЛА В ПОЛЕ ТЯГОТЕНИЯ ЗЕМЛИ § 98. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ЭЛЛИПТИЧЕСКИЕ ТРАЕКТОРИИ § 99. ПОНЯТИЕ О НЕВЕСОМОСТИ. МЕСТНЫЕ СИСТЕМЫ ОТСЧЕТА Раздел четвертый. ДИНАМИКА СИСТЕМЫ И ТВЕРДОГО ТЕЛА § 101. МАССА СИСТЕМЫ. ЦЕНТР МАСС § 102. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ОСИ. РАДИУС ИНЕРЦИИ § 103. МОМЕНТЫ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ПАРАЛЛЕЛЬНЫХ ОСЕЙ. ТЕОРЕМА ГЮЙГЕНСА § 104. ЦЕНТРОБЕЖНЫЕ МОМЕНТЫ ИНЕРЦИИ. ПОНЯТИЯ О ГЛАВНЫХ ОСЯХ ИНЕРЦИИ ТЕЛА § 105. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ПРОИЗВОЛЬНОЙ ОСИ Глава XXII. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС СИСТЕМЫ § 106. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ § 107. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС § 108. ЗАКОН СОХРАНЕНИЯ ДВИЖЕНИЯ ЦЕНТРА МАСС § 109. РЕШЕНИЕ ЗАДАЧ Глава XXIII. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ СИСТЕМЫ § 110.  § 111. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ § 112. ЗАКОН СОХРАНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ § 113. ПРИЛОЖЕНИЕ ТЕОРЕМЫ К ДВИЖЕНИЮ ЖИДКОСТИ (ГАЗА) § 114. ТЕЛО ПЕРЕМЕННОЙ МАССЫ. ДВИЖЕНИЕ РАКЕТЫ Глава XXIV. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ § 115. ГЛАВНЫЙ МОМЕНТ КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ § 116. ТЕОРЕМА ОБ ИЗМЕНЕНИИ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ (ТЕОРЕМА МОМЕНТОВ) § 117. ЗАКОН СОХРАНЕНИЯ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ § 118. РЕШЕНИЕ ЗАДАЧ § 119. ПРИЛОЖЕНИЕ ТЕОРЕМЫ МОМЕНТОВ К ДВИЖЕНИЮ ЖИДКОСТИ (ГАЗА) § 120. УСЛОВИЯ РАВНОВЕСИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ § 121. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ СИСТЕМЫ § 122. НЕКОТОРЫЕ СЛУЧАИ ВЫЧИСЛЕНИЯ РАБОТЫ § 123. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ § 124. РЕШЕНИЕ ЗАДАЧ § 125. СМЕШАННЫЕ ЗАДАЧИ § 126. ПОТЕНЦИАЛЬНОЕ СИЛОВОЕ ПОЛЕ И СИЛОВАЯ ФУНКЦИЯ § 127. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ.  ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИГлава XXVI. ПРИЛОЖЕНИЕ ОБЩИХ ТЕОРЕМ К ДИНАМИКЕ ТВЕРДОГО ТЕЛА § 128. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ § 129. ФИЗИЧЕСКИЙ МАЯТНИК. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ § 130. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА § 131. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ГИРОСКОПА § 132. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА Глава XXVII. ПРИНЦИП ДАЛАМБЕРА § 133. ПРИНЦИП ДАЛАМБЕРА ДЛЯ ТОЧКИ И МЕХАНИЧЕСКОЙ СИСТЕМЫ § 134. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИЛ ИНЕРЦИИ § 135. РЕШЕНИЕ ЗАДАЧ § 136. ДИНАМИЧЕСКИЕ РЕАКЦИИ, ДЕЙСТВУЮЩИЕ НА ОСЬ ВРАЩАЮЩЕГОСЯ ТЕЛА. УРАВНОВЕШИВАНИЕ ВРАЩАЮЩИХСЯ ТЕЛ Глава XXVIII. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ И ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ § 137. КЛАССИФИКАЦИЯ СВЯЗЕЙ § 138. ВОЗМОЖНЫЕ ПЕРЕМЕЩЕНИЯ СИСТЕМЫ. ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ § 139. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ § 140. РЕШЕНИЕ ЗАДАЧ § 141. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ Глава XXIX.  УСЛОВИЯ РАВНОВЕСИЯ И УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ§ 142. ОБОБЩЕННЫЕ КООРДИНАТЫ И ОБОБЩЕННЫЕ СКОРОСТИ § 143. ОБОБЩЕННЫЕ СИЛЫ § 144. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ § 145. УРАВНЕНИЯ ЛАГРАНЖА § 146. РЕШЕНИЕ ЗАДАЧ Глава XXX. МАЛЫЕ КОЛЕБАНИЯ СИСТЕМЫ ОКОЛО ПОЛОЖЕНИЯ УСТОЙЧИВОГО РАВНОВЕСИЯ § 147. ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ РАВНОВЕСИЯ § 148. МАЛЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ § 149. МАЛЫЕ ЗАТУХАЮЩИЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ § 150. МАЛЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ Глава XXXI. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ УДАРА § 151. ОСНОВНОЕ УРАВНЕНИЕ ТЕОРИИ УДАРА § 152. ОБЩИЕ ТЕОРЕМЫ ТЕОРИИ УДАРА § 153. КОЭФФИЦИЕНТ ВОССТАНОВЛЕНИЯ ПРИ УДАРЕ § 154. УДАР ТЕЛА О НЕПОДВИЖНУЮ ПРЕГРАДУ § 155. ПРЯМОЙ ЦЕНТРАЛЬНЫЙ УДАР ДВУХ ТЕЛ (УДАР ШАРОВ) § 156. ПОТЕРЯ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ПРИ НЕУПРУГОМ УДАРЕ ДВУХ ТЕЛ. ТЕОРЕМА КАРНО § 157. УДАР ПО ВРАЩАЮЩЕМУСЯ ТЕЛУ.  ЦЕНТР УДАРА |
Момент инерции твердого тела
Онлайн калькуляторы
На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.
Справочник
Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!
Заказать решение
Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!
Главная Справочник Физика Момент инерции твердого тела
Определение и общие сведения о моменте инерции твердого тела
Это скалярная (в общем случае тензорная) величина.
где – массы материальных точек, на которые разбивают тело; на квадраты расстояний от материальной точки до оси вращения.
Для непрерывного однородного тела, вращающегося около оси, момент инерции чаще определяют как:
где r – функция положения материальной точки в пространстве; – плотность тела; –объем элемента тела.
Тензор инерции
Совокупность величин:
называют тензором инерции. Диагональные элементы тензора: . Тензор инерции является симметричным.
Пусть все недиагональные элементы тензора равны нулю, не равны нулю только диагональные составляющие. Тогда тензор запишем как:
В таком случае оси тела совпадают с осями координат и являются главными осями инерции. Величины:
называют главными моментами инерции. Тензор в виде (4) приведен у диагональному виду. Моменты инерции, находящиеся вне главной диагонали матрицы (3) называются центробежными. Если оси системы координат направлены вдоль главных осей инерции тела, то центробежные моменты инерции равны нулю.
Если главные оси проведены через центр масс тела, то они называются центральными главными осями, а тензор центральным тензором.
Главные оси не всегда для тела не всегда легко отыскать. Но иногда достаточно использовать соображения симметрии. Так, в шаре относительно любой точки главные оси можно найти так.
Одна из главных осей проходит через центр шара, две другие ориентированы произвольно в плоскости, которая перпендикулярна первой оси.
Составляющие момента инерции сплошного тела относительно осей декартовой системы координат определены как:
где – координаты элемента массы тела (), которая обладает объемом .
Момент инерции твердого тела зависит от формы тела и распределения ассы в теле относительно оси вращения.
Величины, равные:
называют радиусами инерции тела по отношению к соответствующим осям системы координат.
Теорема Штейнера
В некоторых случаях вычисление момента инерции существенно облегчает знание теоремы Штейнера (иногда ее называют теоремой Гюйгенса): Момент инерции тела (J) относительно произвольной оси равен моменту инерции относительно оси, которая проведена через центр масс рассматриваемого тела (), плюс произведение массы тела (m) на расстояние между осями в квадрате, при условии, если оси параллельны:
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
Момент инерции тела зависит от (i) массы тела (ii) размера и формы тела (iii) оси вращения тела (iv) всего вышеперечисленного
Вопрос
Обновлено: 20.
05.2019
PRADEEP-СИСТЕМЫ ЧАСТИЦ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ-Множественный выбор вопросов Понимание 2
1 видеоРЕКЛАМА
লিখিত জবাব
A
0003B
(i) и (iii)
C
(ii) и (iii)
Ответ 9(2) Используя вышеприведенное понимание, выберите наиболее подходящий вариант ответа на каждый из следующих вопросов: Маховик массой 40 кг в форме цельного круглого диска диаметром 1 м развивает скорость 120 об/мин. Его момент инерции относительно поперечной оси, проходящей через его центр, равен
11765412
Момент инерции тела относительно данной оси — это инерция вращения тела вокруг этой оси. Оно представлено формулой I=MK2, где M — масса тела, а K — радиус вращения тела вокруг этой оси. Это скалярная величина, которая измеряется в кгм2. когда тело вращается вокруг заданной оси, при этом ось вращения также движется, то суммарный К.Э. тела =К.Е. перевода +К.Э. вращения
E=12mv2+12Iω2
С помощью приведенного выше понимания выберите наиболее подходящую альтернативу для каждого из следующих вопросов:
Кинетическая энергия вращения маховика в приведенном выше случае
11765413
Минимальный момент инерции однородного тела I о и оси.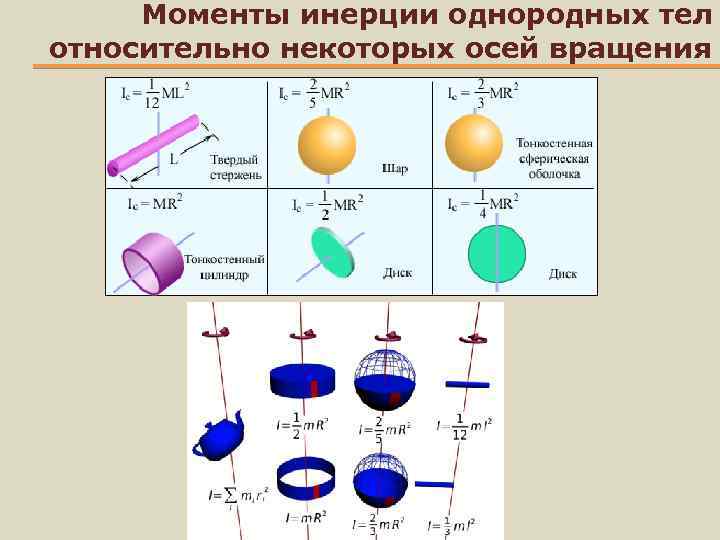
Ось должна проходить через COM тела. Момент инерции зависит от распределения массы вокруг оси вращения.
12229925
क्ष के परितः जड़त्व-आघूर्ण I है तब उस अक्ष के परतिण त्रिज्या है
76224488
500 परितः घूम रहा है। घूर्णन अक्ष से पिण्ड के द्रव्यमान केन्द्र की दू 1.2 ू टर है। पिण्ड का घूर्णन अक्ष के परितः जड़त्व आघूर्ण ड़।ज िए।
131221757
Если кинетическая энергия вращения тела вокруг оси равна 9 Дж, а момент инерции равен 2 кг м2, то угловая скорость тела вокруг оси вращения в рад/с равна
141173485
Момент инерции тела относительно данной оси равен 3,6 кг м2. Первоначально тело находится в состоянии покоя. Для того чтобы произвести вращательный К.Е. 800 Дж, необходимо приложить ускорение 15 рад с относительно этой оси в течение
141173524
Момент инерции тела относительно данной оси вращения зависит от:-
223152665
Момент инерции твердого тела равен _______ кинетической энергии вращения тела с единичной угловой скоростью вращения около заданная ось.
642646105
Кинетическая энергия вращения тела вокруг заданной оси равна 157 Дж. Его момент количества движения относительно этой оси равен 12,5 кг·м2с−1. Найдите частоту вращения тела и момент инерции относительно данной оси?
643020886
Тело массой M вращается вокруг оси с угловой скоростью omega . Если k — радиус вращения тела вокруг данной оси, то его угловой момент равен
643020965
. Тело массой M вращается вокруг оси с угловой скоростью omega. Если K — радиус вращения тела вокруг данной оси, то его угловой момент равен
643069156
Момент инерции тела относительно данной оси вращения зависит от:0003
644650790
РЕКЛАМА.
08:45
5.4: Момент инерции – Физика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 17392
- Тимон Идема
- Делфтский технологический университет через TU Delft Open
Предположим, у нас есть масса m на конце безмассовой палки длиной \(r\), вращающаяся вокруг другого конца палки.
Если мы хотим увеличить скорость вращения, нам нужно применить тангенциальное ускорение в 92\). По аналогии с массой, представляющей инерцию тела, подвергающегося линейному ускорению, мы будем идентифицировать эту величину как инерцию тела, подвергающегося вращательному ускорению, которую мы назовем моментом инерции и обозначим через \(I\):
\[\boldsymbol{\tau}=I \boldsymbol{\alpha} \label{крутящий момент}\]
Уравнение \ref{torque} является вращательным аналогом второго закона Ньютона. Расширяя наш предыдущий пример, мы можем найти момент инерции произвольного набора частиц с массами \(m_\alpha\) и расстояниями до оси вращения \(r_\alpha\) (где \(\alpha\) работает по всем частицам), и запишем: 92\) соответственно. Эти и некоторые другие примеры приведены в таблице 5.1. Ниже мы свяжем момент инерции с кинетической энергией движущегося и катящегося объекта, но сначала приведем две удобные теоремы, которые помогут в их вычислении.
| Объект | Ось вращения | Момент инерции | 9{2} \label{result}\]
|---|
{2}-2 \mathbf{d} \cdot \ int_{V} \mathbf{r} \rho \mathrm{d} V \label{proof} \end{align} \] 92 = \boldsymbol{d}·\boldsymbol{d}\). Последний интеграл в последней строке \ref{proof} равен положению центра масс, которое мы выбрали в начале координат, поэтому последний член равен нулю, и мы получаем \ref{result}. Обратите внимание, что первые две строки таблицы 5.1 (моменты инерции стержня) удовлетворяют теореме об перпендикулярных осях.