|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
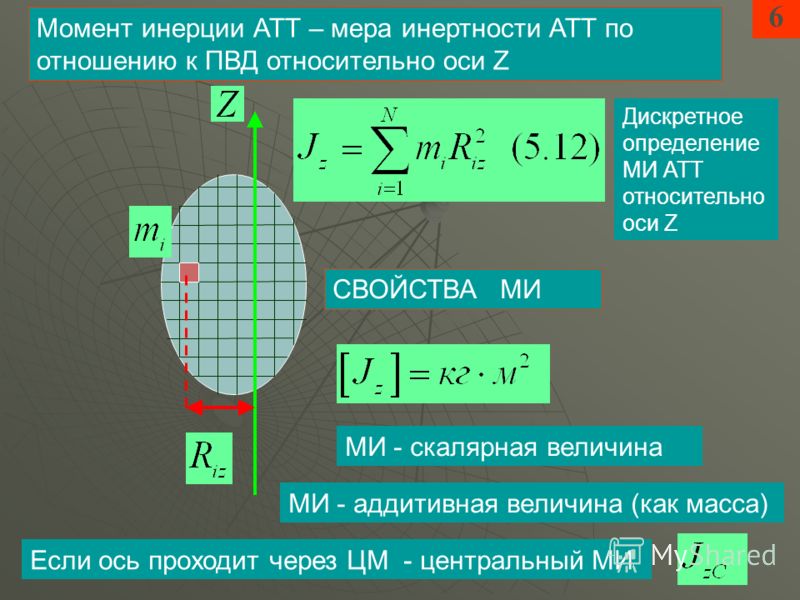
⇐ ПредыдущаяСтр 3 из 13Следующая ⇒ Моментом инерции системы относительно оси вращения называется физическая величина, равная сумме произведения масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси. теоремa Штейнера: момент инерции тела І относительно параллельной оси вращения равен моменту инерции Іс относительно параллельной оси, проходящей через центр масс Например, для обруча на рисунке момент инерции относительно оси O’O’, равен
Момент силы. Моментом силы относительно неподвижной точкиO называется псевдовекторная величина равная векторному произведению радиус-вектора , проведенному из точки O в точку приложения силы, на силу Модуль момента силы: – псевдовектор, его направление совпадает с направлением плоскости движения правого винта при его вращении от к . -где кратчайшее расстояния между линией действия силы и точкой О называется плечом силы. Моментом силы относительно неподвижной оси Z называется скалярная величина равнаяпроекции на эту ось вектора момента силы , определённого относительно произвольной точки O данной оси Z. Если ось Ось, положение которой в пространстве остается неизменнымпривращении вокруг тела в отсутствие внешних сил,называется свободной осью тела. Для тела любой формы и с произвольным распределением массы существует 3 взаимно перпендикулярных, проходящих через центр инерции тела оси, которые могут служить свободными осями:они называются главными осями инерции тела.
Моментом импульса материальной точки относительно некоторой точки О называется вектор , равный векторному произведению радиус-вектора материальной точки относительно точки О на импульс материальной точки Модуль момента импульса
Направление момента импульса определяется по правилу правого винта (вектора и составляют правую тройку векторов). Момент импульса системы материальных точек равен векторной сумме моментов импульсов отдельных материальных точек системы или векторному произведению радиус-вектора центра масс системы на импульс ее центра масс Величина момента импульса твердого тела относительно оси вращения где – момент инерции тела относительно оси z, w – угловая скорость тела. Изотропность пространства (осевая симметрия пространства) приводит к закону сохранения момента импульса: в замкнутых системах момент импульса сохраняется.
Основной закон динамики вращательного движения можно получить из второго закона Ньютона для поступательного движения твердого тела где mi – масса i-й точки; – угловое ускорение; ri – момент инерции i-й материальной точки. Мгновенное значение углового ускорения , есть первая производная угловой скорости по времени , то есть или , где – импульс момента силы – это произведение момента силы на промежуток времени – изменение момента импульса тела, – момент импульса тела есть произведение момента инерции J на угловую скорость , а есть . Поэтому основной закон динамики вращательного движения твердого тела формулируется так: “Импульс момента силы , действующий на вращательное тело, равен изменению его момента импульса ”: или
⇐ Предыдущая12345678910Следующая ⇒ Читайте также: Организация работы процедурного кабинета Статус республик в составе РФ Понятие финансов, их функции и особенности Сущность демографической политии |
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 225; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Момент инерции. Момент инерции материальной точки, обруча, цилиндра. Теорема Штейнера.
- Главная страница 🏠
- 📚 Библиотека
- 👉 Механика 👈
- Ответы на экзаменационные вопросы по курсу Механика
Нужна помощь в написании работы?
Узнать стоимость
Разобьем вращающееся тело на малые элементы Δmi. Расстояния до оси вращения обозначим через ri, модули линейных скоростей – через υi. Тогда кинетическую энергию вращающегося тела можно записать в виде:
Физическая величина зависит от распределения масс вращающегося тела относительно оси вращения. Она называется моментом инерции I тела относительно данной оси:
В пределе при Δm→ 0 эта сумма переходит в интеграл. Единица измерения момента инерции в СИ –
Момент инерции в динамике вращательного движения играет ту же роль, что и масса тела в динамике поступательного движения. Но есть и принципиальная разница. Если масса – внутреннее свойство данного тела, не зависящее от его движения, то момент инерции тела зависит от того, вокруг какой оси оно вращается. Для разных осей вращения моменты инерции одного и того же тела различны.
Для разных осей вращения моменты инерции одного и того же тела различны.
Момент инерции материальной точки: .
На рис. изображены однородные твердые тела различной формы и указаны моменты инерции этих тел относительно оси, проходящей через центр масс.
|
Моменты инерции IC некоторых однородных твердых тел. |
Если твердое тело вращается относительно некоторой неподвижной оси, то его момент инерции I можно выразить через момент инерции IC этого тела относительно оси, проходящей через центр масс тела и параллельной первой.
I = IC + md2
где m – полная масса тела, d- расстояние между осями. Это выражение называют теоремой Штейнера (теоремой о параллельном переносе оси вращения).
Поможем написать любую работу на аналогичную тему
Реферат
Момент инерции.
 Момент инерции материальной точки, обруча, цилиндра. Теорема Штейнера.
Момент инерции материальной точки, обруча, цилиндра. Теорема Штейнера.От 250 руб
Контрольная работа
Момент инерции. Момент инерции материальной точки, обруча, цилиндра. Теорема Штейнера.
От 250 руб
Курсовая работа
Момент инерции. Момент инерции материальной точки, обруча, цилиндра. Теорема Штейнера.
От 700 руб
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Поделись с друзьями
- Содержание
- Материалы 1
- Меню
Материальная точка.
 Поступательное движение твердого тела. Системы отчета. Перемещение, путь, скорость, ускорение.
Поступательное движение твердого тела. Системы отчета. Перемещение, путь, скорость, ускорение.Криволинейное движение. Тангенциальное и нормальное ускорения.
Инерциальные системы отсчета. Масса тел. Силы. Законы динамики Ньютона.
Силы в природе. Упругая сила. Закон Гука.
Сила тяготения. Вес тел. Невесомость.
Силы трения покоя и скольжения
Момент силы.
 Плечо силы.
Плечо силы.Момент инерции. Момент инерции материальной точки, обруча, цилиндра. Теорема Штейнера.
Основной закон динамики вращательного движения.
Материалы по теме:
Момент инерции материальной точки, Лекция
Добавить в избранное (необходима авторизация)
Момент инерции твердого тела
| на главную | к оглавлению |
Организационные, контрольно-распорядительные и инженерно-технические услуги
в сфере жилой, коммерческой и иной недвижимости. Московский регион. Официально.
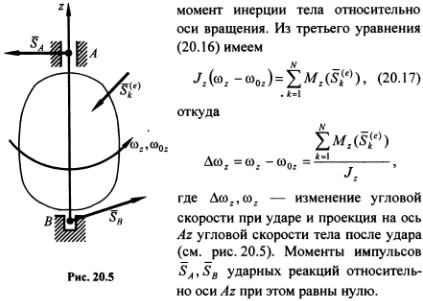
Рассмотрим твердое тело,
которое может вращаться относительно некоторой оси (рис.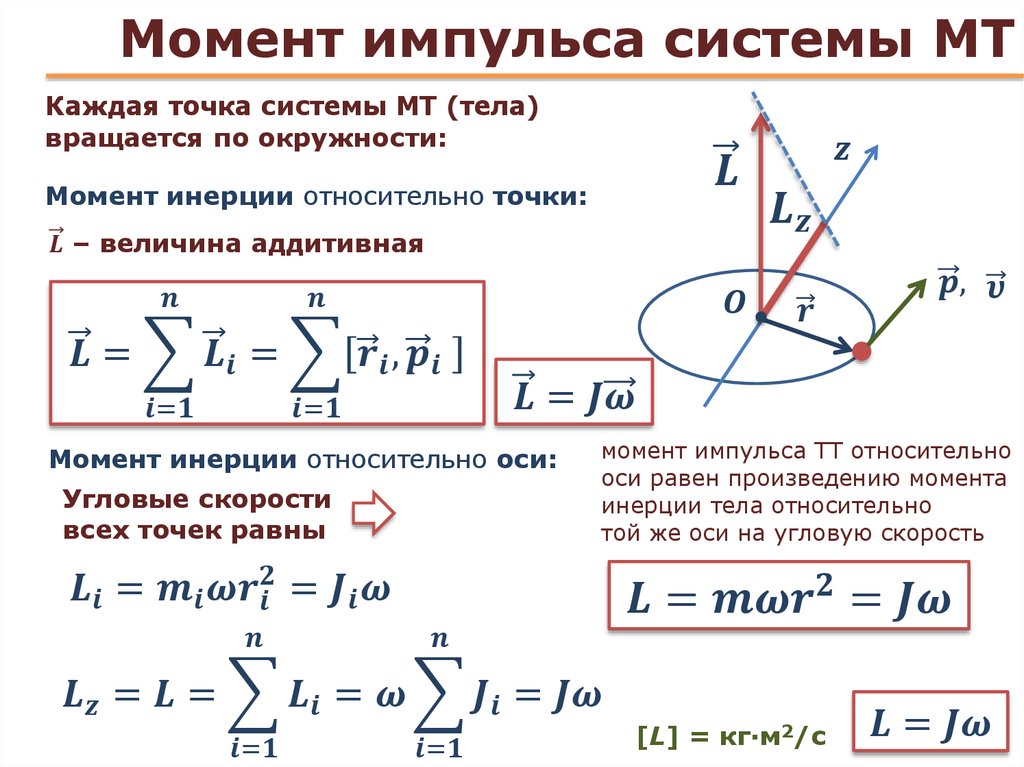 ). Момент импульса i-й
точки тела относительно этой оси определяется формулой:
). Момент импульса i-й
точки тела относительно этой оси определяется формулой:
. (1.84)
Выражая линейную скорость точки через угловую скорость тела и используя свойства векторного произведения, получим
(1.85)
Спроектируем момент импульса на ось вращения: — эта проекция определяет момент относительно этой оси. Получим
. (1.86)
где zi,- координата i—точки вдоль оси Z, a Ri, — расстояние точки от оси вращения. Суммируя по всем частицам тела, получим момент импульса всего тела относительно оси вращения:
. (1.87)
Величина
(1.88)
является моментом инерции тела относительно оси вращения. Момент импульса тела относительно данной оси вращения принимает, таким образом, вид:
Mz= J·ω. (1.89)
(1.89)
Полученная формула аналогична формуле Pz= mVzдля поступательного движения. Роль массы играет момент инерции, роль линейной скорости — угловая скорость. Подставив выражение (1.89) в уравнение для момента импульса (2.74), получим
J·βz = Nz. (1.90)
где βz. — проекция на ось вращения углового ускорения . Это уравнение эквивалентно по форме второму закону Ньютона.
В общем случае несимметричного тела вектор M не совпадает по направлению с осью вращения тела и поворачивается вокруг этой ocи вместе с телом, описывая конус. Из соображений симметрии ясно что для однородного тела, симметричного относительно оси вращения, момент импульса относительно точки, лежащей на оси вращения, совпадает с направлением оси вращения. В этом случае имеет место соотношение:
. (1.91)
(1.91)
Из выражения (1.90) следует, что при равенстве нулю момент внешних сил произведение Jω остается постоянным Jω = const и изменение момента инерции влечет за собой соответствующее изменение угловой скорости вращения тела. Этим объясняется известное явление, состоящее в том, что человек, стоящий на вертящейся скамье, разводя руки в стороны либо прижимая их к туловищу, изменяет частоту вращения.
Из полученных выше выражений ясно, что момент инерции является такой же характеристикой свойства инерции макроскопического тела в отношении вращательного движения, как инертная масса материальной точки в отношении поступательного движения. Из выражения (1.88) следует, что момент инерции вычисляется путем суммирования по всем частицам тела. В случае непрерывного распределения массы тела по его объему естественно перейти от суммирования к интегрированию, вводя плотность тела. Если тело однородно, то плотность определяется отношением массы к объему тела:
. (1.92)
(1.92)
Для тела с неравномерно распределенной массой плотность тела в некоторой точке определяется производной
. (1.93)
Момент инерции представим в виде:
, (1.94)
где DV — микроскопический объем, занимаемый точечной массой.
Поскольку твердое тело состоит из большого числа частиц, практически непрерывно заполняющих весь занимаемый телом объем, в выражении (1.94) микроскопический объем можно считать бесконечно малым, в то же время полагая, что точечная масса «размазана» по этому объему. Фактически мы производим сейчас переход от модели точечного распределения масс к модели сплошной среды, какой в действительности и является твердое тело благодаря большой его плотности. Произведенный переход позволяет в формуле (2.94) заменить суммирование по отдельным частицам интегрированием по всему объему тела:
. (1.95)
(1.95)
Рис. Вычисление момента инерции однородного диска
Здесь величины ρ и r являются функциями точки, например, ее декартовых координат.
Формула (1.95) позволяет вычислять моменты инерции тел любой формы. Вычислим в качестве примера момент инерции однородного диска относительно оси, перпендикулярной к плоскости диска и проходящей через его центр (рис.).
Поскольку диск однороден, плотность можно вынести из-под знака интеграла. Элемент объема диска dV = 2πr·b·dr, где b— толщина диска. Таким образом,
, (1.96)
где R — радиус диска. Введя массу диска, равную произведению плотности на объем диска π·R2 b, получим:
. (1.97)
Нахождение момента
инерции диска в рассмотренном примере облегчалось тем, что тело было однородным
и симметричным, а момент инерции вычислялся относительно оси симметрии тела. В
общем случае вращения тела произвольной формы вокруг произвольной оси,
вычисление момента инерции может быть произведено с помощью теоремы Штейнера:
момент инерции относительно произвольной оси равен сумме момента инерции J0относительно оси, параллельной данной и проходящей через центр инерции тела,
и произведения массы тела на квадрат расстояния между осями:
В
общем случае вращения тела произвольной формы вокруг произвольной оси,
вычисление момента инерции может быть произведено с помощью теоремы Штейнера:
момент инерции относительно произвольной оси равен сумме момента инерции J0относительно оси, параллельной данной и проходящей через центр инерции тела,
и произведения массы тела на квадрат расстояния между осями:
J=J0+ma2. (1.98)
Например, момент инерции диска относительно оси О’ в соответствии с теоремой Штейнера:
(1.99)
2$ в ньютоновской механике полезно вернуться к значению слова «момент».
Этимология моментов и импульсов относится к движению/движению, по-видимому, через латинский глагол «moveo», означающий «двигаться».
По-видимому, первое использование слова «момент» в английском языке имело в виду «важность» рычага, т. е. «равновесие» означает, что блоки на уровне имеют одинаковую важность, «неравновесие» означает, что вращательное движение уровня будет происходить за один раз. направление по сравнению с другим, что делает одно из них более «важным», чем другое.
е. «равновесие» означает, что блоки на уровне имеют одинаковую важность, «неравновесие» означает, что вращательное движение уровня будет происходить за один раз. направление по сравнению с другим, что делает одно из них более «важным», чем другое.
Таким образом, просто из-за «важности» Архимеда исторически говорить о других круговых движениях таким образом, который позволяет легко сравнивать с Архимедом, имеет смысл, поэтому, если мы собираемся использовать одно слово, связанное с латинским «moveo», чтобы относиться к тому, что называется импульсом, мы можем использовать другое слово, когда говорим о специфически вращательном движении, как это установил Архимед. Мы могли бы, например, договориться называть движение вдоль направления одного конкретного листа гиперболического параболоида «двигателем».
Момент векторной величины $\vec{A}$ в трех измерениях определяется как
$$\vec{r} \times \vec{A}.$$
Причина, по которой кто-то вообще хотел бы это сделать, и то, как это связано с приведенным выше обсуждением, заключается в том, что мы думаем о плоском/трехмерном пространстве как о пространстве, в котором мы можем перемещать векторы, как это обычно делается в механике, т. е. мы не рассматривайте их все как зафиксированные в начале координат, тогда мы будем думать о $\vec{A}$ как о стрелке, начинающейся на кончике $\vec{r}$ и указывающей в каком-то направлении.
Если вы разложите вектор $\vec{A}$ в базис, где радиальное движение является одним из ортогональных направлений, скажем, в сферический базис полярных координат, так что
$$\vec{A} = A_r \шляпа{r} + A_{\theta} \шляпа{\theta} + A_{\phi} \шляпа{\phi}$$
(всегда можно выбрать ориентацию, чтобы можно было игнорировать последний компонент и рассматривать его как плоское вращение в данный момент, если хотите, поэтому давайте установим $A_{\phi}=0$.)
тогда ясно
$$\vec{r} \times \vec{A} = 0 + A_{\theta} \vec{r} \times \hat{\theta} + 0 = A_{\theta} \vec{r} \times \ шляпа {\ тета} $ $
таким образом, момент вектора говорит нам, насколько $\vec{A}$ хочет двигаться в направлении (в плоскости, проходящей через начало координат), ортогональном $\hat{r}$ в данный момент времени, т.е. вращаться вокруг вектора $\vec{r}$.
е. мы не рассматривайте их все как зафиксированные в начале координат, тогда мы будем думать о $\vec{A}$ как о стрелке, начинающейся на кончике $\vec{r}$ и указывающей в каком-то направлении.
Если вы разложите вектор $\vec{A}$ в базис, где радиальное движение является одним из ортогональных направлений, скажем, в сферический базис полярных координат, так что
$$\vec{A} = A_r \шляпа{r} + A_{\theta} \шляпа{\theta} + A_{\phi} \шляпа{\phi}$$
(всегда можно выбрать ориентацию, чтобы можно было игнорировать последний компонент и рассматривать его как плоское вращение в данный момент, если хотите, поэтому давайте установим $A_{\phi}=0$.)
тогда ясно
$$\vec{r} \times \vec{A} = 0 + A_{\theta} \vec{r} \times \hat{\theta} + 0 = A_{\theta} \vec{r} \times \ шляпа {\ тета} $ $
таким образом, момент вектора говорит нам, насколько $\vec{A}$ хочет двигаться в направлении (в плоскости, проходящей через начало координат), ортогональном $\hat{r}$ в данный момент времени, т.е. вращаться вокруг вектора $\vec{r}$. Таким образом, момент силы
$$\vec{r} \times \vec{F}$$
это просто удобный способ изолировать движение «вращательных компонентов» силы, в общем случае он пренебрегает радиальным поведением этой силы, которое, очевидно, имеет большое значение. В особых случаях, например, когда $\vec{F}$ всегда является чисто вращательным, это, очевидно, единственное движение. Другой частный случай — когда $\vec{F}$ является чисто радиальным, то это, очевидно, можно использовать (как и в задаче Кеплера) для вывода закона сохранения для вращательного движения системы. Сила, очевидно, настолько важна и интерпретируется как действующая на массу, расположенную в $\vec{r}$, поэтому ей дается дополнительное название «крутящий момент», поскольку это компонент, который «закручивает» частицу вокруг начала координат, из которого мы видим вещи. . Обычно крутящий момент частицы называют скалярной величиной $r F_{\theta}$ или подавляющими индексами $rF$.
Таким образом, момент силы
$$\vec{r} \times \vec{F}$$
это просто удобный способ изолировать движение «вращательных компонентов» силы, в общем случае он пренебрегает радиальным поведением этой силы, которое, очевидно, имеет большое значение. В особых случаях, например, когда $\vec{F}$ всегда является чисто вращательным, это, очевидно, единственное движение. Другой частный случай — когда $\vec{F}$ является чисто радиальным, то это, очевидно, можно использовать (как и в задаче Кеплера) для вывода закона сохранения для вращательного движения системы. Сила, очевидно, настолько важна и интерпретируется как действующая на массу, расположенную в $\vec{r}$, поэтому ей дается дополнительное название «крутящий момент», поскольку это компонент, который «закручивает» частицу вокруг начала координат, из которого мы видим вещи. . Обычно крутящий момент частицы называют скалярной величиной $r F_{\theta}$ или подавляющими индексами $rF$.
В компонентах момент сверху есть
$$r F_{\theta} .$$
Таким образом, любую скалярную величину вида $r B$, где $r$ — длина вектора положения, можно интерпретировать как «момент» вектора, компонент которого в направлении вращения равен $B$.
(Говоря наоборот, скалярная величина $rB$ кодирует понятие «момент», она представляет площадь параллелограмма со сторонами $r$ и $B$. Половина этого, $\frac{1}{2} rB$ — площадь треугольника с основанием $B$ и высотой $r$, что более естественно относится к векторной картине движения в направлении, куда указывает основание треугольника, расположенного в месте окончания высоты, и становится нетривиальным размышление о важности закона равных площадей Кеплера, который можно вывести из этой интерпретации.Чтобы превратить его в векторную величину, мы рассматриваем $B$ как компоненту $\vec{B}$, ортогональную $\vec {r}$ в плоскости, содержащей $\vec{r}$ и $\vec{B}$.) 92 = r (mr)$ (на данном этапе взято из воздуха) как момент некоторого нового вектора, движение которого в направлении, ортогональном $\vec{r}$, имеет величину $mr$. Очевидно, что вектор не является вектором положения $\vec{r}$, умноженным на массу, т. е. $m \vec{r} = m r \hat{r}$, поскольку $\vec{r} \times m \vec{r} = 0$. 2$), так что мы назовем это моментом массы… нет, моментом инерции. Вопрос только в том, почему он по этой логике не выбрал более очевидный «момент массы/материи». 92 = r(mr)$ как момент чего-то отличного от «инерции» изначально («момент материи»), тот факт, что он действует как «вращательная инерция» в $\tau = I \alpha$ пути массы, делает в $F = ma$, а также тот факт, что создатель термина несколько лет спустя переформулировал его как «момент инерции», думая о формировании момента $\vec{r} \times$ как влияющего на левостороннюю сторону $\vec{F} = m \vec{a}$ естественным образом, а в правой части естественно заменить $m$ некоторой скалярной величиной, неудивительно, что термин может быть немного запутанным . 92$ размерности) в $F = ma$ изменится с $m$ на какую-то новую величину с новыми размерностями не только из $r$ в операции $\vec{r} \times$, но и из-за тот факт, что углы, то есть аргументы тригонометрических функций, безразмерны (или измеряются в радианах и т. д.), поэтому, если вам нужен угловой аналог $\vec{F} = m \vec{a}$, размеры множителя ускорения член должен будет измениться, когда ускорение превратится в угловое ускорение (которое имеет размеры только $[T]^{-2}$ от второй производной по времени).
2$), так что мы назовем это моментом массы… нет, моментом инерции. Вопрос только в том, почему он по этой логике не выбрал более очевидный «момент массы/материи». 92 = r(mr)$ как момент чего-то отличного от «инерции» изначально («момент материи»), тот факт, что он действует как «вращательная инерция» в $\tau = I \alpha$ пути массы, делает в $F = ma$, а также тот факт, что создатель термина несколько лет спустя переформулировал его как «момент инерции», думая о формировании момента $\vec{r} \times$ как влияющего на левостороннюю сторону $\vec{F} = m \vec{a}$ естественным образом, а в правой части естественно заменить $m$ некоторой скалярной величиной, неудивительно, что термин может быть немного запутанным . 92$ размерности) в $F = ma$ изменится с $m$ на какую-то новую величину с новыми размерностями не только из $r$ в операции $\vec{r} \times$, но и из-за тот факт, что углы, то есть аргументы тригонометрических функций, безразмерны (или измеряются в радианах и т. д.), поэтому, если вам нужен угловой аналог $\vec{F} = m \vec{a}$, размеры множителя ускорения член должен будет измениться, когда ускорение превратится в угловое ускорение (которое имеет размеры только $[T]^{-2}$ от второй производной по времени). 92 \hat{r} \times \hat{\theta}$ ‘момент материи в точке $\vec{r}$’, но интересует только компонент, ортогональный к $\vec{r}$ так что $m r \hat{\theta}$ поверхностно.
92 \hat{r} \times \hat{\theta}$ ‘момент материи в точке $\vec{r}$’, но интересует только компонент, ортогональный к $\vec{r}$ так что $m r \hat{\theta}$ поверхностно.
Ссылки.
- «Эйлер, Ньютон и основы механики», Мариус Стэн.
- «Theoria Motus Corporum Solidorum seu Rigidorum», Эйлер — переведено и аннотировано Яном Брюсом.
Вращение – Момент инерции
Предыдущий СледующийМомент инерции
Когда дело доходит до поступательного движения, идея массы довольно проста: тяжелые предметы труднее толкать. Это относится и к вращению — тяжелый объект труднее повернуть, — но дело не только в весе. И форма объекта, и точка, вокруг которой он вращается, имеют решающее значение для определения того, насколько легко или сложно его вращать.
Математически мы описываем влияние размера и формы на вращение чем-то, что называется моментом инерции объекта , сокращенно I .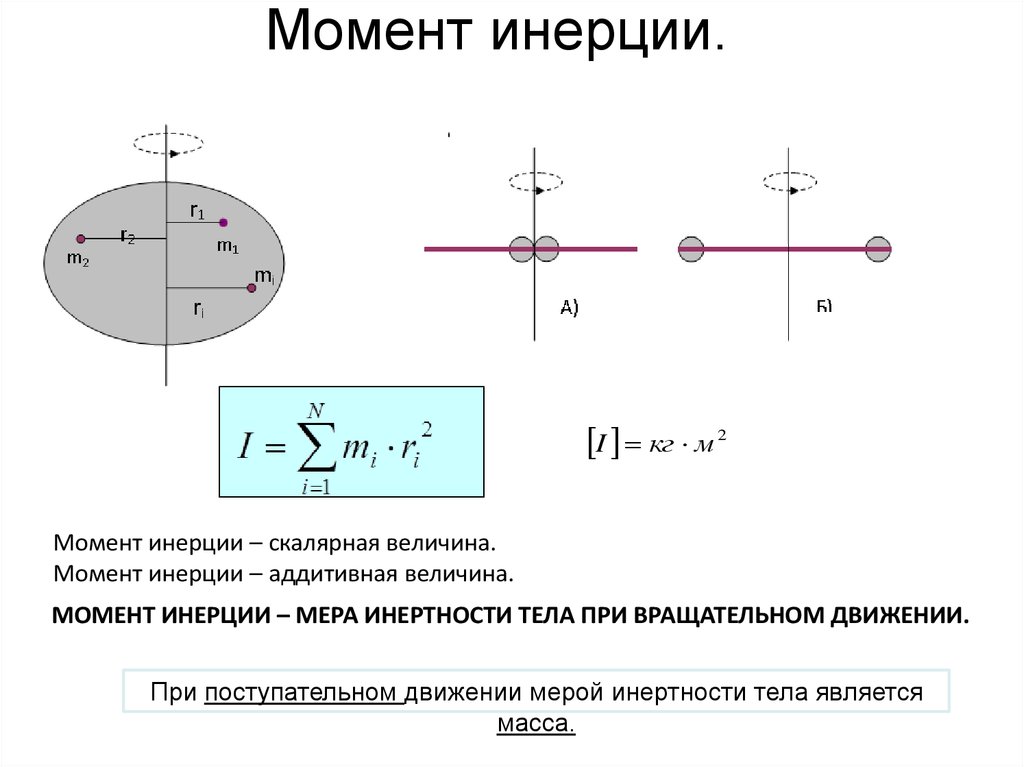 Момент инерции — это мера того, сколько инерции имеет объект — его сопротивление, в данном случае, вращательному движению. Большие и тяжелые объекты будут иметь высокий момент инерции, и их будет трудно поворачивать; меньшие объекты неправильной формы также могут иметь высокие моменты инерции, и их так же трудно повернуть.
Момент инерции — это мера того, сколько инерции имеет объект — его сопротивление, в данном случае, вращательному движению. Большие и тяжелые объекты будут иметь высокий момент инерции, и их будет трудно поворачивать; меньшие объекты неправильной формы также могут иметь высокие моменты инерции, и их так же трудно повернуть.
Короче говоря, чем больше масса объекта вдали от оси, вокруг которой он вращается, тем больше работы требуется, чтобы его повернуть.
Для точки с массой, вращающейся вокруг точки на расстоянии r , ее момент инерции равен:
Мы измеряем момент инерции в кг · м 2 , взвешенная оценка массы по расстоянию.
Если есть целая группа вращающихся точечных масс, их совокупный момент инерции является просто суммой моментов инерции всех отдельных объектов:
-часть аспекта момента инерции и цифра I для сложных твердых тел, таких как сферы или цилиндры. Показательный пример даже для тех, кто не склонен к исчислению: хула-хуп.
Представьте, что обруч сделан из очень-очень маленьких кусков обруча, каждый из которых имеет массу м , и склеены вместе: (радиус обруча). Тогда каждый кусок обруча имеет момент инерции вокруг этой оси вращения I чанк = мр 2 . The moment of inertia of the hoop is the sum of all the chunks: I hoop = m 1 r 2 + m 2 r 2 + m 3 r 2 + …= МР 2 , где – общая масса обруча. Тот же процесс работает с дисками, стержнями, кубами, но процесс суммирования немного сложнее. Вот разбивка некоторых распространенных форм:
Теорема о параллельных осях
Если вы помните весь путь назад к нашему обсуждению импульса, вы, возможно, заметили, что все эти моменты инерции рассчитываются вокруг оси вращения, которая проходит прямо через центр масс объекта. Для другой точки вращения объекта — скажем, стержня, вращающегося вокруг одного конца, как турникет, а не вокруг своего центра — мы используем теорему о параллельной оси , чтобы найти момент инерции объекта. Одна загвоздка в том, что новая ось вращения должна быть параллельна оси, проходящей через центр масс. Если это так, то:
Для другой точки вращения объекта — скажем, стержня, вращающегося вокруг одного конца, как турникет, а не вокруг своего центра — мы используем теорему о параллельной оси , чтобы найти момент инерции объекта. Одна загвоздка в том, что новая ось вращения должна быть параллельна оси, проходящей через центр масс. Если это так, то:
I || — новый момент инерции вокруг новой оси вращения, I см — первоначальный момент инерции вокруг оси, проходящей через центр масс, M — масса объекта, d — расстояние между старой и новой осями вращения. Вращение вокруг оси, не проходящей через центр масс, всегда будет увеличивать I — член Md 2 не может быть отрицательным, потому что другая ось вращения всегда будет иметь большую массу объекта. дальше, чем ось, проходящая через центр масс.
Распространенные ошибки
Помните, что моменты, перечисленные для распространенных форм, верны только в том случае, если ось вращения проходит через центр масс в указанном направлении. Для оси вращения, расположенной в другой точке (но в том же направлении), мы можем использовать теорему о параллельной оси, чтобы получить правильный момент инерции; при другом направлении вращения момент инерции может быть совершенно другим.
Для оси вращения, расположенной в другой точке (но в том же направлении), мы можем использовать теорему о параллельной оси, чтобы получить правильный момент инерции; при другом направлении вращения момент инерции может быть совершенно другим.
Закуска для мозгов
В то время как теорема о параллельных осях проделала огромную работу по объяснению моментов инерции для многих простых и сложных форм, движение одного объекта, которое всегда ускользало от объяснения даже самых проницательных физиков, — это вращение Мика Джаггера вокруг ось микрофонной стойки.
Предыдущий СледующийПодробнее о вращении Навигация
Это продукт премиум-класса
Разблокировать эти функции
Устали от рекламы?
Присоединяйтесь сегодня и никогда больше их не увидите.
Начало работы
Момент инерции – GeeksforGeeks
Движение тел может быть разных типов, таких как линейное движение, круговое движение и вращательное движение. Согласно первому закону движения Ньютона, если объект неподвижен, он будет оставаться в неподвижном состоянии, а если он находится в движении, он будет оставаться в движении, пока к нему не будет приложена внешняя сила. Это связано с инерцией тела. Как линейное движение имеет инерцию, так и вращательное движение имеет момент инерции. В этой статье мы собираемся изучить этот момент инерции. Кроме того, мы собираемся изучить определение, математическое выражение, приложения и теорему и многое другое о моменте инерции. Таким образом, чтобы узнать о моменте инерции, мы должны знать об основной концепции, показанной ниже:0004
Согласно первому закону движения Ньютона, если объект неподвижен, он будет оставаться в неподвижном состоянии, а если он находится в движении, он будет оставаться в движении, пока к нему не будет приложена внешняя сила. Это связано с инерцией тела. Как линейное движение имеет инерцию, так и вращательное движение имеет момент инерции. В этой статье мы собираемся изучить этот момент инерции. Кроме того, мы собираемся изучить определение, математическое выражение, приложения и теорему и многое другое о моменте инерции. Таким образом, чтобы узнать о моменте инерции, мы должны знать об основной концепции, показанной ниже:0004
Центр масс
Центр масс тела или системы частиц — это точка, в которой можно предположить, что вся масса этого тела или системы частиц сосредоточена так, что скорость вращения одного частица, равная полной массе тела с центром в центре масс, точно такая же. Как и движение всего тела. “ Центр масс системы – это точка, в которой вся масса системы может считаться сосредоточенной “.
Вращательное движение твердого тела
Если тело покоится в точке так, что оно может свободно перемещаться вокруг этой точки, то при приложении к телу внешней силы оно не движется в направлении силы, но движется вдоль оси, проходящей через эту точку, начинает двигаться вокруг. это движение тела называется вращательным движением, а ось, вокруг которой вращается тело, называется осью вращения. ” Когда при приложении силы или пары сил к твердому телу тело начинает вращаться вокруг оси, проходящей через него, тогда его движение называется вращательным движением “.
Момент инерции Как линейное движение имеет инерцию, так и вращательное движение имеет момент инерции. Согласно первому закону движения Ньютона, неподвижный объект останется неподвижным, а движущийся объект будет продолжать двигаться прямолинейно с той же скоростью, если к нему не будет приложена внешняя сила, т. е. объект может не меняет свое положение автоматически, но когда к объекту прикладывается внешняя сила для изменения его положения, этот объект сопротивляется ей. Эта склонность объекта называется его Инерция .
Эта склонность объекта называется его Инерция .
Точно так же все во вращательном движении, независимо от того, движется ли оно вокруг оси вращения или способно вращаться, но в состоянии покоя, сопротивляется изменению, вызванному внешней силой. эта тенденция тела называется его Моментом Инерции .
Следовательно, вращательному движению тела противодействует внешняя сила-момент, приложенная для изменения его вращательного состояния, эта тенденция называется его моментом инерции.
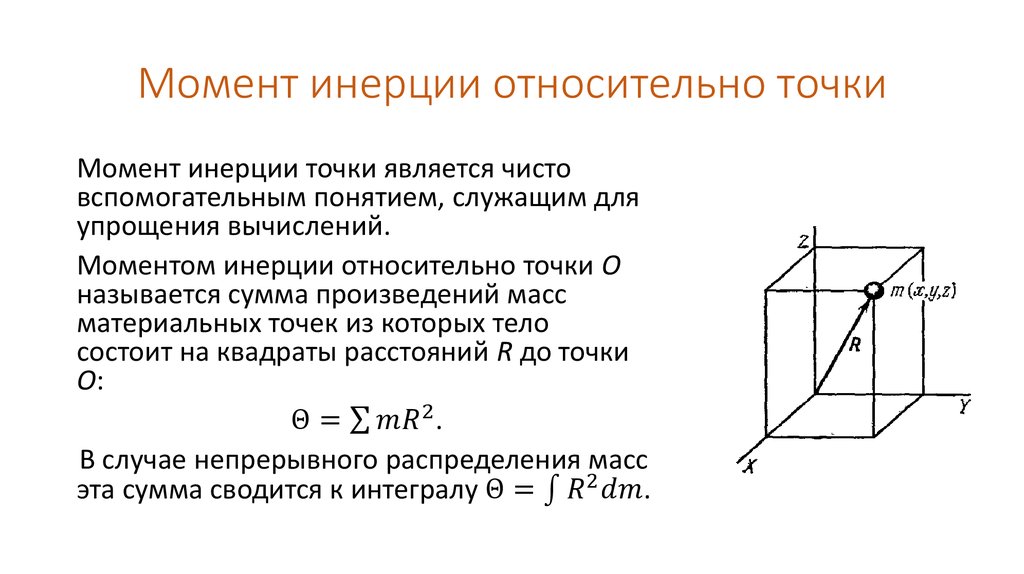
Момент инерции является скалярной величиной. Математически произведение квадрата массы частицы на расстояние от оси вращения называется моментом инерции частицы относительно оси вращения.
Предположим, что частица массой m движется относительно оси вращения XY , тогда момент инерции частицы около XY будет равен I = mr 2 0 0 0 для момента инерции тела
Пусть твердое тело движется с равномерной угловой скоростью ω вокруг оси AB , проходящей через точку O , перпендикулярную плоскости. Предположим, что это тело состоит из множества мелких частиц, масса которых равна m1, m2, m3 и т. д. а их расстояния от оси вращения равны соответственно r1, r2, r3…., и т. д.
Предположим, что это тело состоит из множества мелких частиц, масса которых равна m1, m2, m3 и т. д. а их расстояния от оси вращения равны соответственно r1, r2, r3…., и т. д.
По определению, момент инерции частицы относительно оси AB = Масса частицы * Квадрат расстояния частицы от оси вращения
Итак, Момент инерции первой частицы = m1*r1 2
Момент инерции первой частицы = m2*r2 2
Момент инерции первой частицы = m3*r3 2
……………………………… ………..Так далее.
Теперь момент инерции всего тела относительно оси вращения AB будет равно сумме моментов инерции всех частиц, поэтому
I = m1*r1 2 + m2*r2 2 + m3*r3 2 +……
или I = Σ m*r 2
Здесь I представляют момент инерции всего тела относительно оси вращения, а знак Σ представляет сумму. Из уравнения видно, что момент инерции тела относительно оси вращения равен сумме произведения массы каждой частицы этого тела на квадрат ее перпендикулярного расстояния от оси вращения.
Радиус инерцииПримечание: После изменения размера, формы или оси тела изменится момент инерции.
Радиус инерции тела – это перпендикуляр к расстоянию от оси вращения до точки, в которой момент инерции, полученный путем принятия полной массы тела за центр, равен к фактическому моменту инерции объекта. Обозначается К.
Если масса и радиус вращения тела равны М и К соответственно, то момент инерции тела равен
I = MK 2 ……1
Таким образом, радиус вращения тела равен перпендикуляру к оси вращения, квадрат которого, умноженный на массу этого тела, дает момент инерции этого тела около та ось.
Снова по уравнению 1, K 2 = I/M
или K = √I/m
Таким образом, радиус вращения тела вокруг оси равен квадратному корню из отношения тела относительно этой оси.
Теоремы о моменте инерцииСуществует три типа теорем, которые очень важны в отношении момента инерции:
- Теорема сложения,
- Теорема о вертикальной оси и
- Теорема о параллели ось.

Теорема сложения
Момент инерции системы, состоящей из многих частиц, относительно одной оси вращения равен сумме моментов инерции каждой частицы относительно этой оси. если I 1 , I 2 , I 3 ……..и т. д. – соответственно момент инерции различных частиц системы относительно одной оси вращения, затем общий момент инерции системы.
И = И 1 + И 2 + И 3 + ……………….
Ясно, что если из тела, имеющего момент инерции I , удалить часть момента инерции I’ , то оставшееся тело будет иметь остаточный момент инерции = (I – I’) о одна и та же ось вращения.
Теорема о вертикальной оси
Сумма момента инерции тела относительно двух взаимно перпендикулярных осей, расположенных в плоскости тела, равна моменту инерции тела относительно третьей оси, перпендикулярной две оси и проходит через точку их пересечения.
На рисунке выше. OX и OY имеют две такие оси в плоскости корпуса, которые перпендикулярны друг другу. Третья ось OZ , которая перпендикулярна плоскости корпуса и проходит через точку пересечения осей OX и OY . Если I x , I Y , и I Z – это моменты инерции тела вокруг оси OX , OY и ун. к этой теореме
I x + I y = I z
Теорема о параллельности осей
Согласно этой теореме момент инерции тела относительно данной оси равен сумме момента инерции относительно оси, проходящей через центр масс этого тела, и произведения квадрат массы тела и перпендикулярное расстояние между двумя осями.
Пусть на приведенном выше рисунке мы должны найти момент инерции I O тела, проходящего через точку O и относительно оси, перпендикулярной плоскости, а момент инерции тела, проходящего через центр масс C и относительно оси, параллельной данной оси, равен I C , то согласно этому теорема
I O = I C + Ml 2
где M — масса всего тела, а l — перпендикулярное расстояние между двумя осями.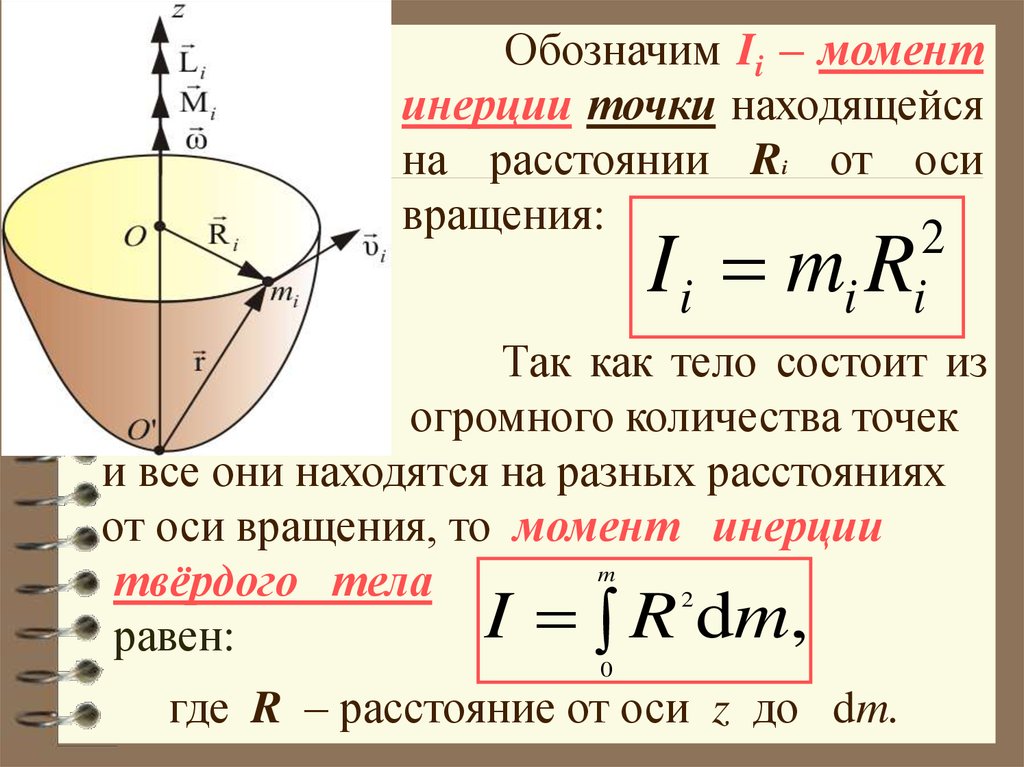
- Сплошная прямоугольная пластина: Если масса пластины равна M, длина l и ширина b, то момент инерции проходит через центр тяжести относительно оси, перпендикулярной плоскости пластины.
I = M( l 2 + b 2 / 12)
- Круговой диск: геометрическая ось
I = 1/2(Mr 2 )
- Однородный тонкий стержень: Если масса стержня равна M, а длина равна l, то момент инерции относительно оси, перпендикулярной длина стержня и проходящая через его центр тяжести
I = Ml 2 /12
- Круговое кольцо: Если масса кольца M и радиус кольца равны r, то момент инерции относительно оси, проходящей перпендикулярно к центру кольца, равен
I = MR 2
- Твердая сфера: , если твердая сфера имеет массу M и радиус R, затем момент инерции около диаметра
 9.9.9.9.9.9.. 9 Imetermet 2/5Mr 2
9.9.9.9.9.9.. 9 Imetermet 2/5Mr 2 Разница между моментом инерции и моментом инерции
| Старший номер | Инерция | Момент инерции |
|---|---|---|
| 1. | Важность линейного движения. | Его значение во вращательном движении. |
| 2. | Это то свойство объекта, которое препятствует изменению состояния объекта при прямолинейном движении. | Моментом инерции называется такое свойство объекта, которое противодействует изменению состояния объекта при вращательном движении. |
| 3. | Инерция объекта зависит только от его массы. | Момент инерции объекта зависит от его массы и распределения массы относительно оси вращения. |
| 4. | Инерция объекта фиксирована. | Момент инерции объекта меняется относительно разных осей вращения. |
Применение момента инерции
- Благодаря большему моменту инерции Земля вращается вокруг своей оси с той же угловой скоростью.
- Небольшое подвижное колесо расположено под мотором детской игрушки. После трения этого колеса о землю и выхода из двигателя, за счет момента инерции колеса, двигатель еще некоторое время продолжает работать.
- Каждый двигатель состоит из большого и тяжелого колеса, прикрепленного к его валу, причем большая часть его массы приходится на его окружность. Следовательно, его момент инерции высок. Это колесо называется маховиком. Крутящий момент, приводящий в движение вал двигателя, продолжает увеличиваться. Поэтому вращение вала может быть не равномерным, но благодаря наличию движущегося колеса с большей инерцией вал продолжает вращаться с почти постоянной скоростью.
- В колесе воловьей повозки, рикши, скутера, велосипеда и т. д. большая часть массы сосредоточена на его окружности или ободе.
 этот обруч или рутина прикреплены к оси колеса жесткими спицами. При этом увеличивается его момент инерции. Поэтому, когда ноги перестают двигаться при езде на велосипеде, колесо еще какое-то время продолжает вращаться.
этот обруч или рутина прикреплены к оси колеса жесткими спицами. При этом увеличивается его момент инерции. Поэтому, когда ноги перестают двигаться при езде на велосипеде, колесо еще какое-то время продолжает вращаться.
Примеры задач
Вопрос 1. Тело массой 500 г вращается вокруг оси. расстояние центра масс кузова от оси вращения 1,2 м. найти момент инерции тела относительно оси вращения.
Решение:
1 900 см Вопрос об оси вращения расстояние от центра масс тела массой 1,2 кг равно 13 см. вычислить радиус вращения и момент инерции относительно оси, проходящей через центр масс.Учитывая, что M = 500 г = 0,5 кг, r = 1,2 м.
Очевидно, можно предположить, что вся масса тела находится в его центре масс. Тогда момент инерции тела относительно оси вращения.
I = Mr 2
=> I = 0,5 * (1,2) 2
=> I = 0,72 кг·м 2

Решение:
Учитывая, что M = 1,0 кг, K = 13 см, l = 12 см, K СМ = ?, I СМ = ?
From Theorem of Parallel Axis I = I CM + Ml 2
=> K 2 = K CM 2 + l 2
or K CM 2 = K 2 – L 2
=> K CM 2 = (13) 2 – (12) 2 = 25
=> K CM = 5
=> K CM = 5
=> K CM = 5
, Момент инерции I СМ = МК см 2I см = 1,0 * (0,05) 2 = 2,5 * 10 -3 кг м 2
Вопрос 3. Кузов 0,1 кг. ось. если расстояние центра масс тела от оси вращения равно 0,5 м, то найти момент инерции тела.
Решение:
Учитывая, что M = 0,1 кг и r = 0,5 м
, значит, I = Mr 2
=> I = 0,1 * (0,5) 2
=> I = 0,025 кг·м 2
Вопрос 4.

 Все правила по сольфеджио
Все правила по сольфеджио



 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь – 161.97.168.212 (0.008 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь – 161.97.168.212 (0.008 с.)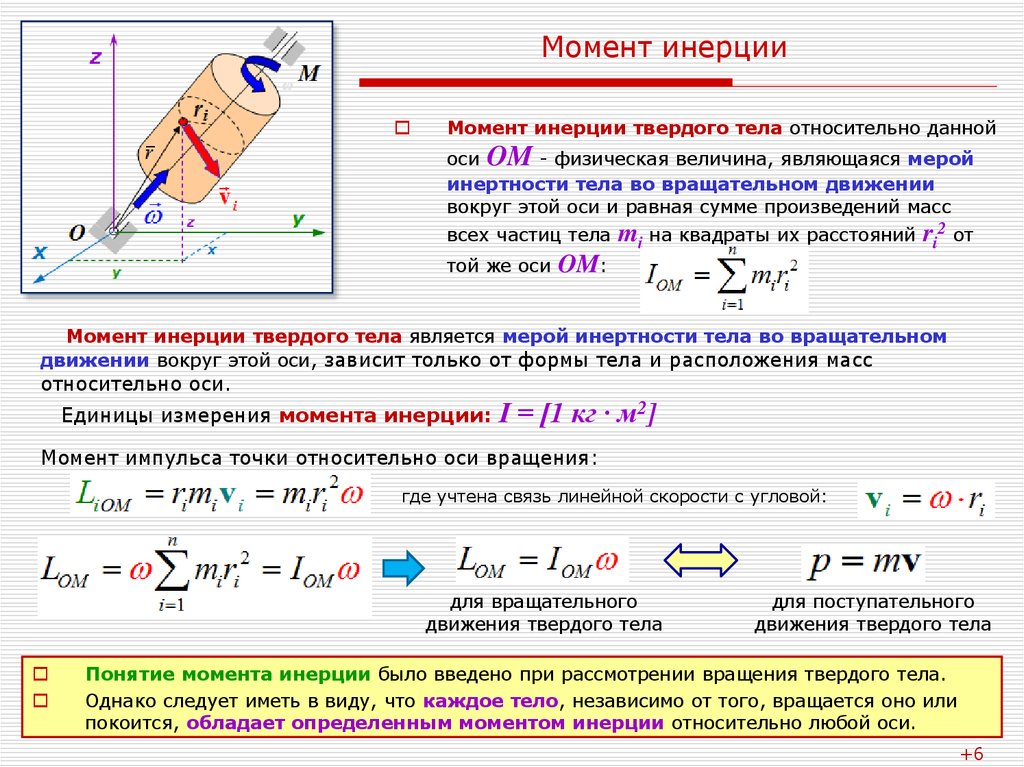 Момент инерции материальной точки, обруча, цилиндра. Теорема Штейнера.
Момент инерции материальной точки, обруча, цилиндра. Теорема Штейнера.
 этот обруч или рутина прикреплены к оси колеса жесткими спицами. При этом увеличивается его момент инерции. Поэтому, когда ноги перестают двигаться при езде на велосипеде, колесо еще какое-то время продолжает вращаться.
этот обруч или рутина прикреплены к оси колеса жесткими спицами. При этом увеличивается его момент инерции. Поэтому, когда ноги перестают двигаться при езде на велосипеде, колесо еще какое-то время продолжает вращаться.