Момент инерции тонкого однородного стержня: 23. Вычисление момента инерции тонкого однородного стержня относительно перпендикулярной оси.

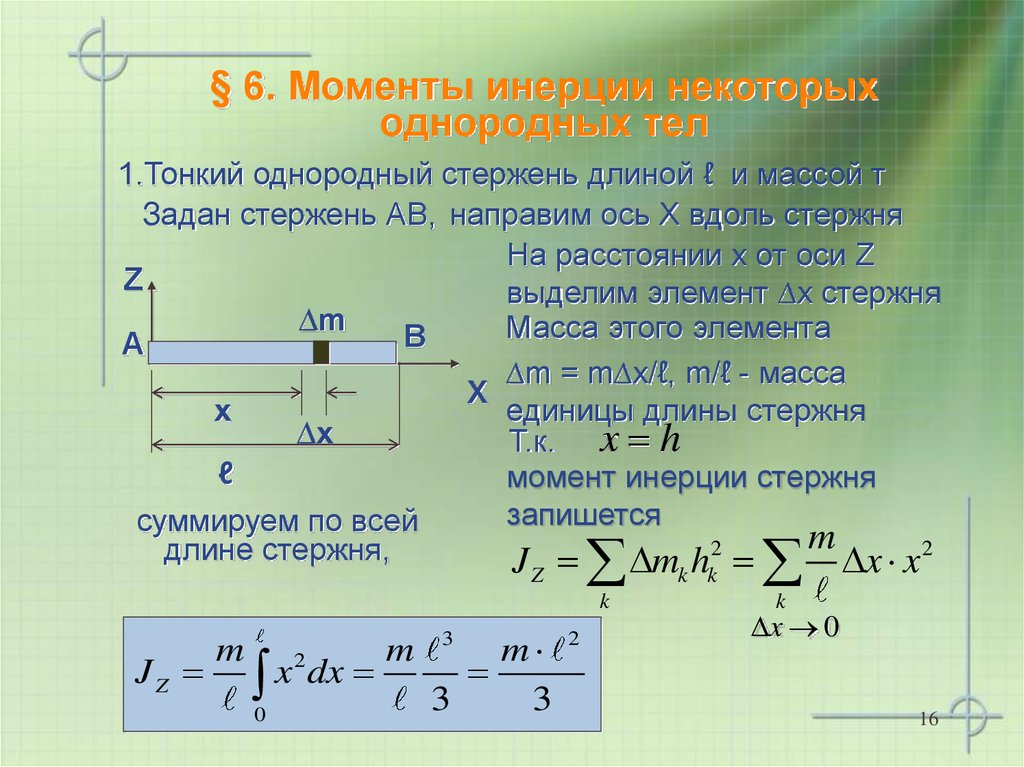
23. Вычисление момента инерции тонкого однородного стержня относительно перпендикулярной оси.

Пусть тонкий стержень имеет длину l и массу m. Разделим его на малые элементы длины dx (рис.27), масса которых . Если выбранный элемент находится на расстоянии x от оси, то его момент инерции , т.е.

Интегрируя последнее соотношение в пределах от 0 до l/2 и удваивая полученное выражение (для учета левой половины стержня), получим

(п.1)

Это выражение может быть получено и другим способом, с помощью метода подобия. Будем считать, что рассматриваемый стержень состоит из двух половин (рис.28). Каждая из них имеет массу m/2 и длину l/2 .

Выражение для момента инерции стержня должно включать его массу и длину, так как это единственные параметры, определяющие его инерционные свойства при вращении. Пусть (п. 2)

где k– неизвестный коэффициент.

Для каждой из половин стержня при вращении вокруг оси AA^` можно найти момент инерции, используя (п.2) (п.3)

Полный момент инерции стержня

(п.4)

Но этот же момент инерции, согласно (п.2) равен kml². Приравнивая (п.4) и (п.2) имеем

(п.5)

или и, следовательно,

(п.6)

т.е. , что совпадает с (п.1)

24. Вычисление момента инерции бесконечно круглого кольца относительно оси, перпендикулярной плоскости кольца.

Для расчета моментов инерции тонкого кольца/диска массы

m и радиуса R выберем систему координат так, чтобы ее оси совпадали с главными центральными осями (рис. 32). Определим момент инерции тонкого однородного кольца/диска относительно оси z , перпендикулярной к плоскости диска. Рассмотрим бесконечно тонкое кольцо с внутренним радиусом r и наружным r+dr. Площадь такого кольца ds=2r $\pi$ dr, а его масса , где S= $\pi$ R² – площадь всего кольца/диска. Момент инерции тонкого кольца найдется по формуле dJ=dmr². Момент инерции всего диска определяется интегралом

(п.18)

Для определения J_x воспользуемся симметрией диска (J_x=J_y) и утверждением (п.10), полученным при расчете момента инерции прямоугольной пластины. При этом из (п.10) получаем

J_z=2J_x (п.19)

Откуда

(п. 20)

25. Вычисление момента инерции однородного сплошного цилиндра (диска) относительно продольной геометрической оси.

Выберем оси системы координат, совпадающие с главными центральными осями так, как показано на рис.33. Определим момент инерции цилиндра относительно оси z. Цилиндр представляет собой набор тонких дисков с массами dm и моментами инерции . Момент инерции цилиндра равен сумме моментов инерций dJ_z тонких дисков

(п.21)

где – радиус цилиндра, – его масса.

Пусть теперь ось вращения проходит через центр масс цилиндра перпендикулярно его продольной оси (рис.33) и совпадает с осью координат x. Представим цилиндр как совокупность тонких дисков толщиной

dz, массой ( l – длина цилиндра). Момент инерции тонкого диска относительно оси Ox dJ^`_x в соответствии с (п. 20) и теоремой Гюйгенса-Штейнера равен

(п.22)

где z – расстояние от диска до центра цилиндра.

Момент инерции всего цилиндра найдем после интегрирования по z (по всей длине цилиндра)

(п.23)

Откуда получаем

(п.24)

Момент инерции стержня однородного и тонкого. Использование теоремы Штейнера. Пример задачи

В физике для описания инерционных качеств поступательного или линейного движения пользуются понятием массы тела. Если же движение рассматривается вокруг некоторой оси вращения, то используют несколько иную физическую характеристику – момент инерции. В данной статье рассмотрим, что это за величина и как можно рассчитать момент инерции тонкого стержня.

Вращение и момент инерции

Инерции момент проще всего ввести для материальной точки. Когда она, обладая массой M, вращается вокруг оси, описывая окружность радиусом R, то момент инерции для нее определяется по формуле:

I = M*R².

Любое реальное тело, какой бы сложной геометрической формой оно не обладало, можно представить как совокупность материальных точек. Это означает, что для всего тела или системы твердых тел величину I можно вычислить, если проинтегрировать по элементарным массам dm выражение выше. Общая формула для определения момента инерции имеет вид:

I = ∫_m(r²*dm).

Через объем и плотность это равенство записывается в таком виде:

I = ∫_V(ρ*r²*dV).

Его часто применяют для вычисления значений I конкретных геометрических объектов.

Физический смысл инерции момента I заключается в том, что он определяет, насколько “сложно” данной силе, создающей некоторый крутящий момент, раскрутить или остановить вращающуюся систему. Иными словами, I характеризует инерционные свойства изучаемой системы.

Самым известным примером использования момента инерции является маховик двигателя внутреннего сгорания в автомобилях. Благодаря большому значению величины I, маховик обеспечивает плавность движения автомобиля, сглаживая любые резкие воздействия на коленчатый вал. Пример иного характера, где также важно знать момент инерции, – это закон сохранения момента импульса. Применяется он для поворота вокруг оси искусственных спутников в космическом пространстве Земли.

Тонкий стержень и оси вращения

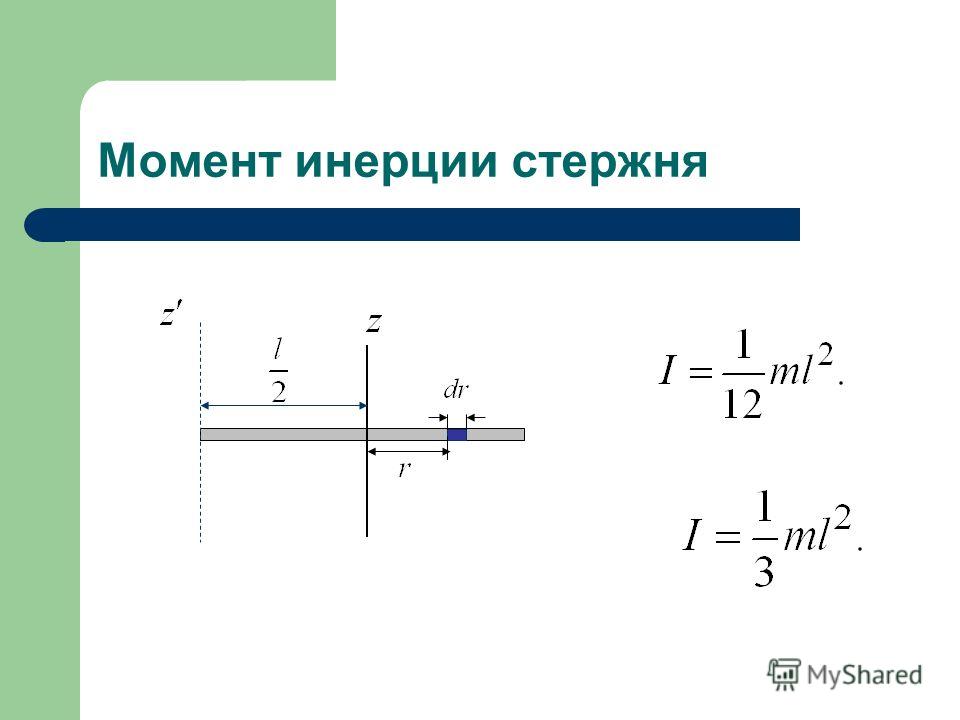
Далее будет рассмотрен момент инерции стержня относительно осей (разных). Вычисления будут проводиться для тонкого стержня, который обладает однородным распределением массы, то есть его плотность во всех точках является постоянной величиной. Под тонким понимают такой стержень, у которого ширина (толщина) намного меньше, чем его длина L. Для обозначения его массы будем использовать букву M.

Из приведенных выше формул следует, что величина I зависит от относительного положения тела и оси вращения. Для стержня можно выделить три основных оси. Одна из них проходит через длину всего стержня. Поскольку его толщина стремится к нулю, то момент инерции для такого положения тела также будет стремиться к этому значению.

Две другие оси перпендикулярны длине рассматриваемого тела. Одна из них проходит через центр масс, назовем ее O₁, вторая – через конец стержня, обозначим ее O₂. Относительно них и вычислим величину I.

Момент инерции относительно O1

В первую очередь выпишем общую формулу. Имеем:

I = ∫_V(ρ*r²*dV).

Обозначим площадь сечения стержня буквой S. Очевидно, что она стремится к нулю, поскольку стержень тонкий. Но это обозначение удобно ввести для выполнения дальнейших расчетов.

Теперь мысленно разобьем стержень на бесконечное количество мелких кусочков, каждый из которых будет иметь сечение S и толщину dl. Заменяя r на l в формуле выше, получаем:

I = ∫_L(ρ*S*l²*dl).

Остается только подставить правильные пределы интегрирования и записать конечную формулу. Поскольку ось O₁ проходит через середину стержня, то пределы интегрирования будут следующими:

I = ∫_-L/2^L/2(ρ*S*l²*dl).

Результатом вычисления этого интеграла является следующая формула:

I = M*L²/12.

Таким образом, момент инерции тонкого стержня определяется его массой и длиной.

Инерции момент относительно O2

Теперь рассмотрим ситуацию, когда ось вращения будет проходить через любой из концов стержня и будет ему перпендикулярна. Соответствующую формулу можно получить из записанного выше интеграла, если правильно подставить пределы интегрирования. Однако мы пойдем несколько иным путем и определим инерции момент с помощью теоремы Штейнера.

Она говорит о том, что если две оси являются параллельными друг другу и одна из них (ось O) проходит через центр масс тела, то момент инерции относительно второй оси может быть вычислен с помощью такого равенства:

I = I₀ + M*h².

Здесь I₀ – момент инерции стержня относительно оси O, h – дистанция между осями.

Эту формулу можно с успехом применить для нашего случая. Поскольку I₀ мы рассчитали в предыдущем пункте статьи относительно оси O₁, и расстояние между O₁ и O₂ составляет L/2, то с использованием теоремы Штейнера получаем следующий результат:

I = I₀ + M*h² = M*L²/12 + M*L²/4 = M*L²/3.

Таким образом, для стержня величина I относительно оси O₂ в 4 раза больше, чем относительно оси O₁. Это означает, что для придания одинакового углового ускорения стержню в случае вращения вокруг оси O₂ следует приложить в 4 раза больший крутящий момент, чем в случае оси O₁.

Пример задачи

Дан тонкий стержень длиною 0,5 м и массой 5 кг. На расстоянии 2/5 от его конца расположена ось вращения, перпендикулярная стержню. Чему равен момент инерции системы?

Для решения задачи воспользуемся теоремой Штейнера. Расстояние между осями O₁ и заданной в задаче равно:

h = 0,25 – 0,2 = 0,05 м.

Тогда получаем момент инерции стержня (однородного):

I = I₀ + M*h² = 0,5²/12 + 0,05² = 0,117 кг*м².

В СИ момент инерции стержня измеряется в указанных единицах.

2}}\)

Использование линейной плотности для определения

дм

Случай тонкого стержня несколько усложняется тем, что r меняется по мере того, как мы перемещаемся с места на место вдоль стержня. Нам нужно варьировать r с одного конца палки на другой. Интеграл больше дм , но не r . Как тогда мы изменим на ?

Хитрость здесь в том, чтобы вызвать плотность объекта. Поскольку мы предполагаем, что стержень имеет однородную плотность и что стержень тонкий, можно с уверенностью сказать, что плотность можно описать следующим образом, где λ  — линейная плотность, полная масса стержня M , а общая длина стержня

R…

\(\color{black}{\lambda = M/R}\)

 

Так как стержень однороден, то если взять любой небольшой кусочек стержня массой дм и длиной др , то получим выражение

\(\color{black}{\lambda = M/R = dm/dr}\)

Можно преобразовать в

\(\color{black}{dm = \lambda \: dr}\) 92,}\)

как и ожидалось.