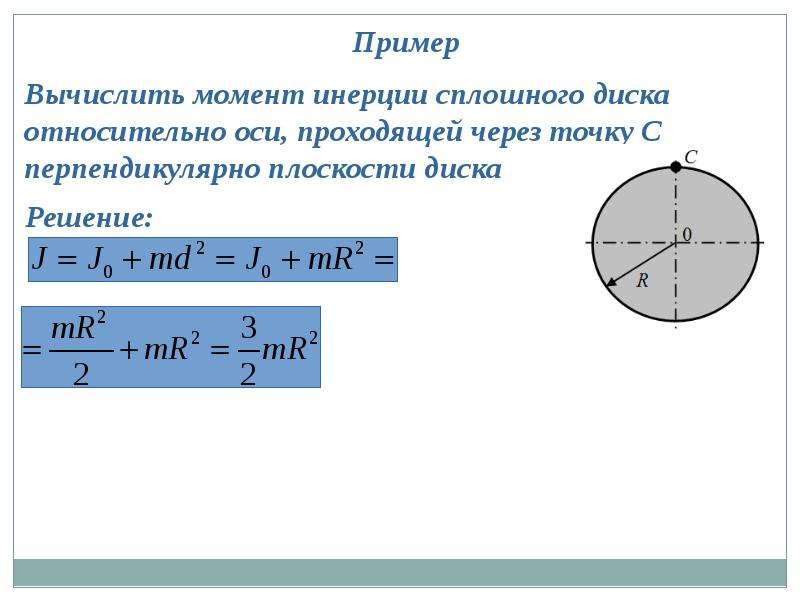
Момент инерции стержня, теория и примеры
Определение и общие понятия момента инерции стержня
Это скалярная (в общем случае тензорная) физическая величина, которую определяют как сумму произведений масс материальных точек () на которые разбивают тело на квадраты расстояний () от них до оси вращения:
Если тело рассматривают как непрерывное, то суммирование в формуле (1) заменяют на интегрирование, массы элементов тела обозначают как , тогда J тела, вращающегося около оси:
где r – функция положения материальной точки в пространстве; – плотность тела; –объем элемента тела. Для однородного тела выражение (2) представим как:
Формула для вычисления момента инерции однородного стержня
Определим формулу для вычисления момента инерции однородного стержня, вращающегося относительно оси (), которая проходит перпендикулярно стержню и идет через его один конец. Масса стержня равна m, длина l (рис.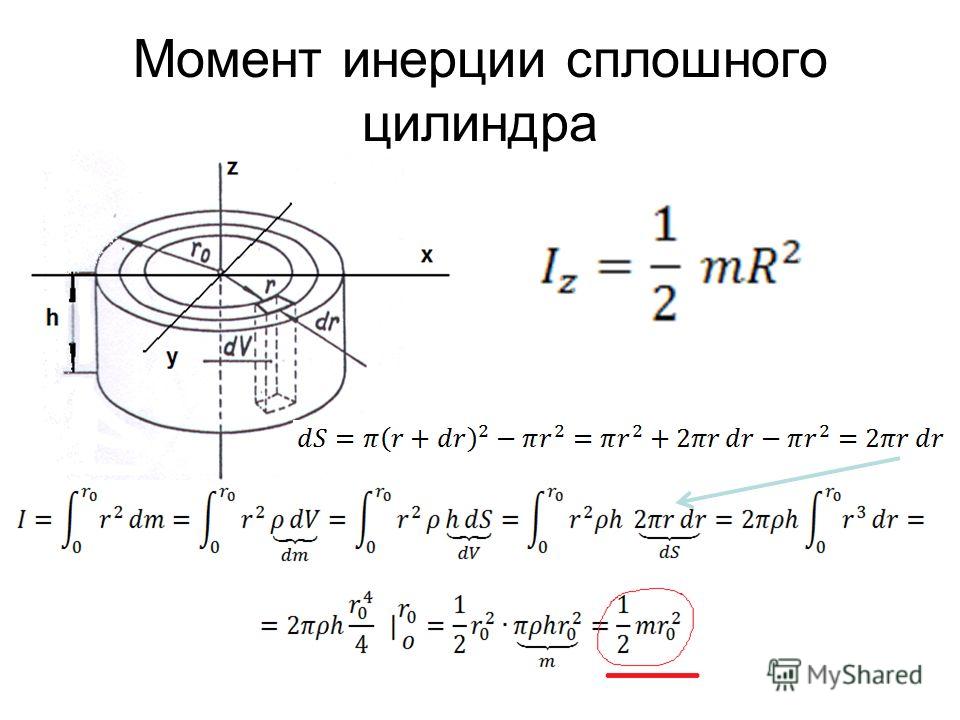
1).
Выделим в объеме стержня материальную точку (), которая находится от оси вращения на расстоянии r. Ее момент инерции равен:
Будем считать, что толщина стержня много меньше, чем его длина, тогда массу можно считать распределенной по длине стержня
Обозначим линейную плотность стержня как , тогда:
где – объем, стержня, который занимает наша материальная точка. Для нахождения момента инерции всего стержня проинтегрируем выражение (4), учитывая (6) и то, что :
Зная из (5), что:
формулу (7) перепишем в виде:
Мы получили, что момент инерции стержня вращающегося относительно оси, перпендикулярной ему и проходящей через один их его концов равен:
в котором расстояние изменяется в пределах: :
Формула (11) дает момент инерции относительно оси, перпендикулярной стержню и проходящей через его центр масс.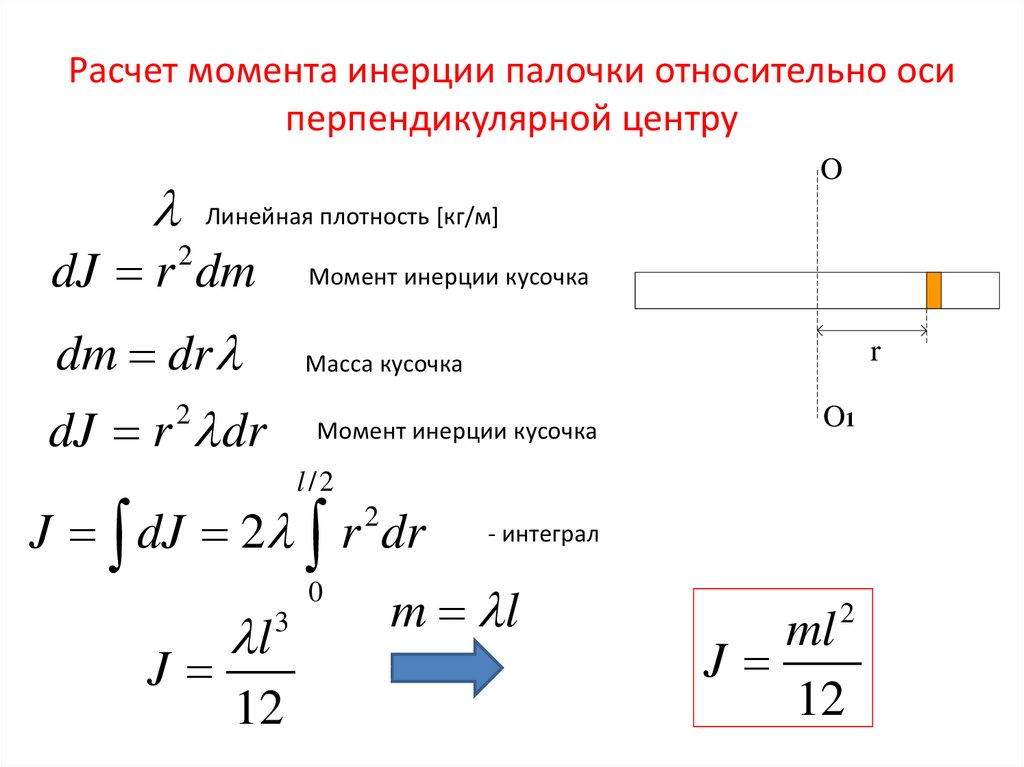
Примеры решения задач
18. Моменты инерции тонкого диска относительно его главных центральных осей.
Для расчета моментов инерции тонкого диска массы m и радиуса R выберем систему координат так, чтобы ее оси совпадали с главными центральными осями (рис.32). Определим момент инерции тонкого однородного диска относительно оси
(п.18)
Для определения Jx воспользуемся симметрией диска (Jx=J
10), полученным при
расчете момента инерции прямоугольной
пластины. При этом из (п.10) получаем Jz=2Jx (п.19)
Откуда (п.20)
17. Определение момента инерции тонкого стержня, относительно оси, проходящей через его середину.
Пусть тонкий стержень имеет длину l и массу m. Разделим его на малые элементы длины dx (рис.27), масса которых . Если выбранный элемент находится на расстоянии x от оси, то его момент инерции , т.е. Интегрируя последнее соотношение в пределах от 0 до l/2 и удваивая полученное выражение (для учета левой половины стержня), получим
(п.1)
Это выражение может быть получено и другим способом, с помощью метода подобия. Будем считать, что рассматриваемый стержень состоит из двух половин (рис.28). Каждая из них имеет массу m/2 и длину l/2 .
Выражение
для момента инерции стержня должно
включать его массу и длину, так как это
единственные параметры, определяющие
его инерционные свойства при вращении.
Пусть
(п.2)
где k– неизвестный коэффициент. Для каждой из половин стержня при вращении вокруг оси AA` можно найти момент инерции, используя (п.2) и теорему Гюйгенса-Штейнера. (п.3)
Полный момент инерции стержня (п.4)
Но этот же момент инерции, согласно (п.2) равен kml2. Приравнивая (п.4) и (п.2) имеем (п.5)
или и, следовательно, (п.6)
т.е. , что совпадает с (п.1)
1.Основные кинематические понятия. Материальная точка. Система отсчета, система координат.
Механика – наз-ся раздел физики, изучающий закономерности взаимодействия простейших форм движения материи.
Механическое движение – взаимное перемещение тел в пространстве в зависимости от времени.
Кинематика – описывает движение тел в пространстве и времени без выяснения причин их движения.
Материальная точка
Возможность рассматривать
тело как материальную точку зависит не
от самого тела, а от характера его
движения. Например, при движении Земли
вокруг солнца Землю можно считать
мат.точкой, если же нас интересует
суточное вращение Земли – то нельзя.Тело отсчета – тело, относительно которого изучается движение рассм-его тела.
Система отсчёта – это тело или совокупность тел, по отношению к которым рассматривается движение других тел. С.О. состоит из тел отсчета, связанной с ним системой координат и прибором для измерения времени (часы).
Радиус-вектор – вектор(r), харак-щий изм-е положения точки за рассм-ый промежуток t.
Вектор перемещения – вектор, харк-щий изменение положения точки за рассм-ый промежуток t.
Система координат – а) если тело движется вдоль прямой линии, то его движение определяется 1 координатой
б) при движении в нек. плоскости:2 координаты
в) при движении в пространстве: 3 координаты
28.
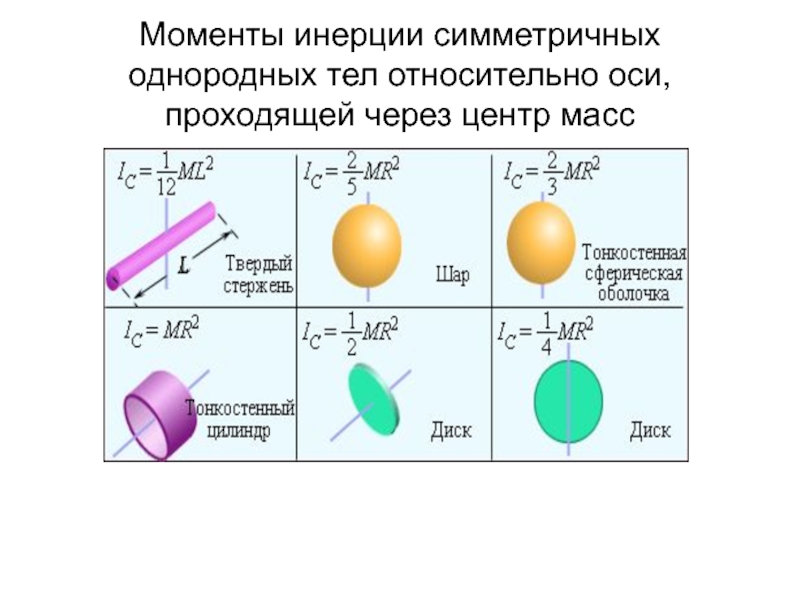Момент инерции для тонкого однородного стержня(формула)Стержень длины L и массы m | [1] | Это выражение предполагает, что стержень имеет вид бесконечно тонкой, но жёсткой проволоки. Это частный случай предыдущего объекта для w = L и h = 0. (через центр) |
через начало стержня –
29. Теория Штейнера(определение М.И. относительно любой оси)Теорема Штейнера. Имеем тело, момент инерции которого относительно оси, проходящей через его центр масс известен. Необходимо определить момент инерции относительно произвольно оси параллельной оси . Согласно теореме Штейнера, момент инерции тела относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс и параллельной данной оси, плюс произведение массы тела на квадрат расстояния между осями:
30.
Кинетическая энергия вращенияКинетическая энергия тела, движущегося произвольным образом, равна сумме кинетических энергий всех n материальных точек па которые это тело можно разбить:
Если тело вращается вокруг неподвижной оси с угловой скоростью
(5.11) |
где – момент инерции тела относительно оси вращения.
В общем случае движение твердого тела можно представить в виде суммы двух движений – поступательного со скоростью, равной скорости центра инерции тела, и вращения с угловой скоростью вокруг мгновенной оси, проходящей через центр инерции. При этом выражение для кинетической энергии тела преобразуется к виду
(5. |
12)где – момент инерции тела относительно мгновенной оси вращения, проходящей через центр инерции.
31. Момент импульса.
Векторное произведение радиуса-вектора материальной точки на ее импульс: называют моментом импульса , этой точки относительно точки О (рис.5.4)
. Вектор иногда называют также моментом количества движения материальной точки. Он направлен вдоль оси вращения перпендикулярно плоскости, проведенной через векторы и и образует с ними правую тройку векторов (при наблюдении из вершины вектора видно, что вращение по кратчайшему расстоянию от к происходит против часовой стрелки).
Векторную сумму моментов импульсов всех материальных точек системы называют моментом импульса (количества движения) системы относительно точки О:
Векторы и взаимно перпендикулярны и лежат в плоскости перпендикулярной оси вращения тела. Поэтому . Сучетом связи линейных и угловых величин
и
направлен вдоль оси вращения тела в ту
же сторону, что и вектор .
Таким образом.
Момент импульса тела относительно оси вращения
т.е.
(5.9) |
Следовательно, момент импульса тела относительно оси вращения равен произведению момента инерции тела относительно той же оси на угловую скорость вращения тела вокруг этой оси.
Момент инерции тонких тел – Энциклопедия по машиностроению XXL
Даны четыре однородных тела одинаковой массы тонкое кольцо, диск, конус и тар. Как относятся между собой моменты инерции этих тел относительно вертикальных осей симметрии [c.97]Моменты инерции тонких и тонкостенных тел. Рассмотрим тонкое тело (стержень) с массой на единицу длины т (s). Здесь s — длина дуги, отсчитываемая вдоль, вообще [c.47]
Моменты инерции.
Момент инерции твердого тела относительно оси радиус инерции. Моменты инерции тела относительно плоскости и полюса. Теорема о моментах инерции относительно параллельных осей (теорема Гюйгенса). Примеры вычисления моментов инерции (моменты инерции однородного тонкого стержня, тонкого круглого кольца или полого цилиндра и круглого диска или сплошного круглого цилиндра). Формула для вычисления момента инерции относительно оси любого направления. Центробежные моменты инерции. Главные и главные центральные оси инерции и их свойства.
[c.8]Сравнивая формулы (4) и (7) можно еще заключить, что радиус инерции тела равен радиусу тонкого кольца с таким же осевым моментом инерции, как и у тела. [c.267]
Вычислим осевые моменты инерции некоторых однородных тел. а) Тонкое однородное кольцо радиуса К и массы М. Проведем через центр кольца О ось Ог, перпендикулярную плоскости кольца (рис. 1.149). В этом случае для любой точки кольца Ни = / , и по формуле (14.
13) момент инерции кольца равен
[c.162]
Момент инерции прямого однородного тонкого стержня постоянного поперечного сечения. Под тонким стержнем понимается цилиндрическое или призматическое тело, поперечные размеры которого малы сравнительно с его длиной. [c.324]
При приближенном вычислении моментов инерции полых цилиндрических тел с тонким ободом (например, маховых колес) иногда пренебрегают толщиной обода и считают всю массу тела равномерно распределенной по его внешней боковой поверхности, В этом случае в предыдущей формуле надо положить г — г, и мы будем иметь [c.327]
Принимая это допущение, мы тем самым берем вместо действительного кольца некоторую гипотетическую модель — кольцо с абсолютно нерастяжимой осью. При равномерном внешнем или внутреннем давлении такое кольцо будет вести себя как абсолютно твердое тело. Перемещения точек нашей модели будут весьма близки к перемещениям действительного кольца, если деформации растяжения оси кольца играют ничтожную роль по сравнению с деформациями изгиба, а это обыкновенно и имеет место в случае тонких колец, так как при уменьшении поперечного сечения кольца площадь сечения убывает как квадрат поперечных размеров, а момент инерции сечения, которым определяется деформация изгиба, убывает как четвертая степень тех же размеров.
Следовательно, уменьшение размеров сечения сопровождается увеличением значения той части перемещений, которые обусловлены деформациями изгиба.
[c.245]
Если рассматривать вырожденную модель реального тела, например бесконечно тонкий стержень длины I, то момент инерции относительно оси, совпадающей со стержнем, будет равен нулю и расстояние до соответствующей точки тензорной поверхности обратится в бесконечность. В этом случае тензорная поверхность представляет собой круглый цилиндр с осью, направленной по стержню. [c.367]
Если возрастает температура, то длина I пружины увеличивается и часы начинают отставать. Для компенсации температурных изменений обычно изменяют момент инерции колеблющегося тела. Обод балансира — не целый, а состоит из двух дуг, каждая из которых менее полуокружности. Каждая дуга прикреплена своим концом к одному из концов стержня ВОВ, и несет на себе малую массу, прикрепленную близ ее свободного конца.
Дуги состоят из двух тонких полос, внешней — сделанной из латуни, а виутренней — из стали При повышении температуры латунная полоса расширяется сильнее, чем стальная, и дуги балансирного колеса загибаются внутрь. Расстояния малых масс от оси сокращаются, и момент инерции всего балансира уменьшается. Правильные положения масс на круговых дугах определяют путем проб, и обычно это оказывается довольно трудоемким делом.
[c.97]
Сравнительно легко вычисляются моменты инерции однородных симметричнь[х тел простой формы относительно их осей симметрии. В качестве примера выведем формулу для момента инерции тонкого однородного стержня длины / и массы т относительно перпендикулярной ему оси Ог, проходящей через середину стержня (рис. 54). Направим ось Ох вдоль стержня, выбрав начало отсчета на оси вращения. Момент инерции а отдельного малого элемента стержня длиной дх, находящегося на расстоянии х от оси вращения, по формуле (19.6) равен [c.66]
Момент инерции однородного цилиндра, полого цилиндра и т п.
относительно геометрической оси. Любое из этих тел мы можем мысленно рачбить на тонкие цилиндрические слои, частицы которых на.ходятся на одинаковом расстоянии от оси. Разобьем цилиндр
[c.211]
Расстояние от начала координат О до точки М, принадлежащей поверхности (12.19), определяется равенством (12.18). Так как момент инерции / тела относительно любой оси всегда положителен и в нуль не обращается, то все точки поверхности (12.19) находятся на конечном расстоянии от начала координат (случай бесконечно тонкого с ержня из рассмотрения временно исключается). Из всех поверхностей второго порядка этому условию удовлетворяет только эллипсоид. Поэтому построенная указанным образом поверхность называется эллипсоидом инерции. [c.282]
Для тел конечнь1х размеров с непрерывным распределением массы момент инерции вычисляется интегрированием согласно определяющей его формуле (19.7). В тривиальном случае, когда все элементы тела находятся на одинаковых расстояниях от оси вращения (примеры тонкий стержень, вращающийся относительно параллельной ему оси тонкостенный цилиндр, вращающийся относительно оси симметрии (рис, 53)), в
[c.
66]
Развитию основ теории и решению конкретных классических динамических задач термовязкоупругости посвящены монографии А. А. Ильюшина и Б. Е. Победри [12], В. Новацкого [421. Ниже приводятся основные соотношения и уравнения термовязкоупругости для массивных тел и тонких пластинок и на основе обобщенной теории термовязкоупругости изучаются динамические температурные напряжения в изотропном полупространстве при заданном на краевой поверхности тепловом потоке и в полубесконечной пластинке [241 при заданной температуре краевой поверхности. Предполагается, что тепловой поток на краевой поверхности полупространства и граничное значение температуры пластинки изменяются в начальный момент времени на некоторую величину, оставаясь далее постоянными. Исследуется влияние тепловой инерции на распределение в них динамических температурных напряжений. [c.292]
Должна лежать в соприкасающейся плоскости той кривой, по которой располагается изогнутая ось, и когДа Бине (В1пе1) ввел уравнение моментов относительно касательной, то Пуассон на основании этого уравнения пришел к заключению,-что крутящий момент постоянен.
Лишь постепенно возникло представление о двух изгибающих пара в двух главных плоскостях, и был найден способ определения меры закручивания. Когда эти элементы теории были получены, стало ясно, что, зная соотношения, связывающие, изгибающие и крутящие моменты с кривизной и степенью кручения и пользуясь обычными условиями равновесия, можно определить форму изогнутой оси, степень кручения стержня вокруг этой оси, а также растягивающую и Перерезы вающую силу в любом данном сечении. Изгибающие и крутящие. пары, а также растягивающая и перерезывающая силы, происходят от усилий, приложенных к, элементам поперечных сечений, и правильные выражения для этих пар и сил следует искать при помощи общей теории. Но здесь возникает затруднение, состоящее в том, Что общие уравнения применимы лишь тогда, когда смещения малы между тем для таких тел, как спиральные пружины, смещения ни в коем случае нельзя считать малыми. КирхГоф (КтеЬЬоК) первый преодолел Это затруднение. Он показал, что общие уравнения применимы со всей строгостью к малой части тонкого стержня, все линейные размеры которой того же порядка малости, что и диаметры, поперечного сечения.
Он считал, что уравнения равновесия или движения такой части можно в первом приближении упростить, пренебрегая силами -инерции и массовыми силами. Исследования, содержащиеся в теории Кирхгофа, носят в значительной своей части кинематический, характер. Когда тонкий стержень подвергается изгибу и скручиванию, то каждый его элемент испытывает деформацию, аналогичную тем деформациям,. которые имеют место в призмах Сен-Венана но соседние элементы должны непрерывным образом переходить один в Другой. Для того чтобы выразить непрерывность этого рода, необходимы некоторые условия. Эти условия принимают форму диференциальных уравнений, которые связывают относительные смещения точек малой части стержня с относительными координатами этих точек и с величинами, которые определяют положение данной части относительно всего стержня в целом. Из этих диференциальных уравнений Кирхгоф получил картину деформации в элементе стерл я и нашел выражение для потенциальной энергии, отнесенной к единице -длины, через относительное удлинение, компоненты кривизны и степень кручения.
Он получил уравнения равновесия и колебаний, варьируя функцию, Выражающую энергию. В случае, когда тонкий стержень подвергается действию внешних сил, приложенных лишь иа его концах, уравнения, которыми определяется форма изогнутой оси, идентичны, как показал Кирхгоф, с уравнениями движения тяжелого твердого тела вокруг неподвижной точки. Эта теорема носит название кинетической аналогии Кирхгофа .
[c.36]
Чертов (Задачи 6-10)
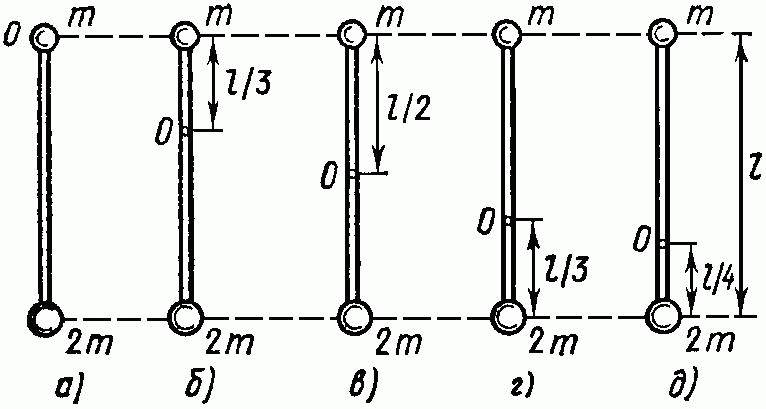
3.6. Определить момент инерции J тонкого однородного стержня длиной l = 30 см и массой т = 100 г относительно оси, перпендикулярной стержню и проходящей через: 1) его конец; 2) его середину; 3) точку, отстоящую от конца стержня на 1/3 его длины.
Дано: Решение:
l = 0,3 м
т = 0,1 кг
J – ?
Ответ: 3×10-3 кг×м2 ; 0,75×10-3 кг×м2 ; ×10-3 кг×м2
3.
7. Определить
момент инерции J тонкого однородного стержня длиной l = 60 см
и массой т = 100 г относительно оси, перпендикулярной ему и проходящей
через точку стержня, удаленную на а = 20 см от одного из его
концов.
Дано: Решение:
l = 0,6 м
т = 0,1 кг
а = 0,2 м
J – ?
Ответ: 4×10-3 кг×м2
3.8. Вычислить момент инерции J проволочного прямоугольника со сторонами а = 12 см и b = 16 см относительно оси, лежащей в плоскости прямоугольника и проходящей через середины малых сторон. Масса равномерно распределена по длине проволоки с линейной плотностью t = 0,1 кг/м.
Дано: Решение:
а = 0,12 м
b = 0,16 м
t = 0,1 кг/м
J – ?
Ответ: 1,4×10-3 кг×м2
3.
9. Два однородных
тонких стержня: АВ длиной l1 = 40 см и массой
m1 = 900 г и
CD длиной
l2 = 40 см и массой
т2 = 400 г скреплены под прямым углом (см. рис. ниже).
Определить момент инерции J
системы стержней относительно оси ОО’,
проходящей через конец стержня АВ параллельно стержню CD.
Дано: Решение:
l1 = 0,4 м
m1 = 0,9 кг
l2 = 0,4 м
т2 = 0,4 кг
J – ?
Ответ: 0,048 кг×м2 ; 0,064 кг×м2 ; 0,112 кг×м2
3.10. Решить предыдущую
задачу для случая, когда ось ОО¢ проходит через
точку А перпендикулярно плоскости чертежа.
Дано: Решение:
l1 = 0,4 м
m1 = 0,9 кг
l2 = 0,4 м
т2 = 0,4 кг
Ответ: 0,114 кг × м2
Помощь студентам в учёбе от Людмилы Фирмаль
Здравствуйте!
Я, Людмила Анатольевна Фирмаль, бывший преподаватель математического факультета Дальневосточного государственного физико-технического института со стажем работы более 17 лет. На данный момент занимаюсь онлайн обучением и помощью по любыми предметам. У меня своя команда грамотных, сильных бывших преподавателей ВУЗов. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И не важно: она по объёму на две формулы или огромная сложно структурированная на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте.
Срок выполнения разный: возможно онлайн (сразу пишите и сразу помогаю), а если у Вас что-то сложное – то от двух до пяти дней.
Для качественного оформления работы обязательно нужны методические указания и, желательно, лекции. Также я провожу онлайн-занятия и занятия в аудитории для студентов, чтобы дать им более качественные знания.
Моё видео:
Как вы работаете?
Вам нужно написать сообщение в WhatsApp (Контакты ➞ тут) . После этого я оценю Ваш заказ и укажу срок выполнения. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за заказ, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл заказа в личные сообщения.
Сколько может стоить заказ?Стоимость заказа зависит от задания и требований Вашего учебного заведения.
На цену влияют: сложность, количество заданий и срок выполнения. Поэтому для оценки стоимости заказа максимально качественно сфотографируйте или пришлите файл задания, при необходимости загружайте поясняющие фотографии лекций, файлы методичек, указывайте свой вариант.
Минимальный срок выполнения заказа составляет 2-4 дня, но помните, срочные задания оцениваются дороже.
Как оплатить заказ?Сначала пришлите задание, я оценю, после вышлю Вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.
Какие гарантии и вы исправляете ошибки?В течение 1 года с момента получения Вами заказа действует гарантия. В течении 1 года я и моя команда исправим любые ошибки в заказе.
Качественно сфотографируйте задание, или если у вас файлы, то прикрепите методички, лекции, примеры решения, и в сообщении напишите дополнительные пояснения, для того, чтобы я сразу поняла, что требуется и не уточняла у вас.
Присланное качественное задание моментально изучается и оценивается.
Теперь напишите мне в Whatsapp или почту (Контакты ➞ тут) и прикрепите задания, методички и лекции с примерами решения, и укажите сроки выполнения. Я и моя команда изучим внимательно задание и сообщим цену.
Если цена Вас устроит, то я вышлю Вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.
Мы приступим к выполнению, соблюдая указанные сроки и требования. 80% заказов сдаются раньше срока.
После выполнения отправлю Вам заказ в чат, если у Вас будут вопросы по заказу – подробно объясню. Гарантия 1 год. В течении 1 года я и моя команда исправим любые ошибки в заказе.
youtube.com/embed/Clc1txB_PxE” frameborder=”0″ allow=”accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture” allowfullscreen=””/> Можете смело обращаться к нам, мы вас не подведем. Ошибки бывают у всех, мы готовы дорабатывать бесплатно и в сжатые сроки, а если у вас появятся вопросы, готовы на них ответить.
В заключение хочу сказать: если Вы выберете меня для помощи на учебно-образовательном пути, у вас останутся только приятные впечатления от работы и от полученного результата!
Жду ваших заказов!
С уважением
Пользовательское соглашение
Политика конфиденциальности
32 Вычисление моментов инерции АТТ
Вычисление моментов инерции АТТ
Пример 1
Найдем момент инерции бесконечно круглого тонкого кольца (окружности).
Момент инерции относительно оси Z (рис. 1), очевидно, равен
, (1)
где R – радиус кольца. Ввиду симметрии Ix = Iy= 1∕2mR2.
Формула (1), очевидно, дает также момент инерции полого однородного цилиндра с бесконечно тонкими стенками относительно его геометрической оси.
Рис. 1
Рекомендуемые файлы
Пример 2
Найдем момент инерции бесконечно тонкого диска. Предполагается, что диск однородный, т.е. вещество распределено в нем с постоянной плотностью. Пусть ось Z, проходит через центр диска С перпендикулярно к его плоскости (рис. 2). Рассмотрим бесконечно тонкое с внутренним радиусом r и наружным радиусом r+dr . Площадь такого кольца . Его момент инерции найдется по формуле IZ = mR2. Момент инерции всего диска определяется интегралом .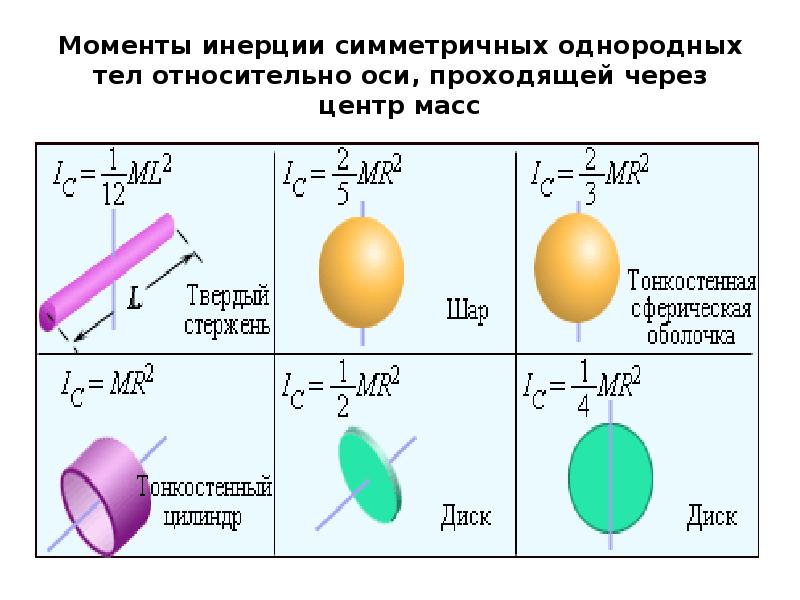
Ввиду однородности диска , где – площадь всего диска. Вводя это выражение под знак интеграла, получим
(2)
Момент инерции относительно диаметра вдвое меньше, как это непосредственно следует из формулы Ix +Iy= Iz, и из соображения симметрии:
(3)
Рис. 2
Пример 3
Найдем момент инерции однородного цилиндра относительно его геометрической оси ОО. Разобьем цилиндр на слои радиуса R и толщины dR. Масса такого слоя равна dm = ρ·dV = ρ·2πRh·dR (dV – объем слоя). Все точки слоя стоят от оси ОО на одинаковое расстояние R. Поэтому вклад слоя в момент инерции равен
(4)
Проинтегрировав это выражение по R в пределах от 0 до r (r – радиус цилиндра), получим искомый момент инерции:
(5),
где – масса цилиндра.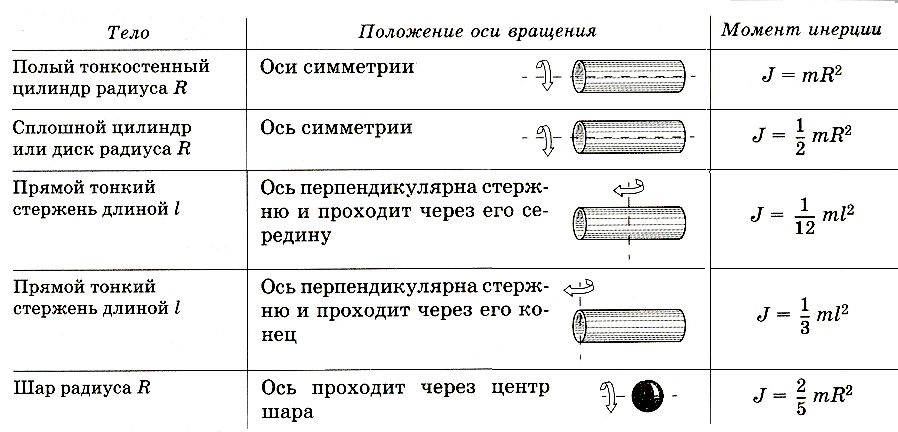
Отметим, что полученное выражение не зависит от высоты цилиндра h. Следовательно, формула (5) определяет и момент инерции тонкого диска относительно перпендикулярной к нему проходящей через его центр оси.
Пример 4
Найдем момент инерции однородной тонкой палочки (прямого тонкого стержня) длиной l относительно центра. Разобьем палочку на одинаковые массы равные dm, возьмем dm, которая будет размещаться на отрезке dx. В формулу можем подставить равные отношения
, (6)
тогда получим . Интегрируем выражение.
. (7)
Используя теорму Гюйгенса-Штейнера найдем момент инерции однородной палочки, если ось перпендикулярна и проходит через ее конец:
(8)
Введем понятие Тензор инерции – матрица, в которой по диагонали располагаются моменты инерции АТТ (для симметричных тел)
(9)
На месте Izz записывается максимальное значение момента инерции АТТ.
Разберемся на примере момента инерции кольца. (см. выше). Так как тело симметрично, то . Значит тензор инерции для кольца :
Если все 3 главных момента инерции равны, т.е. , то тело называется сферическим волчком (шар, сфера…).
Если – симметричный волчок (кольцо, диск, цилиндр, конус…).
Если – несимметричный волчок (параллелепипед).
Тензор инерции цилиндра .
Приведем значения моментов инерции (табл. 1) для некоторых тел (тела считаются однородными, m – масса тела).
Таблица 1.Моменты инерции однородных тел простейшей формы относительно некоторых осей
Тело | Положение оси | Момент инерции |
Полый тонкостенный цилиндр радиусом R | Ось симметрии | mR2 |
Сплошной цилиндр или диск радиусом R | Ось симметрии | 1∕2mR2 |
Прямой тонкий стержень длиной l | Ось перпендикулярна стержню и проходит через его середину | 1∕12ml2 |
В лекции “24 Операционное исчисление” также много полезной информации. Прямой тонкий стержень длиной l | Ось перпендикулярна стержню и проходит через его конец | 1∕3ml2 |
Шар радиусом R | Ось проходит через центр шара | 2∕5mR2 |
Уравнение массового момента инерции
Связанные ресурсы: механические станки
Уравнения массового момента инерции
Сопротивление и механика материалов
Момент инерции массы, обычно обозначаемый I, измеряет степень сопротивления объекта ускорению вращения вокруг оси и является вращательным аналогом массы. Моменты инерции масс имеют размерность масса × длина 2 .Его не следует путать со вторым моментом площади, который используется при расчетах изгиба.
Геометрически простые объекты имеют моменты инерции, которые можно выразить математически, но может быть непросто символически выразить момент инерции более сложных тел.
Точечная масса m (масса) на расстоянии r от оси вращения.
I = м R 2
Где:
I = момент инерции (фунт-м · фут 2 , кг · м 2 )
m = масса (фунт-м, кг)
R = расстояние между осью и массой вращения (футы, м)
Моменты всех остальных моментов инерции объекта вычисляются из суммы моментов.
I = ∑ i m i R i 2 = m 1 R 1 2 + m 2 R 2 2 + ….. + m n R n 2
Массовый момент инерцииИнерция в общем случае может быть выражена как
.I = к м R 2
Где:
k = инерционная постоянная
m = масса (фунт · м, г)
R = расстояние между осью и массой вращения (дюйм., мм)
Общее уравнение и калькулятор Расчет момента инерции массы ator
Некоторые типичные тела и их моменты инерции Момент инерции цилиндраТонкостенный полый цилиндр :
Моменты инерции тонкостенного полого цилиндра сопоставимы с точечной массой и могут быть выражены как:
I = м R 2
Где:
м = масса полости (фунт м, кг)
R = расстояние между осью и тонкостенной полостью (футы, м)
Вычислитель массового момента инерции тонкостенного вала
Массовый момент инерции полого цилиндра (вала):
I = 1/2 м (R i 2 + R o 2 )
Где:
м = масса полости (фунт · м, кг)
R i = расстояние между осью и внутренней полостью (дюймы, мм)
R o = расстояние между осью и внешней полостью (дюймы, мм)
Калькулятор массового момента инерции вала полого цилиндра
Цельный цилиндр :
I = 1/2 м R 2
Где:
м = масса цилиндра (фунт · м, кг)
R = расстояние между осью и внешним цилиндром (дюймы, мм)
Калькулятор массового момента инерции цилиндра со сплошным валом
Массовая инерция сферыТонкостенная полая сфера :
I = 2/3 м R 2
Где:
м = масса полой сферы (фунт · м, кг)
R = расстояние между осью и полостью (дюймы, мм)
Калькулятор массового момента инерции тонкостенной сферы
Твердая сфера :
I = 2/5 м R 2
Где:
м = масса сферы (фунт · м, кг)
R = радиус в сфере (дюймы, мм)
Уравнение и калькулятор цилиндра твердой сферы Момент инерции массы
Плоскость прямоугольная
Моменты инерции для прямоугольной плоскости с осью, проходящей через центр :
I = m (a 2 + b 2 ) / 12
Где:
a, b = короткая и длинная стороны (дюймы, мм)
m = масса шара (фунт · м, кг)
Калькулятор массового момента инерции для прямоугольной плоскости
Моменты инерции для прямоугольной плоскости с осью вдоль кромки:
I = (м 2 ) / 3
Где:
a = длина с обеих сторон (дюймы, мм)
m = масса шара (фунт · м, кг)
Калькулятор массового момента инерции прямоугольной пластины на кромке
Тонкая штангаМоменты инерции тонкого стержня с осью через центр:
I = (м L 2 ) / 12
Где:
L = длина стержня (дюйм.
, мм)
m = масса шара (фунт · м, кг)
Калькулятор момента инерции тонкой штанги
Моменты инерции тонкого стержня с осью:
I = 1/3 м L 2
L = длина стержня (дюймы, мм)
m = масса шара (фунт · м, кг)
Калькулятор момента инерции тонкой штанги о кромке
© Copyright 2000-2021, ООО «Инжиниринг Эдж» www.Engineersedge.com
Все права защищены
Заявление об ограничении ответственности | Обратная связь | Реклама
| Контакты
Момент инерции стержня (Вывод)
Определение момента инерции однородного жесткого стержня
Вычислить / получить момент инерции однородного жесткого стержня длиной L и массой M относительно оси, перпендикулярной стержню и проходящей через точку O на произвольном расстоянии h от одного конца.
РУКОВОДСТВО: (Я проведу вас через это, поскольку вы, возможно, впервые это видите)
- Представьте, что стержень разрезан на бесконечно малое количество кусочков бесконечно тонких ломтиков.
{2} $Примечание: Ожидается, что момент инерции будет максимальным, когда ось находится на одном конце, поскольку теперь массы наиболее удалены от оси вращения. Самый низкий – когда ось находится в центре.
– Всегда проверяйте свое выражение лица после их получения.
Назад к механике (UY1)
Расчет момента инерции обычных форм:
Что такое момент инерции и как его вычислить для стержня »Наука ABC
Инерция – это мера сопротивления, которое тело определенной массы оказывает, когда оно приводится в движение или, наоборот, останавливается. внешняя сила.Инерция, или тенденция объектов сопротивляться изменениям, зависит от массы. Более тяжелые объекты трудно разогнать, когда они находятся в состоянии покоя, и так же трудно остановить при движении, чем более легкие объекты.
Префикс «момент» в физике используется для обозначения вращательного эквивалента линейной величины.
Таким образом, «момент инерции» является вращательным эквивалентом массы для линейного движения. Обозначается он ‘I’ . Точно так же «момент силы» является вращательным эквивалентом линейной силы, также известной как крутящий момент .Как рассчитать момент инерции?
Момент инерции «I» вращающегося объекта относительно его оси вращения определяется произведением его массы на квадрат расстояния от оси вращения. Однако это верно только для однородных или обычных объектов, таких как шар, прикрепленный к струне, вращающейся с определенной угловой скоростью.
Для неоднородных объектов момент инерции рассчитывается как сумма произведений отдельных масс точек и их соответствующего расстояния от оси вращения.Это обобщенное соотношение можно использовать для вычисления момента инерции любой системы, поскольку любой объект может быть составлен как совокупность схожих масс точек и точек.
Чтобы вычислить момент инерции такого непрерывного распределения массы на различных расстояниях, мы используем математический анализ из-за его способности работать с непрерывными переменными.
Мы используем дифференциал элемент массы, бесконечно малый кусок массы дм . Тогда дифференциальный момент инерции равен dI = r²dm .Чтобы вычислить момент инерции ‘I’ всей массы ‘M’, , мы суммируем дифференциальный момент инерции dI , добавленный дм по всей поверхности. Или просто интегрируемся.
Момент инерции стержня
Рассмотрим стержень с массой «M» и длиной «L», так что его линейная плотность λ составляет M / л. В зависимости от положения оси вращения стержень демонстрирует два момента: первый, когда ось проходит перпендикулярно через центр масс стержня, точно через середину; и второй, когда ось расположена перпендикулярно одному из двух ее концов.
Ось, проходящая через центр масс
Подобно бесконечно малому элементу массы дм, рассмотрим бесконечно малый элемент длиной дл , соответствующий ему .
Рисуя начало координат в центре масс, лежащем на линии оси, мы понимаем, что расстояние стержня слева от начала координат до его конца составляет -L / 2, , а расстояние от начала координат до другой конец справа + L / 2. Предполагая, что стержень однороден, линейная плотность остается постоянной, так что:
Подставляя значение дм в наше выражение для расчета момента инерции, мы получаем:
Поскольку переменная интегрирования теперь длина (дл), пределы изменились с ранее изображенного M на требуемую долю L.
Ось через конец
Чтобы вычислить момент инерции стержня, когда ось находится на одном из его концов, мы рисуем начало координат на этом конце.
Статьи по теме
Статьи по теме
Мы должны использовать то же выражение, но с другим пределом. Поскольку ось находится в конце, предел, по которому мы интегрируем, теперь равен нуль (начало координат) до L (противоположный конец).
После интегрирования получаем:
Мы также можем получить тот же результат для момента инерции относительно конца, используя теорему о параллельных осях, , согласно которой:
As L (com, end) равно L / 2, мы находим, что:
Это согласуется с нашим ранее полученным результатом.
Вычисление момента инерции квадратной пластины
Авторские права © Майкл Ричмонд. Эта работа находится под лицензией Creative Commons License.Теорема о параллельных осях позволяет использовать ПРОСТЫЕ части. создать момент инерции СЛОЖНОГО тела. Давайте сделаем пример, чтобы увидеть, как это работает.
Начните с очень простого предмета: длинного тонкого стержня. массой м и длиной L , закрутился вокруг его центра.
Какой момент инерции этого стержня?
Теперь предположим, что я отодвинул стержень от ось вращения на небольшое расстояние x , нравится:
Какой момент инерции у этого смещенного стержня, если я продолжу вращать его вокруг той же оси?
Итак, что, если я объединю два стержня, чтобы получился составной объект? Предположим, я помещаю первый стержень по центру оси, а вторая штанга смещена на расстояние х .
Какой бы суммарный момент инерции этого двухстержневого
комбинация быть?Но зачем останавливаться всего на двух стержнях? Я могу использовать ту же технику, чтобы построить большую конструкцию. из множества стержней, а также вычислить его момент инерции.
Например, я мог бы разместить целую кучу стержней рядом с друг друга, чтобы получилась квадратная тарелка.
Назовем общую массу всей этой прямоугольной пластины M . Он имеет площадь поверхности A = L x L = L 2 .Мы можем определить массу на единицу площади как
Теперь, чтобы выяснить момент инерции этого сложная структура, я рассматриваю только одну деталь за раз. Позвольте мне взять один тонкий стержень, расстояние x от оси и шириной dx .
Масса этого кусочка дМ составляет
и вклад этой детали в момент инерции должен быть
Ладно, теперь твоя очередь: вычислить момент инерции всей квадратной пластины, суммируя вклады от всех маленьких стержней.
- Выразите момент инерции через общая масса M и длина стороны L
- Соответствует ли это значение тому, что указано в вашем учебнике?
Вы можете проверить свои ответы, посмотрев на мое собственное решение.
Авторские права © Майкл Ричмонд. Эта работа находится под лицензией Creative Commons License.
Список формул момента инерции для различных форм
формулы момента инерцииВ этом посте вы узнаете список формул момента инерции для различных форм с примерами.
Состав:- Моменты инерции Определение
- Формула момента инерции
- Уравнение
- Блок
- Намного больше
Продолжайте читать…
Что такое момент инерции?
Момент инерции ( I ) определяется как сумма произведений массы каждой частицы тела и квадрата ее перпендикулярного расстояния от оси. Это также известно как инерция вращения.
Момент инерции отражает распределение массы тела или системы вращающихся частиц относительно оси вращения. Момент инерции зависит только от геометрии тела и положения оси вращения, но не зависит от сил, задействованных в движении.Момент инерции отражает распределение массы тела или системы вращающихся частиц относительно оси вращения. Момент инерции зависит только от геометрии тела и положения оси вращения, но не зависит от сил, задействованных в движении.
Момент инерции играет роль, аналогичную роли инерционной массы в случае прямолинейного и равномерного движения. Это скалярное значение продольного углового момента твердого тела.I = mr²
Для твердого тела, движущегося вокруг фиксированной оси, законы движения имеют ту же форму, что и законы прямолинейного движения, с моментом инерции, заменяющим массу, угловым, заменяющим линейную скорость, угловым моментом, заменяющим линейный момент, и т. Д. Следовательно, кинетическая энергия тела, вращающегося вокруг фиксированной оси с угловой скоростью ω, составляет ½ω², что соответствует ½mv² для кинетической энергии тела массы m, перемещаемой со скоростью v.
См. Также правило Рауса; Теорема о параллельных осях.Уравнение момента инерции
Рассмотрим массу m, прикрепленную к концу безмассового стержня. Предположим, что подшипник в точке поворота O не имеет трения. Пусть система находится в горизонтальной плоскости. Сила F действует на массу, перпендикулярную стержню, и, следовательно, это ускоряет массу в соответствии с:
F = ma
При этом сила заставит массу вращаться вокруг оси O. Так как тангенциальное ускорение связано с угловым ускорением
α уравнением.угловое ускорение = rα
Поскольку вращающий эффект создается крутящим моментом τ, поэтому было бы лучше записать уравнение для вращения в терминах крутящего момента. Это можно сделать, умножив обе части приведенного выше уравнения на r. Таким образом,
rF = τ = крутящий момент = mr²α
Какой вращательный аналог второго закона движения Ньютона?
Здесь F заменяется на τ, a на α и m на mr². Величина mr² известна как момент инерции и обозначается I.Важность момента инерции
Момент инерции играет ту же роль при угловом движении, что и масса при линейном движении. Можно отметить, что момент инерции зависит не только от массы m, но и от r².
Момент инерции Формулы
Вот список формул момента инерции различной формы:
Момент инерции обруча
Момент инерции диска
Момент инерции твердого шара
Момент инерции полого цилиндра
Момент инерции тонкого стержня
Момент инерции прямоугольника
Момент инерции длинного тонкого стержня
Момент инерции сферической оболочки
youtube.com/embed/fHDB7PMUdZE” frameborder=”0″ allowfullscreen=”allowfullscreen”>
Связанные темы:Момент инерции
Момент инерции
следующий: крутящий момент Вверх: Вращательное движение Предыдущее: Центр масс
Момент инерции Рассмотрим расширенный объект, состоящий из элементов.Пусть th элемент обладают массой, вектором положения и скоростью. В полная кинетическая энергия объекта записывается(334)
Предположим, что движение объекта состоит просто из жесткого вращения на угловой скорость . Как следует из разд. 8.4, что(335)
Напишем(336)
где – единичный вектор, выровненный вдоль оси вращения (которая предполагается, что он проходит через начало нашей системы координат). Это следует из
приведенные выше уравнения, что кинетическая энергия вращения объекта принимает
форма (337)
или(338)
Здесь величина называется моментом инерции объекта, и написано(339)
куда – расстояние по перпендикуляру от th элемента до оси вращение.Обратите внимание, что для поступательного движения мы обычно пишем(340)
где представляет собой массу и представляет собой скорость. Сравнение
Уравнения. (338) и (340) предполагают, что момент инерции играет
та же роль во вращательном движении, что и масса в поступательном движении. Для непрерывного объекта аргументы, аналогичные тем, которые используются в разд. 8,5 урожай
(341)
где – массовая плотность объекта, является расстояние по перпендикуляру от оси вращения, и является элементом объема.Наконец, для объекта постоянной плотности приведенное выше выражение сводится к(342)
Здесь – полная масса объекта. Отметим, что интегралы берутся по всей объем объекта.Момент инерции однородного объекта зависит не только от его размера и формы.
объект, но на месте оси, вокруг которой объект вращается. Особенно,
один и тот же объект может иметь разные моменты инерции при вращении вокруг
разные оси.К сожалению, оценка момента инерции данного тела относительно данной оси неизменно вовлекает выполнение неприятного интеграла объема. На самом деле есть только один тривиальный момент инерции расчета, а именно момент инерции тонкого круговое кольцо вокруг оси симметрии, проходящей перпендикулярно в плоскость кольца. См. Рис. 75. Предположим, что это масса кольца, а это его радиус. Каждый элемент кольца разделяет общее перпендикулярное расстояние от ось вращения – i.е. , г. Следовательно, уравнение. (342) сводится к
(343) Рисунок 75: Момент инерции кольца относительно перпендикулярной оси симметрии. В общем, моменты инерции вычислять довольно утомительно. К счастью, есть две мощные теоремы, которые позволяют нам просто связать момент инерции данного тела относительно данной оси до момента инерции того же тела относительно другой оси.Первый из эти теоремы называются теоремой о перпендикулярной оси и применимы только к однородная ламинарная предмет. Рассмотрим ламинарный объект (, т.е. , тонкий плоский объект). однородной плотности. Предположим, для простоты, что объект лежит в плоскости -. Момент инерции объекта относительно -ось задается
(344)
где мы подавили тривиальное -интегрирование, а интеграл берется по протяженности объекта в плоскости.Кстати, Вышеприведенное выражение следует из наблюдения, что когда ось вращения совпадает с осью. Точно так же моменты
инерция объекта относительно осей – и – принимает вид
соответственно. Здесь мы использовали тот факт, что внутри объекта. Отсюда следует при осмотре из предыдущих трех уравнений, которые(347)
См. Рис.76.Рисунок 76: Теорема о перпендикулярной оси. Воспользуемся теоремой о перпендикулярной оси, чтобы найти момент инерции тонкого кольца относительно ось симметрии, лежащая в плоскости кольца. Принятие системы координат, показанной на Рис. 77, из симметрии ясно, что. Теперь мы уже знаем, что где – масса кольца, – его радиус. Следовательно, перпендикулярная ось Теорема говорит нам, что
(348)
или(349)
Конечно, потому что, когда кольцо вращается вокруг оси -оси, его элементы в среднем составляют дальше от оси вращения, чем при вращении вокруг оси. Рисунок 77: Момент инерции кольца относительно компланарной оси симметрии. Вторая полезная теорема относительно моментов инерции называется параллелью . Теорема оси . Теорема о параллельных осях, которая носит довольно общий характер, утверждает, что если момент инерции данного тела относительно оси, проходящей через центр масс этого тела, то момент инерции того же тела относительно второй оси который параллелен первому
(350)
где – масса тела, а – перпендикулярное расстояние между две оси.Чтобы доказать теорему о параллельности осей, выберем начало координат нашего систему координат, чтобы она совпадала с центром масс рассматриваемого тела. Кроме того, давайте сориентируем оси нашей системы координат так, чтобы ось совпадает с первой осью вращения, а вторая ось кусочков – плоскость.
Из уравнения. (328), тот факт, что
центр масс расположен в начале координат означает, что (351)
где интегралы берутся по объему тела.Из уравнения. (342), выражение для первого момента инерции:(352)
поскольку – это перпендикулярное расстояние общей точки от оси -оси. Точно так же выражение для второго момента инерции принимает форма(353)
Вышеприведенное уравнение можно расширить, чтобы получить
Как следует из Ур. (351) и (352) следует, что(355)
что доказывает теорему. Давайте воспользуемся теоремой о параллельности оси, чтобы вычислить момент инерции тонкого кольцо вокруг оси, которая проходит перпендикулярно плоскости кольца и проходит по окружности кольца. Мы знаем, что момент инерции кольца массы и радиус вокруг оси, которая проходит перпендикулярно плоскости кольца и проходит через центр кольца – который совпадает с центром массы кольца – есть. Наша новая ось параллельна этой первоначальной оси, но смещена боком на перпендикулярное расстояние.Следовательно, параллель теорема оси говорит нам, что
(356)
См. Рис.78.Рисунок 78: Применение теоремы о параллельных осях. В качестве иллюстрации прямого применения формулы (342) позвольте нам вычислить момент инерции тонкого круглого диска массы и радиуса, вокруг оси, которая проходит через центр диска и проходит перпендикулярно к плоскость диска.
Выберем нашу систему координат так, чтобы диск
лежит в плоскости – с центром в начале координат. Ось вращения, следовательно,
совпадает с осью. Следовательно, формула (342) сводится к (357)
где интегралы берутся по площади диска, а избыточное -интегрирование был подавлен. Разобьем диск на тонкие кольца. Рассмотрим кольцо радиуса и радиальная толщина.Площадь этого кольца просто . Следовательно, мы можем заменить в приведенных выше интегралах на , чтобы дать(358)
Вышеприведенное выражение дает(359) Расчеты, аналогичные приведенным выше, дают следующие стандартные результаты:
следующий: крутящий момент Вверх: Вращательное движение Предыдущее: Центр масс Ричард Фицпатрик 2006-02-02Формула момента инерции и другие физические формулы
Момент инерции объекта – это числовое значение, которое может быть вычислено для любого твердого тела, которое совершает физическое вращение вокруг фиксированной оси.
Он основан не только на физической форме объекта и его распределении массы, но и на конкретной конфигурации того, как объект вращается. Таким образом, один и тот же объект, вращающийся по-разному, будет иметь разный момент инерции в каждой ситуации.Общая формула
Общая формула для определения момента инерции. Эндрю Циммерман ДжонсОбщая формула представляет собой самое основное концептуальное понимание момента инерции. В принципе, для любого вращающегося объекта момент инерции можно рассчитать, взяв расстояние каждой частицы от оси вращения ( r в уравнении), возведя в квадрат это значение (это член r 2 ), и умножая его на массу этой частицы.Вы делаете это для всех частиц, составляющих вращающийся объект, а затем складываете эти значения вместе, и это дает момент инерции.
Следствием этой формулы является то, что один и тот же объект получает разное значение момента инерции в зависимости от того, как он вращается. Новая ось вращения заканчивается другой формулой, даже если физическая форма объекта остается прежней.
Эта формула представляет собой наиболее грубый подход к вычислению момента инерции.Другие приведенные формулы обычно более полезны и представляют собой наиболее распространенные ситуации, с которыми сталкиваются физики.
Интегральная формула
Общая формула полезна, если объект можно рассматривать как набор дискретных точек, которые можно складывать. Однако для более сложного объекта может потребоваться применить исчисление, чтобы взять интеграл по всему объему. Переменная r – это радиус-вектор от точки до оси вращения.Формула p ( r ) – это функция плотности массы в каждой точке r:
I-sub-P равно сумме i от 1 до N количества m-sub-i, умноженного на r-sub-i в квадрате.
Твердая сфера
Твердая сфера, вращающаяся вокруг оси, проходящей через центр сферы, с массой M и радиусом R , имеет момент инерции, определяемый по формуле:
I = (2/5) MR 2
Полая тонкостенная сфера
Полая сфера с тонкой незначительной стенкой, вращающейся вокруг оси, проходящей через центр сферы, с массой M и радиусом R , имеет момент инерции, определяемый по формуле:
I = (2/3) MR 2
Цельный цилиндр
Сплошной цилиндр, вращающийся вокруг оси, проходящей через центр цилиндра, с массой M и радиусом R , имеет момент инерции, определяемый по формуле:
I = (1/2) MR 2
Полый тонкостенный цилиндр
Полый цилиндр с тонкой незначительной стенкой, вращающейся вокруг оси, проходящей через центр цилиндра, с массой M и радиусом R , имеет момент инерции, определяемый по формуле:
I = MR 2
Полый цилиндр
Полый цилиндр с вращающейся на оси, проходящей через центр цилиндра, с массой M , внутренним радиусом R 1 и внешним радиусом R 2 , имеет момент инерции, определяемый формула:
I = (1/2) M ( R 1 2 + R 2 2 )
Примечание: Если вы взяли эту формулу и установили R 1 = R 2 = R (или, что более уместно, взяли математический предел как R 1 и R 2 приближаются к общему радиусу R ), вы получите формулу для момента инерции полого тонкостенного цилиндра.
Прямоугольная пластина, центральная ось
Тонкая прямоугольная пластина, вращающаяся вокруг оси, перпендикулярной центру пластины, с массой M и длинами сторон a и b , имеет момент инерции, определяемый по формуле:
I = (1/12) M ( a 2 + b 2 )
Прямоугольная пластина, ось вдоль кромки
Тонкая прямоугольная пластина, вращающаяся вокруг оси вдоль одного края пластины, с массой M и длинами сторон a и b , где a – расстояние, перпендикулярное оси вращения, имеет момент инерция определяется по формуле:
I = (1/3) млн лет 2
Тонкая штанга, центральная ось
Тонкий стержень, вращающийся вокруг оси, проходящей через центр стержня (перпендикулярно его длине), с массой M и длиной L , имеет момент инерции, определяемый по формуле:
I = (1/12) ML 2
Тонкая штанга, сквозная ось с одного конца
Тонкий стержень, вращающийся вокруг оси, проходящей через конец стержня (перпендикулярный его длине), с массой M и длиной L , имеет момент инерции, определяемый по формуле:
I = (1/3) ML 2
.
{2} $
Таким образом, «момент инерции» является вращательным эквивалентом массы для линейного движения. Обозначается он ‘I’ . Точно так же «момент силы» является вращательным эквивалентом линейной силы, также известной как крутящий момент .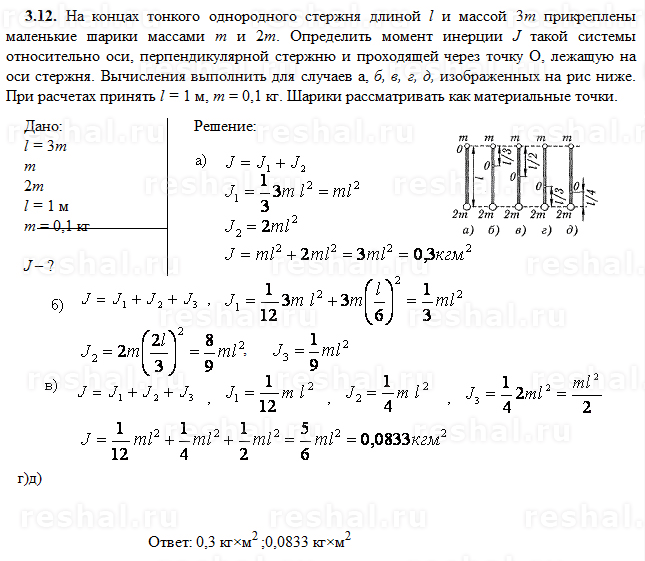
Рисуя начало координат в центре масс, лежащем на линии оси, мы понимаем, что расстояние стержня слева от начала координат до его конца составляет -L / 2, , а расстояние от начала координат до другой конец справа + L / 2.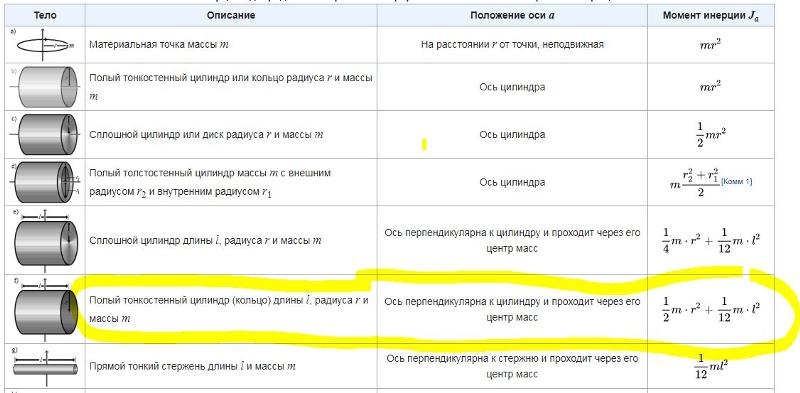 
Какой бы суммарный момент инерции этого двухстержневого
комбинация быть?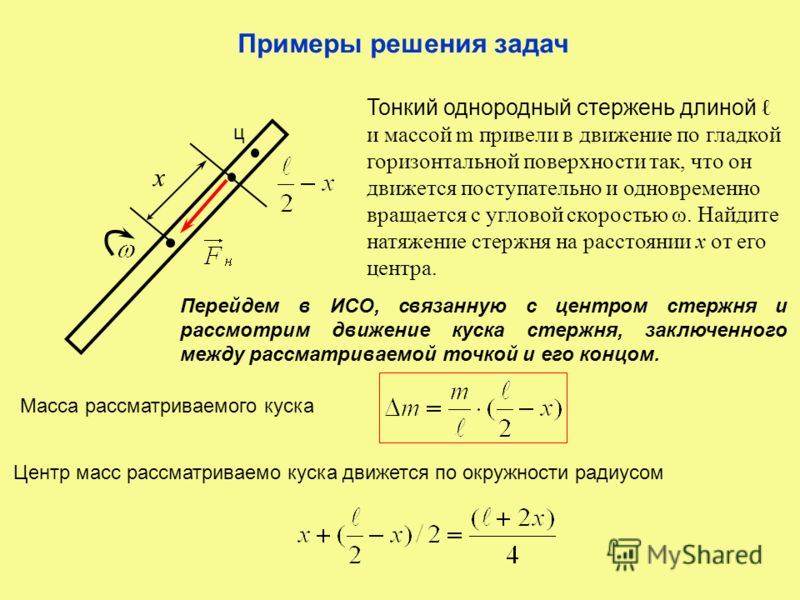
Момент инерции отражает распределение массы тела или системы вращающихся частиц относительно оси вращения. Момент инерции зависит только от геометрии тела и положения оси вращения, но не зависит от сил, задействованных в движении.
См. Также правило Рауса; Теорема о параллельных осях.
Величина mr² известна как момент инерции и обозначается I.
Это следует из
приведенные выше уравнения, что кинетическая энергия вращения объекта принимает
форма 
Сравнение
Уравнения. (338) и (340) предполагают, что момент инерции играет
та же роль во вращательном движении, что и масса в поступательном движении. 
объект, но на месте оси, вокруг которой объект вращается. Особенно,
один и тот же объект может иметь разные моменты инерции при вращении вокруг
разные оси.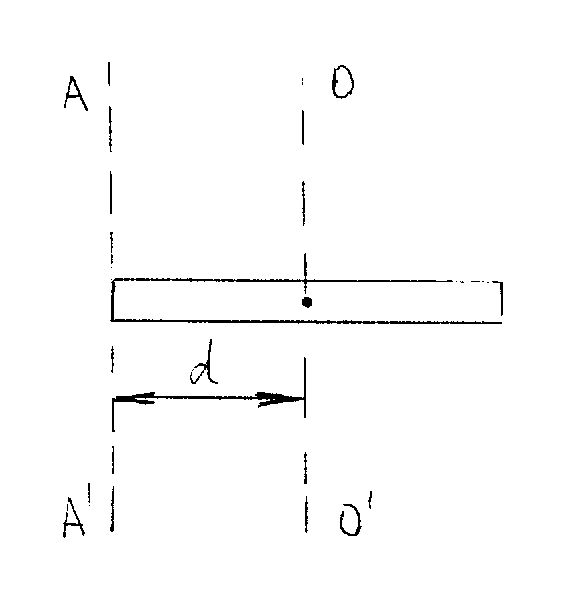
Точно так же моменты
инерция объекта относительно осей – и – принимает вид 
Из уравнения. (328), тот факт, что
центр масс расположен в начале координат означает, что 
Выберем нашу систему координат так, чтобы диск
лежит в плоскости – с центром в начале координат. Ось вращения, следовательно,
совпадает с осью. Следовательно, формула (342) сводится к 
Он основан не только на физической форме объекта и его распределении массы, но и на конкретной конфигурации того, как объект вращается. Таким образом, один и тот же объект, вращающийся по-разному, будет иметь разный момент инерции в каждой ситуации.
