Момент инерции твердого тела
Определение и общие сведения о моменте инерции твердого тела
Это скалярная (в общем случае тензорная) величина.
где – массы материальных точек, на которые разбивают тело; на квадраты расстояний от материальной точки до оси вращения.
Для непрерывного однородного тела, вращающегося около оси, момент инерции чаще определяют как:
где r – функция положения материальной точки в пространстве; – плотность тела; –объем элемента тела.
Тензор инерции
Совокупность величин:
называют тензором инерции. Диагональные элементы тензора: . Тензор инерции является симметричным.
Пусть все недиагональные элементы тензора равны нулю, не равны нулю только диагональные составляющие. Тогда тензор запишем как:
В таком случае оси тела совпадают с осями координат и являются главными осями инерции. Величины:
называют главными моментами инерции.
Если главные оси проведены через центр масс тела, то они называются центральными главными осями, а тензор центральным тензором.
Главные оси не всегда для тела не всегда легко отыскать. Но иногда достаточно использовать соображения симметрии. Так, в шаре относительно любой точки главные оси можно найти так. Одна из главных осей проходит через центр шара, две другие ориентированы произвольно в плоскости, которая перпендикулярна первой оси.
Составляющие момента инерции сплошного тела относительно осей декартовой системы координат определены как:
где – координаты элемента массы тела (), которая обладает объемом .
Момент инерции твердого тела зависит от формы тела и распределения ассы в теле относительно оси вращения.
Величины, равные:
называют радиусами инерции тела по отношению к соответствующим осям системы координат.
Теорема Штейнера
В некоторых случаях вычисление момента инерции существенно облегчает знание теоремы Штейнера (иногда ее называют теоремой Гюйгенса): Момент инерции тела (J) относительно произвольной оси равен моменту инерции относительно оси, которая проведена через центр масс рассматриваемого тела (), плюс произведение массы тела (m) на расстояние между осями в квадрате, при условии, если оси параллельны:
Примеры решения задач
Момент инерции тела – Справочник химика 21
Пример 3.3. Рассчитать частоту собственных колебаний балки см. (рис. 3.11, а), состоящей из двух швеллеров № 12 с суммарным моментом инерции сечения У = = 608 см закрепленное тело — плои(адка с электродвигателем (Пцс = 980 об/мин 102 с 1) общей массой т = 160 кг момент инерции тела Jx = 3,5 кг-м /1 = 2 м 2 = к = 0,5 м.
Массы и моменты инерции тел [c.80]
Момент инерции тела представляет собой сумму моментов инерции материальных точек, составляющих данное тело, и определяется по уравнению [c.66]
Заметьте, что момент инерции тела, являющийся мерой инертности вращающегося твердого тела, зависит не только от его массы, но и от распределения массы в теле относительно оси вращения. Другими словами, размеры и форма тела оказывают значительное влияние на его вращательное движение. [c.193]
Величина момента внешней силы (вращающего момента), приложенного к телу, вращающемуся вокруг неподвижной оси, равна моменту инерции тела относительно этой оси, умноженному на величину углового ускорения тела.
Момент инерции тела [c.193]
Для решения практических задач о вращении твердых тел нужно знать, в каких единицах измеряется момент инерции тела, и уметь определить его численное значение. В соответствии с определением момента инерции тела и формулой [c.193]
В соответствии с определением момента инерции тела и формулой [c.193]
Вычисление момента инерции произвольных тел представляет достаточно сложную задачу. Сравнительно просто вычислить моменты инерции тел вращения. Приведем без доказательства значение моментов инерции тел, эскизы которых показаны на рис. 121.
Ус — момент инерции тела относительно оси, проходящей через центр тяжести (относительно центральной оси) [c.195]
Разность величин движущего вращающего момента и момента сил сопротивления представляет собой результирующий момент внешних сил, который в соответствии с основным уравнением динамики вращающегося тела равен произведению момента инерции тела на величину углового ускорения. Теперь нетрудно сделать практические выводы о вращении тела в зависимости от величины действующих моментов сил. [c.196]
Что такое момент инерции тела и в каких единицах он измеряется  199]
199]
В табл. 23 даны формулы для вычисления моментов инерции тел, которые встречаются при расчете центрифуг. [c.263]
У — относительный момент инерции тела [c.6]
Примечание. и — моменты инерции тела относительно главных осей инерции тела соответственно хх а гг М — масса тела р — плотность материала I — расстояние от центра инерции С тела до его нижнего основания. [c.350]
Основной характеристикой всякого тела по отнощению к его способности совершать вращательные движения является момент инерции тела. Момент инерции жесткого ротатора, представляющего две материальные точки с массами тл и тв, находящиеся на неизменном
Массовый момент инерции тела относительно оси — мера инертности тела во вращательном движении вокруг этой оси. Массовый момент инерции тела вычисляют по формуле [c.321]
Зависимость периода гармонических колебаний от параметров системы играет важную роль во многих технических и физических измерениях, например в определении моментов инерции тел, в измерении магнитных полей. Если известен момент инерции магнита, то из результатов исследования его колебаний в магнитном поле можно найти в отдельности произведение магнитного момента на поле и отношение магнитного момента к полю и вычислить по этим данным магнитное поле. Этим способом Гаусс определял напряжение магнитного поля Земли.
Если известен момент инерции магнита, то из результатов исследования его колебаний в магнитном поле можно найти в отдельности произведение магнитного момента на поле и отношение магнитного момента к полю и вычислить по этим данным магнитное поле. Этим способом Гаусс определял напряжение магнитного поля Земли.
Здесь в свою очередь А, В, С представляют собой моменты инерции тел относительно осей координат, определяемые из соотношений [c.560]
Проекции полного момента количества движения Ь выражаются через моменты инерции и центробежные моменты инерции тела [c.561]
В табл. 66 даны моменты инерции тел, встречающихся при проектировании центрифуг, сепараторов, пальцеврлх мельниц и подобных машин.
Величина I = тг называется моментом инерции. Урав1 ние (6.5) относится к материальной точке. Момент инерции тела представляе умму моментов материальных точек, составляющих данное тело [c. 296]
296]
Такие расчеты можно производить и в более сложных случаях. Напрнмер, мы можем изучить, как много энергии можгга ввести во вращающееся тело. В линейном случае линейный момент р связан с линейной скоростью v через p = mv в случае вращения угловой момент J связан с угловой скоростью и через J = Iw, где /—момент инерции тела. (Необходимо помнить об аналогичных ролях т и 1, V и (О II р и / в линейном случае и в случае вращения, по-
Для большинства тел, применяемых в машиностроении соленчатых валов и шатунов двигателей внутреннего сгорания, роторов паровых и газовых турбин, винтов самолетов, хеталей часового механизма и многих других — математи- еские методы определения моментов инерции малопригодны, главным образом потому, что они оказываются недо- таточно точными. Поэтому моменты инерции тел обычно определяют опытным путем. [c.195]
Здесь величина со вынесена за знак суммы как общий множитель. Величина 2т г нам уже известна.
Величина 1=тг называется моментом инерции. Уравнение (6.5) относится к материальной точке. Момент инерции тела представляет сумму моментов инерции материальных точек, составляющих данное телЪ [c.298]
Момент инерции тела относительно оси Х1Х1, не проходящей через центр инерции [c.350]
Наилучшее направление силы 2 во втором секторе определили с использованием математической модели, решив задачу на минимум суммарного момента поднимателей тела, выразив его как функцию направления силы 2. При этом мы учли еще один способ снижения суммарного момента поднимателей — за счет смещения точки пересечения сил 2 и 3 в сторону от прямой N (рис. 6,6). Правда, при этом векторы 1 и 1 образуют пару сил и сообщают телу вращательный момент, но, благодаря краткости его действия (при высокой частоте шагов) и значительному моменту инерции тела, эта пара сил не успевает вызвать существенного поворота тела.
Чему равен момент инерции системы тел
Рассмотрим материальную точку массой m, которая находится на расстоянии r, от неподвижной оси (рис. 26). Моментом инерции J материальной точки относительно оси называется скалярная физическая величина, равная произведению массы m на квадрат расстояния r до этой оси:
Момент инерции системы N материальных точек будет равен сумме моментов инерции отдельных точек:
(76)
Рис. 26.
К определению момента инерции точки.
Если масса распределена в пространстве непрерывно, то суммирование заменяется интегрированием. Тело разбивается на элементарные объемы dv, каждый из которых обладает массой dm.
В результате получается следующее выражение:
(77)
Для однородного по объему тела плотность ρ постоянна, и записав элементарную массу в виде:
dm = ρdv, преобразуем формулу (70) следующим образом:
(78)
Размерность момента инерции – кг*м 2 .
Момент инерции тела является мерой инертности тела во вращательном движении, подобно тому, как масса тела является мерой его инертности при поступательном движении.
Момент инерции — это мера инертных свойств твердого тела при вращательном движении, зависящая от распределения массы относительно оси вращения. Иными словами, момент инерции зависит от массы, формы, размеров тела и положения оси вращения.
Всякое тело, независимо от того, вращается оно или покоится, обладает моментом инерции относительно любой оси, подобно тому, как тело обладает массой независимо от того, движется оно или находиться в покое. Аналогично массе момент инерции является величиной аддитивной.
В некоторых случаях теоретический расчёт момента инерции достаточно прост. Ниже приведены моменты инерции некоторых сплошных тел правильной геометрической формы относительно оси, проходящей через центр тяжести.
Момент инерции бесконечно плоского диска радиуса R относительно оси, перпендикулярной плоскости диска:
Момент инерции шара радиуса R:
Момент инерции стержня длиной L относительно оси, проходящей через середину стержня перпендикулярно ему:
Момент инерции бесконечно тонкого обруча радиуса R относительно оси, перпендикулярной его плоскости:
Момент инерции тела относительно произвольной оси рассчитывается с помощью теоремы Штейнера:
Момент инерции тела относительно произвольной оси равен сумме момента инерции относительно оси, проходящей через центр масс параллельно данной, и произведения массы тела на квадрат расстояния между осями.
Рассчитаем при помощи теоремы Штейнера момент инерции стержня длиной L относительно оси, проходящей через конец перпендикулярно ему (рис. 27).
К расчету момента инерции стержня
Согласно теореме Штейнера, момент инерции стержня относительно оси O′O′ равен моменту инерции относительно оси OO плюс md 2 . Отсюда получаем:
Очевидно: момент инерции неодинаков относительно разных осей, и поэтому, решая задачи на динамику вращательного движения, момент инерции тела относительно интересующей нас оси каждый раз приходится искать отдельно. Так, например, при конструировании технических устройств, содержащих вращающиеся детали (на железнодорожном транспорте, в самолетостроении, электротехнике и т. д.), требуется знание величин моментов инерции этих деталей. При сложной форме тела теоретический расчет его момента инерции может оказаться трудно выполнимым. В этих случаях предпочитают измерить момент инерции нестандартной детали опытным путем.
Момент силы F относительно точки O
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 10236 — | 7597 — или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
5.2. Момент инерции системы материальных точек
Тело можно представить состоящим из большого числа материальных точек (м.т.), поэтому момент инерции системы м.т.
,
где m i — масса i-й м.т., R i — ее расстояние до полюса 0.
Моментом инерции системы материальных точек или тела относительно полюса (точки) называют алгебраическую сумму произведений масс м. т., из которых состоит тело, на квадрат расстояния их до полюса 0.
т., из которых состоит тело, на квадрат расстояния их до полюса 0.
При непрерывном распределении массы по объему тела момент инерции относительно полюса
В случае момента инерции относительно полюса массу dm умножают на квадрат расстояния до неподвижной точки (полюса), а в случае момента инерции относительно оси — до неподвижной оси.
В декартовой системе координат сумма моментов инерции тела относительно трех взаимно перпендикулярных осей, пересекающих в одной точке 0, равна удвоенному моменту инерции этого тела относительно этого же начала:
Момент инерции тела обладает следующими важнейшими свойствами, имеющими практическое значение.
Момент инерции тела зависит от:
расстояния до оси вращения;
Проявление последнего свойства можно продемонстрировать в видеоопыте “Момент инерции тела в опыте с наклонной плоскостью”.
В этом опыте демонстрируется важнейшее свойство момента инерции тела как меры его инертности при вращательном движении. Два тела одинаковой формы и равной массы, но разное распределение массы по объему, могут иметь разную инертность при вращательном движении, т.е. приобретать разное угловое ускорение под действием одного и того же момента силы. В опыте: сплошной цилиндр имеет меньший момент инерции и поэтому скатывается быстрее.
Момент инерции — скалярная (в общем случае — тензорная) физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Единица измерения СИ: кг·м².
2. Физический смысл момента инерции. Произведение момента инерции тела на его угловое ускорение равно сумме моментов всех сил, приложенных к телу. Сравните. Вращательное движение. Поступательное движение. Момент инерции представляет собой меру инерции тела во вращательном движении
Сравните. Вращательное движение. Поступательное движение. Момент инерции представляет собой меру инерции тела во вращательном движении
Например, момент инерции диска относительно оси О’ в соответствии с теоремой Штейнера:
Теорема Штейнера: Момент инерции I относительно произвольной оси равен сумме момента инерции I0 относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями :
18. Момент импульса твердого тела. Вектор угловой скорости и вектор момента импульса. Гироскопический эффект. Угловая скорость прецессии
Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц, из которых состоит тело относительно оси. Учитывая, что , получим .
Если сумма моментов сил, действующих на тело, вращающееся вокруг неподвижной оси, равна нулю, то момент импульса сохраняется (закон сохранения момента импульса): . Производная момента импульса твердого тела по времени равна сумме моментов всех сил, действующих на тело:.
угловую скорость как вектор, величина которого численно равна угловой скорости, и направленный вдоль оси вращения, причем, если смотреть с конца этого вектора, то вращение направлено против часовой стрелки. Исторически сложилось 2 , что положительным направлением вращения считается вращение «против часовой стрелки», хотя, конечно, выбор этого направления абсолютно условен. Для определения направления вектора угловой скорости можно также воспользоваться «правилом буравчика» (которое также называется «правилом правого винта») − если направление движения ручки буравчика (или штопора) совместить с направлением вращения, то направление движения всего буравчика совпадет с направлением вектора угловой скорости.
Вращающееся тело ( колесо мотоцикла ) стремиться сохранять положение оси вращения в пространстве неизменным .( гироскопический эффект ) Поэтому возможно движение на 2-х колёсах, но не возможно стояние на двух колёсах Этот эфект используется в корабельных и танковых системах наведения орудий. ( корабль качается на волнах, а орудие смотрит в одну точку ) В навигации и др.
( корабль качается на волнах, а орудие смотрит в одну точку ) В навигации и др.
Наблюдать прецессию достаточно просто. Нужно запустить волчок и подождать, пока он начнёт замедляться. Первоначально ось вращения волчка вертикальна. Затем его верхняя точка постепенно опускается и движется по расходящейся спирали. Это и есть прецессия оси волчка.
Главное свойство прецессии — безынерционность: как только сила, вызывающая прецессию волчка, пропадёт, прецессия прекратится, а волчок займёт неподвижное положение в пространстве. В примере с волчком этого не произойдет, поскольку в нём вызывающая прецессию сила — гравитация Земли — действует постоянно.
19. Идеальная и вязкая жидкость. Гидростатика несжимаемой жидкости. Стационарное движение идеальной жидкости. Уравнение Бирнулли.
Идеальной жидкостью назвается воображаемая несжимаемая жидкость, в которой отсутствуют вязкость, внутреннее трение и теплопроводность. Так как в ней отсуствует внутреннее трение, то нет касательных напряжений между двумя соседними слоями жидкости.
вязкая жидкость характеризуется наличием сил трения, которые возникают при ее движении. вязкой наз. жидкость, в которой при движении кроме нормальных напряжений наблюдаются и касательные напряжения
Рассматриваемые в Г. ур-ния относит. равновесия несжимаемой жидкости в поле сил тяжести (относительно стенок сосуда, совершающего движение по нек-рому известному закону, напр. поступательное или вращательное) дают возможность решать задачи о форме свободной поверхности и о плескании жидкости в движущихся сосудах — в цистернах для перевозки жидкостей, топливных баках самолётов и ракет и т. п., а также в условиях частичной или полной невесомости на космич. летат. аппаратах. При определении формы свободной поверхности жидкости, заключённой в сосуде, кроме сил гидростатич. давления, сил инерции и силы тяжести необходимо учитывать поверхностное натяжение жидкости. В случае вращения сосуда вокруг вертик. оси с пост. угл. скоростью свободная поверхность принимает форму параболоида вращения, а в сосуде, движущемся параллельно горизонтальной плоскости поступательно и прямолинейно с пост. ускорением а, свободной поверхностью жидкости является плоскость, наклонённая к горизонтальной плоскости под углом
ускорением а, свободной поверхностью жидкости является плоскость, наклонённая к горизонтальной плоскости под углом
Определение момента инерции твердого тела методом крутильных колебаний
Лабораторная работа 7
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТВЕРДОГО ТЕЛА
МЕТОДОМ КРУТИЛЬНЫХ КОЛЕБАНИЙ
Цель работы: определить момента инерции твердого тела методом крутильных колебаний.
Оборудование: лабораторная установка – крутильный маятник.
1. ОБЩИЕ СВЕДЕНИЯ
Вращательным движением твердого тела называется такое движение, при котором все точки тела описывают окружности, центры которых лежат на одной прямой, называемой осью вращения
В твёрдом теле все точки жестко связаны между собой и могут вращаться вокруг неподвижной оси под действием момента внешней силы. При этом вектор момента силы М и вектор углового ускорения ε всегда направлены в одну сторону и справедлив основной закон динамики вращательного движения
M = I ε
где I – момент инерции твердого тела относительно неподвижной
оси вращения, кг· м2.
Момент инерции I характеризует инертные свойства твердого тела при вращательном движении и зависит от распределения массы тела относительно оси вращения.
Рассмотрим твёрдое тело и выделим в нём материальную точку массой mi. Её удаление от оси вращения обозначим через ri (рис. 1). Тогда линейная скорость этой точки равна
vi = ωiri, где ωi – угловая скорость вращения, рад/с.
Момент импульса относительно оси вращения равен
Li = miViri = miriωi.
Величина равная Ii = miri2 называется
моментом инерции материальной точки.
Для твёрдого тела моменты импульсов складываются по всем материальным точкам, образующим это тело. Тогда суммарный момент импульса равен
или
L = Iω.
Здесь
и есть момент инерции твердого тела относительно оси вращения.
Суммирование производится по всем материальным точкам, входящих в твердое тело.
Практически вычисление такой суммы сводится к вычислению соответствующего интеграла, что для однородных тел симметричной формы труда не составляет, то есть
где ρ – плотность, кг/м3, V – объем, занимаемый телом, м3.
Интегрирование производится по всему объёму тела.
Для любого твёрдого тела можно указать три взаимно
перпендикулярные оси, проходящие через его центр инерции. Эти оси называются
главными осями тела. А момент инерции относительно любой оси вращения
выражается через моменты инерции тела относительно этих главных осей.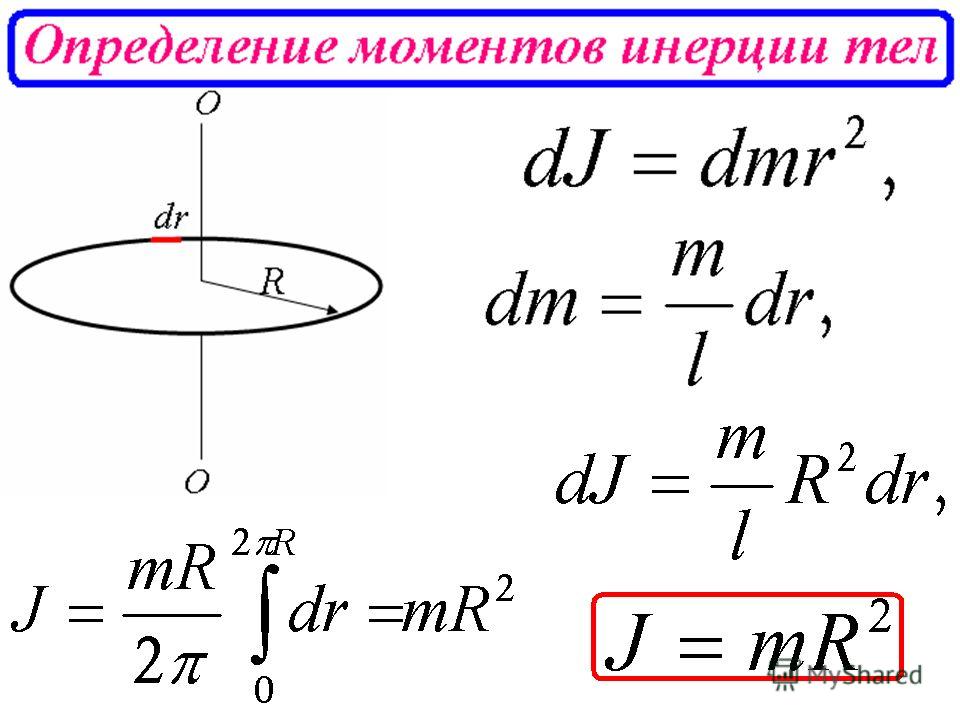
Главные оси просто определить для однородных симметричных тел (шара, куба, параллелепипеда и т.д.). Главные оси инерции таких тел всегда совпадают с осями симметрии тела.
Например, главные оси однородного прямоугольного параллелепипеда проходят через его геометрический центр перпендикулярно граням (рис. 2).
Для тел сложной формы главные оси и моменты инерции определяют экспериментально.
Если известны главные оси твердого тела, то с ними связывают прямоугольную систему координат О, X, У, Z. Начало координат находится в центре инерции твердого тела.
Возьмём произвольную ось вращения, проходящую через центр инерции, ось ОС (рис. 3).
Момент инерции тела относительно оси ОС выражается через моменты инерции главных осей, то есть
I= Ix cos2α + Iy сos2 + Iz cos2 γ (1)
где Ix, Iy, Iz – моменты инерции тела относительно осей ОХ, OY, OZ; α, β, γ –
углы между осью вращения и осями прямоугольной системы координат.
Моменты инерции Ix, Iy, Iz определяются экспериментально. Момент инерции тела относительно произвольной оси вращения находится простым суммированием по формуле (1).
Момент инерции тела зависит от выбора оси вращения. Однако это не значит, что для всякой новой оси момент инерции следует вычислять заново.
Если известен момент инерции тела относительно оси, проходящей через центр инерции, то момент инерции тела относительно любой оси, параллельной первой и смещенной на расстояние d, находится по теореме Штейнера (рис. 4):
где I0 – момент инерции относительно оси вращения, проходящей через центр инерции, кг · м3; m – масса тела, кг; d – расстояние между осями, м.
Используемый в лабораторной работе крутильный маятник позволяет определить момент инерции тел любой формы.
Такой маятник представляет собою рамку, подношенную на
тонкой упругой струне. При повороте рамки из положения равновесия на некоторый
угол Θ, со стороны нити на нее действует упругий момент равный
При повороте рамки из положения равновесия на некоторый
угол Θ, со стороны нити на нее действует упругий момент равный
Mупр = –D Θ, где Θ – угол поворота рамки, рад; D – коэффициент, характеризующий момент упругих сил, Н · м.
При достаточно тонкой и длинной струне зависимость М(Θ) выполняется и для больших углов поворота, а затухания при крутильных колебаниях можно считать малыми.
Пренебрегай затуханиями, движение рамки записывают уравнением для свободных незатухающих колебаний
или
(2)
где – угловое ускорение, рад · с2, вторая производная по времени от угла попорота; ω0 – циклическая частота колебаний, рад/с. Циклическая частота колебаний выражается как
Период таких колебаний равен
(3)
Решение дифференциального уравнения (2) имеет вид
где Θ0 – угловая амплитуда колебаний, рад; α – начальная фаза
колебаний, рад.
Если известен момент инерции I, то найти период колебаний рамки не составляет труда, а следовательно, и найти постоянную D. И наоборот, зная постоянную D, используя формулу (3) можно рассчитать момент инерции тела.
В данной лабораторной работе постоянная D не определяется. Для нахождения момента инерции рамки используется тело с известным моментом инерции. В качестве такого тела взят куб с достаточно идеальными поверхностями и гранями. Его момент инерции относительно оси, походящей через центр, вычисляется по формуле
(4)
где m – масса куба, кг, а – сторона куба, м.
Такой куб жестко закрепляется в рамке крутильного маятника. Если вывести нагруженную рамку из положения равновесия, то она будет совершать крутильные колебания, а её период колебаний равен
2 + … $. Затем используйте уравнения, чтобы уточнить, как момент инерции зависит от массы и расстояния от оси вращения.

Полный пошаговый ответ:
Момент инерции – его также называют моментом инерции массы или инерцией вращения тела. Момент инерции – это сумма произведений массы каждой частицы на квадрат расстояния каждой частицы от оси вращения. Момент инерции основан на концепции центра масс. Центр масс – это воображаемая точка тела, в которой, как можно считать, собрана вся масса тела.2 + … $
Из приведенного выше уравнения мы узнаем несколько важных моментов. Проще говоря, момент инерции тела зависит от распределения массы тела и расстояния от оси вращения.
Момент инерции тела прямо пропорционален его массе и расстоянию частиц тела от оси вращения.
Следовательно, момент инерции зависит от массы и расстояния от оси вращения, а сила и плотность не влияют на момент инерции тела.
Следовательно, варианты A и C являются правильными.
Примечание: Концепция центра масс очень важна для расчета момента инерции. Очень интересна концепция центра масс. Мы знаем, что для расчета электростатической и гравитационной сил, действующих на тело, мы также рассматриваем их как точечный заряд и точечную массу соответственно. По сути, мы считаем, что все заряды и масса сосредоточены в центре. Помните, что этот заряд или масса всегда считается находящейся внутри тела, но в случае центра масс он также может находиться вне тела, например – центр массы банана.
Мы знаем, что для расчета электростатической и гравитационной сил, действующих на тело, мы также рассматриваем их как точечный заряд и точечную массу соответственно. По сути, мы считаем, что все заряды и масса сосредоточены в центре. Помните, что этот заряд или масса всегда считается находящейся внутри тела, но в случае центра масс он также может находиться вне тела, например – центр массы банана.
Момент инерции
Момент инерцииСледующий: Кинетическая энергия вращения вверх: крутящий момент Предыдущая: Статическое равновесие
Момент инерции Второй закон Ньютона, Сила = масса x ускорение, связывает ускорение что объект определенной массы переживает, когда подчиняется данному сила. Аналогичное соотношение между крутящим моментом и угловым ускорение, которое вводит понятие момент инерции :
Так же, как масса – это мера того, насколько легко объект ускоряется.
из-за заданной силы момент инерции объекта
измеряет, насколько легко объект вращается вокруг определенного
точка вращения. Таким образом, объекты с большим моментом инерции
относительно заданной точки будет труднее вращать с заданным крутящим моментом.
Соответственно, больший крутящий момент вызовет большее ускорение.
на конкретном теле.
Таким образом, объекты с большим моментом инерции
относительно заданной точки будет труднее вращать с заданным крутящим моментом.
Соответственно, больший крутящий момент вызовет большее ускорение.
на конкретном теле.
Момент инерции тела, который всегда измеряется относительным
до точки вращения, в целом зависит от
масса объекта и его форма. Возможно, очевидно, что для
единичная масса, движущаяся по кругу фиксированного радиуса, тем больше
радиус тем сложнее изменить угловую скорость.Это
потому что фактическое смещение и, следовательно, линейная скорость
масса пропорциональна радиусу, поэтому больший радиус для
данное угловое смещение означает большее линейное смещение.
В протяженном объекте части, удаленные от оси
вращение вносит больший вклад в момент инерции, чем части
ближе к оси. Итак, как правило, для двух объектов с
такая же общая масса, объект с большей массой расположен дальше от
ось будет иметь больший момент инерции.Например, момент
инерции сплошного цилиндра массой M и радиусом R о линии, проходящей через
его центр MR 2 , а полый цилиндр с
такой же массы и радиуса имеет момент инерции MR 2 . так же
когда крутящаяся фигуристка подтягивает руки к своему телу, она кладет
больше ее масса тела приближается к оси вращения и уменьшается
ее момент инерции.
так же
когда крутящаяся фигуристка подтягивает руки к своему телу, она кладет
больше ее масса тела приближается к оси вращения и уменьшается
ее момент инерции.
Следующий: Кинетическая энергия вращения вверх: крутящий момент Предыдущая: Статическое равновесие modtech @ теория.uwinnipeg.ca
1999-09-29
Зависимость момента инерции от массы
Введение в момент инерции При сравнении линейного и вращательного движения есть множество аналогий. В основе этих сравнений лежат концепции массы с одной стороны и момента инерции с другой. Помимо того, что масса является свойством любого физического объекта, она является мерой сопротивления объекта ускорению, когда к объекту прилагается чистая сила.Второй закон движения Ньютона выражает это в известном уравнении F = ma . По аналогии, момент инерции любого твердого объекта является мерой его сопротивления угловому ускорению вокруг оси, когда к объекту прилагается крутящий момент. Это выражается уравнением τ = Iα .
Это выражается уравнением τ = Iα .
Момент инерции можно определить по уравнению
Момент инерции – это сумма масс частиц, составляющих объект, умноженная на их соответствующие расстояния, возведенные в квадрат от оси вращения .Для непрерывных твердых объектов уравнение будет аналогичным, но с использованием интегралов вместо суммы. Следует отметить, что по определению момент инерции тела зависит не только от конкретной оси, на которой оно вращается, но также от его формы и способа распределения его массы.
Задача № 1 – Подготовка плоского диска и кольца с идентичными массами В этом уроке вы будете сравнивать моменты инерции двух объектов с одинаковыми массами .Вы начнете с использования своих навыков мастера, а также некоторых базовых математических навыков, включая алгебру и геометрию. Вы построите два плоских объекта из картона. Один из объектов будет круглым диском радиусом 3,5 дюйма. Другой объект будет кольцом с внешним радиусом также 3,5 дюйма, , но чья масса идентична массе диска . На рисунке 1 представлена диаграмма с двумя такими объектами.
Другой объект будет кольцом с внешним радиусом также 3,5 дюйма, , но чья масса идентична массе диска . На рисунке 1 представлена диаграмма с двумя такими объектами.
Вы хотите определить толщину кольца x так, чтобы , когда два таких концентрических кольца склеены вместе , масса диска будет идентична массе пары концентрические кольца.Вы вырежете диск и два кольца из трех кусков картона. Можно предположить, что бумага для карточек имеет одинаковую толщину с равномерным распределением массы.
Хорошо, теперь примените эти математические и геометрические навыки, чтобы определить значение x ! Затем вырежьте плоские предметы из картона и соберите кольцо. Если вы правильно выполнили расчеты, диск и кольцо в сборе должны быть очень близки к одной и той же массе при установке на весы.
Задача № 2 – Определить период для дискового и кольцевого маятников Теперь, когда у вас есть два объекта одинаковой формы, но с различным распределением масс, вы готовы к первому шагу в определении их моментов инерции. Вы будете рассматривать каждый объект как физический маятник – любое твердое тело, которое качается в вертикальной плоскости вокруг оси, проходящей через тело. На рисунке 2 показан произвольный физический маятник и его физическая теория. Уравнение в поле позволяет определить момент инерции I любого объекта относительно любой конкретной точки поворота на этом объекте. T, G и d измеримы, а g известен.
Вы будете рассматривать каждый объект как физический маятник – любое твердое тело, которое качается в вертикальной плоскости вокруг оси, проходящей через тело. На рисунке 2 показан произвольный физический маятник и его физическая теория. Уравнение в поле позволяет определить момент инерции I любого объекта относительно любой конкретной точки поворота на этом объекте. T, G и d измеримы, а g известен.
Вы будете измерять период T с помощью магнитометра PocketLab.Крошечный магнит, прикрепленный к нижней части физического маятника, будет вызывать внезапный пик величины магнитного поля каждый раз, когда он проходит мимо PocketLab, в то время как маятник раскачивается назад и вперед. На рисунке 3 показаны изображения экспериментальной установки для двух ваших объектов одинаковой массы. В обоих случаях были выбраны похожие точки поворота – точки поворота близко к краю объекта. Маятники раскачиваются на металлическом стержне, который проходит через небольшие отверстия, пробитые в маятниках. Желательно использовать металлический стержень, который помогает снизить трение в точке поворота.
Желательно использовать металлический стержень, который помогает снизить трение в точке поворота.
Для пояснения механизма поворота на рисунке 4 показан вид устройства под углом. Ось представляет собой тонкий металлический стержень, прикрепленный к кольцевой стойке. Также используется деревянный дюбель (или что-то подобное), поскольку зажимной винт не завинчивается достаточно сильно, чтобы зажать металлический стержень в зажиме. Необходимо надевать защитные очки, чтобы избежать любой возможности ткнуть вас в глаз тонким металлическим стержнем.
Рис. 4 – Вид под углом установки прибора Для успеха этого эксперимента необходимо точное измерение периода T каждого из двух ваших маятников. PocketLab позволяет рассчитать период физического маятника гораздо точнее, чем это возможно с помощью секундомера. Использование PocketLab для этой цели исключает ошибки, связанные с временем реакции при запуске и остановке секундомера. PocketLab также следует установить на максимально возможную скорость передачи данных (50 точек в секунду).Убедитесь, что вы измеряете время за несколько периодов, а затем находите среднее значение. На рисунке 5 показано, как этого можно достичь.
PocketLab также следует установить на максимально возможную скорость передачи данных (50 точек в секунду).Убедитесь, что вы измеряете время за несколько периодов, а затем находите среднее значение. На рисунке 5 показано, как этого можно достичь.
Теперь вы должны быть готовы к измерению периодов ваших двух физических маятников. Эти данные имеют решающее значение для успеха в этом эксперименте!
Задача № 3 – Вычислить экспериментальные моменты инерции Теперь, когда вы определили период для ваших двух физических маятников, вы готовы вычислить экспериментальные моменты инерции, используя уравнение в рамке внизу рисунка 2.Вам нужно будет измерить массу каждого маятника. (Помните, что массы должны быть очень близки к одному и тому же значению!) Вам также необходимо измерить расстояние от точки поворота до центра масс каждого маятника. Вы можете использовать принятое значение 9,81 м / с / с для ускорения свободного падения g . Обязательно выражайте все измерения в системе MKS (метр-килограмм-секунда). Какая единица измерения момента инерции MKS? (Подсказка: посмотрите на определяющее уравнение для момента инерции.)
Обязательно выражайте все измерения в системе MKS (метр-килограмм-секунда). Какая единица измерения момента инерции MKS? (Подсказка: посмотрите на определяющее уравнение для момента инерции.)
Таблицы теоретических моментов инерции различных форм относительно их центра масс легко доступны в Интернете. Эти теоретические моменты инерции определяются с помощью интегрального исчисления, детали которого не важны для нашего исследования. Рисунок 6 суммирует теоретические уравнения момента инерции относительно центра масс для плоского диска и кольца.Однако наши диск и кольцо не вращались вокруг соответствующих центров масс. Они вращались вокруг оси очень близко к их внешним краям . Помните, что момент инерции зависит не только от массы и того, как она распределена, но и от конкретной оси, на которой она вращается.
Как оказалось, существует простая и чрезвычайно полезная теорема, известная как Теорема о параллельных осях , которая выражает связь между моментом инерции I объекта относительно любой оси и его моментом инерция относительно параллельной оси, проходящей через центр масс. Если Ic – это момент инерции относительно центра масс, m – масса объекта, а w – расстояние между двумя осями, эта теорема говорит нам, что момент инерции I определяется выражением уравнение
Если Ic – это момент инерции относительно центра масс, m – масса объекта, а w – расстояние между двумя осями, эта теорема говорит нам, что момент инерции I определяется выражением уравнение
Используйте теорему о параллельных осях вместе с некоторой алгеброй и уравнениями на рисунке 6, чтобы определить уравнения для момента инерции относительно точки, расположенной рядом с краем плоского диска и кольца. Если ваши оси очень близки к внешнему краю диска и кольца, то вы можете считать, что w равно внешнему радиусу.
Наконец, вычислите теоретические значения для этих моментов инерции из ваших уравнений.
Рисунок 6 – Моменты инерции относительно центра масс для диска и кольца Задача № 5 – Определить процентную разницу между экспериментальным и теоретическим моментами инерции Сравнения должны быть выражены как процентная разница между экспериментальным и теоретическим моментом инерции относительно осей у краев, основанная на доле теоретического момента инерции. Разница в процентах будет отрицательной, если ваш экспериментальный результат меньше теоретического, и положительным, если экспериментальный результат больше теоретического.
Разница в процентах будет отрицательной, если ваш экспериментальный результат меньше теоретического, и положительным, если экспериментальный результат больше теоретического.
Ваш экспериментальный момент инерции кольца относительно его краевой оси больше, чем момент инерции диска относительно его краевой оси? Так должно быть, если период кольца был больше периода диска.Проведите обсуждение, которое интуитивно подсказывает, что момент инерции кольца должен быть больше, чем у диска.
Дополнительные уроки PocketLab, посвященные моменту инерцииДинамика вращения падающей измерительной рукоятки
PocketLab Voyager: эксперимент с маховиком
PocketLab Voyager: момент инерции и сохранение углового момента
Вращательное движение: момент инерции
Физический маятник: поиск момента инерции
Определение момента инерции в физике.

Примеры момента инерции в следующих разделах:
Момент инерции
- Первый закон Ньютона, который описывает инерцию тела в линейном движении, может быть расширен до инерции тела, вращающегося вокруг оси, используя момент из инерции .
- Момент инерция также зависит от оси, вокруг которой вы вращаете объект.
- Основная взаимосвязь между моментом при инерции и угловым ускорением заключается в том, что чем больше момент при инерции , тем меньше угловое ускорение.
- Краткое введение в момент из инерция (вращательная инерция ) для студентов, изучающих математику.
- Определите свойство массы , описанной моментом инерцией
Физический маятник
- Период от физического маятника зависит от его момента от инерции относительно его точки поворота и расстояния от его центра с массой .

- В этом случае период маятника зависит от его момента инерции вокруг точки поворота.
- , где α – угловое ускорение, τ – крутящий момент, а I – момент из инерции .
- Момент инерция жесткий стержень вокруг его центра:
- Изменение формы, размера или распределения массы изменит момент из инерции .
- Период от физического маятника зависит от его момента от инерции относительно его точки поворота и расстояния от его центра с массой .
Вращательная кинетическая энергия: работа, энергия и мощность
- Рассмотрение энергии вращения отдельно вокруг оси объекта вращения дает следующую зависимость от момента объекта из инерции :
- , где $ \ omega $ – угловая скорость, а $ I $ – момент инерция вокруг оси вращения .
- Во вращающейся системе момент инерция играет роль массы , а угловая скорость играет роль из линейной скорости.

- Земля имеет момент из инерции , I = 8,04 × 1037 кг · м2.
- Соотношение зависит от момента инерции вращающегося объекта.
Взаимосвязь между крутящим моментом и угловым ускорением
- Крутящий момент равен моменту из инерции , умноженному на угловое ускорение.
- Крутящий момент и угловое ускорение связаны следующей формулой, где – объект момент из инерция и $ \ alpha $ – угловое ускорение.
- Если вы замените крутящий момент силой, а вращательную инерцию инерцией массой и угловое ускорение линейным ускорением, вы получите второй закон Ньютона обратно.
- Чистый крутящий момент вокруг оси вращения равен произведению на инерцию вращения вокруг этой оси и угловое ускорение, как показано на Рисунке 1.
- Силы из двух пальцев компенсируются.

Приложения кратных интегралов
- Как и в случае с одной переменной, можно использовать кратный интеграл, чтобы найти среднее значение для функции по заданному набору.n $ и интегрируемая функция $ f $ над $ D $, среднее значение из $ f $ по его области определяется как:
- , где $ m (D) $ – это величина для $ D $.
- В механике момент инерция рассчитывается как объемный интеграл (тройной интеграл) плотность, взвешенная с квадратом из расстояния от оси:
- В следующем примере электрическое поле, создаваемое распределением зарядов , заданным объемной плотностью заряда $ \ rho (\ vec r) $, получается тройным интегралом от векторной функции:
Вращательные столкновения
- Во время столкновения объектов в замкнутой системе импульс всегда сохраняется.
- Что, если ввести вращательный компонент движения ?
- Как и следовало ожидать, объект с большим моментом из инерции I, такой как Земля, имеет очень большой угловой момент.

- Например, возьмем случай из , когда лучник решает выстрелить стрелой массой m1 в неподвижный цилиндр массой m2 и радиусом r, лежащий на боку.
- Стрела попадает в край цилиндра , заставляя его катиться.
Инерция вращения
- Вращение инерция – это тенденция из вращающегося объекта оставаться вращающимся, если к нему не приложен крутящий момент.
- Вращение инерция , как показано на, это сопротивление объектов изменениям в их вращении.
- Это уравнение является вращательным аналогом второго закона Ньютона (F = ma), где крутящий момент аналогичен силе, угловое ускорение аналогично поступательному ускорению, а mr2 аналогично массе (или инерции ).
- Величина mr2 называется вращательной инерцией или моментом инерцией точечной массой m на расстоянии r от центра вращения .

- Различные формы из объектов имеют разную инерцию вращения , которая зависит от распределения их массы.
Сохранение углового момента
- Закон сохранения углового момента гласит, что когда на объект не действует внешний крутящий момент, никакого изменения углового момента не произойдет.
- Это выражение закона сохранения углового момента .
- Когда она это делает, инерция вращения уменьшается, а скорость вращения увеличивается, чтобы угловой момент $ L = I \ omega $ оставался постоянным.
- (I: вращательная инерция , $ \ omega $: угловая скорость)
- На следующем изображении ее частота вращения из сильно увеличивается, когда она тянет руки, уменьшая ее момент из инерцию .
Сохранение энергии при вращательном движении
- Искры летят, и создается шум и вибрация, когда слои стали отделяются от столба.

- Сила параллельна перемещению, поэтому проделанная чистая работа (W) равна произведению из силы (F) и радиуса (r) диска (это также известно как крутящий момент (τ) ) умноженный на угол (θ) поворота на :
- Кинетическая энергия (К.E.) во вращательном движении связан с моментом из вращением инерцией (I) и угловой скоростью (ω):
- Однако энергия никогда не разрушается; он просто меняет форму от вращения точильного камня на нагрев при приложении трения.
- Заключить взаимозаменяемость силы и радиуса с крутящим моментом и углом вращения при определении силы
- Искры летят, и создается шум и вибрация, когда слои стали отделяются от столба.
Первый закон: инерция
- Первый закон Ньютона движения описывает инерцию .
- Ускорение для объекта параллельно и прямо пропорционально чистой силе, действующей на объект, в направлении для является чистая сила и обратно пропорционально массе объекта.

- Иногда этот первый закон движения называют законом инерции .
- Инерция – это свойство объекта оставаться в состоянии покоя или оставаться в движении с постоянной скоростью.
- Некоторые объекты имеют больше инерции , чем другие, потому что инерция объекта эквивалентна его массе.
Разница между инерцией и моментом инерции
Ключевое отличие: Инерцию можно описать как свойство или тенденцию объекта, который сопротивляется любому изменению его состояния движения. Момент инерции – это измерение сопротивления объекта изменению его вращения. Инерцию можно описать как свойство или тенденцию объекта, который сопротивляется любому изменению его состояния движения.Таким образом, тело остается в покое или продолжает движение, если на него не действует внешняя сила. Латинский корень «инерция» является тем же корнем, что и «инертный», что означает отсутствие способности двигаться. Галилей, ученый семнадцатого века, разработал концепцию инерции, заявив, что движущийся объект имеет тенденцию останавливаться из-за силы трения. Позже Ньютон сформулировал законы движения. Первый закон движения Ньютона фокусируется на инерции. Он описывается как – «В отсутствие внешних сил движение по прямой и с постоянной скоростью продолжается бесконечно.«
Галилей, ученый семнадцатого века, разработал концепцию инерции, заявив, что движущийся объект имеет тенденцию останавливаться из-за силы трения. Позже Ньютон сформулировал законы движения. Первый закон движения Ньютона фокусируется на инерции. Он описывается как – «В отсутствие внешних сил движение по прямой и с постоянной скоростью продолжается бесконечно.«
Момент инерции – это измерение сопротивления объекта изменению его вращения. Момент инерции выражается относительно выбранной оси вращения. Это также известно как инерция вращения. Это зависит от трех сил – массы объекта, формы и относительной точки вращения. Он обозначается символом I. Можно также определить момент инерции как способность противостоять скручивающей силе или крутящему моменту. Момент инерции зависит от формы объекта, и поэтому зависимость можно легко увидеть в различных формулах.Ниже приведены несколько примеров формул, используемых для расчета момента инерции:
Для однородного диска с радиусом r и массой m момент инерции = 1/2 (м x r²).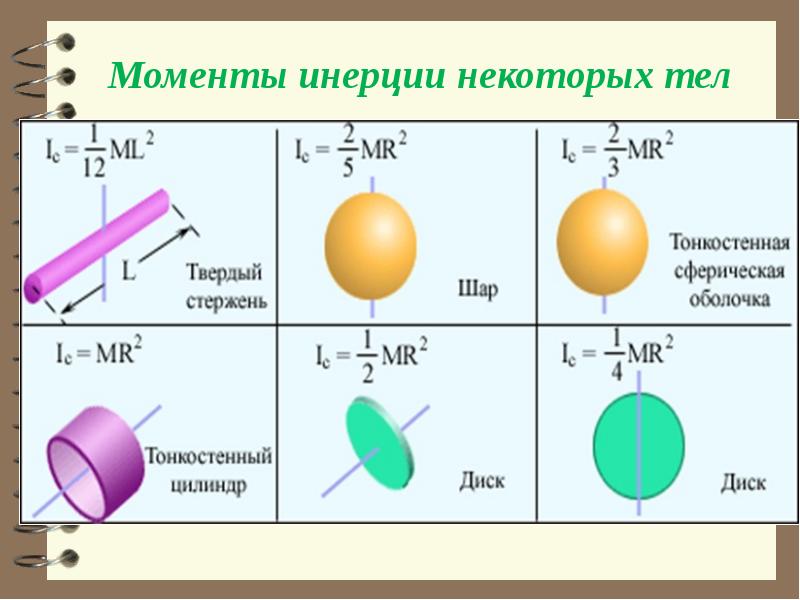
Для твердой сферы I = 2/5 (м x r²).
Точечная частица массы m на орбите на расстоянии r от объекта, момент инерции = (m x r²).
Сравнение инерции и момента инерции:
Инерция | Момент инерции | |
Определение | Инерцию можно описать как свойство или тенденцию объекта, который сопротивляется любому изменению его состояния движения. | Момент инерции – это измерение сопротивления объекта изменению его вращения. Момент инерции выражается относительно выбранной оси вращения. |
Тип | Естественная склонность | Единица измерения |
Формула | Невозможно рассчитать по формуле. | Момент инерции =, , где A – площадь плоскости объекта, а y – расстояние между центроидом объекта и осью x. |
Формы | Никаких других форм | Линейный и угловой момент |
Блок | – | Килограмм метр квадратный |
Зависимость | Масса | Масса и расстояние |
Количественный аспект | Скаляр | Тензор (имеющий как скалярные, так и векторные свойства) |
Другое название | – | Второй момент площади тела. |
Пример | Шар размером с шар для боулинга будет иметь большую инерцию, чем по сравнению с кеглей. | Колесо, в котором большая часть массы лежит около оси, легче разогнаться по сравнению с другим колесом, в котором равная масса распределена по большему диаметру. |
Демонстрация момента инерции | WIRED
Контент
Этот контент также можно просмотреть на сайте, с которого оно создано.
Когда я говорил о балансировке палки, я упомянул момент инерции. Момент инерции отличается от массы, но мне нравится называть его «вращательной массой». Что делает масса? Вещям с большей массой сложнее изменить свое движение (поступательное движение). То же самое и с «вращательной массой». Вещи с большей вращательной массой сложнее изменить вращательное движение. Вот демо.
Демо для Moment of Inertia от Ретта Аллена на Vimeo.
Почему мне нравится эта демонстрация? Во-первых, он использует обычные вещи. Я считаю коробки для сока довольно обычными. Во-вторых, мне это нравится, потому что вы можете передать палку с большим моментом инерции «более сильному» человеку. Так побеждает более слабый. Если вы хотите сделать супер модную версию этого, спрячьте массы внутри тюбика, чтобы две палочки выглядели как у глаз.
Итак, что такое момент инерции? При вращении вокруг фиксированной оси момент инерции является скалярным значением, которое зависит от того, как масса распределена вокруг оси вращения. Технически, если у вас есть точечные массы, то момент инерции будет:
Технически, если у вас есть точечные массы, то момент инерции будет:
Это уравнение говорит – возьмите каждую массу. Умножьте массу на квадрат расстояния до оси и сложите все эти члены. Позвольте мне показать этот расчет для двух клюшек, использованных в демонстрации (при условии безмассовых клюшек).
Для рукояти длиной L с двумя массами масс м момент инерции рукояти с массами на конце будет:
А для второй рукояти массы будут равны намного ближе к оси вращения и, следовательно, я был бы намного меньше.Обратите внимание, что расчет момента инерции зависит от положения оси вращения. Если бы я повернул их около конца, то получил бы другое значение.
Последнее замечание. Я не выводил этот момент инерции выражения, а просто констатировал его. Возможно, позже я вернусь и дам более подробную информацию.
Вращательная инерция – Физика колледжа, главы 1-17
Сводка
- Поймите взаимосвязь между силой, массой и ускорением.

- Изучите вращающий эффект силы.
- Изучите аналогию между силой и крутящим моментом, массой и моментом инерции, а также линейным ускорением и угловым ускорением.
Если вы когда-либо крутили колесо велосипеда или толкали карусель, вы знаете, что для изменения угловой скорости требуется сила, как показано на рисунке 1. Фактически, ваша интуиция надежно предсказывает многие из факторов, которые участвуют в этом процессе. . Например, мы знаем, что дверь открывается медленно, если мы нажимаем слишком близко к ее петлям.Кроме того, мы знаем, что чем массивнее дверь, тем медленнее она открывается. Первый пример подразумевает, что чем дальше от оси приложена сила, тем больше угловое ускорение; другое значение состоит в том, что угловое ускорение обратно пропорционально массе. Эти отношения должны казаться очень похожими на знакомые отношения между силой, массой и ускорением, воплощенные во втором законе движения Ньютона. На самом деле существуют точные вращательные аналоги как силы, так и массы.
Чтобы установить точное соотношение между силой, массой, радиусом и угловым ускорением, подумайте, что произойдет, если мы приложим силу [латекс] \ boldsymbol {F} [/ latex] к точечной массе [латекс] \ boldsymbol {m} [ / latex], который находится на расстоянии [latex] \ boldsymbol {r} [/ latex] от точки поворота, как показано на рисунке 2.Поскольку сила перпендикулярна [латексу] \ boldsymbol {r}, [/ latex], ускорение [латекс] \ boldsymbol {a = \ frac {F} {m}} [/ latex] достигается в направлении [латекса ] \ boldsymbol {F}. [/ latex] Мы можем изменить это уравнение так, чтобы [latex] \ boldsymbol {F = ma} [/ latex], а затем искать способы связать это выражение с выражениями для вращательных величин. Мы отмечаем, что [latex] \ boldsymbol {a = r \ omega}, [/ latex], и подставляем это выражение в [latex] \ boldsymbol {F = ma}, [/ latex], получая
[латекс] \ boldsymbol {F = mr \ alpha}. 2} [/ latex] называется инерцией вращения или моментом инерции точечной массы [латекс] \ boldsymbol {m} [/ latex] на расстоянии [латекс] \ boldsymbol {r} [/ latex] от центр вращения.
2} [/ latex] называется инерцией вращения или моментом инерции точечной массы [латекс] \ boldsymbol {m} [/ latex] на расстоянии [латекс] \ boldsymbol {r} [/ latex] от центр вращения.
ВЫПОЛНЕНИЕ СОЕДИНЕНИЙ: ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Динамика вращательного движения полностью аналогична линейной или поступательной динамике. Динамика связана с силой и массой и их влиянием на движение. Для вращательного движения мы найдем прямые аналоги силе и массе, которые ведут себя так, как мы и ожидали из нашего предыдущего опыта.
Прежде чем мы сможем рассматривать вращение чего-либо, кроме точечной массы, подобной показанной на рисунке 2, мы должны распространить идею инерции вращения на все типы объектов. 2}, [/ latex], где [latex] \ boldsymbol {M} [/ latex] – его общая масса, а [latex] \ boldsymbol {R} [/ latex] – его радиус. (Мы используем [latex] \ boldsymbol {M} [/ latex] и [latex] \ boldsymbol {R} [/ latex] для всего объекта, чтобы отличать их от [latex] \ boldsymbol {m} [/ latex] и [ latex] \ boldsymbol {r} [/ latex] для точечных масс.) Во всех остальных случаях мы должны обращаться к рисунку 3 (обратите внимание, что таблица – это произведение искусства, которое имеет формы, а также формулы) для формул для [латекса] \ жирный символ {I} [/ latex], полученные в результате интегрирования непрерывного тела.2} [/ latex]), как и следовало ожидать из его определения.
2}, [/ latex], где [latex] \ boldsymbol {M} [/ latex] – его общая масса, а [latex] \ boldsymbol {R} [/ latex] – его радиус. (Мы используем [latex] \ boldsymbol {M} [/ latex] и [latex] \ boldsymbol {R} [/ latex] для всего объекта, чтобы отличать их от [latex] \ boldsymbol {m} [/ latex] и [ latex] \ boldsymbol {r} [/ latex] для точечных масс.) Во всех остальных случаях мы должны обращаться к рисунку 3 (обратите внимание, что таблица – это произведение искусства, которое имеет формы, а также формулы) для формул для [латекса] \ жирный символ {I} [/ latex], полученные в результате интегрирования непрерывного тела.2} [/ latex]), как и следовало ожидать из его определения.
Общее соотношение между крутящим моментом, моментом инерции и угловым ускорением:
[латекс] \ boldsymbol {\ textbf {net} \ tau = I \ alpha} [/ латекс]
или
[латекс] \ boldsymbol {\ alpha \: =} [/ latex] [латекс] \ boldsymbol {\ frac {\ textbf {net} \ tau} {I}}, [/ latex]
где net [latex] \ boldsymbol {\ tau} [/ latex] – это общий крутящий момент от всех сил относительно выбранной оси. Для простоты мы будем рассматривать только моменты, действующие под действием сил в плоскости вращения.Такие моменты могут быть положительными или отрицательными и складываются как обычные числа. Отношение в [latex] \ boldsymbol {\ tau = I \ alpha}, \: \ boldsymbol {\ alpha = \ frac {\ textbf {net} \ tau} {I}} [/ latex] является аналогом вращения Ньютона. второй закон и очень широко применяется. Это уравнение действительно для любого крутящего момента , приложенного к любому объекту , относительно любой оси .
Для простоты мы будем рассматривать только моменты, действующие под действием сил в плоскости вращения.Такие моменты могут быть положительными или отрицательными и складываются как обычные числа. Отношение в [latex] \ boldsymbol {\ tau = I \ alpha}, \: \ boldsymbol {\ alpha = \ frac {\ textbf {net} \ tau} {I}} [/ latex] является аналогом вращения Ньютона. второй закон и очень широко применяется. Это уравнение действительно для любого крутящего момента , приложенного к любому объекту , относительно любой оси .
Как и следовало ожидать, чем больше крутящий момент, тем больше угловое ускорение.Например, чем сильнее ребенок толкает карусель, тем быстрее она разгоняется. Кроме того, чем массивнее карусель, тем медленнее она разгоняется при том же крутящем моменте. Основное соотношение между моментом инерции и угловым ускорением состоит в том, что чем больше момент инерции, тем меньше угловое ускорение. Но есть еще один нюанс. Момент инерции зависит не только от массы объекта, но и от его распределения массы относительно оси, вокруг которой он вращается. Например, будет намного легче разогнать карусель, полную детей, если они будут стоять близко к ее оси, чем если все они будут стоять у внешнего края. Масса в обоих случаях одинакова; но момент инерции намного больше, когда дети находятся на грани.
Например, будет намного легче разогнать карусель, полную детей, если они будут стоять близко к ее оси, чем если все они будут стоять у внешнего края. Масса в обоих случаях одинакова; но момент инерции намного больше, когда дети находятся на грани.
ЭКСПЕРИМЕНТ НА ДОМУ
Вырежьте из плотного картона круг радиусом около 10 см. На краю круга напишите числа от 1 до 12, как часы на циферблате. Расположите круг так, чтобы он мог свободно вращаться вокруг горизонтальной оси через его центр, как колесо.(Вы можете свободно прибить круг к стене.) Держите круг неподвижно и с номером 12, расположенным вверху, прикрепите кусок синей замазки (липкий материал, используемый для крепления плакатов к стене) под номером 3. Насколько велик шишка должна быть просто кружить круг? Опишите, как можно изменить момент инерции круга. Как это изменение повлияет на количество синей замазки, необходимое для числа 3, чтобы просто повернуть круг? Измените момент инерции круга, а затем попробуйте повернуть круг, используя разное количество синей замазки. Повторите этот процесс несколько раз.
Повторите этот процесс несколько раз.
СТРАТЕГИЯ РЕШЕНИЯ ПРОБЛЕМ ДЛЯ ВРАЩАТЕЛЬНОЙ ДИНАМИКИ
- Изучите ситуацию, чтобы определить, крутящий момент и масса участвуют во вращении . Нарисуйте тщательный набросок ситуации.
- Определите интересующую систему .
- Нарисуйте схему свободного тела . То есть нарисуйте и обозначьте все внешние силы, действующие на интересующую систему.
- Применить [латекс] \ boldsymbol {\ textbf {net} \ tau = I \ alpha}, \: \ boldsymbol {\ alpha = \ frac {\ textbf {net} \ tau} {I}}, [/ latex ] вращательный эквивалент второго закона Ньютона, чтобы решить задачу .Необходимо соблюдать осторожность, чтобы использовать правильный момент инерции и учитывать крутящий момент относительно точки вращения.
- Как всегда, проверьте правильность решения .
ПОДКЛЮЧЕНИЕ
В статике чистый крутящий момент равен нулю, и нет углового ускорения. При вращательном движении чистый крутящий момент является причиной углового ускорения, как и во втором законе движения Ньютона для вращения.
При вращательном движении чистый крутящий момент является причиной углового ускорения, как и во втором законе движения Ньютона для вращения.
Пример 1: Расчет влияния распределения массы на карусель
Представьте, что отец толкает карусель на игровой площадке на рис. 4. Он прилагает силу 250 Н к краю 50,0 кг карусели, имеющей радиус 1,50 м. Вычислите угловое ускорение, возникающее (а), когда никого нет на карусели, и (б), когда ребенок весом 18,0 кг сидит на расстоянии 1,25 м от центра. Считайте саму карусель однородным диском с незначительным тормозящим трением.
Рис. 4. Отец толкает карусель на детской площадке за край и перпендикулярно ее радиусу, чтобы добиться максимального крутящего момента.Стратегия
Угловое ускорение задается выражением [latex] \ boldsymbol {\ alpha = \ frac {\ textbf {net} \ tau} {I}}: [/ latex]
[латекс] \ boldsymbol {\ alpha \: =} [/ latex] [латекс] \ boldsymbol {\ frac {\ tau} {I}}. 2 = (18.2}}. [/ Latex]
2 = (18.2}}. [/ Latex]
Обсуждение
Угловое ускорение меньше, когда ребенок находится на карусели, чем когда карусель пуста, как и ожидалось. Обнаруженные угловые ускорения довольно велики, отчасти из-за того, что трение считалось незначительным. Если, например, отец продолжал толкать перпендикулярно в течение 2,00 с, он дал бы карусели угловую скорость 13,3 рад / с, когда она пуста, и только 8,89 рад / с, когда на ней сидит ребенок.В оборотах в секунду эти угловые скорости составляют 2,12 об / с и 1,41 об / с соответственно. В первом случае отец разгонялся до 50 км / ч. Летние Олимпийские игры, вот он! Подтверждение этих чисел оставлено читателю в качестве упражнения.
Проверьте свое понимание
1: Крутящий момент является аналогом силы, а момент инерции является аналогом массы. Сила и масса – это физические величины, которые зависят только от одного фактора. Например, масса связана исключительно с количеством атомов различных типов в объекте. Одинаково ли просты крутящий момент и момент инерции?
Одинаково ли просты крутящий момент и момент инерции?
- Чем дальше от оси приложена сила, тем больше угловое ускорение; угловое ускорение обратно пропорционально массе.
- Если мы приложим силу [латекс] \ boldsymbol {F} [/ latex] к точечной массе [латекс] \ boldsymbol {m} [/ latex], которая находится на расстоянии [латекс] \ boldsymbol {r} [/ latex ] от точки поворота, и поскольку сила перпендикулярна [латексу] \ boldsymbol {r}, [/ latex], ускорение [латекс] \ boldsymbol {a = F / m} [/ latex] достигается в направлении [ латекс] \ boldsymbol {F}.[/ latex] Мы можем переписать это уравнение так, чтобы
[латекс] \ boldsymbol {F = ma}, [/ latex]
, а затем поищите способы связать это выражение с выражениями для вращательных величин. Заметим, что [latex] \ boldsymbol {a = r \ alpha}, [/ latex], и мы подставляем это выражение в [latex] \ boldsymbol {F = ma}, [/ latex], получая
[латекс] \ boldsymbol {F = mr \ alpha} [/ латекс]
- Крутящий момент – это эффективность силы при повороте.
 В этом случае, поскольку [latex] \ boldsymbol {F} [/ latex] перпендикулярно [latex] \ boldsymbol {r}, крутящий момент [/ latex] будет просто [latex] \ boldsymbol {\ tau = rF}.2/4}. [/ Латекс])
В этом случае, поскольку [latex] \ boldsymbol {F} [/ latex] перпендикулярно [latex] \ boldsymbol {r}, крутящий момент [/ latex] будет просто [latex] \ boldsymbol {\ tau = rF}.2/4}. [/ Латекс])2: Почему момент инерции обруча имеет массу [латекс] \ boldsymbol {M} [/ latex] и радиус [латекс] \ boldsymbol {R} [/ latex] больше, чем момент инерция диска той же массы и радиуса? Почему момент инерции сферической оболочки, имеющей массу [латекс] \ boldsymbol {M} [/ latex] и радиус [латекс] \ boldsymbol {R} [/ latex], больше, чем у твердой сферы, имеющей такая же масса и радиус?
3: Приведите пример, в котором малая сила вызывает большой крутящий момент.Приведите другой пример, в котором большая сила вызывает небольшой крутящий момент.
4: При уменьшении массы гоночного велосипеда наибольшая выгода достигается за счет уменьшения массы шин и колесных дисков. Почему это позволяет гонщику развивать большее ускорение, чем такое же уменьшение массы рамы велосипеда?
Рис. 5. На изображении показан гоночный велосипед, вид сбоку. Можете ли вы увидеть в конструкции колес этого гоночного велосипеда свидетельство того, что их момент инерции был намеренно уменьшен? (Источник: Хесус Родригес)
5. На изображении показан гоночный велосипед, вид сбоку. Можете ли вы увидеть в конструкции колес этого гоночного велосипеда свидетельство того, что их момент инерции был намеренно уменьшен? (Источник: Хесус Родригес)5: Мяч скользит по трапу без трения.Затем его катят без проскальзывания и с той же начальной скоростью по другому пандусу без трения (с тем же углом наклона). В каком случае он достигает большей высоты и почему?
Задачи и упражнения
1: В этой задаче рассматриваются дополнительные аспекты примера 1. (a) Сколько времени требуется отцу, чтобы дать карусели угловую скорость 1,50 рад / с? б) Сколько оборотов он должен совершить, чтобы получить эту скорость? (c) Если он прикладывает замедляющую силу 300 Н на радиусе 1.35 м, сколько времени ему понадобится, чтобы их остановить?
2: Рассчитайте момент инерции фигуриста с учетом следующей информации.
 (а) Фигурист весом 60,0 кг приблизительно представляет собой цилиндр с радиусом 0,110 м. (b) Фигурист с вытянутыми руками представляет собой цилиндр, который составляет примерно 52,5 кг, имеет радиус 0,110 м и две руки длиной 0,900 м, каждая по 3,75 кг, которые выходят прямо из цилиндра, как стержни, вращающиеся вокруг своей оси. заканчивается.
(а) Фигурист весом 60,0 кг приблизительно представляет собой цилиндр с радиусом 0,110 м. (b) Фигурист с вытянутыми руками представляет собой цилиндр, который составляет примерно 52,5 кг, имеет радиус 0,110 м и две руки длиной 0,900 м, каждая по 3,75 кг, которые выходят прямо из цилиндра, как стержни, вращающиеся вокруг своей оси. заканчивается.3: Трехглавая мышца задней части плеча разгибает предплечье.2}. [/ Latex] Какова сила, действующая на мышцу, если ее эффективное перпендикулярное плечо рычага составляет 1,90 см?
5: Предположим, вы прилагаете усилие 180 Н по касательной к точильному камню массой 75,0 кг радиусом 0,280 м (твердый диск).
(а) Какой крутящий момент прилагается? (b) Какое угловое ускорение предполагает пренебрежимо малое встречное трение? (c) Каково угловое ускорение, если существует противодействующая сила трения 20,0 Н, действующая на 1,50 см от оси?
6: Рассмотрим 12.
 Колесо мотоцикла весом 0 кг показано на рисунке 6. Предположим, что это примерно кольцевое кольцо с внутренним радиусом 0,280 м и внешним радиусом 0,330 м. Мотоцикл стоит на центральной подставке, так что колесо может свободно вращаться. (a) Если приводная цепь оказывает усилие в 2200 Н на радиусе 5,00 см, каково угловое ускорение колеса? (б) Каково тангенциальное ускорение точки на внешнем крае шины? (c) Сколько времени требуется, начиная с состояния покоя, чтобы достичь угловой скорости 80.7 \ textbf {N}} [/ latex] (немного больше, чем тяга ракеты Сатурн V). Как долго Зорч должен продвигаться с этой силой, чтобы достичь своей цели? (Этот период дает Супермену время, чтобы посвятить его другим злодеям.) Ясно покажите, как вы следуете шагам, описанным в Стратегии решения проблем для динамики вращения.
Колесо мотоцикла весом 0 кг показано на рисунке 6. Предположим, что это примерно кольцевое кольцо с внутренним радиусом 0,280 м и внешним радиусом 0,330 м. Мотоцикл стоит на центральной подставке, так что колесо может свободно вращаться. (a) Если приводная цепь оказывает усилие в 2200 Н на радиусе 5,00 см, каково угловое ускорение колеса? (б) Каково тангенциальное ускорение точки на внешнем крае шины? (c) Сколько времени требуется, начиная с состояния покоя, чтобы достичь угловой скорости 80.7 \ textbf {N}} [/ latex] (немного больше, чем тяга ракеты Сатурн V). Как долго Зорч должен продвигаться с этой силой, чтобы достичь своей цели? (Этот период дает Супермену время, чтобы посвятить его другим злодеям.) Ясно покажите, как вы следуете шагам, описанным в Стратегии решения проблем для динамики вращения.8: Автомобильный двигатель может развивать крутящий момент 200 Н ∙ м. Рассчитайте угловое ускорение, возникающее при приложении 95,0% этого крутящего момента к ведущему валу, оси и задним колесам автомобиля, учитывая следующую информацию.
 2/12}.2}. [/ Latex] (а) Сколько времени ей нужно, чтобы полностью изменить свое вращение? б) Что неразумного в результате? (c) Какие посылки необоснованны или непоследовательны?
2/12}.2}. [/ Latex] (а) Сколько времени ей нужно, чтобы полностью изменить свое вращение? б) Что неразумного в результате? (c) Какие посылки необоснованны или непоследовательны?11: Необоснованные результаты
В рекламе утверждается, что автомобилю массой 800 кг помогает его маховик массой 20,0 кг, который может разогнать автомобиль от состояния покоя до скорости 30,0 м / с. Маховик представляет собой диск радиусом 0,150 м. (a) Рассчитайте угловую скорость, которую должен иметь маховик, если 95,0% его энергии вращения используется для набора скорости автомобиля.б) Что неразумного в результате? (c) Какая предпосылка является необоснованной, а какие – несовместимой?
Глоссарий
- крутящий момент
- эффективность поворота силы
- инерция вращения
- сопротивление изменению вращения. Чем больше инерция вращения у объекта, тем труднее его вращать
- момент инерции
- масса, умноженная на квадрат расстояния по перпендикуляру от оси вращения; для точечной массы это [латекс] \ boldsymbol {I = mr ^ 2} [/ latex], и, поскольку любой объект может быть создан из набора точечных масс, это соотношение является основой для всех других моментов инерции
Упражнения
Проверьте свое понимание
1: №Крутящий момент зависит от трех факторов: величины силы, направления силы и точки приложения.
 Момент инерции зависит как от массы, так и от ее распределения относительно оси вращения. Таким образом, хотя аналогии точны, эти вращательные величины зависят от большего числа факторов.
Момент инерции зависит как от массы, так и от ее распределения относительно оси вращения. Таким образом, хотя аналогии точны, эти вращательные величины зависят от большего числа факторов.Задачи и упражнения
1:
(а) 0,338 с
(б) 0,0403 изм.
(в) 0,313 с
3:
[латекс] \ boldsymbol {0.2} \ end {array} [/ latex]
10:
(а) 2,0 мс
(b) Временной интервал слишком короткий.
(c) Момент инерции слишком мал, на один-два порядка величины. Крутящий момент [латекс] \ boldsymbol {500 \ textbf {N} \ cdotp \ textbf {m}} [/ latex] является разумным.
11:
(а) 17500 об / мин
(б) Эта угловая скорость очень велика для диска такого размера и массы. Радиальное ускорение на краю диска> 50 000 gs.
(c) Масса и радиус маховика должны быть намного больше, что позволяет снизить скорость вращения (угловую скорость).











 В этом случае, поскольку [latex] \ boldsymbol {F} [/ latex] перпендикулярно [latex] \ boldsymbol {r}, крутящий момент [/ latex] будет просто [latex] \ boldsymbol {\ tau = rF}.2/4}. [/ Латекс])
В этом случае, поскольку [latex] \ boldsymbol {F} [/ latex] перпендикулярно [latex] \ boldsymbol {r}, крутящий момент [/ latex] будет просто [latex] \ boldsymbol {\ tau = rF}.2/4}. [/ Латекс]) 5. На изображении показан гоночный велосипед, вид сбоку. Можете ли вы увидеть в конструкции колес этого гоночного велосипеда свидетельство того, что их момент инерции был намеренно уменьшен? (Источник: Хесус Родригес)
5. На изображении показан гоночный велосипед, вид сбоку. Можете ли вы увидеть в конструкции колес этого гоночного велосипеда свидетельство того, что их момент инерции был намеренно уменьшен? (Источник: Хесус Родригес) (а) Фигурист весом 60,0 кг приблизительно представляет собой цилиндр с радиусом 0,110 м. (b) Фигурист с вытянутыми руками представляет собой цилиндр, который составляет примерно 52,5 кг, имеет радиус 0,110 м и две руки длиной 0,900 м, каждая по 3,75 кг, которые выходят прямо из цилиндра, как стержни, вращающиеся вокруг своей оси. заканчивается.
(а) Фигурист весом 60,0 кг приблизительно представляет собой цилиндр с радиусом 0,110 м. (b) Фигурист с вытянутыми руками представляет собой цилиндр, который составляет примерно 52,5 кг, имеет радиус 0,110 м и две руки длиной 0,900 м, каждая по 3,75 кг, которые выходят прямо из цилиндра, как стержни, вращающиеся вокруг своей оси. заканчивается. Колесо мотоцикла весом 0 кг показано на рисунке 6. Предположим, что это примерно кольцевое кольцо с внутренним радиусом 0,280 м и внешним радиусом 0,330 м. Мотоцикл стоит на центральной подставке, так что колесо может свободно вращаться. (a) Если приводная цепь оказывает усилие в 2200 Н на радиусе 5,00 см, каково угловое ускорение колеса? (б) Каково тангенциальное ускорение точки на внешнем крае шины? (c) Сколько времени требуется, начиная с состояния покоя, чтобы достичь угловой скорости 80.7 \ textbf {N}} [/ latex] (немного больше, чем тяга ракеты Сатурн V). Как долго Зорч должен продвигаться с этой силой, чтобы достичь своей цели? (Этот период дает Супермену время, чтобы посвятить его другим злодеям.) Ясно покажите, как вы следуете шагам, описанным в Стратегии решения проблем для динамики вращения.
Колесо мотоцикла весом 0 кг показано на рисунке 6. Предположим, что это примерно кольцевое кольцо с внутренним радиусом 0,280 м и внешним радиусом 0,330 м. Мотоцикл стоит на центральной подставке, так что колесо может свободно вращаться. (a) Если приводная цепь оказывает усилие в 2200 Н на радиусе 5,00 см, каково угловое ускорение колеса? (б) Каково тангенциальное ускорение точки на внешнем крае шины? (c) Сколько времени требуется, начиная с состояния покоя, чтобы достичь угловой скорости 80.7 \ textbf {N}} [/ latex] (немного больше, чем тяга ракеты Сатурн V). Как долго Зорч должен продвигаться с этой силой, чтобы достичь своей цели? (Этот период дает Супермену время, чтобы посвятить его другим злодеям.) Ясно покажите, как вы следуете шагам, описанным в Стратегии решения проблем для динамики вращения.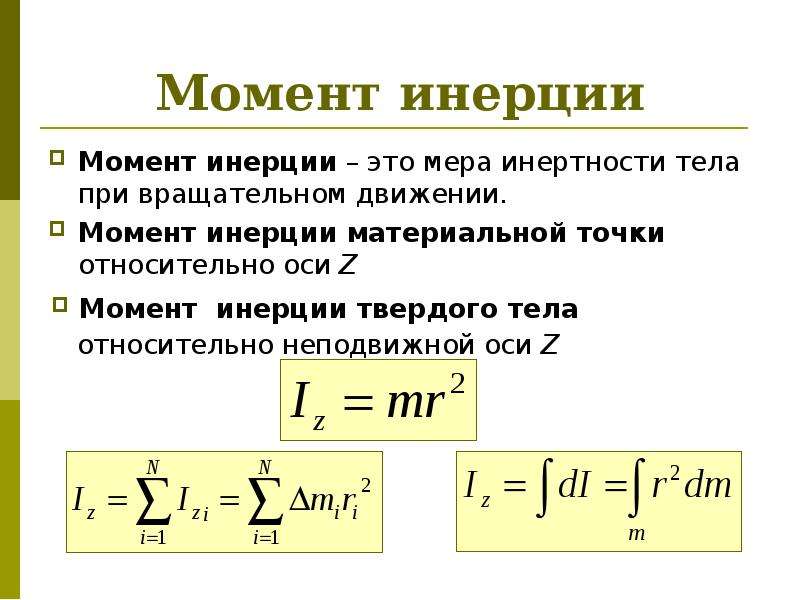 2/12}.2}. [/ Latex] (а) Сколько времени ей нужно, чтобы полностью изменить свое вращение? б) Что неразумного в результате? (c) Какие посылки необоснованны или непоследовательны?
2/12}.2}. [/ Latex] (а) Сколько времени ей нужно, чтобы полностью изменить свое вращение? б) Что неразумного в результате? (c) Какие посылки необоснованны или непоследовательны?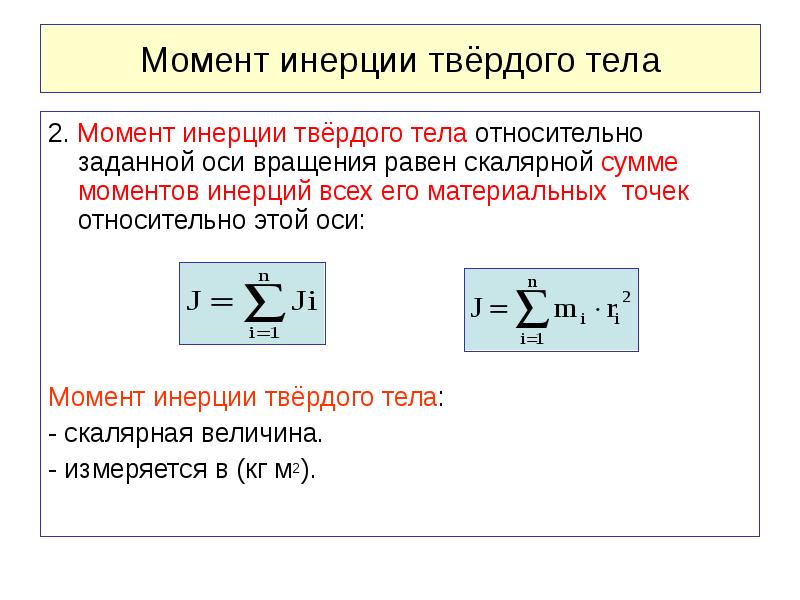 Момент инерции зависит как от массы, так и от ее распределения относительно оси вращения. Таким образом, хотя аналогии точны, эти вращательные величины зависят от большего числа факторов.
Момент инерции зависит как от массы, так и от ее распределения относительно оси вращения. Таким образом, хотя аналогии точны, эти вращательные величины зависят от большего числа факторов.