| ГОСТы, СНиПы Карта сайта TehTab.ru Поиск по сайту TehTab.ru | Навигация по справочнику TehTab.ru: главная страница / / Техническая информация/ / Материалы – свойства, обозначения/ / Сопротивление материалов. Сопромат. / / Таблица. Геометрические характеристики жесткости и прочности для ходовых сечений при кручении прямого бруса. Момент инерции и момент сопротивления при кручении. Положение точки, в которой возникает наибольшее напряжение.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
TehTab.ru Реклама на сайте | Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
В точках В напряжение τ=0
10
Таблица. Кручение. Геометрические характеристики жесткости и прочности для ходовых сечений при кручении прямого бруса. Осевые моменты инерции сечений (статические моменты сечений), осевые моменты сопротивления при кручении. Точка наибольшего напряжения.
Кручение. Геометрические характеристики жесткости и прочности для ходовых сечений при кручении прямого бруса. Осевые моменты инерции сечений (статические моменты сечений), осевые моменты сопротивления при кручении.
Положение точки, в которой возникает наибольшее напряжение. Вариант для печати.Легенда:
|
Легенда:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Форма поперечного сечения бруса |
Момент инерции при кручении JK, см4 |
Момент сопротивления при кручении WK, см3 |
Положение точки, в которой возникает наибольшее напряжение τ=MK/WK |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Круглое |
или Полярный момент инерции Jp=2J |
или |
Наибольшее напряжение возникает во всех точках у наружного контура поперечного сечения | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Кольцо |
или |
или |
Наибольшее напряжение возникает во всех точках у наружного контура поперечного сечения | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Тонкостенное кольцо |
d – средний диаметр |
Все точки находятся в одинаковых условиях (приближенно) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Незамкнутое тонкостенное кольцо | Наибольшее напряжение возникает в точках А. В точках В напряжение τ=0 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Круглое сечение с лыской |
Наибольшее напряжение возникает в середине плоского среза (точка А). В углах τ=0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Круглое с круговым вырезом |
Наибольшее напряжение возникает по дну канавки (точка А) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Значение коэффициентов K1 и K2 в зависимости от r/R
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Сплошное эллиптическое |
Наибольшее напряжение в точках А. Напряжение в точках В |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Прямоугольное |
Наибольшее напряжение возникает в серединах длинных сторон сечения (в точках А), в точках В напряжение | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Значение коэффициентов α, β и γ в зависимости от h/b
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Правильный шести- или восьмиугольник |
Для шестиугольника K’=0,133. Для восьмиугольника K’=0,130. F – площадь сечения |
Для шестиугольника К=0,217 Для восьмиугольника К=0,233 |
Наибольшее напряжение возникают в середине сторон в углах τ=0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Равносторонний треугольник |
Наибольшие напряжения возникают в середине сторон. В углах τ=0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
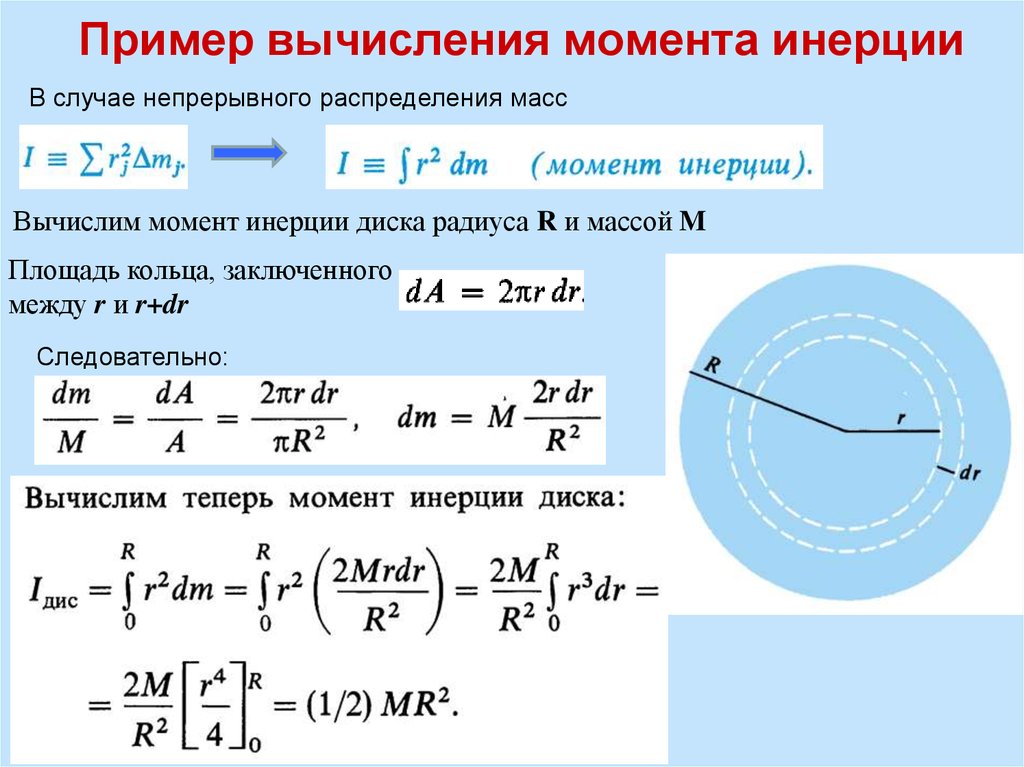
Полярный момент инерции | Энциклопедия MDPI
Полярный момент (инерции), также известный как второй (полярный) момент площади, представляет собой величину, используемую для описания сопротивления деформациям при кручении (прогибу) в цилиндрических (или нецилиндрических) объектах (или сегментах объект) с неизменным поперечным сечением и без существенного искривления или деформации вне плоскости.
Это составляющая второго момента площади, связанная теоремой о перпендикулярной оси. В то время как плоский второй момент площади описывает сопротивление объекта отклонению (изгибу) при воздействии силы, приложенной к плоскости, параллельной центральной оси, полярный второй момент площади описывает сопротивление объекта отклонению при воздействии момента, приложенного в плоскость, перпендикулярная центральной оси объекта (т.е. параллельная поперечному сечению). Аналогично плоскому секундному моменту вычисления площади ([math]\displaystyle{ I_x }[/math],[math]\displaystyle{ I_y }[/math] и [math]\displaystyle{ I_{xy} }[/math ]), полярный второй момент площади часто обозначается как [math]\displaystyle{ I_z }[/math]. Хотя в некоторых инженерных учебниках и академических публикациях оно также обозначается как [math]\displaystyle{ J }[/math] или [math]\displaystyle{ J_z }[/math], этому обозначению следует уделить особое внимание, чтобы оно не стало путают с константой кручения, [math]\displaystyle{ J_t }[/math], используемой для нецилиндрических объектов.
Проще говоря, полярный момент инерции – это сопротивление вала или балки искажению при кручении в зависимости от их формы. Жесткость исходит только от площади поперечного сечения объекта и не зависит от состава его материала или модуля сдвига. Чем больше величина полярного момента инерции, тем больше сопротивление тела кручению.
1. Определение
Схема, показывающая, как вычисляется полярный момент инерции для произвольной формы относительно оси [math]\displaystyle{ O }[/math]. Где [math]\displaystyle{ \rho }[/math] — радиальное расстояние до элемента [math]\displaystyle{ dA }[/math].
Примечание: Хотя термин моментов инерции стал обычным явлением для описания полярных и плоских секундных моментов площади, это в первую очередь конструкция инженерных полей. Срок момент инерции , в области физики и математики, является строго вторым моментом массы, используемым для описания сопротивления массивного объекта вращательному движению, а не его сопротивления деформации кручения.
В то время как полярные и плоские секундные моменты площади интегрируются по всем бесконечно малым элементам данной площади в некотором двумерном поперечном сечении, полярные и плоские секундные моменты массы (по инерции) интегрируются по всем бесконечно малым элементам массы в трехмерном пространстве, занимаемом объектом. Проще говоря, полярных и плоских секундных моментов площади являются показателем жесткости, а момент инерции (секундный момент массы ) является сопротивлением вращательному движению массивного объекта.
Уравнение, описывающее полярный момент площади, представляет собой кратный интеграл по площади поперечного сечения [math]\displaystyle{ A }[/math] объекта. 92 dx \, dy }[/math]
Показано, что полярный момент площади может быть описан как сумма [math]\displaystyle{ x }[/math] и [math]\displaystyle{ y } [/math] плоских моментов площади, [math]\displaystyle{ I_x }[/math] и [math]\displaystyle{ I_y }[/math] [math]\displaystyle{ \therefore J = I_z = I_x + I_y }[/math]
Это также показано в теореме о перпендикулярной оси.
[1] Для объектов, обладающих вращательной симметрией, [2] , таких как цилиндр или полая труба, уравнение можно упростить до: [math]\displaystyle{ J = 2I_x}[/math] или [math] \displaystyle{ J = 2I_y }[/math] 94}{2} }[/math]
2. Единица измерения
Единицей СИ для полярного момента инерции , как и для площади момента инерции , являются метры в четвертой степени ( м 4 ) и дюймов в четвертой степени ( в 4 ) в единицах измерения США и имперских единицах.
3. Ограничения
Полярный момент инерции недостаточен для использования при расчете балок и валов с некруглым поперечным сечением из-за их склонности к короблению при скручивании, вызывая неплоские деформации. В таких случаях следует заменить постоянную кручения, если включена соответствующая постоянная деформации для компенсации эффекта коробления. В рамках этого есть статьи, которые различают полярный момент инерции , [math]\displaystyle{ I_z }[/math] и постоянная кручения , [math]\displaystyle{ J_t }[/math], больше не используется [math]\displaystyle{ J }[/math] для описания полярного момента инерции.
[3]
Для объектов со значительной вариацией поперечного сечения (вдоль оси приложенного крутящего момента), которые невозможно проанализировать по сегментам, возможно, придется использовать более сложный подход. См. 3-D эластичность.
4. Заявка
Хотя полярный момент инерции чаще всего используется для расчета углового смещения объекта, подверженного действию момента (крутящего момента), приложенного параллельно поперечному сечению, предоставленное значение жесткости не имеет никакого отношения к сопротивлению скручиванию, обеспечиваемому объект как функция составляющих его материалов. Жесткость, обеспечиваемая материалом объекта, является характеристикой его модуля сдвига, [math]\displaystyle{ G }[/math]. Объединив эти две функции с длиной вала, [math]\displaystyle{ L }[/math], можно рассчитать угловое отклонение вала, [math]\displaystyle{ \theta }[/math], из-за приложенный крутящий момент, [math]\displaystyle{ T }[/math]: [math]\displaystyle{ \theta = \frac{TL}{JG} }[/math]
Как показано, чем больше модуль сдвига материала и полярный момент площади (т.
е. больше площадь поперечного сечения), тем выше сопротивление кручению.
Полярный момент площади появляется в формулах, описывающих напряжение кручения и угловое смещение.
Напряжения при кручении: [math]\displaystyle{ \tau = \frac{T \, r}{J_z} }[/math], где [math]\displaystyle{ \tau }[/math] — напряжение сдвига при кручении, [math]\displaystyle{ T }[/math] — приложенный крутящий момент, [math]\displaystyle{ r }[/math] — расстояние от центральной оси, а [math]\displaystyle{ J_z }[/math] – полярный момент площади.
Примечание: В круглом валу напряжение сдвига максимально на поверхности вала.
5. Пример расчета
Ротор современной паровой турбины. https://handwiki.org/wiki/index.php?curid=1484887
Расчет радиуса вала паровой турбины для турбоагрегата:
Допущения:
- Мощность на валу 1000 МВт; это типично для крупной атомной электростанции.
- Предел текучести стали, используемой для изготовления вала ( τ выход ) составляет: 250 × 10 6 Н/м 2 .
- Электричество имеет частоту 50 Гц; это типичная частота в Европе. В Северной Америке частота составляет 60 Гц. При этом предполагается, что существует соотношение 1:1 между скоростью вращения турбины и частотой сети.
Угловую частоту можно рассчитать по следующей формуле: [math]\displaystyle{ \omega = 2 \pi f }[/math]
Крутящий момент, передаваемый валом, связан с мощностью следующим уравнением: [ math]\displaystyle{ P = T \omega }[/math]
Таким образом, угловая частота составляет 314,16 рад/с, а крутящий момент 3,1831 × 10 6 Н·м.
Максимальный крутящий момент: [math]\displaystyle{ T_\max = \frac{ \tau_\max J_z }{r} }[/math]
После замены полярного момента инерции следующее выражение получено: [math]\displaystyle{ r = \sqrt[3]{\frac{2 T_\max}{\pi \tau_\max}} }[/math]
Радиус равен r = 0,200 м = 200 мм или диаметром 400 мм. Если добавить коэффициент безопасности 5 и пересчитать радиус с допустимым напряжением, равным 94}{32} }[/math] где:
- [math]\displaystyle{ d }[/math] — внутренний диаметр в метрах (м)
- [math]\displaystyle{ D }[/math] — внешний диаметр в метрах (м)
- [math]\displaystyle{ I_c }[/math] — момент инерции масс в кг·м 2
- [math]\displaystyle{ I_z }[/math] — полярный момент инерции в метрах в четвертой степени (m 4 )
- [math]\displaystyle{ l }[/math] — длина цилиндра в метрах (м)
- [math]\displaystyle{ \rho }[/math] — удельная масса в кг/м 3
Объяснение полярного момента инерции
Полярный момент инерции объекта — это его способность сопротивляться отклонению из-за приложенного крутящего момента.
Он в значительной степени основан на поперечном сечении объекта вдоль оси, к которой приложен крутящий момент.
Содержание
- Как рассчитать полярный момент инерции?
- Сплошное круглое поперечное сечение Полярный момент инерции
- Полое круглое сечение Полярный момент инерции
- Квадратное сечение Полярный момент инерции
- Прямоугольное сечение Полярный момент инерции
- Разница между моментом инерции и полярным моментом инерции Что такое полярное движение6 Инерция против продукта инерции?
Как рассчитать полярный момент инерции?
Скручивание объекта будет происходить вокруг оси, откуда рассчитывается полярный момент инерции. Например, если у вас есть скручиваемая трубка, площадь поперечного сечения, необходимая для расчета, будет равна площади круглого сечения трубки.
По сути, полярный момент инерции — это сопротивление объекта (будь то в форме балки, трубы или вала) деформации (пластической или нет) из-за приложенного крутящего момента.
Обратите внимание, что крутящий момент — это крутящая сила, а кручение — это крутящий момент, возникающий в результате приложенного крутящего момента. Полярный момент инерции полностью зависит от площади поперечного сечения крутящегося объекта, а не от типа материала.
Формула для полярного момента инерции выглядит следующим образом. Это двойной интеграл по площади поперечного сечения:
где:
- Дж = полярный момент инерции (м 4 )
- r = расстояние до элемента dA (м)
- dA = элемент дифференциала площади
Эта общая формула немного сбивает с толку, поскольку включает в себя двойной интеграл и то, что кажется радиусом, несмотря на то, что не каждая площадь поперечного сечения представляет собой круг. К счастью, существуют разные стандартные формулы для расчета полярного момента инерции для цилиндров различного поперечного сечения. Давайте посмотрим на некоторые из наиболее распространенных:
Твердое круглое сечение Полярный момент инерции
где:
- D = диаметр окружности
Полое круглое поперечное сечение Полярный момент инерции
где:
- D = внешний диаметр трубы/окружности (м)
- d = внутренний диаметр трубы/окружности (м)
Квадратное сечение Полярный момент инерции
где:
- a = длина стороны (м)
Прямоугольное поперечное сечение Полярный момент инерции
где:
- б/д = две длины сторон (м)
В этих формулах уже выполнено двойное интегрирование, и они оставлены в упрощенном виде. Существуют также упрощенные формулы для других распространенных площадей поперечного сечения, таких как треугольные, шестиугольные и цилиндры с гнездами переменной формы.
Есть несколько факторов, влияющих на полярный момент инерции. И чем больше полярный момент, тем «жестче» объект, независимо от состава материала или модуля сдвига.
Формулы показывают, что полярный момент инерции можно увеличить, увеличив размер цилиндрического объекта. Этот вывод естественно следует из того факта, что более крупный объект требует большей силы, чтобы осмысленно скрутить его!
Для сравнения, если бы у вас был квадратный цилиндр по сравнению с цилиндрическим цилиндром с одинаковым радиусом, то квадратный цилиндр имел бы более высокий полярный момент инерции. Так почему же мы видим больше примеров круглых цилиндров в реальном мире? Что ж, есть несколько других факторов, которые следует учитывать, когда квадратные сечения могут работать хуже, а круглые цилиндры лучше зацепляются для таких вещей, как гайки, подшипники и шайбы.
Разница между моментом инерции и полярным моментом инерции
Момент инерции, также известный как массовый момент инерции, отличается от своего полярного аналога. Есть несколько других названий этого качества, также известных как: угловая масса, второй момент массы и инерция вращения.
Момент инерции массы представляет собой не сопротивление крутящему моменту, а способность объекта сопротивляться вращению или изменению направления вращения. Это зависит от распределения массы тела относительно оси вращения, а не от его формы, хотя форма может влиять на то, как на самом деле распределяется эта масса. Формула для массового момента инерции:
Для точечной массы:
Для обычного тела:
где:
- I = момент инерции массы (кг-м 2 )
- м = масса (кг)
- r = расстояние между осью и вращающейся массой (м)
- k = инерционная постоянная, зависящая от формы тела (безразмерная)
- τ = приложенный крутящий момент (Н-м)
- α = угловое ускорение (рад/сек 2 )
- L = угловой момент (кг-м 2 /с)
- ω = угловая скорость (рад/с)
Здесь очевидно, что момент инерции массы в гораздо большей степени связан с весом тела и энергией вращения, а также с расстоянием от оси вращения, чем с его формой, хотя форма может играть роль. Полярный момент инерции можно рассматривать как распределение площади относительно оси вращения, тогда как момент массы связан с распределением массы вокруг нее.
Что такое полярный момент инерции и произведение инерции?
Произведение инерции — это еще один способ изучения распределения массы внутри вращающегося объекта, а также того, вращается ли этот объект вокруг оси, которая делает вращение симметричным. Если объект симметричен относительно своей оси вращения, то произведение инерции равно нулю. Если объект не распределен равномерно вокруг своей оси вращения, то у него будет некоторый продукт инерции.
Произведение инерции больше связано с массовым моментом инерции, чем с полярным моментом. Он может быть положительным, отрицательным или нулевым в зависимости от того, где находится объект по отношению к осям координат. Если на самом деле существует ненулевое произведение инерции, можно создать теоретическую ситуацию, в которой вращение симметрично, а произведение равно нулю, сдвинув оси в точку, где они известны как «главные оси».