Момента инерции: Национальный исследовательский университет «Высшая школа экономики»

2}

Чем больше будет масса бусинки, тем труднее будет сдвинуть ее, это логично. Но почему момент инерции материальной точки растет по мере удаления от оси вращения?

Представьте себя лилипутом, который по какой-то неведомой причине решил сообщить бусинке из примера наверху угловую скорость \omega. Не щадя себя, вы разогнались от нуля до некоторой скорости v, после чего, достигнув своей цели, остановились, позволив шарику двигаться дальше.

Теперь увеличим длину практически невесомого стержня в два раза и проделаем тот же самый мысленный эксперимент.

Даже если предположить, что вы не упадете замертво где-то на середине дистанции и сможете бежать с таким же ускорением, как и в первом случае, вы все равно почувствуете разницу. Чем дальше шарик будет находиться от оси вращения, тем труднее будет изменить его угловую скорость, соответственно, тем больше будет его момент инерции.

Кстати, благодаря формуле, представленной наверху, сразу становится понятно, для чего нужно соблюдение всех этих странных теоретических требований.

Если палочка, на которой закреплена бусинка, будет обладать большой массой, то у нее самой будет хороший момент инерции, и это усложнит расчеты. А если бусинка будет иметь большие размеры по отношению ко всей конструкции, то нам будет труднее определить, на каком расстоянии она находится от оси вращения, и это тоже усложнит нахождение момента инерции.

Вы можете сказать: «Для чего нам вообще нужен момент инерции материальной точки? Все равно, безразмерных тел в природе не существует».

Вы правы. Материальная точка – это математическая абстракция. И все-таки есть случаи, когда эта модель работает с хорошей степенью точности. Например, когда вы изучаете движение Луны вокруг Земли, вы запросто можете представить Луну в виде материальной точки и найти ее момент инерции при помощи приведенной выше формулы.

Но, конечно, вращаться могут не только материальные точки, но и другие тела. Например, можно представить, что мы имеем дело не с невесомой палочкой, а с железным стержнем массой m. 2

Теперь больше массы будет находиться ближе к оси вращения, отсюда и уменьшение момента инерции.

Если вас когда-нибудь спросят, чему равен момент инерции такого-то тела, знайте, что это хитрый вопрос. Значение момента инерции, помимо всего прочего, зависит от расположения оси вращения.

Определение моментов инерции модели. Один на один с врагом [Русская школа рукопашного боя]

Определение моментов инерции модели

Момент инерции тела есть мера инертности тела при вращательном движении.

Моментом инерции модели (системы тел) относительно некоторой оси называется физическая величина, равная сумме произведений масс mi отдельных звеньев (тел) на квадрат их расстояний ri от рассматриваемой оси:

Это означает, что в деформирующейся биомеханической системе тел, когда ее звенья отдаляются от оси вращения, момент инерции системы увеличивается.

Основными факторами, влияющими на момент инерции, являются масса и длина тела. На рис. 38 показана зависимость момента инерции (в условных единицах) от позы тела и положения оси вращения.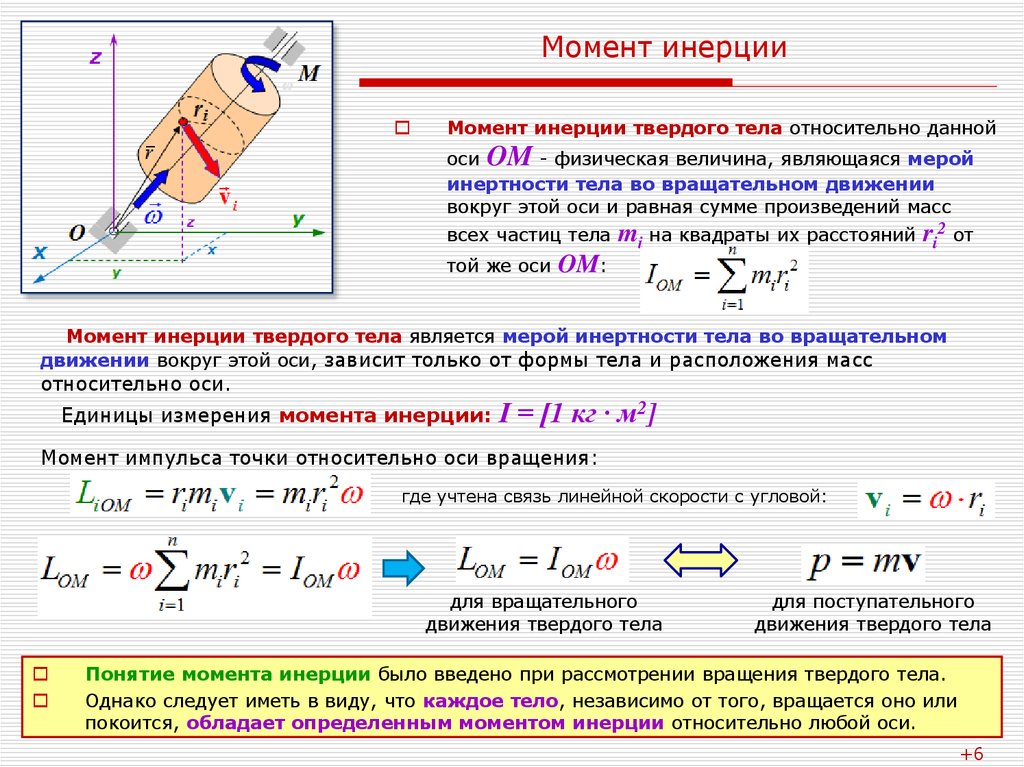

Как видно, изменением позы можно очень сильно влиять на момент инерции. Например, группировка при выполнении сальто (в) уменьшает момент инерции по сравнению с прямым положением тела (г) в три раза.

Момент инерции тела I₀ относительно оси вращения, проходящей через ЦМ, называется центральным.

При его определении можно воспользоваться данными таблицы 4. Расстояния ri относительно оси вращения О—О определяются просто.

Для звеньев тела, расположенных выше оси:

r_i = y_i – y_цм;

для остальных звеньев, расположенных ниже оси:

r_i = y_цм – y_i.

Центральный момент инерции модели:

Таблица 4

Рис. 36

Рис. 37

I₀ = ?miri2 = (m₁r₁2 + m2r22 +…+ mnrn₂) = (5,5.60,4+2,65.2.30+…+1,35.2.95,5)=1,3 кг м₂.

В других случаях предварительно следует вычертить рабочую модель в масштабе и произвести предварительные расчеты.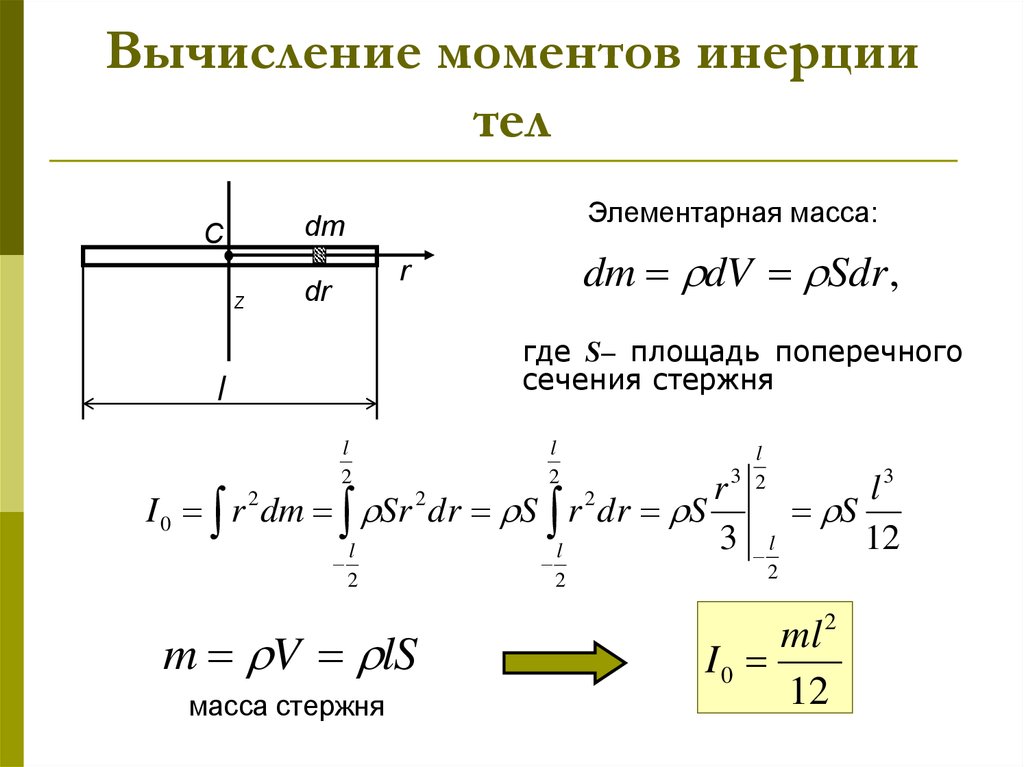

Момент инерции относительно любой оси, параллельной центральной, можно рассчитать по формуле:

Ic = Io + mil₂,

где Ic – искомый момент инерции;

Io – центральный момент инерции;

mi – масса звена;

l – расстояние между осями.

Рис. 38

Инерционное сопротивление увеличивается с отдалением частей тела от оси вращения пропорционально квадрату расстояния. Поскольку материальные точки в теле расположены на разных расстояниях от оси вращения, для ряда задач оказалось удобным ввести понятие «радиуса инерции».

Радиус инерции R_ин – это сравнительная мера инертности данного тела относительно его разных осей. Из выражения для момента инерции относительно данной оси I = MR

ин² следует:

где М – масса тела.

Найдя опытным путем момент инерции Io, можно рассчитать радиус инерции R_ин, величина которого характеризует распределение материальных точек в теле относительно данной оси. Но точное количественное определение этой величины в конкретных случаях нередко затруднено.

Инерционно-массовые характеристики, такие, как масса тела, положение центра масс, величина момента инерции, оказывают существенное влияние на параметры устойчивости, а также на инерционное сопротивление тела вращательному движению.

В частности, чем больше инерционное сопротивление тела, тем меньше угловая скорость его вращения. Например, при вращении тела вокруг вертикальной оси (рис. 38а) с угловой скоростью ?₁ увеличение инерционного сопротивления (I2>I1) разведением рук в стороны (рис. 38б) приводит к уменьшению угловой скорости (?₁<?₁).

Данный текст является ознакомительным фрагментом.

1.2. Определение работы тренера

1.

2. Определение работы тренера Проводя тренерские семинары, я часто задаю участникам вопрос: «В чём заключается работа тренера, что для вас в ней главное?»Действительно, ведь из массы наваливающихся на тренера обязанностей какие-то должны быть более важными, и в конечном

Определение силы ветра

Определение силы ветра В параглайдинге недостаточно знать, что ветер силен или слаб. Он должен быть оценен и измерен более точно, предпочтительно с использованием инструмента — измерителя силы ветра. Если у вас нет такогоинструмента, вы все же можете грубо оценить силу

ОПРЕДЕЛЕНИЕ ПЕДАГОГИЧЕСКИХ ПОКАЗАТЕЛЕЙ

ОПРЕДЕЛЕНИЕ ПЕДАГОГИЧЕСКИХ ПОКАЗАТЕЛЕЙ 1. Контроль физической подготовленностиПедагогический контроль в спортивной деятельности дзюдоистов детско-юношеского возраста приоритетно направлен на изучение показателей их физической подготовленности по

ОПРЕДЕЛЕНИЕ СОЦИАЛЬНО-ПСИХОЛОГИЧЕСКИХ ПОКАЗАТЕЛЕЙ

ОПРЕДЕЛЕНИЕ СОЦИАЛЬНО-ПСИХОЛОГИЧЕСКИХ ПОКАЗАТЕЛЕЙ Наиболее сложный раздел контроля определяет психические состояния, личностно-характерологогические особенности, микроклимат в коллективе дзюдоистов и другие показатели.

Получаемые результаты будут более надежными,

ОПРЕДЕЛЕНИЕ МЕДИКО-БИОЛОГИЧЕСКИХ ПОКАЗАТЕЛЕЙ

ОПРЕДЕЛЕНИЕ МЕДИКО-БИОЛОГИЧЕСКИХ ПОКАЗАТЕЛЕЙ Определение медико-биологических показателей проводится систематически, т. к. выявляет физическое развитие и здоровье занимающихся. У дзюдоистов обычно применяют тестовые методики двух видов.а) Тесты, проводимые в покое,

Определение своих ограничителей

Определение своих ограничителей В главе 5 вы определили свои сильные и слабые стороны с использованием профиля врожденных способностей. Там же была приведена характеристика ряда факторов, связанных с успехом в многоборье. Вы оценили свои способности в области плавания,

Глава 5. Разъяснение 16 моментов, касающихся важного в тайцзицюань

Глава 5.  Разъяснение 16 моментов, касающихся важного в тайцзицюань Подвижность — в пояснице;находчивость — в макушке;пронизанность духом — в спине;текучесть движения — в ци;движение — в ногах;толчок ногой — в стопе;соединение — в ладони;стопа — в пальцах;собирание — в

Массово-инерционные характеристики модели

Массово-инерционные характеристики модели В биомеханике совокупность показателей, характеризующих распределение масс в теле человека, принято называть геометрией масс. Для биомеханических расчетов нужны точные сведения об этих показателях.Таблица 3 К

Определение положения центра масс модели

Определение положения центра масс модели При исследовании движений человека, как правило, возникает необходимость учитывать не только величину массы, но и ее распределение в теле. На распределение массы тела указывает расположение так называемого центра масс

3.

 ИСПОЛЬЗОВАНИЕ ВЫГОДНЫХ МОМЕНТОВ ДЛЯ НАПАДЕНИЯ

3. ИСПОЛЬЗОВАНИЕ ВЫГОДНЫХ МОМЕНТОВ ДЛЯ НАПАДЕНИЯ Можно утверждать, что нет такого мгновения в схватке, когда для самбиста не было бы выгодных для нападения положений, передвижений или действий противника. Но во время борьбы действует так много различных факторов, что

4.3. Процесс развития интеллектуальных способностей подростка-спортсмена: взаимообусловленность актуальной модели интеллекта и модели деятельности

4.3. Процесс развития интеллектуальных способностей подростка-спортсмена: взаимообусловленность актуальной модели интеллекта и модели деятельности Разум есть тот сознаваемый человеком закон, по которому должна совершаться его жизнь. Л. Н. Толстой Процесс развития

Состояние вращения и момент инерции Венеры

• Артикул
• Опубликовано: 29 апреля 2021 г.

• Жан-Люк Марго Orcid: orcid.org/0000-0001-9798-1797 ^1,2 ,
• Дональд Б. Кэмпбелл ³ ,
• Jon D. Giorgini ⁴ ,
• Joseph S. Jao ⁴ ,
• Joseph S. Jao ⁴ ,
• .
• Лоуренс Г. Снедекер ⁴ ,
• Фрэнк Д. Гиго ⁵ и
• …
• Эмбер Бонсолл ⁵  

Природа Астрономия том 5 , страницы 676–683 (2021)Процитировать эту статью

• 1165 доступов

• 11 цитирований

• 742 Альтметрический

• Сведения о показателях

Предметы

• Динамика атмосферы
• Геодинамика
• Внутренние планеты

Abstract

Фундаментальные свойства планеты Венера, такие как распределение ее внутренней массы и вариации продолжительности дня, остались неизвестными. Мы использовали наземные наблюдения радиолокационных спеклов, связанных с вращением Венеры, полученные в 2006–2020 годах, для измерения ориентации ее оси вращения, скорости прецессии вращения, момента инерции и вариаций длины дня. Венера наклонена на 2,6392   ± 0,0008   градуса (1 σ ) по отношению к плоскости своей орбиты. Ось вращения прецессирует со скоростью 44,58 ± 3,3 угл.сек в год (1 σ ), что дает нормированный момент инерции 0,337 ± 0,024 и дает грубую оценку размера ядра. Средний звездный день на Венере в интервале 2006–2020 гг. составляет 243,0226 ± 0,0013 земных суток (1 σ ). Период вращения твердой планеты изменяется на 61 ppm (~20 мин) с возможным суточным или полусуточным воздействием. Изменения длины дня означают, что изменения углового момента атмосферы не менее ~ 4% передаются твердой планете.

Это предварительный просмотр содержимого подписки, доступ через ваше учреждение

Соответствующие статьи

Статьи открытого доступа, цитирующие эту статью.

• Динамика и эволюция мантии Венеры во времени

  • Тобиас Рольф
  • , Мэтт Веллер
  •  … Сюзанна Смрекар

  Обзоры космической науки Открытый доступ 28 ноября 2022 г.

• Недра землеподобных планет и спутников Солнечной системы

  • Дорис Брейер
  • , Тилман Спон
  •  … Николя Рамбо

  Геофизические исследования Открытый доступ 14 декабря 2021 г.

Варианты доступа

Подписаться на журнал

Получить полный доступ к журналу на 1 год

118,99 €

всего 9,92 € за выпуск

Подписаться

Расчет налогов будет завершен во время оформления заказа.

Купить статью

Получите ограниченный по времени или полный доступ к статье на ReadCube.

32,00 $

Купить

Все цены указаны без учета стоимости.

Рис. 1: Пространственно-временная корреляция радарных спеклов Венеры. Рис. 2: Ориентация оси вращения Венеры. Рис. 3: Измерения мгновенного периода вращения Венеры.

Доступность данных

Наборы данных, созданные и/или проанализированные в ходе текущего исследования, можно получить у соответствующего автора по обоснованному запросу.

Доступность кода

Программное обеспечение, используемое для получения и обработки временных рядов радиолокационных эхо-сигналов, можно получить по запросу, связавшись с соответствующим автором.

Каталожные номера

1. Смрекар С.Э., Давайль А. и Сотин К. Внутренняя структура и динамика Венеры. Космические науки. Ред. 214 , 88 (2018).

   Артикул ОБЪЯВЛЕНИЯ Google ученый

2. Дюмулен К., Тоби Г., Верховен О., Розенблатт П. и Рамбо Н. Приливные ограничения внутренней части Венеры. Ж. Геофиз. Рез. Планеты 122 , 1338–1352 (2017).

   Артикул ОБЪЯВЛЕНИЯ Google ученый

3. О’Рурк, Дж. Г., Гиллманн, К. и Тэкли, П. Перспективы древнего динамо и современного остаточного магнетизма земной коры на Венере. Планета Земля. науч. лат. 502 , 46–56 (2018).

   Артикул ОБЪЯВЛЕНИЯ Google ученый

4. Davies, M.E. et al. Период вращения, направление Северного полюса и опорная геодезическая сеть Венеры. Ж. Геофиз. Рез. Планеты 97 , 13141–13151 (1992).

   Артикул ОБЪЯВЛЕНИЯ Google ученый

5. Мюллер, Н. Т., Хелберт, Дж., Эрард, С., Пиччони, Г. и Дроссарт, П. Период вращения Венеры, оцененный по изображениям Venus Express VIRTIS и альтиметрии Магеллана. Икар 217 , 474–483 (2012).

   Артикул ОБЪЯВЛЕНИЯ Google ученый

6. Кэмпбелл, Б. А. и др. Средняя скорость вращения Венеры от 29лет наземных радиолокационных наблюдений. Икар 332 , 19–23 (2019).

   Артикул ОБЪЯВЛЕНИЯ Google ученый

7. “>

   Yoder, CF in Venus II: Geology, Geophysics, Atmosphere, and Solar Wind Environment (eds Bougher, SW et al.) 1087–1124 (Univ. of Arizona Press, 1997).

8. Санчес-Лавега А., Лебоннуа С., Имамура Т., Рид П. и Луз Д. Динамика атмосферы Венеры. Космические науки. Ред. 212 , 1541–1616 (2017).

   Артикул ОБЪЯВЛЕНИЯ Google ученый

9. Horinouchi, T. et al. Как волны и турбулентность поддерживают сверхвращение атмосферы Венеры. Наука 368 , 405–409 (2020).

   Артикул ОБЪЯВЛЕНИЯ MathSciNet Google ученый

10. Дорожная карта для исследования Венеры (Группа по оценке исследования Венеры, 2019 г.).

11. Каула, В. М. Введение в планетарную физику: планеты земной группы (Wiley, 1968).

12. “>

    Уильямс, Дж. Г. Вклады в скорость наклона Земли, прецессию и нутацию. Астрон. J. 108 , 711–724 (1994).

    Артикул ОБЪЯВЛЕНИЯ Google ученый

13. Фолкнер, В. М., Йодер, К. Ф., Юань, Д. Н., Стэндиш, Э. М. и Престон, Р. А. Внутренняя структура и сезонное массовое перераспределение Марса по радиоотслеживанию Mars Pathfinder. Наука 278 , 1749–1751 (1997).

    Артикул ОБЪЯВЛЕНИЯ Google ученый

14. Стэндиш, Э. М. и Уильямс, Дж. Г. в Пояснительное приложение к астрономическому альманаху , 3-е изд. (ред. Урбан, С. Э. и Зайдельманн, П. К.), гл. 8 (Университетские научные книги, 2013 г.).

15. Коноплив А.С., Банердт В.Б. и Шегрен В.Л. Гравитация Венеры: 180-й градус и модель порядка. Икар 139 , 3–18 (1999).

    Артикул ОБЪЯВЛЕНИЯ Google ученый

16. “>

    Коттеро, Л. и Суше, Дж. Вращение твердой Венеры: полная модель прецессии-нутации. Астрон. Астрофиз. 507 , 1635–1648 (2009).

    Артикул ОБЪЯВЛЕНИЯ МАТЕМАТИКА Google ученый

17. Saunders, R. S. et al. Краткое содержание миссии Магеллана. Ж. Геофиз. Рез. Планеты 97 , 13067–13090 (1992).

    Артикул ОБЪЯВЛЕНИЯ Google ученый

18. Шапиро И.И., Кэмпбелл Д.Б. и де Кампли В.М. Нерезонансное вращение Венеры. Астрофиз. Дж. Летт. 230 , L123–L126 (1979).

    Артикул ОБЪЯВЛЕНИЯ Google ученый

19. Зоар, С., Гольдштейн, Р. М. и Рамси, Х. К. Новое радиолокационное определение вектора вращения Венеры. Астрон. J. 85 , 1103–1111 (1980).

    Артикул ОБЪЯВЛЕНИЯ Google ученый

20. “>

    Шапиро И. И., Чандлер Дж. Ф., Кэмпбелл Д. Б., Хайн А. А. и Стейси Н. Дж. С. Вектор вращения Венеры. Астрон. J. 100 , 1363–1368 (1990).

    Артикул ОБЪЯВЛЕНИЯ Google ученый

21. Слейд, М. А., Зоар, С. и Юргенс, Р. Ф. Венера: улучшенный вектор вращения по данным радиолокационных наблюдений Голдстоуна. Астрон. J. 100 , 1369–1374 (1990).

    Артикул ОБЪЯВЛЕНИЯ Google ученый

22. Гольдрайх П. и Пил С. Спин-орбитальная связь в солнечной системе. Астрон. J. 71 , 425–437 (1966).

    Артикул ОБЪЯВЛЕНИЯ Google ученый

23. Гольдрейх П. и Пил С. Спин-орбитальная связь в солнечной системе. II. Резонансное вращение Венеры. Астрон. J. 72 , 662–668 (1967).

    Артикул ОБЪЯВЛЕНИЯ Google ученый

24. “>

    Голд, Т. и Сотер, С. Атмосферные приливы и резонансное вращение Венеры. Икар 11 , 356–366 (1969).

    Артикул ОБЪЯВЛЕНИЯ Google ученый

25. Ингерсолл А. П. и Добровольскис А. Р. Вращение Венеры и атмосферные приливы. Природа 275 , 37–38 (1978).

    Артикул ОБЪЯВЛЕНИЯ Google ученый

26. Добровольскис А. Р. и Ингерсолл А. П. Атмосферные приливы и вращение Венеры. I. Теория приливов и баланс моментов. Икар 41 , 1–17 (1980).

    Артикул ОБЪЯВЛЕНИЯ Google ученый

27. Коррейя, А.К.М. и Ласкар, Дж. Четыре последних состояния вращения Венеры. Природа 411 , 767–770 (2001).

    Артикул ОБЪЯВЛЕНИЯ Google ученый

28. “>

    Биллс, Б. Г. Изменения скорости вращения Венеры из-за орбитальной модуляции эксцентриситета солнечных приливных моментов. Ж. Геофиз. Рез. 110 , E11007 (2005 г.).

    Артикул ОБЪЯВЛЕНИЯ Google ученый

29. Хайд Р., Берч Н. Т., Моррисон Л. В., Ши Д. Дж. и Уайт А. А. Колебания атмосферного углового момента и изменения продолжительности дня. Природа 286 , 114–117 (1980).

    Артикул ОБЪЯВЛЕНИЯ Google ученый

30. Лебоннуа, С. и др. Суперротация атмосферы Венеры проанализирована с помощью модели полной общей циркуляции. Ж. Геофиз. Рез. Планеты 115 , E06006 (2010).

    Артикул ОБЪЯВЛЕНИЯ Google ученый

31. Коттеро, Л., Рамбо, Н., Лебоннуа, С. и Суше, Дж. Различные вклады в скорость вращения Венеры и LOD. Астрон. Астрофиз. 531 , А45 (2011).

    Артикул ОБЪЯВЛЕНИЯ Google ученый

32. Приход, H. F. et al. Десятилетние вариации в модели общей циркуляции Венеры. Икар 212 , 42–65 (2011).

    Артикул ОБЪЯВЛЕНИЯ Google ученый

33. Марго Ж.-Л. Система сбора данных для планетарных радаров. Дж. Астрон. Инструм. 10 , 2150001 (2021).

    Артикул Google ученый

34. Марго, Дж.-Л., Пил, С.Дж., Юргенс, Р.Ф., Слэйд, М.А. и Холин, И.В. Большая долготная либрация Меркурия обнаруживает расплавленное ядро. Наука 316 , 710–714 (2007).

    Артикул ОБЪЯВЛЕНИЯ Google ученый

35. Марго Ж.-Л. Момент инерции Меркурия по данным о вращении и гравитации. Ж. Геофиз. Рез. Планеты 117 , E00L09 (2012).

    Артикул Google ученый

36. Старк А. и др. Первые орбитальные наблюдения MESSENGER за либрациями Меркурия. Геофиз. Рез. лат. 42 , 7881–7889 (2015).

    Артикул ОБЪЯВЛЕНИЯ Google ученый

37. Bendat, J. S. & Piersol, A. G. Случайные данные: процедуры анализа и измерения 2-е изд. (Wiley, 1986).

38. Коррейя, А.К.М., Ласкар, Дж. и Нерон де Сурги, О. Долговременная эволюция вращения Венеры: I. теория. Икар 163 , 1–23 (2003).

    Артикул ОБЪЯВЛЕНИЯ Google ученый

39. Коррейя А.К.М. и Ласкар Дж. Долговременная эволюция вращения Венеры: II. численное моделирование. Икар 163 , 24–45 (2003).

    Артикул ОБЪЯВЛЕНИЯ Google ученый

40. Гросс, Р. в Трактат по геофизике 1-е изд. (изд. Шуберт, Г.) 239–294 (Elsevier, 2007).

41. Гольдрайх П. и Пил С. Дж. Резонансное вращение Венеры? Природа 209 , 1117–1118 (1966).

    Артикул ОБЪЯВЛЕНИЯ Google ученый

42. Наварро Т., Шуберт Г. и Лебоннуа С. Генерация атмосферных горных волн на Венере и ее влияние на скорость вращения твердой планеты. Нац. Geosci. 11 , 487–491 (2018).

    Артикул ОБЪЯВЛЕНИЯ Google ученый

43. Fukuhara, T. et al. Большая стационарная гравитационная волна в атмосфере Венеры. Нац. Geosci. 10 , 85–88 (2017).

    Артикул ОБЪЯВЛЕНИЯ Google ученый

44. “>

    Kouyama, T. et al. Топографическая и локальная временная зависимость больших стационарных гравитационных волн, наблюдаемых в верхней части облаков Венеры. Геофиз. Рез. лат. 44 , 12098–12105 (2017).

    Артикул ОБЪЯВЛЕНИЯ Google ученый

45. Митчелл, Дж. Л. Связь конвективной атмосферной циркуляции с вращением поверхности: свидетельство активной метановой погоды в наблюдаемом дрейфе скорости вращения Титана. Астрофиз. J. 692 , 168–173 (2009).

    Артикул ОБЪЯВЛЕНИЯ Google ученый

46. Грин, ЧП Методы радиолокационных астрономических измерений Технический отчет № 282 (Лаборатория Линкольна Массачусетского технологического института, 1962 г.).

47. Green, PE in Radar Astronomy (eds Evans, JV & Hagfors, T.) Ch. Радарные измерения (McGraw-Hill, 1968).

48. Холин И. В. Пространственно-временная когерентность сигнала, диффузно рассеянного произвольно движущейся поверхностью, для случая монохроматического освещения. Радиофиз. Квант. Электр. 31 , 371–374 (1988).

    Артикул ОБЪЯВЛЕНИЯ Google ученый

49. Холин И.В. Точность измерения параметров вращения тела при монохроматическом освещении и двухэлементном приеме. Радиофиз. Квант. Электр. 35 , 284–287 (1992).

    Артикул ОБЪЯВЛЕНИЯ Google ученый

50. Марго, Дж. Л., Хаук, С. А., Мазарико, Э., Падован, С. и Пил, С. Дж. в Меркурий: вид после MESSENGER (под редакцией Соломона, С.К. и др.) 85–113 (Cambridge Univ. Press, 2018).

51. Duan, X., Moghaddam, M., Wenkert, D., Jordan, R.L. & Smrekar, S.E. X-диапазонная модель диэлектрической проницаемости атмосферы Венеры. Радионауч. 45 , 1–19 (2010).

    Артикул Google ученый

52. Дзиевонски А. М. и Андерсон Д. Л. Предварительная эталонная модель Земли. физ. Планета Земля. Интер. 25 , 297–356 (1981).

    Артикул ОБЪЯВЛЕНИЯ Google ученый

53. Press, W.H., Teukolsky, S.A., Vetterling, W.T. & Flannery, B.P. Numerical Recipes in C 2nd edn (Cambridge Univ. Press, 1992).

54. Уильямс П.К.Г., Клавель М., Ньютон Э. и Рыжков Д. pwkit: Astronomical Utilities in Python ascl:1704.001 (2017).

Скачать ссылки

Благодарности

Эта статья посвящена памяти Рэймонда Ф. Юргенса, который сыграл важную роль в сборе данных для этой работы. Мы благодарим М. А. Слейда, Дж. Т. Лацио, Т. Минтера, К. О’Нила и Ф. Дж. Локмана за помощь в планировании наблюдений. Мы благодарим Б. А. Арчинала, П. М. Дэвиса, С. Лебоннуа, Дж. Л. Митчелла и К. Ф. Уилсона за полезные комментарии и А. Лама за помощь с рис. 1. Обсерватория Грин-Бэнк является объектом Национального научного фонда, управляемым по соглашению о сотрудничестве с ассоциированными университетами. , Inc. Часть этой работы была поддержана Лабораторией реактивного движения, управляемой Калифорнийским технологическим институтом по контракту с НАСА. Мы благодарны за программное обеспечение NASA Navigation and Ancillary Information Facility и ядра данных, которые значительно облегчили это исследование. Ж.-Л.М. частично финансировался за счет гранта НАСА №. NNG05GG18G, NNX09AQ69G, NNX12AG34G и 80NSSC19K0870.

Информация об авторе

Авторы и организации

1. Департамент наук о Земле, планетах и ​​космосе, Калифорнийский университет в Лос-Анджелесе, Лос-Анджелес, Калифорния, США

   Жан-Люк Марго

2. Департамент физики и астрономии Калифорнийского университета в Лос-Анджелесе, Лос-Анджелес , Калифорния, США

   Жан-Люк Марго

3. Кафедра астрономии, Корнельский университет, Итака, штат Нью-Йорк, США

   Дональд Б. Кэмпбелл

4. Лаборатория реактивного движения, Пасадена, Калифорния, США

   Джон Д. Джорджини, Джозеф С. Джао и Лоуренс Г. Снедекер

5. Национальная радиоастрономическая лаборатория, Грин-Бэнк, Западная Вирджиния, США

   Фрэнк Д. Гиго и Эмбер Бонсолл

Авторы

1. Жан-Люк Марго

   Просмотр публикаций автора

   Вы также можете искать этого автора в PubMed Google Scholar

2. Дональд Б. Кэмпбелл

   Посмотреть публикации автора

   Вы также можете искать этого автора в PubMed Google Scholar

3. Jon D. Giorgini

   Просмотр публикаций автора

   Вы также можете искать этого автора в PubMed Google Scholar

4. Joseph S. Jao

   Просмотр публикаций автора

   Вы также можете искать этого автора в PubMed Google Scholar

5. Лоуренс Г. Снедекер

   Посмотреть публикации автора

   Вы также можете искать этого автора в PubMed Google Scholar

6. Frank D. Ghigo

   Просмотр публикаций автора

   Вы также можете искать этого автора в PubMed Google Scholar

7. Amber Bonsall

   Просмотр публикаций автора

   Вы также можете искать этого автора в PubMed Google Scholar

Contributions

J.-L.M. провел расследование и написал программное обеспечение и рукопись. D.B.C. внес свой вклад в методику. J.D.G., J.S.J., L.G.S., F.D.G. и А.Б. способствовал сбору данных. Все авторы просмотрели и отредактировали рукопись.

Автор, ответственный за переписку

Жан-Люк Марго.

Заявление об этике

Конкурирующие интересы

Авторы не заявляют об отсутствии конкурирующих интересов.

Дополнительная информация

Информация о рецензировании Nature Astronomy благодарит Alexandre Correia, Attilio Rivoldini и других анонимных рецензентов за их вклад в рецензирование этой работы.

Примечание издателя Springer Nature сохраняет нейтралитет в отношении юрисдикционных претензий в опубликованных картах и ​​институциональной принадлежности.

Расширенные данные

Расширенные данные Рис. 1 Проиллюстрированы случайные изменения мощности эхо-сигнала радара.

Representative variations in radar echo power ( s p e c k l e s ) from observations of Venus with the Goldstone Solar System Radar and Green Bank Telescope at 8560 МГц, 26 ноября 2016 г. Эхо-сигнал GBT был сдвинут во времени на 20 с, чтобы проиллюстрировать высокую степень корреляции между полученными формами сигналов, когда траектория спекла совмещена с базовой линией антенны.

Расширенные данные Рис. 2 Проиллюстрирована траектория гофрирования волнового фронта, охватывающего антенны Голдстоуна и Грин-Бэнк.

Радиолокационные эхосигналы от Венеры охватывают поверхность Земли во время наблюдений 08 сентября 2020 года. На диаграммах показана траектория спеклов за час до (слева), во время (в центре) и через час после (справа) эпохи максимальной корреляции. Эхосигналы от двух приемных станций (красные треугольники) демонстрируют сильную корреляцию, когда антенны соответствующим образом выровнены по траектории спеклов (зеленые точки показаны с временным интервалом в 1 ~ с).

Расширенные данные Рис. 3 Проиллюстрированы ограничения на ориентацию оси вращения Венеры, полученные с помощью наблюдений радиолокационных спеклов Голдстоуна-GBT.

Каждая цветная линия представляет собой измерение эпохи максимума корреляции, описывающего узкий эллипс ошибки на небесной сфере. Ориентация каждой линии связана с эклиптической долготой проецируемой базовой линии во время наблюдений (дополнительная таблица 2). Наилучшая ориентация оси вращения показана ромбом на пересечении цветных линий. Все измерения прецессированы до эпохи J2000.0. Черная пунктирная линия представляет собой след ориентации оси вращения на небесной сфере в результате прецессии спина между 1950 и 2050.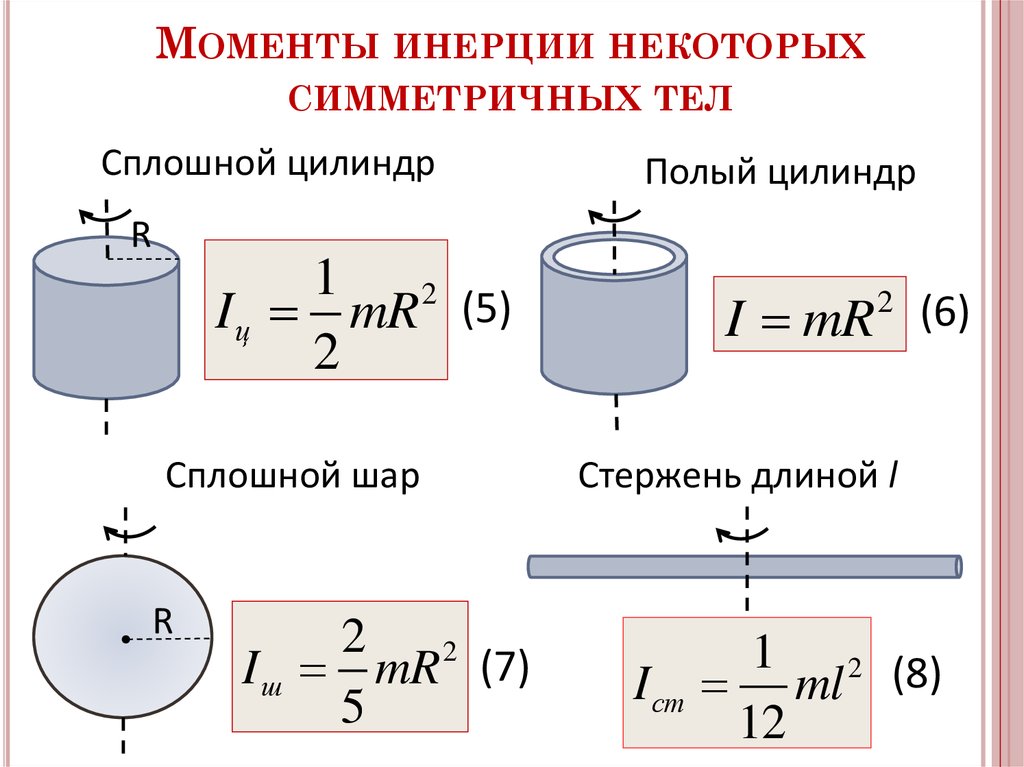

Расширенные данные Рис. 4 Проиллюстрировано распределение нормированных моментов инерции из бутстрап-анализа.

Оценки нормализованного момента инерции Венеры, полученные с помощью радиолокационных спекл-трекингов, предполагают остаточную погрешность в 7% с данными, полученными на сегодняшний день.

Дополнительная информация

Дополнительная информация

Дополнительные таблицы 1–6 и рис. 1–7.

Права и разрешения

Перепечатка и разрешения

Об этой статье

Эту статью цитирует

• Динамика и эволюция мантии Венеры во времени

  • Тобиас Рольф
  • Мэтт Веллер
  • Сюзанна Смрекар

  Обзоры космической науки (2022)

• Недра землеподобных планет и спутников Солнечной системы

  • Дорис Брейер
  • Тилман Спон
  • Николя Рамбо

  Геофизические исследования (2022)

5.

4: Момент инерции – Физика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

17392

• Тимон Идема
• Делфтский технологический университет через TU Delft Open

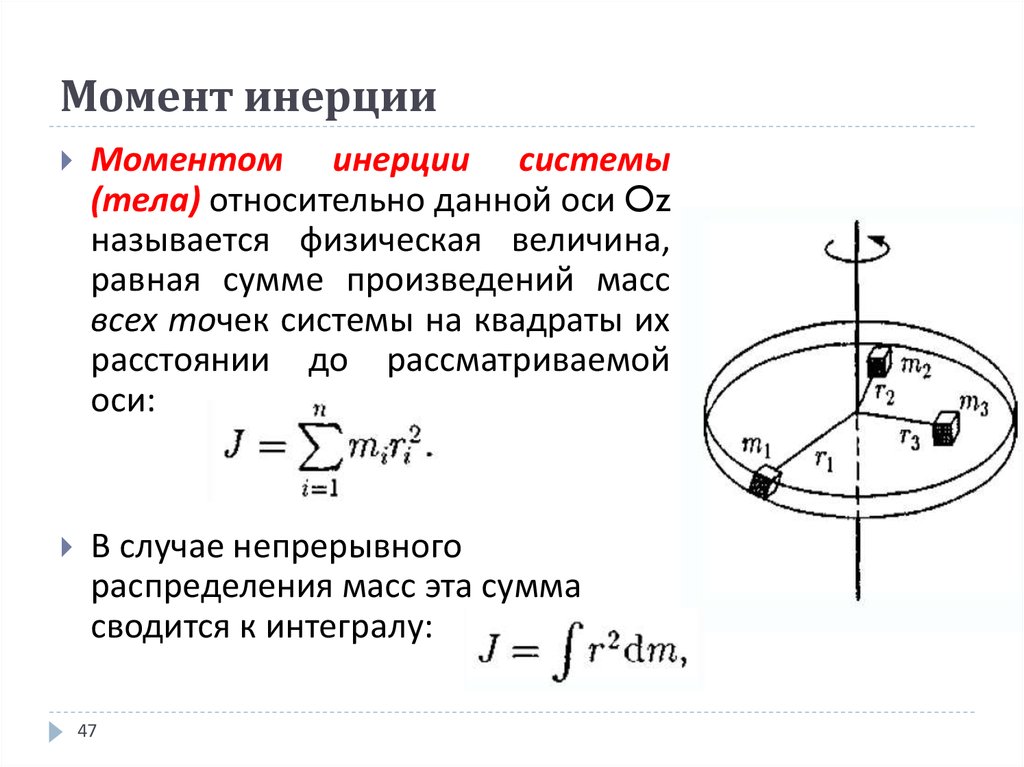
Предположим, у нас есть масса m на конце безмассовой палки длиной \(r\), вращающаяся вокруг другого конца палки. Если мы хотим увеличить скорость вращения, нам нужно применить тангенциальное ускорение на

.

\[\boldsymbol{a}_{\mathrm{t}}=r \boldsymbol{\alpha} \nonumber\] 92\). По аналогии с массой, представляющей инерцию тела, испытывающего линейное ускорение, мы будем идентифицировать эту величину как инерцию тела, подвергающегося вращательному ускорению, которую мы назовем моментом инерции и обозначим через \(I\):

.

\[\boldsymbol{\tau}=I \boldsymbol{\alpha} \label{крутящий момент}\]

Уравнение \ref{torque} является вращательным аналогом второго закона Ньютона. Расширяя наш предыдущий пример, мы можем найти момент инерции произвольного набора частиц с массами \(m_\alpha\) и расстояниями до оси вращения \(r_\alpha\) (где \(\alpha\) работает по всем частицам), и запишем: 92\) соответственно. Эти и некоторые другие примеры приведены в таблице 5.1. Ниже мы свяжем момент инерции с кинетической энергией движущегося и катящегося объекта, но сначала приведем две удобные теоремы, которые помогут в их вычислении.

9{2} \label{result}\]

, где m — масса объекта.

Доказательство

Выберите координаты так, чтобы центр масс находился в начале координат, а исходная ось совпадала с осью \(\hat{z}\). {2}-2 \mathbf{d} \cdot \ int_{V} \mathbf{r} \rho \mathrm{d} V \label{proof} \end{align} \] 92 = \boldsymbol{d}·\boldsymbol{d}\). Последний интеграл в последней строке \ref{proof} равен положению центра масс, которое мы выбрали в начале координат, поэтому последний член равен нулю, и мы получаем \ref{result}. Обратите внимание, что первые две строки таблицы 5.1 (моменты инерции стержня) удовлетворяют теореме об перпендикулярных осях.

Теорема 5.2: Теорема о перпендикулярной оси

Если твердый объект полностью лежит в плоскости, а моменты инерции вокруг двух перпендикулярных осей x и y в этой плоскости равны \(I_x\) и \(I_y\) соответственно, тогда момент инерции вокруг оси z, перпендикулярной плоскости и проходящей через точку пересечения, равен 9{2} \sigma \mathrm{d} A=I_{y}+I_{x}\]

Обратите внимание, что последние две строки таблицы 5.1 (моменты инерции тонкого плоского прямоугольника) удовлетворяют теореме о параллельных осях.

² Подобно одномерным и двумерным аналогам центра масс непрерывного объекта (4.

Таблица 5.1: Моменты инерции для некоторых обычных объектов, все с общей массой M и длиной L / радиусом R

Объект	Ось вращения	Момент инерции