Определение момента инерции махового колеса и силы трения в опоре
Цель работы: изучение законов вращательного движения с помощью маятника Обербека.
1. Краткая теория
Абсолютно твёрдым телом называют тело, расстояние между любыми двумя точками которого в условиях данной задачи остается постоянным. Иначе говоря, это тело, форма и размеры которого не изменяются при его движении. Всякое твёрдое тело можно мысленно разбить на большое число частей, малых по сравнению с размерами всего тела, и рассматривать его как систему (совокупность) материальных точек, жёстко связанных друг с другом.
Центром масс системы материальных точек (центром инерции) называют точку, масса которой равна массе всего тела, а поло
жение в пространстве определяется радиус-вектором rr :
Произвольное движение тела можно представить как совокупность поступательного движения его центра инерции и вращательного движения относительно центра инерции.
Поступательным называется движение, при котором любая прямая, проведенная в теле, остаётся параллельной самой себе.
Второй закон Ньютона для движения центра масс твёрдого тела записывается в виде:− скорость центра масс, F внешн − векторная сумма всех внешних сил, приложенных к телу (обычно индекс опускается).
При вращательном движении тела все его точки описывают окружности, центры которых лежат на одной прямой, называемой осью вращения. Окружности, описываемые точками, находятся в плоскостях, перпендикулярных оси вращения. Ось вращения может находиться как внутри тела, так и вне него.
Чтобы твёрдое тело с закреплённой осью привести во вращательное движение, необходимо хотя бы к одной из его точек прилоr
жить силу F , не проходящую через ось вращения и не параллельную
ей, другими словами, чтобы эта сила создавала вращающий момент.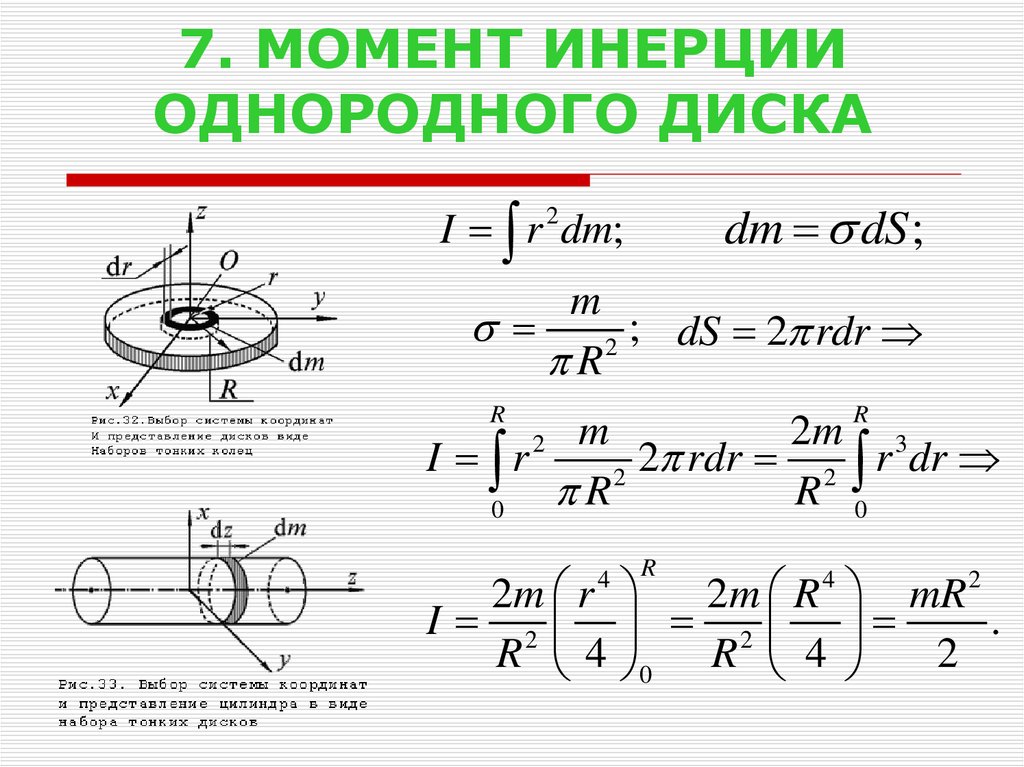
Пусть на твердое тело в точке А действует сила F (рис. 1). Под действием этой силы тело вращается относительно неподвижной оси
О1−О2. Действие силы зависит от ее величины и направления, а также от точки приложения А. Под радиус−вектором точки приложения силы А будем понимать отрезок r, направленный перпендикулярно от
оси вращения к этой точке. Моментом силы F относительно точки О
называется векторное произведение радиус-вектора r на силу F:
Мo = [r,F]. (3)
Момент силы F относительно точки О есть вектор, перпендикулярный к плоскости, содержащей векторы r и F.
Произвольную силу F можно разложить на три взаимно перпендикулярные составляющие: F = Fo + Fr + Fτ. Здесь Fo – осевая составляющая силы, проекция силы на направление оси вращения О1−О2: Fo = Fcosθ ; Fr − радиальная составляющая силы, проекция силы на направление радиус−вектора точки приложения силы А; Fτ −
тангенциальная составляющая силы, которая направлена по касательной к траектории движения точки приложения силы А.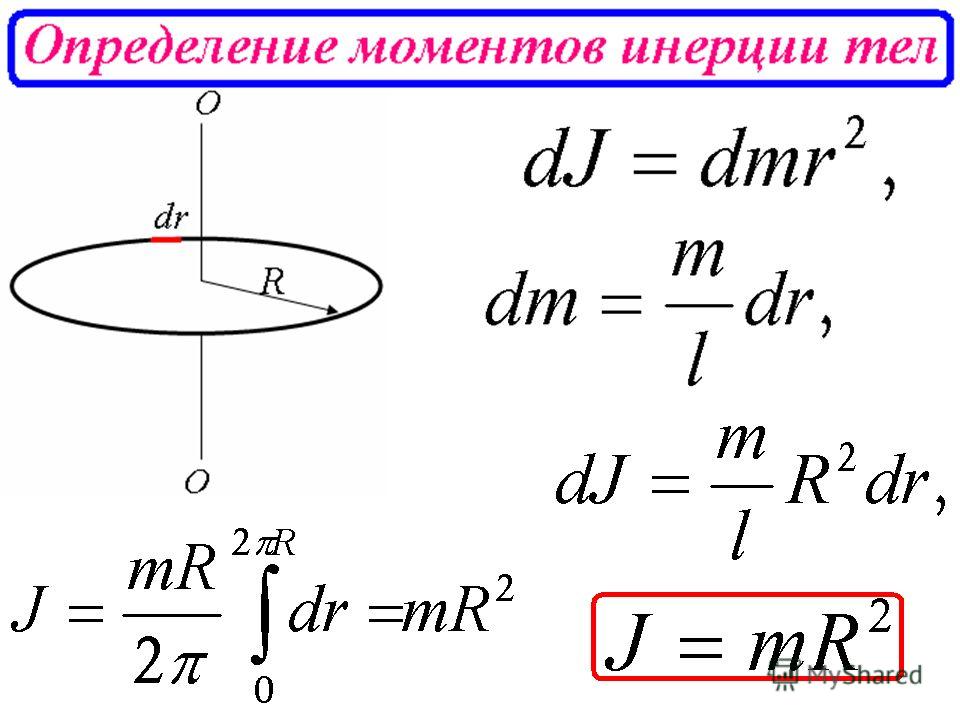
Пусть F′ −
составляющая силы F на плоскость, перпендикулярную оси вращения (можно представить: F = Fo + F′): F ′ = F sinθ . Тогда радиальная составляющая определяется как Fr = F′ cosα = Fsinθ cosα; а тангенциальная составляющая − Fτ = F′ sinα = Fsinθ sinα. Вращение тела относительно оси О1 – О2 происходит только за счет тангенциальной составляющей силы.
7
Вращающим моментом, или моментом силы, относительно оси вращения О1 − О2 называется величина, равная произведению
численного значения радиус-вектора точки приложения силы r и
тангенциальной составляющей силы Fτ :
Mz = r Fτ . (4)
О1
Мz F
Мо ϑ Fτ
ϑ θ
0 F′
Вид сверху
Fτ
0 F′
h r
А А α
Fr Fr
Линия действия силы F′
О
Рис. 1. К определению вращающего момента
Учитывая выражение для Fτ:
Mz = r sin α F ′ = h F ′,
где h = r sinα − плечо силы F ′, это кратчайшее расстояние от оси
вращения до линии действия силы F ′.
другое выражение для вращающего момента:
Mz = h F ′. (5)
Вращающий момент считают векторной величиной, направленной по оси вращения так, что если посмотреть из конца вектора Mz, то вращение будет происходить против часовой стрелки (рис. 1). Тогда вращающий момент можно представить как векторное произведение
радиус−вектора r и силы F ′:
Mz = [ r, F ′] . (6)
Вращающий момент Mz является составляющей (проекцией) момента силы Мo вдоль оси вращения, т.е. вдоль оси z: Mz = Mocos ϑ.
Моментом инерции J материальной точки относительно некоторой оси называется скалярная величина, равная произведению массы материальной точки mi на квадрат расстояния ri от этой точки до оси вращения:
J = mi ri
, [кг•м2] . (7)
8
Момент инерции сплошного тела определяется как сумма моментов инерции всех его частиц:
N
2 2
J = lim ∑ ∆mi ri
N →∞ i=1
= ∫ r dm , (8)
m
где ri − расстояние от i — ой частицы массой ∆mi до оси вращения.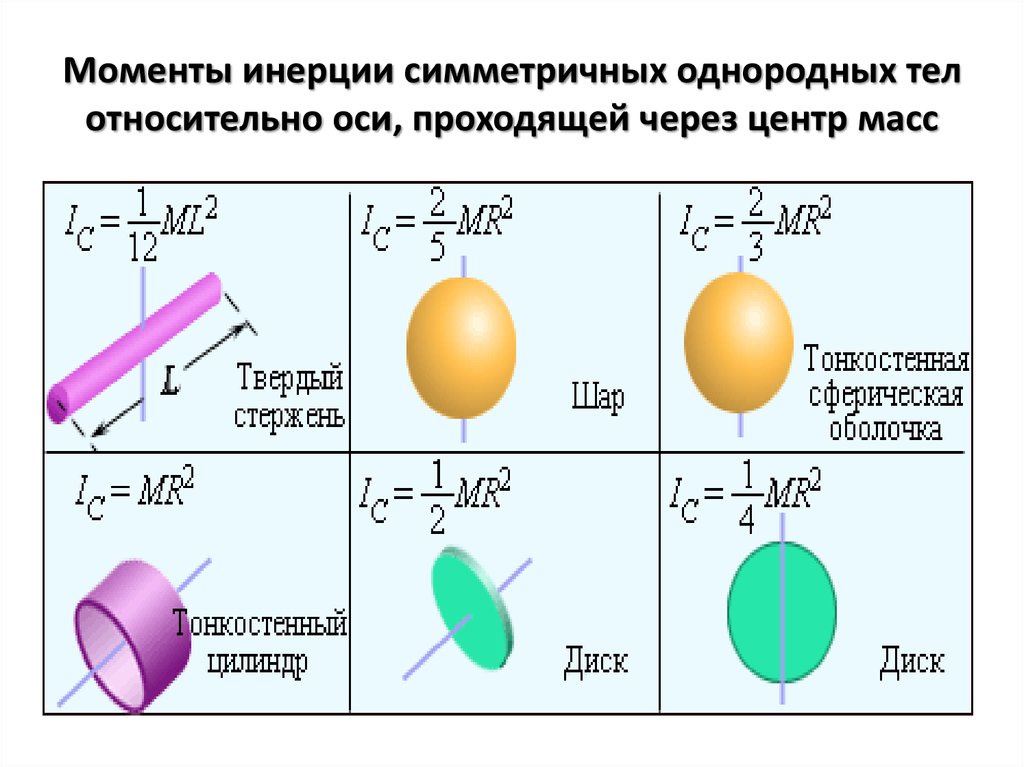
Момент инерции есть скалярная величина, которая определяет инертность тела при вращательном движении и равняется сумме произведений масс отдельных частиц тела на квадрат расстояний от них до оси вращения.
Если тело однородно, т.е. его плотность ρ одинакова по всему объёму. Тогда:
J = ρ ∫ r 2 dV
V
. (9)
Используя формулу (9), можно вычислить моменты инерции однородных тел правильной геометрической формы, результаты некоторых расчетов из них приведены в таблице 1.
Таблица 1
Моменты инерции тел правильной геометрической формы
Тело | Положение оси | Момент инерции |
Полый тонкостенный цилиндр радиусом R | Ось симметрии | mR2 |
Сплошной цилиндр или диск радиусом R | То же | mR2 2 |
Прямой тонкий стержень длиной l | Ось перпендикулярна стержню и проходит через его середину | ml2 12 |
Прямой тонкий стержень длиной l | Ось перпендикулярна стержню и проходит через его конец | ml2 3 |
Шар радиусом R | Ось проходит через центр шара | 2 5 mR2 |
Если ось вращения О1О2 не проходит через центр инерции С (рис.
9
равен сумме момента инерции тела Jc относительно параллельной оси О′О′, проходящей через центр инерции тела С, и произвеО1 O′
l С
O2 O′
дения массы тела m на квадрат расстояния l
от оси вращения до центра инерции:
J = Jc + m l 2 (10)
Закон динамики для тела, вращающегося относительно неподвижной оси О1О2 (рис. 3), записывается в виде
Рис. 3. К определению момента импульса
L = J ωr (12)
− момент импульса тела относительно
оси, т.е. вектор, направленный по оси вращения, как и угловая скорость ωr .
Для i-ой частицы твердого тела второй закон Ньютона: Fidt = dpi. Умножим это уравнение на ri: riFidt = ridpi , Midt = d(ripi). Назовем Li = ripi − моментом импульса материальной точки относительно оси. Для этой величины выполняется правило векторного произведения: Li = [ri, pi].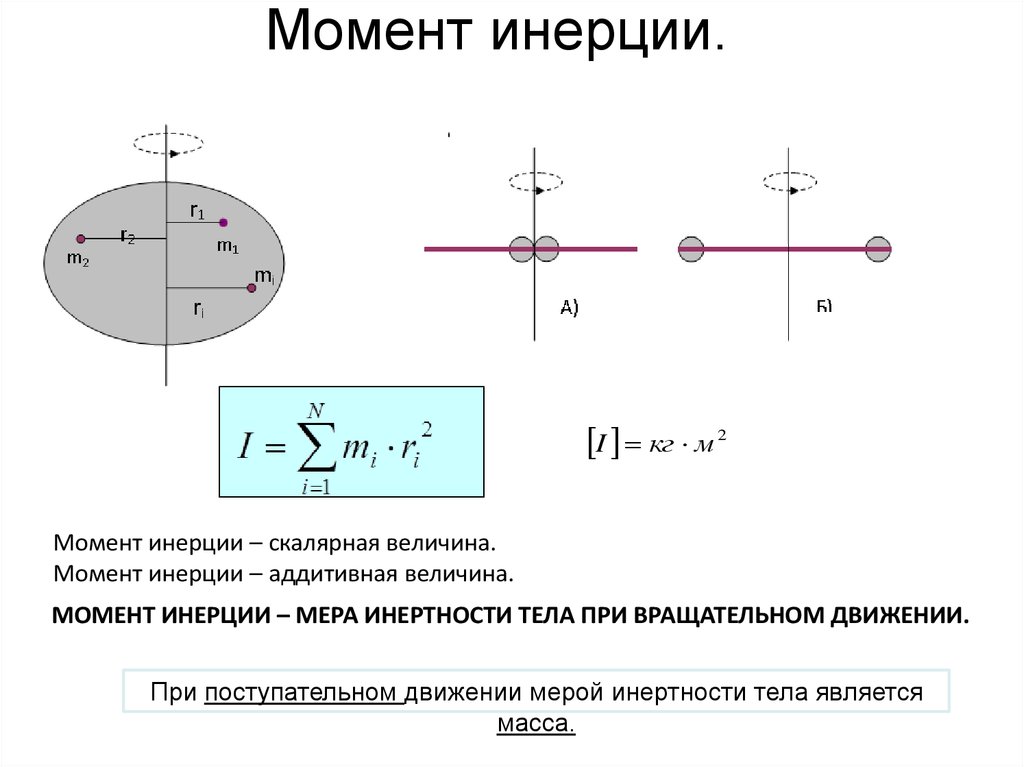
Момент импульса тела определяется как сумма моментов импульса всех его частиц:
Li = Σ [ri, pi]. (13)
При вращательном движении момент импульса играет роль импульса тела.
Основной закон динамики вращательного движения гласит, что скорость изменения момента импульса тела относительно неподвижной оси вращения равна результирующему моменту относительно этой же оси всех внешних сил, действующих на
тело:
dL = M . (14)
dt
10
Сравнивая формулы второго закона Ньютона в дифференциальной форме
dmv F и
dJωr = M,
dt = dt
убеждаемся, что эти формулы аналогичны. Аналогом силы F, входящей в уравнение динамики поступательного движения, является вращающий момент М в случае вращательного движения твёрдого тела, линейной скорости v поступательного движения – угловая скорость
вращающегося тела ωr , массы m – момент инерции тела J.
По учебникам [1 – 3] выучите (выпишите) определения потенциальной и кинетической энергии тел.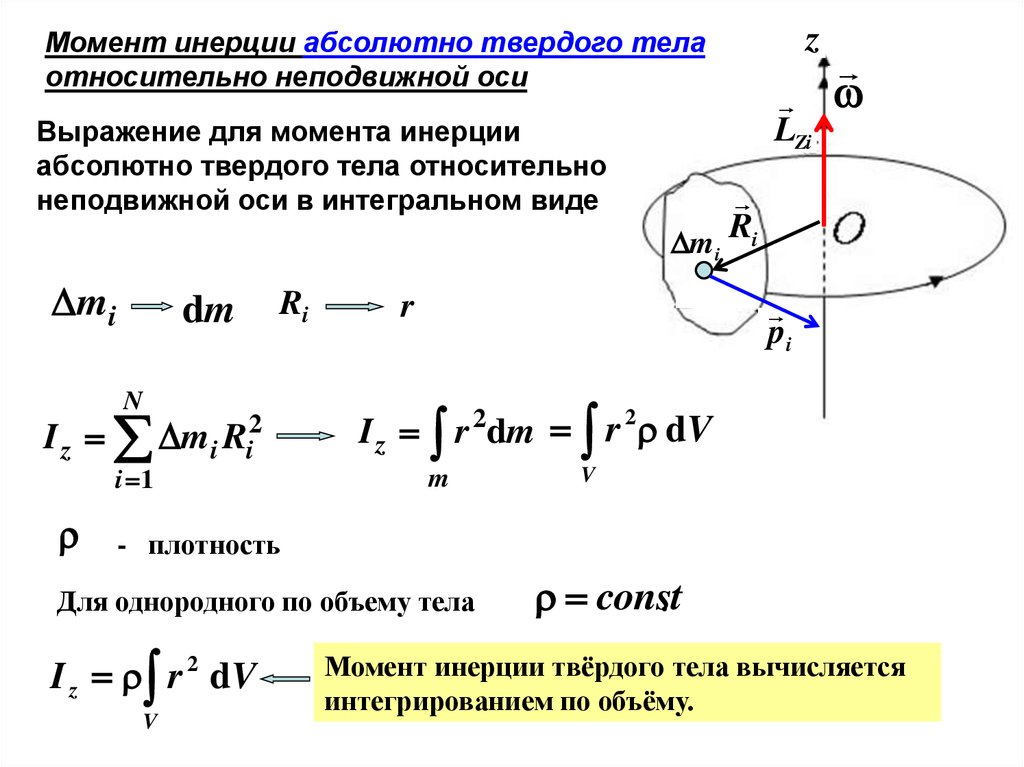
Кинетическая энергия вращающегося твердого тела складывается из кинетических энергий его материальных точек и определяется формулой:
Wк =
Jω 2
2
, (15)
где J − момент инерции тела, ωугловая скорость вращения тела.
2. Описание лабораторной установки и методики измерения
Приборы и принадлежности: маятник Обербека, груз, штангенциркуль, масштабная линейка, секундомер.
Для изучения законов вращательного движения используется маятник Обербека (рис. 4). Прибор состоит из шкива радиусом r , закрепленного на валу, четырех стержней, расположенных под углом
90° друг к другу, и четырех одинаковых цилиндрических грузов m1,
которые можно перемещать вдоль стержней и закреплять на определенном расстоянии от оси вала. Грузы закрепляются симметрично, т.е. так, чтобы центр инерции совпадал с осью вращения. Вращающиеся части прибора представляют собой маховое колесо, момент инерции J которого можно менять за счет перемещения грузов.
Маховое колесо приводится в движение грузом массой m, прикрепленным к концу шнура. Груз на высоте h2 относительно нижней точки падения обладает потенциальной энергией:
Wп1 = Fтh2 = mgh2,
где Fт − сила тяжести груза m; g − ускорение свободного падения.
11
m1 альная энергия переходит в кинетическую энергию поступательного движеR mυ 2
r ния груза
, кинетическую энергию
2
вращательного движения махового коm m Jω 2
1 1 леса
и затрачивается на работу по
2
преодолению сил трения в опорах и сопротивления воздуха. Если сила трения f постоянна, то работа сил трения будет
h2 F равняться A = f h2.
т По закону сохранения энергии поh3 тенциальная энергия груза в верхней
точке равняется сумме кинетических
где υ − скорость груза; ω − угловая скорость маховика.
Движение груза равноускоренное, без начальной скорости, поэтому ускорение а и скорость υ соответственно равны:
a = 2h2 , υ = 2h2 ,
t 2 t
где t − время падения груза с высоты h2.
Угловая скорость махового колеса связана с линейной скоростью груза
ω = υ = 2h2
где r − радиус шкива.
r tr
Маховое колесо, вращаясь по инерции за счет своей кинетической энергии вращательного движения, поднимает груз m на высоту h3 < h2, при этом потенциальная энергия груза увеличивается и на высоте h3 будет Wп2 = mgh3.
12
Уменьшение потенциальной энергии при подъеме груза равно работе по преодолению сил трения:
mgh2 − mgh3 = f (h2 + h3) ,
откуда
f = mg h2 − h3 . (17)
h2 + h3
Подставляя в формулу (16) выражения для υ, ω и f , получим
выражение для вычисления момента инерции махового колеса:
Материал взят из методических указаний Динамика твердого тела (Биктагиров В.В.)
Момент инерции — Студопедия
Рассмотрим материальную точку массой m, которая находится на расстоянии r, от неподвижной оси (рис. 26). Моментом инерции J материальной точки относительно оси называется скалярная физическая величина, равная произведению массы m на квадрат расстояния r до этой оси:
J = mr2(75)
Момент инерции системы N материальных точек будет равен сумме моментов инерции отдельных точек:
(76)
Рис.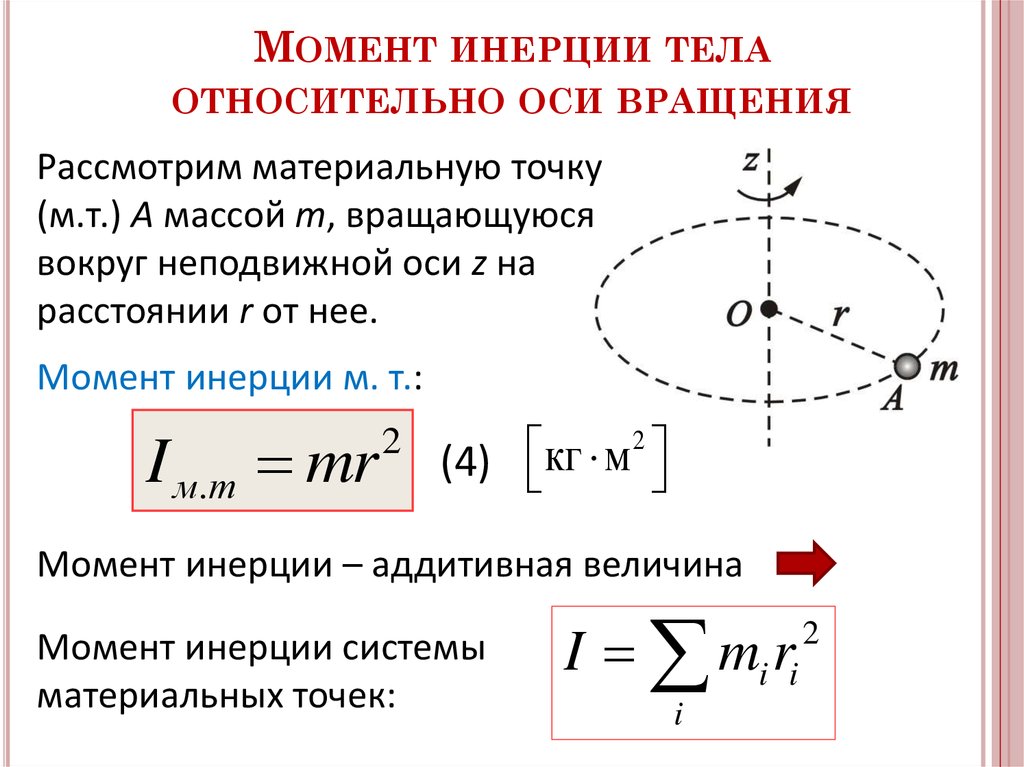
26.
К определению момента инерции точки.
Если масса распределена в пространстве непрерывно, то суммирование заменяется интегрированием. Тело разбивается на элементарные объемы dv, каждый из которых обладает массой dm.
В результате получается следующее выражение:
(77)
Для однородного по объему тела плотность ρ постоянна, и записав элементарную массу в виде:
dm = ρdv, преобразуем формулу (70) следующим образом:
(78)
Размерность момента инерции – кг*м2.
Момент инерции тела является мерой инертности тела во вращательном движении, подобно тому, как масса тела является мерой его инертности при поступательном движении.
Момент инерции — это мера инертных свойств твердого тела при вращательном движении, зависящая от распределения массы относительно оси вращения. Иными словами, момент инерции зависит от массы, формы, размеров тела и положения оси вращения.
Всякое тело, независимо от того, вращается оно или покоится, обладает моментом инерции относительно любой оси, подобно тому, как тело обладает массой независимо от того, движется оно или находиться в покое. Аналогично массе момент инерции является величиной аддитивной.
В некоторых случаях теоретический расчёт момента инерции достаточно прост. Ниже приведены моменты инерции некоторых сплошных тел правильной геометрической формы относительно оси, проходящей через центр тяжести.
Момент инерции бесконечно плоского диска радиуса R относительно оси, перпендикулярной плоскости диска:
Момент инерции шара радиуса R:
Момент инерции стержня длиной L относительно оси, проходящей через середину стержня перпендикулярно ему:
Момент инерции бесконечно тонкого обруча радиуса R относительно оси, перпендикулярной его плоскости:
Момент инерции тела относительно произвольной оси рассчитывается с помощью теоремы Штейнера:
Момент инерции тела относительно произвольной оси равен сумме момента инерции относительно оси, проходящей через центр масс параллельно данной, и произведения массы тела на квадрат расстояния между осями.
Рассчитаем при помощи теоремы Штейнера момент инерции стержня длиной L относительно оси, проходящей через конец перпендикулярно ему (рис. 27).
Рис. 27.
К расчету момента инерции стержня
Согласно теореме Штейнера, момент инерции стержня относительно оси O′O′ равен моменту инерции относительно оси OO плюс md2. Отсюда получаем:
Очевидно: момент инерции неодинаков относительно разных осей, и поэтому, решая задачи на динамику вращательного движения, момент инерции тела относительно интересующей нас оси каждый раз приходится искать отдельно. Так, например, при конструировании технических устройств, содержащих вращающиеся детали (на железнодорожном транспорте, в самолетостроении, электротехнике и т. д.), требуется знание величин моментов инерции этих деталей. При сложной форме тела теоретический расчет его момента инерции может оказаться трудно выполнимым. В этих случаях предпочитают измерить момент инерции нестандартной детали опытным путем.
Рис. 28.
Момент силы F относительно точки O
Момент инерции – определение, формула, значение, факты
Что такое момент инерции?
Момент инерции (MOI) — это сопротивляемость тела его угловому ускорению. Момент инерции можно выразить как; I=mk 2 , где m — масса тела, а k — радиус вращения.
Момент инерции Определение
Момент инерции – это величина, выражающая тенденцию тела сопротивляться внешнему угловому ускорению, которая может быть рассчитана как сумма произведений массы каждой частицы тела на квадрат расстояния до нее от оси, вдоль которой он должен вращаться.
Загрузить формулы для GATE Civil Engineering – Fluid Mechanics
Формула момента инерции
Момент инерции – это резистивная способность поперечного сечения при вращении. Момент инерции также известен как площадь второго момента, которая может быть представлена как n Σ 1 A i y i , где y – расстояние центра тяжести площади от ее оси
Момент инерции также можно выразить как I=p/ω, где p — угловой момент, а ω — угловая скорость тела.
Момент инерции также можно рассчитать по формуле I=L/ω
Где I= момент инерции
L= угловой момент
ω= угловая скорость
Единица момента инерции
Как мы знаем, I =mk 2
Таким образом, единицей измерения момента инерции является кг-м 2
Скачать формулы для GATE Civil Engineering – Environmental Engineering
Момент инерции – очень важная тема физики, которую необходимо изучить. быть понятым, прежде чем применять его к любым реальным проблемам. Момент инерции тела при вращательном движении так же важен, как и масса тела при его поступательном движении. Момент инерции – это свойство сечения, показывающее его способность противостоять вращательному движению.
Момент инерции поперечного сечения показывает сопротивление тела вращению, которое зависит от расстояния накопления массы по поперечному сечению. Момент инерции говорит о свойстве поперечного сечения тела.
Момент инерции твердой сферы
Момент инерции твердой сферы представляет собой присущую ей инерцию, которая обеспечивает сопротивление угловому движению.
Момент инерции зависит от распределения массы, и он больше, если распределение массы больше удалено от оси вращения.
Момент инерции для различных форм
Момент инерции для различных форм зависит от расположения массы относительно центра тела. По мере удаления массы от центра тела увеличивается его момент инерции относительно центра, что делает сечение более прочным.
Теорема о параллельной оси
Момент инерции поперечного сечения зависит от оси, вокруг которой вращается поперечное сечение. Итак, если известен момент инерции относительно его центра, то его можно вычислить относительно любой оси, используя две теоремы.
Теорема о параллельных осях используется для расчета момента инерции твердого тела относительно оси, параллельной центральной оси тела
Согласно теореме о параллельных осях: I=I c +Mh 2
Где I c — момент инерции, M — масса тела, а h — расстояние между новой осью и центральной осью.
Теорема о перпендикулярной оси
Теорема об перпендикулярной оси используется для расчета момента инерции тела относительно оси, перпендикулярной плоскости тела. Теорема перпендикулярной оси очень полезна для нахождения полярного момента инерции и помогает найти жесткость балки при кручении.
Согласно теореме о перпендикулярной оси; I Z =I X +I Y
Влияние вращения оси на момент инерции
Момент инерции зависит от оси вращения тела, а также от распределения массы по всей площади тела. Момент инерции относительно новой оси вращения x’y’ можно рассчитать как
, где I x’y’ – это произведение момента инерции, а θ – вращение преобразованной оси против часовой стрелки.
определение момента+инерции по The Free Dictionary
Момент+инерции – определение момента+инерции по The Free DictionaryМомент+инерции – определение момента+инерции по The Free Dictionary
Слово, не найденное в Словаре и Энциклопедии.