Может ли быть отрицательным момент инерции: Может ли момент инерции быть отрицательным - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Может ли момент инерции быть отрицательным

Моментом инерции называется характеристика, отличающаяся от статического момента тем, что координата входит в подынтегральное выражение в квадрате (рис.4.4). Моменты инерции бывают осевые или экваториальные – формула (4.6.), полярный – (4.7) и центробежный – (4.8).

, . (4.6)

. (4.7)

. (4.8)

Если начало координат совпадает с полюсом, то ρ 2 = z 2 + y 2 , следовательно

Размерность моментов инерции – единица длины в четвёртой степени (например, см 4 ). Отметим, что осевой и полярный моменты инерции всегда положительны. Центробежный момент инерции может быть положительным или отрицательным

в зависимости от положения осей.

Рис.4.5

Очевидно, постепенно поворачивая оси, можно найти такое их положение, при котором центробежный момент инерции равен нулю. Такие оси называются главными осями инерции. Две взаимно перпендикулярные оси, из которых хотя бы одна является осью симметрии фигуры, всегда будут её главными осями инерции, поскольку в этом случае каждой положительной величине zydF соответствует такая же отрицательная по другую сторону от оси симметрии (рис.

4.5) и их сумма по всей площади фигуры равна нулю. Главные оси, проходящие через центр тяжести, называются главными центральными осями. Вычислим моменты инерции прямоугольника относительно главных центральных осей (рис.4.6,а). Оси z и y – главные, т.к. они являются осями симметрии, J_zy = 0.

Для определения осевого момента инерции относительно оси z выделим элементарную площадку в виде полоски, параллельной оси z:

Очевидно, что для определения J_y надо поменять местами стороны прямоугольника.

Главные осевые моменты инерции прямоугольника

, . (4.10)

Вычислим полярный момент инерции круга относительно его центра, а также осевой момент инерции относительно центральной оси. При вычислении полярного момента инерции выделим элементарную площадку в виде тонкого кольца толщиной dρ (рис.4.6,б) и подсчитаем по формуле (4.7)

Полярный момент инерции круга

. (4.11)

Осевой момент инерции круга легко найти из выражения (4. 9), учитывая, что в силу симметрии J_z = J_y . Следовательно,

. (4.12)

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Сдача сессии и защита диплома – страшная бессонница, которая потом кажется страшным сном. 8910 – | 7222 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Моментами инерции сечений называются интегралы следующего вида:

– осевой момент инерции сечения относительно оси у;

– осевой момент инерции сечения относительно оси z;

– центробежный момент инерции сечения;

– полярный момент инерции сечения.

3.2.1. Свойства моментов инерции сечения

Размерность моментов инерции – [длина 4 ], обычно [м 4 ] или [см 4 ].

Осевые и полярный моменты инерции всегда положительные. Центробежный момент инерции может быть положительным, отрицательным или равным нулю.

Оси, относительно которых центробежный момент инерции равен нулю, называются главными осями инерции сечения.

Оси симметрии всегда главные. Если из двух взаимно перпендикулярных осей хотя бы одна является осью симметрии, то обе оси главные.

Момент инерции составного сечения равен сумме моментов инерции элементов этого сечения.

Полярный момент инерции равен сумме осевых моментов инерции.

Докажем последнее свойство. В сечении с площадью А для элементарной площадки dA радиус-вектор ρ и координаты у и z (рис. 6) связаны по теореме Пифагора: ρ 2 = у 2 + z 2 . Тогда

Рис. 6. Связь полярных и декартовых координат

3.2.2. Моменты инерции простейших фигур

В прямоугольном сечении (рис. 7) выберем элементарную площадку dA с координатами y и z и площадью dA = dydz.

Рис. 7. Прямоугольное сечение

Осевой момент инерции относительно оси у

Аналогично получаем момент инерции относительно оси z:

Поскольку у и z – оси симметрии, то центробежный момент D_zy = 0.

Для круга диаметром d вычисления упрощаются, если учесть круговую симметрию и использовать полярные координаты. Возьмем в качестве элементарной площадки бесконечно тонкое кольцо с радиусом ρ и толщиной dρ (рис. 8). Его площадь dA = 2πρdρ. Тогда полярный момент инерции:

Рис. 8. Круглое сечение

Как показано выше, осевые моменты инерции относительно любой центральной оси одинаковы и равны

Момент инерции кольца находим как разность моментов инерции двух кругов – наружного (с диаметром D) и внутреннего (с диаметром d):

Момент инерции I_zтреугольникаопределим относительно оси, проходящей через центр тяжести (рис. 9). Очевидно, ширина элементарной полоски, находящейся на расстоянииуот осиz, равна

Рис. 9. Треугольное сечение

3.3. Зависимости между моментами инерции относительно параллельных осей

При известных величинах моментов инерции относительно осей z и у определим моменты инерции относительно других осей z₁ и y₁, параллельных заданным. Пользуясь общей формулой для осевых моментов инерции, находим

Если оси z и y центральные, то , и

Из полученных формул видно, что моменты инерции относительно центральных осей (когда ) имеют наименьшие значения по сравнению с моментами инерции относительно любых других параллельных осей.

3.4. Главные оси и главные моменты инерции

При повороте осей на угол α центробежный момент инерции становится равным

Определим положение главных главных осей инерции u, v относительно которых

где α_{– угол, на который надо развернуть оси y и z, чтобы они стали главными.}

Поскольку формула дает два значения углаи, то существуют две взаимно перпендикулярные главные оси. Ось максимума всегда составляет меньший угол () с той из осей (z или y), относительно которой осевой момент инерции имеет большее значение. Напомним, что положительные углы откладываются от оси z против хода часовой стрелки.

Моменты инерции относительно главных осей называются главными моментами инерции. Можно показать, что они

Знак плюс перед вторым слагаемым относится к максимальному моменту инерции, знак минус – к минимальному.

Центробежный момент инерции тела

Допустим, что имеется система координат с началом в точке O и осями OX; OY; OZ. По отношению к данным осям центробежными моментами инерции (произведениями инерции) называются величины , которые определяются равенствами:

где – массы материальных точек, на которые разбивают тело; – координаты соответствующих материальных точек.

Центробежный момент инерции обладает свойством симметрии, это следует из его определения:

Если тело можно считать сплошным (непрерывным), то определение центробежного момента инерции записывают как:

Центробежные моменты тела могут быть положительными и отрицательными, при определённом выборе осей OXYZ они могут обращаться в ноль.

Для центробежных моментов инерции существует аналог теоремы Штейнберга. Если рассмотреть две системы координат: и . Одна из этих систем имеет начало координат в центе масс тела (точка C), оси систем координат являются попарно параллельными (). Пусть в системе координат координатами центра масс тела являются (), тогда:

где – масса тела.

Главные оси инерции тела

Пусть однородное тело имеет ось симметрии. Построим координатные оси так, чтобы ось OZ была направлена вдоль оси симметрии тела. Тогда, как следствие симметрии каждой точке тела с массой и координатами соответствует точка, имеющая другой индекс, но такую же массу и координаты: . В результате получаем, что:

так как в данных суммах все слагаемые имеют свою равную по величине, но противоположную по знаку пару. Выражения (4) эквивалентны записи:

Мы получили, что осевая симметрия распределения масс по отношению к оси OZ характеризуется равенством нулю двух центробежных моментов инерции (5), которые содержат среди своих индексов наименование этой оси. В таком случае ось OZ называется главной осью инерции тела для точки О.

Главная ось инерции не всегда является осью симметрии тела. Если тело обладает плоскостью симметрии, то любая ось, которая перпендикулярна этой плоскости, является главной осью инерции для точки O, в которой ось пересекает рассматриваемую плоскость. Равенства (5) отображают условия того, что ось OZ является главной осью инерции тела для точки O (начала координат). Если выполняются условия:

то ось OY будет для точки O главной осью инерции.

В том случае, если выполняются равенства:

то все три координатные оси системы координат OXYZ являются главными осями инерции тела для начала координат.

Моменты инерции тела по отношению к главным осям инерции называются главными моментами инерции тела. Главные оси инерции, которые построены для центра масс тела, носят название главных центральных осей инерции тела.

Если тело обладает осью симметрии, то она является одной из главных центральных осей инерции тела, поскольку центр масс находится на этой оси. В том случае, если тело имеет плоскость симметрии, то ось, нормальная к этой плоскости и проходящая через центр масс тела является одной из главных центральных осей инерции тела.

Понятие главных осей инерции в динамике твердого тела имеет существенное значение. Если вдоль них направить оси координат OXYZ, то все центробежные моменты инерции становятся равными нулю, при этом значительно упрощаются формулы, которые следует применять при решении задач динамики. С понятием о главных осях инерции связано решение задач о динамическом уравнении тела находящегося во вращении и о центре удара.

Момент инерции тела ( и центробежный в том числе) в международной системем единиц измеряются в:

Центробежный момент инерции сечения

Центробежным моментом инерции сечения (плоской фигуры) относительно двух взаимно нормальных осей (OX и OY) называют величину, равную:

выражение (8) говорит о том, что центробежный момент инерции сечения относительно взаимно перпендикулярных осей есть сумма произведений элементарных площадок () на расстояния от них до рассматриваемых осей, по всей площади S.

Единицей измерения моментов инерции сечения в СИ является:

Центробежный момент инерции сложного сечения по отношению к любым двум взаимно нормальным осям равен сумме центробежных моментов инерции составляющих его частей относительно этих осей.

Примеры решения задач

Задание	Получите выражение для центробежного момента инерции прямоугольного сечения относительно осей (X,Y).
Решение	Сделаем рисунок.

Для определения центробежного момента инерции выделим из имеющегося прямоугольника элемент его площади (рис.1) , площадь которой равна:

На первом этапе решения задачи найдем центробежный момент инерции () вертикальной полосы, имеющей высоту и ширину , которая находится на расстоянии от оси Y (учтем, что при интегрировании для всех площадок в избранной вертикальной полоске величина является постоянной):

На втором этапе решения задачи проинтегрируем, двигаясь по горизонтали, учитывая, что :

Центробежный момент – инерция – Большая Энциклопедия Нефти и Газа, статья, страница 1

Центробежный момент – инерция

Cтраница 1

Центробежный момент инерции равен пулю. [1]

Центробежные моменты инерции обычно вычисляются через главные центральные осевые моменты инерции. [2]

Центробежный момент инерции может быть положительным, отрицательным и в частном случае равным нулю. [3]

Центробежный момент инерции относительно этих осей равен нулю. [4]

Центробежный момент инерции может быть положительным, отрицательным и равным нулю. [5]

Центробежный момент инерции может быть положительным, отрицательным или равным нулю. [7]

Центробежный момент инерции относительно осей х, у оказался, как видим, отрицательным. [8]

Центробежный момент инерции может быть положительным, отрицательным и равным нулю. [9]

Центробежный момент инерции имеет размерность см, но в отличие от осевого и полярного моментов инерции он может быть величиной положительной, отрицательной и равной нулю. [10]

Центробежный момент инерции по отношению к осям, из которых хотя бы одна является осью симметрии, равен нулю. [11]

Центробежный момент инерции определяется по осевым моментам инерции, найденным для осей х, у и оси. [12]

Центробежный момент инерции достигает наибольшего по абсолютной величине значения для креста осей, повернутых на: 45 относительно главных осей. Это экстремальное значение равно полуразности главных моментов инерции. Осевые моменты инерции для этого креста осей равны между собой. Наоборот, если для случайного креста осей Ja Jv и Jav ф 0, то главные оси повернуты на: 45 относительно этого креста.

[13]

Центробежные моменты инерции могут быть положительными, отрицательными или равным нулю. [14]

Центробежный момент инерции / у1г1 0, так как ось ляется осью симметрии. [15]

Страницы: 1 2 3 4

Крутящий момент колеса и тормозной момент колеса : Механика и Техника

Заранее извиняюсь за глупые вопросы. Если есть ссылки на литературу по теме – будет здорово.

Нужно читать учебники по теоретической механике. В самом простом учебнике написано примерно следующее:
“Движение твердого тела – это есть комбинация поступательного и вращательного движения”.

Итак, важные термины – поступательное движение и вращательное движение.
У нас был отличный преподаватель по термеху: он разделил доску линией на две части, на левой части написал заголовок “поступательное движение”, на правой – “вращательное движение”. И далее под заголовками написал следующее:

Присмотритесь внимательнее к этим параллелям. Если Вы хорошо изучили в школе поступательное движение, то легко освоите и вращательное движение и все его характеристики , , , , . Они в каком-то смысле похожи на свои аналоги в поступательном движении!
Очень важно, в конце концов, освоить и второй закон Ньютона для вращательного движения.

Каким образом связаны крутящий и тормозной момент колеса?
П.С. У меня небольшие трудности с пониманием, что такое крутящий момент. Я понимаю, что крутящий момент (момент силы) – это векторное произведение вектора, проведенного от оси в ращения к точке приложения силы, и вектора этой силы. Т.е. крутящий момент перпендикулярен плоскости колеса.

Крутящий и тормозной моменты складываются и образуют суперпозицию моментов. Крутящий момент во вращательном движении – это аналог силы в поступательном движении.

Но у телеги есть ограничения по скорости. Она не может ехать быстрее 130 км/ч (например).
Проблема в том, что если не использовать тормозной момент или как-то влиять на крутящий момент (делать его отрицательным?), то телега без проблем достигнет скорости звука.

Крутящий момент в суперпозиции моментов идет со знаком “плюс”, тормозной – со знаком “минус”. Иначе говоря, крутящий момент положителен (направлен вдоль вектора угловой скорости), тормозной – отрицателен (против вектора скорости).
Действительно, если трение очень маленькое, то возникает опасность неуправляемого движения: должно быть предусмотрено устройство для торможения (тормоз). В некоторых случаях тормозят двигателем, то есть тем же устройством, что и создает крутящий момент при разгоне. В этом случае крутящий момент принимает отрицательное значение. Часто тормозят конструктивно другим устройством – так, например, сделано в автомобиле с двигателем внутреннего сгорания. Дело в том, что ДВС не умеет создавать достаточно эффективный тормозящий момент. А вот подавляющее число электродвигателей умеют тормозить, в этом случае они становятся генераторами и превращают кинетическую энергию вращения в электрическую.

ДВС не умеет вращение превращать обратно в бензин. Электрические двигатели обратимы, ДВС – нет.

Почему при постоянном крутящем моменте движение всегда происходит с ускорением?

см. второй закон Ньютона для вращательного движения. Надо только оговориться, что речь не просто про крутящий момент, а про их суперпозицию.

Если в определенный момент времени прекратить сообщать крутящий момент колесу (хм, я не уверен, что правильно выразился), то движение некоторое время все-равно будет увеличиваться из-за инерции колеса? Или сразу должно уменьшаться?

Что значит “движение некоторое время все равно будет увеличиваться…”? Что такое “движение”? Что за величина? Выберите из списка: , , , , . Для ответа на свой вопрос воспользуйтесь вторым законом Ньютона для вращательного движения.

Что такое тормозной момент колеса, как его можно использовать для ограничения скорости?

Для ограничения скорости важен не просто тормозной момент, а тот факт, что любой вращающийся двигатель при увеличении угловой скорости (частоты вращения) рано или поздно теряет способность создавать крутящий момент.

Когда Вы раскручиваете руками карусель, рано или поздно Ваши руки перестают успевать за вращением и крутящий момент падает до нуля, тормозным моментом при этом можно пренебречь. Далее можно посмотреть на второй закон Ньютона, чтобы объяснить ограничение скорости… Также и в случае телеги (поступательного движения). И не важно, что собой представляет двигатель – ракетный, электрический, ДВС, тело человека – все это истощается с ростом скорости (частоты вращения), другими словами, ограничено по мощности…

Геометрические характеристики сечений | ПроСопромат.ру

При решении задач сопротивления материалов разрушению и деформированию, сохранения или потери начальной формы равновесия стержней, как правило, используются следующие геометрические характеристики поперечных сечений, описываемые интегралами

где S_x, S_y – статические моменты площади поперечного сечения (могут быть положительными, отрицательными или равными нулю), J_x, J_y– осевые моменты инерции сечения (положительны, не могут равняться нулю), J_xy – центробежный момент инерции

сечения (может быть положительным, отрицательным или равным нулю), J_ρ– полярный момент инерции сечения (положителен), не равен нулю), dA – элемент площади сечения, х, у – координаты элемента площади.

Размерность статических моментов площади- длина в третьей степени, моментов инерции — длина в четвертой степени.

Для сечения, состоящего из отдельных частей или разделенного на отдельные части (фигуры)

Оси, относительно которых статические моменты площади равны нулю, называются центральными осями. Согласно сути теоремы о моменте равнодействующей (теоретическая механика)

S_x=Ay_c, S_y=Ax_c,

где х_с, у_с – координаты центра тяжести сечения.

Таким образом, применительно к составному сечению

Это формулы для определения координат центра тяжести составного сечения.

Зависимости между геометрическими характеристиками относительно параллельных осей (ОХ||О′Х′, ОУ||О′У′)

где a, b –расстояния между, соответственно, осями

Х и Х_/ и осями Y и Y_/

Если оси Х и У являются центральными, то формулы «перехода» от центральных осей

В случае поворота координатных осей Х и У на угол α зависимости между моментами инерции формулы «перехода» от центральных осей

Из этих формул вытекает замечательное следствие, которое часто используется в качестве контроля, проверки:

Сумма осевых моментов инерции относительно любых двух взаимно перпендикулярных осей не меняется при повороте осей.

Главные оси и главные моменты инерции

В любой точке плоскости существуют такие две взаимно перпендикулярные оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты инерции имеют экстремальные значения (максимальное и минимальное). Такие оси называются главными, а осевые моменты инерции относительно этих осей –главными моментами инерции.

Если главные оси проходят к тому же и через центр тяжести сечения, то они называются главными центральными осями, а осевые моменты инерции – главными центральными моментами инерции.

Практическое значение имеют именно эти главные центральные оси (обозначим их U и V) и главные центральные моменты инерции относительно их, поскольку они входят во все расчетные формулы сопротивления материалов.

Положение главных осей находится из выражения

где – угол между главными и исходными осями.

Этому условию удовлетворяют сразу два значения угла, отличающихся на 90˚, значит формула определяет положение сразу обеих главных центральных осей. Найденное из этого условия значение угла α

0 откладывается между максимальной главной осью и той из центральных осей, относительно которой момент инерции больше.

Главные моменты инерции определяются следующим образом:

Геометрическими характеристиками сечения также являются:

— Радиус инерции

Радиусом инерции называют корень квадратный из отношения момента инерции к площади сечения, эта величина характеризует разброс площади по периферии сечения:

— Осевые моменты сопротивления

Осевой момент сопротивления (W) представляет собой отношение осевого момента инерции относительно оси к расстоянию от этой оси до наиболее удаленной точки сечения:

Все геометрические характеристики для простых фигур можно найти в рубрике

« Таблицы»- см. здесь, а для профилей проката — здесь.

Элементы механики электропривода

Элементы электропривода

Уравнение движения ЭП

где М — вращающий момент двигателя, Н*м,

Мс – приведенный к валу двигателя момент сопротивления РН, Н*м

J – приведенный к валу двигателя момент инерции ЭП, Н*м2

ω — угловая частота вращения двигателя, рад

/с.

Величина называется динамическим или избыточным моментом ЭП. Положительный динамический момент обеспечивает разгон ЭП, отрицательный — замедление.

Мощность двигателя, Вт,

Поскольку (где n измеряется в об/мин),

то

Номинальный момент двигателя можно вычислить по приводимым в паспорте номинальной мощности Рн и номинальной скорости вращения двигателя nн:

Приведенный к валу двигателя момент сопротивления, Н*м,

где j и η — соответственно передаточное отношение и КПД передачи,

Приведенный к валу двигателя момент инерции ЭП, в котором сочетаются вращательное и поступательное движения (например, ЭП лифта):

где: Jд — моменты инерции ротора двигателя, Н*м2

JРM — момент рабочего механизма, Н*м2,

ωрм — частота вращения рабочего механизма, рад /с;

G — вес перемещаемого посредством ЭП груза, кг;

v — линейная скорость перемещения груза, м/с,

g — ускорение силы тяжести, 9,8 м/с2.

Определение времени ускорения и замедления ЭП

Время t1-2 ускорения или замедления ЭП от частоты вращения ω1 до ω2 определяется путем интегрирования уравнения движения ЭП:

В простейшем случае, когда М = const, Мс = const, J= const, no лучим

В частном случае, при пуске двигателя до частоты вращения со, время пуска U с, определяется выражением:

Как рассчитать момент инерции

Как рассчитать момент инерции (MOI) Проблемы в реальном мире

Первым шагом для расчета момента инерции массы является определение местоположения осей X, Y и Z . Точность расчетов (а позже и точность измерений для проверки расчетов) будет полностью зависеть от мудрости, использованной при выборе осей. Теоретически эти оси могут находиться в любом месте относительно рассматриваемого объекта при условии, что оси взаимно перпендикулярны. Однако в реальной жизни, если оси не выбраны так, чтобы их можно было точно измерить и идентифицировать, вычисления момента инерции не имеют смысла.

Момент инерции аналогичен инерции, за исключением того, что он применяется к вращению, а не к линейному движению. Инерция – это тенденция объекта оставаться в покое или продолжать движение по прямой с той же скоростью. Инерцию можно рассматривать как другое слово для обозначения массы. Следовательно, момент инерции – это масса вращения.В отличие от инерции, MOI также зависит от распределения массы в объекте. Чем больше расстояние между массой от центра вращения, тем больше момент инерции.

Формула, аналогичная второму закону движения Ньютона, может быть записана для вращения:
F = Ma (F = сила; M = масса; a = линейное ускорение)
T = IA (T = крутящий момент; I = момент инерции; A = ускорение вращения)

Выбор местоположения опорной оси даже для сложной формы

Три опорные оси необходимы для вычисления центра тяжести, но только одна ось необходима для определения момента инерции. Хотя в качестве опорной можно выбрать любую ось, обычно желательно выбрать ось вращения объекта. Если объект установлен на подшипниках, то эта ось определяется средней линией подшипников. Если объект летит в пространстве, то эта ось является «главной осью» (ось, проходящая через центр тяжести и ориентированная таким образом, что произведение инерции относительно этой оси равно нулю (см. Обсуждение произведения инерции). будет использоваться для расчета момента инерции сложной формы, выберите ось симметрии, чтобы упростить расчет.Эта ось может быть позже переведена на другую ось, если это необходимо, используя правила, изложенные в разделе «Теорема о параллельной оси».

Полярность момента инерции

Значения центра тяжести могут быть как положительными, так и отрицательными, и фактически их полярность зависит от выбора местоположения опорной оси. Значения момента инерции могут быть только положительными, так же как масса может быть только положительной.

Единицы момента инерции

В Соединенных Штатах слово «фунт» часто неправильно используется для обозначения как массы, так и веса.Если единицей веса является фунт, то единицей массы также не может быть фунт, поскольку это нарушит второй закон Ньютона. Однако по причинам, которые были потеряны в древности, в США объект весом 1 фунт часто упоминается как имеющий массу 1 фунт. Это приводит к единицам момента инерции, таким как фунт-дюйм ², где «фунт» относится к весу объекта, а не к его массе. Правильные единицы момента инерции (или произведение инерции): МАССА x РАССТОЯНИЕ ² Когда фунт-дюйм ² или фунт-фут ² используются для определения MOI или POI, величина ДОЛЖНА быть разделена на соответствующее значение. Значение «g» должно быть размерно правильным в инженерных расчетах.Опять же, анализ размеров подтвердит, используются ли правильные единицы измерения. В следующей таблице показаны некоторые из используемых в настоящее время единиц для момента инерции и произведения инерции:

УСТРОЙСТВО КОММЕНТАРИИ
фунт-дюйм ² фунт = вес; необходимо разделить на g = 386,088 дюйм / сек ²
фунт-дюйм-сек ² фунт-дюйм-сек ² = расстояние ² x вес / г; вес / г = масса; правильные размеры
slug-ft ² slug = масса; правильные размеры
кг-м ² кг = масса; правильные размеры

Наиболее распространенные единицы измерения, используемые в U. S. – фунт-дюйм ², даже если размер неверен.

ПРАВИЛО 1 . Если момент инерции или произведение инерции выражены в следующих единицах, то их значения могут использоваться в инженерных расчетах как есть:
Снаряд-фут ², фунт-дюйм-сек ², кг-м ², фунт-фут-сек ², унция-дюйм ²

ПРАВИЛО 2 . Если момент инерции или произведение инерции выражены в следующих единицах, то их значения должны быть разделены на соответствующее значение «g», чтобы сделать их размерно правильными.

фунт-фут ², фунт-дюйм ², унция-дюйм ²

Значение g: 32,17405 фут / сек ² или 386,088 дюйм / сек ²
Не использовать местное значение г, чтобы преобразовать в массу!

Что такое формула момента инерции?

MOI, иногда называемый вторым моментом, для точечной массы вокруг любой оси: I = Mr ²
, где I = MOI (снаряд-фут ² или другая масса-длина ² единиц)
M = масса элемента (пули или другая единица массы)
r = расстояние от точечной массы до исходной оси

Определение радиуса вращения

Момент инерции любого объекта относительно оси через его ЦТ можно выразить следующим образом: формула: I = Mk ², где I = момент инерции
M = масса (снаряд) или другая правильная единица массы
k = длина (радиус вращения) (фут) или любая другая единица длины

Расстояние (k) называется радиусом вращения. Метод расчета радиуса инерции описан в следующих разделах. Рассмотрим сначала тело, состоящее из двух точечных масс каждая с массой M / 2, разделенных расстоянием 2r. Ось отсчета проходит через точку, равноудаленную от двух масс. У каждой массы есть MOI Mr ²/2. Таким образом, их объединенный MOI – Mr ². Во втором примере показана тонкостенная трубка радиуса r. По симметрии ЦТ лежит на средней линии трубы. Опять же, вся масса расположена на расстоянии r от оси отсчета, поэтому ее MOI = Mr ².В этих примерах радиус вращения k = r. Это приводит к определению: «Радиус вращения объекта относительно оси, проходящей через ЦТ, – это расстояние от оси, на котором вся масса объекта может быть сосредоточена без изменения его момента инерции. Радиус вращения всегда отсчитывается от центра тяжести ».

Теорема о параллельной оси для вычисления момента инерции

Если в приведенном выше примере мы хотели определить MOI объекта относительно оси X _a, а не оси X, через CG, то значение можно определить с помощью Теорема о параллельной оси:

Ia = I + d ² M, Поскольку I = k ² M, тогда Ia = M (d ² + k ²)
, где k – радиус вращения.

Эта теорема о параллельных осях очень часто используется при вычислении MOI ракеты или другого аэрокосмического объекта. MOI каждого компонента в ракете сначала измеряется или вычисляется вокруг оси через ее CG, а затем используется теорема о параллельных осях для определения MOI всего транспортного средства с этими компонентами, установленными в их надлежащем месте. Смещение «d» – это расстояние от центра тяжести компонента до центральной линии ракеты.

Полезные приближения

Поскольку момент инерции объекта, смещенного относительно его базовой оси, пропорционален (d ² + k ²), мы можем сделать два наблюдения, которые упростят вычисление MOI:

ПРАВИЛО 1.Если радиус вращения объекта составляет менее 1% от расстояния смещения «d», то MOI объекта вокруг его центра тяжести может быть проигнорирован при вычислении общего MOI, и значение станет d ² M. Например если гироскоп с массой 0,1 снаряда расположен около внешней поверхности ракеты и смещение к центру тяжести гироскопа составляет 3 фута, в то время как радиус вращения гироскопа составляет всего 0,02 фута, то MOI относительно центра Линия движения ракеты за счет гироскопа составляет d ² M = 0,9 снаряда-фут ².Погрешность при использовании этого приближения составляет менее 0,01%.

ПРАВИЛО 2. Если радиус вращения объекта более чем в 100 раз превышает расстояние смещения «d», то смещение объекта можно игнорировать при вычислении общего MOI, и значение становится равным k ² M. Для Например, если ракетный двигатель массой 100 фунтов расположен рядом с центральной линией ракеты, а смещение к ЦТ ракетного двигателя составляет 0,100 дюйма, а радиус вращения ракетного двигателя составляет 12 дюймов, то MOI около центральной линии ракеты из-за ракетного двигателя k ² M = 14400 фунт-дюйм ² (точнее 37. 3 фунта в секунду ²). Опять же, ошибка аппроксимации составляет менее 0,01%. Правило 2 также может применяться к ошибкам выравнивания при вычислении или измерении MOI. Если смещение или несовпадение составляет менее 1% радиуса инерции, то ошибка центровки незначительна.

Эта страница представляет собой отрывок из статьи Ричарда Бойнтона и Курта Вайнера из Space Electronics в 2001 году, которая четыре раза цитировалась в других статьях .

Щелкните здесь, чтобы получить доступ к полному тексту статьи Как рассчитать массовые характеристики – Практическое руководство инженера НЕ ТРЕБУЕТСЯ ВХОД

Дополнительную информацию можно увидеть в полном PDF:

Объединение момента инерции двух объектов
Основная формула с использованием дифференциальных элементов массы
Объединение осевых значений MOI
Объединение поперечных значений MOI
Пример составного MOI
Влияние несоосности
Расчет произведения инерции 9019 Преобразование прямоугольной формы в полярную
Разница между смещением ЦТ и продуктом инерции
Теорема о параллельной оси точки интереса
Сравнение между точкой обзора и точкой интереса И еще 13 страниц после этого

домашнее задание и упражнения – Может момент по инерции быть отрицательным?

домашнее задание и упражнения – Может ли момент инерции быть отрицательным? – Обмен физическими стеками

Сеть обмена стеков

Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.

Посетить Stack Exchange

0
+0
Авторизоваться Зарегистрироваться

Physics Stack Exchange – это сайт вопросов и ответов для активных исследователей, ученых и студентов-физиков.Регистрация займет всего минуту.

Зарегистрируйтесь, чтобы присоединиться к этому сообществу

Кто угодно может задать вопрос

Кто угодно может ответить

Лучшие ответы голосуются и поднимаются наверх

Спросил 6 лет, 5 мес. Назад

Просмотрено 6к раз

$ \ begingroup $ Закрыто. Этот вопрос не по теме. В настоящее время он не принимает ответы.

Хотите улучшить этот вопрос? Обновите вопрос, чтобы он соответствовал теме Physics Stack Exchange.

Закрыт 6 лет назад.

Q: Определите момент инерции однородного круглого диска с радиусом $ r $ и массой $ M $, и ось проходит через точку на окружности.2} {3}. $$ Тяжелая работа! Но все напрасно !! Момент инерции отрицательный ??? Где я ошибся ?? Пожалуйста помоги.

$ \ endgroup $ 5 $ \ begingroup $
с вашим определением $ dA $ вы должны интегрировать между r и 0, потому что вы начинаете в центре, а радиус кольца увеличивается по мере того, как вы идете для (r-x) от x = r до x = 0

Создан 29 ноя.
Вольфрам Джонни
15.1k55 золотых знаков2929 серебряных знаков6464 бронзовых знака
$ \ endgroup $ 4 $ \ begingroup $
Существует общая и простая формула для вычисления момента инерции относительно некоторой оси, если известен момент инерции относительно другой оси. Я почти уверен, что вы сможете найти это в своем учебнике. Теорема является теоремой о параллельных осях.
Вольфрам Джонни
15.1k55 золотых знаков2929 серебряных знаков6464 бронзовых знака
Создан 29 ноя.
Ахметелиахметели
20.9k22 золотых знака2121 серебряный знак4848 бронзовых знаков
$ \ endgroup $ 3 Physics Stack Exchange лучше всего работает с включенным JavaScript
Ваша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой использования файлов cookie.
Принимать все файлы cookie Настроить параметры
Каков физический смысл недиагонального элемента в матрице момента инерции
Основное уравнение, которое содержит $ I $:
$ \ vec {L} = I \ vec {\ omega}
долларов США
где $ \ vec {L} $ – вектор углового момента, а $ \ vec {\ omega} $ – вектор угловой скорости.Тот факт, что $ I $ – тензор (а не только скаляр), означает, что $ \ vec {L} $ и $ \ vec {\ omega} $ не обязательно указывают в одном направлении.
Если вам нужно конкретное матричное представление тензора момента инерции, вы, , можете получить недиагональные элементы. Однако, поскольку по самому своему определению любое матричное представление $ I $ является симметричной матрицей. Любую действительную симметричную матрицу всегда можно диагонализовать ортогональными матрицами. Физически это означает, что по крайней мере для одного выбора осей $ x $, $ y $, $ z $ представление $ I $ будет идеально диагональным, со всеми недиагональными элементами, равными нулю.
Однако …
Это вовсе не означает, что недиагональные элементы не важны. И я не уйду от вопроса об их значении.
Существует также уравнение, описывающее динамику всего бизнеса:
$ \ frac {d \ vec {L}} {dt} = \ vec {\ tau}
долларов США
Это аналогично $ \ frac {d \ vec {p}} {dt} = \ vec {F} $, которое описывает линейное движение; здесь, конечно, $ \ tau $ – крутящий момент, а $ \ vec {L} $ – угловой момент.
Подставив $ \ vec {L} = I \ vec {\ omega} $ и допуская неизменный во времени тензор момента инерции, получаем:
$ I \ frac {d \ vec {\ omega}} {dt} = \ vec {\ tau}
долларов США
Теперь прилагаемый крутящий момент не обязательно должен совпадать с вектором, который диагонализирует ваш $ I $ (такие векторы называются главными осями). Например, сесть за руль своей машины. Он приводится в движение стержнем, проходящим через его ось. Допустим, это ось $ z $. Итак, в этом случае $ \ tau_z $ не равно нулю, а $ \ tau_x $ и $ \ tau_y $ равны нулю.
Приведенное выше уравнение на самом деле представляет собой три уравнения, позвольте мне показать третье явно:
$ I_ {zx} \ frac {d \ omega_x} {dt} + I_ {zy} \ frac {d \ omega_y} {dt} + I_ {zz} \ frac {d \ omega_z} {dt} = \ tau_z $
Теперь, если недиагональные элементы $ I_ {zx} $ и $ I_ {zy} $ равны нулю (при нулевых начальных условиях), ваше колесо просто приобретет $ \ omega_z $, то есть оно начнет хорошо вращаться вокруг ось, на которую вы прикладываете крутящий момент.
Однако, если они не равны нулю … $ \ omega_x $ и $ \ omega_y $ будут , а не , останутся нулевыми. То есть колесо будет стремиться вращаться и вокруг других осей! Таким образом, вы не получите вращения вокруг оси $ z $, и колесо будет качаться! Это условие, при котором вы отвозите свою машину в магазин и балансируете колеса!
Итак, недиагональные элементы на самом деле означают, что любая попытка повернуть тело путем приложения крутящего момента вокруг данной оси не приведет к вращению только вокруг этой оси, а также будет вращение вокруг других осей.
Обратите внимание, что если, например, у нас $ I_ {xy} \ neq 0 $ и $ I_ {xz} = I_ {yz} = 0 $, крутящий момент вокруг оси $ z $ приведет к сбалансированному вращению, а крутящий момент вокруг осей $ x $ или $ y $ не будет …
3.4.4: Продукт инерции – Engineering LibreTexts
Последнее обновление
Сохранить как PDF
Теорема о переносе оси
Участники и атрибуты
Помимо момента инерции, обычно используется произведение инерции.Здесь определяется и обсуждается только продукт области. Произведение инерции, определяемое как \ [I_ {x_ {i} x_ {j}} = \ int_ {A} x_ {i} x_ {j} dA \]. Например, произведение инерции для \ (x \) и \ (y \) оси это \ [I_ {xy} = \ int_ {A} xy dA \] Произведение инерции может иметь положительное или отрицательное значение в отличие от момента инерции. Вычисление произведения инерции не сильно отличается от вычисления момента инерции. Единицы произведения инерции такие же, как и для момента инерции.
Теорема о переносе оси
То же, что и для момента инерции, существует аналогичная теорема. \ [I_ {x’y ‘} = \ int_ {A} x’y’dA = \ int_ {A} \ left (x + \ Delta x \ right) \ left (y + \ Delta y \ right) dA \ ] расширение уравнения 49 приводит к \ [I_ {x’y ‘} = \ int_ {A} xydA + \ int_ {A} x \ Delta ydA + \ int_ {A} \ Delta xydA + \ int_ {A} \ Delta x \ Delta ydA \] Окончательная форма: \ [I_ {x’y ‘} = I_ {xy} + \ Delta x \ Delta y dA \] Следует упомянуть несколько соотношений \ [I_ {xy} = I_ {yx } \] Симметричная область имеет нулевой продукт инерции, потому что интегрирование нечетной функции (асимметричной функции) левой части отменяет правую часть.2} {18} \]
Авторы и авторство
Доктор Геник Бар-Мейр. Разрешается копировать, распространять и / или изменять этот документ в соответствии с условиями лицензии GNU Free Documentation License версии 1. 2 или новее или лицензии Potto.
Расчет момента инерции площади
Расчет момента инерции площади
Щелкните эту ссылку, чтобы загрузить версию этого сообщения в блоге в формате pdf…
Расчет момента инерции площади – метод CAD (FEM аналогичен) по сравнению с Классический ручной расчет Метод .
В этом посте мы рассмотрим несколько моментов, одно из наиболее распространенных значений (момент инерции области «I»), используемых в ряде расчетов запаса прочности, вычислении момента инерции основной площади, ориентации главных осей. , и пример случая с чисто несимметричным изгибом.
Перво-наперво, давайте сделаем простой обзор основ:
Моменты инерции всегда положительные
Минимальные моменты инерции оси всегда проходят через центр масс
Моменты инерции – это мера распределения массы тела относительно набора осей. Представьте себе вращающегося фигуриста. Если человек вытягивает руки, он замедляется, а в противном случае ускоряется. Следовательно, чем меньше инерция, тем более сконцентрирована или ближе масса относительно определенной оси.
Моменты инерции площади указаны для конкретного сечения или двухмерной поверхности
Продукты инерции могут быть положительными, отрицательными или нулевыми
Продукты инерции – это мера симметрии тела относительно набора осей. Они равны нулю относительно любой оси, нормальной к плоскости симметрии
Для любой заданной точки на сечении, например центра тяжести или любой другой точки, существует набор осей, ориентированных таким образом, что все произведения инерции равны нулю
Хотите получать мгновенные обновления о последних сообщениях, подобных этой, и о бесплатной электронной книге?
В настоящее время удобно просто использовать программу CAD, например Solid Works, или препроцессор FEM, такой как FEMAP, чтобы получить все данные, необходимые для данного разреза. Но действительно ли вы понимаете, какие данные он вам дает? Мы можем получить свойства сечения данного сечения, просто нажав несколько кнопок.
Однако время от времени рекомендуется возвращаться к классическому методу расчета момента инерции площади и расчета центра тяжести сечения. Но сначала давайте посмотрим на метод Solid Works получения этих свойств раздела.
Метод Solid Works:
На следующем рисунке показан пример поперечного сечения L-Angle, выделенного голубым цветом.Нас интересуют свойства сечения. Начало координат детали находится в нижнем левом углу выбранного сечения. Мы также можем увидеть настраиваемую систему координат «Custom CSYS» для справки.
Рисунок 1: Деталь угла L для Расчет момента инерции площади
Логично предположить, что центроид этой поверхности будет не на самой поверхности, а где-то в верхнем правом углу. На вкладке «Оценить» в Solid Works есть значок для расчета свойств сечения, как показано ниже. 2. Центроид находится в точке X = 5,2 дюйма и Y = 2,2 дюйма, как и ожидалось, относительно начала координат выбранной системы координат в раскрывающемся меню (–default-). Начало системы координат – по умолчанию – для этой детали находится в нижнем левом углу выбранного сечения. На следующем рисунке показано, как Solid Works отображает результаты расчета момента инерции площади на сечении.
Рис. 4: Секция расчета момента инерции площади, SW CG
Следующий ниже на рисунке 3 – это матрица моментов инерции, представленная в центроиде.Сюда входят значения плоского изгиба и кручения по диагонали матрицы, а также произведения инерции в выбранной системе координат. Мы можем видеть, что продукты инерции, связанные с осью z, равны нулю.
Причина в том, что плоскость xy этого сечения является единственной плоскостью симметрии. Другими словами, на каждой стороне сечения по «z» форма и размер материала одинаковы. Следовательно, все произведения инерции относительно z равны нулю. Все значения в матрице представлены в выбранной системе координат (- по умолчанию – или в системе координат детали на рисунке 3).Но вы можете выбрать любую другую систему координат, например «Custom CSYS». Далее на Рисунке 3 выше мы можем увидеть полярный момент инерции Lzz относительно «z».
Далее мы можем увидеть, как основные моменты области осей инерции отображаются с помощью розовой системы координат в центре тяжести. Угол между выбранной CSYS и этой основной CSYS составляет -17,3 · 108 градусов (по часовой стрелке отрицателен), как показано на рисунке 3 выше. Это система координат, относительно которой все произведения инерции Ixy, Iyz и Ixz равны нулю.Главные моменты инерции всегда сообщаются в центре тяжести относительно главных осей.
Существует другой набор матриц инерции для каждой CSYS, проходящей через заданную точку. Будет один набор осей, относительно которых все продукты инерции равны нулю в любой заданной точке сечения. Но в целом главные оси различны для каждой точки на участке.
Наконец, в нижней части рисунка 3 выше, поскольку начало выбранной системы координат (по умолчанию) не совпадает с центром тяжести сечения, отображается другая «матрица моментов инерции», которая учитывает теорему о параллельных осях w.r.t выбранная система координат вывода (по умолчанию).
Расчет момента инерции площади – Пользовательский CSYS1:
Давайте переместим пользовательский CSYS1 в CG раздела, мы также выровняем этот CSYS1, повернув его вокруг оси «Z» на -17,3108 градусов. Это выравнивает его с основными моментами осей инерции в точке CG. См. Рисунок ниже:
Рис. 5: Расчет момента инерции площади с помощью пользовательского CSYS1 в CG, выровненного с основными осями MI
Используя новый CSYS1, мы снова будем использовать Solid Works для расчета моментов инерции площади секции.
Рис. 6: Расчет момента инерции площади. Пользовательская CSYS выровнена по центру тяжести, моменты инерции
Итак, ясно, что все произведения инерции теперь равны нулю относительно главных осей. Центроид в пользовательском CSYS1 находится в точке (0,0,0), которая является его собственным источником.
Примечательно, что при проверках сечений нагрузки и моменты сечения оцениваются и извлекаются из конечно-элементной модели в ЦТ. Затем они используются в расчетах комбинированного запаса прочности по напряжению (MS) с использованием этих свойств сечения.
Онлайн-курс по конечно-элементному анализу
Классический ручной расчет несимметричного изгиба под углом L:
Хорошо, пока мы узнали, как измерить свойства данного сечения в программе САПР, такой как Solid Works (другие будут аналогичными, включая программы FEM). Теперь давайте рассмотрим другой метод на примере задачи. Та же самая угловая секция, о которой говорилось выше, используется в приведенном ниже примере (для получения более подробной информации щелкните ссылку ниже). В статье вычисляются моменты инерции и напряжения с использованием Классических ручных расчетов для случая несимметричного чистого изгиба.
http://www.engr.colostate.edu/~thompson/hPage/CourseMat/Tutorials/Solid_Mechanics/nonSym.pdf
В статье рассчитаны следующие позиции:
1) Центроид сечения
2) Моменты инерции площади сечения в системе координат плоскости X-Y в центре тяжести (это то, что вы видите в первой матрице на рисунке 3 выше)
3) Моменты инерции главных площадей с использованием метода круга Мора (который вы видите на Рисунке 3 выше)
4) Затем угол, который образуют главные оси относительно системы координат плоскости X-Y по умолчанию (-17.3 градуса на рисунке 3 выше)
5) А затем, как мы определяем угол нейтральной оси относительно основных осей, задав осевые напряжения из-за чистой единичной нагрузки изгибающего момента в ЦТ, равной нулю
6) Наконец, бумага оборачивает его, вычисляя осевые напряжения на крайних точках волокна от нейтральной оси
Хотите получать мгновенные обновления о последних сообщениях, подобных этой, и о бесплатной электронной книге?
Если вам понравился этот пост, почему бы не поделиться им?
Метаматериал сверхширокой запрещенной зоны нулевой частоты с отрицательным моментом инерции и жесткостью
Метаматериалы продемонстрировали большой потенциал для управления распространением волн, поскольку они гибко регулируются. Предлагается новая одномерная модель метаматериала с отрицательным эффективным моментом инерции и отрицательной эффективной жесткостью. Отрицательный эффективный момент инерции и отрицательная эффективная жесткость могут быть достигнуты путем регулировки параметров конструкции в определенных частотных диапазонах. В метаматериале могут образовываться запрещенные зоны в низкочастотном диапазоне с экспоненциальным затуханием волны. Получается плоская полоса, которая соединяет две запрещенные зоны Брэгга для достижения широкой запрещенной зоны в низкочастотном диапазоне, где эффективный момент инерции и эффективная жесткость бесконечны.Нулевую ширину запрещенной зоны можно получить, регулируя структурные параметры. Быстрое затухание волны наблюдается в диапазонах нулевых частот с однократно отрицательными параметрами. Кроме того, сверхширокая запрещенная зона с нулевой частотой достигается за счет оптимизации структурных параметров системы. Кроме того, легко переключаться между брэгговской и локально резонансной запрещенной зоной. Этот новый метаматериал может применяться для изоляции сверхнизкочастотных вибраций.
Метаматериалы с превосходными свойствами – это искусственные структуры, состоящие из периодических материалов или периодических структур [1–3].В метаматериалах могут возникать запрещенные зоны акустических волн или упругих волн. В последние десятилетия было обнаружено, что метаматериалы могут проявлять такие свойства, как отрицательная масса [4–7], отрицательный объемный модуль [8, 9], явления отрицательного преломления [10, 11], топологические эффекты [12, 13] и маскировка невидимости. [14, 15]. Эти характеристики могут быть использованы для разработки и производства новых акустических функциональных устройств и для управления распространением акустических или упругих волн.
Отрицательные эффективные свойства материалов широко исследовались при проектировании метаматериалов.В 2000 году Лю и др. ввели отрицательную эффективную массовую плотность в фононных кристаллах с локальным резонансом путем внедрения тяжелых шариков, покрытых мягким силиконовым каучуком, в эпоксидной смоле [16]. С тех пор было предложено большое количество моделей метаматериалов для достижения отрицательных эффективных параметров путем создания элементарных ячеек [8, 17, 18].
Системы масса-пружина также могут иметь отрицательные эффективные параметры из-за брэгговского рассеяния и механизмов локального резонанса в различных частотных диапазонах.В 2007 году Милтон и Уиллис ввели отрицательную эффективную массу в модель акустического метаматериала с массой в массе. Они подтвердили существование одно-отрицательных или двойных отрицательных свойств [19]. Лю и др. исследовали упругую модель с двойными отрицательными параметрами, построенную с помощью блока хиральной массы-пружины [20]. Ван представляет новую репрезентативную ячейку метаматериалов в попытке предоставить комплексную модель для создания отрицательной массы или отрицательного модуля [21]. В 2018 году Oh и др. предложили спиновой метаматериал и получили ширину запрещенной зоны Брэгга от нулевой частоты [22]. В 2019 году Ван и др. разработали стержень из метаматериала с резонаторами, содержащими механизмы отрицательной жесткости для создания низкочастотной запрещенной зоны [23]. Затем Чжан и др. исследовали темное состояние, нулевой индекс и топологию акустических метаматериалов с отрицательной массой и отрицательной связью [24]. Недавно Бормашенко и др. исследовали метаматериалы с отрицательной эффективной массой, основанные на электромеханической связи, использующей плазменные колебания свободного электронного газа [25].Ли и др. предложили одномерную цепочку из метаматериалов с гетерогенным резонатором для создания объединенных широких запрещенных зон путем настройки параметров [26]. Однако сообщалось о ряде исследований с отрицательной массой или отрицательным модулем упругости. Ограниченные структурой, большинство этих систем являются одноотрицательными системами. Кроме того, мало исследований рассматривали связь поступательного движения и вращательного движения.
С другой стороны, метаматериалы с низкочастотной запрещенной зоной представляют собой интересную область.В 2018 году Чанг и др. разработали одномерную систему масс-пружина с подконструкцией. Они также обнаружили, что связанная брэгговская резонансная запрещенная зона намного шире, чем локальная резонансная одиночная запрещенная зона [27]. Крушинская и др. предложили «аккордеоноподобные» мета-структуры для получения чрезвычайно широкой запрещенной зоны и равномерного затухания волн на низких частотах [28]. В 2019 году Чжоу и др. исследовали резонатор с высокой статической и низкой динамической жесткостью с механизмом инерционного усиления, который способен создавать гораздо меньшую ширину запрещенной зоны, чем чистый резонатор с высокой статической и низкой динамической жесткостью [ 29].В 2020 году Гао и Ван предложили два разных метаматериала с гибридными элементарными ячейками для достижения большей связанной запрещенной зоны [30]. Насколько нам известно, мало работ было посвящено структурам со сверхширокой запрещенной зоной с нулевой частотой, поскольку их сложно спроектировать.
В настоящем исследовании наша основная цель состоит в том, чтобы получить более широкую и более низкую запрещенную зону путем создания периодического метаматериала с отрицательным моментом инерции и жесткости. С этой целью данная статья организована следующим образом.В разделе 2 исследуется кирально связанный одномерный метаматериал с поступательным и вращательным движением. Предлагается концепция отрицательного эффективного момента инерции. В разделе 3 анализируются дисперсионное соотношение, эффективные параметры и коэффициент пропускания одномерной периодической системы. В разделе 4 исследуется распространение волн оптимизированных периодических систем. Наконец, некоторые выводы сделаны в разделе 5.
2.1. Модель и методы
Рассмотрена одномерная периодическая структура на рисунке 1.Система образована периодической структурой с представительной ячейкой, состоящей из одного центрального жесткого диска, одного жесткого рычага и линейных упругих пружин, прикрепленных к дискам, как показано на рисунке 1 (а). Круглые диски, масса и момент инерции которых равны м, и J, , _{, 1,} соответственно, могут свободно вращаться. Момент инерции рычагов Дж ₂. Середина рычага шарнирно закреплена в точке O , а O ₁ соединена с O ₂ диска пружиной k ₂.Расстояние от O до O ₁, R равно расстоянию от O ₂ до центра диска. Дополнительно центр диска соединен с фиксированной точкой O пружиной k ₁. Постоянная решетки системы л . В этой периодической системе и жесткий диск, и рычаг поддерживаются жестким стержнем. Этот жесткий стержень фиксируется при распространении продольной волны по периодической системе.
Увеличить Уменьшить Сбросить размер изображения
Рис. 1. Одномерная система метаматериалов: (а) элементарная ячейка, (б) периодические ячейки.
Загрузить рисунок:
Стандартное изображение Изображение высокого разрешения
Предполагается, что углы поворота как рычага, так и диска малы. Кроме того, игнорируются эффекты демпфирования и гравитации. В текущей модели диск ограничен вращательным движением и поперечным движением.Соседние диски соединяются шарнирно жестким рычагом.
Динамические уравнения элементарной ячейки n можно записать следующим образом:
, где u _n обозначает смещение диска в элементарной ячейке n , θ _n – угловое смещение диска, а α _n – угловое смещение рычага.Основываясь на теории Флоке – Блоха, гармоническое волновое решение одномерной решетчатой системы может быть выражено как
, где и – амплитуды u _n, θ _n и α _n соответственно. В уравнении (2) q и ω – волновое число и круговая частота соответственно. Подставив уравнение (2) в уравнение (1), динамическое уравнение можно переписать как
Если уравнение (3) имеет нетривиальное решение, дисперсионное соотношение этой одномерной системы может быть получено как
Из уравнений (1a) ) и (1b), можно получить
Подставляя уравнение (5) в (1c), получаем
, где
J _eff и k _eff – это эффективный момент инерции и эффективная жесткость системы соответственно.В уравнении (7) ω ₁, ω ₂, ω ₃ и ω ₄ могут быть заданы как
Уравнение (7) ясно показывает, что эффективный момент инерции является функцией ω ₃ и ω ₄, которые управляются вращательным движением дисков и рычагов. Эффективная жесткость является функцией ω ₁, ω ₂ и ω ₃, которые управляются поступательным движением и вращательным движением дисков. Уравнение (6) может быть далее сокращено до
Дисперсионные кривые могут быть получены с помощью уравнения (9).
Метод матрицы переноса используется для анализа свойств пропускания метаматериала. В одномерной периодической системе N элементарных ячеек. Таким образом, рекурсивное соотношение может быть получено как
Угловое смещение n -й эффективной элементарной ячейки составляет α _n. Коэффициент пропускания системы определяется как.Уравнение (10) дает
2.2. Отрицательный эффективный момент инерции и отрицательная жесткость
Динамическое поведение системы контролируется тремя параметрами: λ ₁, λ ₂ и λ ₃, определяемое как
Уравнение (7a ) можно переписать как
, где функции f ₁ и f ₂ задаются как
Уравнение (7b) можно переписать как
, где функции g ₁, g ₂ и g ₃ задаются
Диапазоны отрицательного момента инерции и жесткости контролируются пятью положительными корнями f ₁ = 0, f ₂ = 0 , г ₁ = 0, г ₂ = 0 и г ₃ = 0. Эти корни приняты равными ξ ₁, ξ ₂, η ₁, η ₂ и η ₃ соответственно. Эти диапазоны частот показаны на рисунке 2 для шести различных случаев, different, ②, ③, ④, ⑤ и ⑥, как указано в приложении A. Красные области, синие области и серые области соответствуют частотным диапазонам с отрицательным знаком. момент инерции, отрицательная жесткость и дважды отрицательный соответственно.
Увеличить Уменьшить Сбросить размер изображения
Рис. 2. Отрицательный момент инерции и отрицательные диапазоны жесткости для шести случаев.
Загрузить рисунок:
Стандартное изображение Изображение высокого разрешения
На рисунках 3–5 показано влияние λ ₁, λ ₂ и λ ₃ на безразмерную частоту соответственно. Можно заметить, что для данного ω одно-отрицательное или двойное отрицательное поведение может быть достигнуто путем настройки λ ₁, λ ₂ и λ ₃. Однозначно отрицательный из эффективных параметров соответствует локально резонансной запрещенной зоне. Двойное отрицательное значение эффективных параметров соответствует ширине запрещенной зоны Брэгга или полосе пропускания с отрицательной крутизной.
Увеличить Уменьшить Сбросить размер изображения
Рисунок 3. Частотные диапазоны отрицательных эффективных параметров для (а) λ ₂ = 0,6, λ ₃ = 1, (б) λ ₂ = 1.5, λ ₃ = 1.
Загрузить рисунок:
Стандартное изображение Изображение высокого разрешения
Увеличить Уменьшить Сбросить размер изображения
Рисунок 4. Частотные диапазоны для отрицательных эффективных параметров для (a) λ ₁ = 0,5, λ ₃ = 1. (b) λ ₁ = 1,5, λ ₃ = 1.
Загрузить рисунок:
Стандартное изображение Изображение высокого разрешения
Увеличить Уменьшить Сбросить размер изображения
Рисунок 5. Частотные диапазоны для отрицательных эффективных параметров для (а) λ ₁ = 1, λ ₂ = 0,2, (б) λ ₁ = 1, λ ₂ = 0,8, (в) λ ₁ = 1, λ ₂ = 1,5.
Загрузить рисунок:
Стандартное изображение Изображение высокого разрешения
На рисунке 3 показаны частотные диапазоны отрицательного момента инерции и отрицательной жесткости для различных λ, ₁ с λ, ₂ и λ, ₃.На рисунке 3 розовые области и синие области представляют собой частотные диапазоны с отрицательным моментом инерции и отрицательной жесткостью соответственно. Серийные номера ①, ②, ③, ④, ⑤ и ⑥ соответствуют шести случаям на рисунке 2. На рисунке 3 показано изменение границы для частотных диапазонов отрицательного момента инерции и отрицательной жесткости при λ ₁ для λ ₂ = 0,6, λ ₃ = 1 и λ ₂ = 1. 5, λ ₃ = 1. На рисунке 3 (a) показаны случаи ①, ②, ③ и ④, а на рисунке 3 (b) показаны случаи ⑤ и ⑥.
Когда λ ₁ = 0,5, λ ₃ = 1 и λ ₁ = 1,5, λ ₃ = 1, влияние λ ₂ на Распределение частотных диапазонов с отрицательными параметрами показано на рисунке 4. На рисунке 4 показано, что отрицательная жесткость включает две синие области, когда 0 < λ ₂ <1.Напротив, отрицательная жесткость включает только одну область, когда λ ₂> 1. На рисунке 4 (a) показаны случаи ①, ②, ③, ⑤ и ⑥, а на рисунке 4 (b) показаны случаи ①, ②, ③. , ④ и ⑥.
Влияние структурного параметра λ ₃ показано на рисунке 5. Рисунок 5 (a) соответствует случаю. На рисунке 5 (а) можно увидеть, что момент инерции, связанный с розовыми областями, всегда порождает двойную отрицательность, когда λ ₁ = 1 и λ ₂ = 0. 2. На рисунке 5 (b) показано влияние λ ₃ на частотные диапазоны отрицательности, когда λ ₁ = 1 и λ ₂ = 0,8 и соответствует случаям ②, ③ и ④ . На рисунке 5 (c) показано влияние λ ₃ на частотные диапазоны отрицательности, когда λ ₁ = 1 и λ ₂ = 1,5 и соответствует случаям ⑤ и ⑥.
В этом разделе исследуются дисперсионные характеристики волн в предлагаемом метаматериале.На рисунке 6 показано влияние значений λ, , _{, 1,}, , , _{, 2,} и , , _{, 3,}, на поведение ширины запрещенной зоны в системе. Цветные области представляют диапазон запрещенных зон, а пустые области представляют диапазон полос пропускания. Согласно фиг. 6 (a), средняя полоса пропускания представляет собой плоскую полосу в точке A, , а верхняя полоса пропускания представляет собой плоскую полосу в точке B .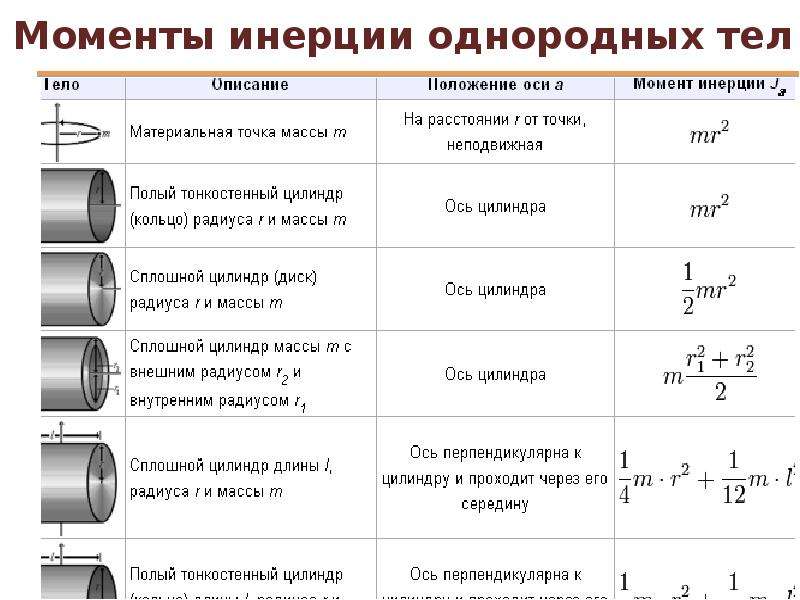 Верхняя запрещенная зона исчезает в точке C . Точка A соединяет нижнюю и верхнюю запрещенные зоны, так что две запрещенные зоны сливаются в одну более широкую запрещенную зону.Аналогичное явление можно наблюдать на рисунке 6 (b). Нижняя запрещенная зона и верхняя запрещенная зона объединяются в одну запрещенную зону в точке D , а верхняя запрещенная зона исчезает в точке F . Верхняя полоса пропускания представляет собой плоскую полосу в точке E . Согласно фиг.6 (c), верхняя граница нижней запрещенной зоны увеличивается намного более постепенно, чем нижняя граница, и ширина запрещенной зоны заметно увеличивается с увеличением λ ₃. Ширина верхней запрещенной зоны сначала уменьшается, но затем увеличивается с увеличением λ ₃.Верхняя запрещенная зона исчезает в точке G .
Увеличить Уменьшить Сбросить размер изображения
Рис. 6. Влияние изменения структурных параметров на поведение запрещенной зоны системы. (а) Влияние изменения λ ₁ на мнимую часть волнового числа при λ ₂ = 0,4 и λ ₃ = 1, (б) влияние λ ₂ изменение мнимой части волнового числа при λ ₁ = 0.5 и λ ₃ = 1, и (c) влияние изменения λ ₃ на мнимую часть волнового числа, когда λ ₁ = 0,5 и λ ₂ = 0,4 .
Загрузить рисунок:
Стандартное изображение Изображение высокого разрешения
На рисунке 7 показаны дисперсия, эффективный момент инерции, обратная эффективная жесткость и коэффициент пропускания метаматериала, когда λ ₁ = 0,5, λ ₂ = 0.4 и λ ₃ = 1. Пять безразмерных частот ξ ₁, ξ ₂, η ₁, η ₂ и η η η полосы соответствуют случаям J _eff = ∞ , J _eff = 0,, и, соответственно. Эти частоты получены в приложении A. Для отображения процесса затухания волны коэффициент пропускания системы с 10 элементарными ячейками показан на рисунке 7 (d).Распространение волн в периодической системе ослабляется в запрещенной зоне, но волны могут распространяться, когда они находятся вне запрещенной зоны. На рисунках 9 (a) и (d) синие области, серые области и темно-желтые области соответствуют ширине запрещенной зоны, вызванной одиночно-отрицательными свойствами, двойными положительными свойствами и двойными отрицательными свойствами, соответственно. Белые области и светло-желтые области соответствуют полосам пропускания, вызванным двойными положительными свойствами и двойными отрицательными свойствами, соответственно.На рисунках 9 (b) и (c) белые области соответствуют положительному моменту инерции или жесткости, а синие области соответствуют отрицательному моменту инерции или жесткости. Дисперсионная кривая получается путем решения уравнений (4) или (9), и результаты те же. Как показано на рисунке 7 (a), в простейшей зоне Бриллюэна есть три полосы пропускания, поскольку каждая элементарная ячейка имеет три степени свободы. Наклоны средней и нижней полос положительные. Следовательно, направления групповой скорости и фазовой скорости совпадают, что означает, что метаматериал имеет как положительный момент инерции, так и положительную жесткость в этом диапазоне частот.Напротив, наклон верхней полосы отрицательный, что означает, что в этом диапазоне частот материал имеет как отрицательный момент инерции, так и отрицательную жесткость. Направление групповой скорости отрицательное, а фазовая скорость положительное. Обратите внимание, что нижняя запрещенная зона состоит из двух частей. Одна часть находится рядом с нижней полосой (серые области), которая имеет двойные положительные свойства и является запрещенной зоной Брэгга. Другая часть находится близко к средней полосе и вызвана локальным резонансом (синие области), соответствующим одноотрицательным свойствам.Верхняя запрещенная зона вызвана брэгговским рассеянием и имеет двойную отрицательную величину. Следовательно, материал будет проявлять разные свойства в разных частотных диапазонах.
Увеличить Уменьшить Сбросить размер изображения
Рис. 7. Дисперсионные характеристики модели с λ ₁ = 0,5, λ ₂ = 0,4 и λ ₃ = 1. (а) Дисперсионное соотношение, (б) эффективный момент инерции, (c) величина, обратная эффективной жесткости, и (d) спектр пропускания системы, состоящей из 10 единиц.
Загрузить рисунок:
Стандартное изображение Изображение высокого разрешения
3.1. Сверхширокая запрещенная зона
На рисунке 8 показаны дисперсионные характеристики модели с λ ₁ = 0,5, λ ₂ = 2/3 и λ ₃ = 1. Когда η ₁ = η ₂ = η ₃, средняя полоса становится плоской. Это означает, что получается более широкая запрещенная зона. Это соответствует точке D на рисунке 6 (b).Из рисунка 8 видно, что две запрещенные зоны могут быть объединены для образования запрещенной зоны путем регулировки λ ₂, и волны быстро затухают. Коэффициент пропускания имеет только один острый резонансный пик при ξ ₁, который очень трудно обнаружить с внешней падающей волны. Как показано на рисунке 8, ширина запрещенной зоны имеет двойные отрицательные (темно-желтые области) и двойные положительные свойства (серые области), когда она выше и ниже этой частоты плоской полосы. Эти две запрещенные зоны объединены плоской полосой в более широкую запрещенную зону Брэгга.Этой плоской полосой частот можно пренебречь. Следовательно, запрещенная зона может использоваться для управления характеристиками пропускания волны в широком диапазоне частот. Точно так же это явление может быть обнаружено, когда λ ₁ = 1,5, λ ₂ = 0,4 и λ ₃ = 1. Это соответствует точке A на рисунке 6 (a).
Увеличить Уменьшить Сбросить размер изображения
Рисунок 8. Дисперсионные характеристики модели с λ ₁ = 0,5, λ ₂ = 2/3 и λ ₃ = 1. (а) Дисперсионное соотношение модели с плоской полосой, (б) эффективный момент инерции, (в) величина, обратная эффективной жесткости, и (г) спектр пропускания системы, состоящей из 10 единиц.
Загрузить рисунок:
Стандартное изображение Изображение высокого разрешения
3.2. Ширина полосы нулевой частоты
На рисунке 9 показано, что нижняя полоса полностью исчезает, когда λ ₁ = 0, а другие параметры такие же, как на рисунке 7.Эта цифра соответствует λ ₁ = 0 на рисунке 6 (a). Три полосы пропускания становятся двумя полосами пропускания при условии k ₁ = 0.
Увеличить Уменьшить Сбросить размер изображения
Рис. 9. Дисперсионные характеристики модели с λ ₁ = 0, λ ₂ = 0,4 и λ ₃ = 1. (a) Дисперсионное соотношение модели с ширина запрещенной зоны при нулевой частоте, (b) эффективный момент инерции, (c) величина, обратная эффективной жесткости, и (d) спектр пропускания системы, состоящей из 10 единиц.
Загрузить рисунок:
Стандартное изображение Изображение высокого разрешения
Согласно уравнениям (15) и (16a), λ ₁ = 0 соответствует эффективной жесткости, равной нулю при ω / ω ₄ = 0. Как видно из рисунков 9 (a) и (c) ширина полосы нулевой частоты получается от 0 до η ₃. Это указывает на то, что данная структура более эффективно сдерживает распространение волн в сверхнизкочастотном диапазоне. В этом частотном диапазоне система представляет положительный эффективный момент инерции и отрицательную эффективную жесткость.Ширина запрещенной зоны нулевой частоты вызвана локальным резонансом. Кроме того, в темно-желтых областях получается еще одна запрещенная зона с отрицательным эффективным моментом инерции и отрицательной эффективной жесткостью. Согласно рисунку 9 (а), наклон нижней полосы положительный, а метаматериал имеет как положительный момент инерции, так и положительную жесткость. Это означает, что скорость волны положительна и волна идет вперед в частотном диапазоне белой области. Наклон верхней полосы отрицательный, и материал имеет отрицательную инерцию и жесткость в частотном диапазоне светло-желтых областей.
Чтобы получить более широкую и меньшую запрещенную зону, необходимо дополнительно оптимизировать структурные параметры. Согласно разделу 3.1 условие изготовления плоских лент: η ₁ = η ₂ = η ₃. Из раздела 3.2 нижняя полоса исчезает, когда λ ₁ = 0. Если оба условия удовлетворяются, может быть достигнута сверхширокая запрещенная зона с нулевой частотой. Как показано на рисунке 10, эта модель превращается в новую систему без k ₁.
Увеличить Уменьшить Сбросить размер изображения
Рис. 10. Одномерная метаматериальная система без k ₁: (а) элементарная ячейка, (б) периодические ячейки.
Загрузить рисунок:
Стандартное изображение Изображение высокого разрешения
На рисунке 11 показано влияние λ ₂ на мнимую часть волнового числа. Как видно из рисунка 11, эти две запрещенные зоны объединяются в более широкую запрещенную зону, когда λ ₂ = 1.Обратите внимание, что значение λ ₃ не влияет на положение запрещенной зоны связи. Отмечены свойства запрещенных зон. Цветные области представляют диапазоны запрещенных зон, а пустые области представляют диапазоны полос пропускания.
Увеличить Уменьшить Сбросить размер изображения
Рис. 11. Влияние изменения λ ₂ на поведение ширины запрещенной зоны в системе.(а) Влияние изменения λ ₂ на мнимую часть волнового числа при λ ₃ = 0,5, (б) влияние изменения λ ₂ на мнимую часть волнового числа когда λ ₃ = 1, и (c) влияние изменения λ ₂ на мнимую часть волнового числа, когда λ ₃ = 1,5.
Загрузить рисунок:
Стандартное изображение Изображение высокого разрешения
На рисунке 12 показаны дисперсионные характеристики модели с λ ₂ = 1 и λ ₃ = 1. Как показано на рисунке 12 (a), все полосы пропускания являются плоскими. Ширина запрещенной зоны с нулевой частотой и верхняя запрещенная зона могут быть объединены для получения сверхширокой запрещенной зоны с нулевой частотой. Согласно рисунку 12 в системе не могут распространяться волны. Другими словами, λ ₂ = 1 делает эффективную жесткость всегда равной нулю. Это означает, что связь между эффективными жесткими рычагами исчезла. Следовательно, эта система может блокировать любую частоту.
Увеличить Уменьшить Сбросить размер изображения
Рисунок 12. Дисперсионные характеристики модели с λ ₂ = 1 и λ ₃ = 1. (а) Дисперсионное соотношение модели со сверхширокой запрещенной зоной с нулевой частотой; (б) спектр пропускания системы в составе 10 единиц.
Загрузить рисунок:
Стандартное изображение Изображение высокого разрешения
На рисунке 13 показаны дисперсионные характеристики модели с λ ₂ → 1 ^– и λ ₃ = 1. Нижняя запрещенная зона – это локально резонансная запрещенная зона с однозначно отрицательными свойствами. Верхняя запрещенная зона имеет двойное отрицательное значение и является запрещенной зоной Брэгга. Напротив, на рисунке 14 показаны дисперсионные характеристики модели с λ ₂ → 1 ⁺ и λ ₃ = 1. Нижняя запрещенная зона является дважды положительной и является запрещенной зоной Брэгга. Верхняя запрещенная зона однозначно отрицательна и представляет собой локально резонансную запрещенную зону. Очевидно, что λ ₂ = 1 является точкой переключения между запрещенной зоной Брэгга и локально резонансной запрещенной зоной.
Увеличить Уменьшить Сбросить размер изображения
Рис. 13. Дисперсионные характеристики модели с λ ₂ → 1 ^– и λ ₃ = 1. (a) Дисперсионное соотношение, (b) эффективный момент инерции, (c) величина, обратная эффективной жесткости, и (d) спектр пропускания системы, состоящей из 10 единиц.
Загрузить рисунок:
Стандартное изображение Изображение высокого разрешения
Увеличить Уменьшить Сбросить размер изображения
Рисунок 14. Дисперсионные характеристики модели с λ ₂ → 1 ⁺ и λ ₃ = 1. (a) Дисперсионное соотношение, (b) эффективный момент инерции, (c) обратная величина эффективная жесткость, (d) спектр пропускания системы, состоящей из 10 единиц.
Загрузить рисунок:
Стандартное изображение Изображение высокого разрешения
В данной статье изучается одномерная модельная система с тремя степенями свободы. Эффективный момент инерции и эффективная жесткость могут иллюстрировать свойства запрещенной зоны, такие как двойное положительное, одиночное отрицательное или двойное отрицательное.В этой статье представлен подробный анализ отрицательного эффективного момента инерции, отрицательной жесткости и перекрывающегося отрицательного момента инерции и отрицательной жесткости. Две запрещенные зоны Брэгга могут быть объединены для получения сверхширокой запрещенной зоны, когда η ₁ = η ₂ = η ₃. Кроме того, полоса пропускания с нулевой частотой может быть достигнута, когда k ₁ = 0. Наклон всех полос пропускания становится нулевым, когда эти два условия выполняются одновременно.Таким образом, получается сверхширокая запрещенная зона с нулевой частотой. Этот результат важен, потому что материал может блокировать все волны с частотами ниже определенного значения. Предполагается, что предложенная модель формирования сверхширокой запрещенной зоны с нулевой частотой станет новым методом создания устройств управления низкочастотными волнами.
Эта работа частично поддержана Национальным научным фондом для выдающихся молодых ученых в рамках гранта № 11925205, частично Национальным фондом естественных наук Китая в рамках грантов №№.11632003 и 513, а также научно-исследовательским проектом Государственной ключевой лаборатории механики и контроля механических конструкций (NUAA).
Данные, подтверждающие выводы этого исследования, доступны по обоснованному запросу авторов.
Частотные диапазоны с отрицательным эффективным моментом инерции обсуждаются в этом приложении. Два положительных корня из f ₁ ⋅ f ₂ = 0, ξ ₁ и ξ ₂ равны
отрицательный момент инерции может быть определен как
Для определения частотных диапазонов для отрицательной эффективной жесткости количество положительных корней из г ₁ ⋅ г ₂ ⋅ г ₃ = 0 содержит два случая.
Случай 1. 0 < λ ₂ <1.
Положительные корни г ₁ ⋅ г ₂ ⋅ г ₃ = 0
Для,, и это означает, что
For, и отношения трех корней могут быть определены как
Диапазон частот для отрицательной жесткости может быть определен как
Корпус 2. λ ₂ ≥ 1.
Положительные корни g ₁ ⋅ g ₂ ⋅ g ₃ = 0 равны
Очевидно,
Частотный диапазон для отрицательной жесткости равен
. пять корней ξ ₁, ξ ₂, η ₁, η ₂ и η ₃.
Футляр ①. .
Соотношения могут быть определены из уравнений (A.2) и (A.5)
Футляр ②. .
Это дает. Таким образом, что приводит к
Согласно уравнениям (A.6) и (A.12), соотношения для пяти корней равны
Футляр ③. .
Когда λ ₁ λ ₃ ≥ 1,. Напротив, когда λ ₁ λ ₃ <1,.Для λ ₁ λ ₃ ≥ 1 и, что означает, что
Следующий результат получается путем обращения к процессу вывода из (A. 12),
На основе уравнений (A.6 ), (A.14) и (A.15) может быть получено следующее соотношение
Для λ ₁ λ ₃ <1 и,
Следовательно, тот же результат, что и уравнения (A .14) и (.15) могут быть получены, и соотношение пяти корней такое же, как и уравнение (.16).
Футляр ④. λ ₁ λ ₃> 1 и.
Ссылаясь на процесс вывода уравнения (A.14), получается следующий результат:
На основе уравнений (A.2), (A.6) и (A.18) пять корней удовлетворяют
Футляр ⑤. λ ₁ λ ₃ <1 и.
За счет ссылки на процесс вывода уравнения (A.14), тот же результат достигается для
Следующее соотношение может быть получено из уравнений (A.9) и (A.20)
Футляр ⑥. .
Ссылаясь на процесс вывода уравнения (A. 14), аналогичные результаты могут быть получены, когда λ ₁ λ ₃ ≤ 1 и
На основании уравнений (A.2) и (A.22) четыре корня удовлетворяют
Для λ ₁ λ ₃> 1 и λ ₂> 1,
Ссылаясь на процесс вывода уравнения (А.14) получается противоположный результат
Следующее соотношение выводится с помощью уравнений (A.2) и (A.25)
Задание пользовательских инерций – MATLAB и Simulink
Определения матрицы инерции
Матрица инерции фиксирует пространственное распределение вещества вокруг локальный кадр, называемый здесь инерционным кадром разрешения. Этот кадр обозначен на рисунке I . Его оси параллельно с локальным опорным кадром, связанным с портом кадра R и соответственно обозначенный R .Однако его происхождение совпадает с местный центр масс.
Матрица инерции состоит из моментов и произведений инерции. В моменты инерции занимают положения диагональной матрицы и измеряют дисперсия или разброс распределения массы вокруг осей инерционная рамка разрешения. Чем больше разброс вокруг оси, тем больший момент инерции, соответствующий этой оси.
Произведения инерции занимают недиагональные положения и измеряют асимметрия распределения массы относительно плоскостей инерции кадр разрешения.Чем больше асимметрия относительно плоскости, тем больше продукты инерции, связанные с любой осью в этой плоскости. Фигура иллюстрирует эти отношения.
Уравнения инерции
Матрица симметрична относительно главной диагональной линии: недиагональные элементы, индексы которых равны друг другу, делят такое же значение. Это ограничение уменьшает количество уникальных продуктов инерция от исходной шестерки (все находящиеся вне диагонали) к три, которые вы должны указать в блоке (с уникальным комбинация индексов):
Произведения инерции, I _ij, определяются с использованием преобладающего, отрицательного, соглашения принят в ряде приложений САПР:
Iyz = −V (yz) ρdv
Izx = −∫V (zx) ρdv
Ixy = −∫V (xy) ρdv
где ρ – массовая плотность, v – объем, а В, – общий объем интеграции. В x , y и z координаты являются декартовыми компонентами вектора расстояния, охватывающего от центра масс к бесконечно малому элементу масс ρ d v . Моменты инерции I _ii определяются аналогично:
Ixx = ∫V (y2 + z2) ρdv
Iyy = ∫V (z2 + x2) ρdv
Izz =
Izz = ∫V (x2 + y2) ρdv
При применении к простым формам, таким как цилиндрические оболочки и прямоугольные балки, эти определения порождают хорошо известные алгебраические уравнения, которые часто публикуются в стандартных технических таблицах.Ты может ссылаться на такие таблицы при указании параметров инерции явно. Полная матрица инерции согласно Simscape Соглашение о многотельности:
Главные оси инерции
Моменты инерции по определению являются положительными числами. Тем не мение, произведение инерции может быть положительным, отрицательным или нулевым. Они равны нулю, если оси инерционной системы разрешения совпадают совпадают с главными осями инерции. Моменты инерции затем называется главными моментами инерции, а матрица инерции имеет вид называется диагональю :
Количество нетривиальных элементов инерционной матрицы, которые вы должны указать, в этом случае сводится к трем – главным моментам инерции. По этой причине главные оси инерции могут быть удобной рамкой, в которой можно указать элементы матрицы инерции. Это инерционная рамка разрешения предполагается в высокосимметричных заданных формах твердого тела блоки.
Однако, как правило, это не относится к экструдированным Твердый или вращающийся Твердые твердые формы, а также не импортированные через Файлы STEP или STL. В экструдированном твердом теле и Вращающиеся твердые формы, рама размещение во многом зависит от того, как вы определяете геометрическую поперечные сечения. В импортированных фигурах это зависит от того, как относительно Местная нулевая координата моделировалась геометрия детали.
Рекомендуется всегда учитывать размещение инерционной рамки разрешения. при явном указании элементов матрицы инерции, особенно при использовании цельного блока.Положение кадра всегда такое центра масс, но его ориентация относительно твердой геометрии, при использовании цельного блока не всегда может совпадать с основным оси инерции.
Упражнение: укажите
Custom Inertia
Рассмотрим прямоугольную балку, показанную на рисунке. Определите его массу, центр масс, моменты инерции и продукты инерции. Укажите рассчитанный параметры явно в Brick Solid блокировка с использованием инерции Custom параметризация.3. Используйте размеры балки:
Ширина x = 3 дюйма
Высота y = 4 дюйма
Длина z = 10 дюймов
Подготовьте модель балки. Добавьте блок Brick Solid в Модель Simscape Multibody. В кирпич Диалоговое окно Solid block, укажите балку геометрия: установите параметр> на [3 4 10] в . Этот массив соответствует размерам балки [ x y z ].
Тип геометрии влияет на размещение локальной ссылки рама ( R ) и, следовательно, инерционность сами расчеты. На панели инструментов визуализации щелкните значок Переключить видимость фреймов. кнопка. Рамка R находится в центре масса и ее оси параллельны размерам балки ( x , y и z ).
Укажите параметры инерции. Рассчитайте инерционные параметры по плотности и размерам балки. Затем укажите рассчитанные значения в Инерция секция кирпича Параметры сплошного блока:
Масса – Произведение на массовую плотность ( ρ ) и объем ( x · y ) · z ):
Центр масс – Координаты центроида относительно локальной системы отсчета ( R ):
Моменты инерции – От стандартного выражения относительно инерционной системы разрешения ( I ):
Продукты инерции – Из симметрии относительно кадра инерции разрешения ( I ):
CAD как источник инерционных данных
Приложения CAD часто предоставляют данные инерции для ваших моделей деталей. Примеры включают программное обеспечение SolidWorks с помощью инструмента массовых характеристик и Программное обеспечение Onshape с помощью его версии того же инструмента. Вы можете сослаться на эти данные и укажите их вручную в Simscape Multibody среда.
Альтернативные условные обозначения инерции
Некоторые приложения САПР, в том числе SolidWorks, используют альтернативную инерцию соглашение об определении элементов матрицы инерции. Это соглашение удаляет знак минус из определений произведения инерции.Например, произведение инерции I _yz принимает следующий вид:
Если ваш источник данных инерции принимает это соглашение, вы должны явно отрицать продукты инерции, прежде чем указывать их значения в среде Simscape Multibody. В качестве примера рассмотрим Матрица инерции SolidWorks, заданная как:
Чтобы правильно указать элементы матрицы в Simscape Multibody среды, вы должны обращаться с ними следующим образом:
Импорт САПР как альтернатива
Вместо того, чтобы ссылаться на данные инерции в модели сборки САПР, вы может импортировать эту модель в среду Simscape Multibody. CAD импорт основан на функции smimport, которая анализирует многотельный файл описания в формате XML и генерирует эквивалентную блок-схему со всеми заранее заданными параметрами блока – параметры инерции включены.
Вы должны экспортировать модель CAD в допустимом формате XML, то есть в формате, соответствующем XML-схему Simscape Multibody, прежде чем вы сможете ее импортировать. Этот вариант может подходит только в том случае, если у вас есть полная сборочная модель САПР. Для индивидуальных Детали САПР, используйте функцию импорта файла STEP твердотельного блока и установите параметр> в Рассчитать из Геометрия.
Для получения дополнительной информации см. Перевод CAD.
Упражнение: ссылка на модель SolidWorks
Определите параметры инерции для L-образной балки, показанной на рисунке. Затем укажите их явно в сплошном блоке, задав параметризацию инерции на Custom . Используйте данные массовых свойств предоставленный в этом примере для модели балки SolidWorks.
Откройте твердотельную модель. В командной строке MATLAB введите smdoc_lbeam_inertia .Открывается простая модель с блоком File Solid, представляющим двутавровая балка сплошная. Откройте файл Solid block и исследуйте его параметры Geometry . В геометрия балки импортируется из файла STEP, ранее экспортированного из модель SolidWorks. Эта геометрия показана на рисунке.
На панели визуализации щелкните Переключить видимость. рамок кнопка. На панели визуализации отображаются два рамы, одна с надписью R , а другая Я .
Рама R – местная ссылка каркас твердый. Это совпадает с тем, что пользователи SolidWorks называют в качестве выходной системы координат детали модель. Эта рамка расположена в нижнем углу L-образной формы на один из двух продольных концов балки. Вы должны указать центр масс относительно этого кадра.
Рама I – цельная рама на заказ включены для вашего удобства. Этот кадр совпадает с инерцией кадр разрешения.Его происхождение находится в центре масс, а его оси параллельны осям локальной системы отсчета. Ты должен укажите моменты и произведения инерции относительно этого Рамка.
Просмотрите данные SolidWorks. Модель SolidWorks предусматривает для L-образной балки следующее Данные о массовых характеристиках:
Массовые характеристики l_beam_solid Конфигурация: по умолчанию Система координат: - по умолчанию - Плотность = 0,10 фунта на кубический дюйм. Масса = 2.19 фунтов Объем = 22,41 кубических дюймов Площадь поверхности = 101,91 квадратных дюйма Центр масс: (дюймы) Х = 0,58 Y = 1,08 Z = 5,00 Главные оси инерции и главные моменты инерции: (фунты * квадратные дюймы) Снято в центре масс. Ix = (0,00; 0,00; 1,00) Px = 2,49 Iy = (0,38, -0,92, 0,00) Py = 18,65 Iz = (0,92, 0,38, 0,00) Pz = 20,35 Моменты инерции: (фунты * квадратные дюймы) Снято в центре масс и выровнено по выходная система координат.Lxx = 20,10 Lxy = -0,60 Lxz = 0,00 Lyx = -0,60 Lyy = 18,89 Lyz = 0,00 Lzx = 0,00 Lzy = 0,00 Lzz = 2,49 Моменты инерции: (фунты * квадратные дюймы) Снято в выходной системе координат. Ixx = 77,40 Ixy = 0,76 Ixz = 6,33 Iyx = 0,76 Iyy = 74,39 Iyz = 11,79 Izx = 6,33 Izy = 11,79 Izz = 5,76
Данные включают координаты центра масс с относительно «выходной системы координат». Эта система координат совпадает с локальной системой отсчета ( R ) соответствующего Simscape Multibody твердый.
Данные включают также матрицу с моментами и произведениями инерция «взята в центре масс и выровнена с выходным система координат.” Эта система координат совпадает с инерционная рамка разрешения ( I ) твердое тело Simscape Multibody.
Укажите параметры инерции. Разверните раздел параметров Inertia в Диалоговое окно файла Solid block. Затем измените параметрирование момента инерции, задав для параметра> значение Custom .В полный набор параметров инерции появляется для вас, чтобы указать.
Установите для параметра Mass значение 2,19 фунта . Это масса соответствующей плотности алюминия.
Установите для параметра Центр масс значение [0,58 1,08 5,00] в . Эти [ x y z ] координаты центра масс отображается в отчете SolidWorks.2 . Эти отрицание [ Lyz Lzx Lxy ] продукты инерции, показанные на Отчет SolidWorks.
Автоматический расчет инерции
Сплошные блоки предоставляют возможность автоматического вычисления большей части инерции параметры при заданной твердотельной геометрии. Этот параметр, доступный в раскрывающемся списке> и по умолчанию включен, требует, чтобы вы указали только геометрические параметры и либо масса, либо массовая плотность.
Блок использует параметры геометрии и массы для вычисления оставшейся параметры инерции – центр масс, моменты инерции и произведения инерция – относительно соответствующей системы отсчета. Расчеты на основе предположения о постоянной плотности массы и униформа.
Вы можете просмотреть результаты расчета внутри сплошного блока в расширяемом разделе с именем Display Inertia . Дан центр масс относительно локальной системы отсчета ( R ), а моменты и произведения инерции относительно инерционной системы разрешение ( I ).Это те же кадры относительно которого вы можете указать эти параметры.
Упражнение: отображение результатов расчетов инерции
Сконфигурируйте твердотельный блок файла smdoc_lbeam_inertia модель для расчета инерции параметры из геометрии твердого тела и его массовая плотность. Затем просмотрите расчетные параметры.
В диалоговом окне файла Сплошной блок, переключите параметр> на Рассчитать от Геометрия.2 . Это значение соответствует к твердой алюминиевой конструкции, и это то же самое предполагается в данных SolidWorks, представленных в разделе Просмотр данных SolidWorks.
Разверните узел Display Inertia и щелкните кнопку Обновить .