Может ли мгновенная скорость изменяться только по модулю пример: Может ли мгновенная скорость изменяться одновременно и по модулю и по направлению? подтвердите свой ответ…

Мгновенная скорость и ее изменение

Современная техника требует большой точности в описании движений, например, при посадке самолёта или стыковке космических кораблей. Поскольку они движутся непрямолинейно и неравномерно, нужно знать их скорости в каждое мгновение в каждой точке траектории.

Как любая траектория состоит из бесконечного числа точек, так и любой интервал времени состоит из бесконечного числа мгновений. И если интервал времени стремится к нулю, превращаясь в «мгновение», то уже известную вам формулу можно применить для определения мгновенной скорости тела:

	=	. .			– мгновенная скорость, м/с – перемещение тела, м   ( если Δt→0 ) Δt – стремящийся к нулю интервал времени, с
		Δt

Итак, мгновенная скорость – векторная физическая величина, равная отношению перемещения к интервалу времени, за который это перемещение произошло, если интервал времени стремится к нулю.

Интервал времени – всегда положительный скаляр, поэтому вектор мгновенной скорости всегда сонаправлен с вектором перемещения при Δt→0.

Для изучения быстрых движений применяют прибор стробоскоп, создающий частые вспышки света через равные интервалы времени (см. рисунок). Сфотографируем полёт тяжёлого шарика со стола при различных частотах вспышек. Все фотографии показывают, что траектория – это ветвь параболы, состоящая из отдельных «точек».

Например, от точки A за Δt→0 шарик совершит бесконечно малое перемещение вправо, поэтому и мгновенная скорость в точке A тоже будет направлена вправо.

 

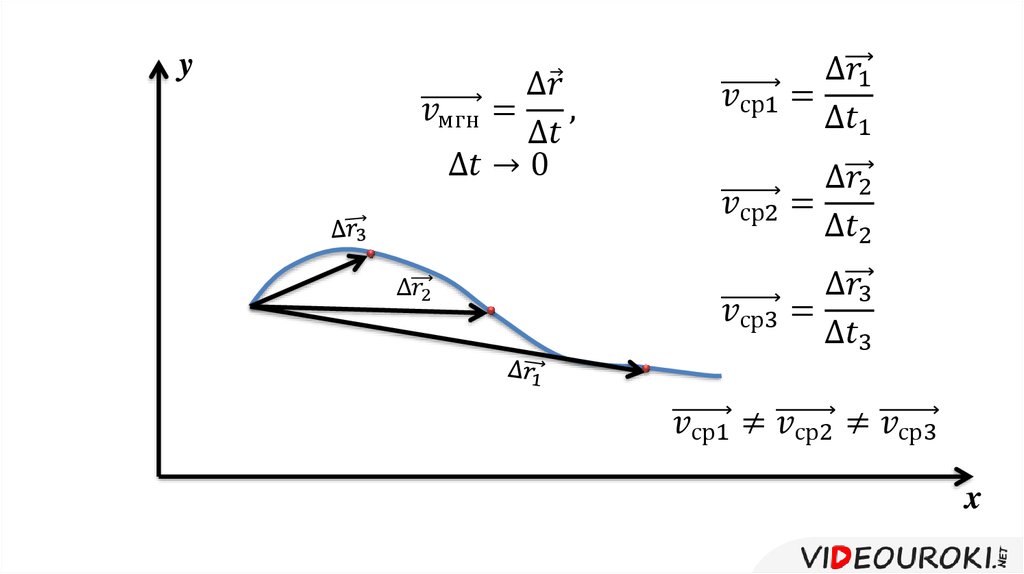
Делая интервалы между вспышками света стробоскопа всё меньше и меньше, мы построим чертёж, показывающий, что векторы мгновенных скоростей всегда располагаются по касательным к траектории тела (см. чертёж справа, красные векторы).

Взгляните: векторы мгновенной скорости меняются не только по направлению, но и по модулю: числовое значение мгновенной скорости возрастает с течением времени.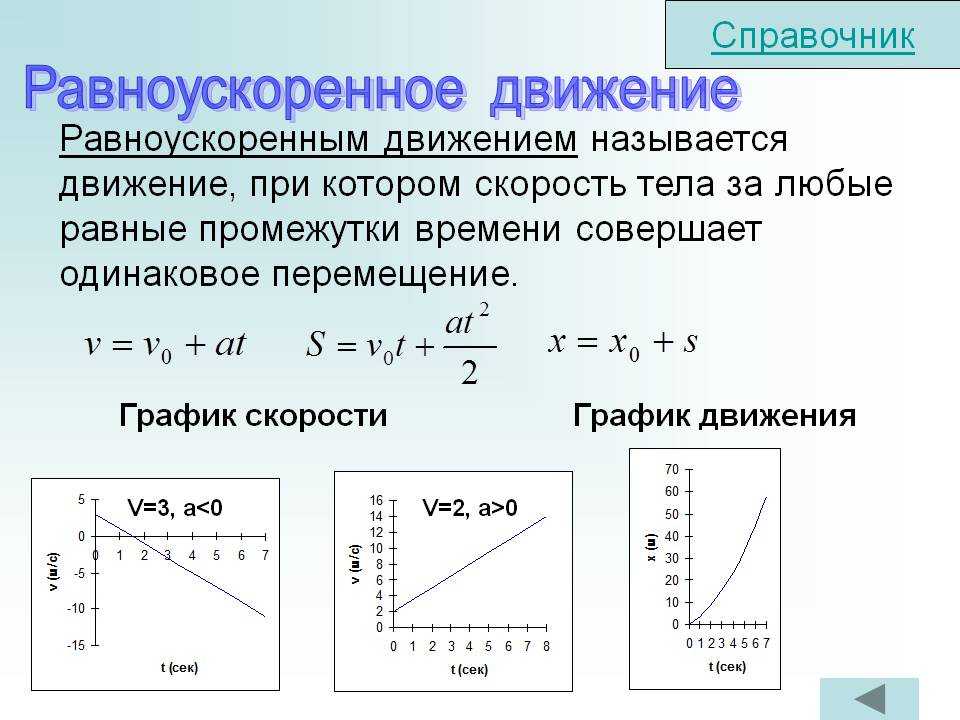 Откуда мы можем это знать? Конечно, только проведя измерения перемещений шарика по его стробоскопическим фотографиям и поделив их на интервалы времени между вспышками света. Эти измерения и вычисления позволят нам начертить векторы скорости в условном, выбранном нами для этого чертежа, масштабе (см. чертёж справа).

Такое движение тела, при котором его мгновенная скорость за любые равные интервалы времени изменяется одинаково, называется равноускоренным движением.

Поскольку мгновенная скорость тела является векторной величиной, то изменение мгновенной скорости – векторная разность: .

Найдём векторную разность двух последних векторов чертежа по «правилу треугольника», изученному нами ранее (см. § 12-г). Параллельным переносом скопируем векторы из точки E и точки F на свободное место на чертеже левее, совместив начала векторов. Построим вектор разности, проведя его от вычитаемого вектора к уменьшаемому вектору. Получим вектор изменения скорости шарика между точкой E и точкой F (мы его показали чёрным цветом).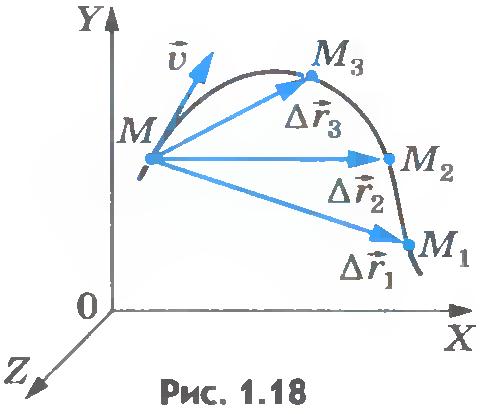 Обратим внимание: этот вектор изменения скорости направлен вниз.

Построив аналогичные векторы для всех других положений шарика, мы убедимся, что все векторы изменения скорости одинаковы – по модулю и по направлению. Значит, свободный полёт тяжёлого шарика – равноускоренное движение, так как мгновенная скорость шарика меняется одинаково за одинаковые интервалы времени.

Опубликовано в разделах: 9 класс, Введение в кинематику

Криволинейное движение – формула, примеры, признаки

4.6

Средняя оценка: 4.6

Всего получено оценок: 192.

4.6

Средняя оценка: 4.6

Всего получено оценок: 192.

Если на тело не действуют внешние силы, оно движется равномерно и прямолинейно. Однако, большинство тел в природе находятся во взаимодействии с другими телами, поэтому наиболее частым видом движения является криволинейное. Рассмотрим особенности такого движения.

Описание криволинейного движения

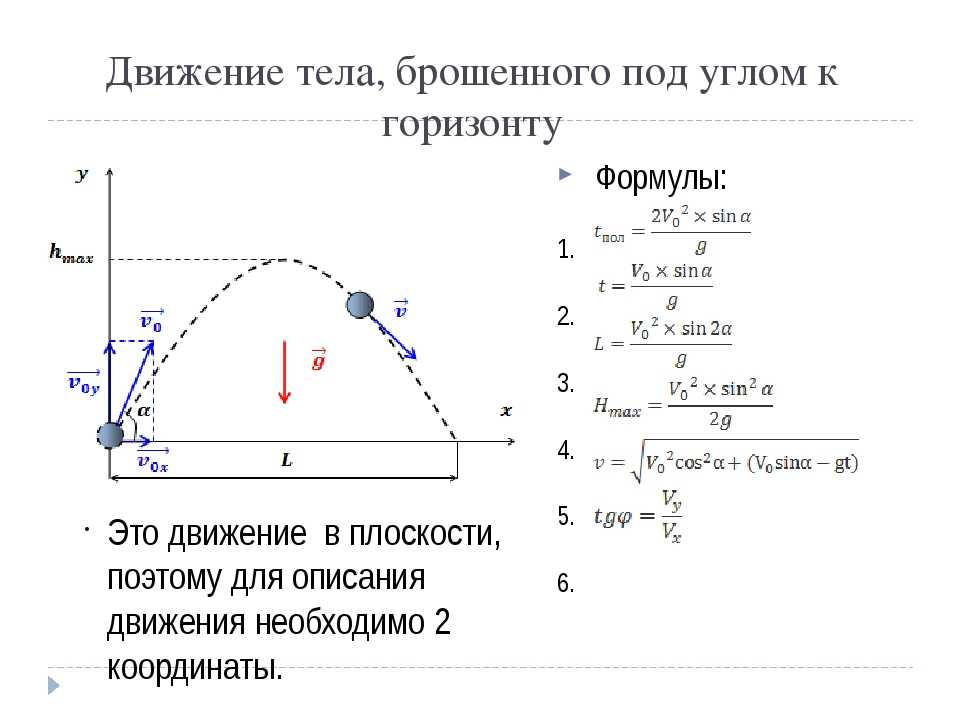
Движение, траектория которого не является прямой линией, называется криволинейным. Примерами криволинейного движения могут являться вращение частей двигателей, колес, дрожание листвы на ветру, полет камня, брошенного под углом к горизонту, и многое другое.

Рис. 1. Криволинейное движение в природе.

Криволинейное движение – это значительно более сложное движение по сравнению с прямолинейным. При прямолинейном движении происходит изменение модулей векторов перемещения, скорости и ускорения. Их направления всегда параллельны вектору перемещения. Если же движение криволинейно, то изменяются не только модули, но и направления. Фактически, изменения направлений векторов перемещения и скорости – это главные признаки криволинейного движения.

Первым методом исследования криволинейного движения является проецирование на координатные оси. Проецированное движение является прямолинейным, и к нему можно применять законы прямолинейного движения.

Вторым методом является разбиение всей траектории пути на короткие участки, каждый из которых неограниченно приближается к прямолинейному, таким образом, в качестве формул криволинейного движения становится возможным использовать формулы прямолинейного движения.

Скорость при криволинейном движении

Перемещение – это вектор от начала рассматриваемой траектории до ее конца. При прямолинейном движении этот вектор одновременно является и траекторией движения, а направление вектора скорости совпадает с направлением вектора перемещения.

При криволинейном движении траектория длиннее вектора перемещения. Однако, чем короче вектор перемещения, тем меньше разница.

Таким образом, если разбить траекторию на много коротких отрезков, движение на каждом из них приблизится к прямолинейному. Направление скорости на каждом отрезке совпадет с направлением отрезка. По мере увеличения числа таких отрезков, каждый из них неограниченно стягивается в точку, имея направление, параллельное к касательной в этой точке.

таким образом, мгновенная скорость криволинейного движения направлена по касательной к траектории движения.

Рис. 2. Мгновенная скорость криволинейного движения.

Ускорение при криволинейном движении

Ускорение – это мера изменения скорости. И если скорость прямолинейного движения постоянна, то и ускорение равно нулю. Для криволинейного движения скорость всегда изменяется. Модуль вектора скорости может оставаться постоянным, но из-за того, что вектор направлен всегда по касательной к траектории, а она не является прямой линией, направление этого вектора будет постоянно меняться. А если вектор скорости постоянно меняется (пусть не по модулю, а только по направлению), значит, при таком движении ускорение всегда присутствует.

Отметим, что если бы направление векторов скорости и ускорения в какой-то момент были бы одинаковыми, то в следующий момент скорость изменила бы только свой модуль, направление ее бы осталось прежним, траектория стала бы прямой линией, движение стало бы прямолинейным.

Криволинейное движение – это всегда движение с ускорением. Причем, направление вектора ускорения никогда не совпадает с направлением вектора скорости.

Рис. 3. Вектор ускорения при криволинейном движении.

Что мы узнали?

Криволинейное движение – это движение по траектории, которая не является прямой. Мгновенная скорость при криволинейном движении всегда направлена по касательной траектории. Ускорение при криволинейном движении всегда присутствует, и его направление всегда отличается от направления вектора скорости.

Тест по теме

Доска почёта

Чтобы попасть сюда – пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.6

Средняя оценка: 4.6

Всего получено оценок: 192.

---

А какая ваша оценка?

Кинематика

– Как работает мгновенная скорость для кругового движения?

Зачем нужна концепция пределов?

Исчисление — неизбежный инструмент в физике. Давайте посмотрим, что мы подразумеваем под ограничениями. Предел функции $f(x)$, когда ее переменная $x$ приближается к некоторому значению, скажем, $a$, — это значение, к которому приближается функция, когда $x$ приближается к $a$. Обозначим приближение $x$ к $a$ как $x\to a$ (произносится как $x$ стремится к значению $a$). То есть основная проблема в пределах состоит в том, чтобы найти значение $f(x)$ при $x\to a$. Назовем эту функцию значением $f(x\to a)$. Математически это выражается следующим образом:

$$\lim_{x\to a}f(x)=f(x\to a)$$

В нашей задаче положение движущейся частицы меняется со временем, поэтому смещение является функцией время. Поэтому обозначим функцию как $s(t)$. Это обозначение означает смещение частицы в момент времени $t$ (или, скажем, положение частицы в момент $t=t$ относительно начального положения в момент $t=t_0$), а не в интервале $(t -t_0)$.
Физическим примером является движущаяся машина. Вы хотите совершить путешествие из $A$ в $B$. Скорость автомобиля, конечно, неравномерна (это главное, зачем нужны вычисления). Автомобиль ускоряется, замедляется и может двигаться с постоянной скоростью и так далее. Затем вы можете проверить среднюю скорость, с которой вы вели машину, взяв отношение пройденного расстояния ко времени, затраченному на поездку.

Однако это всего лишь средняя скорость. Он только говорит вам, что если вы путешествовали с такой же постоянной скоростью, вы преодолеете такое-то расстояние за это время. Но вы знаете, что это не скорость автомобиля в каждое мгновение. Скорость менялась, возможно, вы остановили свою машину.
Концепция среднего значения остается в силе (т. е. дает вам хорошее приближение значения sme) только в том случае, если все значения, для которых вы взяли среднее значение, сопоставимы. В нашем случае, если автомобиль движется около некоторого значения $40 \text{ км/ч}$, все время вы получите в среднем около $40 \text{ км/ч}$, что можно принять за вашу скорость в любой момент времени до очень хорошее приближение. Но, если автомобиль какое-то время стоит, скорость равна нулю, что является очень большим отклонением от среднего значения, и вы никогда не получите точного результата. Они являются фундаментальными, и вы можете знать это. Итак, вообще понятие средней скорости не дает никакой информации о скорости частицы в любой момент; оно давало бы при условии равномерного движения (а это не то, с чем мы сталкиваемся в действительности).

Возможно, вы заметили показания спидометра вашего автомобиля. Он продолжает меняться всякий раз, когда изменяется скорость автомобиля. Этот инструмент дает вам скорость, с которой вы движетесь в настоящий момент. В физике нам нужно узнать скорость частицы во все моменты времени, чтобы проследить ее траекторию. Видите ли, цель механики — выяснить, как частица меняет свое положение во времени. Это решение всех механических проблем.

Как приходит на помощь концепция пределов?

Мы видели определение пределов и проблему реальной жизни, где средняя скорость не работает. Теперь давайте посмотрим, как ограничения могут решить проблему. На самом деле ограничения могут дать нам подсказку, но не решат проблему точно. Прежде чем перейти к вашей проблеме, давайте посмотрим на пример. Рассмотрим функцию

$$f(x)=\frac{1}{\sin x}, \space \space\space 0\le x\le 2\pi$$

Мы знаем, что эта функция не имеет определенное значение в точках $x=0$ и $x=2\pi$, так как в этих точках функция стремится в бесконечность. Даже с ограничениями мы не можем увидеть, каково значение функции в точках $x=0$ и $x=2\pi$. Пределы могут рассказать нам о значении, к которому приближается функция $f(x)$ по мере того, как $x$ приближается к нулю. Поскольку функция синуса симметрична относительно этих двух точек, мы можем анализировать любую из них, скажем, $x=0$. Делаем таблицу, как показано ниже:

$$ \начать{массив}{|с|с|} \hline х& f(x)\\ \hline 1& 1.188395106\\ 0,1 и 10,01668613\\ 0,01 и 100,0016667\\ 0,001 и 1000,000167\\ \vdots& \vdots\\ 0.000000001& 1000000000\\ \vdots& \vdots\\ \hline \конец{массив} $$

Вы можете видеть, что когда $x$ приближается к значению $0$, функция очень быстро возрастает. Здесь мы отмечаем интересную вещь: поскольку $x$ очень близко к нулю, значение функции приблизительно равно $1/x$ (см. последнюю запись). Следовательно, мы можем сказать, что функция изменяется от $\frac{1}{sin x}$ до $\frac{1}{x}$ при $x\to 0$. это 95}{5!}-\cdots\приблизительно x}$, для $x<<1$.

Теперь рассмотрим другой пример

$$g(x)=\frac{sin x}{x}$$

Конечно, есть сингулярность при $x=0$, где мы получаем значение функции в Форма $0/0$. Как и раньше, создаем таблицу со значениями $x$ и соответствующими значениями функций:

$$ \начать{массив}{|с|с|} \hline х& г(х)\\ \hline 1& 0,841470984\\ 0,1& 0,998334166\\ 0,01 и 0,999983333\\ 0,001 и 0,9999999833\\ 0,0001 и 0,999999998\\ \vdots& \vdots\\ \hline \конец{массив} $$

Как видите, значение функции приближается к $1$, когда $x$ приближается к $0$. Следовательно, мы можем сказать

$$\lim_{x\to 0}g(x)=\frac{sin x}{x}=1$$

Это означает, что значение функции приближается к $1$, когда $x$ стремится до $0$. Это не означает, что значение функции при $x=0$ равно $1$. Помните, что мы не можем удалить постоянную сингулярность, используя ограничения. Мы получим соседнее значение около $x=0$. В некоторых функциях, в отличие от того, что мы видели ранее, нет сходимости. В таких случаях мы говорим, что функция не имеет предела в этой конкретной точке.

Как этот предел можно использовать для объяснения мгновенной скорости?

Ну, мы не можем напрямую измерить мгновенную скорость.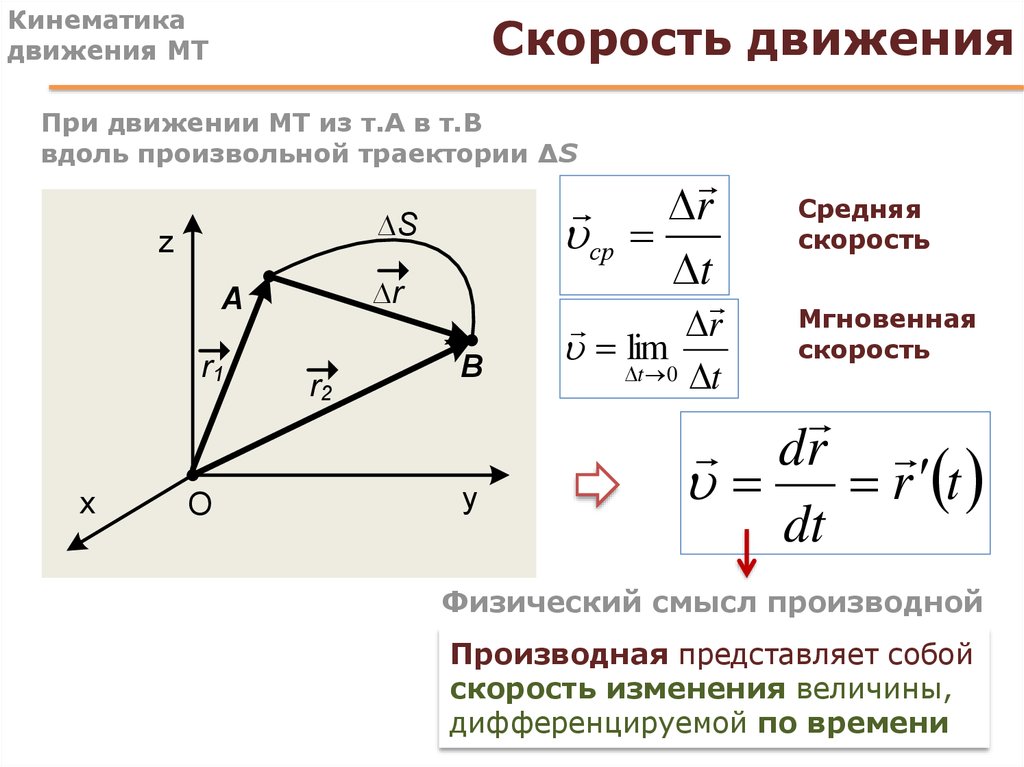 Вам понадобится небольшая длина $\Delta x=x_2-x_1$ и секундомер. Вы запускаете секундомер, когда автомобиль входит в точку $x_1$, и останавливаете, когда он покидает область $x_2$. Конечно, это не скорость в данный конкретный момент. Мы можем измерить событие во временном интервале, здесь временной интервал равен $\Delta t=t_2-t_1$. Однако мы выбираем $\Delta x$ как можно меньше (но также измеримо). Теперь займемся математикой. Чтобы получить мгновенную скорость в определенное время в интервале $\Delta t$, скажем, $t$, так что $t_1 Следовательно, мгновенная скорость определяется как

$$ \bbox[5px,border:2px сплошной красный] { v (t) = \ lim _ {\ Delta t \ to 0} \ frac {\ Delta x} {\ Delta t} } $$

Уравнение означает, что для нахождения мгновенной скорости частицы (т.е. скорости частицы в любой момент времени $t$: $v(t)$) мы берем малое перемещение, которое частица прошла за время интервале $t$, а затем узнать скорость с интервалом времени, стремящимся к нулю около $t$.

Это уравнение справедливо для любых реальных жизненных ситуаций. Но когда вы разделите перемещение на время, вы получите только среднюю скорость, которая, вообще говоря, не равна скорости частицы в какой-то момент внутри интервала времени. Среднее — это все равно, что считать все равным и распределять то, что имеешь, поровну между всеми. Дифференциация (которая является расширением границ) подобна тому, чтобы давать каждому в соответствии с его потребностями. Какой из них вы считаете лучшим способом распространения?

Среднее и мгновенное ускорение – University Physics Volume 1

Движение по прямой

Цели обучения

К концу этого раздела вы сможете:

• Вычислять среднее ускорение между двумя моментами времени.
• Рассчитайте мгновенное ускорение, учитывая функциональную форму скорости.
• Объясните векторную природу мгновенного ускорения и скорости.
• Объясните разницу между средним ускорением и мгновенным ускорением.
• Найдите мгновенное ускорение в указанное время на графике зависимости скорости от времени.

Важность понимания ускорения охватывает наш повседневный опыт, а также обширные пространства космического пространства и крошечный мир субатомной физики. В повседневном разговоре ускорить означает ускорить; при нажатии на педаль тормоза автомобиль замедляется. Например, мы знакомы с ускорением нашего автомобиля. Чем больше ускорение, тем больше изменение скорости за данное время. Ускорение широко используется в экспериментальной физике. В экспериментах с линейным ускорителем частиц, например, субатомные частицы разгоняются до очень высоких скоростей в экспериментах по столкновению, которые сообщают нам информацию о структуре субатомного мира, а также о происхождении Вселенной. В космосе космические лучи — это субатомные частицы, которые были ускорены до очень высоких энергий в сверхновых (взрывах массивных звезд) и активных ядрах галактик. Важно понимать процессы, которые ускоряют космические лучи, потому что эти лучи содержат сильно проникающее излучение, которое может повредить электронику, например, на космическом корабле.

Среднее ускорение

Формальное определение ускорения согласуется с только что описанными понятиями, но является более всеобъемлющим.

Среднее ускорение

Среднее ускорение — это скорость изменения скорости:

[латекс]\stackrel{\text{–}}{a}=\frac{\text{Δ}v}{\text{Δ} t}=\frac{{v}_{\text{f}}-{v}_{0}}{{t}_{\text{f}}-{t}_{0}},[/ латекс]

, где [латекс]\stackrel{\text{−}}{a}[/латекс] — среднее ускорение, v — скорость, а т это время. (Полоса над и означает среднее ускорение .)

Поскольку ускорение представляет собой скорость в метрах, деленную на время в секундах, единицы СИ для ускорения часто обозначают м/с ² , то есть метры в секунду. квадрат или метры в секунду в секунду. Это буквально означает, на сколько метров в секунду скорость изменяется каждую секунду. Напомним, что скорость — это вектор — она имеет как величину, так и направление — это означает, что изменение скорости может быть изменением величины (или скорости), но также может быть и изменением направления. Например, если бегун, движущийся со скоростью 10 км/ч строго на восток, замедляется до остановки, меняет направление и продолжает свой бег со скоростью 10 км/ч строго на запад, его скорость изменилась в результате изменения направления, хотя величина скорости одинакова в обоих направлениях. Таким образом, ускорение возникает, когда скорость изменяется по величине (увеличение или уменьшение скорости) или по направлению, или по тому и другому.

Ускорение как вектор

Ускорение — это вектор в том же направлении, что и изменение скорости, [латекс]\текст{Δ}v[/латекс]. Поскольку скорость является вектором, она может изменяться по величине или по направлению, или по обоим направлениям. Таким образом, ускорение — это изменение скорости или направления, или и того, и другого.

Имейте в виду, что хотя ускорение происходит в направлении изменения скорости, оно не всегда совпадает с направлением движения. Когда объект замедляется, его ускорение противоположно направлению его движения. Хотя это обычно называют замедлением (рисунок), мы говорим, что поезд ускоряется в направлении, противоположном направлению его движения.

Поезд метро в Сан-Паулу, Бразилия, замедляет скорость, приближаясь к станции. Он ускоряется в направлении, противоположном направлению его движения. (кредит: Юсуке Кавасаки)

Термин замедление может вызвать путаницу в нашем анализе, поскольку он не является вектором и не указывает на определенное направление относительно системы координат, поэтому мы его не используем. Ускорение — это вектор, поэтому мы должны выбрать для него соответствующий знак в выбранной нами системе координат. В случае поезда на (Рисунок) ускорение составляет в отрицательном направлении в выбранной системе координат , поэтому мы говорим, что поезд испытывает отрицательное ускорение.

Если объект в движении имеет скорость в положительном направлении по отношению к выбранному началу координат и приобретает постоянное отрицательное ускорение, объект в конце концов приходит в состояние покоя и меняет направление. Если мы подождем достаточно долго, объект пройдет через начало координат в противоположном направлении. Это показано на (рис.).

Объект, движущийся с вектором скорости на восток с отрицательным ускорением, останавливается и меняет направление. Он проходит начало координат, двигаясь в противоположном направлении через достаточно долгое время.

Расчет среднего ускорения: скаковая лошадь покидает ворота
Скаковая лошадь, выходящая из ворот, разгоняется из состояния покоя до скорости 15,0 м/с строго на запад за 1,80 с. Каково его среднее ускорение?

Скаковые лошади ускоряются из ворот. (кредит: Джон Салливан)

Стратегия
Сначала мы рисуем эскиз и назначаем системе координат задачу (Рисунок). Это простая задача, но визуализировать ее всегда полезно. Обратите внимание, что мы назначаем восток как положительный, а запад как отрицательный. Таким образом, в этом случае мы имеем отрицательную скорость.

Укажите систему координат, предоставленную информацию и то, что вы хотите определить.

Мы можем решить эту проблему, идентифицируя [латекс]\текст{Δ}v\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex} }\text{Δ}t[/latex] на основе данной информации, а затем рассчитывая среднее ускорение непосредственно из уравнения [latex]\stackrel{\text{–}}{a}=\frac{\text{Δ} v{\ text {Δ} t} = \ frac {{v} _ {\ text {f}} – {v} _ {0}} {{t} _ {\ text {f}} – {t} _{0}}[/латекс].

Решение
Сначала определите известные значения: [латекс]{v}_{0}=0,{v}_{\text{f}}=-15.0\phantom{\rule{0.2em}{0ex}}\text{ м/с}[/latex] (знак минус указывает направление на запад), Δ t = 1,80 с.

Во-вторых, найдите изменение скорости. Поскольку лошадь движется от нуля до –15,0 м/с, изменение ее скорости равно ее конечной скорости:

[латекс]\текст{Δ}v={v}_{\text{f}}-{v} _{0}={v}_{\text{f}}=-15. 0\phantom{\rule{0.2em}{0ex}}\text{м/с}.[/latex]

Наконец, замените известные значения ([latex]\text{Δ}v\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}\text{Δ}t[ /латекс]) и найти неизвестное [латекс]\stackrel{\text{–}}{a}[/латекс]: 9{2}.[/latex]

Значение
Знак минус для ускорения указывает на то, что ускорение направлено на запад. Ускорение 8,33 м/с ² строго на запад означает, что лошадь увеличивает свою скорость на 8,33 м/с строго на запад каждую секунду; то есть 8,33 метра в секунду за секунду, что мы записываем как 8,33 м/с ² . Это действительно среднее ускорение, потому что езда не плавная. Позже мы увидим, что ускорение такой величины потребовало бы от всадника удержания силы, почти равной его весу. 9{2}.[/латекс]

Мгновенное ускорение

Мгновенное ускорение a или ускорение в определенный момент времени получают с использованием того же процесса, который обсуждался для мгновенной скорости. То есть мы вычисляем среднюю скорость между двумя моментами времени, разделенными [латекс]\текст{Δ}t[/латекс], и приближаем [латекс]\текст{Δ}t[/латекс] к нулю. Результатом является производная функции скорости v ( t ), которая представляет собой мгновенное ускорение и математически выражается как

[latex]a\left(t\right)=\frac{d}{dt}v\left(t\right).[/latex]

Таким образом, аналогично тому, как скорость является производной функции положения, мгновенное ускорение есть производная от функции скорости. Мы можем показать это графически так же, как мгновенную скорость. На (Рисунке) мгновенное ускорение в момент времени t ₀ представляет собой наклон касательной к графику зависимости скорости от времени в момент времени t ₀ . Мы видим, что среднее ускорение [латекс]\stackrel{\text{–}}{a}=\frac{\text{Δ}v}{\text{Δ}t}[/latex] приближается к мгновенному ускорению, поскольку [латекс] \text{Δ}t[/latex] приближается к нулю. Также в части (а) рисунка мы видим, что скорость имеет максимум, когда ее наклон равен нулю. Это время соответствует нулю функции ускорения. В части (b) показано мгновенное ускорение при минимальной скорости, которая также равна нулю, так как наклон кривой и там равен нулю. Таким образом, для данной функции скорости нули функции ускорения дают либо минимальную, либо максимальную скорость.

На графике зависимости скорости от времени мгновенное ускорение представляет собой наклон касательной. (a) Показано среднее ускорение [латекс]\stackrel{\text{–}}{a}=\frac{\text{Δ}v}{\text{Δ}t}=\frac{{v}_{ \text{f}}-{v}_{i}}{{t}_{\text{f}}-{t}_{i}}[/latex] между временами [латекс]\text{Δ} t={t}_{6}-{t}_{1},\text{Δ}t={t}_{5}-{t}_{2}[/латекс] и [латекс]\ текст{Δ}t={t}_{4}-{t}_{3}[/latex]. Когда [latex]\text{Δ}t\to 0[/latex], среднее ускорение приближается к мгновенному ускорению в момент времени t ₀ . На виде (а) показано мгновенное ускорение для точки на кривой скорости при максимальной скорости. В этой точке мгновенное ускорение представляет собой наклон касательной, который равен нулю. В любой другой момент времени наклон касательной и, следовательно, мгновенное ускорение не были бы равны нулю. (b) То же, что и (a), но показано для мгновенного ускорения при минимальной скорости.

Чтобы проиллюстрировать эту концепцию, рассмотрим два примера. Во-первых, показан простой пример с использованием (Рисунок)(b), графика зависимости скорости от времени (Рисунок), для графического определения ускорения. Этот график изображен на (Рисунок)(а) и представляет собой прямую линию. Соответствующий график зависимости ускорения от времени находится по наклону скорости и показан на (Рисунок)(б). В этом примере функция скорости представляет собой прямую линию с постоянным наклоном, поэтому ускорение является постоянным. В следующем примере функция скорости имеет более сложную функциональную зависимость от времени.

(a, b) График зависимости скорости от времени является линейным и имеет отрицательный постоянный наклон (a), равный ускорению, показанному на (b). {2}\phantom{\rule{0.2em}{0ex}}\text{м/с}[ /латекс].

1. Найдите функциональную форму ускорения.
2. Найти мгновенную скорость в момент времени t = 1, 2, 3 и 5 с.
3. Найти мгновенное ускорение при т = 1, 2, 3 и 5 с.
4. Интерпретируйте результаты (c) с точки зрения направлений векторов ускорения и скорости.

Стратегия
Мы находим функциональную форму ускорения, взяв производную функции скорости. Затем вычисляем значения мгновенной скорости и ускорения по заданным функциям для каждого. Для части (d) нам нужно каждый раз сравнивать направления скорости и ускорения. 9{2}[/латекс]

[латекс]v\left(1\phantom{\rule{0.2em}{0ex}}\text{s}\right)=15\phantom{\rule{0.2em}{0ex}}\text{m/ s}[/латекс], [латекс]v\left(2\phantom{\rule{0.2em}{0ex}}\text{s}\right)=20\phantom{\rule{0.2em}{0ex} }\text{м/с}[/латекс], [латекс]v\left(3\phantom{\rule{0.2em}{0ex}}\text{s}\right)=15\phantom{\rule{ 0.2em}{0ex}}\text{м/с}[/latex], [латекс]v\left(5\phantom{\rule{0. {2}[/latex]

При t = 1 с скорость [латекс]v\left(1\phantom{\rule{0.2em}{0ex}}\text{s)}=15\phantom{\rule{0.2em}{0ex }}\text{м/с}[/latex] положительна, а ускорение положительно, поэтому и скорость, и ускорение имеют одно и то же направление. Частица движется быстрее.

При t = 2 с скорость увеличилась до [латекс]v\left(2\phantom{\rule{0.2em}{0ex}}\text{s)}=20\phantom{\rule{0,2 em}{0ex}}\text{м/с}[/latex], где максимально, что соответствует моменту времени, когда ускорение равно нулю. Мы видим, что максимальная скорость возникает, когда наклон функции скорости равен нулю, что равно нулю функции ускорения.

При t = 3 с скорость равна [латекс]v\left(3\phantom{\rule{0.2em}{0ex}}\text{s)}=15\phantom{\rule{0.2em} {0ex}}\text{м/с}[/latex] и ускорение отрицательное. Частица уменьшила свою скорость, и вектор ускорения отрицателен. Частица замедляется.

При t = 5 с скорость равна [латекс]v\left(5\phantom{\rule{0.2em}{0ex}}\text{s)}=-25\phantom{\rule{0. 2em {0ex}}\text{м/с}[/latex] и ускорение становится все более отрицательным. Между временем t = 3 с и t = 5 с частица уменьшила свою скорость до нуля, а затем стала отрицательной, тем самым изменив свое направление. Теперь частица снова ускоряется, но в противоположном направлении.

Мы можем увидеть эти результаты графически на (Рисунок).

(a) Скорость в зависимости от времени. Касательные линии указаны в моменты времени 1, 2 и 3 с. Наклоны касательных линий являются ускорениями. При t = 3 с скорость положительна. При t = 5 с скорость отрицательна, что указывает на то, что частица изменила направление. (b) Ускорение в зависимости от времени. Сравнивая значения ускорений, заданные черными точками, с соответствующими наклонами касательных (наклоны линий, проведенных через черные точки) на (а), мы видим, что они идентичны.

Значение
Проводя численный и графический анализ скорости и ускорения частицы, мы можем многое узнать о ее движении. Численный анализ дополняет графический анализ, давая общее представление о движении. Ноль функции ускорения соответствует максимуму скорости в этом примере. Также в этом примере, когда ускорение положительно и в том же направлении, что и скорость, скорость увеличивается. По мере того, как ускорение стремится к нулю, со временем становясь отрицательным, скорость достигает максимума, после чего начинает уменьшаться. Если мы подождем достаточно долго, скорость также станет отрицательной, указывая на изменение направления. Реальным примером такого типа движения является автомобиль, скорость которого увеличивается до максимума, после чего он начинает замедляться, останавливается, а затем меняет направление.

Проверьте свое понимание Самолет приземляется на взлетно-посадочной полосе, направляясь на восток. Опишите его ускорение.

Если мы возьмем восток за положительное значение, то ускорение самолета будет отрицательным, потому что он движется на запад. Он также замедляется; его ускорение противоположно направлению его скорости.

Почувствуйте ускорение

Вы, вероятно, привыкли ощущать ускорение, когда входите в лифт или нажимаете на педаль газа в машине. Однако ускорение происходит и со многими другими объектами в нашей Вселенной, с которыми у нас нет прямого контакта. (Рисунок) представлены ускорения различных объектов. Мы можем видеть, что величины ускорений простираются на многие порядки.

25; 2; 5; 9.8; 29; 59; 79; 147; 982; 1540; 3200; 30,000; 1,000,000; 1.9 multiplied by 10 in the 9 power.”>

Типичные значения ускорения (кредит: Википедия: порядки величины (ускорение))

Ускорение	Значение (м/с 2 )
Скоростной поезд	0,25
Лифт	2
Гепард	5
Объект в свободном падении без сопротивления воздуха у поверхности Земли	9,8
Максимум космического корабля “Шаттл” во время запуска	29
Пик парашютиста при нормальном раскрытии парашюта	59
Выход самолета F16 из пикирования	79
Катапультирование кресла взрывом из самолета	147
Спринт ракета	982
Самое быстрое пиковое ускорение ракетных саней	1540
Прыгающая блоха 9{9}[/латекс]

В этой таблице мы видим, что типичные ускорения сильно различаются для разных объектов и не имеют ничего общего с размером объекта или его массой. Ускорение также может сильно меняться со временем во время движения объекта. Дрэг-рейсер имеет большое ускорение сразу после старта, но затем оно уменьшается, когда транспортное средство достигает постоянной скорости. Его среднее ускорение может сильно отличаться от его мгновенного ускорения в определенный момент времени во время его движения. (Рисунок) графически сравнивает среднее ускорение с мгновенным ускорением для двух очень разных движений.

Графики зависимости мгновенного ускорения от времени для двух различных одномерных движений. а) Ускорение меняется незначительно и всегда в одном и том же направлении, так как оно положительно. Среднее значение по интервалу почти такое же, как ускорение в любой момент времени. (b) Ускорение сильно различается, возможно, это представляет собой пакет на ленточном конвейере почтового отделения, который ускоряется вперед и назад, когда он толкается. В такой ситуации необходимо рассматривать небольшие промежутки времени (например, от 0 до 1,0 с) с постоянным или почти постоянным ускорением.

Узнайте о графиках положения, скорости и ускорения. Перемещайте человечка вперед-назад с помощью мыши и зарисовывайте его движение. Установите положение, скорость или ускорение, и пусть симуляция переместит человека за вас. Посетите эту ссылку, чтобы использовать симуляцию движущегося человека.

Резюме

• Ускорение — это скорость изменения скорости. Ускорение — это вектор; оно имеет как величину, так и направление. Единицей ускорения в системе СИ является метр в секунду в квадрате.
• Ускорение может быть вызвано изменением величины или направления скорости, или и тем, и другим.
• Мгновенное ускорение a ( t ) является непрерывной функцией времени и дает ускорение в любой конкретный момент времени во время движения. Он рассчитывается из производной функции скорости. Мгновенное ускорение — это наклон графика зависимости скорости от времени.
• Отрицательное ускорение (иногда называемое замедлением) — это ускорение в отрицательном направлении в выбранной системе координат.

Концептуальные вопросы

Возможно ли, чтобы скорость была постоянной, а ускорение не равно нулю?

Нет, в одном измерении постоянная скорость требует нулевого ускорения.

Возможно ли, чтобы скорость была постоянной, а ускорение не равным нулю? Объяснять.

Приведите пример, в котором скорость равна нулю, а ускорение — нет.

Мяч подброшен в воздух, и его скорость равна нулю в точке броска, но ускорение не равно нулю.

Если поезд метро движется влево (имеет отрицательную скорость), а затем останавливается, то как направлено его ускорение? Ускорение положительное или отрицательное?

Знаки плюс и минус используются в одномерном движении для указания направления. Каков знак ускорения, уменьшающего модуль отрицательной скорости? положительной скорости?

Плюс, минус

Гепард может разогнаться из состояния покоя до скорости 30,0 м/с за 7,00 с. Каково его ускорение? 9{2}[/latex]

Доктор Джон Пол Стэпп был офицером ВВС США, который изучал влияние экстремального ускорения на организм человека. 10 декабря 1954 года Стэпп проехал на ракетных санях, разогнавшись из состояния покоя до максимальной скорости 282 м/с (1015 км/ч) за 5,00 с и резко остановившись всего за 1,40 с. Вычислите его (а) ускорение в направлении его движения и (б) ускорение, противоположное направлению его движения. Выразите каждое число, кратное г (9,80 м/с ² ), взяв его отношение к ускорению свободного падения.

Нарисуйте график зависимости ускорения от времени, используя следующий график зависимости скорости от времени.

Пассажирка выезжает из гаража задним ходом с ускорением 1,40 м/с ² . а) За какое время она достигнет скорости 2,00 м/с? б) Если она затем затормозит до остановки через 0,800 с, каково ее ускорение?

Предположим, что межконтинентальная баллистическая ракета выходит из состояния покоя до суборбитальной скорости 6,50 км/с за 60,0 с (фактическая скорость и время засекречены). Чему равно его среднее ускорение в метрах в секунду и кратное г (9,80 м/с ² )?

[латекс]а=11,1г[/латекс]

Самолет, стартовав из состояния покоя, движется по взлетно-посадочной полосе с постоянным ускорением в течение 18 с, а затем взлетает со скоростью 60 м/с.