Лекция по теме “Матрица, действия над матрицами”
I. Определение матрицы.
Матрицей называют совокупность чисел, расположенных в прямоугольной таблице
,
состоящей из m строк и n столбцов.
Числа называют элементами матрицы. Первый индекс в обозначении элемента ( i ) указывает на номер строки, а второй индекс ( j )- на номер столбца, в которых расположен этот элемент.
В нашем случае () матрица называется прямоугольной размера . Если число строк в матрице равно числу столбцов (m=n), то матрицу называют квадратной порядка m.
Матрица, состоящая из одного столбца (n=1), называется матрицей-столбцом, а число строк в ней ( m ) – высотой столбца:
или .
Матрица, имеющая только одну строку (m=1), называется матрицей-строкой, а число столбцов в ней (
или .
Два столбца равны, если они имеют одну одинаковую высоту и равные элементы с одинаковыми номерами. Две строки равны, если они имеют одинаковую длину и равны их соответствующие элементы.
II. Определение детерминанта.
Для квадратной матрицы может быть введено понятие детерминанта (определителя). Детерминант матрицы [A] обозначают
или .
Детерминантом матрицы порядка n>1 называют число
, (1)
где – детерминант матрицы порядка
Матрица порядка 1 состоит из одного числа, и ее детерминант по определению считают равным этому числу:
. (2)
Детерминант матрицы второго порядка в соответствии с (1) и (2) можно вычислить по следующей формуле:
.
Для матрицы третьего порядка
В соответствии с определением детерминант матрицы четвертого порядка может быть выражен через определитель третьего порядка, тот в свою очередь через определители второго порядка и т.д.
Число называют дополнительным минором элемента . Для произвольного элемента матрицы также можно ввести понятия дополнительного минора: – это определитель матрицы, получаемой из исходной вычеркиванием i -ой строки и j-ого столбца. Например, для матрицы [A] третьего порядка дополнительным минором элемента будет определитель
.
Определитель матрицы может быть вычислен по формулам разложения детерминанта по произвольной строке или столбцу:
по строке: , (3)
по столбцу: . (4)
Числа называют алгебраическими
дополнениями элементов матрицы A.
Они равны соответствующим минорам, взятым со своим знаком.
С помощью алгебраических дополнений формулы (3) и (4) могут быть записаны в виде:
, (3¢)
. (4¢)
Пример: записать определитель матрицы третьего порядка, используя формулы разложения по второй строке и третьему столбцу:
III. Свойства детерминантов.
Перечислим следующие основные свойства детерминантов:
1) определитель не изменится, если все строки матрицы заменить столбцами с соответствующими номерами:
.
Cправедливость этого свойства следует из возможности вычисления детерминанта по формулам разложения по строке или столбцу.
2) при перестановке местами двух строк или двух столбцов определителя, он должен быть умножен на -1:
.
3) если определитель имеет два одинаковых столбца или две одинаковые строки, то он равен нулю.
4) умножение всех элементов одного столбца или одной строки на любое число k равносильно умножению определителя на это число:
.
5) если все элементы некоторого столбца или строки матрицы равны нулю, то и ее определитель равен нулю.
6) если соответствующие элементы двух столбцов или двух строк матрицы пропорциональны, то ее определитель равен нулю:
7) если каждый элемент i-ого столбца или строки матрицы представляет собой сумму двух слагаемых, то ее определитель может быть вычислен как сумма двух определителей:
8) если к элементам некоторой строки (или некоторого столбца) матрицы прибавить соответствующие элементы другой строки (или другого столбца), умноженные на одно и тоже число, то величина определителя при этом не изменится:
.
IV. Ранг матрицы.
Рассмотрим некоторую не обязательно квадратную матрицу [A] размером . Выберем какие-нибудь r номеров ее строк и r номеров столбцов
. Минором порядка r матрицы [A] называется определитель матрицы порядка r, образованной элементами, расположенными на пересечении выбранных строк и столбцов.
Если считать, что , то
. (5)
Пусть задана матрица [A] размером :
.
Составим все ее миноры третьего порядка. Они должны включать строки матрицы [A] с номерами 1, 2, 3 и три столбца матрицы [A]. Это могут быть столбцы с номерами 1, 2, 3; или 1, 3, 4; или 2, 3, 4 или 1, 2, 4
Для данной матрицы миноры четвертого порядка не
существуют, т.
к. у нее только три строки. Примерами миноров второго порядка
являются:
Определение: в матрице [A] размером минор порядка r называется базисным, если он отличен от нуля, а все миноры порядка r+1 равны нулю или не существуют. (В последнем случае r равно меньшему из чисел т или п).
В матрице может быть несколько базисных миноров.
Пример. Найдем базисные миноры матрицы:
Миноров третьего порядка для этой матрицы не существует.
, т.к. есть нулевой столбец
Миноры второго порядка, содержащие первый столбец, также равны нулю.
Ненулевыми для данной матрицы оказываются только миноры первого порядка:. Они и являются базисными.
Если матрица нулевая, т.е. все ее элементы равны нулю, то у нее вообще нет базисного минора.
Определение : рангом матрицы называется порядок ее базисного
минора. Если матрица нулевая, то ее ранг считают равным нулю.
В соответствии с определением можно указать ранги матриц, рассмотренных в следующем примере:
V. Действия над матрицами.
Будем рассматривать матрицы [A] и [B] одного и того же размера . Для двух таких матриц вводятся линейные операции сложения и умножения на число. Суммой матриц [A] и [B] является матрица [C] =[A]+[B] того же размера, каждый элемент которой вычисляется по формуле
При умножении матрицы [A] на вещественное число каждый ее элемент умножается на это число:
т.е. в результате умножения матрицы на число получаем матрицу тех же размеров.
Еще одна операция над матрицей – транспонирование.
Транспонирование заключается в замене строк матрицы ее столбцами с
соответствующими номерами.
Если транспонированию подвергается матрица [A]
размером , то результатом будет матрица [A]T
размером , называемая транспонированной по
отношению к матрице [A]. Элементы транспонированной матрицы .
Для двух матриц [A] и [B] размерами и соответственно вводится операция умножения. Произведением матриц [
,
причем , т.е. элемент, стоящий в i -ой строке и j-ом столбце можно найти как сумму произведений элементов матрицы [A], стоящих в i -ой строке, и элементов матрицы [B], стоящих в j -ом столбце.
Перемножать можно только матрицы, для которых число
столбцов в первой равно числу строк во второй матрице. Две квадратные
матрицы можно перемножать только в том случае, когда они имеют одинаковый
порядок. Для операции умножения двух матриц не справедлив переместительный
закон, т.
е. в общем случае
.
Примеры:
При выполнении операций над матрицами полезно иметь в виду следующие соотношения между определителями:
.
Пример: для матриц и
VI. Некоторые специальные виды матриц.
Среди квадратных матриц выделяют некоторые матрицы специальных видов:
1) диагональные матрицы – имеют ненулевые элементы, стоящие только на главной диагонали, т.е. ;
2) единичные матрицы – на главной диагонали стоят единицы, а все остальные элементы – нули:
3) нулевая матрица – все элементы равны нулям;
4) симметричные матрицы – для них выполняется условие
, т.е. ;
5) кососимметричные матрицы: , т.е. .
6) вырожденные матрицы имеют нулевой определитель,
т.
е..
7) унимодулярные матрицы имеют определитель, равный 1.
Перечислим некоторые свойства таких матриц:
Если матрицу [A] сложить с нулевой матрицей [0] , то получим матрицу [A]:
[A]+[0]=[A].
При умножении матрицы [A] на единичную матрицу слева или справа, матрица не изменяется:
.
Матрица [B] называется обратной по отношению к матрице [A], если их произведение равно единичной матрице:
.
Матрицу, обратную к данной, обозначают . Вырожденные матрицы не имеют обратных.
Одним из методов нахождения матрицы, обратной к данной, является метод присоединенной матрицы. В соответствии с этим методом
,
где [AV] – матрица, присоединенная к матрице [A] .
Каждый элемент матрицы [AV] определяется как алгебраическое дополнение соответствующего элемента матрицы [A]; т.е.
.
Пример: найти матрицу, обратную к матрице
Найдем определитель матрицы [А]: .
Найдем алгебраические дополнения элементов матрицы [А]:
и составим присоединенную матрицу
.
Вычислим в соответствии с формулой элементы обратной матрицы:
.
Проверим результат умножением
.
Основы программирования в R
Mатрицы
Создание матрицы
Матрицы в R можно создавать разными способами. Выбор способа зависит от того, какую матрицу мы хотим создать: пустую матрицу (чтобы потом заполнять ее нужными значениями) или матрицу, составленную из уже имеющихся значений, например, из векторов.
Для того чтобы создать пустую матрицу, нужно определить, матрицу какой размерности мы хотим.
Размерность матрицы – число строк и число столбцов в ней. Создадим для начала матрицу \(2 \times 3\), состоящую из нулей:
M <- matrix(0, nrow = 2, ncol = 3) M
## [,1] [,2] [,3] ## [1,] 0 0 0 ## [2,] 0 0 0
Можем посмотреть на ее размерность:
dim(M)
## [1] 2 3
Заполнять эту матрицу другими значениями мы пока не будем – это будет интереснее делать, когда мы узнаем про циклы. А сейчас посмотрим, как собрать матрицу из “готовых” векторов.
Пусть у нас есть три вектора
x <- c(1, 2, 3, 0) y <- c(4, 5, 6, 0) z <- c(7, 8, 9, 0)
и мы хотим объединить их в матрицу. Векторы будут столбцами матрицы:
M_cols <- cbind(x, y, z) # c - от columns M_cols
## x y z ## [1,] 1 4 7 ## [2,] 2 5 8 ## [3,] 3 6 9 ## [4,] 0 0 0
А теперь векторы будут строками матрицы:
M_rows <- rbind(x, y, z) # r - от rows M_rows
## [,1] [,2] [,3] [,4] ## x 1 2 3 0 ## y 4 5 6 0 ## z 7 8 9 0
Другой способ создавать матрицы – разбивать на строки один длинный вектор.
Возьмем вектор:
long_vec <- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 5, 0)
Посиотрим, сколько в нем элементов:
length(long_vec)
## [1] 12
А теперь превратим вектор в матрицу из трех строк и четырех столбцов:
m1 <- matrix(long_vec, 3, 4) # получим матрицу с 3 строками и 4 столбцами m1
## [,1] [,2] [,3] [,4] ## [1,] 1 4 7 0 ## [2,] 2 5 8 5 ## [3,] 3 6 9 0
Конечно, если бы потребовали от R невозможное – матрицу, произведение числа строк и столбцов которой не равно длине вектора, из которого мы пытаемся эту матрицу создать – мы бы получили ошибку:
# m2 <- matrix(long_vec, 4, 5)
Столбцам и строкам матрицы можно дать названия. Посмотрим еще раз на матрицу m1:
m1
## [,1] [,2] [,3] [,4] ## [1,] 1 4 7 0 ## [2,] 2 5 8 5 ## [3,] 3 6 9 0
А теперь дадим столбцам этом матрицы названия.
colnames(m1) <- c("A", "B", "C", "D")
m1## A B C D ## [1,] 1 4 7 0 ## [2,] 2 5 8 5 ## [3,] 3 6 9 0
А теперь назовем строки матрицы:
rownames(m1) <- c("r1", "r2", "r3")
m1## A B C D ## r1 1 4 7 0 ## r2 2 5 8 5 ## r3 3 6 9 0
Можно, конечно, присваивать названия сразу и строкам, и столбцам.
Проделаем это с матрицей M_cols.
dimnames(M_cols) <- list(c("r1", "r2", "r3", "r4"), c("X", "Y", "Z")) # сначала названия строк, затем -- столбцовО том, что такое list – поговорим чуть позже.
Элементы матрицы
Для того, чтобы обратиться к элементу матрицы, необходимо указать строку и столбец, на пересечении которых он находится:
m1[1, 3]
## [1] 7
Если нам нужна отдельная строка (одна строка, все столбцы), то номер столбца нужно не указывать, просто оставить позицию пустой:
m1[1, ] # вся первая строка
## A B C D ## 1 4 7 0
Аналогично для столбцов:
m1[, 2] # весь второй столбец
## r1 r2 r3 ## 4 5 6
Списки
Список предсталяет собой “вектор векторов” в терминах R. Для тех, кто знаком с программированием, может показаться, что списки похожи на массивы. Это так, но списки, в отличие от массивов, могут содержать элементы разных типов. Например, в списке может быть сохранен вектор имен студентов (текстовый, тип character) и вектор их оценок (целочисленный, тип integer).
Пример списка с числовыми значениями:
L <- list(c(1, 2, 3, 4), c(5, 6, 7, 8)) L
## [[1]] ## [1] 1 2 3 4 ## ## [[2]] ## [1] 5 6 7 8
А вот пример списка с элементами разных типов:
grades <- list(c("Ann", "Sam", "Tom"), c(8, 7, 5))
grades## [[1]] ## [1] "Ann" "Sam" "Tom" ## ## [[2]] ## [1] 8 7 5
Так как в списках может храниться большое число разных векторов, для удобства им можно давать названия. Список grades можно было записать и так:
grades <- list(names = c("Ann", "Sam", "Tom"), marks = c(8, 7, 5))И тогда отдельные вектора из списка можно было бы вызывать удобным образом:
grades$names # имена
## [1] "Ann" "Sam" "Tom"
grades$marks # оценки
## [1] 8 7 5
И если мы бы запросили у R структуру этого списка, мы бы увидели названия векторов, которые в него входят.
str(grades)
## List of 2 ## $ names: chr [1:3] "Ann" "Sam" "Tom" ## $ marks: num [1:3] 8 7 5
Можно подумать: зачем нужно знать про списки, если на практике мы обычно будем сталкиваться с другими объектами – базами данных? На самом деле, со списками мы тоже будем встречаться.
Многие статистические функции выдают результат в виде списков. Когда результаты выводятся на экран, это не всегда заметно, но если мы захотим заглянуть внутрь, то увидим, что та же регрессионная выдача представляет собой объект, похожий на список, из которого можно выбрать вектор коэффициентов (coefficients), вектор остатков (residuals), предсказанных значений (fitted.values) и так далее.
А как обращаться к элементам списка, если вектора в нем никак не названы?
Для обращения к элементам списка необходимо использовать двойные квадратные скобки:
L
## [[1]] ## [1] 1 2 3 4 ## ## [[2]] ## [1] 5 6 7 8
L[[1]] # первый элемент списка, вектор (1, 2, 3, 4)
## [1] 1 2 3 4
Если нужно обратиться к “элементу элемента” списка (например, к числу 8 в этом примере) нужно сначала указывать номер вектора, в котором находится элемент, а потом номер самого элемента в этом векторе.
L[[2]][4] # 8 - 4-ый элемент 2ого вектора в списке
## [1] 8
Можно заметить, что список похож на матрицу: для того, чтобы обратиться к элементу, нужно указать “строку” (вектор) и “столбец” (положение в векторе).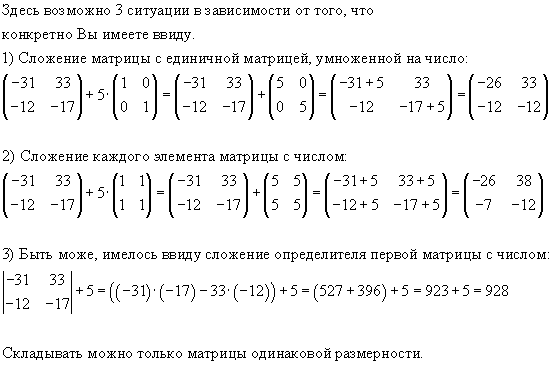
Для того, чтобы добавить элемент в список, нужно четко понимать положение элемента в этом списке: будет ли это элементом самого списка или “элементом элемента”:
L
## [[1]] ## [1] 1 2 3 4 ## ## [[2]] ## [1] 5 6 7 8
L[[3]] <- c(8, 9) # добавили в список третий вектор L
## [[1]] ## [1] 1 2 3 4 ## ## [[2]] ## [1] 5 6 7 8 ## ## [[3]] ## [1] 8 9
L[[3]][3] <- 0 # добавили третий элемент третьего вектора в списке L
## [[1]] ## [1] 1 2 3 4 ## ## [[2]] ## [1] 5 6 7 8 ## ## [[3]] ## [1] 8 9 0
Аналогичным образом можно изменять элементы списка:
L[[1]][1] = 99 # заменим 1 элемент 1 вектора в массиве на 99 L
## [[1]] ## [1] 99 2 3 4 ## ## [[2]] ## [1] 5 6 7 8 ## ## [[3]] ## [1] 8 9 0
Если в списке всего один элемент, при необходимости его можно быстро превратить в обычный вектор с помощью unlist():
small_L <- list(c("a", "b", "c"))
small_L## [[1]] ## [1] "a" "b" "c"
small_vec <- unlist(small_L) small_vec
## [1] "a" "b" "c"
То же можно делать и со списками из нескольких векторов, тогда все склеится в один длинный вектор:
L
## [[1]] ## [1] 99 2 3 4 ## ## [[2]] ## [1] 5 6 7 8 ## ## [[3]] ## [1] 8 9 0
unlist(L)
## [1] 99 2 3 4 5 6 7 8 8 9 0
Калькулятор сложения матриц – 2 3 Сумма
Поиск инструмента
Найдите инструмент в dCode по ключевым словам:Просмотрите полный список инструментов dCode
Добавление матрицы
Инструмент для вычисления сложения матриц в компьютерной алгебре.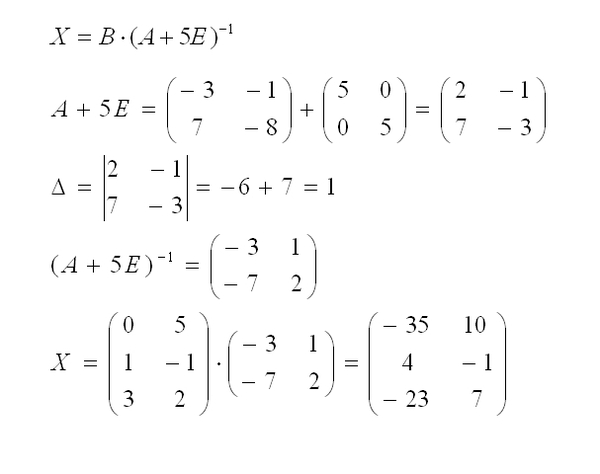
Сумма N матриц обычно получается путем суммирования элементов каждой матрицы.
Результаты
Добавление матрицы – dCode
Метки: Матрица
Поделиться
dCode и многое другое
dCode бесплатен, а его инструменты являются ценным подспорьем в играх, математике, геокэшинге, головоломках и задачах для решения любых задач. день!
Предложение ? обратная связь? Жук ? идея ? Запись в dCode !
Добавление 2 матриц
Matrix M1 Загрузка…
(если это сообщение не исчезнет, попробуйте обновить эту страницу)
Загрузка…
(если это сообщение не исчезнет, попробуйте обновить эту страницу)
Добавление 3-х матриц
Matrix M3 Загрузка…
(если это сообщение не исчезнет, попробуйте обновить эту страницу)
См. также: Калькулятор матриц — прямая сумма матриц
Ответы на вопросы (FAQ)
Что такое сложение матриц? (Определение)
Добавление 2-х матриц отмечено $M_1+M_2$ с $M_1=[a_{ij}]$ ($m$ строк и $n$ столбцов, при этом $m=n$ для квадратной матрицы) и $M_2=[b_{ij}]$ (одинакового размера: $m$ строк и $n$ столбцов).
Сумма этих двух матриц $ M_1 + M_2 = [c_{ij}] $ является матрицей одинакового размера, т.е. $ m $ строк и $ n $ столбцов, где: $$ \forall i, j \quad c_{ij} = a_{ij}+b_{ij} $$
Важное правило: Сложение матриц (матрица A плюс матрица B) может выполняться только с 2 матрицами одинаковой формы/размера/размера (2×2, 2×3, 3×2, 3×3 и т.д.).
Как сложить 2 матрицы?
Добавление матрицы выполняется поэлементно
Пример: $$ \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix} + \begin{bmatrix} 7 & 8 \\ 9 и 10 \\ 11 и 12 \end{bmatrix} = \begin{bmatrix} 1+7 и 2+8 \\ 3+9 и 4+10 \\ 5+11 и 6+12 \end{ bmatrix} = \begin{bmatrix} 8 и 10 \\ 12 и 14 \\ 16 и 18 \end{bmatrix} $$
Для всех матриц A и B одинакового размера A+B = B+A.
Как сложить 2 матрицы в Excel?
Сложение матриц в Excel можно осуществить путем добавления элементов с одинаковыми координатами в каждую матрицу.
Как сложить 2 матрицы разного размера?
Операция сложения (или суммирования) для матриц может быть выполнена только с матрицами одинакового размера (возможны все размеры, при условии, что они абсолютно одинаковы: 3×4, 4×3, 4×4, 5×5 и т.
д.). Тем не менее, существует прямая операция суммирования, которую можно использовать с матрицами разного размера.
Как добавить скаляр к матрице?
Операция прибавления скалярного числа к матрице $[A]+b$ не определена, но иногда подразумевает операцию $[A]+[I]b$ с $I$ единичной матрицей размера, совместимого с A.
Исходный код
dCode сохраняет за собой право собственности на исходный код Matrix Addition. За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Дополнение к матрице», апплета или фрагмента (конвертер, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Дополнение к матрице». функции (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и загрузка всех данных, скрипт, или доступ к API для «Matrix Addition» не является общедоступным, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложении для Android!
Напоминание: dCode можно использовать бесплатно.
Cite dCode
Копирование и вставка страницы «Добавление матрицы» или любых ее результатов разрешено, если вы цитируете dCode!
Ссылка на источник (библиография):
Matrix Addition на dCode.fr [онлайн-сайт], получено 08 февраля 2023 г., https://www.dcode.fr/matrix-addition
Сводка
- Сложение двух матриц
- Что такое сложение матриц? (Определение)
- Как сложить 2 матрицы?
- Как сложить 2 матрицы в Excel?
- Как сложить 2 матрицы разного размера?
- Как добавить скаляр к матрице?
Аналогичные страницы
- Матриксная прямая сумма
- Матричный калькулятор
- Матриксная вычитание
- СПОМОЖНЫ
Опора
- Paypal
- Patreon
- More
Forum/Help
Keywords
addition,sum,plus,matrix,2×2,2×3,3×2,3×3,3×4,4×3,4×4,5×5
Links
▲
Сложение матриц
- Математические сомнения
- Матрица
- Операции
Математическая операция добавления матрицы к другой матрице называется сложением матриц.
Матрицы дополнительно участвуют в некоторых случаях в математике. Каждая матрица состоит из записей (или элементов) в строках и столбцах. Следовательно, матрицы нельзя складывать, как и складывать числа. Следовательно, для добавления матриц требуется специальная системная процедура. Теперь давайте узнаем, как складывать матрицы в математике.
Принцип
Каждая запись матрицы добавляется к соответствующему элементу во второй матрице – это принцип сложения матриц.
Условие
Принцип сложения матриц применим, если расположение записей в матрицах одинаково. Это означает, что возможно сложение матриц одного порядка.
$A$ $\,=\,$ $\begin{bmatrix} a_{11} & a_{12} & a_{13} & \cdots & a_{1n}\\ a_{21} & a_{22 } & a_{23} & \cdots & a_{2n}\\ a_{31} & a_{32} & a_{33} & \cdots & a_{3n}\\ \vdots & \vdots & \vdots & \ ddots & \vdots \\ a_{m1} & a_{m2} & a_{m3} & \cdots & a_{mn} \end{bmatrix}$ и $B$ $\,=\,$ $\begin{bmatrix } b_{11} & b_{12} & b_{13} & \cdots & b_{1n}\\ b_{21} & b_{22} & b_{23} & \cdots & b_{2n}\\ b_ {31} & b_{32} & b_{33} & \cdots & b_{3n}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ b_{m1} & b_{m2} & b_ {m3} & \cdots & b_{mn} \end{bmatrix}$
Матрицы $A$ и $B$ порядка $m \times n$.
Расположение элементов в обеих матрицах одинаковое. Следовательно. Их можно добавлять, добавляя элемент одной матрицы к соответствующему элементу второй матрицы.
$A+B$ $\,=\,$ $\begin{bmatrix} a_{11}+b_{11} & a_{12}+b_{12} & a_{13}+b_{13} & \cdots & a_{1n}+b_{1n}\\ a_{21}+b_{21} & a_{22}+b_{22} & a_{23}+b_{23} & \cdots & a_{2n }+b_{2n}\\ a_{31}+b_{31} и a_{32}+b_{32} и a_{33}+b_{33} & \cdots & a_{3n}+b_{3n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{m1}+b_{m1} & a_{m2}+b_{m2} & a_{m3}+b_{m3} & \cdots & a_{mn}+b_{mn} \end{bmatrix}$
Сумма матриц также является матрицей того же порядка.
Помните, что нельзя складывать матрицы разного порядка, потому что расположение элементов в матрицах разное. Следовательно, невозможно добавить некоторые записи, и в этом случае добавление завершится ошибкой.
Примеры
Давайте узнаем, как складывать матрицы из следующих двух примеров.
$(1).\,\,\,$ $\begin{bmatrix} 1 и 2 \\ 3 и 4 \\ \end{bmatrix}$ $+$ $\begin{bmatrix} 5 и 6 \\ 7 и 8 \\ \end{bmatrix}$
$\implies$ $\begin{bmatrix} 1 & 2 \\ 3 & 4 \\ \end{bmatrix}$ $+$ $\begin{bmatrix} 5 & 6 \\ 7 & 8 \\ \end{ bmatrix}$ $\,=\,$ $\begin{bmatrix} 1+5 и 2+6 \\ 3+7 и 4+8 \\ \end{bmatrix}$
$\,\,\,\ поэтому\,\,\,\,\,\,$ $\begin{bmatrix} 1 & 2 \\ 3 & 4 \\ \end{bmatrix}$ $+$ $\begin{bmatrix} 5 & 6 \\ 7 & 8 \\ \end{bmatrix}$ $\,=\,$ $\begin{bmatrix} 6 & 8 \\ 10 & 12 \\ \end{bmatrix}$
Таким образом, квадратные матрицы могут сложить, чтобы найти сумму матриц.