Подборка по базе: Тема 6. Типы хозяйственных операций и их влияние на баланс.pdf, Актуальность лизинговых операций в деятельности коммерческого ба, 1 урок Свойства информации.docx, 20 операций — НЭБзу_19 Бабкина А.В.doc, ОРГАНИЗАЦИИ СКЛАДСКИХ ОПЕРАЦИЙ профпереподготовка к высшему обра, ОАиП 1 Понятие алгоритма свойства алгоритма.docx, Лекция 2 Психофизиологические свойства специалиста организации.d, 08. Ссылки на некоторые ресурсы для технологии.docx, Понятие алгоритма. Свойства алгоритмов.ppt, Восприятие и его свойства.pptx Некоторые свойства операций над матрицами. Вернёмся к действиям с матрицами. Можно ли к матрице прибавить число? Например: . Ну, или наоборот: Нет. К матрице можно прибавить только другую матрицу, причём точно такого же размера. Матрицу можно умножить на число. Но сложить их нельзя. Результат вычисления определителя – число (справедливо и для разности). Как возвести матрицу в квадрат? Операция определена только для квадратных матриц – «два на два», «три на три» и т.д. Возвести квадратную матрицу в квадрат – это значит, умножить её саму на себя: Пример 1 Возвести в квадрат матрицу Решение: – последовательно (слева направо) перебираем столбцывторой матрицы и «пристраиваем» их к каждой строке первой матрицы. Ответ: Немного о некоммутативности матричного умножения и единичной матрице Коммутативность = Перестановочность. Обычные числа переставлять можно , а матрицы в общем случае не перестановочны: . Рассмотрим некоторые исключения из правила, которые потребуются для выполнения практических задач. Справедливо следующее свойство: если произвольную матрицу умножить слева или справа на единичную матрицу подходящих размеров, то в результате получится исходная матрица: Коммутативность числового множителя относительно умножения матриц Для матриц и действительного числа справедливо следующее свойство: То есть числовой множитель можно (и нужно) вынести вперёд. Пример 2 Вычислить произведение Решение: (1) Согласно свойству перемещаем числовой множитель вперёд. Сами матрицы переставлять нельзя! (2) – (3) Выполняем матричное умножение. (4) Здесь можно поделить каждое число 10, но тогда среди элементов матрицы появятся десятичные дроби, что не есть хорошо. Однако замечаем, что все числа матрицы делятся на 5, поэтому умножаем каждый элемент на . Окончательный ответ лучше оставить в виде , хотя, в принципе, годится и внесение дроби: . Ответ: Как умножить три матрицы? Произведение трёх матриц можно вычислить двумя способами: 1) найти , а затем домножить на матрицу «цэ»: ; 2) либо сначала найти , потом выполнить умножение . Результаты обязательно совпадут, и в теории данное свойство называют ассоциативностью матричного умножения: Пример 3 Перемножить матрицы двумя способами Алгоритм решения двухшаговый: находим произведение двух матриц, затем снова находим произведение двух матриц. 1) Используем формулу . Действие первое: Действие второе: 2) Используем формулу . Действие первое: Действие второе: Ответ: Как возвести матрицу в куб и более высокие степени? Данные операции также определены только для квадратных матриц. Чтобы возвести квадратную матрицу в куб, нужно вычислить произведение: Фактически это частный случай умножения трёх матриц, по свойству ассоциативности матричного умножения: . А матрица, умноженная сама на себя – это квадрат матрицы: Таким образом, получаем рабочую формулу: Пример 4 Возвести матрицу в куб. Решение: Сначала возведём матрицу в квадрат: Матричные выражения Рассмотрим матричное выражение , где – некоторые матрицы. В данном матричном выражении три слагаемых и операции сложения/вычитания выполняются в последнюю очередь. В первом слагаемом сначала нужно транспонировать матрицу «бэ»: , потом выполнить умножение и внести «двойку» в полученную матрицу. Операция транспонирования имеет более высокий приоритет, чем умножение. Скобки, как и в числовых выражениях, меняют порядок действий: – тут сначала выполняется умножение , потом полученная матрица транспонируется и умножается на 2. Во втором слагаемом в первую очередь выполняется матричное умножение , и обратная матрица находится уже от произведения. Если скобки убрать: , то сначала необходимо найти обратную матрицу , а затем перемножить матрицы: . Нахождение обратной матрицы также имеет приоритет перед умножением. С третьим слагаемым всё очевидно: возводим матрицу в куб и вносим «пятёрку» в полученную матрицу. Если матричное выражение имеет смысл, то результат его вычисления является матрицей. Пример 5 Вычислить значение матричного многочлена , если . Решение: Как найти обратную матрицу? Что такое обратная матрица? Здесь можно провести аналогию с обратными числами: рассмотрим, например, оптимистичное число 5 и обратное ему число . Существует два основных метода нахождения обратной матрицы: Рассмотрим квадратную матрицу . Обратную матрицу можно найти по следующей формуле: , где – определитель матрицы , – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы . Понятие обратной матрицы существует только для квадратных матриц, матриц «два на два», «три на три» и т.д. Обозначения: обратная матрица обозначается надстрочным индексом Пример 6: Найти обратную матрицу для матрицы Решаем. 1) Сначала находим определитель матрицы. Если определитель матрицы равен НУЛЮ – обратной матрицы НЕ СУЩЕСТВУЕТ. В рассматриваемом примере , а значит, всё в порядке. 2) Находим матрицу миноров . Матрица миноров имеет такие же размеры, как и матрица , то есть в данном случае . Возвращаемся к нашей матрице 3) Находим матрицу алгебраических дополнений . 4) Находим транспонированную матрицу алгебраических дополнений . – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы . 5) Ответ. Вспоминаем нашу формулу Таким образом, обратная матрица: . Как проверить решение? Необходимо выполнить матричное умножение либо Проверка: Получена единичная матрица– это матрица с единицами на главной диагонали и нулями в остальных местах. Таким образом, обратная матрица найдена правильно. Пример7: Найти обратную матрицу для матрицы Алгоритм точно такой же, как и для случая «два на два». Обратную матрицу найдем по формуле: , где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы . 1) Находим определитель матрицы.
2) Находим матрицу миноров . Матрица миноров имеет размерность «три на три» , и нам нужно найти девять чисел. Рассмотрим несколько миноров: Рассмотрим следующий элемент матрицы: МЫСЛЕННО вычеркиваем строку и столбец, в котором находится данный элемент: необходимо вычислить девять определителей «два на два». Найдем еще один минор в картинках: Окончательный результат: решаем самостоятельно– матрица миноров соответствующих элементов матрицы . 3) Находим матрицу алгебраических дополнений . В матрице миноров необходимо СМЕНИТЬ ЗНАКИ строго у следующих элементов: 4) Находим транспонированную матрицу алгебраических дополнений . – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы . 5) Ответ: Проверка: |
Error
Sorry, the requested file could not be found
More information about this error
Jump to…
Jump to…Согласие на обработку персональных данных Учебно-тематический планАвторы и разработчики курсаИнформация для студентов и преподавателейВводная лекцияIntroductory lectureЛекция о системе обозначений Lecture on the notation systemВидеолекция (часть 1)Lecture (Part 1)Видеолекция 2. Операции над функциями. Свойства функции.Lecture 2. Operations on functions. The properties of the functionТеоретический материал Практическое занятие. Исследование свойств функций по определениюPractical lesson. Investigation of the properties of functions by definitionЗадачи для самостоятельной работыРешения задачТест 1. 1.1(Часть 1). Числовые функцииQuiz 1.1.1 (part 1)Тест 1.1.1(Часть 2). Числовые функцииQuiz 1.1.1 (part 2)Видеолекция 1. Числовая последовательность Lecture 1. Numeric sequenceВидеолекция 2. Предел числовой последовательностиLecture 2. The limit of a numeric sequence.Practical lesson 1. Study of properties of a numerical sequence by conventionПрактическое занятие 1 (часть 2)Теоретический материалЗадачи для самостоятельной работыРешения задачТест 1.1.2. Числовые последовательностиВидеолекция 1. Предел функции в точкеLecture 1. The limit of a function at a pointВидеолекция (часть 2)Практическое занятие 1. Вычисление пределов, неопределенности.Practical lesson 1. Calculation of limits. UncertaintiesПрактическое занятие 2. Вычисление пределов. Замечательные пределы.Practical lesson 2. Calculation of limits. Remarkable limits.Задачи для самостоятельной работыРешения задачТест 1.1.3. Предел функции в точкеВидеолекция. Непрерывность функции в точкеLecture 1. Сontinuity of a function at a pointПрактическое занятие.
1.1(Часть 1). Числовые функцииQuiz 1.1.1 (part 1)Тест 1.1.1(Часть 2). Числовые функцииQuiz 1.1.1 (part 2)Видеолекция 1. Числовая последовательность Lecture 1. Numeric sequenceВидеолекция 2. Предел числовой последовательностиLecture 2. The limit of a numeric sequence.Practical lesson 1. Study of properties of a numerical sequence by conventionПрактическое занятие 1 (часть 2)Теоретический материалЗадачи для самостоятельной работыРешения задачТест 1.1.2. Числовые последовательностиВидеолекция 1. Предел функции в точкеLecture 1. The limit of a function at a pointВидеолекция (часть 2)Практическое занятие 1. Вычисление пределов, неопределенности.Practical lesson 1. Calculation of limits. UncertaintiesПрактическое занятие 2. Вычисление пределов. Замечательные пределы.Practical lesson 2. Calculation of limits. Remarkable limits.Задачи для самостоятельной работыРешения задачТест 1.1.3. Предел функции в точкеВидеолекция. Непрерывность функции в точкеLecture 1. Сontinuity of a function at a pointПрактическое занятие.







 Линейная зависимость векторов. Базис векторного пространстваPractical lesson 2. Linear dependence of vectors and the concept of the basis of the vector systemТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Тест 2.1.2. Арифметическое n-мерное векторное пространствоСправочник (часть 1)Справочник (часть 2)Видеолекция 1. Исследование систем линейных уравненийLecture 1. Study systems of linear equationsВидеолекция 2. Однородная система линейных уравненийLecture 2. Homogeneous system of equationsПрактическое занятие 1. Фундаментальная система решений однородной системы линейных уравненийPractical lesson 1. Fundamental system of solutionsПрактическое занятие 2Practical lesson 2Теоретический материал (лекция 1)Теоретический материал (лекция 2)Задачи для самостоятельной работыРешения задачТест 2.1.3. Исследование систем линейных уравненийСправочникВидеолекция 1. Матрицы и определителиLecture 1.
Линейная зависимость векторов. Базис векторного пространстваPractical lesson 2. Linear dependence of vectors and the concept of the basis of the vector systemТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Тест 2.1.2. Арифметическое n-мерное векторное пространствоСправочник (часть 1)Справочник (часть 2)Видеолекция 1. Исследование систем линейных уравненийLecture 1. Study systems of linear equationsВидеолекция 2. Однородная система линейных уравненийLecture 2. Homogeneous system of equationsПрактическое занятие 1. Фундаментальная система решений однородной системы линейных уравненийPractical lesson 1. Fundamental system of solutionsПрактическое занятие 2Practical lesson 2Теоретический материал (лекция 1)Теоретический материал (лекция 2)Задачи для самостоятельной работыРешения задачТест 2.1.3. Исследование систем линейных уравненийСправочникВидеолекция 1. Матрицы и определителиLecture 1. Matrix determinantВидеолекция 2. Операции над матрицамиLecture 2. Operations on matricesВидеолекция 3. Обратная матрицаLecture 3. Inverse matrixПрактическое занятие 1. Операции над матрицамиPractical lesson 1. The operations on matrices Практическое занятие 2. Вычисление определителейЗадачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Теоретический материал (лекция 3)Тест 2.1.4. МатрицыQuiz 2.1.4. MatricesСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Прямоугольная декартова система координатLecture 1. Rectangular Cartesian coordinate systemТеоретический материалПрактическое занятие. Решение задач в координатахPractical lesson. Solution of problems in coordinatesЗадачи для самостоятельной работыРешения задачТест 2.2.1. Декартова система координатСправочникВидеолекция 1. Скалярное произведение векторовLecture 1. Scalar product of vectorsТеоретический материал (Часть 1)Видеолекция 2.
Matrix determinantВидеолекция 2. Операции над матрицамиLecture 2. Operations on matricesВидеолекция 3. Обратная матрицаLecture 3. Inverse matrixПрактическое занятие 1. Операции над матрицамиPractical lesson 1. The operations on matrices Практическое занятие 2. Вычисление определителейЗадачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Теоретический материал (лекция 3)Тест 2.1.4. МатрицыQuiz 2.1.4. MatricesСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Прямоугольная декартова система координатLecture 1. Rectangular Cartesian coordinate systemТеоретический материалПрактическое занятие. Решение задач в координатахPractical lesson. Solution of problems in coordinatesЗадачи для самостоятельной работыРешения задачТест 2.2.1. Декартова система координатСправочникВидеолекция 1. Скалярное произведение векторовLecture 1. Scalar product of vectorsТеоретический материал (Часть 1)Видеолекция 2. Векторное и смешанное произведения векторовLecture 2. Vector and mixed products of vectorsПрактическое занятие 1. Скалярное произведение векторовPractical lesson 1. Scalar product of vectorsПрактическое занятие 2. Применение произведений векторов при решении задачPractical lesson 2. vector and mixed product of vectors to solve themТеоретический материал (Часть 2)Задачи для самостоятельной работы 1Решения задач 1Тест 2.2.2.(часть 1). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовЗадачи для самостоятельной работы 2Решения задач 2Тест 2.2.2. (часть2). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовСправочник (Часть 1)Справочник (Часть 2)Видеолекция. Уравнения прямой на плоскости и в пространствеLecture. Equation of a straight line on a plane and in spaceТеоретический материалПрактическое занятие 1. Уравнения прямой на плоскостиPractical lesson 1. Related to the equation of a straight line on a planeЗадачи для самостоятельной работы 1Решение задач 1Практическое занятие 2.
Векторное и смешанное произведения векторовLecture 2. Vector and mixed products of vectorsПрактическое занятие 1. Скалярное произведение векторовPractical lesson 1. Scalar product of vectorsПрактическое занятие 2. Применение произведений векторов при решении задачPractical lesson 2. vector and mixed product of vectors to solve themТеоретический материал (Часть 2)Задачи для самостоятельной работы 1Решения задач 1Тест 2.2.2.(часть 1). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовЗадачи для самостоятельной работы 2Решения задач 2Тест 2.2.2. (часть2). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовСправочник (Часть 1)Справочник (Часть 2)Видеолекция. Уравнения прямой на плоскости и в пространствеLecture. Equation of a straight line on a plane and in spaceТеоретический материалПрактическое занятие 1. Уравнения прямой на плоскостиPractical lesson 1. Related to the equation of a straight line on a planeЗадачи для самостоятельной работы 1Решение задач 1Практическое занятие 2. Взаимное расположение прямыхPractical lesson 2. The relative position of straight lines.Задачи для самостоятельной работы 2Решение задач 2Тест 2.2.3. Уравнения прямойСправочникВидеолекция. Уравнение плоскости. Взаимное расположение прямой и плоскостиТеоретический материалПрактическое занятие. Уравнение плоскости. Взаимное расположение прямой и плоскости Practical lesson. Equation of a plane Задачи для самостоятельной работы 1Решение задач 1Задачи для самостоятельной работы 2Практическое занятие 2. Взаимное расположение плоскостейPractical lesson 2. Relative position of planesРешение задач 2Тест 2.2.4. Уравнения плоскостиСправочникВидеолекция 1. ЭллипсLecture 1. EllipseТеоретический материал Часть 1Практическое занятие 1. ЭллипсPractical lesson 1. EllipseЗадачи для самостоятельной работы 1Решение задач 1Видеолекция 2. Гипербола и параболаLecture 2. Hyperbola and parabolaТеоретический материал (Часть 2)Практическое занятие 2. Гипербола и параболаЗадачи для самостоятельной работы 2Решение задач 2Тест 2.
Взаимное расположение прямыхPractical lesson 2. The relative position of straight lines.Задачи для самостоятельной работы 2Решение задач 2Тест 2.2.3. Уравнения прямойСправочникВидеолекция. Уравнение плоскости. Взаимное расположение прямой и плоскостиТеоретический материалПрактическое занятие. Уравнение плоскости. Взаимное расположение прямой и плоскости Practical lesson. Equation of a plane Задачи для самостоятельной работы 1Решение задач 1Задачи для самостоятельной работы 2Практическое занятие 2. Взаимное расположение плоскостейPractical lesson 2. Relative position of planesРешение задач 2Тест 2.2.4. Уравнения плоскостиСправочникВидеолекция 1. ЭллипсLecture 1. EllipseТеоретический материал Часть 1Практическое занятие 1. ЭллипсPractical lesson 1. EllipseЗадачи для самостоятельной работы 1Решение задач 1Видеолекция 2. Гипербола и параболаLecture 2. Hyperbola and parabolaТеоретический материал (Часть 2)Практическое занятие 2. Гипербола и параболаЗадачи для самостоятельной работы 2Решение задач 2Тест 2. 2.5. Кривые второго порядкаСправочник (Часть 1)Справочник (Часть 2)Аттестация по модулю 2Анкета обратной связиИтоговое тестирование по курсу (1-2)Итоговое тестирование по курсу (2)Видеолекция 1. Основные понятия теории вероятностей Lecture 1. Basic concepts of probability theoryВидеолекция 2. Вероятность случайного событияLecture 2. Probability of a random eventПрактическое занятие 1. Классическая вероятностьPractical lesson 1. Classical probabilityЗадачи для самостоятельной работы (часть 1)Решения задач (часть 1)Практическое занятие 2. Операции над событиями. Practical lesson (part 2). Algebra of events. Properties of probabilitiesЗадачи для самостоятельно работы (часть 2)Решения задач (часть 2)Теоретический материалТест 3.1.1. Классическая вероятностьВидеолекция 1. Условная вероятностьLecture 1. Conditional probabilityПрактическое занятие 1. Условная вероятность. Формула полной вероятности. Формула БайесаPractical lesson 1. Conditional probability. The formula of total probability, Bayes ‘ formulaЗадачи для самостоятельной работы.
2.5. Кривые второго порядкаСправочник (Часть 1)Справочник (Часть 2)Аттестация по модулю 2Анкета обратной связиИтоговое тестирование по курсу (1-2)Итоговое тестирование по курсу (2)Видеолекция 1. Основные понятия теории вероятностей Lecture 1. Basic concepts of probability theoryВидеолекция 2. Вероятность случайного событияLecture 2. Probability of a random eventПрактическое занятие 1. Классическая вероятностьPractical lesson 1. Classical probabilityЗадачи для самостоятельной работы (часть 1)Решения задач (часть 1)Практическое занятие 2. Операции над событиями. Practical lesson (part 2). Algebra of events. Properties of probabilitiesЗадачи для самостоятельно работы (часть 2)Решения задач (часть 2)Теоретический материалТест 3.1.1. Классическая вероятностьВидеолекция 1. Условная вероятностьLecture 1. Conditional probabilityПрактическое занятие 1. Условная вероятность. Формула полной вероятности. Формула БайесаPractical lesson 1. Conditional probability. The formula of total probability, Bayes ‘ formulaЗадачи для самостоятельной работы. Условная вероятностьРешения задач. Условная вероятностьВидеолекция 2. Повторные независимые опыты и формула БернуллиLecture 2. Repeated Independent Experiments and the Bernoulli FormulПрактическое занятие 2. Схема БернуллиPractical lesson 2. Bernoulli’s formulaЗадачи для самостоятельной работы. Схема БернуллиРешения задач. Схема БернуллиТеоретический материалТест 3.1.2. Условная вероятностьВидеолекция 1. Дискретные лучайные величиныLecture 1. Discrete random variablesВидеолекция 2. Числовые характеристики дискретных случайных величинПрактическое занятие. Дискретные случайные величиныPractical lesson. Discrete random variablesЗадачи для самостоятельного решенияРешения задачЛабораторная работа. Законы распределения дискретных случайных величинLaboratory work 1. Distribution Laws of Discrete Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.1. Дискретные случайные величиныВидеолекция 1. Непрерывные случайные величиныВидеолекция 2. Частные случаи распределений случайных величинLecture 2.
Условная вероятностьРешения задач. Условная вероятностьВидеолекция 2. Повторные независимые опыты и формула БернуллиLecture 2. Repeated Independent Experiments and the Bernoulli FormulПрактическое занятие 2. Схема БернуллиPractical lesson 2. Bernoulli’s formulaЗадачи для самостоятельной работы. Схема БернуллиРешения задач. Схема БернуллиТеоретический материалТест 3.1.2. Условная вероятностьВидеолекция 1. Дискретные лучайные величиныLecture 1. Discrete random variablesВидеолекция 2. Числовые характеристики дискретных случайных величинПрактическое занятие. Дискретные случайные величиныPractical lesson. Discrete random variablesЗадачи для самостоятельного решенияРешения задачЛабораторная работа. Законы распределения дискретных случайных величинLaboratory work 1. Distribution Laws of Discrete Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.1. Дискретные случайные величиныВидеолекция 1. Непрерывные случайные величиныВидеолекция 2. Частные случаи распределений случайных величинLecture 2.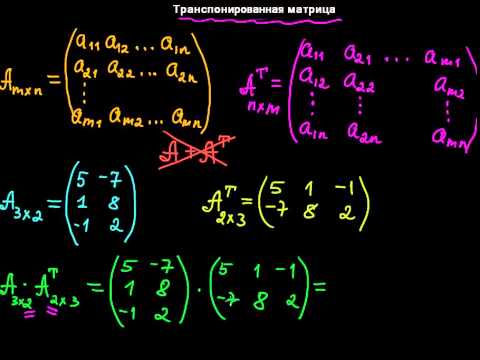 Special cases of distributions of random variablesПрактическое занятие. Непрерывные случайные величиныPractical lesson. Continuous random variableЗадачи для самостоятельного решенияРешения задачЛабораторная работа (видео). Законы распределения непрерывных случайных величинLaboratory work (video). Distribution Laws of Continuous Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.2. Непрерывные случайные величиныТеоретический материалТест 3.3.1. Законы больших чиселВидеолекция 1. Система случайных величин (часть 1)Видеолекция 2. Система случайных величин (часть 2)Lecture 2. Systems of random variables (part 2)Практическое занятие. Система случайных величинЗадачи для самостоятельной работыРешения задачЛабораторная работаРешение задачи (лабораторная работа)Теоретический материалТест 3.4.1. Совместный закон распределенияВидеолекция 1. Характеристическая функция случайной величиныLecture 1. Characteristic function of a random variableВидеолекция 2.
Special cases of distributions of random variablesПрактическое занятие. Непрерывные случайные величиныPractical lesson. Continuous random variableЗадачи для самостоятельного решенияРешения задачЛабораторная работа (видео). Законы распределения непрерывных случайных величинLaboratory work (video). Distribution Laws of Continuous Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.2. Непрерывные случайные величиныТеоретический материалТест 3.3.1. Законы больших чиселВидеолекция 1. Система случайных величин (часть 1)Видеолекция 2. Система случайных величин (часть 2)Lecture 2. Systems of random variables (part 2)Практическое занятие. Система случайных величинЗадачи для самостоятельной работыРешения задачЛабораторная работаРешение задачи (лабораторная работа)Теоретический материалТест 3.4.1. Совместный закон распределенияВидеолекция 1. Характеристическая функция случайной величиныLecture 1. Characteristic function of a random variableВидеолекция 2. Свойства характеристической функции случайной величиныLecture 2. Properties of characteristic functions random variable Практическое занятие 1. Вычисление характеристической функции случайной величиныPractical lesson 1. Calculation of Characteristic Functions Практическое занятие 2. Проверка устойчивости для стандартных распределенийPractical lesson 2. Testing the robustness for standard distributions.Задачи для самостоятельного решения (часть 1)Задачи для самостоятельного решения (часть 2)Решения задач (часть 1)Решения задач (часть 2)Тест 3.4.2. (данное тестирование по теме 1)Видеолекция. Основные понятия математической статистикиLecture. The basic concepts of mathematical statisticsЛабораторная работа (видео). Основные понятия математической статистикиLaboratory work (video). Basic concepts of mathematical statisticsТеоретический материалЛабораторная работа. Основные понятия математической статистикиРешения задач (лабораторная работа)Тест 3.5.1. Основные понятия математической статистикиQuiz 3.
Свойства характеристической функции случайной величиныLecture 2. Properties of characteristic functions random variable Практическое занятие 1. Вычисление характеристической функции случайной величиныPractical lesson 1. Calculation of Characteristic Functions Практическое занятие 2. Проверка устойчивости для стандартных распределенийPractical lesson 2. Testing the robustness for standard distributions.Задачи для самостоятельного решения (часть 1)Задачи для самостоятельного решения (часть 2)Решения задач (часть 1)Решения задач (часть 2)Тест 3.4.2. (данное тестирование по теме 1)Видеолекция. Основные понятия математической статистикиLecture. The basic concepts of mathematical statisticsЛабораторная работа (видео). Основные понятия математической статистикиLaboratory work (video). Basic concepts of mathematical statisticsТеоретический материалЛабораторная работа. Основные понятия математической статистикиРешения задач (лабораторная работа)Тест 3.5.1. Основные понятия математической статистикиQuiz 3. 5.1.Видеолекция. Статистические оценки параметров генеральной совокупности. Lecture. Statistical estimates of general population parametersЛабораторная работа 1 (видео). Статистические оценки параметров генеральной совокупностиLaboratory work 1 (video). Statistical estimators of the parameters of the populationЛабораторная работа 1. Статистические оценки параметров генеральной совокупностиРешения задач 1Лабораторная работа 2 (видео). Минимальный или оптимальный объем выборочной совокупностиLaboratory work 2(video). Minimum or optimal sample sizeЛабораторная работа 2. Минимальный или оптимальный объем выборочной совокупностиРешения задач 2Теоретический материалТест 3.5.2. Статистические оценкиQuiz 3.5.2Видеолекция. Зависимость между величинами. Виды зависимостейLecture. Dependence between quantities. Types of dependenciesТеоретический материал 1Лабораторная работа 1 (видео, часть 1). Парный корреляционный анализLaboratory work 1 (video, part 1). Pair correlation analysisЛабораторная работа 1.
5.1.Видеолекция. Статистические оценки параметров генеральной совокупности. Lecture. Statistical estimates of general population parametersЛабораторная работа 1 (видео). Статистические оценки параметров генеральной совокупностиLaboratory work 1 (video). Statistical estimators of the parameters of the populationЛабораторная работа 1. Статистические оценки параметров генеральной совокупностиРешения задач 1Лабораторная работа 2 (видео). Минимальный или оптимальный объем выборочной совокупностиLaboratory work 2(video). Minimum or optimal sample sizeЛабораторная работа 2. Минимальный или оптимальный объем выборочной совокупностиРешения задач 2Теоретический материалТест 3.5.2. Статистические оценкиQuiz 3.5.2Видеолекция. Зависимость между величинами. Виды зависимостейLecture. Dependence between quantities. Types of dependenciesТеоретический материал 1Лабораторная работа 1 (видео, часть 1). Парный корреляционный анализLaboratory work 1 (video, part 1). Pair correlation analysisЛабораторная работа 1. Парный корреляционный анализЛабораторная работа 1 (видео, часть 2). Множественный корреляционный анализРешение задач 1Лабораторная работа 2 (видео, часть 2). Парный регрессионный анализLaboratory work 2 (video, part 2). Paired Regression AnalysisЛабораторная работа 2. Парный регрессионный анализРешения задач 2Теоретический материал 2Тест 3.5.3. Зависимость между величинамиQuiz 3.5.3Лекция. Статистические гипотезы Теоретический материалЛабораторная работа (видео). Статистический критерий хи-квадратLaboratory work. The Chi-Square StatisticЛабораторная работа 1. Критерий хи-квадратРешения задач (Критерий хи-квадрат)Лабораторная работа 2. Критерий ПирсонаЛабораторная работа (расчетная таблица)Решения задач (Критерий Пирсона)Тест 3.6.1. Проверка статистических гипотез: основные понятияQuiz 3.6.1Видеолекция. Проверка статистических гипотезLecture. Testing statistical hypothesesЛабораторная работа 1 (видео). Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейLaboratory work 1.
Парный корреляционный анализЛабораторная работа 1 (видео, часть 2). Множественный корреляционный анализРешение задач 1Лабораторная работа 2 (видео, часть 2). Парный регрессионный анализLaboratory work 2 (video, part 2). Paired Regression AnalysisЛабораторная работа 2. Парный регрессионный анализРешения задач 2Теоретический материал 2Тест 3.5.3. Зависимость между величинамиQuiz 3.5.3Лекция. Статистические гипотезы Теоретический материалЛабораторная работа (видео). Статистический критерий хи-квадратLaboratory work. The Chi-Square StatisticЛабораторная работа 1. Критерий хи-квадратРешения задач (Критерий хи-квадрат)Лабораторная работа 2. Критерий ПирсонаЛабораторная работа (расчетная таблица)Решения задач (Критерий Пирсона)Тест 3.6.1. Проверка статистических гипотез: основные понятияQuiz 3.6.1Видеолекция. Проверка статистических гипотезLecture. Testing statistical hypothesesЛабораторная работа 1 (видео). Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейLaboratory work 1. Comparison of Sampled Population Means with Known Population VariancesЛабораторная работа 1. Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейРешения задач (лабораторная работа 1)Лабораторная работа 2 (часть 1). Сравнение средних независимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 1). Comparison of means of independent sample populations with unknown variances of general populationsЛабораторная работа 2 (часть 2). Сравнение средних зависимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 2). Comparison of mean dependent sample populations with unknown variances of general populationsЛабораторная работа 2. Проверка статистических гипотез о сравнении средних выборочных совокупностей, если не известны дисперсии генеральных совокупностейРешения задач (лабораторная работа 2)Теоретический материалТест 3.6.2. Проверка гипотезQuiz 3.6.2Аттестация по модулю 3Итоговое тестирование по курсу 1-2-3Итоговое тестирование по курсу для математических специальностейИтоговое тестирование по курсу (3)
Comparison of Sampled Population Means with Known Population VariancesЛабораторная работа 1. Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейРешения задач (лабораторная работа 1)Лабораторная работа 2 (часть 1). Сравнение средних независимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 1). Comparison of means of independent sample populations with unknown variances of general populationsЛабораторная работа 2 (часть 2). Сравнение средних зависимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 2). Comparison of mean dependent sample populations with unknown variances of general populationsЛабораторная работа 2. Проверка статистических гипотез о сравнении средних выборочных совокупностей, если не известны дисперсии генеральных совокупностейРешения задач (лабораторная работа 2)Теоретический материалТест 3.6.2. Проверка гипотезQuiz 3.6.2Аттестация по модулю 3Итоговое тестирование по курсу 1-2-3Итоговое тестирование по курсу для математических специальностейИтоговое тестирование по курсу (3)| A 1,1 = (-1) 1+1 |
|
∆ 1,1 = (-1 4-5 (-2)) = 6
| A 1,2 = (-1) 1+2 |
|
∆ 1,2 = -(2 4-(-2 (-2))) = -4
| A 1,3 = (-1) 1+3 |
|
∆ 1,3 = (2 5-(-2 (-1))) = 8
| A 2,1 = (-1) 2+1 |
|
∆ 2,1 = -(2 4-5 3) = 7
| A 2,2 = (-1) 2+2 |
|
∆ 2,2 = (-1 4-(-2 3)) = 2
| A 2,3 = (-1) 2+3 |
|
∆ 2,3 = -(-1 5-(-2 2)) = 1
| A 3,1 = (-1) 3+1 |
|
∆ 3,1 = (2 (-2)-(-1 3)) = -1
| A 3,2 = (-1) 3+2 |
|
∆ 3,2 = -(-1 (-2)-2 3) = 4
| A 3,3 = (-1) 3+3 |
|
∆ 3,3 = (-1 (-1)-2 2) = -3
Тогда обратную матрицу можно записать как:
| A -1 = 1 / 10 |
|
| A -1 = |
|
Другой алгоритм нахождения обратной матрицы
Приведем другую схему нахождения обратной матрицы.
- Находим определитель данной квадратной матрицы A .
- Находим алгебраические дополнения ко всем элементам матрицы A .
- Записываем алгебраические дополнения элементов строк в столбцы (транспонирование).
- Делим каждый элемент полученной матрицы на определитель матрицы A .
Особый случай : Обратной, по отношению к единичной матрице E , является единичная матрица E .
Действие первое. Вынесение минуса из матрицы (внесение минуса в матрицу).
Действия с матрицами
Данная матрица состоит из шести элементов:
Все числа (элементы) внутри матрицы существуют сами по себе, то есть ни о каком вычитании речи не идет:
Это просто таблица (набор) чисел!
Также договоримся не переставлять числа, если иного не сказано в объяснениях. У каждого числа свое местоположение, и перетасовывать их нельзя!
У каждого числа свое местоположение, и перетасовывать их нельзя!
Рассматриваемая матрица имеет две строки:
три столбца:
СТАНДАРТ: когда говорят о размерах матрицы, то сначала указывают количество строк, а только потом – количество столбцов. Мы только что разобрали по косточкам матрицу «два на три».
Если количество строк и столбцов матрицы совпадает, то матрицу называют квадратной, например:
– матрица «три на три».
Если в матрице один столбец
или одна строка
,
то такие матрицы также называют векторами.
Действие первое. Вынесение минуса из матрицы (внесение минуса в матрицу).
Вернемся к нашей матрице
.
Как вы наверняка заметили, в данной матрице слишком много отрицательных чисел. Это очень неудобно с точки зрения выполнения различных действий с матрицей, неудобно писать столько минусов, да и просто в оформлении некрасиво выглядит.
Вынесем минус за пределы матрицы, сменив у КАЖДОГО элемента матрицы знак:
Действие второе. Умножение матрицы на число.
Пример:
Всё просто, для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число. В данном случае – на тройку.
Еще один полезный пример:
– умножение матрицы на дробь
Сначала рассмотрим то, чего делать НЕ НАДО:
Вносить дробь в матрицу НЕ НУЖНО- это только затрудняет дальнейшие действия с матрицей.
И, тем более, НЕ НАДО делить каждый элемент матрицы на минус семь:
Мы помним, что десятичных дробей с запятой в высшей математике стараются всячески избегать. Единственное, что желательно сделать в этом примере – это внести минус в матрицу:
А вот если бы ВСЕ элементы матрицы делились на 7 без остатка, то тогда можно (и нужно!) было бы поделить.
Пример:
В этом случае можно и НУЖНО умножить все элементы матрицы на 1/2, так как все числа матрицы делятся на 2 без остатка.
Примечание: в теории высшей математики школьного понятия «деление» нет. Вместо фразы «это поделить на это» всегда можно сказать «это умножить на дробь». То есть, деление – это частный случай умножения.
Действие пятое. Умножение матриц.
Как умножить матрицы ?
Пример:
Умножить матрицы
Я буду сразу приводить формулу для каждого случая:
– попытайтесь сразу уловить закономерность.
Пример сложнее:
Умножить матрицы
Формула:
В результате получена так называемая нулевая матрица.
Если в задании предложено умножить матрицу M на матрицу N, то и умножать нужно именно в таком порядке. Ни в коем случае не наоборот.
Ни в коем случае не наоборот.
Переходим к матрицам третьего порядка:
Умножить матрицуы
Формула очень похожа на предыдущие формулы:
А теперь попробуйте самостоятельно разобраться в умножении следующих матриц:
Умножьте матрицы
Ответ.
Как проверить решение? Необходимо выполнить матричное умножение либо
Проверка:
Получена так называемая единичная матрица (с единицами по главной диагонали и нулями в остальных местах).
Таким образом, обратная матрица найдена правильно.
Пример:
Найти обратную матрицу для матрицы
Обратную матрицу найдем по формуле:
,
где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
Как вычислить определитель?
Определитель можно вычислить только для квадратной матрицы.
Обозначения: Если дана матрица
,
то ее определитель обозначают |A|. Также очень часто определитель обозначают латинской буквой D или греческой Δ.
1) Что значит решить (найти, раскрыть) определитель? Вычислить определитель – это значит НАЙТИ ЧИСЛО.
2) Теперь осталось разобраться в том, КАК найти это число. Как Вы догадываетесь, для этого нужно применить определенные правила, формулы и алгоритмы, о чём сейчас и пойдет речь.
Начнем с определителя «два» на «два»:
Сразу рассмотрим пример:
Определитель матрицы «три на три» можно раскрыть 8 способами, 2 из них простые и 6 – нормальные.
Начнем с двух простых способов
Аналогично определителю «два на два», определитель «три на три» можно раскрыть с помощью формулы:
Пример:
Формула длинная и допустить ошибку по невнимательности проще простого. Как избежать досадных промахов? Для этого придуман второй способ вычисления определителя, который фактически совпадает с первым. Называется он способом Саррюса или способом «параллельных полосок».
Как избежать досадных промахов? Для этого придуман второй способ вычисления определителя, который фактически совпадает с первым. Называется он способом Саррюса или способом «параллельных полосок».
Суть состоит в том, что справа от определителя приписывают первый и второй столбец и аккуратно карандашом проводят линии:
Множители, находящиеся на «красных» диагоналях входят в формулу со знаком «плюс». Множители, находящиеся на «синих» диагоналях входят в формулу со знаком минус:
Пример:
Сравните два решения. Нетрудно заметить, что это ОДНО И ТО ЖЕ, просто во втором случае немного переставлены множители формулы, и, самое главное, вероятность допустить ошибку значительно меньше.
Правило Крамера.
А сейчас мы разберём правило Крамера, а также решение системы линейных уравнений с помощью обратной матрицы (матричный метод). Для того чтобы освоить данный параграф Вы должны уметь раскрывать определители «два на два» и «три на три».
Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
Находим главный определитель системы:
Если D=0, то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет/
Если D≠0, то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
И, наконец, ответ рассчитывается по формулам:
Пример
Решить систему по формулам Крамера.
Решение:
Решим систему по формулам Крамера.
значит, система имеет единственное решение.
Ответ: ..
Собственно, здесь опять комментировать особо нечего. Но есть пара замечаний.
Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:
Если под рукой нет компьютера, поступаем так:
1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие. Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).
2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения.
Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:
Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Пример
Решить систему матричным методом
Решение:
Запишем систему в матричной форме: AX=b, где
Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице A нужно было бы поставить нули.
По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице A нужно было бы поставить нули.
.
Согласно формуле нам нужно найти обратную матрицу и выполнить матричное умножение . Алгоритм нахождения обратной матрицы подробно разобран в разделе «Как найти обратную матрицу?»
Обратную матрицу найдем по формуле:
,
где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы A.
Сначала разбираемся с определителем:
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров
Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:
То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце.
В ходе решения расчет миноров лучше расписать подробно.
Порядок расчета миноров совершенно не важен, здесь я их вычислил слева направо по строкам. Можно было рассчитать миноры по столбцам (это даже удобнее).
Таким образом:
– матрица миноров соответствующих элементов матрицы A.
– матрица алгебраических дополнений.
– транспонированная матрица алгебраических дополнений.
Теперь записываем обратную матрицу:
Ни в коем случае не вносим в матрицу, это серьезно затруднит дальнейшие вычисления.Деление нужно было бы выполнить, если бы все числа матрицы делились на 60 без остатка. А вот внести минус в матрицу в данном случае очень даже нужно, это, наоборот – упростит дальнейшие вычисления.
Обратите внимание, что деление на 60 выполняется в последнюю очередь.
Ответ: .
Действия с матрицами
Данная матрица состоит из шести элементов:
Все числа (элементы) внутри матрицы существуют сами по себе, то есть ни о каком вычитании речи не идет:
Это просто таблица (набор) чисел!
Также договоримся не переставлять числа, если иного не сказано в объяснениях. У каждого числа свое местоположение, и перетасовывать их нельзя!
У каждого числа свое местоположение, и перетасовывать их нельзя!
Рассматриваемая матрица имеет две строки:
три столбца:
СТАНДАРТ: когда говорят о размерах матрицы, то сначала указывают количество строк, а только потом – количество столбцов. Мы только что разобрали по косточкам матрицу «два на три».
Если количество строк и столбцов матрицы совпадает, то матрицу называют квадратной, например:
– матрица «три на три».
Если в матрице один столбец
или одна строка
,
то такие матрицы также называют векторами.
Действие первое. Вынесение минуса из матрицы (внесение минуса в матрицу).
Вернемся к нашей матрице
.
Как вы наверняка заметили, в данной матрице слишком много отрицательных чисел. Это очень неудобно с точки зрения выполнения различных действий с матрицей, неудобно писать столько минусов, да и просто в оформлении некрасиво выглядит.
Вынесем минус за пределы матрицы, сменив у КАЖДОГО элемента матрицы знак:
Что такое обратная матрица и как её найти — Журнал «Код»
10.03.2021
Сложная тема из линейной алгебры.
Недавно мы начали говорить о линейной алгебре и матрицах. Сначала всё было хорошо и легко:
Но начав заниматься линейной алгеброй, бывает трудно остановиться. Сегодня мы познакомимся с обратной матрицей и научимся её вычислять. Это навык, который в будущем нам пригодится для решения матричных уравнений.
С точки зрения арифметики материал не сложный. Но он требует вдумчивого чтения для понимания правил. В итоге статья довольно большая, мозги кипят и танки наши быстры.
Читать ли эту статью?
❌ Если вам нужны простые быстрые решения для жизни — нет, можно объявить, что у вас сегодня выходной.
✅ Если вашему мозгу не хватает вызова и новых горизонтов — велком ту зе матрикс.
Обратное — это как?
В математике есть взаимно обратные числа. Они получаются так: вы берёте какое-то число, добавляете отрицательную степень и получаете обратное число:
Они получаются так: вы берёте какое-то число, добавляете отрицательную степень и получаете обратное число:
Обратные числа при умножении друг на друга всегда дают единицу:
Обратная матрица
В линейной алгебре есть обратные матрицы. По свойствам они напоминают обратные числа: если обычную матрицу умножить на обратную к ней, получится единичная матрица.
Единичная матрица работает как единица с числами: если умножить любое число на единицу, получится исходное число; если умножить любую матрицу на единичную матрицу — получится исходная матрица:
Единичная матрица состоит из единиц и нулей: на диагонали находятся единицы; остальные элементы — нули. Единичные матрицы не используются при расчёте обратных матриц, но без них не получится решать матричные уравнения.
Пример квадратной единичной матрицы размером 5×5. Единичная матрица может быть любого размера — состоять из любого количества строк и столбцовКак рассчитать обратную матрицу
Для расчёта обратной матрицы нужно выполнить три действия. Пока что не обращайте внимание на термины:
Пока что не обращайте внимание на термины:
- Разделить единицу на матричный определитель.
- Найти транспонированную матрицу алгебраических дополнений.
- Перемножить полученные значения.
Далее мы по порядку во всём разберёмся.
Формула расчёта обратной матрицы: |A| — матричный определитель; Aᵀᵢⱼ — матрица алгебраических дополненийОпределитель — это особое число, которое «определяет» свойства матрицы.
Порядок вычисления определителя зависит от размера матрицы, которому он соответствует — чем больше матрица, тем сложнее считать определитель. Мы только знакомимся с матрицами, поэтому остановимся на определителях второго и третьего порядка — они подходят для квадратных матриц размером 2×2 и 3×3.
Чтобы найти определитель второго порядка, нам достаточно умножить элементы главной диагонали и вычесть из значения произведение чисел второй диагонали.
Формула для расчёта определителя второго порядка
Пример расчёта определителя второго порядка
Определитель третьего порядка находится путём умножения диагоналей на треугольники. Здесь много операций, поэтому формулу соберём по частям.
Здесь много операций, поэтому формулу соберём по частям.
Сначала работаем по главной диагонали: идём от верхнего левого элемента и движемся к правому нижнему элементу. Перемножаем элементы между собой.
Считаем определитель третьего порядка: 1-й этап — главная диагональ
Прибавляем к произведению элементов первой диагонали произведение первого треугольника. Основание первого треугольника находится параллельно главной диагонали и состоит из элементов А₂₁ и А₃₂. Вершина — элементА₁₃.
Считаем определитель третьего порядка: 2-й этап — первый треугольник
Прибавляем к полученному результату произведение второго треугольника, в котором основание состоит из элементов А₁₂ и А₂₃, а вершина — А₃₁.
Считаем определитель третьего порядка: 3-й этап — второй треугольник
Вычитаем из полученного значения произведение элементов второй диагонали. Вторая диагональ начинается в левом нижнем углу и идёт в правый верхний угол.
Считаем определитель третьего порядка: 4-й этап — вторая диагональ
Вычитаем произведение элементов третьего треугольника, в котором основание — элементы А₁₂ и А₂₁, а вершина — А₃₃.
Считаем определитель третьего порядка: 5-й этап — третий треугольник
Последний шаг: вычитаем произведение четвёртого треугольника, с основанием из элементов А₂₃ и А₃₂ и вершиной А₁₁.
Считаем определитель третьего порядка: 6-й этап — четвёртый треугольник
Общий вид формулы для расчёта определителя третьего порядка
Пример расчёта определителя третьего порядка
Транспонированная матрица алгебраических дополнений вычисляется в три шага:
- Мы из исходной матрицы находим матрицу миноров.
- Меняем в матрице миноров знак некоторых элементов и получаем матрицу алгебраических дополнений.
- Находим транспонированную матрицу из матрицы алгебраических дополнений.
Алгоритм вычислений матрицы миноров и матрицы алгебраических дополнений зависит от размера исходной матрицы — чем она больше, тем сложнее формула расчёта. Поэтому мы рассматриваем только матрицы второго и третьего порядка.
Чтобы найти матрицу миноров второго порядка, нам нужно последовательно зачеркнуть три элемента исходной матрицы:
- Вычёркиваем первую строку и первый столбец исходной матрицы — получаем первый элемент первой строки матрицы миноров.

- Вычёркиваем первую строку и второй столбец — получаем второй элемент первой строки матрицы миноров.
- Вычёркиваем вторую строку и первый столбец — получаем первый элемент второй строки матрицы миноров.
- Вычёркиваем вторую строку и второй столбец — получаем второй элемент второй строки матрицы миноров.
Когда матрица миноров составлена — меняем знаки элементов второй диагонали и получаем матрицу алгебраических дополнений. Теперь берём эту матрицу и проводим транспонирование — меняем расположение строк и столбцов. Готово.
Пример вычисления матрицы миноров из матрицы второго порядка
Пример вычисления матрицы алгебраических дополнений (Aᵢⱼ ) из матрицы миноров второго порядка
Пример вычисления транспонированной матрицы алгебраических дополнений (Aᵀᵢⱼ), полученной из матрицы миноров второго порядка
Матрица миноров третьего порядка рассчитывается по следующему принципу:
- Последовательно вычёркиваем строки и столбцы.
- Получаем четыре элемента и считаем определитель.

- Записываем результат в матрицу миноров третьего порядка.
Чтобы не запоминать порядок вычёркивания элементов — попробуйте схему:
- Определите элемент, который вы ищете для матрицы. Пусть это будет A₁₁.
- Найдите этот же элемент в исходной матрице и отметьте его точкой.
- Проведите от этой точки две линии: вдоль строки и вдоль столбца.
После вычёркивания останется квадратная двухразмерная матрица, определитель которой равен разности произведений двух диагоналей.
Пример вычисления первого элемента матрицы миноров из матрицы третьего порядка. Треугольник, или греческая дельта, — это обозначение определителя вне матрицы
Матрицу миноров третьего порядка удобно находить на бумаге с помощью ручки, карандаша и ластика — записываете исходную матрицу, карандашом вычёркиваете линии, считаете определитель, вытираете линии и повторяете процедуру. Рекомендуем попробовать и сверить результат с нашими расчётами.
1-я строка 1-й элемент:
Δ = 5×1 – 8×6 = -43
1-я строка 2-й элемент:
Δ = 4×1 – 7×6 = -38
1-я строка 3-й элемент:
Δ = 4×8 – 7×5 = -3
2-я строка 1-й элемент:
Δ = 2×1 – 8×3 = -22
2-я строка 2-й элемент:
Δ = 1×1 – 7×3 = -20
2-я строка 3-й элемент:
Δ = 1×8 – 7×2 = -6
3-я строка 1-й элемент:
Δ = 2×6 – 5×3 = -3
3-я строка 2-й элемент:
Δ = 1×6 – 4×3 = -6
3-я строка 3-й элемент:
Δ = 1×5 – 4×2 = -3
Считаем матрицу алгебраических дополнений: берём матрицу миноров и меняем на противоположный знак в четырёх элементах — изменяем А₁₂, А₂₁, А₂₃ и А₃₂. Транспонируем полученную матрицу и можем переходить к последнему действию.
Транспонируем полученную матрицу и можем переходить к последнему действию.
Получаем из матрицы третьего порядка матрицу миноров
Меняем знаки в матрице миноров и получаем матрицу алгебраических дополнений (Aᵢⱼ)
Пример вычисления транспонированной матрицы алгебраических дополнений (Aᵀᵢⱼ), полученной из матрицы миноров третьего порядка
Мы нашли все компоненты для вычисления обратной матрицы. Осталось их подставить в формулу, перемножить и записать ответ:
Пример вычисления обратной матрицы второго порядка: мы внесли дробь в матрицу, но могли этого не делать — просто так захотелось
Пример вычисления обратной матрицы третьего порядка: мы оставили дробь за пределами матрицы и вынесли из матрицы минус. Матрица — это таблица с числами, поэтому не обращайте внимание, если числа получаются большими или неудобными
Господи, зачем всё это?
Мы понимаем, что это всё кажется совершенно оторванным от жизни. Какие-то миноры, детерминанты, о чём вообще речь?
Смотрите:
- Вам не нужно уметь решать все эти уравнения самостоятельно.
 Для этого давно есть мощные алгоритмы.
Для этого давно есть мощные алгоритмы. - Достаточно понимать, из чего всё это складывается. Вот матрица. Вот некий алгоритм, который делает из этой матрицы какую-то другую матрицу. Это всё просто арифметика, числа туда, числа сюда.
- В конце этого пути мы покажем, как из этих кубиков собрано машинное обучение. И вы увидите, что машинное обучение — это просто много алгебры. Просто арифметика, числа туда, числа сюда.
- И вы понимаете, что никакого искусственного интеллекта не существует. Это всё, от начала и до конца, работа с числами и расчёты по формулам. Просто когда это делается в больших масштабах, создаётся иллюзия осмысленной деятельности. Ключевое слово — иллюзия.
«Программисты, которые умеют писать алгоритмы, — нишевая профессия»
Спокойствие, всё будет хорошо.
Текст:
Александр Бабаскин
Редактура:
Максим Ильяхов
Художник:
Даня Берковский
Корректор:
Ирина Михеева
Вёрстка:
Мария Дронова
Соцсети:
Олег Вешкурцев
Получите ИТ-профессию
В «Яндекс Практикуме» можно стать разработчиком, тестировщиком, аналитиком и менеджером цифровых продуктов. Первая часть обучения всегда бесплатная, чтобы попробовать и найти то, что вам по душе. Дальше — программы трудоустройства.
Первая часть обучения всегда бесплатная, чтобы попробовать и найти то, что вам по душе. Дальше — программы трудоустройства.
Начать карьеру в ИТ
Калькулятор суммы матриц – MathCracker.com
Решатели Алгебра
Инструкции: Воспользуйтесь нашим пошаговым калькулятором суммы двух матриц, предоставив две ваши матрицы одинакового размера.
При необходимости измените размер матриц, указав количество строк и количество столбцов. Когда у вас есть правильные размеры, которые вы хотите, вы вводите матрицы (вводя числа и перемещаясь по матрице с помощью “TAB”)
Когда у вас есть правильные размеры, которые вы хотите, вы вводите матрицы (вводя числа и перемещаясь по матрице с помощью “TAB”)
The number of rows and columns provided needs to be integers that are greater than 1. The maximum number of rows is 8, and the maximum number of columns is 8
\(A\) = \begin{bmatrix} & \\ & \end{bmatrix}
\(B\) = \begin{bmatrix} & \\ & \end{bmatrix}
Матрицы являются чрезвычайно полезными математическими объектами, которые служат многим различным целям. Действительно, с матрицами можно
решать системы линейных уравнений
, и вообще, вы можете представлять линейные функции.
Матрицы, как и числа, могут оперировать друг с другом. То есть вы можете их складывать, вычитать и умножать при условии соблюдения определенных основных условий размерности.
И даже при условии, что вы оценить, что матрица обратима , вы можете делить на матрицу, как обычное число.
Как суммировать матрицы?
Матрицы могут быть добавлены при условии, что матрицы имеют одинаковый размер. Итак, если вы хотите добавить две матрицы, вы должны выполнить следующие шаги:
Шаг 1:
Убедитесь, что матрицы, которые вы хотите добавить, имеют одинаковый размер. Для этого вам нужно оценить количество столбцов и строк для обеих матриц и убедиться, что эти числа совпадают.
Для этого вам нужно оценить количество столбцов и строк для обеих матриц и убедиться, что эти числа совпадают.
Это первая и вторая матрицы имеют одинаковое количество строк, а первая и вторая матрицы имеют одинаковое количество столбцов.
Обратите внимание, что вы можете добавлять матрицы, которые не возведены в квадрат, если две матрицы имеют одинаковые размеры.
Шаг 2: Как только вы узнаете, что две добавляемые вами матрицы имеют одинаковый размер, вам нужно добавить каждый соответствующий компонент из каждой из матриц.
То есть, чтобы получить запись в первой строке, первом столбце матрицы суммы, вы возьмете запись в первой строке, первом столбце первой матрицы и добавите к ней запись в первой строке, сначала столбец второй матрицы.
И вы делаете то же самое для всех компонентов. Итак, вы добавляете компонент за компонентом.
Можете ли вы добавить матрицу 3×3 и 3×4?
Строго говоря, нельзя, потому что матрицы 3х3 и 3х4 не имеют одинаковых размеров. Теперь некоторые умные математики утверждают, что вы можете “расширить” “меньшую” матрицу 3×3, чтобы “превратить” ее в матрицу 3×4. Ну, там много слов.
Таким образом, определенно имеет смысл попытаться добавить матрицу 3×3 и 3×4, но для большинства целей мы скажем, что нет, вы не можете их добавить.
И то же самое будет применяться, когда вы пытаетесь добавить матрицы разных размеров. Ответ НЕТ, вы не можете их добавить, но вы определенно можете попытаться придать смысл такой операции.
Ответ НЕТ, вы не можете их добавить, но вы определенно можете попытаться придать смысл такой операции.
Вы умеете вычитать матрицы?
Да! Если у вас есть матрицы одинакового размера, вы можете их вычесть. Так же, как вы делаете с дополнением, чтобы вычесть две матрицы вы вычитаете компонент за компонентом.
Вы можете не только складывать или вычитать матрицы, но и
умножить матрицы
A и B при условии, что количество столбцов A совпадает с количеством строк B.
Калькулятор суммы матриц Матричные операции Калькулятор матриц Добавлен калькулятор двух матриц
линейная алгебра – Почему нельзя делить матрицы?
спросил
Изменено 7 лет назад
Просмотрено 21к раз
$\begingroup$
Мне просто интересно, что если матрицы можно умножать, складывать и вычитать, то почему их нельзя делить?
- линейная алгебра
- абстрактная алгебра
- матрицы
$\endgroup$
10
$\begingroup$
МОЖНО делить по матрицам. Чтобы понять, что означает деление в контексте матриц, давайте посмотрим, что означает деление в контексте действительных чисел.
Чтобы понять, что означает деление в контексте матриц, давайте посмотрим, что означает деление в контексте действительных чисел.
$b/a$ в контексте действительных чисел обозначает действительное число $x$, удовлетворяющее $x \cdot a=b$. Поскольку умножение двух действительных чисел коммутативно, то же самое действительное число $x$ также удовлетворяет условию $a \cdot x = b$.
Аналогично, в контексте матриц $B/A$ означает матрицу $X$ такую, что $X \cdot A = B$. Однако в матричной алгебре умножение не является коммутативным. Следовательно, в общем случае неверно, что $X \cdot A = A \cdot X$. Следовательно, вам нужно указать, делите ли вы матрицу справа или слева. Следовательно, если вы ищете матрицу $X$ такую, что $A \cdot X = B$, $X$ обозначается как $X = A\обратная косая черта B$.
$X = B/A$ означает, что вы делите на матрицу $A$ справа, а $X = A\обратная косая черта B$ означает, что вы делите на матрицу $A$ слева. 9{-1}$.
Однако возникает несколько проблем:
Не все ненулевые матрицы обратимы.
 {-1}$), в то время как для действительных чисел они одинаковы. 9{-1}$ матрицы, которые это делают.
{-1}$), в то время как для действительных чисел они одинаковы. 9{-1}$ матрицы, которые это делают.Для некоторых матриц обратная матрица существует и уникальна, и только для этих матриц можно выполнять деление так, как вы пытаетесь это сделать. На уроке линейной алгебры вы узнаете, что эти матрицы являются квадратными матрицами с определителем, не равным $0$.
$\endgroup$
$\begingroup$
Иногда можно, иногда нельзя. Для квадратных невырожденных матриц вы можете умножить на обратную матрицу, чтобы получить идентичность. Для сингулярных матриц обратные не существуют.
Подробнее об этом см. здесь.
Для неквадратных матриц такие обратные не существуют в том же отношении, но есть близкое приближение, даваемое псевдообратным Муром-Пенроузом.
$\endgroup$
4
$\begingroup$
Вы можете умножать, складывать и вычитать целые числа, но не можете их делить (и всегда получаете целое число).
 Также вы можете складывать и вычитать вещественные функции, но не всегда можете делить, если одна из функций имеет ноль, а другая нет и т. д. Объекты, допускающие сложение, вычитание и умножение (но, возможно, не деление) называются кольцами, и они появляются повсюду в математике.
Также вы можете складывать и вычитать вещественные функции, но не всегда можете делить, если одна из функций имеет ноль, а другая нет и т. д. Объекты, допускающие сложение, вычитание и умножение (но, возможно, не деление) называются кольцами, и они появляются повсюду в математике.$\endgroup$
$\begingroup$
можно умножать и складывать и вычитать матрицы, почему нельзя их делить?
Основная причина заключается в том, что хотя матрица аналогична числу, она более аналогична (параллельной операции) массиву из нескольких чисел, и операция может быть нулевой для одного из компонентов. Например, диагональная матрица может иметь на главной диагонали как несколько нулевых, так и ненулевые элементы, нулевые элементы не позволяют ей иметь обратную, и это единственное, что может предотвратить существование обратной. Объяснение в общем случае по существу такое же, путем диагонализации матрицы или ее небольших модификаций.

$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
SCIRP Открытый доступ
Издательство научных исследований
Журналы от A до Z
Журналы по темам
- Биомедицинские и медико-биологические науки.
- Бизнес и экономика
- Химия и материаловедение.
- Информатика. и общ.
- Науки о Земле и окружающей среде.
- Машиностроение
- Медицина и здравоохранение
- Физика и математика
- Социальные науки. и гуманитарные науки
Журналы по теме
- Биомедицина и науки о жизни
- Бизнес и экономика
- Химия и материаловедение
- Информатика и связь
- Науки о Земле и окружающей среде
- Машиностроение
- Медицина и здравоохранение
- Физика и математика
- Социальные и гуманитарные науки
Публикация у нас
- Подача статьи
- Информация для авторов
- Ресурсы для экспертной оценки
- Открытые специальные выпуски
- Заявление об открытом доступе
- Часто задаваемые вопросы
Публикуйте у нас
- Представление статьи
- Информация для авторов
- Ресурсы для экспертной оценки
- Открытые специальные выпуски
- Заявление об открытом доступе
- Часто задаваемые вопросы
Подпишитесь на SCIRP
Свяжитесь с нами
customer@scirp.  org
org+86 18163351462 (WhatsApp) 1655362766 Публикация бумаги WeChat Недавно опубликованные статьи Недавно опубликованные статьи Наведение мостов в высшем образовании: мультимодальные программы наставничества для поддержки удержания и подготовки к карьере ()
Джеймс Хатсон, Роджер Насер, Майкл Марцано, Райан Кертис, Элизабет Макдональд, Сью Эделе, Барбара Хосто-Марти
Творческое образование Том 13 № 9, 16 сентября 2022 г.

DOI: 10.4236/ce.2022.139178 11 загрузок 57 просмотров
Морфологический признак и физико-химическая характеристика почв под Festuca spp. Доминирующая степь у Высокой горы и горы Хувсгул, Монголия()
Саруул Нарангерел, Ундармаа Джамсран, Маки Асано, Кенджи Тамура
Открытый журнал почвоведения Том 12 № 9, 16 сентября 2022 г.
DOI: 10.4236/ojss.2022.129018 16 загрузок 89 просмотров
Исследование рассеяния энергии волн в зоне прибоя Гвинейского залива: пример автономного порта Котону в прибрежной зоне Бенина()
Освальд Г.
 Акклассато, Ноукпо Бернар Токпохозин, Кристиан Д. Аковану, Аджимон Матиас Хуекпоэха, Ги Эрве Унге, Бруно Базиль Куноухева,
Акклассато, Ноукпо Бернар Токпохозин, Кристиан Д. Аковану, Аджимон Матиас Хуекпоэха, Ги Эрве Унге, Бруно Базиль Куноухева,Journal of Modern Physics Vol.13 No.9, 16 сентября 2022 г.
DOI: 10.4236/jmp.2022.139076 10 загрузок 57 просмотров
Модель скалярного поля обеспечивает возможный мост между общей теорией относительности и квантовой механикой()
Рики В. Остин
Международный журнал астрономии и астрофизики Том 12 № 3, 16 сентября 2022 г.
DOI: 10.4236/ijaa.2022.123014 10 загрузок 57 просмотров
Характеристики состава тела и взаимосвязь между мышечной массой и мышечной силой у пожилых женщин в различных возрастных группах()
Нао Нишиока Ниши, Норико Танака, Наоми Хирано
Успехи в исследованиях старения Том 11 № 5, 16 сентября 2022 г.

DOI: 10.4236/aar.2022.115010 7 загрузок 40 просмотров
Профиль черепно-мозговой травмы в отделениях неотложной помощи больниц — ретроспективное исследование в Республике Молдова ()
Светлана Кочу, Анжела Казаку-Страту, Лилия Киосеа, Георгий Ройновяну, Сергей Чебану, Коринн Пик-Аса
Открытый журнал профилактической медицины Том 12 № 9, 16 сентября 2022 г.
DOI: 10.4236/ojpm.2022.129013 13 загрузок 81 просмотр
Подпишитесь на SCIRP
Свяжитесь с нами
клиент@scirp.  org
org+86 18163351462 (WhatsApp) 1655362766 Публикация бумаги WeChat Бесплатные информационные бюллетени SCIRP
Copyright © 2006-2022 Scientific Research Publishing Inc. Все права защищены.
верхнийКак разделить матрицу в Python? – Leonieclaire.com
Как разделить матрицу в Python?
Обработка матриц в Python
- add() — добавить элементы двух матриц.
- вычитание () — вычитание элементов двух матриц.
- разделить () — разделить элементы двух матриц.
- умножить () — умножить элементы двух матриц.
- точка () — выполняет матричное умножение, а не поэлементное умножение.

Можно ли разделить массивы в Python?
NumPy Поэлементное деление С помощью функции / Operator true_divide() в Python. Мы можем использовать оператор /, чтобы разделить один массив на другой массив и сохранить результаты в третьем массиве. См. следующий пример кода.
Как разделить матрицу на вектор в Numpy?
Матрица — это двумерный массив, а вектор — это просто одномерный массив. Если мы хотим разделить элементы матрицы на элементы вектора в каждой строке, мы должны добавить к вектору новое измерение. Мы можем добавить новое измерение к вектору с помощью метода нарезки массива в Python.
Что делает деление NP?
разделить. Возвращает истинное деление входных данных по элементам. Истинное деление регулирует тип вывода, чтобы представить лучший ответ, независимо от типа ввода. …
Как работает матрица Python?
- Как работают матрицы Python?
- Создайте матрицу Python, используя тип данных вложенного списка.

- Чтобы прочитать данные внутри Python Matrix, используя список.
- Пример 2: Чтобы прочитать последний элемент из каждой строки.
- Пример 3: Распечатать строки в матрице.
- Добавление матриц с помощью вложенного списка.
- Умножение матриц с использованием вложенного списка.
Что такое деление матрицы?
Для матриц нет такого понятия, как деление. Вы можете складывать, вычитать и умножать матрицы, но не можете их делить. Однако существует родственное понятие, которое называется «инверсия». Поскольку умножение на 1/3 равносильно делению на 3, вы также можете умножить обе части на 1/3, чтобы получить тот же ответ: x = 2,9.0005
Можно ли разделить массив?
Разделение массива Массивы также могут иллюстрировать деление. Поскольку деление является обратным или «противоположным» умножению, вы можете использовать массивы, чтобы помочь учащимся понять, как связаны умножение и деление.
Делит ли Numpy быстрее, чем Python?
число.
 разделить(x1, x2) Эквивалентно x1 / x2 с точки зрения широковещательной передачи массива. Похоже, что деление Python обычно работает быстрее, что наводит меня на мысль, что деление Numpy реализует некоторые дополнительные навороты.
разделить(x1, x2) Эквивалентно x1 / x2 с точки зрения широковещательной передачи массива. Похоже, что деление Python обычно работает быстрее, что наводит меня на мысль, что деление Numpy реализует некоторые дополнительные навороты.Как остановить деление на ноль в Python?
Решение 1 Python не может делить число на ноль. Перед выполнением деления или операции по модулю знаменатель должен быть проверен на ненулевое значение.
Что такое матричный Python?
Матрица Python — это специализированный двумерный прямоугольный массив данных, хранящихся в строках и столбцах. Данные в матрице могут быть числами, строками, выражениями, символами и т. д. Матрица — одна из важных структур данных, которую можно использовать в математических и научных расчетах.
Возможно ли разделение матрицы?
Для матриц нет такого понятия, как деление. Вы можете складывать, вычитать и умножать матрицы, но не можете их делить. Поскольку умножение на 1/3 равносильно делению на 3, вы также можете умножить обе части на 1/3, чтобы получить тот же ответ: x = 2.

Какой пример матричного деления в Python?
Это пример матрицы ( foto_dct [3,3], хотя я проделал над ней некоторые операции, 3-й столбец матриц, 3-я строка матриц, если вы помните из шага 1.) Как видите, например, возьмем элемент [0,0] = 613, поэтому после деления мы должны получить [0,0] = 613/16 = 38,3125 (как видите, оно также автоматически округляется?)
Какое деление массива в Python верно?
Элемент массива из первого массива делится на элементы из второго массива (все происходит поэлементно). И arr1, и arr2 должны иметь одинаковую форму. Возвращает истинное деление по элементам. Python традиционно придерживается «этажного разделения». Независимо от типа ввода, истинное деление корректирует ответ наилучшим образом.
Как сделать истинное деление в NumPy в Python?
numpy.divide ¶. numpy.разделить. ¶. Возвращает истинное деление входных данных по элементам. Вместо традиционного для Python «этажного деления» это возвращает истинное деление.
 Истинное деление регулирует тип вывода, чтобы представить лучший ответ, независимо от типа ввода. Массив дивидендов. Массив делителей.
Истинное деление регулирует тип вывода, чтобы представить лучший ответ, независимо от типа ввода. Массив дивидендов. Массив делителей.Как разделить матрицу на более мелкие в Python?
Я сохранил монохромные значения каждого пикселя в матрице под названием «pixelMatrix». Эта команда превращает большую матрицу (128×128) в меньшие (8×8). Теперь, после этого, мне нужно разделить каждую матрица в foto_dct на другую матрицу (называемую Q в этом коде) поэлементно.
Разделить каждую строку матрицы на элементы вектора в R
В этой статье мы обсудим, как разделить каждую строку матрицы на элементы вектора в языке программирования R.
Метод 1: Использование стандартного деленияСначала вычисляется транспонирование матрицы, чтобы поменять местами строки и столбцы.
 Первоначально, если размеры матрицы были n * m , транспонирование преобразует размеры в m * n. Транспонирование матрицы необходимо вычислить, потому что логический оператор деления «/» применяется к столбцам, а нам нужно вычислить деление по строкам. Затем применяется операция деления с использованием матрицы транспонирования в качестве одного операнда и вектора в качестве другого. Затем выполняется транспонирование этого результата, чтобы снова сохранить порядок строк и столбцов.
Первоначально, если размеры матрицы были n * m , транспонирование преобразует размеры в m * n. Транспонирование матрицы необходимо вычислить, потому что логический оператор деления «/» применяется к столбцам, а нам нужно вычислить деление по строкам. Затем применяется операция деления с использованием матрицы транспонирования в качестве одного операнда и вектора в качестве другого. Затем выполняется транспонирование этого результата, чтобы снова сохранить порядок строк и столбцов.Syntax:
t(transpose_matrix/vector)
Example:
R
matrix <-matrix(1:12,ncol=3)Печать(«Оригинальная матрица»)
0(MATRIX)(MATRIX)(MATRIX)(MATRIX)(MATRIX)(MATRIX). 0527 c
0527 c (1:3)trans_mat <-t(matrix)div <-t(trans_mat/vec)print("Division matrix")print(div)Output
[1] «Исходная матрица» [1] [2] [3] [1,] 1 5 9 [2,] 2 6 10 [3,] 3 7 11 [4,] 4 8 12 [1] «Матрица деления» [1] [2] [3] [1,] 1 2,5 3,000000 [2,] 2 3,0 3,333333 [3,] 3 3,5 3,666667 [4,] 4 4.0 4.000000Метод 2: Использование метода развертки()Этот метод на языке R возвращает массив, полученный из входного массива путем подметания сводной статистики.
 Метод используется для вычисления арифметических операций над фреймом данных по выбранной оси. Для построчной операции выбрана ось 2, а операндом становится строка фрейма данных. Результат должен быть сохранен в другой переменной. Время, затрачиваемое на эту операцию, эквивалентно количеству строк во фрейме данных. Тип данных результирующего столбца — это самый большой совместимый тип данных.
Метод используется для вычисления арифметических операций над фреймом данных по выбранной оси. Для построчной операции выбрана ось 2, а операндом становится строка фрейма данных. Результат должен быть сохранен в другой переменной. Время, затрачиваемое на эту операцию, эквивалентно количеству строк во фрейме данных. Тип данных результирующего столбца — это самый большой совместимый тип данных.Синтаксис: Sweep (DF, Axis, VEC, OP)
Параметр:
- DF- DataFrame
- AXIS-. column-wise, use axis = 2
- vec – The vector to apply on the data frame
- op – The operator to apply
Example:
R
матрица <-matrix(1:12,ncol=3)print("Original Matrix")print(matrix)VEC <-C(1: 3)Div <-Sweep(MATRIX, 2, VEC, VEC, VEC,.
print("Division matrix")print(div)Output
[1] "Original Matrix" [1] [2] [3] [1,] 1 5 9 [2,] 2 6 10 [3,] 3 7 11 [4,] 4 8 12 [1] «Матрица деления» [1] [2] [3] [1,] 1 2,5 3,000000 [2,] 2 3,0 3,333333 [3,] 3 3,5 3,666667 [4,] 4 4,0 4,000000Метод 3: Использование метода rep()Метод rep(x) в R используется для репликации значений в векторе x. Он принимает в качестве аргумента аргумент «каждый», где каждый элемент повторяется определенное количество раз. Функция rep() копирует числовые значения, текст или значения вектора определенное количество раз.
Синтаксис: rep ( vec, each = )
Параметр:
- vec : Вектор, значение которого реплицировано.

- каждый: неотрицательное целое число. Другие входные данные будут приведены к целочисленному или двойному вектору, и будет взят первый элемент.
Идея применения метода rep() здесь состоит в том, чтобы создать репликацию вектора и сложить его вместе, чтобы создать количество копий, эквивалентное количеству строк. Далее следует деление задействованных матриц.
Пример:
Ч
matrix <-matrix(1:16,ncol=2)print("Original Matrix")print(Matrix)VEC <-C(1: 2)
110 0528
0528div <- matrix /rep(vec, each = rows)print("Division matrix")print(div)Вывод
[1] «Исходная матрица» [1] [2] [1,] 1 9 [2,] 2 10 [3,] 3 11 [4,] 4 12 [5,] 5 13 [6,] 6 14 [7,] 7 15 [8,] 8 16 [1] «Матрица деления» [1] [2] [1,] 1 4,5 [2,] 2 5,0 [3,] 3 5,5 [4,] 4 6,0 [5,] 5 6,5 [6,] 6 7,0 [7,] 7 7,5 [8,] 8 8,0Метод 4: Использование метода apply()Метод apply() является формой метода сбора, который используется для применения преобразований ко всему указанному объекту.
 Метод apply() принимает в качестве входных данных кадр данных или матрицу и выдает выходные данные в виде вектора, списка или массива.
Метод apply() принимает в качестве входных данных кадр данных или матрицу и выдает выходные данные в виде вектора, списка или массива.Синтаксис: Применить (Матрица, Ось, развлечение)
Параметр:
- Матрикс: Асписная или матрица
- .0014
- ось =1 : манипуляция по строкам
- ось =2 : манипуляция по столбцам
- ось=c(1,2) : манипуляция выполняется на строках и столбцах
- A инъективен ровно тогда, когда у него есть нулевое ядро
- A сюръективен именно тогда, когда он имеет полное изображение.
- A имеет обратное B
- Существует матрица B такая
- Поймите, что означает обратимость квадратной матрицы.
- Узнайте об обратимых преобразованиях и поймите взаимосвязь между обратимыми матрицами и обратимыми преобразованиями.
- Рецепты: вычислить обратную матрицу, решить линейную систему, взяв обратные.
- Изображение: обратное преобразование.
- Словарные слова: обратная матрица , обратное преобразование .

- A−1 обратим, и его обращение равно (A−1)−1=A.
- AB обратим, и его инверсия равна (AB)−1=B−1A−1 (обратите внимание на порядок).
- Уравнения AA-1=In и A-1A=In одновременно отображают A-1 как инверсию A и A как инверсию A-1.
- Мы вычисляем
(B-1A-1)AB=B-1(A-1A)B=B-1InB=B-1B=In.
Здесь мы использовали ассоциативность матричного умножения и тот факт, что InB=B. Это показывает, что B−1A−1 является инверсией AB. - Если det(A)A=0, то A обратим, и A-1=1det(A)Fd-b-caG.
- Если det(A)=0, то A необратима.
- Преобразование T:Rn→Rn обратимо тогда и только тогда, когда оно взаимно однозначно и на.
- Если уже известно, что Т обратимо, то U:Rn→Rn является инверсией T при условии, что либо T◦U=IdRn, либо U◦T=IdRn: необходимо проверить только одно.

Транспонирование результата должно быть вычислено для сохранения порядка после применения метода apply(), поскольку метод apply() возвращает транспонированную матрицу.
Example:
R
|
1111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111159.
[1] [2]
[1,] 1 9[2,] 2 10
[3,] 3 11
[4,] 4 12
[5,] 5 13
[6,] 6 14
[7,] 7 15
[8,] 8 16
[1] «Матрица деления»
[1] [2]
[1,] 1 4,5
[2,] 2 5,0
[3,] 3 5,5
[4,] 4 6,0
[5,] 5 6,5
[6,] 6 7,0
[7,] 7 7,5
[8,] 8 8. 0 Метод 5: Использование оператора %*%
0 Метод 5: Использование оператора %*% Оператор %*% — это особый вид оператора умножения, определенный для умножения матриц. Этот оператор используется для умножения матрицы на ее транспонирование. Первоначально диагональная матрица вычисляется для указанного вектора с помощью функции diag() в R. Она принимает в качестве аргумента вектор, обратный вектору, а затем эта матрица умножается на исходную матрицу для выполнения деления. Это устраняет необходимость явного деления, потому что обратное уже учтено.
Синтаксис: diag( x )
Параметр:
x: вектор, который должен присутствовать в качестве диагональных элементов.
Example:
R
matrix <- matrix (1:16,ncol=2)
print ( "Original Матрица" )
печать (matrix)
vec <- c (1:2)
rows <- nrow (matrix)
div <- matrix %*% diag (1 / vec)
print ( "Division matrix" )
print (дел)
Вывод
[1] «Исходная матрица»
[1] [2]
[1,] 1 9
[2,] 2 10
[3,] 3 11
[4,] 4 12
[5,] 5 13
[6,] 6 14
[7,] 7 15
[8,] 8 16
[1] «Матрица деления»
[1] [2]
[1,] 1 4,5
[2,] 2 5,0
[3,] 3 5,5
[4,] 4 6,0
[5,] 5 6,5
[6,] 6 7,0
[7,] 7 7,5
[8,] 8 8,0
29.
 Деление на ноль для инвертирования матриц
Деление на ноль для инвертирования матриц Пропустил блог. В конце этого эпизода я напишу немного о том, чем я занимался последние несколько месяцев. А пока давайте просто вернемся к графической линейной алгебре.
Чтобы мотивировать себя вернуться к писательству, я привел эпизод, который меня волновал с конца прошлого года, когда я впервые провел исследование. Этот материал тесно связан с Эпизодом 26 о делении на ноль. Если вы не читали или забыли, будет полезно взглянуть, прежде чем продолжить.
Эпизод 26 был довольно популярен — возможно, помогло кликбейтное название. У некоторых людей это вызвало скептицизм: хорошо, значит, этот парень вывел таблицы сложения и умножения, которые, кажется, говорят, что деление на ноль имеет смысл. Но может ли эта странная идея деления на ноль быть полезной или это просто любопытство?
Существуют и другие системы счисления, которые в принципе «позволяют» делить на ноль. Многие из них работают аналогично стандарту IEEE для арифметики с плавающей запятой, который имеет дополнительный объект, называемый NaN (не число). Грубо говоря, это результат всех вычислений, которые не должны иметь смысла, вроде деления на ноль. Затем, если вы добавите и умножите NaN на что-либо еще, у вас все равно будет NaN. Так что это похоже на число черной дыры: как только вы получите его на полпути к своим вычислениям, вы можете быть почти уверены, что что-то пошло не так, и что общий результат будет NaN — что бы вы ни делали, вы никогда не закончите снова с обычным номером.
Грубо говоря, это результат всех вычислений, которые не должны иметь смысла, вроде деления на ноль. Затем, если вы добавите и умножите NaN на что-либо еще, у вас все равно будет NaN. Так что это похоже на число черной дыры: как только вы получите его на полпути к своим вычислениям, вы можете быть почти уверены, что что-то пошло не так, и что общий результат будет NaN — что бы вы ни делали, вы никогда не закончите снова с обычным номером.
В системе счисления из Эпизода 26 дело обстоит иначе. На самом деле три дополнительных элемента ∞, ⊥, ⊤ действительно проявляются в вычислениях. Круто то, что они не провал, как NaN: вам не нужно паниковать, если вы получите, скажем, ⊥ в одном из ваших вычислений. Не исключено, что дело закончится хорошо. Этот выпуск целиком посвящен одному примеру: обращению матриц.
Нам понадобится несколько определений.
Говорят, что матрица A размера n×m равна обратимый когда существует матрица B размером m×n, такая что при составлении в любом направлении вы получаете тождество. На диаграммах:
На диаграммах:
Если такое B существует, мы иногда пишем A -1 = B. Многие матрицы необратимы. Одно из свойств состоит в том, что m=n, то есть все обратимые матрицы квадратные; количество строк равно количеству столбцов.
На самом деле, в большинстве PROP происходит то же самое: обычно инвертировать можно только то, где левая и правая границы имеют одинаковый размер. Следует иметь в виду полезную интуицию: что-то может быть обратимым только в том случае, если это можно отменить. А поскольку провода несут информацию, мы не можем просто выбросить одну или добавить новую и ожидать, что сможем ее отменить.
Назад к определениям. Мы будем говорить, что матрица A размера n × m является инъективной или моно , когда верно следующее.
Обратная сторона А — это не что иное, как симметрия зеркального отображения †, которую мы обсуждали в Эпизоде 27.
Приведенное выше определение, вероятно, кажется немного странным. В большинстве обычных учебников по линейной алгебре определяющим свойством инъективной матрицы размера n × m является то, что она переводит разные m-векторы в разные n-векторы: то есть она является инъективной как функция. На самом деле это эквивалентная формулировка, но мы не думаем о матрицах как о функциях в этом блоге.
В большинстве обычных учебников по линейной алгебре определяющим свойством инъективной матрицы размера n × m является то, что она переводит разные m-векторы в разные n-векторы: то есть она является инъективной как функция. На самом деле это эквивалентная формулировка, но мы не думаем о матрицах как о функциях в этом блоге.
Одно интересное свойство мономатриц состоит в том, что они сокращаемы слева: то есть, если даны две матрицы одинакового размера B, C, для которых определены AB и AC, если AB=AC, то B=C. На самом деле это верно, когда B и C являются линейными отношениями. Схематически:
подразумевает, что
Здесь В и С - линейные отношения, т.е. произвольные диаграммы в IH . Это, конечно, включает случай, когда B и C являются матрицами.
На самом деле инъективность и левосократимость также эквивалентны, т.е. допустив одно, можно доказать другое. Доказательства оставлю в качестве упражнения, а дам подсказку: удобно использовать изложенный в эпизоде 27 факт, что для любого линейного отношения A, A † — его слабая инверсия.
Причудливое инъективное сюръективное . Мы также будем использовать слово epi . Таким образом, матрица размера n×m является сюръективной, если верно следующее:
Точно так же, как мономатрицы сокращаемы слева, эпиматрицы сокращаемы справа; при заданных B и C, таких что BA и CA имеют смысл, если BA=CA, то B=C. С точки зрения обычной линейной алгебры сюръективные матрицы — это те, которые сюръективны как функции; для каждого n-вектора b , существует m-вектор a такой, что A a = b .
И последнее наблюдение , которое нам понадобится позже: любая обратимая матрица одновременно инъективна и сюръективна. Чтобы не останавливаться на достигнутом, я также оставлю доказательство этого в качестве упражнения.
Теперь докажем классический результат линейной алгебры. Это относится к ядрам и образам, которые являются линейными подпространствами, которые мы обсуждали в предыдущем эпизоде.
Лемма о ядре и образе. Предположим, что A является матрицей размера m×n. Тогда:
Доказательство. Свойства 1 и 2 взаимно причудливы, поэтому достаточно доказать только одно. Мы сделаем 1.
Предположим, что A инъективен. Тогда:
Это означает, что A имеет нулевое ядро.
Теперь предположим, что A имеет нулевое ядро; мы хотим показать, что оно должно быть инъективным.
Все, готово, QED.
Следующая лемма очень полезна, поскольку дает нам полезную графическую интуицию относительно обратимых матриц.
Лемма об обратимой матрице
Предположим, что A — квадратная матрица размера m. Тогда следующие эквивалентны
Доказательство . Сначала покажем, что из 1 следует 2. Предполагая 1, предположим, что A имеет обратное B. Поскольку A обратимо, мы знаем, что A инъективно. Итак, у нас есть следующее:
Сначала покажем, что из 1 следует 2. Предполагая 1, предположим, что A имеет обратное B. Поскольку A обратимо, мы знаем, что A инъективно. Итак, у нас есть следующее:
Что дает нам 2. На первом этапе мы использовали предположение, что B является обратным A, а на втором этапе мы использовали тот факт, что A инъективен.
Нам все еще нужно показать, что 2 подразумевает 1. Итак, предположим, что A равно некоторой матрице B, направленной в противоположном направлении, нам нужно показать, что B является обратной матрицей A. Для этого полезно показать, что A должен быть инъективным. Здесь мы можем использовать наши Лемма о ядре и образе .
Итак, по лемме о ядре A инъективен. Теперь мы можем использовать это, чтобы показать, что A, за которым следует B, является тождеством.
Чтобы показать, что B, за которым следует A, также является тождеством, мы можем сделать странную вещь, сначала показав, что B сюръективно.
Наша цель — получить формулу обратной матрицы, если она существует. Отправной точкой является произвольная матрица 2×2, поэтому что-то вроде этого:
Отправной точкой является произвольная матрица 2×2, поэтому что-то вроде этого:
Если существует обратная матрица, то мы знаем, что это также будет матрица 2×2:
Сложность заключается в том, как мы можем вычислить a’, b’, c’ и d’, зная a, b, c и d? Если вы помните свою линейную алгебру, возможно, вы думаете об определителях и сопряженных матрицах. Мы обойдем все это и вместо этого нарисуем несколько картинок.
Давайте начнем с нашей леммы об обратимой матрице . Как диаграммы в IH , мы имеем:
Теперь добавление матрицы к -1 само по себе дает нам нулевую матрицу. Используя это тривиальное наблюдение, мы получаем следующее довольно сложное уравнение:
Мы можем извлечь формулу для каждого из a’, b’, c’ и d’ , подключив некоторые из оборванных проводов в приведенном выше уравнении. Давайте проработаем процедуру для a’.
Первый шаг — поставить нули и отбрасывать в нужных местах с обеих сторон, например:
Делая это, мы получаем первое равенство ниже.
Второе равенство следует из уравнения кости бимоноидов.
Пока все хорошо: но теперь мы можем радикально упростить левую часть. По сути, мы вставили белую единицу в черную коумножение, и наоборот; обычно, когда это происходит, происходит массовое уничтожение. Я оставлю вам графический вывод. После того, как вы удалили большую часть диаграммы, левая часть в итоге будет выглядеть так:
Приятно то, что теперь a’ — это единственный оставшийся элемент обратной матрицы. И мы уже знаем, что диаграмма выше равна нулю, т.е.
Таким образом, мы находимся в ситуации, когда а’ плюс -1, умноженное на некоторый беспорядок, равно 0; таким образом:
Это начинает выглядеть как формула. Мы можем распутать все еще несколько грязную правую сторону выше. Результат:
С точки зрения добросовестной, старомодной синтаксической формулы — если вы увлекаетесь такими вещами — это переводится как:
Обратите внимание, что я не пошел дальше в упрощении знаменателя, потому что d может быть нулем , и в этом случае умножение может не быть коммутативным. Расслабляться; чтобы оценить формулу для конкретных чисел, мы можем использовать наши таблицы сложения и умножения из эпизода 26.
Расслабляться; чтобы оценить формулу для конкретных чисел, мы можем использовать наши таблицы сложения и умножения из эпизода 26.
В a’ нет ничего особенного. Мы адаптируем нашу процедуру, подключив другие комбинации проводов и получив формулы для b’, c’ и d’. Все вместе:
Я нахожу довольно забавным перестановку a, b, c и d в каждой из формул. И никаких определителей, ни помощников не видно!
Давайте сделаем рабочий пример, вычислив обратную матрицу:
Ссылаясь на формулу обратной, мы имеем d=0, поэтому мы будем делить на ноль при вычислении a’. Для этого мы можем обратиться к таблицам умножения и сложения из Эпизода 26. Вот расчет:
Другие вычисления не содержат ничего смешного — мы получаем
Я обещал вам пример, где расширенная рациональная алгебра эпизода 26 может быть полезна. И хотя инвертирование матриц 2×2 не зажжет мир, я надеюсь, что это намек на то, что происходит что-то интересное!
Кстати, формула, которую мы вывели для обращения матриц 2×2, обобщается на произвольные квадратные матрицы. У меня нет места для этого в этом эпизоде, но если есть интерес, я могу вернуться к этой теме. Дай мне знать.
У меня нет места для этого в этом эпизоде, но если есть интерес, я могу вернуться к этой теме. Дай мне знать.
Не писать — все равно, что не ходить в спортзал (в чем, кстати, я тоже виноват). Я имею в виду, что как только вы начинаете не писать, вам трудно вернуться к этому. «Я напишу кое-что на следующих выходных», — говорите вы себе. Прежде чем вы это знаете, прошло полгода. То же самое с (не)ходить в спортзал. Я все еще работаю над этим.
Это были очень напряженные полгода. Помимо преподавания, я побывал в Париже, а точнее, у Жана Кривина, на месяц. Я люблю Париж; В 2005 году я проработал там шесть месяцев постдоком, и было здорово снова оказаться в округе 13 e .
Помимо удовольствия от города, это было действительно продуктивное посещение, и я многому научился. В настоящее время Джин работает над графическим языком программирования высокого уровня для биологов, который имеет много общего со строковыми диаграммами, которыми одержим этот блог.
Среди прочего Джин рассказала мне о семействе строковых диаграммных исчислений для логики, разработанных известным американским логиком XIX века К. С. Пирсом (произносится как «кошелек»; по-видимому, это голландский язык). Джин использует некоторые идеи Пирса для своего языка программирования. Системы Пирса называются экзистенциальными графами и имеют захватывающую историю. Хотя Пирс считал их своим самым важным научным достижением, они оставались неопубликованными при его жизни; Я предполагаю, что из-за отсутствия технологии набора для диаграмм, но, может быть, также из-за того, что его идеи были настолько революционными, что опередили свое время примерно на 100 лет. На самом деле, диаграммы Пирса предшествовали стандартному синтаксическому способу записи логики со всеми перевернутыми буквами А и перевернутыми буквами Е, которые так любят логики. Но его работы были забыты и заново открыты только в 1960-е годы. Они до сих пор являются предметом исследования.
Экзистенциальные графы меня просто поразили. Я планирую как следует понять их в течение следующих нескольких месяцев и, возможно, когда-нибудь напишу о них более серьезно. На данный момент, если вам интересно читать дальше, докторская диссертация Фритьофа Дау кажется отличным ресурсом.
Я планирую как следует понять их в течение следующих нескольких месяцев и, возможно, когда-нибудь напишу о них более серьезно. На данный момент, если вам интересно читать дальше, докторская диссертация Фритьофа Дау кажется отличным ресурсом.
В эти выходные я буду в Порту на семинаре HDRA, а через выходные я лечу в Нью-Йорк на конференцию LiCS. Лето будет насыщенным, но с этого момента я постараюсь работать над блогом более регулярно.
Продолжить чтение с Эпизода 30 – Сущность графической линейной алгебры.
Нравится:
Нравится Загрузка...
Обратные матрицы
Цели
В разделе 3.1 мы научились перемножать матрицы. В этом разделе мы научимся «делить» по матрице. Это позволяет нам элегантно решить матричное уравнение Ax=b:
Ах=b⇐⇒x=A−1b.
Однако при «делении на матрицы» следует соблюдать осторожность, поскольку не каждая матрица имеет обратную, а порядок умножения матриц важен.
, обратное , или , обратное ненулевого числа a, — это число b, которое характеризуется тем свойством, что ab=1. Например, обратное число 7 равно 1/7. Мы используем эту формулировку для определения обратной матрицы.
Определение
Пусть A — матрица размера n × n (квадратная). Мы говорим, что A является обратимым , если существует n × n матрица B такая, что
AB=In и BA=In.
В этом случае матрица B называется обратной из A, и мы пишем B=A−1.
Мы должны потребовать AB=In и BA=In, потому что в общем случае умножение матриц не является коммутативным. Однако в этом следствии в разделе 3.6 мы покажем, что если A и B являются матрицами размера n × n, такими что AB = In, то автоматически BA = In.
Однако в этом следствии в разделе 3.6 мы покажем, что если A и B являются матрицами размера n × n, такими что AB = In, то автоматически BA = In.
Пример
Факты об обратимых матрицах
Пусть A и B — обратимые матрицы размера n × n.
Доказательство
Почему инверсия AB не равна A−1B−1? Если бы это было так, то у нас было бы
In=(AB)(A-1B-1)=ABA-1B-1.
Но нет никаких оснований для того, чтобы ABA-1B-1 равнялась единичной матрице: нельзя поменять местами A-1 и B, поэтому в этом выражении нечего отменять. На самом деле, если In=(AB)(A−1B−1), то мы можем умножить обе части справа на BA, чтобы сделать вывод, что AB=BA. Другими словами, (AB)-1=A-1B-1 тогда и только тогда, когда AB=BA.
На самом деле, если In=(AB)(A−1B−1), то мы можем умножить обе части справа на BA, чтобы сделать вывод, что AB=BA. Другими словами, (AB)-1=A-1B-1 тогда и только тогда, когда AB=BA.
В более общем смысле, обратным произведением нескольких обратимых матриц является произведение обратных в обратном порядке; доказательство такое же. Например,
(АВС)-1=С-1В-1А-1.
До сих пор мы определяли обратную матрицу, не давая никакой стратегии ее вычисления. Мы делаем это сейчас, начиная со специального случая матриц 2×2. Затем мы дадим рецепт для случая n×n.
Определение
Определитель матрицы 2×2 есть число
detFabcdG=ad-bc.
Предложение
Пусть A=FabcdG.
Существует аналогичная формула для обратной матрицы размера n×n, но она не так проста и требует больших вычислительных ресурсов. Заинтересованный читатель может найти его в этом подразделе Раздела 4. 2.
2.
Пример
Следующая теорема дает общую процедуру вычисления A−1.
Теорема
Пусть A — матрица размера n × n, и пусть (A|In) — матрица, полученная путем увеличения A единичной матрицей. Если редуцированная ступенчатая форма строки (A|In) имеет форму (In|B), то A обратима и B=A−1. В противном случае A необратима.
Доказательство
Сначала предположим, что редуцированная ступенчатая форма строки (A|In) не имеет формы (In|B). Это означает, что в первых n столбцах (нерасширенная часть) содержится менее n опорных точек, поэтому у A меньше n опорных точек. Отсюда следует, что Nul(A)A={0} (уравнение Ax=0 имеет свободную переменную), поэтому в Nul(A) существует ненулевой вектор v. Предположим, что существует матрица B такая, что BA=In. Затем
v=Inv=BAv=B0=0,
, что невозможно, так как vA=0. Следовательно, A необратима.
Теперь предположим, что редуцированная ступенчатая форма строки (A|In) имеет вид (In|B). В этом случае все опорные точки содержатся в нерасширенной части матрицы, поэтому расширенная часть не играет роли в сокращении строк: элементы расширенной части не влияют на выбор используемых операций над строками. Следовательно, редукция строк (A|In) эквивалентна решению n систем линейных уравнений Ax1=e1,Ax2=e2,...,Axn=en, где e1,e2,...,en стандартные векторы координат :
Следовательно, редукция строк (A|In) эквивалентна решению n систем линейных уравнений Ax1=e1,Ax2=e2,...,Axn=en, где e1,e2,...,en стандартные векторы координат :
Ax1=e1:C1041000120100-3-4001DAx2=e2:C1041000120100-3-4001DAx3=e3:C1041000120100-3-4001D. Столбцы x1,x2,...,xn матрицы B в приведенной по строкам форме являются решениями следующих уравнений:
AC100D=e1:C1001-6-20100-2-100103/21/2DAC-6-23/2D=e2:C1001-6-20100-2-100103/21/2DAC-2-11/2D=e3:C1001- 6-20100-2-100103/21/2Д. В соответствии с этим фактом в разделе 3.3 произведение Bei является просто i-м столбцом xi матрицы B, поэтому
ei=Axi=ABei
для всех i. По тому же факту i-й столбец матрицы AB равен ei, а это означает, что матрица AB единична. Таким образом, B является инверсией A.
Пример (обратимая матрица)
Пример (необратимая матрица)
В этом подразделе мы научимся решать Ax=b путем «деления на A».
Теорема
Пусть A — обратимая матрица размера n × n, а b — вектор в Rn. Тогда матричное уравнение Ax=b имеет ровно одно решение:
Тогда матричное уравнение Ax=b имеет ровно одно решение:
х=А-1б.
Доказательство
Считаем:
Ax=b=⇒A−1(Ax)=A−1b=⇒(A−1A)x=A−1b=⇒Inx=A−1b=⇒x=A−1b.
Здесь мы использовали ассоциативность матричного умножения и тот факт, что Inx=x для любого вектора b.
Пример (Решение системы 2 × 2 с использованием инверсий)
Пример (Решение системы 3 × 3 с использованием инверсий)
Преимущество решения линейной системы с использованием обратных величин заключается в том, что решение матричного уравнения Ax=b для других или даже неизвестных значений b становится намного быстрее. Например, в приведенном выше примере решение системы уравнений
E2x1+3x2+2x3=b1x1+3x3=b22x1+2x2+3x3=b3,
, где b1,b2,b3 неизвестны, равно
Cx1x2x3D=C232103223D-1Cb1b2b3D=C-6-5932−422−3DCb1b2b3D=C−6b1−5b2+9b33b1+2b2−4b32b1+2b2−3b3D.
Как и в случае умножения матриц, обращение матриц полезно понимать как операцию над линейными преобразованиями. Напомним, что тождественное преобразование на Rn обозначается IdRn.
Напомним, что тождественное преобразование на Rn обозначается IdRn.
Определение
Преобразование T:Rn→Rn является обратимым , если существует преобразование U:Rn→Rn такое, что T◦U=IdRn и U◦T=IdRn. В этом случае преобразование U называется обратным преобразования T, и мы пишем U=T−1.
Инверсия U к T «отменяет» все, что сделал T. У нас есть
T◦U(x)=xandU◦T(x)=x
для всех векторов x. Это означает, что если вы примените T к x, затем примените U, вы получите вектор x обратно, и то же самое в другом порядке.
Пример (функции одной переменной)
Пример (Расширение)
Пример (вращение)
Пример (Отражение)
Не пример (проекция)
Предложение
Как и следовало ожидать, матрица, обратная линейному преобразованию, является обратной матрицей преобразования, как утверждает следующая теорема.
Теорема
Пусть T:Rn→Rn — линейное преобразование со стандартной матрицей A. Тогда T обратимо тогда и только тогда, когда обратимо A, и в этом случае T−1 линейно со стандартной матрицей A−1.
Доказательство
Предположим, что T обратим. Пусть U:Rn→Rn — обратное к T. Мы утверждаем, что U линейно. Нам нужно проверить определяющие свойства в Разделе 3.3. Пусть u,v — векторы в Rn. Затем
u+v=T(U(u))+T(U(v))=T(U(u)+U(v))
по линейности T. Применение U к обеим сторонам дает
U(u+v)=UAT(U(u)+U(v))B=U(u)+U(v).
Пусть c — скаляр. Затем
cu=cT(U(u))=T(cU(u))
по линейности T. Применение U к обеим сторонам дает
U(cu)=UAT(cU(u))B=cU(u).
Поскольку U удовлетворяет определяющим свойствам в разделе 3.3, это линейное преобразование.

 Правило остаётся справедливым, если перемножаются три либо большее количество матриц.
Правило остаётся справедливым, если перемножаются три либо большее количество матриц.

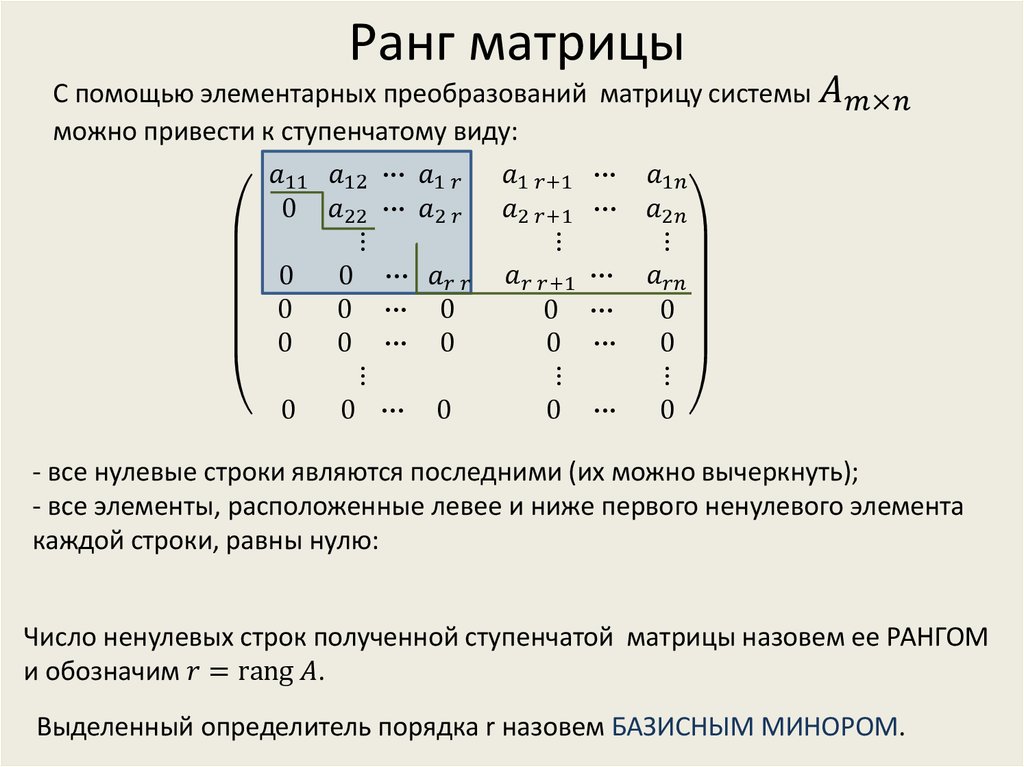 Произведение данных чисел равно единице: . С матрицами всё похоже! Произведение матрицы на обратную ей матрицу равно – единичной матрице, которая является матричным аналогом числовой единицы. Что необходимо знать и уметь для нахождения обратной матрицы? Вы должны уметь решать определители. Вы должны понимать, что такое матрица и уметь выполнять некоторые действия с ними.
Произведение данных чисел равно единице: . С матрицами всё похоже! Произведение матрицы на обратную ей матрицу равно – единичной матрице, которая является матричным аналогом числовой единицы. Что необходимо знать и уметь для нахождения обратной матрицы? Вы должны уметь решать определители. Вы должны понимать, что такое матрица и уметь выполнять некоторые действия с ними.
 Это просто. В матрице миноров нужно ПОМЕНЯТЬ ЗНАКИ у двух чисел: – матрица алгебраических дополнений соответствующих элементов матрицы .
Это просто. В матрице миноров нужно ПОМЕНЯТЬ ЗНАКИ у двух чисел: – матрица алгебраических дополнений соответствующих элементов матрицы . – обратная матрица существует.
– обратная матрица существует.
 {-1}
является обратной по отношению к матрице AB
. Действительно.
{-1}
является обратной по отношению к матрице AB
. Действительно. & … & … \\ {{a}_{m1}} & {{a}_{m2}} & … & {{a}_{mn}} \\\end{matrix} \right]}_{n}\]
& … & … \\ {{a}_{m1}} & {{a}_{m2}} & … & {{a}_{mn}} \\\end{matrix} \right]}_{n}\] {n}{{{a}_{ik}}}\cdot {{b}_{kj}}\]
{n}{{{a}_{ik}}}\cdot {{b}_{kj}}\]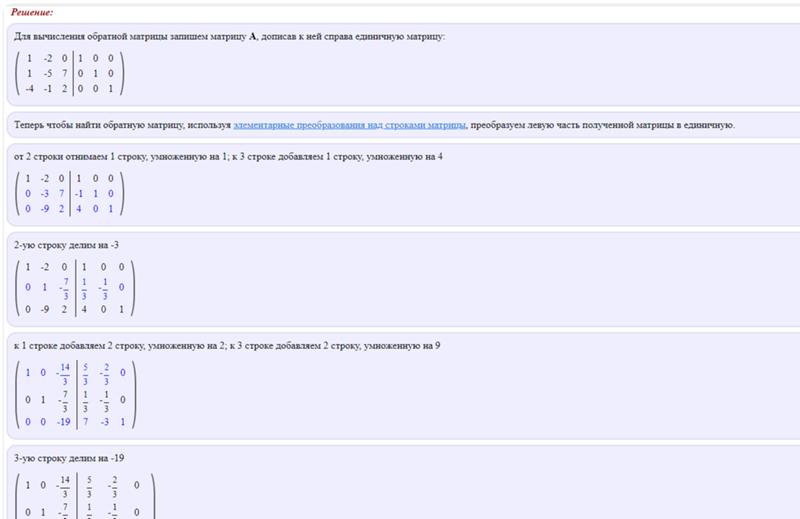 {-1}}$. Тогда эта обратная матрица — единственная.
{-1}}$. Тогда эта обратная матрица — единственная. {-1}} \right|\ne 0.\]
{-1}} \right|\ne 0.\] {t}}$, где $t$ — это (вот сейчас внимание!) сумма номеров всех выбранных строчек и столбцов. Это и будет алгебраическое дополнение.
{t}}$, где $t$ — это (вот сейчас внимание!) сумма номеров всех выбранных строчек и столбцов. Это и будет алгебраическое дополнение. {T}}=\left[ \begin{array}{*{35}{r}} 2 & -1 \\ -5 & 3 \\\end{array} \right]\]
{T}}=\left[ \begin{array}{*{35}{r}} 2 & -1 \\ -5 & 3 \\\end{array} \right]\] {-1}}=\frac{1}{-1}\cdot \left[ \begin{matrix} 2 & -1 & -2 \\ 1 & -1 & -1 \\ -3 & 1 & 2 \\\end{matrix} \right]=\left[ \begin{array}{*{35}{r}}-2 & -1 & 3 \\ 1 & 1 & -1 \\ 2 & 1 & -2 \\\end{array} \right]\]
{-1}}=\frac{1}{-1}\cdot \left[ \begin{matrix} 2 & -1 & -2 \\ 1 & -1 & -1 \\ -3 & 1 & 2 \\\end{matrix} \right]=\left[ \begin{array}{*{35}{r}}-2 & -1 & 3 \\ 1 & 1 & -1 \\ 2 & 1 & -2 \\\end{array} \right]\]
 Поэтому не будем вдаваться в подробности.
Поэтому не будем вдаваться в подробности. {-1}}\]
{-1}}\] Но её мы не трогаем, иначе в третьем столбце начнут «размножаться» только что убранные единицы.
Но её мы не трогаем, иначе в третьем столбце начнут «размножаться» только что убранные единицы. \\ \ \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrr|rrr} 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end{array} \right]\begin{matrix} -6 \\ \updownarrow \\ +1 \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrr|rrr} 0 & 0 & 1 & -18 & 32 & -13 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & 0 & 0 & 4 & -7 & 3 \\\end{array} \right] \\ \end{align}\]
\\ \ \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrr|rrr} 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end{array} \right]\begin{matrix} -6 \\ \updownarrow \\ +1 \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrr|rrr} 0 & 0 & 1 & -18 & 32 & -13 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & 0 & 0 & 4 & -7 & 3 \\\end{array} \right] \\ \end{align}\] Снова составляем присоединённую:
Снова составляем присоединённую: Умножим все три строки на −1, а затем «выжжем» третий столбец, вычитая строку 3 из остальных:
Умножим все три строки на −1, а затем «выжжем» третий столбец, вычитая строку 3 из остальных: 🙂
🙂 ..А n) называется невырожденной , если векторы-столбцы являются линейно независимыми. Число линейно независимых векторов-столбцов матрицы называется рангом матрицы . Поэтому можно сказать, что для того, чтобы существовала обратная матрица, необходимо и достаточно, чтобы ранг матрицы равнялся ее размерности, т.е. r = n.
..А n) называется невырожденной , если векторы-столбцы являются линейно независимыми. Число линейно независимых векторов-столбцов матрицы называется рангом матрицы . Поэтому можно сказать, что для того, чтобы существовала обратная матрица, необходимо и достаточно, чтобы ранг матрицы равнялся ее размерности, т.е. r = n.