Тест дистанционно Сдать 📝 тест МТИ по теоретической механике Теоретическ
Онлайн-сервис
помощи студентам
Видео о сервисе
Эксперты сайта vsesdal.com проводят работу по подбору, обработке и структурированию материала по предложенной заказчиком теме. Результат данной работы не является готовым научным трудом, но может служить источником для его написания.
Теоретическая механика
Сдать тест МТИ по теоретической механике
- Задание
- Обсуждение
520216
Тест дистанционно
Теоретическая механика
Заказ выполнен
Рабочая тетрадь
Раздел 1.
Элементы векторной алгебры и математический аппарат теоретической механики
Тренинг
Контроль
4
4
Элементы векторной алгебры, я сдал.
Раздел 2. Кинематика
Тренинг
Контроль
3
Раздел 3. Кинематика твердого тела
Тренинг
Контроль
Раздел 4. Динамика
Тренинг
Контроль
Раздел 5. Динамика системы материальных точек
Тренинг
Контроль
Раздел 6. Динамика и статика абсолютно твердого тела
Тренинг
Контроль
Раздел 7. Энергия в механике. Работа силы. Силовые поля
Тренинг
Контроль
Раздел 8. Механика Лагранжа
Тренинг
Контроль
Раздел 9. Механика Гамильтона
Тренинг
Контроль
Раздел 10.
Это место для переписки тет-а-тет между заказчиком и исполнителем.
Войдите в личный кабинет (авторизуйтесь на сайте) или
зарегистрируйтесь, чтобы
Закажите подобную или любую другую работу недорого
или
Последние размещенные задания
только что
1 минуту назад
2 минуты назад
2 минуты назад
3 минуты назад
4 минуты назад
6 минут назад
10 минут назад
10 минут назад
12 минут назад
12 минут назад
12 минут назад
12 минут назад
12 минут назад
12 минут назад
12 минут назад
12 минут назад
12 минут назад
Разместите заказ и получите
предложения с ценами
экспертов
Выберите эксперта
по цене и отзывам
Сдайте работу на проверку
преподавателю
Получите положительную оценку,
оплатите работу и оставьте
отзыв эксперту
Узнать стоимость
Узнать стоимость
Заботимся о вас
и вашем времени
Экономия времени
Теперь у вас есть время на друзей, любимые занятия,
работу и семью
Удобный интерфейс
Современный дизайн, созданный для удобства
пользователей сайта
1.
Цена, как известно, зависит от объёма, сложности и срочности. Особенностью «Всё сдал!» является то, что все заказчики работают со экспертами напрямую (без посредников). Поэтому цены в 2-3 раза ниже.
2. Каковы сроки?
Специалистам под силу выполнить как срочный заказ, так и сложный, требующий существенных временных затрат. Для каждой работы определяются оптимальные сроки. Например, помощь с курсовой работой – 5-7 дней. Сообщите нам ваши сроки, и мы выполним работу не позднее указанной даты. P.S.: наши эксперты всегда стараются выполнить работу раньше срока.
3. Выполняете ли вы срочные заказы?
Да, у нас большой опыт выполнения срочных заказов.
4. Если потребуется доработка или дополнительная консультация, это бесплатно?
Да, доработки и консультации в рамках заказа бесплатны, и выполняются в максимально короткие сроки.
5. Я разместил заказ. Могу ли я не платить, если меня не устроит стоимость?
Да, конечно – оценка стоимости бесплатна и ни к чему вас не обязывает.
6. Каким способом можно произвести оплату?
Работу можно оплатить множеством способом: картой Visa / MasterCard, с баланса мобильного, в терминале, в салонах Евросеть / Связной, через Сбербанк и т.д.
7. Предоставляете ли вы гарантии на услуги?
На все виды услуг мы даем гарантию. Если эксперт не справится — мы вернём 100% суммы.
8. Какой у вас режим работы?
Мы принимаем заявки 7 дней в неделю, 24 часа в сутки.
или задать вопрос
Задать вопрос
Тип работыВыберите тип работыКонтрольнаяРешение задачКурсоваяРефератОнлайн-помощьТест дистанционноДипломЛабораторнаяЧертежОтчет по практикеЭссеОтветы на билетыПрезентацияПеревод с ин.
языкаДокладСтатьяСочинениеМагистерская диссертацияКандидатская диссертацияБизнес-планПодбор литературыШпаргалкаПоиск информацииРецензияДругое
Теоретическая механика Синергия МТИ (все ответы на тест экзамен 100 баллов)
Ответы Теоретическая механика Синергия МТИ (тест экзамен 100 баллов). Сборник ответов
1. Автомобиль движется по шоссе со скоростью 72 км/час без пробуксовки. Чему равна скорость точки А на ободе колеса относительно дороги, если колесо имеет радиус R = 50 см.? Все величины выражены в системе СИ
2. Автомобиль массой m = 2 тонны проходит по выпуклому мосту, имеющему радиус кривизны 50 м, со скоростью 54 км/час. Чему равна сила давления автомобиля на мост в наивысшей точке? Ответы выражены в килоньютонах (кН).
3. Автомобиль, трогаясь равноускоренно с места без пробуксовки, развивает скорость 108 км/час за 10 секунд. Чему равно ускорение точки А на ободе колеса относительно дороги в момент времени t = 0,5 с., если колесо имеет радиус R = 50 см.
22. Движение материальной точки в плоскости OXY задано ее декартовыми координатами x(t) = 4 – t? + t?, y(t) = 5t + 4t? – 2t?. Чему равен модуль ускорения точки в момент времени t = 1 с? Все физические величины выражены в системе СИ.
23. Движение материальной точки в плоскости OXY задано ее декартовыми координатами x(t) = 6 – 2t – 6t? + t?, y(t) = 2 – 4t + t?. Чему равен модуль ускорения точки в тот момент времени, когда vy = 0? Все физические величины выражены в системе СИ.
24. Движение материальной точки в плоскости OXY задано ее декартовыми координатами x(t) = 1 + 2t – t?, y(t) = 2 – 3t + t? + t?. Чему равен радиус кривизны траектории движения в точке с координатами.
25. Движение материальной точки в плоскости OXY задано ее декартовыми координатами x(t) = 1 + 3t – t?, y(t) = 2 – t + 3t? – t?. Чему равен угол между векторами скорости и ускорения точки в момент времени t = 1 с? Все физические величины выражены в системе СИ.
26. Движение материальной точки в плоскости OXY задано ее полярными координатами ?(t) = 4cos(?t), ?(t) = ?t.
Чему равен модуль радиального ускорения точки в момент времени t = 0,5 c? Все величины выражены в системе СИ.
27. Движение материальной точки в плоскости OXY задано ее полярными координатами Чему равен модуль радиальной скорости точки в момент времени t = 0,5 c? Все величины выражены в системе СИ. ?(t) = 4cos(?t), ?(t) = ?t
28. Движение материальной точки в плоскости OXY задано ее декартовыми координатами x(t) = 1 + 2t – t?, y(t) = 2 – 3t + t? + t?. Чему равен модуль тангенциального ускорения точки в момент времени t = 1 c? Все величины выражены в системе СИ.
29. Движение материальной точки в плоскости OXY задано ее полярными координатами ?(t) = 4cos(?t), ?(t) = ?t. Чему равен модуль трансверсальной скорости точки в момент времени t = 0,5 c? Все величины выражены в системе СИ.
30. Движение материальной точки в плоскости OXY задано ее полярными координатами ?(t) = 4cos(?t), ?(t) = ?t. Чему равен модуль трансверсального ускорения точки в момент времени t = 0,5 c? Все величины выражены в системе СИ.
31. Движение материальной точки в плоскости OXY по параболе y(x)= x2 задано ее естественной дуговой координатой s(t) = 5 + 4t – t?, отсчитываемой от некоторой точки M0 на параболе в сторону положительных значений x. Чему равен модуль вектора ускорение точки в момент времени t = 1 c, когда она оказалась в вершине параболы? Все величины выражены в системе СИ.
32. Движение материальной точки в плоскости OXY по параболе y(x) = x2 задано ее естественной дуговой координатой s(t) = 5 + 4t – t?, отсчитываемой от некоторой точки M0 на параболе в сторону положительных значений x. Чему равен модуль нормального ускорение точки в момент времени t = 1 c, когда она оказалась в вершине параболы? Все величины выражены в системе СИ.
33. Движение материальной точки в плоскости OXY по параболе y(x) = x2 задано ее естественной дуговой координатой s(t) = 5 + 4t – t?, отсчитываемой от некоторой точки M0 на параболе в сторону положительных значений x. Чему равен модуль тангенциального ускорение точки в момент времени t = 1 c, когда она оказалась в вершине параболы? Все величины выражены в системе СИ.
3. Определить нормальное an ускорения точек на ободе диска в момент времени t = 10 с. Все величины выражены в системе СИ,
40. Из однородного листа цинка вырезали пластину в форме прямоугольного треуголдьника с катетами а = 18см. и b = 24 см. Чему расстояние от центра масс этой пластины до меньшего катета треугольника? Все величины выражены в системе СИ.
41. Математический маятник массой m = 2 кг подвешен на нити длиной l = 0,5 м. Маятник отвели из положения равновесия так, что нить стала горизонтальной и отпустили без начальной скорости. Чему равен модуль вектора момента количества движения относительно точки подвеса в тот момент, когдла нить образует с вертикалью угол 60°? Силами сопротивления движению пренебречь. Все величины выражены в системе СИ.
42. Материальная точка движется вдоль координатной оси OX по закону x(t) = 2 + 3t? – t?. Чему равен модуль скорости точки в момент времени t = 1 с? Все физические величины выражены в системе СИ.
43. Материальная точка движется вдоль координатной оси OX по закону Чему равен модуль скорости точки в тот момент времени, когда ее ускорение равно нулю? Все физические величины выражены в системе СИ.
x(t) = 5 – 2t + 3t? ? t?
44. Материальная точка движется вдоль координатной оси OY по закону y(t) = 2 – t + t?. Чему равен модуль ускорения точки в момент времени t = 1 с? Все физические величины выражены в системе СИ.
45. Материальная точка движется вдоль координатной оси OZ по закону z(t) = 5 + 3t – t?. Чему равен модуль ускорения точки в тот момент времени, когда ее скорость равна нулю? Все физические величины выражены в системе СИ.
46. Материальная точка движется по поверхности сферы радиуса R = 4, так что ее зенитный и азимутальный углы изменяются по закону: ? (t) = ?t/2 , ?(t) = ?t/2. Чему равен модуль азимутального ускорения точки в момент времени t = 2 c? Все физические величины выражены в системе СИ.
47. Материальная точка движется по поверхности сферы радиуса R = 4, так что ее зенитный и азимутальный углы изменяются по закону: ?(t) = ?t/2 , ?(t) = ?t/2. Чему равен модуль зенитной скорости точки в момент времени t = 1 c? Все величины выражены в системе СИ.
48.
2, y(t) = 3 + t. Чему равен модуль вектора момента импульса точки относительно начала координат в момент времени t = 1с? Все величины выражены в системе СИ.
50. Материальная точка с массой m = 2кг движется по конической поверхности. Закон ее двиежния в сферических координатах задан формулами: r(t) = 4 = const, ?(t) = ?/6 = const, ?(t) = 2t. Чему равен модуль вектора равнодействующей силы? Все величины выражены в СИ.
51. Материальная точка с массой m = 2 кг движется по спирали Архимеда в плоскости OXY. Закон ее движения в полярных координатах задан формулами: p(t) = 2t , ?(t) = 3t . Чему равен модуль вектора момента импульса точки относительно начала координат в момент времени t = 1c? Все величины выражены в системе СИ.
52. Маховик начал вращаться равноускоренно и за промежуток времени ?t = 10 с. достиг частоты вращения n = 300 оборотов в минуту. Какое число оборотов N он успел сделать за это время?
53. Однородный сплошной цилиндр массой m=2 кг катится без проскальзывания по горизонтальной поверхности стола со скоростью 6 м/с.
Чему равна полная кинетическая энергия цилиндра в системе отсчета, связанной со столом, если радиус цилиндра R=40 см.? Все величины выражены в системе СИ.
54. Однородный сплошной шар массой m=4 кг, и радиусом R= 30 см скатывается без начальной скорости с вершины наклонной плоскости высотой H=50 см, образующей угол ? = 30° с горизонтом. Чему равна скорость центра масс шара в конце спуска, если движение происходило без проскальзывания? Все величины выражены в системе СИ.
55. Расстояние от Земли до Солнца примерно равно 150 миллионов километров. Чему равна линейная скорость вращения Земли вокруг Солнца? Скорость Земли выражена в километрах за секунду (км/с).
56. Сферические координаты точки M равны M(4, ?/6, ?/2). Чему равен полярный радиус ? этой точки в цилиндрической системе координат?
57. Сферические координаты точки M равны M(8, ?, 0). Чему равна z-координата этой точки в декартовой системе координат?
58. Сферические координаты точки M равны M(8, ?/6, 2?/3). Чему равна x-координата этой точки в декартовой системе координат?
59.
Сферические координаты точки M равны Чему равна y-координата этой точки в декартовой системе координат?
60. Тело движется в поле силы тяжести по гладкой горизонтальной плоскости под действием силы F = 50 H, приложенной под углом 60? к горизорнту. Масса тела равна m = 5кг. Чему равно ускорение тела? Все величины выражены в системе СИ.
61. Три материальные точки с массами m1 = 4 кг, m2 = m3 = 1 кг лежат в одной плоскости OXY в вершинах правильного треугольника со стороной а = 3м. Чему равно расстояние от точки центра масс такой системы до первой точки? Все величины выражены в системе СИ.
62. Три материальные точки с одинаковыми массами m1 = m2 = m3 = 3кг лежат в одной плоскости в вершинах правильного треугольника со стороной а = 20 см. Чему равен JC полярный момент инерции такой системы относительно его центра масс? Все величины выражены в системе СИ.
63. Цилиндрические координаты точки М равны М (3, ?/6 , 4). Чему равен сферический радиус r этой точки в сферической системе координат?
64.
Цилиндрические координаты точки M равны M(4, ?/3, 3). Чему равна x-координата этой точки в декартовой системе координат?
65. Цилиндрические координаты точки M равны M(6, ?/6, 4). Чему равна y-координата этой точки в декартовой системе координат?
66. Цилиндрические координаты точки M равны M(2, ?/4, 3). Чему равна z-координата этой точки в декартовой системе координат?
67. Часовая стрелка Кремлевских Курантов на Спасской башне Московского Кремля имеет длину 2,97 м. Чему равна линейная скорость вращения часовой стрелки Кремлевских Курантов? Все величины выражены в системе СИ.
68. Четыре материальные точки с одинаковыми массами m1 = m2 = m3 = m4 = 2кг лежат в одной плоскости в вершинах квадрата со стороной а = 20 см. Чему равен J-момент инерции такой системы относительно оси, проходящей через середину одной из сторон квадрата перпендикулярно его плоскости. Все величины выражены в системе СИ.
- Введение
- Содержание
- Список литературы
- Отрывок из работы
Введение
1.
Автомобиль движется по шоссе со скоростью 72 км/час без пробуксовки. Чему равна скорость точки А на ободе колеса относительно дороги, если колесо имеет радиус R = 50 см.? Все величины выражены в системе СИ
2. Автомобиль массой m = 2 тонны проходит по выпуклому мосту, имеющему радиус кривизны 50 м, со скоростью 54 км/час. Чему равна сила давления автомобиля на мост в наивысшей точке? Ответы выражены в килоньютонах (кН).
3. Автомобиль, трогаясь равноускоренно с места без пробуксовки, развивает скорость 108 км/час за 10 секунд. Чему равно ускорение точки А на ободе колеса относительно дороги в момент времени t = 0,5 с., если колесо имеет радиус R = 50 см.? Все величины выражены в системе СИ.
4. Вектор задан своими координатами в декартовой прямоугольной системе координат a = (1, 4, 8). Чему равен модуль этого вектора?
5. Вектор задан своими координатами в декартовой прямоугольной системе координат a = (2, 3, 1). Чему равен направляющий косинус cos? угла ?, образованного данным вектором и положительным направлением оси OZ?
6.
Вектор задан своими координатами в декартовой прямоугольной системе координат a = (2, 3, 6). Чему равен направляющий косинус угла ?, образованного данным вектором и положительным направлением оси OX?
7. Вектор задан своими координатами в декартовой прямоугольной системе координат a = (4, 7, 4). Чему равен направляющий косинус cos ? угла ?, образованного данным вектором и положительным направлением оси OY?
8. Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (1, 2, 3), b = (1, 4, 6). Чему равен модуль вектора a + b?
9. Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (2, 2, 1), b = (2, -1, -2). Чему равен модуль вектора a ? b?
10. Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (1, 1, 1), b = (1, -2, -1). Чему равен модуль вектора a ? b?
11. Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (1, -2, 3), b = (1, 2, 1). Чему равен угол между векторами a и b?
12.
Вектор задан своими координатами в декартовой прямоугольной системе координат a = (2, 1, 2). Чему равна длина вектора 4a?
13. Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (2, -1, 2), b = (3, 2, -1). Чему равна x-координата вектора a ? b?
14. Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (1, -1, 1), b = (2, 3, -1). Чему равна y-координата вектора a ? b?
15. Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (-2, 1, 4), b = (1, 2, -1). Чему равна z-координата вектора a ? b?
16. Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (1, 2, 3), b = (1, 2, -1). Чему равно скалярное произведение векторов a ? b?
17. Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (3, 5, 2), b = (1, 2, 1). Чему равен модуль вектора a – b?
18. Две материальные точки с одинаковыми массами m = 2кг соединены невесомым жестким стержнем длиной l = 1м.
-1 вокруг оси, проходящей через центр масс перпендикулярно стержню. Чему будет равна угловая скорость вращения системы ? после того, как одно из тел системы переместится по стержню на расстояние а = 25см в сторону оси вращения (см. рисунок)? Все величины выражены в системе СИ.
19. Движение материальной точки в плоскости OXY задано ее декартовыми координатами x(t) = 1 + 2t – t?, y(t) = 2 – 3t + t? + t?. Чему равен модуль нормального ускорения точки в момент времени t = 1 c? Все величины выражены в системе СИ.
20. Движение материальной точки в плоскости OXY задано ее декартовыми координатами x(t) = 3t – 3t? + 2t?, y(t) = 3t + 2t? – t?. Чему равен модуль скорости точки в момент времени t = 1 с? Все физические величины выражены в системе СИ.
21. Движение материальной точки в плоскости OXY задано ее декартовыми координатами x(t) = 2 + t – 3t? + t?, y(t) = 4 + 2t – t?. Чему равен модуль скорости точки в тот момент времени, когда ?x = 0? Все физические величины выражены в системе СИ.
22. Движение материальной точки в плоскости OXY задано ее декартовыми координатами x(t) = 4 – t? + t?, y(t) = 5t + 4t? – 2t?. Чему равен модуль ускорения точки в момент времени t = 1 с? Все физические величины выражены в системе СИ.
23. Движение материальной точки в плоскости OXY задано ее декартовыми координатами x(t) = 6 – 2t – 6t? + t?, y(t) = 2 – 4t + t?. Чему равен модуль ускорения точки в тот момент времени, когда vy = 0? Все физические величины выражены в системе СИ.
24. Движение материальной точки в плоскости OXY задано ее декартовыми координатами x(t) = 1 + 2t – t?, y(t) = 2 – 3t + t? + t?. Чему равен радиус кривизны траектории движения в точке с координатами.
25. Движение материальной точки в плоскости OXY задано ее декартовыми координатами x(t) = 1 + 3t – t?, y(t) = 2 – t + 3t? – t?. Чему равен угол между векторами скорости и ускорения точки в момент времени t = 1 с? Все физические величины выражены в системе СИ.
26. Движение материальной точки в плоскости OXY задано ее полярными координатами ?(t) = 4cos(?t), ?(t) = ?t.
Чему равен модуль радиального ускорения точки в момент времени t = 0,5 c? Все величины выражены в системе СИ.
27. Движение материальной точки в плоскости OXY задано ее полярными координатами Чему равен модуль радиальной скорости точки в момент времени t = 0,5 c? Все величины выражены в системе СИ. ?(t) = 4cos(?t), ?(t) = ?t
28. Движение материальной точки в плоскости OXY задано ее декартовыми координатами x(t) = 1 + 2t – t?, y(t) = 2 – 3t + t? + t?. Чему равен модуль тангенциального ускорения точки в момент времени t = 1 c? Все величины выражены в системе СИ.
29. Движение материальной точки в плоскости OXY задано ее полярными координатами ?(t) = 4cos(?t), ?(t) = ?t. Чему равен модуль трансверсальной скорости точки в момент времени t = 0,5 c? Все величины выражены в системе СИ.
30. Движение материальной точки в плоскости OXY задано ее полярными координатами ?(t) = 4cos(?t), ?(t) = ?t. Чему равен модуль трансверсального ускорения точки в момент времени t = 0,5 c? Все величины выражены в системе СИ.
31. Движение материальной точки в плоскости OXY по параболе y(x)= x2 задано ее естественной дуговой координатой s(t) = 5 + 4t – t?, отсчитываемой от некоторой точки M0 на параболе в сторону положительных значений x. Чему равен модуль вектора ускорение точки в момент времени t = 1 c, когда она оказалась в вершине параболы? Все величины выражены в системе СИ.
32. Движение материальной точки в плоскости OXY по параболе y(x) = x2 задано ее естественной дуговой координатой s(t) = 5 + 4t – t?, отсчитываемой от некоторой точки M0 на параболе в сторону положительных значений x. Чему равен модуль нормального ускорение точки в момент времени t = 1 c, когда она оказалась в вершине параболы? Все величины выражены в системе СИ.
33. Движение материальной точки в плоскости OXY по параболе y(x) = x2 задано ее естественной дуговой координатой s(t) = 5 + 4t – t?, отсчитываемой от некоторой точки M0 на параболе в сторону положительных значений x. Чему равен модуль тангенциального ускорение точки в момент времени t = 1 c, когда она оказалась в вершине параболы? Все величины выражены в системе СИ.
3. Определить нормальное an ускорения точек на ободе диска в момент времени t = 10 с. Все величины выражены в системе СИ,
40. Из однородного листа цинка вырезали пластину в форме прямоугольного треуголдьника с катетами а = 18см. и b = 24 см. Чему расстояние от центра масс этой пластины до меньшего катета треугольника? Все величины выражены в системе СИ.
41. Математический маятник массой m = 2 кг подвешен на нити длиной l = 0,5 м. Маятник отвели из положения равновесия так, что нить стала горизонтальной и отпустили без начальной скорости. Чему равен модуль вектора момента количества движения относительно точки подвеса в тот момент, когдла нить образует с вертикалью угол 60°? Силами сопротивления движению пренебречь. Все величины выражены в системе СИ.
42. Материальная точка движется вдоль координатной оси OX по закону x(t) = 2 + 3t? – t?. Чему равен модуль скорости точки в момент времени t = 1 с? Все физические величины выражены в системе СИ.
43. Материальная точка движется вдоль координатной оси OX по закону Чему равен модуль скорости точки в тот момент времени, когда ее ускорение равно нулю? Все физические величины выражены в системе СИ.
x(t) = 5 – 2t + 3t? ? t?
44. Материальная точка движется вдоль координатной оси OY по закону y(t) = 2 – t + t?. Чему равен модуль ускорения точки в момент времени t = 1 с? Все физические величины выражены в системе СИ.
45. Материальная точка движется вдоль координатной оси OZ по закону z(t) = 5 + 3t – t?. Чему равен модуль ускорения точки в тот момент времени, когда ее скорость равна нулю? Все физические величины выражены в системе СИ.
46. Материальная точка движется по поверхности сферы радиуса R = 4, так что ее зенитный и азимутальный углы изменяются по закону: ? (t) = ?t/2 , ?(t) = ?t/2. Чему равен модуль азимутального ускорения точки в момент времени t = 2 c? Все физические величины выражены в системе СИ.
47. Материальная точка движется по поверхности сферы радиуса R = 4, так что ее зенитный и азимутальный углы изменяются по закону: ?(t) = ?t/2 , ?(t) = ?t/2. Чему равен модуль зенитной скорости точки в момент времени t = 1 c? Все величины выражены в системе СИ.
48.
2, y(t) = 3 + t. Чему равен модуль вектора момента импульса точки относительно начала координат в момент времени t = 1с? Все величины выражены в системе СИ.
50. Материальная точка с массой m = 2кг движется по конической поверхности. Закон ее двиежния в сферических координатах задан формулами: r(t) = 4 = const, ?(t) = ?/6 = const, ?(t) = 2t. Чему равен модуль вектора равнодействующей силы? Все величины выражены в СИ.
51. Материальная точка с массой m = 2 кг движется по спирали Архимеда в плоскости OXY. Закон ее движения в полярных координатах задан формулами: p(t) = 2t , ?(t) = 3t . Чему равен модуль вектора момента импульса точки относительно начала координат в момент времени t = 1c? Все величины выражены в системе СИ.
52. Маховик начал вращаться равноускоренно и за промежуток времени ?t = 10 с. достиг частоты вращения n = 300 оборотов в минуту. Какое число оборотов N он успел сделать за это время?
53. Однородный сплошной цилиндр массой m=2 кг катится без проскальзывания по горизонтальной поверхности стола со скоростью 6 м/с.
Чему равна полная кинетическая энергия цилиндра в системе отсчета, связанной со столом, если радиус цилиндра R=40 см.? Все величины выражены в системе СИ.
54. Однородный сплошной шар массой m=4 кг, и радиусом R= 30 см скатывается без начальной скорости с вершины наклонной плоскости высотой H=50 см, образующей угол ? = 30° с горизонтом. Чему равна скорость центра масс шара в конце спуска, если движение происходило без проскальзывания? Все величины выражены в системе СИ.
55. Расстояние от Земли до Солнца примерно равно 150 миллионов километров. Чему равна линейная скорость вращения Земли вокруг Солнца? Скорость Земли выражена в километрах за секунду (км/с).
56. Сферические координаты точки M равны M(4, ?/6, ?/2). Чему равен полярный радиус ? этой точки в цилиндрической системе координат?
57. Сферические координаты точки M равны M(8, ?, 0). Чему равна z-координата этой точки в декартовой системе координат?
58. Сферические координаты точки M равны M(8, ?/6, 2?/3). Чему равна x-координата этой точки в декартовой системе координат?
59.
Сферические координаты точки M равны Чему равна y-координата этой точки в декартовой системе координат?
60. Тело движется в поле силы тяжести по гладкой горизонтальной плоскости под действием силы F = 50 H, приложенной под углом 60? к горизорнту. Масса тела равна m = 5кг. Чему равно ускорение тела? Все величины выражены в системе СИ.
61. Три материальные точки с массами m1 = 4 кг, m2 = m3 = 1 кг лежат в одной плоскости OXY в вершинах правильного треугольника со стороной а = 3м. Чему равно расстояние от точки центра масс такой системы до первой точки? Все величины выражены в системе СИ.
62. Три материальные точки с одинаковыми массами m1 = m2 = m3 = 3кг лежат в одной плоскости в вершинах правильного треугольника со стороной а = 20 см. Чему равен JC полярный момент инерции такой системы относительно его центра масс? Все величины выражены в системе СИ.
63. Цилиндрические координаты точки М равны М (3, ?/6 , 4). Чему равен сферический радиус r этой точки в сферической системе координат?
64.
Цилиндрические координаты точки M равны M(4, ?/3, 3). Чему равна x-координата этой точки в декартовой системе координат?
65. Цилиндрические координаты точки M равны M(6, ?/6, 4). Чему равна y-координата этой точки в декартовой системе координат?
66. Цилиндрические координаты точки M равны M(2, ?/4, 3). Чему равна z-координата этой точки в декартовой системе координат?
67. Часовая стрелка Кремлевских Курантов на Спасской башне Московского Кремля имеет длину 2,97 м. Чему равна линейная скорость вращения часовой стрелки Кремлевских Курантов? Все величины выражены в системе СИ.
68. Четыре материальные точки с одинаковыми массами m1 = m2 = m3 = m4 = 2кг лежат в одной плоскости в вершинах квадрата со стороной а = 20 см. Чему равен J-момент инерции такой системы относительно оси, проходящей через середину одной из сторон квадрата перпендикулярно его плоскости. Все величины выражены в системе СИ.
Содержание
1.
Автомобиль движется по шоссе со скоростью 72 км/час без пробуксовки. Чему равна скорость точки А на ободе колеса относительно дороги, если колесо имеет радиус R = 50 см.? Все величины выражены в системе СИ
2. Автомобиль массой m = 2 тонны проходит по выпуклому мосту, имеющему радиус кривизны 50 м, со скоростью 54 км/час. Чему равна сила давления автомобиля на мост в наивысшей точке? Ответы выражены в килоньютонах (кН).
3. Автомобиль, трогаясь равноускоренно с места без пробуксовки, развивает скорость 108 км/час за 10 секунд. Чему равно ускорение точки А на ободе колеса относительно дороги в момент времени t = 0,5 с., если колесо имеет радиус R = 50 см.? Все величины выражены в системе СИ.
4. Вектор задан своими координатами в декартовой прямоугольной системе координат a = (1, 4, 8). Чему равен модуль этого вектора?
5. Вектор задан своими координатами в декартовой прямоугольной системе координат a = (2, 3, 1). Чему равен направляющий косинус cos? угла ?, образованного данным вектором и положительным направлением оси OZ?
6.
Вектор задан своими координатами в декартовой прямоугольной системе координат a = (2, 3, 6). Чему равен направляющий косинус угла ?, образованного данным вектором и положительным направлением оси OX?
7. Вектор задан своими координатами в декартовой прямоугольной системе координат a = (4, 7, 4). Чему равен направляющий косинус cos ? угла ?, образованного данным вектором и положительным направлением оси OY?
8. Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (1, 2, 3), b = (1, 4, 6). Чему равен модуль вектора a + b?
9. Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (2, 2, 1), b = (2, -1, -2). Чему равен модуль вектора a ? b?
10. Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (1, 1, 1), b = (1, -2, -1). Чему равен модуль вектора a ? b?
11. Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (1, -2, 3), b = (1, 2, 1). Чему равен угол между векторами a и b?
12.
Вектор задан своими координатами в декартовой прямоугольной системе координат a = (2, 1, 2). Чему равна длина вектора 4a?
13. Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (2, -1, 2), b = (3, 2, -1). Чему равна x-координата вектора a ? b?
14. Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (1, -1, 1), b = (2, 3, -1). Чему равна y-координата вектора a ? b?
15. Вектора задан
Список литературы
1. Автомобиль движется по шоссе со скоростью 72 км/час без пробуксовки. Чему равна скорость точки А на ободе колеса относительно дороги, если колесо имеет радиус R = 50 см.? Все величины выражены в системе СИ
2. Автомобиль массой m = 2 тонны проходит по выпуклому мосту, имеющему радиус кривизны 50 м, со скоростью 54 км/час. Чему равна сила давления автомобиля на мост в наивысшей точке? Ответы выражены в килоньютонах (кН).
3. Автомобиль, трогаясь равноускоренно с места без пробуксовки, развивает скорость 108 км/час за 10 секунд.
Чему равно ускорение точки А на ободе колеса относительно дороги в момент времени t = 0,5 с., если колесо имеет радиус R = 50 см.? Все величины выражены в системе СИ.
4. Вектор задан своими координатами в декартовой прямоугольной системе координат a = (1, 4, 8). Чему равен модуль этого вектора?
5. Вектор задан своими координатами в декартовой прямоугольной системе координат a = (2, 3, 1). Чему равен направляющий косинус cos? угла ?, образованного данным вектором и положительным направлением оси OZ?
6. Вектор задан своими координатами в декартовой прямоугольной системе координат a = (2, 3, 6). Чему равен направляющий косинус угла ?, образованного данным вектором и положительным направлением оси OX?
7. Вектор задан своими координатами в декартовой прямоугольной системе координат a = (4, 7, 4). Чему равен направляющий косинус cos ? угла ?, образованного данным вектором и положительным направлением оси OY?
8. Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (1, 2, 3), b = (1, 4, 6).
Чему равен модуль вектора a + b?
9. Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (2, 2, 1), b = (2, -1, -2). Чему равен модуль вектора a ? b?
10. Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (1, 1, 1), b = (1, -2, -1). Чему равен модуль вектора a ? b?
11. Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (1, -2, 3), b = (1, 2, 1). Чему равен угол между векторами a и b?
12. Вектор задан своими координатами в декартовой прямоугольной системе координат a = (2, 1, 2). Чему равна длина вектора 4a?
13. Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (2, -1, 2), b = (3, 2, -1). Чему равна x-координата вектора a ? b?
14. Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (1, -1, 1), b = (2, 3, -1). Чему равна y-координата вектора a ? b?
15. Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (-2, 1, 4), b = (1, 2, -1).
-1 вокруг оси, проходящей через центр масс перпендикулярно стержню. Чему будет равна угловая скорость вращения системы ? после того, как одно из тел системы переместится по стержню на расстояние а = 25см в сторону оси вращения (см. рисунок)? Все величины выражены в системе СИ.
19. Движение материальной точки в плоскости OXY задано ее декартовыми координатами x(t) = 1 + 2t – t?, y(t) = 2 – 3t + t? + t?. Чему равен модуль нормального ускорения точки в момент времени t = 1 c? Все величины выражены в системе СИ.
20. Движение материальной точки в плоскости OXY задано ее декартовыми координатами x(t) = 3t – 3t? + 2t?, y(t) = 3t + 2t? – t?. Чему равен модуль скорости точки в момент времени t = 1 с? Все физические величины выражены в системе СИ.
21. Движение материальной точки в плоскости OXY задано ее декартовыми координатами x(t) = 2 + t – 3t? + t?, y(t) = 4 + 2t – t?. Чему равен модуль скорости точки в тот момент времени, когда ?x = 0? Все физические величины выражены в системе СИ.
22. Движение материальной точки в плоскости OXY задано ее декартовыми координатами x(t) = 4 – t? + t?, y(t) = 5t + 4t? – 2t?. Чему равен модуль ускорения точки в момент времени t = 1 с? Все физические величины выражены в системе СИ.
23. Движение материальной точки в плоскости OXY задано ее декартовыми координатами x(t) = 6 – 2t – 6t? + t?, y(t) = 2 – 4t + t?. Чему равен модуль ускорения точки в тот момент времени, когда vy = 0? Все физические величины выражены в системе СИ.
24. Движение материальной точки в плоскости OXY задано ее декартовыми координатами x(t) = 1 + 2t – t?, y(t) = 2 – 3t + t? + t?. Чему равен радиус кривизны траектории движения в точке с координатами.
25. Движение материальной точки в плоскости OXY задано ее декартовыми координатами x(t) = 1 + 3t – t?, y(t) = 2 – t + 3t? – t?. Чему равен угол между векторами скорости и ускорения точки в момент времени t = 1 с? Все физические величины выражены в системе СИ.
26. Движение материальной точки в плоскости OXY задано ее полярными координатами ?(t) = 4cos(?t), ?(t) = ?t.
Чему равен модуль радиального ускорения точки в момент времени t = 0,5 c? Все величины выражены в системе СИ.
27. Движение материальной точки в плоскости OXY задано ее полярными координатами Чему равен модуль радиальной скорости точки в момент времени t = 0,5 c? Все величины выражены в системе СИ. ?(t) = 4cos(?t), ?(t) = ?t
28. Движение материальной точки в плоскости OXY задано ее декартовыми координатами x(t) = 1 + 2t – t?, y(t) = 2 – 3t + t? + t?. Чему равен модуль тангенциального ускорения точки в момент времени t = 1 c? Все величины выражены в системе СИ.
29. Движение материальной точки в плоскости OXY задано ее полярными координатами ?(t) = 4cos(?t), ?(t) = ?t. Чему равен модуль трансверсальной скорости точки в момент времени t = 0,5 c? Все величины выражены в системе СИ.
30. Движение материальной точки в плоскости OXY задано ее полярными координатами ?(t) = 4cos(?t), ?(t) = ?t. Чему равен модуль трансверсального ускорения точки в момент времени t = 0,5 c? Все величины выражены в системе СИ.
31. Движение материальной точки в плоскости OXY по параболе y(x)= x2 задано ее естественной дуговой координатой s(t) = 5 + 4t – t?, отсчитываемой от некоторой точки M0 на параболе в сторону положительных значений x. Чему равен модуль вектора ускорение точки в момент времени t = 1 c, когда она оказалась в вершине параболы? Все величины выражены в системе СИ.
32. Движение материальной точки в плоскости OXY по параболе y(x) = x2 задано ее естественной дуговой координатой s(t) = 5 + 4t – t?, отсчитываемой от некоторой точки M0 на параболе в сторону положительных значений x. Чему равен модуль нормального ускорение точки в момент времени t = 1 c, когда она оказалась в вершине параболы? Все величины выражены в системе СИ.
33. Движение материальной точки в плоскости OXY по параболе y(x) = x2 задано ее естественной дуговой координатой s(t) = 5 + 4t – t?, отсчитываемой от некоторой точки M0 на параболе в сторону положительных значений x. Чему равен модуль тангенциального ускорение точки в момент времени t = 1 c, когда она оказалась в вершине параболы? Все величины выражены в системе СИ.
3. Определить нормальное an ускорения точек на ободе диска в момент времени t = 10 с. Все величины выражены в системе СИ,
40. Из однородного листа цинка вырезали пластину в форме прямоугольного треуголдьника с катетами а = 18см. и b = 24 см. Чему расстояние от центра масс этой пластины до меньшего катета треугольника? Все величины выражены в системе СИ.
41. Математический маятник массой m = 2 кг подвешен на нити длиной l = 0,5 м. Маятник отвели из положения равновесия так, что нить стала горизонтальной и отпустили без начальной скорости. Чему равен модуль вектора момента количества движения относительно точки подвеса в тот момент, когдла нить образует с вертикалью угол 60°? Силами сопротивления движению пренебречь. Все величины выражены в системе СИ.
42. Материальная точка движется вдоль координатной оси OX по закону x(t) = 2 + 3t? – t?. Чему равен модуль скорости точки в момент времени t = 1 с? Все физические величины выражены в системе СИ.
43. Материальная точка движется вдоль координатной оси OX по закону Чему равен модуль скорости точки в тот момент времени, когда ее ускорение равно нулю? Все физические величины выражены в системе СИ.
x(t) = 5 – 2t + 3t? ? t?
44. Материальная точка движется вдоль координатной оси OY по закону y(t) = 2 – t + t?. Чему равен модуль ускорения точки в момент времени t = 1 с? Все физические величины выражены в системе СИ.
45. Материальная точка движется вдоль координатной оси OZ по закону z(t) = 5 + 3t – t?. Чему равен модуль ускорения точки в тот момент времени, когда ее скорость равна нулю? Все физические величины выражены в системе СИ.
46. Материальная точка движется по поверхности сферы радиуса R = 4, так что ее зенитный и азимутальный углы изменяются по закону: ? (t) = ?t/2 , ?(t) = ?t/2. Чему равен модуль азимутального ускорения точки в момент времени t = 2 c? Все физические величины выражены в системе СИ.
47. Материальная точка движется по поверхности сферы радиуса R = 4, так что ее зенитный и азимутальный углы изменяются по закону: ?(t) = ?t/2 , ?(t) = ?t/2. Чему равен модуль зенитной скорости точки в момент времени t = 1 c? Все величины выражены в системе СИ.
48.
2, y(t) = 3 + t. Чему равен модуль вектора момента импульса точки относительно начала координат в момент времени t = 1с? Все величины выражены в системе СИ.
50. Материальная точка с массой m = 2кг движется по конической поверхности. Закон ее двиежния в сферических координатах задан формулами: r(t) = 4 = const, ?(t) = ?/6 = const, ?(t) = 2t. Чему равен модуль вектора равнодействующей силы? Все величины выражены в СИ.
51. Материальная точка с массой m = 2 кг движется по спирали Архимеда в плоскости OXY. Закон ее движения в полярных координатах задан формулами: p(t) = 2t , ?(t) = 3t . Чему равен модуль вектора момента импульса точки относительно начала координат в момент времени t = 1c? Все величины выражены в системе СИ.
52. Маховик начал вращаться равноускоренно и за промежуток времени ?t = 10 с. достиг частоты вращения n = 300 оборотов в минуту. Какое число оборотов N он успел сделать за это время?
53. Однородный сплошной цилиндр массой m=2 кг катится без проскальзывания по горизонтальной поверхности стола со скоростью 6 м/с.
Чему равна полная кинетическая энергия цилиндра в системе отсчета, связанной со столом, если радиус цилиндра R=40 см.? Все величины выражены в системе СИ.
54. Однородный сплошной шар массой m=4 кг, и радиусом R= 30 см скатывается без начальной скорости с вершины наклонной плоскости высотой H=50 см, образующей угол ? = 30° с горизонтом. Чему равна скорость центра масс шара в конце спуска, если движение происходило без проскальзывания? Все величины выражены в системе СИ.
55. Расстояние от Земли до Солнца примерно равно 150 миллионов километров. Чему равна линейная скорость вращения Земли вокруг Солнца? Скорость Земли выражена в километрах за секунду (км/с).
56. Сферические координаты точки M равны M(4, ?/6, ?/2). Чему равен полярный радиус ? этой точки в цилиндрической системе координат?
57. Сферические координаты точки M равны M(8, ?, 0). Чему равна z-координата этой точки в декартовой системе координат?
58. Сферические координаты точки M равны M(8, ?/6, 2?/3). Чему равна x-координата этой точки в декартовой системе координат?
59.
Сферические координаты точки M равны Чему равна y-координата этой точки в декартовой системе координат?
60. Тело движется в поле силы тяжести по гладкой горизонтальной плоскости под действием силы F = 50 H, приложенной под углом 60? к горизорнту. Масса тела равна m = 5кг. Чему равно ускорение тела? Все величины выражены в системе СИ.
61. Три материальные точки с массами m1 = 4 кг, m2 = m3 = 1 кг лежат в одной плоскости OXY в вершинах правильного треугольника со стороной а = 3м. Чему равно расстояние от точки центра масс такой системы до первой точки? Все величины выражены в системе СИ.
62. Три материальные точки с одинаковыми массами m1 = m2 = m3 = 3кг лежат в одной плоскости в вершинах правильного треугольника со стороной а = 20 см. Чему равен JC полярный момент инерции такой системы относительно его центра масс? Все величины выражены в системе СИ.
63. Цилиндрические координаты точки М равны М (3, ?/6 , 4). Чему равен сферический радиус r этой точки в сферической системе координат?
64.
Цилиндрические координаты точки M равны M(4, ?/3, 3). Чему равна x-координата этой точки в декартовой системе координат?
65. Цилиндрические координаты точки M равны M(6, ?/6, 4). Чему равна y-координата этой точки в декартовой системе координат?
66. Цилиндрические координаты точки M равны M(2, ?/4, 3). Чему равна z-координата этой точки в декартовой системе координат?
67. Часовая стрелка Кремлевских Курантов на Спасской башне Московского Кремля имеет длину 2,97 м. Чему равна линейная скорость вращения часовой стрелки Кремлевских Курантов? Все величины выражены в системе СИ.
68. Четыре материальные точки с одинаковыми массами m1 = m2 = m3 = m4 = 2кг лежат в одной плоскости в вершинах квадрата со стороной а = 20 см. Чему равен J-момент инерции такой системы относительно оси, проходящей через середину одной из сторон квадрата перпендикулярно его плоскости. Все величины выражены в системе СИ.
Отрывок из работы
1.
Автомобиль движется по шоссе со скоростью 72 км/час без пробуксовки. Чему равна скорость точки А на ободе колеса относительно дороги, если колесо имеет радиус R = 50 см.? Все величины выражены в системе СИ
2. Автомобиль массой m = 2 тонны проходит по выпуклому мосту, имеющему радиус кривизны 50 м, со скоростью 54 км/час. Чему равна сила давления автомобиля на мост в наивысшей точке? Ответы выражены в килоньютонах (кН).
3. Автомобиль, трогаясь равноускоренно с места без пробуксовки, развивает скорость 108 км/час за 10 секунд. Чему равно ускорение точки А на ободе колеса относительно дороги в момент времени t = 0,5 с., если колесо имеет радиус R = 50 см.? Все величины выражены в системе СИ.
4. Вектор задан своими координатами в декартовой прямоугольной системе координат a = (1, 4, 8). Чему равен модуль этого вектора?
5. Вектор задан своими координатами в декартовой прямоугольной системе координат a = (2, 3, 1). Чему равен направляющий косинус cos? угла ?, образованного данным вектором и положительным направлением оси OZ?
6.
Вектор задан своими координатами в декартовой прямоугольной системе координат a = (2, 3, 6). Чему равен направляющий косинус угла ?, образованного данным вектором и положительным направлением оси OX?
7. Вектор задан своими координатами в декартовой прямоугольной системе координат a = (4, 7, 4). Чему равен направляющий косинус cos ? угла ?, образованного данным вектором и положительным направлением оси OY?
8. Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (1, 2, 3), b = (1, 4, 6). Чему равен модуль вектора a + b?
9. Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (2, 2, 1), b = (2, -1, -2). Чему равен модуль вектора a ? b?
10. Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (1, 1, 1), b = (1, -2, -1). Чему равен модуль вектора a ? b?
11. Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (1, -2, 3), b = (1, 2, 1). Чему равен угол между векторами a и b?
12.
Вектор задан своими координатами в декартовой прямоугольной системе координат a = (2, 1, 2). Чему равна длина вектора 4a?
13. Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (2, -1, 2), b = (3, 2, -1). Чему равна x-координата вектора a ? b?
14. Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (1, -1, 1), b = (2, 3, -1). Чему равна y-координата вектора a ? b?
15. Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (-2, 1, 4), b = (1, 2, -1). Чему равна z-координата вектора a ? b?
16. Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (1, 2, 3), b = (1, 2, -1). Чему равно скалярное произведение векторов a ? b?
17. Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (3, 5, 2), b = (1, 2, 1). Чему равен модуль вектора a – b?
18. Две материальные точки с одинаковыми массами m = 2кг соединены невесомым жестким стержнем длиной l = 1м.
-1 вокруг оси, проходящей через центр масс перпендикулярно стержню. Чему будет равна угловая скорость вращения системы ? после того, как одно из тел системы переместится по стержню на расстояние а = 25см в сторону оси вращения (см. рисунок)? Все величины выражены в системе СИ.
19. Движение материальной точки в плоскости OXY задано ее декартовыми координатами x(t) = 1 + 2t – t?, y(t) = 2 – 3t + t? + t?. Чему равен модуль нормального ускорения точки в момент времени t = 1 c? Все величины выражены в системе СИ.
20. Движение материальной точки в плоскости OXY задано ее декартовыми координатами x(t) = 3t – 3t? + 2t?, y(t) = 3t + 2t? – t?. Чему равен модуль скорости точки в момент времени t = 1 с? Все физические величины выражены в системе СИ.
21. Движение материальной точки в плоскости OXY задано ее декартовыми координатами x(t) = 2 + t – 3t? + t?, y(t) = 4 + 2t – t?. Чему равен модуль скорости точки в тот момент времени, когда ?x = 0? Все физические величины выражены в системе СИ.
22. Движение материальной точки в плоскости OXY задано ее декартовыми координатами x(t) = 4 – t? + t?, y(t) = 5t + 4t? – 2t?. Чему равен модуль ускорения точки в момент времени t = 1 с? Все физические величины выражены в системе СИ.
23. Движение материальной точки в плоскости OXY задано ее декартовыми координатами x(t) = 6 – 2t – 6t? + t?, y(t) = 2 – 4t + t?. Чему равен модуль ускорения точки в тот момент времени, когда vy = 0? Все физические величины выражены в системе СИ.
24. Движение материальной точки в плоскости OXY задано ее декартовыми координатами x(t) = 1 + 2t – t?, y(t) = 2 – 3t + t? + t?. Чему равен радиус кривизны траектории движения в точке с координатами.
25. Движение материальной точки в плоскости OXY задано ее декартовыми координатами x(t) = 1 + 3t – t?, y(t) = 2 – t + 3t? – t?. Чему равен угол между векторами скорости и ускорения точки в момент времени t = 1 с? Все физические величины выражены в системе СИ.
26. Движение материальной точки в плоскости OXY задано ее полярными координатами ?(t) = 4cos(?t), ?(t) = ?t.
Чему равен модуль радиального ускорения точки в момент времени t = 0,5 c? Все величины выражены в системе СИ.
27. Движение материальной точки в плоскости OXY задано ее полярными координатами Чему равен модуль радиальной скорости точки в момент времени t = 0,5 c? Все величины выражены в системе СИ. ?(t) = 4cos(?t), ?(t) = ?t
28. Движение материальной точки в плоскости OXY задано ее декартовыми координатами x(t) = 1 + 2t – t?, y(t) = 2 – 3t + t? + t?. Чему равен модуль тангенциального ускорения точки в момент времени t = 1 c? Все величины выражены в системе СИ.
29. Движение материальной точки в плоскости OXY задано ее полярными координатами ?(t) = 4cos(?t), ?(t) = ?t. Чему равен модуль трансверсальной скорости точки в момент времени t = 0,5 c? Все величины выражены в системе СИ.
30. Движение материальной точки в плоскости OXY задано ее полярными координатами ?(t) = 4cos(?t), ?(t) = ?t. Чему равен модуль трансверсального ускорения точки в момент времени t = 0,5 c? Все величины выражены в системе СИ.
31. Движение материальной точки в плоскости OXY по параболе y(x)= x2 задано ее естественной дуговой координатой s(t) = 5 + 4t – t?, отсчитываемой от некоторой точки M0 на параболе в сторону положительных значений x. Чему равен модуль вектора ускорение точки в момент времени t = 1 c, когда она оказалась в вершине параболы? Все величины выражены в системе СИ.
32. Движение материальной точки в плоскости OXY по параболе y(x) = x2 задано ее естественной дуговой координатой s(t) = 5 + 4t – t?, отсчитываемой от некоторой точки M0 на параболе в сторону положительных значений x. Чему равен модуль нормального ускорение точки в момент времени t = 1 c, когда она оказалась в вершине параболы? Все величины выражены в системе СИ.
33. Движение материальной точки в плоскости OXY по параболе y(x) = x2 задано ее естественной дуговой координатой s(t) = 5 + 4t – t?, отсчитываемой от некоторой точки M0 на параболе в сторону положительных значений x. Чему равен модуль тангенциального ускорение точки в момент времени t = 1 c, когда она оказалась в вершине параболы? Все величины выражены в системе СИ.
3. Определить нормальное an ускорения точек на ободе диска в момент времени t = 10 с. Все величины выражены в системе СИ,
40. Из однородного листа цинка вырезали пластину в форме прямоугольного треуголдьника с катетами а = 18см. и b = 24 см. Чему расстояние от центра масс этой пластины до меньшего катета треугольника? Все величины выражены в системе СИ.
41. Математический маятник массой m = 2 кг подвешен на нити длиной l = 0,5 м. Маятник отвели из положения равновесия так, что нить стала горизонтальной и отпустили без начальной скорости. Чему равен модуль вектора момента количества движения относительно точки подвеса в тот момент, когдла нить образует с вертикалью угол 60°? Силами сопротивления движению пренебречь. Все величины выражены в системе СИ.
42. Материальная точка движется вдоль координатной оси OX по закону x(t) = 2 + 3t? – t?. Чему равен модуль скорости точки в момент времени t = 1 с? Все физические величины выражены в системе СИ.
43. Материальная точка движется вдоль координатной оси OX по закону Чему равен модуль скорости точки в тот момент времени, когда ее ускорение равно нулю? Все физические величины выражены в системе СИ.
x(t) = 5 – 2t + 3t? ? t?
44. Материальная точка движется вдоль координатной оси OY по закону y(t) = 2 – t + t?. Чему равен модуль ускорения точки в момент времени t = 1 с? Все физические величины выражены в системе СИ.
45. Материальная точка движется вдоль координатной оси OZ по закону z(t) = 5 + 3t – t?. Чему равен модуль ускорения точки в тот момент времени, когда ее скорость равна нулю? Все физические величины выражены в системе СИ.
46. Материальная точка движется по поверхности сферы радиуса R = 4, так что ее зенитный и азимутальный углы изменяются по закону: ? (t) = ?t/2 , ?(t) = ?t/2. Чему равен модуль азимутального ускорения точки в момент времени t = 2 c? Все физические величины выражены в системе СИ.
47. Материальная точка движется по поверхности сферы радиуса R = 4, так что ее зенитный и азимутальный углы изменяются по закону: ?(t) = ?t/2 , ?(t) = ?t/2. Чему равен модуль зенитной скорости точки в момент времени t = 1 c? Все величины выражены в системе СИ.
48.
2, y(t) = 3 + t. Чему равен модуль вектора момента импульса точки относительно начала координат в момент времени t = 1с? Все величины выражены в системе СИ.
50. Материальная точка с массой m = 2кг движется по конической поверхности. Закон ее двиежния в сферических координатах задан формулами: r(t) = 4 = const, ?(t) = ?/6 = const, ?(t) = 2t. Чему равен модуль вектора равнодействующей силы? Все величины выражены в СИ.
51. Материальная точка с массой m = 2 кг движется по спирали Архимеда в плоскости OXY. Закон ее движения в полярных координатах задан формулами: p(t) = 2t , ?(t) = 3t . Чему равен модуль вектора момента импульса точки относительно начала координат в момент времени t = 1c? Все величины выражены в системе СИ.
52. Маховик начал вращаться равноускоренно и за промежуток времени ?t = 10 с. достиг частоты вращения n = 300 оборотов в минуту. Какое число оборотов N он успел сделать за это время?
53. Однородный сплошной цилиндр массой m=2 кг катится без проскальзывания по горизонтальной поверхности стола со скоростью 6 м/с.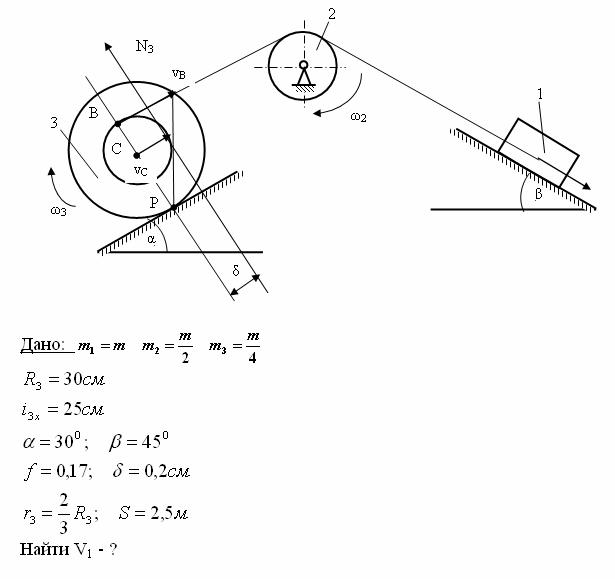
Чему равна полная кинетическая энергия цилиндра в системе отсчета, связанной со столом, если радиус цилиндра R=40 см.? Все величины выражены в системе СИ.
54. Однородный сплошной шар массой m=4 кг, и радиусом R= 30 см скатывается без начальной скорости с вершины наклонной плоскости высотой H=50 см, образующей угол ? = 30° с горизонтом. Чему равна скорость центра масс шара в конце спуска, если движение происходило без проскальзывания? Все величины выражены в системе СИ.
55. Расстояние от Земли до Солнца примерно равно 150 миллионов километров. Чему равна линейная скорость вращения Земли вокруг Солнца? Скорость Земли выражена в километрах за секунду (км/с).
56. Сферические координаты точки M равны M(4, ?/6, ?/2). Чему равен полярный радиус ? этой точки в цилиндрической системе координат?
57. Сферические координаты точки M равны M(8, ?, 0). Чему равна z-координата этой точки в декартовой системе координат?
58. Сферические координаты точки M равны M(8, ?/6, 2?/3). Чему равна x-координата этой точки в декартовой системе координат?
59. Сферические координаты точки M равны Чему равна y-координата этой точки в декартовой системе координат?
60. Тело движется в поле силы тяжести по гладкой горизонтальной плоскости под действием силы F = 50 H, приложенной под углом 60? к горизорнту. Масса тела равна m = 5кг. Чему равно ускорение тела? Все величины выражены в системе СИ.
61. Три материальные точки с массами m1 = 4 кг, m2 = m3 = 1 кг лежат в одной плоскости OXY в вершинах правильного треугольника со стороной а = 3м. Чему равно расстояние от точки центра масс такой системы до первой точки? Все величины выражены в системе СИ.
62. Три материальные точки с одинаковыми массами m1 = m2 = m3 = 3кг лежат в одной плоскости в вершинах правильного треугольника со стороной а = 20 см. Чему равен JC полярный момент инерции такой системы относительно его центра масс? Все величины выражены в системе СИ.
63. Цилиндрические координаты точки М равны М (3, ?/6 , 4). Чему равен сферический радиус r этой точки в сферической системе координат?
64.
Цилиндрические координаты точки M равны M(4, ?/3, 3). Чему равна x-координата этой точки в декартовой системе координат?
65. Цилиндрические координаты точки M равны M(6, ?/6, 4). Чему равна y-координата этой точки в декартовой системе координат?
66. Цилиндрические координаты точки M равны M(2, ?/4, 3). Чему равна z-координата этой точки в декартовой системе координат?
67. Часовая стрелка Кремлевских Курантов на Спасской башне Московского Кремля имеет длину 2,97 м. Чему равна линейная скорость вращения часовой стрелки Кремлевских Курантов? Все величины выражены в системе СИ.
68. Четыре материальные точки с одинаковыми массами m1 = m2 = m3 = m4 = 2кг лежат в одной плоскости в вершинах квадрата со стороной а = 20 см. Чему равен J-момент инерции такой системы относительно оси, проходящей через середину одной из сторон квадрата перпендикулярно его плоскости. Все величины выражены в системе СИ.
💯 Теоретическая механика.ти (все ответы на тест Синергия / МТИ / МосАП, июнь 2022) (Решение → 7278)
- Учебные материалы
Вектор задан своими координатами в декартовой прямоугольной системе координат a = (1, 4, 8).
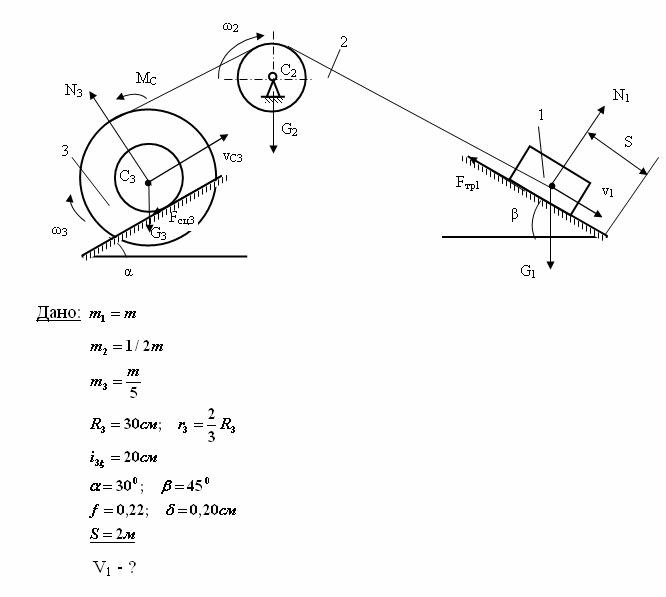Чему равен модуль этого вектора?Тип ответа: Одиночный выбор
- 9
- 32
- 13
- √13
Вектор задан своими координатами в декартовой прямоугольной системе координат a = (2, 1, 2). Чему равна длина вектора 4a?
Тип ответа: Одиночный выбор
- 9
- 4√5
- 12
- 20
Вектор задан своими координатами в декартовой прямоугольной системе координат a = (2, 3, 1). Чему равен направляющий косинус cosγ угла γ, образованного данным вектором и положительным направлением оси OZ?
Тип ответа: Одиночный выбор
- 1) 1/5
- 2) 1/6
- 3) 1/√14
- 4) 1/√6
Вектор задан своими координатами в декартовой прямоугольной системе координат a = (2, 3, 6). Чему равен направляющий косинус угла α, образованного данным вектором и положительным направлением оси OX?
Тип ответа: Одиночный выбор
- 1) 2/3
- 2) 2/11
- 3) 2/√11
- 4) 2/7
Вектор задан своими координатами в декартовой прямоугольной системе координат a = (4, 7, 4).
Чему равен направляющий косинус cos β угла β, образованного данным вектором и положительным направлением оси OY?Тип ответа: Одиночный выбор
- 1) 7/15
- 2) 7/√15
- 3) 7/9
- 4) 7/8
Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (-2, 1, 4), b = (1, 2, -1). Чему равна z-координата вектора a × b?
Тип ответа: Одиночный выбор
- -9
- -5
- 2
- 1
Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (1, -1, 1), b = (2, 3, -1). Чему равна y-координата вектора a × b?
Тип ответа: Одиночный выбор
- -2
- 3
- 5
- 4
Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (1, -2, 3), b = (1, 2, 1). Чему равен угол между векторами a и b?
Тип ответа: Одиночный выбор
- 90°
- 60°
- 30°
- 45°
Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (1, 1, 1), b = (1, -2, -1).
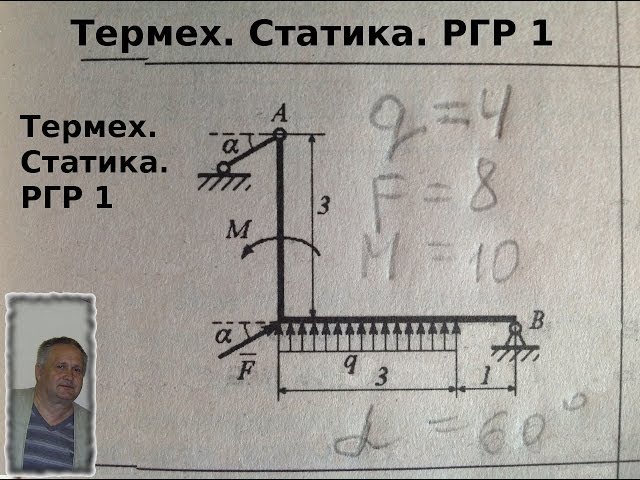Чему равен модуль вектора a × b?Тип ответа: Одиночный выбор
- √30
- 7
- 11
- √14
Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (1, 2, 3), b = (1, 2, -1). Чему равно скалярное произведение векторов a ⋅ b?
Тип ответа: Одиночный выбор
- 0
- 6
- -3
- 2
Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (1, 2, 3), b = (1, 4, 6). Чему равен модуль вектора a + b?
Тип ответа: Одиночный выбор
- 11
- √67
- 27
- √17
Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (2, -1, 2), b = (3, 2, -1). Чему равна x-координата вектора a × b?
Тип ответа: Одиночный выбор
- -3
- 0
- 8
- 7
Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (2, 2, 1), b = (2, -1, -2).
Чему равен модуль вектора a × b?Тип ответа: Одиночный выбор
- 9
- √10
- 1
- √5
Вектора заданы своими координатами в декартовой прямоугольной системе координат a = (3, 5, 2), b = (1, 2, 1). Чему равен модуль вектора a – b?
Тип ответа: Одиночный выбор
- 6
- √14
- 14
- 4√2
Движение материальной точки в плоскости OXY задано ее декартовыми координатами x(t) = 1 + 2t – t², y(t) = 2 – 3t + t² + t³. Чему равен модуль нормального ускорения точки в момент времени t = 1 c? Все величины выражены в системе СИ.
Тип ответа: Одиночный выбор
- 2
- 6
- 4
- 8
Движение материальной точки в плоскости OXY задано ее декартовыми координатами x(t) = 1 + 2t – t², y(t) = 2 – 3t + t² + t³. Чему равен модуль тангенциального ускорения точки в момент времени t = 1 c? Все величины выражены в системе СИ.
Тип ответа: Одиночный выбор
- 2
- 6
- 4
- 8
Движение материальной точки в плоскости OXY задано ее декартовыми координатами x(t) = 1 + 2t – t², y(t) = 2 – 3t + t² + t³.
Чему равен радиус кривизны траектории движения в точке с координатами.Тип ответа: Одиночный выбор
- 1
- √5
- 2
- √17
Движение материальной точки в плоскости OXY задано ее декартовыми координатами x(t) = 1 + 3t – t³, y(t) = 2 – t + 3t² – t³. Чему равен угол между векторами скорости и ускорения точки в момент времени t = 1 с? Все физические величины выражены в системе СИ.
Тип ответа: Одиночный выбор
- 60°
- 30°
- 90°
- 0°
Движение материальной точки в плоскости OXY задано ее декартовыми координатами x(t) = 2 + t – 3t² + t³, y(t) = 4 + 2t – t³. Чему равен модуль скорости точки в тот момент времени, когда αx = 0? Все физические величины выражены в системе СИ.
Тип ответа: Одиночный выбор
- 0
- √5
- 6
- √26
Движение материальной точки в плоскости OXY задано ее декартовыми координатами x(t) = 3t – 3t² + 2t³, y(t) = 3t + 2t² – t³.
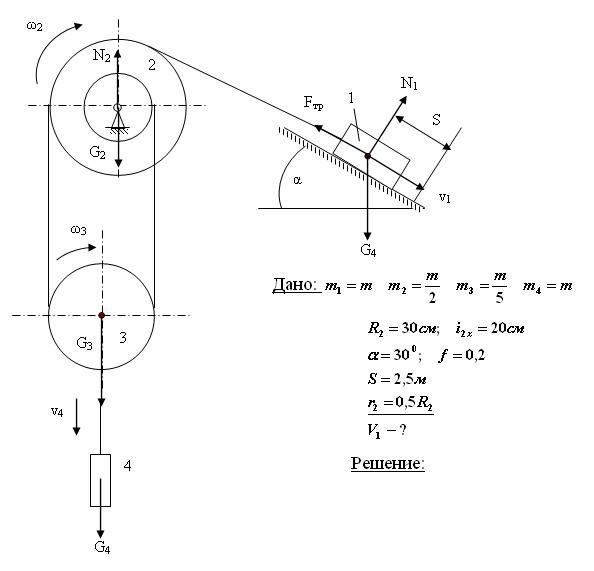Чему равен модуль скорости точки в момент времени t = 1 с? Все физические величины выражены в системе СИ.Тип ответа: Одиночный выбор
- 5
- 6
- √7
- √20
Движение материальной точки в плоскости OXY задано ее декартовыми координатами x(t) = 4 – t² + t³, y(t) = 5t + 4t² – 2t³. Чему равен модуль ускорения точки в момент времени t = 1 с? Все физические величины выражены в системе СИ.
Тип ответа: Одиночный выбор
- 4√2
- 8
- 5√2
- 11
Движение материальной точки в плоскости OXY задано ее декартовыми координатами x(t) = 6 – 2t – 6t² + t³, y(t) = 2 – 4t + t². Чему равен модуль ускорения точки в тот момент времени, когда vy = 0? Все физические величины выражены в системе СИ.
Тип ответа: Одиночный выбор
- 0
- √2
- 2√10
- 2
Движение материальной точки в плоскости OXY задано ее полярными координатами ρ(t) = 4cos(πt), φ(t) = πt. Чему равен модуль радиального ускорения точки в момент времени t = 0,5 c? Все величины выражены в системе СИ.
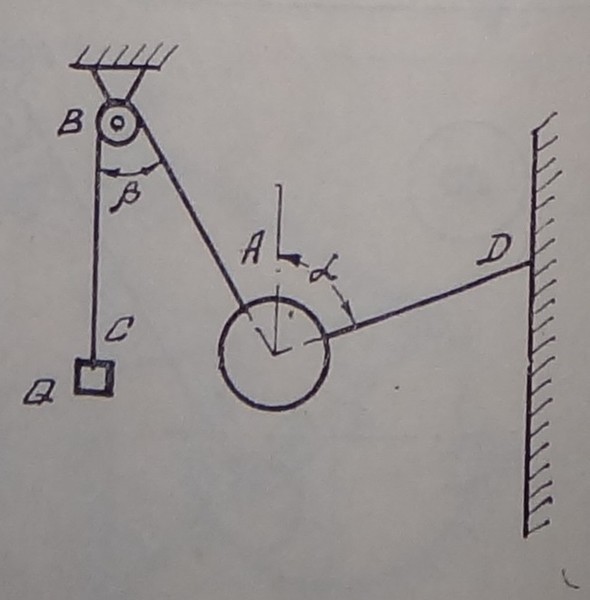
Тип ответа: Одиночный выбор
- 1) 0
- 2) 8π²
- 3) 2π²
- 4) 16π²
Движение материальной точки в плоскости OXY задано ее полярными координатами ρ(t) = 4cos(πt), φ(t) = πt. Чему равен модуль радиальной скорости точки в момент времени t = 0,5 c? Все величины выражены в системе СИ.
Тип ответа: Одиночный выбор
- 1) 0
- 2) 4π
- 3) π/2
- 4) 2π
Движение материальной точки в плоскости OXY задано ее полярными координатами ρ(t) = 4cos(πt), φ(t) = πt. Чему равен модуль трансверсального ускорения точки в момент времени t = 0,5 c? Все величины выражены в системе СИ.
Тип ответа: Одиночный выбор
- 1) 0
- 2) 8π²
- 3) 4π²
- 4) 16π²
Движение материальной точки в плоскости OXY задано ее полярными координатами ρ(t) = 4cos(πt), φ(t) = πt. Чему равен модуль трансверсальной скорости точки в момент времени t = 0,5 c? Все величины выражены в системе СИ.
Тип ответа: Одиночный выбор
- 1) 0
- 2) π/2
- 3) 4π
- 4) 2π
Движение материальной точки в плоскости OXY по параболе y(x) = x2 задано ее естественной дуговой координатой s(t) = 5 + 4t – t², отсчитываемой от некоторой точки M0 на параболе в сторону положительных значений x. Чему равен модуль нормального ускорение точки в момент времени t = 1 c, когда она оказалась в вершине параболы? Все величины выражены в системе СИ.
Тип ответа: Одиночный выбор
- 2
- 6
- 4
- 8
Движение материальной точки в плоскости OXY по параболе y(x) = x2 задано ее естественной дуговой координатой s(t) = 5 + 4t – t², отсчитываемой от некоторой точки M0 на параболе в сторону положительных значений x. Чему равен модуль тангенциального ускорение точки в момент времени t = 1 c, когда она оказалась в вершине параболы? Все величины выражены в системе СИ.
Тип ответа: Одиночный выбор
- 2
- 6
- 4
- 8
Движение материальной точки в плоскости OXY по параболе y(x)= x2 задано ее естественной дуговой координатой s(t) = 5 + 4t – t², отсчитываемой от некоторой точки M0 на параболе в сторону положительных значений x.
Чему равен модуль вектора ускорение точки в момент времени t = 1 c, когда она оказалась в вершине параболы? Все величины выражены в системе СИ.Тип ответа: Одиночный выбор
- 2√5
- 2√17
- 2√10
- 10
Движение материальной точки в пространстве задано ее декартовыми координатами x(t) = 1 + 2t – 3t² + t³, y(t) = 2 + 4t – t², z(t) = 4 – 2t + 2t². Чему равен модуль скорости точки в момент времени t = 1 с? Все величины выражены в системе СИ.
Тип ответа: Одиночный выбор
- 3
- 6
- 3√2
- 2√5
Движение материальной точки в пространстве задано ее декартовыми координатами x(t) = 1 + 2t – t², y(t) = 2 – 3t + t² + t³, z(t) = 2 – t + t². Чему равен модуль ускорения точки в момент времени t = 1 с? Все величины выражены в системе СИ.
Тип ответа: Одиночный выбор
- 7
- 6√2
- √5
- 8
Декартовы координаты точки M равны: M(-2, 2√3, 4). Чему равен полярный угол φ этой точки в цилиндрической системе координат?
Тип ответа: Одиночный выбор
- 1) 2π/3
- 2) 5π/6
- 3) π/3
- 4) π/6
Декартовы координаты точки M равны: M(2, -3, 6).
Чему равен сферический радиус r этой точки в сферической системе координат?Тип ответа: Одиночный выбор
- √5
- 7
- 6
- 5
Декартовы координаты точки M равны: M(6, -8, 4). Чему равен полярный радиус ρ этой точки в цилиндрической системе координат?
Тип ответа: Одиночный выбор
- 2√29
- 10
- 6
- 2√2
Материальная точка движется вдоль координатной оси OX по закону x(t) = 2 + 3t² – t³. Чему равен модуль скорости точки в момент времени t = 1 с? Все физические величины выражены в системе СИ.
Тип ответа: Одиночный выбор
- 0
- 1
- 2
- 3
Материальная точка движется вдоль координатной оси OX по закону x(t) = 5 – 2t + 3t² − t³. Чему равен модуль скорости точки в тот момент времени, когда ее ускорение равно нулю? Все физические величины выражены в системе СИ.
Тип ответа: Одиночный выбор
- 0
- 5
- 1
- 6
Материальная точка движется вдоль координатной оси OY по закону y(t) = 2 – t + t³.
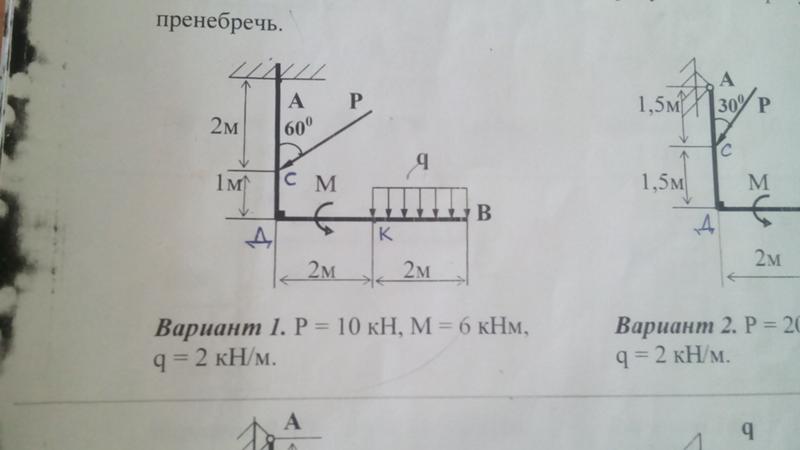Чему равен модуль ускорения точки в момент времени t = 1 с? Все физические величины выражены в системе СИ.Тип ответа: Одиночный выбор
- 0
- 6
- 2
- 8
Материальная точка движется вдоль координатной оси OZ по закону z(t) = 5 + 3t – t³. Чему равен модуль ускорения точки в тот момент времени, когда ее скорость равна нулю? Все физические величины выражены в системе СИ.
Тип ответа: Одиночный выбор
- 0
- 7
- 6
- 8
Материальная точка движется по поверхности сферы радиуса R = 4, так что ее зенитный и азимутальный углы изменяются по закону: θ (t) = πt/2 , φ(t) = πt/2. Чему равен модуль азимутального ускорения точки в момент времени t = 2 c? Все физические величины выражены в системе СИ.
Тип ответа: Одиночный выбор
- 1) 0
- 2) 2π²
- 3) π²
- 4) 8π²
Материальная точка движется по поверхности сферы радиуса R = 4, так что ее зенитный и азимутальный углы изменяются по закону: θ(t) = πt/2 , φ(t) = πt/2.
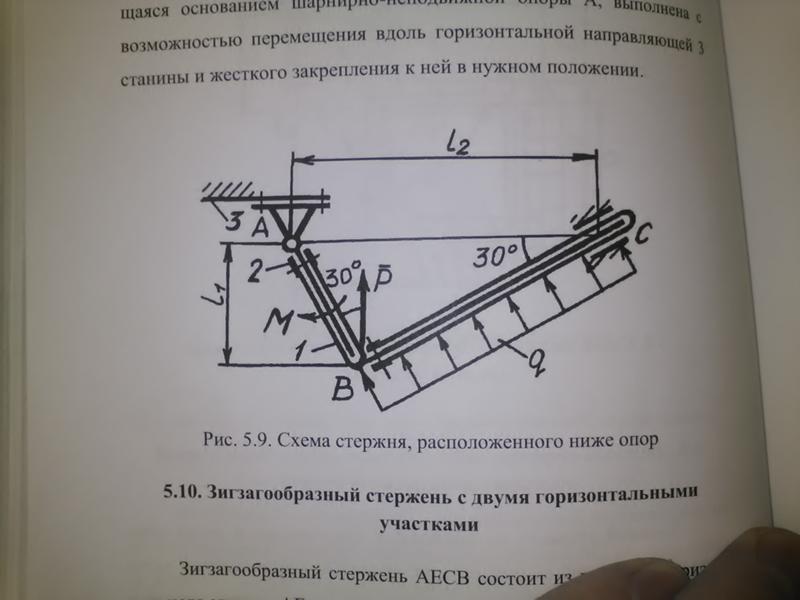Чему равен модуль зенитной скорости точки в момент времени t = 1 c? Все величины выражены в системе СИ.Тип ответа: Одиночный выбор
- 1) 0
- 2) 2π
- 3) 4π
- 4) π/2
Материальная точка движется по поверхности сферы радиуса R = 4, так что ее зенитный и азимутальный углы изменяются по закону: θ(t) = πt/2 , φ(t) = πt/2. Чему равен модуль радиального ускорения точки в момент времени t = 1 c? Все физические величины выражены в системе СИ.
Тип ответа: Одиночный выбор
- 1) 0
- 2) 8π²
- 3) π²
- 4) 2π²
Однородный сплошной цилиндр массой m=2 кг без проскальзывания по горизонтальной поверхности стола со скоростью 6 м/с. Чему равна полная кинетическая энергия цилиндра в системе отсчета, связанной со столом, если радиус цилиндра R=40 см.? Все величины выражены в системе СИ.
Тип ответа: Одиночный выбор
- 54
- 36
- 64
- 72
Однородный сплошной шар массой m=4 кг, и радиусом R= 30 см без начальной скорости с вершины наклонной плоскости высотой H=50 см, образующей угол α = 30° с горизонтом.
Чему равна скорость центра масс шара в конце спуска, если движение происходило без проскальзывания? Все величины выражены в системе СИ.Тип ответа: Одиночный выбор
- 2,6
- 2,0
- 2,2
- 3,1
Сферические координаты точки M равны M(4, π/3, π/6). Чему равна y-координата этой точки в декартовой системе координат?
Тип ответа: Одиночный выбор
- 4
- -2
- 1
- √3
Сферические координаты точки M равны M(4, π/6, π/2). Чему равен полярный радиус ρ этой точки в цилиндрической системе координат?
Тип ответа: Одиночный выбор
- 4
- 2√2
- 2
- 2√3
Сферические координаты точки M равны M(8, π, 0). Чему равна z-координата этой точки в декартовой системе координат?
Тип ответа: Одиночный выбор
- 2√2
- 0
- 8
- -8
Сферические координаты точки M равны M(8, π/6, 2π/3). Чему равна x-координата этой точки в декартовой системе координат?
Тип ответа: Одиночный выбор
- -2
- 2
- 4√3
- 2√3
Цилиндрические координаты точки М равны М (3, π/6, 4).
Чему равен сферический радиус r этой точки в сферической системе координат?Тип ответа: Одиночный выбор
- 6√3
- 5
- 3
- 4
Цилиндрические координаты точки M равны M(2, π/4, 3). Чему равна z-координата этой точки в декартовой системе координат?
Тип ответа: Одиночный выбор
- 6
- 3
- 2
- √2
Цилиндрические координаты точки M равны M(4, π/3, 3). Чему равна x-координата этой точки в декартовой системе координат?
Тип ответа: Одиночный выбор
- 4
- 3
- 2
- 2√3
Цилиндрические координаты точки M равны M(6, π/6, 4). Чему равна y-координата этой точки в декартовой системе координат?
Тип ответа: Одиночный выбор
- 6
- 4
- 3
- 3√3
Техническая механика.ти ЭБС (ответы на тест Синергия / МТИ / МосАП) (Решение → 16016)
Техническая механика.ти ЭБС
- Тема 1.
Теоретическая механика - Тема 2. Сопротивление материалов
- Тема 3. Детали узлов и машин
Теоретическая механика════════════════════
Атомная подводная лодка проекта 941 «Акула» с подводным водоизмещением 48 тысяч тонн находится на глубине 200 м. Чему равна работа силы Архимеда, совершаемая при всплытии лодки на поверхность? Ответы выражены в ГДж=109 Дж.
Тип ответа: Одиночный выбор
- 9,41
- 94,1
- 941
- 9408
Балка длиной 6 м лежит на двух опорах, расположенных на взаимном расстоянии 4,5 м; причем правый конец балки свешивается на 0,5 м. Погонный метр балки весит 66 кг кроме того, на расстоянии 2,25 м от левой опоры балка нагружена сосредоточенной силой 1 т. Определить величину нагрузки, которую нужно приложить к концу левой консоли для того, чтобы изгибающий момент в сечении, где приложена сила 1 т, был бы равен нулю. Определить опорные реакции при этих условиях.
Тип ответа: Одиночный выбор
- 2540 кг
- 3210 кг
- 4130 кг
- 5820 кг
Балка пролетом 2 м свободно лежит на двух опорах, имеет прямоугольное сечение шириной 6 см и высотой 10 см.
Она нагружена сосредоточенной силой 0,5 т, приложенной посредине пролета, и сосредоточенной силой 1 т, приложенной на расстоянии 0,33 м от правой опоры. Определить нормальное напряжение в точке поперечного сечения, отстоящего на 0,33 м от левой опоры. Точка находится на расстоянии 2 см от верхней грани балки. Силы направлены сверху вниз.
Тип ответа: Одиночный выбор
- 52 кг/см2
- 83 кг/см2
- 125 кг/см2
- 213 кг/см2
Балка прямоугольного поперечного сечения пролетом l =4 м, свободно лежащая на двух опорах, загружена сплошной равномерно распределенной нагрузкой q = 4 т/м. Найти величину наибольших касательных напряжений в сечении посредине пролета балки, если размеры сечения 10×20 см2.
Тип ответа: Одиночный выбор
- 100 кг/см2
- 300 кг/см2
- 600 кг/см2
- 900 кг/см2
В каком случае можно применить червячную передачу?
Тип ответа: Одиночный выбор
- Оси валов параллельны.
- Пересекаются под некоторым углом
- Пересекаются под прямым углом
- Скрещиваются под прямым углом
В машиностроении приходится создавать передачи между осями: 1) параллельными; 2) пересекающимися под некоторым углом; 3) пересекающимися под прямым углом; 4) скрещивающимися. В каком случае применение фрикционных передач практически невозможно?
Тип ответа: Одиночный выбор
- Параллельными
- пересекающимися под некоторым углом
- пересекающимися под прямым углом
- скрещивающимися
Велосипедное колесо вращается с частотой n=5 оборотов в секунду. Под действием сил трения оно остановилось через интервал времени Δt = 1 мин. Чему равен модуль углового ускорения колеса ε? Все величины выражены в системе СИ.
Тип ответа: Одиночный выбор
- 50,083
- 0,262
- 0,523
Во фрикционной передаче с коническими катками между пересекающимися осями. Две проволоки, одна стальная, другая медная, имеют одинаковую длину и нагружены одинаковыми осевыми растягивающими усилиями. Медная проволока имеет диаметр 1 мм. Чему равен диаметр стальной проволоки, если обе проволоки удлиняются на одинаковую величину? Тип ответа: Одиночный выбор Для каких целей нельзя применить зубчатую передачу? Тип ответа: Одиночный выбор Для определения мощности, передаваемой валом, замерялись при помощи тензометра удлинения по линии, расположенной под углом 45° к наружной образующей вала. Замеренное относительное удлинение оказалось равным ε = 0,000425. Тип ответа: Одиночный выбор Для работы фрикционной передачи необходима сила, прижимающая катки друг к другу. Какова величина этой силы по отношению к полезному окружному усилию? Тип ответа: Одиночный выбор Из однородного листа стали вырезали пластину в форме прямоугольного треугольника с катетами α=18 см. и b=24 см. Чему расстояние от центра масс этой пластины до вершины прямого угла? Все величины выражены в системе СИ. Тип ответа: Одиночный выбор К нижнему концу троса, закрепленного верхним концом, подвешен груз Р = 7,5 т. К чему приводит износ цепи? Тип ответа: Одиночный выбор Как обычно в червячных передачах передается движение? Тип ответа: Одиночный выбор Какая из написанных зависимостей между межосевым расстоянием (α) и диаметрами зубчатых колес в редуцирующей передаче (d1, d2) неправильная, где u — передаточное число? Тип ответа: Одиночный выбор Какая характеристика плоского ремня не регламентируется стандартом? Тип ответа: Одиночный выбор Какая цель преследуется введением ограничения на максимально возможное отношение толщины ремня к диаметру меньшего шкива? Тип ответа: Одиночный выбор Какие втулочные цепи выпускаются в настоящее время? Тип ответа: Одиночный выбор Каким минимальным значением ограничивают угол захвата ремнем меньшего шкива в плоскоременных передачах? Тип ответа: Одиночный выбор Какую длину цепи целесообразно назначать для цепной передачи? Тип ответа: Одиночный выбор Маховик начал вращаться равноускоренно и за промежуток времени t=10 с. Тип ответа: Одиночный выбор Механизм имеет несколько последовательных передач; при вращении ведущего вала со скоростью 1000 об/мин ведомый вращается со скоростью 80 об/мин. Как правильно назвать этот механизм? Тип ответа: Одиночный выбор Можно ли при неизменной передаваемой мощности с помощью зубчатой передачи получить больший крутящий момент? Тип ответа: Одиночный выбор Мощность энергетических установок атомного крейсера «Петр Великий» примерно равна 103 МВт (140 000 л. Тип ответа: Одиночный выбор Определить диаметр сплошного вала, передающего крутящий момент 1,5 тм, если допускаемое напряжение равно 700 кг/см2. Тип ответа: Одиночный выбор Определить наименьший диаметр стального вала, передающего 18 л.с. при 120 об/мин, если допускаемый угол закручивания равен 1° на длине, равной 15 диаметрам вала. Тип ответа: Одиночный выбор От чего не зависит коэффициент прочности зубьев по изгибным напряжениям (формы зуба)? Тип ответа: Одиночный выбор Под действием постоянной силы F = 50 Н тело массой m=100 кг увеличило за 10 секунд свою скорость до 54 км/час. Тип ответа: Одиночный выбор Полый вал, соединяющий турбину и генератор в гидротехнической установке, имеет наружный диаметр 40 см и внутренний диаметр 22,5 см. Скорость вращения 120 об/мин. Чему равны наибольшие касательные напряжения при передаче валом 10000 л.с.? Тип ответа: Одиночный выбор Полый стальной вал длиной 1,8 м нагружен крутящим моментом 0,6 тм. Определить наружный диаметр вала, если угол закручивания не должен превосходить 2°, а касательное напряжение 700 кг/см2. Тип ответа: Одиночный выбор При вертикальном подъеме груза массой m = 4 кг на высоту h = 2 м. была совершена работа 88 Дж. Чему равно ускорение, с которым двигался груз? Все величины выражены в системе СИ. Тип ответа: Одиночный выбор При каком взаимном расположении валов возможно применение цепной передачи? Тип ответа: Одиночный выбор Приведены формулы для расчета угла подъема витка червяка: где p — шаг; z1 — число заходов червяка; d1 – диаметр червяка; q—характеристика червяка (коэффициент диаметра). В какой формуле допущена ошибка? Тип ответа: Одиночный выбор Разрывающее усилие P приложено к плоскому деревянному образцу сечением 2×4 см2 (см. рисунок) . Предел прочности на растяжение для дерева равен 560 кг/см2? Чему при этом равно скалывающее напряжение в головках этого образца? Тип ответа: Одиночный выбор Расчеты показали, что во фрикционной передаче с точечным контактом рабочих тел допускаемые контактные напряжения могут быть увеличены вдвое. Тип ответа: Одиночный выбор С какой начальной скоростью двигался автомобиль массой m = 2 тонны, если под действием тормозящей силы F = 2 кН он останавливается, пройдя расстояние 50 м.? Все величины выражены в СИ. Тип ответа: Одиночный выбор С чем связывают назначение длины червяка? Тип ответа: Одиночный выбор Сосновая стойка сечением 20х20 см опирается на дубовую подушку, как указано на рисунке. Допускаемое напряжение на смятие для сосны вдоль волокон равно 100 кг/см2, а для дуба поперек волокон 30 кг/см2. Три материальные точки с массами m1= 4 кг, m2=m3=1 кг лежат в одной плоскости OXY в вершинах правильного треугольника со стороной α=3 м. Чему равно расстояние от точки центра масс такой системы до первой точки? Все величины выражены в системе СИ. Тип ответа: Одиночный выбор Три материальные точки с одинаковыми массами m1=m2=m3=3 кг лежат в одной плоскости в вершинах правильного треугольника со стороной a=20 см. Чему равен J–полярный момент инерции такой системы относительно точки, расположенной в одной из его вершин? Все величины выражены в системе СИ. Тип ответа: Одиночный выбор Укажите передаточные механизмы, в которых фрикционные передачи получили наибольшее распространение. Тип ответа: Одиночный выбор Укажите цепи, предназначенные для работы при больших скоростях. Тип ответа: Одиночный выбор Укажите, с каким шагом приводные цепи стандартизованы? С шагом, кратным: Тип ответа: Одиночный выбор Чему равен момент инерции однородного прямого цилиндра массой m=3 кг, высотой H=20 см и радиусом основания R= 20 см относительно оси, проходящей через центр круга в его нижнем основании перпендикулярно высоте цилиндра? Все величины выражены в системе СИ. Тип ответа: Одиночный выбор Чему равен момент инерции тонкой однородной сферы массой m=3 кг и радиуса R= 20 см относительно оси, касающейся поверхности сферы в одной из ее точек? Все величины выражены в системе СИ. Тип ответа: Одиночный выбор Чему равен угол вклинивания клиновых ремней? Тип ответа: Одиночный выбор Чтобы зубчатые колеса могли быть введены в зацепление, что у них должно быть одинаковым? Тип ответа: Одиночный выбор Чтобы уменьшить вес сплошного круглого вала на 20% его заменили полым, наружный диаметр которого в два раза больше внутреннего. Тип ответа: Одиночный выбор Чугунная колонна высотой 3 м кольцевого поперечного сечения имеет наружный диаметр 25 см и толщину стенки 25 мм. Каково абсолютное укорочение колонны при нагрузке 50 тонн. Тип ответа: Одиночный выбор Чугунная колонна высотой 3 м кольцевого поперечного сечения имеет наружный диаметр 25 см и толщину стенки 25 мм. Каково напряжения в поперечном сечении колонны при нагрузке 50 тонн. Тип ответа: Одиночный выбор Чугунная колонна высотой 3 м кольцевого поперечного сечения имеет наружный диаметр 25 см и толщину стенки 25 мм. Все вопросы по 2 бала. На экзамен выбираются 50 вопросов. 1. Что называется силой? а) Давление одного тела на другое б) Мера воздействия одного тела на другое в) Величина взаимодействия между телами г) Мера взаимосвязи между телами (объектами) 2. Назовите единицу измерения силы? а) Паскаль б) Ньютон в) Герц г) Джоуль 3. Чем нельзя определить действие силы на тело? а) числовым значением (модулем) б) направлением в) точкой приложения г) геометрическим размером 4. Какой прибор служит для статического измерения силы? а) амперметр б) гироскоп в) динамометр г) силомер 5. Какая система сил называется уравновешенной? а) Две силы, направленные по одной прямой в разные стороны б) Две силы, направленные под углом 90о друг к другу в) Несколько сил, сумма которых равна нулю г) Система сил, под действием которых свободное тело может находится в покое 6. а) 30 кН, вправо б) 30 кН, влево в) 10 кН, вправо г) 20 кН, вниз 7. Какого способа не существует при сложении сил, действующих на тело? а) геометрического б) графического в) тензорного г) аналитического 8 . Две силы F1=30Н и F2=40Н приложены к телу под углом 900 друг другу. Чему равна их равнодействующая? а) 70Н б)10Н в) 50Н г) 1200Н 9. Чему равна равнодействующая трёх сил, если F1=F2=F3=10 кН? а) 0 кН б) 10 кН в) 20 кН г) 30 кН 10. Что называется моментом силы относительно точки (центра)? а) Произведение модуля этой силы на время её действия б) Отношение силы, действующей на тело, к промежутку времени, в течение которого эта сила действует в) Произведение силы на квадрат расстояния до точки (центра) г)Произведение силы на кратчайшее расстояние до этой точки (центра) 11. а) Когда под действием силы тело движется вперёд б) Когда под действием силы тело вращается по ходу часовой стрелки в) Когда под действием силы тело движется назад г) Когда под действием силы тело вращается против хода часовой стрелки 12. Что называется парой сил? а) Две силы, результат действия которых равен нулю б) Любые две силы, лежащих на параллельных прямых в) Две силы, лежащие на одной прямой, равные между собой, но противоположные по направлению г) Две силы, лежащие на параллельных прямых, равные по модулю, но противоположные по направлению 13. Что называется центром тяжести? а) Это точка, в которой может располагаться масса тела б) Это точка, через которую проходит равнодействующая сил тяжести, действующих на частицы данного тела в) Это точка приложения силы тяжести г) Это точка, в которой совпадают центр симметрии тела и центра тяжести тела 14. б) в) г) 15. Что называется моментом силы относительно точки (центра)? а) Произведение модуля этой силы на время её действия б) Отношение силы, действующей на тело, к промежутку времени, в течение которого эта сила действует в) Произведение силы на квадрат расстояния до точки (центра) г) Произведение силы на кратчайшее расстояние до этой точки (центра) 16. Когда момент силы считается положительным? а) Когда под действием силы тело движется вперёд б) Когда под действием силы тело вращается по ходу часовой стрелки в) Когда под действием силы тело движется назад г) Когда под действием силы тело вращается против хода часовой стрелки 17. Что называется парой сил? а) Две силы, результат действия которых равен нулю б) Любые две силы, лежащих на параллельных прямых в) Две силы, лежащие на одной прямой, равные между собой, но противоположные по направлению г) Две силы, лежащие на параллельных прямых, равные по модулю, но противоположные по направлению 18. а) Это точка, в которой может располагаться масса тела б) Это точка, через которую проходит равнодействующая сил тяжести, действующих на частицы данного тела в) Это точка приложения силы тяжести г) Это точка, в которой совпадают центр симметрии тела и центра тяжести тела 19. Состояние твердого тела не изменится, если: а) Добавить пару сил б) Добавить уравновешивающую силу в) Одну из сил параллельно перенести в другую точку тела г) Добавить уравновешенную систему сил д) Добавить любую систему сил 20. Какое тело считается свободным? а) Имеющее одну точку опоры б)Находящееся в равновесии в) На которое не наложены связи г) Если равнодействующаяся всех сил равна нулю 21. Что называется связью? а) Тело, которое не может перемещаться б) Тело, которое может свободно перемещаться в) Сила, действующая на тело, которое не может перемещаться г) Сила, действующая на тело, которое может перемещаться д) Тело, ограничивающее перемещение данного тела 22. а) Сила, с которой рассматриваемое тело действует на связь б) Тело, ограничивающее свободное движение другого тела в) Сила, с которой связь действует на тело г) Взаимодействие между телом и связью д) Любая неизвестная сила 23. Как направлена реакция нити, шнура, троса: а) Реакция образует произвольный угол с направлением связи; б) Вдоль нити, шнура, троса от рассматриваемого тела; в) Вдоль нити, шнура, троса к рассматриваемому телу; г) Перпендикулярно нити, шнуру, тросу. д) Под углом 45o к нити, шнуру, тросу. 24. Укажите направления реакций связей невесомых стержней AB и BC? а) А б) В в) С г) D 25. Укажите направление реакций связи, если связь – подвижный цилиндрический шарнир. а)А б) В в) С г) D 26. а) А б) В в) С г) D 27. Как направлены реакции связей балки AB, если вес балки не учитывается: а) Вдоль балки АВ б) Параллельно полу в т. А и перпендикулярно балке в т. В в) Перпендикулярно полу в т. А и параллельно полу в т. В г) Перпендикулярно полу в т. А и перпендикулярно балке в т. В 28. Укажите правильную схему с указанием направления реакций связи в опорах A и B а) А б) В в) С г) D 29. Укажите направления реакций невесомых стержней 1, 2, 3. а) А б) В в) С г) D 30. Укажите направление реакций связей в опорах А, В, С. а) А б) В в) С г) D 31. Шар весом P удерживается на гладкой наклонной плоскости при помощи каната DE. а) А б) В в) С г) D 32. Точка A криволинейного бруса AB – цилиндрический шарнир. К концу B привязана нить BC. Укажите направление реакций опор A и B, если вес бруса P а) А б) В в) С г) D 33. Как направлены реакции связей в шарнирах А и В ломаной балки АВ? а) А б) В в) С г) D 34. Укажите направления реакций связи в опоре А и невесомом стержне ВС. а) А б) В в) С г) D 35. Укажите правильное направление реакций связей – нитей 1 и 2, удерживающих шар. а) А б) В в) С г) D 36. Укажите правильное направление реакций в жесткой заделке А. а) А б) В в) С г) D 37. Укажите правильное направление реакций связей в точке A и тросе BD удерживающем балку весом P а) А б) В в) С г) D 38. а) А б) В в) С г) D 39. Укажите правильное направление реакций в точке А. а) А б) В в) С г) D 40. Сходящейся системой сил называется совокупность сил: а) Линии действия которых пересекаются в одной точке б) Лежащих в одной плоскости в) Произвольно расположенных в пространстве г) Параллельных между собой 41. На несвободное тело действует плоская система сходящихся сил. Сколько независимых уравнений равновесия тела можно составить: а) 1 б) 2 в) 3 г) 4 42. Что изучает кинематика? а) Движение тела под действием приложенных к нему сил б) Виды равновесия тела в) Движение тела без учета действующих на него сил г) Способы взаимодействия тел между собой 43. а) Способ измерения времени б) Пространство в) Тело отсчёта г) Система координат, связанная с телом отсчёта 44. Движение тела описывается уравнением 2 . Определите скорость тела через 2с после начала движения. а) 21,4 м/c б) 3,2 м/c в) 12 м/c г) 6,2 м/c 45. Движение тела описывается уравнением . Не делая вычислений, назовите начальную координату тела и его начальную скорость. а) 12м; 7м/c б) 3м; 7м/c в) 7м; 3м/c г) 3м; -5м/c 46. Судно, движущееся с небольшой скоростью, сталкивается с пирсом и останавливается. Какие преобразования энергии происходят в данном процессе? а) Кинетическая энергия судна преобразуется в потенциальную энергию амортизирующих устройств. б) Кинетическая энергия судна преобразуется в его потенциальную энергию. в) Потенциальная энергия амортизирующих устройств преобразуется в её кинетическую энергию. г) Внутренняя энергия амортизирующих устройств преобразуется в кинетическую энергию судна. 47. Как связаны между собой тела (детали), образующие одно звено? а) подвижно б) неподвижно в) шарнирно г) скользящей посадкой 48. Какие кинематические пары подвергаются большему износу: а) низшие б) высшие в) изнашиваются одинаково г) не изнашиваются 49. Какие кинематические пары являются высшими: а) соединение вала с подшипником скольжения б) сцепление зубьев в зубчатых передачах в) соединение ползуна и направляющей г) соединение шариков с дорожкой качения в подшипнике качения 50. Какое звено является ведущим в кривошипно-ползунном механизме поршневого компрессора: а) кривошип б) шатун в) кулиса г) ползун 51. а) кривошип б) шатун в) кулиса г) ползун 52. При действии на ведущее звено механизма уравновешивающей силы или уравновешивающего момента: а) поддерживается движение механизма б) механизм приводится в состояние равновесия в) механизм замедляет движение г) механизм ускоряется 53. Какой вид сварки лучше применить для соединения тонких стальных листов внахлестку: а) газовую сварку б) электродуговую сварку в) контактную сварку г) все равно 54. Какие шпонки обеспечивают лучшее центрирование деталей на валу: а) клиновые шпонки б) призматические шпонки в) обеспечивают одинаково 55. Какой вид соединений обеспечивает большую точность взаимного расположения деталей: а) соединение клиновыми шпонками б) соединение призматическими шпонками в) шлицевое соединение г) обеспечивают одинаково 56. а) треугольную; б) трапецеидальную; в) прямоугольную. 57. Какую резьбу применяют в винтовых парах для передачи движения: а) треугольную б) трапецеидальную 58. Винтовые механизмы применяют: а) для преобразования вращательного движения в поступательное б) преобразования поступательного движения во вращательное в) преобразования вращательного движения относительно одной оси во вращательное относительно другой. 59. Как изменится КПД винтовой пары при увеличении угла подъема винтовой линии при одинаковом значении угла трения: а) КПД увеличится б) КПД уменьшится в) КПД не изменится 60. Передаточное число u больше единицы. Какая это передача: а) понижающая б) повышающая 61. Как следует изменить диаметр ведущего катка фрикционной передачи, чтобы увеличить угловую скорость ведомого вала в два раза: а) уменьшить в два раза б) увеличить в два раза в) увеличить угловую скорость невозможно 62. а) силу нажатия следует увеличить в два раза б) силу нажатия следует увеличить в четыре раза в) силу нажатия следует уменьшить в два раза г) силу нажатия следует уменьшить в четыре раза 63. Как изменится угловая скорость ведомого колеса, если увеличится число его зубьев при неизменном числе зубьев на ведущей шестерне: а) угловая скорость увеличится б) угловая скорость уменьшится в) угловая скорость не изменится 64. Какое звено в червячной передаче является ведущим: а) червяк б) червячное колесо в) шестерня 65. Какая ветвь открытой ременной передачи испытывает при работе большее натяжение: а) ведущая ветвь б) ведомая ветвь в) натяжение одинаково 66. а) диаметр ролика б) шаг цепи в) толщина звеньев цепи 67. Деталь, соединяющая электродвигатель с машиной, работает только на кручение. Как правильно называется эта деталь: а) вал б) ось в) стержень 68. По какому условию прочности следует рассчитывать оси: а) по условию прочности на кручение б) условию прочности на изгиб в) условию прочности на совместное действие изгиба и кручения 69. Две оси, несущие одинаковые нагрузки, изготовлены из стали одной и той же марки. Одна из этих осей неподвижная, другая – вращающаяся. При равной прочности осей какая из них должна иметь больший диаметр: а) вращающаяся б) неподвижная в) должны иметь одинаковую прочность 70. При каком виде трения скольжения почти полностью отсутствует износ трущихся поверхностей: а) при полусухом трении б) сухом трении в) жидкостном трении 71. а) при помощи упругой втулочно-пальцевой муфты б) помощи поперечно-свертной муфты в) помощи втулочной муфты г) помощи кулачковой расширительной муфты Ключи к тестам 4. Таблица 4.1 -Бальные оценки для элементов контроля Таблица 4.2 – Перевод баллов в оценки за аттестационную неделю Таблица 4. Таблица 4. Подготовься вместе с преподавателем с помощью инструментов для совместной работы. Ты сможешь успешно сдать и защитить курсовую или другую работу без пересдач. Срок выполнения Безопасная Проверка работы Поддержка Подробнее о сервисе Оставьте заявку для расчета стоимости заказа Почему студенты выбирают SHelp Прямое взаимодействие Быстрые Выгодная Помощь Гарантированные Как происходит работа Оформление заказа Реализация Получение работы Обратись за помощью уже сейчас! Написание работ по предметам На факультетах, где студенты приобретают инженерные специальности, преподают большое количество дисциплин, требующих решения задач. Ресурс гарантирует, что оставленная студентом заявка на решение задач по теоретической механике максимально быстро найдет своего исполнителя. Профессионалам по силам задачи по кинематике, динамике или статике, определение сил в стержнях плоской формы и реакции опор. Для них не составит труда: Любая из таких задач будет решена в течение определенного заказчиком срока, качественно и ответственно. Отзывы пользователей Замечательные учителя, эффективные уроки. Сдал экзамен на высокие баллы! Владлен Данцов Сергей Марков про репетитора по физике для 7–11 классов Занимался с Владиславом Поймановым. Репетитор объяснял все доступно и понятно, постоянно давал интересные задачи. Занятия помогли мне поступить в НИЯУ МИФИ Задать вопрос ученику Я в восторге от занятий Михаила Юрьевича! Даже самые сложные задачи становятся простыми! Валерия Никитина Дарья Ковтун про репетитора по английскому языку для 10–11 классов Жанна Владимировна Гуджеджиани занималась со мной английским языком полгода. Читать полностью Замечательные учителя, эффективные уроки. Сдал экзамен на высокие баллы! Владлен Данцов Часто задаваемые вопросыМы постарались собрать самые распространенные вопросы и дать на них ответы, Для того, чтобы сделать заказ на услугу вам необходимо заполнить специальную форму на сайте: нужно указать тип работы и номер телефона. Затем менеджер перезвонит Вам в течение 2-3х часов и произведет оценку стоимости заказа. Если стоимость заказа устраивает Вас, Вам нужно сделать предоплату в размере 30% от общей стоимости заказа. После чего мы приступаем к выполнению заказа. Мы оповестим Вас, когда заказ будет готов и после полной оплаты заказа, мы отправим Вам файлы в любом, удобном для Вас, виде. Сроки на все услуги индивидуальны. Если в требованиях к заказу будет указано о необходимости проверки работы на плагиат и будет указан необходимый процент плагиата, мы будем придерживаться данных требований, оказывая услугу нашему клиенту. Основные наши гарантии базируются на том, что мы работаем с нашими клиентами в рамках публичного договора, который определяет основные права и обязанности сторон, порядок работы, а также ответственность сторон в случае несоблюдения условий договора. Заказ можно оплатить безналичным способом путем оплаты по реквизитам, которые указывает наш менеджер в персональной переписке с клиентом. Данные персональной переписки не разглашаются. По результату внесения оплаты (либо предоплаты) клиент отправляет чек об оплате и мы получаем информацию о том, что оплата произведена, после чего, либо приступаем к работе (если внесена предоплата), либо завершаем её (в случаях если производиться полная оплата услуги). При обращении к нам, к вам прикрепляется персональный менеджер, который будет полностью работать с вами в тесном контакте до момента завершения нашего сотрудничества. Наши менеджеры работают круглосуточно и ваше обращение рассматривается в кротчайшие сроки после его поступления. Как проходит обучение с нами?Подберем автора под ваши критерии и образовательную цель. Прямое общение с авторами Обсуждайте детали заказа с авторами в режиме онлайн. Прямое общение с авторами Обсуждайте детали заказа с авторами в режиме онлайн. Эксперты сервиса – преподаватели, доценты и доктора наук, специализирующиеся в различных областях. С помощью отзывов и открытых рейтингов вы можете выбрать наиболее подходящего вам автора и связаться с ним. Прямое общение с авторами Обсуждайте детали заказа с авторами в режиме онлайн. Эксперты сервиса – преподаватели, доценты и доктора наук, специализирующиеся в различных областях. С помощью отзывов и открытых рейтингов вы можете выбрать наиболее подходящего вам автора и связаться с ним. Популярные услуги Строительная механика от 500 Подробнее Курсовые по менеджменту от 500 Подробнее Курсовые по экономике от 500 Подробнее Курсовые по юриспруденции от 500 Подробнее Теоретическая механика от 500 Подробнее Помощь на зачете онлайн от 500 Подробнее Онлайн помощь на экзамене по математике от 500 Подробнее Помощь на контрольной онлайн от 500 Подробнее Помощь в прохождении тестов на дистанционном обучении от 500 Подробнее Помощь в сдаче онлайн тестов от 500 Подробнее Помощь сдачи онлайн тестов через teams от 500 Подробнее Тест по алгебре дистанционно онлайн помощь от 500 Подробнее Помощь в написании диплома от 500 Подробнее Диплом по психологии от 500 Подробнее Написание главы диплома от 500 Подробнее Помощь по написанию диплома по IТ от 500 Подробнее Защита диплома речь заказать от 500 Подробнее Апостиль диплома срочно от 500 Подробнее Дипломная работа колледж от 500 Подробнее Дипломная работа медицинский колледж от 500 Подробнее Дипломная работа по сварке для колледжа от 500 Подробнее Презентация для школы от 500 Подробнее Презентация тема экология от 500 Подробнее Презентация на заказ студенту от 500 Подробнее Доклад с презентацией от 500 Подробнее Перевод на русский язык от 500 Подробнее Перевод на английский язык от 500 Подробнее Перевод публицистических текстов от 500 Подробнее Перевод на французский язык от 500 Подробнее Перевод на немецком языке от 500 Подробнее Диссертация: нюансы написания и как заказать от 500 Подробнее Диссертации по медицине от 500 Подробнее Диссертация на английском языке от 500 Подробнее Диссертации для технических наук от 500 Подробнее Диссертация по праву от 500 Подробнее Диссертации по истории от 500 Подробнее Диссертация по психологии от 500 Подробнее Диссертация по педагогике от 500 Подробнее Диссертация о политике от 500 Подробнее Диссертация по экономике от 500 Подробнее Диссертация по социологии от 500 Подробнее Диссертация по военным наукам от 500 Подробнее Диссертация по физической культуре от 500 Подробнее Диссертация по лингвистике от 500 Подробнее Лабораторная работа по программированию от 500 Подробнее Заказать лабораторные работы по информатике от 500 Подробнее Заказать лабораторные работы по физике от 500 Подробнее Лабораторная работа для ТУСУР от 500 Подробнее Заказать чертеж от руки от 500 Подробнее Заказать чертежи по инженерной графике от 500 Подробнее Чертежи в карандаше: как заказать от 500 Подробнее Заказать чертежи в Компасе от 500 Подробнее Чертежи по начертательной геометрии от 500 Подробнее Купить отчет по производственной практике от 500 Подробнее Заказать отчет по преддипломной практике от 500 Подробнее Готовый отчет по практике от 500 Подробнее Отчет по практике закупки от 500 Подробнее Отчет по практике в СГА от 500 Подробнее Заказать эссе по обществознанию от 500 Подробнее Эссе для написания ЕГЭ от 500 Подробнее Помощь в написании эссе от 500 Подробнее Заказать готовое эссе от 500 Подробнее Эссе по русскому языку от 500 Подробнее Сочинение по литературе от 500 Подробнее Подготовка сочинения по русскому языку от 500 Подробнее Заказать итоговое сочинение от 500 Подробнее Эссе по французскому языку от 500 Подробнее Презентация в Powerpoint от 500 Подробнее Курсовая по уголовному праву от 500 Подробнее Курсовая по педагогике от 500 Подробнее Курсовая работа с подтверждением от антиплагиата от 500 Подробнее Курсовая по финансам от 500 Подробнее Курсовая по программированию от 500 Подробнее Курсовая по сопромату от 500 Подробнее Курсовые по анатомии от 500 Подробнее Курсовая по бухучету от 500 Подробнее Курсовая по теплотехнике от 500 Подробнее Курсовая по гидравлике от 500 Подробнее Курсовая по математике от 500 Подробнее Курсовая работа по деталям машин от 500 Подробнее Курсовые работы по ЭВМ от 500 Подробнее Помощь студентам в написании курсовых от 500 Подробнее Диссертация химических наук от 500 Подробнее Диссертация по филологическим наукам от 500 Подробнее Диссертации по финансовому анализу от 500 Подробнее Государственный орган диссертация от 500 Подробнее Управление организацией диссертация от 500 Подробнее Транспортная сфера диссертация от 500 Подробнее Налоговая диссертация от 500 Подробнее Доклад по радиоэкологии от 500 Подробнее Статья на английском языке от 500 Подробнее Статья для магистратуры от 500 Подробнее Научная статья для студентов от 500 Подробнее Статья для диссертации от 500 Подробнее Реферат по философии от 500 Подробнее Реферат по психологии от 500 Подробнее Реферат по экономике от 500 Подробнее Реферат по социологии от 500 Подробнее Реферат по физкультуре от 500 Подробнее Реферат по менеджменту от 500 Подробнее Реферат по эпидемиологии от 500 Подробнее Онлайн помощь по математике студентам от 500 Подробнее Помощь студентам на контрольной от 500 Подробнее Помощь студентам в написании работ от 500 Подробнее Помощь студентам в программировании на 1С от 500 Подробнее Помощь студентам по программированию от 500 Подробнее Помощь с контрольными работами от 500 Подробнее Остались вопросы? Получите консультацию менеджера! © 2005 – 2020 – Все права защищены стрелка_назад просматривать материалы курса библиотека_книги «
Предыдущий
|
Следующий
» Производные в кинематике Ускорение из положения Стрельба по яблоку Тормозная машина Нарисуйте движение Пешеход и велосипед на перекрестке Суперпозиция гравитации Скользящий блок Толкание сложенных блоков Проблема с мойкой окон Угловое положение по угловому ускорению Автомобиль на вираже Орбитальное круговое движение Прыгающий мяч Центр масс 3 объектов Центр масс однородного стержня Проблема с ракетными салазками Проблема со снегоуборочной машиной Блокировать спуск по пандусу Столкновение и скольжение по неровной поверхности Блок, скользящий вниз по круговому склону Упругое одномерное столкновение Упругое одномерное столкновение снова Гравитационная рогатка Одномерное упругое столкновение в CM Найдите момент инерции диска от падающей массы. Этвуд Машина Два блока и шкив, использующие энергию Блоки и массивный шкив Угловой момент относительно разных точек Угловой момент двух вращающихся частиц Частица попадает в поворотное кольцо Качение колеса без проскальзывания по наклонной плоскости – метод крутящего момента Йойо тянет по земле Качение колеса без проскальзывания по наклонной плоскости «
Предыдущий
|
Следующий
» стрелка_назад просматривать материалы курса библиотека_книги «
Предыдущий
|
Следующий
» Полные конспекты курса также доступны для
скачать (PDF – 67. «
Предыдущий
|
Следующий
» MIT OCW 8.01 – Физика I Классическая механика (37 файлов) Type: Course Bibtex: Ускорьте устранение инцидентов и сократите среднее время восстановления. Начните через 2 минуты с нашим бесплатным, навсегда plan.ads через Carbon Lazure CFHCABLE OSUOSL Greateedbox Seedboxcc Whatbox Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY- NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC- SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC -SA Лицензия: Creative Commons BY-NC -SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY -NC-SA Лицензия: Creative Commons BY-NC- СА Лицензия: Creative Commons BY-NC- SA Лицензия: Creative Commons BY -NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC- SA Лицензия: Creative Commons BY-NC- SA Лицензия: Creative Commons BY -NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY- NC-SA Лицензия : Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC- SA Лицензия: Creative Commons BY- NC-SA Лицензия: Creative Commons BY-NC- SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC -СА Лицензия: Creative Commons BY -NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC- SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY -NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY- NC-SA Лицензия: Creative Commons BY-NC- SA Лицензия: Creative Commons BY-NC- SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC- SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC -SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия : Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY- NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC -SA Лицензия: Creative Commons BY -NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC -SA Лицензия: Creative Commons BY-NC -SA Лицензия: Creative Commons BY -NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC -SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY- NC-SA Лицензия: Creative Commons BY-NC -SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия : Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY -NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY- NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC -SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY- НК-СА Лицензия: Creative Commons BY -NC-SA Лицензия: Creative Commons BY- NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC -SA Лицензия: Creative Commons BY -NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY- NC-SA Лицензия: Creative Commons BY-NC -SA Лицензия: Creative Commons BY- NC-SA Лицензия: Creative Commons BY-NC- SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC -СА Лицензия: Creative Commons BY-NC- SA Лицензия: Creative Commons BY-NC- SA Лицензия: Creative Commons BY-NC -SA Лицензия: Creative Commons BY-NC- SA Лицензия: Creative Commons BY -NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY- NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY- НК-СА Лицензия: Creative Commons BY -NC-SA Лицензия: Creative Commons BY-NC -SA Лицензия: Creative Commons BY -NC-SA Лицензия: Creative Commons BY -NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY -NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY- NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY- НК-СА Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC- SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия : Creative Commons BY-NC-SA Лицензия: Creative Commons BY -NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC- SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC- SA Лицензия: Creative Commons BY -NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY- НК-СА Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Лицензия: Creative Commons BY-NC-SA Скачать Физика I: Классическая механика Решения для итоговых экзаменов | Осень 2008 г. Массачусетский технологический институт и другие экзамены по классической механике в формате PDF только на Docsity! MIT OpenCourseWare http://ocw.mit.edu 8.012 Physics I: Classical Mechanics Fall 2008 Для получения информации о цитировании этих материалов или наших Условий использования посетите: http://ocw.mit.edu/terms. MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Physics Physics 8.012 Fall 2008 Final Exam РЕШЕНИЕ ИМЯ: _________________________________________________ Инструкции: 1. Современные дети не знают, насколько они хороши. Когда я изучал квантовую механику, процесс включал такие этапы, как «посещение лекций». Мало того, что это требовало физического перемещения из уютного дома в полуразрушенные лекционные залы, но — понимаете — вы действительно должны были быть там в заранее оговоренное время! Часто рано утром. В наши дни все, что вам нужно сделать, это запустить YouTube и смотреть лекции в свободное время. Массачусетский технологический институт только что выпустил целый курс по квантовой математике для студентов с любовным названием «8.04», потому что именно так работает Массачусетский технологический институт. Профессором является Аллан Адамс, который, как правило, фантастический лектор, поэтому я подозреваю, что они действительно хороши, хотя я на самом деле не смотрел их все сам. Лекция 1: Введение в суперпозицию Подход Аллана в этом видео на самом деле основан на первых двух главах книги «Квантовая механика и опыт » философа Дэвида Альберта. Я уверен, что это очень смутит философских скептиков, обитающих в разделе комментариев предыдущего поста. Это всего лишь один из многих замечательных онлайн-курсов по физике; Ранее я упоминал курс GR Ленни Сасскинда. Но, будучи в значительной степени вне моих дней, когда я сам ходил на курсы, я действительно не следил за ними. Не стесняйтесь предлагать свои фавориты в комментариях. Подписывайтесь на @seanmcarroll Follow @preposterousuni
7 кг/см2
Наружный диаметр вала равен 40 см, а внутренний 24 см. Модуль упругости G = 8·105кг/см2. Чему равна мощность, передаваемая валом, если он вращается со скоростью 120 об/мин?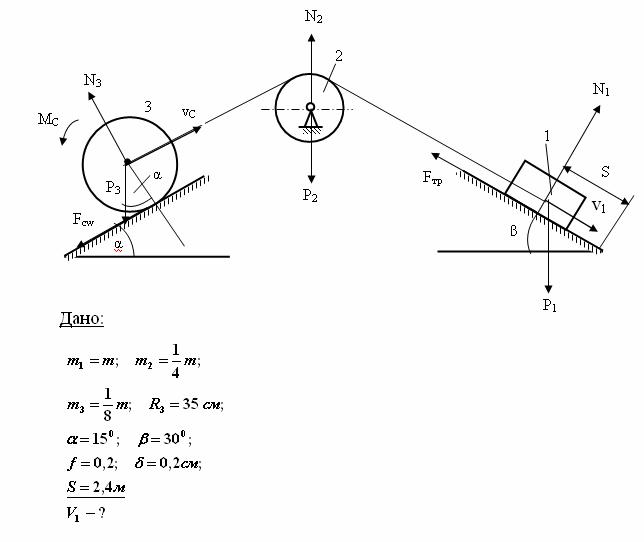
2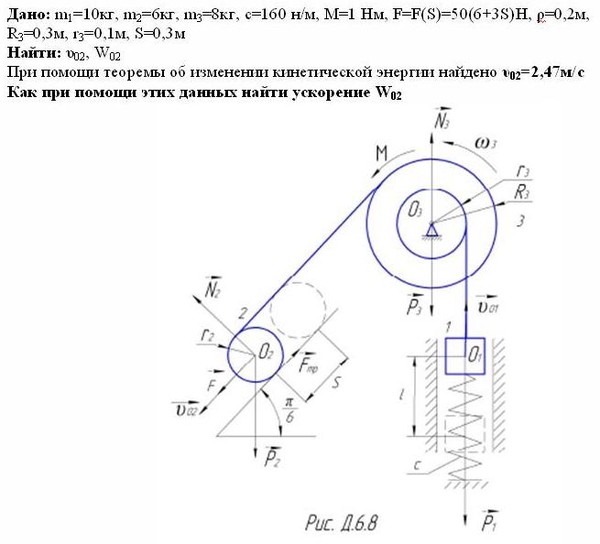
достиг частоты вращения n=300 оборотов в минуту. Какое число оборотов N, он успел сделать за это время?
с.) при максимальной скорости в 32 узла (60 км/час) и полном водоизмещении 25 860 т. Оцените время разгона этого крейсера до максимальной скорости при условии 100% использования мощности силовых установок. Все величины выражены в системе СИ.
Чему была первоначальная скорость тела? Все величины выражены в СИ.
Во сколько раз увеличится нагрузочная способность передачи?
7 кг/см2
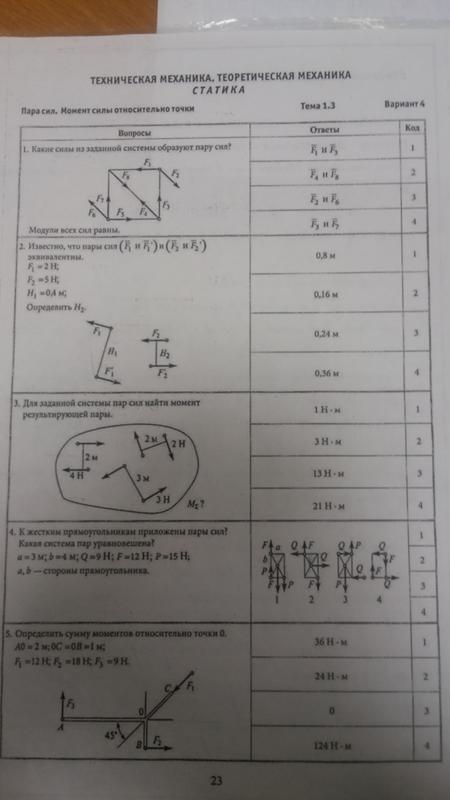Чему будут равны наибольшие касательные напряжения в полом вале, если в сплошном они были равны 600 кг/см2?
-5Тесты по курсу Теоретическая и прикладная механика
Чему равна равнодействующая трёх приложенных к телу сил, если F1=F2=F3=10кН? Куда она направлена?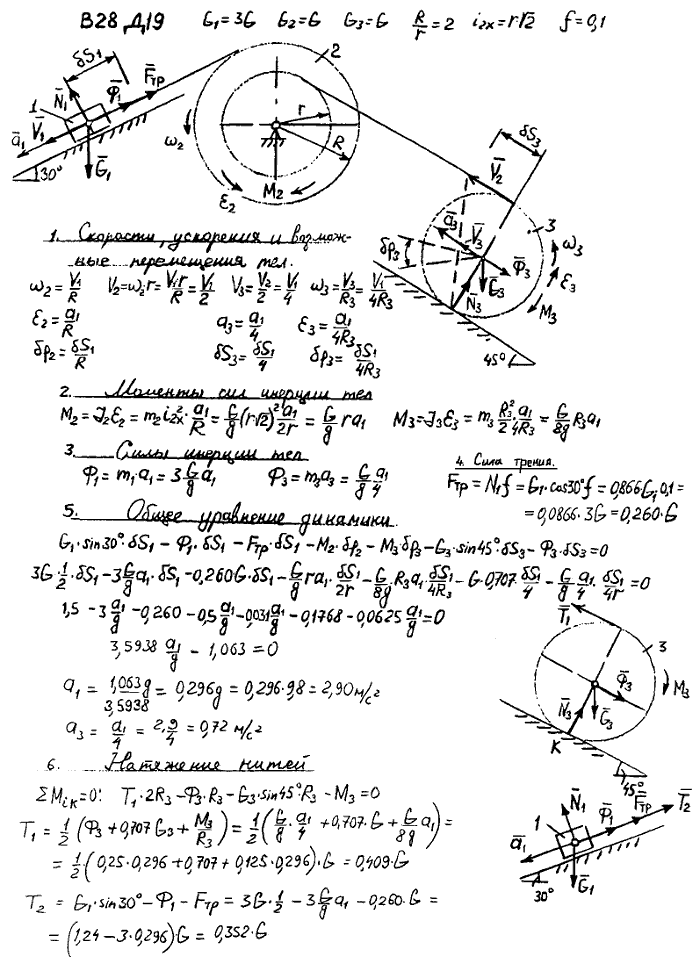
Когда момент силы считается положительным?
Какой формулой нужно воспользоваться, чтобы найти координату с центра тяжести фигуры, выполненной из тонкой проволоки?
Что называется центром тяжести?
Что называется реакцией связи?
Укажите реакцию связи неподвижного шарніра
Определите направление реакций в точках A и D
Укажите правильное направление реакций связей в опорах A, B и веревке CD.
Что из ниже перечисленного не входит в систему отсчёта?
Какое звено является ведущим в кривошипно-ползунном механизме двигателя внутреннего сгорания:
Какую резьбу применяют для крепежных соединений:
Как следует изменить силу нажатия фрикционных цилиндрических катков, если при передаче одного и того же вращающего момента катки заменить другими, с диаметрами в два раза больше первоначальных:
Какой размер является основным для выбора приводной цепи цеп ной передачи: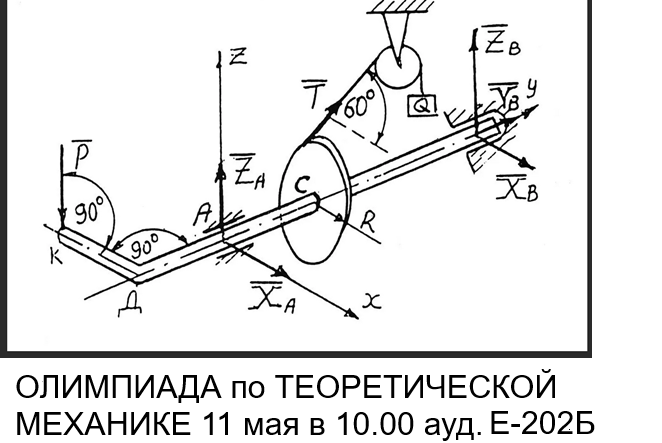
При помощи какой муфты можно компенсировать неточность в расположении геометрических осей валов: №
Вопроса
Правильный ответ
№ Вопроса
Правильный ответ
№
Вопроса
Правильный ответ
б
в
б
б
б
в
г
в
б
в
б
а
г
б
а
в
б
б
в
г
а
в
б
б
а
а
а
г
а
в
г
б
а
г
в
б
в
б
б
г
г
г
а
г
б
б
б
г
б, г
в
а
д
г
в
а
б
в
б
б
г
в
б
а
г
б
в
а
г
а
б
а
Рейтинговая система для оценивания успеваемости курсантов / студентов Элементы учебной деятельности
Максимальный балл на 1-й АО с начала семестра
Максимальный балл за период между 1 АО и 2 АО
Всего за семестр
Посещение занятий
Выполнения лабораторных работ
Выполнения самостоятельных работ на практических занятиях
Поощрительные баллы
Всего максимум за период:
Балы на дату контрольной точки
Оценка
> 90 % от максимальной суммы балов на дату АТ
70% – 89% от максимальной суммы балов на дату АТ
60% – 69% от максимальной суммы балов на дату АТ
< 60 % от максимальной суммы балов на дату АТ
3 – Шкала национальной системы оценивания знаний студентов и ЕКТС (ECTS) Оценка в баллах
Оценка по национальной шкале
Оценка по шкале ECTS
Оценка
Объяснение
90-100
Отлично
А
Отлично (отличное выполнение лишь с незначительным количеством ошибок)
82-89
Хорошо
B
Очень хорошо (выше среднего уровня с несколькими ошибками)
75-81
С
Хорошо (в целом правильное выполнение с определенным количеством существенных ошибок)
67-74
Удовлетворительно
D
Удовлетворительно (неплохо, но со значительным количеством недостатков)
60-66
E
Достаточно (выполнение удовлетворяет минимальным критериям)
35-59
Неудовлетворительно
FX
Неудовлетворительно (с возможностью повторного составления)
1-34
F
Неудовлетворительно (с обязательным повторным курсом)
4 – Критерии оценивания учебных достижений курсантов студентов в кредитно-модульной системе организации учебного процесса и ЕКТС (ECTS)Заказать решение задач по теоретической механике
Заказать решение задач по теоретической механике – быстро, недорого
от 2 часов
сделка
на плагиат
24/7
без посредников
сроки выполнения
партнерская программа
персонального Менеджера
бесплатные доработки В их числе — решение задач по теоретической механике. Овладение предметом предполагает запоминание множества терминов, формул и умение применять их на практике. Если у студента есть время и желание самостоятельно разбираться в сложностях решения таких задач, интернет предлагает не только готовые ответы, но и пояснения для решений из Яблонского или Тарга. Однако если нет ни того, ни другого – выходом из ситуации станет возможность купить готовые решения на сервисе, помощь на котором быстро и недорого оказывают специалисты в области теоретической механики. Отсутствие посредников обеспечит максимально низкую стоимость. Наличие службы поддержки позволит быть в курсе процесса продвижения работы в любой момент времени. Консультант получит оплату только по факту успешной сдачи работы, если потребуются коррективы – внесет их оперативно и бесплатно. Уже на первом занятии она проверила, точнее сказать…
чтобы Вам
было легче разобраться с нашим сервисом. Консультации с рефератами (1 день) занимают куда меньше времени, чем консультации по курсовым работам (2-3 дня). Также время оказания услуги зависит от сезонности (в сессии количество обращений больше, поэтому наши авторы в это время загружены сильнее и, оказать услугу, с маленьким сроком, будет дороже) и от сложности темы и требований к услуге (объем работы, требования к антиплагиату и т.д.). Мы готовы помочь студенту в самые минимальные сроки, но нужно понимать, что это будет стоить дороже, чем услуга со стандартными сроками. В любое случае, пользуясь нашим сервисом, Вы можете быть уверены, что сроки не будут нарушены! Помимо этого наша компания около 6 лет занимается деятельностью в сфере помощи студентам, что соответствующим образом складывается на нашей репутации и отзывах клиентов, которые возвращаются к нам из года в год и получают профессиональную и качественную помощь по волнующим их вопросам. Вне зависимости от того, в каком часовом поясе вы живете, мы стараемся создать для вас наиболее благоприятные условия, которые позволят вам чувствовать себя комфортно в процессе нашего сотрудничества. Персональный менеджер ответить на все ваши вопросы, а также поможет выработать наиболее грамотные и эффективные способы соблюдения ваших интересов.
Помимо этого, на протяжении 6 лет мы сотрудничаем с большим числом авторов по различным дисциплинам, которые имеют высшее профессиональное образование в той области, в которой они оказывают консультацию. Среди наших автор 2 доктора наук, 5 кандидатов наук, а также превалирующее большинство (около 50 человек) экспертом имеющих высшее профессиональной образование в той сфере, в рамках которой вам требуется консультация.
Занятия проходят в удобное для вас время. Эксперты сервиса – преподаватели, доценты и доктора наук, специализирующиеся в различных областях. С помощью отзывов и открытых рейтингов вы можете выбрать наиболее подходящего вам автора и связаться с ним. заданий | Классическая механика | Физика
УРОК № Названия уроков ЗАДАЧИ связанные рабочие примеры 0 Векторы Никто Никто Неделя 1: Кинематика 1 1D-кинематика — положение и скорость Набор задач 1 (PDF) 2 1D-кинематика — ускорение 3 2D-кинематика — положение, скорость и ускорение Неделя 2: Законы Ньютона 4 Законы движения Ньютона Набор задач 2 (PDF) 5 Сила тяжести 6 Контактные силы 7 Напряжение и пружины Глубокое погружение 1 Трение Неделя 3: Круговое движение 8 Круговое движение — положение и скорость Набор задач 3 (PDF) 9 Равномерное круговое движение 10 Круговое движение — ускорение 11 Закон Ньютона 2 и и круговое движение Неделя 4: Силы сопротивления, ограничения и непрерывные системы 12 Шкивы и ограничения Набор задач 4 (PDF) 2 блока и 2 шкива 13 Массивная веревка 14 Силы сопротивления Неделя 5: Импульс и импульс 15 Импульс и импульс Набор задач 5 (PDF) 16 Сохранение импульса 17 Центр масс и движение центра масс Неделя 6: Непрерывный массообмен 18 Относительная скорость и отдача Набор задач 6 (PDF) 19 Непрерывный массообмен Неделя 7: Кинетическая энергия и работа 20 Кинетическая энергия и работа в 1D Набор задач 7 (PDF) 21 Кинетическая энергия и работа в 2D и 3D 22 Консервативные и неконсервативные силы Неделя 8: Потенциальная энергия и энергосбережение 23 Потенциальная энергия Набор задач 8 (PDF) 24 Сохранение энергии 25 Диаграммы потенциальной энергии Неделя 9: Теория столкновений 26 Типы столкновений Набор задач 9 (PDF) 27 Упругие столкновения Глубокое погружение 2 Система отсчета центра масс Неделя 10: Вращательное движение 28 Движение твердого тела Набор задач 10 (PDF) 29 Момент инерции 30 Крутящий момент 31 Вращательная динамика Неделя 11: угловой момент 32 Угловой момент точечной частицы Набор задач 11 (PDF) 33 Угловой момент твердого тела относительно неподвижной оси. 34 Крутящий момент и угловой импульс 90 035 Неделя 12: Вращения и перемещения — Роллинг 90 036 35 Кинематика качения Набор задач 12 (PDF) 36 Динамика качения 37 Кинетическая энергия качения и угловой момент Глубокое погружение 3 Гироскопы чтений | Классическая механика | Физика
9MB)
. УРОК № НАЗВАНИЯ УРОКОВ ЧТЕНИЯ 0 Векторы Неделя 1: Кинематика 1 1D-кинематика — положение и скорость 2 1D-кинематика — ускорение 3 2D-кинематика — положение, скорость и ускорение Неделя 2: Законы Ньютона 4 Законы движения Ньютона 1–7.3 (PDF) 5 Сила тяжести 6 Контактные силы 7 Напряжение и пружины Глубокое погружение 1 Трение Нет чтения Неделя 3: Круговое движение 8 Круговое движение — положение и скорость 2 (PDF, 1,5 МБ) 9 Равномерное круговое движение 10 Круговое движение — ускорение 11 Закон Ньютона 2 и и круговое движение Неделя 4: Силы сопротивления, ограничения и непрерывные системы 12 Шкивы и ограничения 9 (PDF — 1,2 МБ) 13 Массивная веревка 14 Силы сопротивления Неделя 5: Импульс и импульс 15 Импульс и импульс 4 (PDF) 16 Сохранение импульса 17 Центр масс и движение центра масс Неделя 6: Непрерывный массообмен 18 Относительная скорость и отдача 19 Непрерывный массообмен 1–12.3 (PDF, 3,0 МБ) Неделя 7: Кинетическая энергия и работа 20 Кинетическая энергия и работа в 1D 21 Кинетическая энергия и работа в 2D и 3D 22 Консервативные и неконсервативные силы 1 (PDF) Неделя 8: Потенциальная энергия и энергосбережение 23 Потенциальная энергия 24 Сохранение энергии 25 Диаграммы потенциальной энергии 6 (PDF) Неделя 9: Теория столкновений 26 Типы столкновений 27 Упругие столкновения Глубокое погружение 2 Система отсчета центра масс Нет чтения Неделя 10: Вращательное движение 28 Движение твердого тела 29 Момент инерции 30 Крутящий момент 1–17.3 (PDF — 1.9МБ) 31 Вращательная динамика Неделя 11: угловой момент 32 Угловой момент точечной частицы 33 Угловой момент твердого тела относительно неподвижной оси. 34 Крутящий момент и угловой импульс 90 035 Неделя 12: Вращения и перемещения — Роллинг 90 036 35 Кинематика качения 36 Динамика качения 37 Кинетическая энергия качения и угловой момент Глубокое погружение 3 Гироскопы Нет чтения MIT OCW 8.
01 – Физика I – Классическая механика readme.txt 1.81kB ocw-8.01-lec-mit-0035.MP4 62.12MB ocw-8.01-lec-mit-0034.MP4 67.13MB ocw-8.01-lec-mit-0033.MP4 74.11MB ocw-8.01-lec-mit-0032.MP4 68.76MB OCW-8.01-LEC-MIT-0031.MP4 68.40MB OCW-8.01-LEC-MIT-0030.MP4 69.69MB 212124 69.69MB 1212129124 112121212129124 69,69MB 11121212129124 69,69MB 69,69MB121121224 . 0029.MP4 69,60MB OCW-8.01-LEC-MIT-0028.MP4 68,81MB OCW-8.01-LEC-MIT-10027.MP4. OCW-8.01-LEC-MIT -0027.MP4. OCW-8.01-LEC-MIT-100.mp4 OCW-8.01-LEC-MIT-100.mp4 OCW-8.01-LEC-MIT-80021 . -8.01-lec-mit-0026.MP4 70.00MB ocw-8.01-lec-mit-0025.MP4 67.78MB ocw-8.01-lec-mit-0024.MP4 69.64MB ocw-8.01-lec-mit-0023.MP4 73.76MB ocw-8.01- LEC-MIT-0022.MP4 59,82MB OCW-8.01-LEC-MIT-0021.MP4 66,64MB OCW-8.01.64MB-MIT-0025 OCW-8.01.64MB-MIT-0025 . ocw-8.01-lec-mit-0019.MP4 60.87MB ocw-8. 01-lec-mit-0018.MP4 69,40MB OCW-8.01-LEC-MIT-0017.MP4 67,81MB OCW-8.01-LEC-MIT -0016.MP4 68.08.08.01-LEC-MIT -0016.MP4 68.08.01-LEC-MIT -0016.MP4 68.018.08.01-LEC-MIT -0016.MP4 . LEC-MIT-0015.MP4 72.34MB OCW-8.01-LEC-MIT-0014 ocw-8.01-lec-mit-0012.MP4 69.43MB ocw-8.01-lec-mit-0011.MP4 68.38MB ocw-8.01-lec-mit-0010.MP4 69.96MB ocw-8.01-lec-mit-0009.MP4 70.10MB ocw-8.01- LEC-MIT-0008.MP4 66,63MB OCW-8.01-LEC-MIT-0007.MP4 70.09MB OCW-8.01.01-MIT-0006.MP4. OCW-8.01-LEC-MIT -0006.MP40025 . ocw-8.01-lec-mit-0005.MP4 71.14MB ocw-8.01-lec-mit-0004.MP4 72.90MB ocw-8.01-lec-mit-0003.MP4 68.53MB ocw-8.01-lec-mit-0002.MP4 71.54MB ocw-8.01- lec-mit-0001.MP4 57.07MB 8-01Fall-1999.zip 7.09MB
Tags: @article {,
title= {MIT OCW 8.01 - Физика I - Классическая механика},
журнал = {},
автор = {Уолтер Левин},
год = {1999},
URL = {},
лицензия = {BY-NC-SA},
abstract= {Это полный набор видеолекций, записанных в Массачусетском технологическом институте. Домашнюю страницу оригинальных лекций можно найти в MIT OCW: http://ocw. mit.edu/
Этот торрент представляет собой просто перекодирование исходных файлов .rm со скоростью 220 Кбит/с в формат mpeg4, 15 кадров в секунду, 320 x 240 h.264 @ 144 Кбит/с, с монофоническим звуком AAC 32 Кбит/с, так что его можно, например, легко воспроизводить на телефоне во время ваши ежедневные поездки.
Описание курса
--------------------
8.01 - это класс физики для первокурсников в первом семестре по ньютоновской механике, механике жидкости и теории кинетического газа. В дополнение к основным понятиям ньютоновской механики, механики жидкости и теории кинетического газа в этом курсе рассматривается множество интересных тем: двойные звезды, нейтронные звезды, черные дыры, явления резонанса, музыкальные инструменты, звездный коллапс, сверхновые, астрономические явления. наблюдения с очень высоко летающих аэростатов (лекция 35), и вам будет разрешено
заглянуть в интригующий квантовый мир.
Основные моменты этого курса
-------------------------
В этом курсе представлены конспекты лекций, наборы задач с решениями, экзамены с решениями, ссылки на соответствующие ресурсы и полный набор записанных на видео лекций. 35 видеолекций профессора Левина были записаны в кампусе Массачусетского технологического института во время
осень 1999. Профессор Левин хорошо известен в Массачусетском технологическом институте и за его пределами своим динамичным и увлекательным стилем лекций.
Лицензия
-------
Массачусетский технологический институт щедро размещает эти лекции в сети и распространяется под лицензией Creative Commons License (BY-NC-SA), поэтому делиться ими совершенно законно. Поэтому, пожалуйста, раздавайте как можно дольше, чтобы этот удивительный ресурс оставался доступным.},
ключевые слова = {},
условия = {}
}
Случайные механики и примеры: видео -лекции
9007 9007
.
0.1 Векторы и скаляры
Массачусетский технологический институт 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: доктор Мишель Томасик
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 2
Воспроизвести видео 0.2 Векторные операторы
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Мишель Томасик
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 3
Воспроизвести видео 0.3 Системы координат и единичные векторы
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Мишель Томасик
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 4
Воспроизвести видео 0.4 Векторы — величина и направление
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Мишель Томасик NC-SA
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 5
Воспроизвести видео 0,5 Векторная декомпозиция на составляющие
Массачусетский технологический институт 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Мишель Томасик
Дополнительная информация на http://ocw. mit.edu/8-01F16 ://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 6
Воспроизвести видео 0.6 Переход между представлениями
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Мишель Томасик
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 7
Воспроизвести видео 1.0 Неделя 1 Введение
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: профессор Дипто Чакрабарти
Больше информации на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu I. Урок 1: Одномерная кинематика — положение и скорость Лекция 8
Воспроизвести видео 1.1 Системы координат и единичные векторы в 1D
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 9
Воспроизвести видео 1.2 Вектор положения в 1D
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 10
Воспроизведение видео 1. 3 Вектор смещения в 1D
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 11
Воспроизвести видео 1.4 Средняя скорость в 1D
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/8-01F16 ://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 12
Воспроизвести видео 1.5 Мгновенная скорость в 1D
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw. mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 13
Воспроизвести видео 1.7 Рабочий пример: производные в кинематике
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu II. Урок 2: 1D-кинематика — ускорение Лекция 14
Воспроизвести видео 2.1 Введение в ускорение
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw. mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 15
Воспроизвести видео 2.2 Ускорение в 1D
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 16
Воспроизвести видео 2.3 Рабочий пример: ускорение из положения
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 17
Воспроизвести видео 2. 4 Интеграция
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: проф. Дипто Чакрабарти
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu III. Урок 3: 2D-кинематика — положение, скорость и ускорение Лекция 18
Воспроизведение видео 3.1 Система координат и вектор положения в 2D
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 19
Воспроизвести видео 3.2 Мгновенная скорость в 2D
MIT 8. 01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/8-01F16 ://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 20
Воспроизвести видео 3.3 Мгновенное ускорение в 2D
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 21
Воспроизвести видео 3.4 Движение снаряда
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw. mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 22
Воспроизвести видео 3.5 Демонстрация: съемка яблока
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: Калеб Бонюн
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 23
Воспроизведение видео 3.5 Demo: Relative Motion Gun
MIT 8.01 Classical Mechanics, Fall 2016
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: Калеб Бонюн
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu IV. Неделя 1 Примеры работы Лекция 24
Воспроизвести видео PS. 1.1 Три вопроса перед началом
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Мишель Томасик
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 25
Воспроизвести видео PS.1.2 Съемка яблочного решения
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: профессор Дипто Чакрабарти
Дополнительная информация на http://ocw.mit.edu/ термины
Дополнительные курсы на http://ocw.mit.edu Лекция 26
Воспроизвести видео P.1.3 Рабочий пример: тормозной автомобиль
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw. mit.edu/8-01F16
Преподаватель: проф. Анна Фребель
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 27
Воспроизвести видео P.1.4 Sketch the Motion
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 28
Воспроизвести видео P.1.5 Рабочий пример: пешеход и велосипедист на перекрестке
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw. mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 29
Воспроизвести видео 4.0 Неделя 2 Введение
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: профессор Дипто Чакрабарти
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu V. Урок 4: Законы движения Ньютона Лекция 30
Воспроизвести видео 4.1 Первый и второй законы Ньютона
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: проф. Дипто Чакрабарти
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw. mit.edu Лекция 31
Воспроизвести видео 4.2 Третий закон Ньютона
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: профессор Дипто Чакрабарти
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 32
Воспроизвести видео 4.3 Системы отсчета
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: профессор Дипто Чакрабарти
Дополнительная информация на http://ocw.mit.edu/ термины
Дополнительные курсы на http://ocw.mit.edu Лекция 33
Воспроизвести видео 4. 4 Неинерциальные системы отсчета
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: проф. Дипто Чакрабарти
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu VI. Урок 5: Гравитация Лекция 34
Воспроизвести видео 5.1 Универсальный закон всемирного тяготения
Массачусетский технологический институт 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: профессор Анна Фребель
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 35
Воспроизвести видео 5. 2 Рабочий пример: гравитация — суперпозиция
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: проф. Анна Фребель
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 36
Воспроизвести видео 5.3 Гравитация на поверхности Земли: Значение g.
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: профессор Анна Фребель
Дополнительная информация на http ://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu VII. Урок 6: Контактные силы Лекция 37
Воспроизвести видео 6.1 Контактные силы
MIT 8. 01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 38
Воспроизвести видео 6.2 Статическое трение
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu VIII. Урок 7: Натяжение и пружины Лекция 39
Воспроизвести видео 7.1 Толкание Тяга и натяжение
Массачусетский технологический институт 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: профессор Анна Фребель
Дополнительная информация на http://ocw.mit.edu/8-01F16 ://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 40
Воспроизвести видео 7.2 Идеальная веревка
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 41
Воспроизвести видео 7.3 Решение систем шкивов
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Больше информации на http://ocw. mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 42
Воспроизвести видео 7.4 Закон Гука
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu IX. Глубокое погружение: Трение Лекция 43
Воспроизвести видео DD.1.1 Трение в наномасштабе
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: профессор Владан Вулетич
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw. mit.edu X. Примеры работы за неделю 2 Лекция 44
Воспроизвести видео PS.2.1 Рабочий пример — скользящий блок
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 45
Воспроизвести видео PS.2.2 Рабочий пример — сложенные блоки — бесплатные диаграммы тел и применение 2-го закона Ньютона
MIT 8.01 Classical Mechanics, Fall 2016
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: Д-р Петр Доурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw. mit.edu Лекция 46
Воспроизвести видео PS.2.2 Рабочий пример — сложенные блоки — нахождение максимальной силы
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/8-01F16 ://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 47
Воспроизвести видео PS.2.2 Рабочий пример — сложенные блоки — выбор системы из 2 блоков вместе
MIT 8.01 Classical Mechanics, Fall 2016
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/ термины
Дополнительные курсы на http://ocw.mit.edu Лекция 48
Воспроизвести видео PS. 2.3 Схемы кузова стеклоомывателей
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 49
Воспроизвести видео PS.2.3 Средство для мойки окон
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 50
Воспроизвести видео Пара 3-й закон Ньютона
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw. mit.edu/8-01F16
Преподаватель: д-р Мишель Томасик
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 51
Воспроизведение видео Внутренние и внешние силы
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Мишель Томасик
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 52
Воспроизвести видео Применение второго закона Ньютона
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Мишель Томасик
Дополнительная информация на http: //ocw. mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 53
Воспроизвести видео 8.0 Неделя 3 Введение
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: профессор Дипто Чакрабарти
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu XI. Урок 8: Круговое движение — положение и скорость Лекция 54
Воспроизвести видео 8.1 Полярные координаты
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw. mit.edu Лекция 55
Воспроизвести видео 8.2 Круговое движение: векторы положения и скорости
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 56
Воспроизвести видео 8.3 Угловая скорость
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Мишель Томасик
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu XII. Урок 9: Равномерное круговое движение Лекция 57
Воспроизвести видео 9. 1 Равномерное круговое движение
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 58
Воспроизвести видео 9.2 Равномерное круговое движение: направление ускорения
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu XIII. Урок 10: Круговое движение – Ускорение Лекция 59
Воспроизвести видео 10. 1 Круговое движение — ускорение
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 60
Воспроизвести видео 10.2 Угловое ускорение
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 61
Воспроизвести видео 10.3 Рабочий пример — угловое положение от углового ускорения.
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw. mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/8-01F16 ://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu XIV. Урок 11: Второй закон Ньютона и движение по окружности Лекция 62
Воспроизвести видео 11.1 Второй закон Ньютона и движение по окружности
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/8-01F16 ://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 63
Воспроизвести видео 11.2 Рабочий пример — автомобиль на вираже
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 64
Воспроизвести видео 11.3 Демонстрация: вращающийся ковш
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: Калеб Бонюн
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu XV. Неделя 3 Примеры работы Лекция 65
Воспроизвести видео PS.3.1 Рабочий пример — орбитальное круговое движение — радиус
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw. mit.edu/8-01F16
Преподаватель: проф. Анна Фребель : Creative Commons BY-NC-SA
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 66
Воспроизвести видео PS.3.1 Рабочий пример — орбитальное круговое движение — скорость
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: проф. Анна Фребель
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 67
Воспроизвести видео PS.3.1 Рабочий пример — орбитальное круговое движение — период
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: проф. Анна Фребель : Creative Commons BY-NC-SA
Дополнительная информация на http://ocw. mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 68
Воспроизвести видео 12.0 Неделя 4 Введение
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: проф. SA
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu XVI. Урок 12: Шкивы и ограничения Лекция 69
Воспроизвести видео 12.1 Проблемы со шкивами
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 70
Воспроизвести видео 12. 2 Условия ограничений
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/ термины
Дополнительные курсы на http://ocw.mit.edu Лекция 71
Воспроизвести видео 12.3 Virtual Displacement
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 72
Воспроизвести видео 12.4 Решение системы уравнений
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw. mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 73
Воспроизвести видео 12.5 Рабочий пример: 2 блока и 2 шкива
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: проф. Анна Фребель
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu XVII. Урок 13: массивная веревка Лекция 74
Воспроизвести видео 13.1 Подвешивание на веревке между деревьями
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: проф. Анна Фребель
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 75
Воспроизведение видео 13.2 Дифференциальный анализ массивной веревки
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: проф. Дипто Чакрабарти
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 76
Воспроизвести видео 13.3 Элементы дифференциала
Массачусетский технологический институт 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Мишель Томасик
Дополнительная информация на http://ocw. mit.edu/8-01F16 ://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 77
Воспроизвести видео 13.4 Плотность
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Мишель Томасик
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 78
Воспроизвести видео 13.5 Демонстрация: Wrapping Friction
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: Калеб Бонюн
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 79
Воспроизвести видео 13. 6 Краткий обзор дифференциального анализа
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: профессор Дипто Чакрабарти
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu XVIII. Урок 14: Силы сопротивления Лекция 80
Воспроизвести видео 14.1 Введение в силы сопротивления
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 81
Воспроизвести видео 14.2 Силы сопротивления — случай малых скоростей
MIT 8. 01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 82
Воспроизвести видео 14.3 Силы сопротивления — высокоскоростной случай
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/8-01F16 ://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 83
Воспроизвести видео 15.0 Неделя 5 Введение
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw. mit.edu/8-01F16
Преподаватель: профессор Дипто Чакрабарти
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu XIX. Урок 15: Импульс и импульс Лекция 84
Воспроизвести видео 15.1 Импульс и импульс
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: проф. Дипто Чакрабарти
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 85
Воспроизвести видео 15.2 Impulse is a Vector
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Больше информации на http://ocw. mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 86
Воспроизвести видео 15.3 Рабочий пример — прыгающий мяч
Массачусетский технологический институт 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин NC-SA
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 87
Воспроизвести видео 15.4 Импульс системы точечных частиц
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 88
Воспроизвести видео 15. 5 Влияние на систему частиц
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu ХХ. Урок 16: Сохранение импульса Лекция 89
Воспроизвести видео 16.1 Случаи постоянного импульса
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Мишель Томасик
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 90
Воспроизвести видео 16.2 Импульсные диаграммы
MIT 8. 01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/ термины
Дополнительные курсы на http://ocw.mit.edu XXI. Урок 17: Центр масс и движение центра масс Лекция 91
Воспроизвести видео 17.1 Определение центра масс
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/ термины
Дополнительные курсы на http://ocw.mit.edu Лекция 92
Воспроизвести видео 17.2 Рабочий пример — центр масс трех объектов
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: проф. Анна Фребель
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 93
Воспроизвести видео 17.3 Центр масс непрерывной системы
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 94
Воспроизвести видео 17.5 Рабочий пример — центр масс однородного стержня
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw. mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 95
Воспроизвести видео 17.6 Скорость и ускорение центра масс
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 96
Воспроизвести видео 17.7 Сведение системы к точечной частице
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 97
Воспроизвести видео 18. 0 Неделя 6 Введение
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: проф. Дипто Чакрабарти
Дополнительная информация на http ://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu XXII. Урок 18: Относительная скорость и отдача Лекция 98
Воспроизвести видео 18.1 Относительная скорость
Массачусетский технологический институт 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Мишель Томасик
Дополнительная информация на http://ocw.mit.edu/8-01F16 ://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 99
Воспроизвести видео 18. 2 Постановка задачи об отдаче
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 100
Воспроизвести видео 18.3 Решение для скорости относительно земли
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 101
Воспроизвести видео 18.4 Решение для скорости в движущейся системе отсчета
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu XXIII. Урок 19: Непрерывный массообмен Лекция 102
Воспроизвести видео 19.1 Ракетная задача 1. Постановка задачи
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 103
Воспроизвести видео 19.2 Задача 2 о ракетах. Диаграммы импульса
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw. mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 104
Воспроизвести видео 19.3 Ракетная задача 3. Массовые отношения
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин -NC-SA
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 105
Воспроизвести видео 19.4 Ракета Задача 4 – Решение
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw. mit.edu/8-01F16 ://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 106
Воспроизвести видео 19.5 Ракетная задача 5. Тяга и внешние силы
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 107
Воспроизвести видео 19.6 Задача 6 о ракетах. Решение при отсутствии внешних сил
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw. mit.edu Лекция 108
Воспроизвести видео 19.7 Ракетная задача 7. Решение с учетом внешних сил
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu XXIV. Неделя 6 Примеры работы Лекция 109
Воспроизвести видео PS.6.1 Rocket Sled — дифференциальное уравнение
Массачусетский технологический институт 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: проф. Анна Фребель
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw. mit.edu Лекция 110
Воспроизвести видео PS.6.1 Ракетные салазки. Интеграция уравнения ракеты
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: проф. Анна Фребель Creative Commons BY-NC-SA
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 111
Воспроизвести видео Ракетные салазки PS.6.1 — Решение для начальной скорости
Массачусетский технологический институт 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: профессор Анна Фребель Creative Commons BY-NC-SA
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 112
Воспроизвести видео PS. 6.2 Задача со снегоочистителем
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/8-01F16 ://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 113
Воспроизвести видео 20.0 Неделя 7 Введение
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: профессор Дипто Чакрабарти
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu ХХV. Урок 20: Кинетическая энергия и работа в 1D Лекция 114
Воспроизвести видео 20. 1 Кинетическая энергия
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: проф. Анна Фребель
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 115
Воспроизвести видео 20.2 Работа с постоянной силой
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 116
Воспроизвести видео 20.3 Работа с непостоянной силой
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw. mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 117
Воспроизвести видео 20.4 Интеграция adt и adx
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 118
Воспроизвести видео 20.5 Работа – кинетическая энергия Теорема
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw. mit.edu/8-01F16 ://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 119
Воспроизвести видео 20.6 Power
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu ХХVI. Урок 21: Кинетическая энергия и работа в 2D и 3D Лекция 120
Воспроизвести видео 21.1 Свойства скалярного произведения
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit. edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 121
Воспроизвести видео 21.2 Скалярное произведение в декартовых координатах
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 122
Воспроизвести видео 21.3 Кинетическая энергия как скалярное произведение
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 123
Воспроизвести видео 21. 4 Работа в 2D и 3D
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: доктор Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 124
Воспроизвести видео 21.5 Теорема о работе и кинетической энергии в 2D и 3D
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 125
Воспроизвести видео 21.6 Рабочий пример: Блок, спускающийся по пандусу
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/8-01F16 ://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu ХХVII. Урок 22: Консервативные и неконсервативные силы Лекция 126
Воспроизвести видео 22.1 Независимость от траектории — гравитация
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/8-01F16 ://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 127
Воспроизвести видео 22.2 Зависимость от траектории — трение
MIT 8. 01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 128
Воспроизвести видео 22.3 Conservative Forces
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 129
Воспроизвести видео 22.4 Неконсервативные силы
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw. mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 130
Воспроизведение видео 22.5 Краткий обзор работы и кинетической энергии
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: проф. Дипто Чакрабарти
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu XXVIII. Неделя 7 Примеры работы Лекция 131
Воспроизведение видео PS.7.1 Рабочий пример — столкновение и скольжение по шероховатой поверхности
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: проф. Анна Фребель
Дополнительная информация на http://ocw. mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 132
Воспроизвести видео 23.0 Неделя 8 Введение
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: проф. Дипто Чакрабарти
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu XXIX. Урок 23: Потенциальная энергия Лекция 133
Воспроизвести видео 23.1 Введение в потенциальную энергию
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: проф. Дипто Чакрабарти
Дополнительная информация на http ://ocw.mit.edu/terms
Дополнительные курсы на http://ocw. mit.edu Лекция 134
Воспроизвести видео 23.2 Потенциальная энергия гравитации вблизи поверхности Земли
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/ термины
Дополнительные курсы на http://ocw.mit.edu Лекция 135
Воспроизвести видео 23.3 Эталонное состояние потенциальной энергии
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 136
Воспроизвести видео 23. 4 Потенциальная энергия пружины
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 137
Воспроизвести видео 23.5 Потенциальная энергия гравитации
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu ХХХ. Урок 24: Сохранение энергии Лекция 138
Воспроизвести видео 24.1 Механическая энергия и энергосбережение
MIT 8. 01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: проф. Дипто Чакрабарти
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 139
Воспроизвести видео 24.2 Диаграммы энергетического состояния
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 140
Воспроизвести видео 24.3 Рабочий пример — блок, скользящий вниз по круговому склону
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw. mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 141
Воспроизвести видео 24.4 Второй закон Ньютона и закон сохранения энергии
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/8-01F16 ://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu XXXI. Урок 25: Диаграммы потенциальной энергии Лекция 142
Воспроизвести видео 25.1 Сила есть производная потенциала
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw. mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/8-01F16 ://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 143
Воспроизвести видео 25.2 Точки устойчивого и неустойчивого равновесия
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 144
Воспроизвести видео 25.3 Чтение диаграмм потенциальной энергии
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw. mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 145
Воспроизвести видео 26.0 Неделя 9 Введение
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: профессор Дипто Чакрабарти
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu XXXII. Урок 26: Типы столкновений Лекция 146
Воспроизвести видео 26.1 Импульс при столкновениях
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw. mit.edu Лекция 147
Воспроизвести видео 26.2 Кинетическая энергия при столкновениях
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 148
Воспроизвести видео 26.3 Полностью неупругие столкновения
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu XXXIII. Урок 27: Упругие столкновения Лекция 149
Воспроизвести видео 27. 1 Рабочий пример: упругое одномерное столкновение
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 150
Воспроизвести видео 27.2 Относительная скорость в 1D
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/ термины
Дополнительные курсы на http://ocw.mit.edu Лекция 151
Воспроизвести видео 27.3 Уравнение кинетической энергии и импульса
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 152
Воспроизвести видео 27.4 Рабочий пример: снова упругое одномерное столкновение
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 153
Воспроизвести видео 27.5 Рабочий пример: Gravitational Slingshot
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: профессор Анна Фребель
Дополнительная информация на http://ocw. mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 154
Воспроизвести видео 27.6 2D Collisions
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu XXXIV. Глубокое погружение: система отсчета центра масс Лекция 155
Воспроизвести видео DD.2.1 Положение в системе координат
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw. mit.edu Лекция 156
Воспроизвести видео DD.2.2 Относительная скорость не зависит от системы отсчета
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/8-01F16 ://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 157
Воспроизвести видео DD.2.3 Одномерные упругие скорости столкновения в системе координат
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 158
Воспроизвести видео DD. 2.4 Рабочий пример: одномерное упругое столкновение в системе координат
Массачусетский технологический институт 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16 Лицензия: Creative Commons BY-NC-SA
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 159
Воспроизвести видео DD.2.5 Кинетическая энергия в различных системах отсчета
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 160
Воспроизвести видео DD.2.6 Кинетическая энергия в системе координат CM
MIT 8. 01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 161
Воспроизвести видео DD.2.7 Изменение кинетической энергии
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 162
Воспроизвести видео 28.0 Неделя 10 Введение
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: профессор Дипто Чакрабарти
Дополнительная информация на http://ocw. mit.edu/ термины
Дополнительные курсы на http://ocw.mit.edu XXXV. Урок 28: Движение твердого тела Лекция 163
Воспроизвести видео 28.1 Твердые тела
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 164
Воспроизвести видео 28.2 Введение в перенос и вращение
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw. mit.edu Лекция 165
Воспроизвести видео 28.3 Обзор угловой скорости и ускорения
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu XXXVI. Урок 29: Момент инерции Лекция 166
Воспроизвести видео 29.1 Кинетическая энергия вращения
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 167
Воспроизвести видео 29. 2 Момент инерции стержня
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 168
Воспроизвести видео 29.3 Момент инерции диска
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 169
Воспроизвести видео 29.4 Теорема о параллельных осях
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw. mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/ термины
Дополнительные курсы на http://ocw.mit.edu Лекция 170
Воспроизвести видео 29.5 Глубокое погружение — момент инерции сферы
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 171
Воспроизвести видео 29.6 Глубокое погружение. Вывод теоремы о параллельных осях
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw. mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu ХХXVII. Урок 30: Крутящий момент Лекция 172
Воспроизвести видео 30.1 Введение в динамику крутящего момента и вращения
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: проф. Дипто Чакрабарти
Больше информации на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 173
Воспроизвести видео 30.2 Cross Product
MIT 8.01 Classical Mechanics, Fall 2016
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw. mit.edu Лекция 174
Воспроизведение видео 30.3 Перекрестное произведение в декартовых координатах
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 175
Воспроизвести видео 30,4 Крутящий момент
Массачусетский технологический институт 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Мишель Томасик
Дополнительная информация на http://ocw.mit.edu/8-01F16 ://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 176
Воспроизвести видео 30. 5 Крутящий момент от силы тяжести
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu XXXVIII. Урок 31: Вращательная динамика Лекция 177
Воспроизвести видео 31.1 Связь между крутящим моментом и угловым ускорением
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 178
Воспроизвести видео 31. 2 Внутренние крутящие моменты Отменяются в парах
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 179
Воспроизвести видео 31.3 Рабочий пример — определение момента инерции диска при падении массы
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: проф. Анна Фребель
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 180
Воспроизвести видео 31.4 Рабочий пример — машина Этвуда
MIT 8. 01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин NC-SA
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 181
Воспроизвести видео 31.5 Проблемы с массивными шкивами
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Мишель Томасик
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 182
Воспроизвести видео 31.7 Рабочий пример — два блока и шкив, использующий энергию
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw. mit.edu/8-01F16 ://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu XXXIX. Неделя 10 Примеры работы Лекция 183
Воспроизвести видео PS.10.1 Рабочий пример — блоки с трением и массивным шкивом
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/8-01F16 ://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 184
Воспроизвести видео 32.0 Неделя 11 Введение
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: профессор Дипто Чакрабарти
Дополнительная информация на http://ocw. mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu XL. Урок 32: Угловой момент точечной частицы Лекция 185
Воспроизвести видео 32.1 Угловой момент точечной частицы
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 186
Воспроизвести видео 32.2 Расчет углового момента
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Мишель Томасик СА
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit. edu Лекция 187
Воспроизвести видео 32.3 Рабочий пример — угловой момент относительно разных точек
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 188
Воспроизвести видео 32.4 Угловой момент кругового движения
Массачусетский технологический институт 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16 NC-SA
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu XLI. Урок 33: Момент количества движения твердого тела относительно неподвижной оси Лекция 189
Воспроизвести видео 33. 1 Рабочий пример — угловой момент двух вращающихся частиц
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: проф. Анна Фребель
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 190
Воспроизвести видео 33.2 Угловой момент симметричного объекта
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 191
Воспроизвести видео 33.4 Если импульс равен нулю, то угловой момент не зависит от начала координат
MIT 8. 01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 192
Воспроизвести видео 33.5 Кинетическая энергия симметричного объекта
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/8-01F16 ://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu XLII. Урок 34: Крутящий момент и угловой импульс Лекция 193
Воспроизвести видео 34.1 Крутящий момент вызывает изменение углового момента — точечная частица
MIT 8. 01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/8-01F16 ://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 194
Воспроизвести видео 34.2 Крутящий момент вызывает изменение углового момента — система частиц
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/ термины
Дополнительные курсы на http://ocw.mit.edu Лекция 195
Воспроизвести видео 34.3 Угловой импульс
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw. mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 196
Воспроизвести видео 34.4 Демонстрация: демонстрация велосипедного колеса
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: Калеб Бонюн
Больше информации на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 197
Воспроизвести видео 34.5 Рабочий пример — Particle Hits Pivoted Ring
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw. mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 198
Воспроизвести видео 35.0 Неделя 12 Введение
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: профессор Дипто Чакрабарти
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu XLIII. Урок 35: Кинематика качения Лекция 199
Воспроизвести видео 35.1 Перемещение и вращение колеса
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw. mit.edu Лекция 200
Воспроизвести видео 35.2 Катящееся колесо в центре масс рамы
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 201
Воспроизвести видео 35.3 Катящееся колесо в грунтовой раме
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/ термины
Дополнительные курсы на http://ocw.mit.edu Лекция 202
Воспроизвести видео 35. 4 Катание без проскальзывания Скольжение и занос
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 203
Воспроизвести видео 35.5 Точка контакта колеса, катящегося без проскальзывания
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu XLIV. Урок 36: Динамика качения Лекция 204
Воспроизвести видео 36. 1 Трение на катящемся колесе
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 205
Воспроизвести видео 36.2 Рабочий пример — вращение колеса без проскальзывания по наклонной плоскости — метод крутящего момента
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: доктор Питер Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 206
Воспроизвести видео 36.3 Demo: Spool Demo
MIT 8. 01 Classical Mechanics, Fall 2016
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: Калеб Бонюн
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 207
Воспроизведение видео 36.4 Рабочий пример — Йойо тянет по земле
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 208
Воспроизвести видео 36.5 Анализ силы и крутящего момента в задачах перемещения и вращения
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw. mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/8-01F16 ://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu XLV. Урок 37: Кинетическая энергия качения и угловой момент Лекция 209
Воспроизвести видео 37.1 Кинетическая энергия поступательного движения и вращения
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/8-01F16 ://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 210
Воспроизвести видео 37.2 Рабочий пример — качение колеса без проскальзывания по наклонной плоскости
MIT 8. 01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/ термины
Дополнительные курсы на http://ocw.mit.edu Лекция 211
Воспроизвести видео 37.3 Угловой момент поступательного движения и вращения
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: д-р Петр Дурмашкин
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu XLVI. Глубокое погружение: гироскопы Лекция 212
Воспроизвести видео DD.3.1 Глубокое погружение — гироскопы — Бесплатные диаграммы тела, крутящий момент и векторы вращения
MIT 8. 01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: профессор Дипто Чакрабарти
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 213
Воспроизвести видео DD.3.2 Deep Dive — Гироскопы — прецессионные угловые скорости и названные гироскопы
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: проф. Deepto Чакрабарти
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Лекция 214
Воспроизвести видео DD.3.3 Глубокое погружение — Гироскопы — Нутация и полный угловой момент
MIT 8.01 Классическая механика, осень 2016 г.
Посмотреть полный курс: http://ocw.mit.edu/8-01F16
Преподаватель: проф. Дипто Чакрабарти
Дополнительная информация на http://ocw.mit.edu/terms
Дополнительные курсы на http://ocw.mit.edu Физика I: Решения для выпускного экзамена по классической механике | Осень 2008 Массачусетский технологический институт | Экзамены Классическая механика
Решите все СЕМЬ (7) задач. У вас есть 2,5 часа. 2. Показать все работы. ОБЯЗАТЕЛЬНО ОБВЕДИТЕ ВАШ ПОСЛЕДНИЙ ОТВЕТ. 3. Внимательно прочитайте вопросы. 4. Все задания и решения должны быть выполнены в предоставленных буклетах для ответов. Лист полезных уравнений приведен на последней странице. Ваши баллы Задача Максимальный балл Оценщик 1 10 2 15 3 15 4 15 5 15 6 15 7 15 Итого 100 8.012 Осень 2008 г. Заключительный экзамен Без внешней силы импульс фигуриста не меняется; точно так же, поскольку внешних крутящих моментов нет, угловой момент сохраняется. Однако вращательная энергия масштабируется как L2/2I, а момент инерции (I) у фигуриста уменьшается, когда он тянет руки, поэтому его общая механическая энергия должна увеличиваться. (d) [2 балла] Какова размерность гравитационной постоянной G? [M]-1[L]3[T]-2 (e) [2 балла] Наблюдается прецессия гироскопа, вектор угловой скорости вращения которого направлен влево, так что его вектор угловой скорости прецессии направлен под углом, как показано. В каком направлении направлен вектор гравитации? Направление прецессии указывает в противоположном направлении, поскольку вектор вращения первоначально движется в направлении, когда гироскоп падает под действием силы тяжести. Поэтому в этом случае вектор силы тяжести должен быть параллелен вектору прецессии. (f) [БОНУС 2 балла] Дайвер находится в середине погружения, как показано ниже. Основываясь на подсказках на фотографии, укажите в своем буклете для ответов направление, на которое указывает вектор его полного вращения, и определите, выполняет ли ныряльщик сальто вперед или назад. Одна подсказка — это волосы, лежащие в плоскости, перпендикулярной вектору вращения (покрутите веревку, чтобы убедиться в этом). Размещение рук нарушает вырождение, указывая на приложенный крутящий момент, который вызывает поворотное вращение, направление которого указывает на ступни. Таким образом, общий вектор вращения указывает в указанном направлении, а компонент переворота указывает на сальто вперед (голова через ноги). Страница 4 из 25 8.012 Осенний выпускной экзамен 2008 г. Задача 2: Машина Этвуда [15 баллов] α 2M M MR µ d Машина Этвуда состоит из неподвижного шкива радиуса R и однородной массы M (диска), вокруг которого находится эффективно безмассовая проходит нить, соединяющая два блока массой М и 2М. Более легкий блок изначально расположен на расстоянии d от земли. Более тяжелый блок расположен на наклонной плоскости с углом раскрытия α. Между поверхностями этого бруска и наклонной плоскостью имеется коэффициент трения µ. Постоянная сила тяжести действует вниз, и предположим, что струна никогда не проскальзывает. (a) [5 баллов] Определите два условия на угол α, которые позволяют более легкому блоку двигаться вверх или вниз. (b) [10 баллов] Предполагая, что более легкий блок движется вниз, определите его ускорение. Страница 5 из 25 8.012, выпускной экзамен, осень 2008 г. РЕШЕНИЕ ЗАДАЧИ 2 (a) На приведенной выше диаграмме показаны соответствующие силы, воздействующие на два блока и шкив. Два условия для блоков возникают из-за того, движется ли крайний левый блок вверх или вниз, что меняет направление силы трения, действующей на крайний правый блок. Рассмотрим сначала самый левый блок, движущийся вниз; в этом случае Mg > T1 и T1 > T2 (чтобы колесо могло вращаться), а T2 должно быть больше как силы трения (µN = µ2Mgcosα), так и составляющей силы тяжести, параллельной наклонной плоской поверхности (2Mgsinα) на крайний правый блок: Mg R T2 Mg Fs 2Mg T2 N µN T1 T1 Если крайний левый блок движется вверх, то T1 > Mg, T2 > T1 и сила тяжести на крайнем правом блоке должна преодолевать как растяжение, так и трение: Страница 6 из 25 8.012 Падение Выпускной экзамен 2008 г. РЕШЕНИЕ ЗАДАЧИ 3: (a) Рассмотрим некоторый момент времени t, когда из ракеты со скоростью u выбрасывается предмет массой dm. Второй закон Ньютона можно записать как (предполагая, что направление вправо положительно): Импульс системы ракета + топливо до и после выброса топлива можно записать как: место дм/дт. (b) Чтобы поддерживать постоянную скорость, dv/dt = 0, следовательно, тяга равна (c) Когда у ракеты заканчивается топливо, она имеет массу MR и члена тяги нет, следовательно, уравнение в части (a) принимает вид: Это уравнение сепарабельно и может быть непосредственно проинтегрировано: Page 9of 25 8. 012 Fall 2008 Final Exam (d) Как показано на рисунке справа, каждая частица, сталкивающаяся с ракетой, отклоняется на 90º (из-за геометрии), что означает, что каждая частица сообщает ракете импульс Δp = mv в горизонтальном направлении, противоположном движению (он также сообщает импульс mv в вертикальном направлении, но он уравновешивается частицами, ударяющимися о другую сторону носового конуса). Количество частиц, попадающих в ракету в единицу времени, равно простому объему, проносимому ракетой в единицу времени, A∆x/∆t = πR2v. Полный импульс, переданный ракете, составляет: Страница 10 из 25 mv 8.012 Осень 2008 г. Задача 4: Липкие диски [15 баллов] ω0 M 2M 2R 2R M 2M Однородный диск массой M и диаметром 2R движется к другому однородному диску массой 2M и диаметром 2R на поверхности стола без трения. Первый диск имеет начальную скорость v0 и скорость вращения ω0, как указано, в то время как второй диск изначально неподвижен. Когда первый диск соприкасается со вторым («скользящее» столкновение), они моментально прилипают друг к другу и движутся как единый объект. (a) [5 баллов] Каковы скорость и угловая скорость вращения объединенных дисков после столкновения? Укажите как величины, так и направления. (б) [5 баллов] При каком значении ω0 объединенные диски не будут вращаться? (c) [5 баллов] Сколько общей механической энергии теряется при этом столкновении, если предположить, что комбинированная система дисков не вращается? Страница 11 из 25 8.012 Осенний выпускной экзамен 2008 Задача 5: Цилиндрический волчок [15 баллов] M COM r µ = 0 Δp L R Цилиндр массой M, длиной L и радиусом R вращается вокруг своей длинной оси с угловой скоростью на горизонтальной поверхности без трения. . Цилиндр получает резкий горизонтальный удар с импульсом Δp на расстоянии r от его центра масс (ЦМ). Предположим, что постоянное ускорение свободного падения действует вниз. ПРИМЕЧАНИЕ: вам не нужно использовать уравнения Эйлера для решения этой задачи. (a) [5 баллов] Какова поступательная скорость цилиндра после импульса (величина и направление)? (b) [5 баллов] Удар сообщает импульс углового момента цилиндру, который заставляет его подниматься с одного конца. На какой угол α наклонится цилиндр после импульса и какой конец цилиндра приподнимется? Предположим, что импульс углового момента много меньше спинового углового момента. (c) [5 баллов] После того, как цилиндр наклоняется вверх, он фактически становится волчком. Определить скорость его прецессии и направление прецессии. Предположим, что нутационное движение пренебрежимо мало (т. е. α остается фактически постоянным) и что R << L (т. е. что для этой части цилиндр можно аппроксимировать тонким стержнем). (d) [5 баллов БОНУС] При достаточно сильном импульсе цилиндр будет наклоняться достаточно высоко, чтобы прецессировать в противоположном направлении. При каком минимальном угле наклона это должно произойти и какой минимальный импульс необходим? (Обратите внимание, что вы не можете предположить здесь R << L. Эта задача похожа на трюк с «опрокидыванием батареи», на который указал один из учащихся 8.012.) Стр. 14 из 25 8.012 Fall 2008 Final Exam РЕШЕНИЕ ЗАДАЧИ 5: Импульс обеспечивает единственную внешнюю силу для системы, поэтому общий импульс цилиндра - это просто импульс, Δp в направлении y. Следовательно, поступательная скорость цилиндра равна: (b) Угловой импульс, сообщаемый массой r, равен y цилиндру относительно его центра. Этот импульс добавляет вектор ко всем вращательным моментам цилиндра, как показано на рисунке справа. Если предположить, что LS >> ΔL (наше стандартное гироскопическое приближение), то величина полного углового момента по-прежнему равна IωS, но указывает в направлении, смещенном на угол α вверх. Так как это все еще цилиндр, вращающийся вокруг своей оси, правая сторона цилиндра должна быть наклонена вверх на угол α: (c) Когда цилиндр наклонен вверх, сила тяжести и сила тяжести вызывают углубление, обеспечивающее гарантированное N = Mg Mg L/2cosα – Rsinα α нормальная контактная сила на земле нет суммарного крутящего момента на цилиндре, который приведет вектор углового момента вращения к p со скоростью Ω. Давайте измерим угловой mo и крутящий момент относительно центра масс цилиндра (в качестве альтернативы мы могли бы иметь меня относительно точки вращения, но поскольку N = Mg, результат тот же). Горизонтальное плечо рычага между точкой вращения и центром масс равно (L/2)cosα – Rsinα, но, предположив, что L >> R, мы можем опустить второй член. В этом случае крутящий момент равен: Page 15 of 25 8.012 Fall 2008 Final Exam здесь используется наше выражение для производной вектора по времени (LS) во вращающейся системе отсчета. Вектор прецессии должен указывать вдоль направления z, факт, который мы можем установить, учитывая, что гравитация первоначально тянула бы вектор углового момента вращения вниз, поэтому для сохранения полного углового момента вектор углового момента прецессии должен указывать вверх. Вектор прецессии вращает только радиальную составляющую вектора углового момента вращения, следовательно: Решение для скорости прецессии: обратите внимание, что I здесь представляет собой момент инерции относительно оси вращения, а не относительно L/2 R α α 90º-α ось прецессии. из решения (а) это накладывает ограничение на требуемый импульс: обратите внимание, что это приблизительно, поскольку мы больше не удовлетворяем гироскопическому приближению, что LS >> ΔL (действительно, они имеют один и тот же порядок величины в этом случае) . (d) Для прецессии в другом направлении центр масс должен находиться внутри точки вращения диска, что происходит под критическим углом (см. справа): Стр. 16 из 25 8.012 Fall 2008 Final Exam Угловое уравнение движения в вращающаяся система координат: где N снова представляет собой угловую нормальную силу, действующую на шарик, а чистая составляющая углового ускорения равна 0, поскольку θ постоянна во вращающейся системе координат. Отсюда Страница 19of 25 8.012 Fall 2008 Final Exam Задача 7: Центральный потенциал [15 баллов] Частица массы m движется внутри области под действием силы вида Частица изначально находится на расстоянии r0 от источника силы, и первоначально движется со скоростью v0 в тангенциальном направлении. (a) [5 баллов] Найдите и зарисуйте эффективный потенциал этой системы как функцию радиуса от начала координат. Укажите все важные точки перегиба. Может ли частица пройти через начало этой системы отсчета? (б) [5 баллов] Найдите скорость v0, необходимую для того, чтобы частица двигалась по чисто круговой орбите радиусом r0 с этим законом силы. (c) [5 баллов] Вычислите частоту малых колебаний вокруг этого равновесного радиуса. Как период этих колебаний соотносится с периодом обращения? Страница 20 из 25 8.012 Fall 2008 Final Exam РЕШЕНИЕ ЗАДАЧИ 7: (a) Эффективный потенциал возникает из радиального уравнения движения в предположении, что полный угловой момент является постоянным: где угловой момент определяется как Потенциал, возникающий из этого полного закон силы На рисунке выше показан грубый набросок этой функции (при A = 4 и l2 = 2m). Существует одна точка минимального перегиба (равновесия), в которой результирующая сила обращается в нуль: Скорость в полярных координатах Ускорение в полярных координатах Центр масс (ЦМ) твердого тела Элемент объема в цилиндрических координатах Кинетическая энергия Работа Потенциальная энергия (для консервативных силы) где Угловой момент Крутящий момент Вращение с неподвижной осью: 8.012 Осень 2008 г. Выпускной экзамен ПОЛЕЗНЫЕ УРАВНЕНИЯ Стр. 24 из 25 COM Момент инерции однородного стержня COM Момент инерции однородного кольца COM Момент инерции однородного диска COM Момент инерции однородного диска COM однородная сфера Скалярная теорема о параллельной оси Моменты тензора инерции (перестановка x→y→z) Уравнения Эйлера (перестановка 1→2→3) Производная по времени между Фиктивной силой в ускоряющей системе отсчета Фиктивной силой во вращающейся системе отсчета (Ω постоянная) Расширение Тейлора of f(x) 8. 012 Fall 2008 Final Exam Инерциальные и вращающиеся системы отсчета Страница 25 из 25 Открытый курс по квантовой механике Массачусетского технологического института — Шон Кэрролл
Вот первая лекция «Введение в суперпозицию».
Посмотреть это видео на YouTube Твиттер Шона
Обновления блога через Twitter
Последние сообщения
Архивы
Архивы
Выберите Месяц Март 2022 (1) Ноябрь 2021 (2) Январь 2021 (1) Ноябрь 2020 (1) Сентябрь 2020 (2) Август 2020 (5) Июль 2020 (4) Июнь 2020 (5) Май 2020 (4) Апрель 2020 ( 4) март 2020 г. (3) ноябрь 2019 г.(1) сентябрь 2019 г. (1) июль 2019 г. (1) январь 2019 г. (1) ноябрь 2018 г. (1) сентябрь 2018 г. (1) июль 2018 г. (1) июнь 2018 г. (1) май 2018 г. (2) март 2018 г. (1) февраль 2018 г. (2) январь 2018 г. (2) ноябрь 2017 г. (1) октябрь 2017 г. (2) сентябрь 2017 г. (1) июнь 2017 г. (1) май 2017 г. (4) апрель 2017 г. (1) январь 2017 г. (1) декабрь 2016 г. (2) ноябрь 2016 г. (6) сентябрь 2016 г. (2) август 2016 г. (2) июль 2016 г. (1) июнь 2016 г. (1) май 2016 г. (10) апрель 2016 г. (2) март 2016 г. (2) февраль 2016 г. (3) январь 2016 г. (3) декабрь 2015 г. (3) ноябрь 2015 г. (2) октябрь 2015 г. (1) сентябрь 2015 г. (2) август 2015 г. (2) июль 2015 г. (6) июнь 2015 г. (2) май 2015 г. (2) апрель 2015 г. (5) март 2015 г. (6) февраль 2015 г. (5) январь 2015 г. (4) декабрь 2014 г. (4) ноябрь 2014 г. (5) октябрь 2014 г. (5) сентябрь 2014 г. (5) август 2014 г. (4) июль 2014 г. (4) июнь 2014 г. (5) май 2014 г. (6) апрель 2014 г. (8) март 2014 г. (10) февраль 2014 г. (10) январь 2014 г. (6) декабрь 2013 г. (6) ноябрь 2013 г. (7) октябрь 2013 г. (6) сентябрь 2013 г. (5) 2 августа 013 (10) июль 2013 г. (8) июнь 2013 г. (6) май 2013 г. (14) апрель 2013 г. (8) март 2013 г. (7) февраль 2013 г. (13) январь 2013 г. (10) декабрь 2012 г. (15) ноябрь 2012 г. (14) октябрь 2012 г. (11) сентябрь 2012 г. (11) август 2012 г. (14) июль 2012 г. (10) июнь 2012 г. (17) май 2012 г. (8) апрель 2012 г. (15) март 2012 г. (10) февраль 2012 г. (11) январь 2012 г. (8) декабрь 2011 (12) ноябрь 2011 (12) октябрь 2011 (13) сентябрь 2011 (13) август 2011 (14) июль 2011 (12) июнь 2011 (12) май 2011 (18) апрель 2011 (18) март 2011 (15) февраль 2011 (17) Январь 2011 (20) Декабрь 2010 (14) Ноябрь 2010 (16) Октябрь 2010 (19)) Сентябрь 2010 г. (9) Август 2010 г. (4) Июль 2010 г. (3) Июнь 2010 г. (12) Май 2010 г. (11) Апрель 2010 г. (17) Март 2010 г. (16) Февраль 2010 г. (16) Январь 2010 г. (19) Декабрь 2009 г. (15) ) ноябрь 2009 (10) октябрь 2009 (14) сентябрь 2009 (17) август 2009 (16) июль 2009 (16) июнь 2009 (14) май 2009 (13) апрель 2009 (15) март 2009 (13) февраль 2009 (18) ) январь 2009 г. (16) декабрь 2008 г. (18) ноябрь 2008 г. (20) октябрь 2008 г. (19) сентябрь 2008 г. (22) август 2008 г. (18) июль 2008 г. (21) июнь 2008 г. (20) май 2008 г. (6) апрель 2008 г. (17) ) март 2008 (18) февраль 2008 (19) Январь 2008 г. (20) Декабрь 2007 г. (13) Ноябрь 2007 г. (18) Октябрь 2007 г. (10) Сентябрь 2007 г. (15) Август 2007 г. (15) Июль 2007 г. (20) Июнь 2007 г. (16) Май 2007 г. (17) Апрель 2007 г. (16) ) март 2007 г. (17) февраль 2007 г. (16) январь 2007 г. (21) декабрь 2006 г. (17) ноябрь 2006 г. (17) октябрь 2006 г. (13) сентябрь 2006 г. (11) август 2006 г. (11) июль 2006 г. (16) июнь 2006 г. (21) ) май 2006 г. (16) апрель 2006 г. (17) март 2006 г. (19) февраль 2006 г. (18) январь 2006 г. (23) декабрь 2005 г. (30) ноябрь 2005 г. (17) октябрь 2005 г. (24) сентябрь 2005 г. (21) август 2005 г. (32) ) июль 2005 г. (30) июнь 2005 г. (24) май 2005 г. (30) апрель 2005 г. (36) март 2005 г. (45) февраль 2005 г. (30) январь 2005 г. (36) декабрь 2004 г. (31) ноябрь 2004 г. (27) октябрь 2004 г.