исторические факты, правила счета. Как считать на счетах?
Русские счеты более пяти веков добросовестно служили людям, помогая быстрее совершать простые арифметические действия. Удобно и быстро складывать доходы и вычитать из них расходы. Приемы, упрощающие умножение, давались не всем и часто заменялись привычным сложением, а деление было уделом «избранных» и значительно быстрее выполнялось на бумаге.
Счеты в принципе работают только с положительными числами, и если есть необходимость учитывать превышение расходов над доходами (убытки), то расчеты ведутся по модулю числа. Соответствующий знак запоминается или записывается на бумаге, а в необходимый момент вставляется в число. При действиях по умножению и делению нить (проволока, стержень, прут) с 4 косточками – разделитель разрядов (далее по тексту РР) не учитывается, даже если приходится работать с дробями (они преобразуются в целые числа, а после окончания вычислений производится обратная процедура).
Русские счеты – история
Итак, что это такое? Русские счеты — это простейшее механичное устройство для осуществления вычислений. Это сложение, вычитание, деление и умножение. Имеют место две теории появления счет на Руси:
Это сложение, вычитание, деление и умножение. Имеют место две теории появления счет на Руси:
- Заимствование их у китайцев через посредников в лице татаро-монголов в XIV веке нашей эры. Как раз за столетие перед появлением у нас «предков» деревянных счет в Китае они приобрели окончательный вид счетного устройства. Правда они имели 8, а не десять разрядов и 7 косточек, разделенных перегородкой в соотношении 5 и 2. Но русскому человеку только дай что-нибудь усовершенствовать – результат усовершенствования будет отличаться от источника как небо и земля.
- Согласно другой теории, простые счеты – истинно русское изобретение. Они как раз и основываются на десятеричной системе счисления (в Китае в то время была принята пятеричная), которая возникла в Московском государстве, в том числе с XVI века распространилась и на денежную сферу. Имеются документально оформленные ссылки на «дощаный счет» (XVI век).
Как оно было на самом деле, история умалчивает. Но «дощаный» счет до середины XVII века (пока не победил) конкурировал с европейской системой счета на линованных досках типа абак, где он происходил при помощи камешков или специальных жетонов.
Как считать?
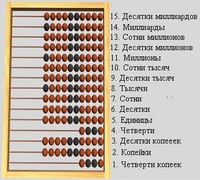
Образец – это старые деревянные счеты. Они имеют 12 поперечных проволочек-прутов (РР отделяет 8 верхних от 3 нижних) с десятью костяшками белого цвета, кроме двух черных посередине на 11 из них (на РР – 4 костяшки). Таким образом, русские счеты могут зафиксировать любое число до 10 миллионов. А если исключить РР, то до 10 миллиардов.
Итак, как считать на счетах? Откладывание чисел производится перемещением костяшек из правого в левое положение, а при наборе слева 10 косточек – они убираются в исходное положение. В следующем разряде в левое положение переводится всего лишь одна косточка. РР отделяет целые числа (сверху) от их соответственно десятых, сотых и тысячных долей и в расчетах участие не принимает (ранее использовался для учета «полушек», которая равнялась ½ «деньги» или ¼ копейки).
Счеты бухгалтерские
Они получили массовое распространение в XIX-XX веках, пока их не вытеснили ЭКВМ (электронно-клавишные вычислительные машины). Кстати, этого не смогли сделать арифмометры, которые считали намного быстрее, но работа на них требовала специальной и довольно сложной подготовки по овладению навыками работы на них, в отличии от счет, обучить работе на которых было в разы легче и быстрее.
Вообще-то искусство работы на бухгалтерских счетах и состоит в том, чтобы знать все способы достижения точного результата действий путем разложения общего на частные более легкие операции. Например, умножение на 25 заменяется умножением на 100 и двукратным последовательным делением результата на 2. Или, как умножение, так и деление на любую степень числа 2 производится последовательным соответствующим действием, число которых равно этой степени.
Как считать на счетах? Другой пример. Умножение на двузначное число из одинаковых цифр «АА» (11, 22 и так далее) заменяется умножением на «А» с переносом результата на разряд вверх (умножение на 10) и сложения этой суммы с предыдущей. От опыта и подготовки человека, работающего на счетах, метода его обучения и зависит скорость вычислений, а также применение им специальных приемов.
Сложение
Сложение на счетах – самая легкая операция. Набирается первое число, потом к нему добавляются костяшки, обозначающее третье и так далее. Надо соблюдать только одно условие. При нехватке косточек для перемещения их в левый ряд – именно столько косточек необходимо оставить в этом ряду, после чего и переместить одну костяшку влево на верхнем пруте. Выполнение происходит сверху вниз (профессионалы могут и наоборот) и складываются только равные разряды (единицы с единицами, десятки с десятками и так далее).
Надо соблюдать только одно условие. При нехватке косточек для перемещения их в левый ряд – именно столько косточек необходимо оставить в этом ряду, после чего и переместить одну костяшку влево на верхнем пруте. Выполнение происходит сверху вниз (профессионалы могут и наоборот) и складываются только равные разряды (единицы с единицами, десятки с десятками и так далее).
Вычитание
Как выполняется вычитание на счетах? Помня, что счеты не работают с отрицательными числами, всегда надо иметь в виду, что вычитание производится из числа более крупного. А если надо сделать наоборот, то все-таки меньшее вычитается из большего, а знак запоминается или записывается. Вычитание на русских счетах производится сверху-вниз, то есть от высших разрядов к низшим. На соответствующей проволоке отбрасывается вправо необходимое число косточек и если их не хватает, то одна косточка переносится вправо в старшем разряде, а на данной проволочке все переносится влево и из них убирается вправо необходимое число.
Умножение
Теперь про умножение на счетах. Древние счеты способствуют повышению скорости проведения действий по умножению, которая значительно превосходит скорость осуществления тех же действий на бумаге. На практике умножение – это многократное сложение искомого с самим собой в числовом выражении. Несколько советов:
- За основу лучше принять большее число, тогда операций будет произведено меньше. Умножение начинается с низшего разряда и идет вверх.
- Складывается число само с собой столько раз, сколько «значит» число в этом разряде (о способах сокращения числа этих операций расскажем в конце настоящего раздела). При переходе к следующему разряду, результат переносится на один прут выше (умножается на 10). И опять та же процедура. Если в разряде «0», то перенос на старший прут происходит, а сложение – нет, и необходимо переходить к дальнейшей процедуре умножения.
- Дробные числа перемножаются как целые, а соответствующий разделитель ставится в итоге всех действий вручную на бумаге.

Способы, упрощающие процесс умножения:
- На 4 – двукратное удвоение.
- На 5 – перенесение на один разряд выше и деление результата на 2.
- На 6 – умножение на 5 плюс начальное число.
- На 7 – троекратное удвоение и минус начальное число.
- На 9 – перенесение на один разряд выше и минус начальное число.
Деление
Как умножение заменяется многократным сложением, так и деление на счетах – это постоянное вычитание. Начинается все с верхнего разряда и идет вниз. Переносится направо число косточек, равных делителю (каждый раз, как это удается на самой верхней проволочке, переносится одна косточка налево) до тех пор, пока слева не окажется косточек меньше чем число, на которое производится деление (делитель).
Затем к процессу подключается нижеследующий разряд. И если в предыдущей проволочке остались косточки, то вычитается делитель уже из двузначного числа. Если нет, то, как в предыдущий раз. Если в низшем разряде вычитание пройдет без остатка косточек слева, то значит деление произведено без остатка. Если слева косточки остались, то в случае необязательного получения в итоге дробного числа – остаток игнорируется, а если обязательно его получение, то вычитание продолжается до нужной точности на прутьях ниже РР, с указанием дробного разделителя на бумаге. Аналогично производится деление на двухзначные, трехзначные (и т. д.) числа, только сначала вычитание идет из соответственно двух, трех и так далее высших разрядов.
Если слева косточки остались, то в случае необязательного получения в итоге дробного числа – остаток игнорируется, а если обязательно его получение, то вычитание продолжается до нужной точности на прутьях ниже РР, с указанием дробного разделителя на бумаге. Аналогично производится деление на двухзначные, трехзначные (и т. д.) числа, только сначала вычитание идет из соответственно двух, трех и так далее высших разрядов.
Как упростить деление
Способы, упрощающие процесс деления:
- На 2 – процесс протекает в обратном порядке – снизу-вверх. На каждом пруте отбрасывается половина косточек, а «лишняя», при их нечетном числе, тоже отбрасывается. В нижнем разряде за это влево переносится 5 косточек.
- На 4 – дважды произведенное деление на 2.
- На 5 – перенос всего числа на один прут вниз (деление на 10) и умножение его на 2.
- На 8 – трижды произведенное деление на 2.
- На 9 – перенесение на один разряд выше и минус начальное число.
Усовершенствование
На протяжении четверти тысячелетия популярности и практической необходимости счет неоднократно предпринимались (часто закончившиеся удачно), попытки усовершенствовать русские счеты. Остановимся только на одной из них. В 1828 г. генерал-майор Ф. М. Свободский представил в соответствующую инстанцию счетный прибор, который не только осуществлял привычные для русских счет действия, но достаточно быстро извлекал кубические корни, возводил числа в степень, вычислял сложные проценты и так далее. Достигалось это только методами сложения и вычитания с фиксацией промежуточных результатов на специальном поле счет. Однако скорость получения искомого результата так поразила комиссию, что она рекомендовала данный прибор к производству и введению специального курса в военных заведениях. Но до реального исполнения решения дело не дошло.
Остановимся только на одной из них. В 1828 г. генерал-майор Ф. М. Свободский представил в соответствующую инстанцию счетный прибор, который не только осуществлял привычные для русских счет действия, но достаточно быстро извлекал кубические корни, возводил числа в степень, вычислял сложные проценты и так далее. Достигалось это только методами сложения и вычитания с фиксацией промежуточных результатов на специальном поле счет. Однако скорость получения искомого результата так поразила комиссию, что она рекомендовала данный прибор к производству и введению специального курса в военных заведениях. Но до реального исполнения решения дело не дошло.
В настоящее время в России счеты применяются только в качестве музейного экспоната или семейной реликвии. Очень редко, если они наличествуют у кого-то в доме, могут использоваться подрастающим поколением для катания по полу, или старшими для массажа ног или спины. А зря! В современном Китае на «Суаньпань» учат учеников младших классов, так как считается, что освоивший такой способ счета ребенок развивается лучше и быстрее, не научившегося работать на этом древнем приспособлении.
Как считать на счетах | Рождённые в СССР
Здравствуйте, дорогие читатели! Я заметил, что современные дети почти разучились совершать в уме простейшие арифметические действия. До того дошло, что вполне обычной стала картина: стоит стайка сорванцов в магазине с пакетами чипсов и мороженым в общей на всех корзинке – и нетерпеливо наблюдает за несложными манипуляциями самого смышленого их собрата. А тот с помощью смартфона высчитывает, хватит ли им ещё и на бутылку «Кока-колы». Да-а, представляю удивление ребят, если бы их любимая Марь Иванна заявила на очередном уроке математики: «А сегодня мы узнаем, как считать на счетах!»
Но ведь, скорее всего, многие из сегодняшних школьников и не слыхивали, что это за диво такое – деревянные счеты. А я помню, как весело было стучать приятными на ощупь костяшками и представлять себя самым важным по детскому разумению человеком в магазине – кассиром, счастливым обладателем больших, «настоящих» счетов! Можно было целый час простоять рядом с кассой, завороженно наблюдая, как кошка за мышкиной беготней, за веселыми деревяшками под ловкими пальцами молодой кассирши, резво облетающими счеты.
Если вам удастся раздобыть счеты, или с детства оставили на память – давайте вместе попробуем вспомнить эти навыки. Хотя бы сложение и вычитание припомним, ведь умножение и деление – более сложные операции на этом инструменте. Хотя я слышал, что сейчас есть люди, желающие и находящие такую возможность, чтобы их детей обучали так называемой ментальной математике. Для этих целей они приобретают малышам счеты абакус. Как считать на них, и что это за счеты? Я думаю, информации на эту тему в сети хватает.
Мы же с вами попытаемся вспомнить уроки счета. Итак, как считать на счетах – инструкция ). Сначала «обнуляем» наши счеты, сбрасывая все кругляшки на правый край. Числа представлены костяшками над тем рядом, где их четыре. Располагаются по разрядам – от единиц над вышеупомянутым рядом разряды увеличиваются к десяткам, сотням и далее. Ниже единиц размещаются четверти, десятые и сотые. Почему центральные костяшки обычно окрашены в черный цвет? Для более удобной ориентации при счете.
Почему центральные костяшки обычно окрашены в черный цвет? Для более удобной ориентации при счете.
Для сложения набираем число, скажем, 937. Для этого влево отбрасываем нужное количество костяшек соответствующего разряда. Теперь, чтобы прибавить к этому, допустим, число 134 – добавляем его поразрядно, начиная с младшего разряда. Это делается для того, чтобы если в одном из разрядов не хватает костяшек – оставить их в данном ряду в том количестве, которого не хватило, и прибавить одну костяшку в старшем над этим ряду.
Разность чисел можно вычислить похожим на нахождение суммы способом, сверху вниз. В ряду, где имеется недостаток костяшек, следует оставить их в количестве, равном 10 минус Х. За Х принимаем число недостающих костяшек и сдвигаем одну костяшку верхнего ряда вправо. Думаю, если вы проделывали эти манипуляции на вытащенных из закромов счетах – разобрались быстро. Но не торопитесь давать объявление: «Учим считать на счетах!» Вот научитесь самостоятельно умножать и делить на них – тогда пора обзаводиться учениками ).
А я во время нашего урока вспомнил еще одно применение этого инструмента для счета, не самое математическое, возможно. После уроков берешь возле пустынной асфальтовой дорожки с уклоном у троих друзей волшебные колесики – и вот уже только ветер свистит в ушах, да как! Считать на счетах любой может научиться, а вы попробуйте удержаться на четвереньках на этом предвестнике скейтборда!
Как называется счет в уме больших чисел. Вычитаем в уме трехзначные числа. Эффективный счёт в уме или разминка для мозга
Одна из главных причин плохих результатов по математике на ОГЭ или ЕГЭ – это неумение считать. Многие школьники затрудняются решить пример даже на листочке, не говоря уже о быстром счете в уме. А ведь некоторые участки мозга атрофируются, если человек не пользуется умственными навыками. Поэтому важно развивать умственные способности в полном объеме.
Основа для развития навыка счета в уме
Некоторые родители считают, что обучать ребенка быстро считать примеры в уме необязательно: в дальнейшем ему это не пригодится, ведь всегда можно воспользоваться калькулятором. Но при этом они забывают о том, что для развития мозга такая тренировка просто необходима: любой изученный метод (прием) счета – это новая нейронная цепочка (связь), чем таких цепочек больше, тем умнее школьник. Поэтому основная польза навыка быстрого счета – это развитие мозга, интеллекта.
Но при этом они забывают о том, что для развития мозга такая тренировка просто необходима: любой изученный метод (прием) счета – это новая нейронная цепочка (связь), чем таких цепочек больше, тем умнее школьник. Поэтому основная польза навыка быстрого счета – это развитие мозга, интеллекта.
Невозможно научиться работать с числами в голове, если иметь слабое представление о них и действиях с ними.
Умение счета развивается постепенно от визуально-наглядного представления чисел и действий с ними до абстрактно-логического:
- Сначала ребенок учится считать в прямом и обратном порядке с помощью стишков, потешек, практических упражнений во время прогулки, принятия пищи игры (посчитать, сколько предметов на столе, машинок в гараже, птичек на дереве). Знакомится с цифрами, узнает, что они обозначают, учится соотносить цифру и количество.
- Затем осваивает понятия «больше — меньше», «поровну», учится сравнивать количество предметов, размеры.
- После этого знакомится со сложением и вычитанием, узнает смысл этих действий.
 Все примеры носят наглядный характер (к двум яблокам ребенок придвигает еще 2 яблока и считает, сколько получится).
Все примеры носят наглядный характер (к двум яблокам ребенок придвигает еще 2 яблока и считает, сколько получится). - Учится считать предметы глазами, проговаривает сначала вслух действия и результат действий, а потом — шепотом:если добавить к 4 машинкам еще 2, то получится 6.
- Многократное повторение действий приведет к тому, что малыш научится распознавать примеры, с которыми уже работал и называть результат вслух, минуя этап проговаривания.
Важно на этапе обучения счету заинтересовать ребенка, поддерживать его в случае неудачи и радоваться вместе с ним победам, пусть даже и маленьким. Когда , навык нужно будет развивать, знакомя школьника с различными приемами и методиками.
Развитие навыка счета в уме
- Совершенствование умения работать с числами в голове.
- Знакомство с новыми приемами и методиками.
- Тренировка умения подбирать оптимальный алгоритм решения в каждом конкретном случае.
Умение работать с числами
Развивать подобный навык позволят упражнения:
- «Назови числа, в которых …» — указывается диапазон и условие, например «Назови числа от 5 до 50, в которых есть цифра 3» или «Назови все двузначные числа, в которых есть цифра 0».
 При выполнении данного упражнения важно сразу прорабатывать все ошибки, допущенные учеником. Если он пропустил число или назвал неправильное, то начинает сначала.
При выполнении данного упражнения важно сразу прорабатывать все ошибки, допущенные учеником. Если он пропустил число или назвал неправильное, то начинает сначала. - «Ведение прогрессии» (диапазон и арифметические действия зависят от возраста и развития навыка счета). Например, «Иди от 5 с шагом 3» или «Иди в обратном порядке от 30 с шагом 4» — для детей начальной школы. Для тех, кто уже выучил таблицу умножения, можно давать задания на умножение и деление: «Иди от 2, умножая все числа на 3».
- «Найди числа от 1 до …» — детям нужно найти и назвать по порядку все числа в таблице.
- «Сравни числа» — дети определяют, какое из них больше (меньше), на сколько;
- «Примеры» — школьникам предлагают решить в уме примеры, сначала простейшие (с маленькими числами), после отработки числа постепенно увеличивают. Не стоит знакомить ребенка с двузначными или трехзначными числами, если он не умеет в совершенстве выполнять действия с числами до 5.
Приемы быстрого счета чисел
К сожалению, единого – универсального – способа, позволяющего решать все примеры одинаково быстро, просто не существует.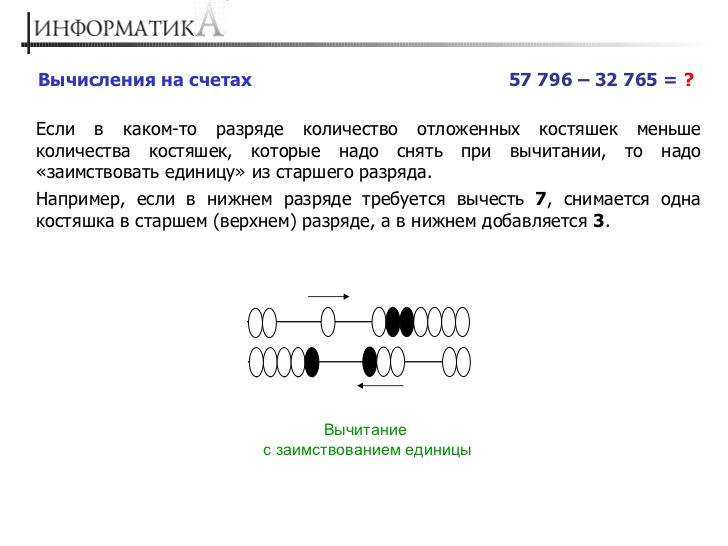
Полезные алгоритмы решения некоторых примеров:
- Чтобы быстро вычесть из числа 7, 8 ил 9, нужно сначала вычесть 10, а затем прибавить 3,2 или 1 соответственно. Например: 45-9=45-10+1=36, или 36-8=36-10+2=28.
- Быстро умножить на 4, 8 и 16 тоже можно. Для этого нужно сначала вспомнить, что 4=2*2, 8=2*2*2, 16=2*2*2*2. Затем просто умножить число на2 несколько раз: 6*16=6*2*2*2*2=96.
- Чтобы умножить число на 9, его сначала увеличивают в 10 раз, а затем от полученного отнимают первый множитель: 27*9=27*10-27=243. Этот прием позволит очень быстро найти результат умножения на 9, если не пользоваться калькулятором.
- Некруглые числа при умножении на 2 удобнее округлить, а затем вычесть или добавить (в зависимости от того, в какую сторону округляли) произведение оставшегося или недостающего числа на 2: 132*2=130*2+2*2=264, или 138*2=140*2-2*2=276.

- Аналогично числа делят на 2: 156/2=150/2+6/2=78, или 156/2=160/2-4/2=78.
- Чтобы умножить на 5, число делят на 2, а затем увеличивают в 10 раз (действия можно произвести наоборот): 27*5=27/2*10 или 27*10/2=135.
- Подобные действия производят при умножении на 25: сначала делят на 4, а потом увеличивают в 100 раз (просто приписывают два нуля): 16*25=16/4*100=400. Конечно, таким способом удобнее пользоваться, когда первый множитель делится без остатка на 4. Определить, делится ли число на 4 без остатка несложно (нетабличные случаи): число, состоящее из двух его последних цифр, должно делиться на 4. Например, число 124 делится на 4 (24/4=6), а 526 – нет (26 не делится на 4 без остатка).
И еще один способ умножения на многозначного числа на однозначное – нужно умножить разрядные слагаемые на второй множитель и результаты сложить. Например, 424*5=400*5+20*5+4*5=2000+100+20=2120.
Чтобы не ошибиться в подсчетах важно уметь прогнозировать будущий результат, и здесь помогут несколько утверждений:
- При умножении однозначных чисел, результат не превышает 81: 9*9=81.

- Аналогично, 99*99=9801, поэтому результат умножения двузначных чисел не должен быть больше этого числа, а при увеличении трехзначных чисел максимальное число – 998001.
Отработка навыка счета в уме
Указанные выше алгоритмы – это основа для развития навыка устного счета. Научиться считать сложные примеры можно только при регулярной тренировке, доведении использования навыка до автоматизма.
Эффективность работы в этом направлении можно повысить, если во время занятий:
- Создать игровую ситуацию , превращающую обыденный учебный процесс в интересный и необычный процесс.
- Поддерживать увлеченность ребенка интересным материалом постоянной сменой деятельности.
- Создать дух соперничества – осознание, что кто-то может сделать лучше, заставит стремиться к новым достижениям, такие занятия будут более эффективны, чем заучивание «в одиночку».
- Фиксировать личные достижения , ставить новые цели по достижению новых вершин.

Умение концентрироваться на решении задачи в любой ситуации (даже когда мешают другие) также способствует развитию навыка счета (да и не только). Тренировать эту способность можно, решая примеры при включенной музыке или, находясь в шумной компании.
Чтобы ребенку не стало скучно, важно научиться бороться с этим чувством. Психологи рекомендуют использовать для этого любые действия: например, рассматривать, что происходит за окном, или наблюдать за движением часовых стрелок. Если малыш научится справляться со скукой, направлять свою энергию в нужное русло, то на уроках он сможет усвоить больший объем информации, что положительно скажется на его успеваемости .
Приемы быстрого счета: магия, доступная всем
Для того чтобы понять, какую роль в нашей жизни играют цифры, поставьте простой эксперимент. Попробуйте некоторое время обойтись без них. Без цифр, без вычислений, без измерений… Вы окажетесь в странном мире, где почувствуете себя абсолютно беспомощным, связанным по рукам и ногам. Как успеть на встречу вовремя? Отличить один автобус от другого? Позвонить по телефону? Купить хлеб, колбасу, чай? Сварить суп или картошку? Без чисел, а значит, без счета жизнь невозможна. Но как тяжело иногда дается эта наука! Попробуйте быстро перемножить 65 на 23? Не получается? Рука сама тянется за мобильником с калькулятором. А, между тем, полуграмотные русские крестьяне 200 лет назад спокойно делали это, пользуясь лишь первым столбиком таблицы умножения – умножением на два. Не верите? А зря. Это – реальность.
Как успеть на встречу вовремя? Отличить один автобус от другого? Позвонить по телефону? Купить хлеб, колбасу, чай? Сварить суп или картошку? Без чисел, а значит, без счета жизнь невозможна. Но как тяжело иногда дается эта наука! Попробуйте быстро перемножить 65 на 23? Не получается? Рука сама тянется за мобильником с калькулятором. А, между тем, полуграмотные русские крестьяне 200 лет назад спокойно делали это, пользуясь лишь первым столбиком таблицы умножения – умножением на два. Не верите? А зря. Это – реальность.
“Компьютер” каменного века
Даже не зная чисел, люди уже пытались считать. Если нашим предкам, обитавшим в пещерах и носившим шкуры, нужно было поменяться чем-либо с соседним племенем, они поступали просто: расчищали площадку и выкладывали, например, наконечник стрелы. Рядом ложилась рыба или горсть орехов. И так до тех пор, пока не заканчивался один из обменных товаров, или глава “торговой миссии” не решал, что уже хватит. Примитивно, но по-своему очень удобно: и не запутаешься, и не обманут.
С освоением скотоводства задачи усложнились. Большое стадо нужно было как-то считать, чтобы знать, все ли козы или коровы на месте. “Счетной машиной” неграмотных, но умных пастухов стала долбленая тыква с камешками. Как только животное покидало загон, пастух клал в тыкву камешек. Вечером стадо возвращалось, и пастух вынимал по камешку с каждым входившим в загон животным. Если тыква пустела, он знал, что со стадом все в порядке. Если оставались камешки – шел искать потерю.
Когда появились цифры, дело пошло веселее. Хотя еще долго у наших предков в ходу было лишь три числительных: “один”, “пара” и “много”.
Можно ли считать быстрее компьютера?
Обогнать устройство, выполняющее сотни миллионов операций в секунду? Невозможно… Но тот, кто говорит так, жестоко лукавит, или просто кое-что умышленно упускает из вида. Компьютер – это лишь набор микросхем в пластике, он не считает сам по себе.
Поставим вопрос по-другому: может ли человек, считая в уме, обогнать того, кто выполняет вычисления на компьютере? И здесь ответ – да.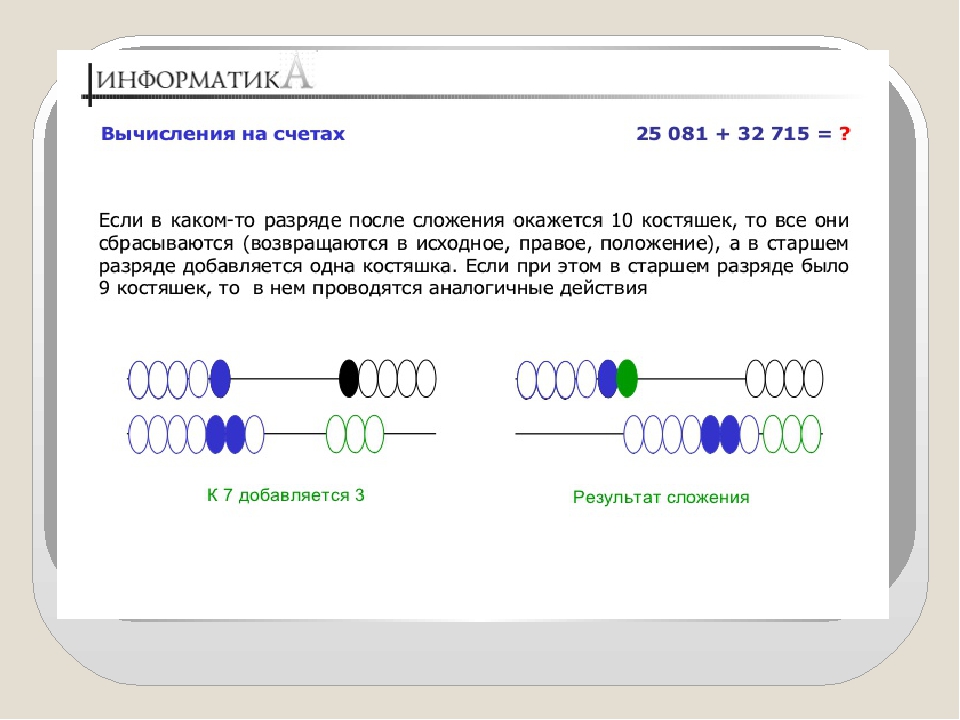 Ведь, чтобы получить ответ от “черного чемоданчика”, данные в него необходимо сначала ввести. Это будет делать человек при помощи пальцев или голосом. А все эти действия имеют ограничения по времени. Непреодолимые ограничения. Сама природа поставила их человеческому телу. Всему – кроме одного органа. Мозга!
Ведь, чтобы получить ответ от “черного чемоданчика”, данные в него необходимо сначала ввести. Это будет делать человек при помощи пальцев или голосом. А все эти действия имеют ограничения по времени. Непреодолимые ограничения. Сама природа поставила их человеческому телу. Всему – кроме одного органа. Мозга!
Калькулятор умеет выполнять лишь две операции: сложение и вычитание. Умножение для него – это множественное сложение, а деление – множественное вычитание.
Наш мозг поступает по-другому.
Класс, где учился будущий король математики, Карл Гаусс, как-то получил задание: сложить все числа от 1 до 100. Карл написал на своей доске абсолютно правильный ответ, как только учитель закончил объяснять задание. Он не стал прилежно складывать числа по порядку, как поступил бы любой уважающий себя компьютер. Он применил открытую им самим формулу: 101 х 50 = 5050. И это далеко не единственный прием, ускоряющий вычисления в уме.
Простейшие приемы быстрого счета
Их изучают в школе. Самое простое: если вам нужно прибавить к любому числу 9, прибавляете 10 и вычитаете 1, если 8 (+ 10 – 2), 7 (+ 10 – 3) и т.д.
Самое простое: если вам нужно прибавить к любому числу 9, прибавляете 10 и вычитаете 1, если 8 (+ 10 – 2), 7 (+ 10 – 3) и т.д.
54 + 9 = 54 + 10 – 1 = 63. Быстро и удобно.
Двухзначные числа складываются так же легко. Если во втором слагаемом последняя цифра больше пяти, число округляется до следующего десятка, а потом “лишнее” вычитается. 22 + 47 = 22 + 50 – 3 = 69. Если ключевая цифра меньше пятерки, то надо сложить сперва десятки, затем единицы: 27 + 51 = 20 + 50 + 7 + 1 = 78.
С трехзначными числами точно так же не возникает никаких трудностей. Складываем их, как читаем, слева на право: 321 + 543 = 300 + 500 + 20 + 40 + 1 + 3 = 864. Гораздо проще, чем в столбик. И гораздо быстрее.
А вычитание? Принцип тот же: вычитаемое округляем до целого и добавляем недостающее: 57 – 8 = 57 – 10 + 2 = 49; 43 – 27 = 43 – 30 + 3 = 16. Быстрее чем на калькуляторе – и никаких претензий от учителя даже во время контрольной!
Нужно ли учить таблицу умножения?
Дети этого, как правило, терпеть не могут. И правильно делают. Ни к чему ее учить! Но не спешите возмущаться. Никто не утверждает, что таблицу не нужно знать.
И правильно делают. Ни к чему ее учить! Но не спешите возмущаться. Никто не утверждает, что таблицу не нужно знать.
Ее изобретение приписывают Пифагору, но, скорее всего, великий математик лишь придал законченную, лаконичную форму тому, что уже было известно. На раскопках древней Месопотамии археологи нашли глиняные таблички с сакраментальным: “2 х 2”. Люди давно пользуются этой в высшей степени удобной системой вычислений и открыли множество способов, которые помогают постичь внутреннюю логику и красоту таблицы, понять – а не тупо, механически зазубрить.
В древнем Китае таблицу начинали учить с умножения на 9. Так проще, и не в последнюю очередь потому, что умножать на 9 можно “на пальцах”.
Положите обе руки на стол ладонями вниз. Первый слева палец – 1, второй – 2 и т.д. Допустим, вам нужно решить пример 6 х 9. Поднимите шестой палец. Пальцы слева покажут десятки, справа – единицы. Ответ 54.
Пример: 8 х 7. Левая рука – первый множитель, правая – второй. На руке пять пальцев, а нам нужно 8 и 7. Загибаем на левой руке три пальца (5 + 3 = 8), на правой 2 (5 + 2 = 7). Загнутых пальцев у нас пять, значит пять десятков. Теперь перемножим оставшиеся: 2 х 3 = 6. Это единицы. Всего 56.
Загибаем на левой руке три пальца (5 + 3 = 8), на правой 2 (5 + 2 = 7). Загнутых пальцев у нас пять, значит пять десятков. Теперь перемножим оставшиеся: 2 х 3 = 6. Это единицы. Всего 56.
Это лишь один из наипростейших приемов “пальцевого” умножения Их много. “На пальцах” можно оперировать числами до 10 000!
У “пальцевой” системы есть бонус: ребенок воспринимает ее как веселую игру. Занимается охотно, испытывает массу положительных эмоций и в итоге очень скоро начинает проделывать все операции в уме, без помощи пальцев.
Делить так же можно при помощи пальцев, но это немного сложнее. Программисты до сих пор пользуются руками, чтобы перевести числа из десятичной системы в двоичную – это удобнее и гораздо быстрее, чем на компьютере. Но в рамках школьной программы научиться быстро делить можно даже без пальцев, в уме.
Допустим, нужно решить пример 91: 13. Столбик? Нет нужды пачкать бумагу. Делимое заканчивается на единицу. А делитель – на тройку. Что там в таблице умножения самое первое, где задействована тройка, а заканчивается на единицу? 3 х 7 = 21. Семерка! Вот и все, мы ее поймали. Надо 84: 14. Вспоминаем таблицу: 6 х 4 = 24. Ответ – 6. Просто? Еще бы!
Семерка! Вот и все, мы ее поймали. Надо 84: 14. Вспоминаем таблицу: 6 х 4 = 24. Ответ – 6. Просто? Еще бы!
Волшебство числа
Большинство приемов быстрого счета похоже на фокусы. Взять хотя бы известнейший пример умножения на 11. Чтобы, например, 32 х 11 нужно написать 3 и 2 по краям, а в середину поставить их сумму: 352.
Для умножения двузначного числа на 101 надо просто записать число два раза. 34 х 101 = 3434.
Для умножения числа на 4 нужно два раза умножить его на 2. Для деления – дважды разделить на 2.
Много остроумных и, главное, быстрых приемов помогают возводить число в степень, извлекать квадратный корень. Знаменитые “30 приемов Перельмана” для математически мыслящих людей будут покруче шоу Коперфильда, потому что они еще и ПОНИМАЮТ что происходит, и как оно происходит. Ну а остальные могут просто наслаждаться красивым фокусом. Например, нужно перемножить 45 на 37. Напишем числа на листе и разделим их вертикальной чертой. Левое число делим на 2, отбрасывая остаток, пока не получим единицу.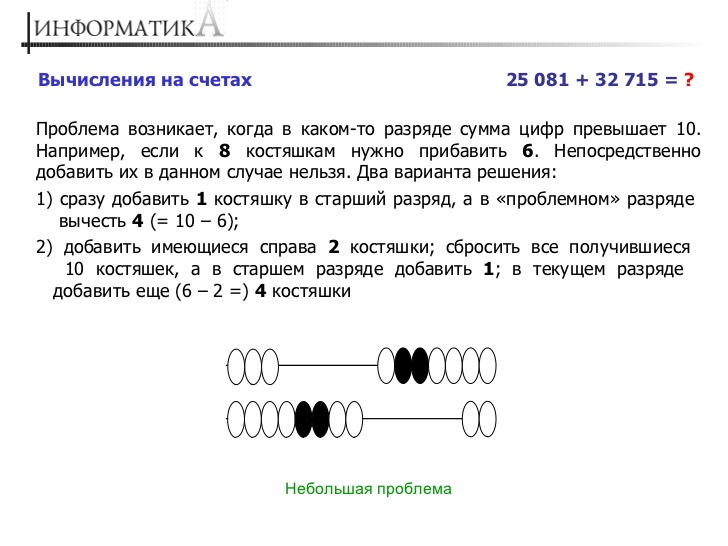 Правое – умножаем до тех пор, пока число строчек в столбике не сравняется. Затем вычеркиваем из ПРАВОГО столбика все те числа, напротив которых в ЛЕВОМ столбике получился четный результат. Оставшиеся числа из правого столбика складываем. Получится 1665. Перемножьте числа привычным способом. Ответ сойдется.
Правое – умножаем до тех пор, пока число строчек в столбике не сравняется. Затем вычеркиваем из ПРАВОГО столбика все те числа, напротив которых в ЛЕВОМ столбике получился четный результат. Оставшиеся числа из правого столбика складываем. Получится 1665. Перемножьте числа привычным способом. Ответ сойдется.
“Зарядка” для ума
Приемы быстрого счета способны здорово облегчить жизнь и ребенку в школе, и маме в магазине или на кухне, и папе на производстве или в офисе. Но мы предпочитаем калькулятор. Почему? Не любим напрягаться. Нам тяжело держать числа, даже двухзначные, в голове. Почему-то не держатся.
Попробуйте выйти на середину комнаты и сесть на шпагат. Почему-то “не сажается”, да? А гимнаст делает это совершенно спокойно, не напрягаясь. Тренироваться нужно!
Самый простой способ тренировки и, одновременно, разминки мозга: устный счет вслух (обязательно!) через число до ста и обратно. Утром, стоя под душем, или готовя завтрак, посчитайте: 2.. 4.. 6.. 100.. . 98.. 96. Можно считать через три, через восемь – главное, делать это вслух. Всего через пару недель регулярных занятий вы удивитесь, насколько ПРОЩЕ станет обращаться с числами.
. 98.. 96. Можно считать через три, через восемь – главное, делать это вслух. Всего через пару недель регулярных занятий вы удивитесь, насколько ПРОЩЕ станет обращаться с числами.
В устном счете, как и везде, есть свои хитрости, и чтобы научиться быстрее считать нужно, знать эти хитрости и уметь применять на практике.
Сегодня мы этим и займемся!
1. Как быстро складывать и вычитать числа
Рассмотрим три случайных примера:
- 25 – 7 =
- 34 – 8 =
- 77 – 9 =
Типа 25 – 7 = (20 + 5) – (5- 2) = 20 – 2 = (10 + 10) – 2 = 10 + 8 = 18
Согласитесь, что такие операции сложно проворачивать в голове.
Но есть более простой способ:
25 – 7 = 25 – 10 + 3, так как -7 = -10 + 3
Намного проще вычесть из числа 10 и прибавить 3, чем городить сложные вычисления.
Вернемся к нашим примерам:
- 25 – 7 =
- 34 – 8 =
- 77 – 9 =
Оптимизируем вычитаемые числа:
- Вычесть 7 = вычесть 10 прибавить 3
- Вычесть 8 = вычесть 10 прибавить 2
- Вычесть 9 = вычесть 10 прибавить 1
Итого получим:
- 25 – 10 + 3 =
- 34 – 10 + 2 =
- 77 – 10 + 1 =
Вот теперь намного интересней и проще!
Посчитайте сейчас представленные ниже примеры этим способом:
- 91 – 7 =
- 23 – 6 =
- 24 – 5 =
- 46 – 8 =
- 13 – 7 =
- 64 – 6 =
- 72 – 19 =
- 83 – 56 =
- 47 – 29 =
2.
 Как быстро умножать на 4, 8 и 16
Как быстро умножать на 4, 8 и 16В случае умножения мы тоже разбиваем числа на более простые, например:
Если помните таблицу умножения, то все просто. А если нет?
Тогда нужно упростить операцию:
Наибольшее число ставим первым, а второе раскладываем на более простые:
8 * 4 = 8 * 2 * 2 = ?
Удваивать числа гораздо легче, нежели чем учетверять или увосьмирять их.
Получаем:
8 * 4 = 8 * 2 * 2 = 16 * 2 = 32
Примеры раскладывания чисел на более простые:
- 4 = 2*2
- 8 = 2*2 *2
- 16 = 22 * 2 2
Отработайте этот способ на следующих примерах:
- 3 * 8 =
- 6 * 4 =
- 5 * 16 =
- 7 * 8 =
- 9 * 4 =
- 8 * 16 =
3. Деление числа на 5
Возьмем следующие примеры:
- 780 / 5 = ?
- 565 / 5 = ?
- 235 / 5 = ?
Деление и умножение с числом 5 всегда очень простые и приятные, ведь пять это половина от десяти.
И как их быстро решить?
- 780 / 10 * 2 = 78 * 2 = 156
- 565 /10 * 2 = 56,5 * 2 = 113
- 235 / 10 * 2 = 23,5 *2 = 47
Для того чтобы проработать этот способ решите следующие примеры:
- 300 / 5 =
- 120 / 5 =
- 495 / 5 =
- 145 / 5 =
- 990 / 5 =
- 555 / 5 =
- 350 / 5 =
- 760 / 5 =
- 865 / 5 =
- 1270 / 5 =
- 2425 / 5 =
- 9425 / 5 =
4.
 Умножение на однозначные числа
Умножение на однозначные числаС умножением немного сложнее, но не сильно, как бы Вы решили следующие примеры?
- 56 * 3 = ?
- 122 * 7 = ?
- 523 * 6 = ?
Без специальных фишек решать их не очень приятно, но благодаря методу «Разделяй и властвуй» мы можем сосчитать их гораздо быстрее:
- 56 * 3 = (50 + 6)3 = 50 3 + 6*3 = ?
- 122 * 7 = (100 + 20 + 2)7 = 100 7 + 207 + 2 7 = ?
- 523 * 6 = (500 + 20 + 3)6 = 500 6 + 206 + 3 6 =?
Нам остается только перемножить однозначные числа, некоторые из которых с нулями и сложить полученные результаты.
Для проработки этой техники решите следующие примеры:
- 123 * 4 =
- 236 * 3 =
- 154 * 4 =
- 490 * 2 =
- 145 * 5 =
- 990 * 3 =
- 555 * 5 =
- 433 * 7 =
- 132 * 9 =
- 766 * 2 =
- 865 * 5 =
- 1270 * 4 =
- 2425 * 3 =
Делимость числа на 2, 3, 4, 5, 6 и 9
Проверьте числа: 523, 221, 232
Число делится на 3, если сумма его цифр делится на 3.
Например, возьмем число 732, представим его как 7 + 3 + 2 = 12. 12 делится на 3, а значит, число 372 делится на 3.
Проверьте, какие из следующих чисел делятся на 3:
12, 24, 71, 63, 234, 124, 123, 444, 2422, 4243, 53253, 4234, 657, 9754
Число делится на 4, если число, состоящее из последних двух его цифр, делится на 4.
Например, 1729. Последние две цифры образуют 20, которое делится на 4.
Проверьте, какие из следующих чисел делятся на 4:
20, 24, 16, 34, 54, 45, 64, 124, 2024, 3056, 5432, 6872, 9865, 1242, 2354
Число делится на 5, если его последняя цифра 0 или 5.
Проверьте, какие из следующих чисел делятся на 5 (самое легкое упражнение):
3, 5, 10, 15, 21, 23, 56, 25, 40, 655, 720, 4032, 14340, 42343, 2340, 243240
Число делится на 6, если оно делится и на 2 и на 3.
Проверьте, какие из следующих чисел делятся на 6:
22, 36, 72, 12, 34, 24, 16, 26, 122, 76, 86, 56, 46, 126, 124
Число делится на 9, если сумма его цифр, делится на 9.
Например, возьмем число 6732, представим его как 6 + 7 + 3 + 2 = 18. 18 делится на 9, а значит, число 6732 делится на 9.
Проверьте, какие из следующих чисел делятся на 9:
9, 16, 18, 21, 26, 29, 81, 63, 45, 27, 127, 99, 399, 699, 299, 49
Игра «Быстрое сложение»
- Ускоряет устный счет
- Тренирует внимание
- Развивает творческое мышление
Отличный тренажер для развития быстрого счета. На экране дана таблица 4х4, а над ней показаны числа. Самое большое число нужно собрать в таблице. Для этого нажмите мышкой на два числа, сумма которых равна этому числу. Например, 15+10 = 25.
Игра “Быстрый счет”
Игра «быстрый счет» поможет вам усовершенствовать свое мышление . Суть игры в том, что на представленной вам картинке, потребуется выбрать ответ «да» или «нет» на вопрос «есть ли 5 одинаковых фруктов?». Идите за своей целью, а поможет вам в этом данная игра.
Игра “Угадай операцию”
Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра “Упрощение”
Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Задание на сегодня
Решить все примеры и тренироваться минимум 10 минут в игре Быстрое сложение.
Очень важно отработать все задания этого урока. Чем лучше Вы будете выполнять задания, тем больше будет пользы. Если Вы чувствуете, что Вам мало заданий – можете сами составлять себе примеры и решать их и тренироваться в математические развивающие игры.
Если Вы чувствуете, что Вам мало заданий – можете сами составлять себе примеры и решать их и тренироваться в математические развивающие игры.
Урок взят из курса “Устный счет за 30 дней”
Научитесь быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. Научу использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Другие развивающие курсы
Деньги и мышление миллионера
Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.
Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
Скорочтение за 30 дней
Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.
Развитие памяти и внимания у ребенка 5-10 лет
В курс входит 30 уроков с полезными советами и упражнениями для развития детей. В каждом уроке полезный совет, несколько интересных упражнений, задание к уроку и дополнительный бонус в конце: развивающая мини-игра от нашего партнера. Длительность курса: 30 дней. Курс полезно проходить не только детям, но и их родителям.
Длительность курса: 30 дней. Курс полезно проходить не только детям, но и их родителям.
Супер-память за 30 дней
Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.
Секреты фитнеса мозга, тренируем память, внимание, мышление, счет
Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.
Зачем нужен устный счет, если на дворе 21 век, и всевозможные гаджеты способны едва ли не молниеносно производить любые арифметические операции? Можно даже не тыкать в смартфон пальцем, а дать голосовую команду – и немедленно получить правильный ответ. Сейчас это успешно проделывают даже школьники младших классов, которым лень самостоятельно делить, умножать, складывать и вычитать.
Сейчас это успешно проделывают даже школьники младших классов, которым лень самостоятельно делить, умножать, складывать и вычитать.
Но у этой медали есть и обратная сторона: ученые предупреждают, что если не тренировать, не нагружать работой и облегчать ему задачи, он начинает лениться, его снижаются. Точно так же без физических тренировок слабеют и наши мышцы.
О пользе математики говорил еще Михаил Васильевич Ломоносов, называющий ее прекраснейшей из наук: «Математику уже за то любить надо, что она ум в порядок приводит».
Устный счет развивает внимание, быстроту реакции. Недаром появляются все новые и новые методики быстрого устного счета, предназначенные и для детей, и для взрослых. Одна из них – японская система устного счета, в которой используются древние японские счеты «соробан». Сама методика была разработана в Японии 25 лет назад, а сейчас ее с успехом применяют и в некоторых наших школах устного счета. В ней используются визуальные образы, каждый из которых соответствует определенному числу. Такое обучение развивает правое полушарие мозга, отвечающее за пространственное мышление, построение аналогий и пр.
Такое обучение развивает правое полушарие мозга, отвечающее за пространственное мышление, построение аналогий и пр.
Любопытно, что всего за два года ученики таких школ (сюда принимают детей в возрасте 4–11 лет) учатся совершать арифметические действия с 2-значными, а то и 3-значными цифрами. Малыши, не знающие таблицы умножения, здесь умеют умножать. Они складывают и вычитают большие числа, не записывая их столбик. Но, конечно же, цель обучения – это сбалансированное развитие правого и .
Овладеть устным счетом можно и с помощью задачника «1001 задача для умственного счета в школе», составленного еще в 19 веке сельским учителем и известным педагогом-просветителем Сергеем Александровичем Рачинским. В пользу этого задачника говорит тот факт, что он выдержал несколько изданий. Эту книгу можно найти и скачать в Интернете.
Люди, практикующиеся в быстром счете, рекомендуют книгу Якова Трахтенберга «Система быстрого счета». История создания этой системы весьма необычна. Чтобы выжить в концлагере, куда его отправили нацисты в 1941 г. , и не утратить ясность ума, цюрихский профессор математики занялся разработкой алгоритмов математических действий, позволяющих быстро считать в уме. А после войны написал книгу, в которой система быстрого счета изложена настолько понятно и доступно, что она и сейчас пользуется спросом.
, и не утратить ясность ума, цюрихский профессор математики занялся разработкой алгоритмов математических действий, позволяющих быстро считать в уме. А после войны написал книгу, в которой система быстрого счета изложена настолько понятно и доступно, что она и сейчас пользуется спросом.
Хорошие отзывы и о книге Якова Перельмана «Быстрый счет. Тридцать простых примеров устного счета». Главы этой книге посвящены умножению на однозначное и двузначное число, в частности умножению на 4 и 8, 5 и 25, на 11/2, 11/4, ѕ, делению на 15, возведению в квадрат, вычислениям по формуле.
Простейшие способы устного счета
Быстрее овладеют этим навыком люди, обладающие определенными способностями, а именно: способностью к логическому мышлению, умением сконцентрироваться и сохранять в краткосрочной памяти несколько образов одновременно.
Не менее важно знание специальных алгоритмов действийи некоторых математических законов, позволяющих , а также умение выбрать наиболее эффективный для данной ситуации.
Ну и, конечно же, не обойтись без регулярных тренировок!
В числе самых распространенных приемов быстрого счета следующие:
1. Умножение двузначного числа на однозначное
Умножить двузначное число на однозначное проще всего, разложив его на две составляющие. Например, 45 – на 40 и 5. Далее каждую составляющую умножаем на нужное число, к примеру на 7, отдельно. Получаем: 40 × 7 = 280; 5 × 7 = 35. Затем получившиеся результаты складываем: 280 + 35 = 315.
2. Умножение трехзначного числа
Умножать в уме трехзначное число также намного проще, если разложить его на составляющие, но представив множимое так, чтобы с ним легче было производить математические действия. Например, нам нужно умножить 137 на 5.
Представляем 137 как 140 − 3. То есть получается, что мы теперь должны умножить на 5 не 137, а 140 − 3. Или (140 − 3) х 5.
Зная таблицу умножения в пределах 19 х 9, можно сосчитать еще быстрее. Раскладываем число 137 на 130 и 7. Далее умножаем на 5 сначала 130, а затем 7, и результаты складываем. То есть 137 × 5 = 130 × 5 + 7 × 5 = 650 + 35 = 685.
То есть 137 × 5 = 130 × 5 + 7 × 5 = 650 + 35 = 685.
Разложить можно не только множимое, но и множитель. Например, нам нужно умножить 235 на 6. Шесть мы получаем, умножив 2 на 3. Таким образом, 235 сначала множим на 2 и получаем 470, а затем 470 умножаем на 3. Итого 1410.
Это же действие можно произвести иначе, представив 235 как 200 и 35. Получается 235 × 6 = (200 + 35) × 6 = 200 × 6 + 35 × 6 = 1200 + 210 = 1410.
Таким же образом, раскладывая числа на составляющие, можно выполнять сложение, вычитание и деление.
3. Умножение на 10-ть
Как умножать на 10, известно всем: просто приписать к множимому нуль. Например, 15 × 10 = 150. Исходя из этого, не менее просто умножать и на 9. Сначала к множимому припишем 0, то есть умножим его на 10, а затем от получившегося числа отнимем множимое: 150 × 9 = 150 × 10 = 1500 − 150 = 1 350.
4. Умножение на 5-ть
Легко умножать и на 5. Следует всего лишь умножить нужно число на 10, а получившийся результат разделить на 2.
5. Умножение на 11-ть
Интересно умножать двузначные числа на 11. Возьмем, к примеру, 18. Мысленно раздвинем 1 и 8, и между ними впишем сумму этих чисел: 1 + 8. У нас получится 1 (1 + 8) 8. Или 198.
6. Умножение на 1,5
При необходимости умножить какое-нибудь число на 1,5 делим его на два и прибавляем получившуюся половинку к целому: 24 × 1,5 = 24 / 2 + 24 = 36.
Это лишь самые простые способы устного счета, с помощью которых мы можем тренировать свой мозг в быту. Например, подсчитывать стоимость покупок, стоя в очереди в кассу. Или же совершать математические действия с цифрами на номерах проезжающих мимо машин. Те же, кто любит «играться» с цифрами и хочет развить свои мыслительные способности, могут обратиться к книгам вышеупомянутых авторов.
Чувство числа, минимальные навыки счета – такой же элемент человеческой культуры, как речь и письмо. И если вы легко считаете в уме, то ощущаете иной уровень управления реальностью. Кроме того, подобное умение развивает мыслительные способности: концентрацию на предметах и вещах, память, внимание к деталям и переключение между потоками познания. И если вас интересует, как научиться быстро считать в уме,
секрет прост: нужно постоянно тренироваться.
И если вас интересует, как научиться быстро считать в уме,
секрет прост: нужно постоянно тренироваться.
Тренировка памяти: миф или реальность?
В математике все просто для тех смышленых личностей, которые щелкают уравнения как семечки. Другим людям сложнее научиться Но нет ничего невозможного, все реально, если много тренироваться. Существуют следующие математические действия: вычитание, сложение, умножение, деление. Каждое из них имеет свои особенности. Чтобы понять все сложности, нужно один раз разобраться в них, а далее будет все намного проще. Если вы будете тренироваться по 10 минут каждый день, то через несколько месяцев выйдете на приличный уровень и познаете истину счета математических чисел.
Многим людям непонятно, как можно варьировать цифрами в уме. Как стать властелином цифр, чтобы это выглядело не глупо и незаметно со стороны? Когда под рукой нет калькулятора, мозг начинает интенсивно обрабатывать информацию, стараясь посчитать необходимые числа в уме. Но не у всех людей получается добиться желаемых результатов, так как каждый из нас – это индивидуальная личность со своими пределами возможностей. Если вы хотите понять, в уме,
то вам следует изучить всю необходимую информацию, вооружившись ручкой, блокнотом и терпением.
Но не у всех людей получается добиться желаемых результатов, так как каждый из нас – это индивидуальная личность со своими пределами возможностей. Если вы хотите понять, в уме,
то вам следует изучить всю необходимую информацию, вооружившись ручкой, блокнотом и терпением.
Таблица умножения спасет ситуацию
Мы не будем говорить о тех людях, у которых уровень IQ выше 100, к таким индивидам особые требования. Поговорим о среднестатистическом человеке, который с помощью таблицы умножения может научиться многим манипуляциям. Итак, как быстро считать в уме без потери здоровья, сил и времени? Ответ прост: вызубрите таблицу умножения! На самом деле здесь нет ничего трудного, главное – иметь напор и терпение, а цифры сами сдадутся перед вашей целью.
Для такого занятного дела нужен будет смышленый напарник, который сможет вас проверить и составит вам компанию в этом требующем терпения процессе. Человек, который знает, в уме даже самого ленивого ученика. Как только вы сможете оперативно умножать, вести устный подсчет будет для вас обыденным делом. К сожалению, волшебных методов не существует. Как быстро вы сможете овладеть новым навыком, зависит только от вас. Упражнять свой мозг можно не только с помощью таблицы умножения, существует более увлекательное занятие – это чтение книг.
К сожалению, волшебных методов не существует. Как быстро вы сможете овладеть новым навыком, зависит только от вас. Упражнять свой мозг можно не только с помощью таблицы умножения, существует более увлекательное занятие – это чтение книг.
Книги и отсутствие калькулятора тренируют ваш мозг
Чтобы как можно быстрее научиться вести вычислительную деятельность устно, нужно постоянно закалять свой мозг новой информацией. Но как научиться быстро считать в умеза короткое время? Тренировать память можно только полезными книгами, благодаря которым универсальной будет не только работа вашего мозга, но и, как бонус, – улучшение памяти и получение полезных знаний. Но чтение книг — это не предел тренировок. Только когда вы сможете забыть о калькуляторе, ваш мозг начнет быстрее перерабатывать информацию. Старайтесь считать в уме при любом случае, продумывайте сложные математические примеры. Но если вам тяжело все это делать самостоятельно, то заручитесь поддержкой профессионала, который быстро вас всему научит.
Вам может быть сложно понять, как научиться быстро считать в уме,когда не дружишь с математикой и нет хорошего учителя, который смог бы облегчить задачу. Но не стоит пасовать перед трудностями. Изучив все необходимые рекомендации, вы с легкостью сможете быстро научиться считать в уме и удивить своих сверстников новыми способностями.
- Умение работать с большими числами – выход за рамки общего развития.
- Знание «хитростей» счета поможет вам быстро преодолеть все препятствия.
- Регулярность важнее интенсивности.
- Не стоит торопиться, старайтесь поймать свой ритм.
- Делайте акцент на правильных ответах, а не на скорости запоминания.
- Проговаривайте действия вслух.
- Не расстраивайтесь, если у вас не выходит, ведь главное – это начать.
Никогда не сдавайтесь перед трудностями
В ходе тренировки у вас может появиться много вопросов, на которые вы не знаете ответов. Это вас не должно пугать. Ведь вы не можете на первых порах знать, как быстро считать
без предварительной подготовки. Дорогу осилит только тот, кто всегда идет вперед. Трудности должны только закалять вас, а не тормозить желание присоединиться к людям с нестандартными возможностями. Даже если вы уже на финишной прямой, возвращайтесь к самому легкому, тренируйте свой мозг, не давайте ему возможности расслабиться. И помните, чем больше вы будете проговаривать информацию в слух, тем быстрее будете запоминать.
Дорогу осилит только тот, кто всегда идет вперед. Трудности должны только закалять вас, а не тормозить желание присоединиться к людям с нестандартными возможностями. Даже если вы уже на финишной прямой, возвращайтесь к самому легкому, тренируйте свой мозг, не давайте ему возможности расслабиться. И помните, чем больше вы будете проговаривать информацию в слух, тем быстрее будете запоминать.
НЕ ментальная арифметика – Школа скорочтения в г. Благовещенск
НЕ ментальная арифметика – Школа скорочтения в г. БлаговещенскГлавная » Курсы » НЕ ментальная арифметика
Для детей, которые испытывают проблемы с примерами: медленно вычитают, складывают, умножают и делят, а простые уравнения и задачи не могут освоить и вовсе
Гарантированные результаты:
- Улучшение навыков счета: по сравнению с первоначальным уровнем в 3-10 раз
- Освоение принципов быстрого счета, умножения и деления и доведение этого навыка до автоматизма
- Быстрое решение простых уравнений, математических ребусов и примеров со смешанными действиями
Программа для детей 5-12 лет
Методика одобрена Министерством Образования РФ
Программа для детей 5-12 лет
Методика одобрена Министерством Образования РФ
Почему ребенок испытывает сложности со счетом и решением задач? Есть несколько причин:
Непонимание принципов быстрых операций
Отсутствие комплексной программы и индивидуального подхода
Счёт кажется скучным, нет правильной мотивации
Курс помогает:
- освоить базовые принципы счета и простейших математических операций
- понять алгоритмы быстрого умножения и деления
- освоить решение математических ребусов
- привить любовь к математике
Курс развивает:
- навыки счета
- умение решать примеры со смешанными действиями
- понимание принципов разгадывания ребусов
Курс ориентирован на:
- обучение быстрому счету
- освоение навыков сложения, вычитания, умножения и деления 2-х и 3-х значных чисел
Наша цель – помочь ребенку освоить не только алгоритм быстрого счета и основных математических операций, но и полюбить математику
Мы покажем ребенку, что решение уравнений и разгадывание математических ребусов не только просто, но и интересно.
На занятиях ребенку предлагаются разноплановые упражения, которые призваны развить внимание и мышление.
Наши ученики умеют концентрироваться на выполнении задачи и делают это с удовольствием Очень часто ребенка пугают логические задачи, часто страхи связаны не только с наполнением материала, но и со строгостью учителя.
Дети, прошедшие наш курс, избавляются от этих страхов раз и навсегда.
Работа с родителями Мы посоветуем и порекомендуем только лучшие варианты по развитию навыков вашего ребенка. В течение курса вы можете узнавать, какая динамика наблюдается у вашего ребенка в ходе обучения и что можно ожидать после его завершения.
Постоянная обратная связь: мы всегда рады рассказать об успехах вашего ребенка и ответить на волнующие вас вопросы.
Посмотрите 2-минутное
видео про процесс обучения
в школе скорочтения
и развития интеллекта TurboRead
Привить ребенку любовь к математике и научить быстро считать в уме – реально! Секрет успеха прост:
Оригинальная методика: мы предлагаем комплексное развитие различных навыков при помощи различных упражнений, ориентированных на развитие памяти, внимания и математического мышления
Индивидуальный подход: каждому ребенку мы предлагаем собственный вариант обучения, согласно особенностям его развития и восприятия материала
Наша основная цель: успех вашего ребенка
Оригинальный формат: использование игры и смены деятельности позволяет исключить скуку и недопонимание в обучении
Наши педагоги: любят детей, свою работу и всегда открыты новому и интересному!
Посмотрите, чему научится ваш ребенок
Мы ориентируемся не только на возраст, но и на уровень подготовки ребенка при определении в группу
5-6 лет
НЕ ментальная
арифметика с 06-8 лет
Сложение
и вычитание8-9 лет
Таблица
умножения9-12 лет
Умножение
и деление
Не ментальная арифметика с 0
До обучения
Ребенок не знаком со счетом.
У него отсутствует понимание принципов сложения и вычитания.
После обучения
Ребенок осваивает сложение и вычитание в пределах первого десятка, в сильных группах — в пределах 20.
Обучение начинается с относительно несложных задач и математических ребусов.
Ребята выполняют задания на развитие мышления, внимания и памяти.
Сложение и вычитание
До обучения
Ребенок уверенно складывает и вычитает в пределах первого десятка.
Быстро решает простые примеры, но испытывает трудности с двузначными и трехзначными числами.
После обучения
Ребенок уверенно выполняет операции по сложению и вычитанию двух- и трехзначных чисел.
Упражнения, которые даются ребятам, ориентированы на увеличение уровня памяти, внимания и мышления.
Запишите вашего ребенка на курс “Сложение и вычитание”, 6-8 летТаблица умножения
До обучения
Ребенок освоил около половины таблицы умножения, но затрудняется с математическими операциями на двузначные и трехзначные числа.
После обучения
Ребенок быстро делит и умножает в уме двузначные и трехзначные числа.
Упражнения, предлагаемые ребенку, помогают ему справиться с внутренней неуверенностью, повышают уровень памяти и развивают мышление.
Запишите вашего ребенка на курс “Таблица умножения”, 8-9 летУмножение и деление
До обучения
Ребенок уверенно выполняет операции по сложению и вычитанию двух- и трехзначных чисел, но не понимает принцип умножения и деления.
После обучения
Даже если ребенок к концу курса не выучил всю таблицу умножения, он понимает сам принцип, по которому происходит умножение.
Он может с легкостью делить и умножать в уме двузначные и трехзначные числа.
Упражнения, предлагаемые ребенку, помогают ему справиться с внутренней неуверенностью, повышают уровень памяти и развивают мышление.
Посмотрите результаты наших учеников
Сидорова Дарья (6л)
Результаты до:
- Примеры на + 6 верных примеров из 15
- Примеры на – 6 верных из 15
Результаты после:
- Примеры на + 15 верных примеров из 15
- Примеры на – 14 верных примеров 15
Курманова Гузель (7л)
Результаты до:
- Примеры на + 8 верных примеров из 15
- Примеры на – 8 верных из 15
Результаты после:
- Примеры на + 15 верных примеров из 15
- Примеры на – 13 верных из 15
Марфина Анастасия (7л)
Результаты до:
- Примеры на + 8 верных из 15
- Примеры на – 6 верных из 15
Результаты после:
- Примеры на + 15 верных из 15
- Примеры на – 15 верных из 15 Задачи 7/7
Тонев Дмитрий (6л)
Результаты до:
- Примеры на + 5 верных из 15
- Примеры на – 7 верных из 15
Результаты после:
- Примеры на + 15 верных из 15
- Примеры на – 15 верных из 15
Как проходят занятия
Объём тренинга 10-12 практических занятий
по 60 минут
Методические пособия предоставляются на занятиях, ребенку не нужно ничего носить с собой!
Место обучения Уютные, современные
аудитории находятся по адресу:
Прочитайте довольные отзывы
учеников и их родителей
Виктория Третьякова 15 июня, 2018
Узнали о школе случайно, пришли на пробный урок и. .. с тех пор мы с удовольствием посещаем занятия. Персонал внимательные, программа интересная ребёнок бежит на уроки с энтузиазмом . Результат тоже радует рекомендую занятия всем знакомым без тени сомнений или колебаний !!!!! Спасибо вам
.. с тех пор мы с удовольствием посещаем занятия. Персонал внимательные, программа интересная ребёнок бежит на уроки с энтузиазмом . Результат тоже радует рекомендую занятия всем знакомым без тени сомнений или колебаний !!!!! Спасибо вам
Ольга Евгеньева 17 марта, 2020
В центр ходим уже не в первый раз. Ребёнку очень нравиться заниматься, на занятия не идём, а бежим! Занятия проходят в игровой форме, где дети не только учатся чему-то новому, но открыто и с интересом участвуют на всех занятиях. Хочу выразить огромную благодарность Центру и школе скорочтения, а именно Ольге! За ее труд, за тёплое отношение к детям, за методику, которая раскрывает и развивает способности ребёнка, и помогает в дальнейшем без труда выполнять домашние задания. Спасибо!!!
Екатерина Алексеева 18 июня, 2018
Очень полезное знание Школа дала моему сыну! Теперь он читаем в три разв быстрее! В процессе учебного года много раз его выручал Новый навык! Огромная благодарность преподавателю Ольге!
Любовь Метальникова 6 июля, 2018
Рекомендую всем мамам отвезти в Центр своего ребенка. Доброжелательная обстановка, динамичные и занимательные занятия пролетают мгновенно, ребенок с удовольствием идёт на занятия!
Светлана Кушакова 16 июня, 2018
Прошли обучение в школе скорочтения. Если честно даже не ожидади таких результатов. Очень рекомендую всем, кто сомневается
Виктория Панкратова 9 апреля, 2018
Напишу просто результаты пришли с скорость 18 слов в минуту, понимание текста было 0%. При окончании школы скорочтения скорость 28, понимание текста 100%. Ребёнок уходил со слезами на глазах, не хотел уходить. Ольга нашла подход к каждому ученику из нашей группы. Очень скептически была настроена на эти курсы, но к моменту обращения в школу было попробовано все что можно, что бы научить сына читать. Подкупило ещё то что в договоре прописано что если курс не даёт результат, деньги возвращают. Очень советую. Придём ещё в сентябре. Спасибо школе скорочтения и лично Ольге!
Ольга Амосова 5 июня, 2018
Прошли курс «Техника чтения». Пришли со знанием алфавита, слоги складывали плохо. После курса ребенок зачитал! Появилось уверенное слоговое чтение, некоторые слова читает словом. У ребёнка появилась уверенность в себе и своих силах. Теперь читает с удовольствием! Мы остались очень довольны Школой и данным курсом!
Екатерина Протасова 6 июня, 2018
Хотела бы выразить огромную благодарность Школе скорочтения и бесподобному преподавателю Юлие! Моя дочь Дарья прошла курс “Чтение словами”. Всего за 10 занятий по этой уникальной методике Дарья, прежде всего, полюбила самостоятельное чтение????, начала читать словами, у неё появилось полное понимание и запоминание прочитанного!????На курсах царила комфортная, благоприятная атмосфера! Спасибо большое! Вернёмся к вам обязательно на курс “Скорочтение”!
Ольга Шмакова 10 июля, 2018
В такое чудо трудно поверить, но это произошло!!! Моя внучка Вика читает, а самое главное получает огромное удовольствие от самого процесса, потому что стало интересно и понятно прочитанное. Результат потрясающий: от 102 слов в минуту до 235 слов, но не механического чтения, а понимание прочитанного 100%, а было всего 30%.С первого занятия была в восторге, и так же с желанием и ожиданием все десять занятий. Огромное спасибо Юля Николаевна за ваш талант и доброту. Мы все в восторге, не верится до сих пор, что такой прогресс за столь короткое время! Всем советую дать шанс вашему ребенку поверить в себя и обрести уверенность в завтрашнем дне.
Антонина Головина 12 июня, 2018
Прошли курс “Чтение вслух”. Основными целями ставили перед собой снять страх и неуверенность при чтении вслух, а также осознанность чтения. Большое спасибо Юлии Николаевне за профессионализм, за чуткое отношение к ученикам, за ее сопереживание, умение внушить уверенность в успех. И, конечно, за индивидуальный подход, подбор заданий для решения проблем каждого ребенка. Планируем пройти еще один крус, позже определимся с направлением. А пока продолжим заниматься по имеющимся материалам.
Марина Усова 14 августа, 2018
Добрый день! Хочу выразить огромную благодарность”Школе скорочтения для детей”.
В какой-то момент я потеряла всякую надежду, что мой сын – 7 лет, будет с удовольствием брать книгу в руки. Случайно я узнала, что в нашем городе есть курсы “Скорочтение для детей” по методике Шамиля Ахмадуллина. И мы решили попробовать. Прошли собеседование и записались на курс “Чтение словами”. Уже после третьего занятия я заметила положительные результаты. Простые тексты сыну стали даваться с легкостью. Он с удовольствием делал домашние задания, а на занятия шёл с большим желанием. Все занятия проходили в игровой форме и Ваня не замечал, как пролетали 60 минут урока. К окончанию курса результаты превзошли мои ожидания: он стал читать словами и читает уверенно, с выражением, а главное, понимает прочитанное. Появилось желание обсуждать книги.
Хочу выразить свою признательность педагогам школы, Юлии Николаевне и Ксении. Спасибо вам за доброту, терпение, за добрые слова! Желаю вам успехов в вашем очень нужном деле, как для детей, так и для их родителей!
Обязательно придем в ” Школу скорочтения” ещё раз, только уже на другой курс.
Дипломы и сертификаты
Ответы на часто
задаваемые вопросы
- Для чего нужно собеседование?
Бесплатное собеседование – это наша с вами Встреча. На нем вы знакомитесь с нашей программой и задаете свои вопросы педагогу, а мы определяем текущий уровень ребенка, тестируем его в интересующем вас направлении. Кроме того, можно пообщаться с тренером, который подскажет, насколько подходит методика для вашего ребенка и даст рекомендации по курсам. Все это поможет принять окончательное решение – подходит ли вам наша методика.
- Можно ли присутствовать на занятиях?
Мы не практикуем открытые занятия по той простой причине, что это сильно отвлекает детей и тормозит учебный процесс. Мы считаем, что занятия должны быть максимально продуктивными. Но в течение всего курса проходят родительские собрания, где можно задать вопросы на волнующие темы, a также ознакомиться с результатами обучения ребенка.
- Будут ли домашние задания?
Домашние задания даются на повторение пройденного материала на занятия, но для их выполнения потребуется не более 15 минут свободного времени в день.
- Специалисты какого уровня проводят занятия (опыт, образование, сертификаты и т.д.)?
Все педагоги у нас имеют психологическое и педагогическое образование, у некоторых специалистов за плечами не одно высшее образование. Методическую подготовку по ведению занятий у педагогов проводит руководитель школы лично. Шамиль Тагирович Ахмадуллин является автором более 40 книг и пособий по эффективному обучению детей, из них 17 книг стали бестселлерами. О том, что в школе работают профессионалы, вы поймёте после общения с тренером на собеседовании.
- Занятия ведет сам Шамиль Ахмадуллин?
Нет, Шамиль Тагирович не занимается преподавательской деятельностью, он разрабатывает методику, пишет пособия. Кроме того, он занимается методической подготовкой педагогов, поэтому компетентность педагогов не вызывает сомнений.
Сайт уважает и соблюдает законодательство РФ. Также мы уважаем ваше право и соблюдаем конфиденциальность при заполнении, передаче и хранении ваших конфиденциальных сведений.
Мы запрашиваем ваши персональные данные исключительно для информирования об оказываемых услугах сайта.
Персональные данные – это информация, относящаяся к субъекту персональных данных, то есть, к потенциальному покупателю. В частности, это фамилия, имя и отчество, дата рождения, адрес, контактные реквизиты (телефон, адрес электронной почты), семейное, имущественное положение и иные данные, относимые Федеральным законом от 27 июля 2006 года № 152-ФЗ «О персональных данных» к категории персональных данных.
Если Вы разместили ваши контактные данных на сайте, то Вы автоматически согласились на обработку данных и дальнейшую передачу ваших контактных данных менеджерам нашего сайта.
В случае отзыва согласия на обработку своих персональных данных мы обязуемся удалить ваши персональные данные в срок не позднее 3 рабочих дней.
Счет в уме – тренировка умственных способностей
В современном мире огромное значение придается саморазвитию. Так в сферу интересов многих людей попадает умение быстро считать в уме. Существует целый ряд методик, позволяющих устно выполнять операции даже с большими числами. Рассмотрим самые популярные из них и определим, как они справляются со своей задачей.
Польза навыков устного счета
Числа – это то, что окружает современного человека повсюду. Мы знакомимся с ними в детстве на уроках математики или еще до школы. Именно в это время прививаются первичные навыки счета, позволяющие производить более сложные вычисления в дальнейшем. В начальной школе большое значение уделяется устному счету. Учителя проверяют то, насколько хорошо ребенок умеет складывать, вычитать, умножать и делить небольшие числа в уме. Но чем старше становится ученик, тем реже он считает устно, предпочитая производить вычисления на бумаге или с помощью калькулятора.
Во взрослой жизни тенденция отказа от устного счета сохраняется. Совершая покупки или выполняя отчет по работе, гораздо проще воспользоваться умными помощниками, чем тратить время и силы на попытки подсчитать все в уме. Но в нужный момент гаджетов или листа бумаги может не оказаться под рукой. В таких ситуациях человек невольно задумывается о том, насколько полезным может быть навык быстрого устного счета, ведь вычисления в уме позволяют сделать любую работу, связанную с цифрами, более продуктивной. Но как этого можно добиться?
Первым способом является знание хитростей математики. Существует целый ряд приемов, позволяющих не только складывать и вычитать, но умножать и делить двузначные и трехзначные числа. Но у данного подхода есть свои минусы, главным из которых является невозможность применять один и тот же прием для разных чисел. К тому же, многие способы включают в себя сразу несколько действий. Учитывая то, что вычисления ведутся устно, бывает сложно сохранять концентрацию и не сбиваться.
Более продуктивной альтернативой математическим хитростям является такая методика счета в уме, как ментальная арифметика. Она позволяет научиться производить операции даже с многозначными числами за считанные секунды. К ее плюсам можно отнести уже то, что ей может обучиться как маленький ребенок, так и взрослый. В чем же секрет этой техники?
Как научиться считать ментально
Ментальная арифметика – это методика, позволяющая научиться считать в уме без использования подручных средств. В ее основе лежит умение производить вычисления на абакусе – специальных счетах, известных еще с древних времен. Обучение этой технике проходит поэтапно. Сначала ученику предстоит освоить принципы работы абакуса, научиться использовать его для простейших операций с небольшими числами. Требуется хорошо закрепить эти навыки, довести их до автоматизма. Только тогда, когда удастся производить вычисления не задумываясь, можно будет перейти к следующему этапу тренировок.
Теперь у ученика появляется другая задача – научиться представлять абакус в своем воображении и считать уже на нем. Сначала изучается сложение и вычитание небольших чисел, затем осваивается умножение и деление. Постепенно уровень сложности растет, и ученик переходит к операциям с многозначными числами. Этому этапу тренировок счета в уме уделяется особенно много времени и внимания, но результат будет стоить потраченных усилий. Так удастся производить вычисления даже быстрее, чем при использовании калькулятора, но и это не является главным плюсом данной методики.
Помимо быстрого устного счета, ментальная арифметика развивает множество других функций человеческого интеллекта. Обычно при подсчетах используется только левое полушарие мозга, которое отвечает за логическое мышление и аналитические способности, а правое, отвечающее за креативное мышление и фантазию, не задействуется. Но ментальный счет имеет совершенно другой подход, ведь в его основе лежат вычисления на воображаемых счетах, а значит правое полушарие также будет использоваться. Рассмотрим то, как это отражается на умственных способностях человека.
Тренировка интеллектуальных способностей
Человеческий мозг нуждается в тренировке. Только получая нагрузку на различные области интеллекта, удается совершенствовать свои способности. Ментальная арифметика отлично справляется с этой задачей, так как задействует оба полушария мозга одновременно. Благодаря этому удается:
- улучшить память. Обучение включает в себя упражнения, в которых нужно производить операции с целыми рядами чисел подряд. Из-за этого приходится одновременно держать в уме итог промежуточных вычислений и новые части задания. Такая разносторонняя нагрузка способствует развитию памяти.
- повысить концентрацию. Работа с большим объемом чисел требует высокой сосредоточенности. Обучаясь ментальной арифметике, человек также учится сохранять внимание на процессе вычислений. Концентрация, которая развивается в процессе занятий, будет очень полезна и в других сферах деятельности.
- укрепить межполушарные связи. Те или иные задачи нагружают в большей степени или левое, или правое полушарие мозга. Ментальная арифметика позволяет укрепить связь между ними, благодаря чему удается добиться более продуктивной работы как в творческих, так и в аналитических областях.
- развить творческие способности и фантазию. Креативное мышление важно в самых разных сферах деятельности. Ментальная арифметика хоть и подразумевает работу с числами, но также способствует повышению и творческих способностей человека.
- улучшить логические способности. Выполнение большого количества операций с числами развивает левое полушарие мозга, что положительно сказывается на логических и аналитических функциях интеллекта.
- увеличить количество процессов, которые можно выполнять одновременно. Освоение ментальной арифметики формирует многозадачность, благодаря которой можно научиться считать большое количество чисел в уме и параллельно выполнять другие действия – рассказывать стихотворение или петь песню. Умение выполнять несколько дел одновременно очень полезно в повседневной жизни.
Помимо перечисленных плюсов, ментальная арифметика несет в себе различные преимущества для каждой возрастной группы. Для детей такие занятия – это способ полюбить математику, улучшить успеваемость в школе и повысить мотивацию к учебе. Для взрослых эта техника является отличным инструментом саморазвития, ведь она позволяет приобрести навыки, которые пригодятся и в работе, и в быту. Все это делает данную методику отличным вариантом для тех, кто хочет улучшить свои способности. Осталось определиться с тем, как лучше организовать сам процесс обучения.
Ментальная арифметика – методика обучения быстрому счету в уме
Как и многие другие программы, данную методику можно освоить самостоятельно. Но поиск нужного материала, отсутствие помощи педагога и необходимость соблюдать регулярность тренировок могут стать серьезной преградой для обучения. Именно поэтому большинство людей отдает предпочтение очным курсам, а не самостоятельным тренировкам. Но и у такого подхода есть свои минусы:
- приходится тратить время на дорогу. Из-за современного ритма жизни, потеря пусть даже и одного часа на дорогу очень ощутима. Далеко не у каждого взрослого или ребенка есть на это время.
- нельзя регулировать график и время занятий. Сменный график работы у взрослых или наличие секций у детей может препятствовать посещению курсов ментальной арифметики. Из-за этого такие занятия являются не тем вариантом, который удобен для всех.
- нет возможности индивидуально подобрать нагрузку. У каждого человека свое количество свободного времени, которое он может посвятить саморазвитию. Групповые тренировки подразумевают постоянное посещение. Тренер не сможет ждать тех, кто не справляется с нагрузкой из-за пропуска занятий.
Все это приводит к востребованности онлайн-обучения, в том числе, и ментальной арифметике. Теперь изучать быстрый счет в уме можно прямо из дома и тогда, когда это удобно. Так как для занятий достаточно компьютера и выхода в интернет, можно беспрепятственно путешествовать, не пропуская онлайн-уроки. А возможность индивидуально подобрать нагрузку и график тренировок позволяет самосовершенствоваться даже самым занятым маленьким и взрослым ученикам.
Умножение и деление чисел в Excel
Умножение и деление в Excel не представляют никаких сложностей: достаточно создать простую формулу. Не забывайте, что все формулы в Excel начинаются со знака равенства (=), а для их создания можно использовать строку формул.
Умножение чисел
Предположим, требуется определить количество бутылок воды, необходимое для конференции заказчиков (общее число участников × 4 дня × 3 бутылки в день) или сумму возмещения транспортных расходов по командировке (общее расстояние × 0,46). Существует несколько способов умножения чисел.
Умножение чисел в ячейке
Для выполнения этой задачи используйте арифметический оператор * (звездочка).
Например, при вводе в ячейку формулы =5*10 в ячейке будет отображен результат 50.
Умножение столбца чисел на константу
Предположим, необходимо умножить число в каждой из семи ячеек в столбце на число, которое содержится в другой ячейке. В данном примере множитель — число 3, расположенное в ячейке C2.
-
Введите =A2*$B$2 в новом столбце таблицы (в примере выше используется столбец D). Не забудьте ввести символ $ в формуле перед символами B и 2, а затем нажмите ввод.
Примечание: Использование символов $ указывает Excel, что ссылка на ячейку B2 является абсолютной, то есть при копировании формулы в другую ячейку ссылка всегда будет на ячейку B2. Если вы не использовали символы $ в формуле и перетащили формулу вниз на ячейку B3, Excel изменит формулу на =A3*C3, которая не будет работать, так как в ячейке B3 нет значения.
-
Перетащите формулу вниз в другие ячейки столбца.
Примечание: В Excel 2016 для Windows ячейки заполняются автоматически.
Перемножение чисел в разных ячейках с использованием формулы
Функцию PRODUCT можно использовать для умножения чисел, ячеек и диапазонов.
Функция ПРОИЗВЕД может содержать до 255 чисел или ссылок на ячейки в любых сочетаниях. Например, формула =ПРОИЗВЕДЕНИЕ(A2;A4:A15;12;E3:E5;150;G4;h5:J6) перемножает две отдельные ячейки (A2 и G4), два числа (12 и 150) и три диапазона (A4:A15, E3:E5 и h5:J6).
Деление чисел
Предположим, что вы хотите узнать, сколько человеко-часов потребовалось для завершения проекта (общее время проекта ÷ всего людей в проекте) или фактический километр на лилон для вашего последнего меж страны(общее количество километров ÷ лилонов). Деление чисел можно разделить несколькими способами.
Деление чисел в ячейке
Для этого воспользуйтесь арифметическим оператором / (косая черта).
Например, если ввести =10/5 в ячейке, в ячейке отобразится 2.
Важно: Не забудьте ввести в ячейку знак равно(=)перед цифрами и оператором /. в противном случае Excel интерпретирует то, что вы введите, как дату. Например, если ввести 30.07.2010, Excel может отобразить в ячейке 30-июл. Если ввести 36.12.36, Excel сначала преобразует это значение в 01.12.1936 и отобразит в ячейке значение “1-дек”.
Примечание: В Excel нет функции DIVIDE.
Деление чисел с помощью ссылок на ячейки
Вместо того чтобы вводить числа непосредственно в формулу, можно использовать ссылки на ячейки, такие как A2 и A3, для обозначения чисел, на которые нужно разделить или разделить числа.
Пример:
Чтобы этот пример проще было понять, скопируйте его на пустой лист.
Копирование примера
-
Создайте пустую книгу или лист.
-
Выделите пример в разделе справки.
Примечание: Не выделяйте заголовки строк или столбцов.
Выделение примера в справке
-
Нажмите клавиши CTRL+C.
-
Выделите на листе ячейку A1 и нажмите клавиши CTRL+V.
-
Чтобы переключиться между просмотром результатов и просмотром формул, которые возвращают эти результаты, нажмите клавиши CTRL+’ (ударение) или на вкладке “Формулы” нажмите кнопку “Показать формулы”.
|
A |
B |
C |
|
|
1 |
Данные |
Формула |
Описание (результат) |
|
2 |
15000 |
=A2/A3 |
Деление 15000 на 12 (1250). |
|
3 |
12 |
Деление столбца чисел на константу
Предположим, вам нужно разделить каждую ячейку в столбце из семи чисел на число, которое содержится в другой ячейке. В этом примере число, на которые нужно разделить, составляет 3, содержалось в ячейке C2.
|
A |
B |
C |
|
|
1 |
Данные |
Формула |
Константа |
|
2 |
15000 |
=A2/$C$2 |
3 |
|
3 |
12 |
=A3/$C$2 |
|
|
4 |
48 |
=A4/$C$2 |
|
|
5 |
729 |
=A5/$C$2 |
|
|
6 |
1534 |
=A6/$C$2 |
|
|
7 |
288 |
=A7/$C$2 |
|
|
8 |
4306 |
=A8/$C$2 |
-
В ячейке B2 введите =A2/$C$2. Не забудьте в формуле включить символ $ перед символами C и 2.
-
Перетащите формулу в ячейке B2 вниз в другие ячейки в столбце B.
Примечание: Символ $ указывает Excel, что ссылка на ячейку C2 является абсолютной, то есть при копировании формулы в другую ячейку ссылка всегда будет на ячейку C2. Если вы не использовали в формуле символы $ и перетащили формулу вниз на ячейку B3, Excel изменит формулу на =A3/C3, которая не будет работать, так как в ячейке C3 нет значения.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
См. также
Умножение столбца чисел на одно и то же число
Умножение на процентное значение
Создание таблицы умножения
Операторы вычислений и порядок операций
Рабочая программа краткосрочного курса “Быстрый счет без калькулятора” (6 класс)
Хоть и считается, что математика наводит ужас на значительную часть населения, но деньги считать умеют все. И вот как раз влет это умеют делать люди, далекие от математики.
Помнится, бабушка моего мужа показывала ему на пальцах таблицу умножения на 9. Никакого образования, только огромная практика торговли редиской и клубникой на рынке!
Так вот сегодня я предлагаю вам несколько интересненьких приемов устного счета. Ведь сколько бы замечательных гаджетов (телефоны, смартфоны, айподы и айпады, ай, да чего там…) своя голова она всегда лучше.
Итак, читаем, тут же проверяем и запоминаем приемы вычисления в уме.
1. Умножение на 11
Умножать на 11 чуть сложнее, чем умножать на 10. Закономерность здесь такая:
53 х 11 = 583
Шаг 1 — Складываем две цифры двузначного числа: 5 + 3 = 8
Шаг 2 — Помещаем результат между двумя числами двузначного числа: 583
59 х 11 = 649
Шаг 1 — 5 + 9 = 14
Шаг 2 — Перекидываем единицу налево, если сумма на предыдущем шаге оказалась больше 9: 5 + 1 = 6 (справа остается второй символ, в данном случае это четверка)
Шаг 3 — На первый символ мы единицу уже перекинули, получили 6. Далее у нас осталась 4, которую ставим в центр, и дописываем 9: 649
2. Быстрое возведение в квадрат
Этот прием поможет быстро возвести в квадрат двузначное число, которое заканчивается на 5.
85 х 85 = 7225
Шаг 1 — Умножаем первую цифру на первую цифру, увеличенную на единицу: 8 x (8 + 1) = 72
Шаг 2 — Дописываем к получившемуся результату 25: 7225
45 x 45 = 2025
Шаг 1 — 4 х (4 + 1) = 20
Шаг 2 — 2025
3. Умножение на 5
Большинство людей очень просто запоминает таблицу умножения на 5, но, когда приходится иметь дело с большими числами, сделать это становится сложнее. Или нет? Этот прием невероятно прост.
Возьмите любое число, разделите на 2 (другими словами, поделите пополам). Если в результате получилось целое число, припишите 0 в конце. Если нет, не обращайте внимание на запятую и в конце добавьте 5.
Это срабатывает всегда:
2682×5 = (2682 / 2) & 5 или 0
2682 / 2 = 1341 (целое число, поэтому добавьте 0)
13410
Давайте попробуем другой пример:
5887×5
2943,5 (дробное число, пропустите запятую, добавьте 5)
29435
4. Умножение на 9
Это просто. Чтобы умножить любое число от 1 до 9 на 9, посмотрите на руки. Загните палец, который соответствует умножаемому числу (например 9×3 – загните третий палец), посчитайте пальцы до загнутого пальца (в случае 9×3 – это 2), затем посчитайте после загнутого пальца (в нашем случае – 7). Ответ – 27.
5. Умножение на 4
Это очень простой прием, хотя очевиден лишь для некоторых. Хитрость в том, что нужно просто умножить на 2, а затем опять умножить на 2:
58×4 = (58×2) + (58×2) = (116) + (116) = 232
6. Подсчет чаевых
Если вам нужно оставить 15% чаевых, есть простой способ сделать это.
Высчитайте 10% (разделите число на 10), а потом добавьте получившееся число к его половине и получите ответ:
15% от $25 = (10% от 25) + ((10% от 25) / 2)
$2.50 + $1.25 = $3.75
И, как следствие): чтобы умножить число на 1,5 нужно к исходному числу прибавить его половину. Например,
34*1,5 = 34+17=51
125*1,5= 125+62,5=187,5
7. Сложное умножение
Если вам нужно умножать большие числа, причем одно из них — четное, вы можете просто перегруппировать их, чтобы получить ответ:
32×125 все равно, что:
16×250 все равно, что:
8×500 все равно, что:
4×1000 = 4,000
8. Деление на 5
На самом деле делить большие числа на 5 очень просто. Все, что нужно,— просто умножить на 2 и перенести запятую: 195 / 5
Шаг1: 195×2 = 390
Шаг2: Переносим запятую: 39,0 или просто 39.
2978 / 5
Шаг1: 2978×2 = 5956
Шаг2: 595,6
9. Вычитание из 1000
Чтобы выполнить вычитание из 1000, можете пользоваться этим простым правилом: Отнимите от 9 все цифры, кроме последней. А последнюю цифру отнимите от 10:
1000-648
Шаг1: от 9 отнимите 6 = 3
Шаг2: от 9 отнимите 4 = 5
Шаг3: от 10 отнимите 8 = 2
Ответ: 352
И, напоследок, несколько математических трюков:
Интересные результаты:
1 х 1 = 1
11 х 11 = 121
111 х 111 = 12321
1111 х 1111 = 1234321
11111 х 11111 = 123454321
111111 х 111111 = 12345654321
1111111 х 1111111 = 1234567654321
11111111 х 11111111 = 123456787654321
111111111 х 111111111 = 12345678987654321
1 х 9 + 2 = 11
12 х 9 + 3 = 111
123 х 9 + 4 = 1111
1234 х 9 + 5 = 11111
12345 х 9 + 6 = 111111
123456 х 9 + 7 = 1111111
1234567 х 9 + 8 = 11111111
12345678 х 9 + 9 = 111111111
123456789 х 9 + 10 = 1111111111
9 х 9 + 7 = 88
98 х 9 + 6 = 888
987 х 9 + 5 = 8888
9876 х 9 + 4 = 88888
98765 х 9 + 3 = 888888
987654 х 9 + 2 = 8888888
9876543 х 9 + 1 = 88888888
98765432 х 9 + 0 = 888888888
1 х 8 + 1 = 9
12 х 8 + 2 = 98
123 х 8 + 3 = 987
1234 х 8 + 4 = 9876
12345 х 8 + 5 = 98765
123456 х 8 + 6 = 987654
1234567 х 8 + 7 = 9876543
12345678 х 8 + 8 = 98765432
123456789 х 8 + 9 = 987654321
Любимая цифра.
Предложите задумать свою любимую цифру. А теперь выполните умножение (на калькуляторе) числа 15873 на любимую цифру, умноженную на 7. Например, если любимая цифра 5, то умножить нужно на 35. Получится произведение, записанное только любимой цифрой.
Возможен и второй вариант: умножить число 12345679 на любимую цифру, умноженную на 9, в нашем случае это число 45.
Объяснение этого фокуса достаточно простое: если умножить 15873 на 7, то получится 111111, а если умножить 12345679 на 9, то получится 111111111.
Угадать возраст.
Умножаем число своих лет на 10, затем любое однозначное число умножить на 9, из первого произведения вычесть второе и сообщить полученную разность. В этом числе “фокусник” должен цифру единиц сложить с цифрой десятков – получится число лет.
Всегда девятка
Предложите кому-нибудь написать число из трех разных цифр, под ним — написать число из этих же цифр, но в обратном порядке. Затем вычесть меньшее из большего. Когда зритель это сделает, скажите ему, что в середине числа стоит девятка.
Секрет фокуса: Вы будете правы, потому что девятка всегда будет в середине независимо от того, какие цифры написаны.
Людей из группы выделяют как по умению красиво и правильно говорить, так и по умению быстро считать в уме, и относят их, как правило, к категории умных. Школьнику умение быстро считать в уме позволяет более успешно учиться, а инженеру и ученому сократить время получения результата их деятельности.
УС нужен не только школьникам, но и инженерам, учителям, медицинским работникам, ученым и руководителям разного уровня. Кто быстро считает, тому легче учиться и работать. УС – это не игрушка, хотя и развлекает. Он позволяет вернуться ученику на те “рельсы”, с которых он упал когда-то; повышает скорость и качество восприятия информации; дисциплинирует и производит точность во всем; приучает замечать детали и мелочи; приучает к экономии; создает образы предметов и явлений; позволяет предвидеть будущее и развивает интеллект человека.
«Евроремонт» в голове нужно начинать с простых арифметических действий, которые позволяют структурировать мозг.
Умение быстро считать в уме дает ученику уверенность в себе. Как правило, быстрее всех считают в уме те, кто хорошо учится в школе или в ВУЗе. Если отстающего ученика научить быстро считать в уме, то это обязательно благотворно повлияет на его успеваемость, и не только в естественных, но и во всех других предметах. Это доказано практикой.
Произвольное внимание и интерес во время устного счета меняет блуждающий взгляд отстающего ученика на фиксированный, а концентрация внимания достигает нескольких этажей глубины предмета или процесса, который изучается.
“Изучение математики дисциплинирует мышление, приучает к правильному словесному выражению мыслей, к точности, сжатости и ясности речи, воспитывает настойчивость, умение достигать намеченной цели, развивает работоспособность, способствует правильной самооценке владения предметом, который изучается”. (Кудрявцев Л.Д. – член-кор. РАН. 2006.).
Ученик, который научился быстро считать в уме, как правило, начинает и быстрее мыслить.
Тот, кто по своей природе хорошо считает, естественно обнаружит ум и в любой другой науке, а тот, кто считает медленно, учась этому искусству и овладевая им, сможет улучшить свой ум, сделать его острее (Платон).
Приобретенных навыков устного счета одним хватит на 5 — 10 лет, а другим на всю жизнь.
Нашим потомкам будет легче учиться и получать знания. Однако, культура устного счета всегда будет являться неотъемлемой частью общечеловеческой культуры.
Кто быстро считает в уме, тот, как правило, ясно мыслит, быстро воспринимает и глубже видит.
Освоение УС развивает образное, диаграммное и системное мышление, расширяет оперативную память, диапазон восприятия, приучает к мышлению на несколько ходов вперед, повышает качество мышления, оперируя количественными характеристиками объектов.
УС повышает ясность мышления, уверенность в себе, а также волевые качества (терпение, усидчивость, выносливость, трудолюбие). Приучает к глубокой и устойчивой концентрации внимания, домысливанию и договариванию начатых фраз (особенно у дошкольников и учеников начальных классов).
5 реальных способов удвоить свои деньги
Каждый хочет удвоить свои деньги. К счастью, есть способы приумножить свои деньги, которые не связаны с мошенничеством быстрого обогащения или выигрышем в лотерею.
Эти законные способы создания богатства не требуют огромных доходов для начала. Хотя вы не можете быстро удвоить свои деньги, правило 72 показывает, что со временем это возможно.
Правило 72 дает оценку того, когда ваши деньги удвоятся.Например, если вы разделите 72 на восьмипроцентную норму прибыли, вы увидите, что ваши деньги удвоятся за девять лет. В это время уменьшится более высокая окупаемость инвестиций.
Эти методы приумножения денег доступны каждому.
Как приумножить деньги
Хотите узнать, как приумножить свои деньги? Или вы ищете законных идей пассивного дохода , которые пополнят ваш банковский счет?
* Сделка дня : КИТ Банк платит.45 процентов на их счетах денежного рынка . Заработайте в 7 раз больше среднего по стране, открыв счет всего на 100 долларов. Все вклады застрахованы FDIC на сумму не более 250 000 долларов на каждого вкладчика.
Вот пять простых способов начать приумножать свои деньги прямо сейчас.
1. Инвестируйте в фондовый рынок
Когда вы пытаетесь узнать, как удвоить свои деньги, инвестирование в фондовый рынок – лучший способ увеличить свое богатство в долгосрочной перспективе.
Фондовый рынок может быть рискованным, и вы можете потерять деньги.Однако вы также можете зарабатывать деньги, инвестируя в фондовый рынок.
S&P 500, который считается ведущим индексом фондового рынка, с 1957 года имел среднюю годовую доходность в размере восьми процентов. При таком уровне вы удвоили бы свои вложения в течение девяти лет.
Что делать, если у вас нет денег для инвестирования или вы не знаете, с чего начать? Вы все еще можете инвестировать в фондовый рынок и приумножить свои деньги.
Главное – немедленно начать инвестировать. Чем раньше вы начнете инвестировать, тем меньше денег вы сможете сэкономить из-за сложных процентов.
Возьмем для примера достижение чистой стоимости активов в 1 миллион долларов. Вот то, что вам нужно откладывать каждый месяц для достижения этой цели, начиная с 20 лет.
SoFi Wealth – отличный выбор, если вы хотите начать инвестировать, но вам нужна помощь. Платформа помогает управлять вашими инвестициями, чтобы быть уверенным, что вы достигли поставленных целей.
ДляSoFi Wealth требуется минимальный баланс в размере 1 доллара США, и она не взимает никаких комиссий за управление.
Если у вас есть старый план 401 (k) или IRA, вы можете переместить их в SoFi Wealth, чтобы получить их помощь.
Как насчет плана 401 (k)?
Вы новичок в инвестировании или предпочитаете не иметь нескольких инвестиционных счетов? Ваш спонсируемый сотрудником план 401 (k) является подходящей альтернативой инвестированию через брокерскую компанию, такую как SoFi Invest.
Большинство работодателей предлагают соответствовать вашему взносу до определенной суммы. Это мгновенно увеличит ваши деньги, так что больше будет поступать на рынок и работать на вас.
Многие планы 401 (k) содержат бесплатные образовательные ресурсы, которые помогут вам узнать больше об инвестировании.Большинство планов также включают индексные фонды в качестве вариантов инвестирования.
Это позволяет вам отслеживать рынок, не платя обременительных комиссий в активно управляемый фонд.
Прочтите наше руководство по , как настроить свой первый план 401 (k) , если вы новичок в этом инструменте личных финансов.
2. Инвестиции в недвижимость
Многие люди считают, что фондовый рынок – единственный способ приумножить богатство. Благодаря краудфандингу недвижимость становится выгодным вариантом инвестиций для большего числа людей. Это также позволяет диверсифицировать инвестиции, чтобы снизить риски.
Раньше требовалось значительных денежных средств, чтобы инвестировать в недвижимость . В качестве альтернативы вам нужно было управлять собственностью.
Crowdfunding позволяет находить инвестиции в недвижимость с минимальными ресурсами. Это также позволяет избежать самостоятельного управления имуществом.
Теперь вы можете инвестировать в недвижимость всего за 10 долларов с помощью таких платформ, как Fundrise . Как и на фондовом рынке, инвестирование в недвижимость может быть рискованным. Однако он предлагает множество выгодных возможностей.
Доходность без учета комиссий составила 7,4 процента по состоянию на 2020 год.
Платформа, такая как Fundrise, поможет вам найти недвижимость, соответствующую вашему профилю риска. Сюда могут входить:
- Апартаменты
- Коммерческая недвижимость
- Новостройка
Fundrise позволяет инвестировать в недвижимость, не занимаясь физическим управлением. Для пользователей доступны пенсионные или не пенсионные счета.
Roofstock – еще один хороший вариант для инвестиций в недвижимость.Платформа ориентирована на аренду недвижимости под ключ.
Для инвестирования с Roofstock не требуется минимального баланса. У вас должно быть 20 процентов, и вы можете инвестировать с IRA.
3. Открыть сберегательный счет
Сберегательный счет– это классический способ приумножить свои деньги. Хотя на удвоение ваших денег с помощью сберегательного счета уйдут годы, это надежный способ без особых усилий приумножить ваши деньги.
Процентные ставки по сберегательным счетам в прошлые годы были значительно выше.До Великой рецессии они приближались к пяти процентам. Сейчас трудно найти что-либо выше одного процента.
К сожалению, нынешняя пандемия только усугубляет ситуацию.
Сберегательные счетапредлагают ликвидность, которая необходима для любого инвестиционного плана. Ликвидность полезна разными способами, в том числе:
- Финансирование идеи малого бизнеса
- Накопление на инвестиционную недвижимость
- Ликвидность для управления бизнес-расходами
ЦИТ Банк – отличный выбор для сбережений.На денежном рынке ЦИТ Банка выплачивается 0,45 процента, и требуется только минимальный баланс в 100 долларов.
Счет работает как сберегательный. Он застрахован FDIC на сумму до 250 000 долларов США и взимает 0 долларов США в качестве комиссии.
Вы также можете использовать счет для снятия средств и оплаты счетов.
4. Одолжите деньги кому-нибудь другому
Один из наиболее уникальных способов приумножить ваши деньги – это одалживать их другим людям через одноранговые (P2P) займы. Это отличный вариант, если у вас мало денег для вложения или вы хотите диверсифицировать свои вложения.
Вы можете одолжить свои деньги другим через такую платформу, как LendingClub.
Люди используют такие платформы, как LendingClub, чтобы получить беззалоговый личный заем . Они используют ссуды практически на все, в том числе:
- Консолидация долга
- Финансирование реконструкции дома
- Рефинансирование автокредита
Вы можете финансировать ссуды поэтапно от 25 долларов. Вы также можете выбрать, какие ссуды вы хотите финансировать. Это помогает распределить риски и максимизировать прибыль.
LendingClub утверждает, что предлагает инвесторам доходность от четырех до восьми процентов. Ваша доходность зависит от того, насколько хорошо вы распределяете риск.
P2P-займы могут быть рискованными, как и на фондовом рынке. Имейте в виду, что риск дефолта может повлиять на вашу прибыль.
Тем не менее, займы P2P могут быть хорошим способом помочь кому-то приумножить ваши деньги.
5. Выплата долга
Выплата долга – это законный способ приумножить ваши деньги. Люди часто спорят о выплате долга против выплаты долга.инвестирование. Что важнее – извечный вопрос.
Ответ в сторону, убийство долгов – это способ приумножить ваши деньги, которым не уделяют должного внимания.
Выплата долга помогает вам создать богатство, поскольку долг является одной из составляющих уравнения чистой стоимости активов.
Выплачивая долг, вы экономите деньги, которые пошли бы на выплату процентов. Затем эти деньги можно использовать другими способами.
Долг, особенно потребительский долг с высокими процентами, носит ограничительный характер. Это не даст вам создать потоки пассивного дохода, которые жизненно важны для накопления богатства.
Если у вас есть задолженность по кредитной карте, рассмотрите возможность объединения с SoFi . Кредитор предлагает ставки всего 5,99% и не имеет скрытых комиссий.
Это может позволить вам снизить ставку, быстрее выплатить долг и получить больше средств для инвестирования.
Когда вы начнете выплачивать долг, постарайтесь совместить его с меньшими расходами. Когда вы приближаетесь к долговой свободе и имеете больше денег для инвестирования, вы можете воспользоваться преимуществами фондового рынка или недвижимости.
Это может помочь вам удвоить ваши деньги за восемь или девять лет.
Вложение при выплате долга – личное решение. Вы можете делать и то, и другое одновременно, но это продлит время, необходимое для освобождения от долгов. Делайте то, что лучше для вас, и со временем все наладится.
Итог
Создание богатства – это то, к чему стремится большинство людей, но считает, что это сложно или невозможно. Благодаря обилию инструментов и ресурсов найти законные способы накопления богатства никогда не было так просто.
Когда вы будете искать способы удвоить свои деньги, помните правило 72.Разделите 72 на норму прибыли, и вы увидите, сколько времени вам понадобится, чтобы добиться успеха.
Хотя успех не может прийти в одночасье, он произойдет быстрее, чем вы думаете, если вы будете твердо привержены делу.
Какие из ваших любимых способов приумножить свое богатство? Как диверсифицировать свои вложения?
Вас направили на веб-сайт SoFi Wealth, LLC («SoFi Invest») от компании Frugal Rules и Ink Harmony, LLC, солиситора SoFi Invest («Солиситор»).Адвокат, направивший вас на эту веб-страницу, получит компенсацию от SoFi Invest, если вы вступите в консультативные отношения или в платную подписку на консультационные услуги. Компенсация солиситору может составлять до 1500 долларов. С вас не будут взиматься какие-либо сборы или какие-либо дополнительные расходы за то, что Адвокат направит вас в SoFi Invest. Адвокат может продвигать и / или может рекламировать услуги инвестиционного консультанта SoFi Invest, а также может предлагать независимый анализ и обзоры услуг SoFi Invest.SoFi Invest и Солиситор не находятся в общей собственности или иным образом не связаны между собой. Дополнительная информация о SoFi Invest содержится в ее форме ADV Part 2A, доступной здесь .
Похожие сообщенияТри шага к увеличению ваших сбережений и повышению благосостояния
Совет 1. Положите свои сбережения на автопилот
Когда дело доходит до сбережений, первый шаг – сделать это привычкой.
Многие финансовые консультанты рекомендуют начинать с фонда на случай чрезвычайной ситуации, который является ключом к тому, чтобы не дотянуться до кредитной карты, когда всплывает что-то неожиданное, например, сломанный прибор или счет за медицинское обслуживание.Или, что еще хуже, потерю работы и дохода.
Больше от Инвестируйте в себя:
4 шага по сокращению расходов на 2020 год
Следуйте этим правилам, а чего нельзя делать, когда начинаете инвестировать
Бесплатные онлайн-инструменты, которые помогут вам стать более успешным инвестором
как минимум шесть месяцев или больше расходов, отложенных, если вы являетесь главой семьи.
Хотя эта сумма может показаться большой, думайте о малом: например, хорошей целью является накопление до 1000 долларов на банковском счете к концу года.
Если вы разбили это на недельную цель сбережений, это примерно эквивалентно откладыванию 20 долларов каждую пятницу.
Для этого настройте прямой перевод из своей зарплаты на специальный сберегательный счет. В некоторых случаях ваш отдел кадров может даже сделать это за вас.
Совет 2: заново продумайте, где спрятать деньги
По мере того, как ваши сбережения будут расти, они начнут увеличиваться. Вот где процентные ставки играют решающую роль.
По данным FDIC, средняя ставка по сберегательному счету составляет всего 0.09% или даже меньше в некоторых крупнейших розничных банках. Онлайн-банки платят в 10-20 раз больше. Чтобы получить максимальную отдачу от своих денег, покупайте товары по более высокой ставке сбережений.
«Это действительно окупится в долгосрочной перспективе», – сказала Ариэль О’Ши, специалист по банковскому делу и инвестициям NerdWallet.
Онлайн-банки могут предлагать высокодоходные счета, потому что у них меньше накладных расходов, чем у традиционных обычных банков.
Лучшие из них также предлагают льготы, такие как отсутствие минимального баланса и бесплатный доступ к банкомату.Вы даже можете связать онлайн-сберегательный счет с текущим счетом в местном банке, чтобы получить доступ к наличным деньгам, когда они вам понадобятся.
Чтобы получить еще более высокую доходность, вложить деньги на фондовый рынок было гораздо лучше, чем просто хранить их в наличных деньгах.
Как правило, если вы берете на себя больший риск, вознаграждение со временем увеличивается. Однако вероятность потерять деньги также увеличивается.
Вот где может помочь финансовый советник, робот-консультант или даже приложения.
Совет 3. Увеличьте свои пенсионные сбережения
Ваш пенсионный план на рабочем месте, или 401 (k), предлагает еще одну возможность приумножить ваши деньги – благодаря совпадению с работодателем.
Вы хотите внести как минимум достаточно денег на свой пенсионный счет на рабочем месте, чтобы получить полный соответствующий взнос компании. «Это бесплатные доллары, – сказал О’Ши.
«Выбор работодателя – один из единственных способов получить гарантированный возврат своих инвестиций», – добавила она.«Это может быть 50% или 100% доходности».
В то же время включите функцию автоматической эскалации, если ваш работодатель предлагает ее, которая автоматически увеличит вашу норму сбережений на 1% или 2% каждый год.
Если вы работаете в малом бизнесе или самостоятельно откладываете деньги через индивидуальный пенсионный счет, вы можете применить тот же подход.
«Ваша цель должна заключаться в увеличении этих взносов до предела», – сказал О’Ши.
ПОДПИСАТЬСЯ: Money 101 – это 8-недельный курс обучения финансовой свободе, который еженедельно доставляется на ваш почтовый ящик.
ПРОВЕРИТЬ: Почему январь – прекрасное время для вложения денег через Grow with Acorns + CNBC.
Раскрытие информации: NBCUniversal и Comcast Ventures являются инвесторами в Acorns .
Понимание основ бухгалтерского учета (ALOE и балансовые отчеты) – более подробное объяснение
В бухгалтерии математика обычно не хуже умножения. Но бухгалтерский учет не связан с математикой – это около концепций , и некоторые из них меня сбили с толку.У бухгалтерского учета есть простые и удивительно элегантные способы отслеживания бизнеса.
Так что же такое бухгалтерский учет?
Откровенно говоря, учет – это отслеживание вещей (да, это еще не все, но держитесь меня). Какие вещи мы можем отслеживать?
- Активов: Штат внутри компании
- Обязательства: Прочие вещи
- Собственный капитал (также известный как капитал) : Вещи, принадлежащие владельцам
Достаточно просто.Как они связаны?
Активы = Обязательства + Собственный капитал
Проще говоря, все, что есть у компании, принадлежит владельцам или кому-то еще . Подумайте об уравнении так:
- активы = обязательства + собственный капитал
- сотрудников = чужое + собственное
Эта формула (также называемая ALOE) сначала может показаться странной. Почему мы добавляем к обязательств и собственного капитала? Потому что мы смотрим с точки зрения компании , а не акционеров.Если у компании что-то есть, это может быть кому-то еще.
С точки зрения собственника, собственный капитал = активы – обязательства. Это уравнение выглядит более естественным, но часто нас не интересует точка зрения владельца. Мы хотим знать о компании.
Что такое баланс?
Балансовый отчет – это документ, в котором отслеживаются активы, обязательства и собственный капитал компании в определенный момент времени. Как известно, если у компании что-то есть, то это принадлежит кому-то .Стороны должны уравновесить. Итак, давайте сделаем пример.
Предположим, мы открываем компанию с $ 100 наличными:
Активы:
Наличные: 100
Обязательства:
Никто
Собственный капитал:
Доступность: 100
Компания имеет краткосрочные инвестиции на $ 100, а у владельцев есть акции на $ 100 (как в компании представлена собственность).
Теперь предположим, что мы берем ссуду в банке на 150 долларов. Бухгалтерский баланс принимает следующий вид:
Активы:
Наличные: 250
Обязательства:
Кредиты: 150
Собственный капитал
Доступность: 100
Сейчас у нашей компании $ 250, но $ 150 принадлежит банку, а $ 100 принадлежит владельцам.Извините, ребята, вы не можете взять ссуду и сделать свою долю в компании более ценной.
Далее купим здание за 200 $:
Активы:
Наличные: 50
Дом: 200
Обязательства:
Кредиты: 150
Собственный капитал
Доступность: 100
Покупка здания не делает нашу компанию более ценной: мы реорганизовали наши активы. Вместо \ $ 250 наличными у нас \ $ 50 наличными и \ $ 200 в “строительстве”. Наша доля в компании (\ $ 100) ничуть не изменилась. А мы до сих пор должны банку 150 долларов.
На самом деле это не так, не так ли?
Это так. Что ж, настоящие бухгалтеры используют более изящные термины («дебиторская задолженность» против «неплательщиков, которые должны мне») и имеют более крупный и плохой баланс. Но основная идея та же: показать, чего стоит компания и кто чем владеет.
Взгляните на баланс небольшой интернет-компании:
Активы делятся на краткосрочные и долгосрочные; чистая стоимость компании составляет около 18 миллиардов долларов (по состоянию на декабрь 2006 г.).Это выше 10 миллиардов долларов в 2005 году.
Существует множество причин, по которым активы могут быть переоценены или недооценены в бухгалтерских книгах. Как вы измеряете импульс? Моральный дух сотрудников? Бренд? Лояльность клиентов?
Бухгалтеры пытаются количественно оценить подобные вещи с помощью нематериальных терминов, таких как «гудвилл», но это непросто. На самом деле стоимость большинства компаний в несколько раз превышает их заявленные активы; Рыночная капитализация Google более чем в 10 раз превышает балансовую стоимость (но узнайте больше об акциях, чтобы понять, почему рыночная капитализация не совсем правильная).
Теперь рассмотрим другую сторону уравнения, обязательства и собственный капитал:
Вау, у Google не так много обязательств! Всего 1,4 миллиарда долларов (из общей суммы 18 миллиардов долларов) и нет долгосрочного долга. То, что он действительно должен, является «кредиторской задолженностью» – эквивалентом счета по кредитной карте (обычно оплачиваемого в короткие сроки).
Теперь вы можете изучить компанию и увидеть, сколько она стоит (на бумаге) и в чем заключается ценность. У Google нет «инвентаря» (когда-либо покупал у них готовый продукт?), Но у него много денег, инвестиций и оборудования.Долгов и других обязательств очень мало, поэтому на бумаге она кажется очень стабильной; в ближайшее время они не разорятся (есть и другие документы, которые показывают, насколько прибыльна компания).
УBlockbuster, например, 2,5 миллиарда активов, но 1,9 миллиарда причитаются другим (сохраненный баланс здесь). Акционерам осталось немного. Фактически, у него 700 миллионов «нематериальных активов», поэтому на самом деле у него отрицательных реальных материальных активов. Плохой знак – если вы ликвидировали компанию сегодня, она не могла выплатить свой долг.
Правила игры
Бухгалтерия имеет много правил, но основное из них таково: используйте двойную бухгалтерию .
Этот причудливый термин означает, что все изменения происходят парами:
- Если активы падают, обязательства или собственный капитал также должны уменьшиться
- Если активы растут, обязательства или собственный капитал также должны увеличиваться
Каждое изменение активов должно иметь соответствующее изменение, чтобы сбалансировать уравнение.Существует формальная система «дебетов и кредитов», описывающая эти изменения, но концепция проста: если вы вносите изменение в одну сторону, вы должны также вносить изменения в другую.
Есть еще чему поучиться
Бухгалтерский учет гораздо больше, но основы у вас есть:
- Если у компании что-то есть, лучше бы кому-то владеть
- В балансе перечислены активы, обязательства и собственный капитал на определенный момент времени; все должно составлять
- Изменения должны производиться парами : если активы, обязательства или собственный капитал изменяются, то также сильно меняется что-то еще
Любая система может быть интересной (даже «забавной»), если вы посмотрите на причины, по которым она была создана, и на проблему, которую она пытается решить.Могли бы вы, , упростить отчет о том, сколько стоит компания и кому что причитается?
Наслаждайтесь.
Другие сообщения из этой серии
- Правило 72
- Понимание основ бухгалтерского учета (ALOE и балансы)
- Понимание долга, рисков и кредитного плеча
- Что нужно знать о фондовом рынке
- Понимание принципа Парето (Правило 80/20)
- Сочетание простоты и сложности
Умножение – объяснения и примеры
Что такое умножение?
Умножение – это математическая операция по нахождению результата двух или более чисел путем повторного сложения чисел.
Умножение обычно обозначается крестиком (x). Однако также используются другие символы, такие как звездочка (*), точка (.) И фраза «время».
Части умноженияПредложение умножения состоит из двух частей: математического выражения и произведения. Математическое выражение состоит из множителей и оператора или символа умножения.
Например, в математическом выражении: 5 x 2 = 10, часть «2 x 5» представляет собой математическое выражение, состоящее из 2 и 5 как факторов и операторов.В данном случае произведение равно 10.
Мы можем далее разбить множители на множимое и множимое:
- Множаемое – это число, умноженное на другое число.
- Множитель – это число, на которое нужно умножить.
- Произведение является результатом умножения.
Свойства умножения
Изучение свойств умножения помогает упростить и решить математические задачи, связанные с умножением.
В умножении свойство коммутативности означает, что умножение двух или более чисел не влияет на окончательный ответ.В общем, для предложения умножения: m x n = n x m. Например, 4 x 5 – это то же самое, что 5 x 4. Это свойство также применяется при умножении большой группы чисел. Например, 4 x 3 x 2 = 2 x 3 x 4.
При умножении ассоциативное свойство утверждает, что группировка чисел не влияет на окончательный ответ при умножении ряда чисел вместе. Обычно группировки в любом математическом выражении обозначаются круглыми или квадратными скобками. Мы можем суммировать это свойство как: m x (n x p) = (m x n) x p.Например, (2 x 4) x 6 = 2 x (4 x 6).
Это свойство указывает, что умножение любого числа на единицу не меняет его значения. Другими словами, это свойство можно записать как 1 x a = a. Например, 1 x 8 = 8.
Свойство распределения для умножения утверждает, что выражение, состоящее из сложения или вычитания значений, умноженных на число, эквивалентно сумме или разности чисел выражений.
В общем случае m x (n + p) = m x n + m x p, а m x (n – p) = m x n – m x p.Например, 2 x (3 + 4) = 2 x 3 + 2 x 4.
Таблица умноженияМассив – это сетка / диаграмма умножения, состоящая из чисел в строках и столбцах. Умножение с использованием таблицы умножения проще, потому что произведение двух чисел находится путем подсчета количества строк и умножения на соответствующее количество столбцов.
Например, , в ручке, состоящей из 9 в столбце и 6 в строке, продукт в сетке равен 54.
| x | 1 | 2 | 3 | 4 | 4 5 8 | 9 | 10 | 11 | 12 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 1 | 2 | 79053 | 9058 | 9 | 10 | 11 | 12 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | 2 | 4 | 6 | 8 | 10 | 905 905 12 905 1220 | 22 | 24 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | 3 | 6 | 9 | 12 | 90 513 1518 | 21 | 24 | 27 | 30 | 33 | 36 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | 4 | 8 | 20 | 905 2832 | 36 | 40 | 44 | 48 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | 5 | 10 | 15 | 20 | 25 | 905 90550 | 55 | 60 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 905 90572 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 905 13 6370 | 77 | 84 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 64 905 905 905 88 | 96 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 905 905 905 905 905 905 90510 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 905 11 | 120 9 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 | 110 | 121 | 132 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12 | 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 | 132 | 120 | 132 Как составить предложения умножения? Умение составлять предложения умножения – важный навык для учащихся, поскольку он подготавливает их к практическому использованию математики.Учащийся, который знает, как составлять свои собственные предложения для умножения, может взглянуть на сетку чисел четыре на четыре и обязательно скажет, что сетка состоит из 16 элементов. Как составить предложение из слова ЗадачаСоздание предложений умножения, кажется, сбивает студентов с толку. Однако после прочтения и понимания этой статьи учащимся будет легче решать задачи со словами. Например, предположим, что Мэри собрала корзину апельсинов, если у нее достаточно апельсинов, чтобы разместить 15 апельсинов в 3 ряда.Сколько апельсинов она собрала? В этом примере предложение умножения можно записать как 15 x 3 = 45. Таким образом, Мэри собрала 45 апельсинов. Практические вопросы
Ответы
Как Multiply выбирает рекомендуемый мне сберегательный счет? | умножить | УмножьтеЕсли вы решите создать продукт или учетную запись, мы рекомендуем, чтобы провайдер мог заплатить нам комиссию за отправку вашего бизнеса.Так Multiply зарабатывает достаточно денег, чтобы помочь нам сохранить ваш финансовый план свободным. Сумма, которую нам платит поставщик, никогда не влияет на то, какие продукты вы показываете в плане. Но мы подумали, что вам может быть интересно узнать, какие факторы или критерии действительно входят в уравнение при выборе наших продуктов. Так что же важно в сберегательном счете? Ян и Стивен, наша группа по исследованию продуктов, продумывают, что важно для клиентов на сберегательном счете.Эти принципы помогают нам выбирать поставщиков, исходя из ваших интересов: Цена: Каждый хочет получить максимум за свои деньги, и выбор сберегательного счета ничем не отличается, мы стараемся, чтобы наши рекомендации учитывали процентную ставку, которую вы » Я получу деньги. Простота настройки: Сейчас 2019 год, а это значит, что вам не нужно тащить кучу документов в местное отделение, чтобы создать сберегательный счет. Вот почему мы рекомендуем только онлайн-провайдеров, которые легко настроить. Доступность: Некоторые продукты для сбережения денежных средств доступны только определенным группам людей, например существующим клиентам поставщика. Чтобы убедиться, что наши рекомендации подходят большинству людей, мы отфильтровываем поставщиков с такими ограничениями. Гибкость: Мы считаем, что финансовые продукты, которые вы покупаете, должны соответствовать вашей жизни. Поэтому мы отсеиваем продукты, которые не являются гибкими, например, мы не рекомендуем ISA, которые не принимают входящие переводы. Безопасность: Будь то фонд на черный день или депозит на новый дом, вы должны знать, что ваши сбережения в безопасности. Вот почему мы рекомендуем только безопасные и безопасные продукты. Все рекомендуемые нами счета защищены FSCS, что означает, что деньги, которые вы в них вкладываете, защищены до 85 000 фунтов стерлингов. А как вы решите, какой тип аккаунта мне подходит? Тип сберегательного счета, который вам нужен, будет зависеть от ваших обстоятельств или цели.Например, если вы израсходовали всю свою квоту на ISA за год, Multiply не порекомендует вам открыть еще одну. Точно так же, если мы порекомендовали вам создать резервный фонд, мы всегда будем рекомендовать учетную запись с мгновенным доступом, то есть без штрафных санкций за досрочное снятие средств, если вам это необходимо. Типы счетов, которые мы в настоящее время рекомендуем: Сберегательные счета с мгновенным доступом Мгновенный доступ Cash ISA Как вы обновляете свои рекомендации? Мы пересматриваем наш список поставщиков каждые четыре недели.Вдобавок к этому мы всегда обновляем, когда:
Если у вас есть какие-либо отзывы или мысли, дайте нам знать, связавшись с закрытой группой сообщества в Facebook или написав нам в Твиттере @ MultiplyAI Умножить или добавить в первую очередь? Обучение правилам порядка операцийЧто первично в порядке операций?Со временем математики согласовали набор правил, называемый порядком операций , чтобы определить, какую операцию выполнить в первую очередь.Когда выражение включает только четыре основных операции, вот правила:
При упрощении выражения, такого как \ (12 \ div 4 + 5 \ times 3-6 \), сначала вычислите \ (12 \ div 4 \), поскольку порядок операций требует сначала оценки любого умножения и деления (в зависимости от того, что первый) слева направо перед вычислением сложения или вычитания. В данном случае это означает сначала вычисление \ (12 \ div 4 \), а затем \ (5 \ times 3 \).После того, как все умножение и деление будут завершены, продолжайте, добавляя или вычитая (в зависимости от того, что наступит раньше) слева направо. Шаги показаны ниже.
Рассмотрим в качестве примера другое выражение:
Иногда мы можем захотеть убедиться, что сначала выполняется сложение или вычитание. Группировка символов , таких как круглых скобок \ (() \), скобок \ ([] \) или фигурных скобок \ (\ {\} \), позволяет нам определить порядок, в котором выполняются определенные операции. выполненный. Порядок операций требует, чтобы операции внутри символов группировки выполнялись перед операциями вне их.Например, предположим, что выражение 6 + 4 заключено в круглые скобки:
Обратите внимание, что выражение имеет совершенно другое значение! Что, если вместо этого мы заключим \ (7 – 3 \) в круглые скобки?
Этот набор скобок дает еще один ответ. Итак, когда используются круглые скобки, правила порядка операций следующие:
|


 Все примеры носят наглядный характер (к двум яблокам ребенок придвигает еще 2 яблока и считает, сколько получится).
Все примеры носят наглядный характер (к двум яблокам ребенок придвигает еще 2 яблока и считает, сколько получится). При выполнении данного упражнения важно сразу прорабатывать все ошибки, допущенные учеником. Если он пропустил число или назвал неправильное, то начинает сначала.
При выполнении данного упражнения важно сразу прорабатывать все ошибки, допущенные учеником. Если он пропустил число или назвал неправильное, то начинает сначала.