Начальная фаза что такое: Белорусский государственный университет транспорта - БелГУТ (БИИЖТ) - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Белорусский государственный университет транспорта – БелГУТ (БИИЖТ)

Начальная фаза колебаний – точки, формулы, единица измерения в физике

словосочетание начальной фазы | значение и примеры использования

События

Анонсы

Новости

БелГУТ на Доске почета

КУДА ПОСТУПАТЬ

Предложения

Видеотека

Фотогалерея

Понятие фазы колебательного процесса

Значение начальной фазы колебательного процесса

Что мы узнали?

Тест по теме

Как поступить в БелГУТ

Как получить место

Оценка доклада

Содержание

Электронная очередь на
централизованное тестирование

в общежитии БелГУТа

ГОРЯЧАЯ ЛИНИЯ
по вопросам приемной кампании

Все события

Все анонсы

Поздравление с Днем Победы Председателя Совета Рес. ..
С ПРАЗДНИКОМ ВЕЛИКОЙ ПОБЕДЫ!…
68-я студенческая научно-техническая конференция…
С днем Печати!
Фестиваль военно-патриотической песни среди иностр…
XXXII Международный фестиваль искусств «Славянский…
Вопросы к собеседованию для прошедших обучение в Н…
Олимпиада по теории вероятностей…

Летний оздоровительный лагерь для детей сотруднико…
Славим мир, труд, май!

Университет

Абитуриентам

Студентам

Конференции

Приглашения

Поздравление с Днем Победы Председателя Совета Рес…

С ПРАЗДНИКОМ ВЕЛИКОЙ ПОБЕДЫ!…

68-я студенческая научно-техническая конференция…

С днем Печати!

Университет

Международные связи

Спорт

ИВР

Жизнь студентов

Новости подразделений

Университет

Праздничный концерт и торжественное собрание в ОКЦ. ..
05 мая 2023

Университет

Слава Героям – митинг на Аллее Героев
05 мая 2023

Университет

Макет лагеря «Дулаг-121» выполнен студентами БелГУТа для выставки о ла…
05 мая 2023

Университет

Поклонимся тем, кто отдал свои жизни за Победу…
05 мая 2023

Университет

Презентуем патриотический проект «Альбом памяти»…
05 мая 2023

Студенческая жизнь

Мы помним о тех, кто не вернулся с поля боя…
05 мая 2023

Университет

Новый номер газеты «Вести БелГУТа»
05 мая 2023

Спорт

Победа в Республиканской Универсиаде по вольной борьбе. ..
05 мая 2023

Студенческая жизнь

Наши Первая вице-Мисс и самый харизматичный Мистер Студенчества Гомель…
05 мая 2023

Другие новости

Мы тоже должны быть едины и сплочены, как эти братья……
Парад под окнами… Потапенко Василий Данилович…
Интерактивный квест по мемориалам г. Гомеля…

Горек хлебушек блокадный
Материалы V Международной научно-практической конференции «Научные и м…
Дорогами мира и созидания. Братская могила в деревне Огородня…
Дорогами мира и созидания. Братская могила в деревне Старые Дятловичи…
Дорогами мира и созидания. Братская могила по ул. Интендантская…
Звезда Победы
Дорогами мира и созидания. Братская могила в д. Юрковичи…
Стратегическая сессия «Молодежь союзного государства в условиях новых…

Достижения университета

Все факультеты

Все предложения

Все видео

Все фото

4.6

Средняя оценка: 4.6

Всего получено оценок: 68.

4.6

Средняя оценка: 4.6

Всего получено оценок: 68.

Одной из характеристик колебательного процесса в физике является фаза. Особенно важным этот параметр становится, когда сравниваются два колебания одинаковой частоты. Начальная фаза колебаний характеризует начало отклонения, когда система выводится из равновесия.

Любой колебательный процесс может быть представлен в виде бесконечной суммы простейших гармонических колебаний. Гармоническое колебание — это колебание, которое совершается по закону круговых функций (синуса или косинуса).

Рис.

1. График гармонической функции.

Формула гармонического колебания имеет следующий вид:

$$X = X_m sin(\omega t+\varphi)$$

где:

$t$ — текущий момент времени;
$X$ — текущее значение параметра;
$X_m$ — амплитудное (максимальное) значение параметра;
$\omega$ — частота;
$\varphi$ — начальная фаза.

Из представленной формулы можно увидеть, что при изменении значения времени $t$ аргумент круговой функции постоянно возрастает. Этот аргумент $(\omega t+\varphi)$ называется фазой. Единица измерения фазы — радиан, и поскольку круговая функция имеет период $2\pi$, то фаза, как правило, рассматривается только в диапазоне от нуля до $2\pi$.

Рис. 2. Фаза колебания.

Из формулы также видно, что фаза — это линейная функция от времени, которая монотонно возрастает от значения $\varphi$. Поэтому это значение называется начальной фазой.

Точка начальной фазы колебаний характеризует значение параметра функции в нулевой момент времени. Учитывая, что для того, чтобы система начала колебаться, она должна быть выведена из положения равновесия, начальная фаза колебаний характеризует именно это начальное отклонение, которое хорошо видно на графике функции.

Для нитяного или пружинного маятника зачастую начальная фаза колебаний также характеризует точку максимального отклонения.

Но наибольшее значение начальная фаза колебаний принимает для случая, когда происходит два и более колебательных процесса одинаковой частоты. При одинаковой частоте разность фаз колебаний в этих процессах будет постоянна. Следовательно, именно от начальной фазы зависит взаимное значение колебаний.

Например, если в обоих колебательных процессах, происходящих с равной частотой, начальные фазы будут равны, то нулевые и амплитудные значения обоих процессов будут всегда достигаться одновременно. Говорят, что процессы происходят синфазно.

Если начальная фаза в одном процессе будет равна нулю, а в другом — $\pi$, то в этом случае нулевые значения будут достигаться процессами одновременно, а вот амплитудные — нет.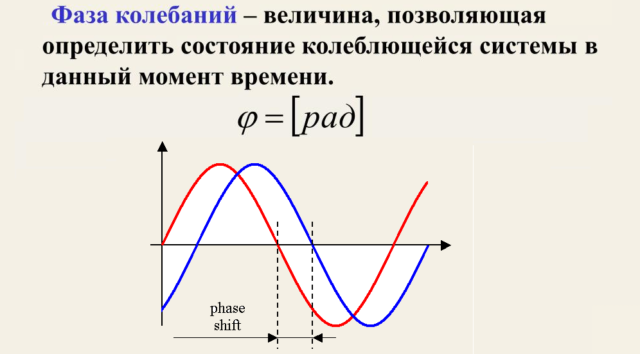

Более того, в момент, когда амплитуда одного процесса будет максимально положительной, амплитуда другого процесса будет максимально отрицательной. Говорят, что эти два процесса происходят в противофазе.

При других начальных фазах такие процессы будут меняться «с отставанием» или «с опережением», в зависимости от конкретных значений. И, поскольку их частота одинакова, то отставание или опережение будет постоянно. Нулевые и амплитудные значения никогда не будут достигнуты одновременно.

Рис. 3. Разность фаз колебаний.

Фаза колебания — это аргумент гармонической функции в ее формуле. Фактически это конкретный момент колебания. Начальная фаза — это аргумент в нулевой момент времени. Наибольшее значение начальная фаза колебаний играет при сравнении различных колебаний с одинаковой частотой.

Доска почёта

Чтобы попасть сюда – пройдите тест.

Пока никого нет. Будьте первым!

4.6

Средняя оценка: 4.6

Всего получено оценок: 68.

А какая ваша оценка?

11
Дата : 2023-05-11

26
Дата : 2023-05-26

30
Дата : 2023-05-30

Эти слова часто используются вместе. Нажмите на ссылки ниже, чтобы изучить значения. Или посмотрите другие словосочетания с фазой.

Эти примеры взяты из корпусов и источников в Интернете. Любые мнения в примерах не отражают мнение редакторов Кембриджского словаря, издательства Кембриджского университета или его лицензиаров.

Только начальный фаза дается для каждой части.

Из Кембриджского корпуса английского языка

Эти примеры взяты из корпусов и из источников в Интернете. Любые мнения в примерах не отражают мнение редакторов Кембриджского словаря, издательства Кембриджского университета или его лицензиаров.
Фазовый угол: определение, формула и символ
Знаете ли вы, что могут быть две точные волны, разница между которыми лишь в том, что одна из них смещена от определенной точки отсчета? Волна — это пространственный и временной процесс, в котором переносится энергия. Периодическая волна — это волна, которая повторяется в зависимости от положения и времени. Математически периодические волны используются для описания колебаний и простого гармонического движения, которое описывает движение систем пружины и массы. Этот тип волны описывается двумя характеристиками: величиной и фазой. В этой статье мы обсудим понятие фазового угла в периодической волне.
Фазовый угол
В предыдущих статьях мы обсуждали дифференциальное уравнение, описывающее колебательное движение, особенно простое гармоническое движение. Мы знаем, что решение, удовлетворяющее уравнению, выражается как
$$x=A\sin\left(\omega t+\phi_0\right).$$
Где $A$ – амплитуда в метрах $( \mathrm m)$, $\omega$ – угловая частота в радианах в секунду $(\frac{\mathrm{rad}}{\mathrm s})$, а $\phi_0$ – начальная фаза в радианах $(\mathrm{rad})$.
Фазовый угол — это угловая составляющая периодической волны, которая определяется как аргумент синусоидальной функции $\omega t+\phi_0$. Выбирая $\phi_0$, мы указываем начальную позицию колеблющегося объекта , чтобы убедиться, что у нас есть правильное уравнение с позицией осциллятора, независимо от того, где он мог быть расположен в точке $t=0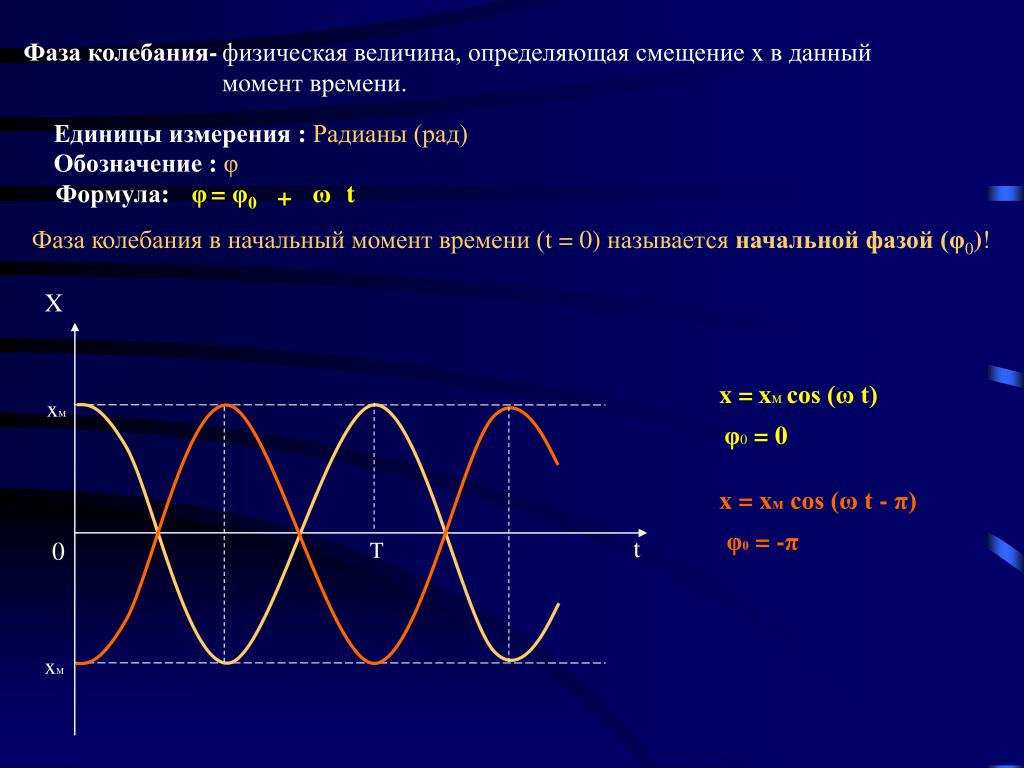$. Мы можем переформулировать приведенное выше уравнение в терминах символа $\phi$ для фазового угла.
$$\begin{align*}\phi&=\omega t+\phi_0,\\x&=A\sin\left(\phi\right).\end{align*}$$ 9{-1}\left(\frac{x_0}A\right),$$
где $A$ — амплитуда в метрах, $(\mathrm m)$ и $x_0$ — начальная положение объекта в точке $t=0$ в метрах $(\mathrm m)$.
Простой гармонический осциллятор имеет амплитуду $3,0\;\mathrm{см}$ и частоту $4,0\;\mathrm{Гц}$. В момент времени $t=0$ его положение равно $y=3.0\;\mathrm{см}$. Где он находится в момент времени $t=0.3\;\mathrm s$?
Амплитуда равна $A=0,03\;\mathrm м$, а угловая частота равна $\omega=2\pi f=2\pi(4,0\;\mathrm{Гц})=8\pi\ {\ textstyle \ frac {\ mathrm {rad}} {\ mathrm s}} $. Теперь мы можем определить начальную фазу, 9{-1}\left(\frac{0.03\;\mathrm m}{0.03\;\mathrm m}\right),\\\phi_0&=\frac\pi2.\end{align*}
Теперь мы знаем положение осциллятора в любой момент времени,
$$y(t)=0.03\sin\left(8\pi t+\frac\pi2\right). $$
Мы можем найти положение осциллятора во время $t=0,3\;\mathrm s$,
\begin{align*}y(0,3\;\mathrm s)&=(0,03\;\mathrm m)\sin\left((8\ пи \; {\ textstyle \ frac {\ mathrm {rad}} {\ mathrm s}}) (0,3 \; \ mathrm s) \; + \; \ frac \ pi2 \; \ mathrm {rad} \ right), \\y(0,3\;\mathrm с)&=0,0093\;m.\end{align*}
Положение осциллятора задается уравнением:
$$y=(0.04\;\mathrm m)\sin\left((6\pi\;{ \textstyle\frac{\mathrm{rad}}{\mathrm s}})t-\frac\pi2\;\mathrm{rad}\;\right).$$
Где находится осциллятор в момент времени $t =0$?
\begin{align*}y(0\;\mathrm s)&=(0,04\;\mathrm m)\sin\left((6\pi\;{\textstyle\frac{\mathrm{rad}} {\mathrm s}})(0\;\mathrm s)-\frac\pi2\;\mathrm{rad}\;\right),\\y(0\;\mathrm s)&=-0,04\; \mathrm m.\end{align*}
Начальная фаза определяет, используется ли функция синуса или косинуса для описания положения колеблющегося объекта. Например, если $\phi_0=\frac\pi2$ мы можем использовать функцию косинуса вместо функции синуса с начальной фазой. Это связано с тригонометрическим тождеством $\sin\left(\frac\pi2+\theta\right)=\cos\left(\theta\right)$. В приведенной ниже таблице поясняется, как два выражения дают одинаковые результаты в любое время.
Уравнение
$t=0$
$t=\frac\pi{2\omega}$
$\sin\left(\omega t+\;\frac\pi2 \right)$
1
$\cos\left(\omega t\right)$
1 9000 3
В качестве примечания: фазовый угол играет очень важную роль в экспериментальной физике, особенно в электронике, где существует прямая связь между напряжением и синусоидальными функциями. В электронике фазовый угол относится к угловому смещению между формами сигналов напряжения и тока в цепи переменного тока.
Понимание начальной фазы на графике
Мы рассмотрели теоретическое определение фазового угла и начальной фазы. Как мы понимаем влияние изменения начальной фазы синусоидальной функции? Легче понять, если мы на самом деле представляем синусоидальные функции на графике.
Рис. 1. Различные примеры начальных фаз для визуализации влияния регулировки начальной фазы на синусоидальную функцию.
На изображении выше мы видим, что при начальном значении $x=0$, $f(0)=\sin\left(0\right)=0$. Для той же синусоидальной функции с начальной фазой $\phi_0=\frac{-\pi}4$, $f(0)=\sin\left(0-\frac\pi4\right)=-\frac {\sqrt2}2$ и $f(\frac\pi4)=\sin\left(\frac\pi4-\frac\pi4\right)=0$. Мы замечаем, что функция синуса сместилась по горизонтали вправо на величину $\frac\pi4$. Если мы изменим начальную фазу на $\phi_0=-\pi$, мы заметим, что функция синуса сдвинется вправо на величину $\pi$. Здесь мы замечаем закономерность: отрицательная начальная фаза сдвинет функцию по горизонтали вправо, а положительная начальная фаза сдвинет функцию по горизонтали влево. Наглядно это представлено на рисунке ниже.
Рис. 2 – Синусоидальная функция: случай, когда начальная фаза равна нулю.
Рис. 3 – Влияние положительной начальной фазы на синусоидальную функцию.