Начальная скорость физика формула: Какие существуют кинематические формулы? (статья) - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Урок 3. равноускоренное движение материальной точки – Физика – 10 класс

Физика, 10 класс

Урок 3.Равноускоренное движение материальной точки

Перечень вопросов, рассматриваемых на уроке:

1) изучение равноускоренного движения;

2) изучение понятий мгновенной скорости, ускорения и скорости равноускоренного движения;

3) вывод формул скорости и пути равноускоренного движения;

4) построения графиков координат и пути равноускоренного движения.

Глоссарий по теме

Неравномерное движение – если тело за одинаковые промежутки времени проходит разные расстояния – то такое движение называется неравномерным.

Скорость – это векторная величина равная отношению пути, пройденного телом за некоторый период времени, к величине этого периода времени.

Средняя скорость при неравномерном движении – отношение вектора перемещения тела к промежутку времени, за который это перемещение произошло.

Мгновенная скорость – это векторная физическая величина, численно равная пределу, к которому стремится средняя скорость за бесконечно малый промежуток времени:

Ускорение – это физическая величина, численно равная изменению скорости за единицу времени. Равноускоренное движение – скорость тела за равные промежутки времени изменяется одинаково, то есть движется с постоянным ускорением.

Основная и дополнительная литература по теме урока:

Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н.. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 31-54

1.Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н.. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 40 – 41

Открытые электронные ресурсы:

2. http://kvant.mccme.ru/1983/10/p33.htm

Основное содержание урока.

Неравномерное движение тел может быть не только прямолинейным, но и криволинейным.

Полное описание неравномерного движения тела, возможно при знании его положения и скорости в каждый момент времени. Скорость точки в данный момент времени называется мгновенной скоростью ()

Любая точка в движении при определённой скорости перемещается из начального положения в конечное. Эту скорость называют средней скоростью перемещения точки.

Определяется по формуле:

Кроме мгновенной и средней скоростей перемещения для описания движения чаще пользуются средней путевой скоростью.

Эта средняя скорость определяется отношением пути к промежутку времени, за которое этот путь пройден:

Скорости тел при движении меняются по модулю, по направлению или же одновременно как по модулю, так и по направлению.

Изменения скорости теле могут происходить как быстро, так и медленно.

Ускорением тела называется предел отношения изменения скорости к промежутку

Времени ∆t, в течении которого это изменение призошло, при стремлении ∆t к нулю.

Ускорение обозначается буквой .

Определяется по формуле:

Единица ускорения – м/с²

Выясним зависимости точки от времени при её движении с постоянным ускорением. Для этого воспользуемся формулой:

Пусть _о– скорость точки в начальный момент времени t_o, а – в некоторый момент времени t, тогда:

∆t = t_o,

и формула для ускорения примет вид:

Если начальный момент времени _{принять равным нулю, то получим:}

Отсюда получим формулу для определения скорости точки в любой момент времени при её движении с постоянным ускорением:

Вектору уравнению соответствуют в случае движения на плоскости два скалярных уравнения для проекций скорости на координатные оси X и Y:

𝑣_х= 𝑣_ох + 𝒂_хt;

𝑣_у = 𝑣_оу = 𝒂_уt.

Мы научились, таким образом, находить скорость материальной точки при движении с постоянным ускорением.

Теперь получим уравнения, которые позволяют рассчитывать для этого движения положение точки в любой момент времени.

Допустим, движение с постоянным ускорением совершается в одной плоскости, пусть это будет плоскость XOY. Если вектор начальной скорости и вектор ускорения не лежат на одной прямой, то точка будет двигаться по кривой линии. Следовательно, в этом случае с течением времени будут изменяться обе ее координаты

х и у. Обозначим через х_ои у_окоординаты в начальный момент времени t_о = 0, а через х и у координаты времени.

Тогда за время ∆t = t – t_o= t изменения координат будут равны

∆х = х – х_ои ∆у = у – у_о

Отсюда:

х = х_о + ∆х,

у = у_о + ∆у

График зависимости v(t)

По формуле для площади трапеции имеем:

Учитывая, что 𝑣ₓ = 𝑣ₒₓ + 𝒂ₓt, получаем формулу:

В обычных условиях задачи даются значения (модули) скоростей и ускорений:

При движении точки в плоскости ХОY двум уравнениям соответствует одно векторное уравнение:

Разбор тренировочных заданий

1. Куда движутся тела и как изменяются их скорости, векторы начальных скоростей и ускорений которых показаны на рисунке 1?

Направление движения определяем по направлению скорости, изменение скорости – по направлению ускорения и скорости.

Решение:

Тело 1 движется вправо; направления ускорения и скорости совпадают, следовательно, скорость его увеличивается.

Тело 2 движется вправо; ускорение направлено в противоположную сторону скорости, следовательно, скорость его уменьшается.

Тело 3 движется влево; направления ускорения и скорости совпадают, следовательно, скорость его увеличивается.

Тело 4 движется влево; ускорение направлено в противоположную сторону скорости, следовательно, скорость его уменьшается.

2. Электропоезд тормозит с ускорением 0,40 м/с². Определите, за какое время он остановится, если тормозной путь равен 50 м.

Решение:

При прямолинейном движении путь электропоезда равен перемещению s = ∆r.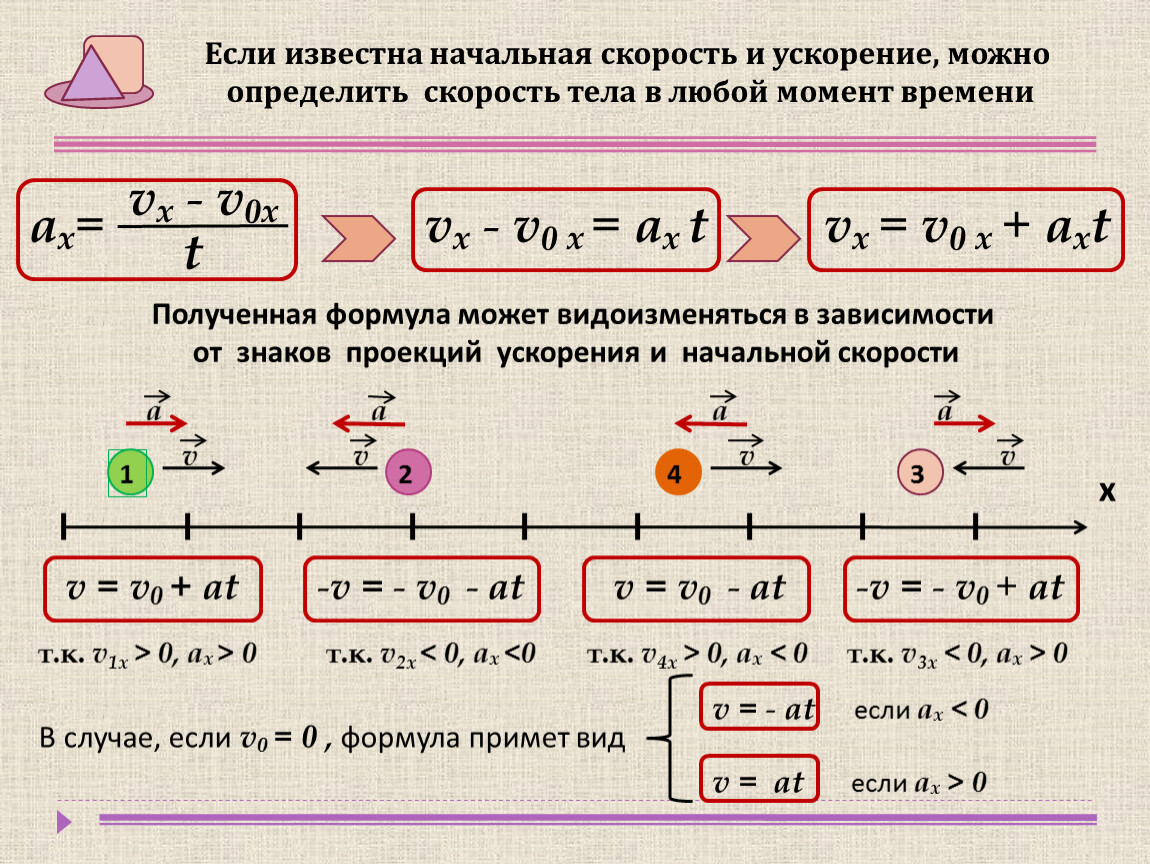

Тогда:

Ответ: t ≈ 16 c.

Движение тела, брошенного вертикально вверх и вниз

Если некоторое тело будет свободно падать на Землю, то при этом оно будет совершать равноускоренное движение, причем скорость будет возрастать постоянно, так как вектор скорости и вектор ускорения свободного падения будут сонаправлены между собой.

Если же подбросить некоторое тело вертикально вверх и при этом считать, что сопротивление воздуха отсутствует, то можно считать, что оно тоже совершает равноускоренное движение с ускорением свободного падения, которое вызвано силой тяжести. Только в этом случае скорость, которую мы придали телу при броске, будет направлена вверх, а ускорение свободного падения направлено вниз, то есть они будут противоположно направлены друг к другу. Поэтому скорость будет постепенно уменьшаться.

Через некоторое время наступит момент, когда скорость станет равняться нулю. В этот момент тело достигнет своей максимальной высоты и на какой-то момент остановится. 2}2.\) Из последней формулы можно найти время падения тела с высоты h: $t = \sqrt{\frac{2h}g} .$ Подставляя найденное время в формулу для скорости, получим модуль скорости тела в момент падения: $υ= \sqrt{2gh}.$

Если тело подбросить, то оно сначала движется равнозамедленно вверх, достигает максимальной высоты, а затем движется равноускоренно вниз. Учитывая, что при $y = h_{max}$ скорость $υ_y = 0$ и в момент достижения телом первоначального положения $y = 0$, можно найти

$t_1=υ_0\cdot g $ – время подъема тела на максимальную высоту;

$h_{max}$ – максимальная высота подъема тела;

$t_2=2t_1=\frac{2υ_0}g $ – время полета тела;

$v_{2y}=-v_0$ – проекция скорости в момент достижения телом первоначального положения.

Скорость при прямолинейном равноускоренном движении тела

Цели урока:

обучающая: повторить понятия равноускоренного движения, ускорения; научить учащихся определять проекцию вектора мгновенной скорости, которую будет иметь тело к концу любого заданного промежутка времени, сформировать навыки построения графика скорости и его анализа.

развивающая: развитие умения наблюдать и анализировать конкретные ситуации; выделять определенные признаки; рассмотрение свойств объектов на основе анализа количественных и качественных характеристик.

воспитывающая: воспитание дисциплины и норм поведения, творческого отношения к изучаемому предмету; стимулирование активности учащихся.

Методы:

словесный — беседа;

наглядный — видеоурок, записи на доске;

контролирующий — тестирование или устный опрос, решение задач.

Связи:

межпредметные: математика — линейная зависимость, график линейной функции;

внутрипредметные: равноускоренное движение, ускорение.

Ход урока:

1. Организационный этап.

Добрый день. Прежде чем мы приступим к уроку, хотелось бы, чтобы каждый из вас настроился на рабочий лад.

2. Актуализация знаний.

На прошлом уроке, мы с вами рассмотрели такой вид движения, при котором тело, за любые равные промежутки времени совершает разные перемещения. Как мы назвали такое движение? {неравномерное}

Какое движение мы назвали ускоренным? {это когда скорость тела увеличивается с течением времени}

А замедленным? {когда скорость тела уменьшается с течением времени}.

Ответьте на вопрос, а что такое средняя скорость? {Средняя скорость показывает, чему равно перемещение, которое тело в среднем совершает за единицу времени}

А всегда ли мы можем пользоваться понятием средней скорости при решении задач? Приведите примеры.

Как мы с вами назвали скорость тела в данный момент времени или в данной точке траектории? {мгновенной скоростью}

Как направлена мгновенная скорость? {Она направлена по касательной к траектории в каждой её точке в сторону перемещения}

Что является основной характеристикой неравномерного движения?

{Ускорение — физическая векторная величина, характеризующая быстроту изменения скорости и численно равная отношению изменения скорости тела к промежутку времени, в течение которого это изменение произошло}.

Откройте тетради и запишите число и тему нашего урока: Скорость тела при равноускоренном движении тела.

3. Объяснение нового материала.

Скачать видеоурок Скорость при прямолинейном равноускоренном движении тела

Нам известно, что при прямолинейном равноускоренном движении ускорение тела можно рассчитать по формуле;

Выразим из этой формулы скорость, которую могло бы иметь тело в конце промежутка времени Δt.

Получим

Или

Мы получили формулу, которая называется уравнением скорости при равноускоренном движении.

Напомним, что по формулам, записанным в векторном виде, вычисления вести нельзя.

Перепишем нашу формулу в проекции на ось х.

Таким образом, зная проекцию вектора начальной скорости и проекцию вектора ускорения, можно вычислить проекцию вектора мгновенной скорости, которую будет иметь тело к концу любого заданного промежутка времени.

Представим зависимость проекции вектора скорости от времени при равноускоренном движении в виде графика.

Из курса математики вам известна линейная функция

у = kx + b,

где х — аргумент, k — постоянный коэффициент, b — свободный член. Графиком этой функции является прямая линия.

Функция

υ_x = υ_0x + a_xΔt

тоже линейная с аргументом Δt, постоянным коэффициентом а_хи свободным членом υ_0х. Значит, графиком этой функции тоже должна быть прямая линия. Расположение этой линии по отношению к осям координат определяется значениями проекции начальной скорости и ускорения.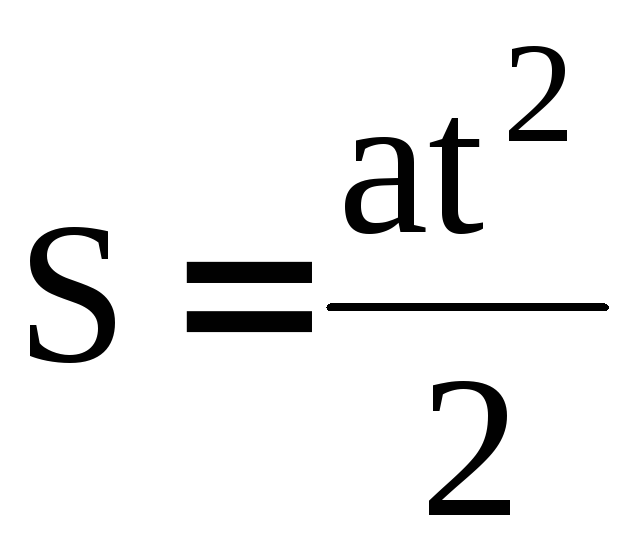

Рассмотрим, какой вид будет иметь график скорости в зависимости от знаков проекций ускорения и начальной скорости.

Если проекция вектора скорости тела и его ускорение направлены по оси Ох, то уравнение примет вид

В этом случае скорость тела с течением времени возрастает. При этом график скорости образует с положительным направлением оси t острый угол.

Если же проекция вектора скорости тела и его ускорение направлены против оси Ох, то уравнение примет вид

Скорость тела с течением времени возрастает, но тело, при этом, движется в отрицательном направлении. График скорости образует с положительным направлением оси t тупой угол.

В случае, если скорость тела направлена по оси Ох, а ускорение — против оси Ох, то формула принимает вид

Скорость тела убывает от некоторого значения до нуля. График скорости образует с положительным направлением оси t тупой угол.

Когда ускорение направлено по оси х, а начальная скорость против оси х, то формула принимает вид:

скорость тела с течением времени возрастает. Но при этом график скорости образует с положительным направлением оси t тупой угол.

Если в начальный момент времени тело покоилось, то уравнение примет вид

если проекция вектора ускорения направлена по оси Ох, то скорость тела возрастает и график скорости, в этом случае, образует с положительным направлением оси t острый угол и начинается в точке (0;0).

Или

если проекция вектора ускорения направлена против оси х. Скорость тела возрастает, но при этом тело движется в отрицательном направлении, но так же начинается в точке (0;0).

И последнее, если проекции начальной скорости и ускорения равны нулю, то тело с течением времени не изменяет своего положения и графиком скорости является прямая, совпадающая с осью времени (тело покоится).

4. Этап обобщения и закрепления нового материала

Подведем основные итоги:

Ø Зная проекцию вектора начальной скорости и проекцию вектора ускорения, можно вычислить проекцию вектора мгновенной скорости, которую будет иметь тело к концу любого заданного промежутка времени, по формуле:

Ø Зависимость проекции вектора скорости от времени при равноускоренном движении есть линейная функция, графиком которой является прямая линия.

Ø Расположение этой линии по отношению к осям координат определяется значениями проекции начальной скорости и ускорения.

5. Рефлексия

Хотелось бы услышать ваши отзывы о сегодняшнем уроке: что вам понравилось, что не понравилось, чем бы хотелось узнать еще.

Равномерное прямолинейное движение | ЮКлэва

Всё в мире находится в движении.

Каждый день, когда мы выходим из дома, мы стараемся рассчитать, насколько быстро доберемся до школы или работы.

Может, однажды мы захотим научиться чему-то новому и купим машину.

А физика объяснит тебе, как не попасть в аварию и как всюду успевать.

Приступим!

СодержаниеО том, как решить основную задачу механикиРавномерное прямолинейное движениеОпределение равномерного прямолинейного движенияСкоростьРешение основной задачи механики для равномерного прямолинейного движенияГрафики равномерного прямолинейного движенияПостроение графикаЗависимость графика от проекции скоростиВстречаГрафик зависимости проекции скорости от времени. Нахождение проекции перемещенияРешение простейших задач и задач на графики равномерного прямолинейного движенияТекстовые задачиЗадачи на графикиСредняя скорость по перемещению. Средняя путевая скоростьОтносительность движения. Операции над скоростямиРешение задач на среднюю скорость и действия со скоростямиЗадачи в плоскостиКраткое содержание, основные формулы и определенияЗаключение

О том, как решить основную задачу механики

Мы помним, что основная задача механики – указать положение тела в пространстве в любой момент времени, не только в настоящем, но и в будущем.

Мы узнали это, когда только начали изучать кинематику.

Итак, что нужно знать для того, чтобы найти положение тела в пространстве?

Неплохо было бы знать, где оно находилось в начале своего движения, его начальные координаты. Ведь нам важно, откуда мы выдвигаемся в путь.

Зависят ли начальные координаты тела от времени? Совсем нет: мы просто принимаем то, что тело где-то есть.

А еще нам важно знать, как далеко оказалось тело от своего начального положения и куда вообще двигалось. Важно знать перемещение этого тела.

Давай опробуем свои силы! Думаю, мы уже готовы решить главную задачу!

Рассмотрим какое-то тело. Оно подвигалось, изменило свое положение, оказалось в другой точке.

Назовем ее конечной и постараемся найти ее координаты, то есть узнать положение тела после совершенного им перемещения.

Помним, что перемещение – вектор, поэтому изобразим его:

Уже сейчас мы можем указать начальные координаты тела! Нет чисел – не пугаемся, используем буквы:

Нам нужно узнать конечное положение тела. Отметим координаты тела в конце, их нам и нужно найти, чтобы определить положение тела в конце:

Но как найти эти координаты, зная лишь начальное положение тела и его перемещение? Как нам попасть из ${{x}_{0}}$ в $x$ и из ${{y}_{0}}$ в $y$ ?

Все очень просто! Если есть вектор, то какая-нибудь проекция-то найдется, правда? Отметим их:

Теперь ответить на вопрос, как добраться из начала в конец становится очень легким: просто нужно прибавить к начальной точке проекцию перемещения для нужной оси!

То есть положение точки в любой момент времени можно записать так:

$x={{x}_{0}}+{{S}_{x}}$ — для оси Х

$y={{y}_{0}}+{{S}_{y}}$ — для оси Y

Поздравляю! Мы только что решили основную задачу механики!

Правда, сделали это в общем виде… Но перемещение ведь может быть очень разнообразным! Как вообще его найти? Не всегда же оно будет дано!

Это зависит от движения тела.

Равномерное прямолинейное движение

Определение равномерного прямолинейного движения

Самым простым движением по праву считается равномерное прямолинейное движение. Мы начнем с него.

Давай попробуем дать ему определение.

Всегда стоить помнить, что знать определения наизусть вовсе не обязательно. Главное – научиться строить его самостоятельно.

Успех любого хорошего определения заключается в правильной его структуре.

Равномерное прямолинейное движение – это движение. Мы нашли главное слово нашего определения. Давай развивать его.

Мы уже знаем, что такое движение. Давай дополним это определение.

Что значит равномерное? Равная мера… Но что является этой самой равной мерой?

Тело проходит равные пути. Логично, что происходит это за какие-то промежутки времени.

А за какие промежутки? За равные. За секунду, за минуту, за час. Не обязательно за ОДНУ секунду, ОДНУ минуту, ОДИН час. Равными промежутками времени могут быть, например, три часа или две секунды.

Но что значит прямолинейное? Можно сказать, что это движение по прямой. Но давайте объясним это, исходя из уже знакомых нам понятий.

Представь: какое-то тело движется, у нас в руках секундомер.

Прошла секунда – тело переместилось на метр. Еще секунда – еще метр. В том же направлении.

То есть тело совершает равные перемещения!

Поэтому…

Равномерное прямолинейное движение — такое движение, при котором тело за любые равные промежутки времени совершает равные перемещения.

С перемещением намного проще объяснить, почему за равные промежутки времени можно принимать абсолютно любое количество единиц времени.

Пусть тело совершает за 1 секунду перемещение $vec{S}$.

Тогда за две секунды совершает перемещение $2vec{S}$:

Будет ли тело все еще совершать равные перемещения за каждые 2 секунды? Конечно! Давай посмотрим:

Скорость

Равномерное прямолинейное движение тоже бывает разным: быстрым и медленным.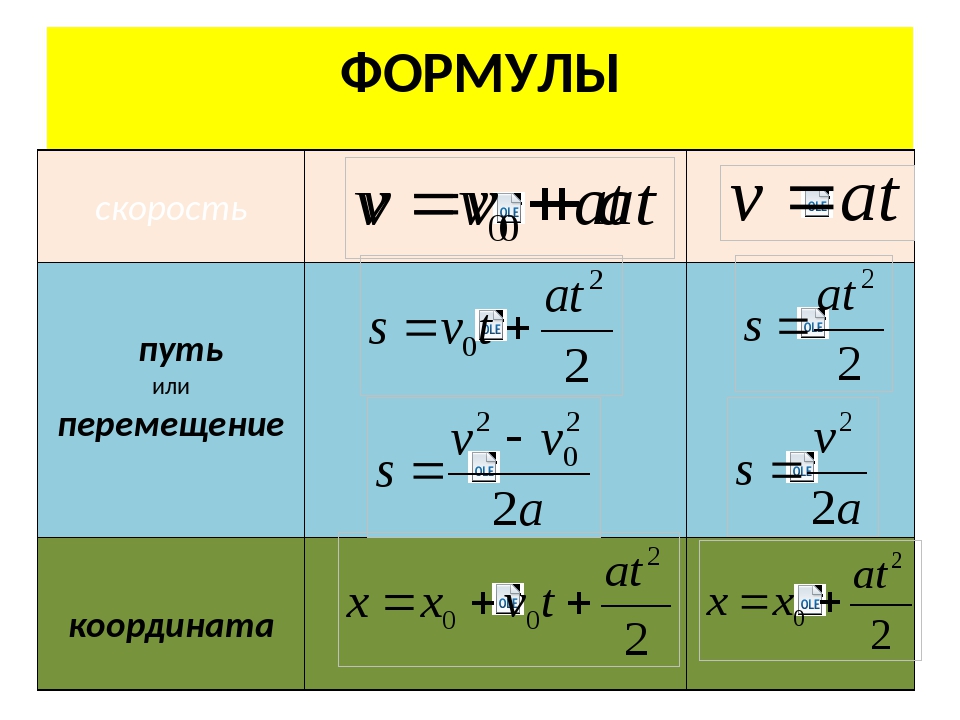 Чтобы охарактеризовать его, существует скорость.

Чем большее перемещение совершает тело за промежуток времени, тем больше его скорость. Это очевидно: за одно и то же время гепард преодолевает расстояние во много раз большее, чем термит.

То есть скорость прямо пропорциональна перемещению!

А еще мы помним, что нам действительно важно направление скорости, ведь нам важно направление движения. То есть скорость – величина векторная. Давай убедимся в этом.

Скорость равномерного прямолинейного движения есть физическая величина, равная отношению вектора перемещения ко времени, за которое оно произошло.

Запишем это в виде формулы:

$vec{V}=frac{{vec{S}}}{t}$

Векторы с обеих сторон, верно, но… Мы ведь учились умножать векторы, а не делить их. При делении тоже вектор получается?

Да. Ведь любое деление можно представить в виде умножения, смотри:

$vec{V}=frac{1}{t}cdot vec{S}$

Время – скалярная величина. Оно не имеет направления. Поэтому можно сказать, что скорость есть перемещение, умноженное на скаляр, то есть тоже вектор! Более того, вектор перемещения и скорости сонаправлены.

Подробнее о свойствах векторов можно прочитать в Большой теории по векторам.

Помнишь, мы чуть выше выясняли, будет ли тело все так же совершать одинаковые перемещения за 2 секунды, а не за одну? Причем эти перемещения сами будут в два раза больше. Значит отношение останется прежним, вот так:

$vec{V}=frac{2vec{S}}{2t}=frac{{vec{S}}}{t}$

Отсюда делаем вывод:

Скорость равномерного прямолинейного движения постоянна.

Как это записать? Кажется, очевидно, но это «задачка со звездочкой». Вот так:

$vec{V}=overrightarrow{const}$

Мы не можем приравнять векторную величину к скалярной. Поэтому над константой тоже нужно ставить вектор.

Решение основной задачи механики для равномерного прямолинейного движения

Из уравнения скорости можно легко выразить перемещения, что сделает нас на шаг ближе к конкретному решению основной задачи.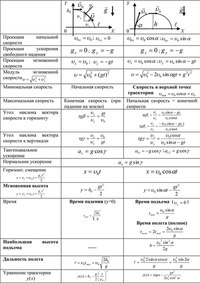 Давай сделаем это:

$vec{S}=vec{V}cdot t$

Из свойств векторов мы помним, что это будет справедливо и для проекций:

${{S}_{x}}={{V}_{x}}cdot t$

${{S}_{y}}={{V}_{y}}cdot t$

Стоп-стоп-стоп… Мы что, можем уже с помощью этого определить положение точки?

Да, почему нет? Просто подставим это вместо проекций перемещения туда, где мы решали основную задачу механики в общем виде:

$x={{x}_{0}}+{{V}_{x}}cdot t$

$y={{y}_{0}}+{{V}_{y}}cdot t$

Обычно в задачах по физике мы стараемся выбрать оси так, чтобы было проще работать с проекциями. Мы стараемся расположить их так, чтобы как можно больше векторов располагалось параллельно один осям и перпендикулярно другим, вот так:

Проекция перемещения на ось Y будет равняться нулю, мы можем не обращать на нее внимания.

По оси Y тело вообще не меняло своего положения, верно?

Именно поэтому в задачах чаще всего мы будем использовать упрощенный вариант нахождения конечного положения тела. Его координата будет описана лишь одним числом.

То есть используем лишь одну ось:

$x={{x}_{0}}+{{V}_{x}}cdot t$

Работаем с проекциями. Настораживаемся. Вспоминаем о знаках.

Здесь все просто: если проекция скорости положительна, тело движется вдоль оси. Если она отрицательна, тело движется против оси.

Помни, что работаем мы с координатной осью! Начальное положение тела тоже может быть отрицательным. Это зависит лишь от того, как расположено тело относительно начала координат:

Графики равномерного прямолинейного движения

Построение графика

Очень важно уметь описывать движение графиком. Это может значительно упростить решение задачи.

Давай посмотрим, как с помощью графика описать равномерное прямолинейное движение.

Любой график – множество точек, который показывает зависимость одного значения от другого. Эта зависимость определяется каким-то уравнением.

Например, когда мы строим параболу, мы руководствуемся уравнением $y={{x}^{2}}$. {2}}\). Это показывает, что функция $f$ зависит от значения $x$.

Давай аналогично составим график движения тела. Вспомним то главное уравнение:

$x={{x}_{0}}+{{V}_{x}}cdot t$

Иными словами, это график зависимости координаты тела от времени. Давай так и запишем:

$x(t)={{x}_{0}}+{{V}_{x}}cdot t$

Начинаем работать с уравнением. Предположим, что нам известна проекция скорости и начальное положение тела. Работать с конкретными числами удобнее.

Пусть: ${{V}_{x}}=0.5$м/с и ${{x}_{0}}=3$м

Тогда уравнение имеет вид: $x=3+0.5cdot t$

Нарисуем оси и обозначим их. Так как у нас даны единицы измерения (метры и секунды), мы обязательно должны подписать их рядом с названиями осей!

Теперь можем взять и рассмотреть положение тела в любую секунду: хоть в первую, хоть в двенадцатую!

Отметим точки и соединим их. Получим график движения.

А теперь вопрос на засыпку: может ли время быть отрицательным?

Могу ли я указать положение тела в минус третью секунду? Могу.

Для этого стоит помнить, что «нулевая» секунда – момент, когда мы запускаем секундомер, когда мы только начинаем наблюдать за телом. Но оно могло двигаться и до того, как мы включили таймер, верно?

Давай покажем движение тела до наших наблюдений пунктирной линией:

Зачастую точки пересечения графика с осями несут в себе очень важную информацию!

Например, когда мы только включили секундомер ($t=0$с), тело находилось в начальном положении (${{x}_{0}}=3$м), и это видно по графику!

А когда координата тела была равна нулю?

Все очень просто: за 6 секунд до того, как мы включили секундомер! Прямая пересекает ось времени в точке -6.

Итак, мы выяснили, что…

График равномерного прямолинейного движения представляет собой прямую.

Точка пересечения ее с осью Х есть координата в начальный момент времени.

Точка пересечения с осью времени показывает ту секунду, когда тело находится в начале координат.

И действительно, само уравнение $x={{x}_{0}}+{{V}_{x}}cdot t$ уже напоминает стандартное уравнение прямой, которое мы изучаем на математике: $y=kx+m$, где $m$ — точка пресечения графика с осью Х, а $k$ — коэффициент наклона прямой.

В нашем случае роль коэффициента наклона играет проекция скорости.

Зависимость графика от проекции скорости

Давай изобразим несколько графиков в общем виде, то есть без каких-либо конкретных значений. Например, пусть у нас есть два движущихся тела, вот так:

Чем отличаются движения этих двух тел?

Ну, прежде всего, у них разные начальные положения. Ладно.

А что насчет проекции скорости?

Рассмотрим первое тело. С течением времени оно все больше удаляется от начала координат. А вот второе к нему приближается: оно даже достигает начала координат через некоторое время (когда пересекает ось).

Значит, первое тело идет вдоль оси, а второе против нее, то есть к началу! Мы помним, что это определяет знак проекции скорости.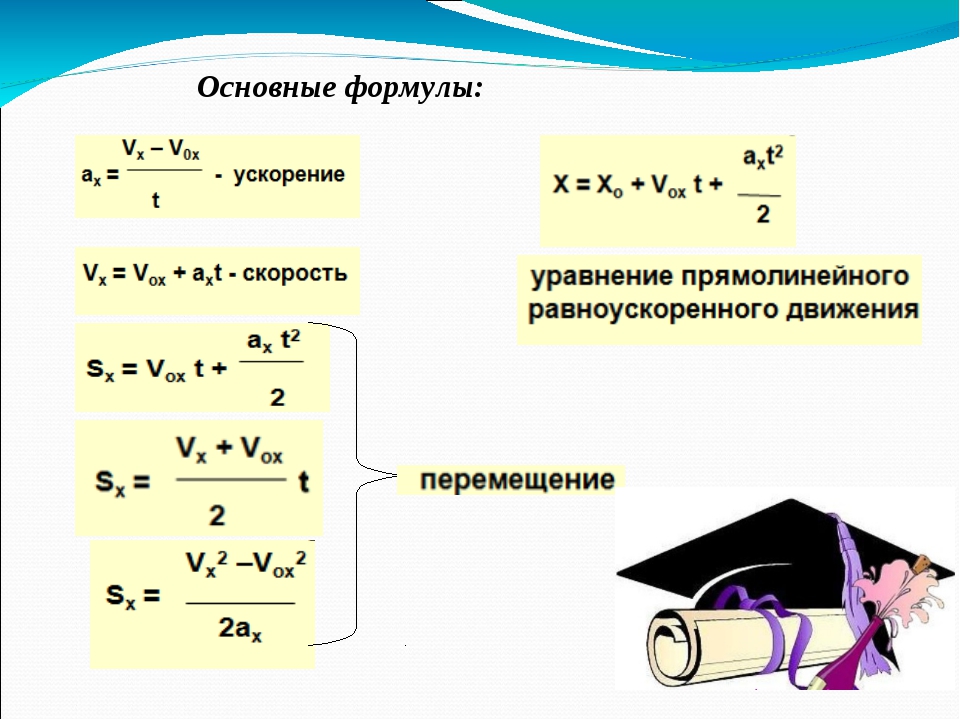

А именно: проекция скорости первого тела положительна. Проекция скорости второго тела отрицательна.

Со знаками разобрались. А как быть, если попросят узнать, какая проекция скорости больше?

Рассмотрим следующий график. Чтобы было легче его анализировать, представим, что два тела имеют одинаковое положение, когда мы включаем секундомер:

Чтобы понять, чья скорость больше, рассмотрим определенный промежуток времени, отделим его вертикальной пунктирной линией. А еще обозначим начальную и конечную координаты тел в этот промежуток времени:

Теперь посмотрим, чем отличаются графики. Ну так, навскидку. Они отличаются наклоном.

График движения второго тела расположен к оси Х значительно ближе. Что это значит?

Рассмотрим, какое расстояние прошло первое тело, обозначим его на рисунке. Оно численно равно проекции перемещения, убедимся с помощью формулы:

$Delta {{x}_{1}}={{x}_{1}}-{{x}_{01}}={{S}_{x}}_{1}$

Теперь рассмотрим расстояние, которое преодолело второе тело:

$Delta {{x}_{2}}={{x}_{2}}-{{x}_{02}}={{S}_{x}}_{2}$

Видим, что за одинаковый промежуток времени второе тело прошло значительно большее расстояние! Это значит, что его скорость больше.

Чем ближе к оси Х расположена прямая, тем больше скорость движения тела.

А что будешь делать с таким графиком?

Координата тела с течением времени не меняется. Значит ли это, что тело не движется вовсе?

Нет. Тело не движется лишь по этой оси. Но по какой-нибудь другой оси оно двигаться может. Например, вот так:

Тело не меняет координаты по оси Х, однако движется по оси Y.

Если мы видим такой график, мы можем лишь утверждать, что проекция скорости равна нулю. О самой скорости говорить не можем.

Встреча

Помнишь самый первый рисунок с двумя телами? Вот этот:

В нем есть одна интересная деталь. Графики движения тел пересекаются.

Со временем все понятно: оно для всех идет одинаково, ничего не поделаешь.

А вот с координатой интереснее: ведь мы можем утверждать, что в какой-то момент тела встретились. То есть в какой-то момент их координаты на оси Х стали равны. Обозначим момент встречи и координату («место») встречи:

Встреча – такое событие, при котором координаты тел в один и тот же момент времени совпадают.

Это еще один момент, о котором стоит помнить при решении задач на графики.

А еще стоит обратить внимание на то, что координаты тел должны совпадать в один момент времени! Если в лесу мимо дуба пробежала лань, а через несколько дней мимо этого же дуба пробежал енот, мы не можем сказать, что они встретились. Просто у них совпала траектория.

График зависимости проекции скорости от времени. Нахождение проекции перемещения

Рассмотрим несколько другой график. График зависимости проекции скорости от времени при равномерном прямоли… Стоп, чего? Какой зависимости? Скорость ведь постоянная и не меняется со временем.

Ты абсолютно прав. А график-то начертить можем, вот так:

Скучный график. Просто прямая, параллельная оси времени. Проекция скорости не меняется, а время всё идет и идет.

Давай хоть что-то найдем по графику. Хоть площадь под ним. Обозначим эту область:

Получили прямоугольник. Его площадь ищем путем перемножения двух соседних сторон, то есть мы берем проекцию скорости и умножаем еще на время.

Где-то мы это слышали.

Верно, ведь именно так ищется проекция перемещения!

${{S}_{x}}={{V}_{x}}cdot t$

Совпадение? Не думаю.

Искать проекцию перемещения таким способом можно не только для равномерного прямолинейного движения, но и для других его видов!

Проекция перемещения тела численно равна площади под графиком скорости тела.

Решение простейших задач и задач на графики равномерного прямолинейного движения

Текстовые задачи

Задача 1. Охарактеризуйте движение соседки, которая спускается по лестнице и одновременно с этим закатывает рукава, услышав в 11 часов вечера громкую музыку из квартиры снизу, если уравнение ее движения: $x=2cdot t$, а ось направлена вниз по лестнице.

Решение:

Итак, для начала вспомним уравнение движения в общем виде:

$x={{x}_{0}}+{{S}_{x}}$

Соответствует ли уравнение движения соседки уравнению выше? Конечно!

Почему? По глазам вижу, догадываешься! Потому что его можно записать так:

$x=0+2cdot t$

Начальная координата соседки равна нулю: соседка двигалась из начала координат. С этим разобрались. Осталось определить тип ее движения.

Она движется вниз по лестнице. Значит, идет по прямой в одном направлении. Это прямолинейное движение.

Она свирепеет и ускоряется? Нет. Она движется равномерно. Давай вспомним уравнение движения для равномерного прямолинейного движения:

$x={{x}_{0}}+{{V}_{x}}cdot t$

И еще раз посмотрим на наше:

$x=0+2cdot t$

Сопоставляем их и понимаем, что рядом с временем расположена проекция скорости. Она, как видим, положительна и равна 2 м/с. Соседка двигается вдоль оси. Ось направлена вниз и соседка движется туда же!

Подробно мы разбирали зависимость направления от знака проекции в Большой теории по векторам.

Таким образом, соседка совершает равномерное прямолинейное движение вдоль оси из начала координат, а проекция ее скорости на эту ось равняется 2 м/с.

Задача 2. Таракан Вася совершает равномерное прямолинейное движение вдоль линейки (соответствующей оси Х) на столе семиклассника Вовы, который, старательно уча уроки, уже неделю не выносит из комнаты мусор. Проекция скорости таракана на эту ось 0.1 м/с. Вова берет секундомер и начинает отсчет в тот момент, когда таракан находится на втором сантиметре линейки. На каком сантиметре линейки окажется таракан через две секунды?

Решение:

Первое правило решающих физику: увидеть тему и писать формулы по теме.

Второе правило решающих физику: увидеть тему и писать ВСЕ формулы по теме. Могут пригодиться.

Знаем тип движения! Равномерное прямолинейное!

Знаем уравнение равномерного прямолинейного движения! Пишем:

$x={{x}_{0}}+{{V}_{x}}cdot t$

Делов-то! Начнем подставлять известные величины для таракана. Из задачи знаем, что в начале отсчета таракан находится на втором сантиметре линейки…

Стоп. «Сантиметре…»

Никогда не теряй бдительность, боец. Всегда проверяй величины.

Переведем все, что есть, в СИ. Скорость – в м/с. Отлично, уже есть. Как быть с линейкой? Просто перевести сантиметры в метры!

Таракан был на втором сантиметре, а значит на 0. 02 метре линейки!

Теперь можем записать уравнение его движения:

$x=0.02+0.1cdot t$

Чтобы узнать, где окажется таракан через 2 секунды, просто подставим цифру 2 в это уравнение:

$x=0.02+0.1cdot 2=0.22$м

На 0.22 метре линейки! Получили ответ. Но в задаче спрашивается, на каком сантиметре будет находится таракан. Переводим наш ответ в сантиметры и получаем, что таракан будет находится на 22-ом сантиметре линейки!

Задача 3. По коридору мчится восьмиклассник Петя, уравнение его движения можно описать следующим уравнением: $x=6+2cdot t$. За ним несётся разъяренный директор Максим Михайлович, уравнение его движения: $x=3+3cdot t$. Догонит ли директор Петю и, если догонит, когда и на каком метре коридора это произойдет? Скорость измерять в м/с, время в секундах.

Решение:

Итак, давай разберемся. Что вообще значит «догонит»? То же самое, что «встретит», верно?

Мы знаем, что такое встреча. Это такое событие, при котором координаты тел в один и тот же момент времени совпадают.

Чтобы понять, встретятся ли они вообще, давай построим графики движения Пети (П) и директора (Д):

Видим, что прямые пересекаются. В какой-то момент времени их координаты действительно одинаковы.

Но как узнать, в какой?

Что-что? Видно по графику? Ну уж нет! Думаешь, там координата 12? А вдруг там 11.999?

Всегда нужно проверять себя аналитически.

Запишем два уравнения:

${{x}_{P}}=6+2cdot t$ — Пети

${{x}_{D}}=3+3cdot t$ — директора

При встрече у них одинаковые координаты: ${{x}_{P}}={{x}_{D}}$

Да… Наверное, другие части уравнений приравнять будет полезнее:

$6+2cdot t=3+3cdot t$

Отсюда легко вычислить время встречи:

$t=3$ c

Значит, через три секунды после начала отсчета их координаты будут одинаковы, они встретятся. Найдем место встречи, просто подставив время в одно из двух (какое больше нравится 🙂 ) уравнений:

${{x}_{B}}=6+2cdot 3=12$ м

Директор догонит Петю через 3 секунды. Это произойдет на 12-ти метрах от начала коридора.

Задачи на графики

Задача 4. Написать уравнение движение тела, если график этого движения:

Решение:

Какое это движение? Видим, что графиком движения является прямая. Значит, это равномерное прямолинейное движение.

Удивительно, но начнем с уравнения:

$x={{x}_{0}}+{{V}_{x}}cdot t$

График очень информативный. По крайней мере мы уже знаем начальную координату: ${{x}_{0}}=8$ м

Имеем:

$x=8+{{V}_{x}}cdot t$

Как найти проекцию скорости? Ну, давай ее выразим для начала.

${{V}_{x}}=frac{x-8}{t}$ м/с

Дальше все очень просто: сделаем так, чтобы она осталось единственной неизвестной. Подставим в уравнение координату и время из графика, абсолютно любую пару, вот так:

Считаем:

${{V}_{x}}=frac{6-8}{2}=-1$ м/с

Проекция скорости отрицательна. И правда: с течением времени тело приближается к началу координат, то есть движется против оси.

Подставим в уравнение:

$x=8-t$ — уравнение движения тела.

Задача 5. Тело движется вдоль оси Х. Описать движение на каждом участке графика. Найти проекции скоростей. Построить графики проекции скорости и пройденного пути от времени.

Решение:

Опишем движение. Какое оно?

«Ха! Это не прямая, — скажешь ты, — а ломаная!»

И будешь абсолютно прав.

А я скажу: «А что такое ломаная? Это просто соединенные между собой отрезки! А отрезки — части прямых!»

Поэтому давай рассматривать этот график частями!

С первым отрезком все понятно: равномерное прямолинейное движения, ведь эта часть графика – прямая. С течением времени тело приближается к началу координат, значит движется против оси.

Найдем проекцию скорости.

Для начала, что есть скорость?

Мы помним, что скорость – отношение перемещения к промежутку времени.

$vec{V}=frac{{vec{S}}}{t}$

Знаем, что это справедливо и для проекций:

${{V}_{x}}=frac{{{S}_{x}}}{t}$

Ну, время у нас есть. А проекцию перемещения откуда взять?

Давай вспомним, что это такое. Перемещение – вектор, проведенный из начального положения тела в конечное. А проекция перемещения – проекция этого вектора. Логично, правда? То есть:

${{S}_{x}}=x-{{x}_{0}}$

Подробнее о проекциях можно узнать в Большой теории по векторам.

Вот и нашли проекцию скорости:

${{V}_{x}}=frac{x-{{x}_{0}}}{t}$

Подставим в уравнение выше значения необходимых величин:

${{V}_{x}}=frac{4-10}{2}=-3$ м/с

Проекция скорости на первом участке графика равна -3м/с.

Второй отрезок необычнее: тело не меняет координату. Тело на этом участке неподвижно.

Так как в условии сказано, что тело движется именно вдоль оси Х, модуль проекции скорости на эту ось равен длине вектора скорости.

Так как тело не меняет координату, проекция его перемещения равна нулю. А значит и проекция скорости равна нулю.

Третий отрезок описывает равномерное прямолинейное движение. Тело отдаляется от начала координат и движется туда же, куда направлена ось.

Найдем проекцию скорости на третьем участке:

${{V}_{x}}=frac{9-4}{12-7}=1$ м/с

Так. Давай разберемся, почему там 12-7.

Помнишь, мы считаем отношение проекции перемещения к ПРОМЕЖУТКУ времени. А от 7 до 12 секунды промежуток времени составляет 5 секунд.

Проекция скорости на третьем участке равна 1м/с.

Всё нашли, осталось лишь построить графики! Начнем с графика зависимости проекции скорости от времени. Начертим и обозначим оси, обязательно обозначив единицы измерения и помня, что проекция может быть отрицательна:

Работаем с первой частью:

Мы выяснили, что в течение первых двух секунд проекция скорости была постоянна (как-никак, равномерное прямолинейное движение 🙂 ) и равна -3 м/с.

Давай нарисуем!

На втором участке проекция скорости равна нулю, а на третьем – единице.

Избавимся от вспомогательных линий и получим:

Что-то мне подсказывает, что на графике пути тоже будет три участка. Приступим.

Нарисуем оси и обозначим их:

Логично будет утверждать, что, пока тело не начало двигаться, оно и путь никакой не прошло. Отметим это точкой на графике:

Первые две секунды тело двигалось равномерно со скоростью 3 метра в секунду. Значит, за две секунды тело прошло $3cdot 2=6$ метров! Отметим это!.. Нет, не так, на графике отметим:

Движемся дальше. Мы знаем, что на втором участке тело было неподвижно, а значит путь никакой не проходило. За промежуток времени второго участка тело не прошло никакой путь.

Однако суммарно за всё свое движение тело все так же прошло 6 метров:

На третьем участке тело движется. Значит, суммарно пройденный путь увеличится. Оно двигалось со скоростью 1м/с. Посмотрим сколько оно прошло за 5 (12-7) секунд.

Оно пройдет 5 метров.

Добавим их к нашим уже пройденным 6 метрам и получим 11 метров:

Остается только соединить точки прямой:

Задача 6. Найти проекцию перемещения тела по графику:

Решение:

Определимся, из чего вообще складывается то, что нам нужно найти. В разные промежутки времени тело двигалось с разными постоянными скоростями.

Значит, проекция перемещения складывается из проекций перемещения в разных промежутках времени! Их 6:

${{S}_{x}}={{S}_{x1}}+{{S}_{x2}}+{{S}_{x3}}+{{S}_{x4}}+{{S}_{x5}}+{{S}_{x6}}$

Попробуем найти первую проекцию. Помнишь, мы знаем, что проекция перемещения есть площадь под графиком?

«Под графиком» означает «между графиком и осью», то есть вот эта:

Что ж, давай найдем перемещение:

Проекция скорости есть -2м/с, а промежуток времени – 3с.

Поэтому: ${{S}_{x1}}=-2cdot 3=-6$м

Попробуем найти площадь второго прямоугольника:

Сразу обрати внимание на то, что промежуток времени – с третьей по пятую секунду, то есть 2 секунды!

${{S}_{x2}}=2cdot 2=4$м

Аналогично для остальных:

${{S}_{x3}}=3cdot 3=9$м

${{S}_{x4}}=2cdot 1=2$м

${{S}_{x5}}=1cdot 1=1$м

${{S}_{x6}}=-3cdot 2=-6$м

Посмотрим, чему равна проекция перемещения:

${{S}_{x}}=-6+4+9+2+1-6=4$м

Тяжело в учении – легко в бою. Давай поднажмём и составим график зависимости проекции перемещения от времени.

Когда мы включили таймер, она была равна нулю:

В конце первого промежутка времени она становится равна -6м:

А, ну дальше-то все легко: отмечаем 4, потом отмечаем 9… Нет!

Мы ведь работаем с ОБЩЕЙ проекцией. А общая проекция есть сумма.

Тогда в конце второго промежутка проекция будет равна:

${{S}_{x}}={{S}_{x1}}+{{S}_{x2}}$

Дальше – больше слагаемых.

Следующая точка: $-6+4=-2$ м

А после нее:$-6+4+9=7$ м и т.д.

Теперь соединяем точки по порядку:

Задача 7. Постройте траекторию движения колибри, если начальное положение его по оси Х – 1 м, по оси Y – 3 м, а проекция его скорости на оси, расположенные перпендикулярно друг другу, описывается следующими графиками:

Решение:

Увидел сложную задачу – пиши всё, что знаешь! Зачем? Так надо! Пиши!

Скорость изменяется скачками, но на отдельных промежутках она постоянна. Тело движется равномерно.

Тело изменяет свое положение в пространстве. Изменяет свою координату.

Вспомним, как записывается уравнение координаты тела при равномерном прямолинейном движении:

$x={{x}_{0}}+{{V}_{x}}cdot t$

$y={{y}_{0}}+{{V}_{y}}cdot t$Мы учились делать это раньше. Построим графики зависимости координаты от времени.

Итак, по оси Х у нас 3 участка, обозначим их вспомогательными линиями на нашем новом графике:

Начнем с первого участка. Знаем проекцию скорости и даже начальную координату! Подарок судьбы.

$x=1+2cdot t$

Строим его на первом промежутке:

Теперь координата тела – 17м и тело начинает двигаться с другой скоростью. Из координаты 17 тело движется со скоростью… А, ни с какой скоростью. Проекция скорости на эту ось равна нулю, поэтому:

$x=17+0cdot t$

Координата не меняется. Рисуем:

Тело на 17 м. Оттуда продолжаем движение с проекцией скорости -2 м/с.

Тогда: $x=17-2cdot t$

Аналогично строим график для оси Y. Теперь у нас есть два графика:

Построим траекторию движения в плоскости. Для этого нам нужны оси Х и Y одновременно!

Давай построим их:

Всегда бери длину с запасом! Чтобы потом не перечерчивать оси. Наибольшее значение по Х – 17м. По Y – 15м. На всякий случай будем брать 20Х20.

Давай будем анализировать по секундам. Каковы были координаты тела в момент начала отсчета? Давай посмотрим.

В начальный момент времени координата по Х равна 1м, по Y – 3м. В конечный момент по Х координата равна 13, по Y – 15м.

Отметим эти точки:

Дальше будем рассматривать «переломные моменты». Для первого графика это 8 и 10с, для второго – 4 и 6с.

То есть секунды: 4, 6, 8, 10.

Запишем координаты точек для нужных нам секунд:

4: (9;15)

6: (13; 9)

8: (17;11)

10: (17;13)

Отметим их и соединим прямой, укажем последовательность:

Задача решена!

Теперь ты знаешь, как работать с графиками равномерного прямолинейного движения и их уравнениями! Движемся дальше. Иронично звучит 🙂

Средняя скорость по перемещению. Средняя путевая скорость

Хочешь, покажу фокус?

Смотри.

Из горной пещеры вылетает дракон, а за ним в ту же секунду выбегает доблестный рыцарь. Дракон хочет разрушить замок, находящийся от пещеры на расстоянии 7 километров. Задача рыцаря – добраться до замка первым и остановить дракона.

Рыцарь скачет на лошади прямо к замку по равнине в течении 20 минут. Он обнаруживает, что мост через реку на пути к замку разрушен, поэтому решает переплыть реку, и (спасибо его хорошей подготовке) у него уходит лишь 5 минут на то, чтобы снять с себя доспехи и сделать это. Затем в течении 10 минут он продолжает движение к замку.

Дракон после вылета из пещеры движется вперед и вверх, на это у него уходит 15 минут. На какой-то высоте он останавливается, потому что видит стаю пролетающих мимо уток. Драконы, динозавры, птицы… Смекаешь, да? Он решает поиграться со своими «родственниками», на что у него уходит 15 минут. Затем он вспоминает о замке и стремительно пикирует к нему на протяжении 5 минут.

Давай всё это изобразим для наглядности:

Дракон и рыцарь совершили одинаковые перемещения, так? 7 км, ведь они оказались у замка, двигаясь из пещеры.

Давай посчитаем время каждого в пути. И для дракона, и для рыцаря оно составило 35 минут. Они прибыли к замку одновременно.

Так что ж получается… Они совершили одинаковое перемещение за одинаковый промежуток времени.

Но их траектории были очень различны! И двигались они по-разному!

Для того, чтобы описать это, существует средняя скорость по перемещению.

Средняя скорость тела – векторная физическая величина, равная отношению перемещения тела на определенном участке траектории ко времени, за которое оно совершено.

Можно в виде формулы: ${{vec{V}}_{cp}}=frac{{vec{S}}}{t}$

Средняя скорость дракона и рыцаря по перемещению одинакова, ведь они пришли одновременно в одно и то же место.

Есть подвох, о котором тебе на математике не рассказали. Ты все время работал не с этой средней скоростью. А с этой:

Средняяпутеваяскорость — это отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден.

Понял, да? Путевая – про путь, а не про перемещение. Средняя путевая скорость совпадает (по модулю) со средней скоростью по перемещению только в том случае, если тело двигалось по прямой в одном направлении.

Средняя путевая скорость дракона сильно отличается от средней путевой скорости рыцаря.

Если не помнишь, в чем отличие пути от перемещения, советую посмотреть основные определения кинематики!

Относительность движения. Операции над скоростями

Давай вспомним одну из важнейших вещей, когда мы говорим про движение. Мы давали ему определение, когда говорили о кинематике в целом.

Это тело отсчета. То тело, относительно которого мы рассматриваем движение.

Мы уже знаем, что относительно одного тела тело может нестись с бешеной скоростью, а относительно другого не двигаться вовсе.

От системы отсчета зависит изменение положения тела. А что еще от нее зависит? Траектория зависит?

Оказывается, да!

Однажды человек изобрел колесо и изменил мир. Давай воспользуемся этим изобретением для того, чтобы найти ответ на вопрос выше.

Возьмем какую-то точку на колесе и пусть оно катится по дороге! Как движется эта точка относительно оси колеса? По кругу.

А относительно Земли?

Вот так:

Круто, да?

Эта кривая называется циклоида. И она точно отличается от траектории движения точки относительно оси колеса.

Сегодня мы научимся определять и связывать скорости в разных системах отсчета.

А еще на относительности основан главный закон скоростей – закон об их сложении.

Поступим как настоящие ученые. Готовые формулы – для слабаков. Мы будем выводить их сами.

Рассмотрим ситуацию.

По реке плывет плот (П) со спортсменом (С). На берегу реки сидит рыбак (Р) и наблюдает за этим. В какой-то момент пловец прыгает с плота и движется к другому берегу реки. Их несёт течение реки.

Давай изобразим это:

Давай нарисуем вектор перемещения спортсмена относительно плота и назовем его относительным перемещением:

Теперь нарисуем вектор перемещения плота, которого несет течение. Назовем этот вектор переносным:

А теперь посмотрим, как спортсмен двигался относительно рыбака, и назовем вектор этого перемещения абсолютным:

Ты только посмотри! У нас тут треугольник!

Нет, оставь свои теории заговора и иллюминатов. Не тот треугольник. Треугольник суммы векторов!

Переносное перемещение и относительное в сумме дают абсолютное!

${{vec{S}}_{a}}={{vec{S}}_{n}}+{{vec{S}}_{o}}$

Как связать перемещение со скоростью? Нужно поделить его на время!

Та-а-ак… А его откуда брать?

Оно для всех течёт одинаково. Смело делим:$frac{{{{vec{S}}}_{a}}}{t}=frac{{{{vec{S}}}_{n}}}{t}+frac{{{{vec{S}}}_{o}}}{t}$И получаем:${{vec{V}}_{a}}={{vec{V}}_{n}}+{{vec{V}}_{o}}$А теперь давай разбираться.

Что такое абсолютная скорость? В нашем случае это скорость пловца относительно берега.

Абсолютная скорость – скорость движения тела относительно неподвижной системы отсчета.

Что такое переносная скорость? Скорость плота, скорость течения реки относительно берега.

Переносная скорость – скорость движущейся системы отсчета относительно неподвижной.

Что такое относительная скорость? Это скорость спортсмена относительна плота.

Относительная скорость – скорость движения тела относительно подвижной системы отсчета.

Таким образом,

Скорость движения тела относительно неподвижной системы отсчёта равна векторной сумме скорости этого тела относительно движущейся системы отсчета и скорости движущейся системы отсчета относительно неподвижной.

Иначе говоря:

Абсолютная скорость есть векторная сумма относительной и переносной скоростей.

Чем хороши векторные уравнения? Они не заставляют тебя думать о знаках.

Знаки ты определишь в проекциях. Это будет зависеть от условия задачи.

Внимание, практика!

Решение задач на среднюю скорость и действия со скоростями

Задача 8 (продолжение задачи 3 🙂 ). Поймавший Петю директор пишет замечание в его дневник, его ручка движется по листу бумаги со скоростью 0.05 м/с. Через 3 секунды Петя взмолится перед Максимом Михайловичем, его ручка станет двигаться со скоростью 0.03 м/с на протяжении 4 секунд. А если бедному ученику повезёт и ручка начнет плохо писать, то, чтобы расписать ее, директор будет давить на нее сильнее в течение 5 секунд и скорость ее станет равна 0.01 м/с. Найдите среднюю путевую скорость ручки. Зная, что длина красноречивого замечания равна 24 см, найдите среднюю скорость ручки по перемещению.

Решение:

Если в задаче много букв – составляй ее план. Давай это сделаем и переведем все в СИ, если необходимо.

3с – 0.05 м/с

4с – 0.03 м/с

5с – 0.01 м/с

24см=0.24м

Что значит «длина замечания»? Фактически, расстояние от начала до конца, то есть это кратчайшая ПРЯМАЯ. Запишем ее как вектор – получим перемещение.

Ведь перемещение есть вектор, проведенный из начального положение в конечное.

Давай посчитаем, сколько времени директор писал замечание:

$3+4+5=12$ с

Значит, мы уже можем найти среднюю скорость по перемещению!

Сделаем это:

${{V}_{cp}}=frac{0.24}{12}=0.02$ м/с

Почему там не вектор? Помни: мы не можем приравнивать векторные величины к скалярным. Когда нам сказали, чему равно перемещение, нам дали ДЛИНУ вектора перемещения. А длина есть величина скалярная.

Приступим к средней путевой скорости. Для начала нам нужно найти путь, время у нас уже есть.

Путь будет состоять из трёх участков, в которых тело двигалось с разными скоростями:$L={{L}_{1}}+{{L}_{2}}+{{L}_{3}}$Каждый из них можно найти умножением скорости на участке на время движения с этой скоростью.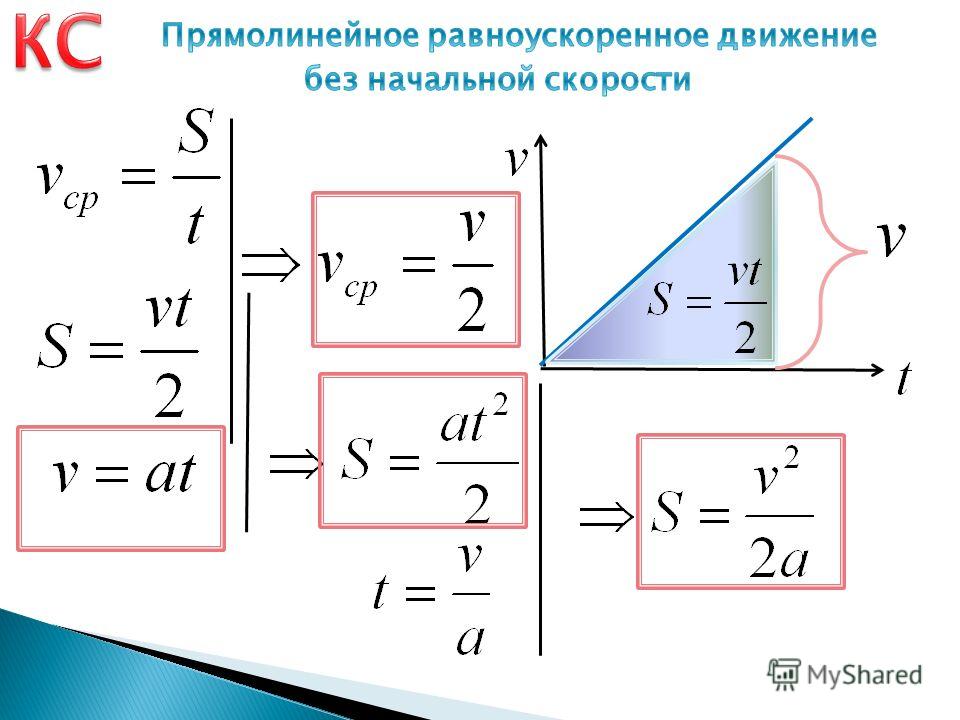 Вот так:$L={{V}_{1}}cdot {{t}_{1}}+{{V}_{2}}cdot {{t}_{2}}+{{V}_{3}}cdot {{t}_{3}}$Давай подставим:$L=0.05cdot 3+0.03cdot 4+0.01cdot 5=0.32$А теперь можем найти среднюю путевую скорость:${{V}_{cpL}}=frac{0.32}{12}approx 0.027$ м/сЗадача решена!

Задача 9. В небе летят два вертолёта. Скорость одного из них – 350 км/ч, другого – 400 км/ч. Найти скорость второго вертолёта относительно первого.

Решение:

Вот тебе дело: найди одно очень важное потерянное условие.

Дело в том, что в задаче не сказано, летят ли они в одном направлении или в разных. Рассмотрим оба случая.

Случай 1. Вертолеты движутся в одном направлении.

Давай вспомним главное уравнение:

${{vec{V}}_{a}}={{vec{V}}_{n}}+{{vec{V}}_{o}}$Мы ищем скорость одного вертолета относительно другого. Скорость одного движущегося тела относительно другого движущегося тела называется относительной. Выразим ее:${{vec{V}}_{o}}={{vec{V}}_{a}}-{{vec{V}}_{n}}$Помним, что с векторами рука об руку идут их проекции.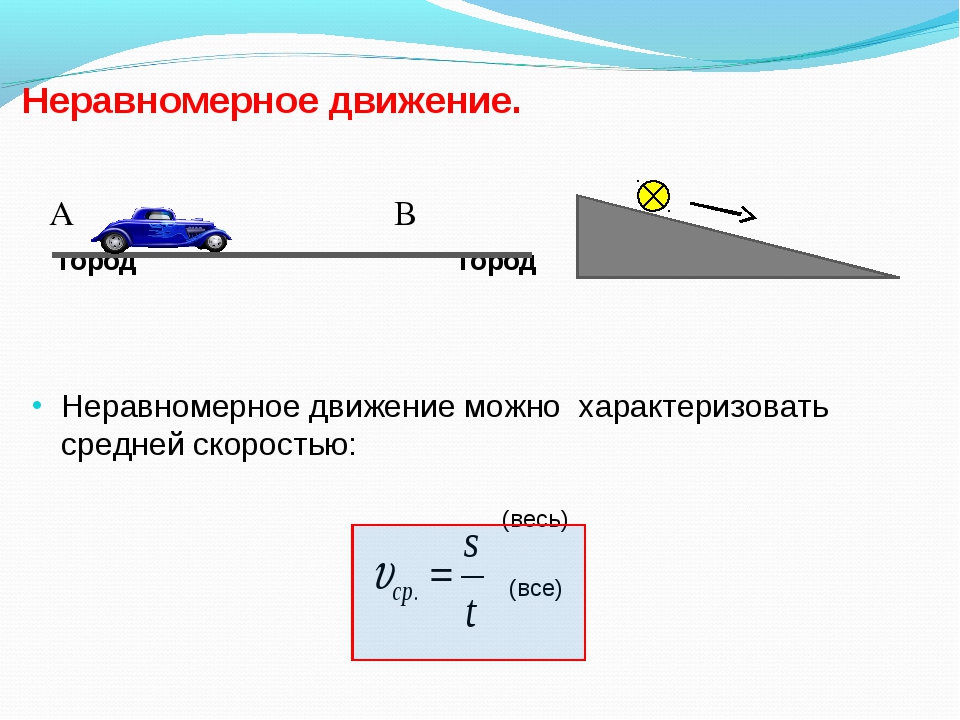 Давай начертим схему задачи и построим ось, на которую будем проецировать векторы скорости:

Всё это, конечно, здорово, но какая скорость абсолютная, а какая переносная?

Давай разбираться.

Переносная скорость – скорость движущейся системы отсчета относительно неподвижной.

В система отсчета, которую требует задача, все происходит относительно первого вертолета. Он – тело отсчета.

Значит, переносная скорость – скорость первого вертолета относительно земли.

Абсолютная скорость – скорость движения тела относительно неподвижной системы отсчета. То есть это скорость второго вертолета, данная в задаче.

Вернемся к уравнению и запишем его по-новому:${{vec{V}}_{o}}={{vec{V}}_{a}}-{{vec{V}}_{n}}$${{vec{V}}_{o}}={{vec{V}}_{2}}-{{vec{V}}_{1}}$Мы помним, что с векторами рука об руку идут проекции. Давай запишем это уравнение в проекции на ось Х.

Обе этих скорости направлены по направлению оси. Значит, их проекции положительны:${{V}_{ox}}={{V}_{2x}}-{{V}_{1x}}$Мы выбрали ось так, чтобы векторы были ей параллельны, поэтому мы смело можем утверждать, что проекции по модулю равны длинам векторов:${{V}_{o}}={{V}_{2}}-{{V}_{1}}$Считаем:${{V}_{o}}=400-350=50$ км/ч

Случай 2. Вертолеты движутся в разных направлениях.

Нарисуем схему снова:

Нетрудно догадаться, что теперь проекция уравнения на ось будет иметь другой вид. Проекция скорости первого вертолета будет отрицательна: она направлена против оси.${{vec{V}}_{o}}={{vec{V}}_{2}}-{{vec{V}}_{1}}$${{V}_{o}}={{V}_{2}}-(-{{V}_{1}})={{V}_{2}}+{{V}_{1}}$Скорости складываются. И правда: оба вертолета стремятся отдалиться друг от друга, никто никого не догоняет.${{V}_{o}}=400+350=750$ км/ч

Таким образом, скорость второго вертолета относительно первого равна 50 км/ч, если они движутся в одном направлении, и 750 км/ч, если движутся в разных.

Задача 10. Дядя Стэн, с уверенностью открыв сезон рыбалки, мчится на моторной лодке против течения реки в течение 3 ч и преодолевает 4 км, пока не вспоминает, что забыл дома свой любимый сборник анекдотов. Скорость течения реки – 2.5 км/ч. Сколько времени понадобится Стэну, чтобы преодолеть то же самое расстояние, возвращаясь обратно?

Решение:

Давай сделаем рисунок. Это в большинстве случаев упрощает задачу!

Сначала нарисуем реку с течением:

А теперь лодку Стэна, которая плывет против течения. Обозначим ее собственную скорость.

Давай посмотрим, как мы можем связать эти две скорости с путем и временем.

Для начала вспомним формулу:${{vec{V}}_{a}}={{vec{V}}_{n}}+{{vec{V}}_{o}}$Пройденный путь и время будет определять абсолютная скорость – та, что характеризует движение тела относительно неподвижной системы отсчета. В нашем случае – берега.

Можно объяснять проекциями, а можно просто понять. Куда легче плыть? По течению или против? Конечно, по течению! Оно подгоняет тебя.

В нашей ситуации Стэн сначала плывет против течения. Абсолютная скорость будет меньше собственной скорости лодки, ведь ее тормозит течение.

Давай запишем:${{V}_{a1}}={{V}_{L}}-{{V}_{T}}$ или $frac{L}{{{t}_{1}}}={{V}_{L}}-{{V}_{T}}$, где ${{t}_{1}}$ — время против течения

Хорошо. Посмотрим, что может дать нам вторая часть задачи.

Здесь лодка идет по течению. Уравнение имеет вид:

$frac{L}{{{t}_{2}}}={{V}_{L}}+{{V}_{T}}$, где ${{t}_{2}}$ — время по течению

Таким образом, у нас есть система уравнений:$frac{L}{{{t}_{2}}}={{V}_{L}}+{{V}_{T}}$$frac{L}{{{t}_{1}}}={{V}_{L}}-{{V}_{T}}$Нам неизвестна собственная скорость лодки. А нам она и не нужна! Вычтем одно уравнение из другого и получим:$frac{L}{{{t}_{2}}}-frac{L}{{{t}_{1}}}=2cdot {{V}_{T}}$Отсюда нужно выразить время по течению:${{t}_{2}}=frac{L}{2cdot {{V}_{T}}+frac{L}{{{t}_{1}}}}$Считаем:${{t}_{2}}=frac{4}{2cdot 2.5+frac{4}{3}}approx 0.6$ ч

36 минут потребуется Стэну, чтобы приплыть обратно.

Задача 11. По узкой лесной тропе колонной длиной в 30 метров идут туристы со скоростью 5 км/ч. Замыкающий посылает одного туриста в начало строя, чтобы тот передал гиду карту местности. Турист бежит в начало строя со скоростью 8 км/ч и, выполнив поручение, тут же бежит обратно с той же скоростью. Сколько времени потребуется туристу, чтобы добежать до начала строя и вернуться обратно?

Решение:

Начнем с рисунка. Есть колонна определенной длины (пусть будет l), она движется с определенной скоростью. Из начала выходит турист (Т) и движется с другой скоростью:

Смотри. Пока турист движется, колонна тоже движется. Значит туда он пробежит путь больше, чем обратно:

Выглядит сложно.

Ну да, конечно! Это как идти в школу в соседнем дворе и для этого каждый раз покупать билет в Антарктиду.

Нужно выбрать удобную систему отсчета!

Сделаем так, чтобы колонна была неподвижна. Будем рассматривать все относительно нее. Можно даже представить, что ты один из туристов 🙂

Сделаем другую картинку!

Если ты один из туристов, будет очевидно, что туда и обратно “посыльный” будет двигаться с разной скоростью.

Например, когда ты едешь по шоссе, кто кажется быстрее: машины, которые обгоняют твою или машины, которые едут на встречу? Очевидно, что те, кто едут навстречу.

Теперь осталось определить, с какой скоростью турист движется туда и обратно.

Изначально он движется с колонной в одном направлении, то есть пытается ее обогнать. Результирующая скорость будет меньше его собственной:

${{V}_{1}}={{V}_{T}}-{{V}_{K}}$${{V}_{1}}=8-5=3$ км/чКогда он движется обратно, колонна будет идти ему навстречу. Результирующая скорость будет больше:${{V}_{2}}={{V}_{T}}+{{V}_{K}}$${{V}_{2}}=8+5=13$ км/чСлишком быстро? Посиди и подумай. Мне не удастся просто вложить знания в твою голову. Ты сам тоже должен стараться!

Итак, из чего складывается время, затраченное туристом? Из времени туда и обратно!$t={{t}_{1}}+{{t}_{2}}$Время в пути есть путь, деленный на скорость. Давай подставим:$t=frac{l}{{{V}_{1}}}+frac{l}{{{V}_{2}}}=frac{l}{{{V}_{T}}-{{V}_{K}}}+frac{l}{{{V}_{T}}+{{V}_{K}}}$Теперь можем посчитать!$t=frac{0.03}{3}+frac{0.03}{13}approx 0.0123$ч

Или приблизительно 44 секунды!

Задача решена! Оказывается, она очень простая, если верно выбрать систему отсчета.

Задачи в плоскости

Задача 12. Индейцы переплывают реку. Один из них, Красный Джо, встает напротив маленького причала и прыгает в воду, начиная плыть в его сторону со скоростью 2 м/с. Расстояние от причала до берега – 120 м. Течение реки имеет скорость 3 км/ч. Куда на самом деле приплывет Красный Джо, позабывший духовную (и не только) связь своей скорости с рекой, и сколько времени на это уйдет?

Решение.

Итак, в мыслях индейцах он плыл бы так:

И это было бы верно, если бы он плыл в стоячей воде! Но течение изменяет его движение:

Он движется вперед и его еще переносит река! Обозначим расстояние, на которое его перенесет от причала, за Х. Его и нужно найти.

Еще нам дано расстояние до причала. Покажем на рисунке:

Как можно найти Х? Давай посмотрим, как движется тело по горизонтали. Оно просто смещается со скоростью течения, верно?

Значит, Х можно найти самым простым уравнением пути, которое мы знаем еще с пятого класса!$X={{V}_{T}}cdot t$Но как найти время?

Для этого нужно понять, что сносить его будет ровно столько времени, сколько он движется вперед.

То есть это то же время, что он затратил бы в стоячей воде, чтобы переплыть реку!$t=frac{l}{{{V}_{K}}}$Подставим в уравнение выше:$X={{V}_{T}}cdot frac{l}{{{V}_{K}}}$ Теперь можем ответить на все вопросы задачи! Только не забудь перевести все в единую систему единиц измерения.

В задачах на движение не особенно важно (если не сказано иное), какие использовать единицы измерения. Главное, чтобы везде в решении они были одинаковые, например, везде километры или везде метры, везде часы или везде секунды. Как тебе удобно.

3 км/ч примерно равняется 0.83 м/с.

Подставляем значения в формулы:

$X=0.83cdot frac{120}{2}=49.8$м

Найдем время:

$t=frac{120}{2}=60$c

Таким образом, Красному Джо потребуется 1 минута на то, чтобы переплыть реку и оказаться на расстоянии 49.8 метров от причала.

Но есть и другой способ решения, если этот кажется тебе подозрительно легким 🙂

Попробуем решить эту задачу геометрией!

Вектор скорости течения параллелен отрезку Х, который нам нужно найти. Давай используем параллельный перенос и поставим его в более удобное место:

Сумма векторов скорости Красного Джо и течения даст нам абсолютную скорость – скорость, с которой тело движется относительно берега.

Вектор абсолютной скорости будет лежать на пунктире, конец которого – положение Джо после преодоления реки.

А теперь рассмотрим подобные треугольники:

Теперь запишем для них уравнение подобия, используя известные нам величины:$frac{l}{{{V}_{K}}}=frac{X}{{{V}_{T}}}$Отсюда можем легко найти Х:$X=frac{lcdot {{V}_{T}}}{{{V}_{K}}}$У нас получилась та же самая формула!

Задача 13. При скорости ветра 12 м/с капли дождя падают под углом 30 градусов к вертикали. При какой скорости ветра они будут падать под углом 45 градусов?

Решение:

Приятно и легко смотреть на дождь в окне. А еще легче решить эту задачу.

Если в физике видишь углы, ты точно будешь использовать тригонометрию. От нее не убежишь.

Начертим рисунок. Прежде всего, у нас есть вектор скорости ветра и какая-то вертикаль:

Как бы падали капли без ветра? Просто вниз:

Для удобства будем рассматривать одну каплю.

В этой задаче ветер можно сравнить с течением реки! Давай сделаем рисунок по этому сравнению!

Но где тут угол? Все просто: это будет угол вектора суммы!

Именно этот вектор принадлежит абсолютной скорости – той, что описывает движение капли относительно земли (и вертикали)

Давай разбираться. Скорость капли при отсутствии ветра нам неизвестна.

Не пугайся. Надежда на то, что неизвестные сократятся, всегда умирает последней.

Нам известна скорость ветра. И угол.

Рассмотрим получившийся у нас треугольник: он прямоугольный, его гипотенуза – абсолютная скорость. Она тоже неизвестна.

Давай попробуем с помощью угла связать два катета этого треугольника! Здесь поможет тангенс. Это отношение противолежащего катета к прилежащему, то есть:$tgalpha =frac{{{V}_{B}}}{{{V}_{K}}}$Без векторов, потому что мы рассматриваем их длины и работаем с треугольником!

Давай выразим скорость капли в безветренную погоду, она ведь не изменится, она просто дана (вообще-то не дана, ну ладно) нам как факт.{o}}}=frac{12cdot 3}{sqrt{3}}approx 20.8\) м/сЗадача решена!

Краткое содержание, основные формулы и определения

Сегодня ты узнал:

Как решить основную задачу механики в общем виде;
Равномерное прямолинейное движение — такое движение, при котором тело за любые равные промежутки времени совершает равные перемещения;
Скорость равномерного прямолинейного движения есть физическая величина, равная отношению вектора перемещения ко времени, за которое оно произошло;
Скорость равномерного прямолинейного движения постоянна;
Как решить основную задачу механики для равномерного прямолинейного движения;
Как строить и анализировать графики равномерного прямолинейного движения;
Графиком равномерного прямолинейного движения является прямая;
Встреча – такое событие, при котором координаты тел в один и тот же момент времени совпадают;
Проекция перемещения тела численно равна площади под графиком скорости тела;
Как строить траекторию движения тела;
Средняя скорость тела – векторная физическая величина, равная отношению перемещения тела на определенном участке траектории ко времени, за которое оно совершено;
Средняя путеваяскорость — это отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден;
Траектория движения тела зависит от выбора системы отсчета;
Как доказать закон сложения скоростей;
Абсолютная скорость есть векторная сумма относительной и переносной скоростей;

А еще ты научился решать задачи разного уровня сложности!

Ой, я что, не сказал? Там сложные были!

Ты, наверное, и не заметил 😉

Заключение

Мы разобрались с самым простым видом движения.

Необходимо очень хорошо разбираться даже в тех вещах, которые кажутся очевидными.

Дальше будет легче, ведь у нас уже есть хорошая база! Теперь будут меняться лишь характеристики движения.

Надеюсь, тебе понравились задачи 🙂

Все ли было понятно? Узнал ли ты что-то, о чем не рассказывали в школе?

Остались вопросы? Пиши в комментариях!

Поделитесь в социальных сетях:

Projectile Motion
Projectile Motion Движение снаряда
Объект бросает прямо вверх с вершины здания высотой h футов с начальной скоростью v футов в секунду. Высота объекта как функция времени может быть смоделирована функцией h (t) = –16t ² + vt + h, где h (t) – высота объекта (в футах) через t секунд после него. брошен.
Если нам задана начальная скорость (или скорость) объекта и высота здания, мы можем использовать эту модель, чтобы определить, сколько времени требуется, чтобы объект достиг разной высоты.Эта модель предполагает, что объект не попадает в верхнюю часть здания на обратном пути к земле и что сопротивление ветра минимально.

Вот шаги, необходимые для решения проблем движения снаряда:
Шаг 1 : Установите данное уравнение равным соответствующей высоте.
Шаг 2 : Решите уравнение, найденное на шаге 1, установив уравнение равным нулю и разложив уравнение на множители.
Шаг 3 : В зависимости от проблемы определите, какой ответ или ответы верны. Не забудьте указать единицы в своем окончательном ответе.
Пример 1 – Мяч бросается прямо с вершины здания высотой 128 футов с начальной скоростью 32 фута в секунду. Высота шара как функция времени может быть смоделирована функцией h (t) = –16t ² + 32t + 128.Сколько времени потребуется, чтобы мяч коснулся земли?
Шаг 1 : Установите данное уравнение равным соответствующей высоте. В этом случае мы устанавливаем уравнение равным нулю, потому что высота земли равна нулю.
Шаг 2 : Решите уравнение, найденное на шаге 1, установив уравнение равным нулю и разложив уравнение на множители.
Шаг 3 : В зависимости от проблемы определите, какой ответ или ответы верны.Не забудьте указать единицы в своем окончательном ответе. В этом случае есть только один положительный ответ, который имеет смысл, потому что мяч ударяется о землю только один раз.
Пример 2 – Мяч подбрасывается прямо с вершины здания высотой 288 футов с начальной скоростью 48 футов в секунду. Высота мяча как функция времени может быть смоделирована функцией h (t) = –16t ² + 48t + 288. Когда мяч достигнет высоты 320 футов?
Шаг 1 : Установите данное уравнение равным соответствующей высоте.В этом случае мы устанавливаем уравнение равным 320, потому что мы хотим определить, когда высота будет 320 футов.
Шаг 2 : Решите уравнение, найденное на шаге 1, установив уравнение равным нулю и разложив уравнение на множители.
Шаг 3 : В зависимости от проблемы определите, какой ответ или ответы верны. Не забудьте указать единицы в своем окончательном ответе.В этом случае есть два положительных ответа, которые имеют смысл, потому что мяч достигнет 320 футов один раз на пути вверх и еще раз на пути вниз.
Щелкните здесь для практических задач
Пример 3 – Ракета запускается прямо с вершины здания высотой 24 фута с начальной скоростью 92 фута в секунду. Высота ракеты как функция времени может быть смоделирована функцией h (t) = –16t ² + 92t + 24.Сколько времени потребуется, чтобы ракета упала на землю?
Шаг 1 : Установите данное уравнение равным соответствующей высоте. В этом случае мы устанавливаем уравнение равным нулю, потому что высота земли равна нулю.
Шаг 2 : Решите уравнение, найденное на шаге 1, установив уравнение равным нулю и разложив уравнение на множители.
Шаг 3 : В зависимости от проблемы определите, какой ответ или ответы верны.Не забудьте указать единицы в своем окончательном ответе. В этом случае есть только один положительный ответ, который имеет смысл, потому что мяч ударяется о землю только один раз.
Щелкните здесь для практических задач
Пример 4 – Мяч падает прямо в воздухе с высоты 4 фута с начальной скоростью 64 фута в секунду. Высота шара как функция времени может быть смоделирована функцией h (t) = –16t ² + 64t + 4.Когда мяч достигнет высоты 52 футов?
Шаг 1 : Установите данное уравнение равным соответствующей высоте. В этом случае мы устанавливаем уравнение равным 52, потому что мы хотим определить, когда высота будет 52 фута.
Шаг 2 : Решите уравнение, найденное на шаге 1, установив уравнение равным нулю и разложив уравнение на множители.
Шаг 3 : В зависимости от проблемы определите, какой ответ или ответы верны.Не забудьте указать единицы в своем окончательном ответе. В этом случае есть два положительных ответа, которые имеют смысл, потому что мяч достигнет 52 футов один раз на пути вверх и еще раз на пути вниз.
Щелкните здесь для практических задач
3.5: Движение с постоянным ускорением (Часть 1)
Цели обучения
Определите, какие уравнения движения следует использовать для решения неизвестных.
Используйте соответствующие уравнения движения, чтобы решить задачу о преследовании двух тел.
Вы можете догадаться, что чем больше ускорение, скажем, у автомобиля, удаляющегося от знака «Стоп», тем больше смещение автомобиля за данный момент времени. Но мы не разработали конкретное уравнение, которое связывает ускорение и смещение. В этом разделе мы рассмотрим некоторые удобные уравнения кинематических отношений, начиная с определений смещения, скорости и ускорения. Сначала мы исследуем движение одного объекта, называемого движением одного тела. Затем мы исследуем движение двух объектов, называемых задачами преследования двух тел .
Обозначение
Во-первых, сделаем несколько упрощений в обозначениях. Принятие начального времени равным нулю, как если бы время измерялось секундомером, является большим упрощением. Поскольку прошедшее время равно \ (\ Delta \) t = t _f – t ₀, взяв t ₀ = 0, значит \ (\ Delta \) t = t _f, последнее время на секундомере. . Когда начальное время принимается равным нулю, мы используем индекс 0 для обозначения начальных значений положения и скорости. То есть x ₀ – это начальная позиция , а v ₀ – начальная скорость .Мы не ставим нижние индексы на окончательные значения. То есть t – это последнее время , x – это конечное положение , а v – это конечная скорость . Это дает более простое выражение для истекшего времени: \ (\ Delta \) t = t. Это также упрощает выражение для смещения x, которое теперь равно \ (\ Delta \) x = x – x ₀. Кроме того, он упрощает выражение для изменения скорости, которое теперь равно \ (\ Delta \) v = v – v ₀. Подводя итог, используя упрощенные обозначения, с начальным временем, принятым равным нулю,
\ [\ Delta t = t \]
\ [\ Delta x = x – x_ {0} \]
\ [\ Delta v = v – v_ {0}, \]
, где нижний индекс 0 обозначает начальное значение, а отсутствие нижнего индекса означает конечное значение в любом рассматриваемом движении.
Теперь мы делаем важное предположение, что ускорение постоянно. Это предположение позволяет нам избегать использования расчетов для определения мгновенного ускорения. Поскольку ускорение постоянно, среднее и мгновенное ускорения равны, то есть
\ [\ bar {a} = a = константа \ ldotp \]
Таким образом, мы можем использовать символ a для ускорения в любое время. Предположение, что ускорение является постоянным, не серьезно ограничивает ситуации, которые мы можем изучить, и не ухудшает точность нашего лечения.Во-первых, ускорение постоянно в большом количестве ситуаций. Кроме того, во многих других ситуациях мы можем точно описать движение, приняв постоянное ускорение, равное среднему ускорению для этого движения. Наконец, для движения, во время которого ускорение резко меняется, например, когда автомобиль разгоняется до максимальной скорости, а затем тормозит до остановки, движение можно рассматривать в отдельных частях, каждая из которых имеет собственное постоянное ускорение.
Смещение и положение от скорости
Чтобы получить наши первые два уравнения, мы начнем с определения средней скорости:
\ [\ bar {v} = \ frac {\ Delta x} {\ Delta t} \ ldotp \]
Замена упрощенных обозначений для \ (\ Delta \) x и \ (\ Delta \) t дает
\ [\ bar {v} = \ frac {x – x_ {0}} {t} \ ldotp \]
Решение относительно x дает нам
\ [x = x_ {0} + \ bar {v} t, \ label {3.10} \]
, где средняя скорость
\ [\ bar {v} = \ frac {v_ {0} + v} {2} \ ldotp \ label {3.11} \]
Уравнение \ (\ bar {v} = \ frac {v_ {0} + v} {2} \) отражает тот факт, что при постоянном ускорении v – это просто среднее значение начальной и конечной скоростей. Рисунок \ (\ PageIndex {1} \) графически иллюстрирует эту концепцию. В части (а) рисунка ускорение является постоянным, а скорость увеличивается с постоянной скоростью. Средняя скорость на 1-часовом интервале от 40 км / ч до 80 км / ч составляет 60 км / ч:
\ [\ bar {v} = \ frac {v_ {0} + v} {2} = \ frac {40 \; км / ч + 80 \; км / ч} {2} = 60 \; км / ч \ ldotp \]
В части (b) ускорение не является постоянным.В течение 1-часового интервала скорость ближе к 80 км / ч, чем к 40 км / ч. Таким образом, средняя скорость больше, чем в части (а).
Рисунок \ (\ PageIndex {1} \): (a) График зависимости скорости от времени с постоянным ускорением, показывающий начальную и конечную скорости v ₀ и v. Средняя скорость равна \ (\ frac {1} {2} \) (v ₀ + v) = 60 км / ч. (б) График зависимости скорости от времени с изменением ускорения со временем. Средняя скорость не выражается в \ (\ frac {1} {2} \) (v ₀ + v), но превышает 60 км / ч.
Решение для окончательной скорости по ускорению и времени
Мы можем вывести еще одно полезное уравнение, манипулируя определением ускорения:
\ [a = \ frac {\ Delta v} {\ Delta t} \ ldotp \]
Подстановка упрощенных обозначений для \ (\ Delta \) v и \ (\ Delta \) t дает нам
\ [a = \ frac {v – v_ {0}} {t} \; (константа \; a) \ ldotp \]
Решение относительно v дает
\ [v = v_ {0} + at \; (константа \; a) \ ldotp \ label {3.12} \]
Пример 3.7: Расчет окончательной скорости
Самолет приземляется с начальной скоростью 70,0 м / с, а затем замедляется со скоростью 1,50 м / с. ² в течение 40,0 с. Какова его конечная скорость?
Стратегия
Сначала мы идентифицируем известные: v ₀ = 70 м / с, a = -1,50 м / с ², t = 40 с.
Во-вторых, мы идентифицируем неизвестное; в данном случае это конечная скорость v _f.
Наконец, мы определяем, какое уравнение использовать. Для этого мы выясняем, какое кинематическое уравнение дает неизвестное в терминах известных.{2}) (40,0 \; s) = 10,0 \; м / с \ ldotp \]
Рисунок \ (\ PageIndex {2} \) – это эскиз, на котором показаны векторы ускорения и скорости.
Рисунок \ (\ PageIndex {2} \): Самолет приземляется с начальной скоростью 70,0 м / с и замедляется до конечной скорости 10,0 м / с, прежде чем направиться к терминалу. Обратите внимание, что ускорение отрицательное, потому что его направление противоположно его скорости, которая положительна.
Значение
Конечная скорость намного меньше начальной скорости, требуемой при замедлении, но все же положительная (см. Рисунок).В реактивных двигателях обратная тяга может поддерживаться достаточно долго, чтобы остановить самолет и начать движение назад, на что указывает отрицательная конечная скорость, но в данном случае это не так.
Помимо полезности при решении задач, уравнение v = v ₀ + at дает нам представление о взаимосвязях между скоростью, ускорением и временем. Мы видим, например, что
Конечная скорость зависит от того, насколько велико ускорение и как долго оно длится
Если ускорение равно нулю, то конечная скорость равна начальной скорости (v = v ₀), как и ожидалось (другими словами, скорость постоянна)
Если a отрицательно, то конечная скорость меньше начальной
Все эти наблюдения соответствуют нашей интуиции.Обратите внимание, что всегда полезно исследовать основные уравнения в свете нашей интуиции и опыта, чтобы убедиться, что они действительно точно описывают природу. {2} \; (константа \; a) \ ldotp \ label {3.13} \]
Пример 3.8: Расчет смещения ускоряющегося объекта
Драгстеры могут развивать среднее ускорение 26,0 м / с ². Предположим, драгстер ускоряется из состояния покоя с этой скоростью в течение 5,56 с. Рисунок \ (\ PageIndex {3} \). Как далеко он пролетит за это время?
Рисунок \ (\ PageIndex {3} \): пилот Top Fuel американской армии Тони «Сержант» Шумахер начинает гонку с контролируемого выгорания. (Источник: подполковник Уильям Термонд. Фотография предоставлена армией США.)
Стратегия
Сначала нарисуем эскиз Рисунок \ (\ PageIndex {4} \).{2} \), когда мы идентифицируем v ₀, a и t из постановки задачи.
Рисунок \ (\ PageIndex {4} \): эскиз ускоряющегося драгстера.
Решение
Во-первых, нам нужно определить известные. Запуск из состояния покоя означает, что v ₀ = 0, значение a равно 26,0 м / с ², а значение t равно 5,56 с. {2} \ ldotp \]
Подстановка идентифицированных значений a и t дает
\ [x = \ frac {1} {2} (26.{2} = 402 \; м \ ldotp \]
Значение
Если мы переведем 402 м в мили, мы обнаружим, что пройденное расстояние очень близко к четверти мили, стандартному расстоянию для дрэг-рейсинга. Итак, наш ответ разумный. Это впечатляющий водоизмещение всего за 5,56 с, но первоклассные драгстеры могут преодолеть четверть мили даже за меньшее время. Если бы драгстеру была присвоена начальная скорость, это добавило бы еще один член в уравнение расстояния. Если в уравнении использовать те же ускорение и время, пройденное расстояние будет намного больше.{2} + 2a (x – x_ {0}) \) идеально подходит для этой задачи, поскольку он связывает скорости, ускорение и смещение и не требует информации о времени.
Решение
Сначала мы идентифицируем известные значения. Мы знаем, что v ₀ = 0, поскольку драгстер запускается из состояния покоя. {2} = 0 + 2 (26.{2} + 2a (x – x_ {0}) \) может дать дополнительную информацию об общих отношениях между физическими величинами:
Конечная скорость зависит от величины ускорения и расстояния, на котором оно действует.
При фиксированном ускорении машина, едущая вдвое быстрее, не просто останавливается на удвоенном расстоянии. Чтобы остановиться, нужно гораздо дальше. (Вот почему у нас есть зоны с пониженной скоростью возле школ.)
Авторы и указание авторства
Сэмюэл Дж.Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами. Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Двумерные уравнения кинематики
Двумерные уравнения кинематики
3.2. Уравнения кинематики в двух измерениях
Рисунок 3.3 Космический корабль движется с постоянным ускорением a _х параллельно оси x.Нет движения в направлении y, и двигатель y выключен.
Чтобы понять, как смещение, скорость и ускорение применяются к двумерному движению, рассмотрим космический корабль, оснащенный двумя двигателями, установленными перпендикулярно друг другу. Эти двигатели создают единственные силы, которые испытывает аппарат, и предполагается, что космический аппарат находится в начале координат, когда t ₀ = 0 с, так что r ₀ = 0 м. В более позднее время t смещение космического корабля Dr = r – r ₀ = r.Относительно осей x и y смещение r имеет компоненты вектора x и y соответственно.
На рисунке 3.3 работает только двигатель, ориентированный вдоль направления x, и транспортное средство ускоряется в этом направлении. Предполагается, что скорость в направлении y равна нулю, и она остается нулевой, поскольку двигатель y выключен. Движение космического корабля в направлении x описывается пятью кинематическими переменными x, a _x, v _x, v _0x и t.Здесь символ «x» напоминает нам, что мы имеем дело с компонентами x векторов смещения, скорости и ускорения. (См. Разделы 1.7 и 1.8 для обзора компонентов вектора.) Переменные x, a _x, v _x и v _0x являются скалярными компонентами (или для краткости «компонентами»). Как обсуждается в разделе 1.7, эти компоненты являются положительными или отрицательными числами (с единицами измерения), в зависимости от того, указывают ли соответствующие компоненты вектора вдоль оси + x или –x. Если космический аппарат имеет постоянное ускорение в направлении x, движение точно такое же, как описано в главе 2, и можно использовать уравнения кинематики.Для удобства эти уравнения записаны в левом столбце таблицы 3.1.
Interactive LearningWare 3.1
Лисица пробегает 85 м на юг за 18 с. Он начинает с отдыха и останавливается на незначительное время в конце бега. Затем он снова взлетает и пробегает 62 м на восток за 21 секунду. Во время этого второго пробега его ускорение постоянное. Для всего 39-секундного интервала найдите величину и направление средней скорости лисы (а) и (б) среднего ускорения.Укажите направления относительно юга.
Сопутствующее домашнее задание: Проблемы 10
Таблица 3.1 Уравнения кинематики для двумерного движения с постоянным ускорением
Рисунок 3.4 аналогичен рисунку 3.3, за исключением того, что теперь работает только двигатель y, а космический корабль ускоряется в направлении y. Такое движение можно описать с помощью кинематических переменных y, a _y, v _y, v _0y и t.И если ускорение в направлении y постоянно, эти переменные связаны уравнениями кинематики, как написано в правом столбце таблицы 3.1. Как и их аналоги в направлении x, скалярные компоненты y, a _y, v _y и v _0y могут быть положительными (+) или отрицательными (-) числами (с единицами измерения).
Рисунок 3.4 Космический корабль движется с постоянным ускорением a _г параллельно оси y.Нет движения в направлении x, и двигатель x выключен.
Если оба двигателя космического корабля работают одновременно, результирующее движение происходит частично по оси x и частично по оси y, как показано на рисунке 3.5. Тяга каждого двигателя придает автомобилю соответствующую составляющую ускорения. Двигатель x ускоряет корабль в направлении x и вызывает изменение компонента x скорости. Точно так же y-двигатель вызывает изменение y-компоненты скорости. Важно понимать, что x-часть движения происходит точно так же, как если бы y-часть не происходила вообще. Аналогично, y-часть движения происходит точно так же, как если бы x-часть движения не существовала. Другими словами, движения по осям x и y не зависят друг от друга.
Рисунок 3.5 Двумерное движение космического корабля можно рассматривать как комбинацию отдельных движений по осям x и y.
ОБЗОР КОНЦЕПЦИЙ Независимость движений по осям x и y лежит в основе двумерной кинематики. Это позволяет нам рассматривать двумерное движение как два отдельных одномерных движения, одно для направления x, а другое – для направления y. Как показано на диаграмме «Обзор концепций» на рис. 3.6, все, что мы узнали в главе 2 о кинематике в одном измерении, теперь будет применяться отдельно к каждому из двух направлений. Поступая таким образом, мы сможем описать переменные x и y по отдельности, а затем объединить эти описания, чтобы понять двумерную картину.В примере 4 этот подход применяется к движущемуся космическому кораблю.
Рисунок 3.6 ОБЗОР КОНЦЕПЦИИ В двух измерениях движение по направлению x и движение по направлению y не зависят друг от друга. В результате каждый может быть проанализирован отдельно в соответствии с процедурами для одномерной кинематики, описанными в главе 2. На космическом корабле “Челленджер” движение в перпендикулярных направлениях контролируется двигателями.На фотографиях показан “Челленджер” на орбите с активированными двигателями. (С любезного разрешения НАСА).
Пример 1 Движущийся космический корабль
Проверьте свое понимание 2
Моторная лодка, трогаясь с места, сохраняет постоянное ускорение. По прошествии определенного времени t его смещение и скорость равны r и v. Каковы были бы его смещение и скорость в момент времени 2, если предположить, что ускорение останется прежним?
(а) 2р и 2в (б) 2р и 4в (в) 4р и 2в (г) 4р и 4в
Справочная информация: Когда объект ускоряется, его перемещение и скорость зависят от времени.Если ускорение постоянное, применяются уравнения кинематики в таблице 3.1.
По аналогичным вопросам (в том числе расчетным аналогам) обратитесь к Тесту самооценки 3.1. Этот тест описан в конце раздела 3.3.
Следующая стратегия рассуждений дает обзор того, как уравнения кинематики применяются для описания движения в двух измерениях, например, в примере 1.
Авторские права © 2000-2003 John Wiley & Sons, Inc. или связанных компаний. Все права защищены.
Расчет с постоянным ускорением – Nexus Wiki
Если у нас есть постоянное ускорение – скорость либо увеличивается, либо уменьшается с одинаковой скоростью – тогда мы можем выяснить много полезного. В этом разделе мы предположим, что мы движемся по линии. Мы могли бы путешествовать взад и вперед, но мы не будем рассматривать изменения угла нашего движения.Поэтому мы отбросим $ \ hat {i} $ или $ \ hat {j} $, которые выбирают, по какой линии мы движемся, и работаем только с одной координатой. Для удобства мы назовем его $ x $.
Скорость
Если ускорение постоянное, значит, скорость изменяется с постоянной скоростью. Тогда наше уравнение, определяющее ускорение, равно
.
$$ a_0 = \ frac {\ Delta v} {\ Delta t} $$
или
$$ a_0 = \ frac {v_2 – v_1} {\ Delta t} $$
где $ v_1 $ – наша скорость в начале временного интервала (начальная скорость), а $ v_2 $ – наша скорость в конце временного интервала (конечная скорость).
Если мы решим окончательную скорость, мы получим
$$ v_2 = v_1 + a_0 (t_2 – t_1) $$
Поскольку мы выбрали конкретное время, все в этом уравнении является константой. Но мы можем выбрать один или несколько из них, чтобы снова превратить их в переменную. В частности, давайте назовем $ t_2 $, «$ t $» и будем рассматривать его как независимую переменную. Затем мы можем увидеть, как выглядит скорость как функция времени. «Конечная скорость», поскольку она соответствует скорости в момент времени $ t_2 $, станет зависимой переменной $ v $.
Если вам это кажется немного странным, привыкните к этому. В физике, поскольку мы склонны описывать как общие, так и конкретные ситуации, мы часто позволяем константе «блуждать», становясь переменной. И мы часто фиксируем переменную на определенном значении, чтобы уравнение применялось к конкретной ситуации.
Это дает нам уравнение для $ v $ (которое выполняется между временем t ₁ и некоторым более поздним временем t, которое не указано)
$$ v (t) = v_t + a_0 (t – t_1) $$
Если мы построим эту скорость как функцию $ t $, мы получим цифру, которая выглядит как та, что слева на рисунках ниже.Если мы хотим выяснить, какова средняя скорость в этом временном интервале, мы должны найти постоянную линию, чтобы площади под кривой истинной скорости равнялись площади под линией средней скорости (константа). Мы делаем это, настраивая линию средней скорости так, чтобы светло-розовая область (область, которая больше не включалась) и светло-голубая область (теперь добавленная область) были равны.
Совершенно ясно, как если подумать о том, как изменяется скорость, так и глядя на график, что средняя скорость будет на полпути между конечными точками; то есть, если а постоянна, то
$$ \ langle v \ rangle = \ frac {v_1 + v_2} {2} $$
Поскольку мы знаем, что определение средней скорости – это «та скорость, которая, если вы постоянно будете следовать ей, будет производить такое же смещение», мы можем видеть, что если ускорение постоянное:
$$ \ Delta v = a \ Delta t $$
$$ \ Delta x = \ langle v \ rangle \ Delta t $$
$$ \ Delta v = v_2 – v_1 $$
$$ \ langle v \ rangle = \ frac {v_1 + v_2} {2} $$
Каждое из этих 4 уравнений имеет четкое и понятное концептуальное значение и позволяет вам рассчитывать все, что вам нужно, исходя из того, что вы знаете, когда ускорение является постоянным.Иногда сложнее всего вспомнить, какое уравнение работает для $ \ Delta v $, а какое – для $ \ langle v \ rangle $. Легко сохранить ясность, если помнить о значениях «изменение» и «среднее» и думать о том, какими они были бы, если бы скорость была постоянной.
Тренировка: расчет с постоянным ускорением
Джо Рэдиш 10.09.11
CC | Физика и поступательное движение
Поскольку физика MCAT часто полагается на вычисления, эта часть раздела теста по физическим наукам часто вызывает у студентов чрезмерный уровень беспокойства.Как репетитор MCAT и репетитор физики, я могу помочь вам преодолеть ваше беспокойство по поводу этого раздела MCAT. Считайте, что это первое из серии неопределенных по продолжительности и частоте, которая поможет демистифицировать те концепции, которые могут пригодиться в разделе физики во время тестового дня.
Поступательное движение для MCAT означает, что что-то движется не более чем в двух измерениях без вращения. Это движение можно разбить, описав скорость и ускорение в направлении X (слева направо в модели на странице) или направлении Y (вверх-вниз на странице).Скорость рассчитывается как расстояние, разделенное на время, а ускорение – это изменение скорости, деленное на время, необходимое для того, чтобы это изменение произошло.
Например: автомобиль, который проезжает шестьдесят миль за час, имеет скорость 60 миль / час. Автомобиль, разгоняющийся с нуля до шестидесяти миль в час за 4 секунды, имеет ускорение 15 миль в секунду2. (Примечание: единицы выстраиваются в линию! Скорость [расстояние / время], деленная на время, дает вам единицы расстояния / времени2!)
Существует четыре формулы поступательного движения, которые вы обязательно должны запомнить в день экзамена.Это:
d = v _o t + ¹/₂ a * t ²
v _o = v _t + a * t
d = ¹/₂ (v _o + v _t) * t
v _x ² = v _o ² + 2a * d
(d = расстояние, v _o = начальная скорость, v _t = конечная скорость, t = время, a = ускорение)
Эти уравнения легче понять, если вы знаете, откуда они взялись.
1.d = v
_o t + ¹/₂ a * t ²
Первое уравнение разбивает расстояние, которое объект преодолевает, на две составляющие: скорость и ускорение. Расстояние, обусловленное начальной скоростью, просто умножается на скорость (автомобиль, идущий со скоростью 30 миль в час за 2 часа, преодолевает 60 миль [30 миль / час x2 часа = 60 миль]).
Вторая составляющая – ускорение. Поскольку ускорение может очень быстро добавить большую скорость объекту (а точнее, потому что так работает расчет), ускорение умножается на время в квадрате и делится на 2.
2.v
_o = V _T + a * t
Это уравнение определяет ускорение! Скорость движения объекта определяется как скорость, с которой он двигался вначале, плюс скорость ускорения, умноженная на время ускорения. Например, автомобиль, движущийся со скоростью 10 метров в секунду, который затем ускоряется со скоростью 5 метров в секунду ² в течение 2 секунд, будет двигаться со скоростью 40 метров в секунду по истечении этих 2 секунд! (30 метров в секунду + 5 миль в секунду ² * 2 секунды = 40 метров в секунду!)
3.d =
¹/₂ (v _o + v _t) * t
Это уравнение пригодится, когда ускорение неизвестно. Предположим, вы знаете начальную и конечную скорости объекта и время движения. Все это уравнение говорит о том, что пройденное расстояние – это СРЕДНЯЯ величина этих двух скоростей, умноженная на время!
Например: автомобиль заводится со скоростью 30 миль в час и через 2 часа движется со скоростью 60 миль в час с постоянным ускорением.Средняя скорость (¹/₂ [30 + 60]) составляет 45 миль в час. Поскольку скорость 45 миль в час, 2 часа – это 90 миль, машина должна проехать 90 миль! В 95% случаев MCAT предполагает постоянное ускорение.
4. v
_x ² = v _o ² + 2a * d
Это уравнение очень полезно, когда не указано время, но не указаны ускорение и расстояние. Это немного сложнее понять интуитивно, но если это полезно, его можно получить, решив уравнение (2) для переменной t, а затем подставив это выражение вместо t в уравнение (3).По сути, если вы знаете начальную скорость объекта, его ускорение и пройденное расстояние, вы можете вычислить его конечную скорость!
Продолжая решать практические задачи, вы заметите, что БОЛЬШОЕ большинство задач трансляционной физики MCAT – это просто эти 4 формулы, применяемые с небольшими вариациями.
В следующий раз перейдем к свободному падению …
Учебные пособия и практические занятия д-ра Юэ-Лин Вонга
Общая физика :: Движение снаряда :: Как рассчитать # 1
Проблема №1: Найти туда, куда приземлится пушечное ядро, учитывая начальную скорость ( v ₀ ) и угол стрельбы ( θ ₀ )
(параметры, значения которых известны, выделены красным.Основное направление решения проблемы: попытаться вывести уравнения которые используют эти параметры с известными значениями.)
Пошаговое описание решения:
Разложите вектор начальной скорости на компоненты x и y.
Начальная скорость:
x-составляющая: v _x0 = v ₀ × cos θ ₀
y-составляющая: v _y0 = v ₀ × sin θ ₀

Анализируйте горизонтальное и вертикальное движение независимо:
Вертикальное движение: использовать постоянную ускорение (g)
v _y = v _y0 – g × t
, где g – сила тяжести (9.8 м / сек) или в свободном падении ускорение, а t – прошедшее время.
Когда объект достигает вершины его траектория движения параболы, v _y = 0 .
т.е. v _y0 – g × t _макс = 0
Þ т _макс = v _y0 / g

где t _max – время, за которое объект достигает максимума. высота.
Шаг 2
Вычислить:
т _макс
От:
v _y0
Попробуйте:
Используйте значения v _y0 , полученные выше для расчета времени (t _max), когда объект достигает своего максимума высота:
т _макс = v _y0 / g
t _max = м / сек./ 9,8 м / сек. = 0,408 сек.

Итак, теперь вы знаете, сколько времени требуется, чтобы объект достиг вершины его траектория движения параболы. После этого он начнет падать.
Как узнать это время, чтобы выяснить, где пушечное ядро приземлится и горизонтальное положение, когда оно достигнет самая высокая точка?
Из-за симметрии вертикального движения требуется столько же времени, чтобы пушечное ядро вернулось на землю (предположим, что пушечное ядро мяч был запущен на уровне земли).Таким образом, весь путь пушки мяч, от выстрела до возвращения на землю, занимает:

Шаг 3
Вычислить:
т _всего
От:
т _макс
Попробуйте:
Используйте t _max, полученный выше для расчета общего времени (t _всего) для пушечное ядро для возврата на землю:
т _всего = 2 × т _макс
т _всего = 2 × сек.= 0,816 сек.
Например, если пушечному ядру требуется 3 секунды, чтобы достичь максимума точки на его траектории движения параболы, то для это вернуться с самой высокой точки. Общее время на пушку Возвращение мяча в землю после выстрела составляет 6 секунд.
Эта информация о времени может быть использована для расчета, где ядро приземлится. (См. Анализ горизонтального движения ниже)
Горизонтальное движение: использовать постоянную скорость (v _x)
v _x = v _x0
горизонтальное расстояние (d _x), которое прошло пушечное ядро при приземлении на землю:
[при обработке этой директивы произошла ошибка]
Уравнения движения снаряда – Изучение – ScienceFlip
Уравнения движения снаряда – выучить
Уравнения движения снаряда
Следующие уравнения применяются к задачам движения снаряда:
Где:
= начальная скорость в
= конечная скорость в
= время в
= смещение в
= ускорение свободного падения ()
Уравнения и векторный анализ
Поскольку задачи о движении снаряда анализируются по компонентам горизонтального и вертикального вектора, уравнения должны быть записаны с индексами, чтобы отразить этот анализ, например:
Важность направления
Движение снаряда имеет дело со многими переменными, которые являются векторами.Это означает, что направление является очень важным фактором при анализе проблем движения снаряда.
По горизонтали: Поскольку снаряды могут двигаться только в одном направлении по горизонтали, мы, естественно, делаем это направление положительным.
Вертикально: Поскольку снаряды могут двигаться в обоих направлениях по вертикали, направление (вверх или вниз) должно быть отмечено как положительное. Все проанализированные здесь проблемы будут считаться положительными *. Ключевым результатом этого является то, что ускорение свободного падения всегда будет положительным ().
* Неважно, какое направление вы выберете в качестве положительного, оба будут вычислять один и тот же ответ, если направление остается неизменным на протяжении всей работы.
Ниже приведены общие значения, которые могут потребоваться во многих задачах движения снаряда:
Достигнута максимальная высота ()
Время полета ()
Диапазон ()
Эти переменные часто являются звеном для решения более сложных задач, состоящих из нескольких частей.
Достигнута максимальная высота ()
Максимальная достигнутая высота учитывает вертикальную часть движения снаряда. Ключевым моментом здесь является то, что на максимальной высоте будет вертикальная скорость.
Используя уравнение: и напишите это с вертикальными индексами:
Учитывая следующее:
Мы выводим следующее уравнение для максимальной высоты:
Время полета ()
Для снаряда, который запускается и завершает свою траекторию на одной и той же высоте, общее время полета будет в 2 раза больше времени, которое требуется снаряду для достижения максимальной высоты:
Используя уравнение: и напишите это с вертикальными индексами:
Учитывая следующее:
Мы выводим следующее уравнение для времени достижения максимальной высоты:
Учитывая:
Диапазон ()
Дальность полета снаряда учитывает горизонтальную часть движения снаряда.Ключевым моментом здесь является то, что снаряд имеет постоянную горизонтальную скорость
.
Используя уравнение: и записав это с горизонтальными индексами:
Учитывая следующее:
(горизонтальный вектор начальной скорости,)
(горизонтальная скорость постоянна)
Мы выводим следующее уравнение для диапазона:
Пример 1:
Снаряд запускается со скоростью 15 м / с под углом 40 ° к горизонтали, как показано ниже.Он приземляется на той же высоте, на которой был запущен. Вычислить:
а) Максимальная высота
б) Время полета
в) Диапазон
Ответы:
a) Использование:
Где: (с учетом положительного значения вниз)
(отрицательно, так как начальная вертикальная скорость увеличена)
Следовательно, максимальная достигнутая высота = 4.

Шаг 1 :	Установите данное уравнение равным соответствующей высоте.
Шаг 2 :	Решите уравнение, найденное на шаге 1, установив уравнение равным нулю и разложив уравнение на множители.
Шаг 3 :	В зависимости от проблемы определите, какой ответ или ответы верны. Не забудьте указать единицы в своем окончательном ответе.

Шаг 1 : Установите данное уравнение равным соответствующей высоте. В этом случае мы устанавливаем уравнение равным нулю, потому что высота земли равна нулю.
Шаг 2 : Решите уравнение, найденное на шаге 1, установив уравнение равным нулю и разложив уравнение на множители.
Шаг 3 : В зависимости от проблемы определите, какой ответ или ответы верны.Не забудьте указать единицы в своем окончательном ответе. В этом случае есть только один положительный ответ, который имеет смысл, потому что мяч ударяется о землю только один раз.

Урок 3. равноускоренное движение материальной точки – Физика – 10 класс

Движение тела, брошенного вертикально вверх и вниз

Скорость при прямолинейном равноускоренном движении тела

Равномерное прямолинейное движение | ЮКлэва

О том, как решить основную задачу механики

Равномерное прямолинейное движение

Определение равномерного прямолинейного движения

Скорость

Решение основной задачи механики для равномерного прямолинейного движения

Графики равномерного прямолинейного движения

Построение графика

Зависимость графика от проекции скорости

Встреча

График зависимости проекции скорости от времени. Нахождение проекции перемещения

Решение простейших задач и задач на графики равномерного прямолинейного движения

Текстовые задачи

Задачи на графики

Средняя скорость по перемещению. Средняя путевая скорость

Относительность движения. Операции над скоростями

Решение задач на среднюю скорость и действия со скоростями

Задачи в плоскости

Краткое содержание, основные формулы и определения

Заключение

Projectile Motion

3.5: Движение с постоянным ускорением (Часть 1)

Обозначение

Смещение и положение от скорости

Решение для окончательной скорости по ускорению и времени

Авторы и указание авторства

Двумерные уравнения кинематики

Расчет с постоянным ускорением – Nexus Wiki

Скорость

CC | Физика и поступательное движение

1.d = v

2.v

3.d =

4. v

Учебные пособия и практические занятия д-ра Юэ-Лин Вонга

Уравнения движения снаряда – Изучение – ScienceFlip

Оставить комментарий Отменить ответ