Конспект урока по математике на тему “Вычисление пределов функции”
Тема: «Вычисление пределов функции»
Цель: закрепить и усовершенствовать практические приемы вычисления предела функции.
Задачи:
образовательные:
· формировать умения и навыки вычисления пределов;
· познакомить обучающихся со способами раскрытия неопределенностей и других;
· сформировать у обучающихся навыки вычисления предела многочлена и отношения многочленов;
· сформировать у обучающихся навыки применения первого и второго замечательных пределов для раскрытия неопределенностей.
развивающие:
· развивать мышление обучающихся при выполнении упражнений;
· создать условия для развития у студентов умений формулировать промежуточные проблемы, предлагать пути их решения;
· создать условия для развития у студентов монологической и диалогической математической речи;
· формировать умения
и навыки самостоятельно умственного труда.
воспитательные:
· способствовать воспитанию дисциплинированности, усидчивости, навыков самостоятельности и умения работать индивидуально.
Тип урока: практическая работа.
Формы и методы: словесный, наглядный, исследовательский, фронтальная работа, самостоятельная работа.
Оборудование: карточки для обучающихся, опорные конспекты, решение типовых примеров, компьютер, презентация по теме «Предел функции».
Структура занятия:
1. Организационный момент (1 минута)
2. Сообщение темы занятия. Постановка цели и задач занятия. Мотивация. (3 минуты)
3. Актуализация прежних знаний (сопровождается демонстрацией слайдов). (7 минут)
а) фронтальный опрос;
б) устный счет.
4. Воспроизведение изученного и его применение в стандартных условиях. (5 минут)
5. Перенос
приобретенных знаний и их применение в новых или измененных условиях с целью
формирования умений.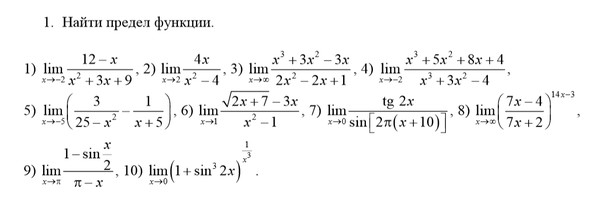 (50 мин.)
(50 мин.)
а) решение примеров у доски с комментированием;
б) самостоятельное выполнение обучающимися заданий под контролем преподавателя;
в) исследование.
6. Проверка умений обучающихся самостоятельно применять полученные знания. (15 мин.)
7. Повторение основных понятий. Разгадывание кроссворда.(5 мин.)
8. Подведение итогов занятия, рефлексия. (3 минуты)
9. Домашнее задание. (1 минута)
Ход занятия
1. Организационный момент.
Перед началом занятия преподаватель проводит проверку подготовленности кабинета к занятию.
Приветствие обучающихся, определение отсутствующих, заполнение группового журнала.
2. Сообщение темы занятия. Постановка цели и задач занятия. Мотивация.
Сообщается тема занятия: «Вычисление пределов функции». Вместе с обучающимися преподаватель формулирует цель и задачи занятия.
Значение теории пределов для математики трудно
переоценить – это центральное понятие математического анализа, на основе
которого формируются понятия производной, дифференциала и интеграла.
Понятие предела функции имеет большое значение для построения графиков функций. Кроме того, в дальнейшем мы будем изучать понятие производной и без знания предела функции рассмотрение этого понятия невозможно.
Понятие непрерывности играет важную роль, т.к. многие физические процессы характеризуются тем, что плавное изменение физических величин сменяется скачкообразно. То есть количественные изменения переходят в качественные. Это один из основных законов диалектики.
Но предел нашел применение не только в математике. Предельный анализ в экономике исследует изменяющиеся величины затрат или результатов при изменении объемов производства или потребления на основе анализа их предельных значений. Задачи на темы: рост вклада, рост населения страны, распад радиоактивного вещества, размножение бактерий решаются с помощью второго замечательного предела.
Но такое признание теория пределов имела не всегда. В
17 веке известный математик Мишель Ролль писал, что эта наука есть коллекция
гениальных ошибок. А великий французский мыслитель – Вольтер заметил, что
исчисление пределов представляет собой искусство вычислять и точно измерять
вещи, существование которых не может быть доказано. Начальный период развития
новых ветвей математики, связанных с понятиями функции, бесконечно малых
величин, пределов и производных, был охарактеризован Марксом как «мистический».
А великий французский мыслитель – Вольтер заметил, что
исчисление пределов представляет собой искусство вычислять и точно измерять
вещи, существование которых не может быть доказано. Начальный период развития
новых ветвей математики, связанных с понятиями функции, бесконечно малых
величин, пределов и производных, был охарактеризован Марксом как «мистический».
Многие десятилетия величайшие математики, в том числе Ньютон и Лейбниц, предпринимали попытки дать строгое определение предела. Но лишь в 19 веке великому французскому математику Огюстену Луи Коши удалась это сделать.
3. Актуализация прежних знаний (сопровождается демонстрацией слайдов).
а) Фронтальный опрос.
Ответы на вопросы теоретической части темы:
– предел функции в точке;
– односторонние пределы;
– предел функции при x стремящемся к бесконечности;
– основные теоремы о пределах;
– правила вычисления пределов;
– раскрытие неопределенностей;
– первый замечательный предел;
–
второй
замечательный предел.
б) Устный счет.
Для нахождения предела данных функций заменим аргумент x его предельным значением.
4. Воспроизведение изученного и его применение в стандартных условиях.
Задание 1
На рис. изображены графики функций. Установите для каждой из функции имеет ли она предел в точке х=2. если имеет, то чему он равен?
Ответы:
;;;не существует.
Задание 2.
Общее
правило: Когда
дан любой предел, сначала просто пытаемся подставить число в функцию.
Найти предел функции в точке:
Решение. Функция определена в точке х = π/6. Получим:
5. Перенос приобретенных знаний и их применение в новых или измененных условиях с целью формирования умений.
Решение примеров у доски с комментированием.
Рассмотрим теперь такие примеры, когда применение
свойств предела становится возможным лишь после некоторых предварительных
преобразований.
Общее правило: если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида , то для ее раскрытия нужно разложить числитель и знаменатель на множители.
Для этого чаще всего нужно решить квадратное уравнение и (или) использовать формулы сокращенного умножения.
Задание 3.
а) Найти
Решение. Здесь имеем неопределенность 0/0. Для того чтобы раскрыть эту неопределенность, разложим числитель и знаменатель дроби на множители и до перехода к пределу сократим дробь на множитель х-2. В результате получим
Итак, чтобы найти предел частного двух функций, где пределы делимого и делителя равны 0, нужно преобразовать функцию таким образом, чтобы выделить в делимом и делителе сомножитель, предел которого равен 0, и, сократив дробь на этом сомножитель, найти предел частного.
Самостоятельное выполнение обучающимися заданий под контролем преподавателя.
Один
обучающийся решает пример 2б) на вращающейся доске. Остальные решают
самостоятельно. Затем обсуждается решение.
Остальные решают
самостоятельно. Затем обсуждается решение.
б)
в) Найти
Сначала попробуем подставить -1 в дробь:
Разложим числитель и знаменатель на множители
Для того чтобы
разложить числитель на множители, нужно решить квадратное уравнение:
Сначала находим дискриминант:
И квадратный корень из него: .
Далее находим
корни:
Таким образом:
Знаменатель. Знаменатель уже является простейшим множителем, и упростить его никак нельзя.
Очевидно, что можно сократить на :
Теперь и подставляем -1 в выражение, которое осталось под знаком предела:
Самостоятельное выполнение обучающимися заданий под контролем преподавателя.
Один обучающийся решает пример 2г) на вращающейся доске. Остальные решают самостоятельно. Затем обсуждается решение.
г) Найти
Решение. Здесь имеем
неопределенность 0/0. Для того чтобы раскрыть эту неопределенность, разложим
числитель на множители и до перехода к пределу сократим дробь на множитель х+2.
Здесь предел делителя равен 0. Таким образом, знаменатель дроби неограниченно убывает и стремиться к 0, а числитель приближается к -1. Ясно, что вся дробь неограниченно растет, что условно записывается так: .
Задание 4.
Рассмотрим метод умножения числителя и знаменателя на сопряженное выражение.
Общее правило: Когда в числителе (знаменателе) находится разность корней (или корень минус какое-нибудь число), то для раскрытия неопределенности используют метод умножения числителя и знаменателя на сопряженное выражение.
а) Найти предел
Получена
неопределенность вида ,
которую нужно устранять.
В числителе находится разность корней. А от корней в математике принято, по-возможности, избавляться. По формуле разности квадратов:
Умножаем числитель на сопряженное выражение:
Число лучше
вынести за значок предела.
Теперь осталось
разложить числитель и знаменатель на множители и сократить «виновников»
неопределённости, ну а предел константы – равен самой константе:
Самостоятельное выполнение обучающимися заданий под контролем преподавателя.
Один обучающийся решает пример 2б) на вращающейся доске. Остальные решают самостоятельно. Затем обсуждается решение.
б) Найти предел
Разложим числитель
на множители:
Умножим числитель и знаменатель на сопряженное выражение
Перейдем к примерам нахождения предела функции на бесконечности.
Общее правило: для того, чтобы раскрыть неопределенность необходимо разделить числитель и знаменатель на в старшей степени.
Задание 5.
а) Найти предел
Снова в числителе и знаменателе находим в старшей степени:
Максимальная степень в числителе: 3
Максимальная степень в знаменателе: 4
Выбираем наибольшее значение, в данном случае
четверку.
Согласно нашему алгоритму, для раскрытия неопределенности делим числитель и
знаменатель на .
Полное оформление задания может выглядеть так:
Разделим числитель и знаменатель на
Исследование.
Группа делится на 2 группы. Каждая группа получает задание и выполняет его общими усилиями.
б) Найти
Решение. При x->∞ имеем неопределенность вида ∞/∞. Чтобы раскрыть эту неопределенность, разделим числитель и знаменатель на x3.Тогда получим
в) Найти
Решение. Разделив числитель и знаменатель на x3 и перейдя к пределу, получим
поскольку числитель последней дроби стремиться к пределу, отличному от нуля, а знаменатель – к нулю.
После решения
примера в группах. Представитель каждой группы поясняет решение своего примера.
Представитель каждой группы поясняет решение своего примера.
Все три примера на доске. Ответьте на вопросы:
Что общего в этих трех примерах?
Какие отличия?
Какие можно сделать выводы?
Общее | Различия | Выводы |
1.все пределы на бесконечности 2.пределы от дробно-рациональных функций 3.ответы в каждом примере не случайные | показатели степеней равны в 1 примере показатели степеней разные во 2 и в 3 примерах: Во 2 примере – у числителя показатель больше, чем у знаменателя; В 3 примере – у числителя показатель меньше, чем у знаменателя;
| 1.если показатели степеней числителя и знаменателя равны, то предел равен отношению коэффициентов при этих степенях 2. то предел равен бесконечности 3. если показатель степени числителя меньше показателя степени знаменателя, то предел равен 0. |
На основании открытого правила вычислить значение пределов устно:
1 группа | 2 группа | 3 группа |
г) Найти
Решение. При стремлении аргумента x к бесконечности имеем неопределенность вида ∞/∞. Чтобы раскрыть ее, разделим числитель и знаменатель дроби на x. Тогда получим
Задание 6.
Рассмотрим примеры, в которых
используются замечательные пределы.
а) Найти предел
Если мы замечаем в пределе синус, то это нас сразу должно наталкивать на мысль о возможности применения первого замечательного предела.
Выражение под знаком предела у нас похоже на первый замечательный предел, но это не совсем он, под синусом находится , а в знаменателе .
В подобных случаях
первый замечательный предел нам нужно организовать самостоятельно, используя
искусственный прием. Ход рассуждений может быть таким: «под синусом у нас ,
значит, в знаменателе нам тоже нужно получить ».
А делается это очень просто:
Обведенное выражение у нас превратилось в единицу и исчезло в произведении:
Теперь только осталось избавиться от трехэтажности дроби:
б) Найти
Решение. Произведем подстановку kx=y. Отсюда следует, что при , а x=y/k. Тогда получим
Так как
в). Найти
Решение. Имеем
Здесь мы разделили числитель и
знаменатель дроби на x (это можно сделать, так как но
x<>0), а затем воспользовались результатом предыдущего примера.
г) Найти
Решение. Преобразуем числитель к виду 1-cos8x=2sin24x. Далее находим
Самостоятельное выполнение обучающимися заданий под контролем преподавателя.
Один обучающийся решает примеры 2д) и 2е) на вращающейся доске. Остальные решают самостоятельно. Затем обсуждается решение.
д) Найти
Решение. 1 способ. Здесь имеет место неопределенность вида 0/0. Применяя известную тригонометрическую формулу и выполняя элементарные преобразования, получим
2 способ. Преобразуем числитель следующим образом:
Следовательно,
е) Найти
Решение. Заменив tg x на sin x/cos x, получим
Задание 7.
а). Найти предел
Когда выражение под знаком предела находится в степени – это первый признак того, что нужно попытаться применить второй замечательный предел.
Но сначала, как всегда, пробуем подставить бесконечно большое число в выражение .
Нетрудно заметить, что при основание степени , а показатель – , то есть имеется, неопределенность вида :
Данная
неопределенность как раз и раскрывается с помощью второго замечательного
предела. Но, как часто бывает, второй замечательный предел не лежит на блюдечке
с голубой каемочкой, и его нужно искусственно организовать. Рассуждать можно
следующим образом: в данном примере параметр ,
значит, в показателе нам тоже нужно организовать .
Для этого возводим основание в степень ,
и, чтобы выражение не изменилось – возводим в степень :
Но, как часто бывает, второй замечательный предел не лежит на блюдечке
с голубой каемочкой, и его нужно искусственно организовать. Рассуждать можно
следующим образом: в данном примере параметр ,
значит, в показателе нам тоже нужно организовать .
Для этого возводим основание в степень ,
и, чтобы выражение не изменилось – возводим в степень :
Когда задание оформляется от руки, карандашом помечаем:
Практически всё готово, страшная степень превратилась в симпатичную букву :
При этом сам
значок предела перемещаем в показатель:
б) Найти
Решение. Запишем основание степени в виде , а показатель степени – в виде . Следовательно,
в). Найти
Решение. Имеем
=
6. Проверка умений обучающихся самостоятельно применять полученные знания.
Самостоятельная работа (4 варианта).
Вариант – 1 · · · · | Вариант – 2 · · · · |
Вариант – 3 · · · · | Вариант – 4 · · · · |
7. Повторение
основных понятий.
Повторение
основных понятий.
Разгадывание кроссворда.
|
|
| 3.Б |
| ||||||||||||||
|
| Е | ||||||||||||||||
|
| С |
| 4.Н |
| |||||||||||||
|
| 1.О |
| К | Е | |||||||||||||
|
| Д |
| 2. |
| О | П | |||||||||||
|
| Н | Р | Н | Р | |||||||||||||
1. Н | Е | О | П | Р | Е | Д | Е | Л | Е | Н | Н | О | 5.С | Т | Ь |
| ||
|
| С |
| Д |
| Ч |
| Р |
| К |
| |||||||
Т | Е | Н | Ы |
| 2. | А | З | Р | Ы | В | А | |||||||
О | Л | О | В |
| Ч |
|
| |||||||||||
Р |
| С | Н | О | ||||||||||||||
3. К | О | Ш | И | Т | О | К | ||||||||||||
| Н |
| Ь | Й |
| |||||||||||||
Н |
|
| ||||||||||||||||
И |
| |||||||||||||||||
М |
| |||||||||||||||||
И | ||||||||||||||||||
ПО ГОРИЗОНТАЛИ:
1. Выражение,
значение которого не определено, – это неопределенность;
Выражение,
значение которого не определено, – это неопределенность;
2. Если f(x) не определена в точке х0 или не является непрерывной в этой точке, то точка х0 называется точкой разрыва функции f(x).
3. Французский математик, который ввел строгое определение предела. – Коши.
ПО ВЕРТИКАЛИ:
1. Пределы функции в точке слева и справа называются односторонними пределами функции в этой точке.
2. Если для любого найдется такое число, что для всех х, удовлетворяющих условию , будет выполнятся неравенство , то число А – предел функции при х, стремящемся к а.
3. Сколь угодно большое(малое), безграничное число – это бесконечность.
4. Функция y=f(x) называется непрерывной в точке х0, если существует предел функции в этой точке и он равен значению функции в этой точке.
5. Разность односторонних
пределов функции f(х) в точке разрыва , если они различны – это скачок функции.
8.
8.Подведение итогов занятия, рефлексия.
Студенты под руководством преподавателя подводят итоги занятия. Преподаватель называет оценки.
В качестве рефлексии обучающимся предлагается ответить на вопросы и высказать свои мнения.
Цель: осознание обучающимися своей учебной деятельности, самооценка результатов своей деятельности.
Рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности, адекватное понимание причин успеха или неуспеха.
- Что нового узнали на занятии?
- Какую цель мы ставили в начале урока?
- Наша цель достигнута?
- Что нам помогло справиться с затруднением?
- Какие знания нам пригодились при выполнении заданий на уроке?
- Как вы можете оценить свою работу?
- На следующем занятии мне бы хотелось…
9.Домашнее задание.
Вычислить пределы
1. а) б)
2. а) б)
а) б)
3. а) б)
4. а) б)
Теорема косинусов и синусов треугольника. Формулы и примеры
Поможем понять и полюбить математику
Начать учиться
202.6K
9 класс — насыщенное новыми знаниями время. Чтобы не запутаться в теории по геометрии, рекомендуем сделать карточки с информацией по каждой теме. В этой статье вы найдете самое важное про теорему косинусов.
Формулировка и доказательство теоремы косинусов
Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Формула Теоремы Пифагора:
a2> + b2> = c2>, где a, b — катеты, с — гипотенуза.
Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними. Формула теоремы косинусов: a2 = b2 + c2 – 2bc cos α |
В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:
BC2 = (x2 – x1)2 + (y2 – y1)2
В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).
cos2α + sin2α = 1 — основное тригонометрическое тождество.
BC2 = a2 = (b cos α – c)2 + b2sin2α = b2cos2α + b2sin2α – 2bc cos α + c2 = b2(cos2α + sin2α) – 2bc cos α + c2
Что и требовалось доказать.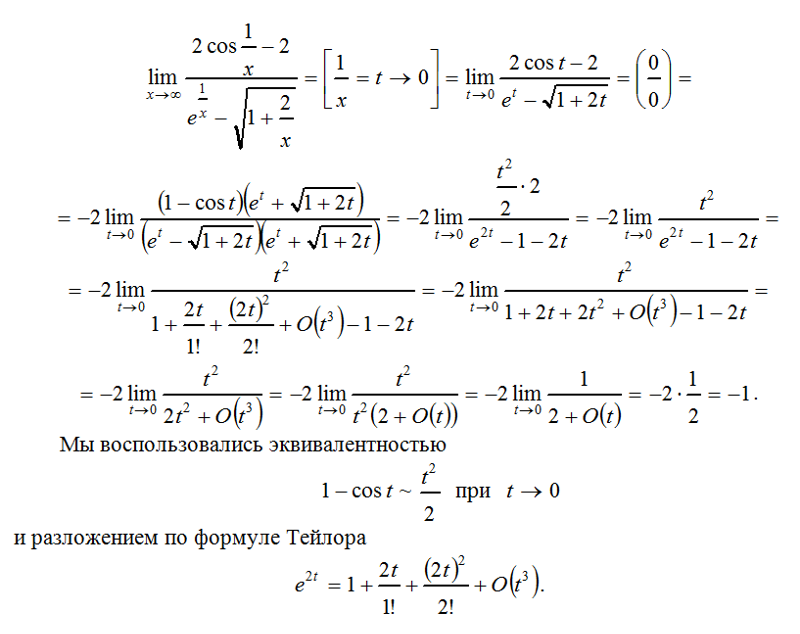
Совет: чтобы быстрее разобраться в сложной теме, запишитесь на онлайн-курсы по математике для детей и подростков.
С помощью теоремы косинусов можно найти косинус угла треугольника:
- Когда b2 + c2 – a2 > 0, угол α будет острым.
- Когда b2 + c2 – a2 = 0, угол α будет прямым.
- Когда b2 + c2 – a2 < 0, угол α будет тупым.
Запоминаем
Когда угол α прямой, то теорема косинусов превращаеся в теорему Пифагора.
Сформулируем еще одно доказательство теоремы косинусов.
Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:
- AD = b × cos α,
- DB = c – b × cos α.

Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
- h2 = b2 – (b × cos α)2
- h2 = a2 – (c – b × cos α)2
Приравниваем правые части уравнений:
- b2 – (b × cos α)2 = a2 – (c – b × cos α)2
либо
- a2 = b2 + c2 – 2bc × cos α
Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.
Определим стороны b и c:
- b2 = a2 + c2 – 2ac × cos β;
- c2 = a2 + b2 – 2ab × cos γ.
Демоурок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Формулировка теоремы для каждой из сторон треугольника
Теорема косинусов справедлива для всех сторон треугольника, то есть:
a2 = b2 + c2 – 2bc cos α
b2 = c2 + a2 – 2ca cos β
c2 = a2 + b2 – 2ab cos γ
Теорема косинусов может быть использована для любого вида треугольника.
Косинусы углов треугольника
Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:
Аналогично:
Определение угла с помощью косинуса
А теперь обратим внимание на углы.
Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).
Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.
Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.
Рассмотрение пределов изменения cos α и sin α
Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.
Предел изменения косинуса: -1 < cos α < 1.
Предел изменения синуса: 0 < sin α ≤ 1.
- Если cos α > 0, то α ∈ (0°;90°)
- Если cos α < 0, то α ∈ (90°;180°)
- Если cos α = 0, то α = 90°
Примеры решения задач
При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.
Пример 1. Дан треугольник АВС. Найти длину СМ.
Дан треугольник АВС. Найти длину СМ.
∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.
Как решаем:
- Так как АМ + МВ = 9, а AM/MB = 1/2, то АМ = 3, МВ = 6.
Из треугольника АВС найдем cos B: - Из треугольника СМВ по теореме косинусов найдём СМ:
Ответ: СМ = .
Пример 2. Дан треугольник АВС, в котором a2 + b2 < c2. Доказать, что ∠C — тупой угол.
Как доказываем:
- Для доказательства нужно вспомнить теорему косинусов для угла ∠C:
- Так как a2 + b2 < c2, то cos C < 0, следовательно, ∠C — тупой.

Что и требовалось доказать.
Эта задача нам показала, что с помощью теоремы косинусов можно определить тупой угол или острый.
- Если c2 = a2 + b2, то ∠C = 90°.
- Если c2 < a2 + b2, то ∠C — острый.
Больше объяснений по этой и другим темам вы найдете в справочнике по математике — с формулами, чертежами и примерами решения задач.
Шпаргалки по математике родителей
Все формулы по математике под рукой
Лидия Казанцева
Автор Skysmart
К предыдущей статье
Теоремы, которые точно пригодятся на ЕГЭ
К следующей статье
139.9K
Векторное произведение векторов
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Лучший инструмент для поиска предела функции
Калькулятор лимита
| Лим( | ) | |
| xabcdfghklmnopqrstuvwyz | → |
Используйте inf для +∞ и -inf для -∞
Сторона: Двусторонняя Правосторонняя (+) Левосторонняя (-)
Решение:
Если вы в настоящее время изучаете как оценить пределы функций , без сомнения, калькулятор пределов , который мы предлагаем вам здесь, будет вам очень полезен. С помощью Калькулятора пределов вы можете рассчитать односторонние пределы и двусторонние пределы .
С помощью Калькулятора пределов вы можете рассчитать односторонние пределы и двусторонние пределы .
Содержание
- 1 Калькулятор пределов
- 2 Инструкции по использованию калькулятора пределов
- 3 Определение предела функции
- 4 Правила предела
- 5 Методы нахождения предела функции
Инструкции по использованию Калькулятора лимитов
Взглянув на калькулятор, вы заметите, что он очень интуитивно понятен, что делает его использование очень простым. Чтобы найти предел функции, вам просто нужно выполнить следующие простые шаги:
- Напишите функцию, предел которой вы хотите оценить, для этого вы должны использовать список допустимых функций.
- Затем выберите переменную и к какому значению приближается переменная.
- Выберите тип предела, который вы хотите рассчитать, у вас есть три варианта:
- Двусторонний предел
- Односторонний предел:
- Правосторонний (+)
- Левосторонний (-)
- Наконец, нажмите кнопку расчета, чтобы получить результат.

| Допустимые функции и символы | Описание | |
|---|---|---|
| квт() | Квадратный корень | |
| лн() | Натуральный логарифм | |
| журнал() | Основание логарифма 10 9 | Экспоненты |
| абс() | Абсолютное значение | |
| sin(), cos(), tan(), csc(), sec(), cot() | Основные тригонометрические функции | |
| asin(), acos(), atan(), acsc(), asec(), acot() | Обратные тригонометрические функции | |
| sinh(), cosh(), tanh(), csch(), sech(), coth() | Гиперболические функции | |
| asinh(), acosh(), atanh(), acsch(), asech(), acoth() | Обратные гиперболические функции | |
| число пи | PI-номер (π = 3,14159. ..) ..) | |
| е | Число Непера (e= 2,71828…) | |
| я | Для обозначения мнимой составляющей комплексного числа. | |
| инф | ∞ |
Определение предела функции
Предел функции можно определить как значение L, к которому f(x) приближается, когда независимая переменная x приближается к определенному значению x 92. Предел этой функции при приближении x к 2, обозначаемый как lim(x→2)f(x), равен 4. Это связано с тем, что по мере приближения x к 2 значение f(x) становится все ближе и ближе к 4.
Предел этой функции при приближении x к 2, обозначаемый как lim(x→2)f(x), равен 4. Это связано с тем, что по мере приближения x к 2 значение f(x) становится все ближе и ближе к 4.
Предел функции можно использовать для описания поведения функции вблизи определенной точки, даже если функция в этой точке не определена. Например, функция g(x) = 1/x не определена при x = 0, но мы все же можем говорить о пределе этой функции при приближении x к 0. В этом случае предел равен бесконечности, так как при x достигает ближе и ближе к 0 значение g(x) становится все больше и больше.
Пределы — важное понятие в математике, потому что они позволяют нам описывать поведение функций в точках, где функция не может быть определена, и они играют центральную роль в развитии исчисления.
Правила ограничения
Свойства пределов — это набор алгебраических правил и процедур, используемых для их вычисления. Понятие предела является фундаментальным для исчисления, и определение его значения не должно быть сложной задачей, если вы знаете эти правила. Ниже приведен список основных свойств лимитов:
Ниже приведен список основных свойств лимитов:
| Предел константы | lim x → a к = к |
| Постоянное множественное правило | LIM x → A ( K · F ( x ) = K · LIM x → A ( F ( → A ( F ( → A ( F ()) ) ( F ()) ) ( F ()) A ( F ()))). |
| Сумма функций | lim x → a ( f ( x )+ g ( x )) = lim x → a ( f ( x ))+ lim x → a ( g ( x )) |
| Различие функций | lim x → a ( f ( x )- g ( x )) = lim x → a ( f ( x ))- lim х → а ( г ( х )) |
| Произведение функций | LIM x → A ( F ( x ) · G ( x )) = LIM x → A ( F ( x ). → a ( г ( x )) → a ( г ( x )) |
| Частное функций | lim x → a f ( x ) г ( x ) = lim x → a ( f ( x )) lim x → a ( г ( x ))  ;   i f    lim x → a ( г ( x )) ≠ 0 |
| Правило предельной степени | lim x → a ( f ( x ) n ) = ( lim x → a ( f f )0028 ( x ))) п |
| Пределы основного закона | lim x → a (√ n f ( x )) = √ n lim x → a ( f ( x )) |
| Предел полиномиальной функции | lim x → a ( p ( x )) = ( p ( a )) |
Методы нахождения предела функции
Прямая подстановка: Этот метод включает в себя просто подстановку значения, к которому x приближается, в функцию и просмотр результата.
 Если выход представляет собой конечное число, то это значение предела. Если на выходе бесконечность или неопределенное значение, нам нужно использовать другой метод.
Если выход представляет собой конечное число, то это значение предела. Если на выходе бесконечность или неопределенное значение, нам нужно использовать другой метод.Разложение на множители. Этот метод включает преобразование выражения функции в более простые термины, а затем использование свойств пределов для нахождения предела.
Правило Лопиталя: Этот метод включает в себя получение производной функции по x и нахождение предела производной. Если производная имеет конечный предел при приближении x к определенному значению, то исходная функция также имеет конечный предел при этом значении.
Расширение ряда: Этот метод включает расширение функции в ряд Тейлора вокруг точки, где берется предел. Затем можно рассчитать предел, взяв соответствующий член в разложении.
Асимптотическое расширение: Этот метод включает в себя нахождение выражения для функции, которая становится точной в пределе, когда x приближается к определенному значению.
 Затем можно рассчитать предел, взяв соответствующий член в разложении.
Затем можно рассчитать предел, взяв соответствующий член в разложении.Численные методы: В некоторых случаях может потребоваться использование численных методов для аппроксимации предела функции. Одним из распространенных методов является использование компьютерной программы для оценки функции в большом количестве точек вблизи точки, где берется предел, а затем использование этих значений для оценки предела.
– Googlesuche
AlleBilderVideosNewsMapsShoppingBücher
suchoptionen
Калькулятор непрерывности функций – Symbolab
www.symbolab.com › … › Функции › Поиск непрерывности функции
Бесплатный 900 калькулятор -шаг.
Калькулятор непрерывности — AllMath
www.allmath.com › калькулятор непрерывности
Калькулятор непрерывности определяет, является ли функция непрерывной или прерывистой. Этот непрерывный калькулятор находит результат шагами за пару секунд.
Этот непрерывный калькулятор находит результат шагами за пару секунд.
Онлайн-калькулятор разрыва – Wolfram|Alpha
www.wolframalpha.com › калькуляторы › разрыв…
Больше, чем просто онлайн-инструмент для изучения непрерывности функций. Wolfram|Alpha — отличный инструмент для поиска неоднородностей функции.
Калькулятор непрерывности
www.meracalculator.com › математика › расчет непрерывности…
Калькулятор непрерывности. Введите функцию 🛈. Пример загрузки. ⌨. Переменная: 🛈. x, y, z, u, v, t, w, θ. Ограничение (n): 🛈. Рассчитать сброс. Отвечать. Показать шаги …
Определить, является ли непрерывное f(x) = квадратным корнем из x/(x-2) | Mathway
www.mathway.com › популярные задачи › Исчисление
Примеры исчисления; Шаг 1.2.1. Найдите все значения, при которых выражение переключается с отрицательного на положительное, установив каждый множитель равным 0 0 и решив. х=0 …
Ähnliche Fragen
Как рассчитывается значение непрерывности?
Каковы 3 условия непрерывности?
Что делает функцию калькулятора непрерывной?
Как узнать, непрерывно это или прерывисто?
Поиск непрерывности в графическом калькуляторе [Calc] – YouTube
www. youtube.com › смотреть
youtube.com › смотреть
18.03.2020 · Поиск непрерывности в графическом калькуляторе [Calc]. Смотреть позже. Делиться. Копировать ссылку. Информация …
Dauer: 3:19
Прислан: 18.03.2020
Непрерывность Липшица – Десмос
www.desmos.com › калькулятор
Untitled Graph. Войдите или зарегистрируйтесь. 1. 2. питается от. питаться от. “х” х. “у” у. «а» в квадрате а 2. «а» Верхний индекс, «б» , базовая линия а б.
Калькулятор коррекции непрерывности
www.criticalvaluecalculator.com › Continuity-correc…
Калькулятор коррекции непрерывности. Количество попыток (N) Количество успехов (n) Вероятность успеха (0 < p < 1). Рассчитать предварительный загрузчик
Калькулятор уравнения непрерывности — Онлайн-инструмент расчета потока
drr.ikcest.org › приложение › sca75
Описание приложения. расход=площадь потока×расход. Пример использования. Исходные данные: Площадь циркуляции, сечение циркуляции -10 кв.

 если
показатель степени числителя больше показателя степени знаменателя,
если
показатель степени числителя больше показателя степени знаменателя, П
П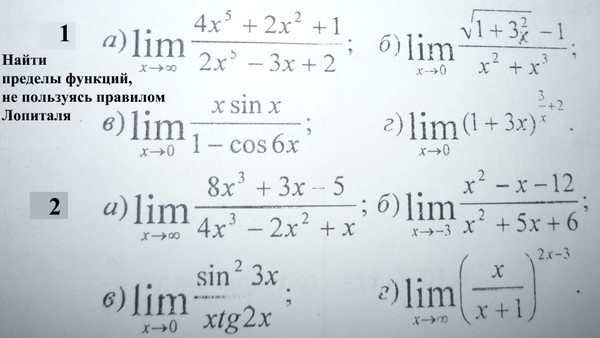 Р
Р



 Если выход представляет собой конечное число, то это значение предела. Если на выходе бесконечность или неопределенное значение, нам нужно использовать другой метод.
Если выход представляет собой конечное число, то это значение предела. Если на выходе бесконечность или неопределенное значение, нам нужно использовать другой метод. Затем можно рассчитать предел, взяв соответствующий член в разложении.
Затем можно рассчитать предел, взяв соответствующий член в разложении.