lim x→2 [f(x) + g(x)] (б) lim x→0 [f(x) − g(x)] (в) lim x→−1 [f(x)g(x) )] (d) lim x→3 f(x) g(x) (e) lim x→2 [x2f(x)] (f) f(−1) + lim x→−1 g(x)
Исчисление
Эдди Б.
спросил 21.01.21Подписаться І 1
Подробнее
Отчет
1 ответ эксперта
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Ким Г. ответил 21.01.21
Репетитор
4.9 (46)
Студент Йельского университета, получающий степень магистра статистики и докторскую степень в области общественного здравоохранения
Об этом репетиторе ›
Об этом репетиторе ›
Привет, Эдди! Отличные вопросы! Похоже, этот вопрос просит нас понять логику ограничений для нескольких функций, даже если у нас не обязательно есть для них точные уравнения.
а) Чтобы найти предел как x -> 2 f(x) + g(x) , полезно помнить важное свойство пределов: что предел суммы двух функций равен сумме пределы . Это означает, что мы должны отдельно найти предел при x -> 2 для f(x) и предел при x -> 2 0f g(x), а затем сложить их вместе. Сделаем так:
i) f(x): Посмотрим на x = 2 на графике f. Начиная с x = 1 и двигаясь к x = 2 («левая» сторона), мы видим, что по мере того, как мы все ближе и ближе подходим к x = 2, функция f(x) становится все ближе и ближе к f(x) = -1 (точка (2,-1)). Таким образом, у нас есть хорошее предположение, что предел = 2,
ii) g(x): Давайте теперь посмотрим на график g(x). Используя ту же логику, я могу начать с x = 1 и двигаться к x = 2.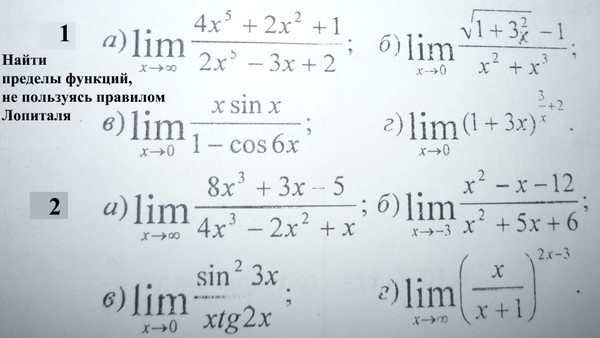 При этом я замечаю, что график приближается к точке (2, 2) (т. е. g(x) = 2). То же самое произойдет, если я начну с x = 3 и перейду в другую сторону, поэтому наш предел для g(x) равен 2,9.0003
При этом я замечаю, что график приближается к точке (2, 2) (т. е. g(x) = 2). То же самое произойдет, если я начну с x = 3 и перейду в другую сторону, поэтому наш предел для g(x) равен 2,9.0003
Сложите их вместе, и мы получим ответ:
Теперь, когда мы установили основную логику нахождения предела в части (а), мы можем подойти к остальным аналогичным образом. :
б) Опять же здесь я могу использовать свойство, аналогичное тому, что использовалось выше: что предел разности равен разнице пределов. Это означает, что все, что мне нужно сделать, это найти предел при x -> 0 для f(x), найти предел при x -> 0 для g(x) и затем вычесть два. Но ждать! Я сразу вижу проблему. График g(x) имеет два «предела» при x = 0; когда вы начинаете с -1 и направляетесь к нулю, мы приближаемся к точке (0,3), но если мы начинаем с 1, мы приближаемся к (0,1). Поскольку правосторонний и левосторонний предел не равны друг другу, предела для g не существует! Это означает, что 
c) Аналогично частям (a) и (b), предел продукта равен произведению предела. Итак, давайте снова рассмотрим f(x) и g(x) по отдельности. Я собираюсь выйти из строя для этого, и вы поймете, почему. Предел для g(x) довольно прост: мы начинаем с x = -2 и направляемся к x = -1, чтобы найти график, приближающийся к (-1, 2). То же самое для другой стороны, поэтому предел x ->
Что происходит с f? Похоже, если мы посмотрим влево от оси y, у нас есть гладкая кривая в каждой точке , кроме x = -1, где есть «пробел» в (-1,1) и «скачок» к точке (-1,3). Означает ли это, что наш ответ равен 3, так как это то, чему равно f(x), когда мы подставляем x = -1? Не совсем! Вот где пределы отличаются от нашей обычной алгебры. Мы используем ту же логику, что и для частей (a) и (b) — начинаем с -2 и приближаемся к -1. К чему подходит функция ? Похоже на точку (-1,1). То же самое, если мы начнем с x = 0. Таким образом, предел x -> -1 для f (x) на самом деле равен 1! Умножьте это на предел для g(x), и мы получим 2 x 1 = 1.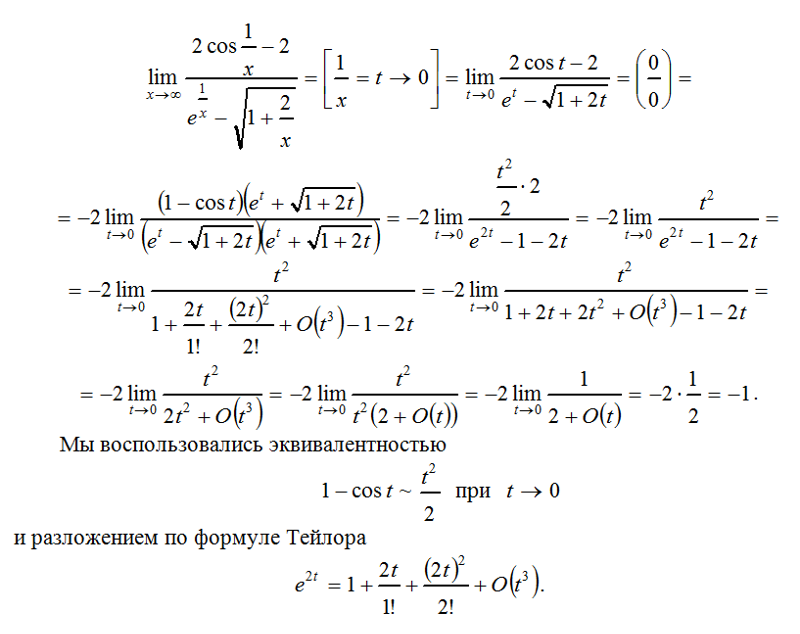
d) Снова отметим, что предел произведения равен произведению пределов, это намного проще, чем части (b) и (c) – так как нет странных пробелов, скачков или острых точек ни на одном из графиков при x = 3, мы можем просто перемножить f(3) и g(3) вместе, чтобы получить наш ответ – и поскольку g(3) равно нулю, а все, что умножено на ноль, равно нулю, наш предел будет равен ноль.
e) У меня есть некоторые проблемы с пониманием того, что именно задает этот вопрос (просто потому, что Wyzant иногда затрудняет использование математических обозначений), но вот мой лучший вариант. Здесь мы используем принцип, что  0037 -2 х 2 = -4.
0037 -2 х 2 = -4.
f) Наконец, этот вопрос заставляет нас еще раз взглянуть на то, что мы обнаружили в части (c) — что f(-1) не обязательно равно пределу при x -> -1 f(x) .
Надеюсь, это поможет! ЛМК, если есть еще вопросы 🙂
Голосовать за 0 голос против
Подробнее
Отчет
Все еще ищете помощи? Получите правильный ответ, быстро.
Получите бесплатный ответ на быстрый вопрос.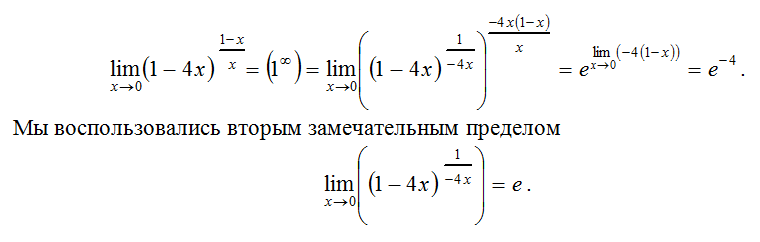
Ответы на большинство вопросов в течение 4 часов.
ИЛИ
Найдите онлайн-репетитора сейчас
Выберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.
Поиск пределов: определение, правила и функции
Подобно бусам на нитке, ведущей к подвеске, точки на графике могут привести вас к пределу функции. Как мы можем использовать точки на графике для оценки пределов? Хороший вопрос! Здесь мы рассмотрим некоторые из различных способов нахождения пределов функций!
Нахождение пределов в исчислении
Существует множество способов найти предел функции!
Вы можете использовать определение предела \(\epsilon\), \(\delta\) и написать доказательство. См. Пределы функции для примеров этого метода.
Вы можете посмотреть на график или таблицу значений, чтобы увидеть, каким может быть предел.
 См. Поиск пределов с помощью графика или таблицы для множества примеров нахождения пределов таким способом.
См. Поиск пределов с помощью графика или таблицы для множества примеров нахождения пределов таким способом.Вы можете посмотреть на ограничение слева и справа функции и посмотреть, совпадают ли они. См. Односторонние ограничения для определений и примеров использования этого метода.
Вы можете использовать законы пределов, которые являются уже доказанными теоремами для нахождения предела. Если ваша функция хороша, люди часто находят предел именно так. Для получения дополнительной информации о свойствах пределов см. Законы о предельных значениях
Вам может понадобиться использовать специальную теорему для нахождения предела, такую как теорема сжатия или теорема о промежуточном значении. Оба они очень полезны, и теорема о промежуточном значении появится позже в таких темах, как нахождение максимального значения функции. См. «Теорему о сжатии» или см. «Теорему о промежуточном значении», чтобы узнать, как их использовать.
Здесь вы увидите пример способов нахождения предела функции.
Использование определения предела
Чтобы просмотреть определение предела функции, см. Пределы функции.
Возьмем \(f(x)=k\), где \(a\) и \(k\) – постоянные действительные числа. Верно ли, что
\[lim_{x \rightarrow a} f(x)=k\]
Ответ:
Да. Используя определение, для любого заданного \(\epsilon > 0\)
\[|f(x)-k|=|k-k|=0< \epsilon\]
независимо от того, какую \(\delta\) вы используете. Таким образом, константные функции имеют предел, которого вы от них ожидаете.
Возьмем \(f(x)=x\), и пусть \(a\) будет постоянным действительным числом. Откуда вы знаете, что
\[lim_{x \rightarrow a} f(x)=a\]
Ответ:
У вас может возникнуть соблазн сказать: «Конечно, предел равен \(a\) – функция – это просто строка”. На самом деле этого почти достаточно. Вы не можете использовать какие-либо свойства пределов, но вы можете использовать определение и взять \(\delta = \epsilon\), чтобы показать, что предел равен \(a\). 92+7\), а \(а\) — постоянное действительное число. Найдите
92+7\), а \(а\) — постоянное действительное число. Найдите
\[lim_{x \rightarrow a} f(x)\]
Ответ:
Обратите внимание, что функция представляет собой просто сумму и произведение степеней \(x\) вместе с константой \( 7\). Вы уже знаете, что
\(lim_{x \rightarrow a} x=a\) и \(lim_{x \rightarrow a} 7 =7\)
из двух приведенных выше примеров, что означает условия для применения Правило суммы, правило произведения и правило константы выполняются. Затем их применение дает 92+7\]
Нахождение пределов графически
Ниже приведен пример использования графика для нахождения предела функции. Дополнительные сведения о подобных проблемах см. в разделе Поиск пределов с помощью графика или таблицы.
Рассмотрим функцию
\[f(x)=\dfrac{1}{4}(x+1)(x-1)(x-5)\]
Найдите предел функции как \( х \стрелка вправо 3 \).
Ответ:
Сначала начертите график функции и составьте таблицу значений рядом с \(x=3\). Хотя у функции больше корней, чем показано на графике, поскольку вас интересует только предел как \(x \стрелка вправо 3\), имеет смысл увеличить масштаб функции.
Хотя у функции больше корней, чем показано на графике, поскольку вас интересует только предел как \(x \стрелка вправо 3\), имеет смысл увеличить масштаб функции.
Использование графика с несколькими точками для нахождения предела функции, выделенной красным цветом.
| \(x\) | \(f(x)\) |
| 2.5 | -3.28 |
| 2.55 | -3.37 |
| 2.6 | -3.46 |
| 2.65 | -3.54 |
| 2.7 | -3.62 |
| 2.75 | -3.69 |
| 2.8 | -3.76 |
| 2.85 | -3.83 |
| 2.9 | -3.89 |
| 2.95 | -3.95 |
| 3.0 | -4.0 |
| 3.05 | -4.05 |
| 3.1 | -4.09 |
| 3.15 | -4.13 |
3. 2 2 | -4.16 |
| 3.25 | -4.18 |
| 3.3 | -4.20 |
| 3.35 | -4.22 |
| 3.4 | -4.22 |
| 3.45 | -4.46 |
Table 1. Limit example points.
Точки на графике соответствуют точкам в таблице. Как на графике, так и в таблице видно, что по мере того, как \(x\) становится все ближе и ближе к \(x= 3\), значения функции все ближе и ближе к \(-4\). Это означает, что
\[ lim_{x \rightarrow 3} f(x)=-4\]
.
Обратите внимание, что при поиске предела значение функции в точке \(x=3\) на самом деле не интересует, потому что в определении говорится, что нужно смотреть близко к \(x=3\), но не к \(x=3 \).
Алгебраическое нахождение пределов
Другие примеры алгебраического нахождения пределов приведены в отдельной статье. См. раздел «Нахождение пределов конкретных функций».

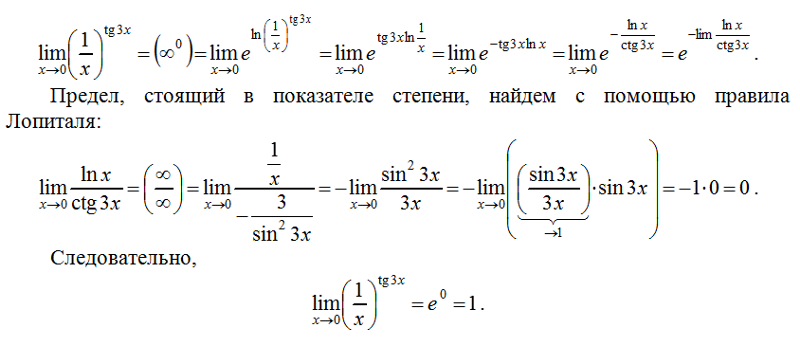 См. Поиск пределов с помощью графика или таблицы для множества примеров нахождения пределов таким способом.
См. Поиск пределов с помощью графика или таблицы для множества примеров нахождения пределов таким способом.