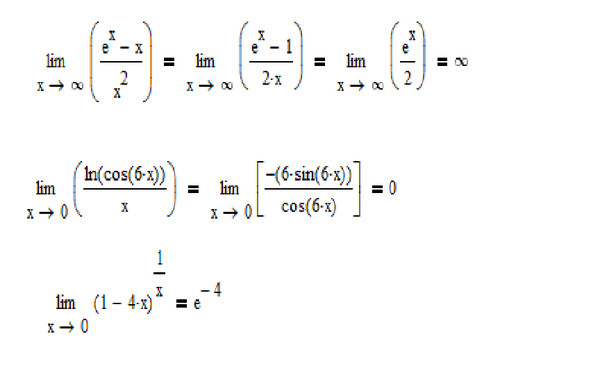Найти предел используя правило лопиталя онлайн: Правило Лопиталя онлайн

Калькулятор онлайн.Решение пределов. Решение пределов онлайн

Правило Лопиталя (п. Л.) облегчает вычисление пределов функций. Например, надо найти предел функции, которая является отношением функций стремящихся к нулю. Т.е. отношение функций это неопределенность 0/0. Раскрыть ее поможет . В пределе отношение функций можно заменить отношением производных этих функций. Т.е. надо производную числителя разделить на производную знаменателя и от этой дроби взять предел.

1. Неопределенность 0/0. Первое п.Л.

Если = 0, то , если последний существует.

2. Неопределенность вида ∞/∞ Второе п. Л.

Нахождение пределов такого типа называется раскрытием неопределенностей.

Если = ∞, то , если последний существует.

3. Неопределенности 0⋅∞, ∞- ∞, 1 ∞ и 0 0 сводятся к неопределенностям 0/0 и ∞/∞ путем преобразований. Такая запись служит для краткого указания случая при отыскании предела. Каждая неопределенность раскрывается по своему. Правило Лопиталя можно применять несколько раз, пока не избавимся от неопределенности.

Применение правила Лопиталя приносит пользу тогда, когда отношение производных удается преобразовать к более удобному виду легче, чем отношение функций.

• 0⋅∞ произведение двух функций, первая стремится к нулю, вторая к бесконечности;
• ∞- ∞ разность функций, стремящихся к бесконечности;
• 1 ∞ степень, ее основание стремится к единице, а показатель к бесконечности;
• ∞ 0 степень, ее основание стремится к бесконечности, а степень к нулю;
• 0 0 степень, ее основание стремится к 0 и показатель тоже стремятся к нулю.

Пример 1. В этом примере неопределенность 0/0

Пример 2. Здесь ∞/∞

В этих примерах производные числителя делим на производные знаменателя и подставляем предельное значение вместо х.

Пример 3. Вид неопределенности 0⋅∞ .

Неопределенность 0⋅∞ преобразуем к ∞/∞, для этого х переносим в знаменатель в виде дроби 1/x , в числителе пишем производную от числителя, а в знаменателе производную от знаменателя.

Пример 4 Вычислить предел функции

Здесь неопределенность вида ∞ 0 Сначала логарифмируем функцию, затем найдем от нее предел

Для получения ответа надо е возвести в степень -1, получим e -1 .

Пример 5. Вычислить предел от если x → 0

Решение. Вид неопределенности ∞ -∞ Приведя дробь к общему знаменателю перейдем от ∞-∞ к 0/0. Применим правило Лопиталя, однако снова получим неопределенность 0/0, поэтому п. Л. надо применить второй раз. Решение имеет вид:

= = = =
= =

Пример 6 Решить

Решение. Вид неопределенности ∞/∞, раскрыв ее получим

В случаях 3), 4), 5) сначала логарифмируют функцию и находят предел логарифма, а затем искомый предел е возводим в полученную степень.

Пример 7. Вычислить предел

Решение. Здесь вид неопределенности 1 ∞ . Обозначим A =

Тогда lnA = = = = 2.

Основание логарифма е, поэтому для получения ответа надо е возвести в квадрат, получим e 2 .

Иногда бывают случаи, когда отношение функций имеет предел, в отличие от отношения производных, которое не имеет его.

Рассмотрим пример:

Т.к. sinx ограничен, а х неограниченно растет, второй член равен 0.

Эта функция не имеет предела, т. к. она постоянно колеблется между 0 и 2, к этому примеру неприменимо п. Л.

Раскрытие неопределённостей вида 0/0 или ∞/∞ и некоторых других неопределённостей, возникающих при вычислении предела отношения двух бесконечно малых или бесконечно больших функций значительно упрощается с помощью правила Лопиталя (на самом деле двух правил и замечаний к ним).

Суть правил Лопиталя

состоит в том, что в случае, когда вычисление предела отношений двух бесконечно малых или бесконечно больших функций даёт неопределённости видов 0/0 или ∞/∞, предел отношения двух функций можно заменить пределом отношения их производных и, таким образом, получить определённный результат.

Перейдём к формулировкам правил Лопиталя.

Правило Лопиталя для случая предела двух бесконечно малых величин . Если функции f (x ) и g (x a a , причём в этой окрестности g “(x a равны между собой и равны нулю

().

Правило Лопиталя для случая предела двух бесконечно больших величин

. Если функции f (x ) и g (x ) дифференцируемы в некоторой окрестности точки a , за исключением, может быть, самой точки a , причём в этой окрестности g “(x )≠0 и если и если пределы этих функций при стремлении икса к значению функции в точке a равны между собой и равны бесконечности

(),

то предел отношения этих функций равен пределу отношения их производных

().

Иными словами, для неопределённостей вида 0/0 или ∞/∞ предел отношения двух функций равен пределу отношения их производных, если последний существует (конечный или бесконечный).

Замечания .

1. Правила Лопиталя применимы и тогда, когда функции

f (x ) и g (x ) не определены при x = a .

2. Если при вычисления предела отношения производных функций f (x ) и g (x ) снова приходим к неопределённости вида 0/0 или ∞/∞, то правила Лопиталя следует применять многократно (минимум дважды).

3. Правила Лопиталя применимы и тогда, когда аргумент функций (икс) стремится не к конечному числу a , а к бесконечности (x → ∞).

К неопределённостям видов 0/0 и ∞/∞ могут быть сведены и неопределённости других видов.

Раскрытие неопределённостей видов “ноль делить на ноль” и “бесконечность делить на бесконечность”

Пример 1.

x =2 приводит к неопределённости вида 0/0. Поэтому производную каждой функции и получаем

В числителе вычисляли производную многочлена, а в знаменателе – производную сложной логарифмической функции . Перед последним знаком равенства вычисляли обычный предел , подставляя вместо икса двойку.

Пример 2. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:

Решение. Подстановка в заданную функцию значения x

Пример 3. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:

Решение. Подстановка в заданную функцию значения x =0 приводит к неопределённости вида 0/0.

Поэтому вычисляем производные функций в числителе и знаменателе и получаем:

Пример 4. Вычислить

Решение. Подстановка в заданную функцию значения икса, равного плюс бесконечности, приводит к неопределённости вида ∞/∞. Поэтому применим правило Лопиталя:

Замечание. Переходим к примерам, в которых правило Лопиталя приходится применять дважды, то есть приходить к пределу отношений вторых производных, так как предел отношения первых производных представляет собой неопределённость вида 0/0 или ∞/∞.

Применить правило Лопиталя самостоятельно, а затем посмотреть решение

Раскрытие неопределённостей вида “ноль умножить на бесконечность”

Пример 12.

Вычислить

.

Решение. Получаем

В этом примере использовано тригонометрическое тождество .

Раскрытие неопределённостей видов “ноль в степени ноль”, “бесконечность в степени ноль” и “один в степени бесконечность”

Неопределённости вида , или обычно приводятся к виду 0/0 или ∞/∞ с помощью логарифмирования функции вида

Чтобы вычислить предел выражения , следует использовать логарифмическое тождество , частным случаем которого является и свойство логарифма .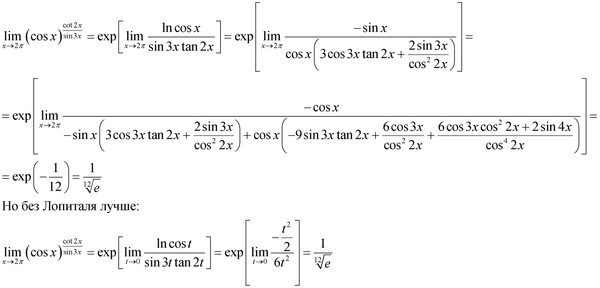

Используя логарифмическое тождество и свойство непрерывности функции (для перехода за знак предела), предел следует вычислять следующим образом:

Отдельно следует находить предел выражения в показателе степени и возводить

e в найденную степень.

Пример 13.

Решение. Получаем

.

.

Пример 14. Вычислить, пользуясь правилом Лопиталя

Решение. Получаем

Вычисляем предел выражения в показателе степени

.

.

Пример 15. Вычислить, пользуясь правилом Лопиталя

• Правило Лопиталя и раскрытие неопределённостей
• Раскрытие неопределённостей видов “ноль делить на ноль” и “бесконечность делить на бесконечность”
• Раскрытие неопределённостей вида “ноль умножить на бесконечность”
• Раскрытие неопределённостей видов “ноль в степени ноль”, “бесконечность в степени ноль” и “один в степени бесконечность”
• Раскрытие неопределённостей вида “бесконечность минус бесконечность”

Правило Лопиталя и раскрытие неопределённостей

Раскрытие неопределённостей вида 0/0 или ∞/∞ и некоторых других неопределённостей значительно упрощается с помощью правила Лопиталя.

Суть правила Лопиталя состоит в том, что в случае, когда вычисление предела отношений двух функций даёт неопределённости видов 0/0 или ∞/∞, предел отношения двух функций можно заменить пределом отношения их производных и, таким образом, получить определённный результат.

Вообще, под правилами Лопиталя понимаются несколько теорем, которые могут быть переданы в следующей одной формулировке.

Правило Лопиталя . Если функции f (x ) и g (x ) дифференцируемы в некоторой окрестности точки , за исключением, может быть, самой точки , причём в этой окрестности

(1)

Иными словами, для неопределённостей вида 0/0 или ∞/∞ предел отношения двух функций равен пределу отношения их производных, если последний существует (конечный или бесконечный).

В равенстве (1) величина , к которой стремится переменная, может быть либо конечным числом, либо бесконечностью, либо минус бесконечностью.

К неопределённостям видов 0/0 и ∞/∞ могут быть сведены и неопределённости других видов.

Раскрытие неопределённостей видов “ноль делить на ноль” и “бесконечность делить на бесконечность”

Пример 1. Вычислить

x =2 приводит к неопределённости вида 0/0. Поэтому применим правило Лопиталя:

Пример 2. Вычислить

Решение. Подстановка в заданную функцию значения x

Пример 3. Вычислить

Решение. Подстановка в заданную функцию значения x =0 приводит к неопределённости вида 0/0. Поэтому применим правило Лопиталя:

Пример 4. Вычислить

Решение. Подстановка в заданную функцию значения икса, равного плюс бесконечности, приводит к неопределённости вида ∞/∞. Поэтому применим правило Лопиталя:

Замечание. Если предел отношения производных представляет собой неопределённость вида 0/0 или ∞/∞, то можно снова применить правило Лопиталя, т.е. перейти к пределу отношения вторых производных, и т.д.

Пример 5. Вычислить

Решение. Находим

Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных дают неопределённость вида ∞/∞.

Пример 6. Вычислить

Представьте стаю воробьёв с выпученными глазами. Нет, это не гром, не ураган и даже не маленький мальчик с рогаткой в руках. Просто в самую гущу птенчиков летит огромное-огромное пушечное ядро. Именно так правила Лопиталя расправляются с пределами, в которых имеет место неопределённость или .

Правила Лопиталя – очень мощный метод, позволяющий быстро и эффективно устранить указанные неопределенности, не случайно в сборниках задач, на контрольных работах, зачётах часто встречается устойчивый штамп: «вычислить предел, не пользуясь правилом Лопиталя ». Выделенное жирным шрифтом требование можно с чистой совестью приписать и к любому пределу уроков Пределы. Примеры решений , Замечательные пределы . Методы решения пределов , Замечательные эквивалентности , где встречается неопределённость «ноль на ноль» либо «бесконечность на бесконечность». Даже если задание сформулировано коротко – «вычислить пределы», то негласно подразумевается, что вы будете пользоваться всем, чем угодно, но только не правилами Лопиталя.

Всего правил два, и они очень похожи друг на друга, как по сути, так и по способу применения. Кроме непосредственных примеров по теме, мы изучим и дополнительный материал, который будет полезен в ходе дальнейшего изучения математического анализа.

Сразу оговорюсь, что правила будут приведены в лаконичном «практическом» виде, и если вам предстоит сдавать теорию, рекомендую обратиться к учебнику за более строгими выкладками.

Первое правило Лопиталя

Рассмотрим функции , которые бесконечно малЫ в некоторой точке . Если существует предел их отношений , то в целях устранения неопределённости можно взять две производные – от числителя и от знаменателя. При этом: , то есть .

Примечание : предел тоже должен существовать, в противном случае правило не применимо.

Что следует из вышесказанного?

Во-первых, необходимо уметь находить производные функций , и чем лучше – тем лучше =)

Во-вторых, производные берутся ОТДЕЛЬНО от числителя и ОТДЕЛЬНО от знаменателя. Пожалуйста, не путайте с правилом дифференцирования частного !!!

И, в-третьих, «икс» может стремиться куда угодно, в том числе, к бесконечности – лишь бы была неопределённость .

Вернёмся к Примеру 5 первой статьи о пределах , в котором был получен следующий результат:

К неопределённости 0:0 применим первое правило Лопиталя:

Как видите, дифференцирование числителя и знаменателя привело нас к ответу с пол оборота: нашли две простые производные, подставили в них «двойку», и оказалось, что неопределённость бесследно исчезла!

Не редкость, когда правила Лопиталя приходится применять последовательно два или бОльшее количество раз (это относится и ко второму правилу). Вытащим на ретро-вечер Пример 2 урока о замечательных пределах :

На двухъярусной кровати снова прохлаждаются два бублика. Применим правило Лопиталя:

Обратите внимание, что на первом шаге в знаменателе берётся производная сложной функции . После этого проводим ряд промежуточных упрощений, в частности, избавляемся от косинуса, указывая, что он стремится к единице. Неопределённость не устранена, поэтому применяем правило Лопиталя ещё раз (вторая строчка).

Я специально подобрал не самый простой пример, чтобы вы провели небольшое самотестирование. Если не совсем понятно, как найдены производные , следует усилить свою технику дифференцирования, если не понятен фокус с косинусом, пожалуйста, вернитесь к замечательным пределам . Не вижу особого смысла в пошаговых комментариях, так как о производных и пределах я уже рассказал достаточно подробно. Новизна статьи состоит в самих правилах и некоторых технических приёмах решения.

Как уже отмечалось, в большинстве случаев правила Лопиталя использовать не нужно, но их зачастую целесообразно применять для черновой проверки решения. Зачастую, но далеко не всегда. Так, например, только что рассмотренный пример значительно выгоднее проверить через замечательные эквивалентности .

Второе правило Лопиталя

Брат-2 борется с двумя спящими восьмёрками . Аналогично:

Если существует предел отношения бесконечно больших в точке функций: , то в целях устранения неопределённости можно взять две производные – ОТДЕЛЬНО от числителя и ОТДЕЛЬНО от знаменателя. При этом: , то есть при дифференцировании числителя и знаменателя значение предела не меняется .

Примечание : предел должен существовать

Опять же, в различных практических примерах значение может быть разным , в том числе, бесконечным. Важно, чтобы была неопределённость .

Проверим Пример №3 первого урока: . Используем второе правило Лопиталя:

Коль скоро речь зашла о великанах, разберём два каноничных предела:

Пример 1

Вычислить предел

Получить ответ «обычными» методами непросто, поэтому для раскрытия неопределённости «бесконечность на бесконечность» используем правило Лопиталя:

Таким образом, линейная функция более высокого порядка роста , чем логарифм с основанием бОльшим единицы ( и т.д.). Разумеется, «иксы» в старших степенях тоже будут «перетягивать» такие логарифмы. Действительно, функция растёт достаточно медленно и её график является более пологим относительно того же «икса».

Пример 2

Вычислить предел

Ещё один примелькавшийся кадр. В целях устранения неопределённости , используем правило Лопиталя, причём, два раза подряд:

Показательная функция, с основанием, бОльшим единицы ( и т.д.) более высокого порядка роста , чем степенная функция с положительной степенью .

Похожие пределы встречаются в ходе полного исследования функции , а именно, при нахождении асимптот графиков . Также замечаются они и в некоторых задачах по теории вероятностей . Советую взять на заметку два рассмотренных примера, это один из немногих случаев, когда лучше дифференцирования числителя и знаменателя ничего нет.

Далее по тексту я не буду разграничивать первое и второе правило Лопиталя, это было сделано только в целях структурирования статьи. Вообще, с моей точки зрения, несколько вредно излишне нумеровать математические аксиомы, теоремы, правила, свойства, поскольку фразы вроде «согласно следствию 3 по теореме 19…» информативны только в рамках того или иного учебника.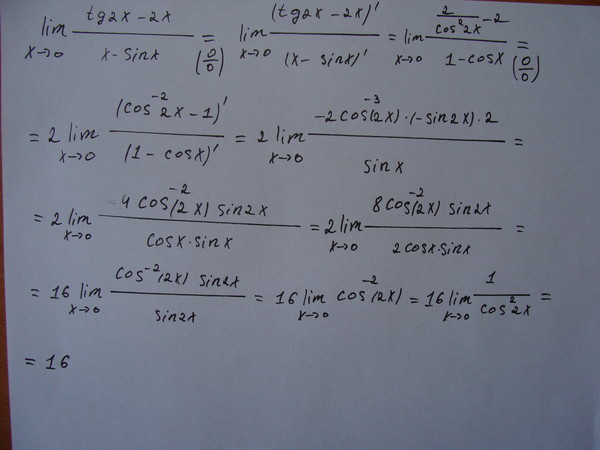 В другом источнике информации то же самое будет «следствием 2 и теоремой 3». Такие высказывания формальны и удобны разве что самим авторам. В идеале лучше ссылаться на суть математического факта. Исключение – исторически устоявшиеся термины, например, первый замечательный предел или второй замечательный предел .

Продолжаем разрабатывать тему, которую нам подкинул член Парижской академии наук маркиз Гийом Франсуа де Лопиталь. Статья приобретает ярко выраженную практическую окраску и в достаточно распространённом задании требуется:

Для разминки разберёмся с парой небольших воробушков:

Пример 3

Предел можно предварительно упростить, избавившись от косинуса, однако проявим уважение к условию и сразу продифференцируем числитель и знаменатель:

В самом процессе нахождения производных нет чего-то нестандартного, так, в знаменателе использовано обычное правило дифференцирования произведения .

Рассмотренный пример разруливается и через замечательные пределы , похожий случай разобран в конце статьи Сложные пределы .

Пример 4

Вычислить предел по правилу Лопиталя

Это пример для самостоятельного решения. Нормально пошутил =)

Типична ситуация, когда после дифференцирования получаются трех- или четырёхэтажные дроби:

Пример 5

Вычислить предел, используя правило Лопиталя

Напрашивается применение замечательной эквивалентности , но путь жёстко предопределён по условию:

После дифференцирования настоятельно рекомендую избавляться от многоэтажности дроби и проводить максимальные упрощения . Конечно, более подготовленные студенты могут пропустить последний шаг и сразу записать: , но в некоторых пределах запутаются даже отличники.

Пример 6

Вычислить предел, используя правило Лопиталя

Пример 7

Вычислить предел, используя правило Лопиталя

Это примеры для самостоятельного решения. В Примере 7 можно ничего не упрощать, слишком уж простой получается после дифференцирования дробь. А вот в Примере 8 после применения правила Лопиталя крайне желательно избавиться от трёхэтажности, поскольку вычисления будут не самыми удобными. Полное решение и ответ в конце урока. Если возникли затруднения – тригонометрическая таблица в помощь.

И, упрощения совершенно необходимы, когда после дифференцирования неопределённость не устранена .

Пример 8

Вычислить предел, используя правило Лопиталя

Поехали:

Интересно, что первоначальная неопределённость после первого дифференцирования превратилась в неопределённость , и правило Лопиталя невозмутимо применяется дальше. Также заметьте, как после каждого «подхода» устраняется четырёхэтажная дробь, а константы выносятся за знак предела. В более простых примерах константы удобнее не выносить, но когда предел сложный, упрощаем всё-всё-всё. Коварство решённого примера состоит ещё и в том, что при , а , поэтому в ходе ликвидации синусов немудрено запутаться в знаках. В предпоследней строчке синусы можно было и не убивать, но пример довольно тяжелый, простительно.

На днях мне попалось любопытное задание:

Пример 9

Если честно, немного засомневался, чему будет равен данный предел. Как демонстрировалось выше, «икс» более высокого порядка роста, чем логарифм, но «перетянет» ли он логарифм в кубе? Постарайтесь выяснить самостоятельно, за кем будет победа.

Да, правила Лопиталя – это не только пальба по воробьям из пушки, но ещё и кропотливая работа….

В целях применения правил Лопиталя к бубликам или уставшим восьмёркам сводятся неопределённости вида .

Расправа с неопределённостью подробно разобрана в Примерах №№9-13 урока Методы решения пределов . Давайте для проформы ещё один:

Пример 10

Вычислить предел функции, используя правило Лопиталя

На первом шаге приводим выражение к общему знаменателю, трансформируя тем самым неопределённость в неопределённость . А затем заряжаем правило Лопиталя:

Здесь, к слову, тот случай, когда четырёхэтажное выражение трогать бессмысленно.

Неопределённость тоже не сопротивляется превращению в или :

Пример 11

Вычислить предел функции с помощью правила Лопиталя

Предел здесь односторонний, и о таких пределах уже шла речь в методичке Графики и свойства функций . Как вы помните, графика «классического» логарифма не существует слева от оси , таким образом, мы можем приближаться к нулю только справа.

Правила Лопиталя для односторонних пределов работают, но сначала необходимо разобраться с неопределённостью . На первом шаге делаем дробь трёхэтажной, получая неопределённость , далее решение идёт по шаблонной схеме:

После дифференцирования числителя и знаменателя избавляемся от четырёхэтажной дроби, чтобы провести упрощения. В результате нарисовалась неопределённость . Повторяем трюк: снова делаем дробь трёхэтажной и к полученной неопределённости применяем правило Лопиталя ещё раз:

Готово.

Исходный предел можно было попытаться свести к двум бубликам:

Но, во-первых, производная в знаменателе труднее, а во-вторых, ничего хорошего из этого не выйдет.

Таким образом, перед решением похожих примеров нужно проанализировать (устно либо на черновике), К КАКОЙ неопределённости выгоднее свести – к «нулю на ноль» или к «бесконечности на бесконечность».

В свою очередь на огонёк подтягиваются собутыльники и более экзотические товарищи . Метод трансформации прост и стандартен.

Предел функции, правило Лопиталя

Применение правила Лопиталя необходимо для вычисления пределов при получении неопределенностей вида 00 и ∞∞.

Имеются неопределенности вида 0·∞ и ∞-∞.

Самой важной частью правила Лопиталя является дифференцирование функции и нахождение ее производной.

Определение 1

Когда limx→x0f(x)g(x)=00 или ∞∞ и функции  f(x), g(x) являются дифференцируемыми в пределах точки х0, тогда limx→x0f(x)g(x)=limx→x0f'(x)g'(x).

Если неопределенность нерешаема после применения правила Лопиталя, тогда необходимо снова его применить. Для полного понятия рассмотрим несколько примеров.

Пример 1

Произвести вычисления, применив правило Лопиталя limx→0sin2(3x)x·cos(x).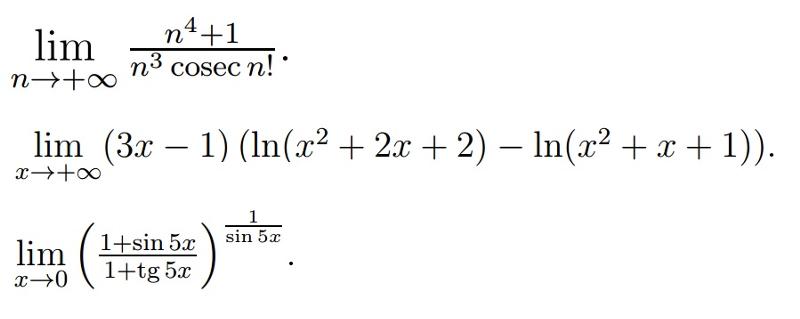

Решение

Для решения по правилу Лопиталя для начала необходимо произвести подстановку. Получаем, что limx→0sin2(3x)x·cos(x)=sin2(3·0)0·cos(0)=00.

Теперь можно переходить к вычислению пределов, используя правило. Получаем, что

limx→0sin2(3x)x·cos(x)=00=limx→0sin2(3x)’x·cos(x)’=limx→02sin(3x)(sin(3x))’x’·cos(x)+x·(cos(x))’==limx→06 sin(3x)cos(3x)cos(x)-x·sin(x)=6sin(3·0)cos(3·0)cos(0)-0·sin(0)=01=0

Ответ: limx→0sin2(3x)x·cos(x)=0.

Пример 2

Вычислить предел заданной функции limx→∞ln(x)x.

Решение

Производим постановку бесконечностью. Получаем, что

limx→∞ln(x)x=ln(∞)∞=∞∞

Полученная неопределенность указывает на то, что необходимо применить правило Лопиталя. Имеем, что

limx→∞ln(x)x=∞∞=limx→∞ln(x)’x’=limx→∞1×1=1∞=0

Ответ: limx→∞ln(x)x=0

Пример 3

Вычислить предел заданной функции limx→0+0(x4ln(x))

Решение

Производим подстановку значения x. получаем, что

limx→0+0(x4ln(x))=(0+0)4·ln(0+0)=0·(-∞)

Решение привело к неопределенности вида ноль умноженный на отрицательную бесконечность.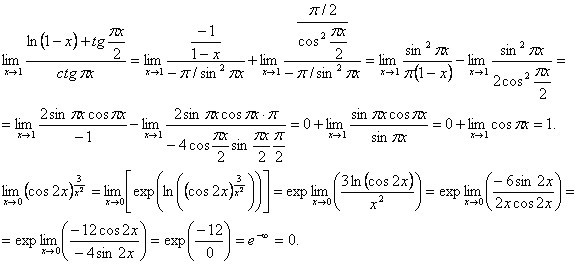 Это указывает на то, что необходимо обратиться к таблице неопределенностей и принять решения для выбора метода нахождения этого предела. После преобразования применяем правило Лопиталя. Получаем, что

limx→0+0(x4ln(x))=0·(-∞)=limx→0+0ln(x)x-4=ln(0+0)(0+0)-4=-∞+∞

Приход к неопределенности говорит о том, что необходимо повторное применение этого правила. Имеем, что

limx→0+0(x4ln(x))=0·(-∞)=limx→0+0ln(x)x-4=-∞+∞==limx→0+0(ln(x))'(x-4)’=limx→0+01x-4-5=-14limx→0+01x-4=-14·1(0+0)-4==-14·(0+0)4=0

Ответ: limx→0+0(x4ln(x))=0

Пример 4

Выполнить вычисление предела функции limx→0ctg2(x)-1×2.

Решение

После подстановки получаем

limx→0ctg2(x)-1×2=∞-∞

Наличие неопределенности указывает на то, что следует использовать правило Лопиталя. Получаем, что

limx→0ctg2(x)-1×2=∞-∞=limx→0cos2(x)sin2(x)-1×2==limx→0x2cos2(x)-sin2(x)x2sin2(x)=limx→0x cos x-sin xx cos x+sin xx2sin2(x)==limx→0x cos x-sin xx sin2(x)x cos x+sin xx=limx→0xcos x-sinxxsin2(x)cos x+sin xx==limx→0cos x+sin xxlimx→0xcos x-sin xxsin2(x)=2limx→0x cosx-sin xx sin2 (x)==20·cos(0)-sin(0)0·sin2(0)=00

Для последнего перехода использовался первый замечательный предел. После чего приходим к решению по Лопиталю. Получим, что

2limx→0x cosx-sin xx sin2 (x)=00=2limx→0(x cosx -sin x)'(x sin2(x))’==2limx→0cos x-x sin x-cos xsin2(x)+2x sin x cos x=2limx→0-xsin(x)+2x cos x=00

Так как неопределенность не ушла, необходимо еще одно применение правила Лопиталя. Получаем предел вида

2limx→0-xsin(x)+2x cos x=00=2limx→0-x’sin(x)+2x cos x’==2limx→01cos x+2cos x-2xsin x=-2·13·cos(0)-2·0·sin(0)=-23

Ответ: limx→0ctg2(x)-1×2=-23

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Вычислить предел, используя правило Лопиталя

Вычислить предел, используя правило Лопиталя

Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3 Архитектура Биология География Другое Иностранные языки Информатика История Культура Литература Математика Медицина Механика Образование Охрана труда Педагогика Политика Право Программирование Психология Религия Социология Спорт Строительство Физика Философия Финансы Химия Экология Экономика Электроника

Сравнение бесконечно больших функций | Сравниваем старшие степени: , следовательно, числитель более высокого порядка роста, чем знаменатель, и сразу можно сказать, что предел будет равен бесконечности. | Метод замены переменной в пределе | Бесконечно малые функции. Сравнение бесконечно малых | Может ли функция быть бесконечно малой на бесконечности? | Сравнение бесконечно малых функций | Что принципиально важно во всех рассмотренных примерах? | Замечательные эквивалентности в пределах | Первое правило Лопиталя | Второе правило Лопиталя |

Читайте также: I. Прочитайте текст и заполните пропуски 1- 5 в нем, используя части предложений A- F. VII. Напишите 10 предложений о распорядке дня Майкла, используя следующую таблицу. А1. ПРАВИЛО ОБОСНОВАННОСТИ АРГУМЕНТОВ. Аргумент в диалоге должен быть высказыванием, обоснованным вне данного диалога и независимо от его тезиса. Б) Расскажите о себе, используя слова и выражения из а). Билет №46.Стимулирующая и сдерживающая денежно-кредитная политика. Монетарное правило М.Фридмена (автоматическая денежно-кредитная политика). Вам дается возможность самим творить физическое тело, используя кирпичики материи, клеточек ваших, напитывая их Светом Любви Вселенской. Виды дисперсий и правило их сложения

Для разминки разберёмся с парой небольших воробушков:

Пример 3

Вычислить предел по правилу Лопиталя

Предел можно предварительно упростить, избавившись от косинуса, однако проявим уважение к условию и сразу продифференцируем числитель и знаменатель:

В самом процессе нахождения производных нет чего-то нестандартного, так, в знаменателе использовано обычное правило дифференцирования произведения .

Рассмотренный пример разруливается и через замечательные пределы, похожий случай разобран в конце статьи Сложные пределы.

Пример 4

Вычислить предел по правилу Лопиталя

Это пример для самостоятельного решения. Нормально пошутил =)

Типична ситуация, когда после дифференцирования получаются трех- или четырёхэтажные дроби:

Пример 5

Вычислить предел, используя правило Лопиталя

Напрашивается применение замечательной эквивалентности, но путь жёстко предопределён по условию:

После дифференцирования настоятельно рекомендуюизбавляться от многоэтажности дробии проводить максимальные упрощения. Конечно, более подготовленные студенты могут пропустить последний шаг и сразу записать: , но в некоторых пределах запутаются даже отличники.

Пример 6

Вычислить предел, используя правило Лопиталя

Пример 7

Вычислить предел, используя правило Лопиталя

Это примеры для самостоятельного решения. В Примере 7 можно ничего не упрощать, слишком уж простой получается после дифференцирования дробь. А вот в Примере 8 после применения правила Лопиталя крайне желательно избавиться от трёхэтажности, поскольку вычисления будут не самыми удобными. Полное решение и ответ в конце урока. Если возникли затруднения – тригонометрическая таблица в помощь.

И, упрощения совершенно необходимы, когда после дифференцирования неопределённостьне устранена.

Пример 8

Вычислить предел, используя правило Лопиталя

Поехали:

Интересно, что первоначальная неопределённость после первого дифференцирования превратилась в неопределённость , и правило Лопиталя невозмутимо применяется дальше. Также заметьте, как после каждого «подхода» устраняется четырёхэтажная дробь, а константы выносятся за знак предела. В более простых примерах константы удобнее не выносить, но когда предел сложный, упрощаем всё-всё-всё. Коварство решённого примера состоит ещё и в том, что при , а , поэтому в ходе ликвидации синусов немудрено запутаться в знаках. В предпоследней строчке синусы можно было и не убивать, но пример довольно тяжелый, простительно.

На днях мне попалось любопытное задание:

Пример 9

Вычислить предел функции, используя правило Лопиталя

Если честно, немного засомневался, чему будет равен данный предел. Как демонстрировалось выше, «икс» более высокого порядка роста, чем логарифм, но «перетянет» ли он логарифм в кубе? Постарайтесь выяснить самостоятельно, за кем будет победа.

Да, правила Лопиталя – это не только пальба по воробьям из пушки, но ещё и кропотливая работа….

В целях применения правил Лопиталя к бубликам или уставшим восьмёркам сводятся неопределённости вида .

Расправа с неопределённостью подробно разобрана в Примерах №№9-13 урокаМетоды решения пределов. Давайте для проформы ещё один:

Пример 10

Вычислить предел функции, используя правило Лопиталя

На первом шаге приводим выражение к общему знаменателю, трансформируя тем самым неопределённость в неопределённость . А затем заряжаем правило Лопиталя:

Здесь, к слову, тот случай, когда четырёхэтажное выражение трогать бессмысленно.

Неопределённость тоже не сопротивляется превращению в или :

Пример 11

Вычислить предел функции с помощью правила Лопиталя

Предел здесь односторонний, и о таких пределах уже шла речь в методичке Графики и свойства функций. Как вы помните, графика «классического» логарифма не существует слева от оси , таким образом, мы можем приближаться к нулю только справа.

Правила Лопиталя для односторонних пределов работают, но сначала необходимо разобраться с неопределённостью . На первом шаге делаем дробь трёхэтажной, получая неопределённость , далее решение идёт по шаблонной схеме:

После дифференцирования числителя и знаменателя избавляемся от четырёхэтажной дроби, чтобы провести упрощения. В результате нарисовалась неопределённость . Повторяем трюк: снова делаем дробь трёхэтажной и к полученной неопределённости применяем правило Лопиталя ещё раз:

Готово.

Исходный предел можно было попытаться свести к двум бубликам:

Но, во-первых, производная в знаменателе труднее, а во-вторых, ничего хорошего из этого не выйдет.

Таким образом, перед решением похожих примеров нужно проанализировать (устно либо на черновике), К КАКОЙ неопределённости выгоднее свести – к «нулю на ноль» или к «бесконечности на бесконечность».

В свою очередь на огонёк подтягиваются собутыльники и более экзотические товарищи . Метод трансформации прост и стандартен:

Пример 12

Вычислить предел функции с помощью правила Лопиталя

Для устранения неопределённости используем основное логарифмическое тождество: . В данном случае :

На предпоследнем шаге, согласно известному школьному свойству, «сносим» синус из степени за пределы логарифма, получая произведение . На последнем шаге перемещаем значок предела в показатель (поскольку экспоненциальная функция непрерывна, да и предел относится, прежде всего, к верхнему этажу).

Чтобы не мельчить, вычислим предел показателя отдельно:

С неопределённостью разбираемся уже знакомым способом – делаем дробь трёхэтажной, получая долгожданную неопределённость , к которой применимо правило Лопиталя:

Метаморфозы продолжаются, теперь вылезла неопределённость «ноль на ноль». В принципе, можно избавиться от косинуса, указав, что он стремится к единице. Но мудрая стратегия заключается в том, чтобы никто ни до чего не докопался. Поэтому сразу применим правило Лопиталя, как этого требует условие задачи:

Не торопитесь, предел не равен нулю! Мы вычислили только предел показателя. В конце решения главное не забыть про экспоненту, я сейчас сам чуть про неё не забыл =) Окончательно:

В ряде случаев после использование основного логарифмического тождества удаётся миновать неопределённость :

Пример 13

Вычислить предел по правилу Лопиталя

Очередной папуас тоже сдаётся перед формулой . В данном случае :

В результате сразу получена неопределённость , что облегчает задачу. Предел показателя для удобства вычислим отдельно:

В итоге:

Аналогичное задание для самостоятельного решения:

Пример 14

Вычислить предел по правилу Лопиталя

Полное решение и ответ в конце урока.

Предел с неопределённостью по правилу Лопиталя, если честно, у себя не нашёл, но для полноты картины решим многострадальный шестой пример урока Замечательные пределы:

Пример 15

Вычислить с помощью правила Лопиталя

Решайте =)

В заключение хочу успокоить гринписовцев – ни один воробей от оружия серьёзно не пострадал, пределы – птицы юркие, да и ядра формы обтекаемой. Вспоминаем обычное требование: «…не пользуясь правилом Лопиталя». С беспощадной действительностью соприкоснёмся в статье Сложные пределы.

Желаю успехов!

Решения и ответы:

Пример 4

Пример 6

Пример 7

Пример 9

Пример 14
Используем основное логарифмическое тождество и преобразование :

Вычислим предел показателя:

Таким образом:

Пример 15
Используем основное логарифмическое тождество:

Вычислим предел показателя:

Таким образом:

Автор: Емелин Александр

 

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

 

Сложные пределы

 

В данной статье будут рассмотрены пределы повышенной сложности, и заключительный практикум по теме предназначен, прежде всего, для читателей со средним и высоким уровнем подготовки. Если ваши навыки вычисления пределов невелики или вовсе отсутствуют, пожалуйста, начните с вводного урока Пределы функций. Примеры решений. Многие методы решения пределов, о которых пойдёт речь, уже знакомы и сложность будет состоять преимущественно в технике вычислений. Кроме того, мы рассмотрим примеры с более редкими замечательными пределами, которые до сей поры были обделены моим вниманием.

Пока не знаю, сколько будет примеров, 15-ть, 20-ть или больше, но в любом случае программа предстоит насыщенная, поэтому сразу приступим к зачистке территории:

Пример 1

Найти предел, не пользуясь правилом Лопиталя

При подстановке «единицы» в выражение под знаком предела, получается неопределённость , которая устраняется стандартным методом: числитель и знаменатель необходимо разложить на множители, а затем что-нибудь сократить. Разложить на множители…. Были бы у нас многочлены второй степени – без проблем. Но как раскладывать кубические многочлены? Познакомимся с новым приёмом, который основан на одной из теорем алгебры. Сначала кратко передам теоретическую суть:

Рассмотрим многочлен положительной степени. Если число является корнем уравнения , то многочлен делится на многочлен без остатка. В результате деления получается многочлен , при этом: .

Да, многочлены, как и числа, можно делить друг на друга. Термины те же:
– делимое;
– делитель;
– частное.

Начнём оформлять решение и детально разберём техническую сторону вопроса:

Разложим числитель и знаменатель на множители.

Числитель: поскольку число является корнем уравнения , то многочлен делится на многочлен без остатка. Деление выполняется столбиком. В школе столбиком мы делили числа, и принцип деления многочленов весьма похож. Записываем начальный шаблон: Обратите внимание на очень важную вещь: в многочлене в явном виде отсутствует «икс» в первой степени. При делении ОБЯЗАТЕЛЬНО прописываем все недостающие слагаемые, прикрепляя к ним нулевые коэффициенты.

Теперь в углу нужно разоблачить незнакомца :

Каким он должен быть? Девчонки, признавайтесь =) …Нет-нет-нет, он должен быть ТАКИМ, чтобы при его умножении на «икс» получилось :

Очевидно, что данному критерию удовлетворяет . Действительно, . Записываем первый трофей:

Далее нашего героя необходимо умножить на делитель :
, а результат записать во второй строке слева:

Проводим отчёркивание и из первой строки почленно вычитаем вторую строку:

Если подробно, (ноль под чертой не пишем),

Сносим сверху следующее слагаемое:

Алгоритм идёт на следующий круг. Снова ищем одночлен , он должен быть ТАКИМ, чтобы при его умножении на «икс» получилось :

В данном случае . Рисуем его справа под чертой:

и умножаем на делитель :
, результат записываем в 4-ую строку:

Ещё раз отчёркиваем и проводим почленное вычитание: (ноль под чертой не пишем), :

Сносим сверху последнее слагаемое:

Организуем завершающий цикл. Необходимо подобрать третье слагаемое , которое при умножении на «икс» даёт :

Уравнению соответствует корень , который записываем справа под чертой:

Умножаем на делитель :
, результат записываем в 6-ую строку:

Выполняем завершающее отчёркивание и почленное вычитание:

В итоге получился ноль, и это значит, что все вычисления выполнены правильно. Иными словами, многочлен поделился на без остатка. Таким образом:

Желающие могут раскрыть скобки в правой части и убедиться, что получится исходный многочлен .

Рассмотренный алгоритм на самом деле не сложен, и рука набивается довольно быстро.

Знаменатель. Разборки аналогичны. Так как число является корнем уравнения , то соответствующий многочлен делится на без остатка:

В итоге

Открываем решение и записываем всё, что нажито непосильным трудом:

Приключения продолжаются – после сокращения неопределённость не устранена. Но уже легче, квадратные трёхчлены можно разложить на множители тривиальным способом, рассмотренным на первом уроке про пределы функций. Тем не менее, в целях закрепления алгоритма продолжим деление. Да простит меня сервак =)

Числитель. Поскольку число является корнем уравнения , то соответствующий многочлен делится на без остатка. Поехали. На первом шаге подбираем ТАКИМ образом, чтобы при его умножении на «икс» получить :

Искомое значение :

Умножаем на делитель :
, результат записываем слева, отчёркиваем и проводим почленное вычитание:

Из первой строки сносим оставшееся слагаемое:

Второе значение при умножении на «икс» должно давать «икс»:

Очевидно, что :

Умножаем на делитель :
, результат записываем ниже, отчёркиваем и проводим почленное вычитание:

В остатке получился ноль, значит, деление выполнено верно. Таким образом:

Аналогично расправляемся со знаменателем:

То есть

Снова открываем решение и получаем окончательный ответ:

Выполним проверку. Дважды используем правило Лопиталя:

Сравните трудоёмкость двух способов решения. Думаю, теперь вам понятно, почему запрещают применять правило Лопиталя =)

Времени и сил на первый пример совсем не жалко, так как необходимость делить многочлены время от времени возникает в других задачах, в частности, при нахождении нулей функции, в интегралах от дробно-рациональной функции. Поэтому с энтузиазмом отнесёмся к другим пределам… …они будут ещё длиннее =) Никто не знает, вдруг в жизни пригодится. Хах. Вспомнился заезженный анекдот в тему: если к вам на улице подошли Свидетели Иеговы, перехватите инициативу – начните им рассказывать про тройные интегралы.

Пример 2

Найти предел, не пользуясь правилом Лопиталя

Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

Вернёмся к другому известному способу решения пределов, повысив их сложность:

Пример 3

Найти предел, не пользуясь правилом Лопиталя

Неопределённость ликвидируется стандартным методом – умножением и делением на сопряженное выражение. Единственное отличие, приём используется два раза:

1) для устранения разности домножаем числитель и знаменатель на сопряженное выражение ;

2) для устранения разности домножаем числитель и знаменатель на сопряженное выражение .

Далее дважды используется формула . Сама техника решения подробно рассмотрена на уроке Пределы. Примеры решений.

Оформляем:

Оба вышеуказанных действия выгоднее выполнить «за один присест». Умножим числитель и знаменатель на сопряженные выражения:

Проверим решение по правилу Лопиталя:

Пример 4

Найти предел, не пользуясь правилом Лопиталя

Это более сложный пример для самостоятельного решения.

Иногда в пределах рассматриваемого типа приходится использовать не только формулу разности квадратов , но и формулу разности кубов:

Пример 5

Найти предел

Неопределённость устраняется умножением и делением на сопряженное выражение. Аналогичные, но более простые пределы мы рассмотрели в Примерах №№11-13 урокаМетоды решения пределов. Только здесь работает формула разности кубов:

В данном случае . И, согласно формуле, для разности сопряженным выражением будет вот этот вот страх:

Умножим и разделим на сопряженное выражение, чтобы использовать формулу :

Тоже знакомая картина….

Старшая степень числителя: 2
Старшая степень знаменателя: 2

Таким образом, числитель и знаменатель одного порядка роста, и сразу можно сказать, что предел равен конечному числу.

Разделим числитель и знаменатель на :

Готово.

Пример 6

Найти предел

Это пример для самостоятельного решения. После умножения/деления на сопряженное выражение и упрощений предел будет сведён к случаю Примеров №№1-3 статьи о бесконечно малых функциях. Полное решение и ответ в конце урока.

А сейчас обещанные на уроке Методы решения пределов плюшки на замену переменной. Повышенной сложности:

Пример 7

Найти предел, не пользуясь правилом Лопиталя

Аргумент стремится к не самому распространённому числу: , с ходу и не сообразишь, есть здесь вообще неопределённость или нет. Поэтому откроемтригонометрическую таблицу, и выпишем следующие значения:

Проверим предел на наличие неопределённости:

Да, действительно, два бублика.

Проведём предварительный анализ. В пределе находятся тригонометрические функции, и решение, скорее всего, сведётся к первому замечательному пределу. В этой связи напрашивается замена, после которой новая переменная будет стремиться к нулю.

Но перед заменой целесообразно провести некоторое упрощение выражения. В пределе есть тангенс, а работать с этой функцией неудобно (как и с котангенсом тоже). Таким образом, сначала лучше свести всё дело к синусам и косинусам. Пример свирепый, поэтому я закомментирую каждый шаг:

(1) Используем формулу .
(2) Дробь числителя приводим к общему знаменателю.
(3) Избавляемся от трёхэтажности дроби, а также от косинуса, указывая, что .
(4) Выносим константу за значок предела.

Неопределённость никуда не делась, но от тангенса мы избавились, что уже является небольшим достижением

Проведем замену переменной:
Если , то
Ну и ещё – из замены нужно выразить: .

(5) Выполняем подстановку в соответствии с выполненной заменой.
(6) Используем тригонометрические формулы:

(7) Используя значения , упрощаем выражение.
(8) Раскрываем скобки в числителе и знаменателе.
(9) Приводим подобные слагаемые в числителе.
(10) Константу –2 выносим за значок предела. В знаменателе переставляем слагаемые.

И снова два нуля, причём не видно как решать предел дальше…. Но если хорошенько пошуршать в тригонометрических формулах, то история закончится счастливым концом:

(11) Используем формулы половинного угла: . В числителе избавляемся от косинуса, указывая, что .
(12) В знаменателе выносим за скобки .
(13) Сокращаем числитель и знаменатель на .

Забавно, что всё обошлось даже без замечательного предела.

Не знаю, кто и на каком месте будет рвать себе волосы, но правило Лопиталя даёт ответ фантастически быстро:

Пример 8

Найти предел, не пользуясь правилом Лопиталя

Это пример для самостоятельного решения. В тригонометрической таблиценет информации об отрицательных значениях угла. Понятие ориентации угла дано в статьеПростейшие задачи с прямой на плоскости. Наглядная иллюстрация с конкретными примерами также фигурирует при нахождении аргумента комплексного числа. Чтобы воспользоваться таблицей, прибавляем один «оборот»: , то есть и – это один и тот же угол. Таким образом:

Полное решение и ответ в конце урока

Как-то незаслуженно оказались забыты степени:

Пример 9

Найти предел

На повестке дня неопределённость , и решение, очевидно, нужно свести к замечательной формуле . Но в нашем пределе нет единицы, только одинокий косинус. Что делать? Организуем!

(1) Приводим основание степени к виду , для этого используем искусственный приём: прибавляем и вычитаем единицу. Таким образом:
(2) В целях применения 2-го замечательного предела возводим основание в степень , и, чтобы ничего не изменилось – в обратную степень .
(3) Используем замечательный предел .
(4) Теперь в показателе необходимо устранить неопределённость 0:0. Сначала меняем знак в числителе: , минус выносим из предела.
(5) В числителе используем формулу .
(6) Искусственно преобразуем знаменатель, чтобы получить два первых замечательных предела.

Очень кстати в одном примере подвернулись сразу оба замечательных предела, и после их повторения во второй части статьи рассмотрим:

 

---

Дата добавления: 2015-07-25; просмотров: 670 | Нарушение авторских прав

---

	|	следующая страница ==>
Показательная функция, с основанием, бОльшим единицы ( и т.д.) более высокого порядка роста, чем степенная функция с положительной степенью.	|	Замечательные пределы с экспонентой и логарифмом

---

mybiblioteka.su – 2015-2022 год. (0.044 сек.)

Правило Лопиталя для вычисления пределов, примеры с подробным решением, доказательство » Kupuk.

net

Одной из основных теорем в математическом анализе является правило Лопиталя. Этот закон, предложенный французским учёным, используется для вычисления пределов функций, когда формулы Тейлора применить невозможно. Идейно он достаточно простой, однако его доказательство содержит технические тонкости, на которые следует обратить пристальное внимание.

Общие сведения

Важным понятием в высшей математике является определение бесконечности. Эта неопределённость обозначается символом ∞. Когда её упоминают, то имеют в виду как бесконечно малое число, так и большое. Для записи предела функций используется знак лимита, например, lim 0k (y). В нижней части указывается аргумент со стрелочкой, обозначающей, к чему именно стремится неопределённость. Если предел известный, то он называется конечным, в ином случае — бесконечным.

Когда нельзя установить, является ограничение бесконечным или конечным, то говорят, что предела для рассматриваемой функции не существует. Это возможно, например, когда ограничение тригонометрической функции стремится к бесконечности. Существует несколько способов вычисления пределов: правило Лопиталя, формулы Тейлера, графический метод, подставление неизвестного в функцию.Указанные способы можно применять для нахождения того или иного предела, но для неопределённости вида 0/0 или ∞/∞, а также вычисления отношений бесконечно малых или больших выражений лучше всего использовать закон Лопиталя. Состоит он из двух правил:

• Для бесконечно малых величин. Когда функции k (y) и d (y) можно дифференцировать в некоторой области точки, исключая саму её, при этом в этой окрестности производная выражения неравна нулю, а пределы этих функций равны нулю, то отношение ограничения этих функций будет равно пределу отношения их производных.
• Для бесконечно больших значений. Если две функции k (y) и d (y) можно дифференцировать по окрестности взятой точки, но при этом её саму исключить, учитывая, что в рассматриваемой окрестности производная d (y) не равняется нулю, то когда функции в этой точке равны бесконечности, предел отношения этих выражений тождественен отношению их производных.

Другими словами, смысл теоремы Лопиталя заключается в том, что когда нужно найти ограничение для двух функций, отношение которых даёт неопределённость 0/0 или ∞/∞, то можно взять производные этих выражений и найти их отношение. Это действие приведёт к получению искомого ответа. Метод позволяет упростить вычисление сложных показательных степенных функций. Его можно применять и при умножении неопределённостей или их вычитании. Например, 0 * ∞, ∞ — ∞.

Доказательство правила

Лопиталь после знакомства с Бернулли смог систематизировать метод Иоганна и издать в 1696 году книгу «Анализ бесконечно малых», где подробно изложил способы решения задач с неопределённостями. Математически его описание состоит из четырёх пунктов:

• lim k (y) = lim d (y) = 0 (∞).
• Графики k (y) и d (y) приближаются к линейному виду.
• d (y)’ ≠ 0.
• lim k (y)’ / d (y)’ = lim k (y) / d (y).

Пусть имеется два дифференцируемых выражения, при этом d (y) во всех точках имеет не нулевую производную. При y, стремящемся к a, d стремится к бесконечности. Если предел отношения производных конечного предела или бесконечного равняется числу L, тогда ограничение отношений производных этих функций также будет тождественно этому числу. То есть lim k (y) / d (y) = L, при y → a. Исходя из определения Гейне и Коши, рассматривать можно только монотонные последовательности, которые стремятся к a.

Взяв произвольный ряд, который может расти yn → a, верно утверждать, что в соответствии со следствием теоремы Дарбу и условием d (y)’ ≠ 0, рассматриваемая функция будет строго монотонной. А это означает, что последовательность d (yn) будет такой же. В тоже время из условия lim d (y) = ∞ следует, что d (yn) → ∞. При этом бесконечность может быть как со знаком минус, так и плюс.

Рассмотрим теорему Штольца, а именно отношение: (k (yn+1) — k (yn)) / (d (yn+1) — d (yn)) = k'(Cn) / d'(Cn) = L. Из неё следует, что k (y) / d (y) → L. То есть всегда найдётся такая точка Cn, которая будет принадлежать множеству (Yn+1,Yn). Так как множество стремится к L, то и точка, принадлежащая ему, тоже будет приближаться к L. Поэтому можно утверждать, что и выражение lim k (y) / d (y) → L.

Аналогичным образом первому доказывается и второй случай, когда lim k (y) = lim d (y) = 0. Если предел отношения производных будет L, то ограничения отношений функций будет также равняться этому числу. Из теоремы Дарбу и монотонности получим, что d (Yn) → 0, кроме того k (Yn) → 0. Используя правило Штольце, можно будет утверждать, что k (y) / d (y) → L.

Но на практике часто для решения примеров правило Лопиталя оказывается недостаточным. Это справедливо для заданий, в которых y стремится не к конечному числу, а к бесконечному. Поэтому для таких задач используется следствие из теоремы. Согласно ему, при k → 0 и d → 0, а y → + ∞. Тогда существует предел lim k'(y) / d'(y) = AЄR и предел отношений lim k (y) / d (y) = A. Этот вспомогательный закон очень важен и то же может быть доказан.

Следствие из утверждения

Перед доказательством следствия нужно условиться, что в выражении a будет всегда больше либо равно единице. Это возможно исходя из того, что если a будет меньше единицы, то доказывать нужно будет правило только от единицы до плюс бесконечности. Кроме этого, необходимо ввести замену вида t = 1/y. Она необходима, так как во многом облегчает сведение доказательства к теореме Лопиталя.

Пусть имеется функция K (t), равная k, и D (t), равная d. При этом аргумент последней будет 1/t. Так как по условию правила функции k и d определены на интервале от a до плюс бесконечности, то можно сказать, что функции K и D известны на интервале от нуля до единицы, делённом на a. Это верно из-за того, что если в исходной функции k и d икс подходил достаточно близко к плюс бесконечности, то в силу сделанной ранее замены t будет приближаться к нулю. Если же икс близок к a, то t будет приближаться к значению 1/a.

Так как a больше либо равняется единице, то интервал от нуля до единицы, делённой на a, будет определён корректно. Чтобы воспользоваться теоремой Лопиталя, нужно доказать, что предел lim K'(t) / D'(t) при t, стремящемся к нулю, равняется A. В силу того, что K (t) = k (1/t) и D (t) = d (1/t), можно написать: lim K'(t) / D'(t) = lim k'(1/t)’ / d'(1/t)’ .

Теперь нужно воспользоваться теоремой о производной композиции, условия которой выполнены. Вначале нужно взять производную внутренней функции, а затем внешней. Должно получиться следующее выражение: lim -1/ t 2 k ‘(1/ t) / (-1/ t 2) * d ‘ (1/ t) = lim K ‘(t) / D ‘(t) = lim k ‘(y)/ d (y) = A.

Отсюда можно утверждать, что предел отношений K'(t) / D'(t) будет равняться A. Все условия теоремы Лопиталя выполнены. А это значит, что существует предел отношения функций при t, стремящемся к нулю, равный A. Теперь можно снова применить теорему о пределе композиций и от переменной t перейти обратно к иксу: lim K (t)/D (t) = lim k (y)/(d (y) = A.

Таким образом можно сделать вывод, что требуемое утверждение верно. Использование правила и следствия позволяет выполнить быстрый расчёт неопределённости 0/0 или ∞/∞. При этом другого вида выражение можно свести к этой неопределённости. Это намного упрощает работу, особенно если необходимо логарифмировать или возводить в степень.

Решение примеров

Закрепить правило лучше всего на соответствующих примерах. Существуют типовые задания, чаще всего встречающиеся на контрольных работах. Например, требуется найти предел отношения натурального логарифма от тангенса икс к котангенсу два икс, когда неизвестное стремится к p /4. Помощь в решении окажет правило Лопиталя, которое при сравнении с альтернативными методами окажется на порядок проще.

Для того чтобы понять, какого вида неопределённость в задании, нужно в числитель и знаменатель подставить p/4. Тогда: ln td p /4 = ln 1 = 0 и ctd p /2 = 0. По правилу можно свести нахождение предела функций к вычислению их производных. Искомый предел: A = lim (lntdy ‘) / (ctd 2 y)’ = lim (ctdy * 1/ cos 2 y) / 2 (-1/ sin 2 2 y) = lim (-sin 2 y)(2 * siny * cosy) = (-½) * lim (sin 2 2 y / siny * cosy) = — ½ * 1/½ = -1. Таким образом, решение будет равняться минус единице.

Пусть есть выражение вида: lim y½ (p — 2 arctd √ y) = A. Нужно определить предел при иксе, стремящемся к плюс бесконечности. Чтобы воспользоваться правилом, исходное выражение нужно привести к дробному виду. Для этого выражение можно переписать как lim (p — 2 arctd √ y) / y½. В этом случае имеет место неопределённость 0/0. Поэтому можно рассматривать отношение производной делимого на делитель: A = lim (2 *(1/1+ y) * ½ * y -½ ) / ½ * y -3/2 = lim 2y/(1+y) = 2 lin 1 /(1+ 1/ y) = 2.

Замечательным случаем является неопределённость вида ∞/∞. Например, требуется найти предел lim k (y) при иксе, стремящемся к бесконечности, где функция k (y) = y /ey. По теореме Лопиталя A = lim (y)’ / (ey)’, а это выражение есть не что иное, как lim 1/ey, равняющийся нулю. Теперь можно рассмотреть пример сложнее.

Пусть дано выражение нормальной функции со степенью: lim yy = A, где A = lim k (y). Проэкспоненцируя эту функцию, выражение можно привести к виду: yy = ey *lny. Если найти, к чему стремится показатель экспоненты, то это и будет решением рассматриваемого примера. Можно записать: lim y * lny = lim lny /1/ y = lim (1/ y)/(-1/ y 2 ) = 0. Если предел в показателе экспоненты стремится к нулю, то можно написать, что он будет равняться e0, то есть единице. А это и будет искомый предел: lim k (y) = 1 при иксе, стремящемся к плюс бесконечности.

Закон Лопиталя является хорошим помощником при вычислении особо экзотических пределов. При этом можно попробовать составить выражение, отвечающее условиям правила и из неявного вида функции. Для этого можно использовать раскрытие скобок, дополнительно умножить или разделить функцию на однородный многочлен.

Использование онлайн-калькулятора

Не всегда задания, попадающиеся на практике, довольно легко привести к условию, отвечающему правилу. Да и нередко сама функция настолько умудрённая, что для определения производной понадобится не только проявить внимание и усидчивость, но и затратить довольно много времени. Поэтому в таких случаях есть резон решать задания на онлайн-калькуляторе с подробным решением. Правило Лопиталя отлично поддаётся автоматизированному вычислению.

Такую услугу предлагают более десятка специализированных на математических расчётах сайтов. Доступ к вычислениям предоставляется полностью бесплатно. От пользователя даже не требуется регистрации и указания персональных данных. Работают они на основе алгоритмов, заложенных в программный код используемого онлайн-приложения. Пользователю нужно лишь только подключение к интернету и любой веб-обозреватель.

Все его действия сводятся к введению в предложенную форму условия примера и нажатия кнопки «Рассчитать». После этого программа автоматически вычислит ответ и выведет его на дисплей. При этом в большинстве случаев вместе с ответом приложение отобразит пошаговый расчёт с комментариями. Это позволит потребителю не просто получить готовый ответ, но и разобраться в решении.

Из наиболее популярных сайтов можно выделить следующую пятёрку:

• Math.semestr.
• Kontrolnaya-rabota
• Planetcalc.
• Math34.
• Webmath.

Все эти сайты имеют интуитивно понятный интерфейс на русском языке. Кроме предоставления услуги онлайн-калькулятора, на их страницах содержится вся необходимая теория, помогающая понять, как происходит нахождение ответа. А также приведены несколько типовых примеров с подробным решением.

Пользоваться такими сайтами сможет даже пользователь, ничего не понимающий в математическом анализе. Но решая различные примеры, со временем он поймёт суть идеи правила и сможет самостоятельно вычислять пределы функций. При этом такие сайты являются отличным подспорьем как инженерам, проводящим сложные вычисления, так и студентам, проверяющим свои навыки.

калькулятор пределов (решатель) – с шагами

Калькулятор лимита с шагами

онлайн калькулятор пределов поможет вам найти предел функции по отношению к переменной. Это онлайн-инструмент, который помогает вам вычислять значение функции, когда вход приближается к определенному значению.

Калькулятор пределов с шагами показывает пошаговое решение пределов вместе с графиком и расширением ряда. Он использует все предельные правила, такие как сумма, произведение, частное и правило Лопиталя, для расчета точного значения.

Вы можете оценить пределы относительно \(\text{x, y, z, v, u, t}\) и \(w\) с помощью этого калькулятора пределов.

Это не то. С помощью этого инструмента вы также можете найти,

1. Правый предел (+)
2. Левый предел (-)
3. двусторонний предел

Как работает калькулятор лимитов?

Чтобы оценить предел с помощью этого решателя пределов, выполните следующие шаги.

• Введите функцию в данное поле ввода.
• Выберите соответствующую переменную.
• Введите предельное значение.
• Выберите сторону ограничения. т. е. левое, правое или двустороннее.
• Нажмите кнопку «Рассчитать», чтобы получить результат.
• Используйте кнопку «Сброс», чтобы ввести новые значения, и значок клавиатуры  , чтобы ввести дополнительные значения.

Вы найдете ответ под инструментом. Нажмите «Показать шаги», чтобы просмотреть пошаговое решение.

Что такое предел в исчислении?

Предел функции — это значение, к которому f(x) приближается по мере приближения x к некоторому числу. Пределы можно использовать для определения производных, интегралов и непрерывности, находя предел данной функции. x приближается к 0, равен 1.

Каков предел, когда x приближается к бесконечности ln(x)?

Предел ln(x) при стремлении x к бесконечности равен +∞. Предел этого натурального логарифма может быть доказан доведением до абсурда.

• Если x >1ln(x) > 0, предел должен быть положительным.
• Поскольку ln(x2) − ln(x1) = ln(x2/x1). Если x2>x1, разность положительна, поэтому ln(x) всегда возрастает.
• Если lim x→∞ ln(x) = M ∈ R, мы имеем ln(x)

Некоторые теоремы о дифференцируемых функциях. Правило Лопиталя. (Семинар 11)

Похожие презентации:

Основные теоремы о дифференцируемых функциях, правило Лопиталя. Лекция 11

Правило Лопиталя

Основные теоремы о дифференцируемых функциях, правило Лопиталя. (Лекция 11)

Теоремы о среднем. Правило Лопиталя

Логарифмическая производная. Производные высших порядков. Теоремы Роля, Лагранжа, Коши. Правило Лопиталя. (Лекция 6)

Правило Лопиталя

Правило Лопиталя раскрытия неопределенности вида

Производная сложной функции. Производная обратной функции. Производная функции, заданной неявно. Теорема. (Семинар 8)

Дифференциальное исчисление. Лекция 1

Дифференциальное исчисление

Семинар 11. Некоторые теоремы о дифференцируемых функциях. Правило
Лопиталя.
1.Теорема о корнях производной (теорема Ролля)
Если функция y=f(x) непрерывна и дифференцируема на отрезке [a,b] и на концах
отрезка f(a)=f(b)=0, то существует внутри отрезка [a,b] по крайней мере одна
точка x=c, a<c<b, в которой производная f’(x) обращается в 0.
2.Теорема о конечных приращениях (теорема Лагранжа)
Если y=f(x) непрерывна и дифференцируема на отрезке [a,b], то внутри отрезка [a,b]
найдется, по крайней мере, одна точка c, a<c<b, что
f(b)-f(a)=f’(c)(b-a) (1)
3.Теорема об отношении приращений двух функций (теорема Коши)
Если f ( x), ( x) непрерывные и дифференцируемые функции на отрезке [a,b],
причем ‘ ( x) 0 при x [a, b]
f (b) f (a) f ‘ (c)
(b) (a) ‘ (c)
то найдется такая точка x=c, a<c<b, что
(1).
Понятие о правиле Лопиталя
Рассмотрим отношение f ( x) ( x)
где функция ( x), ( x) определены и
( x)
дифференцируемы в окрестности U
точки а. Может случиться, что при
a
x a, ( x), ( x) стремятся к 0 или к то есть обе функции одновременно
являются бесконечно малыми или бесконечно большими. Тогда в точке а
функция f(x) имеет неопределенность вида 0 или (1).
0
В этом случае, используя производные ‘ ( x), ‘ ( x) можно сформулировать простое
правило для нахождения предела функции f(x) при x a
то есть дать способ
раскрытия неопределенностей вида (1). Это правило Лопиталя.
Теорема
Предел отношения двух бесконечно малых или бесконечно больших функций равен
пределу отношения их производных (конечному или бесконечному), если
последний существует.
lim x a
( x)
‘ ( x)
lim x a
( x)
‘ ( x)
0
Указанные виды неопределенностей
или
не являются единственными.
0
Возможны неопределенности 0 то есть f ( x) ( x) ( x) причём
( x) 0, ( x) , x a Или неопределенность
причём
то есть f ( x) ( x) ( x)
( x) , ( x) , x a Возможны и другие неопределенности. Для раскрытия этих
неопределенностей их стараются с помощью тождественных преобразований
0
свести к неопределенностям вида или и затем применить правило Лопиталя.
0
Примеры с решениями
1. Выполняется ли теорема Ролля для функции f ( x) x 2 6 x 100 если a=1, b=5?
При каком значении с?
Решение. Так как функция f(x) непрерывна и дифференцируема при всех значения х и
ее значения на концах отрезка [1;5] равны: f(1)=f(5)=95, то теорема Ролля на этом
отрезке выполняется. Значение с определяется из уравнения f’(x)=2x-6=0, то есть
с=3
2. Показать, что производная многочлена f ( x) x 3 x 2 x 1 имеет
действительный корень в интервале (-1;1)
Решение. Найдем корни данного многочлена: x 3 x 2 x 1 0 ( x 1) 2 ( x 1) 0
то есть x1 x2 1; x3 1
Так как f(-1)=f(1)=0, то по теореме Ролля f’(x) имеет корень в интервале (-1;1).
Найдем корни производной: f ‘ ( x) 3x 2 2 x 1 0 x1 1 / 3; x2 1
Таким образом, между корнями функции содержится корень производной, равный 1/3.
3.На дуге AB кривой y 2 x x 2 найти точку М, в которой касательная
параллельна хорде AB, если A(1;1) и B(3;-3)
Решение. Функция y 2 x x 2
непрерывна и дифференцируема при этих значениях
х. По теореме Лагранжа между двумя значениями a=1 и b=3 существует значение
x=c, удовлетворяющее равенству f(b)-f(a)=f’(c)(x-a), где f’(x)=2-2x. Подставив
соответствующие значения, получим f(3)-f(1)=f’(c)(3-1), -4=4(1-с). Отсюда с=2,
f(2)=0. Таким образом, точка М имеет координаты (2;0).
4. На дуге АВ кривой, заданной параметрическими уравнениями x t 2 ; y t 3
найти точку М, в которой касательная параллельна хорде АВ, если точкам А и В
соответствуют значения t=1 и t=3.
Решение. Угловой коэффициент хорды АВ равен y(3) y(1)
а угловой
x(3) x(1)
коэффициент касательной в точке М (при t=c) равен
yt’ (c)
xt’ (c)
где
xt’ 2t ; y t’ 3t 2
‘
Для определении с по теореме Коши получаем уравнение
y (3) y (1) y t (c)
x(3) x(1) xt’ (c)
или
27 1 3c 2
13 3
c
9 1
2c
4 2
Найденное значение с=13/6 удовлетворяет неравенству 1<c<3. Подставив значение
t=c в уравнения кривой получим x=169/36; y=2197/216.
5. Применяя правило Лопиталя найти пределы.
1. lim 2 x 1 0 lim 2 x ln 2 ln 2 ln 2
x 0
2.
lim x
3. lim
4.
x 0
sin x
0
x 0
cos x
1
x 2
2x
2
lim x x lim x x 0
x
e
e
e
x ln x 0 lim x 0
ln x
lim x 0
1
x
1
x lim
x 0 x 0
1
x2
1
x cos x sin x 0
cos x 1
lim x 0 (ctgx ) lim x 0
lim x 0
x
x sin x
sin x x
0
lim x 0
cos x x sin x cos x
x sin x
sin x
0
lim x 0
lim x 0
0
sin x
sin x x cos x
sin x x cos x
1 1
cos x
x
Примеры для самостоятельного решения.
1. Проверить справедливость формулы Коши для функций f ( x) x 3и ( x) x 2 1 в
интервале [1,2].
2. Написать формулу Коши для функций f ( x) e 2 x и ( x) 1 e x в
интервале [a,b].
3. Проверить справедливость теоремы Ролля для функции y 3 x 2 3x 2 в
интервале [1,2].
4.
Проверить справедливость теоремы Ролля для функции y ln sin x
в
интервале , 5
6 6
5. Написать формулу Лагранжа для функции y x(1 ln x)в интервале [a.b].
6.Проверить справедливость теоремы Лагранжа для функции y ln x в
интервале 1, e
7. Применяя правило Лопиталя найти пределы.
x 2 1 ln x
1) lim
x 1
ex e
x 3 3x 2 2
6) lim 3
x 1 x 4 x 2 3
x sin x
2) lim
x 0
x3
xn
3) lim x
x e
e x e x
7) lim
x 0 ln( 1 x)
4) lim ( x 2 ln x)
x 0
ln( x a)
x a ln( e x e a )
8) lim
1
1
5) lim x
x 0 x
e 1
ln x
x 0 1 2 ln sin x
9) lim
ln x
x x n
10) lim

English     Русский Правила

Правило Лопиталя — Math Insight

Правило Лопиталя — окончательный способ упростить оценку пределы. Он не оценивает пределы напрямую, а только упрощает оценка при правильном использовании .

По сути, это правило является окончательной версией «трюков отмены», применимы в ситуациях, когда более приземленный подлинный алгебраический отмена может быть скрытой или невидимой.

Предположим, мы хотим оценить $$\lim_{x\rightarrow a}{f(x)\over g(x)}$$ где предел $a$ также может быть равен $+\infty$ или $-\infty$ дополнительно на «обычные» номера. Предположим, что либо $$\lim_{x\rightarrow a}f(x)=0 \hbox{ и } \lim_{x\rightarrow a} г(х)=0$$ или $$\lim_{x\rightarrow a}f(x)=\pm\infty\hbox{и} \lim_{x\rightarrow a} г(х)=\pm\infty$$ (Знаки $\pm$ не обязательно должны быть одинаковыми). Тогда мы не можем просто «подключиться» для оценки предела, и они традиционно называются неопределенные формы . Неожиданный трюк, который часто срабатывает состоит в том, что (удивительно) мы имеем право взять производную от и в числителе, и в знаменателе: $$\lim_{x\rightarrow a}{f(x)\over g(x)}= \lim_{x\rightarrow a}{f'(x)\над g'(x)}.$$ Нет, это , а не частное правило . Нет, не очень понятно, почему это тоже помогло бы, но посмотрим на примерах.

Пример 1

Найти $\lim_{x\стрелка вправо 0}\,(\sin\,x)/x$.

Решение: и числитель, и знаменателя имеют предел $0$, поэтому мы имеем право применить L’Hospital’s правило: $$\lim_{x\стрелка вправо 0}\,{\sin\,x\over x}= \lim_{x\стрелка вправо 0}\,{\cos\,x\более 1}. $$ В новом выражении 92}} } .$$

В этот момент мы можем заменить каждый ${1\over x}$ на $0$, обнаружив, что предел равен $${{1\более 2}+0 \более \sqrt{1+0+0}}+ { 0 \over \sqrt{1+0 }}={1\over 2}.$$

Важно понимать, что в дополнение к фактическому применения правила Лопиталя, может быть необходимо немного поэкспериментировать , чтобы все уладилось так, как вы хочу. Метод проб и ошибок не только возможен, он необходим .

Упражнения 9-}, \lim_{x\to \infty}, {\small\textrm{и}} \lim_{x\to -\infty}$ в общем случае через $\lim$ в дальнейшем.

Правило Лопиталя для $\displaystyle\frac{0}{0}$

Предположим, что $\lim f(x)=\lim g(x)=0$. затем

1. Если $\displaystyle \lim\, \frac{f'(x)}{g'(x)}=L$, то $\displaystyle \lim\, \frac{f(x)}{g( х)}=\lim \frac{f'(x)}{g'(x)}=L$.
2. Если $\displaystyle \lim\, \frac{f'(x)}{g'(x)}$ стремится к $+\infty$ или $-\infty$ в пределе, то и $\displaystyle \frac{f(x)}{g(x)}$. 9х}{2x}=\текст{не существует}. $

Если числитель и знаменатель стремятся к $\infty$ или $-\infty$, правило Лопиталя остается в силе.

Правило Лопиталя для $\displaystyle\frac{\infty}{\infty}$

Предположим, что $\lim f(x)$ и $\lim g(x)$ бесконечны. затем

1. Если $\displaystyle \lim\, \frac{f'(x)}{g'(x)}=L$, то $\displaystyle \lim\, \frac{f(x)}{g(x)}=\lim \frac{f'(x)}{g'(x)}=L$.
2. Если $\displaystyle \lim\, \frac{f'(x)}{g'(x)}$ стремится к $+\infty$ или $-\infty$ в пределе, то и $\displaystyle\frac{f(x)}{g(x)}$ тоже. 9х=1.\]

   Обратите внимание, что правило Лопиталя применимо только к неопределенным формам. Для ограничения в первом примере этого руководства L’Hôpital’s Правило не применяется и даст неправильный результат 6. Правило Лопиталя мощное и удивительно простое в использовании. вычислить неопределенные формы типа $\frac{0}{0}$ и $\frac{\infty}{\infty}$.

   ---

   Ключевые понятия

   Правило Лопиталя для $\frac{0}{0}$

   Предположим, что $\lim f(x) = \lim g(x) = 0$. затем

   1. Если $\displaystyle\lim \frac{f'(x)}{g'(x)} = L,$, то $\displaystyle\lim \frac{f(x)}{g(x)} = \displaystyle\lim \frac{f'(x)}{g'(x)} = L$.
   2. Если $\displaystyle\lim \frac{f'(x)}{g'(x)}$ стремится к $+\infty$ или $-\infty$ в пределе, то и $\frac{f(x)}{g(x)}$ тоже.

   Правило Лопиталя для $\frac{\infty}{\infty}$
   Предположим, что $\lim f(x)$ и $\lim g(x)$ оба бесконечны. затем

   1. Если $\displaystyle\lim \frac{f'(x)}{g'(x)} = L$, то $\displaystyle\lim \frac{f(x)}{g(x)} = \displaystyle\lim \frac{f'(x)}{g'(x)} = L$.
   2. Если $\displaystyle\lim \frac{f'(x)}{g'(x)}$ стремится к $+\infty$ или $-\infty$ в пределе, то и $\frac{f(x)}{g(x)}$ тоже.

   ---

   [Я готов пройти тест.] [Мне нужно просмотреть больше.]
   

   Исчисление

   – Расчет предела по правилу Лопиталя

   спросил 4 года, 7 месяцев назад

   Изменено 4 года, 7 месяцев назад 92}\right )}{\cos x} \\ & =\lim_{x\стрелка вправо 0}\frac{2x\cdot \cos \left (\frac{1}{x}\right )+\sin \left (\frac{1}{x}\right )}{\cos x}=\lim_{x\rightarrow 0}\left (2x\cdot \cos \left (\frac{1}{x}\right )+ \sin \left (\frac{1}{x}\right )\right ) \\ & =\lim_{x\rightarrow 0}\left (2x\cdot \cos \left (\frac{1}{x} \right )\right )+\lim_{x\rightarrow 0}\left (\sin \left (\frac{1}{x}\right )\right )\end{align*}

   Мы вычисляем два предела отдельно

   • $\lim_{x\стрелка вправо 0}\left (2x\cdot \cos \left (\frac{1}{x}\right )\right )$ :

   \begin{equation*}\left |\cos \left (\frac{1}{x}\right )\right |\leq 1 \Rightarrow -1\leq \cos \left (\frac{1}{ x}\right )\leq 1 \Rightarrow -2x\leq 2x\cdot \cos \left (\frac{1}{x}\right )\leq 2x\end{equation*} мы рассматриваем предел $x\rightarrow 0$ и мы получаем \begin{equation*}\lim_{x\rightarrow 0} \left (2x\cdot \cos \left (\frac{1}{x}\right ) \right )=0\end{equation *}

   • Как вычислить предел $\lim_{x\стрелка вправо 0}\left (\sin \left (\frac{1}{x}\right )\right )$ ?

   пределы исчисления

   $\endgroup$

   4

   $\begingroup$

   Чтобы использовать правило Лопиталя, нужно проверить, существует ли $\lim_{x\rightarrow 0}\dfrac{f'(x)}{g'(x)}$. Таким образом, в этом случае синусоида тополога $\sin(1/x)$ не имеет предела всякий раз, когда $x\rightarrow 0$, поэтому правило Лопиталя не применяется.

   Теперь используйте трюк, например \начать{выравнивать*} \lim_{x\стрелка вправо 0}\dfrac{x}{\sin x}=1 \конец{выравнивание*} и что \начать{выравнивать*} \lim_{х\стрелка вправо 0}х\cos(1/x)=0 \конец{выравнивание*} сделать вывод, что предельное значение равно нулю.

   Для доказательства $x\cos(1/x)\rightarrow 0$ всякий раз, когда $x\rightarrow 0$: \начать{выравнивать*} |х\cos(1/х)|\leq|х|, \конец{выравнивание*} а теперь используйте теорему сжатия, чтобы заключить, что $\lim_{x\rightarrow 0}x\cos(1/x)=0$ из-за того, что $\lim_{x\rightarrow 0}|x|=0$.

   Чтобы утверждать, что синусоидальная кривая тополога не имеет предела, поскольку $x\rightarrow 0$, просто пусть $a_{n}=\dfrac{1}{2n\pi}$ и $b_{n}=\dfrac{ 1}{2n\pi+\pi/2}$, поэтому $a_{n},b_{n}\rightarrow 0$, но $\sin(1/a_{n})=0\rightarrow 0$ и $\sin (1/b_{n})=1\rightarrow 1$, функция имеет две различные предельные точки всякий раз, когда $x\rightarrow 0$, поэтому предела не существует. 9+$, $1/x\to \infty$ .

   Поэтому sin(1/x) прыгает вверх и вниз между $-1$ и $1$ бесконечно много раз.

   Таким образом, предела $$\lim_{x\rightarrow 0}\left (\sin \left (\frac{1}{x}\right )\right )$$ не существует.

   Вам нужно попробовать другой подход, чтобы обойти это ограничение.

   $\endgroup$

   1

   $\begingroup$

   Правило Лопиталя не является альфой и омегой расчета пределов! Когда она работает, формула Тейлора при заказе $1$ тоже работает, и она менее опасна. 92}x\cos\frac1x=x\,O(1)=O(x),$$ а последний стремится к $0$, когда $x$ стремится к $0$.

   $\endgroup$

   3

   Твой ответ

   Зарегистрируйтесь или войдите в систему

   Зарегистрируйтесь с помощью Google

   Зарегистрироваться через Facebook

   Зарегистрируйтесь, используя электронную почту и пароль

   Опубликовать как гость

   Электронная почта

   Обязательно, но не отображается

   Опубликовать как гость

   Электронная почта

   Требуется, но не отображается

   Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

   Правило Лопиталя – Mathauditor

   Как пользоваться Калькулятором правила Лопиталя?

   Вычисления по математике очень сложны, и на их выполнение требуется много времени. делать. Как правило, требуется много времени, чтобы их понять и понять. решено. Однако у нас есть доступные инструменты и калькуляторы, которые сделать эти сложные вычисления относительно простыми и быстрыми. К счастью, сейчас мы живем в цифровом мире. В этом цифровой мир, бесчисленные онлайн-инструменты доступны для решения сложные математические теоремы в кратчайшие сроки. Правило Лопиталя калькулятор является одним из онлайн-инструментов, доступных для этого сложный расчет легко и быстро. Это может быть полезно в случае, если мы имеют дело с исчислением, в частности с пределами и непрерывностью функции для оценки пределов неопределенных форм.

   Прежде чем погрузиться в глубокое море, как использовать правило Лопиталя калькулятор для оценки предела неопределенных форм, мы будем сначала просмотрите термины, связанные с этим правилом L Hospital. Некоторые из полезные термины в правиле L Hospital: Исчисление, Предел, Непрерывность, Производные и т. д.

   Исчисление — это раздел математики, который помогает нам понимать слегка изменяющиеся значения, связанные с функцией. это также нахождение и свойства производных и интегралов функций путем суммирования бесконечно малых разностей. В исчислении Ограничения и Непрерывность существуют, чтобы лучше понять использование «правила больницы L».

   Предел в правиле Лопиталя

   Предел в математике — это значение, которое функция «адресует» как вход «адресует» некоторое значение, и ограничения имеют значение в исчисление и математический анализ для определения интегралов, производных и непрерывность. Синтаксис предела функции приведен ниже. –
   Lim f (n) =L
   n→c

   Непрерывность в правиле Лопиталя

   В исчислении функция может быть непрерывной в точке x = a – если – и только если – при выполнении нижеперечисленных условий.

   1. Функция определена при x = a; т. е. f (a) равно вещественному количество.
   2. Предел функции x с адресом a- существует.
   3. Предел функции как x, адресованной a, равен значение функции при x = a.

   Производные в калькуляторе правила Госпиталя

   Производная – это мгновенная скорость колебания функцию относительно одной из своих переменных. Это равнозначно нахождению наклон касательной к функции в точке.

   Калькулятор L’ Hospital

   Правило L’ Hospital по математике позволяет оценить Предел неопределенных форм. Применение этого правила преобразует и неопределенная форма к выражению, которое может быть вычислено замена быстро. Это реализовано в правиле Лопиталя. калькулятор.

   В калькуляторе правила Лопиталя мы должны вводить только значения, и это засчитает желаемый результат в кратчайшие сроки.

   Например, когда мы будем вводить значения неопределенных форм введите 00 или ∞∞. Пусть a будет либо конечным числом, либо бесконечным числом. Его можно использовать только в том случае, когда прямая замена дает неопределенная форма, т. е. 0/0 или ±∞/±∞. 92 х→4 х→∞

   Шаг 1: В 1-м пределе, если мы поместим x=4, мы получим 0/0, и во 2-м пределе, если мы введем бесконечность, мы можем получить ∞/минус ∞, т. е. если x стремится к бесконечности, многочлен будет следовать тому же пути, что и следует его наиболее значительная сила. Оба называются неопределенными формы. В обоих случаях существуют конкурирующие правила, и это не ясно, что даст близкий результат.

   Шаг 2: В случае 0/0 мы обычно думаем о фрагменте, который имеет числитель 0 как равный 0. Однако мы должны думать о элемент, в котором знаменатель ведет к 0, в пределе, как бесконечен или может вообще не существовать. Точно так же мы должны думать о фрагмент, в котором числитель и знаменатель равны 1. Итак, что даст близкий результат? Или не будет предоставлять немедленный результат, и все они «скомпрометированы», и Лимит будет достичь какого-либо другого результирующего значения?

   В случае с ∞/−∞ возникает такая же проблема. Если числитель фрагмента стремится к бесконечности, мы должны думать о весь фрагмент становится бесконечным. Кроме того, если знаменатель уходя в бесконечность, в Предел, мы должны думать о фрагменте как о приводит к нулю. Мы также имеем случай фрагмента, в котором числитель и знаменатель совпадают (без учета – (знак минус) и поэтому мы можем получить -1. Повторюсь, непонятно, какой из них приблизится к результатам, если какой-либо из них будет иметь точное результат.

   Шаг 3: Со 2-м пределом есть другая проблема, которая бесконечность не является числом, и поэтому мы даже не будем рассматривать это как число. Как правило, он не будет действовать так, как мы ожидаем. если бы это было число. Это проблема с неопределенными формами. Это просто непонятно, что происходит в пределе. Есть и другие типы неопределенных форм, а также. Некоторые другие типы:

   (0) (±∞) 1∞ 00 ∞0 ∞−∞

   Кроме того, правило Госпиталя по правилу Лопиталя калькулятор уточняет оценку лимитов и находит лимит.

   У этого есть эмулирующие правила, которые сообщают нам, что может случиться, и это просто не зафиксировано, какие из правил, если таковые имеются, будут близки к результат. Определение этого раздела заключается в том, как мы можем справиться с такого рода ограничения.

   Итак, в конечном итоге вы должны выполнить следующие шаги при использовании Калькулятор по правилу Лопиталя.

   1. Шаг 1: Прежде всего, введите предел, который вы хотите найти.
   2. Шаг 2: Затем введите значения x и y в расчеты.
   3. Шаг 3: После этого нажмите кнопку «Отправить», чтобы получить оценка введенных вами значений в качестве входных данных.
   4. Шаг 4: И вы получите соответствующий вывод.

   Bottom Line

   Однако при использовании калькулятора правил Лопиталя вам следует введите значения для x и y в зависимости от того, что вы даете в качестве входных данных к этому. Очень эффективно решать такого рода математические проблема с использованием калькулятора правил Лопиталя.

   L’Hopital’s Rule – Math Hints

   Этот раздел содержит:

   • • L’Hoptital’s Rule
     • Подробнее
   9000 2 9000 2 помните в исчислении, когда вы берете ограничения (как мы делали в разделе «Ограничения и непрерывность »). В книгах по математическому анализу это правило, похоже, не представлено до разделов «Техники интеграции», так что вот оно!

   При использовании ограничений вы можете получить то, что мы называем неопределенными формами , которые представляют собой  \(\displaystyle \frac{0}{0}\) или \(\displaystyle \frac{\infty }{\infty } \). Причина, по которой эти дроби называются неопределенными, заключается в том, что мы не знаем, существует ли предел, или если он существует, мы не знаем, что это такое. Ранее мы научились применять к ним некоторые алгебраические действия (например, разложение на множители и вычеркивание или умножение на сопряженные числа), чтобы попытаться найти предел.

   По сути, правило Лопиталя говорит о том, что в некоторых случаях, чтобы получить предел частного, вы можете просто взять предел частного производных числителя (вверху) и знаменателя (внизу) .

   Вот более формальное определение:

   Правило Лопиталя :

   c}}{\mathop{{\lim }}}\frac{{f\left( x \right)}}{{g\left( x \right)}}\) is \(\displaystyle \frac{0 }{0}\) или \(\displaystyle \frac{\infty}{\infty }\) или \(\displaystyle \frac{{-\infty}}{{-\infty }}\) или \(\ displaystyle \frac{{-\infty }}{\infty }\) или \(\displaystyle \frac{\infty }{{-\infty }}\), затем

   \(\displaystyle \underset{{x\to c}}{\mathop{{\lim }}}\frac{{f\left(x\right)}}{{g\left(x\right) }}=\underset{{x\to c}}{\mathop{{\lim }}}\frac{{{f}’\left( x \right)}}{{{g}’\left( x \right)}}\) (пока предел справа существует или бесконечен).

    

   Это говорит о том, что если у вас есть две функции, пределы которых соответствуют приведенным выше условиям, вы можете брать производную от верхней и нижней функций снова и снова, пока не получите пределы, которые «работают».

   Вот несколько примеров с использованием как алгебраических методов, так и метода Лопиталя. Помните, что в L’Hôpital, когда вы работаете с частными, вам не нужно правило частных; вы просто берете производную от верха (числителя) и низа (знаменателя), а потом берете предел.

   Помните, что если вы не можете получить предел после взятия производных верхней и нижней части, снова возьмите производную, а затем попробуйте (вы можете делать это бесконечно!) калькулятор , введя очень маленькое число (если предел достигает 0 ) или очень большое число (если предел достигает \(\infty \)), чтобы увидеть, получите ли вы близкий ответ.

   Find Limits	Algebraic Solution	L’Hôpital’s Rule Solution
   \(\displaystyle \underset{{x\to \infty }}{\mathop{ {\lim }}}\,\frac{{3x+2}}{{5x-1}}\)   Неопределенная форма: \(\displaystyle \frac{\infty }{\infty }\)	Каждое слагаемое можно разделить на \(x\), так как это высшая степень (показатель степени). Затем помните, что \(\displaystyle \underset{{x\to \infty}}{\mathop{{\lim }}}\frac{1}{x}=0\): \(\displaystyle \begin{align } \ underset {{x \ to \ infty}} {\ mathop {{\ lim }}} \ frac {{3x + 2}} {{5x-1}} & = \ underset {{x \ to \ infty} {\ mathop {{\ lim }}} \ frac {{\ frac {{3x}} {x} + \ frac {2} {x}}} {\ frac {{5x}} {x} – \ frac{1}{x}}}\\&=\frac{{3+\frac{2}{x}}}{{5-\frac{1}{x}}}=\frac{3}{ 5}\end{align}\)	Возьмем производную от верхней и нижней части дроби, а затем возьмем предел:   \(\displaystyle \underset{{x\to \infty}}{\mathop{{\lim }}}\,\frac{{3x+2}}{{5x-1}}=\underset{ {x\to \infty}}{\mathop{{\lim }}}\,\frac{3}{5}\,\,=\frac{3}{5}\)   Поскольку существует нет \(x\) в ответе, мы можем игнорировать \(x\) переход к \(\infty \). Намного легче!
   \(\displaystyle \underset{{x\to 0}}{\mathop{{\lim }}}\frac{{\sin 4x}}{{3x}}\)   Неопределенная форма: \(\displaystyle \frac{0}{0}\)	Нам нужно получить это в виде \(\displaystyle \underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{{\sin x}}{x} \) (переместите \(\displaystyle \frac{1}{3}\) наружу, а затем умножьте на \(\displaystyle \frac{4}{4}\)) поскольку \(\displaystyle \underset{ {x\to 0}}{\mathop{{\lim}}}\,\frac{{\sin x}}{x}=1\): \(\displaystyle \begin{align}\underset{{ х \ к \, 0}} {\ mathop {{\ lim}}} \ frac {{\ sin 4x}} {{3x}} & = \ frac {1} {3} \ cdot \ underset {{x \ к \,0}}{\mathop{{\lim}}}\frac{{\sin 4x}}{x}\\&=\frac{1}{3}\cdot \frac{4}{4} \cdot \underset{{x\to \,0}}{\mathop{{\lim }}}\frac{{\sin 4x}}{x}\\&=\frac{1}{3}\cdot \ frac {4} {1} \ underset {{x \ to \, 0}} {\ mathop {{\ lim }}} \ frac {{\ sin 4x}} {{4x}} \\ & = \ frac {4}{3}\cdot 1=\frac{4}{3}\end{align}\) 9{2}}-1}}&=\underset{{x\to -\,\infty}}{\mathop{{\lim }}}\frac{1}{{2x}}\\&=\underset {{x\to -\,\infty}}{\mathop{{\lim }}}\frac{0}{2}=0\end{align}\) Так как нет \(x\) в ответе мы можем игнорировать переход \(x\) в \(-\infty\).
   \(\displaystyle \underset{{h\to 0}}{\mathop{{\lim }}}\frac{{\sqrt[3]{{h+27}}-3}}{ h}\)   Неопределенная форма: \(\displaystyle \frac{0}{0}\)	Слишком сложно для алгебраических вычислений! 9049{{-\frac{2}{3}}}}=\frac{1}{{27}}\end{align}\)
   \(\displaystyle \underset{{t\to 0 }}{\mathop{{\lim }}}\,\frac{{\sin \left({\pi +t} \right)}}{t}\)   Неопределенная форма: \(\displaystyle \frac{0}{0}\)	Не знаю, как это сделать алгебраически!	Возьмите производную от верхней и нижней части дроби, а затем возьмите предел: \(\displaystyle \begin{align}\underset{{t\to 0}}{\mathop{{\lim }}} \ frac {{\ sin \ left ( {\ pi + t} \ right)}} {t} & = \ underset {{t \ to 0}} {\ mathop {{\ lim}}} \ frac {{\ cos \left( {\pi +t} \right)}}{1}\\&=\cos \left({\pi +0} \right)=-1\end{align}\)

   Изучите эти правила и практикуйтесь, практикуйтесь, практикуйтесь!

   ---

   Используйте клавиатуру MathType, чтобы ввести задачу Limit , а затем нажмите «Отправить» (стрелка справа от задачи), чтобы решить задачу, используя Правило Лопиталя . Вы также можете нажать на 3 точки в правом верхнем углу, чтобы развернуть, например, проблемы.

   Если вы нажмете «Нажмите, чтобы просмотреть шаги», вы перейдете к  Mathway  сайт, на котором вы можете зарегистрироваться для получения полной версии  (этапы включены) программного обеспечения. Вы даже можете получить рабочие листы по математике.

   Вы также можете перейти на сайт Mathway здесь, где вы можете зарегистрироваться или просто использовать программное обеспечение бесплатно без подробных решений. Существует даже приложение Mathway для вашего мобильного устройства. Наслаждаться!

   Переходим к Суммы Римана и площадь по предельному определению  — вы готовы!

   Что такое правило Лопиталя (Правило Лопиталя)?

   Правило Лопиталя (правило Лопиталя) произносится как «правило лопиталя», и это правило является очень важным правилом исчисления, которое используется для оценки странных пределов, которые приводят к неопределенным формам (таким как 0/0, ∞/ ∞ и др. ). Эти типы лимитов

   • не могут быть рассчитаны путем прямой подстановки лимита и/или
   • можно оценить, но с использованием очень долгой процедуры.

   Давайте посмотрим на правило Лопиталя вместе с его формулировкой, доказательством и примерами. Кроме того, давайте рассмотрим некоторые распространенные заблуждения, которые могут возникнуть при применении этого правила.

   1.	История правил Лопиталя
   2.	Что такое правило больницы L?
   3.	Формула правила Лопиталя
   4.	Доказательство правила Лопиталя
   5.	Когда и как применять правило Лопиталя?
   6.	Неправильные представления о правиле Лопиталя
   7.	Часто задаваемые вопросы о правиле Лопиталя

   История правила Лопиталя

   Правило Лопиталя имеет различные названия, такие как правило Лопиталя, правило Лопиталя, правило Бернулли и т. д., и используется для оценки пределов неопределенных форм. Впервые оно было введено швейцарским математиком Иоганном Бернулли в 1694 году и поэтому известно как правило Бернулли. Позже оно было разработано французским математиком Гийомом де л’Опиталем и поэтому стало популярным под названием правила Лопиталя.

   Давайте рассмотрим пример, прежде чем смотреть, что говорит это правило: lim _{x → 2} (x ² – 4) / (x – 2). Первое, что мы обычно делаем для оценки предела, — это подставляем предел. Давайте посмотрим, что происходит, когда мы применяем ограничение. Получаем (2 ² – 4) / (2 – 2) = 0/0. Это неопределенная форма (поскольку 0/0 не определено). Но попробуем упростить этот предел по-другому. Мы знаем, что x ² – 4 можно записать как (x + 2) (x – 2) (используя формулу a² – b²). Так лим _{x → 2} (x ² – 4) / (x – 2) = lim _{x → 2} [(x + 2) (x – 2)] / (x – 2) = lim _{x → 2} (x + 2) = 2 + 2 = 4. Из-за факторизации мы могли легко вычислить этот предел.

   Возьмем другой предел lim _{x → 0} (sin x) / x (действительное значение которого равно 1, и это будет доказано позже), который также дает нам неопределенную форму 0 / 0, но ее нелегко вычислить, так как другой. Правило Лопиталя упрощает процесс нахождения пределов, дающих неопределенные формы, путем применения предела. Прежде чем приступить к его изучению, давайте просто посмотрим, какими могут быть другие неопределенные формы.

   Неопределенные формы:

   Неопределенная форма — это то, что не может быть определено математически. Неопределенные формы могут быть вида 0/0, ±∞/±∞, 0 × ∞, ∞ – ∞, 0 ⁰ , 1 ^∞ , ∞ ⁰ и т. д. Но наиболее распространены неопределенные формы, встречающиеся в то время как применение правила Лопиталя – 0/0 и ± ∞ / ± ∞.

   Что такое правило больницы L?

   Правило Лопиталя гласит, что предел отношения двух функций (где знаменатель НЕ равен 0), который приводит к неопределенной форме при прямом применении предела, равен пределу отношения их производные. Давайте посмотрим на математическое определение правила Лопиталя ниже.

   Формула правила Лопиталя

   Правило Лопиталя гласит, что для любых двух непрерывных функций f(x) и g(x) lim _{x → a} f(x)/g(x) является неопределенной формой, тогда lim _{x → a} f(x) / g(x) = lim _{x → a} f’ (x) / g'(x), где

   • ‘a’ — любое действительное число, или ∞, или – ∞.
   • lim _{x → a} f(x) / g(x) является неопределенной формой, когда применяется x = a.
   • f'(x) является производной от f(x)
   • g'(x) является производной от g(x) и g'(a) ≠ 0,

   Доказательство правила Лопиталя

   Мы знаем, что правило Лопиталя применяется, когда предел имеет вид 0/0 и ±∞/±∞. Предположим, что lim _{x → a} f(x)/g(x) = 0/0, т. е. f(a)/g(a) = 0/0, что означает f(a) = 0 и g( а) = 0. Рассмотрим левую часть правила и в конечном итоге добьемся правой части.

   LHS = lim _{x → a} f(x) / g(x)

   = lim _{x → a} [ f(x) – f(a) ] / [ g(x) – g(a) ] (∵ f(a) = g (a) = 0)

   Деление числителя и знаменателя на (x – a),

   = lim _{x → a} \(\dfrac{\frac{f(x)-f(a)}{x-a}} {\ frac {g (x) -g (a)} {xa}} \)

   = \(\ frac {lim_ {x → a} \ frac {f (x) -f (a)} {xa} }{ lim_{x → a}\frac{g(x)-g(a)}{x-a}}\)

   По определению производной

   = f'(a) / g'(a)

   = lim _{x → a} f’ (x) / g'(x)

   = RHS

   Таким образом, правило Лопиталя доказано. Это доказательство расширяется до пределов с другими неопределенными формами, такими как ± ∞ / ± ∞ (хотя это доказательство сложное и продвинутое).

   Когда и как применять правило Лопиталя?

   Правило Лопиталя следует применять только тогда, когда lim _{x → a} f(x) / g(x) приводит к неопределенной форме прямым применением предела. В таких случаях мы просто дифференцируем числитель и знаменатель (используя формулы производных) по отдельности, а затем применяем предел. Вот те же самые примеры, которые были упомянуты в первом разделе и очень легко решаются с помощью правила Лопиталя.

   • lim _{x → 2} (x ² – 4) / (x – 2) = 0/0 прямым применением предела (x = 2).
     Используя правило Лопиталя:
     lim _{x → 2} (x ² – 4) / (x – 2) = lim _{x → 2} (2x) / (1) = 2(2) = 4
     (это следует из правила мощности)
   • lim _{x → 0} (sin x) / x = 0 / 0, когда применяется x = 0.
     Используя правило Лопиталя:
     lim _{x → 0} (sin x) / x = lim _{x → 0} (cos x) / 1 = cos 0 = 1
     (это следует из формулы производной sin x)

   Иногда предел все еще приводит к неопределенной форме даже после однократного применения правила Лопиталя. В этом случае мы можем применять одно и то же правило снова и снова по мере необходимости.

   Многократное применение правила Лопиталя:

   Мы можем применять правило Лопиталя столько раз, сколько потребуется. Каждый раз, когда мы применяем правило, мы вычисляем производные функций числителя и знаменателя отдельно, а затем применяем предел. Но перед каждым применением этого правила просто убедитесь, что текущий предел приводит к неопределенной форме. Вот пример.

   Пример: Оценка предела lim _{x → 0} (1 – cos 2x) / x ² .

   Решение:

   Непосредственным применением предела x → 0 мы получаем (1 – cos 0) / 0 = (1 – 1) / 0 = 0 / 0, что является неопределенной формой. Поэтому применим правило Лопиталя. Мы знаем, что производные от 1 – cos 2x и x ² равны 2 sin 2x и 2x соответственно. Тогда приведенный выше предел принимает вид:

   lim _{x → 0} (2 sin 2x / 2x) = lim _{x → 0} (sin 2x / x)

   Теперь попробуем применить ограничение. Тогда мы получаем (sin 0)/0 = 0/0, что снова является неопределенной формой. Итак, мы снова применяем правило Лопиталя. Мы знаем, что производные от sin 2x и x равны 2 cos 2x и 1 соответственно. Тогда приведенный выше предел принимает вид:

   lim _{x → 0} (2 cos 2x / 1) = 2 cos 0 = 2(1) = 2.

   Следовательно, lim _{x → 0} (1 – cos 2x) / х ² = 2.

   Неправильные представления о правиле Лопиталя

   В некоторых случаях мы склонны применять правило Лопиталя, но это приводит к неправильному результату. Поэтому мы должны быть осторожны при применении этого правила. Давайте посмотрим, где мы можем ошибиться при применении правила.

   Когда нельзя применять правило Лопиталя?

   Применение правила Лопиталя, когда предел НЕ дает неопределенной формы, дает неверный результат. Например:

   lim _{x → 2} (3x + 1) / (2x + 2) = (3(2) + 1) / (2(2) + 2) = 7/6 (правильный ответ)

   Ограничение не привело к неопределенной форме, поэтому мы не можем применить правило Лопиталя. Посмотрим, что мы получим, если подадим заявку. Мы знаем, что производные от 3x + 1 и 2x + 2 равны 3 и 2 соответственно. Таким образом, приведенный выше предел после применения правила становится:

   lim _{x → 2} (3/2) = 3/2 (неправильный ответ)

   ☛ Поэтому сначала примените ограничение и убедитесь, что в результате получается неопределенная форма перед применением правила.

   Упрощайте дробь перед каждым применением:

   Когда мы применяем правило Лопиталя несколько раз, каждый раз упрощайте рациональное выражение, прежде чем каждый раз применять ограничение. В противном случае получаем неверный ответ. Вот пример.

   lim _{x → 1} (x ³ – 1) / (x ² – 1)
   = lim _{x → 1} (3x ² /2x)
   = lim _{х → 1} (3x / 2)
   = 3(1)/2
   = 3/2 (правильный ответ)

   Но что произойдет, если мы не упростим дробь (на третьем шаге) и попытаемся снова применить правило Лопиталя?

   lim _{х → 1} (х ³ – 1) / (х ² – 1)
   = lim _{x → 1} (3x ² /2x)
   = lim _{x → 1} (6x / 2)
   = lim _{х → 1} 3x
   = 3(1)
   = 3 (неправильный ответ)

   ☛ Таким образом, упрощаем все до минимума перед применением правила.

   Важные примечания к правилу Лопиталя:

   • Предел дроби двух функций (что приводит к неопределенной форме) равен пределу дроби их производных.
   • Не применяйте правило Лопиталя, если ограничение не приводит к неопределенной форме.
   • Мы можем применять правило Лопиталя столько раз, сколько потребуется, но перед каждым применением мы должны проверять, не дает ли предел на этом конкретном шаге неопределенную форму.
   • Когда мы пытаемся применить правило Лопиталя для произведения f(x) · g(x), сначала запишем его в виде дроби (т.е. либо как f(x)/(1/g(x)) либо как g(x) / (1/ f(x)) ).

   ☛ Связанные темы:

   • Калькулятор пределов
   • Интегральный калькулятор
   • Калькулятор производных
   • Калькулятор определенных интегралов

   Часто задаваемые вопросы о правиле Лопиталя

   Что такое правило Лопиталя в исчислении?

   Правило Лопиталя в исчислении очень хорошо работает при оценке пределов, значение которых является неопределенным значением после прямого применения предела. Чтобы применить это правило, мы просто заменяем заданную долю функций долей их производных, а затем применяем предел. Мы всегда можем применить это правило столько раз, сколько потребуется.

   Как применять правило Лопиталя?

   Чтобы применить правило Лопиталя для оценки предела lim _{x → a} f(x)/g(x):

   • Сначала проверьте, приводит ли f(a)/g(a) к неопределенной форме, такой как 0/0, ∞/∞ и т. д. 90 106
   • Если да, найдите производные f'(x) и g'(x).
   • Тогда заданный предел получается путем вычисления предела lim _{x → a} f'(x)/g'(x).

   Что такое формула правил больницы L?

   Формула правила L Hopitals lim _{x → a} f(x) / g(x) = lim _{x → a} f’ (x) / g'(x), где левосторонний предел дает неопределенную форму, применяя предел x = a. Здесь f'(x) и g'(x) — производные соответствующих функций.

   Как узнать, применимо ли правило L’Hospital?

   Чтобы вычислить любой предел как x → a, мы сначала подставим x = a в данное выражение. Если это приводит к неопределенным значениям, таким как 0/0, ∞/∞, ∞/0 и т. д., то мы применяем правило Лопиталя.

   Когда нельзя использовать правило Лопиталя?

   Когда применение предела к дроби функций приводит к любому действительному числу, или ∞, или -∞, тогда мы не должны применять правило Лопиталя к этому пределу.

   Можно ли использовать правило Лопиталя несколько раз?

   Да, мы можем использовать правило Лопиталя несколько раз. Но перед каждым применением правила убедитесь, что применение ограничения дает неопределенное значение, например 0/0.

   Как произносится правило Лопиталя?

   Правило Лопиталя на самом деле называется правилом Лопиталя (которое было выведено французским математиком Гийомом де л’Опиталем) и произносится как “правило лопиталя”. Он используется для оценки пределов, которые приводят к неопределенной форме.

   Как применять правило Лопиталя для экспонент?

   При нахождении пределов, если в выражении присутствует переменная, сначала пометьте предел как L, а затем примените логарифмирование к обеим частям.