Замечательные пределы (1)
Замечательные пределы.
При вычислении пределов функций при х → х0 или х → ∞ часто возникают проблемы из-за того, что функция не определена при х → х0 (х → ∞).
Первым примером такой функции является функция .
Первым замечательным пределом называется предел этой функции при х → 0:
(1)
Пример 1.
Вычислить предел функции при х → 0.
Решение. Подставляя значение аргумента х = 0 в заданную функцию, видим что функция в заданной точке не определена (имеет неопределенность вида ). Для нахождения предела заданной функции попробуем привести ее к первому замечательному пределу. Используя формулу преобразования тригонометрических функций , получим:
дальнейшие преобразования проведем с
использованием основных теорем о
пределах.
Второй сомножитель в полученном выражении совпадает с формулой (1). Первый сомножитель так же эквивалентен формуле (1) так как может быть записан в виде: , где z = 2х.
Пример 2.
Найти:
Задание: найти пределы, используя первый замечательный предел и эквивалентность бесконечно малых величин:
=
2.
3.
4.
Второй замечательный предел.
Если вычислять значения членов последовательности при натуральных значениях номера n числовой последовательности, то получим:
у1 = 2; у2 = 2,25; у3 = 2,37; у4 = 2,441; у5 =
2,488; … … у10 = 2,59; … у50 = 2,69; у100 = 2,71.
у10 = 2,59; … у50 = 2,69; у100 = 2,71.
Из приведенных значений видно, что числовая последовательность является монотонной неубывающей. Это обусловлено увеличением показателя степени при увеличении номера
Ограничение возрастания рассматриваемой числовой последовательности обусловлено стремлением к единице основания степени при увеличении номера n числовой последовательности.
Данная числовая последовательность имеет предел:
. (2)
Формулу (2) называют вторым замечательным пределом.
Число е в математике еще называют
числом Эйлера, неперовым числом. Число е является иррациональным и с
точностью до шестой значащей цифры оно
равно
Число е является иррациональным и с
точностью до шестой значащей цифры оно
равно
е = 2,71828….
Если рассматривать числовую последовательность как значения некоторой функции при x = n, то получим другую запись второго замечательного предела:
(3)
Причем этот предел равен е при х → +∞ и при х → –∞, и формулу (3) можно записать в виде:
(4)
Если в формуле (3) произвести замену независимой переменной (при х → ∞, z → 0) получим еще одну форму записи второго замечательного предела:
(5)
Пример 3.
Вычислить предел функции .
Решение. Для решения приведем данный
предел ко второму замечательному пределу
в записи формулы (4).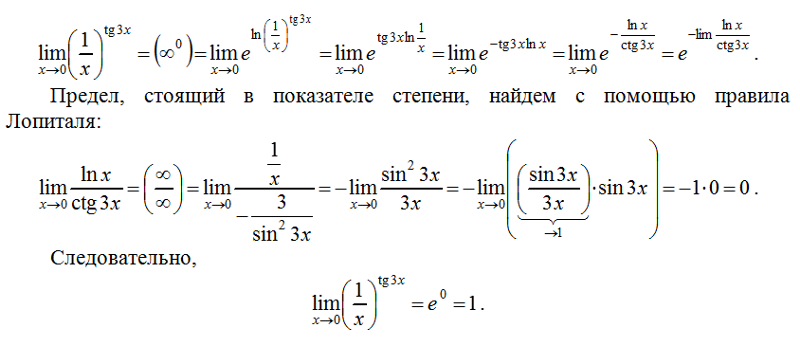
1. Умножим числитель и знаменатель дроби на 2 и числитель почленно разделим на знаменатель:
.
2. Сделаем замену переменной и решим по формуле (5):
.
Помогите найти предел функции двух переменных : Анализ-I
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе “Помогите решить/разобраться (М)”.
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
| MaxMelnikov |
| ||
28/03/09 |
| ||
| |||
| |
| |||
01/03/06 |
| |||
| ||||
| MaxMelnikov |
| ||
28/03/09 |
| ||
| |||
| Someone |
| |||
23/07/05 |
| |||
| ||||
| ASA |
| ||
30/01/09 |
| ||
| |||
| Atata379 |
| ||
09/02/12 |
| ||
| |||
| Someone |
| |||
23/07/05 |
| |||
| ||||
| Atata379 |
| ||
09/02/12 |
| ||
| |||
| Shtorm |
| ||
14/02/10 |
| ||
| |||
| AKM |
| |||
18/05/09 |
| |||
| ||||
| Shtorm |
| ||
14/02/10 |
| ||
| |||
| kw_artem |
| ||
17/01/12 |
| ||
| |||
| AKM |
| |||
18/05/09 |
| |||
| ||||
| Shtorm |
| ||
14/02/10 |
| ||
| |||
| Munin |
| |||
30/01/06 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 15 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
Нахождение пределов: свойства пределов
Результаты обучения
- Нахождение предела суммы, разности и произведения.

- Найдите предел многочлена.
- Найдите предел силы или корня.
- Найдите предел частного.
Нахождение предела суммы, разности и произведения
Построение графика функции или изучение таблицы значений для определения предела может быть громоздким и занимать много времени. Когда это возможно, более эффективно использовать свойства пределов , который представляет собой сборник теорем для нахождения пределов.
Знание свойств пределов позволяет нам напрямую вычислять пределы. Мы можем складывать, вычитать, умножать и делить пределы функций, как если бы мы выполняли операции над самими функциями, чтобы найти предел результата. Точно так же мы можем найти предел функции, возведенной в степень, возведя предел в эту степень. Мы также можем найти предел корня функции, взяв корень предела. Используя эти операции над пределами, мы можем найти пределы более сложных функций, найдя пределы их более простых составляющих функций.
A Общее примечание: свойства пределов
Пусть [латекс]а,к,А[/латекс] и [латекс]В[/латекс] представляют действительные числа, а [латекс]f[/латекс] и [латекс ]g[/latex] — функции, такие, что [latex]\underset{x\to a}{\mathrm{lim}}f\left(x\right)=A[/latex] и [latex]\underset{ x\to a}{\mathrm{lim}}g\left(x\right)=B[/latex]. Для пределов, которые существуют и являются конечными, свойства пределов суммированы в таблице ниже.
| Константа, к | [латекс]\underset{x\to a}{\mathrm{lim}}k=k[/latex] |
| Постоянное время функции | [латекс]\underset{x\to a}{\mathrm{lim}}\left[k\cdot f\left(x\right)\right]=k\underset{x\to a}{\mathrm{ lim}}f\left(x\right)=kA[/latex] |
| Сумма функций | [латекс]\underset{x\to a}{\mathrm{lim}}\left[f\left(x\right)+g\left(x\right)\right]=\underset{x\to a }{\mathrm{lim}}f\left(x\right)+\underset{x\to a}{\mathrm{lim}}g\left(x\right)=A+B[/latex] |
| Различие функций | [латекс]\underset{x\to a}{\mathrm{lim}}\left[f\left(x\right)-g\left(x\right)\right]=\underset{x\to a }{\mathrm{lim}}f\left(x\right)-\underset{x\to a}{\mathrm{lim}}g\left(x\right)=AB[/latex] |
| Произведение функций | [латекс]\underset{x\to a}{\mathrm{lim}}\left[f\left(x\right)\cdot g\left(x\right)\right]=\underset{x\to a}{\mathrm{lim}}f\left(x\right)\cdot \underset{x\to a}{\mathrm{lim}}g\left(x\right)=A\cdot B[/latex ] 9{n}[/latex], где [latex]n[/latex] — целое положительное число | .
| n -й корень функции, где n — натуральное число | [латекс] \ underset {x \ to a} {\ mathrm {lim}} \ sqrt [n] {f \ left (x \ right)} = \ sqrt [n] {\ underset {x \ to a} { \mathrm{lim}}\left[f\left(x\right)\right]}=\sqrt[n]{A}[/latex] |
| Полиномиальная функция | [латекс]\underset{x\to a}{\mathrm{lim}}p\left(x\right)=p\left(a\right)[/latex] |
Пример 1. Алгебраическое вычисление предела функции
Оценить [латекс]\занижение{х\до 3}{\mathrm{lim}}\влево(2x+5\вправо)[/латекс].
Показать решение
Попробуйте
Оцените следующий предел: [latex]\underset{x\to -12}{\mathrm{lim}}\left(-2x+2\right)[/latex].
Показать решение
Попробуйте
Нахождение предела многочлена
Не все функции или их пределы предполагают простое сложение, вычитание или умножение. Некоторые могут включать полиномы. Напомним, что многочлен — это выражение, состоящее из суммы двух или более слагаемых, каждое из которых состоит из константы и переменной, возведенных в неотрицательную целую степень. Чтобы найти предел полиномиальной функции, мы можем найти пределы отдельных членов функции, а затем сложить их вместе. Кроме того, предел полиномиальной функции при приближении [latex]x[/latex] к [latex]a[/latex] эквивалентен простому вычислению функции для [latex]a[/latex] .
Напомним, что многочлен — это выражение, состоящее из суммы двух или более слагаемых, каждое из которых состоит из константы и переменной, возведенных в неотрицательную целую степень. Чтобы найти предел полиномиальной функции, мы можем найти пределы отдельных членов функции, а затем сложить их вместе. Кроме того, предел полиномиальной функции при приближении [latex]x[/latex] к [latex]a[/latex] эквивалентен простому вычислению функции для [latex]a[/latex] .
Как: Для заданной функции, содержащей многочлен, найти ее предел.
- Используйте свойства пределов, чтобы разбить многочлен на отдельные члены.
- Найдите пределы отдельных терминов.
- Сложите ограничения вместе.
- В качестве альтернативы оцените функцию для [latex]a[/latex] . 9{3}+5\вправо)[/латекс].
Показать решение
Попробуйте
Нахождение предела степени или корня
Когда предел включает в себя степень или корень, нам нужно другое свойство, которое поможет нам оценить его.
 Квадрат предела функции равен пределу квадрата функции; то же самое относится и к высшим силам. Точно так же квадратный корень из предела функции равен пределу квадратного корня функции; то же верно и для высших корней. 9{2}+6x+8}{x – 2}\right)[/latex] , можем ли мы определить предел функции, когда [latex]x[/latex] приближается к [latex]a[/latex] ?
Квадрат предела функции равен пределу квадрата функции; то же самое относится и к высшим силам. Точно так же квадратный корень из предела функции равен пределу квадратного корня функции; то же верно и для высших корней. 9{2}+6x+8}{x – 2}\right)[/latex] , можем ли мы определить предел функции, когда [latex]x[/latex] приближается к [latex]a[/latex] ?Да. Некоторые функции можно алгебраически переставить, чтобы можно было оценить предел упрощенной эквивалентной формы функции.
Нахождение предела частного
Нахождение предела функции, выраженной в виде частного, может оказаться более сложной задачей. Нам часто нужно переписать функцию алгебраически, прежде чем применять свойства предела. Если знаменатель равен 0, когда мы применяем свойства предела напрямую, мы должны переписать частное в другой форме. Один из подходов состоит в том, чтобы записать частное в факторизованной форме и упростить. 9{2}-11x+28}{7-x}\справа)[/латекс].
Показать решение
Попробуйте
Пример 6.
 Оценка предела частного путем поиска ЖК-дисплея }{x}-\frac{1}{5}}{x – 5}\right)[/latex].
Оценка предела частного путем поиска ЖК-дисплея }{x}-\frac{1}{5}}{x – 5}\right)[/latex].Показать решение
Попробуйте
Вычислите [латекс]\underset{x\to -5}{\mathrm{lim}}\left(\dfrac{\frac{1}{5}+\frac{1}{x}} {10+2x}\справа)[/латекс].
Показать решение
Как сделать: Учитывая предел функции, содержащей корень, используйте сопряжение для оценки.
- Если частное не находится в неопределенной форме [латекс]\влево(\фракция{0}{0}\вправо)[/латекс], оценить напрямую.
- В противном случае перепишите сумму (или разность) двух частных как одно частное, используя наименьший общий знаменатель (LCD) .
- Если в числителе есть корень, рационализируйте числитель; умножьте числитель и знаменатель на сопряженное числителя. Напомним, что [latex]a\pm \sqrt{b}[/latex] являются сопряженными.
- Упростить.
- Оценить полученный предел.

Пример 7. Вычисление предела, содержащего корень, с помощью сопряжения {x}\right)[/latex].
Показать решение
Попробуйте
Оцените следующий предел: [латекс]\underset{h\to 0}{\mathrm{lim}}\left(\dfrac{\sqrt{16-h}-4}{h}\right )[/латекс].
Показать решение
Попробуйте
Пример 8. Оценка предела частного функции с помощью факторизации
Оценить [латекс]\underset{x\to 4}{\mathrm{lim}}\left(\dfrac{4-x}{\sqrt{x}-2}\right)[/latex].
Показать решение
Попробуйте
Оцените следующий предел: [латекс]\underset{x\to 3}{\mathrm{lim}}\left(\dfrac{x – 3}{\sqrt{x}-\sqrt{3) }}\справа)[/латекс].
Показать решение
Как: Имея частное с абсолютными значениями, оценить его предел.
- Попробуйте разложить или найти ЖК.
- Если предел не может быть найден, выберите несколько значений рядом и по обе стороны от входа, где функция не определена.
 9{+}}{\mathrm{lim}}\dfrac{6-x}{|x – 6|}[/latex].
9{+}}{\mathrm{lim}}\dfrac{6-x}{|x – 6|}[/latex].Показать решение
Ключевые понятия
- Свойства пределов могут использоваться для выполнения операций над пределами функций, а не над самими функциями.
- Предел полиномиальной функции можно найти, найдя сумму пределов отдельных членов.
- Предел функции, возведенной в степень, равен той же степени предела функции. Другой метод — прямая замена.
- Предел корня функции равен соответствующему корню предела функции.
- Один из способов найти предел функции, выраженной в виде частного, состоит в том, чтобы записать частное в факторизованной форме и упростить.
- Еще один метод нахождения предела сложной дроби — найти ЖК.
- Предел, содержащий функцию, содержащую корень, может быть оценен с помощью сопряжения.
- Пределы некоторых функций, выраженных в виде частных, можно найти с помощью факторизации.
- Одним из способов оценки предела частного, содержащего абсолютные значения, является использование числовых данных.
 Настройка его по частям также может быть полезной.
Настройка его по частям также может быть полезной.
Глоссарий
- свойства пределов
- сборник теорем для нахождения пределов функций путем выполнения математических операций над пределами
Пределы – Пределы и графики
Учителя и профессора математики по всему миру пытаются ввести ограничения в это большое, огромное дело. Мы здесь, чтобы установить рекорд. На самом деле, это наша миссия: доказать, что пределы — одна из самых простых математических идей.
Представьте, что сейчас полночь, и мы уже несколько часов готовимся к выпускному экзамену по математике. Нам нужно перекусить, срочно. Итак, мы направляемся на кухню и видим гигантский шоколадный торт, стоящий прямо посреди стола. Торт выглядит идеально, поэтому мы начинаем двигаться к нему.
Когда мы приближаемся к торту, расстояние между нами и тортом сокращается вдвое, скажем, с 10 футов до 5 футов. Это длинная кухня, хорошо. По мере того как мы продолжаем, расстояние снова сокращается вдвое до 2,5 фута, до 1,25 фута, до 0,625 фута и так далее.
 По мере того, как мы идем дальше, расстояние между нами и этим тортом продолжает сокращаться вдвое.
По мере того, как мы идем дальше, расстояние между нами и этим тортом продолжает сокращаться вдвое.Это представляет огромную проблему, потому что по этой логике мы никогда не доберемся до торта. #midnightsnackprobs
Хотя все мы знаем, что в конечном итоге мы сможем прорваться и откусить огромный кусок вкусного пирога, эта идея приблизиться к чему-то, на самом деле никогда не реально добраться туда, — это именно то, как можно описать предел .
Пример задачи
Оценить предел f ( x ) = x + 3, так как x приближается к 1. Другими словами, оцените:
Прежде чем мы приступим к работе, давайте удостоверимся, что мы поняли используемую нотацию. «lim» говорит, что мы смотрим на предел функции справа. Под «lim» у нас x -> 1. Это означает, что мы смотрим на данную функцию, поскольку x приближается к 1.
На словах мы читаем это как «предел x + 3 как x приближается к 1″.

Эта запись спрашивает нас, что происходит с функцией, когда значения x приближаются к 1, но не совсем касаются его. Как выглядит значение y по мере того, как x приближаются к 1? Посмотрим на график функции.
Нетрудно заметить, что значения y увеличиваются до y = 4, поскольку x приближается к 1. Таким образом, мы бы сказали, что «предел приближается к 4, когда x приближается к 1″. Это слишком много слов для математического ответа, поэтому мы можем вместо этого написать:
Ужасно важно знать, что это предел только потому, что график приближается к 4 по обе стороны от 1. Да, число 1 имеет две стороны. У одного есть положительная сторона и отрицательная сторона — мы можем подойти к нему слева или справа. Проверьте следующую задачу-o.
Пример задачи
Оцените предел этой функции, когда x приближается к 0.
Это наш второй предел, и у нас уже есть странные ломаные графики.
 Без проблем. Как мы уже говорили, ноль имеет отрицательную (или левую) сторону, а также положительную (или правую) сторону. Чтобы мы могли сказать, что предел существует, предел слева и справа должен быть одним и тем же.
Без проблем. Как мы уже говорили, ноль имеет отрицательную (или левую) сторону, а также положительную (или правую) сторону. Чтобы мы могли сказать, что предел существует, предел слева и справа должен быть одним и тем же.Значит, мы видим здесь проблему. Левая рука спорит с правой. «Скоро будет 4». «Вы слепы, это будет 0». Когда у нас возникают такие разногласия, мы говорим, что «предела не существует». Да, это написано с большой буквы, потому что мы действительно имеем это в виду.
Если вы хотите выглядеть по-крупному, используйте аббревиатуру «Не существует» как DNE. Кто угодно поймет, о чем вы говорите. #mathswag
Пример задачи
Использовать график функции f ( x ) для оценки заданных пределов.
a)
Поскольку значения y одинаковы как слева, так и справа, мы можем сказать, что .
Подождите, что? Но функция не определена при x = a ; по крайней мере, так сказал нам наш учитель предварительного исчисления, что означают открытые кружки.


 Решал только с одной переменной, и те давались тяжело. Помогите найти предел или же доказать что его не существует:
Решал только с одной переменной, и те давались тяжело. Помогите найти предел или же доказать что его не существует: 
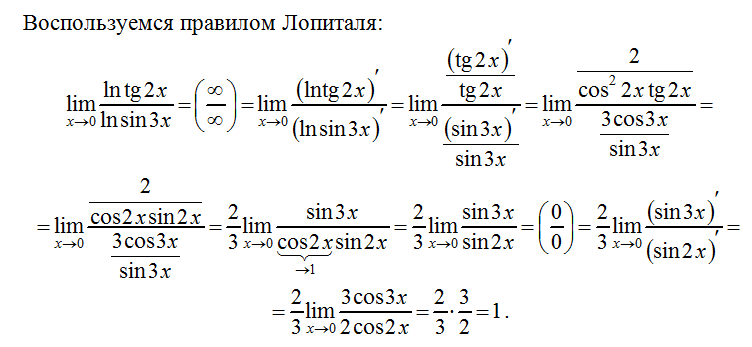 е. найти пределы:
е. найти пределы: е. найти пределы:
е. найти пределы: По-моему нужно так:
По-моему нужно так: 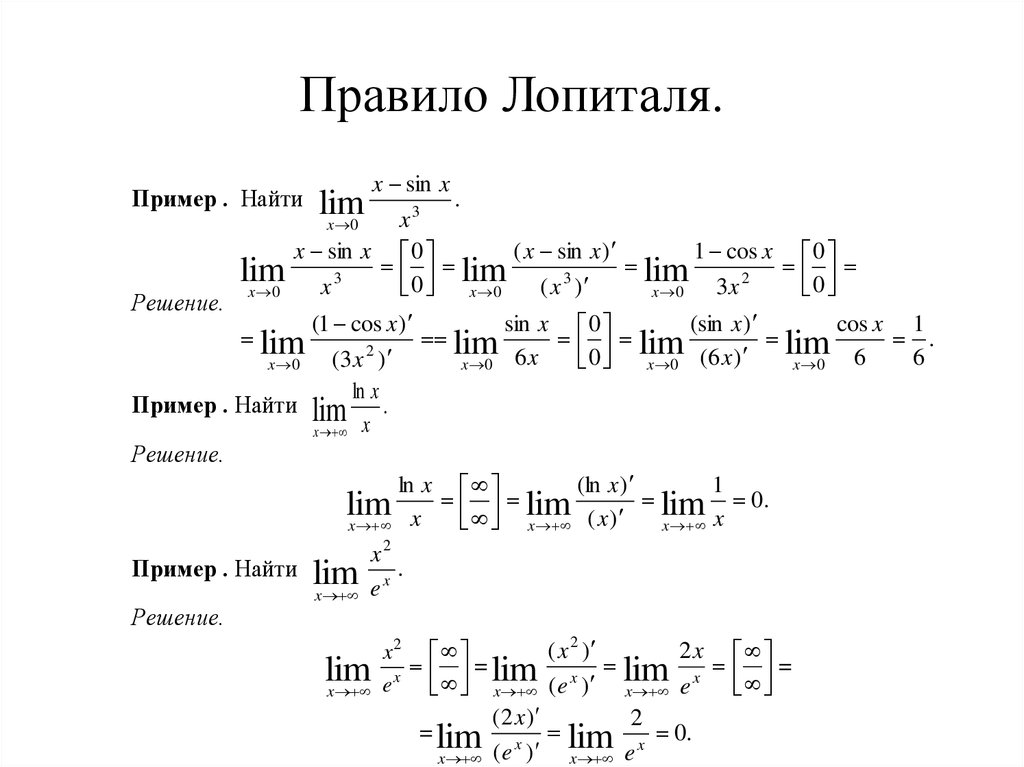 ..
.. 02.2012, 00:31
02.2012, 00:31 
 .. хочу найти о них какую-нибудь информацию. Спасибо за ответ.
.. хочу найти о них какую-нибудь информацию. Спасибо за ответ. Решал только с одной переменной, и те давались тяжело. Помогите найти предел или же доказать что его не существует:
Решал только с одной переменной, и те давались тяжело. Помогите найти предел или же доказать что его не существует:  е. предел зависит от пути, т.е. предела по двум переменным нет.
е. предел зависит от пути, т.е. предела по двум переменным нет. е. предел зависит от пути, т.е. предела по двум переменным нет.
е. предел зависит от пути, т.е. предела по двум переменным нет. 07.2012, 00:22
07.2012, 00:22 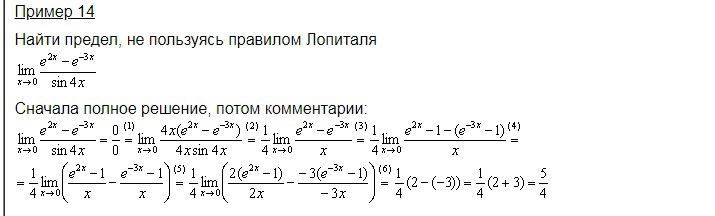 07.2012, 12:13
07.2012, 12:13 
 07.2012, 19:02
07.2012, 19:02  Следовательно если есть хотя бы в одном направлении значит просто – есть. Значит по аналогии и в пространстве – если есть хотя бы в одном направлении значит просто – есть.
Следовательно если есть хотя бы в одном направлении значит просто – есть. Значит по аналогии и в пространстве – если есть хотя бы в одном направлении значит просто – есть. А мне один раз уже закрыли мою тему, мотивировав, что таких тем уже полно и дескать не надо плодить – пишите в уже созданных.
А мне один раз уже закрыли мою тему, мотивировав, что таких тем уже полно и дескать не надо плодить – пишите в уже созданных. Соответственно, у функции типа предела в бесконечности нет, поскольку упомянутая kw_artem
Соответственно, у функции типа предела в бесконечности нет, поскольку упомянутая kw_artem

 Квадрат предела функции равен пределу квадрата функции; то же самое относится и к высшим силам. Точно так же квадратный корень из предела функции равен пределу квадратного корня функции; то же верно и для высших корней. 9{2}+6x+8}{x – 2}\right)[/latex] , можем ли мы определить предел функции, когда [latex]x[/latex] приближается к [latex]a[/latex] ?
Квадрат предела функции равен пределу квадрата функции; то же самое относится и к высшим силам. Точно так же квадратный корень из предела функции равен пределу квадратного корня функции; то же верно и для высших корней. 9{2}+6x+8}{x – 2}\right)[/latex] , можем ли мы определить предел функции, когда [latex]x[/latex] приближается к [latex]a[/latex] ? Оценка предела частного путем поиска ЖК-дисплея }{x}-\frac{1}{5}}{x – 5}\right)[/latex].
Оценка предела частного путем поиска ЖК-дисплея }{x}-\frac{1}{5}}{x – 5}\right)[/latex].
 9{+}}{\mathrm{lim}}\dfrac{6-x}{|x – 6|}[/latex].
9{+}}{\mathrm{lim}}\dfrac{6-x}{|x – 6|}[/latex]. Настройка его по частям также может быть полезной.
Настройка его по частям также может быть полезной. По мере того, как мы идем дальше, расстояние между нами и этим тортом продолжает сокращаться вдвое.
По мере того, как мы идем дальше, расстояние между нами и этим тортом продолжает сокращаться вдвое.
 Без проблем. Как мы уже говорили, ноль имеет отрицательную (или левую) сторону, а также положительную (или правую) сторону. Чтобы мы могли сказать, что предел существует, предел слева и справа должен быть одним и тем же.
Без проблем. Как мы уже говорили, ноль имеет отрицательную (или левую) сторону, а также положительную (или правую) сторону. Чтобы мы могли сказать, что предел существует, предел слева и справа должен быть одним и тем же.